Open Access Article
Open Access ArticleControlled coherent dynamics of [VO(TPP)], a prototype molecular nuclear qudit with an electronic ancilla†
Simone
Chicco
ab,
Alessandro
Chiesa
 ab,
Giuseppe
Allodi
ab,
Giuseppe
Allodi
 a,
Elena
Garlatti
ab,
Matteo
Atzori
cd,
Lorenzo
Sorace
a,
Elena
Garlatti
ab,
Matteo
Atzori
cd,
Lorenzo
Sorace
 c,
Roberto
De Renzi
c,
Roberto
De Renzi
 a,
Roberta
Sessoli
a,
Roberta
Sessoli
 c and
Stefano
Carretta
c and
Stefano
Carretta
 *ab
*ab
aUniversità di Parma, Dipartimento di Scienze Matematiche, Fisiche e Informatiche, I-43124 Parma, Italy. E-mail: stefano.carretta@unipr.it
bUdR Parma, INSTM, I-43124 Parma, Italy
cDipartimento di Chimica “Ugo Schiff” & INSTM, Università Degli Studi di Firenze, I-50019 Sesto Fiorentino, Italy
dLaboratoire National des Champs Magnétiques Intenses (LNCMI), Univ. Grenoble Alpes, INSA Toulouse, Univ. Toulouse Paul Sabatier, EMFL, CNRS, F-38043 Grenoble, France
First published on 5th August 2021
Abstract
We show that [VO(TPP)] (vanadyl tetraphenylporphyrinate) is a promising system to implement quantum computation algorithms based on encoding information in multi-level (qudit) units. Indeed, it embeds a nuclear spin 7/2 coupled to an electronic spin 1/2 by hyperfine interaction. This qubit–qudit unit can be exploited to implement quantum error correction and quantum simulation algorithms. Through a combined theoretical and broadband nuclear magnetic resonance study, we demonstrate that the elementary operations of such algorithms can be efficiently implemented on the nuclear spin qudit. Manipulation of the nuclear qudit can be achieved by resonant radio-frequency pulses, thanks to the remarkably long coherence times and the effective quadrupolar coupling induced by the strong hyperfine interaction. This approach may open new perspectives for developing new molecular qubit–qudit systems.
1 Introduction
Molecular Nanomagnets (MNMs) have been proposed for a long time as promising units of a future quantum computing architecture. Indeed, many molecules consisting of a ground spin 1/2 doublet were synthesized, thus providing the two-level elementary unit of the established quantum-computing paradigm.1,2 Great efforts have been devoted to improve the coherence times of these systems, by following tailored synthetic strategies,3–13 and to link complexes together in order to fit specific requirements of quantum computation schemes.14–22 However, the peculiar feature which makes MNMs different and potentially preferable over any other established quantum-computing platform is represented by their intrinsic multi-level structure.23,24 Indeed, the presence of many low-energy levels, with long coherence and easily accessible through microwave or radio-frequency pulses opens a range of new possibilities. By encoding information in multi-level (qudit) systems, the number of units and operations required to implement an algorithm25–28 could be significantly reduced, compared to the conventional, two-level encoding. For instance, the extra levels of the qudit can be used to encode qubits with embedded quantum-error correction, a fundamental step to make the quantum hardware resistant to environmental noise29–34 and still far from being realized even by the most advanced technologies.35–40 Other examples are provided by the Toffoli gate,41 the Deutsch,42 Grover,43 Quantum Fourier Transform, or Quantum Phase Estimation algorithms, which can be implemented much faster and using fewer operations on a qudit than on multiple qubits.25 Moreover, quantum simulation schemes have recently been put forward, exploiting the qudit multi-level structure to represent bosonic fields.44In many cases, the coupling of the qudit with a spin 1/2 ancilla can provide an additional tool, e.g. to detect errors occurring on the qudit,33 or to simulate photons interacting with matter.44
The simplest chemical realization of such a platform is provided by a single magnetic-ion complex, embedding a nuclear32,33,43 spin I coupled by hyperfine interaction to an electronic spin doublet. A good candidate should fulfill the following requirements: (i) an electronic and nuclear energy level structure yielding well distinguished transitions; (ii) nuclear and electronic coherence times much longer than the time required to manipulate the system; (iii) the capability to coherently control the qudit dynamics, thus implementing the elementary operations which can then be combined into relevant algorithms.
Here we show that the [VO(TPP)] (TPP = tetraphenylporphyrinate) molecular complex (1) meets the aforementioned requirements and hence is a prototypical qubit–qudit system to realize such quantum computing platform. Indeed, it provides a large spin (I = 7/2, eight levels) nuclear qudit, coupled by hyperfine interaction to an electronic spin 1/2. Recent studies on the same45,46 and very similar compounds47 have reported remarkable electron spin coherence times, thus suggesting this system also as a very promising candidate qudit. However, to actually demonstrate this, we now need to focus on nuclear spin degrees of freedom. Detecting the magnetic resonance signal of a nuclear spin of a paramagnetic ion is challenging and typically beyond the instrumental limits of the nuclear magnetic resonance (NMR) technique. In this system, however, performing pulsed NMR sequences is permitted by both the favorable physical properties of this diluted spin system, detailed below, and the employment of custom NMR hardware optimized for study of magnetic materials.48 By measuring single-crystal NMR spectra on a targeted frequency and magnetic field range, we characterize in detail the nuclear spin Hamiltonian of 1, including small quadrupolar interactions, and the hyperfine coupling with the electronic qubit.
The small quadrupolar coupling could make it very hard to individually manipulate each nuclear spin transition using fast resonant radio-frequency pulses. We overcome this limitation by taking advantage of the slight mixing between the electronic and nuclear spin wave-function, arising from the strong hyperfine coupling with the electronic ancilla. The effectiveness of our approach in controlling the nuclear spin state by radio-frequency pulses is demonstrated by numerical simulations and experimental coherent manipulation of the involved pair of targeted levels. This paves the way to a proof-of-principle implementation of qudit algorithms. In particular, we show by numerical simulations how to implement the elementary steps of quantum error correction (QEC) algorithms.
By removing the strict requirements on the nuclear quadrupole interaction, our approach largely extends the class of electro-nuclear spin systems suitable to implement quantum-error correction,33 quantum simulation44 and in general qudit-based algorithms.25 In particular, vanadium-based complexes,5,6,10,49 characterized by very long nuclear and electronic coherence but with small nuclear quadrupole coupling, become extremely promising.
2 Results
In the following subsections we combine NMR measurements with theoretical arguments and simulations, to illustrate step-by-step why [VO(TPP)] complex is a very promising qubit–qudit system, suitable, e.g., to implement QEC and quantum simulation algorithms. The steps are the following:(1) Synthesize a molecular complex embedding a transitions metal ion characterized by an electronic spin 1/2 coupled to a large nuclear spin.
(2) Characterize the system by broadband NMR to derive the spin Hamiltonian parameters and
(2.1) Identify an operating regime in which nuclear transitions required to implement algorithms are well resolved and individually addressable.
(3) Measure nuclear spin coherence times, to check they are sufficiently longer than operating times.
(4) Simulate the actual implementation of qudit algorithms, showing they can be decomposed into elementary operations we can easily access.
(5) Demonstrate we can actually implement each of these elementary operations by resonant radio-frequency pulses, i.e. measure Rabi oscillations between targeted transitions involved in the algorithm.
2.1 Synthesis: a multi-level nuclear spin and a spin 1/2 ancilla
The first step is represented by synthesizing the suitable system. Vanadyl is a promising core unit of our quantum computing platform, since it provides a nuclear spin with 8 levels (thanks to the large value of I = 7/2 for 51V, with natural abundance of 99.85%) and an electronic spin doublet to be used as ancilla.The complex [VO(TPP)] (Fig. 1) has been prepared as reported in ref. 45 and 50 and it has been magnetically diluted (2%) in its diamagnetic analogue [TiO(TPP)], prepared with the same method, by cocrystallization. Slow solvent evaporation (CH3COCH3) of the mixture of isostructural starting materials provides single crystals of [Ti0.98V0.02O(TPP)], hereafter 1, that assume the shape of a square pyramid with well developed (±1,±1,±1) faces and dimensions of ca. 0.4 × 0.4 × 0.2 mm3 (see Fig. S1†). The system crystallizes in the tetragonal I4 space group, as [Ti(OTPP)], with the four-fold symmetry axis c corresponding to the direction of the V![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O (Ti
O (Ti![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) bond (see Fig. 1). A description of the molecular and crystal structure of [VO(TPP)] and [TiO(TPP)] is reported in ref. 45.
O) bond (see Fig. 1). A description of the molecular and crystal structure of [VO(TPP)] and [TiO(TPP)] is reported in ref. 45.
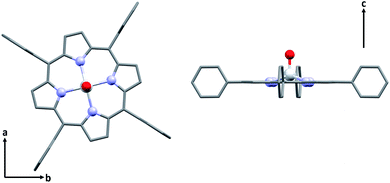 | ||
| Fig. 1 Molecular structure of [VO(TPP)] viewed along c axis (left) and ab plane (right). Hydrogen atoms are omitted for clarity. | ||
2.2 Characterization by broadband NMR
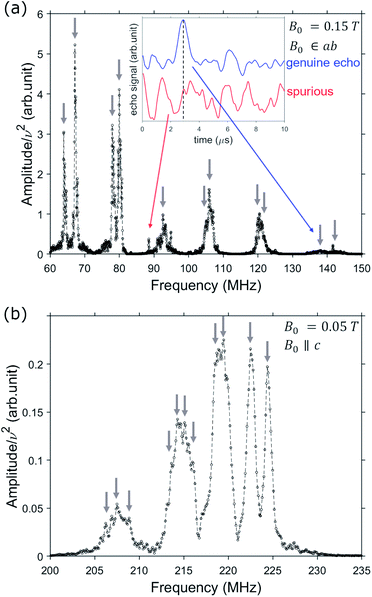
The second step is a thorough experimental characterization, which is needed first to get a precise determination of the spin Hamiltonian parameters (in particular those involving the nuclear spin and its interaction with the electronic one); and second, to understand if different nuclear transitions can be resolved in the spectra, possibly by choosing proper experimental conditions. This is mandatory to implement any qudit-based algorithm, whose elementary operations can be decomposed in terms of ΔmI = ±1 transitions between nuclear spin states.51V NMR spectra are measured by a broadband home-built NMR spectrometer (see ESI† and ref. 48) at fixed temperature T = 1.4 K on a single crystal of 1, where dilution of VO in diamagnetic TiO reduces inter-molecular dipole–dipole interactions. We collect spectra by measuring Hahn-echoes as a function of frequency, for different applied static fields B0 in the range 0.05–0.3 T, along the two orthogonal crystal directions, corresponding to the two inequivalent symmetry directions of the [VO(TPP)] molecule: ab plane and c axis (see Fig. 2 and ESI† for further details). NMR spectra are collected at discrete equally spaced frequency points and reconstructed by merging frequency shifted fast Fourier transform of spin echoes, according to a variant of the method described in ref. 51.
The usual condensed matter paramagnetic regime corresponds to hyperfine field fluctuations faster than the nuclear Larmor frequency, resulting in exceedingly large nuclear relaxation rates. This sets the detection of their NMR signal outside the time window of the standard pulsed NMR technique. Here, in contrast, this is possible thanks to the synergy between the characteristics of our home-made spectrometer and the physical properties of 1. Indeed, on the one hand our broadband spectrometer allows us to apply short pulses and to detect short-living signals.48 On the other hand, the measured electronic spin-lattice relaxation of 1 (ref. 45) are much longer than the duration of the spin-echo sequence, which thus provides a snapshot of the electronic environment of 51V. Examples of spectra measured for different applied fields are reported in Fig. 2, as a function of frequency. The inset shows how nuclear spin excitations (indicated by arrows) can be distinguished from noise, by examining the time dependence of the detected echo signal.
The system is described by the spin Hamiltonian:
| H0 = ηA·Ŝ + pÎz2 + μBŜ·gS·B0 + μNgNηB0 | (1) |
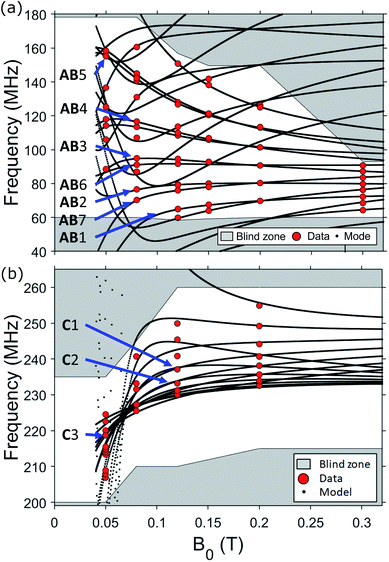
Conversely, hyperfine tensor (A) and quadrupolar coupling (p) are fitted to reach the best agreement between simulated and measured spectra, as a function of the applied magnetic field (Fig. 3). We find Ax,y = −170 ± 1 MHz, Az = −480 ± 1 MHz, and a tiny quadrupolar coupling p = −0.35 ± 0.07 MHz.
The full set of observed NMR peaks as a function of the static field B0 is reported in Fig. 3, in both measured directions. It is worth noting that experimental transition frequencies are in excellent agreement with simulations using spin Hamiltonian (1) and best fit parameters listed above.
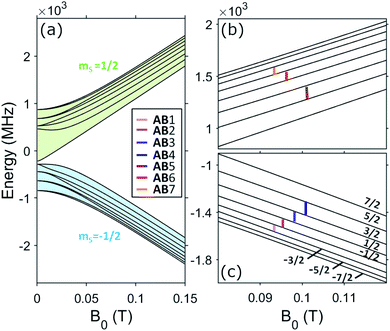
The resulting energy levels diagram, obtained from diagonalization of spin Hamiltonian (1) with magnetic field applied in the xy plane (e.g. along x), is shown in Fig. 4. Despite the mixing between electronic and nuclear spins induced by the significant transverse components of the hyperfine interaction (Ay and Az) with respect to the static field direction, for B0 ≳ 0.25 T, gxμBB0 > |Az| and the eigenstates are at least 98% factorized. In these conditions, the eigenstates can be labeled by the components of S and I parallel to the external field, i.e. |mS, mI〉. We now need to answer the question: are the differences between the nuclear energy gaps (δ(mI) = (EmI+1 − EmI) − (EmI − EmI−1)) sufficiently large to fulfill point 2.1 above, i.e. to be resolved and individually addressed by resonant radio-frequency pulses? This question is crucial to exploit the nuclear spin as an actually working qudit, because any quantum computing operation on the nuclear spin qudit can be decomposed in terms of rotations between pairs of consecutive mI levels. For large B0 or small transverse hyperfine couplings, this difference is directly given by the nuclear quadrupolar interaction (δmI = 2p for B0 parallel to z). The effect of the quadrupolar coupling on the energy level diagram of an I = 7/2 qudit is shown in Fig. 5(a). It can be clearly understood by making an analogy with the zero-field splitting of an electronic spin S. In the case of an electronic spin S, the Zeeman interaction with the external field splits the state in equally spaced levels, while the zero-field splitting term makes all energy gaps different. Conversely, in the here-examined case of a nuclear spin I coupled to a polarized electronic spin, the effective field is mainly given by the longitudinal component of the hyperfine interaction, Ax/2, while the quadrupolar coupling introduces the anisotropy distinguishing the gaps. The resulting effect on the NMR spectrum is analogous to that observed in electron paramagnetic resonance (EPR): a single peak for isotropic systems, seven distinct peaks if the electronic/nuclear spin is subject to anisotropy.
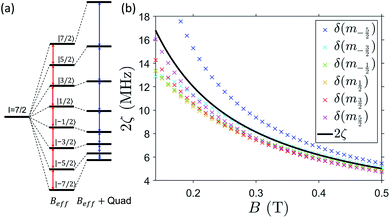 | ||
| Fig. 5 (a) Schematic representation of the energy-levels splitting of an I = 7/2 spin in presence of an effective field Beff and with the addition of a quadrupole coupling, making the gaps inequivalent (note that the effect of quadrupole is here exaggerated for clarity). (b) Difference between the energy gap of consecutive nuclear transitions δ(mI) = (EmI+1 − EmI) − (EmI − EmI−1) in the mS = −1/2 subspace, as a function of static field, applied along x. Results from diagonalization of the effective rank-2 pseudo-quadrupolar Hamiltonian (2) are shown in black, in very good agreement with results from exact diagonalization of the full Hamiltonian (1) (colored crosses), especially at large B0. | ||
Unfortunately, the quadrupole moment of 51V nuclei is one of the smallest among metals (∼1/4 of that of Cu and 1/50 of that of Yb). We show below that such a small quadrupolar term (also occurring in other 3d-ion based molecular nanomagnets) is not a limiting factor in terms of addressability of nuclear transitions.
2.2.1 Effective quadrupole coupling
We overcome the small p hurdle by properly tuning the applied field. In this way, we meet a condition in which the strong transverse hyperfine interaction effectively splits the different nuclear energy gaps, thus acting as an effective sizable pseudo-quadrupolar contribution. In order to explore the best conditions for our aims, it is very useful to start from Hamiltonian (1) and build a simpler approximate model, although our analysis is then based on the exact diagonalization. With the effective quadrupole coupling concept, we provide a simple and intuitive picture of the resulting effect on the NMR spectrum, for a fixed orientation of the electronic spin. Formally, the effective quadrupole is derived by restricting to the mS = −1/2 subspace and considering the effect of hyperfine interaction up to second-order perturbation theory with respect to the Zeeman term. In this regime, the resulting Hamiltonian is perfectly analogous to that of a single electronic spin S, whose energy levels are split by zero-field splitting (and by the magnetic field). Here, the effective quadrupole plays the same role of the zero-field splitting in EPR and distinguishes the peaks in the NMR spectrum. By making all the gaps significantly different, this solves the small-quadrupole issue and enables manipulation of the nuclear qudit.The effect is maximized by applying the static field B0 in the xy plane. Indeed, with this choice, the largest component of A is perpendicular to B0. We thus fix B0 along x in the following experiments and simulations. The resulting low-energy effective Hamiltonian includes a pseudo-Zeeman term BeffIx (with 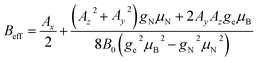 ) and an effective quadrupole interaction of the form
) and an effective quadrupole interaction of the form
| Hq = pxeff[Ix2 − I(I + 1)/3] + preff(Iz2 − Iy2) | (2) |
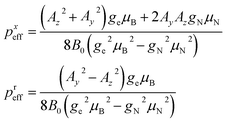 | (3) |
2.3 Phase memory time
Besides being well resolved, nuclear spin transitions must also be characterized by coherence times longer than the time required to manipulate the qudit. To demonstrate this, we investigate nuclear spin dephasing rates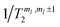 for different mI → mI ± 1 transitions (vertical colored lines in Fig. 4(b) and (c)), as a function of the applied field. Analogous results with B0 parallel to c are reported in the ESI (Fig. S4†). The phase memory time is extracted from the decay of the spin-echo amplitude M(τ) after application of the Hahn echo sequence 2π/3–τ–2π/3 (see ESI†), as a function of the delay τ between the exciting and refocusing pulses.53 These decays are accurately fitted by a single exponential function (Fig. 6 and ESI†). We note that this sequence (originally proposed by Hahn53) is shorter than the standard π/2–τ–π one (thus more favorable in case of short T2) and more tolerant to imperfect pulse calibrations. The effect of the echo sequence is to compensate inhomogeneous broadening effects, as well as static contribution to the effective field induced on the central spin by its interaction with the surrounding spin bath. Further enhancement of the system phase memory time could be achieved by using more complex refocusing sequences, such as Carr–Purcell–Meiboom–Gill (CPMG), as shown in ref. 32 in a similar setup. The extracted phase memory times
for different mI → mI ± 1 transitions (vertical colored lines in Fig. 4(b) and (c)), as a function of the applied field. Analogous results with B0 parallel to c are reported in the ESI (Fig. S4†). The phase memory time is extracted from the decay of the spin-echo amplitude M(τ) after application of the Hahn echo sequence 2π/3–τ–2π/3 (see ESI†), as a function of the delay τ between the exciting and refocusing pulses.53 These decays are accurately fitted by a single exponential function (Fig. 6 and ESI†). We note that this sequence (originally proposed by Hahn53) is shorter than the standard π/2–τ–π one (thus more favorable in case of short T2) and more tolerant to imperfect pulse calibrations. The effect of the echo sequence is to compensate inhomogeneous broadening effects, as well as static contribution to the effective field induced on the central spin by its interaction with the surrounding spin bath. Further enhancement of the system phase memory time could be achieved by using more complex refocusing sequences, such as Carr–Purcell–Meiboom–Gill (CPMG), as shown in ref. 32 in a similar setup. The extracted phase memory times 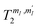 are reported in Fig. 6, as a function of the applied field. We find
are reported in Fig. 6, as a function of the applied field. We find 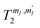 increasing from 10 to 60 μs with increasing B0, for all transitions. These values are much longer than the time required to implement elementary operations (see below), thus suggesting 1 as a very promising qudit.
increasing from 10 to 60 μs with increasing B0, for all transitions. These values are much longer than the time required to implement elementary operations (see below), thus suggesting 1 as a very promising qudit.
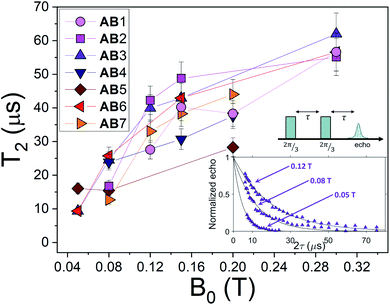 | ||
Fig. 6 Nuclear spin dephasing times  , measured at T = 1.4 K, with the Hahn-echo sequence depicted, as a function of the applied field B0 in the ab plane. The label of the transitions is the same reported in Fig. 4(b) and (c). Inset: Hahn echo sequence and examples of the echo decay amplitude for transition AB3 at different applied fields, fitted by an exponential function ∝ e−2τ/T2. , measured at T = 1.4 K, with the Hahn-echo sequence depicted, as a function of the applied field B0 in the ab plane. The label of the transitions is the same reported in Fig. 4(b) and (c). Inset: Hahn echo sequence and examples of the echo decay amplitude for transition AB3 at different applied fields, fitted by an exponential function ∝ e−2τ/T2. | ||
Concerning the behavior of  as function of B0, we first note that since the dilution of [VO(TPP)] in the diamagnetic [TiO(TPP)] matrix strongly suppresses the electron–electron spin dipolar coupling, the decoherence of the central 51V nuclear spin is primarily ruled by the interaction with neighbouring magnetic nuclei. For the low magnetic fields examined here, this interaction is mediated by virtual excitations of the electronic spin component of the system wave-function, whereas direct coupling between nuclear spins is much smaller. As a consequence, the reduction of electron-nuclear mixing with increasing B0 is responsible of the observed increase of T2 with magnetic field, as already reported in similar experiments32 and in a theoretical work on Si:Bi quantum dots.54 A secondary source of decoherence (limited by dilution) is represented by the interaction of the probed nuclei with surrounding electronic spins. This effect is also reduced by increasing B0, due to the consequent increment in electronic polarization and suppression of electronic spins fluctuations, as shown in related works on molecular spin systems.55–57
as function of B0, we first note that since the dilution of [VO(TPP)] in the diamagnetic [TiO(TPP)] matrix strongly suppresses the electron–electron spin dipolar coupling, the decoherence of the central 51V nuclear spin is primarily ruled by the interaction with neighbouring magnetic nuclei. For the low magnetic fields examined here, this interaction is mediated by virtual excitations of the electronic spin component of the system wave-function, whereas direct coupling between nuclear spins is much smaller. As a consequence, the reduction of electron-nuclear mixing with increasing B0 is responsible of the observed increase of T2 with magnetic field, as already reported in similar experiments32 and in a theoretical work on Si:Bi quantum dots.54 A secondary source of decoherence (limited by dilution) is represented by the interaction of the probed nuclei with surrounding electronic spins. This effect is also reduced by increasing B0, due to the consequent increment in electronic polarization and suppression of electronic spins fluctuations, as shown in related works on molecular spin systems.55–57
2.4 Application: quantum error correction using the nuclear qudit
Having demonstrated both the individual addressability of nuclear spin transitions (based on the effective quadrupole concept) and their remarkable coherence, we now move to investigate the feasibility of qudit-based algorithms.As an example, we consider quantum-error correction, whose implementation represents a mandatory step for any quantum computing platform, in order to overcome unavoidable errors and to scale above the capabilities of classical devices. Spin qudits allow one to embed error-correction within single objects, a crucial simplification compared to standard platforms which require many units to be linked together.24
Here we show how to implement the encoding operation of the qudit QEC algorithm proposed in ref. 33 and we demonstrate by realistic numerical simulations and measurements that this can be achieved on 1. Encoding means replacing logical units |0L〉 and |1L〉 represented by individual mI components (e.g. |0L〉 → |1/2〉 and |1L〉 → |−1/2〉) with superposition of mI states, such as
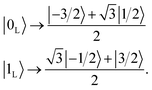 | (4) |
These superpositions enable one to correct the harmful effect of pure dephasing on the spin qudit, with the help of the electronic ancilla (see ref. 33). The larger the number of levels in the superposition, the larger the number of dephasing errors which can be corrected by the algorithm. We start from the four levels 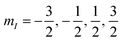 , of the
, of the 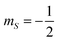 multiplet (whose transitions are labelled AB1,2,3 in the energy levels diagram of Fig. 4), which are already sufficient to correct the leading (first order) dephasing error,33,58 by means of the encoding shown in eqn (4). Coherence within these four levels has also been fully probed by Hahn-echo measurements. To simulate the time evolution of the system subject to the sequence of pulses needed for the encoding, we start from the sound Hamiltonian extracted in Section 2.2, and we numerically solve the Lindblad equation for the system density matrix ρ:
multiplet (whose transitions are labelled AB1,2,3 in the energy levels diagram of Fig. 4), which are already sufficient to correct the leading (first order) dephasing error,33,58 by means of the encoding shown in eqn (4). Coherence within these four levels has also been fully probed by Hahn-echo measurements. To simulate the time evolution of the system subject to the sequence of pulses needed for the encoding, we start from the sound Hamiltonian extracted in Section 2.2, and we numerically solve the Lindblad equation for the system density matrix ρ:
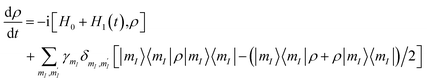 | (5) |
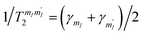 . Given the very close values of the measured
. Given the very close values of the measured 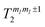 (Fig. 6), we assume in our simulations an average T2 for all mI, mI ± 1 pairs. Decoherence between ΔmI > 1 states is ruled by the rates
(Fig. 6), we assume in our simulations an average T2 for all mI, mI ± 1 pairs. Decoherence between ΔmI > 1 states is ruled by the rates 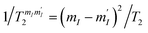 .33,60 Note that our simulations are a perfect reproduction of the experimental scenario, because they employ the Hamiltonian parameters fitted in Section 2.2 and the measured dephasing times.
.33,60 Note that our simulations are a perfect reproduction of the experimental scenario, because they employ the Hamiltonian parameters fitted in Section 2.2 and the measured dephasing times.
Starting from a generic superposition of mI = ±1/2, the encoding operation on the four considered levels corresponds to the transformation:
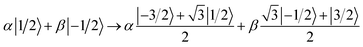 | (6) |
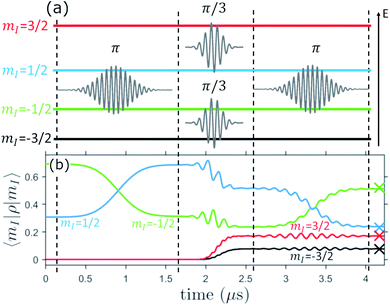
This can be decomposed into the sequence of transitions between adjacent levels reported in Fig. 7(a), i.e. a π pulse between the central mI = +1/2 and −1/2 levels, followed by two π/3 pulses between ±1/2 and ±3/2 (which are performed in parallel) and a final π pulse again between the +1/2 and −1/2 levels.
Simulations reported in Fig. 7(b) are performed with B0 = 0.3 T ![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) . This constitutes a good trade-off, between a limited entanglement of electronic and nuclear spin (yielding long T2 ∼ 50–60 μs), and spectral separation of the different transitions (thanks to the sizable effective quadrupole). The system is controlled by using Gaussian-shaped pulses of amplitude B1 = 1 mT.‡ The resulting time evolution of the calculated squared absolute value of the components of the system state is reported in Fig. 7(b). This produces an encoded superposition which is essentially coincident with the exact value (see crosses) and hence demonstrates that 1 is suitable to implement the QEC algorithm. We note that small residual errors on the encoded state (of the order of a few %) could be further reduced by using quantum control techniques to speed-up transitions,61,62 while keeping a small leakage to neighboring levels.
. This constitutes a good trade-off, between a limited entanglement of electronic and nuclear spin (yielding long T2 ∼ 50–60 μs), and spectral separation of the different transitions (thanks to the sizable effective quadrupole). The system is controlled by using Gaussian-shaped pulses of amplitude B1 = 1 mT.‡ The resulting time evolution of the calculated squared absolute value of the components of the system state is reported in Fig. 7(b). This produces an encoded superposition which is essentially coincident with the exact value (see crosses) and hence demonstrates that 1 is suitable to implement the QEC algorithm. We note that small residual errors on the encoded state (of the order of a few %) could be further reduced by using quantum control techniques to speed-up transitions,61,62 while keeping a small leakage to neighboring levels.
2.5 Coherent NMR manipulation of the nuclear qudit
As a last step, we show by targeted pulse NMR measurements that we can actually coherently manipulate all the nuclear spin transitions involved in the sequence reported in Section 2.4. To this end, we perform Rabi experiments on each of the three ΔmI = ±1 transitions, namely |−3/2〉 → |−1/2〉 (AB1), |− 1/2〉 → |1/2〉 (AB2) and |1/2〉 → |3/2〉 (AB3). Measurements reported in Fig. 8 are performed on our home-built pulse-NMR spectrometer, by a first θ exciting pulse of increasing length, followed by a fixed π refocusing pulse of proper amplitude B1 to excite a single transition at a time (as discussed in detail in the ESI†). The resulting oscillations are modelled by an exponentially damped sinusoidal function f(t) ∝ e−tλ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(2πνRt). For each excited transition, the measured Rabi frequency νR increases linearly with oscillating field amplitude B1 in agreement with expectations for an rf field induced nutation (see ESI†). The damping rate (λ) of the measured Rabi oscillations shows a strong dependence on B1, indicating that this decay is dominated by inhomogeneities of the applied radio-frequency field. However, for achievable pulse intensities the decay time
sin(2πνRt). For each excited transition, the measured Rabi frequency νR increases linearly with oscillating field amplitude B1 in agreement with expectations for an rf field induced nutation (see ESI†). The damping rate (λ) of the measured Rabi oscillations shows a strong dependence on B1, indicating that this decay is dominated by inhomogeneities of the applied radio-frequency field. However, for achievable pulse intensities the decay time 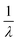 is always remarkably longer that the duration of a π rotation, in the range 0.3–1 μs, as shown in Fig. 8 and also in Fig. S5.† The long decay times allow many successive operations of nuclear spin state manipulation before the coherence is lost.
is always remarkably longer that the duration of a π rotation, in the range 0.3–1 μs, as shown in Fig. 8 and also in Fig. S5.† The long decay times allow many successive operations of nuclear spin state manipulation before the coherence is lost.
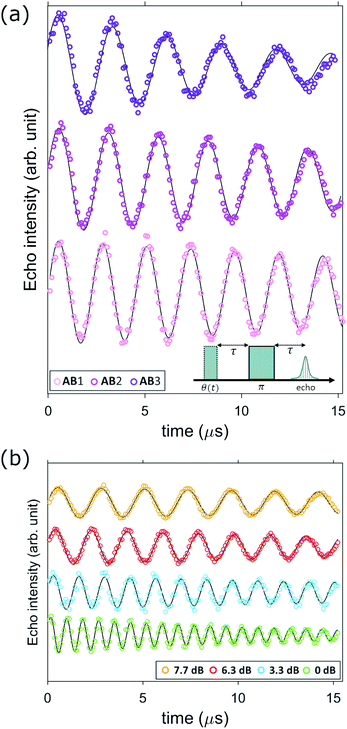 | ||
| Fig. 8 (a) Nuclear Rabi oscillations induced on transitions AB1, 2, 3 at fixed static field B0 = 0.3 T, approximately parallel to x (∼2° uncertainty) by the linearly polarized (z) rf pulse sequence depicted in the inset (with variable first pulse length θ(t)) and fixed radio frequency attenuation 7.7 dB. (b) Nuclear Rabi oscillations induced on transition AB1 (f = 72.25 MHz) at fixed field (B0 = 0.3 T) for different applied pulse intensities, showing the expected scaling of Rabi frequency with B1 (Fig. S5 and S6†). Experiments are performed at T = 1.4 K. | ||
We finally note that the inclusion of the additional available levels mI = ±5/2 and mI = ±7/2 would allow us to improve the encoding of Section 2.4 and thus to correct further dephasing errors (i.e. not only first but also second and third order errors).
3 Discussion and conclusions
Summarizing, we have studied [VO(TPP)] as an important representative of a class of vanadyl-based molecular qudits. These are characterized by an 8-level nuclear spin coupled to an electronic qubit, particularly promising for quantum computing applications,25 such as quantum-error correction33 or quantum simulation.44 In this respect, the 8 levels of the spin qudit could be used to encode a system characterized by several degrees of freedom, such as a photon or a phonon mode interacting with an atom.44 In this scheme, the qudit levels mI = 7/2, 5/2, …, −7/2 would represent states with n = 0, 1, …, 7 photons, thus enabling the simulation of the interaction between matter and a quantized field even in the ultra-strong coupling regime. Such a simulation could be implemented by a sequence of pulses resonant with nuclear or electronic spin transitions, along the lines of ref. 44. Remarkably, the 8 available nuclear levels (instead of 4 or 6 as in ref. 44) enlarge the range of models to be simulated.In general, operations involved in quantum computing algorithms on the qudit can be decomposed into elementary transitions between pairs of ΔmI = ±1 nuclear spin levels. Each of these transitions must then be individually addressable and characterized by long coherence times.
We have demonstrated that these conditions are fulfilled by the investigated system through an extensive NMR study on single crystals. In particular, we characterize the nuclear spin Hamiltonian, its interaction with the electronic ancilla and its coherence properties. Starting from this in-depth characterization, we show that nuclear transitions involved in the encoding step of a qudit-based QEC code33 can be individually addressed by resonant radio-frequency pulses. This is made possible by the remarkably long coherence times and by the robust hyperfine interaction with the electronic spin, which acts as an effective quadrupole coupling distinguishing the various transitions, even in the absence of a real quadrupole coupling. This scheme enables coherent manipulation of the qudit and hence the implementation of sequences of transitions, such as those required by QEC codes.
By removing the strict requirements on the quadrupole interaction, our work will significantly enlarge the list of suitable qubit–qudit systems for quantum computing applications. In these conditions, not only rare-earth,32 but also transition metal complexes could be very promising, thanks to their remarkable coherence times, despite their smaller intrinsic quadrupole interaction. In particular, V-based compounds, usually not considered due to their small quadrupole coupling, become very attractive, by combining two great advantages. First, among all transition-metal and rare-earth MNMs, they possess the largest nuclear spin (7/2), thus providing a sizable number of levels for the implementation of qudit algorithms. Second, the record electronic coherence for a MNM was reported on a vanadium(IV) complex,5 which is only an example of a large family of highly coherent compounds.6,10,49 The [VO(TPP)] case examined here shows indeed values of nuclear T2 significantly longer than those reported in ref. 32 for [Yb(trensal]), whose nuclear spin was characterized by a much stronger value of p. The generality of this conclusion is further confirmed by the subsequent observation of a detectable effective quadrupole also in another coordination geometry of vanadium complex.63
It is finally worth noting that the examined compound presents some additional appealing features. [VO(TPP)], though seldom investigated, belongs to a class of molecules that can be evaporated and organized in ordered arrays on different substrates.64 The V![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group is readily accessible in these flat molecules,65 with the potential to perform single spin EPR by using a Scanning Probe Microscopy, as recently reported for a phthalocyanine complex.66 Equally relevant is the possibility to couple more porphyrin rings to induce interactions between the coordinated metal ions,67 as required for the implementation of quantum gates. Last but not least, chemical functionalization of the porphyrin allowed to arrange the [VO(TPP)] units into a metal–organic framework without affecting its magnetic properties.45 This, together with its remarkable coherence times, makes it a good candidate for a magnetic field sensor. To this aim, the hyperfine coupling with a spin 7/2 nucleus could be a useful resource to enhance sensitivity of a [VO(TPP)]-based quantum meter close to level anti-crossings,68–70 such as those occurring below 0.05 T.
O group is readily accessible in these flat molecules,65 with the potential to perform single spin EPR by using a Scanning Probe Microscopy, as recently reported for a phthalocyanine complex.66 Equally relevant is the possibility to couple more porphyrin rings to induce interactions between the coordinated metal ions,67 as required for the implementation of quantum gates. Last but not least, chemical functionalization of the porphyrin allowed to arrange the [VO(TPP)] units into a metal–organic framework without affecting its magnetic properties.45 This, together with its remarkable coherence times, makes it a good candidate for a magnetic field sensor. To this aim, the hyperfine coupling with a spin 7/2 nucleus could be a useful resource to enhance sensitivity of a [VO(TPP)]-based quantum meter close to level anti-crossings,68–70 such as those occurring below 0.05 T.
Data availability
Data shown in the paper are available from the corresponding author upon reasonable request.Author contributions
R. S. and S. C. conceived the work and planned the experiment. S. Ch., A. C., G. A., E. G. and R. D. R. performed NMR measurements, with data analysis and determination of model parameters. S. Ch. and A. C. performed numerical simulations. M. A., L. S. and R. S. synthesized and preliminary characterized the sample. S. Ch., A. C. and S.C. wrote the manuscript, with inputs from all the authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has received funding from the European Union's Horizon 2020 Research and Innovation Programme (FET-OPEN project FATMOLS) under grant agreement No. 862893, the European Project “Scaling Up quantum computation with MOlecular spins” (SUMO) of the call QuantERA, cofunded by Italian Ministry of University and Research (MUR), and by the Italian Ministry of Education and Research (MUR) through PRIN Project 2017 Q-chiSS “Quantum detection of chiral-induced spin selectivity at the molecular level”.Notes and references
- A. Gaita-Ariño, F. Luis, S. Hill and E. Coronado, Nat. Chem., 2019, 11, 301–309 CrossRef PubMed.
- M. Atzori and R. Sessoli, J. Am. Chem. Soc., 2019, 141, 11339 CrossRef CAS PubMed.
- C. J. Wedge, G. A. Timco, E. T. Spielberg, R. E. George, F. Tuna, S. Rigby, E. J. L. McInnes, R. E. P. Winpenny, S. J. Blundell and A. Ardavan, Phys. Rev. Lett., 2012, 108, 107204 CrossRef CAS PubMed.
- K. Bader, D. Dengler, S. Lenz, B. Endeward, S.-D. Jiang, P. Neugebauer and J. van Slageren, Nat. Commun., 2014, 5, 5304 CrossRef CAS PubMed.
- J. M. Zadrozny, J. Niklas, O. G. Poluektov and D. E. Freedman, ACS Cent. Sci., 2015, 1, 488 CrossRef CAS PubMed.
- M. Atzori, L. Tesi, E. Morra, M. Chiesa, L. Sorace and R. Sessoli, J. Am. Chem. Soc., 2016, 138, 2154–2157 CrossRef CAS PubMed.
- M. Atzori, E. Morra, L. Tesi, A. Albino, M. Chiesa, L. Sorace and R. Sessoli, J. Am. Chem. Soc., 2016, 138, 11234–11244 CrossRef CAS PubMed.
- M. Atzori, L. Tesi, S. Benci, A. Lunghi, R. Righini, A. Taschin, R. Torre, L. Sorace and R. Sessoli, J. Am. Chem. Soc., 2017, 139, 4338–4341 CrossRef CAS PubMed.
- M. Atzori, S. Benci, E. Morra, L. Tesi, M. Chiesa, R. Torre, L. Sorace and R. Sessoli, Inorg. Chem., 2018, 57, 731–740 CrossRef CAS PubMed.
- C.-J. Yu, M. J. Graham, J. M. Zadrozny, J. Niklas, M. D. Krzyaniak, M. R. Wasielewski, O. G. Poluektov and D. E. Freedman, J. Am. Chem. Soc., 2016, 138, 14678–14685 CrossRef CAS PubMed.
- M. Fataftah, J. M. Zadrozny, S. C. Coste, M. J. Graham, D. M. Rogers and D. E. Freedman, J. Am. Chem. Soc., 2016, 138, 1344 CrossRef CAS PubMed.
- M. J. Graham, J. M. Zadrozny, M. Shiddiq, J. S. Anderson, M. S. Fataftah, S. Hill and D. E. Freedman, J. Am. Chem. Soc., 2014, 136, 7623–7626 CrossRef CAS PubMed.
- J. Zadrozny and D. E. Freedman, Inorg. Chem., 2015, 54, 12027–12031 CrossRef CAS PubMed.
- F. Luis, A. Repollés, M. J. Martínez-Pérez, D. Aguilá, O. Roubeau, D. Zueco, P. J. Alonso, M. Evangelisti, J. S. A. Camón, L. A. Barrios and G. Aromí, Phys. Rev. Lett., 2011, 107, 117203 CrossRef CAS PubMed.
- D. Aguilà, D. Barrios, V. Velasco, O. Roubeau, A. Repollés, P. Alonso, J. Sesé, S. Teat, F. Luis and G. Aromí, J. Am. Chem. Soc., 2014, 136, 14215 CrossRef PubMed.
- A. Ardavan, A. M. Bowen, A. Fernandez, A. J. Fielding, D. Kaminski, F. Moro, C. A. Muryn, M. D. Wise, A. Ruggi, E. J. L. McInnes, K. Severin, G. A. Timco, C. R. Timmel, F. Tuna, G. F. S. Whitehead and R. E. P. Winpenny, npj Quantum Inf., 2015, 1, 15012 CrossRef.
- A. Chiesa, G. F. S. Whitehead, S. Carretta, L. Carthy, G. A. Timco, S. J. Teat, G. Amoretti, E. Pavarini, R. E. P. Winpenny and P. Santini, Sci. Rep., 2014, 4, 7423 CrossRef CAS PubMed.
- J. Ferrando-Soria, E. Moreno-Pineda, A. Chiesa, A. Fernandez, S. A. Magee, S. Carretta, P. Santini, I. Vitorica-Yrezabal, F. Tuna, E. J. L. McInness and R. E. P. Winpenny, Nat. Commun., 2016, 7, 11377 CrossRef CAS PubMed.
- J. Ferrando-Soria, et al. , Chem, 2016, 1, 727–752 CAS.
- M. Atzori, A. Chiesa, E. Morra, M. Chiesa, L. Sorace, S. Carretta and R. Sessoli, Chem. Sci., 2018, 9, 6183 RSC.
- E. Garlatti, T. Guidi, S. Ansbro, P. Santini, G. Amoretti, J. Ollivier, H. Mutka, G. Timco, I. J. Vitorica-Yrezabal, G. F. S. Whitehead, R. E. P. Winpenny and S. Carretta, Nat. Commun., 2017, 8, 14543 CrossRef CAS PubMed.
- G. Timco, S. Marocchi, E. Garlatti, C. Barker, M. Albring, V. Bellini, F. Manghi, E. J. L. McInnes, R. G. Pritchard, F. Tuna, W. Wernsdorfer, G. Lorusso, G. Amoretti, S. Carretta, M. Affronte and R. E. P. Winpenny, Dalton Trans., 2016, 45, 16610–16615 RSC.
- E. Moreno-Pineda, C. Godfrin, F. Balestro, W. Wernsdorfer and M. Ruben, Chem. Soc. Rev., 2018, 47, 501–513 RSC.
- S. Carretta, D. Zueco, A. Chiesa, A. Gómez-León and F. Luis, Appl. Phys. Lett., 2021, 118, 240501 CrossRef CAS.
- Y. Wang, Z. Hu, B. C. Sanders and S. Kais, Front. Phys., 2020, 8, 479 Search PubMed.
- P. Imany, J. A. Jaramillo-Villegas, M. S. Alshaykh, J. M. Lukens, O. D. Odele, A. J. Moore, D. E. Leaird, M. Qi and A. M. Weiner, npj Quantum Inf., 2019, 5, 59 CrossRef.
- E. O. Kiktenko, A. K. Fedorov, O. V. Man’ko and V. I. Man’ko, Phys. Rev. A, 2015, 91, 042312 CrossRef.
- B. Mischuck and K. Mølmer, Phys. Rev. A, 2013, 87, 022341 CrossRef.
- M. H. Michael, M. Silveri, R. Brierley, V. V. Albert, J. Salmilehto, L. Jiang and S. M. Girvin, Phys. Rev. X, 2016, 6, 031006 Search PubMed.
- C. Cafaro, F. Maiolini and S. Mancini, Phys. Rev. A, 2012, 86, 022308 CrossRef.
- V. V. Albert, J. P. Covey and J. Preskill, Phys. Rev. X, 2020, 10, 031050 CAS.
- R. Hussain, G. Allodi, A. Chiesa, E. Garlatti, D. Mitcov, A. Konstantatos, K. Pedersen, R. D. Renzi, S. Piligkos and S. Carretta, J. Am. Chem. Soc., 2018, 140, 9814–9818 CrossRef CAS PubMed.
- A. Chiesa, E. Macaluso, F. Petiziol, S. Wimberger, P. Santini and S. Carretta, J. Phys. Chem. Lett., 2020, 11, 8610–8615 CrossRef CAS PubMed.
- E. Macaluso, M. Rubín, D. Aguilà, A. Chiesa, J. I. M. L. A. Barrios, P. J. Alonso, O. Roubeau, F. Luis, G. Aromí and S. Carretta, Chem. Sci., 2020, 11, 10337 RSC.
- F. Tacchino, A. Chiesa, S. Carretta and D. Gerace, Adv. Quantum Technol., 2019, 1900052 Search PubMed.
- A. Chiesa, F. Tacchino, M. Grossi, P. Santini, I. Tavernelli, D. Gerace and S. Carretta, Nat. Phys., 2019, 15, 455–459 Search PubMed.
- F. Arute, et al. , Science, 2020, 369, 1084–1089 CrossRef CAS PubMed.
- P. J. Ollitrault, A. Baiardi, M. Reiher and I. Tavernelli, Chem. Sci., 2020, 11, 6842–6855 RSC.
- A. Kandala, A. Mezzacapo, K. Temme, M. Takita, M. Brink, J. M. Chow and J. M. Gambetta, Nature, 2017, 549, 242–246 CrossRef CAS PubMed.
- C. D. Bruzewicz, J. Chiaverini, R. McConnell and J. M. Sage, Appl. Phys. Lett., 2019, 6, 021314 Search PubMed.
- B. P. Lanyon, M. Barbieri, M. P. Almeida, T. Jennewein, T. C. Ralph, K. J. Resch, G. J. Pryde, A. G. Jeremy, L. O'Brien and A. G. White, Nat. Phys., 2009, 5, 134–140 Search PubMed.
- E. Kiktenko, A. Fedorov, A. Strakhov and V. Man'ko, Phys. Lett. A, 2015, 379, 1409–1413 CrossRef CAS.
- C. Godfrin, A. Ferhat, R. Ballou, S. Klyatskaya, M. Ruben, W. Wernsdorfer and F. Balestro, Phys. Rev. Lett., 2017, 119, 187702 CrossRef CAS PubMed.
- F. Tacchino, A. Chiesa, R. Sessoli, I. Tavernelli and S. Carretta, J. Mater. Chem. C, 2021 10.1039/d1tc00851j.
- T. Yamabayashi, M. Atzori, L. Tesi, G. Cosquer, F. Santanni, M.-E. Boulon, E. Morra, S. Benci, R. Torre, M. Chiesa, L. Sorace, R. Sessoli and M. Yamashita, J. Am. Chem. Soc., 2018, 140, 12090–12101 CrossRef CAS PubMed.
- C. Bonizzoni, A. Ghirri, F. Santanni, M. Atzori, L. Sorace, R. Sessoli and M. Affronte, npj Quantum Inf., 2020, 6, 68 CrossRef.
- I. Gimeno, A. Urtizberea, J. Román-Roche, D. Zueco, A. Camón, P. J. Alonso, O. Roubeau and F. Luis, Chem. Sci., 2021, 12, 5621–5630 RSC.
- G. Allodi, A. Banderini, R. De Renzi and C. Vignali, Rev. Sci. Instrum., 2005, 76, 083911 CrossRef.
- E. Garlatti, L. Tesi, A. Lunghi, M. Atzori, D. J. Voneshen, P. Santini, S. Sanvito, T. Guidi, R. Sessoli and S. Carretta, Nat. Commun., 2020, 11, 1751 CrossRef CAS PubMed.
- D. Feng, Z.-Y. Gu, J.-R. Li, H.-L. Jiang, Z. Wei and H.-C. Zhou, Angew. Chem., Int. Ed., 2012, 51, 10307–10310 CrossRef CAS PubMed.
- W. G. Clark, M. E. Hanson, F. Lefloch and P. Ségransan, Rev. Sci. Instrum., 1995, 66, 2453–2464 CrossRef CAS.
- N. J. Stone, International Atomic Energy Agency, INDC(NDS)-0658, 2014, vol. 45, p. 11 Search PubMed.
- E. L. Hahn, Phys. Rev., 1950, 80, 580 CrossRef.
- S. J. Balian, G. Wolfowicz, J. J. L. Morton and T. S. Monteiro, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 045403 CrossRef.
- S. Takahashi, R. Hanson, J. van Tol, M. S. Sherwin and D. D. Awschalom, Phys. Rev. Lett., 2008, 101, 047601 CrossRef PubMed.
- S. Takahashi, J. van Tol, C. C. Beedle, D. N. Hendrickson, L.-C. Brunel and M. S. Sherwin, Phys. Rev. Lett., 2009, 102, 087603 CrossRef PubMed.
- A. Ghirri, A. Chiesa, S. Carretta, F. Troiani, J. van Tol, S. Hill, I. Vitorica-Yrezabal, G. A. Timco, R. E. P. Winpenny and M. Affronte, J. Phys. Chem. Lett., 2015, 6, 5062–5066 CrossRef CAS PubMed.
- S. J. Lockyer, A. Chiesa, G. A. Timco, E. J. L. McInnes, T. S. Bennett, I. J. Vitorica-Yrezebal, S. Carretta and R. E. P. Winpenny, Chem. Sci., 2021, 12, 9104 RSC.
- D. G. Tempel and A. Aspuru-Guzik, Chem. Phys., 2011, 391, 130–142 CrossRef CAS.
- W. Zhong, Z. Sun, J. Ma, X. Wang and F. Nori, Phys. Rev. A, 2013, 87, 022337 CrossRef.
- N. V. Vitanov, A. A. Rangelov, B. W. Shore and K. Bergmann, Rev. Mod. Phys., 2017, 89, 015006 CrossRef.
- M. Werninghaus, D. J. Egger, F. Roy, S. Machnes, F. K. Wilhelm and S. Filipp, npj Quantum Inf., 2021, 7, 14 CrossRef.
- M. Atzori, E. Garlatti, G. Allodi, S. Chicco, A. Chiesa, A. Albino, R. D. Renzi, E. Salvadori, M. Chiesa, S. Carretta and L. Sorace, Inorg. Chem., 2021, 60, 11273–11286 CrossRef CAS PubMed.
- J. M. Gottfried, Surf. Sci. Rep., 2015, 70, 259–379 CrossRef CAS.
- L. Malavolti, M. Briganti, M. Hänze, G. Serrano, I. Cimatti, G. McMurtrie, E. Otero, P. Ohresser, F. Totti, M. Mannini, R. Sessoli and S. Loth, Nano Lett., 2018, 18, 7955–7961 CrossRef CAS PubMed.
- X. Zhang, C. Wolf, Y. Wang, H. Aubin, T. Bilgeri, P. Willke, A. Heinrich and T. Choi, 2021, DOI:10.21203/rs.3.rs-134144/v1.
- N. Wili, S. Richert, B. Limburg, S. J. Clarke, H. L. Anderson, C. R. Timmel and G. Jeschke, Phys. Chem. Chem. Phys., 2019, 21, 11676–11688 RSC.
- F. Troiani and M. G. A. Paris, Phys. Rev. B, 2016, 94, 115422 CrossRef.
- L. Ghirardi, I. Siloi, P. Bordone, F. Troiani and M. G. A. Paris, Phys. Rev. A, 2018, 97, 012120 CrossRef CAS.
- C. L. Degen, F. Reinhard and P. Cappellaro, Rev. Mod. Phys., 2017, 89, 035002 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sc01358k |
| ‡ This allows us to obtain a small leakage to neighboring levels, while limiting the duration of the pulses and hence the effect of dephasing acting during the operation. |
| This journal is © The Royal Society of Chemistry 2021 |