Open Access Article
Open Access ArticleKinetic effects of molecular clustering and solvation by extended networks in zeolite acid catalysis
Jason S.
Bates
 and
Rajamani
Gounder
and
Rajamani
Gounder
 *
*
Charles D. Davidson School of Chemical Engineering, Purdue University, 480 Stadium Mall Drive, West Lafayette, IN 47907, USA. E-mail: rgounder@purdue.edu
First published on 24th February 2021
Abstract
Reactions catalyzed within porous inorganic and organic materials and at electrochemical interfaces commonly occur at high coverage and in condensed media, causing turnover rates to depend strongly on interfacial structure and composition, collectively referred to as “solvent effects”. Transition state theory treatments define how solvation phenomena enter kinetic rate expressions, and identify two distinct types of solvent effects that originate from molecular clustering and from the solvation of such clusters by extended solvent networks. We review examples from the recent literature that investigate reactions within microporous zeolite catalysts to illustrate these concepts, and provide a critical appraisal of open questions in the field where future research can aid in developing new chemistry and catalyst design principles.
1. Introduction
Catalytic reactions that occur at high pore occupancy within zeolites and porous materials are of both practical and fundamental interest. Practical applications include biomass conversions,1–4 selective oxidations of hydrocarbons and oxygenates,5–7 and alkene oligomerization.8–12 Zeolites provide a well-defined materials platform to probe the mechanistic details of solvent effects in catalysis,13 because their reaction environments can be systematically varied via synthetic and post-synthetic changes to pore topology, size, and chemical functionality. This structural diversity can be leveraged to elucidate new reactivity paradigms such as mechanisms involving solvated and mobilized cation active sites14–16 or solvent-mediated charge interactions that influence free energy landscapes.17,18 These findings regarding the effects of solvation on the kinetics and mechanisms of catalytic reactions in zeolites have broader implications both for heterogeneous catalysts in condensed phases (e.g., Fischer–Tropsch synthesis,19–22 organic synthesis23), and for adjacent sub-fields of catalysis where solvation at interfaces or within confining environments is critical, including catalysis at electrochemical interfaces24–28 and within enzymes29–31 and metal–organic frameworks (MOFs).32,33 Solvation alters the free energy landscapes of reactions that occur in solution, including situations where solvent rearrangement occurs along reaction coordinates,34 and where non-equilibrium solvation dynamics motivate revisions of “classical” organic reaction mechanisms.35The prevalence of solvent effects in heterogeneous catalysis in condensed media has motivated developing quantitative kinetic, spectroscopic, and theoretical assessments of solvent structures and their interactions with reaction intermediates and transition states. In our research, we have found it useful to conceptually delineate “solvent effects” into two parts: (i) molecular clustering, which describes the local structures and molecularity of reaction intermediates and transition states bonded closely to the active center, and (ii) the solvation of such clusters by extended solvent networks, which considers the thermodynamic consequences of the arrangements of solvent molecules and charged moieties in response to reactant adsorption, transition state formation, and confinement within porous environments. This conceptual division is manifested mathematically in transition state theory treatments of kinetic rate expressions that provide a quantitative basis to measure solvent effects, as we discuss in Section 2. Examples from the recent literature that illustrate these two distinct effects are concisely reviewed in Sections 3 and 4, and an outlook is provided in Section 5 to identify opportunities for future research into the fundamentals of solvation in zeolite catalysis.
2. Kinetic implications of solvation
Quantitatively precise descriptions of solvation require reliable measurements of the catalytic turnover rate, because transition state theory formalisms enable rigorously relating turnover rates to molecular-level properties of bound adsorbates, transition states, and solvent molecules. Thus, turnover rates must be measured in kinetic regimes uncorrupted by transport phenomena, and normalized by the number of catalytically relevant active sites (L).36 Upon satisfying these conditions, measured turnover rates, which are proportional to the concentration of transition states,37 can be expressed in terms of the free energies of the apparent initial state (IS) and transition state (TS), according to recently derived transition state theory-based treatments of multistep reaction networks38 (cf. eqn (2.2.13) in that work):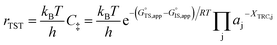 | (1) |
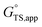 is the apparent transition state Gibbs free energy,
is the apparent transition state Gibbs free energy,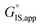 is the apparent initial state Gibbs free energy, aj is the thermodynamic activity of species j, and XTRC,j is the degree of thermodynamic rate control39 of species j. In this general form, j includes both fluid-phase species and adsorbed intermediates. Following the treatment of Foley and Bhan38 (cf. eqn (2.1.12)):
is the apparent initial state Gibbs free energy, aj is the thermodynamic activity of species j, and XTRC,j is the degree of thermodynamic rate control39 of species j. In this general form, j includes both fluid-phase species and adsorbed intermediates. Following the treatment of Foley and Bhan38 (cf. eqn (2.1.12)): | (2) |
Thus, the apparent free energy of activation for a multistep reaction network reflects a weighted average of the standard-state Gibbs free energies of the individual species and transition states involved in elementary steps. The terms in eqn (1) and (2) readily illustrate, without requiring further simplification, how molecular clustering and solvation influences rates. The  term reflects the mechanistic pathway by which the reaction proceeds, and thus captures both the chemical identity and the thermodynamic stability of the kinetically relevant transition states within the summation (XRC,i ≠ 0), which depends on their size, molecularity, and solvation by the surrounding environment. The
term reflects the mechanistic pathway by which the reaction proceeds, and thus captures both the chemical identity and the thermodynamic stability of the kinetically relevant transition states within the summation (XRC,i ≠ 0), which depends on their size, molecularity, and solvation by the surrounding environment. The  term similarly depends on the structures of the most abundant reactive intermediates (MARI; XTRC,i ≠ 0), also referred to as the catalyst resting state, which are often solvent-reactant clusters stabilized at active sites within micropores. The thermodynamic activities (aj) of chemical species contain activity coefficients (γj) that reflect solvation when their Gibbs free energies depart from those at standard state in the limit of low surrounding pore occupancy. Kinetic, spectroscopic, and theoretical interrogation of the apparent IS and TS under reaction conditions is required to derive mechanism-based rate expressions as a more specific embodiment of eqn (1) that enable quantifying the kinetic effects of solvation.
term similarly depends on the structures of the most abundant reactive intermediates (MARI; XTRC,i ≠ 0), also referred to as the catalyst resting state, which are often solvent-reactant clusters stabilized at active sites within micropores. The thermodynamic activities (aj) of chemical species contain activity coefficients (γj) that reflect solvation when their Gibbs free energies depart from those at standard state in the limit of low surrounding pore occupancy. Kinetic, spectroscopic, and theoretical interrogation of the apparent IS and TS under reaction conditions is required to derive mechanism-based rate expressions as a more specific embodiment of eqn (1) that enable quantifying the kinetic effects of solvation.
Knowledge of the apparent IS and TS under a given set of conditions enables writing the overall reaction as an apparent rate-determining step of the form: IS → TS, where the IS collectively describes the MARI species and the additional fluid-phase species required to traverse from the IS to the TS. Fluid-phase species may have both positive or negative stoichiometric coefficients (by convention, species that are consumed en route to the apparent TS have negative stoichiometric coefficients) if MARI species of the IS contain spectating components and thus require desorption of molecules to form the TS. Quasi-equilibrium between the IS and TS can be expressed as an equilibrium constant:
 | (3) |
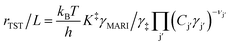 | (4) |
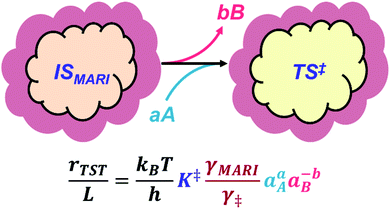
The quantitative effects of clustering and solvation are collectively illustrated in Fig. 1, where a clustered MARI (IS) forms the transition state (‡), a process that may be accompanied by the incorporation of reactant molecules (A) and/or the removal of spectating molecules (B). The corresponding rate expression shows how the identities and solvation of clustered intermediates and transition states determine kinetic rate constants viaeqn (1)–(4). Next, we highlight case studies from the recent literature that investigate reactions within microporous zeolites to illustrate these concepts, discussing separately the effects of molecular clusters and of their solvation by extended networks.
3. Reactant and solvent clustering at active sites
Reactant and solvent molecules bind closely to active sites in zeolites to form IS and TS clusters of diverse structures, which change in relative abundance as kinetic and pore occupancy regimes in turn change in response to external chemical potential. The growth of molecular clusters thus reflects changes in the identity of the apparent IS and TS (and their associated Gibbs free energies) in eqn (1), prior to the onset of solvation effects described by the activity coefficients of a single clustered structure (eqn (4)). A simple case describes reactant clustering that occurs in the absence of a solvent where both the IS and TS can change structure and molecularity, as illustrated by alkanol dehydration via bimolecular pathways to form ether products within small-pore Brønsted acid zeolites. Di Iorio et al.43 measured turnover rates of methanol dehydration to dimethyl ether (415 K, per H+) on H-CHA zeolites, and showed that rates were inhibited at high methanol pressures (>10 kPa). Methanol adsorption isotherms coupled to in situ IR spectra and DFT calculations showed that methanol clusters of increasing molecularity prevail with increasing pore occupancy, while simultaneously granting access to alternative mechanistic pathways wherein transition states of higher molecularity eliminate ether and water products.44 The combined changes to both apparent IS and TS structures leads to apparent kinetic inhibition when the molecularity of the preferred TS (3 CH3OH) is smaller than that of the MARI species (>3 CH3OH), according to DFT evidence.44 Later experimental kinetic analyses45 confirmed that clusters of higher molecularity inhibit methanol dehydration turnover rates by using mixed ethanol–methanol feeds to quantify formation rates of parallel products from identical MARI species, which allow separating the kinetic contributions of different TS structures (numerator terms in product formation rate expressions) from an identical IS (common denominator terms in such rate expressions). Furthermore, turnover rates to form methyl ethyl ether (373 K, per H+) on H-CHA zeolites are inhibited by methanol clusters more severely than turnover rates to form dimethyl ether, because the former pathways prefer bimolecular transition states rather than trimolecular ones (Fig. 2a),45 demonstrating that zeolite frameworks select IS and TS cluster sizes that maximize dispersive and hydrogen-bonding interactions within confining voids. Thus, kinetic inhibition by alkanol reactants is not observed on medium- and large-pore Brønsted acid zeolite topologies that do not stabilize IS clusters of higher molecularity than the apparent TS under equivalent reaction conditions (e.g., MFI, MTT, MTW, MOR, Beta, SFH, FAU),46,47 but is generally observed on small-pore topologies possessing window-cage motifs that readily stabilize higher-molecularity IS clusters (e.g., CHA, AEI, LTA, LEV).44 In the case of unimolecular dehydration of 1-propanol on H-MFI zeolites (413–433 K), when H+ become saturated by clusters containing at least two propanol molecules, an apparent TS stabilized by reactant clustering also contributes to propene formation rates.48 Taken together, these studies show that reactant clusters at the IS can be identified by quantitative measurements of their coverage (i.e., pore occupancy) and spectroscopic characterization of their structure in situ, and in turn require kinetic interrogation of their corresponding clustered TS.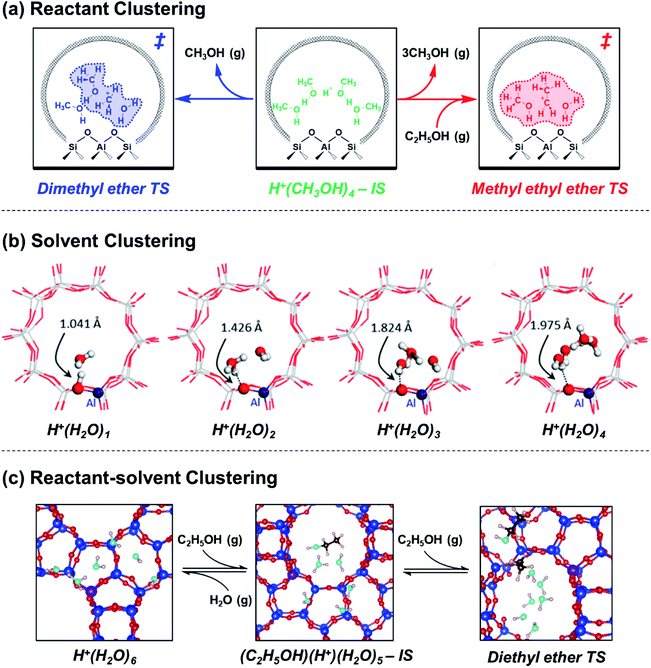 | ||
| Fig. 2 Effects of molecular clustering on initial and transition states of reactions catalyzed by Brønsted acid zeolites. Clusters are shown that consist of (a) reactants,45 (b) solvents,52 or (c) reactant-solvent mixtures.53 (a) Adapted from ref. 45 with permission from Elsevier, copyright 2020. (b) Adapted from ref. 52 with permission from the American Chemical Society, copyright 2019. (c) Adapted from ref. 53 with permission from the Royal Society of Chemistry, copyright 2020. | ||
Aqueous and organic solvents also form clusters within acid zeolites, which become part of the extra-lattice conjugate base that stabilizes the Brønsted acid proton together with the deprotonated lattice. In the context of water, Lercher and coworkers elucidated the structures and dynamics of confined hydronium ions under widely varying coverages and their departure from solution-phase behavior. H2O initially hydrogen-bonds with Si–O(H)–Al groups at coverages up to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1,49,50 then forms H+(H2O)n clusters that delocalize positive charge distant from compensating framework [AlO4/2]− (Fig. 2b).51,52 These clusters reach their maximum size as H+(H2O)7–8 in H-MFI zeolites according to adsorption isotherms,17,531H and 1H–29Si CP MAS NMR spectra,52 and ab initio molecular dynamics (AIMD) simulations.52,53 AIMD simulations showed that confined H+(H2O)n possess more compressed structures and different proton hopping dynamics than their solution-phase counterparts.52,54 In our recent work,53 extended hydrogen-bonded networks of H2O were found to solvate H+(H2O)n clusters after they reach their maximum size (n = 6–7 in H-Beta zeolites, Fig. 2c), as indicated by adsorption isotherms and in situ transmission IR spectra. Xu and coworkers have studied the effects of solvent identity on the adsorption behavior of proton-solvent clusters. The identity of liquid solvent molecules (H2O, CH3CN, C2H5OH) changes the number of H+ that are able to protonate pyridine, relative to those that decompose n-propylamine in the gas phase, in H-MFI and H-MOR but not in H-FAU or H-Beta; these findings suggest that different spatial constraints around clusters and their propensity to delocalize positive charge modify their accessibility and ability to protonate organic bases.55 The thermodynamics of pyridine adsorption and protonation were disentangled using adsorption isotherms measured by attenuated total reflectance (ATR)-IR on H-Beta zeolites and their siliceous analogues to show that protons are less stable within clusters of lower polarity, which protonate pyridine more readily (Kprot: 1,4-dioxane > C2H5OH > CH3CN > H2O).56 Such protonation equilibrium constant differences can be related to
1,49,50 then forms H+(H2O)n clusters that delocalize positive charge distant from compensating framework [AlO4/2]− (Fig. 2b).51,52 These clusters reach their maximum size as H+(H2O)7–8 in H-MFI zeolites according to adsorption isotherms,17,531H and 1H–29Si CP MAS NMR spectra,52 and ab initio molecular dynamics (AIMD) simulations.52,53 AIMD simulations showed that confined H+(H2O)n possess more compressed structures and different proton hopping dynamics than their solution-phase counterparts.52,54 In our recent work,53 extended hydrogen-bonded networks of H2O were found to solvate H+(H2O)n clusters after they reach their maximum size (n = 6–7 in H-Beta zeolites, Fig. 2c), as indicated by adsorption isotherms and in situ transmission IR spectra. Xu and coworkers have studied the effects of solvent identity on the adsorption behavior of proton-solvent clusters. The identity of liquid solvent molecules (H2O, CH3CN, C2H5OH) changes the number of H+ that are able to protonate pyridine, relative to those that decompose n-propylamine in the gas phase, in H-MFI and H-MOR but not in H-FAU or H-Beta; these findings suggest that different spatial constraints around clusters and their propensity to delocalize positive charge modify their accessibility and ability to protonate organic bases.55 The thermodynamics of pyridine adsorption and protonation were disentangled using adsorption isotherms measured by attenuated total reflectance (ATR)-IR on H-Beta zeolites and their siliceous analogues to show that protons are less stable within clusters of lower polarity, which protonate pyridine more readily (Kprot: 1,4-dioxane > C2H5OH > CH3CN > H2O).56 Such protonation equilibrium constant differences can be related to 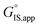 terms of solvated H+ in catalytic reactions via Born–Haber thermochemical cycles. These studies show that solvent molecules and clusters, whether water or organic species, exhibit distinct structures and behavior when active sites are confined within a porous environment.
terms of solvated H+ in catalytic reactions via Born–Haber thermochemical cycles. These studies show that solvent molecules and clusters, whether water or organic species, exhibit distinct structures and behavior when active sites are confined within a porous environment.
Mixtures of solvent and reactant molecules further generate a diverse array of reactant-solvent clusters that can inhibit catalysis in some cases, and facilitate catalysis in others. In the case of ethanol dehydration catalysis, we showed using in situ infrared spectra and volumetric adsorption isotherms that the stabilization of (C2H5OH)(H+)(H2O)5–6 clusters within H-zeolites leads to inhibition of diethyl ether formation rates because H+ prefers to reside within H2O clusters as H3O+, and thus gives rise to −1 reaction orders in H2O that reflect the desorption of one H2O molecule from H3O+ into the gas phase.53 The resulting TS cluster does not require further H2O desorption, consistent with AIMD and metadynamics simulations (Fig. 2c). This interpretation is consistent with prior studies of solution-phase alkanol dehydration by Dumesic and coworkers,57–59 highlighting that solvent clusters stabilize positive charge at the IS in Brønsted acid catalysis. Coadsorbed water also decreases the turnover rate of 1-propanol dehydration catalyzed by H-MFI zeolites because it stabilizes the IS more than the TS, according to activation enthalpy measurements and DFT calculations by Lercher and coworkers.48,60 In these examples of alkanol–water clustering, the inclusion of H2O in clusters introduces new terms to 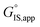 and
and 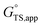 expressions whose net effect is to increase apparent free energies of activation.
expressions whose net effect is to increase apparent free energies of activation.
Reactant–solvent clustering can increase reaction rates when it preferentially stabilizes the TS, however, as shown by Haw et al.61 by cosolvating acetone with nitromethane to facilitate acetone dimerization. Similarly, coadsorbed H2O at low coverage can facilitate proton transfer steps within H-MFI zeolites;62,63 however, larger H+(H2O)n clusters (n ≥ 4) can inhibit H+ transfer to cyclohexanol reactants.64 Additional kinetic studies in the aqueous phase report zero-order dependences in alkanols (substituted cyclohexanols, ethanol),65–69 highlighting that IS clusters often include coadsorbed reactant. Bulk solutions that contain reactants in binary solvent mixtures lead to increasingly complex intrapore reactant–solvent structures whose reactant concentrations respond to differences in cosolvent composition.70 In one case, 500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 CH3CN
1 CH3CN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O solvent mixtures form H2O clusters (IS) at Si–OH groups within Ti-Beta zeolites that become disrupted by alkene epoxidation transition states, providing entropic gains that increase turnover rates relative to Ti-Beta zeolites with lower Si–OH densities.71,72 These concepts are also reflected in studies of solvated catalysis in non-zeolitic materials, including water-facilitated pathways in Fischer–Tropsch synthesis on supported Ru catalysts21,22 and water inhibition of H2 activation at Au–TiO2 interfaces.73 Thus, careful treatment of how reactants associate with and disrupt solvent clusters and their associated transition states are required to predict whether the changes to IS and TS configurations lead to increases or decreases in turnover rates through
H2O solvent mixtures form H2O clusters (IS) at Si–OH groups within Ti-Beta zeolites that become disrupted by alkene epoxidation transition states, providing entropic gains that increase turnover rates relative to Ti-Beta zeolites with lower Si–OH densities.71,72 These concepts are also reflected in studies of solvated catalysis in non-zeolitic materials, including water-facilitated pathways in Fischer–Tropsch synthesis on supported Ru catalysts21,22 and water inhibition of H2 activation at Au–TiO2 interfaces.73 Thus, careful treatment of how reactants associate with and disrupt solvent clusters and their associated transition states are required to predict whether the changes to IS and TS configurations lead to increases or decreases in turnover rates through 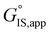 and
and 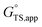 terms.
terms.
In summary, reactants, solvents, and their mixtures form molecular clusters when confined within microporous voids, and such clusters constitute different IS and TS terms in kinetic rate expressions. Molecular clusters lead to kinetic behavior distinct from both the low-coverage limits characteristic of low-pressure gas-phase conditions and the high-coverage limit characteristic of bulk solution phase conditions. Thus, in situ spectroscopic, theoretical, and kinetic characterizations are required to identify clustered structures and determine how they are influenced by their confining environment. Once such clusters are characterized, it becomes possible to observe and quantify their solvation by extended networks as a departure from kinetic dependences described by clustering alone.
4. Extended networks of solvent and charge
Molecular clusters that assemble around proton active sites also reside within a solvating medium, comprised of both the solid zeolite framework and any non-clustered solvent molecules that are contained within its porous voids. Charged moieties or solvent molecules can form extended networks within zeolitic pores that solvate apparent IS and TS differently, influencing rate expressions through their activity coefficients (γMARI, γ‡). Extended hydrogen-bonded networks of H2O form within zeolites that contain polar functional groups (e.g., Si–OH, Si–O(H)–Al), but not within nonpolar analogues74 (unless pressures exceed 50 MPa![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 75). When H2O networks are stabilized within polar Ti-Beta zeolites, glucose–fructose isomerization TS are entropically destabilized relative to their bound IS, leading to ∼6× lower turnover rates (368–383 K, per Lewis acidic Ti) than on nonpolar Ti-Beta zeolites.41 The different solvation of the TS relative to IS within polar and nonpolar Ti-Beta zeolites is thus a case of different γMARI/γ‡ ratios (cf.eqn (4)) that quantitatively encode the impact of solvation on the free energies of TS/IS-solvent ensembles. In a contrasting example, Di Iorio et al.76 showed that 2-butanol solvents, which are less polar than water, preferentially form extended hydrogen-bonded networks within hydrophobic Sn-Beta-F zeolites; this increases cyclohexanone transfer hydrogenation turnover rates because adsorption of cyclohexanone and formation of a coadsorbed hydride shift TS disrupts 2-butanol solvent networks stabilized in the IS, resulting in entropic stabilization (Fig. 3a). Dissecting the individual contributions of adsorption and TS formation relative to its precursors highlighted the dominance of adsorption entropies to form the IS in this chemistry, whereas the TS entropy dominates in the case of aqueous glucose–fructose isomerization within Ti-Beta zeolites. In both cases, the organization of the solvent within an extended network that is confined in either polar or nonpolar micropores leads to kinetically significant entropic differences in the stabilization of IS and TS moieties.
75). When H2O networks are stabilized within polar Ti-Beta zeolites, glucose–fructose isomerization TS are entropically destabilized relative to their bound IS, leading to ∼6× lower turnover rates (368–383 K, per Lewis acidic Ti) than on nonpolar Ti-Beta zeolites.41 The different solvation of the TS relative to IS within polar and nonpolar Ti-Beta zeolites is thus a case of different γMARI/γ‡ ratios (cf.eqn (4)) that quantitatively encode the impact of solvation on the free energies of TS/IS-solvent ensembles. In a contrasting example, Di Iorio et al.76 showed that 2-butanol solvents, which are less polar than water, preferentially form extended hydrogen-bonded networks within hydrophobic Sn-Beta-F zeolites; this increases cyclohexanone transfer hydrogenation turnover rates because adsorption of cyclohexanone and formation of a coadsorbed hydride shift TS disrupts 2-butanol solvent networks stabilized in the IS, resulting in entropic stabilization (Fig. 3a). Dissecting the individual contributions of adsorption and TS formation relative to its precursors highlighted the dominance of adsorption entropies to form the IS in this chemistry, whereas the TS entropy dominates in the case of aqueous glucose–fructose isomerization within Ti-Beta zeolites. In both cases, the organization of the solvent within an extended network that is confined in either polar or nonpolar micropores leads to kinetically significant entropic differences in the stabilization of IS and TS moieties.
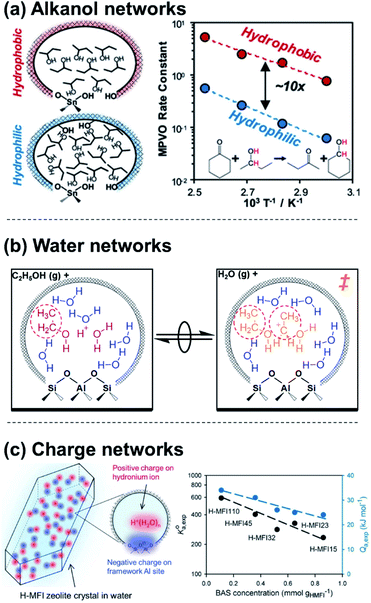 | ||
| Fig. 3 Examples of (a) extended alkanol networks within non-polar Sn-Beta zeolites,76 (b) extended H2O networks within Brønsted acid zeolites,53 and (c) adsorption properties that depend on networks of charge and their density within Brønsted acid zeolites.17 (a) Adapted from ref. 76 with permission from the American Chemical Society, copyright 2020. (b) Adapted from ref. 53 with permission from the Royal Society of Chemistry, copyright 2020. (c) Adapted from ref. 17 with permission from John Wiley and Sons, copyright 2019. | ||
The extended structure and reorganization of networks around the IS and TS are further influenced by the topology of the confining environments that host them. During ethanol dehydration catalysis on Brønsted acid zeolites, the presence of extended H2O networks surrounding (C2H5OH)(H+)(H2O)5–6 clusters can be controlled by varying water chemical potentials up to and beyond the point of intrapore condensation, and measured by in situ IR spectra under catalytically relevant conditions.53 Whereas (C2H5OH)(H+)(H2O)5–6 clusters alone inhibit diethyl ether formation by localizing charge at H3O+ (−1 order in PH2O), their further solvation by H2O networks results in more severe inhibition (up to −3 order in PH2O). This deviation from the limiting water pressure order dependence caused by clusters (−1) rigorously reflects the ratio of IS and TS activity coefficients (γEWn/γ‡) and thus enables its quantification by experiment. This ratio decreases with increasing extents of solvation because the bimolecular ether formation TS disrupts H2O networks to a greater extent than the corresponding IS (a (C2H5OH)(H+)(H2O)5–6 cluster), which is smaller and more polar because it contains one fewer ethyl group (Fig. 3b). These activity coefficient ratios (γEWn/γ‡) quantify free energy penalties for solvent reorganization along the reaction coordinate, which is constrained by the shape of confining pores. Thus, pore shapes that impede H2O reorganization cause more severe orders of H2O inhibition, as observed within zeolite topologies that require water networks to compress from cages through restricting windows (i.e., CHA, AEI).53 These insights about the role of topology and intrapore functional group polarity in mediating solvation can be extended to MOFs and other porous materials that are capable of stabilizing different extended H2O networks,77 and are reminiscent of the effects of adsorbate crowding on metal surfaces where dense adlayers lead to different stabilization of the IS and TS.22,78 In these cases, quantifying the effects of extended solvent networks on the IS and TS is enabled by kinetic measurements and characterizations that monitor the formation of these networks over widely varying coverage ranges.
The specific arrangement and proximity of protonated molecular clusters within zeolites can also lead to distinct solvation phenomena. Lercher and coworkers17,67 concluded that H2O networks can mediate charge interactions that manifest as different activity coefficients for the adsorption of cyclohexanol and phenol within MFI zeolites of different charge density, as determined by bulk Al content (Si/Al = 15–110). The saturation uptakes of both organic molecules systematically decreased with Al content, which was attributed to their preferential adsorption in hydrophobic regions of porous voids that are unoccupied by H+(H2O)7–8 clusters, whose molecularity was corroborated by volumetric adsorption isotherms. Concomitant decreases in the cyclohexanol adsorption constant with H+ density were rationalized by treating the zeolite as a “quasi solid electrolyte” that destabilizes adsorbed organic molecules when H+(H2O)7–8 form densely populated networks of positive charge, in analogy to the effects of ionic strength in solution (Fig. 3c). Although networks of solvent molecules can mediate charge interactions that destabilize adsorbates, specific arrangements of charged reactant molecules can stabilize transition states. Hoffman et al.18 recently reported that alkanol dehydration transition states become stabilized when H+ active sites are arranged in proximal positions of zeolite lattices, which form rigid networks of charge that facilitate hydrogen bonding between transition states and coadsorbed reactant clusters. Non-ideal charge interactions have similarly been described for polyoxometalate clusters,79 and solvent-enabled expansion of the length scales over which charge interactions mediate reactions has been demonstrated for other solid Brønsted acids,80 metals,81,82 and oxides.83 The specific arrangement and density of charged moieties within solids thus afford additional ways to modify the relative stabilities of IS and TS.
In summary, extended networks of solvent and charge influence the free energies of IS and TS clusters through activity coefficient terms in kinetic rate expressions. The existence of such networks, their shape, and their specific arrangements are determined by the topology and composition of the solid that confines them. Systematic quantification of these influences of solvation using activity coefficients thus provides a method to study the effects of material properties on reactivity.
5. Outlook
In the foregoing sections, we reviewed two conceptually distinct ways in which “solvent effects” are mathematically codified in kinetic rate expressions and summarized examples from the recent literature in which solvation can be interpreted using this conceptual framework, wherein the dominant kinetic effects reflect consequences of either molecular clustering or extended networks of solvent and charge. Here, we provide an outlook on future research that can provide additional insights into the fundamental principles of molecular clustering and of extended networks that influence the reactivity of active sites in zeolites under conditions of high pore occupancy.Zeolites behave as “solid solvents”,84,85 which impose spatial constraints on the structures of confined clusters and networks, and contain chemical moieties that provide specific interactions with their molecular constituents, leading to the formation of unique clustered configurations of the IS and TS that otherwise do not form in bulk liquid media at the same chemical potential.52,65 Such diverse clustered structures and their consequences for adsorption86 and catalysis87 have also been recently recognized in supramolecular environments. Unifying the limiting regimes of low and high pressures that are characteristic of the kinetic behavior in gaseous and condensed phases, respectively, thus requires kinetic and spectroscopic data measured in intermediate regimes of fluid-phase chemical potential to interrogate the clustered intermediates that form. Studies that survey a wide range of fluid-phase chemical potential, and the rich catalytic behavior engendered by variations in the structures of confined clusters and networks, provide opportunities to develop kinetic models that more accurately account for the nature of clustered intermediates across coverage regimes that vary from dilute to full pore occupancy. Such kinetic models are often challenged to describe the complexities of experimental realities, which include not only realistic representations of high coverage, but also cluster–cluster interactions that may depend on the spatial arrangements of chemical moieties (e.g., framework Al, other defect sites) in the zeolite lattice.18 Unique molecular configurations that arise when multicomponent mixtures fill micropores at high coverage are reported for alkane mixtures88 and aqueous solutions of alcohols,89,90 suggesting that unique configurations of other mixtures may prevail at high coverage and provide opportunities to investigate their consequences for catalysis. Such insights will inform new strategies to design catalysts that prefer advantageous clustering motifs (either IS or TS) by modifying the surrounding spatial constraints provided by porous solids91 and their arrangements of atoms and charges. Further, identifying cosolvents that preferentially stabilize a clustered TS over the IS offers another approach to influence reactivity, a concept demonstrated in a simpler case where alkane or alkene cosolvents stabilize (non-clustered) alkene dimerization TS.10,12 In contrast to alkanol dehydration, where the proton stabilizes clusters in the IS that inhibit rates, alternative cases may describe situations where the IS is a neutral moiety that becomes protonated at the TS, and thus solvation within a cluster preferentially stabilizes the more highly-charged TS and increases the rate. Examples of such systems are found in electrochemistry, such as in proton transfer or concerted proton-electron transfer steps.28 Overall, molecular clustering offers a mechanism to influence reactivity, and to provide hypothesis-driven models and generate intuition about the structure of clusters and their consequences for reactivity.
The formation of extended networks can lead to non-ideal thermodynamic behavior that often becomes superimposed on changes in clustered structures. The influence of extended solvent networks can be quantified by non-ideal activity coefficients obtained experimentally by the approach outlined on H-Beta zeolites in our prior work53 and by Liu et al.78 on CO-covered Ru surfaces, in which the identification of kinetic regimes prior to and including the formation of solvent networks enables quantifying activity coefficients. These approaches require the ability to systematically vary solvent coverages during kinetic measurements and to connect them to spectroscopic data and theoretical calculations that corroborate proposals for the identity of the clustered and networked structures. Conceptually analogous approaches have been used in electrochemical systems, where the size of water domains at the electrode interface was systematically varied within an organic cosolvent.28 The quantification of IS and TS activity coefficients via experimental kinetic measurements creates opportunities for theory to develop detailed models of relevant solvent structures and solvated reaction coordinates that may provide the foundation for predictive models of activity coefficient relationships that are validated by experimental data. The use of advanced theoretical methods such as AIMD, augmented by metadynamics and umbrella sampling techniques, will aid in assessing the thermodynamic subtleties of confined solvent structure and reaction dynamics within porous materials, such as the consequences of anharmonicity for IS and TS entropies.92
Our prior study53 represents only a small portion of the catalyst design space that can be explored to influence extended solvent networks and their effects on non-ideal thermodynamic behavior. The influence of pore size and shape on the activity coefficients that reflect the reorganization of solvent networks to accommodate IS and TS structures is relatively unexplored within a broad range of zeolite topologies and for different chemistries. Furthermore, the confining voids of zeolites are a “solid solvent” that enforces the specific positioning of active sites, reacting moieties, and solvent molecules. Thus, specific interactions provided by moieties associated with the zeolite lattice, such as the polarity introduced by Si–OH and Si–O(H)–Al groups and which varies with their density and arrangement,18,74 can be leveraged to influence the structure and reorganization of solvent networks. Work by Eckstein et al.17 shows that the density of H+(H2O)n influences activity coefficients, prompting further questions about whether their local proximity or the arrangement of the lattice Al sites that bind H+(H2O)n may also play a role. A related question concerns the length scales over which solvent networks can influence the thermodynamics of IS and TS. Long-range interactions may be sensitive to crystal-scale structural properties such as the degree of crystallinity or faulting,93 or the presence of less ordered94,95 or hierarchical pore structures. The design of porous materials to direct the structure and arrangement of solvent and charge networks offers promise to exert more precise control over reactivity through differences in the stabilization of kinetically relevant IS and TS moieties.
In conclusion, we affirm that quantitative kinetic descriptions of catalytic behavior continue to serve as an indispensable tool to navigate research efforts intended to model and predict the effects of solvation within porous materials, and to implement such knowledge in the development of new catalytic chemistries. Collaborations between experimental researchers and theoreticians can accelerate such research efforts by providing complementary insights into, and more precise definitions of, the distinct mechanistic origins of “solvent effects” in catalysis. Quantitative knowledge of the rate constants and thermodynamic activities that describe the IS and TS structures prevalent during catalysis are essential components of the foundation to support the aspirational goal of designing—rather than discovering—catalysts for their intended purpose.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The authors acknowledge financial support by the National Science Foundation DMREF program (1922173-CBET). We thank Brandon L. Foley, James W. Harris, and David L. Bruns for helpful technical discussions and their careful review of this manuscript.References
- Y. Román-Leshkov and M. E. Davis, ACS Catal., 2011, 1, 1566–1580 CrossRef
.
- T. Ennaert, J. V. Aelst, J. Dijkmans, R. D. Clercq, W. Schutyser, M. Dusselier, D. Verboekend and B. F. Sels, Chem. Soc. Rev., 2016, 45, 584–611 RSC
.
- H. Y. Luo, J. D. Lewis and Y. Román-Leshkov, Annu. Rev. Chem. Biomol. Eng., 2016, 7, 663–692 CrossRef CAS
.
- P. Sudarsanam, E. Peeters, E. V. Makshina, V. I. Parvulescu and B. F. Sels, Chem. Soc. Rev., 2019, 48, 2366–2421 RSC
.
- R. J. Saxton, Top. Catal., 1999, 9, 43–57 CrossRef CAS
.
- C. Perego, A. Carati, P. Ingallina, M. A. Mantegazza and G. Bellussi, Appl. Catal., A, 2001, 221, 63–72 CrossRef CAS
.
- A. Corma, L. T. Nemeth, M. Renz and S. Valencia, Nature, 2001, 412, 423–425 CrossRef CAS
.
- J. P. G. Pater, P. A. Jacobs and J. A. Martens, J. Catal., 1998, 179, 477–482 CrossRef CAS
.
- Y. T. Kim, J. P. Chada, Z. Xu, Y. J. Pagan-Torres, D. C. Rosenfeld, W. L. Winniford, E. Schmidt and G. W. Huber, J. Catal., 2015, 323, 33–44 CrossRef CAS
.
- I. Agirrezabal-Telleria and E. Iglesia, J. Catal., 2017, 352, 505–514 CrossRef CAS
.
- I. Agirrezabal-Telleria, I. Luz, M. A. Ortuño, M. Oregui-Bengoechea, I. Gandarias, N. López, M. A. Lail and M. Soukri, Nat. Commun., 2019, 10, 2076 CrossRef
.
- I. Agirrezabal-Telleria and E. Iglesia, J. Catal., 2020, 389, 690–705 CrossRef CAS
.
- N. S. Gould and B. Xu, Chem. Sci., 2018, 9, 281–287 RSC
.
- C. Paolucci, I. Khurana, A. A. Parekh, S. Li, A. J. Shih, H. Li, J. R. D. Iorio, J. D. Albarracin-Caballero, A. Yezerets, J. T. Miller, W. N. Delgass, F. H. Ribeiro, W. F. Schneider and R. Gounder, Science, 2017, 357, 898–903 CrossRef CAS
.
- K. T. Dinh, M. M. Sullivan, K. Narsimhan, P. Serna, R. J. Meyer, M. Dincă and Y. Román-Leshkov, J. Am. Chem. Soc., 2019, 141, 11641–11650 CrossRef CAS
.
- R. Y. Brogaard, M. Kømurcu, M. M. Dyballa, A. Botan, V. Van Speybroeck, U. Olsbye and K. De Wispelaere, ACS Catal., 2019, 9, 5645–5650 CrossRef CAS
.
- S. Eckstein, P. H. Hintermeier, R. Zhao, E. Baráth, H. Shi, Y. Liu and J. A. Lercher, Angew. Chem., Int. Ed., 2019, 58, 3450–3455 CrossRef CAS
.
- A. J. Hoffman, J. S. Bates, J. R. Di Iorio, S. V. Nystrom, C. T. Nimlos, R. Gounder and D. Hibbitts, Angew. Chem., Int. Ed., 2020, 59, 18686–18694 CrossRef CAS
.
- E. Iglesia, Appl. Catal., A, 1997, 161, 59–78 CrossRef CAS
.
- A. K. Dalai, T. K. Das, K. V. Chaudhari, G. Jacobs and B. H. Davis, Appl. Catal., A, 2005, 289, 135–142 CrossRef CAS
.
- D. D. Hibbitts, B. T. Loveless, M. Neurock and E. Iglesia, Angew. Chem., Int. Ed., 2013, 52, 12273–12278 CrossRef CAS
.
- F. Anaya and D. E. Resasco, ACS Catal., 2020, 10, 4433–4443 CrossRef CAS
.
- F. Zhang and H. Li, Chem. Sci., 2014, 5, 3695–3707 RSC
.
- N. Dubouis and A. Grimaud, Chem. Sci., 2019, 10, 9165–9181 RSC
.
- M. T. M. Koper, Chem. Sci., 2013, 4, 2710–2723 RSC
.
- Z.-Q. Zhang, S. Banerjee, V. S. Thoi and A. Shoji Hall, J. Phys. Chem. Lett., 2020, 11, 5457–5463 CrossRef CAS
.
- X. Yang, J. Nash, N. Oliveira, Y. Yan and B. Xu, Angew. Chem., Int. Ed., 2019, 58, 17718–17723 CrossRef CAS
.
- N. Dubouis, A. Serva, R. Berthin, G. Jeanmairet, B. Porcheron, E. Salager, M. Salanne and A. Grimaud, Nat. Catal., 2020, 3, 656–663 CrossRef CAS
.
- F. Garczarek and K. Gerwert, Nature, 2005, 439, 04231 Search PubMed
.
- P. W. Snyder, M. R. Lockett, D. T. Moustakas and G. M. Whitesides, Eur. Phys. J.: Spec. Top., 2014, 223, 853–891 Search PubMed
.
- J. Åqvist, M. Kazemi, G. V. Isaksen and B. O. Brandsdal, Acc. Chem. Res., 2017, 50, 199–207 CrossRef
.
- J. Canivet, A. Fateeva, Y. Guo, B. Coasne and D. Farrusseng, Chem. Soc. Rev., 2014, 43, 5594–5617 RSC
.
- H. Kim, S. Yang, S. R. Rao, S. Narayanan, E. A. Kapustin, H. Furukawa, A. S. Umans, O. M. Yaghi and E. N. Wang, Science, 2017, 356, 430–434 CrossRef CAS
.
- H. Wang, M. Park, R. Dong, J. Kim, Y.-K. Cho, T. Tlusty and S. Granick, Science, 2020, 369, 537–541 CrossRef CAS
.
- V. A. Roytman and D. A. Singleton, J. Am. Chem. Soc., 2020, 142, 12865–12877 CrossRef CAS
.
- M. Boudart, Chem. Rev., 1995, 95, 661–666 CrossRef CAS
.
- C. Eckert and M. Boudart, Chem. Eng. Sci., 1963, 18, 144–147 CAS
.
- B. L. Foley and A. Bhan, J. Catal., 2020, 384, 231–251 CrossRef CAS
.
- C. Stegelmann, A. Andreasen and C. T. Campbell, J. Am. Chem. Soc., 2009, 131, 8077–8082 CrossRef CAS
.
- R. J. Madon and E. Iglesia, J. Mol. Catal. A: Chem., 2000, 163, 189–204 CrossRef CAS
.
- M. J. Cordon, J. W. Harris, J. C. Vega-Vila, J. S. Bates, S. Kaur, M. Gupta, M. E. Witzke, E. C. Wegener, J. T. Miller, D. W. Flaherty, D. D. Hibbitts and R. Gounder, J. Am. Chem. Soc., 2018, 140, 14244–14266 CrossRef CAS
.
- M. C. Allen, A. J. Hoffman, T. Liu, M. S. Webber, D. Hibbitts and T. J. Schwartz, ACS Catal., 2020, 10, 6771–6785 CrossRef CAS
.
- J. R. Di Iorio, C. T. Nimlos and R. Gounder, ACS Catal., 2017, 7, 6663–6674 CrossRef CAS
.
- J. R. Di Iorio, A. J. Hoffman, C. T. Nimlos, S. Nystrom, D. Hibbitts and R. Gounder, J. Catal., 2019, 380, 161–177 CrossRef CAS
.
- J. S. Bates and R. Gounder, J. Catal., 2020, 390, 178–183 CrossRef
.
- A. J. Jones, S. I. Zones and E. Iglesia, J. Phys. Chem. C, 2014, 118, 17787–17800 CrossRef CAS
.
- R. Gounder, A. J. Jones, R. T. Carr and E. Iglesia, J. Catal., 2012, 286, 214–223 CrossRef CAS
.
- Y. Zhi, H. Shi, L. Mu, Y. Liu, D. Mei, D. M. Camaioni and J. A. Lercher, J. Am. Chem. Soc., 2015, 137, 15781–15794 CrossRef CAS
.
- A. Zecchina, F. Geobaldo, G. Spoto, S. Bordiga, G. Ricchiardi, R. Buzzoni and G. Petrini, J. Phys. Chem., 1996, 100, 16584–16599 CrossRef CAS
.
- M. Krossner and J. Sauer, J. Phys. Chem., 1996, 100, 6199–6211 CrossRef CAS
.
- A. Vjunov, M. Wang, N. Govind, T. Huthwelker, H. Shi, D. Mei, J. L. Fulton and J. A. Lercher, Chem. Mater., 2017, 29, 9030–9042 CrossRef CAS
.
- M. Wang, N. R. Jaegers, M.-S. Lee, C. Wan, J. Z. Hu, H. Shi, D. Mei, S. D. Burton, D. M. Camaioni, O. Y. Gutiérrez, V.-A. Glezakou, R. Rousseau, Y. Wang and J. A. Lercher, J. Am. Chem. Soc., 2019, 141, 3444–3455 CrossRef CAS
.
- J. S. Bates, B. C. Bukowski, J. Greeley and R. Gounder, Chem. Sci., 2020, 11, 7102–7122 RSC
.
- P. Liu and D. Mei, J. Phys. Chem. C, 2020, 124, 22568–22576 CrossRef CAS
.
- N. S. Gould and B. Xu, J. Catal., 2018, 358, 80–88 CrossRef CAS
.
- N. S. Gould, S. Li, H. J. Cho, H. Landfield, S. Caratzoulas, D. Vlachos, P. Bai and B. Xu, Nat. Commun., 2020, 11, 1–13 Search PubMed
.
- M. A. Mellmer, C. Sener, J. M. R. Gallo, J. S. Luterbacher, D. M. Alonso and J. A. Dumesic, Angew. Chem., Int. Ed., 2014, 53, 11872–11875 CrossRef CAS
.
- M. A. Mellmer, C. Sanpitakseree, B. Demir, P. Bai, K. Ma, M. Neurock and J. A. Dumesic, Nat. Catal., 2018, 1, 199–207 CrossRef CAS
.
- T. W. Walker, A. K. Chew, H. Li, B. Demir, Z. C. Zhang, G. W. Huber, R. C. V. Lehn and J. A. Dumesic, Energy Environ. Sci., 2018, 11, 617–628 RSC
.
- D. Mei and J. A. Lercher, AIChE J., 2017, 63, 172–184 CrossRef CAS
.
- J. F. Haw, T. Xu, J. B. Nicholas and P. W. Goguen, Nature, 1997, 389, 832–835 CrossRef CAS
.
- K. Chen, J. Damron, C. Pearson, D. Resasco, L. Zhang and J. L. White, ACS Catal., 2014, 4, 3039–3044 CrossRef CAS
.
- K. Chen, A. Gumidyala, M. Abdolrhamani, C. Villines, S. Crossley and J. L. White, J. Catal., 2017, 351, 130–135 CrossRef CAS
.
- D. Mei and J. A. Lercher, J. Phys. Chem. C, 2019, 123, 25255–25266 CrossRef CAS
.
- Y. Liu, A. Vjunov, H. Shi, S. Eckstein, D. M. Camaioni, D. Mei, E. Baráth and J. A. Lercher, Nat. Commun., 2017, 8, 14113 CrossRef
.
- H. Shi, S. Eckstein, A. Vjunov, D. M. Camaioni and J. A. Lercher, Nat. Commun., 2017, 8, 15442 CrossRef
.
- S. Eckstein, P. H. Hintermeier, M. V. Olarte, Y. Liu, E. Baráth and J. A. Lercher, J. Catal., 2017, 352, 329–336 CrossRef CAS
.
- P. H. Hintermeier, S. Eckstein, D. Mei, M. V. Olarte, D. M. Camaioni, E. Baráth and J. A. Lercher, ACS Catal., 2017, 7, 7822–7829 CrossRef CAS
.
- L. Milakovic, P. H. Hintermeier, Q. Liu, H. Shi, Y. Liu, E. Baráth and J. A. Lercher, J. Catal., 2020, 390, 237–243 CrossRef CAS
.
- L. Qi, R. Alamillo, W. A. Elliott, A. Andersen, D. W. Hoyt, E. D. Walter, K. S. Han, N. M. Washton, R. M. Rioux, J. A. Dumesic and S. L. Scott, ACS Catal., 2017, 7, 3489–3500 CrossRef CAS
.
- D. T. Bregante, A. M. Johnson, A. Y. Patel, E. Z. Ayla, M. J. Cordon, B. C. Bukowski, J. Greeley, R. Gounder and D. W. Flaherty, J. Am. Chem. Soc., 2019, 141, 7302–7319 CrossRef CAS
.
- D. T. Bregante and D. W. Flaherty, ACS Catal., 2019, 9, 10951–10962 CrossRef CAS
.
- K. B. Sravan Kumar, T. N. Whittaker, C. Peterson, L. C. Grabow and B. D. Chandler, J. Am. Chem. Soc., 2020, 142, 5760–5772 CrossRef CAS
.
- B. C. Bukowski, J. S. Bates, R. Gounder and J. Greeley, Angew. Chem., Int. Ed., 2019, 58, 16422–16426 CrossRef CAS
.
- N. Desbiens, I. Demachy, A. H. Fuchs, H. Kirsch-Rodeschini, M. Soulard and J. Patarin, Angew. Chem., Int. Ed., 2005, 44, 5310–5313 CrossRef CAS
.
- J. R. Di Iorio, B. A. Johnson and Y. Román-Leshkov, J. Am. Chem. Soc., 2020, 142, 19379–19392 CrossRef CAS
.
- A. J. Rieth, K. M. Hunter, M. Dincă and F. Paesani, Nat. Commun., 2019, 10, 4771 CrossRef
.
- J. Liu, D. Hibbitts and E. Iglesia, J. Am. Chem. Soc., 2017, 139, 11789–11802 CrossRef CAS
.
- T. J. Wilke and M. A. Barteau, J. Catal., 2020, 382, 286–294 CrossRef CAS
.
- G. Li, B. Wang, B. Chen and D. E. Resasco, J. Catal., 2019, 377, 245–254 CrossRef CAS
.
- Z. Zhao, R. Bababrik, W. Xue, Y. Li, N. M. Briggs, D.-T. Nguyen, U. Nguyen, S. P. Crossley, S. Wang, B. Wang and D. E. Resasco, Nat. Catal., 2019, 2, 431–436 CrossRef CAS
.
- D. Muñoz-Santiburcio, M. F. Camellone and D. Marx, Angew. Chem., Int. Ed., 2018, 57, 3327–3331 CrossRef
.
- G. Li, B. Wang and D. E. Resasco, ACS Catal., 2020, 10, 5373–5382 CrossRef CAS
.
- E. G. Derouane, J. Mol. Catal. A: Chem., 1998, 134, 29–45 CrossRef CAS
.
- R. Gounder and E. Iglesia, Chem. Commun., 2013, 49, 3491–3509 RSC
.
- F. Sebastiani, T. A. Bender, S. Pezzotti, W.-L. Li, G. Schwaab, R. G. Bergman, K. N. Raymond, F. D. Toste, T. Head-Gordon and M. Havenith, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 32954–32961 CrossRef CAS
.
- W. Zhang, G. Cheng, G. L. Haller, Y. Liu and J. A. Lercher, ACS Catal., 2020, 10, 13371–13376 CrossRef CAS
.
- T. J. H. Vlugt, R. Krishna and B. Smit, J. Phys. Chem. B, 1999, 103, 1102–1118 CrossRef CAS
.
- P. Bai, M. Tsapatsis and J. I. Siepmann, Langmuir, 2012, 28, 15566–15576 CrossRef CAS
.
- R. F. DeJaco, P. Bai, M. Tsapatsis and J. I. Siepmann, Langmuir, 2016, 32, 2093–2101 CrossRef CAS
.
- J. W. Harris, J. S. Bates, B. C. Bukowski, J. Greeley and R. Gounder, ACS Catal., 2020, 10, 9476–9495 CrossRef CAS
.
- G. Collinge, S. F. Yuk, M.-T. Nguyen, M.-S. Lee, V.-A. Glezakou and R. Rousseau, ACS Catal., 2020, 10, 9236–9260 CrossRef CAS
.
- J. S. Bates, B. C. Bukowski, J. W. Harris, J. Greeley and R. Gounder, ACS Catal., 2019, 9, 6146–6168 CrossRef CAS
.
- D. Jo, J. Zhao, J. Cho, J. H. Lee, Y. Liu, C. Liu, X. Zou and S. B. Hong, Angew. Chem., Int. Ed., 2020, 59, 17691–17696 CrossRef CAS
.
- J. P. S. Mowat, M. A. Miller, M. M. Galey, W. Sinkler, S. Prabhakar, L. Xu, C. L. Nicholas and C. P. Nicholas, Chem.–Eur. J., 2018, 24, 17779–17787 CrossRef CAS
.
| This journal is © The Royal Society of Chemistry 2021 |