Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Ruddlesden Popper 2D perovskites as Li-ion battery electrodes†
Angus
Mathieson
 abc,
Mohammad
Rahil‡
d,
Youcheng
Zhang‡
bc,
Wesley M.
Dose
abc,
Mohammad
Rahil‡
d,
Youcheng
Zhang‡
bc,
Wesley M.
Dose
 ae,
Jung Tae
Lee
f,
Felix
Deschler
*g,
Shahab
Ahmad
ae,
Jung Tae
Lee
f,
Felix
Deschler
*g,
Shahab
Ahmad
 *d and
Michael
De Volder
*d and
Michael
De Volder
 *a
*a
aInstitute for Manufacturing, Department of Engineering, University of Cambridge, 17 Charles Babbage Rd, Cambridge, CB3 0FS, UK. E-mail: mfld2@cam.ac.uk
bCavendish Laboratories, Department of Physics, University of Cambridge, 17 JJ Thomson Ave, Cambridge, CB3 0HE, UK
cCambridge Graphene Centre, Department of Engineering, University of Cambridge, 9 JJ Thomson Ave, Cambridge, CB3 0HE, UK
dAdvanced Energy Materials Group, Department of Physics, Indian Institute of Technology Jodhpur, 342037 Jodhpur, Rajasthan, India. E-mail: shahab@iitj.ac.in
eDepartment of Chemistry, University of Cambridge, Lensfield Road, Cambridge, CB2 1EW, UK
fDepartment of Plant & Environmental New Resources, College of Life Science, Kyung Hee University, 1732 Deogyeong-daero, Republic of Korea
gWalter Schottky Institut, Fakultät für Physik, 458, Technische Universität München, 85748 Garching bei 459, München, Germany. E-mail: felix.deschler@wsi.tum.de
First published on 7th April 2021
Abstract
Hybrid metal halide perovskites, typically known for their photovoltaic applications, have recently gained traction as a potential energy-storage material due to their promising gravimetric capacities as lithium-ion battery electrode materials. Here we investigate the effect of tuning the layering properties of the quasi two-dimensional Ruddlesden Popper (RP) layered perovskite series (BA)2(MA)n−1PbnX3n+1 (BA – butylammonium, MA – methylammonium, X – halide (I− and Br−)) from n = 1 to n = 4 and the equivalent bulk crystal structure MAPbX3. The interaction between the insertion of lithium ions and the layering arrangement of the perovskite structure are studied electrochemically and compared to a reported three-stage energy storage mechanism in bulk perovskites. The layering structure that optimises both capacity and stability is determined to be n = 4, providing a compromise between the number of active layers and the lithium ion access between them provided by the BA organic chain, thus demonstrating initial and stabilised gravimetric capacities of 575.5 mA h g−1 and 89.9 mA h g−1 respectively. The effect of changing the halide within the perovskite structure is investigated and demonstrates a greater gravimetric capacity for the lighter bromide species compared to the commonly used iodide. Finally, high molarity electrolytes and tailored cut-off potentials are used to improve the stability of the RP layered perovskite electrodes.
Introduction
The importance of hybrid perovskites (HPs) as photovoltaic technologies1,2 is well-established. Not only are they capable of achieving standalone photovoltaic power conversion efficiencies (PCEs) of 25%,3 but are also predicted to be able to bolster the performance of existing semiconductor technologies up to 32% PCE4 in tandem configurations. A plethora of further technologies such as light-emitting diodes (LEDs),5,6 lasers7 and photodetectors8 have also benefited from the utilisation of hybrid perovskite materials, owing in part to the large number of different compositions in the perovskite portfolio and their relative ease of fabrication. The effect of altering the perovskite composition to tune the optical properties has been well studied,9 for instance by changing the halide content and the choice of organic cations.10–13In 2015, Xia et al.14 first reported that HPs can be used as an anode material in Li-ion batteries (LIBs), and compared the gravimetric capacities of methylammonium (MA) lead bromide (MAPbBr3) and methylammonium lead iodide (MAPbI3), synthesised using a hydrothermal method and yielding gravimetric capacities of 121 mA h g−1 initially and 9 mA h g−1 after 200 cycles respectively. Higher gravimetric discharge capacities have subsequently been reported by Tathavadekar et al.15 for the one-dimensional (1D) benzidine lead iodide with needle-like morphology of 646 mA h g−1, 508 mA h g−1 for the two-dimensional (2D) layered butylammonium (BA) lead iodide (BAPbI4), and 202 mA h g−1 for the traditional MAPbI3 bulk phase after 50 cycles. While these capacities are promising, particularly compared to commercial graphite anodes (theoretical capacity of 372 mA h g−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ),16 relatively little attention and resource have been dedicated to the further development of this application due to the unstable behaviour of hybrid perovskites in the Li-ion battery environment.17–19 Consequently, the composition-function and structure–function relationships for hybrid perovskite electrodes remain poorly understood.
),16 relatively little attention and resource have been dedicated to the further development of this application due to the unstable behaviour of hybrid perovskites in the Li-ion battery environment.17–19 Consequently, the composition-function and structure–function relationships for hybrid perovskite electrodes remain poorly understood.
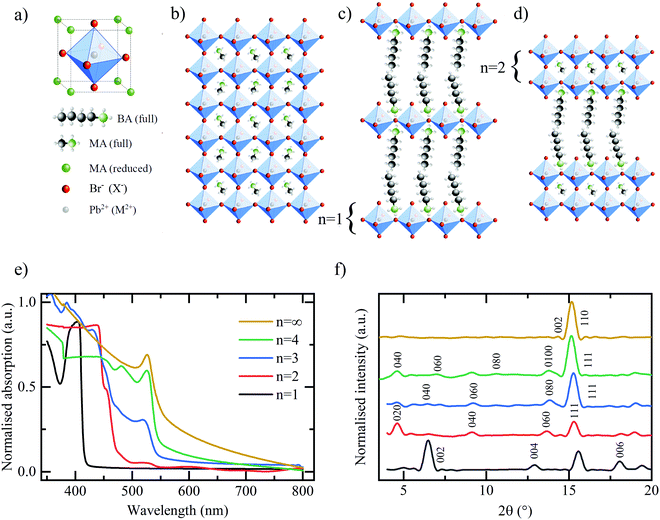
A conventional, hybrid bulk perovskite with the formula MAPbX3 (where MA – methylammonium, Pb – divalent lead cation, X – halide) comprises the unit cell shown in Fig. 1(a). A central divalent cation (in this example Pb2+) has six-fold coordination with a halide anion (in this case I− or Br−) forming the octahedral cage as shown. This in turn is surrounded by the secondary, organic cation (in this example MA+) exhibiting cubic symmetry. The resultant crystal structure is shown in Fig. 1(b). Quasi two-dimensional RP layered perovskites are formed by introducing an organic cationic chain of greater length than the MA, such as the butylammonium (BA) used in this work, resulting in a final composition described by (BA)2(MA)n−1MnX3n+1.13,20,21 In doing so, since the longer chain is now unable to populate the space between the lead-halide octahedra in its standard configuration, the corner-sharing octahedra are forced apart, thus forming a layered quasi-2D structure as shown in Fig. 1(c). The individual layers of (MA)n−1PbnX3n+1 may be thought of as being isolated both physically and electronically from one another by the intercalating BA cation.22 By varying the stoichiometric ratio of the BA:MA during the perovskite synthesis it is possible to vary the number of (MA)n−1PbnX3n+1 in each layer. The extreme case of n = 1 is shown in Fig. 1(c) and an intermediate stage n = 2 in Fig. 1(d). Therefore, the RP family of compounds provides a rich collection of building blocks with which to tune the composition and structure for optimal performance, but also to gain insight into how these properties affect the lithium ion storage mechanism in these materials.
Recent studies18,23 indicate that the lithium insertion into hybrid perovskites can be broken down into three main processes, which are summarised below. All subsequent potentials herein are with reference to the Li/Li+ redox couple.
(I) Between 2.1 V and 1.5 V, lithium ion insertion into the perovskite structure takes place, with charge compensation by the reduction of the Pb2+ cation.17 It has been suggested that at the end of this stage both the original perovskite phase and a lithiated perovskite phase coexist.
(II) A conversion reaction occurs at ∼1.4 V, resulting in the decomposition of the perovskite structure and the likely formation of lithium halide, an organic halide product, and metallic Pb.17,24
(III) Below 1.0 V a multi-stage, (partially) reversible alloy reaction between lithium and metallic lead takes place. Given the irreversible nature of the conversion reaction in step II, the lead alloying/dealloying reactions are proposed to be the only source of reversible capacity for hybrid perovskite anodes.
In this paper, we systematically investigate the effect of changing the number of inorganic lead-halide sheets (i.e. n) on the electrochemical performance of bromide- and iodide-based RP perovskites of type (BA)2(MA)n−1MnX3n+1, for n = 1, 2, 3, 4, ∞, and find that an optimum performance point, referring to both maximum capacity and capacity retention, is reached at n = 4, indicating a compromise between lead content and packing structure in addition to a better gravimetric performance from the lighter Br− halide systems. Furthermore, methods to maintain the perovskite structure are explored by modification of the cycling potential window, i.e. cutting-off the discharge cycle at 1.8 V vs. Li/Li+ in order to prevent the irreversible conversion reaction in step II, whilst maintaining the upper potential of 2.8 V vs. Li/Li+. In this way, we assess the intrinsic reversibility of 2D hybrid perovskites with regards to lithium insertion/extraction.
Results and discussion
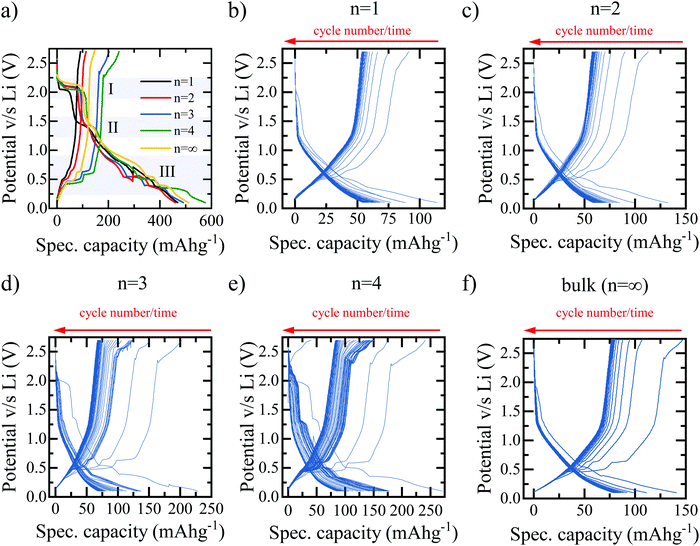
The hybrid perovskite materials are characterised using a combination of UV-vis absorption and X-ray diffraction (XRD) spectroscopy to confirm the characteristic shifts in the bandgap and crystallographic spacing associated with the layering order of the RP perovskite series. The UV-vis absorption spectra in Fig. 1(e) demonstrates the expected shift in bandgap absorption from ∼400 nm for the purely 2D (BA)2PbBr4 through to ∼550 nm for the bulk MAPbBr3 samples.13 Shared peaks and similarities between the spectra, particularly for the n = 2, 3, 4 phases, indicates a lack of perfect phase purity. This is confirmed by the corresponding photoluminescence (PL) spectra shown in Fig. S1 (ESI†). Despite containing the correct stoichiometric ratios of MA:BA:PbBr2 the method of preparation required for LIB electrode deposition does not meet the strict protocol that allows for the formation of perfect phase-purity – specifically the lack of substrate surface control and annealing temperature.25 However, the clear colour changes between samples, as shown in Fig. S2 (ESI†) in conjunction with the observed differences in absorption spectra and PL emission, provide adequate confidence that the dominant structures in the electrodes are that of the desired RP phase and layering number. The XRD spectra in Fig. 1(f) confirm the clear, out-of-plane 〈002〉 layering peak expected of the 2D n = 1 (BA)2PbBr4 and corresponding shifts of the 〈0k0〉 peaks for the n = 2, 3, 4 samples. Finally, the XRD spectra for the bulk MAPbBr3 confirms the expected 3D simple cubic structure associated with this species.26Fig. 2 shows the galvanostatic charge–discharge curves for the first 100 cycles of the bromide based layered perovskites. The first discharge and charge cycles for the layered perovskite series from n = 1 to n = 4 are shown in Fig. 2(a). The overall profile is consistent between samples insofar as it may be broken down into three distinct regions – in accordance with the findings of previous work.23 First, a discharge plateau is observed in all samples at ∼2.1 V believed to correspond to the initial lithium ion insertion into the perovskite structure. Although the potential at which this mechanism occurs is roughly consistent across the samples, the capacity associated with the insertion is observed to increase with an increasing number of layers (n-value) of MAn−1PbnBr3n+1 between the BA separator layer. Therefore, it may be concluded that a greater number of lead-bromide octahedra facilitates the insertion of a greater number of lithium ions into the perovskite structure. This would indicate that the lithium ions preferentially intercalate into the sheets of the layered perovskite, where there are more active sites for the lithium to insert, and not into the space provided by the larger organic cation. There appears no consistent trend with the capacity associated with the second process – the conversion reaction – as a function of the perovskite layering number.
The final stage of the mechanism, occurring below 1.0 V in all five samples and comprising multiple plateaus, is that of the multistage alloying reactions between the metallic lead formed in the conversion reaction and lithium ions18,19,23 – these reactions are summarised in Table S1 (ESI†).27,28 The combined capacity associated with this mechanism is observed to increase with the layering n-number, from 109.8 mA h g−1 for n = 1 to 202.1 mA h g−1 for n = ∞. This can be explained, at least in part, by the larger proportion of lead per unit of mass present in (BA)2(MA)n−1PbnBr3n+1 perovskites with a larger n-value.
Cycles from 2 to 100 for each material are shown in Fig. 2(b)–(f), with Fig. 2(b)–(e) corresponding to an increasing number of lead-bromide octahedra between the BA organic spacer cation from n = 1 to n = 4 respectively, and Fig. 2(f) corresponding to the bulk perovskite MAPbBr3 – which represents the n = ∞ limit. It is clear that in all cases, the discharge and charge curves vary both in profile and capacity from the first cycle. The prominence of each individual plateau is reduced compared to the first discharge cycle indicating that it is indeed likely that the conversion reaction at 1.5 V changes the crystal structure of perovskite irreversibly and therefore limits the utilisation of the insertion and conversion mechanisms to the first cycle only.
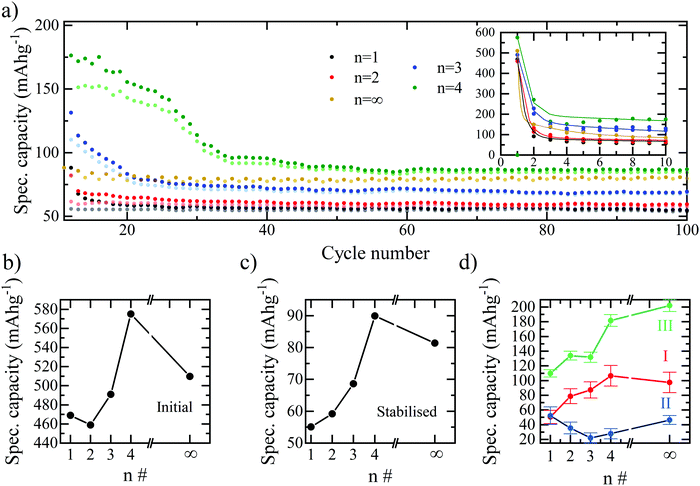
The combined effect is that both the initial discharge capacity and the stabilised capacity (e.g. after 60 cycles) both increase with the number of inorganic layers, as shown in Fig. 3. The trend would imply that the greatest specific capacity should be reached by the bulk perovskite, with a larger amount of lithium insertion at the start and a greater availability of lead for the alloying reactions. However, we observe a decrease in capacity for n = ∞ relative to n = 4, therefore, it is concluded that additional effects limit the bulk perovskite from reaching its true electrochemical capability such as ionic diffusion and morphological restrictions due to the absence of the BA interlayer separator.29 If this is the case, there should exist an optimum layering structure that maximises the number of inorganic layers – which seemingly facilitate higher gravimetric capacity – with enough organic spacer layers accommodating ionic diffusion29 and structural flexibility whilst maintaining as much of the electrochemically active octahedra as possible. Based on our results, the optimum performance appears to be reached at n = 4. Configurations beyond n = 4 were not tested here due to the difficulty in achieving phase-purity of n > 4 RP structures. Furthermore, the differentiation in structural and behavioural properties in the higher layering ordered structures diminish and tend towards that of the bulk, particularly in the case of imperfect phase purity.25
The specific capacity of the bromide series plotted versus cycle number in Fig. 3a summarises the results above. Fig. 3a also accentuates an interesting effect for the n = 3 and n = 4 samples, whereby after the initial drop in capacity, following the first discharge cycle, the capacity appears to stabilise for ∼20 (n = 3) and ∼30 (n = 4) cycles before dropping again. A possible explanation for this effect is that more active sites become accessible to the lithium ions during each of the first 20–20 cycles, with the additional capacity associated with these sites offsetting the expected drop, and thus the capacity of the overall electrode is temporarily observed to remain higher. This could be due to a slow wetting process associated with the viscous, high molarity electrolyte (5 M LiTFSI). I.e. at the beginning of the cycling process, the electrolyte is not able to penetrate the entire electrode and only does so after the time allowed for the first ∼20 cycles. It is also apparent in the charge–discharge curves for the n = 3 and n = 4 samples that unlike n = 1 and n = 2, the insertion plateau at 2.1 V also appears in the second discharge curve. This could be explained by the incomplete lithiation and conversion of the perovskite occurring in the n = 3 and n = 4 samples, or again, the slow wetting process not allowing the lithiation and subsequent conversion of the entirety of the available perovskite in the first discharge cycle. Fig. 3b and c show the specific capacity trend with increasing n-number for the initial discharge and stabilised capacities, respectively. The optimal structure for both the initial discharge capacity and stabilised capacity is confirmed as n = 4. A breakdown of the capacity attributable to each of the electrochemical processes and how they are affected by the layering number is provided in Fig. 3d. As expected, the specific capacity associated with the lead-alloy reactions (process III) increases linearly with the number of layers and is therefore directly related to the lead content of the electrode. An increase from n = 1 to n = 4 is also observed for process I – the lithium intercalation – due to the increased number of active sites for lithium insertion within the structure. This drops off for n = ∞ due to the packing structure and lack of pathways to the active sites provided by the BA spacer cation and therefore a reduction in the number of insertion processes.
The same series of measurements were repeated for an iodide based RP series of n = 1 − n = 4 and the bulk structure MAPbI3. The potential profiles are shown in Fig. S4 (ESI†). The three-step mechanism is again observed with plateaus in the initial discharge cycle (Fig. S4(a), ESI†) corresponding to lithium ion insertion (∼2.1 V), conversion (∼1.4 V) and multi-stage Li–Pb alloying reactions (<1.0 V). However, the gravimetric capacities are generally lower in all cases for the iodide series compared to the bromide series. Due to the inherent differences between bromide and iodide anions (e.g. electronegativity, chemical “softness” and the resulting bond length, and unit cell size), we hypothesised that the two classes of materials would exhibit different electrochemical performance in a Li-ion battery. It is correct that the gravimetric capacity is greater in a bromide-based perovskite, however, once normalised for the differing atomic masses of the two halides, the resulting performance is comparable – as shown in Fig. S4(f) (ESI†). Therefore, it may be concluded that under identical galvanostatic cycling, the resulting performance metrics of the two halide compositions are comparable and not influenced heavily by the subtle differences afforded by the different halide content. This holds for all layering numbers, n = 1–4 and the bulk perovskite.
At a finer level of detail, there are subtle differences in the shapes of the charge–discharge curves for the two halide compositions, such as the relative durations of individual plateaus and thus their associated capacity. Unlike the bromide n = 3 and n = 4 samples, no recurrence of the plateau at 2.1 V is observed in the second discharge cycle of the equivalent iodide based cells – indicating that complete insertion and conversion was achieved in the first cycle. This may indicate that the access experienced by the lithium ions to the active material is greater in the iodide samples, which could be explained by the slightly larger lattice parameter in the iodide based perovskite compared to the bromide (∼133 pm and ∼114 pm respectively).30 Similar to the bromide series, a clear trend in both the initial discharge capacity and the stabilised capacity, with the highest capacities again achieved with n = 4, is observed for iodide series – this is summarised in Fig. S5 (ESI†).
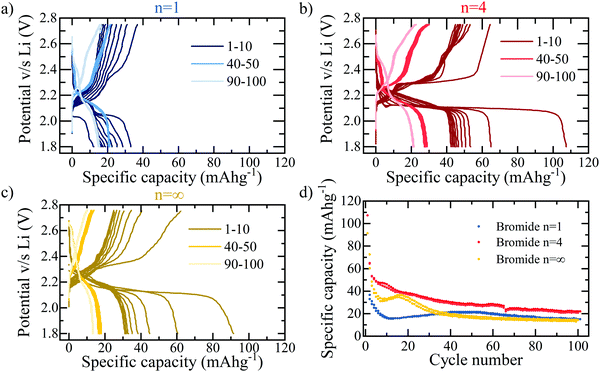
The loss in capacity after passing the conversion process at ∼1.5 V may be discouraging; however, if the cut-off voltage is adapted such that the 1.5 V threshold for conversion reactions is not passed, as shown in Fig. 4, the initial insertion reaction does show usable, reversible capacity. For the purpose of this work, this allows the study of this initial process, to develop an understanding for the lithium intercalation and interaction into hybrid perovskite structures; for commercial applications, this demonstrates a potentially feasible window of device usability, if the associated capacity is capable of being improved further. Fig. 4a and b compare the n = 1 and n = 4 bromide based layered RP perovskite respectively, cycled within a reduced potential window of 2.8–1.8 V at 30 mA g−1. It is immediately apparent that the n = 4 sample yields consistently higher capacities for the insertion reaction – with an initial discharge capacity of 108 mA h g−1 compared to the 32 mA h g−1 of n = 1. It may be concluded therefore, that the insertion reaction into the perovskite phase favours the higher stacking number, implying that the lithium ions preferentially insert into the active sites provided by the lead-halide layers rather than the organic spacer, in concurrence with previous studies.29,31
Compared to electrodes used commercially in LIBs, the coulombic efficiency of hybrid perovskite cells remains low, particularly in the first cycle (for example in n = 4, a coulombic efficiency of 60% is observed in the first cycle), even within the more stable potential window shown in Fig. 4. This is believed to be due to instability issues between the polar organic solvents present in the electrolyte and the perovskite active material. Using a 1 M LiPF6 (in ethylene carbonate/dimethyl carbonate) (LP30) electrolyte demonstrates this to a great extent with a colour change associated with the dissolution of the perovskite into the lead-halide precursor visible to eye within 30 seconds of contact. Although such dramatic and immediate results are not observed for the 5 M electrolyte used in this work, the dissolution process, although much slower will still be present. The resulting electrochemical performance of cells using 1 M LP30 electrolyte is predictably very poor. However, in this work the stability has been dramatically improved by increasing the molar concentration of the electrolyte to 5 M, thereby reducing the presence of free solvent into which the perovskite dissolution will take place32 and using only a minimal amount (10 μL of electrolyte solution for an electrode with active area of diameter ϕ = 12 mm), slowing down the dissolution reaction and making the electrochemical characterisation shown herein possible.
Conclusion
We demonstrate that out of the iodide and bromide based RP layered perovskite structures, an optimum composition for LIB performance (based on capacity and stability) is reached with the n = 4 bromide species (BA)2(MA)3Pb4Br13. This is believed to be due to reaching a suitable compromise between the number of electrochemically active layers (which increases with the amount of (MA)n−1PbnBr3n+1 per unit mass) and the spacing between layers facilitating adequate ionic migration of the lithium ions to access the active material – provided by the spacer BA cations. Further, we show how the choice of halide species plays an important role in the overall gravimetric performance of hybrid perovskite electrodes, with bromide based perovskites establishing a better overall gravimetric capacity, due to bromide's inherently lower atomic mass. An irreversible conversion reaction occurring at 1.4 V during the first discharge cycle is avoided by choosing a reduced potential window of 2.8–1.8 V and allows the testing of the first electrochemical process at 2.1 V as the main source of reversible lithium storage. Again, an optimal structure is reached at n = 4, demonstrating an initial discharge capacity of 108 mA h g−1 compared to 32 mA h g−1 for the n = 1 structure coupled with an improved reversibility. A significant contribution to the poor coulombic efficiencies of the hybrid perovskite electrodes could be attributed to the presence of organic solvents in the battery electrolyte and a step forward in mitigating this issue is made in this work with the use of a high molarity electrolyte.Methods
Perovskite synthesis
Powders of the various perovskites studied in this report were prepared by using a slow evaporation technique. First, solutions of Ruddlesden–Popper hybrid perovskites were prepared by mixing stoichiometric amounts of the precursor powders in dimethylformamide (DMF) under an argon atmosphere. The precursors are listed in Table S2 (ESI†) for reference. The resulting solutions were stirred using a magnetic stirrer at 70 °C for 1 hour to ensure total and homogeneous dissolution. After cooling, the solution was transferred to a vacuum oven and dried overnight at 60 °C. The powder precipitate was collected and stored again under an argon atmosphere. At this stage, the powders exhibited vivid colours depending on the relevant band gap of each composition, as shown in Fig. S2 (ESI†).Electrolyte solution preparation
A high concentration electrolyte was synthesised by adding 5 M of bistrifluoromethanesulfonimide lithium (LiTFSI) salt (Sigma Aldrich >99%) to 1 mL of ethylene carbonate (EC) (Sigma Aldrich) and propylene carbonate (PC) (Sigma Aldrich) in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 vol ratio. The solution was stirred magnetically for 4 days prior to usage to ensure total dissolution of the LiTFSI salt.
1 vol ratio. The solution was stirred magnetically for 4 days prior to usage to ensure total dissolution of the LiTFSI salt.
Electrode fabrication
Electrode fabrication was undertaken in an argon atmosphere with H2O and O2 < 0.5 ppm. The electrode slurry consisted of 85 wt% as prepared perovskite powder, 5 wt% polyvinylidene difluoride (PVDF, Arco Ltd) binder, and 10 wt% conductive carbon (Super-P, Alfa Aesar), and was produced stepwise, as follows. The perovskite powder was added to anhydrous N-methyl-2-pyrrolidone (NMP, Sigma Aldrich) into which it re-dissolved. The PVDF binder was then added and the solution stirred magnetically overnight to ensure homogeneity. Finally, the Super-P was added and the resulting solution was sonicated for 3 hours in an ultrasonic bath. The solution was then used to deposit perovskite electrodes by drop casting on pre-cut circular (ϕ = 12 mm diameter) copper foil. 6.3 μL of solution was dropped, corresponding to a mass loading of 0.36 mg cm−2 of active material. After drop casting, the as coated electrodes were annealed at 90 °C overnight (at least 12 h) to ensure complete removal of the NMP.Cell construction
2032 coin cells (Cambridge Energy Solutions) were fabricated under a dry, argon atmosphere (H2O and O2 < 0.5 ppm) to prevent the degradation of the hygroscopic electrolyte and lithium metal. The perovskite electrode was placed in the base of a standard coin cell casing and 5 μL of electrolyte was placed on top. Two layers of an electronically insulating, porous polymer separator (polyethylene/polypropylene, MTI) were placed on top of the electrode. After placement, 10 μL of electrolyte solution was added to wet the separators. A metallic lithium counter/reference electrode was placed on top followed by stainless steel spacers and a spring to form compression within the cell. The top casing was placed on top and the whole cell sealed by a mechanical press. A schematic representation of the final structure is shown in Fig. S9 (ESI†) where the individual components are separated for clarity.Material characterisation
To measure the crystallographic structures of the layered perovskites, XRD spectra were taken using a Bruker D8 Advance powder X-ray diffractometer. The varying size of the effective quantum wells formed by the layered perovskites were captured using UV-vis spectroscopy, using a PerkinElmer UV-vis NIR Spectrometer (Lambda 750).All electrochemical measurements were taken using a CT3001A battery cycler from Landt Instruments at 30 mA g−1 in galvanostatic charge–discharge mode.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
S. A. and M. D. V. acknowledges financial support from DST-UKIERI (DST/INT/UK/P-167/2017). S. A. acknowledge SERB-ECRA (ECR/2018/002056) and UGC Start-Up (30-422/2018 BSR) research grants. The authors acknowledge technical help by Pramod Rajput in the initial perovskite synthesis. The authors acknowledge and thank Dr Buddha Deka-Boruah for the collection of the UV-vis spectra. The authors acknowledge and thank Dr Sascha Feldmann for the collection of the PL spectra of the bromide-based species. A. M. acknowledges support from the EPSRC Graphene CDT EP/L016087/1. F. D. acknowledges funding from the Winton Program for the Physics of Sustainability and the DFG Emmy Noether Program.References
- J. Huang, Y. Yuan, Y. Shao and Y. Yan, Understanding the physical properties of hybrid perovskites for photovoltaic applications, Nat. Rev. Mater., 2017, 2(7), 17042 CrossRef CAS.
- S. D. Stranks, R. L. Z. Hoye, D. Di, R. H. Friend and F. Deschler, The Physics of Light Emission in Halide Perovskite Devices, Adv. Mater., 2018, 31(9), 1803336 Search PubMed.
- M. A. Green, Y. Hishikawa, E. D. Dunlop, D. H. Levi, J. Hohl-Ebinger and A. W. Y. Ho-Baillie, Solar cell efficiency tables (version 51), Prog. Photovolt. Res. Appl., 2020, 26(1), 3–12 CrossRef.
- M. T. Hörantner and H. J. Snaith, Predicting and optimising the energy yield of perovskite-on-silicon tandem solar cells under real world conditions, Energy Environ. Sci., 2017, 10, 1983–1993 RSC.
- N. Wang, L. Cheng, R. Ge, S. Zhang, Y. Miao, W. Zou, C. Yi, Y. Sun, Y. Cao, R. Yang, Y. Wei, Q. Guo, Y. Ke, M. Yu, Y. Jin, Y. Liu, Q. Ding, D. Di, L. Yang, G. Xing, H. Tian, C. Jin, F. Gao, R. H. Friend, J. Wang and W. Huang, Perovskite light-emitting diodes based on solution-processed self-organized multiple quantum wells, Nat. Photonics, 2016, 10, 699–704 CrossRef CAS.
- S. D. Stranks and H. J. Snaith, Metal-halide perovskites for photovoltaic and light-emitting devices, Nat. Nanotechnol., 2015, 10(5), 391–402 CrossRef CAS PubMed.
- B. R. Sutherland and E. H. Sargent, Perovskite photonic sources, Nat. Photonics, 2016, 10(4), 295–302 CrossRef CAS.
- X. Hu, X. Zhang, L. Liang, J. Bao, S. Li, W. Yang and Y. Xie, High-Performance Flexible Broadband Photodetector Based on Organolead Halide Perovskite, Adv. Funct. Mater., 2014, 24(9), 7373–7380 CrossRef CAS.
- G. E. Eperon, S. D. Stranks, C. Menelaou, M. B. Johnston, L. M. Herz and H. J. Snaith, Formamidinium lead trihalide: a broadly tunable perovskite for efficient planar heterojunction solar cells, Energy Environ. Sci., 2014, 7, 982 RSC.
- M. R. Filip, G. E. Eperon, H. J. Snaith and F. Giustino, Steric engineering of metal-halide perovskites with tunable optical band gaps, Nat. Commun., 2014, 5, 12 Search PubMed.
- J. H. Noh, S. H. Im, J. H. Heo, T. N. Mandal and S. I. Seok, Chemical Management for Colorful, Efficient, and Stable Inorganic–Organic Hybrid Nanostructured Solar Cells, Nano Lett., 2013, 13(3), 1764–1769 CrossRef CAS PubMed.
- H. J. Snaith, Perovskites: The Emergence of a New Era for Low-Cost, High-Efficiency Solar Cells, J. Phys. Chem. Lett., 2013, 4(10), 3623–3630 CrossRef CAS.
- C. C. Stoumpos, D. H. Cao, D. J. Clark, J. Young, J. M. Rondinelli, J. I. Jang, J. T. Hupp and M. G. Kanatzidis, Ruddlesden–Popper Hybrid Lead Iodide Perovskite 2D Homologous Semiconductors, Chem. Mater., 2016, 28(4), 2852–2867 CrossRef CAS.
- H.-R. Xia, W.-T. Sun and L.-M. Peng, Hydrothermal synthesis of organometal halide perovskites for Li-ion batteries, Chem. Commun., 2015, 51, 13787–13790 RSC.
- M. Tathavadekar, S. Krishnamurthy, A. Banerjee, S. Nagane, Y. Gawli, A. Suryawanshi, S. Bhat, D. Puthusseri, A. D. Mohite and S. Ogale, Low-dimensional hybrid perovskites as high performance anodes for alkali-ion batteries, J. Mater. Chem. A, 2017, 5, 18634–18642 RSC.
- J.-M. Tarascon and M. Armand, Issues and challenges facing rechargeable lithium batteries, Nature, 2001, 414(11), 359–367 CrossRef CAS PubMed.
- J. A. Dawson, A. J. Naylor, C. Eames, M. Roberts, W. Zhang, H. J. Snaith, G. Bruce and M. S. Islam, Mechanisms of Lithium Intercalation and Conversion Processes in Organic–Inorganic Halide Perovskites, ACS Energy Lett., 2017, 2(7), 1818–1824 CrossRef CAS.
- N. Vicente, D. Bresser, S. Passerini and G. Garcia-Belmonte, Probing the 3-step Lithium Storage Mechanism in CH3 NH3 PbBr3 Perovskite Electrode by Operando -XRD Analysis, ChemElectroChem, 2018, 6(11), 456–460 Search PubMed.
- D. Ramirez, Y. Suto, N. C. Rosero-Navarro, A. Miura, K. Tadanaga and F. Jaramillo, Structural and Electrochemical Evaluation of Three- and Two-Dimensional Organohalide Perovskites and Their Influence on the Reversibility of Lithium Intercalation, Inorg. Chem., 2018, 57(3), 4181–4188 CrossRef CAS.
- D. H. Cao, C. C. Stoumpos, O. K. Farha, J. T. Hupp and M. G. Kanatzidis, 2D Homologous Perovskites as Light-Absorbing Materials for Solar Cell Applications, J. Am. Chem. Soc., 2015, 137(6), 7843–7850 CrossRef CAS.
- G. Grancini, C. Roldan-Carmona, I. Zimmermann, E. Mosconi, X. Lee, D. Martineau, S. Narbey, F. Oswald, F. D. Angelis, M. Graetzel and M. K. Nazeeruddin, One-Year stable perovskite solar cells by 2D/3D interface engineering, Nat. Commun., 2017, 8(6), 15684 CrossRef CAS.
- G. Grancini and M. K. Nazeeruddin, Dimensional tailoring of hybrid perovskites for photovoltaics, Nat. Rev. Mater., 2018, 4(11), 4–22 Search PubMed.
- N. Vicente and G. Garcia-Belmonte, Methylammonium Lead Bromide Perovskite Battery Anodes Reversibly Host High Li-Ion Concentrations, J. Phys. Chem. Lett., 2017, 8(3), 1371–1374 CrossRef CAS PubMed.
- S. Ahmad, C. George, D. J. Beesley, J. J. Baumberg and M. D. Volder, Photo-Rechargeable Organo-Halide Perovskite Batteries, Nano Lett., 2018, 18(2), 1856–1862 CrossRef CAS PubMed.
- C. Liang, H. Gu, Y. Xia, Z. Wang, X. Liu, J. Xia, S. Zuo, Y. Hu, X. Gao, W. Hui, L. Chao, T. Niu, M. Fang, H. Lu, H. Dong, H. Yu, S. Chen, X. Ran, L. Song, B. Li, J. Zhang, Y. Peng, G. Shao, J. Wang, Y. Chen, G. Xing and W. Huang, Two-dimensional Ruddlesden–Popper layered perovskite solar cells based on phase-pure thin films, Nat. Energy, 2021, 6, 38–45 CrossRef CAS.
- K.-H. Wang, L.-C. Li, M. Shellaiah and K. W. Sun, Structural and Photophysical Properties of Methylammonium Lead Tribromide (MAPbBr3) Single Crystals, Sci. Rep., 2017, 7, 13643 CrossRef PubMed.
- S. M. Wood, C. H. Pham, A. Heller and C. B. Mullins, Communication - Stages in the Dynamic Electrochemical Lithiation of Lead, J. Electrochem. Soc., 2016, 163, A1027–A1029 CrossRef CAS.
- M. N. Obrovac and V. L. Chevrier, Alloy Negative Electrodes for Li-Ion Batteries, Chem. Rev., 2014, 114(11), 11444–11502 CrossRef CAS PubMed.
- M. He, L. Zhang and J. Li, Theoretical investigation on interactions between lithium ions and two-dimensional halide perovskite for solar-rechargeable batteries, Appl. Surf. Sci., 2020, 11, 148509 Search PubMed.
- R. Ohmann, L. K. Ono, H.-S. Kim, H. Lin, M. V. Lee, Y. Li, N.-G. Park and Y. Qi, Real-Space Imaging of the Atomic Structure of Organic–Inorganic Perovskite, J. Am. Chem. Soc., 2015, 137(12), 16049–16054 CrossRef CAS PubMed.
- S. Ahmad, K. Kanaujia, W. Niu, J. J. Baumberg and G. V. Prakash, In situ Intercalation Dynamics in Inorganic–Organic Layered Perovskite Thin Films, ACS Appl. Mater. Interfaces, 2014, 6(6), 10238–10247 CrossRef CAS PubMed.
- J. Wang, Y. Yamada, K. Sodeyama, C. H. Chiang, Y. Tateyama and A. Yamada, Superconcentrated electrolytes for a high-voltage lithium-ion battery, Nat. Commun., 2016, 7, 12032 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ma00020a |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2021 |