 Open Access Article
Open Access ArticlePolymorphism in metal halide perovskites
Aida
Alaei
 ,
Abigail
Circelli
,
Yihang
Yuan
,
Yi
Yang
,
Abigail
Circelli
,
Yihang
Yuan
,
Yi
Yang
 and
Stephanie S.
Lee
and
Stephanie S.
Lee
 *
*
Department of Chemical Engineering and Materials Science, Stevens Institute of Technology, Hoboken, NJ, USA. E-mail: stephanie.lee@stevens.edu
First published on 18th November 2020
Abstract
Metal halide perovskites (MHPs) are frontrunners among solution-processable materials for lightweight, large-area and flexible optoelectronics. These materials, with the general chemical formula AMX3, are structurally complex, undergoing multiple polymorph transitions as a function of temperature and pressure. In this review, we provide a detailed overview of polymorphism in three-dimensional MHPs as a function of composition, with A = Cs+, MA+, or FA+, M = Pb2+ or Sn2+, and X = Cl−, Br−, or I−. In general, perovskites adopt a highly symmetric cubic structure at elevated temperatures. With decreasing temperatures, the corner-sharing MX6 octahedra tilt with respect to one another, resulting in multiple polymorph transitions to lower-symmetry tetragonal and orthorhombic structures. The temperatures at which these phase transitions occur can be tuned via different strategies, including crystal size reduction, confinement in scaffolds and (de-)pressurization. As discussed in the final section of this review, these solid-state phase transformations can significantly affect optoelectronic properties. Understanding factors governing these transitions is thus critical to the development of high-performance, stable devices.
Introduction
As conversion efficiencies of metal halide perovskite (MHP) solar cells skyrocket past 25%,1 research in the fundamental parameters governing MHP performance in optoelectronic devices, including solar cells, light-emitting diodes, transistors, and sensors, continues to rise exponentially. This class of materials, adopting the general perovskite composition of AMX3 where X represents halide ions of Cl−, Br− or I−, exhibit superior light absorption and charge mobilities compared to their organic molecular and polymeric counterparts,2 as well as remarkable defect tolerance that enables their high performance upon solution processing.3,4Intricately tied to the performance of these materials is the specific arrangement adopted by the ions within the crystalline lattice. All MHPs exhibit different polymorphs, i.e. solid-state crystal structures, as a function of temperature and pressure. The optoelectronic properties of MHPs can vary significantly depending on the specific polymorph present. CsPbI3, FAPbI3 and CsSnI3, for example, all adopt a non-perovskite, insulating phase at room temperature that cannot be used as active layers in optoelectronic devices.5–8 Significant research effort has thus focused on developing methods to trap the metastable, active perovskite phases of these compounds.9,10 In other systems, the relationship between polymorphism and optoelectronic properties is less drastic, but important nonetheless. The MAPbI3 tetragonal-to-cubic transition, for example, occurs within the operating range of solar cells around 330 K and can impact, for example, charge carrier dynamics.11 Understanding and controlling polymorphism in this class of materials is necessary to ensure long-lasting, reliable performance of MHP-based optoelectronic devices.
In this review, we aim to present a systematic and comprehensive picture of polymorphism in three-dimensional MHPs, beginning with a general classification of perovskite polymorphs and a comparison of all the known polymorph transition temperatures across 17 different three-dimensional MHPs. These MHPs represent “pure” compositions, rather than mixed compositions in which one or all of the components is a mixture of different ionic species (e.g. MAxCs1−xPbySn1−yClzBr3−z). Overall, all MHPs adopt a high-symmetry cubic phase at elevated temperatures, transitioning to lower-symmetry polymorphs upon decreasing temperature as a result of octahedral tilting. For MHPs with organic A-site cations, the orientation and motion of the cation with respect to the metal–halide framework must also be considered. Strategies, including crystal size reduction and pressurization, employed to shift polymorph transition temperatures and relative thermodynamic stabilities are discussed. An overview of how optoelectronic properties vary with different polymorphs is also provided.
Classifying perovskite polymorphs
First discovered by Russian mineralogist Lev Perovski, perovskites are a class of materials that adopt the structure of calcium titanium oxide, with a general chemical formula of AMX3. In the perovskite structure, X ions form corner-sharing octahedra with M ion centers, while A ions occupy the spaces between octahedra. A schematic of the perovskite structure highlighting the corner sharing octahedra is provided in Fig. 1A. This particular structure represents an orthorhombic phase in which the octahedra are tilted relative to one another. The extent and direction of octahedral tilting define the different perovskite polymorphs and are a consequence of a mismatch between the sizes of the ions comprising the perovskite structure.12 The ideal size of the A-site cation can be predicted by the Goldschmidt tolerance factor, t:13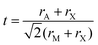 | (1) |
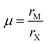 | (2) |
 | ||
| Fig. 1 (A) Perovskite structure comprising corner-sharing octahedra. (B) Plot of octahedral factors versus tolerance factors based on anion-dependent cationic radii. Blue circles represent compounds that form the perovskite structure at room temperature and pressure, while red x's represent those that do not. Adapted from ref. 15. Copyright 2016, Royal Society of Chemistry. | ||
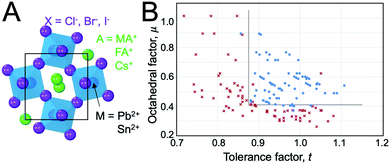
At ambient pressure, perovskites can undergo multiple solid-state phase transitions as a function of temperature. In the highest-symmetry cubic structure with a M–X–M angle of 180° that appears at elevated temperatures, the corner-sharing octahedra are aligned in all directions. With decreasing temperature, the octahedra tilt due to a mismatch between the size of the A-site cation and the metal–halide framework. Polymorphs thus represent different extents of tilting of the corner-sharing octahedra. The tilting can be described in Glazer notation,17 which assigns either an in-phase (+) or out-of-phase (−) rotation of octahedra along each of the three spatial dimensions, x (first position), y (second position), and z (third position). The amplitude of these rotations is indicated by lower case letters. As detailed by Bechtel and co-workers in Fig. 2A, a perovskite structure characterized as a+b0b0 in Glazer notation exhibits in-phase octahedral tilting along the x-axis, with no tilting along other axes.12 On the other hand, a structure characterized as a−b0b0 exhibits out-of-phase octahedral tilting in the x direction. For a structure characterized by a+b−b−, in-plane octahedral rotation occurs along the x-direction, while out-of-plane tilting occurs along the y- and z-directions. The amplitude of tilting is the same in the y- and z-directions, but different from the x-direction, as indicated by the different lowercase letters a and b. In general, perovskites undergo a cubic-to-tetragonal transition, followed by a tetragonal-to-orthorhombic transition with decreasing temperature. The cubic, tetragonal, and orthorhombic phases are represented by the Greek letters α, β and γ, respectively. Fig. 2B displays the general classification for these phases.18 For all MHPs characterized thus far, octahedral tilting in the γ-phase is characterized by a+b−b−, resulting in Pnma symmetry, while the tetragonal phase can adopt either P4/mbm symmetry with in-phase octahedral tilting denoted by a0a0c+ or I4/mcm symmetry with out-of-phase octahedral tilting denoted by a0a0c−. Fig. 2C displays a flow diagram of phase transitions observed in hybrid and all-inorganic perovskites, including those outside of the halide perovskite family.18
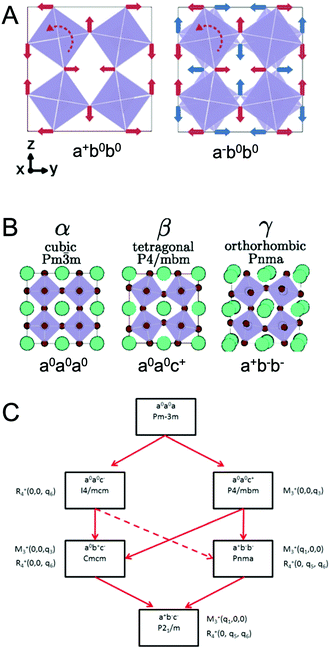 | ||
| Fig. 2 (A) Illustrations of different octahedral tilting directions and their corresponding identifier in Glazer notation. (B) Solid-state phases observed in MHPs, from the high-temperature, high-symmetry cubic structure to the low-temperature, low-symmetry orthorhombic structure. Adapted with permission from ref. 12. Copyright 2018, American Physical Society. (C) Flow diagram of phase transitions in organic MHPs and all-inorganic MHPs. The dashed red line indicates that transitions from I4/mcm to Pnma symmetry must be a first order transition. Reproduced with permission from ref. 18. Copyright 2016, Royal Society of Chemistry. | ||
For the sub-class of optoelectronically-active perovskites that are the topic of this review, the use of halide anions (e.g. Cl−, Br−, I−) in the X position imposes restrictions on the options for A and M cations. Compared to other anions common to perovskite structures, such as O2−, halide anions have smaller negative charge and larger ionic radii.19 As such, A-site cations have thus far been limited to organic methylammonium and formamidinium and inorganic cesium, while MII cations are largely restricted to heavier group IV elements (e.g. Sn2+ and Pb2+).19
Fig. 3 displays the solid-state phase transition temperatures and space groups reported for bulk MHP crystals, including CsPbCl3,20–23 CsPbBr3,24–26 CsPbI3,27,28 CsSnCl3,29,30 CsSnBr3,31,32 CsSnI3,29,33,34 MAPbCl3,35–37 MAPbBr3,36,38–40 MAPbI3,36,41–43 MASnCl3,30 MASnBr3,8 MASnI3,44,45 FAPbCl3,46 FAPbBr3,47 FAPbI3,6,8 FASnBr3,48 and FASnI3.47 To the best of our knowledge, the crystal structure of FASnCl3 has not been reported. As observed from the figure, all perovskites adopt a cubic Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m structure at elevated temperatures. In general, chlorine-based derivatives retain the cubic structure to relatively lower temperatures compared to bromine and iodine derivatives with the same A-site and metal cations. With a smaller ionic radius, the tolerance factors for chlorine derivatives are closer to 1, rendering the cubic phase more stable. For all derivatives, the symmetry of the crystal structure decreases as temperature is lowered, following the flow diagram displayed in Fig. 2C. Furthermore, MHPs with organic A-site cations generally form the cubic phase at room temperature due to the relatively larger size of these cations compared to Cs+. For reference, Cs+ has an ionic radius of 1.88 Å.15 Estimated effective ionic radii generally fall in the range of 2.03–2.38 Å for MA+ and 2.24–2.53 Å for FA+.15,49–51
m structure at elevated temperatures. In general, chlorine-based derivatives retain the cubic structure to relatively lower temperatures compared to bromine and iodine derivatives with the same A-site and metal cations. With a smaller ionic radius, the tolerance factors for chlorine derivatives are closer to 1, rendering the cubic phase more stable. For all derivatives, the symmetry of the crystal structure decreases as temperature is lowered, following the flow diagram displayed in Fig. 2C. Furthermore, MHPs with organic A-site cations generally form the cubic phase at room temperature due to the relatively larger size of these cations compared to Cs+. For reference, Cs+ has an ionic radius of 1.88 Å.15 Estimated effective ionic radii generally fall in the range of 2.03–2.38 Å for MA+ and 2.24–2.53 Å for FA+.15,49–51
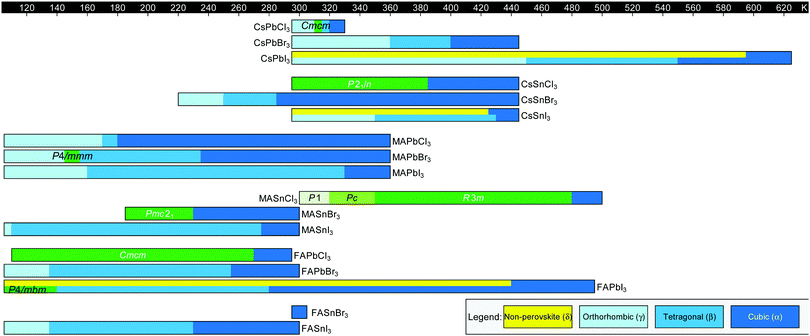 | ||
Fig. 3 Summary of phase transition temperatures in halide perovskites reported in the literature collected at ambient pressure as a function of composition.6,8,20–48 Cubic structures exhibit Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m symmetry, tetragonal structures exhibit either I4/mcm or P4/mbm symmetry, and the orthorhombic phase exhibits Pnma symmetry, unless otherwise noted. Green colors indicate phases not represented by the above categories. m symmetry, tetragonal structures exhibit either I4/mcm or P4/mbm symmetry, and the orthorhombic phase exhibits Pnma symmetry, unless otherwise noted. Green colors indicate phases not represented by the above categories. | ||
We note there are some discrepancies in the literature on phase transition temperatures and space groups observed for specific compositions. In 1987, for example, Poglitsch and Weber reported the space groups of the low temperature phases of MAPbCl3, MAPbBr3 and MAPbI3 to be P2221, Pna21, and Pna21, respectively.36 These assignments have been reassigned to Pnma based on recent high resolution X-ray and neutron diffraction experiments.35,43,52 For MAPbBr3, there are further conflicting reports about the existence of a P4/mmm tetragonal phase in between the orthorhombic phase and I4/mcm tetragonal phase, with neutron scattering52 and X-ray diffraction experiments53 unable to detect this phase.
Polymorphism in all-inorganic perovskites
For perovskites comprising halide anions in the X-site, cesium is the only elemental ion with a sufficiently large radius to support the perovskite framework.19 To date, the most promising inorganic halide perovskites for optoelectronic devices are CsPbX3 and CsSnX3 where X = Cl−, Br−, or I−.54 The first reports on the crystal structures of these compounds date back to the late 1950s to early 1970s,29,55–57 but it was not until 2015 that the first all-inorganic light-emitting diodes comprising CsPbBr3 as the photoactive layer58 and solar cells comprising CsPbI3 as the photoactive layer59 were successfully fabricated. Since then, inorganic MHP-based devices have been demonstrated for a variety of devices,60,61 including photodetectors,62,63 solar cells,64,65 transistors66,67 and light-emitting diodes.68–70 Promisingly, CsPbI3-based solar cells recently achieved record efficiencies of 19%.71Compared to MHPs utilizing organic molecules as the A-site cation, inorganic MHPs comprising inorganic Cs+ cations are expected to exhibit enhanced thermal stability.54 However, these inorganic perovskites have other critical issues related to degradation and polymorph transitions. Sn-Based perovskites exhibit smaller bandgaps compared to their Pb-based counterparts, 1.3 eV for CsSnI3 compared to 1.7 eV for CsPbI3, but suffer from rapid oxidation of Sn2+ to the more stable state of Sn4+. In the Pb family, CsPbCl3 and CsPbBr3 are air-stable in the perovskite phase at ambient temperatures and pressures but their relatively large bandgaps of 2.99 and 2.31 eV72 make them less attractive for light harvesting applications. On the other hand, the perovskite phases of CsPbI3 possess reasonable bandgaps around 1.7 eV but these phases are only stable at elevated temperatures. Of all the CsMX3 compounds, CsPbI3 and CsSnI3 have the smallest tolerance factors of 0.89 and 0.91 (based on anion-dependent A-site cation radii) and octahedral factors of 0.47 and 0.44, respectively.15 This mismatch between the A-site cation size and the perovskite framework renders these systems less stable compared to other CsMX3 compounds where M = Pb2+ or Sn2+ and X = Cl− or Br−. At room temperature, CsPbI3 and CsSnI3 both exist in a yellow, non-perovskite polymorph,55,73 referred to as the δ phase, exhibiting large bandgaps of around 2.8 and 2.55 eV, respectively.34,74 The δ phase is characterized by isolated double MX6 octahedra (Fig. 4A).
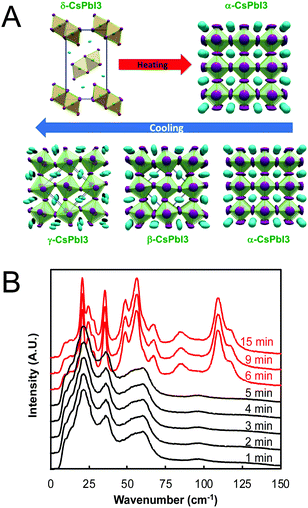 | ||
| Fig. 4 (A) Temperature-dependent phase transitions of CsPbI3 at ambient pressure. Reproduced with permission from ref. 27. Copyright 2018, American Chemical Society. (B) Room-temperature low-frequency Raman spectra of a drop cast CsPbI3 film as a function of exposure time to air (λex = 976 nm). CsPbI3 initially adopted the γ phase (black) upon cooling from 610 K before converting to the δ phase (red) between 5 and 6 min of air exposure. Adapted with permission from ref. 78. Copyright 2020, Royal Society of Chemistry. | ||
While all four phases of CsSnI3 were identified and characterized29,75 decades prior to the fabrication of the first perovskite-based solar cell by Kojima and coworkers in 2009,76 some confusion initially surrounded the room temperature perovskite structure of CsPbI3. Many early reports on CsPbI3-based optoelectronic devices described the room temperature metastable perovskite phase as the cubic α phase. Recent studies, however, have found that CsPbI3 undergoes the same cubic-tetragonal and tetragonal–orthorhombic phase transitions upon cooling as other perovskites.27,28Fig. 4A displays the phase transitions of CsPbI3 as a function of the thermal history. At room temperature, CsPbI3 adopts the non-perovskite δ phase. Upon heating above 587 K, this phase converts directly to the cubic α phase.27 If the α phase is then slowly cooled, it undergoes a transition to the tetragonal β phase at 554 K and then to the orthorhombic γ phase at 457 K. Comparing two different methods of stabilizing the black phase of CsPbI3 at room temperature via Rietveld refinement of powder diffraction patterns, Sutton and coworkers confirmed that the γ phase is present at room temperature, not the cubic α phase.28
At room temperature, the γ phases of both CsSnI3 and CsPbI3 are unstable and will spontaneously convert to the insulating δ phases,75 even when stored under vacuum.77 Using low-frequency Raman spectroscopy to monitor phonon modes in a CsPbI3 crystalline film deposited via drop casting from dimethyl sulfoxide onto a SiO2 substrate, we found this transition to occur within 6 min of air exposure (Fig. 4B).78 The transition itself was rapid and completed within time resolution limit of the measurements (e.g. within one minute). Stabilizing the active black phases of these compounds at room temperature has thus been an area of intense research focus over the past five years.
Polymorphism in organometallic perovskites
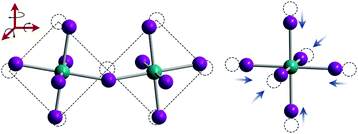
Organic MHPs with methylammonium (MA+) and formamidinium (FA+) as the A-site cation represent the most extensively studied compositions of MHPs for optoelectronic applications to-date. These ions are larger than Cs+, resulting in tolerance factors closer to, and in some cases larger than 1.79 As displayed in Fig. 3, phase transitions in organic MHPs are similar to inorganic perovskites. These compounds adopt a high symmetry cubic phase at elevated temperatures and transition to lower symmetry structures via octahedral tilting upon cooling. Unlike inorganic MHPs with a simple atomic A-site cation, however, phase transitions in organic MHPs possess additional complexity associated with orientation and rotation of the asymmetric molecular cations in the interstices of the corner-sharing MX6 octahedra.80 The specific orientations adopted by the A-site cation may in turn affect optoelectronic properties, such as the bandgap.81In the cubic phase, which is stable above 330 K, early magnetic resonance experiments found that the MA+ cation can rotate on the picosecond timescale within the interstitial spaces between corner-sharing PbI6 octahedra.105 In 2015, Weller and co-workers used neutron powder diffraction to provide a comprehensive picture of MA+ cation dynamics in the range of 100–352 K.43Fig. 5A displays a MAPbI3 unit cell in the cubic phase, with atomic displacement parameter (ADP) ellipsoids representing a 50% probability of locations of the hydrogen atoms at the ends of the MA+ cations. As observed from the figure, the MA+ ion appears disordered in the cubic phase. Later studies revealed preferential alignment of the MA+ cations based on four-fold rotational symmetry of the C–N axis and three-fold rotational symmetry about the C–N axis.97,106,107 Employing single crystal neutron diffraction studies, Ren and coworkers found that the MA+ cations preferentially align along the [011] (edge), [111] (diagonal), and [100] (face) directions.108 These experiments also revealed that the middle point of the C–N bond is located slightly off-center due to interactions between the amine group of MA+ and iodine atoms.
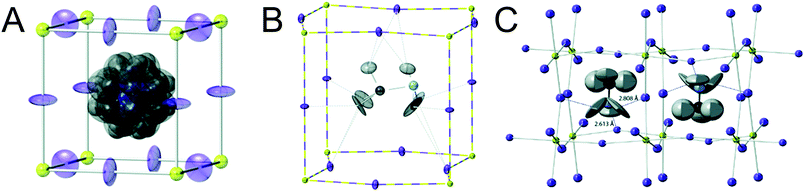 | ||
| Fig. 5 Depictions of MA+ cation orientations in the (A) cubic phase with ADP ellipsoids at 50% probability, (B) one orientation of the tetragonal phase with ADP ellipsoids at 50% probability, and (C) orthorhombic phase with ADP ellipsoids at 90% probability of MAPbI3, as determined by powder neutron diffraction experiments. Adapted with permission from ref. 43. Copyright 2015, Royal Society of Chemistry. | ||
Upon decreasing the temperature below 330 K, MAPbI3 undergoes a phase transition to the tetragonal β phase. Here the PbI6 octahedra are tilted compared to the cubic phase, with an average Pb–I–Pb bond angle of 165.3°. Fig. 5b displays one configuration of the tetragonal phase at 180 K for MAPbI3 with ADP ellipsoids at 50% probability.43 In this phase, the NH3 group adopts four distinct positions, while the CH3 group adopts eight distinct positions.108 Although the organic cation is more confined in the tetragonal phase compared to cubic phase, and exhibits slower rotational dynamics,105 four-fold rotation of (C–N) axis C4 and three-fold rotation around (C–N) axis C3 is still possible.97,106,107 Elastic and quasi-elastic neutron scattering techniques and group theoretical analysis revealed the room temperature relaxation times of and around the C–N axis to be approximately 5 and 1 ps, respectively.94,106
It should be noted that the crystal structure classification of tetragonal MAPbI3 is still being debated, in part due to extensive twinning that complicates structure determination.109,110 A centrosymmetric I4/mcm space group for tetragonal MAPbI3 was proposed by Poglitsch and Weber in 1987.36 In 2013, Stoumpos and coworkers reported instead a non-centrosymmetric I4cm space group due to off-centering of the MA+ cation along the c-axis.111 A later report suggested that non-centrosymmetric tetragonal MAPbI3 was achieved through static distortion of the Pb–I framework via second harmonic generation analysis.112 Subsequent second harmonic generation rotational anisotropy experiments capable of distinguishing surface and bulk signals, however, determined that tetragonal MAPbI3 indeed adopts the centrosymmetric I4/mcm space group.113 Structural rearrangement at perovskite surfaces may lead to the formation of noncentrosymmetric domains that are not present in the bulk, as observed in low-temperature scanning tunneling microscopy images of MAPbBr3 crystals.114 Non-centrosymmetric structures in MHPs are expected to exhibit ferroelectricity and Rashba splitting due to spin–orbit coupling interactions with charge carriers. With significant implications to fundamental device physics and applications, intensive research efforts continue to focus on definitive structure determination in these materials.
As displayed in Fig. 5C, the MA+ cation is in its most confined state in the low temperature orthorhombic γ phase (T < 160 K), for which the average Pb–I–Pb bond angle of 154.51°. In this phase, the MA+ cations are completely ordered in an alternating head-to-tail configuration with the NH3 groups of MA+ closer to the inorganic framework compared to the CH3 groups.43 Relaxation times of the MA+ cation were found to be orders of magnitude larger than those expected for a rigid rotator in the same temperature range due to restrictions on motion imposed by the Pb–I framework.115 This configuration promotes hydrogen bonding between the NH3 group of the MA+ cation and the framework.43,116 While four-fold rotation is not allowed in this polymorph, three-fold rotation about the C–N axis is possible,97,106,107 with estimated activation energies of 56 meV and 120 meV for rotations of the CH3 and NH3 tails, respectively.117 Using infrared spectroscopy to examine vibrational modes in MAPbI3 single crystals, Schuck and coworkers found that the vibrational mode associated with symmetrical NH3 bending shifted to lower frequencies upon transitioning from the tetragonal to orthorhombic structure due to hydrogen bonding between the amine group on the organic cation and halide ions.118 Interestingly, the strength of the interaction depended on the halide composition, with the largest effect observed for I− compared to Cl− and Br−.
These experimental results have been supported by extensive computational modelling of MA+ rotational dynamics.18,94,95,102,119–122 Recent molecular dynamics simulations of phase transitions in organic MHPs have found that phase transitions are the result of dipole–dipole interactions between organic cations and hydrogen bonding with the Pb–I lattice.116 Reduced cation movement with decreasing temperature increases the strength of these interactions, resulting in lattice deformation.121 Combining DFT calculations and ab initio molecular dynamics, Deretzis and Magna found that vibrational features of MAPbI3 are strongly affected by the orientation of the organic cation in the low temperature orthorhombic phase, with the tetragonal–orthorhombic phase transition occurring to relax stress via rearrangement of the MA+ cation in an orientation that can reduce local stretching of ionic bonds in the inorganic framework.120
For FA+ cations, there are three primary axes of rotation, with rotation about the N–N axis the dominant motion in all phases above 50 K.107 As displayed in Fig. 6A, FA+ cations are completely disordered in the high temperature cubic phase and can rotate freely within the inorganic framework.127 In this phase, the carbon atom of the FA+ cation is located at the center of the inorganic framework.128 In the lower temperature tetragonal phase, FA+ cations rotate between preferred orientations, as displayed in Fig. 6B. In this phase, FA+ cations in adjacent inorganic cages reorient with respect to each other by changing the H–C bond direction. This preferred orientation is influenced by PbI6 octahedral tilting, as demonstrated by both experimental and simulation results.127,129 In the low-temperature orthorhombic phase, FA+ cation rotation is arrested but unlike MA+ cations, FA+ cations do not exhibit any long range order.127 Instead, their configuration can be described by a glass-like, disordered state.107
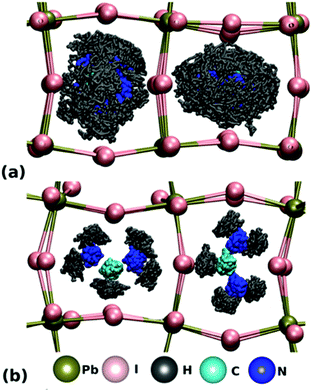 | ||
| Fig. 6 Molecular dynamics simulations of FA cations within Pb–I frameworks in the (A) pseudocubic phase and (B) tetragonal phase. Reproduced with permission from ref. 127. Copyright 2018, American Chemical Society. | ||
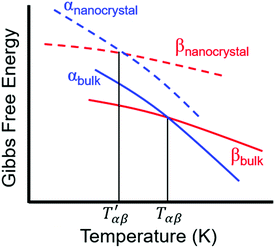 | ||
| Fig. 7 Comparison of the dependence of the Gibbs free energy on temperature for different polymorphs of a bulk crystal and nanocrystal. Adapted with permission from ref. 130. Copyright 2019, American Chemical Society. | ||
Influence of crystal size on polymorph transitions
One of the most promising emerging strategies to stabilize MHPs is to reduce the average crystal size.130 The total Gibbs free energy of a crystal, GT, can be expressed as a sum of the volume free energy, GV, and the total surface free energy:131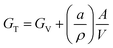 | (3) |
For relatively small crystals, on the other hand, the surface free energy contribution to the total Gibbs free energy can be significant. Fig. 7 illustrates the shift in Gibbs free energy upon crystal size reduction of two polymorphs of a compound as a function of temperature. As can be seen from the figure, at temperatures above Tαβ, the α phase is favored due to its lower Gibbs free energy compared to the β phase. Tαβ represents the temperature at which phase co-existence occurs. Below Tαβ, the β phase is thermodynamically preferred. For nanocrystals with large A/V ratios (represented by dashed lines), the Gibbs free energy of both phases increases due to an increased contribution from the surface free energy. If the surface free energy of the β phase is larger than the surface free energy of the α phase, the final result is a lowering of the phase transition temperature from Tαβ to 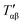 . Indeed, lower surface free energies of higher symmetry polymorphs compared to lower symmetry polymorphs have been recorded for a variety of metal oxide systems.132–135 For CsPbI3, DFT calculations found the surface energies of the high symmetry γ phase and low symmetry δ phase to be 0.13 and 2.57 J m−2, respectively.136
. Indeed, lower surface free energies of higher symmetry polymorphs compared to lower symmetry polymorphs have been recorded for a variety of metal oxide systems.132–135 For CsPbI3, DFT calculations found the surface energies of the high symmetry γ phase and low symmetry δ phase to be 0.13 and 2.57 J m−2, respectively.136
Perovskite quantum dots (PQDs)
At the smallest length scale, many research efforts have focused on the synthesis of perovskite quantum dots (PQDs) with dimensions in the range of 2–20 nm.137,138 Lowering of solid-state phase transition temperatures in these systems has been widely reported, although some confusion has surrounded the precise solid-state phases adopted by PQDs. In the first report of metal halide PQDs in 2015, Protesescu and coworkers synthesized all-inorganic cesium lead halide perovskite QDs (CsPbX3, X= Cl, Br, I, and mixed Cl/Br, Br/I), with sizes in the range of 4–15 nm. XRD patterns collected on the PQDs were used to assign the cubic α phase to all compositions.139 These phases were reported to be stable, with only CsPbI3 transitioning to the orthorhombic, non-perovskite δ phase upon several months of storage. A later report using synchrotron radiation and atomic pair distribution (PDF) to characterize both elastic and inelastic X-ray scattering from PQDs prepared in the same manner, however, found that CsPbCl3, CsPbBr3 and CsPbI3 QDs all existed in the room temperature γ phase observed in bulk crystals.140 Here the authors found that the presence of twin boundaries in some cases gave rise to “apparent higher symmetry” observed via X-ray diffraction. In general, while the main peaks in the XRD patterns of the γ phase are similar to those of the α phase, the presence of weak superstructure peaks indicate octahedral tilting in the perovskite framework. These findings are supported by ab initio DFT simulations that found crystal size reduction to below 5.6 nm and 2.7 nm were needed to thermodynamically stabilize γ-CsPbI3 and α-CsPbI3, respectively.141In 2018, Cottingham and Brutchey experimentally examined phase transitions in CsPbBr3 PQDs with average diameters of 9 nm using temperature-dependent, synchrotron radiation-based total X-ray scattering techniques.142 At room temperature, these PQDs were found to exist in the γ phase.143 The γ-β transition was observed between 50–59 °C, while the β-α transition was observed between 108–117 °C. These ranges represent phase transition temperature depressions of at least 29 and 13 °C, respectively, compared to those observed in bulk crystals. In the analogous organic–inorganic hybrid system of MAPbBr3, Liu and coworkers used temperature-dependent photoluminescence measurements to identify the β-α transition for PQDs with an average diameter of 3.7 ± 0.6 nm at 150 K,144 compared to ∼236 K in the bulk.40 Close agreement was found between the experimental data and the predicted phase transition temperature between the paraelectric α phase and ferroelectric β-phase following Ginzburg–Landau–Devonshire theory. Fig. 8 displays the size dependence of the critical temperature and Gibbs free energy, decrease and increase, respectively, with decreasing crystal size. As observed from the figure, the critical temperature drops to 0 K for particle diameters below 2 nm, in agreement with the authors’ observation of the absence of phase transitions for PQDs with average diameters of 1.7 ± 0.4 nm.
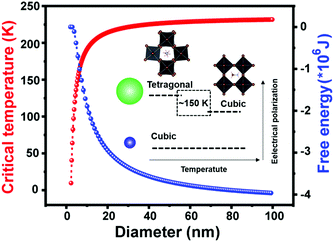 | ||
| Fig. 8 Critical temperature and Gibbs free energy versus particle diameter for MAPbBr3 PQDs based on Ginzburg–Landau–Devonshire theory. Reproduced with permission from ref. 144. Copyright 2019, American Chemical Society. | ||
Coexistence of the γ and α phases of CsPbBr3 PQDs has also been reported. Recently, Brennan and coworkers examined the crystal structure of CsPbBr3 nanocubes with average edge lengths 5 nm and 10 nm via lattice-resolved transmission electron microscopy imaging at progressive defocus values.145 Finite Fourier transforms of experimental images and simulated images of the α and γ phases suggest that 10 nm diameter CsPbBr3 nanocubes mainly adopt the cubic α phase, with some γ phase present. For 5 nm diameter nanocubes, on the other hand, only the α phase was found to be present.
Scaffold-confined crystals
Another method of controlling polymorphism via crystal size reduction is to confine crystallization within nanoporous scaffolds, such as controlled porous glass, selectively-etched block copolymers and anodized aluminium oxide.130,146 This strategy has been successfully employed to shift phase transition temperatures, including melting points, in a number of different organic and inorganic systems, as summarized in several reviews.130,147,148Recently, our group examined the phase stability of MAPbI3 crystals confined within the cylindrical nanopores of anodized aluminium oxide scaffolds with average pore diameters of 100–250 nm (Fig. 9A).149,150 Temperature-dependent X-ray diffraction measurements in the range of 293–373 K and photoluminescence measurements in the range of 4–300 K revealed the α–β transition temperature to shift from 330 K for bulk crystals to 170 K for nanoconfined crystals. Similarly, the β–γ transition was observed at 80 K for nanoconfined crystals, compared to 150 K in the bulk. Fig. 9B displays a comparison of the Gibbs free energy curves as a function of temperature for the different bulk and nanoconfined phases that is consistent with our experimental observations.
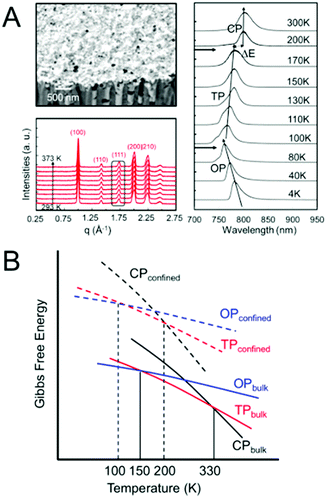 | ||
| Fig. 9 (A) SEM image of MAPbI3 confined within 100 nm diameter nanopores of anodized aluminum oxide templates. Temperature-dependent X-ray diffraction measurements revealed only the cubic phase to be present in the range of 293–373 K, while temperature-dependent photoluminescence measurements revealed the tetragonal (TP)–cubic (CP) phase transition to occur between 170–200 K and the orthorhombic (OP)-TP transition to occur between 80 and 100 K. (B) Comparison of the dependence of the Gibbs free energy on temperature for different polymorphs of a compound in the bulk and nanocrystal state. Reproduced with permission from ref. 130. Copyright 2019, American Chemical Society. | ||
Examining nanoconfined CsPbI3 crystallization as a function of AAO pore diameter, Ma and coworkers found that the black phase of CsPbI3 (reported as the α phase but weak superstructure peaks in the XRD patterns likely indicate the γ phase was present) became thermodynamically stable within 41 nm diameter pores or smaller.151 DFT calculations suggested that stabilization of the black CsPbI3 phase at room temperature was due both to increased surface area of nanoconfined crystals and strain introduced at the pore walls. By tuning the processing conditions, we discovered that γ-CsPbI3 could be stabilized in AAO pores as large as 250 nm.152 Using wet annealing method in which spun cast samples with solvent remained were immediately annealed at a minimum temperature 373 K, γ-CsPbI3 was formed within the AAO nanopores. Once formed, nanoconfined γ-CsPbI3 was found to be stable in a range of 4–610 K and for a period of at least 120 days of storage in air. Using chemical vapor deposition to infiltrate the 250 nm pores of AAO scaffolds, Waleed and coworkers recently reported stabilization of α-CsPbI3 at room temperature.153 In comparison, CsPbI3 deposited via spin coating in the same nanopores was found to adopt the orthorhombic γ phase, indicating that processing conditions play a crucial role in determining final crystal structures. Nanoconfined stabilization of the metastable α phase of FAPbI3 from conversion to the thermodynamically stable δ-phase at room temperature has also been reported,154 although shifting of polymorph transitions temperatures was not reported.
Influence of pressure on phase transitions
Solid state phase transitions are a function of both temperature and pressure. Enabled by advances in synchrotron-based pressurized configurations for high-resolution diffraction measurements,155 pressured-induced phase transitions in MHPs have been intensely studied in recent years. Compared to other perovskites, MHPs exhibit high compressibility and pressure-dependent tunability of optoelectronic properties.156,157 Several reviews have already been published on pressure-induced phase transitions in MHPs and the role of pressure in modulating electronic landscapes,155,157–159 so we will only provide a brief overview here.In general, MHPs undergo similar phase transitions upon pressurization in the range of atmospheric to 50 GPa.159 At lower pressures, structural changes are characterized by compression of Pb–I bonds and/or octahedral tilting, as displayed in Fig. 10.160 At higher pressures, MHPs amorphize, a process which is reversible upon pressure reduction. MAPbCl3, for example, undergoes a cubic-to-cubic isostructural transition upon increasing the pressure from atmospheric pressure to 0.8 GPa due to a continuous decrease in the Pb–Cl bond length.161 Increasing the pressure further to 2.4 GPa was found to induce octahedral tilting such that the crystal structure transitions to an orthorhombic unit cell with Pnma symmetry. Fig. 11 summarizes the pressure-dependent phase behavior of 12 perovskites, including CsPbCl3,162 CsPbBr3,163 CsPbI3,164 CsSnBr3,165 MAPbCl3,161 MAPbBr3,166 MAPbI3,167 MASnCl3,161 MASnBr3,165 MASnI3,168 FAPbBr3,169 and FAPbI3.170 CsPbCl3, CsPbBr3 and MaPbCl3 all exhibit an isostructural phase transition in which the crystal symmetry is retained upon increasing pressure via symmetric compression of the M–X bond. We note that there are some discrepancies in reported pressure-induced phase transitions, for example in widely studied MAPbI3,167,171–174 which partially result from differing ambient pressure phase assignments.
 | ||
| Fig. 10 Pressure-induced rotation of PbI6 octahedra (left) and Pb–I bond compression (right). Reproduced with permission from ref. 160. Copyright 2017, American Chemical Society. | ||
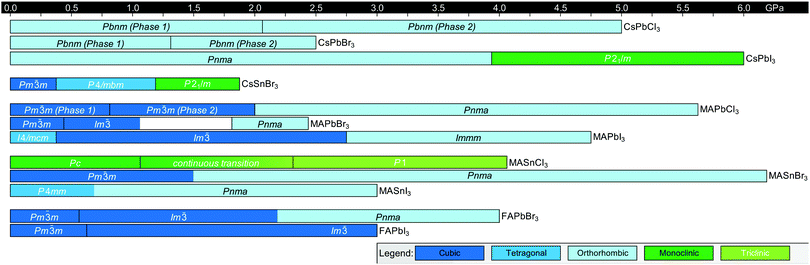 | ||
| Fig. 11 Summary of room-temperature phase transition pressures in halide perovskites as a function of composition reported in the literature.162–170 The white section in the data for MAPbBr3 indicates a region where data was not available. | ||
In the opposite direction, lowering the pressure can also impact solid state phase transitions in MHPs. Decreasing the pressure to 10−3 mbar was recently found to shift the tetragonal to cubic phase transition temperature of MAPbI3 higher by 40 °C, from ∼323–363 K.175 Furthermore, the tetragonal and cubic phases were observed to coexist until a temperature of 140 °C was reached. This shift was attributed to a reduction in temperature-induced volume expansion rate of MAPbI3 upon pressure reduction.
Promisingly, recent reports have found that some pressure-induced changes can be retained upon cycling back to ambient pressure. For FAPbI3 exposed to pressures of 7.1 GPa, it was found that unit cell parameters at ambient pressure after compression were smaller compared to before compression, as evidenced by a shift in diffraction peaks to higher 2-theta values.176 This structural change resulted in a narrower bandgap of previously compressed versus uncompressed FAPbI3. Recently, quenching MAPbI3 from a high pressure state was found to result in retention of bandgap reduction upon pressurization.177 Partial retention of pressure-induced structural changes has also been reported for 2D perovskites.178,179
Polymorph-dependent optoelectronic properties
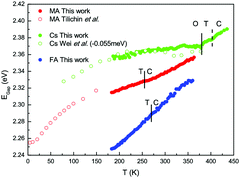
Among compounds adopting the AMX3 perovskite crystal structure, those incorporating halide ions in the X position have sufficiently small bandgaps, from ∼1.2–1.7 eV,42 to absorb visible light and transport charge carriers for use in solar cells and other optoelectronic devices. First principle calculations have found that the bandgap is determined by the metal–halide framework, with A-site cations contributing minimally to the band structure.180,181 The valence band maximum comprises antibonding metal s and halogen p orbitals, while the conduction band minimum primarily comprises empty metal p orbitals.181,182 The band structure of MHPs is sensitive to slight changes in the M–X framework due to lattice contractions and octahedral tilting.183 Thus while not directly contributing to the band structure, A-site cations indirectly influence band structures through altering the M–X framework.These trends are exemplified in a recent comparison of the temperature-dependent optical bandgaps of CsPbBr3, MAPbBr3, and FAPbBr3 single crystals.184 As observed from Fig. 12, optical bandgaps decrease with increasing tolerance factors of 0.92, 1.04, and 1.14 for CsPbBr3, MAPbBr3, and FaPbBr3, respectively.15,185,186 Overall, the bandgaps of halide perovskites are strongly correlated to the M–X–M bond angle,187,188 which can range from 150–180°, as described in detail in a 2015 account by Stoumpos and Kanatzidis.19 Upon bending, interactions between M p orbitals and X p antibonding orbitals increases, resulting in an increase of the bandgap.183 Significant efforts in the field have focused on exploiting the relationship between A-site cation size, the extent of M–X–M bond angle distortion, and the overall bandgap of the system through the engineering of mixed composition MHPs.189–195 For a series of MAPb(I1−xBrx)3 compounds, for example, Noh and coworkers reported the ability to continuously tune the bandgap from 1.6 to 2.3 eV by increasing the value of x from 0 to 1.196Fig. 13 displays the bandgaps of six different MHPs as a function of the X–M–X bond angle.157 As observed from the figure, the bandgap decreases as this angle approaches 180°.
 | ||
| Fig. 12 Comparison of optical bandgap of MAPbBr3, CsPbBr3, and FAPbBr3 single crystals. Cubic, tetragonal and orthorhombic phases are indicated by C, T, and O labels, respectively. Reproduced with permission from ref. 184. Copyright 2020, American Chemical Society. | ||
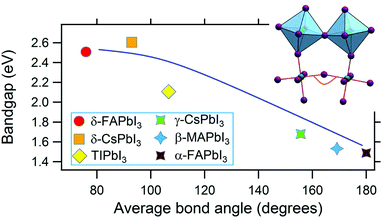 | ||
| Fig. 13 Graph of the bandgap versus M–X–M bond angle in MHPs. Reproduced with permission from ref. 157. Copyright 2019, Elsevier. | ||
Following this trend of widening bandgaps with increased octahedral tilting among different MHP compounds, one might expect that within a single compound, the bandgap should decrease with increasing temperatures as MHPs transition from low-symmetry to high-symmetry structures. It has been demonstrated experimentally, however, that the bandgaps of MHPs increase with increasing temperature.197 Indeed, the temperature dependence of the optical bandgaps of CsPbBr3, MAPbBr3, and FAPbBr3 in Fig. 12 all display a positive temperature coefficient, with monotonically increasing bandgaps with increasing temperature. For widely studied MAPbI3, a blue shift in the bandgap with increasing across the tetragonal-cubic transition has been recorded via temperature-dependent photoluminescence,198–203 spectroscopic ellipsometry,204 and vis-NIR absorption spectroscopy205 even though the nominal Pb–I–Pb angle increases from 165.3 to 180° across the tetragonal-cubic transition.
Through a combination of temperature-dependent UV-vis absorption and ab initio simulations, Quarti and coworkers found that MAPbI3 monotonically blue-shifts through this transition due to large fluctuations in the M–X framework on the picosecond time scale that increase with increasing temperature.206 At temperatures above tetragonal-to-cubic phase transition, MAPbI3 was found to adopt the cubic structure on average, but in fact fluctuates between highly distorted configurations, resulting in an increase in the bandgap compared to the tetragonal phase. Computational modeling has attributed the increase in bandgap upon temperature increase to electron–phonon coupling and thermal expansion.197,207,208
Interestingly, we recently observed a ∼30 meV red shift in the PL spectrum of MAPbI3 across the tetragonal-cubic transition when MAPbI3 crystals were nanoconfined in the ∼20–250 diameter pores of AAO (Fig. 9),150 opposite of the trend observed in bulk crystals. By increasing the surface area-to-volume ratio of these crystals, nanoconfinement shifted the relative Gibbs free energies of the α, β, and γ phases such that the α–β transition temperature was lowered from ∼330 K to between 170–200 K. At these lower temperatures, thermal fluctuations in the M–X framework are likely suppressed, resulting in a narrowing of the bandgap upon transitioning to the cubic phase with I–Pb–I angles of 180°. This narrowing of the bandgap of α-MAPbI3 compared to β-MAPbI3 is predicted when considering static structures.27,209,210
Examining pressure-induced changes in optoelectronic properties of MHPs has also advanced a fundamental understanding of the relationship between molecular structure and band structure. Pressure-induced compression of M–X–M bonds results in a decrease in the bandgap due to increased overlap between Pb 6s and I 5p orbitals, increasing the valence band energy and decreasing the overall bandgap.171,211 A linear positive correlation between Pb–I–Pb bond length and the bandgap, for example, has been reported for MAPbI3.172 On the other hand, octahedral tilting reduces this overlap, resulting in an increase in bandgap at higher pressures.159,167,172
Beyond the bandgap, the impact of polymorphic phase transitions on other optoelectronic properties varies for different compositions and temperature ranges. For CsPbI3, CsSnI3, and FAPbI3, polymorph transitions to their non-perovskite δ-phases destroy device performance as these phases are insulating. For transitions between α, β, and γ phases, the impact on optoelectronic properties is less catastrophic, but can be detrimental nonetheless. While many questions still remain about optoelectronic processes in these materials,212,213 recent temperature-dependent studies have begun to track photophysical processes across polymorph transitions, particularly in widely studied MAPbI3.
In 2015, for example, Milot and coworkers used temperature-dependent time-resolved PL and THz conductivity measurements to examine charge recombination in MAPbI3.11 The rate of monomolecular recombination was observed to increase smoothly in the range of 8–340 K. On the other hand, the temperature dependence of bimolecular and Auger recombination rates were found to depend on the polymorph, as displayed in Fig. 14. In particular, Auger recombination rates significantly increased upon transition from the tetragonal to orthorhombic phase. In a later study, pulse-radiolysis time-resolved microwave conductivity experiments on MAPbI3 and MAPbBr3 further revealed abrupt increases in charge carrier mobilities and lifetimes when crystals transitioned from the tetragonal to the orthorhombic phase.214 While MA+ cations can rotate in the tetragonal phase, their orientation becomes fixed in the orthorhombic phase to form charged domains that reduce charge recombination. This ordering of the MA+ cation was found to result in smaller dielectric constants and larger exciton binding energies compared to the tetragonal phase, contributing to a faster rate of ground state bleaching recovery in the former phase.215 In contrast, no abrupt changes across the tetragonal–orthorhombic phase transition for FAPbI3 was observed due to the fact that FA+ retain rotational freedom in the low-temperature orthorhombic phase.216
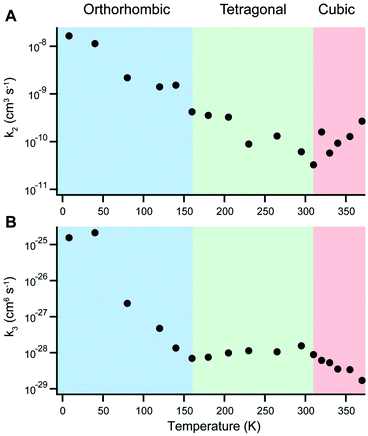 | ||
| Fig. 14 Temperature dependence of (A) bimolecular and (B) Auger recombination rates for MAPbI3. Reproduced with permission from ref. 11. Copyright 2015, Wiley. | ||
Because the MA+ cations can rotate in all directions in both the tetragonal and cubic phases of MAPbI3, their role in modulating photophysical processes across the tetragonal-cubic transition may be less pronounced compared to the orthorhombic–tetragonal transition. Examining temperature-dependent dielectric properties of MAPbI3 using microwave conductance experiments found that cation rotation was too slow to influence charge carrier mobilities and lifetimes in the range of 160–300 K.217 Recent temperature-dependent photoconductivity experiments on FAPbBr3, on the other hand, revealed multiple discontinuities in the peak intensities and peak locations, only two of which corresponded to crystallographic phase changes from the cubic to tetragonal phase at 266 K and the tetragonal to orthorhombic phase at 153 K.218Fig. 15 displays the photoconductivity characteristics, heat capacity, and mean square displacement (MSD) of hydrogen atoms as a function of temperature. Five distinct discontinuities can be observed in the temperature-dependent excitonic peak center, represented by gray circles in Fig. 15a. These five transitions were all found to correspond to discontinuities in the temperature-dependent MSD of hydrogen, as measured by elastic neutron scattering (Fig. 15c). These results suggest that FA+ rotational dynamics may induce local temperature-dependent distortions through dynamic coupling to the M–X framework.
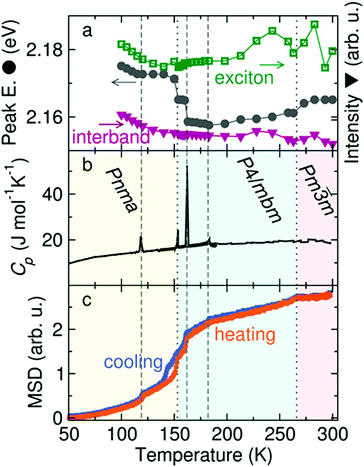 | ||
| Fig. 15 (a) Plot of the excitonic peak intensity (green squares), excitonic peak center (gray circles) and interband intensity (purple triangles) extracted from photoconductivity data as a function of excitation wavelength and temperature for FAPbBr3. (b) Differential scanning calorimetry scan for FAPbBr3, with crystallographic phases at different temperatures labelled. (c) Mean squared displacement of hydrogen upon heating and cooling of FAPbBr3 measured via elastic neutron scattering. Dotted and dashed lines represent discontinuities in the spectra that do and do not correspond to solid-state phase transitions, respectively. Reproduced with permission from ref. 218. Copyright 2019, American Chemical Society. | ||
One of the main applications for MHPs is in emerging photovoltaics to harvest renewable solar energy. Depending on the location and specific use, solar panels can be exposed to a wide range of temperatures, inducing polymorph transitions in the MHP active layer during device operation. Monitoring structural phase transitions in MAPbI3 active layers during solar cell operation, Zhang and coworkers observed a drop in photocurrent from 20 mA cm−2 at 240 K to 1 mA cm−2 at 140 K.219 This large difference in photocurrent was attributed to a phase transition from the tetragonal to orthorhombic phase upon lowering the temperature. In these devices, power conversion efficiencies of <0.1% were measured at temperatures below 160 K when the orthorhombic phase was present, compared to a maximum efficiency of 16% at 300 K for tetragonal MAPbI3.219 Recent time-of-flight and electrical conductivity measurements on MAPbI3 solar cells have further revealed a balancing of electron and hole mobilities at the tetragonal-cubic phase transition.220
Conclusion
The chemical diversity and flexibility of MHPs has given rise to myriad possibilities of structures and compositions for use in optoelectronic devices. Systematic experimental and computational studies of the relationships between A-site, M-site and X-site ion sizes and the crystal structure of MHPs, as well as temperature-dependent measurements of these crystals via high-resolution X-ray and neutron diffraction, have provided a comprehensive understanding of the factors governing polymorphism in this class of materials. In general, MHPs with tolerance factors closer to 1 will adopt a cubic structure at room temperature, whereas octahedral tilting in MHPs with tolerance factors farther from 1 result in orthorhombic or tetragonal crystal structures under ambient conditions. MHPs transition from lower to higher symmetry with increasing temperature, but higher to lower symmetry with increasing pressure. More complex and less understood are how slight changes in bond lengths and angles, as well as A-site cation dynamics, affect the electronic structure and optoelectronic processes, such as exciton recombination and charge transport. Looking forward, optoelectronic characterization across phase transitions will provide further mechanistic insights into the interplay between charges and the metal halide framework. The role of strategies to shift solid-state phase transition temperatures, for example via size reduction or nanoconfinement, and to kinetically trap metastable phases, such as through pressure cycling, have the potential to improve both the performance and reliability of MHP-based devices. Looking towards future commercialization, suppression of polymorph transitions that negatively impact device performance will be necessary, and research on structure–property–function relationships across these solid-state transitions will undoubtedly play a critical role in the advancement of MHPs for optoelectronic applications.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge support from the National Science Foundation under Award No. CMMI-AM-1846178. The authors are also grateful for support from the PSEG Foundation to advance energy innovation at Stevens.References
- NREL, Best Res. Effic. Chart | Photovolt. Res. | NREL, 2020, https://www.nrel.gov/pv/cell-efficiency.html.
- J. Yan and B. R. Saunders, RSC Adv., 2014, 4, 43286–43314 RSC.
- K. X. Steirer, P. Schulz, G. Teeter, V. Stevanovic, M. Yang, K. Zhu and J. J. Berry, ACS Energy Lett., 2016, 1, 360–366 CrossRef CAS.
- J. Kang and L. W. Wang, J. Phys. Chem. Lett., 2017, 8, 489–493 CrossRef CAS.
- J. A. Steele, H. Jin, I. Dovgaliuk, R. F. Berger, T. Braeckevelt, H. Yuan, C. Martin, E. Solano, K. Lejaeghere, S. M. J. Rogge, C. Notebaert, W. Vandezande, K. P. F. Janssen, B. Goderis, E. Debroye, Y. K. Wang, Y. Dong, D. Ma, M. Saidaminov, H. Tan, Z. Lu, V. Dyadkin, D. Chernyshov, V. Van Speybroeck, E. H. Sargent, J. Hofkens and M. B. J. Roeffaers, Science, 2019, 365, 679–684 CrossRef CAS.
- D. H. Fabini, C. C. Stoumpos, G. Laurita, A. Kaltzoglou, A. G. Kontos, P. Falaras, M. G. Kanatzidis and R. Seshadri, Angew. Chem., Int. Ed., 2016, 55, 15392–15396 CrossRef CAS.
- E. L. Da Silva, J. M. Skelton, S. C. Parker and A. Walsh, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 144107 CrossRef.
- S. Masi, A. F. Gualdrón Reyes and I. Mora-Seró, ACS Energy Lett., 2020, 5, 1974–1985 CrossRef CAS.
- J. Shi, Y. Wang and Y. Zhao, Energy Environ. Mater., 2019, 2, 73–78 CrossRef CAS.
- Y. Fan, H. Meng, L. Wang and S. Pang, Sol. RRL, 2019, 3, 1900215 CrossRef.
- R. L. Milot, G. E. Eperon, H. J. Snaith, M. B. Johnston and L. M. Herz, Adv. Funct. Mater., 2015, 25, 6218–6227 CrossRef CAS.
- J. S. Bechtel and A. Van Der Ven, Phys. Rev. Mater., 2018, 2, 025401 CrossRef CAS.
- V. M. Goldschmidt, Naturwissenschaften, 1926, 14, 477–485 CrossRef CAS.
- L. Q. Jiang, J. K. Guo, H. B. Liu, M. Zhu, X. Zhou, P. Wu and C. H. Li, J. Phys. Chem. Solids, 2006, 67, 1531–1536 CrossRef CAS.
- W. Travis, E. N. K. Glover, H. Bronstein, D. O. Scanlon and R. G. Palgrave, Chem. Sci., 2016, 7, 4548–4556 RSC.
- C. Li, X. Lu, W. Ding, L. Feng, Y. Gao and Z. Guo, Acta Crystallogr., Sect. B: Struct. Sci., 2008, 64, 702–707 CrossRef CAS.
- A. M. Glazer, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1972, B28, 3384–3392 CrossRef.
- J. Even, M. Carignano and C. Katan, Nanoscale, 2016, 8, 6222 RSC.
- C. C. Stoumpos and M. G. Kanatzidis, Acc. Chem. Res., 2015, 48, 2791–2802 CrossRef CAS.
- Y. Fujii, S. Hoshino, Y. Yamada and G. Shirane, Phys. Rev. B: Solid State, 1974, 9, 4549–4559 CrossRef CAS.
- S. Hirotsu and S. Sawada, Phys. Lett. A, 1969, 28, 762–763 CrossRef CAS.
- S. Plesko, R. Kind and J. Roos, J. Phys. Soc. Jpn., 1978, 45, 553–557 CrossRef CAS.
- C. Carabatos-Nédelec, M. Oussaïd and K. Nitsch, J. Raman Spectrosc., 2003, 34, 388–393 CrossRef.
- C. C. Stoumpos, C. D. Malliakas, J. A. Peters, Z. Liu, M. Sebastian, J. Im, T. C. Chasapis, A. C. Wibowo, D. Young Chung, A. J. Freeman, B. W. Wessels and M. G. Kanatzidis, Cryst. Growth Des., 2013, 13, 2722–2727 CrossRef CAS.
- S. Hirotsu, T. Suzuki and S. Sawada, J. Phys. Soc. Jpn., 1977, 43, 575–582 CrossRef CAS.
- M. Rodová, J. Brožek, K. Knížek, K. Nitsch, J. Brooek, K. Knííek and K. Nitsch, J. Therm. Anal. Calorim., 2003, 71, 667–673 CrossRef.
- A. Marronnier, G. Roma, S. Boyer-Richard, L. Pedesseau, J. M. Jancu, Y. Bonnassieux, C. Katan, C. C. Stoumpos, M. G. Kanatzidis and J. Even, ACS Nano, 2018, 12, 3477–3486 CrossRef CAS.
- R. J. Sutton, M. R. Filip, A. A. Haghighirad, N. Sakai, B. Wenger, F. Giustino and H. J. Snaith, ACS Energy Lett., 2018, 3, 1787–1794 CrossRef CAS.
- D. E. Scaife, P. F. Weller and W. G. Fisher, J. Solid State Chem., 1974, 9, 308–314 CrossRef CAS.
- K. Yamada, Y. Kuranaga, K. Ueda, S. Goto, T. Okuda and Y. Furukawa, Bull. Chem. Soc. Jpn., 1998, 71, 127–134 CrossRef CAS.
- D. H. Fabini, G. Laurita, J. S. Bechtel, C. C. Stoumpos, H. A. Evans, A. G. Kontos, Y. S. Raptis, P. Falaras, A. Van Der Ven, M. G. Kanatzidis and R. Seshadri, J. Am. Chem. Soc., 2016, 138, 11820–11832 CrossRef CAS.
- R. H. Andrews, J. D. Donaldson, J. Silver and E. A. D. White, J. Mater. Sci., 1975, 10, 1449–1451 CrossRef CAS.
- K. Yamada, S. Funabiki, H. Horimoto, T. Matsui, T. Okuda and S. Ichiba, Chem. Lett., 1991, 801–804 CrossRef CAS.
- I. Chung, J. H. Song, J. Im, J. Androulakis, C. D. Malliakas, H. Li, A. J. Freeman, J. T. Kenney and M. G. Kanatzidis, J. Am. Chem. Soc., 2012, 134, 8579–8587 CrossRef CAS.
- L. Chi, I. Swainson, L. Cranswick, J. H. Her, P. Stephens and O. Knop, J. Solid State Chem., 2005, 178, 1376–1385 CrossRef CAS.
- A. Poglitsch and D. Weber, J. Chem. Phys., 1987, 87, 6373–6378 CrossRef CAS.
- A. Bernasconi, K. Page, Z. Dai, L. Z. Tan, A. M. Rappe and L. Malavasi, J. Phys. Chem. C, 2018, 122, 28265–28272 CrossRef CAS.
- W. M. I. P. Swainson, R. P. Hammond, C. Soulliere and O. Knop, J. Solid State Chem., 2003, 176, 97–104 CrossRef.
- T. Baikie, N. S. Barrow, Y. Fang, P. J. Keenan, P. R. Slater, R. O. Piltz, M. Gutmann, S. G. Mhaisalkar and T. J. White, J. Mater. Chem. A, 2015, 3, 9298–9307 RSC.
- N. Onoda-Yamamuro, O. Yamamuro, T. Matsuo and H. Suga, J. Phys. Chem. Solids, 1992, 53, 277–281 CrossRef CAS.
- T. Baikie, Y. Fang, J. M. Kadro, M. Schreyer, F. Wei, S. G. Mhaisalkar, M. Graetzel and T. J. White, J. Mater. Chem. A, 2013, 1, 5628 RSC.
- C. C. Stoumpos, C. D. Malliakas and M. G. Kanatzidis, Inorg. Chem., 2013, 52, 9019–9938 CrossRef CAS.
- M. T. Weller, O. J. Weber, P. F. Henry, A. M. Di Pumpo and T. C. Hansen, Chem. Commun., 2015, 51, 4180–4183 RSC.
- Y. Takahashi, R. Obara, Z.-Z. Lin, Y. Takahashi, T. Naito, T. Inabe, S. Ishibashi and K. Terakura, Dalton Trans., 2011, 40, 5563 RSC.
- Y. Takahashi, H. Hasegawa, Y. Takahashi and T. Inabe, J. Solid State Chem., 2013, 205, 39–43 CrossRef CAS.
- S. Govinda, B. P. Kore, D. Swain, A. Hossain, C. De, T. N. Guru Row and D. D. Sarma, J. Phys. Chem. C, 2018, 122, 13758–13766 CrossRef CAS.
- E. C. Schueller, G. Laurita, D. H. Fabini, C. C. Stoumpos, M. G. Kanatzidis and R. Seshadri, Inorg. Chem., 2018, 57, 695–701 CrossRef CAS.
- C. Ferrara, M. Patrini, A. Pisanu, P. Quadrelli, C. Milanese, C. Tealdi and L. Malavasi, J. Mater. Chem. A, 2017, 5, 9391–9395 RSC.
- M. R. Filip, G. E. Eperon, H. J. Snaith and F. Giustino, Nat. Commun., 2014, 5, 5757 CrossRef CAS.
- G. Kieslich, S. Sun and A. K. Cheetham, Chem. Sci., 2014, 5, 4712–4715 RSC.
- J. Gebhardt and A. M. Rappe, Adv. Mater., 2019, 31, 1–15 CrossRef.
- I. P. Swainson, R. P. Hammond, C. Soullière, O. Knop and W. Massa, J. Solid State Chem., 2003, 176, 97–104 CrossRef CAS.
- C. A. López, M. V. Martínez-Huerta, M. C. Alvarez-Galván, P. Kayser, P. Gant, A. Castellanos-Gomez, M. T. Fernández-Díaz, F. Fauth and J. A. Alonso, Inorg. Chem., 2017, 56, 14214–14219 CrossRef.
- W. Xiang and W. Tress, Adv. Mater., 2019, 31, 1902851 CrossRef CAS.
- C. K. Moller, Mat. Fys. Medd. Dan. Vid. Sels., 1959, 32, 1 CAS.
- Y. Fujii, S. Hoshino, Y. Yamada and G. Shirane, Phys. Rev. B: Solid State, 1974, 9, 4549–4559 CrossRef CAS.
- T. Sakudo, H. Unoki, Y. Fujii, J. Kobayashi and M. Yamada, Phys. Lett. A, 1969, 28, 542–543 CrossRef CAS.
- N. Yantara, S. Bhaumik, F. Yan, D. Sabba, H. A. Dewi, N. Mathews, P. P. Boix, H. V. Demir and S. Mhaisalkar, J. Phys. Chem. Lett., 2015, 6, 4360–4364 CrossRef CAS.
- G. E. Eperon, G. M. Paternò, R. J. Sutton, A. Zampetti, A. A. Haghighirad, F. Cacialli and H. J. Snaith, J. Mater. Chem. A, 2015, 3, 19688–19695 RSC.
- J. Liang, J. Liu and Z. Jin, Sol. RRL, 2017, 1, 1700086 CrossRef.
- X. Li, F. Cao, D. Yu, J. Chen, Z. Sun, Y. Shen, Y. Zhu, L. Wang, Y. Wei, Y. Wu and H. Zeng, Small, 2017, 13 Search PubMed.
- P. Ramasamy, D. H. Lim, B. Kim, S. H. Lee, M. S. Lee and J. S. Lee, Chem. Commun., 2016, 52, 2067–2070 RSC.
- C. Li, C. Han, Y. Zhang, Z. Zang, M. Wang, X. Tang and J. Du, Sol. Energy Mater. Sol. Cells, 2017, 172, 341–346 CrossRef CAS.
- K. P. Marshall, M. Walker, R. I. Walton and R. A. Hatton, Nat. Energy, 2016, 1, 1–9 Search PubMed.
- T. Bin Song, T. Yokoyama, C. C. Stoumpos, J. Logsdon, D. H. Cao, M. R. Wasielewski, S. Aramaki and M. G. Kanatzidis, J. Am. Chem. Soc., 2017, 139, 836–842 CrossRef.
- C. Huo, X. Liu, X. Song, Z. Wang and H. Zeng, J. Phys. Chem. Lett., 2017, 8, 4785–4792 CrossRef CAS.
- S. Zhou, G. Zhou, Y. Li, X. Xu, Y.-J. Hsu, J. Xu, N. Zhao and X. Lu, ACS Energy Lett., 2020, 23, 2614–2623 CrossRef.
- H. Cho, C. Wolf, J. S. Kim, H. J. Yun, J. S. Bae, H. Kim, J.-M. Heo, S. Ahn and T.-W. Lee, Adv. Mater., 2017, 29, 1700579 CrossRef.
- Z. Shi, S. Li, Y. Li, H. Ji, X. Li, D. Wu, T. Xu, Y. Chen, Y. Tian, Y. Zhang, C. Shan and G. Du, ACS Nano, 2018, 12, 1462–1472 CrossRef CAS.
- C. Wu, Y. Zou, T. Wu, M. Ban, V. Pecunia, Y. Han, Q. Liu, T. Song, S. Duhm and B. Sun, Adv. Funct. Mater., 2017, 27, 1700338 CrossRef.
- Y. Wang, X. Liu, T. Zhang, X. Wang, M. Kan, J. Shi and Y. Zhao, Angew. Chem. Int. Ed., 2019, 58, 16691–16696 CrossRef CAS.
- S. Tao, I. Schmidt, G. Brocks, J. Jiang, I. Tranca, K. Meerholz and S. Olthof, Nat. Commun., 2019, 10, 1–10 CrossRef CAS.
- P. Mauersberger and F. Huber, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1980, 36, 683–684 CrossRef.
- R. J. Sutton, G. E. Eperon, L. Miranda, E. S. Parrott, B. A. Kamino, J. B. Patel, M. T. Hörantner, M. B. Johnston, A. A. Haghighirad, D. T. Moore and H. J. Snaith, Adv. Energy Mater., 2016, 6, 1502458 CrossRef.
- K. Yamada, S. Funabiki, H. Horimoto, T. Matsui, T. Okuda and S. Ichiba, Chem. Lett., 1991, 801–804 CrossRef CAS.
- A. Kojima, K. Teshima, Y. Shirai and T. Miyasaka, J. Am. Chem. Soc., 2009, 131, 6050–6051 CrossRef CAS.
- C.-Y. Chen, H.-Y. Lin, K.-M. Chiang, W.-L. Tsai, Y.-C. Huang, C.-S. Tsao and H.-W. Lin, Adv. Mater., 2017, 29, 1605290 CrossRef.
- Y. Yang, J. P. Robbins, L. Ezeonu, Y. Ma, N. Sparta, X. Kong, S. Strauf, S. G. Podkolzin and S. S. Lee, J. Mater. Chem. C, 2020, 8, 8896–8903 RSC.
- Z. Xiao and Y. Yan, Adv. Energy Mater., 2017, 7, 1701136 CrossRef.
- P. S. Whitfield, N. Herron, W. E. Guise, K. Page, Y. Q. Cheng, I. Milas and M. K. Crawford, Sci. Rep., 2016, 6, 35685 CrossRef CAS.
- C. Motta, F. El-Mellouhi, S. Kais, N. Tabet, F. Alharbi and S. Sanvito, Nat. Commun., 2015, 6, 1–7 Search PubMed.
- D. Weber, Z. Naturforsch. B, 1978, 33, 1443–1445 Search PubMed.
- A. Poglitsch and D. Weber, J. Chem. Phys., 1987, 87, 6373–6378 CrossRef CAS.
- N. Onoda-Yamamuro, T. Matsuo and H. Suga, J. Phys. Chem. Solids, 1990, 51, 1383–1395 CrossRef CAS.
- D. H. Fabini, T. Hogan, H. A. Evans, C. C. Stoumpos, M. G. Kanatzidis and R. Seshadri, J. Phys. Chem. Lett., 2016, 7, 376–381 CrossRef CAS.
- D. H. Fabini, C. C. Stoumpos, G. Laurita, A. Kaltzoglou, A. G. Kontos, P. Falaras, M. G. Kanatzidis and R. Seshadri, Angew. Chem. Int. Ed., 2016, 55, 15392–15396 CrossRef CAS.
- I. Anusca, S. Balčiūnas, P. Gemeiner, Š. Svirskas, M. Sanlialp, G. Lackner, C. Fettkenhauer, J. Belovickis, V. Samulionis, M. Ivanov, B. Dkhil, J. Banys, V. V. Shvartsman and D. C. Lupascu, Adv. Energy Mater., 2017, 7, 1700600 CrossRef.
- J. H. Lee, J. H. Lee, E. H. Kong and H. M. Jang, Sci. Rep., 2016, 6, 305–353 Search PubMed.
- J. H. Lee, N. C. Bristowe, J. H. Lee, S. H. Lee, P. D. Bristowe, A. K. Cheetham and H. M. Jang, Chem. Mater., 2016, 28, 4259–4266 CrossRef CAS.
- J. S. Bechtel, R. Seshadri and A. Van Der Ven, J. Phys. Chem. C, 2016, 120, 12403–12410 CrossRef CAS.
- M. A. Carignano, Y. Saeed, S. A. Aravindh, I. S. Roqan, J. Even and C. Katan, Phys. Chem. Chem. Phys., 2016, 18, 27109–27118 RSC.
- J. Even, M. Carignano and C. Katan, Nanoscale, 2016, 8, 6222–6236 RSC.
- I. P. Swainson, C. Stock, S. F. Parker, L. Van Eijck, M. Russina and J. W. Taylor, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 100303 CrossRef.
- T. Chen, B. J. Foley, B. Ipek, M. Tyagi, J. R. D. Copley, C. M. Brown, J. J. Choi and S.-H. Lee, Phys. Chem. Chem. Phys., 2015, 17, 31278–31286 RSC.
- A. M. A. Leguy, J. M. Frost, A. P. McMahon, V. G. Sakai, W. Kockelmann, C. Law, X. Li, F. Foglia, A. Walsh, B. C. O’Regan, J. Nelson, J. T. Cabral and P. R. F. Barnes, Nat. Commun., 2015, 6, 7124 CrossRef.
- K. Druzbicki, R. S. Pinna, S. Rudić, M. Jura, G. Gorini and F. Fernandez-Alonso, J. Phys. Chem. Lett., 2016, 7, 4701–4709 CrossRef CAS.
- B. Li, Y. Kawakita, Y. Liu, M. Wang, M. Matsuura, K. Shibata, S. Ohira-Kawamura, T. Yamada, S. Lin, K. Nakajima and S. F. Liu, Nat. Commun., 2017, 8, 1–9 CrossRef.
- W. M. J. Franssen, S. G. D. Van Es, R. Dervişoğlu, G. A. De Wijs and A. P. M. Kentgens, J. Phys. Chem. Lett., 2017, 8, 61–66 CrossRef CAS.
- C. Roiland, G. Trippé-Allard, K. Jemli, B. Alonso, J. C. Ameline, R. Gautier, T. Bataille, L. Le Pollès, E. Deleporte, J. Even and C. Katan, Phys. Chem. Chem. Phys., 2016, 18, 27133–27142 RSC.
- B. A. Rosales, L. Men, S. D. Cady, M. P. Hanrahan, A. J. Rossini and J. Vela, Chem. Mater., 2016, 28, 6848–6859 CrossRef CAS.
- S. Govinda, B. P. Kore, D. Swain, A. Hossain, C. De, T. N. Guru Row and D. D. Sarma, J. Phys. Chem. C, 2018, 122, 42 CrossRef.
- A. A. Bakulin, O. Selig, H. J. Bakker, Y. L. A. Rezus, C. Müller, T. Glaser, R. Lovrincic, Z. Sun, Z. Chen, A. Walsh, J. M. Frost and T. L. C. Jansen, J. Phys. Chem. Lett., 2015, 6, 3663–3669 CrossRef CAS.
- J. Gong, M. Yang, X. Ma, R. D. Schaller, G. Liu, L. Kong, Y. Yang, M. C. Beard, M. Lesslie, Y. Dai, B. Huang, K. Zhu and T. Xu, J. Phys. Chem. Lett., 2016, 7, 2879–2887 CrossRef CAS.
- Y. Guo, O. Yaffe, D. W. Paley, A. N. Beecher, T. D. Hull, G. Szpak, J. S. Owen, L. E. Brus and M. A. Pimenta, Phys. Rev. Mater., 2017, 1, 042401 CrossRef.
- R. E. Wasylishen, O. Knop and J. B. Macdonald, Solid State Commun., 1985, 56, 581–582 CrossRef CAS.
- B. J. Foley, B. Ipek, M. Tyagi, J. R. D. Copley, C. M. Brown, J. J. Choi, S.-H. H. Lee, T. Chen, B. J. Foley, B. Ipek, M. Tyagi, J. R. D. Copley, C. M. Brown, J. J. Choi, S.-H. H. Lee, J. R. D. Copley, C. M. Brown, J. J. Choi and S.-H. H. Lee, Phys. Chem. Chem. Phys., 2015, 17, 31278–31286 RSC.
- D. H. Fabini, Ting, A. Siaw, C. C. Stoumpos, G. Laurita, D. Olds, K. Page, J. G. Hu, M. G. Kanatzidis, S. Han and R. Seshadri, DOI:10.1021/jacs.7b09536.
- Y. Ren, I. W. H. Oswald, X. Wang, G. T. McCandless and J. Y. Chan, Cryst. Growth Des., 2016, 16, 2945–2951 CrossRef CAS.
- J. Breternitz, M. Tovar and S. Schorr, Sci. Rep., 2020, 10, 16613 CrossRef CAS.
- M. Szafrański and A. Katrusiak, J. Phys. Chem. Lett., 2016, 7, 3458–3466 CrossRef.
- C. C. Stoumpos, C. D. Malliakas and M. G. Kanatzidis, Inorg. Chem., 2013, 52, 9019–9038 CrossRef CAS.
- Y. Rakita, O. Bar-Elli, E. Meirzadeh, H. Kaslasi, Y. Peleg, G. Hodes, I. Lubomirsky, D. Oron, D. Ehre and D. Cahen, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E5504–E5512 CrossRef CAS.
- K. Frohna, T. Deshpande, J. Harter, W. Peng, B. A. Barker, J. B. Neaton, S. G. Louie, O. M. Bakr, D. Hsieh and M. Bernardi, Nat. Commun., 2018, 9, 1–9 CrossRef CAS.
- R. Ohmann, L. K. Ono, H. S. Kim, H. Lin, M. V. Lee, Y. Li, N. G. Park and Y. Qi, J. Am. Chem. Soc., 2015, 137, 16049–16054 CrossRef CAS.
- A. Mattoni, A. Filippetti, M. I. Saba and P. Delugas, J. Phys. Chem. C, 2015, 119, 17421–17428 CrossRef CAS.
- J.-H. Lee, N. C. Bristowe, P. D. Bristowe and A. K. Cheetham, Chem. Commun., 2015, 51, 6434 RSC.
- J. Li, M. Bouchard, P. Reiss, D. Aldakov, S. Pouget, R. Demadrille, C. Aumaitre, B. Frick, D. Djurado, M. Rossi and P. Rinke, J. Phys. Chem. Lett., 2018, 9, 3969–3977 CrossRef CAS.
- G. Schuck, D. M. Többens, M. Koch-Müller, I. Efthimiopoulos and S. Schorr, J. Phys. Chem. C, 2018, 122, 5227–5237 CrossRef CAS.
- F. Brivio, J. M. Frost, J. M. Skelton, A. J. Jackson, O. J. Weber, M. T. Weller, A. R. Goñi, A. M. A. Leguy, P. R. F. Barnes and A. Walsh, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 144308 CrossRef.
- I. Deretzis and A. La Magna, Nanoscale, 2017, 9, 5896–5903 RSC.
- S. Maheshwari, M. B. Fridriksson, S. Seal, J. Meyer and F. C. Grozema, J. Phys. Chem. C, 2019, 123, 14652–14661 CrossRef CAS.
- S. Kanno, Y. Imamura, A. Saeki and M. Hada, J. Phys. Chem. C, 2017, 121, 14051–14059 CrossRef CAS.
- O. J. Weber, D. Ghosh, S. Gaines, P. F. Henry, A. B. Walker, M. S. Islam and M. T. Weller, Chem. Mater., 2018, 30, 3768–3778 CrossRef CAS.
- Y. Li, F. Z. Liu, M. Waqas, T. L. Leung, H. W. Tam, X. Q. Lan, B. Tu, W. Chen, A. B. Djurišić and Z. B. He, Small Methods, 2018, 2, 1700387 CrossRef.
- W. S. Yang, B. W. Park, E. H. Jung, N. J. Jeon, Y. C. Kim, D. U. Lee, S. S. Shin, J. Seo, E. K. Kim, J. H. Noh and S. Il Seok, Science, 2017, 356, 1376–1379 CrossRef CAS.
- E. Smecca, Y. Numata, I. Deretzis, G. Pellegrino, S. Boninelli, T. Miyasaka, A. La Magna and A. Alberti, Phys. Chem. Chem. Phys., 2016, 18, 13413–13422 RSC.
- O. J. Weber, D. Ghosh, S. Gaines, P. F. Henry, A. B. Walker, M. S. Islam and M. T. Weller, Chem. Mater., 2018, 30, 3768–3778 CrossRef CAS.
- A. Franz, D. M. Többens, F. Lehmann, M. Kärgell and S. Schorr, Res. Pap. Acta Crystallogr., 2020, 76, 267–274 CAS.
- D. H. Fabini, T. A. Siaw, C. C. Stoumpos, G. Laurita, D. Olds, K. Page, J. G. Hu, M. G. Kanatzidis, S. Han and R. Seshadri, J. Am. Chem. Soc., 2017, 139, 16875–16884 CrossRef CAS.
- X. Kong, K. Zong and S. S. Lee, Chem. Mater., 2019, 31, 4953–4970 CrossRef CAS.
- G. T. Rengarajan, D. Enke, M. Steinhart and M. Beiner, Phys. Chem. Chem. Phys., 2011, 13, 21367–21374 RSC.
- J. M. McHale, A. Auroux, A. J. Perrotta and A. Navrotsky, Science, 1997, 277, 788–789 CrossRef CAS.
- R. C. Garvie, J. Phys. Chem., 1978, 82, 218–224 CrossRef CAS.
- D. Fu and H. Suzuki, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 3125–3129 CrossRef CAS.
- P. Ayyub, S. Chattopadhyay, M. Multani and B. Road, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 6135–6138 CrossRef CAS.
- B. Zhao, S. F. Jin, S. Huang, N. Liu, J. Y. Ma, D. J. Xue, Q. Han, J. Ding, Q. Q. Ge, Y. Feng and J. S. Hu, J. Am. Chem. Soc., 2018, 140, 11716–11725 CrossRef CAS.
- K. Hong, Q. Van Le, S. Y. Kim and H. W. Jang, J. Mater. Chem. C, 2018, 6, 2189–2209 RSC.
- Y. Wei, Z. Cheng and J. Lin, Chem. Soc. Rev., 2019, 48, 310–350 RSC.
- L. Protesescu, S. Yakunin, M. I. Bodnarchuk, F. Krieg, R. Caputo, C. H. Hendon, R. X. Yang, A. Walsh and M. V. Kovalenko, Nano Lett., 2015, 15, 3692–3696 CrossRef CAS.
- F. Bertolotti, L. Protesescu, M. V. Kovalenko, S. Yakunin, A. Cervellino, S. J. L. Billinge, M. W. Terban, J. S. Pedersen, N. Masciocchi and A. Guagliardi, ACS Nano, 2017, 11, 3819–3831 CrossRef CAS.
- R. X. Yang and L. Z. Tan, J. Chem. Phys., 2020, 152, 034702 CrossRef CAS.
- P. Cottingham and R. L. Brutchey, Chem. Mater., 2018, 30, 6711–6716 CrossRef CAS.
- P. Cottingham and R. L. Brutchey, Chem. Commun., 2016, 52, 5246–5249 RSC.
- L. Liu, R. Zhao, C. Xiao, F. Zhang, F. Pevere, K. Shi, H. Huang, H. Zhong and I. Sychugov, J. Phys. Chem. Lett., 2019, 10, 5451–5457 CrossRef CAS.
- M. C. Brennan, M. Kuno and S. Rouvimov, Inorg. Chem., 2019, 58, 1555–1560 CrossRef CAS.
- B. D. Hamilton, J.-M. Ha, M. A. Hillmyer and M. D. Ward, Acc. Chem. Res., 2012, 45, 414–423 CrossRef CAS.
- Q. Jiang and M. D. Ward, Chem. Soc. Rev., 2014, 43, 2066–2079 RSC.
- B. D. Hamilton, J. M. Ha, M. A. Hillmyer and M. D. Ward, Acc. Chem. Res., 2012, 45, 414–423 CrossRef CAS.
- S. Lee, J. Feldman and S. S. Lee, Cryst. Growth Des., 2016, 16, 4744–4751 CrossRef CAS.
- X. Kong, K. Shayan, S. Lee, C. Ribeiro, S. Strauf and S. S. Lee, Nanoscale, 2018, 10, 8320–8328 RSC.
- S. Ma, S. H. Kim, B. Jeong, H. C. Kwon, S. C. Yun, G. Jang, H. Yang, C. Park, D. Lee and J. Moon, Small, 2019, 15, 1–12 Search PubMed.
- X. Kong, K. Shayan, S. Hua, S. Strauf and S. S. Lee, ACS Appl. Energy Mater., 2019, 2, 2948–2955 CrossRef CAS.
- A. Waleed, M. M. Tavakoli, L. Gu, S. Hussain, D. Zhang, S. Poddar, Z. Wang, R. Zhang and Z. Fan, Nano Lett., 2017, 17, 4951–4957 CrossRef CAS.
- L. Gu, D. Zhang, M. Kam, Q. Zhang, S. Poddar, Y. Fu, X. Mo and Z. Fan, Nanoscale, 2018, 10, 15164–15172 RSC.
- Q. Li, L. Zhang, Z. Chen and Z. Quan, J. Mater. Chem. A, 2019, 7, 16089–16108 RSC.
- Y. Lee, D. B. Mitzi, P. W. Barnes and T. Vogt, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 020103 CrossRef.
- G. Liu, L. Kong, W. Yang and H. K. Mao, Mater. Today, 2019, 27, 91–106 CrossRef CAS.
- M. Szafrański and A. Katrusiak, J. Phys. Chem. Lett., 2017, 8, 2496–2506 CrossRef.
- X. Lü, W. Yang, Q. Jia and H. Xu, Chem. Sci., 2017, 8, 6764–6776 RSC.
- A. Jaffe, Y. Lin and H. I. Karunadasa, ACS Energy Lett., 2017, 2, 1549–1555 CrossRef CAS.
- L. Wang, K. Wang, G. Xiao, Q. Zeng and B. Zou, J. Phys. Chem. Lett., 2016, 7, 5273–5279 CrossRef CAS.
- L. Zhang, L. Wang, K. Wang and B. Zou, J. Phys. Chem. C, 2018, 122, 15220–15225 CrossRef CAS.
- L. Zhang, Q. Zeng and K. Wang, J. Phys. Chem. Lett., 2017, 8, 49 CrossRef.
- G. Yuan, S. Qin, X. Wu, H. Ding and A. Lu, Phase Transitions, 2018, 91, 38–47 CrossRef CAS.
- M. Coduri, T. A. Strobel, M. Szafran, A. Katrusiak, A. Mahata, F. Cova, S. Bonomi, E. Mosconi, F. De Angelis and L. Malavasi, J. Phys. Chem. Lett., 2019, 10, 25 Search PubMed.
- Y. Wang, X. Lü, W. Yang, T. Wen, L. Yang, X. Ren, L. Wang, Z. Lin and Y. Zhao, DOI:10.1021/jacs.5b06346.
- J. Fang, S. Jiang, Y. Fang, R. Li, H. Xiao, J. Crowley, C. Wang, T. J. White, W. A. Goddard, Z. Wang, T. Baikie and J. Fang, Angew. Chem., Int. Ed., 2016, 55, 6540–6544 CrossRef.
- X. Lü, Y. Wang, C. C. Stoumpos, Q. Hu, X. Guo, H. Chen, L. Yang, J. S. Smith, W. Yang, Y. Zhao, H. Xu, M. G. Kanatzidis and Q. Jia, Adv. Mater., 2016, 28, 8663–8668 CrossRef.
- L. Wang, K. Wang and B. Zou, J. Phys. Chem. Lett., 2016, 7, 2556–2562 CrossRef CAS.
- H. Zhu, T. Cai, M. Que, J. P. Song, B. M. Rubenstein, Z. Wang and O. Chen, J. Phys. Chem. Lett., 2018, 9, 4199–4205 CrossRef CAS.
- A. Jaffe, Y. Lin, C. M. Beavers, J. Voss, W. L. Mao and H. I. Karunadasa, ACS Cent. Sci., 2016, 2, 201–209 CrossRef CAS.
- M. Szafrański and A. Katrusiak, J. Phys. Chem. Lett., 2016, 7, 3458–3466 CrossRef.
- L. Kong, G. Liua, J. Gong, Q. Hu, R. D. Schaller, P. Dera, D. Zhang, Z. Liu, W. Yang, K. Zhu, Y. Tang, C. Wang, S. H. Wei, T. Xu and H. K. Mao, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 8910–8915 CrossRef CAS.
- F. Capitani, C. Marini, S. Caramazza, P. Postorino, G. Garbarino, M. Hanfland, A. Pisanu, P. Quadrelli and L. Malavasi, J. Appl. Phys., 2016, 119, 185901 CrossRef.
- A. Halder, Y. Rakita, D. Cahen and S. K. Sarkar, J. Phys. Chem. Lett., 2020, 11, 1473–1476 CrossRef CAS.
- G. Liu, L. Kong, J. Gong, W. Yang, H. Mao, Q. Hu, Z. Liu, R. D. Schaller, D. Zhang and T. Xu, Adv. Funct. Mater., 2017, 27, 1604208 CrossRef.
- S. Bonomi, I. Tredici, B. Albini, P. Galinetto, A. Rizzo, A. Listorti, U. A. Tamburini and L. Malavasi, Chem. Commun., 2018, 54, 13212–13215 RSC.
- G. Liu, J. Gong, L. Kong, R. D. Schaller, Q. Hu, Z. Liu, S. Yan, W. Yang, C. C. Stoumpos, M. G. Kanatzidis, H. K. Mao and T. Xu, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 8076–8081 CrossRef CAS.
- G. Liu, L. Kong, P. Guo, C. C. Stoumpos, Q. Hu, Z. Liu, Z. Cai, D. J. Gosztola, H. K. Mao, M. G. Kanatzidis and R. D. Schaller, ACS Energy Lett., 2017, 2, 2518–2524 CrossRef CAS.
- Y. H. Chang, K. Matsuishi and C. H. Park, J. Korean Phys. Soc., 2004, 44, 889–893 CAS.
- F. Brivio, A. B. Walker and A. Walsh, APL Mater., 2013, 1, 042111 CrossRef.
- C. Grote and R. F. Berger, J. Phys. Chem. C, 2015, 119, 22832–22837 CrossRef CAS.
- R. Prasanna, A. Gold-Parker, T. Leijtens, B. Conings, A. Babayigit, H. G. Boyen, M. F. Toney and M. D. McGehee, J. Am. Chem. Soc., 2017, 139, 11117–11124 CrossRef CAS.
- G. Mannino, I. Deretzis, E. Smecca, A. La Magna, A. Alberti, D. Ceratti and D. Cahen, J. Phys. Chem. Lett., 2020, 11, 2490–2496 CrossRef CAS.
- C. J. Bartel, C. Sutton, B. R. Goldsmith, R. Ouyang, C. B. Musgrave, L. M. Ghiringhelli and M. Scheffler, Sci. Adv., 2019, 5, eaav0693 CrossRef CAS.
- M. Becker, T. Klüner and M. Wark, Dalton Trans., 2017, 46, 3500–3509 RSC.
- J. L. Knutson, J. D. Martin and D. B. Mitzi, Inorg. Chem., 2005, 44, 4699–4705 CrossRef CAS.
- M. R. Filip, G. E. Eperon, H. J. Snaith and F. Giustino, Nat. Commun., 2014, 5, 1–9 Search PubMed.
- N. Pellet, P. Gao, G. Gregori, T.-Y. Yang, M. K. Nazeeruddin, J. Maier and M. Grätzel, Angew. Chem., 2014, 126, 3215–3221 CrossRef.
- J. H. Noh, S. H. Im, J. H. Heo, T. N. Mandal and S. Il Seok, Nano Lett., 2013, 13, 1764–1769 CrossRef CAS.
- A. Walsh, J. Phys. Chem. C, 2015, 119, 5755–5760 CrossRef CAS.
- D. Luo, L. Yu, H. Wang, T. Zou, L. Luo, Z. Liu and Z. Lu, RSC Adv., 2015, 5, 85480–85485 RSC.
- A. K. Jena, A. Kulkarni and T. Miyasaka, Chem. Rev., 2019, 119, 3036–3103 CrossRef CAS.
- Z. Li, M. Yang, J.-S. Park, S.-H. Wei, J. J. Berry and K. Zhu, Chem. Mater., 2016, 28, 284–292 CrossRef CAS.
- G. E. Eperon, K. H. Stone, L. E. Mundt, T. H. Schloemer, S. N. Habisreutinger, S. P. Dunfield, L. T. Schelhas, J. J. Berry and D. T. Moore, ACS Energy Lett., 2020, 5, 1856–1864 CrossRef CAS.
- J. H. Noh, S. H. Im, J. H. Heo, T. N. Mandal and S. Il Seok, Nano Lett., 2013, 13, 1764–1769 CrossRef CAS.
- A. Francisco-López, B. Charles, O. J. Weber, M. I. Alonso, M. Garriga, M. Campoy-Quiles, M. T. Weller and A. R. Goñi, J. Phys. Chem. Lett., 2019, 10, 2971–2977 CrossRef.
- V. D’Innocenzo, G. Grancini, M. J. P. Alcocer, A. R. S. Kandada, S. D. Stranks, M. M. Lee, G. Lanzani, H. J. Snaith and A. Petrozza, Nat. Commun., 2014, 5, 1–6 Search PubMed.
- Y. Yamada, T. Nakamura, M. Endo, A. Wakamiya and Y. Kanemitsu, Appl. Phys. Express, 2014, 7, 032302 CrossRef.
- W. Zhang, M. Saliba, S. D. Stranks, Y. Sun, X. Shi, U. Wiesner and H. J. Snaith, Nano Lett., 2013, 13, 4505–4510 CrossRef CAS.
- R. L. Milot, G. E. Eperon, H. J. Snaith, M. B. Johnston and L. M. Herz, Adv. Funct. Mater., 2015, 25, 6218–6227 CrossRef CAS.
- H. Diab, G. Trippé-Allard, F. Lédée, K. Jemli, C. Vilar, G. Bouchez, V. L. R. Jacques, A. Tejeda, J. Even, J. S. Lauret, E. Deleporte and D. Garrot, J. Phys. Chem. Lett., 2016, 7, 5093–5100 CrossRef CAS.
- J. H. Lee, N. C. Bristowe, J. H. Lee, S. H. Lee, P. D. Bristowe, A. K. Cheetham and H. M. Jang, Chem. Mater., 2016, 28, 4259–4266 CrossRef CAS.
- Y. Jiang, A. M. Soufiani, A. Gentle, F. Huang, A. Ho-Baillie and M. A. Green, Appl. Phys. Lett., 2016, 108, 061905 CrossRef.
- M. N. F. Hoque, N. Islam, Z. Li, G. Ren, K. Zhu and Z. Fan, ChemSusChem, 2016, 9, 2692–2698 CrossRef CAS.
- C. Quarti, E. Mosconi, J. M. Ball, V. D’Innocenzo, C. Tao, S. Pathak, H. J. Snaith, A. Petrozza and F. De Angelis, Energy Environ. Sci., 2016, 9, 155–163 RSC.
- W. A. Saidi, S. Poncé and B. Monserrat, J. Phys. Chem. Lett., 2016, 7, 5247–5252 CrossRef CAS.
- J. Y. Yang and M. Hu, J. Phys. Chem. Lett., 2017, 8, 3720–3725 CrossRef CAS.
- S. X. Tao, X. Cao and P. A. Bobbert, Sci. Rep., 2017, 7, 1–9 CrossRef.
- J. Kim, S. C. Lee, S. H. Lee and K. H. Hong, J. Phys. Chem. C, 2015, 119, 4627–4634 CrossRef CAS.
- D. Ghosh, A. Aziz, J. A. Dawson, A. B. Walker and M. S. Islam, Chem. Mater., 2019, 31, 4063–4071 CrossRef CAS.
- L. M. Herz, J. Phys. Chem. Lett., 2018, 9, 6853–6863 CrossRef CAS.
- J. Peng, Y. Chen, K. Zheng, T. Pullerits and Z. Liang, Chem. Soc. Rev., 2017, 46, 5714–5729 RSC.
- M. C. Gélvez-Rueda, D. H. Cao, S. Patwardhan, N. Renaud, C. C. Stoumpos, G. C. Schatz, J. T. Hupp, O. K. Farha, T. J. Savenije, M. G. Kanatzidis and F. C. Grozema, J. Phys. Chem. C, 2016, 120, 16577–16585 CrossRef.
- H. Wang, L. Whittaker-Brooks and G. R. Fleming, J. Phys. Chem. C, 2015, 119, 19590–19595 CrossRef CAS.
- M. C. Gélvez-Rueda, N. Renaud and F. C. Grozema, J. Phys. Chem. C, 2017, 121, 23392–23397 CrossRef.
- V. M. Caselli, M. Fischer, D. Meggiolaro, E. Mosconi, F. De Angelis, S. D. Stranks, A. Baumann, V. Dyakonov, E. M. Hutter and T. J. Savenije, J. Phys. Chem. Lett., 2019, 10, 5128–5134 CrossRef CAS.
- E. M. Mozur, J. C. Trowbridge, A. E. Maughan, M. J. Gorman, C. M. Brown, T. R. Prisk and J. R. Neilson, ACS Mater. Lett., 2019, 1, 260–264 CrossRef CAS.
- H. Zhang, X. Qiao, Y. Shen, T. Moehl, S. M. Zakeeruddin, M. Grätzel and M. Wang, J. Mater. Chem. A, 2015, 3, 11762–11767 RSC.
- J. Peng, Y. Sun, Y. Chen, Y. Yao and Z. Liang, ACS Energy Lett., 2016, 1, 1000–1006 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2021 |
