Syngas molecules as probes for defects in 2D hexagonal boron nitride: their adsorption and vibrations

Abstract

Single-layer, defect-laden hexagonal boron nitride (dh-BN) is attracting a great deal of attention for its diverse applications: catalysis on the one hand, and single photon emission on the other. As possible probes for identifying some common defects in single-layer h-BN, we present results of ab initio calculations for the adsorption and vibrational characteristics of syngas molecules (H₂, CO, CO₂) on dh-BN containing one of four types of defects: nitrogen vacancy (V_N), boron vacancy (V_B), Stone–Wales defect (SW), and nitrogen substituted by boron (B_N). Through a comparative examination of adsorption features, charge transfer, electronic structure, and vibrational spectrum, we obtain a deep understanding of the interaction of these molecules with dh-BN and the role of the defect states. We find that while CO, CO₂ and atomic hydrogen chemisorb, molecular H₂ physisorbs on dh-BN with the four considered defect types. V_N and V_B show strong affinity for CO and CO₂ since the defect states induced by them lie close to the Fermi level. SW does not favor adsorption of these small molecules, as the process for each is endothermic. In the case of B_N, CO adsorbs strongly but CO₂ only weakly. Vibrational frequencies of notable modes localized at the adsorbed molecules are analyzed and suggested as measures for identification of the defect type. Through a simple comparison of adsorption characteristics of the molecules on these defects, we propose dh-BN with V_N to be a good catalyst candidate for CO₂ hydrogenation.

---

Introduction

Similar to other two dimensional (2D) materials, single-layer hexagonal boron nitride (h-BN) has received considerable attention in the past few years owing to its novel properties that make it amenable for various applications.¹ Structurally analogous to graphene, single-layer h-BN has B and N atoms arranged in a hexagonal lattice and bound together by strong covalent bonds. It is a wide bandgap material with high chemical stability² and ideally suited as a reliable support for other 2D materials.³ Its unique properties have also suggested its potential usage in optoelectronics⁴ and photo-catalysis.⁵ Even more remarkable have been the recent findings of its suitability as a thermal catalyst^1,6,7 and as a single photon emitter,^8–10 pointing to the important role of defects. This is to be expected as pristine h-BN is chemically inert because of the lack of dangling bonds.¹¹ It therefore calls for prudent ways to activate the basal plane of h-BN. Taking cues from prior studies on MoS₂,^12–17 proposals have been made to activate single-layer h-BN by the creation of defects,^18,19 deposition of metal atoms or molecules,^20–23 creation of grain-boundaries,²⁴ and application of strain to the defective surface.²⁵ Quite akin to defect-laden single-layer MoS₂ (with sulfur vacancies), which calculations predict to be a possible catalyst for hydrogenation of syngas to alcohol,¹² single-layer h-BN can be chemically activated for similar reactions, in the presence of point or line defects. Indeed, in the above mentioned experimental and theoretical study⁶ showing propane hydrogenation, the activity was traced to the presence of defects. While nitrogen vacancy has been proposed as the most active defect, interestingly for both catalytic⁶ and single-photon emissive⁸ properties, the role of other types of defects cannot be ruled out. Defects are, however, not easy to characterize experimentally, notwithstanding the nanometer resolution scanning tunnelling microscopy (STM) studies by Feng et al.⁹ Small molecules such as H₂, CO, CO₂, the syngas trio, could, however, serve as a probe of defects through their adsorption and vibrational characteristics on defect-laden hexagonal boron nitride (dh-BN).

Beyond serving as probes of defects, an in-depth understanding of the relative propensity of common defect types in facilitating adsorption of syngas molecules on dh-BN is the first step in rational designing of dh-BN for specific hydrogenation reactions. The topic is of broad interest since h-BN is readily available and thermally stable. With appropriate defects it could serve as a metal-free catalyst for hydrogenation of CO/CO₂ even at temperatures higher than ambient. To probe the catalytic propensity of h-BN toward such hydrogenation, it is thus essential that we gain fundamental insights into the interactions between h-BN and syngas, as presented in this work. It should be noted that adsorption of H₂, CO, and CO₂ (syngas) on other catalysts leading to promising reaction pathway of their conversion into useful (value-added) chemical products, i.e., simple to higher alcohols, formaldehyde, formic acid, and higher hydrocarbons has been the subject of several studies.^26–28 Furthermore, thermodynamic and kinetic favorability of adsorption of syngas molecules on the catalyst surface are critical for efficiently and selectively promoting hydrogenations of CO and CO₂.²⁹ Additionally, catalyst material should be thermally stable, chemically active and selective for the desired reaction products. Historically, metal-based catalysts have been widely investigated for syngas hydrogenation reactions, as they typically demonstrate good catalytic activity and product selectivity.^26–28 The optimal catalyst material is, however, often an expensive, non-abundant metal and/or can be easily oxidized and deactivated. Copper-based catalysts²⁸ are, of course, not expensive but they have poor thermal stability, and hence not suitable for high-temperature reactions without a thermal stabilizer. Cerium-based catalysts³⁰ have also shown good activity and selectivity for CO₂ hydrogenation, but are easily deactivated by a small coverage of deposited carbon. There is thus the need to develop more cost-effective catalyst than presently available.

With the above in mind, we present here results of ab initio calculations, based on density functional theory (DFT) of the adsorption and vibrational characteristics of syngas on dh-BN with one of four possible types of defects – nitrogen vacancy (V_N), boron vacancy (V_B), Stone–Wales (SW), and nitrogen substituted by boron (B_N) – which have been shown to have affinity towards the selected adsorbates.⁶ We examine favorable adsorption sites and orientation of these molecules on dh-BN and analyze the unique local atomic environment and electronic structure of dh-BN as modified by the adsorbed molecules (H₂, CO and CO₂). Quite importantly, we calculate and analyze vibrational frequencies of modes localized at the adsorbed molecules and nearby defect sites to identify notable modes as possible signatures of the adsorption, and thereby the defect type. Based on the DFT-calculated thermodynamics for syngas-adsorption, we suggest that the h-BN with nitrogen vacancy may serve as a potential metal-free catalyst material for hydrogenation of CO₂, fully recognizing that the results presented here are only a first step towards a comprehensive understanding of catalyst reactivity and selectivity.

In the next section, we introduce details of our computational methodology. We next present results and discussion, starting with the geometrical and electronic structure of the four types of point defects in h-BN considered in this work, followed by the adsorption and vibrational analysis of H₂, CO, and CO₂ on the defects and discussion of implications of our results towards the catalytic activity of h-BN. Finally, we provide main conclusions of this work.

Computational details

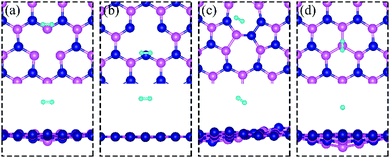
All calculations are performed by using spin-polarized DFT, implemented in the Quantum Espresso Code,³¹ employing plane-wave basis set and the projected-augmented-wave (PAW) method^32,33 for interaction between electrons and nuclei. We use the vdW-DF2 functional³⁴ for exchange–correlation of electrons as it is found to produce excellent lattice constant of h-BN. We use the plane wave basis set with kinetic energy cut-off of 45 Ry and charge density with 180 Ry. We construct a (6 × 6) supercell of single layer hexagonal boron nitride (h-BN) with periodic boundary conditions along in-plane directions and a vacuum of 20 Å to avoid the spurious interaction between periodical images. To model a defect-laden h-BN system (dh-BN), we remove either a boron or a nitrogen atom or substitute a nitrogen atom by boron or rotate a B–N bond by 90°. The lateral dimensions of the resulting dh-BN are optimized so that the system is stress free. The relaxed structures of our model systems of h-BN with the four defects are shown in Fig. 1. To investigate the adsorption characteristics of H₂, CO and CO₂ we begin by placing a molecule at the defect site and at the neighboring atoms near the defect sites and perform ionic relaxations to obtain the lowest-energy adsorption configuration. All systems are relaxed until their energy converges with a threshold of 10⁻⁶ eV and the residual force on each atom reaches below 0.005 eV Å⁻¹. For calculations of relaxed geometry, we sample the Brillouin zone with one k-point (zone center: Γ point) and for electronic density of states, we use a 12 × 12 × 1 k-point mesh. As shown in the ESI,† usage of Γ-point sampling produces system total energy within 7 meV of that obtained with larger k-point sampling, thereby justifying our usage of Γ point sampling.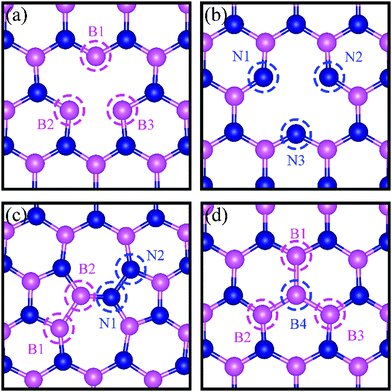

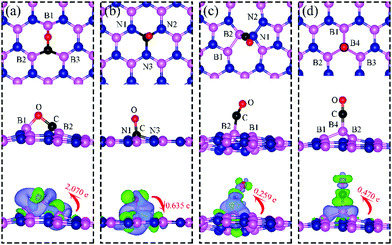
Fig. 1 Schematic representation of h-BN model systems with defects: (a) V_N, (b) V_B, (c) SW, and (d) B_N. Blue and magenta balls represent N and B atoms, respectively.

The adsorption energy is defined as 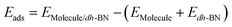, where, , 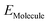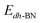are the total energy of the molecule on dh-BN, isolated molecule, and dh-BN, respectively. We calculate charge density difference upon adsorption of molecules on dh-BN using: 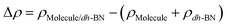, where 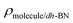, , 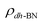and are charge density of the molecule on dh-BN, dh-BN itself, and the isolated molecule, respectively. The charge on each atom is calculated using Bader analysis^35,36 which allows estimation of the charge transfer between the molecule and dh-BN. Vibration frequencies were calculated using the finite-difference method as implemented in the Phonopy package,³⁷ in which we use a displacement of 0.01 Å to maintain validity of the harmonic approximation and avoid numerical errors that would otherwise introduce chaotic behavior in the result. Zero-point energy (ZPE) correction for the total energy of each system is calculated as 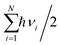, where 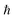is the Planck constant, ν_i is the frequency of vibrational mode i (i = 1…N, where N is the total number of vibrational modes of the system).

Results and discussions

Geometrical and Electronic Structure of dh-BN

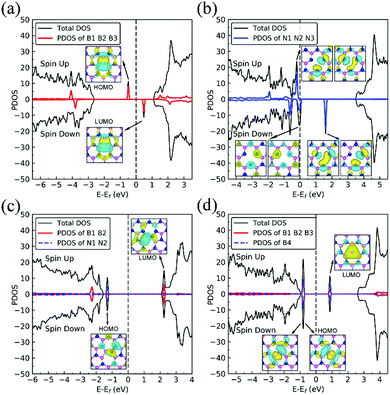
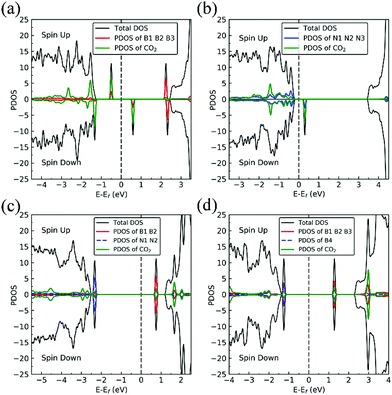
We present in Fig. 1 the geometry of the considered four types of defects in single-layer h-BN, V_N, V_B, SW, and B_N. To explore their electronic structure, we show the spin dependent density of states of each defect in Fig. 2.

Fig. 2 Spin-polarized projected density of states (PDOS) of dh-BN with defects: (a) V_N, (b) V_B, (c) SW, and (d) B_N. The inset displays the wave function of the defect states with isosurface value of 0.001 |e| Å⁻¹.

Nitrogen vacancy (V_N)

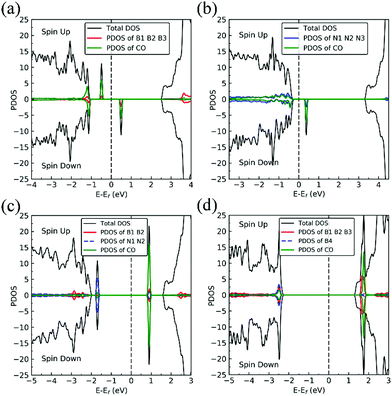
The presence of a nitrogen vacancy on h-BN leads to a local geometric change (Fig. 1a) as reflected by changes in bond lengths and bond angles. The shortest B and N bond length (d_(B2–N)) is 1.492 Å, to be compared to 1.455 Å of pristine h-BN, whereas the angle between N, B and N atoms (θ_(N–B2–N)) is 113.6° as opposed to 120° in pristine h-BN. Also, the separation between N atoms, d_(N–N), is changed from 2.485 to 2.471 Å (0.5% change).

From spin-polarized calculations of electronic density of states in Fig. 2a, we find that dh-BN (V_N) is a spin-polarized system – the effect arising from the unpaired electrons produced by the N vacancy. Of critical importance are the two mid-gap states, one is spin-up—the highest occupied molecular orbital (HOMO)—and the other is spin-down—the lowest unoccupied molecular orbital (LUMO). These states are separated by 0.98 eV. The HOMO and LUMO wave functions (inserts in Fig. 2a) adapt the same symmetry and are π-type dominated by p_z orbitals of B1, B2 and B3 atoms (see Fig. 1a).

Boron vacancy (V_B)

The existence of a boron vacancy on single-layer h-BN leads to the following geometrical change at the defect (Fig. 1b): as compared to those in pristine h-BN, the bond between N and B atoms (d_(B–N1)) shortens from 1.455 to 1.410 Å (3.1% change); the angle between B, N and B atoms (θ_(B–N1–B)) enlarges from 120° to 126.6° (5.5% change); and the distance between N atoms, d_(N–N), elongates from 2.520 to 2.662 Å (5.6% change). The dh-BN with V_B also possesses spin-polarized electronic DOS, as indicated by the calculated spin-up and -down DOS shown in Fig. 2b. The presence of B vacancy leads naturally to undercoordinated nearest-neighboring N atoms, N1, N2, and N3 (Fig. 1b). The PDOS (blue curve Fig. 2b) show the mid-gap state (above the Fermi level) to be composed mainly of contributions from the N1/N2/N3 atoms in the spin down channel, On the other hand, the half-occupied state at the Fermi level, has partial contributions from N1/N2/N3, and also contributions from other surrounding N atoms (see inset). These results are in qualitative agreement with previous studies.^38–40

Stone–Wales (SW) defect

The Stone–Wales (SW) defect is created by rotation of a B–N bond by 90° around its midpoint, as shown in Fig. 1c. The bond lengths of B1–B2, B2–N1, N1–N2 are found to be 1.686, 1.375 and 1.478 Å, respectively. The PDOS of dh-BN (SW), shown in Fig. 2c, indicates that occupied and unoccupied defect states are not spin-polarized. The unoccupied defect states (LUMO) above the Fermi level are mainly contributed by the B1 and B2 atoms with a small contribution from the atoms surround B1 and B2 while the occupied defect states (HOMO) below the Fermi level have main contributions from N1 and N2 atoms. The LUMO states are σ-type dominated by p_x and p_y orbitals from the B–B bond, while the HOMO states are π-type, in agreement with ref. 41.

B substitution for N (B_N)

B_N defects are formed by the substitution of a B atom for N at the lattice of pristine h-BN as shown in Fig. 1d. The B–B and N–B bond lengths are found to be 1.627 and 1.452 Å, respectively. The PDOS plot, Fig. 2d, for dh-BN with B_N displays a large bandgap with non-spin-polarized defect-related gap states. Since boron has two fewer valence electrons than nitrogen, dangling bonds are formed. In the defect levels below and above the Fermi level, the atom B4 makes larger contribution than the sum of the contributions from atoms B1, B2, and B3. Note that B4 and their surrounding boron atoms in single layer dh-BN (B_N) resemble the geometry in the boron nitride nanotube with B_N defect and display similar electronic structure to those found by H. Choi et al.⁴² We also find that the B_N defect introduces unoccupied defect states (LUMO) in the middle of the energy gap and occupied defect states (HOMO) near the valence band edge. These are σ-type orbitals with similar geometric structure in comparison with those in the nanotube with B_N.⁴²

Adsorption of small molecules on dh-BN

Hydrogen molecule on dh-BN

Fig. 3 shows the optimized geometries of H₂ on dh-BN with V_N, V_B, SW, and B_N. We find that the H₂ molecule only physisorbs on dh-BN with adsorption energy of −0.07, −0.05, −0.08 and −0.08 eV, at V_N, V_B, SW and B_N, respectively. The H–H bond length on all four defects is 0.737 Å, which is almost identical to that in the gas phase (0.736 Å). The H–B bond lengths, d_(H-B), are 3.359, 3.267, and 3.357 Å, for H₂ on V_N, SW and B_N, respectively. Similarly, the H–N bond length, d_(H–N), for H₂ on V_B is 3.285 Å. Electron transfer from dh-BN to H₂ is found to be negligible (0.005, 0.004, 0.002, and 0.004 electrons, on V_N, V_B, SW, and B_N, respectively). Such small electron transfer reflects the fact that the H₂ molecule is physisorbed on dh-BN, consistent with almost-unchanged H–H bond lengths.

Fig. 3 Optimized structures of H₂ adsorbed at favored sites of h-BN with (a) V_N, (b) V_B, (c) SW, and (d) B_N. The magenta, blue, white balls represent the B, N and H atoms, respectively. The top and bottom panel shows the top and side views, respectively.

Adsorption of two atomic hydrogens on dh-BN

Since H₂ does not chemisorb in molecular form on dh-BN with V_N, V_B, SW and B_N, we turn to investigate the adsorption of the dissociated molecule in the form of two atomic hydrogens on dh-BN. Binding geometries of two atomic hydrogens (2 H) on the four considered types of dh-BN are shown in Fig. 4. The geometries of the most stable adsorption sites are similar to those in previous work by Nash et al.⁶ The calculated energetic and geometric parameters, including the adsorption energy, H–H distance, and the distance of formed B(N)–H bond, are summarized in Table 1.

Fig. 4 Optimized structures of two hydrogen atoms adsorbed at energetically favorable sites on dh-BN with (a) V_N, (b) V_B, (c) SW, and (d) B_N. The magenta, blue, cyan balls represent B, N and H atoms, respectively. The top and middle panel show the top and side views, respectively. Bottom panel: Corresponding side view of geometric structure with charge density difference plot. The green and violet isosurfaces with isovalue of ±0.003 e Å⁻³, represent accumulation and depletion of charge, respectively. The red arrow shows the direction of electron transfer evaluated with Bader charge analysis.

Table 1 The adsorption energy without (E_ads) and with (E_ads′) ZPE correction, geometrical parameters, and notable frequencies for adsorption of 2 atomic Hydrogen on dh-BN

Defects	Sites	E ads (eV)	E ads′ (eV)	Bond lengths (Å)	Notable frequencies (cm^−1)
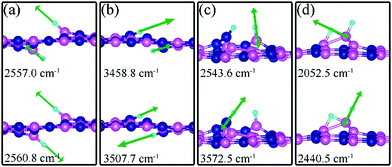
VN	B1, B2	−1.61	−1.28	d (H–H) = 3.087, d(H1–B1) = 1.189, d(H2–B2) = 1.189	2557.0 cm^−1, 2560.8 cm^−1
VB	N1, N2	−4.74	−4.22	d (H–H) = 1.869, d(H1–N1) = 1.012, d(H2–N2) = 1.009	3458.8 cm^−1, 3507.7 cm^−1
SW	B3, N1	1.16	1.41	d (H–H) = 1.687, d(H1–N1) = 1.004, d(H2–B3) = 1.190, d(B3–N1) = 2.632	2543.6 cm^−1, 3572.5 cm^−1
BN	B1, B4	−1.51	−1.32	d (H–H) = 1.757, d(H2–B4) = 1.207, d(H1–B4)= 1.274, d(H1–B1) = 1.315, d(B1–B4) = 1.858	2052.5 cm^−1, 2440.5 cm^−1

---

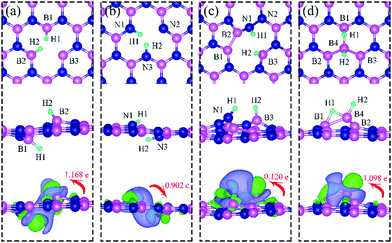
On dh-BN with V_N, two hydrogen atoms prefer to bind to B atoms near N vacancy such that they are on the opposite side of the dh-BN sheet, with respect to each other, and the difference in their z coordinates is 2.938 Å (Fig. 4a). The adsorption energy of 2 H is found to be −1.61 eV. On dh-BN with V_B, shown in Fig. 4b, 2 H prefer to attach to N atoms near the B vacancy in such a way that again the two H atoms are on the opposite side of the sheet but now with a difference in their z-position of 1.550 Å. The adsorption energy of 2 H on dh-BN with V_B is −4.74 eV, an extremely exothermic adsorption. For 2 H adsorption on dh-BN with SW, the H atoms prefer to stay on the same side of the sheet, as shown in Fig. 4c, in which one hydrogen attaches to B3 while the other attaches to N1. We find that the adsorption of 2 H atoms on SW breaks the bond of B3–N1, with the distance d_(B3–N1) of 2.632 Å, largely increased from 1.492 Å in the absence of the H atoms. This adsorption is endothermic with energy of +1.16 eV, the positive sign signifying that it is not favored, mainly because there is no undercoordinated site at SW. For the case of 2 H adsorption on dh-BN with B_N, one hydrogen prefers to adsorb on the central boron atom (B4) whereas the other prefers to stay at the bridge between B1 and B4, as shown in Fig. 4d. The adsorption energy of this configuration is −1.51 eV.

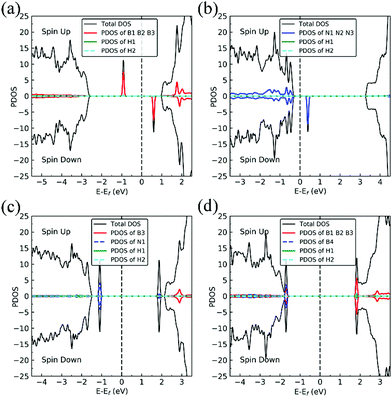
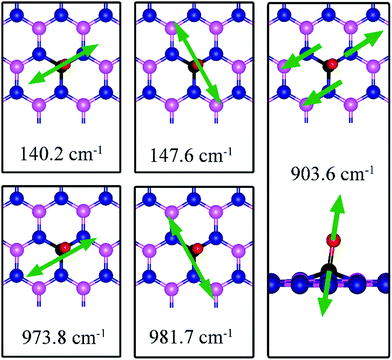
Charge density difference (CDD) plots, shown in the bottom panels of Fig. 4, indicate noticeable rearrangement of electron density and electron transfer. For V_N and B_N, the dh-BN donates 1.168 and 1.098 electrons to the atomic hydrogens, respectively. For V_B, the defect gains 0.902 electrons from atomic hydrogens. In the case of SW, 0.120 electrons transfer from dh-BN to atomic hydrogens. We also find that adsorption of 2 H affects electronic density of states of dh-BN (Fig. 5) in different ways depending on the defect type. For instance, comparison of Fig. 2a with Fig. 5a shows that 2 H adsorption increases the HOMO–LUMO gap for dh-BN with V_N. For V_B type defect, Fig. 5b attests to the disappearance of the defect states near the Fermi level (see Fig. 2b) on 2 H adsorption, leaving only the mid-gap state with spin down channel now drawn closer to the valence band, as compared to pristine V_B. For the case of SW, adsorption of 2 H leads to only a slight change of the HOMO–LUMO gap. Finally, for the case of B_N, adsorption of 2 H widens the HOMO–LUMO gap, such that HOMO and LUMO lie at the top of the valence and bottom of conduction bands, respectively. Overall, our calculations indicate that hydrogen atoms adsorb most strongly on dh-BN with a V_B defect (E_ads = −4.74 eV) and not at all when the defect is SW (E_ads = +1.04 eV). The inclusion of zero-point energy correction changes the binding energy of 2 H to dh-BN to −1.28, −4.22, +1.41, and −1.32 eV with V_N, V_B, SW, and B_N, respectively. The adsorption of H on dh-BN creates either B–H, N–H bonds, or both. The vibrational frequencies of the stretching mode of the bonds should serve as an identifier of the defect sites to which H adsorbs. The notable vibrational frequencies of such modes are listed in Table 1 and their corresponding vibrational patterns are shown in Fig. 6.

Fig. 5 Spin-polarized total density of states (TDOS) (black line), projected density of states (PDOS) in defect regions (red or blue) and spin-polarized PDOS of adsorbed hydrogens (green and cyan) on 2 H–dh-BN with (a) V_N, (b) V_B, (c) SW, and (d) B_N, respectively. The position of the Fermi level (E_F) is indicated by dashed line.

Fig. 6 Notable displacement patterns of two hydrogen atoms adsorbed on dh-BN with (a) V_N, (b) V_B, (c) SW, and (d) B_N defect. The magenta, blue, black and light blue balls represent the B, N, and H atoms, respectively. Arrows indicate displacement directions.

CO on dh-BN

Carbon monoxide (CO) is one of the major common toxic gases in the atmosphere and is the main component of syngas, the essential reactant for (higher) alcohol synthesis. Fig. 7 shows the geometric structure of the lowest energy configuration of CO adsorbed on V_N, V_B, SW, and B_N. Table 2 summarizes the binding energy, geometric parameters, and notable frequencies for CO binding on the four types of defects in h-BN.

Fig. 7 Top and side views of the most energetically favorable configurations of adsorbed CO on dh-BN with (a) V_N, (b) V_B, (c) SW, and (d) B_N type defect. The magenta, blue, black and red balls represent the B, N, C, and O atoms, respectively. The top and middle panel shows the top and side views, respectively. Bottom: The corresponding side views of the geometric structures with the charge density difference. The green and violet isosurfaces with isovalue of ±0.003 e Å⁻³, represent the accumulation and depletion of electron, respectively. The red arrow shows the electron transfer in direction and value using Bader charge analysis.

Table 2 The adsorption energy without (E_ads) and with (E_ads′) ZPE correction, geometrical parameters, and notable frequencies for adsorption of CO on dh-BN. Note that the frequency of the CO stretch mode is 2115.0 cm⁻¹ in the gas phase

Defects	E ads (eV)	E ads′ (eV)	Bond length (Å) and Bond angle (°)	Notable frequencies (cm^−1)
VN	−3.45	−3.22	d (C–O) = 1.403, d(C–B2) = 1.528, d(O–B1) = 1.417, θ(C–O–B1) = 93.5°	330.5, 352.9, 1069.2
VB	−4.70	−4.45	d (C–O) = 1.387, d(C–N1) = 1.495, θ(O–C–N1) = 110.8°	140.2, 147.6, 903.6, 973.8, 981.7
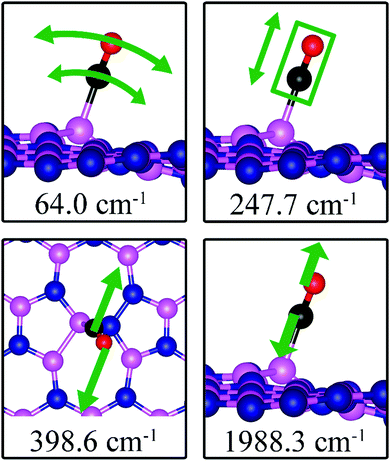
SW	0.42	0.46	d (C–O) = 1.150, d(C–B2) = 1.631, θ(O–C–B2) = 159.0°	64.0, 247.7, 398.6, 1988.3
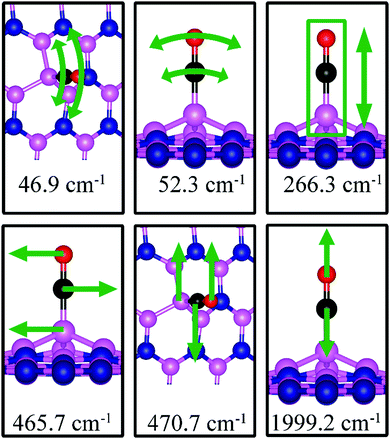
BN	−2.53	−2.43	d (C–O) = 1.163, d(C–B4) = 1.444, θ(B4–C–O) = 179.9°	46.9, 52.3, 266.3, 465.7, 470.7, 1999.2

---

CO adsorption on V_N

On V_N, CO binds at the defect sites with the O atom bonded to B1 and the C atom bonded to B2 and B3, as shown in Fig. 7a, in agreement with prior results.^43,44 The adsorption causes out-of-plane displacement of the B1 atom by about 1 Å, which is quite large. The CO bond length increases from 1.134 Å (gas phase) to 1.403 Å (adsorbed), while d_(C–B2) (d_(C–B3)) and d_(O–B) are calculated to be 1.528 and 1.417 Å, respectively. The CO bond length of 1.403 Å suggests that a bond order of 1, i.e. adsorption causes scission of the two π-bonds of the CO molecule, making it ready for a further reaction such as dissociation or hydrogenation. The adsorption energy of CO on dh-BN (V_N) is −3.45 eV, which is not far from −4.04 eV or −3.97 eV reported elsewhere.^43,44 The adsorption energy is −3.22 eV with ZPE correction. The Bader charge analysis shows that 2.070 electrons are transferred from dh-BN to the CO molecule. As shown in the bottom panel of Fig. 7a, a sizable electron density accumulation (green region) appears between B and C, and between B and O, which verifies formation of the B–C and B–O bonds. A loss of electron density (violet region) is shown around the C–O bond, confirming that adsorption weakens the C–O bond by breaking its two π-bonds. In Fig. 8a, which contains PDOS of CO adsorption on dh-BN (V_N), the orbital mixing between the occupied states of CO molecules (in red line) and the states of B atoms (around the vacancy in blue line). This obvious overlap of states of CO and V_N indicates the strong chemisorption of the CO molecule caused by dangling bonds of the B atoms around the vacancy site. In addition, the peaks in the density of states shift toward the higher energy since a charge transfer takes place from the dh-BN surface to the CO molecule.

Fig. 8 Spin-polarized TDOS (black line), PDOS of defect area (red or blue) and PDOS of adsorbed CO (green line) of CO–dh-BN with (a) V_N, (b) V_B, (c) SW, and (d) B_N, respectively. The position of the Fermi level (E_F) is indicated by dashed line.

The strong adsorption of CO on V_N with both C and O bond to Boron atoms of dh-BN significantly affects the CO stretching mode. We found that its frequency is 1069.2 cm⁻¹, as compared to that of 2115.0 cm⁻¹ of the isolated CO molecule. This is a large shift and reflects the strong bond of CO with the support. In addition, we found that there are several vibrational modes that show a strong coupling between CO and dh-BN whose frequencies are listed in Table 2 and whose vibrational patterns are shown in Fig. 9.

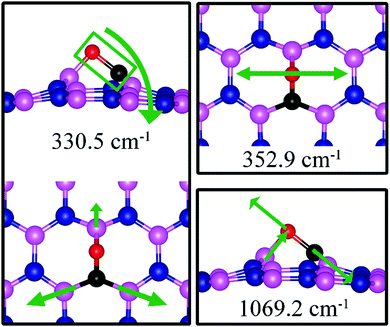Fig. 9 Notable vibrational modes of CO adsorbed on dh-BN with V_N. The magenta, blue, black and red balls represent the B, N, C, and O atoms, respectively. Arrows indicate vibrational patterns.

CO adsorption on V_B

The most stable adsorption configuration of CO adsorption on V_B is shown in Fig. 7b. In this configuration, CO binds to N1, N2 and N3 atoms in a vertical orientation via C–N bond, which is similar to that previously reported.^43,44 C–O bond length increases from 1.134 Å, in gas phase CO, to 1.387 Å, while d_(C–N) is found to be 1.495 Å. The CO bond length is larger than that of a typical bond order 2, but smaller than that of bond order 1. The calculated adsorption energy of −4.70 eV (−4.45 eV with ZPE correction) is smaller than that (−5.63 or −5.86 eV) reported elsewhere.^43,44 The difference may arise from the form of the exchange–correlation functional used in the DFT calculations or from differences in the geometry of the reference structure, as we discuss below. The Bader charge analysis shows that about 0.635 electrons are transferred from the CO molecule to the support. In the bottom panel of Fig. 7b, a sizable electron density accumulation (green region) appeared between the C and N atoms, which affirms the strong interaction between the CO molecule and N atoms around the vacancy. A loss of electron density (violet region) surrounds the region between C and O atoms, which shows a weakened C–O bond. In Fig. 8b, PDOS of CO adsorption on dh-BN at V_B around the Fermi level shows orbital mixing between the occupied states of the CO molecule and orbitals of B atoms, indicating chemisorption of CO on dh-BN.

As for CO on V_N, the strong adsorption of CO on V_B significantly affects the CO stretching mode. We found that its frequency is 903.6 cm⁻¹, as compared to 2115.0 cm⁻¹ of the isolated CO molecule. Such large change is consistent with the elongation of CO bond length upon adsorption. In addition, we found several vibrational modes that show strong coupling between CO and dh-BN, whose frequencies are listed in Table 2 and whose displacement patterns are illustrated in Fig. 10.

Fig. 10 Notable vibrational modes of CO adsorption on dh-BN with V_B. The magenta, blue, black and red balls represent the B, N, C, and O atoms, respectively. Arrows indicate vibrational patterns.

CO adsorption on SW

The most energetically favorable configuration of CO adsorption on SW is shown in Fig. 7c. Here CO adsorbs at the B site by pulling the B atom out from the dh-BN plane, resulting in C–O bond length of 1.150 Å and C–B bond length of 1.631 Å. The adsorption energy of CO is found to be 0.42 eV (0.46 eV with ZPE correction), which is significantly different from −0.58 eV reported in a previous study.⁴⁵ While both studies show similar adsorption configuration, the large difference in binding energies is puzzling, even after accounting for differences in the exchange correlation functional used in DFT calculations. One plausible reason for such discrepancy could be how the reference system for calculating binding energy, i.e., h-BN with SW defect, was created and optimized. We performed tests for couple of scenarios. For example, if the reference clean SW defect system is flat and without minimized stress, its energy is 0.87 eV higher than the clean SW defect system we use, which is stress free and not flat. Secondly, if the reference system is prepared as a non-flat sheet but stress is not minimized, its energy is 0.39 eV higher than ours. If such higher energy structures of clean SW defect system were used in ref. 45, it would boost the binding energy of CO significantly as such adsorption would break symmetry making the dh-BN non-flat or creating perturbation to release stress. Moreover, our result of positive binding energy, i.e., endothermic adsorption, of CO molecule is reasonable because B atom has 3 valence electrons and prefers to make 3 covalent bonds. In the SW defect, it already has 3 covalent bonds. Making another covalent bond with the adsorbed CO molecule is thus not energetically favorable. A similar rationale led to the conclusion that CO does not chemically bind to SW in BN nanotube.⁴⁶ To further validate our results, we calculate the physisorption energy of CO on SW to find that it is −0.14 eV, indicating CO preference to be in the physisorbed state. We also performed Nudged Elastic Band^47,48 calculations between the physisorbed and chemisorbed configurations (Fig. S1 in ESI†) and found that there is a barrier of 0.57 eV for the physisorbed molecule to adsorb chemically on the SW defect and a barrier of 0.01 eV for the chemisorbed CO to desorb. The latter together with the positive binding energy indicate a weak chemisorption of the CO molecule at SW defect. Bader charge analysis of chemisorbed CO on SW shows 0.259 electrons transferred from the surface to CO. The charge density difference plot of CO on dh-BN (SW) as shown in the bottom panel of Fig. 7c indicates a sizable electron density accumulation (green region) between the B and C atoms, consistent with the formation of B–C bond. However, the B–C bond length is 1.631 Å, longer than that for CO on V_N and V_B defects, indicating that the strength of CO binding on dh-BN with SW is weaker than that for the two other defects, consistent with calculated positive adsorption energies. The PDOS in Fig. 8c shows that the conduction band moves toward lower energy and that the valence band shifts toward higher energy, reducing the band gap of dh-BN, albeit the energy gap is still large and there is no available electronic state that is at or close to the Fermi level.

As the strength of adsorption of CO on SW is much reduced compared to that on V_B and V_N, the CO stretching frequency is found to be 1988.3 cm⁻¹. This mode is softer than that in isolated CO molecule due to the reduction in strength of CO bond and its elongation upon adsorption. In addition, we find several vibrational modes that show strong contribution from C and O movements whose frequencies are listed in Table 2 and whose displacement patterns are shown in Fig. 11.

Fig. 11 Notable vibrational modes of CO adsorption on dh-BN with SW defect. The magenta, blue, black and red balls represent the B, N, C, and O atoms, respectively. Arrows indicate vibrational patterns. The rectangular encloses the atoms that concertedly move.

CO adsorption on B_N

Fig. 7d shows the energetically favored CO adsorption configuration on dh-BN with B_N, in which CO binds perpendicularly on top of the central B atom (labeled as B4) with an adsorption energy of −2.53 eV (−2.43 eV with ZPE correction). The calculated bond length d_(C–B) and d_(C–O) are 1.444 Å and 1.163 Å (elongated by ∼0.03 Å from that in gas-phase), respectively. CDD plot of CO on dh-BN with B_N shown in the bottom panel of Fig. 7d indicates a sizable electron density accumulation (green region) between the B and C atoms, confirming the strong interaction between the CO molecule and its neighboring B atoms around the defect area. A small loss of electron density (violet region) is seen over the C–O bond, indicating weakening of the C–O bond, consistent with its elongation (from 1.134 Å in gas phase to 1.163 Å). A large loss of electron density (violet region) is found over the B4–B1, B4–B2 and B4–B3 bonds, suggesting that the bonds are weakened on CO adsorption. Bader charge analysis shows a net 0.470 electrons transferred from dh-BN (with B_N) to CO. After CO adsorption on dh-BN with B_N, the peaks in density of states shift toward lower energy, as shown in Fig. 8d. More importantly, the defect states merge with the valence and conduction bands, suggesting the absence of dangling bonds and the inability of more molecules to adsorb, thus passivating the catalytic activity of dh-BN with B_N.

The stretching frequency of the adsorbed CO molecule on dh-BN with B_N is found to be 1999.2 cm⁻¹. This mode is slightly softer than that in isolated CO molecule commensurate with small reduction in strength of the CO bond as a result of slight elongation upon adsorption. Here again we find several vibrational modes that show strong coupling between CO and dh-BN, displacement patterns of six of which are shown in Fig. 12.

Fig. 12 Notable vibrational modes of CO adsorption on dh-BN with B_N. The magenta, blue, black and red balls represent the B, N, C, and O atoms, respectively. Arrows indicate vibrational patterns. The rectangular encloses the atoms that are concertedly move together.

CO₂ on dh-BN

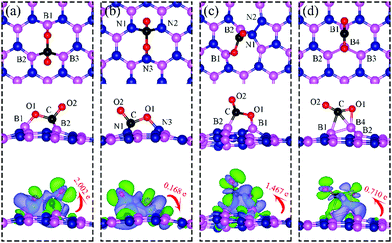
The geometric structure of CO₂ adsorption on V_N, V_B, SW, and B_N are shown in Fig. 13. The corresponding adsorption energies and geometric parameters are summarized in Table 3.

Fig. 13 Top and side views of the most energetically favorable configurations of adsorbed CO₂ on the dh-BN with (a) V_N, (b) V_B, (c) SW, and (d) B_N. The magenta, blue, black and red balls represent the B, N, C, and O atoms, respectively. The top and middle panel shows the top and side views, respectively. Bottom: The corresponding side views of the geometric structures with the charge density difference plot. The green and violet isosurfaces with isovalue of ±0.003 e Å⁻³, represent the accumulation and depletion of electron, respectively. The red arrow shows the electron transfer in direction and value.

Table 3 The adsorption energy without (E_ads) and with (E_ads′) ZPE correction and geometrical parameters for adsorption of CO₂ on dh-BN. Note that the frequency of the CO stretch mode is 2115.0 cm⁻¹ in the gas phase

Defects	E ads (eV)	E ads′ (eV)	Bond length (Å) and Bond angle (°)	Notable frequencies (cm^−1)
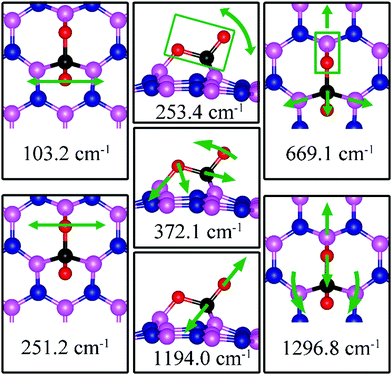
VN	−1.83	−1.72	d (C–O1) = 1.438, d(C–O2) = 1.311, d(C–B2) = 1.672, d(O1–B1) = 1.382, θ(O1–C–O2) = 113.7°	103.2, 251.2, 253.4, 372.1, 669.1, 1194.0, 1296.8
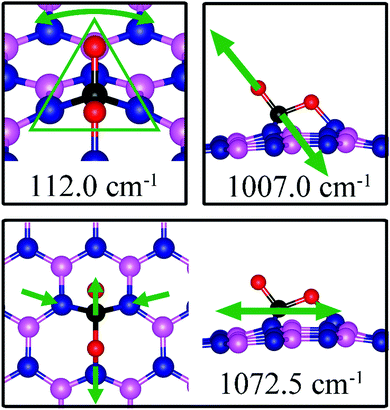
VB	−0.75	−0.59	d (C–O1) = 1.409, d(C–O2) = 1.353, d(C–N1) = 1.496, d(O1–N3) = 1.446, θ(O1–C–O2) = 107.1°	112.0, 1007.0, 1072.5
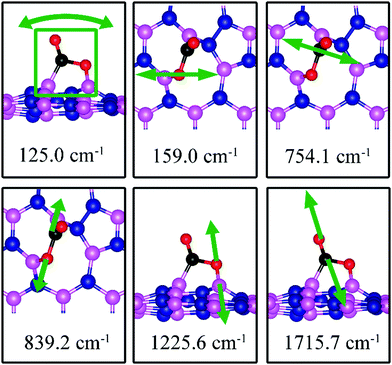
SW	0.49	0.51	d (C–O1) = 1.405, d(C–O2) = 1.209, d(C–B2) = 1.582, d(O1–B1) = 1.412, θ(O1–C–O2) = 121.9°	125.0, 159.0, 754.1, 839.2, 1225.6, 1715.7
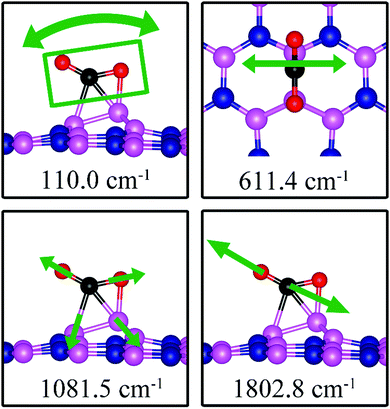
BN	−0.10	−0.11	d (C–O1) = 1.273, d(C–O2) = 1.206, d(C–B1) = 1.989, d(C–B4) = 1.807, d(O1–B4) = 1.661, θ(O1–C–O2) = 139.6°	110.0, 611.4, 1081.5, 1802.8

---

CO₂ adsorption on V_N

On dh-BN with V_N, CO₂ binds at the defect site, with an adsorption energy of −1.83 eV (−1.72 eV with ZPE correction), indicating a strong chemisorption of the CO₂ molecule at the vacancy site. As shown in Fig. 13a, the adsorption pulls B1, B2 and B3 atoms slightly out of the dh-BN plane and the CO₂ molecule lies in the proximity of three boron sites near the vacancy with bond lengths, d_(O1–B1), and d_(C–B2) (d_(C–B3)), of 1.382 and 1.672 Å, respectively. The molecule is bent with the O1–C–O2 angle of 113.7°. The bond lengths, d_(C–O1) and d_(C–O2), are 1.438 and 1.311 Å, respectively (both are longer than that of 1.172 Å of gas phase CO₂), indicating that the original C–O bonds are stretched upon interaction between CO₂ and dh-BN with V_N. Bader charge analysis shows that about 2.002 electrons transferred from dh-BN to the CO₂ molecule. CDD plot of CO₂ on dh-BN with V_N, shown in the bottom panel of Fig. 13a, indicates a sizable electron density accumulation (green region) appearing between the B2 (B3) and C atoms and between the B1 and O atoms, consistent with the formation of new bonds B2(B3)–C and B1–C. A loss of electron density (violet region) between C–O is also consistent with the elongation and weakening of the C–O bond. PDOS shown in Fig. 14a indicates overlaps, i.e., hybridizations, between states of CO₂ molecule and the states of B atoms, indicating the chemisorption of CO₂ on the dh-BN with V_N and the strong interaction between the molecule and the dh-BN sheet. We also find that the defect states, i.e., the ones near the Fermi level, are mostly contributed from CO₂ and shifted toward lower energy, closer to VBM. This phenomenon indicates that the defect states have migrated (transferred) to the adsorbed CO₂ molecules.

Fig. 14 Spin-polarized total density of states (TDOS) (black line), and spin-polarized PDOS of defect area (red line or blue line) and of adsorbed CO₂ (green line) of CO₂–dh-BN with (a) V_N, (b) V_B, (c) SW, and (d) B_N, respectively. The position of the Fermi level (E_F) is indicated by dashed line.

Since CO₂ adsorbs on dh-BN with a bent configuration, the normal vibrational modes of CO₂ molecule (symmetric stretching, antisymmetric stretching, bending) are absent. Instead, we found few notable vibrational modes that include contributions from the adsorbed CO₂ molecules, as shown in Fig. 15, with their frequencies listed in Table 3. Among them, the CO stretching mode is of particular interest as it is infra-red active and its frequency is 1194.0 cm⁻¹, which is different from that (1069.2 cm⁻¹) of the adsorbed CO molecule on the same defect.

Fig. 15 Notable vibrational modes of CO₂ adsorption on dh-BN with V_N. The magenta, blue, black and red balls represent the B, N, C, and O atoms, respectively. Arrows indicate vibrational patterns. The rectangular encloses the atoms that move together.

CO₂ adsorption on V_B

On dh-BN with V_B, CO₂ binds at the N sites with an adsorption energy of −0.75 eV (−0.59 eV with ZPE correction). Fig. 13b shows the corresponding adsorption configuration, close to that reported in previous work,⁴⁹ which also reported a binding energy of −0.62 eV. In this configuration, CO₂ lies in between the three N sites with bond lengths, d_(C–N1) and d_(O1–N3), of 1.496 Å and 1.446 Å, respectively. The bond lengths, d_(C–O1) and d_(C–O2), are 1.409 and 1.353 Å (longer than that 1.172 Å of an isolated molecule), respectively, indicating weakening of the C–O bonds. The Bader charge analysis shows 0.168 electrons transferred from the molecule to the dh-BN. CDD plot of CO₂ on dh-BN with V_B shown in Fig. 13b shows a sizable electron density accumulation (green region) between the N and C atoms, confirming the formation of N–C bond, and a loss of electron density (violet region) between the C and O atoms, consistent with the weakening of C–O bonds. PDOS shown in Fig. 14b indicates hybridizations of electronic states of the adsorbed CO₂ molecule and defects states of dh-BN with V_B, confirming the chemisorption of the molecule. It also suggests that the dangling bonds at the N atoms at the defect site of dh-BN are partially saturated, as the contributions of N atoms to the defect states are reduced as compared to that in the absence of CO₂.

Similar to the case of CO₂ adsorbed on the dh-BN with V_N, the molecule is found to adsorb with a bent configuration on V_B. Thus the normal vibrational modes of CO₂ molecule (symmetric stretching, antisymmetric stretching, bending) are not present. We found again three notable vibrational modes that show contributions from the adsorbed CO₂ molecules, as shown in Fig. 16, with their frequencies listed in Table 3. The CO stretching mode that points outward from dh-BN has a frequency of 1007.0 cm⁻¹. This mode is also infrared active and we assign this mode as a signature for the identification of the adsorption of CO₂ on the dh-BN with V_N.

Fig. 16 Notable vibrational modes of CO₂ adsorption on dh-BN with V_B. The magenta, blue, black and red balls represent the B, N, C, and O atoms, respectively. Arrows indicate vibrational patterns. The trapezium-like shape in 141.8 cm⁻¹ mode encloses the group of atoms that concertedly vibrate together.

CO₂ adsorption on SW

On dh-BN with SW, CO₂ binds at two B sites with an adsorption energy of +0.49 eV (0.51 eV with ZPE correction) indicating that the adsorption is endothermic. As shown in Fig. 13c, the adsorbed CO₂ pulls the B atom out of the dh-BN plane. The two C–O bond lengths are found to be 1.405 Å (C–O1) and 1.209 Å (C–O2). The bond lengths, d_(C–B2) and d_(O1–B1), are 1.582 and 1.412 Å, respectively. Bader charge analysis shows 1.467 electrons transferred from dh-BN with SW to the molecule. CDD plot of CO₂ on dh-BN with SW, as shown in Fig. 13c, indicates a sizable electron density accumulation (green region) between the B and C atoms and between the B and O atoms, suggesting covalent bond formation between the pairs of atoms and a large loss of electron density in the region between the B1 and B2 atoms, indicating weakening of the B–B bond of the defect. PDOS, as shown in Fig. 14c, indicates that the conduction band moves toward lower energy while the valence band shifts toward higher energy, as in the case of CO on dh-BN with SW. It also shows that contributions from B1, B2, N1, and N2 atoms to the defect states are still dominant while only a small contribution of the adsorbed CO₂ is observed. As in the case of CO adsorption on SW, we find a preferred physisorbed state of CO₂ with a binding energy of −0.14 eV. By performing Nudged Elastic Band calculation (see Fig. S1 in ESI†), we find a barrier of 1.71 eV between the physisorbed and chemisorbed configurations. However, if CO₂ is already chemically adsorbed on SW, the reverse barrier is also very high at 1.08 eV (see Fig. S1 in ESI†), which means CO₂ will remain chemically adsorbed. Interestingly, the above findings lead to the conclusion that CO₂ chemisorption on SW is not weak.

The calculated vibrational frequencies for the above configurations display four notable modes that are localized at or near the adsorbed CO₂. Their vibrational patterns are shown in Fig. 17 and their frequencies are listed in Table 3. We find the CO stretching mode that points outward from the defect to have a frequency of 1715.7 cm⁻¹. This mode is infrared active and could be the signature of this defect site.

Fig. 17 Notable vibrational modes of CO₂ adsorption on dh-BN with SW. The magenta, blue, black and red balls represent the B, N, C, and O atoms, respectively. Arrows indicate vibrational patterns. The square in 124.6 cm⁻¹ mode figure (left) encloses all atoms that concertedly vibrate together.

CO₂ adsorption on B_N

On dh-BN with B_N as shown in Fig. 13d, the adsorbed CO₂ molecule undergoes structural distortion to a bent geometry with C–O bond order reduction similar to that reported for CO₂ chemisorbed on B-rich BNNTs.⁴² The O1–C–O2 bond angle is 139.6°, and the C–O1 and C–O2 bonds are significantly elongated to 1.273 and 1.206 Å, respectively, indicating bond-order reductions. The B4 atom at the defect site is pulled out of dh-BN plane considerably by ∼1 Å. The adsorption energy of CO₂ adsorbed at the B_N is found to be −0.10 eV (−0.11 eV with ZPE correction), which is significantly lower than that of −0.74 eV reported for B-rich BNNTs.⁴² Bader charge analysis shows 0.710 electrons are transferred from the dh-BN to the molecule. CDD plot of CO₂ on dh-BN with B_N, as shown in Fig. 13d, indicates a sizable electron density accumulation (green region) in the region between the B and C atoms and between the B and O atoms and a large loss of electron density (violet region) in the region between the B1 and B2 atoms, indicating the weakening of B–B bond. The CO₂ adsorption on dh-BN with B_N thus causes the density of states to shift toward higher energy (Fig. 14d), consistent with the direction of electron transfer from dh-BN to the CO₂ molecule.

We found two notable vibrational modes that display a large contribution from the adsorbed CO₂ molecule. The displacement patterns of these modes are shown in Fig. 18 and their frequencies are listed in Table 3. The CO stretching mode that points outward from the dh-BN plane has a frequency of 1802.8 cm⁻¹. This mode is infrared active and we assign it as the signature of the adsorption configuration discussed above.

Fig. 18 Notable vibrational modes of CO₂ adsorption on dh-BN with B_N. The magenta, blue, black and red balls represent the B, N, C, and O atoms, respectively. Arrows indicate vibrational patterns. The rectangular in the left figure encloses atoms that concertedly vibrate together.

Propensity for chemical activity of dh-BN

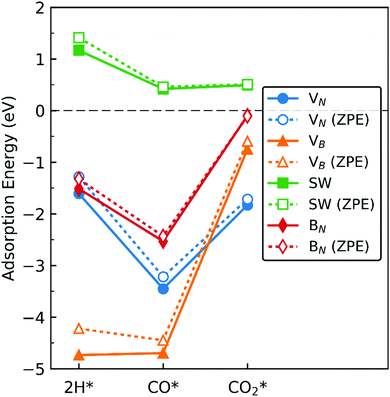
In this section we extrapolate the implications of our findings of adsorption energies of the molecules toward catalytic application of dh-BN for hydrogenation of CO and CO₂, bearing in mind that to facilitate these reactions we should be taking into account co-adsorption and diffusion of syngas molecules, and subsequent reaction steps which are beyond the scope of the present study. Fig. 19 shows comparison of the adsorption energy of 2 H, CO, and CO₂. We do not include H₂ in the above since it only physisorbs on these dh-BN. As indicated by the positive energies in Fig. 19, on dh-BN with SW, the adsorption of 2 H, CO and CO₂ are endothermic, suggesting low chemical reactivity of dh-BN with SW. This is consistent with the fact that B and N atoms have 3 valence electrons and in SW defect each has 3 covalent bonds. Creating covalent bonds with adsorbate molecules is thus energetically not favorable. In the case of the adsorption of 2 H, B–H and N–H bond formations lead to the breaking of the original B–N bond of the SW defect. With CO₂ adsorption B–C and B–O bond formations lead to breaking of the original B–B bond of the SW defect to compensate the formations of B–C and B–O bonds, i.e., to warrant that each B atom has 3 covalent bonds. The energy gained in the formations of new bonds and energy lost in the breaking of the original bond in SW defect compete with each other. Their cooperative effect does not offer an exothermic process. Because of such unfavorable adsorptions, hydrogenation of CO or CO₂ are not feasible on such a defect.

Fig. 19 Adsorption energy of 2 H, CO, and CO₂ on the dh-BN with (a) V_N, (b) V_B, (c) SW, and (d) B_N, shown with circle, triangle, square, and diamond markers, respectively. Values without and with ZPE corrections are shown in solid and empty markers, respectively. The markers for each defect types are connected with solid or dotted lines for guiding the eyes.

On dh-BN with V_B, on the other hand, adsorption energies of 2 H and CO are similar and in the range from −4 to −5 eV, suggesting rather strong adsorption. Such strong adsorption, however, often leads to difficulties, i.e., high energetics barrier, in the removal or diffusion of the adsorbates (reactants) and for co-adsorption to occur. It is most likely that the V_B sites will remain occupied by H or CO during a reaction, thus deactivating the site. Moreover, with the V_B defect adsorption of CO₂ is substantially weaker than that of 2 H, making it less likely that the site is occupied by 2 H. We thus conclude that dh-BN with V_B is also not suitable for CO₂ hydrogenation. Similarly, on dh-BN with B_N, adsorption of CO₂ is a weak chemisorption, implying that CO₂ could easily desorb before it would have the opportunity to react with other species under reaction conditions. On the other hand, the strength of 2 H and CO adsorptions are similar and strong for stable adsorption. However, the PDOS for 2 H and CO on dh-BN with B_N, as shown in Fig. 5 and 8, respectively, do not show any mid-gap state, indicating there is no dangling bond available for more molecules to adsorb. The above lead us to surmise that for such a defect co-adsorption is less likely to occur. The situation is different for dh-BN with V_N. With this particular defect we find that while the binding of CO is strong (adsorption energy of −3.22 eV with ZPE correction)—suggesting that CO could occupy and deactivate the site—the adsorption energies of 2 H and CO₂ are in a similar range that is not too strong to block active sites nor too weak to be unstable. The above comparisons lead us to suggest that dh-BN with V_N could be a potential catalyst for CO₂ hydrogenation. This is in agreement with a similar conclusion obtained for the hydrogenation of olefins.⁶

Our results presented above suggest that the strength of binding of the adsorbates depends on the availability of undercoordinated sites of the defects. For the creation of V_B and V_N vacancy defects, three covalent bonds together with three valence electrons were removed. As a result, the number of electrons in the system is odd and the system is spin-polarized because there is an unpaired electron. More importantly, they create 3 undercoordinated sites at the defects. The situation is different for the case of BN and SW defects, in which all atoms do have 3 covalent bonds and all electrons are paired. As a result, there is no undercoordinated site at the defect.

Conclusions

Our systematic analysis of the electronic structure and vibrational dynamics of syngas molecules adsorbed on defect-laden single-layer h-BN, using DFT-based calculations, has allowed us to make a distinction among four types of defects (V_N, V_B, SW, and B_N) that we considered. We find that CO and CO₂ molecules chemisorb on dh-BN for each of the four defect types, while H₂ only physisorbs on these defects. On the other hand, atomic hydrogen adsorbs on the defects. The above conclusions are also supported by an analysis of the partial density of electronic states and charge density difference plots. In addition, our calculations of vibrational frequencies for the considered adsorptions point to a number of notable vibrational modes that could help in the identification of defect type, through their experimental examination such as infrared absorption spectroscopy of the adsorbed molecules on dh-BN.

Our results provide fundamental insights into the interaction of syngas molecules and dh-BN through which we can prescreen the defect type that would make the basal plane of the dh-BN catalytically active for CO and CO₂ hydrogenation reactions. In particular, by comparing the adsorption energy of the molecules on dh-BN with each of the four defect types, accompanied with analysis of their electronic and geometric structures, we suggest that dh-BN with V_N (nitrogen vacancy) as a good candidate catalyst for CO₂ hydrogenation. We await experimental results that validate our findings.

On a more general note, although we have focused mostly on the chemical activity of defect-laden h-BN in this work, as we mention in the introduction, this interesting low-dimensional material is also being proposed as a single photon emitter in which defects play a major and their characterization is a challenge. Our work provides signatures in the vibrational modes of the adsorbed molecules that are strikingly different for the four defect types and thus could serve to identify them in experiments such as infra-red absorption spectroscopy which is commonly available. We hope our work encourages colleagues to undertake such measurements as a probe of the nature of the defect in h-BN that gives rise to several novel properties.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

It is a pleasure to submit this work to a volume dedicated to Peter Toennies with whom TSR has had many fruitful scientific interactions over the years. She also remembers very fondly discussions with JPT at Schloss Ringberg and a particular challenging hike in the area which fortunately ended well. We also thank Richard Blair and Hannah Stern for many helpful discussions. This work was supported in part by the U.S. Department of Energy, under Grant DE-FG02-07ER15842. The DFT calculations were performed in part using the computing resources at STOKES in the Advanced Research Computing Center at University of Central Florida, and at the National Energy Research Scientific Computing Center (NERSC). TSR is also indebted to the Miller Foundation, University of California, Berkeley, for the award of a Visiting Miller Professorship which facilitated some of the work presented here.

Notes and references

1. Y. Lin and J. W. Connell, Nanoscale, 2012, 4, 6908–6939.
2. K. Watanabe, T. Taniguchi and H. Kanda, Nat. Mater., 2004, 3, 404–409.
3. R. Decker, Y. Wang, V. W. Brar, W. Regan, H.-Z. Tsai, Q. Wu, W. Gannett, A. Zettl and M. F. Crommie, Nano Lett., 2011, 11, 2291–2295.
4. Y. Li, Y. Rao, K. F. Mak, Y. You, S. Wang, C. R. Dean and T. F. Heinz, Nano Lett., 2013, 13, 3329–3333.
5. J. Di, J. Xia, M. Ji, B. Wang, S. Yin, Q. Zhang, Z. Chen and H. Li, Appl. Catal., B, 2016, 183, 254–262.
6. D. J. Nash, D. T. Restrepo, N. S. Parra, K. E. Giesler, R. A. Penabade, M. Aminpour, D. Le, Z. Li, O. K. Farha, J. K. Harper, T. S. Rahman and R. G. Blair, ACS Omega, 2016, 1, 1343–1354.
7. J. T. Grant, C. A. Carrero, F. Goeltl, J. Venegas, P. Mueller, S. P. Burt, S. E. Specht, W. P. McDermott, A. Chieregato and I. Hermans, Science, 2016, 354, 1570–1573.
8. T. T. Tran, K. Bray, M. J. Ford, M. Toth and I. Aharonovich, Nat. Nanotechnol., 2016, 11, 37–41.
9. J. Feng, H. Deschout, S. Caneva, S. Hofmann, I. Lončarić, P. Lazić and A. Radenovic, Nano Lett., 2018, 18, 1739–1744.
10. R. Bourrellier, S. Meuret, A. Tararan, O. Stéphan, M. Kociak, L. H. G. Tizei and A. Zobelli, Nano Lett., 2016, 16, 4317–4321.
11. M. Topsakal, E. Aktürk and S. Ciraci, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 115442.
12. D. Le, T. B. Rawal and T. S. Rahman, J. Phys. Chem. C, 2014, 118, 5346–5351.
13. T. B. Rawal, D. Le and T. S. Rahman, J. Phys.: Condens. Matter, 2017, 29, 415201.
14. T. B. Rawal, D. Le and T. S. Rahman, J. Phys. Chem. C, 2017, 121, 7282–7293.
15. P. E. Evans, H. K. Jeong, Z. Hooshmand, D. Le, T. B. Rawal, S. N. Alvillar, L. Bartels, T. S. Rahman and P. A. Dowben, J. Phys. Chem. C, 2018, 122, 10042–10049.
16. C. S. Merida, D. Le, E. M. Echeverria, A. E. Nguyen, T. B. Rawal, S. Naghibi Alvillar, V. Kandyba, A. Al-Mahboob, Y. Losovyj, K. Katsiev, M. D. Valentin, C.-Y. Huang, M. J. Gomez, I. H. Lu, A. Guan, A. Barinov, T. S. Rahman, P. A. Dowben and L. Bartels, J. Phys. Chem. C, 2018, 122, 267–273.
17. H. Li, C. Tsai, A. L. Koh, L. Cai, A. W. Contryman, A. H. Fragapane, J. Zhao, H. S. Han, H. C. Manoharan, F. Abild-Pedersen, J. K. Norskov and X. Zheng, Nat. Mater., 2016, 15, 48–53.
18. B. Huang and H. Lee, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 245406.
19. C. Jin, F. Lin, K. Suenaga and S. Iijima, Phys. Rev. Lett., 2009, 102, 195505.
20. R. Schimmenti, R. Cortese, D. Duca and M. Mavrikakis, ChemCatChem, 2017, 9, 1610–1620.
21. S. Lin, X. Ye, R. S. Johnson and H. Guo, J. Phys. Chem. C, 2013, 117, 17319–17326.
22. X. Liu, T. Duan, C. Meng and Y. Han, RSC Adv., 2015, 5, 10452–10459.
23. Q. Sun, Z. Li, D. J. Searles, Y. Chen, G. M. Lu and A. Du, J. Am. Chem. Soc., 2013, 135, 8246–8253.
24. A. L. Gibb, N. Alem, J. H. Chen, K. J. Erickson, J. Ciston, A. Gautam, M. Linck and A. Zettl, J. Am. Chem. Soc., 2013, 135, 6758–6761.
25. C. K. Oliveira, E. F. A. Gomes, M. C. Prado, T. V. Alencar, R. Nascimento, L. M. Malard, R. J. C. Batista, A. B. de Oliveira, H. Chacham, A. M. de Paula and B. R. A. Neves, Nano Res., 2015, 8, 1680–1688.
26. I. N. Remediakis, F. Abild-Pedersen and J. K. Norskov, J. Phys. Chem. B, 2004, 108, 14535–14540.
27. Y. Choi and P. Liu, J. Am. Chem. Soc., 2009, 131, 13054–13061.
28. Y. Yang, J. Evans, J. A. Rodriguez, M. G. White and P. Liu, Phys. Chem. Chem. Phys., 2010, 12, 9909–9917.
29. H. Wu, X. Fan and J.-L. Kuo, Int. J. Hydrogen Energy, 2012, 37, 14336–14342.
30. W. Wang, S. Wang, X. Ma and J. Gong, Chem. Soc. Rev., 2011, 40, 3703–3727.
31. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502.
32. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
33. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
34. K. Lee, E. D. Murray, L. Z. Kong, B. I. Lundqvist and D. C. Langreth, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 081101.
35. W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204.
36. R. F. Bader, Acc. Chem. Res., 1985, 18, 9–15.
37. A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5.
38. S. Azevedo, J. R. Kaschny, C. M. C. de Castilho and F. de Brito Mota, Eur. Phys. J. B, 2009, 67, 507–512.
39. S. Yu, L. Li, Z. Lai, J. Hao and K. Zhang, Mater. Res. Express, 2017, 4, 116302.
40. R. Muhammad, Y. Shuai and H.-P. Tan, J. Mater. Chem. C, 2017, 5, 8112–8127.
41. R. Wang, J. Yang, X. Wu and S. Wang, Nanoscale, 2016, 8, 8210–8219.
42. H. Choi, Y. C. Park, Y. H. Kim and Y. S. Lee, J. Am. Chem. Soc., 2011, 133, 2084–2087.
43. Z. L. Liu, Q. Z. Xue, T. Zhang, Y. H. Tao, C. C. Ling and M. X. Shan, J. Phys. Chem. C, 2013, 117, 9332–9339.
44. K. Mao, L. Li, W. Zhang, Y. Pei, X. C. Zeng, X. Wu and J. Yang, Sci. Rep., 2014, 4, 5441.
45. Y.-H. Zhang, K.-G. Zhou, X.-C. Gou, K.-F. Xie, H.-L. Zhang and Y. Peng, Chem. Phys. Lett., 2010, 484, 266–270.
46. C. Tabtimsai, A. Nonsri, N. Gratoo, N. Massiri, P. Suvanvapee and B. Wanno, Monatsh. Chem., 2014, 145, 725–735.
47. G. Henkelman and H. Jonsson, J. Chem. Phys., 2000, 113, 9978–9985.
48. G. Henkelman, B. P. Uberuaga and H. Jonsson, J. Chem. Phys., 2000, 113, 9901–9904.
49. Y. Jiao, A. Du, Z. Zhu, V. Rudolph, G. Q. Lu and S. C. Smith, Catal. Today, 2011, 175, 271–275.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp05943a

‡ Present address: Department of Physics, University of Houston, Houston, TX 77204, USA.

---