Open Access Article
Open Access ArticleMimicking bone–metal exchanges with synthetic nanocrystalline apatites†
Jingxian
Wang
,
Damien
Bourgeois
 * and
Daniel
Meyer
* and
Daniel
Meyer
Institut de Chimie Séparative de Marcoule, ICSM, CEA, CNRS, ENSCM, Univ. Montpellier, BP 17171, Marcoule, 30207 Bagnols-sur-Cèze, France. E-mail: damien.bourgeois@umontpellier.fr
First published on 13th October 2020
Abstract
Deciphering the mechanisms of metal exchanges between blood plasma and bone requires the reproduction of this complex physicochemical system: bone mineral is a poorly crystalline non-stoichiometric apatite, in equilibrium with blood plasma, a supersaturated calcium phosphate solution. Careful control of synthesis of nanocrystalline apatites possessing similar structural features as bone mineral, followed by preliminary contact with adequate buffered solution enabled the set-up of in vitro experiments that can account for solid/liquid exchange under biomimetic conditions. The interaction between uranium(VI) and bone mineral was studied according to this model, and the results obtained are in full agreement with available biological data, and demonstrate that existing information using crystalline apatites is not relevant. Uranium accumulation in bone is thus not the result of the precipitation of a uranium phosphate phase, but is due to simple diffusion into the surface amorphous layer, which can be described as physical sorption using the Langmuir model.
Introduction
Bone is a sophisticated organ, highly vascularized, and permanently regenerating through dissolution-mineralization cycles in which various bone cells intervene.1 Apart from supporting the body and assuring its shape, the skeleton has several functions, including the storage of minerals.2 This essential well-known function enables calcium and magnesium storage and release according to metabolic needs for these elements. Less often mentioned is the aptitude the skeleton to store and release essential oligo elements such as zinc, and to immobilize unwanted exogenous metals.3,4 Chemical poisons such as lead or uranium, or radiological poisons such as plutonium and americium, can be sequestered in a stable matrix preventing further damage to soft organs such as the brain (lead), kidneys (lead and uranium) or liver (plutonium and americium).5,6 Bone is composed of mineralized apatite, and organic macromolecules, mostly type I collagen.7 The bone mineral is a non-stoichiometric poorly crystalline carbonated apatite.8 Several studies have proven that a hydrated amorphous layer is present on the surface of biological bone mineral,9 and is the place for ion exchange in bone with basic ions (Ca2+, Mg2+, CO32−, HPO42−, etc.).10,11 This amorphous layer is labile and hydrophilic, and very difficult to analyze directly. Thus it is not fully understood, and difficult to model. As a consequence, the understanding of chemical mechanisms associated with the biological functions of bone mineral often relies on synthetic apatite, instead of real bone samples. This approach also avoids the variability of biological systems according to species, genders, etc. which necessitates the use of multiple replicates in animal studies. In order to mimic biological functions, synthetic apatite should lead to results similar to those observed in biological systems.12 The simplest approach lies in the preparation of minerals with a structure analogous to bone minerals. However, chemical reactivity also has to be considered.In vivo, the accepted mechanism for exchange of common cations from plasma to bone is considered to involve diffusion into the amorphous layer eventually followed by further diffusion into the bone apatite crystal. The latter step depends on metal size and valence of the considered cation. More precisely, several elementary steps can occur, such as chemical complexation and surface sorption on the mineral surface, ion exchange with calcium, in the hydrated layer and/or within the apatite lattice, and precipitation of a poorly soluble compound.3,10 Detailed in vitro study of the effect of an exogenous cation requires a well-defined chemical system in which solid and liquid phases are in equilibrium, similar to bone, which is continuously irrigated by blood plasma. Considering bone–blood exchange, such a chemical system is difficult to obtain as blood plasma is a supersaturated calcium phosphate and carbonate solution, and bone mineral is a hierarchical assembly of fragile poorly crystalline nanoparticles.
In this paper, a general methodology for the in vitro study of metal exchanges between blood plasma and bone is described. The approach is motivated by the need for detailed studies on exchange mechanisms between the bone apatite and uranium(VI) under physiological conditions.13 Uranium ions have some detrimental effects on our environment and health,14,15 and they have been the object of several studies, analyzed in detail by environmental agencies of different countries.16,17 Furthermore, there is no satisfactory treatment of contaminated persons yet.18 Kinetics and thermodynamics of metal exchange are key to envision the decorporation of an exogenous metal after contamination.19 Apatite minerals are known for their high affinity for numerous metals including uranium(VI).20,21 They have been proposed as remediation materials in the case of water contaminated with uranium(VI).22,23 There are three mechanisms proposed to describe uranium exchange with apatite minerals: (1) apatite dissolution and uranium containing phase precipitation, such as chernikovite, (H3O)2(UO2)2(PO4)2·nH2O and autunite, Ca(UO2)2(PO4)2·nH2O; (2) ion exchange of uranyl cation UO22+ with Ca2+; and (3) uranium(VI) complexation and sorption at the mineral surface.24 However, all these mechanisms were not established under conditions extrapolatable to physiological ones. These conditions are very important in the case of uranium(VI) because the speciation of this metal is strongly influenced by ions25 and proteins26,27 present in biological media: in the presence of uranium(VI), carbonate ions lead to the formation of soluble complexes, whereas phosphate ions leads to precipitates.28,29 In addition, the apatite in the above presented models is crystalline apatite, which has different features from bone matrix mineral, and especially does not possess a distinct surface layer.
Carbonated nanocrystalline apatites (NCAs) have been proposed as a bone mineral surrogate for in vitro studies, including sorption of bis-phosphonates and nucleotides at physiological pH.30–32 The direct adaptation to uranium(VI) of the proposed experimental set-up led to complete uranium(VI) sorption within a few minutes, in total disagreement with the distribution of uranium in the body after contamination.33,34 Based on this intriguing result, we embarked on a precise description of the chemical behavior of NCAs prepared according to the well-established wet precipitation methods mentioned above.31 By varying precipitation parameters, and including a maturation period,35 various apatites were obtained. These apatite samples were fully characterized by transmission electron microscopy (TEM), powder X-ray diffraction (PXRD) and Fourier-transform infrared spectroscopy (FT-IR), and used in exchange experiments. In a first step, we detailed the dynamic equilibrium with calcium and phosphorous from the blood plasma with the bone mineral surrogates at physiological pH = 7.4. This step led to the development of a so-called “pre-equilibration” step, which plays a crucial role on adjusting the apatite surface ions. Afterwards, the kinetics and thermodynamics of equilibrium between pre-equilibrated apatites and solutions containing carbonated uranium(VI), as well as calcium and phosphate ions, have been studied, and an exchange mechanism under conditions mimicking the physiological ones is proposed.
Results and discussion
Solid characterization and chemical composition
The synthetic apatite samples employed in the study are listed in Table 1. As described before, we prepared nanocrystalline carbonated apatites (NCAs) according to the procedure reported in the literature.10,31 In this procedure, a calcium containing solution is rapidly added to a phosphate containing solution. A precipitate appears instantaneously, and the resulting mixture is left to stand for 1 day or 30 days in order to obtain NCA mimicking, respectively, the young and mature bone mineral (NCA-ref samples). The experimental procedure has been changed by the controlled slow addition of the calcium solution (NCA-modif samples), after facing reproducibility issues in exchange experiments employing the NCA-ref samples. Modification of the addition rate of reagents during preparation of nanocrystalline apatites through wet precipitation is a classical approach that has been previously employed in order to modify the physicochemical features of the nanocrystalline apatites.36 To our knowledge, such an approach has never been reported for NCAs. The newly prepared NCAs were thus fully characterized and compared to biomimetic apatite-collagen complex (ACC), prepared by slow growth of apatite on collagen-coated glass slides. Latter samples have been proven to possess similar features to bone mineral.37 Furthermore, they have been successfully used to mimic bone matrix in cell cultures,38 also in the presence of exogenous metals such as uranium.39 But it is impossible to use ACC mineral for systematic chemical experiments, as the mineral quantity obtained through this method is very low (max 5 mg per glass slide), and attached to a glass slide (microscope cover slip) through a collagen layer. It was possible however to recover few mg through scratching with a razor blade, in order to compare synthetic apatite samples with ACC. Characterization of the presented samples is focused on physical and chemical data relevant to solid/liquid exchanges in solution. ACC mineral is a very good reference, although more recent methods have been proposed in order to prepare calcium phosphate biomaterials and develop the biological understanding of apatites.40| Sample | Synthesis conditions | Specific surface (m2 g−1) | Mean crystal size (Å) | ||
|---|---|---|---|---|---|
| Addition duration | Maturation duration | (002) | (130) | ||
| NCA-ref-young | 1 min | 1 day | 202 ± 20 | 135 | 60 |
| NCA-modif-young | 30 min | 1 day | 247 ± 25 | 125 | 35 |
| NCA-modif-mature | 30 min | 30 days | 223 ± 22 | 180 | 50 |
| ACC | NA | NA | ND | 270 | 65 |
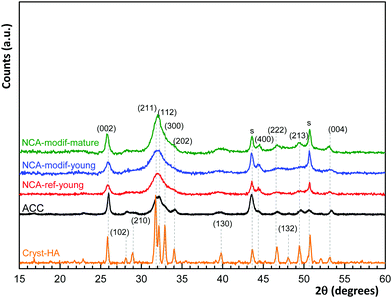
In Fig. 1, PXRD highlights the sole presence of a crystalline apatite phase (PDF file 01-079-5683) in all the samples, without showing the other carbonate phase. Similar to ACC, all synthetic NCAs are poorly crystalline materials, with the strong characteristic diffraction lines at 2θ = 31.8° (2 1 1), 32.2° (1 1 2) and 32.9° (3 0 0), well visible on a crystalline sample (Cryst-HA, commercially available), merging to a broad peak from 30° to 33.5°. The mean crystal sizes have been estimated from (002) and (130) lines according to the Scherrer equation, and are given in Table 1. ACC and synthetic NCAs have nano-scale sizes and exhibit an elongated crystal shape along the c-axis. As expected, NCA-modif-mature has a larger crystal size than NCA-modif-young, suggesting that the maturation is not altered by the rate of precipitation.
Morphology of the samples was characterized using TEM and data are shown in Fig. 2. Biomimetic ACC is composed of long plate-like nanocrystals with dimensions of about 60 nm × 30 nm × 4 nm, close to those of natural bone apatite. Synthetic NCAs also present this plate-like morphology. NCA-ref-young and NCA-modif-young have similar particle sizes, about 30 nm × 15 nm × 4 nm. This shows that the speed of addition of the calcium solution does not significantly affect the particle size. In agreement with PXRD data, NCA-modif-mature is composed of particles of larger dimensions than those of the young samples, but still smaller than those of the ACC samples. This further confirms that apatite gradually crystallizes during maturation. The dimensions of particles obtained from TEM are larger than those determined by PXRD analysis. This difference is in full agreement with previously reported data,31 and is attributed principally to the presence of the hydrated layer, visible on TEM images, but not detected by X-ray diffraction. The specific surface areas of synthetic NCAs determined using the Brunauer–Emmett–Teller (BET) method (N2 adsorption) are also reported in Table 1. The ACC sample could not be analyzed using BET as the available quantity is too low. As expected, the surface area of all the samples is inversely proportional to the average particle size. The specific surface areas of all NCAs are close to 200 m2 g−1, in full agreement with previous reports.9 Matured apatite has a more ordered crystal domain, and accordingly slightly lower surface area than young apatite. Therefore, the use of modified synthetic NCAs to represent bone apatite seems appropriate as these have analogous physical features to bone mineral, and are easy to prepare on a large scale, in a reproducible manner.41
 | ||
| Fig. 2 TEM images of synthetic apatites (a) NCA-modif-young; (b) NCA-ref-young; (c) NCA-modif-mature; (d) biomimetic apatite ACC, purchased stoichiometric apatite. | ||
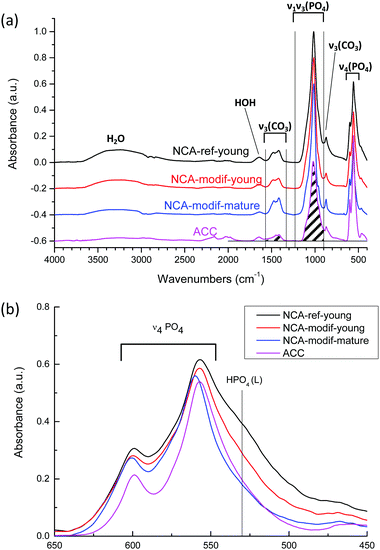
The chemical compositions of the different apatite samples are listed in Table 2. Calcium and phosphorus contents were determined through elemental analysis (ICP-OES) after total dissolution of solid in 10% nitric acid. The carbonate content was evaluated using FTIR (Fig. 3(a)), based on the area ratio between ν3(CO3) and ν1ν3(PO4) absorbance bands.42,43 According to this reported methodology, the ν3(CO3) contribution was integrated from 1570 to 1330 cm−1. The ν1ν3(PO4) was integrated from 1230 to about 900 cm−1. The local minimum around 900 cm−1 was selected as the lower limit for each apatite spectrum. The carbonate content was then calculated according to eqn (1):
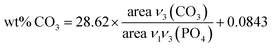 | (1) |
| Sample | Ca (wt %) | P (wt %) | CO3 (wt %) | Ca/P | Ca/(P + C) |
|---|---|---|---|---|---|
| NCA-ref-young | 33.86 ± 0.24 | 16.71 ± 0.19 | 3.2 | 1.57 | 1.43 |
| NCA-modif-young | 31.84 ± 0.27 | 15.03 ± 0.19 | 3.2 | 1.64 | 1.47 |
| NCA-modif-mature | 32.78 ± 0.41 | 15.11 ± 0.12 | 5.3 | 1.68 | 1.42 |
| ACC | 29.28 ± 0.20 | 14.41 ± 0.15 | 1.7 | 1.57 | 1.48 |
| Stoichiometric HA | 39.89 | 18.50 | 0 | 1.67 | 1.67 |
As shown in Table 2, the Ca/P ratios of synthetic NCAs were found between 1.5 and 1.7, while the Ca/(P + C) is around 1.4–1.5, indicating the non-stoichiometry of the synthetic apatite. The rate of addition of the calcium solution in the wet precipitation method does not affect the carbonate content, and the carbonate content increased during maturation. It has been reported that bone mineral and wet synthetic apatite are non-stoichiometric due to lattice substitution and ion vacancies, and to the non-apatitic environment on the apatite surface.44 Bone mineral is composed of an apatitic core and non-apatitic surface layer, around 55% versus 45% volume fraction, respectively.45 The non-apatitic layer is amorphous calcium phosphate, and contains phosphate, hydrogenophosphate, carbonate and calcium ions.9 Additionally, CO32− and HPO42− are also present in the crystalline apatite domains.45 In the FTIR spectra, the non-apatite layer is identified by the labile CO3, HPO4 and PO4 groups, well visible as shoulders at 866 cm−1 in the ν2CO3 domain, 530 cm−1 and 617 cm−1 in the ν4PO4 domain, respectively.35 Here the ν4PO4 domains of different apatites were compared (Fig. 3(b)). All synthetic NCAs display an apparent shoulder at 530 cm−1 from labile HPO42− adsorption. This confirms the presence of the non-apatitic environment. NCA-modif-young has a smaller labile HPO42− adsorption band than NCA-ref-young, showing that the labile environment decreases upon increase of the calcium solution addition duration. Afterwards, during maturation, the further decrease of labile HPO42− is associated with increasing CO32− content, which is associated with apatite domain growth. According to the literature,9,10 labile HPO42− is substituted by CO32− firstly in the non-apatitic layer, and then CO32− progressively enters the apatite lattice during apatite maturation.
Set-up of pre-equilibration procedure for solid/liquid exchange
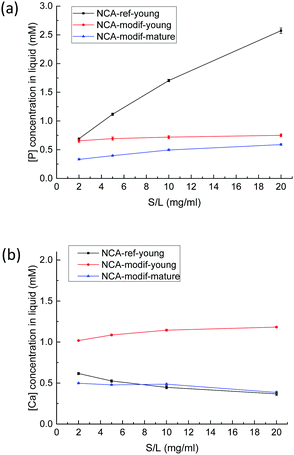
Before examination of other ions, the evolution of calcium and phosphate ions when NCAs are immersed in Tris buffer solution at pH = 7.4 was analyzed. Total calcium content (Ca) and phosphorus (P) content in solution were monitored, with no consideration of the precise speciation of these elements. It is supposed that calcium is mostly present as Ca2+ ions, and phosphorus as H2PO4− and HPO42− ions. Whatever is the sample considered, as soon as the solid contacts the liquid, both Ca and P are released from solid into solution, then Ca and P concentrations do not significantly evolve and slowly stabilize within 1 hour. Equilibration between solid and liquid is expected, and dissolution of the solid phase is very rapid (less than 1 min), presumably because of its nm-size. Although no data regarding the dissolution of NCAs into buffered solution are available to our knowledge, the Ca and P concentrations observed are well in agreement with numerous available data on calcium phosphate phase dissolution.46 Ca and P concentrations found are in the mM order of magnitude, which is fully compatible with the occurrence of amorphous calcium phosphate, and well above theoretical concentrations that would arise from dissolution of a pure hydroxyapatite phase. In other words, the resulting solution is supersaturated regarding hydroxyapatite. More intriguing is the extreme variability of the Ca/P ratio in solution: values ranging from 0.1 to 8 have been obtained according to the solid considered and the solid/liquid ratio employed. This is typical of a non-congruent dissolution, and demonstrates that surface chemistry of the solid particles pilot the dissolution process. The solid/liquid ratio (S/L, expressed in g L−1) appears thus as the key experimental parameter to study as it is theoretically directly sensitive to surface desorption. As shown in Fig. 4, with NCA-ref-young, increasing S/L ratio leads to higher P release in the liquid, while Ca concentration is low with a regular decrease. It reflects that NCA-ref-young has excess P on its surface.Considering the large amount of P released, it seems unlikely that what we call surface chemistry is limited to physical desorption processes of sole HPO42− ions, without association with counter ions. The dissolution of an amorphous phosphate impurity, containing either Na+ or NH4+, was first suspected, but all the samples have been thoroughly washed with deionized water after precipitation and filtering. We examined the influence of number of washings, amount of water used, and washing with dilute Ca2+ solution,47 and these parameters did not exhibit any influence. Furthermore, analysis of washing solutions did not reveal abnormal P or Ca concentration values. The surfaces of bone mineral and synthetic NCAs have been described as a highly hydrophilic amorphous calcium phosphate phase.9 This important hydrated layer can be considered as an ion reservoir that is capable of ion exchange with the surrounding fluid. Thus, it seems reasonable that ion exchange occurs, possibly between HPO42− and HO− or Cl− ions. It was impossible to evidence a decrease in one of these ions (or both). In the buffer solution, HO− concentration is stable, and Cl− concentration is much more important than the variation in P concentration. Ion exchanges between surface HPO42− and OH− ions in the solution have never been reported to our knowledge. During the previous sorption studies performed at physiological pH mentioned in the introduction, pH evolution has not been controlled, but only monitored, and a moderate decrease has been reported, especially in the blank experiments.48 On the other hand, exchanges between surface Ca2+ ions and H+ ions present in the solution have already been observed on crystalline apatite.49 In the present study, all solutions are buffered, and the absence of significant pH evolution cannot preclude the exchange of HO− ions between solution and solid.
In contrast to the important P release observed with NCA-ref-young, the amount of Ca released is low, and increasing the S/L ratio led to a slightly decreasing Ca concentration in solution, as detailed in Fig. 4(b). With NCA-modif-young neither Ca nor P concentration changes significantly according to the S/L ratio, suggesting the absence of strong Ca or P excess on the surface. Similarly, NCA-modif-mature does not lead to variable Ca or P release into the solution according to the S/L ratio. Yet, mature apatite leads to lower dissolution than young apatite, as both Ca and P concentrations in the liquid are lower. This is in full agreement with the structural features of both samples, which indicate that matured samples are more crystalline, and exhibit a smaller hydrated layer. With the studied biomimetic apatites, surface chemistry is thus likely to be the result of ion exchange between hydrated surface layer and solution.
Our work further suggests that the NCA synthesis directly influences the exchangeable ion content in the surface layer. This point was further backed by the study of the influence of the addition rate of the Ca solution on the P solution. The amount of P released during exchange with buffer solution at pH = 4 is inversely proportional to the addition duration (see Fig. SI1, ESI†). Rapid addition of calcium solution is expected to yield a defined number of solid particle nuclei that further grow into a phosphate rich solution, whereas slow addition of calcium solution will continuously generate new particle nuclei that will grow in a solution continuously supplied with Ca, thus more balanced in Ca and P. Accordingly, NCA-modif-young particles are slightly smaller than NCA-ref particles, and the developed surface is slightly higher. The pH of the solution was followed during the synthesis: initial pH is 7.9, and whatever the speed of addition, the pH never drops below the final value, 7.4, as the solution is buffered by phosphate and carbonate ions. Maturation then leads to particles of greater size with a smaller hydrated layer, still balanced in Ca and P, but less prone to Ca and P desorption. In other words, final Ca and P concentrations in solutions obtained after immersion of NCA-modif samples in buffered solutions can be seen as the result of solution saturation through dissolution of the amorphous hydrated calcium phosphate layer, with apparent solubility product depending on the thickness of this layer. As an illustration, the evolution of Ca and P in solution in the case of the NCA-modif-young sample is given in the ESI† (Fig. SI2): Ca and P concentrations are well stable over 2 h, with a Ca/P ratio found between 1.6 and 1.8.
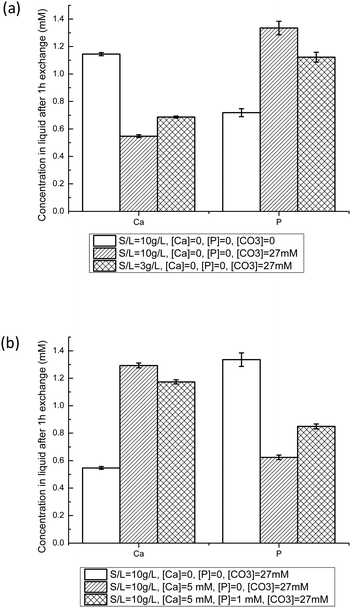
Equilibration experiments between NCAs and buffered solution (pH = 7.4) containing Ca2+, HPO42− and/or HCO3− were then performed. It has to be mentioned that all solutions are supersaturated regarding hydroxyapatite and calcium carbonate (calcite and aragonite).46 Such solutions have to be freshly prepared, and showed good stability over 24 h. Furthermore, we did not observe any rapid precipitation of another solid phase, nor detect an unwanted crystalline phase with PXRD on samples analyzed after exchange experiments for Ca concentrations below 5 mM and P concentrations below 1.5 mM. As a comparison, the simulated body fluid (SBF) method developed in order to form a calcium phosphate film on solid supports relies on similar solutions, and leads to mineralization of surfaces after several days only.50Fig. 5 displays the Ca and P concentrations in liquid after 1 h with NCA-modif-young. The final Ca and P concentrations are affected by S/L ratio, and initial HCO3−, Ca2+ and HPO42− concentrations. As shown in Fig. 5(a), the presence of HCO3− in initial solution leads to a decrease in Ca and an increase in P concentrations. This observation can be explained by substitution of phosphate ions with carbonate ions in the amorphous layer. Meanwhile, as more phosphate is released from the solid in a solution with a very weakly altered carbonate content, the Ca release is reduced in order to reach the solubility equilibrium. It cannot be excluded that the P release leads to a re-precipitation of calcium phosphate or calcium carbonate in the surface layer, but we did not observe a significant increase of Ca concentration at short times, followed by a decrease of Ca. It is likely that the carbonate-phosphate exchange and the solubility equilibrium are concomitant events.
When HCO3− ions are present, the S/L ratio now also influences the final Ca and P concentrations: decreasing S/L ratio from 10 mg L−1 to 3 mg mL−1 leads to a Ca/P ratio of 0.63 instead of 0.42. A lower S/L ratio leads to lower phosphate-carbonate exchange, thus to a decrease in P and concomitant increase in Ca. However, the final concentrations are very different from those obtained in a system without carbonate ions (Ca/P = 1.63). In order to obtain Ca and P concentrations close to those observed in blood plasma (free [Ca2+] about 1.2 mM,51 and total P about 1 mM), it is thus necessary to add Ca2+ as well as HPO42− ions into the buffered 27 mM HCO3− solution. Fig. 5(b) illustrates the effects of adding Ca and P in the initial liquid on S/L exchange results. Adding Ca increases Ca and decreases P final concentrations. Similarly, adding P increases P but decreases Ca final concentrations. These observations could be explained by control through the apparent solubility product of the amorphous calcium phosphate layer, or through the previously proposed metastable solubility equilibrium (MES) constant.52 We tried to derive various ionic products corresponding to different calcium phosphate phases, but no constant value could be obtained throughout the different experimental conditions with a given apatite sample. Results depicted in Fig. 5(b) suggest that Ca is easier to incorporate onto the hydrated layer than P: the Ca concentration decrease is about 75%, whereas the P one is only about 15%. With the established trends regarding the influence of initial Ca and P concentrations, at the given S/L ratio and HCO3− concentration, it was possible to obtain conditions in which the final Ca and P concentrations are close to the targeted ones. A similar study was performed with the NCA-modif-mature sample. All results are given in Table 3. Details on the impact of HCO3− ions and variation in initial Ca and P concentrations are available in the ESI† (Fig. SI3).
| Solid/liquid exchange conditions | Liquid concentrations after pre-equilibration | ||||||
|---|---|---|---|---|---|---|---|
| S/L (mg mL−1) | Surface area per mL (m2 mL−1) | [Ca]ini (mM) | [P]ini (mM) | [HCO3]ini (mM) | [Ca]fin (mM) | [P]fin (mM) | |
| [Ca]ini and [P]ini: initial Ca2+ and HPO42− concentrations in liquid before exchange; [Ca]fin [P]fin: final Ca and P concentrations after exchange determined by ICP-OES. | |||||||
| NCA-modif-young | 10 | ∼2.5 | 5 | 1 | 27 | 1.2 | 0.8 |
| NCA-modif-young | 3 | ∼0.7 | 2.5 | 1 | 27 | 1.2 | 1 |
| NCA-modif-mature | 3 | ∼0.7 | 2.5 | 1.25 | 27 | 0.9 | 0.8 |
We then checked that removing the supernatant and replacing it with a new buffered solution containing 27 mM HCO3− ions, 1.2 mM Ca and 1 mM P did not lead to significant changes in the Ca and P concentrations after contact. The synthetic NCAs, having different synthesis parameters, have different surface conditions that can interfere when studying the impact of exogenous ions. Thus, the first S/L contact with a solution not mimicking blood plasma is a ‘pre-equilibration’ step that enables adaption of the different surface hydrated layers of the apatite samples. In vivo bone mineral is permanently contacting blood plasma, which contains free calcium, phosphate and carbonate ions, and is in dynamic equilibrium with these ions. The modified NCAs, after pre-equilibration, are thus ready for detailed studies of S/L exchanges, using variable parameters such as developed surface area, all other conditions remaining equal. To obtain further information, use of a commercial apatite sample was attempted. This sample is a highly crystalline apatite (see Fig. 1, Cryst-HA sample), and not structurally nor chemically representative of bone mineral (see Fig. SI4, ESI†). Furthermore, it was not possible to obtain with this material a suitable equilibrated solid/liquid system as with NCAs. Experimental data gathered on the commercial crystalline apatite are given in the ESI† (Fig. SI5 and Table SI1).
Solid/liquid exchange in the presence of U(VI)
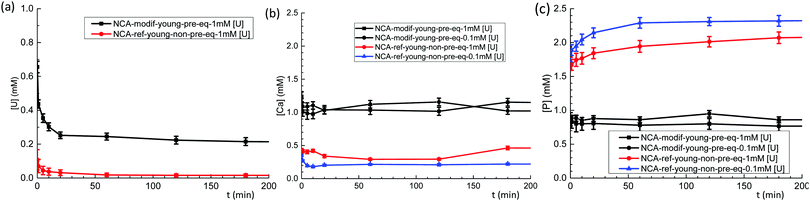
Behavior of exogenous U(VI) was then studied in S/L exchange experiments. U(VI) was introduced in a buffered (pH = 7.4) carbonated calcium phosphate solution with initial concentrations between 0.1 mM and 1.4 mM. Such solutions are stable over several hours, the precipitation of U(VI) being prevented by the presence of HCO3− ions. The slow release of CO2 from the solutions requires, however, that fresh solutions are prepared every day. To study the influence of solid preparation conditions on U(VI) exchange, kinetic tests were performed on NCA-ref-young without pre-equilibration, and compared to NCA-modif-young with pre-equilibration. Fig. 6(a–c) show evolution of U, Ca, and P concentrations in solution during S/L exchange. It can be observed that U(VI) concentration in solution drops much more rapidly when exchange occurs with non-pre-equilibrated NCA-ref-young than pre-equilibrated NCA-modif-young (Fig. 6(a)). The final U(VI) concentration reached at equilibrium is also different: about 98% U(VI) is incorporated in NCA-ref-young after 1 h, and the sorption of U(VI) with NCA-modif-young pre-equilibrated is not complete. As detailed before, NCA-ref-young has excess P available in its surface layer, while NCA-modif-young has neither extra Ca nor P in its surface layer.Fig. 6(b) and (c) show that NCA-ref-young releases its excess P and incorporates Ca since the beginning of the exchange. Thus, the evolution of Ca and P concentrations observed is not related only to the presence of U(VI) in the system. Without U(VI), expected concentrations of Ca and P are 0.25 and 2.3 mM, respectively (very close to those obtained in the presence of 0.1 mM U(VI)). It is likely that the rapid incorporation of uranium is due to the large release of P with the NCA-ref-young. It can be related to the easy precipitation of uranyl phosphates (which could not be detected by XRD due to the low quantity of such a phase if present). Lower initial U(VI) concentration increases P concentration in the liquid during exchange, and consequently the Ca concentration decreases. With the pre-equilibrated NCA-modif-young sample, both Ca and P concentrations remain stabilized around the initial value (1 mM), almost insensible to the initial U(VI) concentration. This suggests that U(VI) incorporation by the solid is a simple process, not impacted by Ca and P: it is neither a straight calcium–uranium ion exchange, nor a uranyl phosphate precipitation. Such in vitro experiments are in full agreement with available in vivo data. Uranium(VI) is described to be only partially stored in the skeleton (maximum load about 20% of initial burden), and the target organs are kidneys. The fixation of U(VI) in the skeleton occurs within hours, and can be prevented in part by the injection of bicarbonate. Furthermore, it is very likely also mediated by bone cells.53,54 An instantaneous fixation by bone mineral such as what is observed with the NCA-ref-young sample would lead to a much higher fraction in the skeleton.
Considering the observed kinetics, characterization of the incorporation of U(VI) under thermodynamic conditions was accomplished using a 1 h duration for experiments. This corresponds to a very short time considering biological events, relevant for the study of metal accumulation in bones. As the maturation process is slow (30 days of maturation to prepare the NCA-modif-mature sample), we neglect in the data interpretation the evolution of the crystalline core of the NCAs, as well as exchanges between the crystalline core and external hydrated layer. Diffusion of ions from the hydrated layer into the crystal lattice has indeed been described to be a slow process.3,10 The amount of U(VI) incorporated on apatite surface Qads (μmol m−2) as a function of U(VI) equilibrium concentration in liquid Ceq (mM) is plotted in Fig. 7(a). The curves can be fitted using the Langmuir isotherm model, classically employed to describe physical sorption, according to eqn (2):
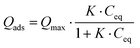 | (2) |
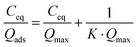 | (3) |
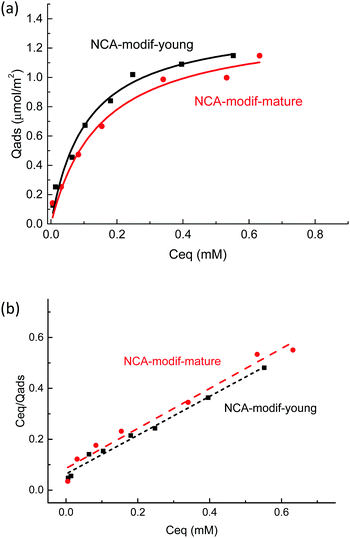 | ||
| Fig. 7 (a) U(VI) adsorption isotherms by NCA-modif-young, NCA-modif-mature and HA-ref and (b) linear regression of NCA-modif-young and NCA-modif-mature using Langmuir isotherm models. | ||
Altogether, our results highlight the specific behavior of NCAs in the presence of U(VI) under conditions close to the physiological ones. Available information given in previously published studies dedicated to uranium removal from groundwater using crystalline apatite is not relevant for the description of bone–blood plasma exchanges.22,56 In this case, it was demonstrated that U(VI) precipitates with the phosphate released from the apatite to form chernikovite (a mixed hydrogen uranium(VI) phosphate) when apatite dissolution provides sufficient phosphate ions.23,24 Further understanding of the detailed mechanism of uranium chemistry during the exchange process will be the next step, including exact location of the metal in the apatite particle (hydrated layer vs. crystalline core) and its speciation (phosphato vs. carbonato species), and evolution over longer durations (diffusion into the crystalline core). These points are relevant in order to evaluate complete reversibility of the incorporation process and possible decorporation of uranium embedded in the skeleton after contamination.
Conclusions
We report here the first in vitro study where important parameters such as pH, and Ca and P concentrations are well controlled during synthetic bone mineral-blood plasma exchanges. We demonstrated that with adapted biomimetic apatites and a pre-equilibration step, it is possible to mimic the biological system in order to study the physicochemical impact of an exogenous metallic cation. Previously reported nanocrystalline apatites suffer from excessive P release from their surface, and have a strong impact on calcium phosphate balance of the S/L system. With the pre-equilibrated modified apatite samples, it is possible to study bone–metal exchange using various conditions without perturbation brought by the initial apatite-solution equilibrium. Application to uranium(VI) revealed that bone–blood exchange is likely to occur via diffusion of ions in the hydrated surface layer of the mineral, analogous to a sorption process, which can be well described using classical Langmuir isotherms. This mechanism is in good agreement with in vivo data treating uranium accumulation in bone, and different to the mechanism previously reported with crystalline apatite on groundwater remediation. The approach proposed is general and relevant to other chemicals that may interact with bone mineral. Various metallic cations are prone to accumulating in the bone, such as heavier actinides (plutonium and americium) and heavy metals (lead). Organic molecules such as bisphosphonates are known to interfere with bone mineralization. In both cases, our findings should enable decoupling of the complex bone mineral-blood plasma equilibrium from the specific effect of exogenous chemicals, and subsequently lead to better understanding of the peculiar chemical features of the skeleton.Experimental
Carbonated nanocrystalline apatite (NCAs) synthesis
NCAs were prepared according to an adaptation of a precipitation method previously reported.31 To a phosphate-carbonate solution prepared by dissolution of NaHCO3 (4.0 g) and (NH4)2HPO4 (3.95 g) in deionized water (67 mL) was added a calcium solution at room temperature (T = 22 °C) over 30 min under constant agitation, prepared by dissolution of NaHCO3 (0.085 g) and Ca(NO3)2·4H2O (2.3 g) in deionized water (33 mL) adjusted to pH 6.3 through addition of an aqueous 1 M HNO3 solution. A precipitate appeared immediately and the final pH of the mixture was 7.4. The agitation was stopped, and the suspension left to settle and to mature in an airtight container for 1 day (young samples) or 30 days (mature samples). After maturation, the precipitate was filtered on a Büchner funnel and washed 3 times with deionized water (100 mL). The collected wet precipitate was lyophilized at −110 °C under 2 Torr for 48 h. After grinding, NCA was obtained as a white powder and stored in the freezer.Material characterization and chemical analysis
X-ray diffractograms were obtained using a Bruker D8 Advance Powder X-ray diffractometer in Bragg–Brentano geometry with CuKα1 radiation (λ = 1.5406 Å). The diffraction pattern was collected from 2θ = 10° to 60° with the step size of 0.05° and 4 s dwell time per step.The specific surface areas of solids were measured using the Brunauer–Emmett–Teller (BET) method (N2 adsorption) using a Tristar II apparatus.
Morphology of solids was observed by transmission electron microscopy (TEM) using both a JEOL 1200 EXII TEM and a JEOL 2200 FS high-resolution TEM (HRTEM) at the acceleration voltage of 120 kV (point to point resolution: 4 Å) and 200 kV (point to point resolution: 1.9 Å), respectively. The samples were prepared by dispersing the solid in ethanol and depositing the suspension on a carbon coated copper grid.
Fourier-transform infrared spectroscopy (FTIR) analysis was performed on a PerkinElmer Spectrum 100 series spectrometer equipped with a Universal ATR diamond top plate at room temperature. The wavelength range of 380–4000 cm−1 was acquired with a resolution of 4 cm−1 by transmission. The carbonate content is directly correlated to the area ratio of ν3(CO3) and ν1ν3(PO4) bands, which were determined from the processed spectra using Origin Pro 8.1 software.
The calcium and phosphorus contents of the solid were determined after complete dissolution by elemental analysis. The solids were dissolved in an aqueous 1 M HNO3 solution (10 mL), and the resulting solution diluted 10 fold using a 2% aqueous HNO3 solution, and analyzed by inductively coupled plasma atomic emission spectroscopy (ICP-AES) using SpectroArcos apparatus.
Solid/liquid exchange experiments
Solid pre-equilibration with liquid was performed by contacting dry apatite powders (between 2.0 and 20 mg according to the S/L ratio targeted) and a 1 mL solution containing Ca2+, HPO42− and 27 mM NaHCO3 buffered at pH = 7.4 using 50 mM trishydroxymethylmethylamine (Tris) and an aqueous 0.1 M HCl solution to adjust the pH. The resulting suspension was placed on a rotatory shaker (40 rpm) for 1 h. The solid was left to settle for 5 min, then 750 μL of the supernatant was removed and replaced by the same total volume of aqueous solution by successive addition of different aqueous solutions buffered at pH = 7.4 and containing (1) HCO3− (200 mM), (2) carbonated uranium(VI) (20 mM UO2(NO3)2 and 200 mM HCO3−), (3) buffer alone in order to obtain targeted final concentrations of U(VI) (0.1 to 1.4 mM), Ca (1.2 mM), P (1 mM) and carbonate (27 mM), (4) Ca2+ (25 mM), and (5) HPO42− (10 mM). The resulting suspension was placed on a rotatory shaker (40 rpm) for 1 min to 24 h. The tubes were centrifuged for 2 min at 6400 rpm, and the supernatant was aliquoted and diluted 10 fold using a 2% aqueous HNO3 solution, and analyzed by ICP-AES for Ca and P determination. The diluted solution was again diluted 100 fold using 1% aqueous extra pure HNO3, and analyzed by inductively coupled plasma mass spectroscopy (ICP-MS) using ThermoFisher iCAP-RQ apparatus.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are grateful to the Agence Nationale de la Recherche (ANR) for funding (ANR-16-CE34-0003-01).Notes and references
- J. A. Gokhale, A. L. Boskey and P. G. Robey, Osteoporosis, Elsevier, 2001, pp. 107–188 Search PubMed.
- M. Berglund, A. Åkesson, P. Bjellerup and M. Vahter, Toxicol. Lett., 2000, 112–113, 219–225 CrossRef CAS.
- C. Vidaud, D. Bourgeois and D. Meyer, Chem. Res. Toxicol., 2012, 25, 1161–1175 Search PubMed.
- Trace metals and fluoride in bones and teeth, ed. N. D. Priest and F. L. Van de Vyver, CRC Press, Boca Raton, Fla, 1990 Search PubMed.
- F. Bronner, Principles of Bone Biology, Elsevier, 2008, pp. 515–531 Search PubMed.
- P. Froidevaux, F. Bochud and M. Haldimann, Chemosphere, 2010, 80, 519–524 CrossRef CAS.
- C. Rey, C. Combes, C. Drouet and M. J. Glimcher, Osteoporos. Int., 2009, 20, 1013–1021 CrossRef CAS.
- C. Combes, S. Cazalbou and C. Rey, Minerals, 2016, 6, 34 CrossRef.
- C. Rey, C. Combes, C. Drouet, S. Cazalbou, D. Grossin, F. Brouillet and S. Sarda, Prog. Cryst. Growth Charact. Mater., 2014, 60, 63–73 CrossRef CAS.
- S. Cazalbou, D. Eichert, X. Ranz, C. Drouet, C. Combes, M. F. Harmand and C. Rey, J. Mater. Sci.: Mater. Med., 2005, 16, 405–409 CrossRef CAS.
- V. E. Badillo-Almaraz and J. Ly, J. Colloid Interface Sci., 2003, 258, 27–32 CrossRef CAS.
- Z. Xia, M. M. Villa and M. Wei, J. Mater. Chem. B, 2014, 2, 1998 RSC.
- G. Chatelain, D. Bourgeois, J. Ravaux, O. Averseng, C. Vidaud and D. Meyer, J. Biol. Inorg. Chem., 2015, 20, 497–507 CrossRef CAS.
- T. Gritsaenko, V. Pierrefite-Carle, T. Lorivel, V. Breuil, G. F. Carle and S. Santucci-Darmanin, Biochim. Biophys. Acta, Gen. Subj., 2017, 1861, 715–726 CrossRef CAS.
- Y. Ran, S. Wang, Y. Zhao, J. Li, X. Ran and Y. Hao, J. Environ. Radioact., 2020, 222, 106357 CrossRef CAS.
- Danish EPA, 2013.
- Agency for Toxic Substances and Disease Registry, 2013.
- Y.-C. Yue, M.-H. Li, H.-B. Wang, B.-L. Zhang and W. He, Environ. Health Prev. Med., 2018, 23, 18 CrossRef.
- A. E. V. Gorden, J. D. Xu, K. N. Raymond and P. Durbin, Chem. Rev., 2003, 103, 4207–4282 CrossRef CAS.
- G. R. Choppin, J. Radioanal. Nucl. Chem., 2007, 273, 695–703 CrossRef CAS.
- P. Thakur, R. C. Moore and G. R. Choppin, Radiochim. Acta, 2005, 93, 385–391 CAS.
- C. C. Fuller and J. R. Bargar, Abstr. Pap. Am. Chem. Soc., 2001, 222, U491 Search PubMed.
- C. C. Fuller, J. R. Bargar, J. A. Davis and M. J. Piana, Environ. Sci. Technol., 2002, 36, 158–165 CrossRef CAS.
- C. C. Fuller, J. R. Bargar and J. A. Davis, Environ. Sci. Technol., 2003, 37, 4642–4649 CrossRef CAS.
- L. Götzke, G. Schaper, J. März, P. Kaden, N. Huittinen, T. Stumpf, K. K. K. Kammerlander, E. Brunner, P. Hahn, A. Mehnert, B. Kersting, T. Henle, L. F. Lindoy, G. Zanoni and J. J. Weigand, Coord. Chem. Rev., 2019, 386, 267–309 CrossRef.
- G. Creff, C. Zurita, A. Jeanson, G. Carle, C. Vidaud and C. Den Auwer, Radiochim. Acta, 2019, 107, 993–1009 CAS.
- S. Ameziane-Le Hir, D. Bourgeois, C. Basset, A. Hagege and C. Vidaud, Metallomics, 2017, 9, 865–875 RSC.
- M. Sutton and S. R. Burastero, Chem. Res. Toxicol., 2004, 17, 1468–1480 Search PubMed.
- D. Gorman-Lewis, P. C. Burns and J. B. Fein, J. Chem. Thermodyn., 2008, 40, 335–352 CrossRef CAS.
- K. Hammami, H. El-Feki, O. Marsan and C. Drouet, Appl. Surf. Sci., 2016, 360, 979–988 CrossRef CAS.
- P. Pascaud, P. Gras, Y. Coppel, C. Rey and S. Sarda, Langmuir, 2013, 29, 2224–2232 CrossRef CAS.
- S. Sarda, M. Iafisco, P. Pascaud-Mathieu, A. Adamiano, M. Montesi, S. Panseri, O. Marsan, C. Thouron, A. Dupret-Bories, A. Tampieri and C. Drouet, Langmuir, 2018, 34, 12036–12048 CrossRef CAS.
- D. M. Taylor and R. W. Leggett, Radiat. Prot. Dosim., 2003, 106, 281 Search PubMed.
- F. Paquet, P. Houpert, E. Blanchardon, O. Delissen, C. Maubert, B. Dhieux, A. M. Moreels, S. Frelon, P. Voisin and P. Gourmelon, Health Phys., 2006, 90, 139–147 CrossRef CAS.
- S. Cazalbou, C. Combes, D. Eichert, C. Rey and M. J. Glimcher, J. Bone Miner. Metab., 2004, 22, 310–317 CrossRef.
- E. Bouyer, F. Gitzhofer and M. I. Boulos, J. Mater. Sci.: Mater. Med., 2000, 11, 523–531 CrossRef CAS.
- Y. Doi, T. Horiguchi, Y. Moriwaki, H. Kitago, T. Kajimoto and Y. Iwayama, J. Biomed. Mater. Res., 1996, 31, 43–49 CrossRef CAS.
- T. Shibutani, H. Iwanaga, K. Imai, M. Kitago, Y. Doi and Y. Iwayama, J. Biomed. Mater. Res., 2000, 50, 153–159 CrossRef CAS.
- G. Chatelain, D. Bourgeois, J. Ravaux, O. Averseng, C. Vidaud and D. Meyer, Biomed. Mater., 2014, 9, 015003 CrossRef.
- S. V. Dorozhkin, J. Mater. Sci., 2009, 44, 2343–2387 CrossRef CAS.
- C. Rey, C. Combes, C. Drouet, H. Sfihi and A. Barroug, Mater. Sci. Eng., C, 2007, 27, 198–205 CrossRef CAS.
- A. Krajewski, M. Mazzocchi, P. L. Buldini, A. Ravaglioli, A. Tinti, P. Taddei and C. Fagnano, J. Mol. Struct., 2005, 744–747, 221–228 CrossRef CAS.
- A. Grunenwald, C. Keyser, A. M. Sautereau, E. Crubézy, B. Ludes and C. Drouet, J. Archaeol. Sci., 2014, 49, 134–141 CrossRef CAS.
- S. Cazalbou, C. Combes, D. Eichert and C. Rey, J. Mater. Chem., 2004, 14, 2148 RSC.
- Y. Wang, S. Von Euw, F. M. Fernandes, S. Cassaignon, M. Selmane, G. Laurent, G. Pehau-Arnaudet, C. Coelho, L. Bonhomme-Coury, M.-M. Giraud-Guille, F. Babonneau, T. Azaïs and N. Nassif, Nat. Mater., 2013, 12, 1144–1153 CrossRef CAS.
- L. Wang and G. H. Nancollas, Chem. Rev., 2008, 108, 4628–4669 CrossRef CAS.
- C. Drouet, N. Vandecandelaere and C. Rey, MATEC Web Conf., 2013, 7, 04008 CrossRef.
- F. Errassifi, PhD thesis, Cadi Ayad University, 2011.
- I. S. Harding, N. Rashid and K. A. Hing, Biomaterials, 2005, 26, 6818–6826 CrossRef CAS.
- T. Kokubo and H. Takadama, Biomaterials, 2006, 27, 2907–2915 CrossRef CAS.
- A. A. Mir, B. Goyal, S. K. Datta, S. Ikkurthi and A. Pal, J. Lab. Physicians, 2016, 8, 071–076 CrossRef CAS.
- A. A. Baig, J. L. Fox, Z. Wang, W. I. Higuchi, S. C. Miller, A. M. Barry and M. Otsuka, Calcif. Tissue Int., 1999, 64, 329–339 CrossRef CAS.
- D. Bourgeois, B. Burt-Pichat, X. Le Goff, J. Garrevoet, P. Tack, G. Falkenberg, L. Van Hoorebeke, L. Vincze, M. A. Denecke, D. Meyer, C. Vidaud and G. Boivin, Anal. Bioanal. Chem., 2015, 407, 6619–6625 CrossRef CAS.
- V. Pierrefite-Carle, S. Santucci-Darmanin, V. Breuil, T. Gritsaenko, C. Vidaud, G. Creff, P. L. Solari, S. Pagnotta, R. Al-Sahlanee, C. D. Auwer and G. F. Carle, Arch. Toxicol., 2017, 91, 1903–1914 CrossRef CAS.
- C. Drouet, M.-T. Carayon, C. Combes and C. Rey, Mater. Sci. Eng., C, 2008, 28, 1544–1550 CrossRef CAS.
- F. G. Simon, V. Biermann and B. Peplinski, Appl. Geochem., 2008, 23, 2137–2145 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ma00398k |
| This journal is © The Royal Society of Chemistry 2020 |