Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Vibrational mode frequency correction of liquid water in density functional theory molecular dynamics simulations with van der Waals correction†
Kai
Zhong
ab,
Chun-Chieh
Yu
 b,
Mayank
Dodia
b,
Mischa
Bonn
b,
Mayank
Dodia
b,
Mischa
Bonn
 b,
Yuki
Nagata
b,
Yuki
Nagata
 *b and
Tatsuhiko
Ohto
*c
*b and
Tatsuhiko
Ohto
*c
aHefei National Laboratory for Physical Sciences at the Microscale, Collaborative Innovation Center of Chemistry for Energy Materials, CAS Center for Excellence in Nanoscience, School of Chemistry and Materials Science, University of Science and Technology of China, Hefei, Anhui 230026, P. R. China
bMax Planck Institute for Polymer Research, Ackermannweg 10, 55128 Mainz, Germany. E-mail: nagata@mpip-mainz.mpg.de
cGraduate School of Engineering Science, Osaka University, 1-3 Machikaneyama, Toyonaka, Osaka 560-8531, Japan. E-mail: ohto@molectronics.jp
First published on 22nd May 2020
Abstract
The frequencies and spectral lineshapes of the stretch and bending modes of water provide invaluable information on the microscopic structures of water in aqueous solutions and at the water/solid interfaces. Density functional theory molecular dynamics (DFT-MD) simulation has been used not only for predicting the properties of water but also for interpreting the vibrational spectra of water. Since the accuracy of the DFT-MD simulations relies on the choice of the exchange–correlation functionals and dispersion correction schemes employed, the predicted vibrational spectra at different levels of DFT theory differ significantly, prohibiting precise comparison of simulated spectra with experimental data. Here, we simulate the vibrational density of states for liquid heavy water based on various DFT-MD trajectories. We find that DFT-MD simulations tend to predict excessive inhomogeneous broadening for the stretch mode of water. Furthermore, we develop a frequency correction scheme for the stretch and bending modes of liquid water, which substantially improves the prediction of the vibrational spectra.
1. Introduction
The molecular structure of water is simple, yet the ensemble of water molecules leads to unique properties of liquid water, such as the higher density in the liquid phase than in the solid phase and large surface tension of water. These unique properties arise from the complex hydrogen-bond (H-bond) network of water. Understanding the relationship between the local conformation of water and H-bond strength is essential for clarifying the properties of various aqueous systems.Information on the H-bond of water has been gained through vibrational spectroscopy such as infrared (IR) and Raman spectroscopy.1,2 Typically, the IR spectrum of liquid water consists of three major bands; the O–H stretch mode, H–O–H bending mode, and librational modes of water. The O–H stretch and H–O–H bending modes have been widely used as reporters of the H-bond strength.3–6 When the H-bond of water becomes stronger, the frequency of the O–H stretch mode is lowered4 and the frequency of the H–O–H bending mode is elevated.7 As such, frequency shifts of the O–H stretch mode in aqueous solutions reflect how the solute–water interactions alter the strength and structure of the H-bond network of water.7–10 The target of the vibrational spectroscopy of water can be further expanded, when the vibrational technique is combined with a surface-specific technique.11–13 As such, vibrational spectroscopy becomes a valuable technique for probing the microscopic structure of interfacial water.
There are, however, several challenges associated with interpreting the vibrational spectra of water. First of all, the vibrational bands of the water spectra are often broad and featureless, making it difficult to assign specific features to the molecular conformations. Secondly, for more complex, composite aqueous solutions, it is often not clear which interaction is leading to which feature of the vibrational spectra. Simulating vibrational spectra based on the trajectories sampled by molecular dynamics (MD) simulation is a direct and powerful route to interpret the vibrational spectra, because it allows us to identify the contribution of water molecules in the bulk and near the solute molecules.5,14–18
When a solute–water interaction is complicated, developing accurate force field models for computing the vibrational spectra is not straightforward. In contrast with MD simulations using force field models, a density functional theory (DFT)-MD simulation computes the forces acting on the atoms based on DFT, which allows us to simulate complex solute–water interactions without using force field models.19–28 However, the predictive powers of DFT-MD simulations regarding the water properties rely heavily on the choice of the exchange–correlation (XC) functionals and van der Waals (vdW) corrections.29–35 Likewise, the peak frequencies in the vibrational spectra of liquid water are strongly affected by the XC functionals and vdW corrections.36–38
To correct the peak frequency, one can use the dataset of scaling factors that are available for many XC functionals.39–41 These datasets, however, do not work well for water vibrational spectroscopy, as these datasets are often created to correct for gas-phase frequencies. Furthermore, the scaling factors are generally parametrized for a set of small molecules, which may provide inaccurate numerical values for the liquid water peak frequencies. As such, generating the correction scheme for the vibrational frequency of water is urgently required for achieving reliable interpretation of the vibrational spectra of water, based on the DFT-MD simulation with available XC functionals and vdW corrections. Note that, although the vibrational spectra will be affected by several factors including nuclear quantum effects,42,43 the scheme for correcting the frequency being presented here include these effects only implicitly; the correction factor provides a practical approach to estimate the frequency of liquid water, while accurate high-level simulation requires nuclear quantum simulation, high-level XC functional, and accurate basis sets, resulting in a computationally expensive simulation.
In this work, we calculated the vibrational density of states (VDOS) spectra for bulk heavy water (D2O) with various DFT methods and vdW methods. We find that the O–D stretch frequency is highly sensitive to the XC functionals and vdW correction schemes. In particular, DFT-MD simulations tend to predict a broader peak than the experimental data, indicating that DFT-MD describes an excessive inhomogeneous environment of bulk water. On the other hand, the D–O–D bending frequency is rather insensitive to the choice of DFT methods. Furthermore, we developed a frequency correction scheme to reproduce the stretch and bending peaks for water. These correction factors are employed to evaluate the heterogeneity of the O–D stretch mode of heavy water.
2. Simulation procedures
2.1 MD Trajectories
We used the mixed Gaussian and plane wave approach as implemented in the CP2K code. For the Gaussian part, the TZV2P basis set which is constructed using triple-zeta valence Gaussian basis with two sets of polarization functions was used for all BOMD simulations. We set the plane wave density cutoff of 320 Ry. Only for the M06-L-D3(0), we used a cutoff of 1200 Ry, because the M06-L functional requires a finer integration grid.43 Norm-conserving Goedecker–Teter–Hutter pseudopotentials67,68 were used to describe the core electrons. To accelerate the MD simulations, D2O was used instead of H2O, and the time step was set to 0.5 fs. We simulated 160 D2O molecules in the 16.63 Å × 16.63 Å × 44.10 Å cell in a slab configuration at 300 K in the NVT ensemble. The canonical sampling through velocity rescaling method69 was employed as the thermostat. The cutoff radius of the vdW interactions was set to 10 Å.
We ran 10 independent simulations from previously generated configurations from the simulation at the revPBE-D3(0) level of theory.32 From each simulation, a 16 ps MD trajectory was generated after 5 ps equilibration run. The length of the trajectories were total ≥500 ps for BLYP, BLYP-D2, BLYP-D3(0), BLYP-D3(BJ), PBE, PBE-D2, PBE-D3(0), PBE-D3(BJ), revPBE-D3(0) and revPBE-D3(BJ) GGA functionals, ≥150 ps for PBE-D3m(BJ), PBE-DRSLL, PBE-rVV10, optB88-DRSLL, revPBE-D2, revPBE-DRSLL, revPBE-rVV10 GGA functionals, M06-L-D3(0), B97M-rV meta-GGA functionals, B3LYP-D3(0), HSE06-D3(0), revPBE0-D3(0) hybrid-GGA functionals, and 160 ps for revPBE-D3(0) hybrid functionals without ADMM.
2.2. VDOS spectra calculation based on MD trajectories
VDOS is computed for the bulk D2O molecules by using the velocity–velocity autocorrelation: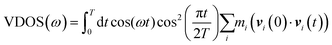 | (1) |
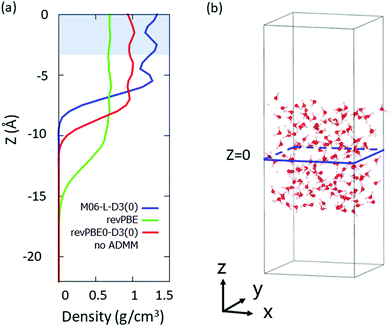
We selected the bulk D2O molecules as a D2O molecule with the z-coordinate of its oxygen atom |z| < 3 Å, where we set the origin point of z = 0 as a center of mass of the system. The region which we used for the VDOS calculation is highlighted in Fig. 1(a), while the snapshot of the simulation is drawn in Fig. 1(b).
3. Results
3.1. VDOS Spectra
Fig. 2 displays the calculated VDOS spectra with various combinations of the XC functionals and the vdW corrections, together with the reference POLI2VS data. Fig. 2 demonstrates that the spectral shapes of the O–D stretch mode are very sensitive to the choice of the DFT functional, whereas the D–O–D bending mode is comparatively insensitive. When we focus on the linewidth of the O–D stretch peak, one can recognize that the VDOS spectra computed from the DFT-MD trajectories are generally broader than the reference VDOS spectra. For example, the VDOS spectra computed from the revPBE0-D3(0) and SCAN functionals show much broader FWHMs (299 and 327 cm−1, respectively) than the reference POLI2VS data (FWHM of 259 cm−1). Since the linewidths of the spectra arise mainly from inhomogeneous broadening, this excessive broadening of the O–D stretch peak indicates that the DFT-MD simulations tend to sample a larger variety of the H-bond strengths than classical MD simulation.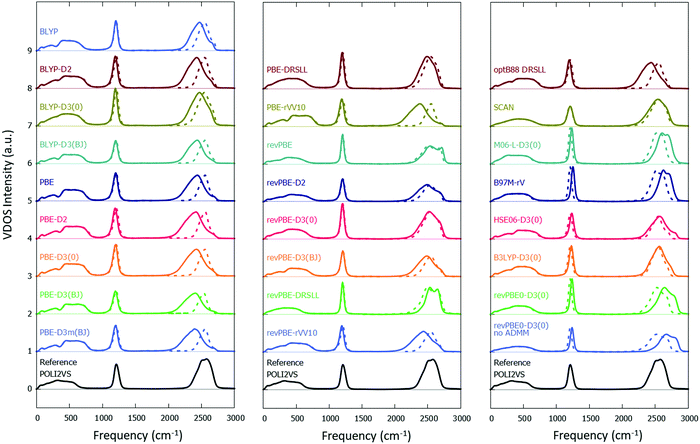 | ||
| Fig. 2 Simulated VDOS spectra for D2O with different DFT methods. The solid and dotted lines represent the simulated VDOS spectra without frequency correction and with frequency correction viaeqn (2) and (4), respectively. The reference data was obtained from the POLI2VS model. | ||
The comparison between the FWHM of the VDOS obtained from DFT-MD simulations and classical MD simulation is sharply contrasted with the comparison of their respective simulated IR spectra. Specifically, the reported linewidths of the IR stretch mode spectra using the revPBE0-D3(0) and SCAN functionals (FWHMs of 251 cm−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 36 and 246 cm−1,37 respectively) exhibit good agreement with the simulated IR spectra (FWHM of 257 cm−1
36 and 246 cm−1,37 respectively) exhibit good agreement with the simulated IR spectra (FWHM of 257 cm−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 82). These different trends in the VDOS spectra and IR spectra can be explained as follows. The linewidth of the IR spectrum of neat D2O is determined not only by the inhomogeneous broadening but also by the intermolecular/intramolecular vibrational coupling1,5,84 as well as the frequency-dependent transition dipole moment.85 Thus, the good agreement between the FWHMs in the IR spectra and poor agreement between the FWHMs in the VDOS data indicates that the FWHM of the IR spectra is dominated by the inhomogeneous broadening in the DFT-MD simulations, while in the classical MD simulations, the FWHM is largely determined by intermolecular/intramolecular vibrational coupling as well as the frequency-dependent transition dipole moment.
82). These different trends in the VDOS spectra and IR spectra can be explained as follows. The linewidth of the IR spectrum of neat D2O is determined not only by the inhomogeneous broadening but also by the intermolecular/intramolecular vibrational coupling1,5,84 as well as the frequency-dependent transition dipole moment.85 Thus, the good agreement between the FWHMs in the IR spectra and poor agreement between the FWHMs in the VDOS data indicates that the FWHM of the IR spectra is dominated by the inhomogeneous broadening in the DFT-MD simulations, while in the classical MD simulations, the FWHM is largely determined by intermolecular/intramolecular vibrational coupling as well as the frequency-dependent transition dipole moment.
Among the DFT-MD simulations considered in this study, the B97M-rV and M06-L-D3(0) levels of theory provide reasonable linewidths of the O–D stretch mode, in line with ref. 42. However, we also reported that these methods are inadequate for describing the water properties and the surface-specific vibrational spectra of water.34 This means that there is room for improving the XC functionals and vdW corrections. Finally, we note that, although a small 1500 cm−1 peak can be seen in the experimental data, it cannot be properly captured in the VDOS data, as this peak arises from the combination of bending and librational motions, and the VDOS calculation cannot capture such combination band properly. A high-level computational scheme would be needed to reproduce this combination band of water.86,87
3.2. Frequency correction factor
To correct the bandwidth as well as the peak position, we developed a correction scheme for the O–D stretch mode of D2O. For correcting the frequency, we assumed the expression as;| ωstr,ref = aωstr,DFT-MD + b | (2) |
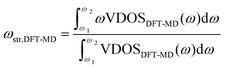 | (3) |
| DFT methods | ω str (cm−1) | Free O–D frequency (cm−1) | ω bend (cm−1) |
|---|---|---|---|
| BLYP | 2458 | 2688 | 1204 |
| BLYP-D2 | 2413 | 2688 | 1194 |
| BLYP-D3(0) | 2465 | 2688 | 1194 |
| BLYP-D3(BJ) | 2410 | 2687 | 1201 |
| PBE | 2411 | 2725 | 1201 |
| PBE-D2 | 2381 | 2725 | 1191 |
| PBE-D3(0) | 2399 | 2723 | 1197 |
| PBE-D3(BJ) | 2369 | 2718 | 1197 |
| PBE-D3m(BJ) | 2375 | 2718 | 1197 |
| PBE-DRSLL | 2490 | 2687 | 1199 |
| PBE-rVV10 | 2357 | 2712 | 1194 |
| revPBE | 2569 | 2740 | 1204 |
| revPBE-D2 | 2495 | 2732 | 1204 |
| revPBE-D3(0) | 2530 | 2737 | 1204 |
| revPBE-D3(BJ) | 2481 | 2732 | 1207 |
| revPBE-DRSLL | 2567 | 2697 | 1204 |
| revPBE-rVV10 | 2424 | 2712 | 1194 |
| optB88-DRSLL | 2417 | 2692 | 1194 |
| SCAN | 2527 | 2738 | 1213 |
| M06-L-D3(0) | 2628 | 2699 | 1234 |
| B97M-rV | 2645 | 2805 | 1251 |
| HSE06-D3(0) | 2562 | 2819 | 1234 |
| B3LYP-D3(0) | 2554 | 2773 | 1227 |
| revPBE0-D3(0) | 2657 | 2837 | 1237 |
| revPBE0-D3(0) no ADMM | 2686 | 2847 | 1237 |
| Reference | 2540 | 2714 | 1209 |
To determine two parameters, a and b, one needs to have the additional relation of ωstr,ref with ωstr,DFT-MD. This relation can be obtained from the peak frequency of the free O–D stretch in the DFT-MD simulated and experimental sum-frequency generation (SFG) spectra. At the free surface of water, a small fraction of water molecules finds itself with one non-hydrogen bonded OH/OD group that sticks into the vapor phase. The frequency of this free OH/OD group can be determined using sum-frequency generation spectroscopy. The free O–D stretch frequency of 2714 cm−1 is obtained from ref. 89, while the simulated free O–D stretch frequencies using DFT-MD simulations were obtained from ref. 34. The results are summarized in Table 1.
From the relation for the VDOS O–D stretch data and the free O–D stretch data, we obtained the parameters a and b. The parameters are listed in Table 2, while the O–D stretch spectra modified by using eqn (2) are plotted with the broken lines in Fig. 2. The frequency-corrected VDOS spectra of the O–D stretch mode show close agreement with the reference data. This illustrates that the frequency correction scheme is powerful for predicting the vibrational frequency and lineshape of the O–D stretch mode.
| DFT methods | a | b (cm−1) | c |
|---|---|---|---|
| BLYP | 0.757 | 679 | 1.004 |
| BLYP-D2 | 0.633 | 1013 | 1.013 |
| BLYP-D3(0) | 0.780 | 617 | 1.013 |
| BLYP-D3(BJ) | 0.628 | 1027 | 1.007 |
| PBE | 0.554 | 1204 | 1.007 |
| PBE-D2 | 0.506 | 1335 | 1.015 |
| PBE-D3(0) | 0.537 | 1252 | 1.010 |
| PBE-D3(BJ) | 0.499 | 1358 | 1.010 |
| PBE-D3m(BJ) | 0.507 | 1336 | 1.010 |
| PBE-DRSLL | 0.883 | 341 | 1.008 |
| PBE-rVV10 | 0.490 | 1385 | 1.013 |
| revPBE | 1.018 | −75 | 1.004 |
| revPBE-D2 | 0.734 | 709 | 1.004 |
| revPBE-D3(0) | 0.841 | 412 | 1.004 |
| revPBE-D3(BJ) | 0.693 | 821 | 1.002 |
| revPBE-DRSLL | 1.338 | −895 | 1.004 |
| revPBE-rVV10 | 0.604 | 1076 | 1.013 |
| optB88-DRSLL | 0.633 | 1010 | 1.013 |
| SCAN | 0.825 | 455 | 0.997 |
| M06-L-D3(0) | 0.946 | 54 | 0.980 |
| B97M-rV | 1.088 | −338 | 0.966 |
| HSE06-D3(0) | 0.677 | 806 | 0.980 |
| B3LYP-D3(0) | 0.791 | 520 | 0.985 |
| revPBE0-D3(0) | 0.967 | −29 | 0.977 |
| revPBE0-D3(0) no ADMM | 1.081 | −364 | 0.977 |
We further obtained the correction factor c for the D–O–D bending mode via;
| ωbend,ref = cωbend,ref,DFT-MD | (4) |
These correction factors can be also used to predict the vibrational spectra of H2O by scaling the vibrational frequency axis with the factor of 1/0.735 in the D2O spectra.89 In fact, the vibrational spectra lineshapes of H2O and D2O become quite similar after the frequency axis is scaled by this factor.90 Finally, we note that our correction scheme include a red-shift induced by nuclear quantum effects. For the DFT-MD simulation with the nuclear quantum effects such as the ring-polymer MD simulation91 and centroid MD simulation,92 we recommend using the coefficients, a and c, divided by a factor of 0.96.
3.3. Decomposition of the O–D stretch spectra
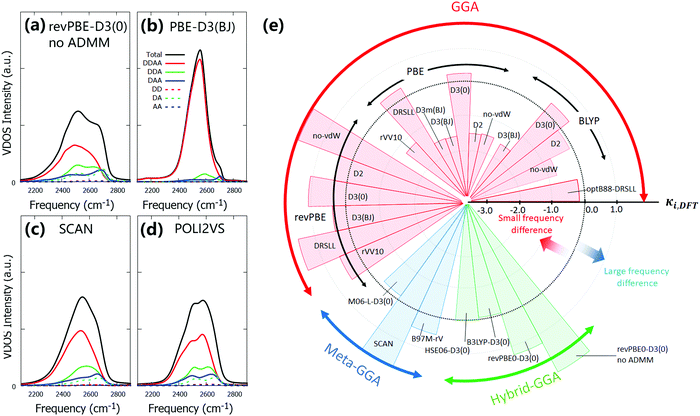
By establishing the frequency correction scheme for the DFT-MD trajectories, we can compare the individual spectra simulated at different DFT levels. Here, we investigate the level of heterogeneity of the O–D stretch spectra at different DFT levels of theory. To do so, we decomposed the spectra based on the number of donating and accepting hydrogen bonds (DDAA, DDA, DAA, DD, DA, AA, and others). The hydrogen bond formation was judged at time t = 0 in eqn (1)via the geometry of water dimer; when the O⋯O distance is less than 3.5 Å and the O⋯O–D angle is less than 30 degrees, the hydrogen bond is formed.93A few representative frequency-corrected DFT-MD spectra with O–D stretch decomposition are shown in Fig. 3(a)–(d). The computed spectra with other DFT methods are given in the ESI.† The data show that the O–D stretch mode is dominated by the contribution of the DDAA species, while the other water species, such as DDA and DAA, also contribute to the water spectra. The DDAA species constitute the lowest frequency component, and the water species with a smaller number of the hydrogen bond acceptor or donor provide higher frequency component, as is expected.4 However, one can see a marked difference of the frequency shift between the DDAA and the DDA/DAA/DD/DA/AA species. To quantify this, we computed the quantities of
| Δωi,DFT = ωi,DFT − ωDDAA | (5) |
| κi,DFT = (Δωi,DFT − Δωi,ff)/Δωi,sd | (6) |
4. Conclusion
We have computed the VDOS spectra of heavy water for the DFT-MD trajectories with various DFT methods and compared them with the reference data. We found that different DFT methods provide a variety of the O–D stretch mode peak frequency and linewidth in the VDOS spectra. In particular, the VDOS spectra of the DFT-MD simulations tend to show a broader linewidth than the reference POLI2VS VDOS spectrum, indicating that the DFT-MD simulations excessively sample the inhomogeneous environments of water stretch mode. Subsequently, we developed the frequency correction scheme for the stretch mode and bending mode. Our data shows that the correction proposed here can improve the prediction and interpretation of the vibrational spectra of D2O. By further scaling the frequency axis of the O–D stretch mode to the O–H stretch mode via a factor of 1/0.735, one can also predict the O–H stretch spectra reasonably.The correction scheme was further applied to evaluate the homogeneity of the O–D stretch spectra. By decomposing the corrected VDOS into the contributions from differently hydrogen-bonded water species, we revealed that the HSE06-D3(0), B3LYP-D3(0), revPBE-D2, revPBE-D3(BJ) and BLYP-D2 levels of theory predict a reasonable homogeneity of water frequencies with the classical MD simulation.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge the financial support from MaxWater project of Max Planck Society. This research used computational resources of Oakforest-PACS provided by Multidisciplinary Cooperative Research Program in Center for Computational Sciences, University of Tsukuba. Open Access funding provided by the Max Planck Society.References
- F. Perakis, L. De Marco, A. Shalit, F. Tang, Z. R. Kann, T. D. Kühne, R. Torre, M. Bonn and Y. Nagata, Vibrational Spectroscopy and Dynamics of Water, Chem. Rev., 2016, 116, 7590–7607 CrossRef CAS PubMed.
- H. J. Bakker and J. L. Skinner, Vibrational Spectroscopy as a Probe of Structure and Dynamics in Liquid Water, Chem. Rev., 2010, 110, 1498–1517 CrossRef CAS PubMed.
- M. Falk, The Frequency of the H–O–H Bending Fundamental in Solids and Liquids, Spectrochim. Acta, Part A, 1984, 40, 43–48 CrossRef.
- R. Rey, K. B. Møller and J. T. Hynes, Hydrogen Bond Dynamics in Water and Ultrafast Infrared Spectroscopy, J. Phys. Chem. A, 2002, 106, 11993–11996 CrossRef CAS.
- B. M. Auer and J. L. Skinner, IR and Raman Spectra of Liquid Water: Theory and Interpretation, J. Chem. Phys., 2008, 128, 224511 CrossRef CAS PubMed.
- Y. Ni and J. L. Skinner, IR and SFG Vibrational Spectroscopy of the Water Bend in the Bulk Liquid and at the Liquid-Vapor Interface, Respectively, J. Chem. Phys., 2015, 143, 014502 CrossRef PubMed.
- L. Piatkowski and H. J. Bakker, Vibrational Dynamics of the Bending Mode of Water Interacting with Ions, J. Chem. Phys., 2011, 135, 214509 CrossRef CAS PubMed.
- J. Hunger, K. J. Tielrooij, R. Buchner, M. Bonn and H. J. Bakker, Complex Formation in Aqueous Trimethylamine-N-Oxide (TMAO) Solutions, J. Phys. Chem. B, 2012, 116, 4783–4795 CrossRef CAS PubMed.
- J. G. Davis, K. P. Gierszal, P. Wang and D. Ben-Amotz, Water Structural Transformation at Molecular Hydrophobic Interfaces, Nature, 2012, 491, 582–585 CrossRef CAS PubMed.
- R. Biswas, W. Carpenter, J. A. Fournier, G. A. Voth and A. Tokmakoff, IR Spectral Assignments for the Hydrated Excess Proton in Liquid Water, J. Chem. Phys., 2017, 146, 154507 CrossRef PubMed.
- V. Ostroverkhov, G. A. Waychunas and Y. R. Shen, New Information on Water Interfacial Structure Revealed by Phase-Sensitive Surface Spectroscopy, Phys. Rev. Lett., 2005, 94, 046102 CrossRef PubMed.
- A. Eftekhari-Bafrooei and E. Borguet, Effect of Surface Charge on the Vibrational Dynamics of Interfacial Water, J. Am. Chem. Soc., 2009, 131, 12034–12035 CrossRef CAS PubMed.
- H. C. Allen, N. N. Casillas-Ituarte, M. R. Sierra-Hernández, X. Chen and C. Y. Tang, Shedding Light on Water Structure at Air-Aqueous Interfaces: Ions, Lipids, and Hydration, Phys. Chem. Chem. Phys., 2009, 11, 5538–5549 Search PubMed.
- T. Yagasaki and S. Saito, Ultrafast Intermolecular Dynamics of Liquid Water: A Theoretical Study on Two-Dimensional Infrared Spectroscopy, J. Chem. Phys., 2008, 128, 154521 CrossRef PubMed.
- S. Imoto, S. S. Xantheas and S. Saito, Molecular Origin of the Difference in the HOH Bend of the IR Spectra between Liquid Water and Ice, J. Chem. Phys., 2013, 138, 054506 CrossRef PubMed.
- M. M. Skinner, A. A. Martin and B. C. Moore, Is Lipid Correction Necessary in the Stable Isotope Analysis of Fish Tissues?, Rapid Commun. Mass Spectrom., 2016, 30, 881–889 CrossRef CAS PubMed.
- K. Usui, J. Hunger, M. Sulpizi, T. Ohto, M. Bonn and Y. Nagata, Ab Initio Liquid Water Dynamics in Aqueous TMAO Solution, J. Phys. Chem. B, 2015, 119, 10597–10606 CrossRef CAS.
- T. Ohto, E. H. G. Backus, C.-S. Hsieh, M. Sulpizi, M. Bonn and Y. Nagata, Lipid Carbonyl Groups Terminate the Hydrogen Bond Network of Membrane-Bound Water, J. Phys. Chem. Lett., 2015, 6, 4499–4503 CrossRef CAS.
- Y. Nagata, S. Yoshimune, C. S. Hsieh, J. Hunger and M. Bonn, Ultrafast Vibrational Dynamics of Water Disentangled by Reverse Nonequilibrium Ab Initio Molecular Dynamics Simulations, Phys. Rev. X, 2015, 5, 021002 Search PubMed.
- C. Zhang, D. Donadio, F. Gygi and G. Galli, First Principles Simulations of the Infrared Spectrum of Liquid Water Using Hybrid Density Functionals, J. Chem. Theory Comput., 2011, 7, 1443–1449 CrossRef CAS PubMed.
- T. Ohto, K. Usui, T. Hasegawa, M. Bonn and Y. Nagata, Toward Ab Initio Molecular Dynamics Modeling for Sum-Frequency Generation Spectra; an e Cient Algorithm Based on Surface-Specific Velocity-Velocity Correlation Function, J. Chem. Phys., 2015, 143, 124702 CrossRef PubMed.
- R. Iftimie and M. E. Tuckerman, The Molecular Origin of the “Continuous” Infrared Absorption in Aqueous Solutions of Acids: A Computational Approach, Angew. Chem., Int. Ed., 2006, 45, 1144–1147 CrossRef CAS PubMed.
- W. Chen, M. Sharma, R. Resta, G. Galli and R. Car, Role of Dipolar Correlations in the Infrared Spectra of Water and Ice, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 245114 CrossRef.
- H. S. Lee and M. E. Tuckerman, Dynamical Properties of Liquid Water from Ab Initio Molecular Dynamics Performed in the Complete Basis Set Limit, J. Chem. Phys., 2007, 126, 164501 CrossRef PubMed.
- M. Sharma, R. Resta and R. Car, Intermolecular Dynamical Charge Fluctuations in Water: A Signature of the H-Bond Network, Phys. Rev. Lett., 2005, 95, 187401 CrossRef PubMed.
- B. Das, B. Sharma and A. Chandra, Effects of tert-Butyl Alcohol on Water at the Liquid–Vapor Interface: Structurally Bulk-like but Dynamically Slow Interfacial Water, J. Phys. Chem. C, 2018, 122, 9374–9388 CrossRef CAS.
- G. Melani, Y. Nagata, J. Wirth and P. Saalfrank, Vibrational Spectroscopy of Hydroxylated α-Al2O3(0001) Surfaces with and without Water: An Ab Initio Molecular Dynamics Study, J. Chem. Phys., 2018, 149, 014707 CrossRef PubMed.
- L. W. Pinkley, P. P. Sethna and D. Williams, Optical Constants of Water in the Infrared: Influence of Temperature, J. Opt. Soc. Am., 1977, 67, 494–499 CrossRef CAS.
- I.-C. Lin, A. P. Seitsonen, I. Tavernelli and U. Rothlisberger, Structure and Dynamics of Liquid Water from Ab Initio Molecular Dynamics—Comparison of BLYP, PBE, and RevPBE Density Functionals with and without van der Waals Corrections, J. Chem. Theory Comput., 2012, 8, 3902–3910 CrossRef CAS PubMed.
- M. J. Gillan, D. Alfè and A. Michaelides, Perspective: How Good Is DFT for Water?, J. Chem. Phys., 2016, 144, 130901 CrossRef PubMed.
- S. Grimme, A. Hansen, J. G. Brandenburg and C. Bannwarth, Dispersion-Corrected Mean-Field Electronic Structure Methods, Chem. Rev., 2016, 116, 5105–5154 Search PubMed.
- T. Ohto, M. Dodia, S. Imoto and Y. Nagata, Structure and Dynamics of Water at the Water-Air Interface Using First-Principles Molecular Dynamics Simulations within Generalized Gradient Approximation, J. Chem. Theory Comput., 2019, 15, 595–602 CrossRef CAS PubMed.
- M. Dodia, T. Ohto, S. Imoto and Y. Nagata, Structure and Dynamics of Water at the Water–Air Interface Using First-Principles Molecular Dynamics Simulations. II. NonLocal vs Empirical van der Waals Corrections, J. Chem. Theory Comput., 2019, 15, 3836–3843 CrossRef CAS PubMed.
- T. Ohto, M. Dodia, J. Xu, S. Imoto, F. Tang, F. Zysk, T. D. Kühne, Y. Shigeta, M. Bonn and X. Wu, et al., Accessing the Accuracy of Density Functional Theory through Structure and Dynamics of the Water–Air Interface, J. Phys. Chem. Lett., 2019, 10, 4914–4919 CrossRef CAS PubMed.
- J. G. Brandenburg, A. Zen, D. Alfè and A. Michaelides, Interaction between Water and Carbon Nanostructures: How Good Are Current Density Functional Approximations?, J. Chem. Phys., 2019, 151, 164702 Search PubMed.
- O. Marsalek and T. E. Markland, Quantum Dynamics and Spectroscopy of Ab Initio Liquid Water: The Interplay of Nuclear and Electronic Quantum Effects, J. Phys. Chem. Lett., 2017, 8, 1545–1551 CrossRef CAS PubMed.
- J. Xu, M. Chen, C. Zhang and X. Wu, First-Principles Study of the Infrared Spectrum in Liquid Water from a Systematically Improved Description of H-Bond Network, Phys. Rev. B, 2019, 99, 205123 CrossRef CAS.
- M. J. DelloStritto, S. M. Piontek, M. L. Klein and E. Borguet, Effect of Functional and Electron Correlation on the Structure and Spectroscopy of the Al2O3 (001)–H2O Interface, J. Phys. Chem. Lett., 2019, 3, 2031–2036 CrossRef PubMed.
- J. P. Merrick, D. Moran and L. Radom, An Evaluation of Harmonic Vibrational Frequency Scale Factors, J. Phys. Chem. A, 2007, 111, 11683–11700 CrossRef CAS.
- D. O. Kashinski, G. M. Chase, R. G. Nelson, O. E. Di Nallo, A. N. Scales, D. L. Vanderley and E. F. C. Byrd, Harmonic Vibrational Frequencies: Approximate Global Scaling Factors for TPSS, M06, and M11 Functional Families Using Several Common Basis Sets, J. Phys. Chem. A, 2017, 121, 2265–2273 CrossRef CAS PubMed.
- I. M. Alecu, J. Zheng, Y. Zhao and D. G. Truhlar, Computational Thermochemistry: Scale Factor Databases and Scale Factors for Vibrational Frequencies Obtained from Electronic Model Chemistries, J. Chem. Theory Comput., 2010, 6, 2872–2887 CrossRef CAS PubMed.
- L. Ruiz Pestana, O. Marsalek, T. E. Markland and T. Head-Gordon, The Quest for Accurate Liquid Water Properties from First Principles, J. Phys. Chem. Lett., 2018, 9, 5009–5016 CrossRef CAS PubMed.
- L. Ruiz Pestana, N. Mardirossian, M. Head-Gordon and T. Head-Gordon, Ab Initio Molecular Dynamics Simulations of Liquid Water Using High Quality Meta-GGA Functionals, Chem. Sci., 2017, 8, 3554–3565 RSC.
- J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Quickstep: Fast and Accurate Density Functional Calculations Using a Mixed Gaussian and Plane Waves Approach, Comput. Phys. Commun., 2005, 167, 103–128 CrossRef CAS.
- J. Hutter, M. Iannuzzi, F. Schiffmann and J. VandeVondele, Atomistic Simulations of Condensed Matter Systems, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 15–25 CAS.
- J. P. Perdew, K. Burke and E. Matthias, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- A. D. Becke, Density-Functional Exchange-Energy Approximation with Correct Asymptotic Behavior, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS.
- Y. Zhang and W. Yang, Comment on “Generalized Gradient Approximation Made Simple.”, Phys. Rev. Lett., 1998, 80, 890 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, A New Local Density Functional for Main-Group Thermochemistry, Transition Metal Bonding, Thermochemical Kinetics, and Noncovalent Interactions, J. Chem. Phys., 2006, 125, 194101 CrossRef PubMed.
- N. Mardirossian and M. Head-Gordon, Mapping the Genome of Meta-Generalized Gradient Approximation Density Functionals: The Search for B97M-V, J. Chem. Phys., 2015, 142, 074111 CrossRef PubMed.
- A. D. Becke, Density-functional Thermochemistry. III. The Role of Exact Exchange, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- S. H. Vosko, L. Wilk and M. Nusair, Accurate Spin-Dependent Electron Liquid Correlation Energies for Local Spin Density Calculations: A Critical Analysis, Can. J. Phys., 1980, 58, 1200–1211 CrossRef CAS.
- C. Adamo and V. Barone, Toward Reliable Density Functional Methods without Adjustable Parameters: The PBE0 Model, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, Hybrid Functionals Based on a Screened Coulomb Potential, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, Influence of the Exchange Screening Parameter on the Performance of Screened Hybrid Functionals, J. Chem. Phys., 2006, 125, 224106 CrossRef.
- M. Guidon, J. Hutter and J. VandeVondele, Auxiliary Density Matrix Methods for Hartree−Fock Exchange Calculations, J. Chem. Theory Comput., 2010, 6, 2348–2364 CrossRef CAS PubMed.
- S. Grimme, Semiempirical GGA-Type Density Functional Constructed with a Long-Range Dispersion Correction, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef.
- S. Grimme, S. Ehrlich and L. Goerigk, Effect of the Damping Function in Dispersion Corrected Density Functional Theory, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- D. G. A. Smith, L. A. Burns, K. Patkowski and C. D. Sherrill, Revised Damping Parameters for the D3 Dispersion Correction to Density Functional Theory, J. Phys. Chem. Lett., 2016, 7, 2197–2203 CrossRef CAS PubMed.
- M. Dion, H. Rydberg, E. Schröder, D. C. Langreth and B. I. Lundqvist, van der Waals Density Functional for General Geometries, Phys. Rev. Lett., 2004, 92, 246401 CrossRef CAS.
- G. Román-Pérez and J. M. Soler, Efficient Implementation of a van der Waals Density Functional: Application to Double-Wall Carbon Nanotubes, Phys. Rev. Lett., 2009, 103, 096102 Search PubMed.
- R. Sabatini, T. Gorni and S. de Gironcoli, Nonlocal van der Waals Density Functional Made Simple and Efficient, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 041108 Search PubMed.
- O. A. Vydrov and T. Van Voorhis, Nonlocal van der Waals Density Functional: The Simpler the Better, J. Chem. Phys., 2010, 133, 244103 CrossRef PubMed.
- M. F. Kropman, H.-K. Nienhuys, S. Woutersen and H. J. Bakker, Vibrational Relaxation and Hydrogen-Bond Dynamics of HDO:H2O, J. Phys. Chem. A, 2001, 105, 4622–4626 CrossRef CAS.
- S. Goedecker, M. Teter and J. Hutter, Separable Dual-Space Gaussian Pseudopotentials, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703–1710 CrossRef CAS PubMed.
- G. Bussi, D. Donadio and M. Parrinello, Canonical Sampling through Velocity Rescaling, J. Chem. Phys., 2007, 126 Search PubMed.
- J. Sun, R. C. Remsing, Y. Zhang, Z. Sun, A. Ruzsinszky, H. Peng, Z. Yang, A. Paul, U. Waghmare and X. Wu, et al., Accurate First-Principles Structures and Energies of Diversely Bonded Systems from an Efficient Density Functional, Nat. Chem., 2016, 8, 831–836 CrossRef CAS PubMed.
- J. Sun, A. Ruzsinszky and J. Perdew, Strongly Constrained and Appropriately Normed Semilocal Density Functional, Phys. Rev. Lett., 2015, 115, 036402 CrossRef PubMed.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni and I. Dabo, et al., QUANTUM ESPRESSO: A Modular and Open-Source Software Project for Quantum Simulations of Materials, J. Phys.: Condens. Matter, 2009, 21, 395502 Search PubMed.
- P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. Buongiorno Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli and M. Cococcioni, et al., Advanced Capabilities for Materials Modelling with Quantum ESPRESSO, J. Phys.: Condens. Matter, 2017, 29, 465901 CrossRef CAS PubMed.
- D. Vanderbilt, Optimally Smooth Norm-Conserving Pseudopotentials, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 32, 8412–8415 CrossRef CAS.
- D. R. Hamann, M. Schlüter and C. Chiang, Norm-Conserving Pseudopotentials, Phys. Rev. Lett., 1979, 43, 1494–1497 CrossRef CAS.
- W. G. Hoover, Canonical Dynamics: Equilibrium Phase-Space Distributions, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697 CrossRef.
- G. J. Martyna, M. L. Klein and M. Tuckerman, Nosé–Hoover Chains: The Canonical Ensemble via Continuous Dynamics, J. Chem. Phys., 1992, 97, 2635–2643 CrossRef.
- I.-F. W. Kuo, C. J. Mundy, M. J. McGrath and J. I. Siepmann, Time-Dependent Properties of Liquid Water: A Comparison of Car−Parrinello and Born−Oppenheimer Molecular Dynamics Simulations, J. Chem. Theory Comput., 2006, 2, 1274–1281 CrossRef CAS PubMed.
- M. Chen, H.-Y. Ko, R. C. Remsing, M. F. Calegari Andrade, B. Santra, Z. Sun, A. Selloni, R. Car, M. L. Klein and J. P. Perdew, et al., Ab Initio Theory and Modeling of Water, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 10846–10851 Search PubMed.
- R. Khatib, T. Hasegawa, M. Sulpizi, E. H. G. Backus, M. Bonn and Y. Nagata, Molecular Dynamics Simulations of SFG Librational Modes Spectra of Water at the Water–Air Interface, J. Phys. Chem. C, 2016, 120, 18665–18673 CrossRef CAS.
- H. Ito and Y. Tanimura, Simulating Two-Dimensional Infrared-Raman and Raman Spectroscopies for Intermolecular and Intramolecular Modes of Liquid Water, J. Chem. Phys., 2016, 144, 074201 CrossRef PubMed.
- T. Hasegawa and Y. Tanimura, A Polarizable Water Model for Intramolecular and Intermolecular Vibrational Spectroscopies, J. Phys. Chem. B, 2011, 115, 5545–5553 CrossRef CAS PubMed.
- Y. Nagata, T. Hasegawa, E. H. G. Backus, K. Usui, S. Yoshimune, T. Ohto and M. Bonn, The Surface Roughness, but Not the Water Molecular Orientation Varies with Temperature at the Water–Air Interface, Phys. Chem. Chem. Phys., 2015, 17, 23559–23564 RSC.
- J. Schaefer, E. H. G. Backus, Y. Nagata and M. Bonn, Both Inter- and Intramolecular Coupling of O–H Groups Determine the Vibrational Response of the Water/Air Interface, J. Phys. Chem. Lett., 2016, 7, 4591–4595 CrossRef CAS PubMed.
- S. A. Corcelli and J. L. Skinner, Infrared and Raman Line Shapes of Dilute HOD in Liquid H2O and D2O from 10 to 90 °C, J. Phys. Chem. A, 2005, 109, 6154–6165 CrossRef CAS.
- H. Liu, Y. Wang and J. M. Bowman, Quantum Local Monomer IR Spectrum of Liquid D2O at 300 K from 0 to 4000 cm−1 Is in Near-Quantitative Agreement with Experiment, J. Phys. Chem. B, 2016, 10, 2824–2828 CrossRef.
- H. Liu, Y. Wang and J. M. Bowman, Quantum Calculations of the IR Spectrum of Liquid Water Using Ab Initio and Model Potential and Dipole Moment Surfaces and Comparison with Experiment, J. Chem. Phys., 2015, 142, 194502 CrossRef PubMed.
- F. Tang, T. Ohto, S. Sun, J. R. Rouxel, S. Imoto, E. H. G. Backus, S. Mukamel, M. Bonn and Y. Nagata, Molecular Structure and Modeling of Water–Air and Ice–Air Interfaces Monitored by Sum-Frequency Generation, Chem. Rev., 2020, 120, 3633–3667 CrossRef CAS PubMed.
- X. Xu, Y. R. Shen and C. Tian, Phase-Sensitive Sum Frequency Vibrational Spectroscopic Study of Air/Water Interfaces: H2O, D2O, and Diluted Isotopic Mixtures, J. Chem. Phys., 2019, 150, 144701 CrossRef PubMed.
- S. Y. Venyaminov and F. G. Prendergast, Water (H2O and D2O) Molar Absorptivity in the 1000–4000 cm−1 Range and Quantitative Infrared Spectroscopy of Aqueous Solutions, Anal. Biochem., 1997, 248, 234–245 CrossRef CAS PubMed.
- I. R. Craig and D. E. Manolopoulos, Quantum Statistics and Classical Mechanics: Real Time Correlation Functions from Ring Polymer Molecular Dynamics, J. Chem. Phys., 2004, 121, 3368–3373 CrossRef CAS PubMed.
- J. Cao and G. A. Voth, The Formulation of Quantum Statistical Mechanics Based on the Feynman Path Centroid Density. II. Dynamical Properties, J. Chem. Phys., 1994, 100, 5106–5117 CrossRef CAS.
- A. Luzar and D. Chandler, Hydrogen-Bond Kinetics in Liquid Water, Nature, 1996, 379, 55–57 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp06335h |
| This journal is © the Owner Societies 2020 |