Reversible temperature-induced polymorphic phase transitions of [Y(OAr)₃] and [Ce(OAr)₃] (Ar = 2,6-^tBu₂-4-MeC₆H₂): interconversions between pyramidal and planar geometries

Abstract

In studying the crystal structure of [Y(O-2,6-^tBu₂-4-MeC₆H₂)₃] [1] at different temperatures, three phase transitions were observed. Three polymorphs contained a 1 : 1 ratio of planar and pyramidal isomers of 1 with an increasing number of molecules in the asymmetric unit, but the fourth polymorph at 100 K had a 3 : 2 ratio favouring the planar geometry. These phase transitions were reversible and involved very subtle changes in the molecular conformation, which must happen in situ over all the molecules in the crystal. For [Ce(O-2,6-^tBu₂-4-MeC₆H₂)₃] [2] with one 4f-electron, a disorder/order transition was observed, similar to the first phase transition for 1, with two different molecules observed in the asymmetric unit at 100 K {Σ(O–Ln–O) = 341.3° and 351.7°}. The study of these polymorphic systems has been complemented by computational studies in the gas phase and solid state that confirm that these complexes lie in a very shallow potential energy surface that allow molecules to transition between planar and pyramidal structures upon a change in temperature.

---

Introduction

The identification of three-coordinate rare-earth compounds was an important milestone in the chemistry of group 3 and the f-block.^1–4 The first of these complexes to be characterised utilised the hexamethyldisilazide {N(SiMe₃)₂, or N′′} ligand, which is sterically very bulky, inhibiting bridged motifs, and imparts good hydrocarbon solubility to the compounds. These properties are important because low-coordinate rare-earth complexes are very reactive to water and other donor/protic solvents, through either coordination or reaction with the strongly basic, anionic ligands, so hydrocarbon solvents must be used in their preparation. 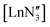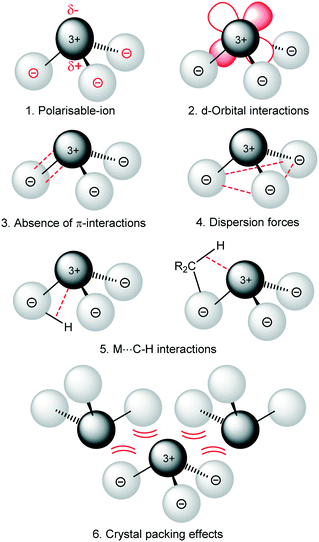Many solid-state structures of are known and show the metal to be situated on a three-fold rotation axis and in a trigonal pyramidal geometry, with the metal disordered 0.34–0.65 Å above and below the plane of the three N atoms.^5–17 Recently, the analogous Ln(II) 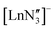‘ate’ complexes with non-interacting cryptand-encapsulated alkali-metal cations have also been structurally characterised with similar disorder of the Ln atoms 0.27–0.52 Å above and below the plane.¹⁷ The adoption of a trigonal pyramidal geometry, rather than a trigonal planar geometry, was unexpected according to predictions based on VSEPR and a number of hypotheses have been proposed to explain this (Fig. 1).^18–24 These explanations are also likely to underpin the non-linearity of several two-coordinate group 2 compounds as well.^19,25–29 Despite many years of disagreement, it has more recently been proposed that the polarisable-ion model (Fig. 1, 1) is not in competition with the presence of d-orbital interactions (2), which have been identified as very important factors in enforcing the non-planar geometry.^19,23,30 In fact, they could be two facets of the same mechanism.¹⁹ The presence of π-interactions with the directly bonded ligand donor atoms tend to decrease pyramidality (3).^19,20 The influence of London dispersion forces (4) has become an important topic of consideration in inorganic chemistry.^31,32 Dispersion forces have been highlighted as important contributors to the bent geometry in 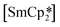²⁷ and 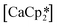,³³ but were found to be less important when using a different set of techniques in the study of 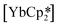.²⁸ A brief DFT study on 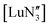demonstrated only minor differences in geometry computed with and without dispersion corrections, suggesting only a relatively minor contribution.¹⁸ The shallow nature of the potential energy surface and the small amount of energy required for these deformations/interconversions has been alluded to.²⁰ Metal C–H agostic interactions (5) are another potential complication to the system,³³ but for [Ln{CH(SiMe₃)₂}₃], the influence of these interactions has been suggested by Boyde et al. to have been overstated,¹⁸ with more evidence for β-agostic Si–C bonds than γ-agostic C–H bonds.^23,34 Crystal-packing effects must also be taken into account (6).^21,35 In the solid state, [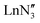, including Sc] are all pyramidal, and it has been established that at least some 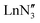(where Ln = La, Ce or Pr) remain in this geometry in the gas phase.²¹ However, 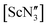was found by electron diffraction to be planar in the gas phase.³⁵ The conclusion from this study was that crystal packing may play a role in the pyramidality of 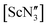in the solid state (potentially emphasising the shallow potential-energy surface of this molecule),³⁵ but crystal-packing effects cannot explain the pyramidality in the other 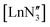complexes.²¹ Near linear Ln(II) bis(amides)^36,37 and planar Ln(III)^24,38 and U(III)³⁹ tris(amides) have recently been realised through the use of extremely sterically bulky ligands that use steric constraints to enforce the geometries anticipated by VSEPR.

Fig. 1 Possible factors leading to pyramidal geometries in 3-coordiante Ln complexes.

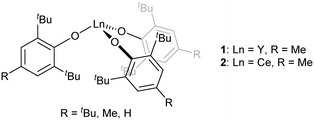
[Ln(OAr)₃] are another well-known class of three-coordinate rare earth species that are stable when the Ar groups are large (Fig. 2, Ar = 2,6-^tBu₂-4-RC₆H₂; R = ^tBu, Me, H).^40–44 With the smaller aryl group 2,6-ⁱPr₂C₆H₃, dimers with arene interactions were observed instead.⁴⁵ Conventionally, [Ln(OAr)₃] complexes with Ar = 2,6-^tBu₂-4-RC₆H₂; R = ^tBu, Me, H would be predicted to have almost identical geometries and reactivities because the peripheral para-R groups would be expected to have a minimal influence on the mainly ionic-bonding of the aryloxide ligand. However, it was observed that the uranium analogue [U(OAr)₃] with para-^tBu was found to bind strongly to N₂ whereas the analogous compound with para-H did not.⁴⁶ In transition metal terphenyl compounds, the influence of remote para-ⁱPr groups was recently found to be important as well.⁴⁷ Remote substitution might, however, be expected to change crystal packing effects.

Fig. 2 Monomeric rare earth tris(aryloxide) complexes.

The geometry of f-block complexes has become a very important consideration due to the single molecule magnet (SMM) properties of many of these systems,^48,49 including three coordinate 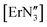,⁵⁰ [Er{CH(SiMe₃)₂}₃] and [Er(O-2,6-^tBu₂-4-MeC₆H₂)₃].⁴³ Herein, we explore the phase transitions observed for [Y(OAr)₃] and [Ce(OAr)₃] (Ar = 2,6-^tBu₂-4-RC₆H₂, R = Me), which in turn highlights the fine balance in the energies between planar and trigonal pyramidal geometries in these complexes, and the influence of the para-substituent.

Results and discussion

Phase transitions in the crystal structures of 1 and 2 (R = Me)

In the course of synthesising rare-earth starting materials for an investigation into ‘ate’ complex formation,⁵¹ [Y(OAr)₃] (1) and [Ce(OAr)₃] (2), (Ar = 2,6-^tBu₂-4-RC₆H₂, R = Me) were synthesised and their crystal structures determined. It was noted that 1 had a large unit cell at 100 K with Z′ = 5. This is in contrast to 2 which had Z′ = 1 at 200 K and was isomorphous to the analogous Er and Sc crystal structures.^40,43 The Sc, Ce and Er compounds crystallise in the space group P1̄, with one molecule in the asymmetric unit. The structure of 2 shows Ce disordered over two positions with Σ(O–Ce–O) equal to 349.7(2)° and 356.3(2)°, i.e. the second Ce atom position does not lead to a planar geometry, but rather a second, albeit shallow, pyramid (see Fig. S3 in the ESI‡). The Ce–O bond lengths are 2.198(2), 2.098(2) and 2.183(2) Å for pyramidal or 2.117(2), 2.161(2) and 2.130(2) Å for the near-planar geometry. The Sc complex (at room temperature), with its smaller ionic radius (average Sc–O = 1.869(15) Å), adopted a near-planar conformation (Σ(O–Sc–O) = 358.5°),⁴⁰ which resembles the gas-phase structure of 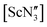.³⁵ The Er complex, with an average Er–O bond length of 2.043(4) Å (at 120 K), is pyramidal (Σ(O–Er–O) = 342.2(5)°).⁴³ We recollected diffraction data of the Y compound 1 at various temperatures noting a number of phase transitions as the temperature was increased. At 160 K, the structure was determined to be isomorphous to the analogous Sc, Ce and Er structures with Z′ = 1, but displaying 50 : 50 disorder between planar and pyramidal geometries (Σ(O–Y–O) = 360.0(2)° and 347.7(2)° respectively (Fig. 3)), unlike the disorder between the two different pyramidal geometries seen for 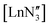.^{9,11–14,16,52} The three aryloxide ligands adopt different orientations of the ^tBu groups and slightly different torsion angles with respect to the plane of the three oxygen atoms, leading to a significant deviation from C₃ geometry. In each geometry, there are different Y⋯H short contacts (see below). Thus, in the crystal structures of [Ln(OAr)₃] Ln = Ce, Y, Er, Sc; Ar = 2,6-^tBu₂-4-MeC₆H₂, the metal can adopt a planar or pyramidal configuration without changing the overall crystal packing.

Fig. 3 Molecular geometry of [Y(OAr)₃] (1) in the crystal structure at 160 K (A) and the two independent molecules observed in the structure at 140 K (B, planar and C, pyramidal). Most H atoms have been removed for clarity. Disordered atoms from the second part of A (which have 50% occupancy) are coloured orange.

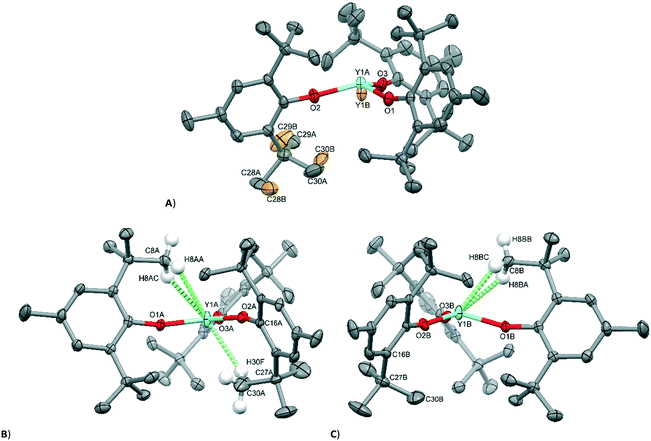
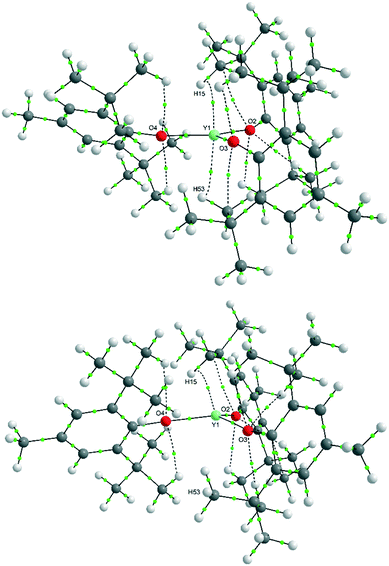
A variable-temperature study showed that upon cooling 1 from 160 K to 140 K, the disordered molecules separate into two distinct sites, one pyramidal (Σ(O–Y–O) = 348.2(2)°) and one planar (Σ(O–Y–O) = 359.9(2)°) such that Z′ = 2. This same transition was observed for 2 upon cooling from 200 K to 190 K and produced two ordered but different molecular geometries (Σ(O–Ce–O) = 341.3(2)° and 351.7(2)°). On further cooling of 1 to 120 K, a second phase transition occurs that sees the unit cell double in volume again such that there are now two planar and two pyramidal molecules in the asymmetric unit (and Z′ = 4). A final phase transition was seen when data for 1 were collected at 100 K, when Z′ increases to 5 to show three planar and two pyramidal molecules in the asymmetric unit (Table 1, Fig. 4). Structures with Z′ ≥ 5 are rare, making up fewer than 0.07% of structures in the CSD.⁵³ There is now an unequal population of the two different geometries with planar favoured. Further cooling was not possible using our equipment, and no further transitions for 2 were observed down to 100 K. Notably, all structures adopt approximately the same crystal packing. This is possible because the geometric differences between the planar and pyramidal forms are subtle (Fig. 3A).

Table 1 Unit cells for phases of 1

T/K	160 K	140 K	120 K	100 K
a/Å	9.7113(3)	9.7054(5)	9.6914(4)	9.6910(6)
b/Å	15.0872(4)	25.1144(12)	25.0653(1)	25.0295(17)
c/Å	15.6649(5)	17.7491(9)	35.4181(14)	45.485(3)
α/°	70.506(2)	92.271(3)	92.297(2)	76.182(4)
β/°	83.665(2)	91.056(3)	91.122(2)	86.604(3)
γ/°	82.160(2)	98.699(3)	98.890(2)	80.933(3)
V/Å^3	2138.20(11)	4271.8(4)	8490.6(6)	10 577.0(12)
Z′	1	2	4	5

---

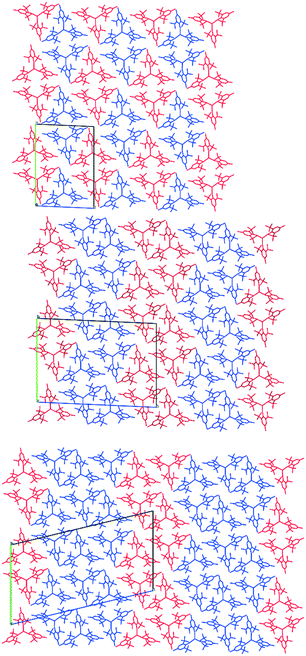Fig. 4 Crystal structures of 1 at 140 K (top), 120 K (middle) and 100 K (bottom), viewed along the a-axis with the unit cell highlighted. Planar conformations are shown in blue and pyramidal in red.

In the pyramidal conformation, two H atoms on one of the methyl groups (C8) appear to form a bifurcated C–H⋯Y interaction with H⋯Y distances of 2.44 Å and 2.53 Å, Y⋯C(8) = 2.91 Å to make a pseudo-tetrahedral geometry (Fig. 3C). In the planar conformation, this bifurcated interaction is still present (albeit with longer C–H⋯M distances of 2.52 Å and 2.54 Å, Y⋯C(8) = 2.96 Å).§ However, an additional CH⋯Y short contact is also present, forming a pseudo-trigonal bipyramidal geometry (Fig. 3B). This is facilitated by rotation of one of the ^tBu groups by ca. 16° such that the torsion angle O2–C16–C27–C30 changes from 52.8° in the pyramidal geometry to 36.9° in the planar form. Thus, the transformation from a planar to pyramidal geometry affects only four atoms: the central Y atom, and the three terminal carbon atoms of one tertiary butyl group (C28–C30). This is most obvious in the structure at 160 K, where two molecules are disordered over the same site, where differentiation of atomic positions is possible for only these four atoms.

Comparison to structural data of [Ln(OAr)₃]; Ar = 2,6-^tBu₂-4-RC₆H₃, R = H

As crystal data are also available for a series of [Ln(OAr)₃] complexes (Ar = 2,6-^tBu₂-4-RC₆H₂, R = H); M = Y, Ce, Pr, Nd, Sm, Gd, Dy, Er, Yb and Lu,⁴⁴ comparisons are facilitated. All of these para-H structures share the same unit cell parameters and crystallise in either P2₁ or P2₁/c with either two or one molecules in the asymmetric unit respectively. As noted by Boyle et al.,⁴⁴ complexes of metals up to and including Er crystallise in P2₁, but Yb and Lu crystallise in P2₁/c with disorder evident in one ^tBu group. However, all of these structures are trigonal pyramidal, and where disorder does exist, it is between two pyramidal geometries, where the metal atoms sits above or below the plane of the three oxygen atoms. There is an inverse correlation between the Ln–O bond length and the pyramidality of the LnO₃ moiety (see ESI‡). Thus, as the ionic radius of the Ln(III) ion decreases, the LnO₃ moiety becomes more planar. This is as expected from the point of view of sterics: to maximise the distance between the bulky ^tBu groups, complexes with smaller metal ions adopt a more planar structure. A half-shell effect is also visible here, with Gd breaking the general trend.

Conformational analysis

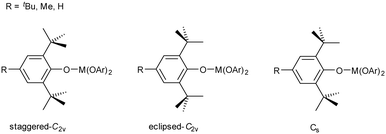
It is apparent that these aryloxide ligands can adopt different conformations of the ortho-^tBu groups, which can be either staggered or eclipsed with respect to the C–O bond. Two geometries of the ligand with local C_2v symmetry are possible, where the ^tBu groups are either both staggered or both eclipsed, and one geometry with local C_s symmetry, with one staggered and one eclipsed ^tBu group (Fig. 5). In the crystal structures of [Y(OAr)₃] and [Ce(OAr)₃] (R = Me, described herein) and the Sc and Er structures previously described,^40,43 two of the ligands adopt the staggered-C_2v (s-C_2v) conformation and the third ligand adopts the C_s conformation. Having at least one eclipsed ^tBu group allows a short contact between the hydrogen atoms on the methyl group closest to the metal and the metal (Fig. 3B and C).

Fig. 5 s-C_2v, e-C_2v and C_s conformations (local symmetry) of the aryloxide ligand.

In all of the R = H structures, the OAr ligands adopt the s-C_2v geometry, except where disorder in the ^tBu group (a rotation of 60°) is present in the later, more planar complexes (Yb and Lu). This changes the conformation of one aryloxide ligand from s-C_2v to C_s and facilitates the formation of a short CH⋯Ln contact. This suggests that as the structure becomes more planar – owing to the decreasing M–O bond length – a C–H⋯Ln interaction can balance the energetic cost of increasing planarity.

A search of the CSD for the 2,6-^tBu₂-4-RC₆H₂ moiety bonded to X, where X is any atom, revealed that for R = H or Me, the e-C_2v conformation is rare (0.5 and 1.5% of ligands respectively), and around 90% adopt the s-C_2v conformation; the rest adopt the C_s conformation. This suggests that there is an energetic cost to the C_s conformation compared to the s-C_2v conformation. Interestingly, when R = ^tBu, the population of these conformations changes substantially, such that the populations of e-C_2v, s-C_2v and C_s are 17.2, 24.5 and 58.3% respectively (see Fig. S5, Table S3 in ESI‡). This may well have implications for the reactivity of complexes of the ligand with R = ^tBu, such as leading to facile dinitrogen binding in uranium complexes of this ligand.⁴⁶ However, no crystal structure data are available for M(OAr)₃, R = ^tBu (i.e. three such moieties on M where X = O). The only crystallographically determined Ln structure, with Yb, has an additional molecule of THF bound,⁵⁴ and analogous U compounds have dinitrogen bound.⁴⁶

Gas phase computational analysis of [Y(OAr)₃]

In order to quantify some of these results and probe the energetic preference for planar or pyramidal metal centres, gas phase optimisations for [Y(OAr)₃], Ar = 2,6-^tBu₂-4-RC₆H₂; R = H, Me and ^tBu, in planar and pyramidal forms were computed. With three ligands on each metal centre (i.e. six ^tBu groups in the 2- and 6-positions), there are 24 conformations of the complex that might arise (see Table S4, Fig. S6 in ESI‡). In practice, only one is seen for R = Me (with two s-C_2v ligands and one C_s ligand), and two are seen for R = H (mostly three s-C_2v ligands, but also two s-C_2v ligands and one C_s ligand arising from disorder in one of the ^tBu groups). Thus, these two conformations were studied in both planar and pyramidal forms. Notably, geometry optimisations started in the planar geometry where all ligands were in the s-C_2v conformation always converged to a geometry where one aryl group changes to C_s. This suggests that the planar conformer of [Ln(OAr)₃] (Ar = 2,6-^tBu₂-4-RC₆H₂) can only exist when supported by a C–H⋯M short contact. A summary of the other results (Table 2) shows that the energy differences between these conformers are small. However, the pyramidal form where all of the ligands are s-C_2v (as seen in the crystal structures of R = H) was consistently computed to be the lowest in energy. The planar and pyramidal (s-C_2v)₂C_s conformers, which are seen in the crystal structures where R = Me, are computed to differ in energy by up to 10 kJ mol⁻¹. However, optimisation of the structure of [Y(OMes)₃] (Mes = 2,4,6-Me₃C₆H₂) always converged to a planar geometry; thus in the absence of C–H⋯Ln interactions, a planar form was computed to be lowest in energy.

Table 2 Computed relative free energy difference at 298 K (enthalpy in parentheses) for conformers of [Y(OAr)₃] (Ar = 2,6,-^tBu₂-4-RC₆H₂) in kJ mol⁻¹

R	Pyramidal (s-C2v)3	Pyramidal (s-C2v)2Cs	Planar (s-C2v)2Cs
H	0.2 (0.0)	0.0 (2.5)	7.2 (3.5)
Me	0.0 (0.0)	0.1 (2.3)	10.0 (3.5)
^tBu	0.0 (0.0)	2.2 (2.5)	9.6 (3.0)

---

Despite the computations confirming both a planar and pyramidal minimum, and an additional (s-C_2v)₃ pyramidal form, the pyramidality of the YO₃ moiety was computed to be much shallower in the gas phase optimisations {Σ(O–Y–O) = 355°} than seen in the crystal structure (346.4°).¶ The Y–O bond lengths are also longer (2.07 Å cf. ≈ 2.04 Å in the crystal structure). To study these in more depth, we also examined the outcome of these computations using QTAIM⁵⁵ analysis. The QTAIM analysis (Tables S3 and S4‡) identified bond critical points (BCP) for C–H⋯Y which correlate with only the very shortest contacts in the computed structures. For the pyramidal conformer: CH⋯Y = 2.478 Å at the top of the apex, and for the planar conformer: CH⋯Y = 2.497 Å at the top of the apex and CH⋯Y = 2.491 Å on the opposite side of the plane of the three oxygen atoms. The “bifurcated” interaction is not supported by the QTAIM analysis. Indeed, the calculated electron densities (ρ) of the bcps are very small (∼0.015) for these Y⋯H interactions and so despite being short, are very weak. The optimised structures showed no significant increase in bond lengths for the C–H bonds that formed the shortest contacts to Y compared to other similar C–H bonds in the structure. In fact, there are computed to be many BCPs for O⋯H and C⋯H interactions of a similar magnitude of electron density (Fig. 6).

Fig. 6 QTAIM plot of bond paths with BCPs (green) for planar (top) and pyramidal Y(OAr)₃, (bottom) conformers showing the presence of multiple weak O⋯H interactions in addition to the Y⋯H interactions (ρ cut-off = 0.015). Weak (ρ < 0.05) bond paths are shown as dashed lines. NB: numbering scheme differs to crystal structure.

In fact, the only notable difference is in the ρ of the C–H bonds forming short contacts to the metal compared to similar C–H bonds. In the pyramidal conformer, the value for the former is 0.262, which is slightly lower than the average value for the latter [0.268(1)]. In the planar structure, the values are very similar (see ESI‡ for full details). Thus, we consider these interactions too weak to be considered agostic.

Solid-state computations

Given that there appears to be a slight energetic preference for Y to adopt a pyramidal conformation, and the Y⋯H interactions are weak, it is likely that the peculiarities of the phase changes happen mostly because of packing preferences. If there is an entropic preference for the molecule to be pyramidal at room temperature, this effect will be minimised at low temperature, i.e. as the crystal is cooled. Using periodic DFT calculations as implemented in CP2K, we computed the relative SCF energy of various crystalline phases, shown in Fig. 7. Artificial crystal structures were created from the 160 K structure in that either the planar conformer was chosen (A-160), or the pyramidal conformer (B-160), by removing the disordered atoms of the unwanted conformer. By expanding the symmetry to P1, we could also create a structure that had one planar and one pyramidal conformer (C). This was then compared to the structure at 140 K, which has a different packing of the planar and pyramidal conformers (D). In a similar fashion, we also constructed the planar-only (A-140) and pyramidal only (B-140) structures from the crystal at 140 K.||

Fig. 7 Schematic representation of packing of planar and pyramidal molecules in solid-state calculations, viewed down the a-axis. Each triangle represents a column of identical molecules. A) all planar conformers, B) all pyramidal conformers, C) artificial packing in P1 created from disordered structure at 160 K, D) packing in 140 K structure.

For all structures, the positions of all atoms were allowed to refine, but the cell parameters were fixed. This was done sequentially, by firstly relaxing only the H atom positions, then expanding to include C, then O and finally Y atoms. When the yttrium atoms were finally allowed to relax, some changes in geometry did occur, but only for the cells at 160 K. In these cases, the originally planar molecules converged to a very shallow pyramid [Σ(O–Y–O) ≈ 358°] and the originally pyramidal molecules flattened somewhat (such that Σ(O–Y–O) ≈ 352°). This suggests that the disorder at 160 K is likely to be dynamic. However, for the computations from the cells at 140 K, the planar molecules remained planar (Σ(O–Y–O) = 360°) and the pyramidal molecules remained pyramidal (Σ(O–Y–O) = 345°), with the geometry of individual molecules closely matching that seen in the crystal structures. Relative (SCF) energies are given in Table 3.

Table 3 Relative SCF energies of (simulated) crystalline forms of 1^a

Structure	Derived from	Relative energy (kJ mol^−1)
a Relative energies are given for the cell at 140 K, which is double the size of the cell at 160 K.
(A-160)	160 K all planar	11.1
(B-160)	160 K all pyramidal	3.3
(C)	160 K planar/pyramidal	6.7
(D)	140 K planar/pyramidal (crystal)	0.0
(A-140)	140 K all planar	7.7
(B-140)	140 K all pyramidal	1.6

---

Given that these solid state structures have four Y(OAr)₃ molecules in the unit cell, the energetic differences between the various packing arrangements are slight. However, the packing seen at 140 K is computed to be the lowest in energy, and has equal numbers of planar and pyramidal molecules. The position of planar and pyramidal conformers in every second row of the molecules was observed to be an important factor in the overall energy of the structure (see Fig. 7). Thus, if both the packing arrangements in the crystal structures and molecular conformations have differences of only a few kJ mol⁻¹, it can be concluded that in the case of Y, the preference for a planar or pyramidal conformation can be easily influenced by packing forces, and that the conformer seen in the crystal structure is not necessarily a good indicator of the structure in the gas phase. However, given that only a disordered/order phase change was seen for the analogous cerium structure, the interplay of energetics of molecular conformation versus packing energies is subtle, and predictions even between Y and similar lanthanides is not straightforward.

Conclusions

In the absence of any possible C–H⋯Y interactions, the energy of [Y(OMes)₃] is minimised by adopting a planar conformation. However, if the coordination number can be increased by means of C–H⋯Y interactions, however weak, then the yttrium can adopt a pyramidal configuration, which can be described as a pseudo-tetrahedral coordination with a C–H⋯Y interaction taking up the apical coordination site. The coordination number may be further increased in a planar configuration by a second short contact, such that the structure becomes pseudo-trigonal bipyramidal, with the CH⋯Y short contacts at the apical positions. The energy difference between the geometries for 1 and 2 is very small, and both are accessible. In the solid state, subtle differences in packing arrangements of molecules are large enough to dictate whether an individual molecule adopts a planar or pyramidal configuration.

For [Ln(OAr)₃] (Ar = 2,6-^tBu₂-4-RC₆H₂), the preference to be pyramidal is stronger than for Y. As the Ln–O bond length shortens, the increase in energy induced by the trend towards planarity (owing to the steric repulsion between bulky ligands) is balanced by an additional C–H⋯Ln interaction. The preference to be pyramidal or planar may well be influenced by the nature of a remote para-group on the aryl ring, because of its influence on the conformation of the bulky groups in the 2- and 6-positions of the aryl ring. The energetically higher conformation of the eclipsed orientation (as suggested by its lower incidence in crystal structures) allows short CH⋯Y interactions, so the influence of conformation on metal geometry and the occurrence of balancing C–H⋯M interactions should not be discounted when considering the properties and reactivity of these species.

Experimental Details

Computational methods: gas-phase optimisations

DFT computations were run with Gaussian 09 (Revision D.01).⁵⁶ Yttrium atoms were described with Stuttgart–Dresden relativistic effective core potentials⁵⁷ and 6-31G*^58,59 basis sets were used for all other atoms. Optimisations used the BP86 (ref. 60 and 61) functional and all stationary points were fully characterised as minima using analytical frequency calculations (all positive eigenvalues). QTAIM studies were carried out using AIMAll (version 17.11.14).⁶² For the QTAIM analyses, bond critical points were visualised with AIMStudio.⁶²

Solid-state calculations

Periodic electronic structure calculations were carried out at the Kohn–Sham DFT level of theory, employing the Gaussian plane wave (GPW) formalism as implemented in the QUICKSTEP⁶³ module within the CP2K program suite version 2.5.1.^64,65 Double-ζ valence potential molecularly optimised basis sets in their short-range variant (DZVP-MOLOPT-SR-GTH)⁶⁶ were used on all atomic species (Y, O, C, H) with Goedecker–Teter–Hutter (GTH) pseudo potentials^67–69 describing the interaction between the core electrons and the valence shell electrons. The generalized gradient approximation (GGA) to the exchange–correlation functional according to Perdew–Burke–Ernzerhof (PBE)⁷⁰ was used in combination with Grimme's D3-correction⁷¹ for dispersion interactions. The auxiliary plane wave basis set was truncated at a cut-off of 500 Ry. The maximum force convergence criterion was set to 10⁻⁴ Hartree per Bohr, whilst default values were used for the remaining criteria. The convergence criterion for the self-consistent field (SCF) accuracy was set to 10⁻⁷ E_h for geometry optimisations. The positions of all atoms were optimised sequentially from the lightest to the heaviest atoms using fixed unit cell parameters and periodic boundary conditions (PBC), with starting structures obtained from the crystal structure at 140 K or by editing the crystal structure obtained at 160 K by deleting disordered atoms. All energies are reported as uncorrected electronic SCF energies.

Synthetic details

All reactions were performed under an oxygen-free nitrogen atmosphere using standard Schlenk-line techniques or by using an MBRAUN UNIlab Plus glovebox. Anhydrous THF was obtained from an MBRAUN SPS-800. 40–60 petroleum ether was distilled from sodium wire; n-hexane was dried over molecular sieves. Benzene-d₆ was dried over molten potassium and distilled. All anhydrous solvents were degassed before use and stored over activated molecular sieves. NMR spectra were recorded on Bruker AVI400 or AVIII400 spectrometers and the chemical shifts δ are noted in parts per million (ppm) calibrated to the residual proton resonances of the deuterated solvent. [M(N′′)₃] M = Y, Ce (ref. 72) and [M(O-2,6-^tBu₂-4-MeC₆H₂)₃] M = Y, Ce (ref. 41, 73 and 74) were synthesised as previously described. Elemental analysis was performed by Mr Stephen Boyer at London Metropolitan University.

X-ray crystallographic studies

Single crystals of the samples were grown from unstirred reaction mixtures of [M(N′′)₃] and HO-2,6-^tBu₂-4-MeC₆H₂ in n-hexane. They were covered in inert oil and placed under the cold stream of a Bruker X8 APEXII four-circle diffractometer cooled to 100 K, or another temperature as required. Exposures were collected using Mo Kα radiation (λ = 0.71073). Indexing, data collection and absorption correction were performed using the APEXII suite of programs.⁷⁵ Structures were solved using direct methods (SHELXT)⁷⁶ and refined by full-matrix least-squares (SHELXL)⁷⁶ interfaced with the programme OLEX2 (ref. 77) (Tables S1 and S2‡).

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

MFH acknowledges a Fellowship from the Daphne Jackson Trust, with funding from the RSC and the EPSRC. RJN and SMM acknowledge funding from the Carnegie Trust for a Research Incentive Grant (RIG007547). BET acknowledges funding from EPSRC grant number EP/M024210/1. The authors thank Prof Stuart Macgregor for useful discussions.

Notes and references

1. D. C. Bradley, J. S. Ghotra and F. A. Hart, J. Chem. Soc., Chem. Commun., 1972, 349–350.
2. D. C. Bradley, J. S. Ghotra and F. A. Hart, J. Chem. Soc., Dalton Trans., 1973, 1021–1023.
3. P. O'Brien, Coord. Chem. Rev., 2000, 209, 35–47.
4. T. Spallek, O. Heß, M. Meermann-Zimmermann, C. Meermann, M. G. Klimpel, F. Estler, D. Schneider, W. Scherer, M. Tafipolsky, K. W. Törnroos, C. Maichle-Mössmer, P. Sirsch and R. Anwander, Dalton Trans., 2016, 45, 13750–13765.
5. D. H. Woen, G. P. Chen, J. W. Ziller, T. J. Boyle, F. Furche and W. J. Evans, Angew. Chem., Int. Ed., 2017, 56, 2050–2053.
6. M. Westerhausen, M. Hartmann, A. Pfitzner and W. Schwarz, Z. Anorg. Allg. Chem., 1995, 621, 837–850.
7. J. Sundermeyer, A. Khvorost and K. Harms, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2004, 60, m1117–m1119.
8. G. Scarel, C. Wiemer, M. Fanciulli, I. L. Fedushkin, G. K. Fukin, G. A. Domrachev, Y. Lebedinskii, A. Zenkevich and G. Pavia, Z. Anorg. Allg. Chem., 2007, 633, 2097–2103.
9. J. W. S. Rees, O. Just and D. S. Van Derveer, J. Mater. Chem., 1999, 9, 249–252.
10. M. Niemeyer, Z. Anorg. Allg. Chem., 2002, 628, 647–657.
11. P. B. Hitchcock, A. G. Hulkes, M. F. Lappert and Z. Li, Dalton Trans., 2004, 129–136.
12. W. A. Herrmann, R. Anwander, F. C. Munck, W. Scherer, V. Dufaud, N. W. Huber and G. R. J. Artus, Z. Naturforsch., B: J. Chem. Sci., 1994, 49, 1789–1797.
13. J. S. Ghotra, M. B. Hursthouse and A. J. Welch, J. Chem. Soc., Chem. Commun., 1973, 669–670.
14. E. D. Brady, D. L. Clark, J. C. Gordon, P. J. Hay, D. W. Keogh, R. Poli, B. L. Scott and J. G. Watkin, Inorg. Chem., 2003, 42, 6682–6690.
15. A. M. Bienfait, B. M. Wolf, K. W. Tornroos and R. Anwander, Inorg. Chem., 2018, 57, 5204–5212.
16. R. A. Andersen, D. H. Templeton and A. Zalkin, Inorg. Chem., 1978, 17, 2317–2319.
17. A. J. Ryan, L. E. Darago, S. G. Balasubramani, G. P. Chen, J. W. Ziller, F. Furche, J. R. Long and W. J. Evans, Chem. – Eur. J., 2018, 24, 7702–7709.
18. N. C. Boyde, S. C. Chmely, T. P. Hanusa, A. L. Rheingold and W. W. Brennessel, Inorg. Chem., 2014, 53, 9703–9714.
19. M. Kaupp, Angew. Chem., Int. Ed., 2001, 40, 3534–3565.
20. L. Perrin, L. Maron and O. Eisenstein, Faraday Discuss., 2003, 124, 25–39.
21. T. Fjeldberg and R. A. Andersen, J. Mol. Struct., 1985, 129, 93–105.
22. C. E. Myers, L. J. Norman and L. M. Loew, Inorg. Chem., 1978, 17, 1581–1584.
23. L. Perrin, L. Maron, O. Eisenstein and M. F. Lappert, New J. Chem., 2003, 27, 121–127.
24. C. A. P. Goodwin, N. F. Chilton, L. S. Natrajan, M.-E. Boulon, J. W. Ziller, W. J. Evans and D. P. Mills, Inorg. Chem., 2017, 56, 5959–5970.
25. R. L. De Kock, M. A. Peterson, L. K. Timmer, E. J. Baerends and P. Vernooijs, Polyhedron, 1990, 9, 1919–1934.
26. R. F. Koby and T. P. Hanusa, J. Organomet. Chem., 2018, 857, 145–151.
27. S. Labouille, C. Clavaguéra and F. Nief, Organometallics, 2013, 32, 1265–1271.
28. N. Kaltsoyannis and M. R. Russo, J. Nucl. Sci. Technol., 2002, 39, 393–399.
29. T. K. Hollis, J. K. Burdett and B. Bosnich, Organometallics, 1993, 12, 3385–3386.
30. K. J. Donald and R. Hoffmann, J. Am. Chem. Soc., 2006, 128, 11236–11249.
31. D. J. Liptrot and P. P. Power, Nat. Rev. Chem., 2017, 1, 0004.
32. J. Klimeš and A. Michaelides, J. Chem. Phys., 2012, 137, 120901.
33. R. Pal, S. Mebs, M. W. Shi, D. Jayatilaka, J. M. Krzeszczakowska, L. A. Malaspina, M. Wiecko, P. Luger, M. Hesse, Y.-S. Chen, J. Beckmann and S. Grabowsky, Inorg. Chem., 2018, 57, 4906–4920.
34. D. L. Clark, J. C. Gordon, P. J. Hay, R. L. Martin and R. Poli, Organometallics, 2002, 21, 5000–5006.
35. T. Fjeldberg and R. A. Andersen, J. Mol. Struct., 1985, 128, 49–57.
36. N. F. Chilton, C. A. P. Goodwin, D. P. Mills and R. E. P. Winpenny, Chem. Commun., 2015, 51, 101–103.
37. C. A. P. Goodwin, N. F. Chilton, G. F. Vettese, E. Moreno Pineda, I. F. Crowe, J. W. Ziller, R. E. P. Winpenny, W. J. Evans and D. P. Mills, Inorg. Chem., 2016, 55, 10057–10067.
38. C. A. P. Goodwin, K. C. Joslin, S. J. Lockyer, A. Formanuik, G. A. Morris, F. Ortu, I. J. Vitorica-Yrezabal and D. P. Mills, Organometallics, 2015, 34, 2314–2325.
39. C. A. P. Goodwin, F. Tuna, E. J. L. McInnes, S. T. Liddle, J. McMaster, I. J. Vitorica-Yrezabal and D. P. Mills, Chem. – Eur. J., 2014, 20, 14579–14583.
40. P. B. Hitchcock, M. F. Lappert and A. Singh, J. Chem. Soc., Chem. Commun., 1983, 1499–1501.
41. H. A. Stecher, A. Sen and A. L. Rheingold, Inorg. Chem., 1988, 27, 1130–1132.
42. H.-D. Amberger, H. Reddmann, C. Guttenberger, B. Unrecht, L. Zhang, C. Apostolidis, O. Walter and B. Kanellakopulos, Z. Anorg. Allg. Chem., 2003, 629, 1522–1534.
43. H. Zhang, R. Nakanishi, K. Katoh, B. K. Breedlove, Y. Kitagawa and M. Yamashita, Dalton Trans., 2018, 47, 302–305.
44. L. A. M. Steele, T. J. Boyle, R. A. Kemp and C. Moore, Polyhedron, 2012, 42, 258–264.
45. D. M. Barnhart, D. L. Clark, J. C. Gordon, J. C. Huffman, R. L. Vincent, J. G. Watkin and B. D. Zwick, Inorg. Chem., 1994, 33, 3487–3497.
46. S. M. Mansell, N. Kaltsoyannis and P. L. Arnold, J. Am. Chem. Soc., 2011, 133, 9036–9051.
47. J. Pratt, A. M. Bryan, M. Faust, J. N. Boynton, P. Vasko, B. D. Rekken, A. Mansikkamäki, J. C. Fettinger, H. M. Tuononen and P. P. Power, Inorg. Chem., 2018, 57, 6491–6502.
48. R. J. Blagg, L. Ungur, F. Tuna, J. Speak, P. Comar, D. Collison, W. Wernsdorfer, E. J. L. McInnes, L. F. Chibotaru and R. E. P. Winpenny, Nat. Chem., 2013, 5, 673.
49. D. N. Woodruff, R. E. P. Winpenny and R. A. Layfield, Chem. Rev., 2013, 113, 5110–5148.
50. P. Zhang, L. Zhang, C. Wang, S. Xue, S.-Y. Lin and J. Tang, J. Am. Chem. Soc., 2014, 136, 4484–4487.
51. S. G. Rachor, P. A. Cleaves, S. D. Robertson and S. M. Mansell, J. Organomet. Chem., 2018, 857, 101–109.
52. P. G. Eller, D. C. Bradley, M. B. Hursthouse and D. W. Meek, Coord. Chem. Rev., 1977, 24, 1–95.
53. K. M. Steed and J. W. Steed, Chem. Rev., 2015, 115, 2895–2933.
54. G. Deacon, T. Feng, S. Nickel, M. Ogden and A. White, Aust. J. Chem., 1992, 45, 671–683.
55. R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Clarendon Press, 1994.
56. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, J. B. Foresman Farkas, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, 2013.
57. D. Andrae, U. Huermann, M. Dolg, H. Stoll and H. Preu, Theor. Chim. Acta, 1990, 77, 123–141.
58. W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261.
59. P. C. Hariharan and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213–222.
60. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100.
61. J. P. Perdew, Phys. Rev. B, 1986, 33, 8822–8824.
62. T. A. Keith, AIMAll (Version 17.11.14), 2017.
63. J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Comput. Phys. Commun., 2005, 167, 103–128.
64. J. Hutter, M. Iannuzzi, F. Schiffmann and J. Van de Vondele, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2013, 4, 15–25.
65. The CP2K developers group http://www.cp2k.org).
66. J. VandeVondele and J. Hutter, J. Chem. Phys., 2007, 127, 114105.
67. M. Krack, Theor. Chem. Acc., 2005, 114, 145–152.
68. C. Hartwigsen, S. Goedecker and J. Hutter, Phys. Rev. B, 1998, 58, 3641–3662.
69. S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B, 1996, 54, 1703–1710.
70. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
71. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
72. F. T. Edelmann and W. A. Herrmann, Synthetic Methods of Organometallic and Inorganic Chemistry, Volume 6, 1997: Volume 6: Lanthanides and Actinides, Thieme, 2014.
73. A. G. Avent, C. F. Caro, P. B. Hitchcock, M. F. Lappert, Z. Li and X.-H. Wei, Dalton Trans., 2004, 1567–1577.
74. M. F. Lappert and A. Singh, Inorg. Synth., 1990, 27, 168.
75. Bruker, APEX2 V2009–5, Bruker AXS Inc., Madison, Wisconsin, USA, 2009.
76. G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112–122.
77. O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341.

---

Footnotes

† Additional research data supporting this publication are available from Heriot-Watt University's research data repository at DOI: http://10.17861/c8b6b503-6574-4cf0-b719-4c1f4f80371a.

‡ Electronic supplementary information (ESI) available: Additional analytical, crystallographic and computational data. CCDC 1875486–1875491. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c9ce00184k

§ Unfortunately, the crystal structure data do not support an in-depth analysis of the C–H bond lengths, and all the H atoms were refined used a riding model.

¶ When the computations were repeated with Grimme D3 dispersion corrections, the pyramidality was much more pronounced than in the crystal. Thus, the computations were repeated for R = Me using the coordinates extracted from the crystal structure at 140 K (which has one pyramidal and one planar conformation), where only the positions of the hydrogen and carbon atoms were allowed to refine and the positions of all other atoms were fixed. The computed SCF energy for these suggested the planar form (for R = Me) to be lower in energy by 2.3 kJ mol⁻¹ (whereas the SCF difference for the fully optimised structures was 0.2 kJ mol⁻¹). Although the difference is more pronounced than the fully optimised structures, it is still a very small difference.

|| The volume of the unit cell at 140 K is double compared to that at 160 K, but the decrease in relative size is only 0.1%, so we judge this to be a fair comparison.

---