Open Access Article
Open Access ArticleCurve crossing in a manifold of coupled electronic states: direct quantum dynamics simulations of formamide†
K. Eryn
Spinlove
 *abd,
Gareth W.
Richings
*abd,
Gareth W.
Richings
 c,
Michael A.
Robb
c,
Michael A.
Robb
 d and
Graham A.
Worth
d and
Graham A.
Worth
 *a
*a
aDept. of Chemistry, University College London, 20 Gordon St., London, UK. E-mail: g.a.worth@ucl.ac.uk
bSchool of Chemistry, University of Birmingham, Birmingham, B15 2TT, UK
cDept. of Chemistry, University of Warwick, Gibbet Hill, Coventry, CV4 7AL, UK
dDept. of Chemistry, Imperial College London, London, SW7 2AZ, UK
First published on 16th May 2018
Abstract
Quantum dynamics simulations are an important tool to evaluate molecular behaviour including the, often key, quantum nature of the system. In this paper we present an algorithm that is able to simulate the time evolution of a molecule after photo-excitation into a manifold of states. The direct dynamics variational multi-configurational Gaussian (DD-vMCG) method circumvents the computational bottleneck problems of traditional grid-based methods by computing the potential energy functions on-the-fly, i.e. only where required. Unlike other commonly used direct dynamics methods, DD-vMCG is fully quantum mechanical. Here, the method is combined with a novel on-the-fly diabatisation scheme to simulate the short-time dynamics of the key molecule formamide and its acid analogue formimidic acid. This is a challenging test system due to the nature and large number of excited states, and eight coupled states are included in the calculations. It is shown that the method is able to provide unbiased information on the product channels open after excitation at different energies and demonstrates the potential to be a practical scheme, limited mainly by the quality of the quantum chemistry used to describe the excited states.
1 Introduction
Photochemistry is an area of chemistry in which quantum effects play a key role in how molecules behave. After absorbing a photon, a molecule is promoted into an excited electronic state and subsequently evolves on the excited state potential energy surface. In many cases, this state is one of a whole manifold of electronic states close in energy that are coupled by the nuclear motion, termed vibronic coupling. This coupling can lead to a breakdown of the Born–Oppenheimer approximation and it is not valid to separate the electronic and nuclear motion. To correctly simulate the time evolution of a molecule after photo-excitation it is therefore necessary to solve the time-dependent Schrödinger equation (TDSE) for the nuclear wavepacket created by the photon absorption.A variety of dynamics methods have been developed with a view of solving the TDSE. Generally these methods fall into two categories, termed semi-classical if the nuclei are treated using classical equations of motion which are coupled to the electronic motion, or quantum if the nuclei are treated quantum mechanically. Quantum molecular dynamics methods attempt to directly solve the full TDSE for both nuclei and electrons. Using a grid-based representation, standard approaches provide a pictorial representation of the evolving wavepacket and information can be extracted from the wavepacket over the course of a calculation. However, these exact methods suffer from exponential scaling with an increase in the number of degrees of freedom, and powerful numerical methods are required to describe the time evolution of the system. The multi-configuration time-dependent Hartree (MCTDH) method,1–3 and the derivative multi-layer MCTDH method,4 are probably the most powerful algorithms at present for quantum dynamics able to solve the TDSE for many tens of degrees of freedom.
A significant drawback of grid-based methods is the requirement for global potential energy surfaces that must be computed and fit to analytic functions before any calculations are performed. This presents a major bottleneck for polyatomic systems due to the huge number of quantum-chemistry calculations and complex fitting procedure required, although recent work by one of us is beginning to alleviate this problem.5–7 Direct dynamics that compute the potential on-the-fly are thus receiving significant interest at present as they circumvent this problem by only calculating the potential in regions of space visited by the system. Most direct dynamics methods, however, use a semi-classical description of the evolving system, with surface hopping methods being the most popular approach. In these, an ensemble, or swarm, of trajectories are propagated on the adiabatic surfaces of a system, which are supplied by an external electronic structure method. In regions dominated by non-adiabatic effects, hopping can occur between surfaces. A variety of approaches has been developed with differing methods by which the trajectories are described and propagated, the manner by which the hopping occurs, and the effect a successful hop has on the ensemble.8–11
A novel semi-classical method is exact factorization.12,13 Using a wavefunction ansatz in which the nuclear and electronic parts are factorised, similar to the Ehrenfest method, it has explicit time-dependent electronic motion. In addition, the electronic motion is explicitly coupled to the nuclear coordinate. The method has only been applied to one-dimensional systems but could prove to be a promising alternative method for direct dynamics.
Semi-classical dynamics methods have much better scaling than quantum dynamics methods, and provide a suitable framework for direct dynamics calculations, but are unfortunately not guaranteed to converge on the correct result due to the missing nuclear correlation. The underlying classical structure also means that they cannot correctly describe tunnelling through a barrier. A different approach is ab initio multiple spawning (AIMS).14–16 In this, the nuclear wavepacket is described by a superposition of Gaussian basis functions, known as Gaussian wavepackets (GWPs). The expansion coefficients solve the full TDSE while the GWPs follow classical trajectories making them suitable for direct dynamics. In principle AIMS can reach the full quantum solution, but the use of classical trajectories leads to slow convergence. AIMS has been used successfully in many applications.
A relatively recent development that can be used in direct-dynamics simulations and provides a full quantum treatment of the nuclei is the variational multi-configurational Gaussian method (DD-vMCG).17–19 Similar to multiple spawning, it uses a superposition of GWPs as a basis set for the nuclei. The equations of motion for both GWPs and expansion coefficients are, however, variational and the GWPs follow coupled “quantum” trajectories rather than classical trajectories. Initial test calculations show that the method converges quickly on the full solution, but suffers from numerical instabilities. It also has the drawback that a diabatic representation must be used for the wavefunction and it is not clear how to diabatise a set of potentials on-the-fly.
Recently, a propagation diabatisation method was introduced.20 This uses the relationship between adiabatic and diabatic wavefunctions to provide global diabatic surfaces from the quantum chemistry data. The relationship, however, is only exact for a complete set of states and its practical behaviour must be evaluated. Formamide (FAM), also known as methanamide, provides a suitable test system. Over the years since its first published synthesis in 1863,21 it has been an important, but until relatively recently, often disregarded compound.
FAM has a number of industrial uses, e.g. as a precursor to hydrogen cyanide and as a formylating agent. It is also the smallest, most stable compound containing the four most abundant elements in the universe. FAM itself has been generally detected in the interstellar medium,22 in comets23,24 including Hale-Bopp, on icy grains around the protostellar object W33A,25 and from sources SgrA and SgrB2.26,27 In recent years, support has been growing in the apperception of FAM as a key abiotic precursor to the synthesis of pyrimidines and nucleobases in prebiotic Earth, supporting the RNA world theory. A comprehensive review, “Formamide and the origin of life” by Saladino et al.,28 details the diverse conditions under which FAM has been used in the synthesis of nucleic acid bases and nucleosides, the phosphorylation of nucleosides, as a catalyst for the oligomerization and polymerization of nucleotides, and the synthesis of pre-metabolic components. As the Hadean Earth was not shielded from solar radiation, it is reasonable to consider not only the effects of temperature, catalysis and concentration but also the photoactivity of FAM in its viability as a precursor to prebiotic life.
Despite the plethora of information regarding the behaviour, uses and function of FAM, to date there have been a limited number of computational studies, even though it was the subject of early molecular orbital (MO) calculations.29 Most of the recent work focuses on the ground state tautomerism and the importance of solvation for the proton transfer process30,31 and the thermal decomposition pathways,32,33 as well as the nature of the excited states and possible processes.34–38 As of yet, however, there are no published full quantum dynamics studies on the behaviour of FAM or its acid analogue formimidic acid (FIM) after photo-excitation, despite the potential importance of light in prebiotic chemistry. A direct dynamics surface hopping study of protonated formamide has been carried out.39 In this paper we apply the DD-vMCG method to the excited state dynamics of formamide and formamidic acid to demonstrate the utility of the method as well as to shed some light on the excited state dynamics of these key molecules.
2 Background theory: DD-vMCG
The variational multi-configurational Gaussian (vMCG)40–43 ansatz has the form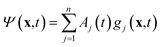 | (1) |
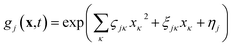 | (2) |
It then follows that by defining the relationships
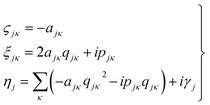 | (3) |
Eqn (2) can be written in the more intuitive Heller form:44,45
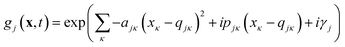 | (4) |
In this form it can be seen that the quadratic parameters, ς, represent the widths of the Gaussian functions, the linear parameters, ξ, represent the momentum, p, and centre coordinate, q, of the functions, and the scalar parameters, η, represent the remaining parameters, including the phase, γ, of the functions.
As with the MCTDH method, the Dirac–Frenkel variational principle is applied to the wavefunction ansatz to obtain equations of motion for the expansion coefficients
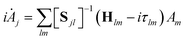 | (5) |
| Sjl = 〈gj|gl〉 and Hjl = 〈gj|Ĥ|gl〉 | (6) |
By collecting the GWP time-dependent parameters in a vector,
| Λj = {ξj,ηj} | (7) |
| iΛ = [C]−1Y | (8) |
| Cjα,lβ = ρjl(S(αβ)jl − [S(α0)S−1S(0β)]jl) | (9) |
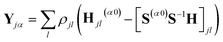 | (10) |
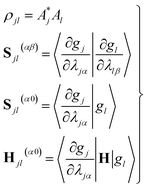 | (11) |
Furthermore, τ can explicitly be written as a function of the time derivative of the Gaussian parameters using the chain rule:
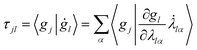 | (12) |
In order to maintain the normalisation of the Gaussians during the propagation, the diagonal of the overlap time-derivative matrix, τ, can be set to zero. This defines the evolution of the otherwise undefined scalar parameters.
To evaluate the matrix elements of the potential function, the local harmonic approximation (LHA) is used, i.e. the potential energy is expanded to second order around each GWP time-dependent centre coordinate, qj(t):
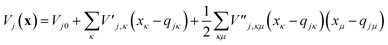 | (13) |
In addition, if rectilinear coordinates are used, the kinetic energy operator can be taken to have a separable form, i.e.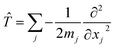 , then the separable part of the Hamiltonian can be expanded as a power series in terms of the Gaussian moments Mjlκ = 〈gj|xκ|gl〉 and Mjlκμ = 〈gj|xκxμ|gl〉 as
, then the separable part of the Hamiltonian can be expanded as a power series in terms of the Gaussian moments Mjlκ = 〈gj|xκ|gl〉 and Mjlκμ = 〈gj|xκxμ|gl〉 as
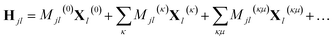 | (14) |
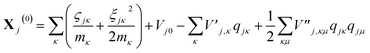 | (15) |
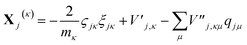 | (16) |
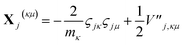 | (17) |
The Y-vector can also be separated into two parts:
| Y = Y0 + YR | (18) |
The part of the Hamiltonian that can be expressed in terms of S(0α) is represented by Y0, with the remaining part of the Hamiltonian expressed by YR, known as the residual term. The residual term includes both of the correlation terms, as well as the higher order terms of the separable part of the Hamiltonian. Using the relationship between the overlap matrix elements, S(αβ), and the Gaussian moments, M, and comparing eqn (9) and (10), eqn (18) can be rewritten as
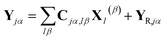 | (19) |
Consequently, the equation of motion for the Gaussian parameters can be further simplified to
i![[capital Lambda, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e138.gif) = X + C−1YR = X + C−1YR | (20) |
The significance of this so-called “CX formalism” is realised when the practical implications are considered. As the C-matrix is inverted during propagation, the removal of part of the Hamiltonian from the C−1Y-term results in a reduction of possible numerical errors and hence increases the stability of the propagation. Another desirable feature is that the parameter equations of motion can be divided into classical and non-classical parts.
The separation of classical and non-classical parts is achieved in the vMCG method by putting only the classical Gaussian propagation terms into X with the remaining (quantum) contributions kept in the YR term.
When frozen GWPs are used, only the scalar and linear parameters are varied with time. Consequently, the Hamiltonian can be written in terms of eqn (15) and (16) as
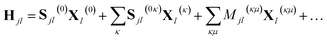 | (21) |
In this form, the linear parameter of the equations of motion eqn (20) can be written
i![[small xi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e15b.gif) jκ = −i2ςjκ jκ = −i2ςjκ![[q with combining dot above]](https://www.rsc.org/images/entities/i_char_0071_0307.gif) jκ − ṗjκ jκ − ṗjκ | (22) |
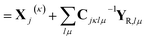 | (23) |
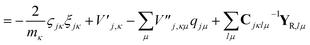 | (24) |
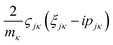 and
and 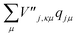 are added to YR, defining
are added to YR, defining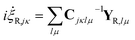 | (25) |
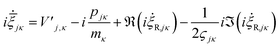 | (26) |
![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) jκ = qjκ + ipjκ is propagated (as opposed to ξjκ = −2ςjκqjκ + ipjκ). If the last two terms are ignored, the GWPs will follow classical trajectories. It should also be stated that for coherent states in an appropriate-width harmonic well, the last two terms of this expression cancel.
jκ = qjκ + ipjκ is propagated (as opposed to ξjκ = −2ςjκqjκ + ipjκ). If the last two terms are ignored, the GWPs will follow classical trajectories. It should also be stated that for coherent states in an appropriate-width harmonic well, the last two terms of this expression cancel.
2.1 The direct-dynamics variational multi-configurational Gaussian method
Using the LHA, eqn (13), the Hamiltonian matrix elements required to integrate the equations of motion (eqn (5) and (8)) need only the energies, gradients and Hessians at the centres of the Gaussians at each time step. These values are easily evaluated on-the-fly via an interface with an external quantum chemistry software package. It is, however, undesirable to carry out these time-consuming electronic structure calculations for every point reached by the GWPs. The DD-vMCG method as implemented in the Quantics package46 bypasses this issue by creating a database of electronic energies and other calculated information and, when possible, uses this information to construct the PESs.47 The idea of using a database to store the information has been used before in both classical trajectory48,49 and quantum trajectory50 methods.Instead of calling the external electronic structure program at each time step, the database is consulted. The Euclidean norm of the difference vector between all points of the new molecular geometry and all existing geometries in the database is then calculated as a method by which the distance between two structures can be measured. If the lowest value of the calculated norm is higher than the predefined value then the electronic structure program is called in order to calculate the energy, gradient and Hessian of the PES, the LHA constructed, and the information is stored in the database. Additional information such as the dipole moments, derivative couplings and MO coefficients may also be stored.
If the lowest value of the norm is lower than the predefined value, a modified Shepard interpolation50 is carried out in order to obtain the energy, gradient and Hessian for the LHA. This Shepard weighted interpolation has the form
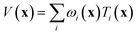 | (27) |
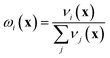 | (28) |
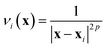 | (29) |
Following earlier work, p = 2 was used.43 This set of equations (eqn (27)–(29)) is used to gain the interpolated energy, gradient and Hessian. The choice of the parameter to trigger a new calculation appears to be system-dependent,43 though running an exploratory set of calculations varying this value will yield informative results. It should also be noted, from a practical perspective, that if an electronic structure calculation fails to complete, this interpolation is also used.
Although the use of the database in this way can significantly reduce the amount of real time required for a full propagation, there remains the issue of the evaluation of the Hessian matrix, which is a computationally intensive process. Various methods for the approximation of the Hessian exist requiring only a reference Hessian, and the current gradient information. Here, the Powell Hessian update algorithm51 is used, where the updated Hessian is calculated using the following equation
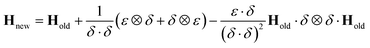 | (30) |
At the first point in a DD-vMCG calculation, when it is performed using an empty database, an electronic structure calculation is carried out in order to obtain the energy, gradient and full Hessian, and this data is used as the reference. In the case where a populated database is used, the first entry in the database is used as the reference. The propagation continues and when the calculation reaches a point where a new electronic structure calculation is required, as opposed to an extrapolated point, only the energy and gradient at this new point are calculated. The DD-vMCG program then calculates the Euclidean norm distance between the reference and the new point, as well as calculating the distances between the reference and all other points in the database. The points in the database are then divided into two subsets. The first, “internal” subset of points comprises points which are closer to the reference than the new point. The second, “external” subset of points comprises the points which are further away from the reference than the new point. The gradient at the new point and the gradient and Hessian of each of the points in the internal subset in turn is used to obtain a set of Powell-updated Hessians for the new point, Hi. As the distances between the new point and the internal points, di, have been calculated, the Hessian at the new point is given by the weighted sum
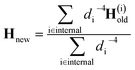 | (31) |
The new Hessian is then added to the database and each of the Hessians in the external subset are updated in a similar manner, including the new Hessian as part of the internal subset. The performance of this Hessian update procedure has been tested, the details of which can be found in ref. 43.
A final important feature to note in the DD-vMCG method is the form of the potential energy surface, specifically the representation of the states in the calculation. Although the external electronic structure programs calculate points along adiabatic surfaces, the wavepacket is propagated along the diabatic surfaces. Given the prerequisites for the DD-vMCG method, a method by which the diabatic surfaces can be calculated is required which can even-handedly account for on-the-fly calculated surfaces with multiple states and an unknown number of state crossings. The method by which this is carried out is known as propagation diabatisation.
A unitary transformation matrix, S, can be defined as between the adiabatic, ψ, and diabatic, φ, electronic functions.
| Sji = 〈ψj|φi〉 | (32) |
If the adiabatic and diabatic states form complete sets, the gradient of these matrix elements can be written
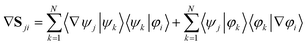 | (33) |
| 〈φk|∇φi〉 = 0, ∀i,k | (34) |
Using the definition of the non-adiabatic coupling vector,
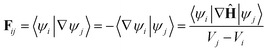 | (35) |
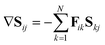 | (36) |
This relationship, first derived by Baer,52 is strictly correct only when a complete basis set is used. It completely defines a diabatic basis once an initial S matrix is defined at a specific point, referred to as selecting the gauge for the transformation. For example, the adiabatic and diabatic representations can be set to be equal at the Franck–Condon point.
The key equation to propagation diabatisation is the matrix form of this equation
| ∇S = −FS | (37) |
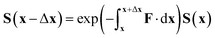 | (38) |
However, in this form it can be seen that in order to solve this equation an exponential of a matrix expression must be taken. It can also be seen that the integral of a function with an unknown analytic form must be taken. The second of these issues can be overcome using a simple numerical integration along the straight line between x and x + Δx using the trapezium rule, resulting in a matrix of scalar parameters. The first issue is not as straightforward to solve.
The equation for the propagation, eqn (38), does not guarantee that a unitary matrix S(x) will return a unitary matrix for S(x − Δx). Following the Esry and Sadeghpour53 method, which uses the Cayley–Hamilton form of the propagator, the unitarity of the transformation matrix can be maintained, resulting in
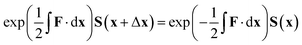 | (39) |
As mentioned previously, this method is correct only for a complete basis set of states. However, tests to date indicate that this propagation diabatisation scheme provides smooth, diabatic potential energy surfaces.20
3 Methods
3.1 Electronic structure
In a DD-vMCG calculation, external quantum chemistry programs are needed in order to calculate the energy, gradient and Hessian required for the propagation. The use of a large basis set and a high level of theory would enable higher accuracy in the results; however, these computationally intensive calculations would present a severe bottleneck to the propagations over even relatively short timescales in terms of the memory and both the computational and real time for taken for the calculation. An important consideration, particularly relevant in quantum chemistry calculations involving a large number of excited states, is the stability of the quantum chemistry calculations to the movement of atoms away from equilibrium geometries. A final consideration is that the DD-vMCG method is relatively new and computational studies have, so far, been carried out testing the ability of the code to handle large numbers of degrees of freedom, but thus far no studies have been carried out examining the ability of the code to handle large numbers of excited states. Consequently a balance between accuracy, stability, computational expense, and time expense in the calculations carried out by an external quantum chemistry software must be considered from the outset of an investigation.Due to the lack of computational investigations into the excited states of FAM and FIM, it was unknown as to how many excited states would be needed in the quantum chemistry calculations. Consequently, an overall emphasis on efficiency in the quantum chemistry calculations was made, whilst maintaining the intention of gaining as accurate a description of the excited states of the molecules as possible within a reasonable time constraint.
In order to be able to successfully carry out a direct dynamics calculation involving multiple states, it is necessary for the non-adiabatic couplings between all of the states to be calculated. This is particularly important when the system of interest has a manifold of excited states in close proximity between which multiple crossings and intersections may occur. Consequently, the logical choice when considering the excited state dynamics of a system from a chemical perspective is the use the complete active space self-consistent field (CASSCF) method. All electronic structure calculations in the following sections used the Molpro 2015 program54 which has a very efficient CASSCF procedure55 and is able to provide all of the derivative couplings between states as required for the direct dynamics.
The use of the CASSCF is, however, by no means a “black box” method. It is known that a poor selection of active space size, occupancy and orbitals can lead to poorly converged calculations and instabilities. This problem is often exacerbated with the inclusion of excited states leading to even further instabilities in the calculation. It is these issues that present a major difficulty in the use of the DD-vMCG method. In addition, the inclusion of a nitrogen atom in the system is known to increase the difficulty in the accurate selection of the orbitals within the active space. As a result, as opposed to attempting to enforce a particular selection of orbitals on a specified number of excited states, a new analytical procedure for the systematic identification of the orbitals required alongside the number of excited states was developed in order to minimise the difficulties in this CASSCF selection process.
Before any active space orbitals and number of excited states can be chosen, the chemical features of the system in question must be considered. It was decided that the initial selection of orbitals should have the capacity to describe a potential proton transfer between the two isomers. It is known that π–π* transitions are optically bright, so in addition to the description of a proton transfer, a sufficient description of the π-bonding network would be required. In addition, due to the system size, it was also decided that, in the interest of efficiency, a relatively large active space could be chosen so as to maximise the number of configuration interactions to be calculated with the caveat that a smaller basis set would be required in order to minimise the time-scaling issue.
Consequently, the orbital selection for FAM should include the description of the N–H(1) σ-bond and σ*-bond, the lone-pair acceptor on the oxygen and a description of the π-bonding network containing at least one π-bonding molecular orbital and one π*-bonding molecular orbital. The selection of orbitals to be included in the active apace for FIM should hence contain the complementary O–H(1) σ and σ* molecular orbitals, as well as the lone-pair acceptor on the nitrogen and the relevant π- and π*-bonding molecular orbitals. It was also decided that the active space for the FAM and the FIM should be the same size. Finally, while the choice of the 6-311++G** basis set would yield more accurate results, in the interest of efficiency and given the choice of a large active space and the as-of-yet unknown number of excited states required for the calculation, a 6-31G* basis set would be used as a compromise. After extensive testing with different CAS spaces and including different numbers of excited states, it was decided to use 10 electrons in 8 orbitals, and 8 states with equal weights were to be calculated.
The results from the studies using a state-averaged CAS(10,8) with different numbers of states are shown in the ESI.† As a result of these studies it can be seen that not only is the character of the active space important to state-averaged calculations, but also the number of states included in the calculation. This representation of the results of the state-averaged CAS calculations serves both as a tool for the selection of the active space size and the number of excited states, and as a demonstration that the analysis of the numerical and pictographic results of CAS calculations are intrinsically linked. Fig. 1 shows the pictures of the molecular orbitals of FAM and FIM in the active space from the final choice, which included 8 singlet states. The accompanying labels are used below in the state-averaged CAS characterisations.
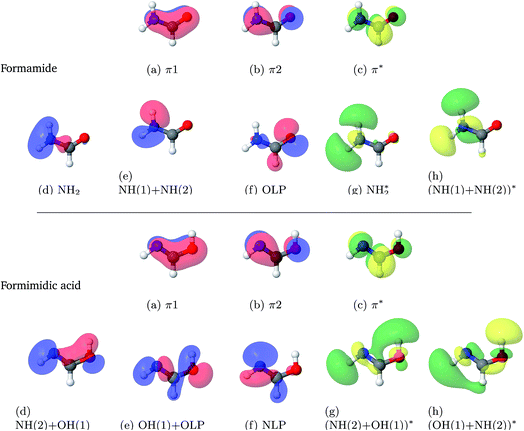 | ||
| Fig. 1 Molecular orbitals of formamide (top) and formimidic acid (bottom) from SA8-CAS(10,8)/6-31G* calculations. | ||
3.2 Direct dynamics
The dynamics calculations were propagated using the ground state normal modes of the molecules with the widths of the Gaussian wavepackets defined by the frequencies. The initial distribution of the Gaussians comprised a single fully populated Gaussian at the Franck–Condon point around which the rest of the zero populated Gaussians are distributed, with an overlap of 0.5. In order to ensure the stability of the initial electronic structure calculation, the Gaussians were distributed in momentum space, as opposed to configuration space. The use of the single fully populated Gaussian at this point ensures that the initial wavepacket is the ground state vibrational wavefunction. As there were 8 states included in the electronic structure calculation, a preliminary calculation was made with a vertical excitation to S1 using 8 Gaussian basis functions, with a propagation time of 150 fs.These results allowed the selection and placement of complex absorbing potentials (CAPs). These are negative, imaginary potentials which are used to absorb a wavepacket. In grid based calculations, they are placed at the ends of grids to ensure that the wavepacket is not reflected off the end of the grid, resulting in the decoherence. In a direct dynamics calculation, if a rapid dissociation occurs, the dissociating atom or fragment gains momentum as it gets further away from the main molecule. This has a direct impact on the integrator in that rapidly decreasing time step sizes must be taken in order to gain a valid description of the system as a whole. Additional issues arise in that these rapidly changing geometries result in a larger number of points requiring electronic structure calculations. At these widely spaced geometries, the electronic structure calculations will take longer to run, and may fail. Consequently, the use of CAPs in the DD-vMCG method essentially provides a cut-off point to dissociative motion along normal mode coordinates.
The CAPs are defined as
| iW = ηΘ(k(x − x0))n | (40) |
The DD-vMCG method builds a database of geometries, energies and other information, such as molecular orbitals, along the course of a propagation. Multiple runs of a calculation, using the database constructed from previous calculation(s), will result in fewer electronic structure calculations required, as well as the opportunity for further regions of configuration space to be explored. Consequently, the databases from this first set of calculations were used for subsequent calculations.
A second set of calculations was propagated starting on the S1, S2 and S3 states and with 8, 24 and 48 GWPs, each with a propagation time of 150 fs. The databases constructed from these propagations were then merged into one database which was then used for the final propagations on the three states, with 48 GWPs. The final databases for both formamide and formimidic acid at the end contained approximately 6500 structures. It is the results of this final set of calculations that are used for the following analysis.
4 Results
4.1 Electronic structure
The first question to be answered is what are the ground state structures of FAM and FIM? Optimised structures at the CCSD/6-311+G* level of theory were first obtained for the two structures and the transition state for proton transfer from the N to the O. It was found, in agreement with previous work,37 that the minimum structure of FAM has a non-planar structure with the NH2 group having a pyramidalisation angle of 25.4°. The minimum energy of the planar structure with Cs symmetry was therefore also obtained. The energies of these structures relative to the FAM non-planar minimum are listed in Table 1. It can be seen that FIM is approximately 0.5 eV less stable than FAM, and there is an appreciable barrier to proton transfer on the ground state surface of approximately 2.5 eV. The barrier to NH2 inversion in FIM is, however, tiny, of the order of 0.01 eV. The wells are thus too shallow to contain vibrational states and the molecule will appear to be planar for spectroscopic processes. The planar structure was thus taken as the starting structure for the dynamics. Table 1 also includes labels distinguishing the 3 hydrogen atoms that are used in the following analysis.In Table 2 the normal modes of formamide and formimidic acid are listed, calculated at the CCSD/6-311+G* and the SA8-CAS(10,8)/6-31G* levels of theory. The relevant frequencies and characterisations are also shown. All frequencies were calculated on structures optimised at the relevant level of theory. The normal mode vectors are shown graphically in the ESI.†
| Label | Formamide | Formimidic acid | ||||
|---|---|---|---|---|---|---|
| Frequency (cm−1) | Character | Frequency (cm−1) | Character | |||
| CCSD/6-311+G* | CAS(10,8)/SA8 6-31G* | CCSD/6-311+G* | CAS(10,8)/SA8 6-31G* | |||
| ν 1 (A′′) | 350.35i | 320.66i | NH2 oop wag | 596.58 | 630.43 | OH oop wag |
| ν 2 (A′) | 576.24 | 598.06 | H1 ip rocking | 611.55 | 635.19 | H2 + H1 ip wag |
| ν 3 (A′′) | 619.77 | 601.74 | NH2 oop torsion | 846.36 | 911.91 | H2 + H3 oop in-phase |
| ν 4 (A′′) | 1045.95 | 1014.98 | H3 oop bend | 1066.07 | 1062.53 | H3 + H2 oop out-of-phase |
| ν 5 (A′) | 1079.99 | 1108.68 | H2 ip rocking | 1097.61 | 1150.16 | NH ip bend |
| ν 6 (A′) | 1293.11 | 1356.26 | H3 H1 ip out-of-phase | 1232.28 | 1284.95 | H1 + H2 + H3 ip wag |
| ν 7 (A′) | 1443.86 | 1397.43 | H3 ip bend | 1404.31 | 1447.58 | H1 + H2 in-phase ip wagging |
| ν 8 (A′) | 1680.88 | 1803.58 | NH2 ip bend | 1437.46 | 1515.33 | H3 ip bend |
| ν 9 (A′) | 1827.88 | 2031.85 | CO stretch | 1750.26 | 1854.47 | CH3 ip rocking |
| ν 10 (A′) | 3008.20 | 2640.00 | CH stretch | 3155.30 | 3126.07 | NH stretch |
| ν 11 (A′) | 3636.12 | 3855.27 | NH2 sym stretch | 3554.58 | 3379.82 | OH stretch |
| ν 12 (A′) | 3772.01 | 4029.16 | NH2 anti-sym stretch | 3776.70 | 3449.48 | CH + OH stretch |
For formamide, in the first row of Table 2, it can be seen that the normal mode, ν1, is an imaginary frequency. This is the NH2 inversion mode that connects the global C1 minimum as discussed above. It can be seen that the frequencies calculated at the two levels of theory are close to each other with the largest difference for ν12 where the CASSCF frequency is higher by approximately 250 cm−1. As the structure has Cs symmetry, there exist two categories of normal mode representing in-plane and out-of-plane motion, where only three modes, ν1, ν3 and ν4, represent this out-of-plane motion. It should be noted that despite the fact that the motion of H(2) and H(3) appear to have their “own” vibrational modes, the motion of H(1) is always coupled to the motion of other atoms.
The normal mode frequencies of formimidic acid are seen to be all in good agreement between the 2 methods. As with FAM, there exist two categories of normal mode representing in-plane and out-of-plane motion where only three modes, ν1, ν3 and ν4, represent this out-of-plane motion.
Excitation energies, oscillator strengths and characterisations from the SA8-CAS(10,8)/6-31G* calculations of FAM and FIM are summarised in Table 3. The orbitals are shown in Fig. 1. It can be seen that the S6 state, characterised as a π–π* transition, is the brightest state for both FAM and FIM, while the S3 and S5 states have smaller but significant oscillator strengths. In FAM, the S6 and S3 states are both a mixture of π–π* and Olp–NH2* transitions, while S5 is predominantly Olp–NH2*, where Olp is the oxygen lone pair. In FIM, the S6 and S3 states are both characterised as being a mixture of π–π* and Nlp–(NH(2) + OH(1))* character, where Nlp is the nitrogen lone pair, while S5 is predominantly Nlp–(NH(2) + OH(1)*). The S1 (Nlp–π*) state in FIM also has a small, but significant, oscillator strength. It can also be seen that the oscillator strengths of the S3 and S5 states of FIM are greatly increased in comparison to the same states in FAM. This comparative increase in the oscillator strength in the S3 state is likely due to the dominant π–π* transition in the FIM, which is only a secondary contribution to the equivalent state in FAM.
| Formamide | Formimidic acid | |||||
|---|---|---|---|---|---|---|
| Energy (eV) | Oscillator strength (au) | Main configurations | Energy (eV) | Oscillator strength (au) | Main configurations | |
| S1 | 5.607 | 0.0008 | 0.69 (Olp–Pi*) | 6.935 | 0.0105 | 0.687 (Nlp–Pi*) |
| S2 | 8.015 | 0.0004 | 0.66 (Pi–NH + NH) | 8.935 | 0.0009 | 0.56 (Pi–(OH + NH)*) + 0.35 (Pi–(NH + OH)*) |
| S3 | 8.159 | 0.0225 | 0.54 (Olp–NH + NH) + 0.34 (Pi–Pi*) | 9.117 | 0.1325 | 0.48 (Pi–Pi*) + 0.37 (Nlp–(OH + NH)*) |
| S4 | 9.118 | 0.0000 | 0.66 (Pi–NH + NH) | 10.079 | 0.0045 | 0.56 (Pi–(NH + OH)*) + 0.36 (Pi–(OH + NH)*) |
| S5 | 10.033 | 0.0710 | 0.63 (Olp–NH + NH) | 10.137 | 0.1723 | 0.48 (Nlp–(NH + OH)*) + 0.47 (Nlp–(OH + NH)*) |
| S6 | 10.574 | 0.7258 | 0.44 (Pi–Pi*) + 0.37 (Olp–NH + NH) | 11.267 | 0.4634 | 0.41 (Nlp–(NH + OH)*) + 0.39 (Pi–Pi*) + 0.30 (Nlp–(OH + NH)*) |
| S7 | 11.450 | 0.0013 | 0.55 (Pi–NH + NH) + 0.36 (Pi–Pi*) | 11.831 | 0.0000 | 0.676 (OH + Olp–Pi*) |
Table 4 compares the results from the SA8-CAS(10,8)/6-31G* calculations on formamide with literature values. Experiments have determined five main bands in the UV absorption spectrum, which have been assigned to three valence (nπ* and ππ*) and two Rydberg states. The presence of Rydberg states is well-known in small nitrogen-containing molecules, and a basis set with diffuse functions is required to treat them correctly. The calculations of Hirst et al.,34 Serrano-Andrés and Fülscher35 and Antol et al.37 all include diffuse functions and obtain a large number of Rydberg states. For example, Serrano-Andrés and Fülscher, using a huge 15-orbital active space and large atomic natural orbital (ANO) basis set specifically designed for this, obtained 22 states in the 5 eV range between the nπ* and higher ππ* states. These Rydberg states are not included in our calculations as the basis set was chosen for efficiency in the direct dynamics. It can be seen that the CAS space chosen, however, places the valence states with reasonable accuracy compared to the other calculations and experiment. It would also be expected that as the molecule moves away from the high symmetry starting point that the Rydberg states will mix strongly with the valence states and the description of these will be adequate for our purposes of testing the DD-vMCG method with a realistic, but challenging system.
| Band | Expt.56,57 | This work | Hirst34 | Serrano-Andrés35 | Antol37 |
|---|---|---|---|---|---|
| CAS(10,8) | MRCI/CAS(6,13) | CASPT2(6,15) | MRCISD | ||
| 6-31G* | 6-31+G** | ANO | aug-cc-pVDZ | ||
| W 1A′′ (nπ*) | 5.82 (0.002) | 5.61 (0.001) | 5.86 (0.001) | 5.61 (0.001) | 5.78 (0.001) |
| R1 1A′′ | 6.35 | 8.01 (0.001) | 6.14 (0.022) | 6.52 (0.024) | 6.77 (0.022) |
| V1 1A′ (ππ*) | 7.36 (0.37) | 8.16 (0.022) | 7.40 (0.156) | 7.41 (0.371) | 7.71 (0.338) |
| R2 1A′ | 7.72 | 10.03 (0.071) | 7.50 (0.041) | 7.72 (0.101) | 7.84 (0.017) |
| Q 1A′ (ππ*) | 9.23 | 10.57 (0.726) | 7.94 (0.149) | 10.50 (0.131) |
4.2 Quantum dynamics simulations
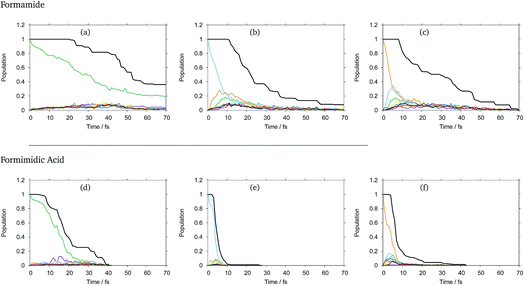
The diabatic state populations as a function of time for formamide and formimidic acid after vertical excitation to the S1, S2 and S3 states for each of the 8, 24 and 48 GWP propagations are shown in the ESI.† These demonstrate that the results are not changing significantly with increasing basis set, but the results become smoother. It can be seen, most significantly in the S1 plots, that the increase from 8 to 24 GWPs resulted in a more smooth representation of the decay and redistributions of the density into the different states, while the improvement from the 24 to 48 GWP is less significantly pronounced. This implies that the calculations are reaching convergence.In Fig. 2 the diabatic state populations from the 48 GWP propagations are shown, with a comparison to the total density. The diabatic state populations give information as to how the total wavepacket has been distributed, along the period of propagation, into the various states included in the calculation. The amount of the population absorbed by the CAPs cannot directly be separated from the population transfer in the analysis of this set of graphs. However, by also plotting the total density with the diabatic state populations, the features of population transfer can more easily be resolved from the population that is being absorbed by the CAP. It can be seen that in both molecules, the timescale for the decay from the S1 state is significantly longer than that from the higher lying states, and that FAM has a longer lifetime than FIM after all excitations.
In FAM, approximately 20% of the population is still in the S1 state after 70 fs, while the population decay from the higher lying states is complete by around 30 fs. It can be seen that in the S1 state, density begins to flow into the CAPs after around 20 fs, while in the S2 state this begins to occur after 10 fs and in the S3 state this occurs after around 8 fs, indicating that the initial drop in the population at the beginning of the propagation is due to population transfer. In the S1 state, as mentioned previously, the rate of population transfer is significantly slower than in the other excited states. It can also be seen that the population transfer is relatively evenly distributed across all of the excited states in the calculation.
In the S2 state it can be seen that after approximately 6 fs about 25% of the population has been transferred to the S3 (orange) state, with around 18% of the population being transferred to the S1 (green) state by 9 fs. A similar fast population transfer is also seen in the S3 plot, where about 32% of the population is transferred to the S2 (light blue) state with the next most significant population transfer going into the S1 state. Population transfer also takes place from the S3 to S4 (yellow) states.
In FIM after excitation to S1, the most significant diabatic state population transfer is into the S0 state at about 15 fs, and the population transfer is complete by around 30 fs. The transfer is, however, minor. It can be seen instead that the decrease in total density follows the trend in the decreasing population of the S1 state, suggesting that the S1 state is displaying dissociative behaviour. In the S2 state, the decrease in the total density occurs rapidly between 4 and 10 fs, with relatively little population transfer occurring to S1 and S3. In the S3 state, it can be seen that there is a fast population transfer, mostly to the S2 state, but also to the S5 and S6 states and a small amount to the S4 state, and the total density does not decrease over this short timescale. It appears that in this S3 calculation, when the S1 and S7 states become populated, the total density proceeds to decrease rapidly, supporting the suggestion that the S1 and perhaps the S7 states are dissociative.
As a result of this analysis it can be seen that while dissociative behaviour can be seen in all sets of results, it is not possible from this analysis to state conclusively that particular states exhibit dissociative behaviours, or to know what the products are. A useful description of the distribution of the products of a calculation can be obtained by assigning a weight to a particular GWP. An estimate can then be obtained of the density going into the channel described by the trajectory at the centre of a GWP. The density is given by
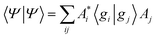 | (41) |
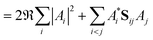 | (42) |
When the overlaps between the functions are divided evenly, the gross Gaussian population,58 or GGP, is hence defined where
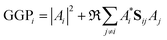 | (43) |
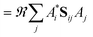 | (44) |
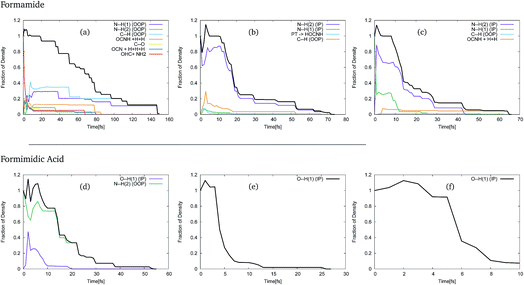
In order to use these GGPs, it is first necessary to perform a visual inspection of the geometries defined by the trajectory of the centre of the GWPs. The fraction of the density, defined by the GGP, along each of the product channels was then categorised, allowing analysis of the product distribution. The results of this analysis of the trajectories of the GWPs for formamide and formimidic acid can be seen in Fig. 3. It should be noted that the >1 population in the first few femtoseconds of the propagation is likely due to numerical instabilities in the method.
In Fig. 3, representing the product distribution of FAM, upon cursory inspection it can be seen that while the product distribution in the S2 and S3 states is dominated by one behaviour, the number of product channels, and hence the product distribution in the S1 state, is more evenly distributed between the possible pathways. In the S1 state, it can be seen that dissociation in the first 70 to 80 fs of the propagation occurs along a multitude of pathways, the principal of which represent the N–H(1) and C–H out-of-plane motions, which correspond to the ν1, ν2 and ν3 vibrational modes of the system. It is in the movement in these channels that the density continues after 80 fs, until all of the Gaussians have been absorbed by the caps. In both the S2 and the S3 states, the principal product channel is defined by the N–H(2) bond stretching. In the S2 state it can be seen that a very small amount of proton transfer occurs. In this process, the H(1) dissociates and the H(3) subsequently transfers to the oxygen. Although the proton transfer involving the H(1) atom was expected, this mechanism of proton transfer was somewhat unexpected. In the S3 state it can be seen that a secondary product channel to the nuclear motion in the first 12 fs is observed along the N–H(1) stretching mode. It should be noted that while the C–H out-of-plane bond-breaking is observed in all three of these states, NH2 and NH1 bond-breaking is along in-plane motion for S2 and S3, but out-of-plane motion for S1.
In Fig. 3, representing the product distribution of FIM, upon cursory inspection it can be seen that while the number of product channels for the S1 state is greater than in the S2 and S3 states, as was the case with FAM, only two product channels are seen. In all three states the O–H(1) in-plane stretching motion, characterised as the ν11 mode, to the point of dissociation is seen, while in the S1 state the N–H(2) out-of-plane motion, characterised in a combination of the ν3 and ν4 modes, is also seen. In the S1 state it is the N–H(2) out-of-plane motion that is dominant, though the timescale over which the O–H(1) stretching motion is seen is comparable to the timescale in the S2 state.
As a result of this investigation it can be seen that a number of different product channels are available in the dynamics of formamide, whereas the OH stretching motion in formimidic acid is dominant.
During the course of direct dynamics propagation, the energies are calculated and stored in the database. As a result, 1- and 2-dimensional cuts of the potential energy surfaces can be made. By looking at the adiabatic and diabatic representation of the same mode, or modes, regions displaying non-adiabatic features such as avoided crossings, or conical intersections, can be determined. From a practical perspective, these surfaces can also be used to determine if the direct dynamics calculations have been propagated for sufficient time periods, if the diabatisation scheme has been successful, and other technical faults which are displayed as discontinuities on the surfaces. Using the observations of the GWP trajectories, the surface cuts were selected along the modes which were most clearly important for the dissociation of the molecules.
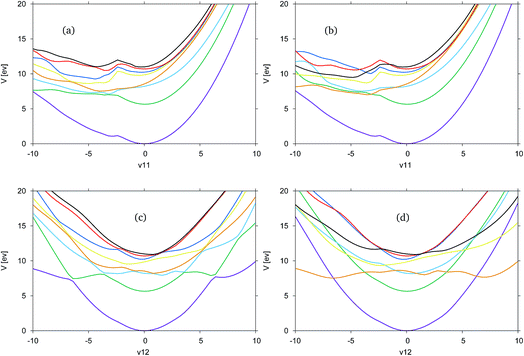
In Fig. 4, the adiabatic and diabatic cuts of the potential energy surfaces of FAM along the ν11 and ν12 modes are shown, characterised as the N–H2 symmetric and anti-symmetric stretching modes. The NH dissociations occur along a combination of the modes. The potential energy surfaces are smooth, with the diabatic states correctly crossing between states.
Along ν11 in Fig. 4(a) and (b), there is a dissociative channel in the negative displacement direction shown as the green, S1 state in the adiabatic representation, which in the diabatic representation becomes the orange, previously S3, state. However, in both the diabatic and adiabatic representations it can be seen that there exists a kink in the surfaces, approximately located at a displacement of −2. From the shape of the curves at this point it is likely that there is a higher energy state which cuts down through most of the states, and is not represented in the CAS space used.
Along ν12 in Fig. 4(c) and (d) at the Franck–Condon point it can be seen that the blue, S2, and orange, S3, states are very close in energy and crossing between these states occurs very close to the Franck–Condon point. It is this orange state, in the diabatic picture, that leads to the NH-dissociation channel. It should be noted that these curves are not symmetric.
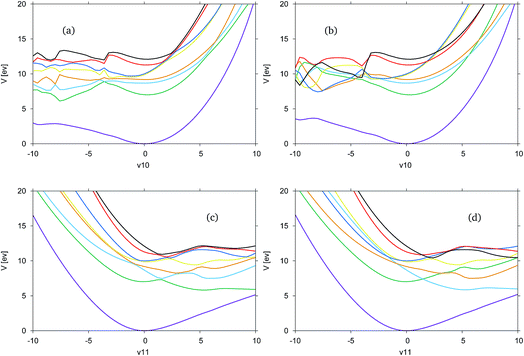
In Fig. 5 the adiabatic and diabatic cuts of the potential energy surface along the ν10 (Fig. 5(a) and (b)) and ν11 (Fig. 5(c) and (d)) modes of formimidic acid, characterised as the N–H2 and the OH stretching modes, are shown. These modes represent the equivalent modes to the ν11 and ν12 of FAM. In Fig. 5(a) and (b) there appears to be a major failure in the calculation in the negative direction along the mode, at about −4. This has been identified as a failure in the electronic structure calculations. Consequently, the only comments that can be made about this representation are that the dark blue (S5) and yellow (S4) states are very close in energy along the positive direction of the mode, and that the crossings between these and the red (S6) and black (S7) states are well-resolved. It appears as if there may be a dissociative state in the negative direction along the mode though it is unclear as to whether this state originates from a state within the precalculated manifold.
In Fig. 5(c) and (d) it can be seen that the surfaces are much more smooth and they clearly show a dissociative state which is the green, S1, state in the adiabatic representation, or the light blue, S2, state in the diabatic representation. As the states are well-resolved in this mode it is clear that the OH dissociative pathway was open to the dynamics of the molecule. In the diabatic representation there is a good representation of the crossings between the states, although a region approximately located at 2, in the positive direction shows a significant convergence of the yellow, blue, red and black states, S4 to S7, and it is unclear if this region has been correctly resolved.
5 Conclusions
In this paper we have presented a study of the photo-dissociation dynamics of two key molecules, formamide and formimidic acid, using a new fully quantum mechanical direct dynamics algorithm. The method is able to capture the entire quantum nature of the coupled nuclear and electronic motions after photo-excitation into a manifold of states. Here, eight states were considered with the coupling between them treated using a novel propagation diabatisation scheme. It provides potential surfaces from quantum chemistry calculations on-the-fly, thus circumventing the need for pre-fitted global surfaces, and the diabatic surfaces cross smoothly where crossing points are found in the adiabatic surfaces. This should provide a significant step forward when calculating the quantum dynamics of polyatomic molecules as the provision of global diabatic surfaces is a prohibitive step in most cases.A feature of the method that is also useful is that the Gaussian wavepacket basis functions are free to travel anywhere, and thus any open channels can be explored. The local nature of the basis functions allows a simple analysis of the importance of the different channels by analysing the trajectories of the GWP centres and weighting them by the Gross Gaussian Populations that are related to the density carried by each basis function. In the case of formamide and formimidic acid, it is found that both molecules dissociate in less than 100 fs, with FIM being the faster of the two. The simulations, moreover, show that the dissociation in both cases depends on the initial excitation, i.e. the starting energy. In both cases, excitation to S2 or S3 results in very fast direct dissociation of a single hydrogen atom – the O–H bond in FIM or the N–H or C–H bonds in FAM. In contrast, excitation to S1 leads to a longer lifetime and more open channels. In the case of FIM, the main dissociation is now the N–H bond, while in FAM, a number of fragmentations occur. Thus, in both cases, hydrogen loss appears to lend a degree of photostability to the molecule.
The study also shows the limitations of the present method. The main problem is the quantum chemistry. Despite careful initial benchmarking, the CASSCF calculations are seen to have problems in the N–H dissociation channels, resulting in non-smooth surfaces. The algorithm also needs to be improved to retain the symmetry of the surfaces. Further work is required to remedy these problems. The diabatic surfaces also need to be tested beyond visual inspection for any inconsistencies. The potential of the method is, however, clear, and should lead to a powerful tool able to simulate quantum mechanical behaviour in a straightforward way.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded in part by the EPSRC through a DTA award to Eryn Spinlove.References
- H.-D. Meyer, U. Manthe and L. S. Cederbaum, Chem. Phys. Lett., 1990, 165, 73–78 CrossRef.
- M. H. Beck, A. Jäckle, G. A. Worth and H.-D. Meyer, Phys. Rep., 2000, 324, 1–105 CrossRef.
- H.-D. Meyer, F. Gatti and G. A. Worth, Multidimensional Quantum Dynamics: MCTDH Theory and Applications, Wiley VCH, 2009 Search PubMed.
- H. Wang and M. Thoss, J. Chem. Phys., 2003, 119, 1289–1299 CrossRef.
- G. Richings and S. Habershon, Chem. Phys. Lett., 2017, 683, 228–233 CrossRef.
- G. Richings and S. Habershon, J. Chem. Theory Comput., 2017, 13, 4012–4024 CrossRef PubMed.
- G. Richings and S. Habershon, J. Chem. Phys., 2018, 148, 134116 CrossRef PubMed.
- M. D. Hack and D. G. Truhlar, J. Phys. Chem. A, 2000, 104, 7917–7926 CrossRef.
- M. Richter, P. Marquetand, J. González-Vázquez, I. Sola and L. González, J. Chem. Theory Comput., 2011, 7, 1253–1258 CrossRef PubMed.
- S. Mai, P. Marquetand and L. González, Int. J. Quantum Chem., 2015, 115, 1215–1231 CrossRef.
- C. C. Martens, J. Phys. Chem. Lett., 2016, 7, 2610–2615 CrossRef PubMed.
- A. Abedi, N. T. Maitra and E. K. U. Gross, Phys. Rev. Lett., 2010, 105, 123002 CrossRef PubMed.
- S. K. Min, F. Agostini, I. Tavernelli and E. K. Gross, J. Phys. Chem. Lett., 2017, 8, 3048–3055 CrossRef PubMed.
- J. Quenneville, M. Ben-Nun and T. J. Martínez, J. Phys. Chem. A, 2000, 104, 5161–5175 Search PubMed.
- M. Ben-Nun and T. J. Martínez, Adv. Chem. Phys., 2002, 121, 439–512 CrossRef.
- B. Curchod and T. Martinez, Chem. Rev., 2018, 118, 3305–3336 CrossRef PubMed.
- G. A. Worth, M. A. Robb and I. Burghardt, Faraday Discuss., 2004, 127, 307–323 RSC.
- B. Lasorne, M. A. Robb and G. A. Worth, Phys. Chem. Chem. Phys., 2007, 9, 3210–3227 RSC.
- G. A. Worth, M. A. Robb and B. L. Lasorne, Mol. Phys., 2008, 106, 2077–2091 CrossRef.
- G. W. Richings and G. A. Worth, J. Phys. Chem. A, 2015, 119, 12457–12470 CrossRef PubMed.
- A. W. Hofmann, J. Am. Chem. Soc., 1863, 16, 72–74 RSC.
- P. M. Solomon, Phys. Today, 1973, 26, 32–40 CrossRef.
- D. Bockelée-Morvan, D. C. Lis, J. E. Wink, D. Despois, J. Crovisier, R. Bachiller, D. J. Benford, N. Biver, P. Colom, J. K. Davies, E. Gérard, B. Germain, M. Houde, D. Mehringer, R. Moreno, G. Paubert, T. G. Phillips and H. Rauer, Astron. Astrophys., 2000, 353, 1101–1114 Search PubMed.
- D. C. Lis, D. M. Mehringer, D. Benford, M. Gardner, T. G. Phillips, D. Bockelée-Morvan, N. Biver, P. Colom, J. Crovisier, D. Despois and H. Rauer, Earth, Moon, Planets, 1997, 78, 13–20 CrossRef.
- W. A. Schutte, A. C. A. Boogert, A. G. G. M. Tielens, D. C. B. Whittet, P. A. Gerakines, J. E. Chiar, P. Ehrenfreund, J. M. Greenberg, E. F. van Dishoeck and T. de Graauw, Astron. Astrophys., 1999, 343, 966–976 Search PubMed.
- W. H. Flygare, R. C. Benson, H. L. Tigelaar, R. H. Rubin and G. W. J. Swenson, Molecules in the galactic environment, John Wiley and Sons Inc, New York, 1973 Search PubMed.
- C. A. Gottlieb, P. Palmer, L. J. Rickard and B. Zuckerman, Astrophys. J., 1973, 182, 699–710 CrossRef.
- R. Saladino, C. Crestini, S. Pino, G. Costanzo and E. Di Mauro, Phys. Life Rev., 2012, 9, 84–104 CrossRef PubMed.
- M. A. Robb and I. G. Csizmadia, Theor. Chim. Acta, 1968, 10, 2 CrossRef.
- X. C. Wang, J. Nichols, M. Feyereisen, M. Gutowski, J. Boatz, A. D. J. Haymet and J. Simons, J. Phys. Chem., 1991, 95, 10419–10424 CrossRef.
- D. Guzmán-Angel, R. Inostroza-Rivera, S. Gutiérrez-Oliva, B. Herrera and A. Toro-Labbé, Theor. Chem. Acc., 2016, 135, 37 Search PubMed.
- V. S. Nguyen, H. L. Abbott, M. M. Dawley, T. M. Orlando, J. Leszczynski and M. T. Nguyen, J. Phys. Chem. A, 2011, 115, 841–851 CrossRef PubMed.
- V. S. Nguyen, T. M. Orlando, J. Leszczynski and M. T. Nguyen, J. Phys. Chem. A, 2013, 117, 2543–2555 CrossRef PubMed.
- J. D. Hirst, D. M. Hirst and C. L. Brooks III, J. Phys. Chem., 1996, 100, 13487–13491 CrossRef.
- L. Serrano-Andrés and M. P. Fülscher, J. Am. Chem. Soc., 1996, 118, 12190–12199 CrossRef.
- N. A. Besley and J. D. Hirst, J. Am. Chem. Soc., 1999, 121, 8559–8566 CrossRef.
- I. Antol, M. Vazdar, M. Barbatti and M. Eckert-Maksić, Chem. Phys., 2008, 349, 308–318 CrossRef.
- N. V. Tukachev, V. A. Bataev, A. V. Abramenkov and I. A. Godunov, Comput. Theor. Chem., 2016, 1080, 23–32 CrossRef.
- I. Antol, M. Barbatti, M. Eckert-Maksić and H. Lischka, Monatsh. Chem., 2008, 139, 319–328 CrossRef.
- I. Burghardt, M. Nest and G. A. Worth, J. Chem. Phys., 2003, 119, 5364–5378 CrossRef.
- G. A. Worth and I. Burghardt, Chem. Phys. Lett., 2003, 368, 502–508 CrossRef.
- I. Burghardt, K. Giri and G. A. Worth, J. Chem. Phys., 2008, 129, 174104–174114 CrossRef PubMed.
- G. W. Richings, I. Polyak, K. E. Spinlove, G. A. Worth, I. Burghardt and B. Lasorne, Int. Rev. Phys. Chem., 2015, 34, 269–308 Search PubMed.
- E. J. Heller, J. Chem. Phys., 1975, 62, 1544–1555 CrossRef.
- E. J. Heller, J. Chem. Phys., 1981, 75, 2923–2931 CrossRef.
- G. A. Worth, K. Giri, G. W. Richings, M. H. Beck, A. Jäckle and H.-D. Meyer, Quantics package, Version 1.1, 2015 Search PubMed.
- B. Lasorne, M. J. Bearpark, M. A. Robb and G. A. Worth, Phys. Chem. Chem. Phys., 2006, 432, 3210–3227 Search PubMed.
- J. Ischtwan and M. A. Collins, J. Chem. Phys., 1994, 100, 8080–8088 CrossRef.
- M. A. Collins and D. H. Zhang, J. Chem. Phys., 1999, 111, 9924–9931 CrossRef.
- T. J. Frankcombe, M. A. Collins and G. A. Worth, Chem. Phys. Lett., 2010, 489, 242–247 CrossRef.
- T. J. Frankcombe, J. Chem. Phys., 2014, 140, 114106–114108 CrossRef PubMed.
- M. Baer, Chem. Phys. Lett., 1975, 35, 112–118 CrossRef.
- B. Esry and H. Sadeghpour, Phys. Rev. A: At., Mol., Opt. Phys., 2003, 68, 42706 CrossRef.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz, P. Celani, W. Györffy, D. Kats, T. Korona, R. Lindh, A. Mitrushenkov, G. Rauhut, K. R. Shamasundar, T. B. Adler, R. D. Amos, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, E. Goll, C. Hampel, A. Hesselmann, G. Hetzer, T. Hrenar, G. Jansen, C. Köppl, Y. Liu, A. W. Lloyd, R. A. Mata, A. J. May, S. J. McNicholas, W. Meyer, M. E. Mura, A. Nicklass, D. P. O’Neill, P. Palmieri, D. Peng, K. Pflüger, R. Pitzer, M. Reiher, T. Shiozaki, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson and M. Wang, MOLPRO, version 2015.1, a package of ab initio programs, 2015, http://www.molpro.net Search PubMed.
- P. J. Knowles and H.-J. Werner, Chem. Phys. Lett., 1985, 115, 259–267 CrossRef.
- H. Basch, J. Chem. Phys., 1968, 49, 5007–5018 CrossRef.
- J. M. Gingell, N. J. Mason, H. Zhao, I. C. Walker and M. R. F. Siggel, Chem. Phys., 1997, 220, 191–205 CrossRef.
- C. S. M. Allan, B. Lasorne, G. A. Worth and M. A. Robb, J. Phys. Chem. A, 2010, 114, 8713–8729 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Structures, normal mode vectors, CASSCF analysis. See DOI: 10.1039/c8fd00090e |
| This journal is © The Royal Society of Chemistry 2018 |