DOI:
10.1039/C8FD00096D
(Paper)
Faraday Discuss., 2018,
212, 175-190
Heavy Rydberg states: large amplitude vibrations†
Received
21st May 2018
, Accepted 21st June 2018
First published on 21st June 2018
Abstract
Extremely large vibrational amplitude (≈8700 a.u.) heavy Rydberg levels in the H![[H with combining macron]](https://www.rsc.org/images/entities/char_0048_0304.gif) 1Σ+g state, located only 25 cm−1 below the ion-pair dissociation limit, are reported. The calculations are done using a hybrid log derivative/multichannel quantum defect approach that accounts for predissociation and is capable of dealing with any number of long-range closed channels, and of providing positions and widths for the heavy Rydberg resonances. In this case, resonance positions can be reproduced qualitatively using a simple diabatic model (however, the resonance widths cannot). Absolute quantum defects are derived for the vibrational series ranging from ν = 0 to ν = 2010. The influence of the Coulomb potential and continuity of heavy Rydberg behavior throughout the 1Σ+g manifold of states is demonstrated.
1Σ+g state, located only 25 cm−1 below the ion-pair dissociation limit, are reported. The calculations are done using a hybrid log derivative/multichannel quantum defect approach that accounts for predissociation and is capable of dealing with any number of long-range closed channels, and of providing positions and widths for the heavy Rydberg resonances. In this case, resonance positions can be reproduced qualitatively using a simple diabatic model (however, the resonance widths cannot). Absolute quantum defects are derived for the vibrational series ranging from ν = 0 to ν = 2010. The influence of the Coulomb potential and continuity of heavy Rydberg behavior throughout the 1Σ+g manifold of states is demonstrated.
1 Introduction
The electrostatic Coulomb potential between particles of opposite charge can support extremely long-range states in atoms and molecules. For instance, in a recent experiment, a Rb atom within a Bose–Einstein condensate was excited to an electronic (Rb+e−) Rydberg state with a mean radius of orbit close to 4 μm, thus exceeding the short axis of the entire 65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atom condensate.1
000 atom condensate.1
The vibrational levels of ionically bound states in diatomic molecules are known to form Rydberg series2,3 and such vibronic states are now sometimes referred to as ‘heavy Rydberg’ states.4–8 Heavy Rydberg (HR) states are analogous of electronic Rydberg states but with the Rydberg electron replaced by a negative ion. Thus both the center of mass and the reduced mass of HR states differ significantly from those of electronic Rydberg states. However, in either case a system bound by a Coulomb potential at long range will support an infinite number of bound levels and the vibrational levels of a HR state will form a Rydberg series with well-defined effective quantum numbers n* and quantum defects. The vibrational quantum number ν is a measure of the number of nodes in a given vibrational state and simply replaces the radial quantum number n normally associated with electronic Rydberg states;3 note that ν is a node count so ν + 1 = n.
HR states have attracted much recent interest and substantial progress has been made in their identification. The ion-pair (IP) states of molecular hydrogen, the hydrogen halides, diatomic halogens and several other molecules exhibit extended vibrational progressions that have been shown to be HR in character over much of their range.8–25 Heavy Rydberg behaviour is diagnostic of the dominance of the Coulomb potential in a progression of vibrational levels. The large electronic transition moments associated with valence ↔ IP state transitions (which must always be parallel), when combined with good Franck–Condon factors, makes ion-pair states effective doorway states for photochemical reactions involving charge transfer. In homonuclear HR states a large transition dipole connects g/u pairs of HR states that correlate with the same ionic products and this can lead to amplified spontaneous emission.
There is an intimate connection between ion-pair states and electronic Rydberg states that lie in the same energy region. Their electronic configurations are related by a one or two-electron transfer between molecular orbitals. Asaro and Dalgarno pointed out in 1985 (ref. 2) that the vibrational states in LiF would acquire Rydberg character with increasing excitation. The year before, Mies pioneered the idea that multichannel quantum defect theory (MQDT, see e.g.ref. 26) could be applied to vibrational states in diatomics,27,28 and in 1988 published a paper that explicitly discussed the Rydberg-like properties of rotational–vibrational states in alkalihalides.3 Around the same time, Zewail and co-workers published their wave packet experiments on NaI,29,30 which were almost immediately followed up by time-dependent calculations.31,32 In the experiment, a surprisingly strong dependence on the excitation energy was observed for the lifetime of the wave packet. Chapman and Child eventually demonstrated that in the energy domain, this could be understood in terms of a periodic interferometric modulation of the widths of the states constituting the wave packets.33 Later, this modulation, which can span several orders of magnitude, was shown to cause Fano q-parameter reversals in lineshapes,34,35 and more recently, was proposed as the basis for the excitation of long-range ion-pair states in ultracold Rb gas.36
The present article is inspired by the observation of photoexcited HR states with high principal quantum number (n > 1000) by Ubachs et al.,4,5,7,8 predominantly in H2. Molecular hydrogen has attracted intense interest from both theoreticians and spectroscopists over many decades.8,9,11,12,14,15,19–21,24,25 The potential energy curves for many of the electronic states of H2 below the ionisation energy can now be calculated to high precision and there is close agreement between experiment and theory for the rovibronic term-values of most of the isotopomers which include mass-dependent non-adiabatic corrections.15 Mixing between HR and electronic Rydberg states provides doorway states that give access to the HR manifold. We present close-coupled channel calculations in H2, using a hybrid log derivative/MQDT method19,20 in an energy range that corresponds to principal quantum numbers n ≈ 2000. These HR states are embedded in the ionization and dissociation continua. We account for the non-adiabatic couplings to the neutral states of H2, leading to dissociation into neutral atoms, and focus on the high energy long-range states between the n = 3 and the ion-pair dissociation limit. This is the region employed for threshold ion-pair production spectroscopy (TIPS) and zero ion kinetic energy (ZIKE) techniques, and is of interest to astrophysicists, especially as it closely relates to the process of mutual neutralization, H+ + H− → H(nl) + H(n′l′), recently discussed by Larson et al.37
2 Properties of Rydberg states
HR states are bound by the long-range ion-pair potential,38| | 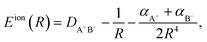 | (1) |
where R is the internuclear distance, DA+B− is the ion-pair dissociation energy, and αA+ and αB− are the polarizabilities of the two ions respectively. Atomic units are used throughout. The dominant term in Eion(R) is the Coulomb potential, 1/R, which supports an infinite number of bound states and whose properties underpin the scaling laws shared by all Rydberg systems.39 The energies of bound Rydberg states are given by the Rydberg formula,| | 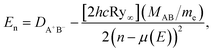 | (2) |
where n is the principal quantum number and μ(E) is the quantum defect. The quantity in brackets, [2hcRy∞], corresponds to one atomic unit of energy. Ry∞ is the Rydberg constant for an electron associated with an infinite-mass positive charge, and (MAB/me) is the mass scaling factor given by the ratio of the reduced mass MAB of A+B− and the electron mass me. The quantum defect, μ(E), gives the shift in the position of each Rydberg energy level compared to the pure Coulomb potential (see discussion below).
All scaling laws for Rydberg states originate from the properties of the Coulomb potential and the Rydberg formula. Since the energy levels scale as n−2, the level spacing scales as n−3 (with the same scaling implied for line widths and conversely n3 for lifetimes). The size of the Rydberg states scales as the classical outer turning point Rtp,
| | 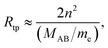 | (3) |
with the same
n2 scaling of the dipole moment.
It is important to note the effect of the reduced mass MAB in eqn (2) and (3), which is illustrated in Fig. 1. As a consequence of this mass scaling, heavy Rydberg states which by definition have (MAB/me) ≫ 1 are more compact and have a larger proportion of the wave function contained in the short-range interaction region for a given n. The mass scaling also has an obvious influence on the distribution of energy levels, as illustrated for the H-atom and H+H− in Fig. 1. In electronic Rydberg states, represented here by the H-atom, almost all energy levels occupy a narrow band just below the ionization limit, while the HR states in H+H− occupy a much wider energy band.
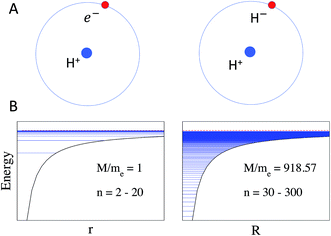 |
| | Fig. 1 (A) Schematic of Rydberg states in the H-atom (left) and in the H+H− heavy Rydberg system (right) in which H− is assumed to be a point charge. (B) The effect of the increased mass on Rydberg energy levels is demonstrated by the distribution of states according to the Rydberg formula using the effective mass of the H-atom on the left with MAB = me = 1 and n = 2–20, and the H2 molecule on the right with MAB = 918 and n = 30–300. Note that for the H2 molecule the states would be perturbed by short-range repulsive interactions, not included in this schematic (see later). Energy levels are indicated by horizontal lines. | |
The quantum defect μ(E) in eqn (2) can be related to the asymptotic phase shift in the scattering of the two opposite-charge fragments,26 with non-zero quantum defects μ(E) ≠ 0 indicative of shorter range interactions. Consider for instance the first electronically excited state of molecular hydrogen, the H2(B1Σ+u) state, which has an ionic configuration H+H− derived from the molecular orbital configuration σ1gσ1u for radial separations R < 10 a.u. where it crosses the atom-pair asymptote H(1s) + H(2s) leading to dissociation. The potential below this crossing is thus coulombic albeit modified by a small polarization term, until, on the inner branch of the potential, nuclear repulsion and electron-pair repulsion begin to dominate at short range. The resulting inner wall, present in all molecular ion-pair potentials, restricts the available phase space for vibration and results in large negative quantum defects.3 This is in contrast to the positive quantum defects for electronic Rydberg series in which the Rydberg electron can penetrate through inner valence shells to experience an increased effective nuclear charge giving a positive quantum defect. The energy dependence of the quantum defect generally decreases with increasing principal quantum number, as the Coulomb waves become increasingly similar in the interaction region, although the onset of this effect is slower in HR states due to mass scaling.19 As a general remark in the context of H2, note that HR states can only appear in the singlet manifolds of states, since the singlet H−(1s2) negative ion is the only stable form of the anion.
3 Theory
3.1 Overview
The HR states can be regarded as a long-range collision complex between two opposite-charge fragments. The complex can decay by predissociation, radiative decay, or ionisation. The following approach considers predissociation, with radiative decay slow enough to be ignored in the first approximation and the coupling to ionisation having a comparatively small influence on line positions, as will be argued later. The problem is treated using a hybrid log derivate-MQDT approach applied across the three distinct regions shown in Fig. 2. The inner region A is the interaction region, where the nonadiabatic interaction between the colliding fragments must be accounted for (using numerical integration of the close-coupled equations by the log derivative method, Section 3.2), the intermediate region B is the long-range region which supports heavy Rydberg resonances in the closed ion-pair channel (treated using an MQDT approach for channel elimination, Section 3.3). Finally, in the asymptotic region C, all interactions between the collision fragments have ceased.
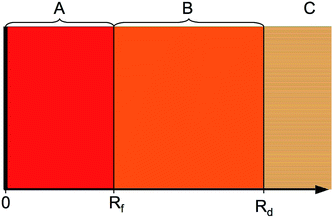 |
| | Fig. 2 The calculations proceed through three regions. The inner interaction region A (0 < R < Rf) has strong non-adiabatic couplings and we solve the close-coupled equations using the log derivative method. The intermediate region B (Rf < R < Rd) has no inter-channel couplings, but some channels contain long-range potentials capable of supporting large-amplitude resonances. These asymptotically closed channels are eliminated by an MQDT procedure. Finally, region C (R > Rd) is the asymptotic region. | |
3.2 Interaction region
We consider first the interaction region (region A: 0 < R < Rf in Fig. 2) corresponding to the collision complex. The theory of nonadiabatic atom–atom collisions is well-established (see e.g.ref. 37, 40 and 41). The dynamics are governed by a set of close-coupled partial differential equations,| | 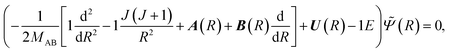 | (4) |
where MAB is the reduced mass and U(R) contains the N′ clamped-nuclei electronic energy curves, E is the total energy, and A(R) and B(R) are the N′ × N′ nonadiabatic coupling matrices. The leading first-derivative coupling terms can be eliminated by a Cayley transform,| | 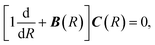 | (5) |
with boundary condition C(R → ∞) = 1. The matrix C(R) defines the adiabatic–diabatic transformation. This allows us to transform eqn (4) into the standard form,where Ψ is a N′ × N′ matrix, with each column being a linearly independent solution, Ψ′′ indicates the second derivative with respect to R, and the matrix W consists of| | 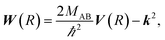 | (7) |
where the N′ × N′ matrix V contains the diagonal potentials (including the angular momentum components) and the off-diagonal coupling elements. The diagonal matrix k contains the asymptotic channel wave vectors k2 = (2MAB/ℏ2)ε, where ε has diagonal elements εi = E − Ei, with E being the total energy and Ei being the threshold energy in each channel i.
Eqn (6) is solved using the log derivative method,42–44 which propagates the log derivative matrix Y, defined as
where
Ψ′ indicates the first derivative with respect to
R. Propagation of
Y eliminates stability problems that can arise when the integration is started deep inside a classically forbidden region, or if it enters regions where a subset of channels are classically forbidden. Differentiation of
eqn (8) and removal of the second derivative using
eqn (6) gives a non-linear first order differential equation,
known as the matrix Riccati equation. Since
Y is undefined when det|
Ψ| = 0, standard integration techniques are not applicable and a form of invariant embedding must be used instead (see the extensive literature on the log derivative method,
e.g.ref. 42–44).
The matrix is propagated out to the matching radius Rf, at which point we assume that the channel interactions have vanished. At that point, the matrix is used to calculate the wave function in the form
where the wave function
Ψ is a
N ×
N matrix with each column corresponding to one solution, and
F and
G are diagonal
N ×
N matrices containing energy-normalized Milne functions.
45 These coincide with the analytic Coulomb and Riccati–Bessel functions once the polarization term in
eqn (1) vanishes. The crucial entity is the
N ×
N reaction matrix
K, which summarizes all interactions for
R <
Rf, and which is independent of
R,
i.e. d
K/d
R = 0, in the absence of channel interactions. Since channels closed already at
Rf are excluded from
Ψ, note that
N ≤
N′. The matrix
K is obtained by
| | | K = G−1F + G−1B−1G−1Ω, | (11) |
where
B =
Y −
G′
G−1, and only the
N ×
N (open–open) parts of the matrices are considered in
eqn (11) (and
eqn (10)), since the components associated with the
N′−
N closed channels have vanished. For energy-normalized Milne wave functions in natural units, the Wronskian matrix is given by
Ωij(
R) = π
−1δij. The calculations of the matrix
K (or equivalently
S) would normally constitute the end-point of the calculation. However, in the presence of HR resonances, the long-range ion-pair potential supports resonances in the external region B (
Rf <
R <
Rd), the treatment of which will be discussed in the next section.
3.3 Intermediate region
We consider here the situation where the intermediate region (region B: Rf < R < Rd in Fig. 2) contains long-range potentials capable of supporting additional vibrational resonances. Assume that among the N channels in the R > Rf wave function in eqn (10), there exists a subset of Nc asymptotically closed channels, for instance due to the ion-pair Coulomb potential, such that N = No + Nc, where No are the asymptotic channels that remain open for R > Rd. The Nc closed channels can be eliminated using multichannel quantum defect theory (MQDT).26,46 For energies close to the threshold, where the wave functions in the Coulomb channels extend to large distances, this procedure is more efficient than integrating all N channels to asymptotic distances.
In essence, the elimination procedure uses the N linearly independent solutions given by the column vectors of Ψ in eqn (10) to form No superpositions with correct asymptotic boundary conditions. This can be expressed as
where
Φ is a
N ×
No matrix,
Ψ a
N ×
N matrix, and the coefficient matrix
Z is
N ×
No. As before, each column is one solution.
Rewriting the matrix K as
| | 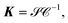 | (13) |
where
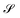
and
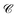
are
N ×
N matrices, and the coefficient matrix
Z as
| | 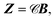 | (14) |
allows us to express
eqn (12) as
| | 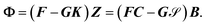 | (15) |
The component of the wave function given by eqn (15) for channel i and solution j is
| | 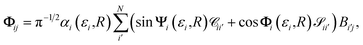 | (16) |
where
ϕi(
εi,
R → ∞) =
βi(
εi) for closed channels, with
βi(
εi) the accumulated phase
R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Rf
Rf → ∞ at energy
εi.
‡ At large distances
R → ∞ the wave function must be zero in closed channels, meaning that
| | 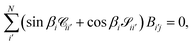 | (17) |
which in matrix form is
| | 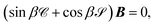 | (18) |
with sin
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β
β and cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β
β diagonal
N ×
N matrices with elements (sin
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β
β)
ii = sin
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β
β(
εi).
For asymptotically open channels, eqn (16) has ϕi(εi,R → ∞) = kiR + δi, assuming the asymptotic potential is constant. We can rewrite the sum as
| | 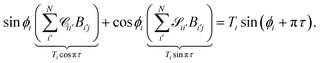 | (19) |
To obtain a condition similar in form to the closed channel condition in eqn (17), while ensuring that each open channel has the same asymptotic phase shift πτ, we can define
| | 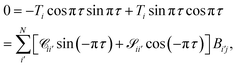 | (20) |
which in matrix form becomes
| | 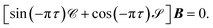 | (21) |
The unknowns in eqn (18) and (21) are the N × No coefficient matrix B and the No eigenphases τ. A numerically convenient method to obtain all these in a single calculation is to combine eqn (18) and (21) in the form of a generalized eigenvalue equation,
| | ΓB = tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) πτΛB, πτΛB, | (22) |
where the
N ×
N matrices
Γ and
Λ are defined as
| | 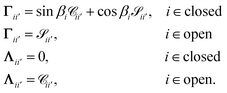 | (23) |
The main remaining steps are to normalize the continuum eigenvectors in B and to calculate the scattering matrix S. According to the definitions of T in eqn (19), we have that
| | 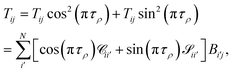 | (24) |
or in matrix form,
| | 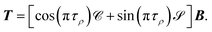 | (25) |
The matrix T can be shown to be orthogonal46 and becomes unitary, TT† = 1, if it is normalised according to 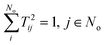 . This condition fixes the overall normalization of the N coefficients Bij for each j.
. This condition fixes the overall normalization of the N coefficients Bij for each j.
We can now obtain the No × No scattering matrix S− for incoming wave boundary conditions, appropriate for photodissociation. Combining the final wave function in eqn (15) with the definition of the coefficients T in eqn (19) gives the wave function for solution j in channel i (i, j ∈ No) as follows,
| | 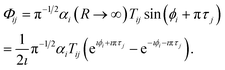 | (26) |
Henceforth we will use the asymptotic value of the open channel phase, ϕi(εi,R → ∞) = kiR + δi.
The following superposition corresponds to an asymptotic wave function incoming boundary condition,
| | 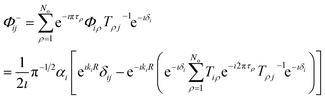 | (27) |
and we can identify the asymptotic open–open (
No ×
No) scattering matrix
S−(
E) as
| | 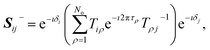 | (28) |
where
τρ is the asymptotic phase in channel
i and the unitary matrix
T is defined as
T =
CB cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
π
τ +
SB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
sin
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
π
τ. The matrix
S−(
E) will have strong energy-dependence reflective of the sharp long-range resonances, characterized by rapid change in the total eigenphase of the scattering matrix. The positions of the resonances can be obtained from the derivative of the cumulative eigenphase,
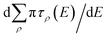
, and the width is obtained from the full width at half maximum (FWHM) for each peak. The positions of the peaks allow us to determine the value of the quantum defect by reference to
eqn (2). The shifts compared to the pure Coulomb potential are expressed in terms of either the quantum defect itself,
μ(
E), or equivalently the effective quantum number,
n* =
n −
μ(
E).
4 Calculations
The ab initio potential energy curves and the non-adiabatic couplings are taken from Wolniewicz et al.12,38 for states 2–61Σ+g and from Detmer et al.47 for 7–91Σ+g. The non-adiabatic couplings are particularly strong for R < 20 a.u. The potential energy curves are shown in Fig. 3. The figure includes the ion-pair potential and the ionisation limit in terms of the H+2 ground state. Weakly avoided crossings between the ion-pair potential and the adiabatic potential energy curves appear at R ≈ 36 a.u. (H(1s) + H(3l) dissociation limit) and R ≈ 280 a.u. (H(1s) + H(4l) dissociation limit). Table 1 includes indicative principal quantum numbers to provide a sense of the outer turning point on the ion-pair potential for the vibrational states at corresponding energies.
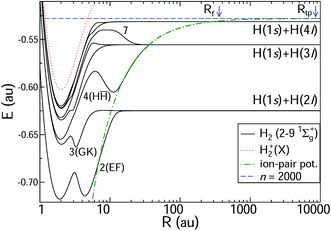 |
| | Fig. 3 Potential energy curves for H2 of 1Σ+g symmetry. The potential energy curves are taken from Wolniewicz et al. for states 2–6 (ref. 12 and 38) and from Detmer et al. for states 7–9.47 The H+2 ground-state potential is also included, as is the ion-pair potential. The position of the n = 2000 HR state is indicated by a vertical line, with the classical turning point Rtp at 8700 a.u. and the position of Rf (see Fig. 2). The unusual barrier shape in the region of R ≈ 10 on the excited potential energy curves can be understood using a simple Fermi model as contact potential interactions between a colliding H(1s) atom and an almost-Rydberg H(3l) atom.48,49 Note that the scale of the axis for the internuclear distance R is logarithmic. For R > 60 a.u. the potential energy curves are continued analytically. | |
Table 1 Table of features in 1Σ+g potential energy curves. For each feature we include the principal quantum number n* and the classical outer turning point in the ion-pair potential at the corresponding energy
| Feature |
n* |
R
tp (a.u.) |
| H(1s) + H(2l) dissociation limit |
68.72 |
11.08 |
| H(1s) + H(3l) dissociation limit |
128.52 |
36.05 |
| H(1s) + H(4l) dissociation limit |
362.30 |
286 |
| Outer well state 7 (at R = 33.8 a.u.) |
128.68 |
36.13 |
| Barrier on state 7 (at R = 8.7 a.u.) |
193.53 |
81.56 |
| At n = 100 energy |
100 |
22 |
| At n = 200 energy |
200 |
87 |
| At n = 1000 energy |
1000 |
2177 |
| At n = 2000 energy |
2000 |
8709 |
At large internuclear distances (R > 10 a.u.) the ion-pair (HR) states are accurately described by the Coulomb interaction energy between the positive and negative ion given by eqn (1) with the ion-pair dissociation energy DH+H− = −0.527751014 a.u. (ref. 38 and 50) and the polarizability of H−(1s2) αH− = 211.897 (a.u.)3 (see ref. 51 and also footnote§). The reduced mass for H2 is MH2 ≈ 918.0764 a.u.53
For the model diabatic calculation, we construct an effective diabatic potential Eion,diab(R) from the H![[H with combining macron]](https://www.rsc.org/images/entities/char_0048_0304.gif) 1Σgab initio adiabatic state calculated by Wolniewicz38 and the asymptotic ion-pair potential in eqn (1).50,51 The potentials are merged as follows,
1Σgab initio adiabatic state calculated by Wolniewicz38 and the asymptotic ion-pair potential in eqn (1).50,51 The potentials are merged as follows,
| | Eion,diab(R) = γ(R)Eion(R) + (1 − γ(R))EH![[H with combining macron]](https://www.rsc.org/images/entities/char_0048_0304.gif) (R), (R), | (29) |
where the mixing function
γ(
R) is defined as
γ(
R < 33) = 0, 0 <
γ(33 <
R < 35.5) = (
R − 33)/2.5 < 1, and finally
γ(
R > 35.5) = 1. Resonance positions on the diabatic model potential are determined using the shooting method, while all other calculations are done using the full machinery described in Sections 3.2 and 3.3.
5 Results and discussion
Tables of calculated long-range vibrational HR resonances for J = 0, 1, and 2 in the energy interval [−0.554933, −0.536094] a.u., corresponding to principal quantum numbers n = 130–235, are provided in the ESI,† listing the energy, effective quantum number and FWHM width of each resonance. This energy region corresponds to previous measurements by Ubachs et al.7,8 The overall agreement for line (resonance) positions is good. In contrast, the calculated widths, which decrease from 26 cm−1 to 2.4 cm−1 across the range n = 130–235, are systematically narrower than those observed in experiments. The source of this discrepancy must relate to decay channels other than predissociation that are not included in the present calculations, with ionisation most likely since these states are known to exhibit autoionisation.19
The main physics underpinning the progression of line positions across the range n = 160–230 is assessed by comparison to the simple diabatic model constructed from H![[H with combining macron]](https://www.rsc.org/images/entities/char_0048_0304.gif) 1Σ+g and the ion-pair potential (see Section 4). A comparison between the line positions resulting from the full log derivative–MQDT hybrid calculation and the model in this energy region show that the model follows the pattern of line positions closely, with only a comparatively small and almost constant off-set (Fig. 4).
1Σ+g and the ion-pair potential (see Section 4). A comparison between the line positions resulting from the full log derivative–MQDT hybrid calculation and the model in this energy region show that the model follows the pattern of line positions closely, with only a comparatively small and almost constant off-set (Fig. 4).
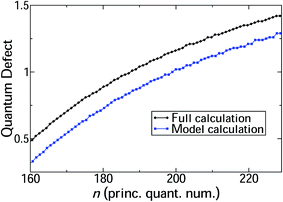 |
| | Fig. 4 Quantum defects for J = 0 HR states in the range n = 160–230 calculated using the full log derivative/MQDT approach outlined in the article, as well as a simple diabatic model (see text for details). The model calculations follow the trend for the full calculation closely. | |
It therefore appears that a large portion of the energy dependence in the quantum defect, μ(E), can be attributed to the vibrational wavefunction accumulating phase on the diabatic H![[H with combining macron]](https://www.rsc.org/images/entities/char_0048_0304.gif) potential. The model diabatic potential and a bound state on that potential are shown in Fig. 5. Note that states on the model potential are technically bound states, and that the model in its current form cannot make predictions of line widths. Given the importance of interferometric lifetime modulation in HR states, and the complexity of the H2 potentials in the interaction region, it is doubtful that a meaningful simplified model could be constructed for the lifetimes (widths).
potential. The model diabatic potential and a bound state on that potential are shown in Fig. 5. Note that states on the model potential are technically bound states, and that the model in its current form cannot make predictions of line widths. Given the importance of interferometric lifetime modulation in HR states, and the complexity of the H2 potentials in the interaction region, it is doubtful that a meaningful simplified model could be constructed for the lifetimes (widths).
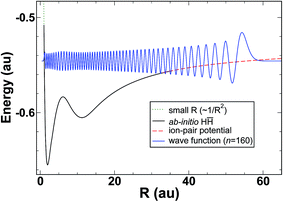 |
| | Fig. 5 Effective potential (merged H![[H with combining macron]](https://www.rsc.org/images/entities/char_0048_0304.gif) and ion-pair potential) together with the bound n = 160 radial wavefunction. and ion-pair potential) together with the bound n = 160 radial wavefunction. | |
We now proceed to the part of the HR spectrum just below the ion-pair dissociation limit. Using the hybrid log derivative–MQDT approach we calculate a narrow range with principal quantum number 1990 < n < 2010 as shown in Fig. 6 for total angular momenta J = 0, 1, and 2. The line positions are quite regular, with nearly constant quantum defects μ(E) across the range. The widths, on the other hand, exhibit modulation across the range, with different variation in line widths for the different angular momenta J = 0, 1, 2. The calculated width for the state n = 2000 is 5 × 10−4 cm−1, corresponding to a lifetime of approximately 10 ns. This is almost an order of magnitude shorter than the observed lifetimes reported by Ubachs et al.4 Since one would normally expect the calculations to over-estimate lifetimes on the basis that not all decay channels are included in the calculations, this lends support to the notion that such high-n HR states have a strong tendency to undergo J-mixing by external fields, analogous to the l-mixing that occurs in electronic zero electron kinetic energy (ZEKE) spectroscopy.
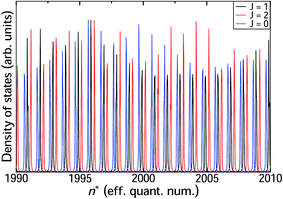 |
| | Fig. 6 Progression of heavy Rydberg resonances around the principal quantum number n = 2000 for J = 0, 1 and 2. These states have classical turning points at around Rtp = 8700 a.u. | |
Term values of the vibrational levels supported by the adiabatic H![[H with combining macron]](https://www.rsc.org/images/entities/char_0048_0304.gif) potential of Wolniewicz have been calculated up to ν = 39 (Eb = 8000 cm−1) and we include a complete table of resonances in the energy region Eb = 1800–6000 cm−1(ESI†) calculated by solving the close-coupled equations for seven 1Σ+g states. If the vibrational numbering is known, the absolute quantum defect follows from −μ(Eb) = n* − ν − 1 − J, where
potential of Wolniewicz have been calculated up to ν = 39 (Eb = 8000 cm−1) and we include a complete table of resonances in the energy region Eb = 1800–6000 cm−1(ESI†) calculated by solving the close-coupled equations for seven 1Σ+g states. If the vibrational numbering is known, the absolute quantum defect follows from −μ(Eb) = n* − ν − 1 − J, where 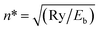 . Such μ(Eb) plots, both from model potentials and experimentally, for a wide range of ion-pair states have been shown to be nearly linear over a wide range of Eb values as the dissociation limit is approached. Thus, if experimental Tv values are used from fragmentary spectra in which the absolute vibrational numbering is not known, ν is adjusted so that the ν(Eb) values for a partial progression lie on the μ(Eb) plot extrapolated from regions of known numbering. If the numbering is changed by ±1, clear discontinuities in the sections of the μ(Eb) plot result.
. Such μ(Eb) plots, both from model potentials and experimentally, for a wide range of ion-pair states have been shown to be nearly linear over a wide range of Eb values as the dissociation limit is approached. Thus, if experimental Tv values are used from fragmentary spectra in which the absolute vibrational numbering is not known, ν is adjusted so that the ν(Eb) values for a partial progression lie on the μ(Eb) plot extrapolated from regions of known numbering. If the numbering is changed by ±1, clear discontinuities in the sections of the μ(Eb) plot result.
The various calculated μ(Eb) values for the H![[H with combining macron]](https://www.rsc.org/images/entities/char_0048_0304.gif) state are summarized in Fig. 7. The high vibrational levels presented in this paper cover the range Eb = 25.5–25 cm−1 and, if positioned on the extrapolated μ(Eb) plot, indicate a quantum defect of −63.8 at Eb 25 cm−1. The condition n ≫ μ is sometimes taken to define HR behaviour, and this is certainly fulfilled by the levels in Fig. 7. The broader μ(Eb) dependence in Fig. 7 indicates that there is no abrupt transition from a HR region to one deeper in the potential well in which the vibrational spacing becomes sensitive to the position of the inner wall of the potential, even after interruptions by avoided crossings that predissociate parts of the progression. In the H
state are summarized in Fig. 7. The high vibrational levels presented in this paper cover the range Eb = 25.5–25 cm−1 and, if positioned on the extrapolated μ(Eb) plot, indicate a quantum defect of −63.8 at Eb 25 cm−1. The condition n ≫ μ is sometimes taken to define HR behaviour, and this is certainly fulfilled by the levels in Fig. 7. The broader μ(Eb) dependence in Fig. 7 indicates that there is no abrupt transition from a HR region to one deeper in the potential well in which the vibrational spacing becomes sensitive to the position of the inner wall of the potential, even after interruptions by avoided crossings that predissociate parts of the progression. In the H![[H with combining macron]](https://www.rsc.org/images/entities/char_0048_0304.gif) state, the potential has a potential maximum at Eb ∼ 12
state, the potential has a potential maximum at Eb ∼ 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 and the vibrational numbering to larger Eb is that of the outer well only, whose outer wall continues initially to have a dominantly coulombic potential.
000 cm−1 and the vibrational numbering to larger Eb is that of the outer well only, whose outer wall continues initially to have a dominantly coulombic potential.
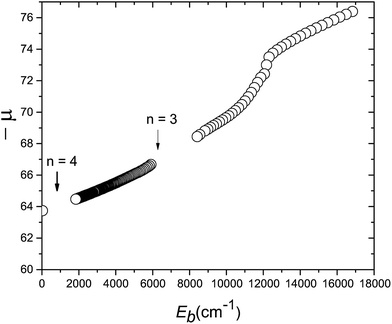 |
| | Fig. 7 Quantum defect plot for the vibrational levels of the H![[H with combining macron]](https://www.rsc.org/images/entities/char_0048_0304.gif) 1Σ+g state for ν′ = 0 up to ν′ = 2010. The absolute quantum defects, −μ(Eb), are plotted as a function of the binding energy Eb below the ion-pair dissociation limit. Previously calculated term values for ν′ = 0–40 are taken from ref. 54. The break in slope at Eb ≈ 13 1Σ+g state for ν′ = 0 up to ν′ = 2010. The absolute quantum defects, −μ(Eb), are plotted as a function of the binding energy Eb below the ion-pair dissociation limit. Previously calculated term values for ν′ = 0–40 are taken from ref. 54. The break in slope at Eb ≈ 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 corresponds to the top of the barrier between the electronic and heavy Rydberg potentials (ν′ = 16). Calculated resonances lie between Eb = 2000 and 6000 cm−1 (see the ESI†). The highest energy resonances, close to the ion-pair dissociation limit, are indicated by the extrapolated point close to the vertical axis (Eb ≈ 25 cm−1). Note that the point on the y-axis corresponds to the states shown in detail in Fig. 6. Finally, the position of the crossings for n = 3 and n = 4 limits are indicated by arrows. 000 cm−1 corresponds to the top of the barrier between the electronic and heavy Rydberg potentials (ν′ = 16). Calculated resonances lie between Eb = 2000 and 6000 cm−1 (see the ESI†). The highest energy resonances, close to the ion-pair dissociation limit, are indicated by the extrapolated point close to the vertical axis (Eb ≈ 25 cm−1). Note that the point on the y-axis corresponds to the states shown in detail in Fig. 6. Finally, the position of the crossings for n = 3 and n = 4 limits are indicated by arrows. | |
6 Conclusions
The vibrational energy levels of the H![[H with combining macron]](https://www.rsc.org/images/entities/char_0048_0304.gif) state of H2 have been calculated very close to dissociation, between the n = 3 and n = 4 asymptotes, under fully coupled conditions with the six other 1Σ+g states. All of the H
state of H2 have been calculated very close to dissociation, between the n = 3 and n = 4 asymptotes, under fully coupled conditions with the six other 1Σ+g states. All of the H![[H with combining macron]](https://www.rsc.org/images/entities/char_0048_0304.gif) levels are subject to weak predissociation into the H + H* (n = 3) channel and their widths indicate lifetimes ∼10 ns (n ∼ 2000) arising from this. The absolute quantum defects associated with these levels are close to 64 and, with n ∼ 2000, they clearly can be classified as heavy Rydberg states.
levels are subject to weak predissociation into the H + H* (n = 3) channel and their widths indicate lifetimes ∼10 ns (n ∼ 2000) arising from this. The absolute quantum defects associated with these levels are close to 64 and, with n ∼ 2000, they clearly can be classified as heavy Rydberg states.
The calculations presented here complete the sequence of HR vibrational levels associated with the EF1Σ+g and H![[H with combining macron]](https://www.rsc.org/images/entities/char_0048_0304.gif) 1Σ+g states, the observed resonance structure and the higher n1Σ+g states that are bound by the Coulomb potential. This is the first report of HR states above the n = 4 limit. HR behavior has now been observed from ν = 0 of the outer F1Σ+g potential, through the vibrational levels of the H
1Σ+g states, the observed resonance structure and the higher n1Σ+g states that are bound by the Coulomb potential. This is the first report of HR states above the n = 4 limit. HR behavior has now been observed from ν = 0 of the outer F1Σ+g potential, through the vibrational levels of the H![[H with combining macron]](https://www.rsc.org/images/entities/char_0048_0304.gif) 1Σ+g state and up to within ≈25 cm−1 of the ion-pair dissociation limit.
1Σ+g state and up to within ≈25 cm−1 of the ion-pair dissociation limit.
The analogous vibrational systems in the 1Σ+u manifold have been shown to have HR character from ν = 0 of the B1Σ+g state, through the B![[B with combining macron]](https://www.rsc.org/images/entities/char_0042_0304.gif) 1Σ+u state, and diabatically through the n = 3 asymptote up to the limit of the published resonance structure. However, the region between the n = 4 asymptote and the ion-pair dissociation limit for the 1Σ+u manifold remains to be investigated.
1Σ+u state, and diabatically through the n = 3 asymptote up to the limit of the published resonance structure. However, the region between the n = 4 asymptote and the ion-pair dissociation limit for the 1Σ+u manifold remains to be investigated.
Work is underway to include ionisation by coupling the inner-most region (R < 10 a.u.) to the electronic continuum via a generalised R-matrix approach. The conceptual framework for incorporating ionisation and dissociation within an R-matrix formalism is already established.55–58 Judging by the present calculations, the effect of including ionisation on the line positions will be comparatively minor. In contrast, one should expect the effect on the line widths to be more significant, and a full account of the mixing with electronic Rydberg states will provide an understanding of how valence and electronic Rydberg states channel excitation intensity to heavy Rydberg states.
Conflicts of interest
There are no conflicts of interest to declare.
Acknowledgements
A. K. acknowledges support from a Royal Society of Edinburgh Sabbatical Fellowship (58507).
References
- K. S. Kleinbach, F. Engel, T. Dieterle, R. Löw, T. Pfau and F. Meinert, Phys. Rev. Lett., 2018, 120, 193401 CrossRef CAS PubMed.
- C. Asaro and A. Dalgarno, Chem. Phys. Lett., 1985, 118, 64–66 CrossRef CAS.
- S. Pan and F. H. Mies, J. Chem. Phys., 1988, 89, 3096 CrossRef CAS.
- E. Reinhold and W. Ubachs, Phys. Rev. Lett., 2002, 88, 013001 CrossRef CAS PubMed.
- R. C. Shiell, E. Reinhold, F. Magnus and W. Ubachs, Phys. Rev. Lett., 2005, 95, 213002 CrossRef CAS PubMed.
- E. Reinhold and W. Ubachs, Mol. Phys., 2005, 103, 1329–1352 CrossRef CAS.
- M. O. Vieitez, T. I. Ivanov, E. Reinhold, C. A. de Lange and W. Ubachs, Phys. Rev. Lett., 2008, 101, 163001 CrossRef CAS PubMed.
- M. O. Vieitez, T. I. Ivanov, E. Reinhold, C. A. de Lange and W. Ubachs, J. Phys. Chem. A, 2009, 113, 13237 CrossRef CAS PubMed.
- E. E. Marinero, R. Vasudev and R. N. Zare, J. Chem. Phys., 1983, 78, 692–699 CrossRef CAS.
- K. P. Lawley and R. J. Donovan, J. Chem. Soc., Faraday Trans., 1993, 89, 1885 RSC.
- S. Yu and K. Dressler, J. Chem. Phys., 1994, 101, 7692 CrossRef CAS.
- L. Wolniewicz and K. Dressler, J. Chem. Phys., 1994, 100, 444 CrossRef CAS.
- E. Reinhold, W. Hogervorst and W. Ubachs, Phys. Rev. Lett., 1997, 78, 2543 CrossRef CAS.
- E. Reinhold, W. Hogervorst and W. Ubachs, Chem. Phys. Lett., 1998, 296, 411 CrossRef CAS.
- E. Reinhold, W. Hogervorst, W. Ubachs and L. Wolniewicz, Phys. Rev. A: At., Mol., Opt. Phys., 1999, 60, 1258–1270 CrossRef CAS.
- M. Cannon, C. Wang and F. Dunning, Chem. Phys. Lett., 2009, 479, 30 CrossRef CAS.
- S. Mollet and F. Merkt, Phys. Rev. A: At., Mol., Opt. Phys., 2010, 82, 032510 CrossRef.
- M. Cannon, C. H. Wang, F. B. Dunning and C. O. Reinhold, J. Chem. Phys., 2010, 133, 064301 CrossRef CAS PubMed.
- A. Kirrander, J. Chem. Phys., 2010, 133, 121103 CrossRef PubMed.
- A. Kirrander and Ch. Jungen, Phys. Rev. A: At., Mol., Opt. Phys., 2011, 84, 052512 CrossRef.
- R. C. Ekey Jr and E. F. McCormack, Phys. Rev. A: At., Mol., Opt. Phys., 2011, 84, 020501 CrossRef.
- R. J. Donovan, K. P. Lawley and T. Ridley, J. Chem. Phys., 2015, 142, 204306 CrossRef PubMed.
- R. J. Donovan, K. P. Lawley and T. Ridley, Chem. Phys., 2015, 463, 145–148 CrossRef CAS.
- K. P. Lawley and R. J. Donovan, Chem. Phys. Lett., 2016, 659, 192–195 CrossRef CAS.
- A. M. Chartrand, R. J. Donovan, K. P. Lawley and E. F. McCormack, Chem. Phys. Lett., 2017, 676, 140–143 CrossRef CAS.
-
Ch. Jungen, Handbook of High-resolution Spectroscopy, Wiley, 2010 Search PubMed.
- F. H. Mies, J. Chem. Phys., 1984, 80, 2514 CrossRef CAS.
- F. H. Mies and P. S. Julienne, J. Chem. Phys., 1984, 80, 2526 CrossRef CAS.
- T. S. Rose, M. J. Rosker and A. H. Zewail, J. Chem. Phys., 1988, 88, 6672–6673 CrossRef CAS.
- T. S. Rose, M. J. Rosker and A. H. Zewail, J. Chem. Phys., 1989, 91, 7415–7436 CrossRef CAS.
- S. E. Choi and J. C. Light, J. Chem. Phys., 1989, 90, 2593–2604 CrossRef CAS.
- V. Engel and H. Metiu, J. Chem. Phys., 1989, 90, 6116–6128 CrossRef CAS.
- S. Chapman and M. S. Child, J. Phys. Chem., 1991, 95, 578 CrossRef CAS.
- S. T. Cornett, H. R. Sadeghpour and M. J. Cavagnero, Phys. Rev. Lett., 1999, 82, 2488 CrossRef CAS.
- N. Balakrishnan, B. D. Esry, H. R. Sadeghpour, S. T. Cornett and M. J. Cavagnero, Phys. Rev. A: At., Mol., Opt. Phys., 1999, 60, 1407 CrossRef CAS.
- A. Kirrander, S. Rittenhouse, M. Ascoli, E. E. Eyler, P. L. Gould and H. R. Sadeghpour, Phys. Rev. A: At., Mol., Opt. Phys., 2013, 87, 031402 CrossRef.
- M. Stenrup, Å. Larson and N. Elander, Phys. Rev. A: At., Mol., Opt. Phys., 2009, 79, 012713 CrossRef.
- L. Wolniewicz, J. Chem. Phys., 1998, 108, 1499 CrossRef CAS.
-
T. F. Gallagher, Rydberg Atoms, Cambridge University Press, 1st edn, 1994 Search PubMed.
- F. Mrugala and D. Secrest, J. Chem. Phys., 1983, 79, 5960 CrossRef CAS.
- P. Quadrelli, K. Dressler and L. Wolniewicz, J. Chem. Phys., 1990, 92, 7461 CrossRef CAS.
-
D. E. Manolopoulos, PhD thesis, University of Cambridge, Cambridge, 1988.
- D. E. Manolopoulos, J. Chem. Phys., 1986, 85, 6425 CrossRef CAS.
- J. M. Hutson, Comput. Phys. Commun., 1994, 84, 1 CrossRef CAS.
- Ch. Jungen and F. Texier, J. Phys. B: At., Mol. Opt. Phys., 2000, 33, 2495 CrossRef CAS.
- C. H. Greene and Ch. Jungen, Adv. At. Mol. Phys., 1985, 21, 51 CAS.
- T. Detmer, P. Schmelcher and L. S. Cederbaum, J. Chem. Phys., 1998, 109, 9694 CrossRef CAS.
- A. S. Dickinson and F. X. Gadea, Phys. Rev. A: At., Mol., Opt. Phys., 2002, 65, 052506 CrossRef.
- A. S. Dickinson and F. X. Gadea, J. Mol. Struct.: THEOCHEM, 2003, 621, 87 CrossRef CAS.
- C. L. Pekeris, Phys. Rev., 1962, 126, 1470 CrossRef CAS.
- A. Dalgarno, Adv. Phys., 1962, 11, 281 CrossRef CAS.
-
A. A. Radtzig and B. M. Smirnov, Reference Data on Atoms, Molecules, and Ions, Springer-Verlag, 1985 Search PubMed.
- G. Staszewska and L. Wolniewicz, J. Mol. Spectrosc., 2002, 212, 208 CrossRef CAS.
- L. Wolniewicz and K. Dressler, J. Chem. Phys., 1985, 82, 3292–3299 CrossRef CAS.
- A. Kirrander, H. H. Fielding and Ch. Jungen, J. Chem. Phys., 2007, 127, 164301 CrossRef CAS PubMed.
- A. Kirrander, H. H. Fielding and Ch. Jungen, J. Chem. Phys., 2010, 132, 024313 CrossRef CAS PubMed.
- A. Kirrander, Ch. Jungen and H. H. Fielding, Phys. Chem. Chem. Phys., 2010, 12, 8948 RSC.
- A. Kirrander, Ch. Jungen and H. H. Fielding, J. Phys. B, 2008, 41(7), 074022 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8fd00096d |
| ‡ Calculated numerically by inwards integration, see Jungen and Texier.45 |
| § Note that the electron affinity can be calculated as Eea = DH+H− − EH− − EH and that the value of the electron affinity obtained this way differs somewhat from the value −0.0277196153 a.u. reported by Radtzig et al.52 |
|
| This journal is © The Royal Society of Chemistry 2018 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Christian
Jungen
b,
Robert J.
Donovan
a and
Kenneth P.
Lawley
a
*a,
Christian
Jungen
b,
Robert J.
Donovan
a and
Kenneth P.
Lawley
a
![[H with combining macron]](https://www.rsc.org/images/entities/char_0048_0304.gif) 1Σ+g state, located only 25 cm−1 below the ion-pair dissociation limit, are reported. The calculations are done using a hybrid log derivative/multichannel quantum defect approach that accounts for predissociation and is capable of dealing with any number of long-range closed channels, and of providing positions and widths for the heavy Rydberg resonances. In this case, resonance positions can be reproduced qualitatively using a simple diabatic model (however, the resonance widths cannot). Absolute quantum defects are derived for the vibrational series ranging from ν = 0 to ν = 2010. The influence of the Coulomb potential and continuity of heavy Rydberg behavior throughout the 1Σ+g manifold of states is demonstrated.
1Σ+g state, located only 25 cm−1 below the ion-pair dissociation limit, are reported. The calculations are done using a hybrid log derivative/multichannel quantum defect approach that accounts for predissociation and is capable of dealing with any number of long-range closed channels, and of providing positions and widths for the heavy Rydberg resonances. In this case, resonance positions can be reproduced qualitatively using a simple diabatic model (however, the resonance widths cannot). Absolute quantum defects are derived for the vibrational series ranging from ν = 0 to ν = 2010. The influence of the Coulomb potential and continuity of heavy Rydberg behavior throughout the 1Σ+g manifold of states is demonstrated.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atom condensate.1
000 atom condensate.1
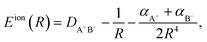
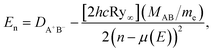
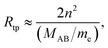
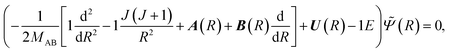
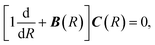
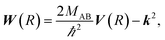
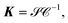
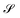 and
and 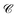 are N × N matrices, and the coefficient matrix Z as
are N × N matrices, and the coefficient matrix Z as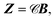
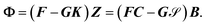
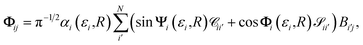
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Rf → ∞ at energy εi.‡ At large distances R → ∞ the wave function must be zero in closed channels, meaning that
Rf → ∞ at energy εi.‡ At large distances R → ∞ the wave function must be zero in closed channels, meaning that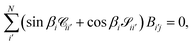
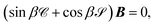
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β and cos
β and cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β diagonal N × N matrices with elements (sin
β diagonal N × N matrices with elements (sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β)ii = sin
β)ii = sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β(εi).
β(εi).
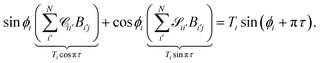
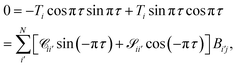
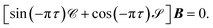
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) πτΛB,
πτΛB,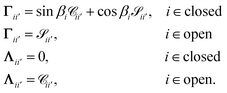
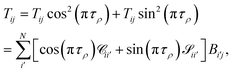
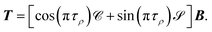
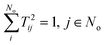 . This condition fixes the overall normalization of the N coefficients Bij for each j.
. This condition fixes the overall normalization of the N coefficients Bij for each j.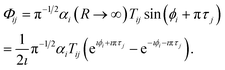
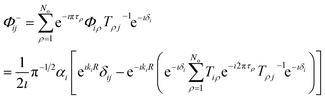
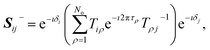
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) πτ + SB
πτ + SB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) πτ. The matrix S−(E) will have strong energy-dependence reflective of the sharp long-range resonances, characterized by rapid change in the total eigenphase of the scattering matrix. The positions of the resonances can be obtained from the derivative of the cumulative eigenphase,
πτ. The matrix S−(E) will have strong energy-dependence reflective of the sharp long-range resonances, characterized by rapid change in the total eigenphase of the scattering matrix. The positions of the resonances can be obtained from the derivative of the cumulative eigenphase, 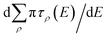 , and the width is obtained from the full width at half maximum (FWHM) for each peak. The positions of the peaks allow us to determine the value of the quantum defect by reference to eqn (2). The shifts compared to the pure Coulomb potential are expressed in terms of either the quantum defect itself, μ(E), or equivalently the effective quantum number, n* = n − μ(E).
, and the width is obtained from the full width at half maximum (FWHM) for each peak. The positions of the peaks allow us to determine the value of the quantum defect by reference to eqn (2). The shifts compared to the pure Coulomb potential are expressed in terms of either the quantum defect itself, μ(E), or equivalently the effective quantum number, n* = n − μ(E).

![[H with combining macron]](https://www.rsc.org/images/entities/char_0048_0304.gif) 1Σgab initio adiabatic state calculated by Wolniewicz38 and the asymptotic ion-pair potential in eqn (1).50,51 The potentials are merged as follows,
1Σgab initio adiabatic state calculated by Wolniewicz38 and the asymptotic ion-pair potential in eqn (1).50,51 The potentials are merged as follows,![[H with combining macron]](https://www.rsc.org/images/entities/char_0048_0304.gif) (R),
(R),![[H with combining macron]](https://www.rsc.org/images/entities/char_0048_0304.gif) 1Σ+g and the ion-pair potential (see Section 4). A comparison between the line positions resulting from the full log derivative–MQDT hybrid calculation and the model in this energy region show that the model follows the pattern of line positions closely, with only a comparatively small and almost constant off-set (Fig. 4).
1Σ+g and the ion-pair potential (see Section 4). A comparison between the line positions resulting from the full log derivative–MQDT hybrid calculation and the model in this energy region show that the model follows the pattern of line positions closely, with only a comparatively small and almost constant off-set (Fig. 4).![[H with combining macron]](https://www.rsc.org/images/entities/char_0048_0304.gif) potential. The model diabatic potential and a bound state on that potential are shown in Fig. 5. Note that states on the model potential are technically bound states, and that the model in its current form cannot make predictions of line widths. Given the importance of interferometric lifetime modulation in HR states, and the complexity of the H2 potentials in the interaction region, it is doubtful that a meaningful simplified model could be constructed for the lifetimes (widths).
potential. The model diabatic potential and a bound state on that potential are shown in Fig. 5. Note that states on the model potential are technically bound states, and that the model in its current form cannot make predictions of line widths. Given the importance of interferometric lifetime modulation in HR states, and the complexity of the H2 potentials in the interaction region, it is doubtful that a meaningful simplified model could be constructed for the lifetimes (widths).
![[H with combining macron]](https://www.rsc.org/images/entities/char_0048_0304.gif) and ion-pair potential) together with the bound n = 160 radial wavefunction.
and ion-pair potential) together with the bound n = 160 radial wavefunction.
![[H with combining macron]](https://www.rsc.org/images/entities/char_0048_0304.gif) potential of Wolniewicz have been calculated up to ν = 39 (Eb = 8000 cm−1) and we include a complete table of resonances in the energy region Eb = 1800–6000 cm−1(ESI†) calculated by solving the close-coupled equations for seven 1Σ+g states. If the vibrational numbering is known, the absolute quantum defect follows from −μ(Eb) = n* − ν − 1 − J, where
potential of Wolniewicz have been calculated up to ν = 39 (Eb = 8000 cm−1) and we include a complete table of resonances in the energy region Eb = 1800–6000 cm−1(ESI†) calculated by solving the close-coupled equations for seven 1Σ+g states. If the vibrational numbering is known, the absolute quantum defect follows from −μ(Eb) = n* − ν − 1 − J, where 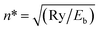 . Such μ(Eb) plots, both from model potentials and experimentally, for a wide range of ion-pair states have been shown to be nearly linear over a wide range of Eb values as the dissociation limit is approached. Thus, if experimental Tv values are used from fragmentary spectra in which the absolute vibrational numbering is not known, ν is adjusted so that the ν(Eb) values for a partial progression lie on the μ(Eb) plot extrapolated from regions of known numbering. If the numbering is changed by ±1, clear discontinuities in the sections of the μ(Eb) plot result.
. Such μ(Eb) plots, both from model potentials and experimentally, for a wide range of ion-pair states have been shown to be nearly linear over a wide range of Eb values as the dissociation limit is approached. Thus, if experimental Tv values are used from fragmentary spectra in which the absolute vibrational numbering is not known, ν is adjusted so that the ν(Eb) values for a partial progression lie on the μ(Eb) plot extrapolated from regions of known numbering. If the numbering is changed by ±1, clear discontinuities in the sections of the μ(Eb) plot result.![[H with combining macron]](https://www.rsc.org/images/entities/char_0048_0304.gif) state are summarized in Fig. 7. The high vibrational levels presented in this paper cover the range Eb = 25.5–25 cm−1 and, if positioned on the extrapolated μ(Eb) plot, indicate a quantum defect of −63.8 at Eb 25 cm−1. The condition n ≫ μ is sometimes taken to define HR behaviour, and this is certainly fulfilled by the levels in Fig. 7. The broader μ(Eb) dependence in Fig. 7 indicates that there is no abrupt transition from a HR region to one deeper in the potential well in which the vibrational spacing becomes sensitive to the position of the inner wall of the potential, even after interruptions by avoided crossings that predissociate parts of the progression. In the H
state are summarized in Fig. 7. The high vibrational levels presented in this paper cover the range Eb = 25.5–25 cm−1 and, if positioned on the extrapolated μ(Eb) plot, indicate a quantum defect of −63.8 at Eb 25 cm−1. The condition n ≫ μ is sometimes taken to define HR behaviour, and this is certainly fulfilled by the levels in Fig. 7. The broader μ(Eb) dependence in Fig. 7 indicates that there is no abrupt transition from a HR region to one deeper in the potential well in which the vibrational spacing becomes sensitive to the position of the inner wall of the potential, even after interruptions by avoided crossings that predissociate parts of the progression. In the H![[H with combining macron]](https://www.rsc.org/images/entities/char_0048_0304.gif) state, the potential has a potential maximum at Eb ∼ 12
state, the potential has a potential maximum at Eb ∼ 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 and the vibrational numbering to larger Eb is that of the outer well only, whose outer wall continues initially to have a dominantly coulombic potential.
000 cm−1 and the vibrational numbering to larger Eb is that of the outer well only, whose outer wall continues initially to have a dominantly coulombic potential.
![[H with combining macron]](https://www.rsc.org/images/entities/char_0048_0304.gif) 1Σ+g state for ν′ = 0 up to ν′ = 2010. The absolute quantum defects, −μ(Eb), are plotted as a function of the binding energy Eb below the ion-pair dissociation limit. Previously calculated term values for ν′ = 0–40 are taken from ref. 54. The break in slope at Eb ≈ 13
1Σ+g state for ν′ = 0 up to ν′ = 2010. The absolute quantum defects, −μ(Eb), are plotted as a function of the binding energy Eb below the ion-pair dissociation limit. Previously calculated term values for ν′ = 0–40 are taken from ref. 54. The break in slope at Eb ≈ 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 corresponds to the top of the barrier between the electronic and heavy Rydberg potentials (ν′ = 16). Calculated resonances lie between Eb = 2000 and 6000 cm−1 (see the ESI†). The highest energy resonances, close to the ion-pair dissociation limit, are indicated by the extrapolated point close to the vertical axis (Eb ≈ 25 cm−1). Note that the point on the y-axis corresponds to the states shown in detail in Fig. 6. Finally, the position of the crossings for n = 3 and n = 4 limits are indicated by arrows.
000 cm−1 corresponds to the top of the barrier between the electronic and heavy Rydberg potentials (ν′ = 16). Calculated resonances lie between Eb = 2000 and 6000 cm−1 (see the ESI†). The highest energy resonances, close to the ion-pair dissociation limit, are indicated by the extrapolated point close to the vertical axis (Eb ≈ 25 cm−1). Note that the point on the y-axis corresponds to the states shown in detail in Fig. 6. Finally, the position of the crossings for n = 3 and n = 4 limits are indicated by arrows.![[H with combining macron]](https://www.rsc.org/images/entities/char_0048_0304.gif) state of H2 have been calculated very close to dissociation, between the n = 3 and n = 4 asymptotes, under fully coupled conditions with the six other 1Σ+g states. All of the H
state of H2 have been calculated very close to dissociation, between the n = 3 and n = 4 asymptotes, under fully coupled conditions with the six other 1Σ+g states. All of the H![[H with combining macron]](https://www.rsc.org/images/entities/char_0048_0304.gif) levels are subject to weak predissociation into the H + H* (n = 3) channel and their widths indicate lifetimes ∼10 ns (n ∼ 2000) arising from this. The absolute quantum defects associated with these levels are close to 64 and, with n ∼ 2000, they clearly can be classified as heavy Rydberg states.
levels are subject to weak predissociation into the H + H* (n = 3) channel and their widths indicate lifetimes ∼10 ns (n ∼ 2000) arising from this. The absolute quantum defects associated with these levels are close to 64 and, with n ∼ 2000, they clearly can be classified as heavy Rydberg states.
![[H with combining macron]](https://www.rsc.org/images/entities/char_0048_0304.gif) 1Σ+g states, the observed resonance structure and the higher n1Σ+g states that are bound by the Coulomb potential. This is the first report of HR states above the n = 4 limit. HR behavior has now been observed from ν = 0 of the outer F1Σ+g potential, through the vibrational levels of the H
1Σ+g states, the observed resonance structure and the higher n1Σ+g states that are bound by the Coulomb potential. This is the first report of HR states above the n = 4 limit. HR behavior has now been observed from ν = 0 of the outer F1Σ+g potential, through the vibrational levels of the H![[H with combining macron]](https://www.rsc.org/images/entities/char_0048_0304.gif) 1Σ+g state and up to within ≈25 cm−1 of the ion-pair dissociation limit.
1Σ+g state and up to within ≈25 cm−1 of the ion-pair dissociation limit.![[B with combining macron]](https://www.rsc.org/images/entities/char_0042_0304.gif) 1Σ+u state, and diabatically through the n = 3 asymptote up to the limit of the published resonance structure. However, the region between the n = 4 asymptote and the ion-pair dissociation limit for the 1Σ+u manifold remains to be investigated.
1Σ+u state, and diabatically through the n = 3 asymptote up to the limit of the published resonance structure. However, the region between the n = 4 asymptote and the ion-pair dissociation limit for the 1Σ+u manifold remains to be investigated.


