Implications of flexible spacer rotational processes on the liquid crystal behavior of 4,5-dihydroisoxazole benzoate dimers†
Aline
Tavares
*a,
Josene M.
Toldo
a,
Guilherme D.
Vilela
a,
Paulo F. B.
Gonçalves
a,
Ivan H.
Bechtold
b,
Stuart P.
Kitney
c,
Stephen M.
Kelly
d and
Aloir A.
Merlo
*a
aInstitute of Chemistry, UFRGS, Porto Alegre, RS, Brazil. E-mail: aloir.merlo@ufrgs.br
bDepartment of Physics, UFSC, Florianópolis, Brazil
cPolar OLED, University of Hull, Hull, England, UK
dDepartment of Chemistry, University of Hull, Hull, UK
First published on 21st October 2015
Abstract
The synthesis of some novel non-symmetric liquid crystal dimers, {3-[4-(octyloxyphenyl)]-4,5-dihydroisoxazol-5-yl}alkyl 4-(decyloxy)benzoates (5a–d) and 4-{3-[4-(octyloxyphenyl)]-4,5-dihydroisoxazol-5-yl}alkyl 4-{[6-(octyloxy)naphthalen-2-yl]ethynyl}benzoate (9a–d), are reported. The liquid-crystalline properties, theoretical calculations based on the conformational aspects of the flexible alkyl spacer and X-ray experiments are discussed. The syntheses of the key intermediates, 2-{3-[4-(octyloxy)phenyl]-4,5-dihydroisoxazol-5-yl}alkanol (3a–d), presenting the flexible alkyl spacer were achieved through [3+2] cycloaddition reactions between nitrile oxides, which were generated in situ by oxidation of the respective aromatic oximes, and dipolarophile alkenols (CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH(CH2)nOH, n = 1, 2, 3, and 4). The benzoates 5a–d were synthesized through esterification of 3a–d and p-n-decyloxybenzoic acid (4). The esters 9a–d were synthesized through derivatization of isoxazolines 3a–d into 4-{3-[4-(octyloxyphenyl)]-4,5-dihydroisoxazol-5-yl}alkyl 4-bromobenzoate (7a–d) followed by a Sonogashira reaction with 2-ethynyl-6-octyloxynaphthalene (8). 5a and 5b showed a monotropic smectic C phase. 9a/c displayed a enantiotropic nematic (N) mesophase, whereas 9b/d showed a monotropic nematic mesophase. No mesophase was observed for 7a–d. An odd–even effect was observed for 5a–d and 9a–d associated with the crystal to isotropic phase transition and crystal to nematic phase, respectively, as the length of the spacer was increased from 1 to 4 carbon atoms. The transitional properties were higher for odd-numbered members (n = 1 and 3) for all of the series studied. The X-ray data of compounds 5a and 5b are in agreement with polarizing optical microscopy observations with the assignment of an SmC mesophase. Density functional theory calculations using the B3LYP hybrid functional with the level 6-311G(d,p) basis set were performed for molecules 5a–d to correlate the conformation of the flexible spacer and the transitional properties. The conformational analysis showed that the most stable conformation for 5a–d is one where all of the carbon atoms of the flexible spacer are orientated at 180° (antiperiplanar orientation) except for 5a because the spacer is too short. The odd-numbered members have a more bent shape and are less elongated molecules than the even-numbered members. Thus, mesomorphic behavior is dictated by the conformational constraint imposed by the flexible spacer on the mesogenic groups.
CH(CH2)nOH, n = 1, 2, 3, and 4). The benzoates 5a–d were synthesized through esterification of 3a–d and p-n-decyloxybenzoic acid (4). The esters 9a–d were synthesized through derivatization of isoxazolines 3a–d into 4-{3-[4-(octyloxyphenyl)]-4,5-dihydroisoxazol-5-yl}alkyl 4-bromobenzoate (7a–d) followed by a Sonogashira reaction with 2-ethynyl-6-octyloxynaphthalene (8). 5a and 5b showed a monotropic smectic C phase. 9a/c displayed a enantiotropic nematic (N) mesophase, whereas 9b/d showed a monotropic nematic mesophase. No mesophase was observed for 7a–d. An odd–even effect was observed for 5a–d and 9a–d associated with the crystal to isotropic phase transition and crystal to nematic phase, respectively, as the length of the spacer was increased from 1 to 4 carbon atoms. The transitional properties were higher for odd-numbered members (n = 1 and 3) for all of the series studied. The X-ray data of compounds 5a and 5b are in agreement with polarizing optical microscopy observations with the assignment of an SmC mesophase. Density functional theory calculations using the B3LYP hybrid functional with the level 6-311G(d,p) basis set were performed for molecules 5a–d to correlate the conformation of the flexible spacer and the transitional properties. The conformational analysis showed that the most stable conformation for 5a–d is one where all of the carbon atoms of the flexible spacer are orientated at 180° (antiperiplanar orientation) except for 5a because the spacer is too short. The odd-numbered members have a more bent shape and are less elongated molecules than the even-numbered members. Thus, mesomorphic behavior is dictated by the conformational constraint imposed by the flexible spacer on the mesogenic groups.
Introduction
Liquid crystal oligomers (LCOs) are a special class of soft materials formed of two or more anisotropic-shaped cores connected by flexible spacers, normally alkyl chains.1 The core is usually a mesogenic group and the simplest LCOs are termed dimers which have just two mesogenic units linked chemically to a single methylene chain.2 The first reports about liquid crystal dimers were by Vorländer3 at the beginning of the 1920s and by Rault4 some years later. However, these important reports appear to have been a forgotten past until the early 1980s, when they were rediscovered again and gained new interest.5 The vast majority of LCOs are composed of two symmetric rod-like mesogenic units,6 whereas their non-symmetrical analogues7 have two different mesogenic groups connected by a flexible alkyl chain and less frequently by oligo(ethyleneoxide),8 oligo(siloxane)9 and sulfur–sulfur links10 in the chain. In this context, the length and parity of the flexible spacer are important parameters that have a great influence on the transitional properties.11 Dimers and higher oligomers, such as trimers12–14 and tetramers,15,16 have a special level of attention due to their ability to act as model compounds for semi-flexible main-chain liquid crystal polymers.17,18 Also, from the academic point of view these oligomers are interesting because they behave differently to conventional liquid crystals of low molar mass.19,20Mostly, LCOs have an aryl group as the mesogenic unit and a few examples of LCOs incorporating 5- and 6-membered rings such as 1,3,4-oxadiazoles and pyridyl-based dimers respectively, have also been published, with their transitional properties having been investigated.21,22 Compounds containing a 4,5-dihydroisoxazole moiety have been prepared recently and the liquid crystalline behavior evaluated.23 To the best of our knowledge, however, there have been no examples of non-symmetric 4,5-dihydroisoxazole-based liquid crystal dimers reported in the literature.
We have previously reported24 the synthesis of liquid-crystalline 3,5-disubstituted isoxazolines, where the number of carbon atoms of the terminal aliphatic chains exerts a strong influence on the molecular shape and mesomorphic behavior. In this work, we report the synthesis and transitional properties of two new homologous series of non-symmetrical 3,5-disubstituted 4,5-dihydroisoxazole benzoate liquid crystal dimers with emphasis on the dependence of the liquid-crystalline transition temperatures on the number of methylene carbon atoms of the flexible spacer. Density functional theory (DFT) calculations combined with X-ray analysis provided supporting information in this study.
Results and discussion
Synthesis and description of liquid-crystalline behavior
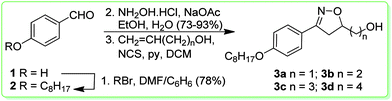
The synthetic route used for the preparation of the isoxazolines 3a–d is shown in Scheme 1. We selected the aldehyde 2 as a precursor for the reactive arylnitrile oxide.25 Thus, the aldehyde 2 was synthesized through alkylation of 4-hydroxybenzaldehyde 1 with octylbromide in 78% yield. The isoxazolines were obtained by a [3+2] 1,3-dipolar cycloaddition26 of nitrile oxide, formed by the in situ oxidation reaction of 4-octyloxybenzaldehyde oxime and four different dipolarophile alkenols – CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH(CH2)nOH, n = 1, 2, 3, and 4. The final key isoxazolines 3a–d were obtained in low yields (33–36%).
CH(CH2)nOH, n = 1, 2, 3, and 4. The final key isoxazolines 3a–d were obtained in low yields (33–36%).
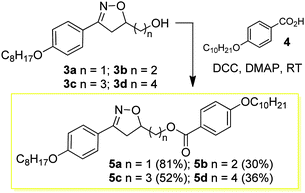
The design and synthesis of the liquid crystals 5a–d and 9a–d was based on creating the structural characteristics necessary for the occurrence of a mesophase through a short and quick synthesis. Thus, the first homologous series 5a–d, (see reaction Scheme 2) was prepared through the esterification of compounds 3a–d and 4-n-decyloxybenzoic acid 4 in the presence of DCC and catalytic amounts of DMAP in a THF solution at room temperature. The compounds 7a–d, prepared from the esterification reaction between compounds 3a–d and 4-bromobenzoic acid 6 in the presence of DCC and catalytic amounts of DMAP in THF, were precursors for the synthesis of the liquid-crystalline materials 9a–d. The yields reported for the compounds 5a–d and 7a–d refer to the pure compounds after purification via recrystallization or column chromatography to remove the undesirable byproduct urea.
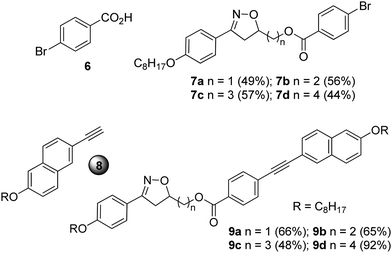
The compounds 9a–d were prepared using a Sonogashira cross-coupling reaction between the intermediates 7a–d and the terminal alkyne 827 in the presence of a palladium catalyst, i.e., (PPh3)2PdCl2, CuI, PPh3 in NEt3 (Chart 1).
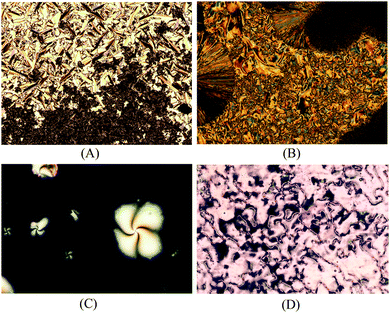
The mesophase identification for the LC compounds 5a–d as well as for 9a–d was made using polarizing optical microscopy (POM). The smectic C mesophase (SmC) was assigned through the observation of a typical broken fan texture (at the top of Fig. 1(A) for 5a) and a schlieren texture (at the bottom of Fig. 1(C) for 9b). For compound 5b, the mesophase SmC range was very narrow and it appears very quickly before the crystallization takes places [Fig. 1(B)]. The DSC traces for 5b display a shoulder along a peak related to the transition temperature of the crystal phase to the isotropic phase. The SmC mesophase for 5c and 5d was detected and the texture persists for just a few seconds followed by fast crystallization. No POM images or shoulders in the DSC traces for these compounds could be acquired. Identification of the nematic mesophase for compounds 9a–d was made from the observation of the typical schlieren texture with two- and four-point brushes and a planar texture [Fig. 1(C) and (D)]. The low enthalpy values associated with the transition of the nematic mesophase to the isotropic state corroborate this assignment (see Table 1).
| Entry | Transition phase temperatures | ΔT,e °C | Enthalpy, ΔH | Entropy, ΔS/Rg | ||
|---|---|---|---|---|---|---|
| Heating | Cooling | Meltf | I/phase/Cr | |||
| a Onset temperatures (Tonset). Data obtained from DSC (2nd cycle) with a rate of heating and cooling of 10 °C min−1; Cr = crystal phase, SmC = smectic C mesophase, N = nematic mesophase, and I = isotropic liquid. b Temperatures were obtained through optical microscopy. c SmC or d N mesophases were observed only on fast cooling – samples were exposed to room temperature. e Mesophase range upon cooling for compounds 5a–b and 9d and upon heating for 9a and 9c. For 9b the temperature range was too small to be measured. f Enthalpy values (second cycle heating/cooling) obtained in the Cr–I transition for the series 5a–d and the Cr–N transition for the series 9a–d. g Values of melting entropy obtained in the Cr–I transition for the series 5a–d and 9b/d and Cr–N for 9a/c. R = 8.31 J K−1 mol−1. | ||||||
| 5a | Cr 103 I | I 83 SmC 74 Cr | 9 | 17.9 | I/3.1 SmC/10.4 Cr | 24.0 |
| 5b | Cr 72 I | I 61 SmC 54 Cr | 7 | 8.7 | — | 12.5 |
| 5c | Cr 85 I | I 66 Crc | — | 23.0 | — | 32.4 |
| 5d | Cr 68 I | I 57 Crc | — | 13.4 | — | 19.5 |
| 7a | Cr 115 Ib | I 104 Cr | — | — | — | — |
| 7b | Cr 90 Ib | I 77 Cr | — | — | — | — |
| 7c | Cr 99 Ib | I 81 Cr | — | — | — | — |
| 7d | Cr 73 Ib | I 61 Cr | — | — | — | — |
| 9a | Cr 150 N 163 I | I 162 N 136 Cr | 13 | 13.0 | I/0.4 N/13.2 Cr | 15.4 |
| 9b | Cr 130 I | I Nd 120 Cr | — | 10.0 | I/—/10.5 Cr | 12.4 |
| 9c | Cr 136 N 145 I | I 144 N 126 Cr1 116 Cr2 | 9 | 9.3 | I/0.9 N/0.8 Cr1 8.5 Cr2 | 11.5 |
| 9d | Cr 130 I | I 122 N 112 Cr | 10 | 12.7 | I/0.5 N/11.5 Cr | 15.8 |
Compounds 5a–d are composed of two terminal alkyl chains – eight carbon atoms on the isoxazoline side and ten carbon atoms on the ester side. The number of carbon atoms in the flexible spacer was varied. So, compounds 5a–d have n = 1, 2, 3, and 4 in the flexible spacer, respectively.
The transition temperatures shown in Table 1 were obtained through a combination of POM and DSC analysis. Compounds 5a and 5b, upon a second cooling cycle, exhibit a monotropic phase with two exothermic peaks at 83 °C and 61 °C, respectively. These peaks were associated with the transition temperature when the samples enter the SmC mesophase from the isotropic state. Upon further cooling, 5a and 5b displayed a crystallization peak from the SmC mesophase, at 74 °C and 54 °C, respectively. For the higher homologues 5c and 5d, the DSC traces show only peaks related to the crystal phase to isotropic phase transition. However, samples of 5c and 5d when analyzed using POM upon fast cooling, displayed a monotropic SmC phase before recrystallization. For compounds that belong to the homologous series 9a–d the terminal alkyl chain was fixed at eight carbon atoms (n-octyl). The variation in the flexible spacer was made in the same way as described for 5a–d. According to the DSC data [Table 1, Fig. 1(C) and (D) and Fig. S31 (ESI†)], the 9a and 9c homologues of this series exhibit an enantiotropic nematic mesophase, while 9b and 9d display a monotropic nematic mesophase. When heated, the temperature range decreased by increasing the number of methylene units in the aliphatic chain, e.g., for 9a ΔT = 13 °C and for 9c ΔT = 9 °C. For 9b and 9d, a monotropic nematic mesophase was observed which was more persistent for 9d, whereas 9b displayed a nematic mesophase for a few seconds through quick cooling from the isotropic state to under room temperature. Under this circumstance the nematic mesophase grew along with the crystal formation.
Compounds 9a–d have a more pronounced rod-like or lath-like structure than compounds 5a–d and 7a–d and, consequently, they exhibit an enantiotropic mesophase at higher temperatures than compounds 5a–d.
The melting points for 5a–d, 7a–d and 9a–d displayed an odd–even effect as the length and parity of the flexible spacer was varied. The values of the melting point alternate as the length of the flexible spacer chain increase with odd-numbered members exhibiting higher values. The alternation is attenuated by increasing the spacer length. Values of the entropy associated with the melting points of 5a–d displayed the odd–even effect while those for 9a–d did not follow the tendency observed for 5a–d, probably due to the nature of the mesophase accompanying the crystal phase (Fig. 2). The melting processes followed the same tendency as noted for the melting points of the compounds.
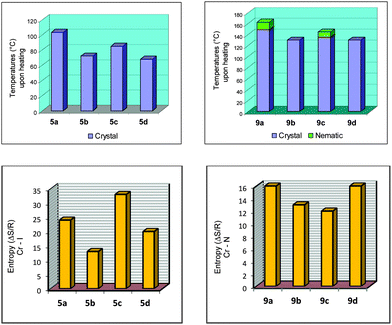 | ||
| Fig. 2 Bar graphs for 5a–d and 9a–d. Plots of temperatures (°C) upon heating (top) and entropy values for Cr → I for 5a–b and Cr → N for 9a–d (ΔS/R) (bottom). | ||
For the homologous series 9a–d the odd–even effect based on the mesomorphic behavior is also barely observed upon cooling the samples from the isotropic phase. A stable nematic mesophase was observed for 9a and 9c, however, for 9b and 9d the nematic mesophase was only visible during the cooling cycle. 9b displayed the N mesophase upon cooling with a very short period of time [Fig. 1(C)]. Upon cooling, all samples showed a nematic mesophase. The correlation between the length and parity of the flexible spacer is not an easy task to achieve considering that upon heating 9b and 9d did not display mesomorphic behavior. The influence of the flexible spacer for compounds 9a–d is more visible and more pronounced due to the more anisotropic shape of the molecules of this series than the series 5a–d. The naphthyl group connected by triple bond to the benzoate moiety induces the formation of a stable mesophase when compared to the series 5a–d. However, a conformational issue associated with the methylene chain flexible spacer alters the molecular packing in the mesophase, and consequently induces a dependence of the intermolecular interaction between the aromatic ring and the size of the flexible spacer. When we move along the carbon skeleton of the flexible spacer, the aromatic rings rotate around the last carbon bond to produce a set of distinct conformations for 9a/c and 9b/d (see the Theoretical calculations section). Obviously, the transitional properties analysis in this article suffers a drawback because the nematic phase behavior is only stable for 9a and 9c. However, upon heating or cooling the melting points exhibit an even–odd effect as shown in Fig. 2 for the 5a–d and 9a–d series. The odd-numbered members have the highest values (9a and 9c) and the even-numbered members have the lowest values (9b and 9d). The odd-numbered members displayed higher values of melting point than the even-numbered members.
The dependence of the entropy changes associated with the nematic crystal-isotropic transition on the number of methylene units (n) present in the flexible spacer of non-dimeric LC 9a–d does not follow a regular tendency due to the nature of the nematic phase observed in this series of liquid crystals (Fig. 2, bottom). Anyway, it is possible to state that the differences between odd and even membered dimers reflect, at least, the difference in their average molecular shapes, which are governed to a large extent by the parity of the flexible spacer.1
Transitions from a more ordered mesophase to the isotropic state have higher entropy than transitions between a disordered phase to the isotropic state. Less ordered phases, such as the nematic phase, display lower entropy values and consequently, when they undergo a transition to the isotropic liquid state are less sensitive to structural parameters, such as variation in the flexible spacer, due to the absence of short- or long-positional order of the molecules.
Bar graphs are also presented for all of the compounds in this study, 5a–d and 9a–d, to get a better view of the odd–even effect. Fig. 2, at the top, represents the melting points for 5a–d and the transition temperatures upon heating for 9a–d. At the bottom of Fig. 2, plots of the entropy values for Cr → I for 5a–b and Cr → N for 9a–d (ΔS/R) are shown.
Theoretical calculations
Theoretical calculations were performed to evaluate the influence of the number of methylene carbon atoms in the flexible spacer chain on the most stable conformation of the compounds of the series 5a–d. DFT calculations were carried out in order to obtain the optimized geometries and conformational distributions for the molecules 5a–d. All of the calculations were performed with the Gaussian 0328 computational package and the geometries were optimized under vacuum using the B3LYP29 hybrid functional with the level 6-311G(d,p) basis set. In order to compare the energies, geometries and dipoles moments with the ones obtained in the gas phase, the structure of 5a was calculated using the PCM model for the solvent effect and water and cyclohexane as solvents with high and low dielectric constants, respectively.30 Calculations were performed considering that the molecular shape has a prominent effect in liquid crystal behavior and is primarily determined by the rotational process.31 The study here is guided by the fact that 5a–d and 9a–d containing a five-membered heterocyclic ring, named Δ2-isoxazolines, are connected to a benzoate moiety core by a flexible aliphatic spacer. The spacers in liquid crystal dimers contribute to the molecular anisotropy and exert control over the relative orientation of the two mesogenic groups.The Δ2-isoxazolines present a non-traditional bent-shape as a consequence of the tetrahedral carbon atoms C4 and C5 in the heterocyclic ring. Deviations from linearity as well as the non-coplanarity of the aryl groups bonded to C3 and C5 of isoxazoline have a pronounced influence on the mesophase formation as well as on the liquid crystal mesophase stability. To compensate these geometrical constraints, the elongating molecular strategy is applied for. Previous results have shown that stable mesophase formation is reached when highly anisotropic groups are linked to the C3 and C5 isoxazoline carbon atoms.24
For mesogens composed of flexible molecules a large number of conformational states can be obtained due to being arranged antiparallel or inclined for odd and even dimers and degrees of freedom related to the alkyl chains. In fact, calculations performed in this work showed a set of lowest energy conformations for 5a–d with energy barriers lower than 1.0 kcal mol−1 in the gas phase as well as in the condensed phase.
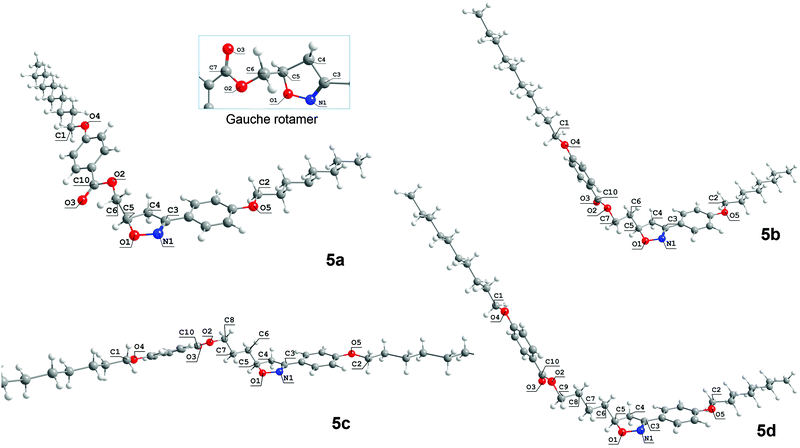
Fig. 3 represents the lowest energy conformations obtained for 5a–d. It is interesting to notice that the favored geometry for 5a is slightly different to 5c and quite different to 5b and 5d because of the dihedral angle ϕ1. For 5a, the dihedral angle ϕ1 is related to the O1–C5–C6–O2 atoms, whereas for 5b–d the dihedral angle ϕ1 is defined between the C4–C5–C6–C7 carbon atoms. In this way, the antiperiplanar arrangement of the carbon skeleton of the flexible spacer is obtained with different atoms as the length of spacer increases. Upon increasing from 1 to 4 methylene units in the flexible spacer the preferred rotamers are those that contain all of the methylene units in a trans conformation, except for 5a. 5a prefers a conformation where the two polar bonds O1–C5 and C6–O2 are oriented at an angle of 173.3° to minimize the electrostatic repulsion that occurs in the gauche rotamer, where the ϕ1 angle is equal to 61.8°.
This conformational preference for 5a can be explained by a destabilizing interaction that occurs when the O1–C5 bond of the heterocyclic ring and C6–O2 of the ester group are in the gauche position. In the gauche arrangement (inset at the top of Fig. 3), despite O1 being on the opposite side to the carbonyl oxygen O3, O1 and O2 are closer than in the anti conformation. To avoid this unfavorable electrostatic repulsion, 5a shows a more bent-shape form where the O2 and O1 oxygen atoms have adopted an antiperiplanar disposition. However when the size of the flexible spacer increases through the addition of methylene carbon atoms, this destabilization is no longer observed and now it is its preference for all trans conformations for the flexible spacers which is prevailing.
This preference can be explained by minimization of the destabilizing electrostatic interaction created by the gauche conformations, thus avoiding the syn-pentane effect. A destabilizing syn-pentane interaction is created when a hydrocarbon chain is folded such that a g+ dihedral angle is followed by one g− along the backbone.32 This effect, primarily of steric origin, results in conformers substantially higher in energy and, for this reason, linear hydrocarbon chains in alkanes adopt conformations that are free of syn-pentane interactions.33 This effect can be clearly seen in the even-numbered members 5b and 5d, and the odd-numbered member 5c.
Statistically, there are a lot of rotamers that contribute to the equilibrium of 5a–d because of the great number of internal degrees of freedom for these molecules. For 5a, considering the terminal alkyl chains are all trans, there are two conformations with a small energy difference between them. One of them is more elongated (the gauche conformer) and the other, the most stable, is more bent-shaped and less elongated (the anti rotamer in Fig. 3 – 5a). The energy barrier to convert the most stable rotamer obtained for 5a into the gauche rotamer is 0.67 kcal mol−1. The molecular length of the gauche rotamer is 34.8 Å which is about 6 Å bigger than the anti rotamer. We can overlook the contribution of all of the conformers to the equilibrium if we restrict the conformers to a discrete number such as the anti and gauche conformers.34 In doing so the populations in the equilibrium are roughly estimated to be in favor of the more bent-shaped conformer (anti) than the less bent-shaped conformer (gauche).
The relative orientation of the two molecular planes depends on the conformation of the flexible spacer (see Fig. S33, ESI†). The most stable conformer of 5a presents two slightly collinear and twisted planes composed of the aromatic rings, isoxazoline ring and terminal alkyl chains. The estimated angle between these two planes is about 32.5° from the side view (see the ESI†). 5c has similar planes which are shifted by about 60° when compared to the planes of 5a. These two planes are now separated by 21.5° from the side view. Individually, each rotamer of 5a has two independent planes which are organized in an edge-to-edge manner. From the top view it is possible to see that the planes are nearly flattened to the normal. For the even-numbered members 5b and 5d these planes are bent. The rotamers of 5b and 5d are organized in a face-to-face manner with an estimated angle between the planes of 98.5° and 102° for 5b and 5d, respectively. The top view of these planes shows that they are tilted to the normal.
Table 2 shows the data for the most stable conformations of 5a–d. The dipole moments, molecular lengths and some dihedral angles obtained for the anti conformation of 5a in the gas phase, in water and cyclohexane are shown. For 5b–d the data were collected only in the gas phase. Both the gas phase and condensed phase calculations for 5a pointed to same conformation as being the most stable conformer, but when solvent effects were taken into account the dipole moment increases with the increase of the solvent dielectric constant.
| Entry | μ (Debye) | Dihedral angle, ϕ1 (°) | Dihedral angle, ϕ2e (°) | Dihedral angle, ϕ3f (°) | Molecular length (Å) |
|---|---|---|---|---|---|
| a Cyclohexane. b Water. c Dihedral angle between the O1–C5–C6–O2 atoms. d Dihedral angle between the C4–C5–C6–C7 atoms. e Dihedral angle N1–C3–O5–C2. f Dihedral angle O2–C10–O4–C1. | |||||
| 5a | 7.7 | 173.3c | 179.4 | 176.5 | 28.96 |
| 5a | 8.5 | 174.7c | 176.2 | 176.9 | 29.70 |
| 5a | 9.8 | 177.0c | 175.1 | 176.8 | 29.80 |
| 5b | 5.4 | 175.6d | 179.8 | 178.0 | 33.25 |
| 5c | 3.0 | 176.7d | 0.660 | 0.86 | 36.93 |
| 5d | 5.0 | 176.9d | 176.5 | 178.6 | 37.45 |
The values of dihedral angles ϕ2, defined by N1–C3 and O5–C2, and ϕ3, defined by O2–C10–O4–C1, ensure that the alkyl chains and aromatic rings are in the same molecular plane on each side of the molecules. The aliphatic side chains all have trans conformations. The carbonyl oxygen, O3, is always on the opposite side to the O1–N1 polar bond of the isoxazoline ring, except for 5a. In this structure, the carbonyl oxygen is on the same side of the O1–N1 polar bond as a consequence of the antiperiplanar arrangement.
The main feature of this conformational analysis is related to changes in the dihedral angle related to the flexible spacer (ϕ1). The ϕ2 and ϕ3 dihedral angles are about 180.0° for 5a, 5b, and 5d and about 0° for 5c. Thus, the 5a, 5b, and 5d molecules display an antiperiplanar orientation of the imine group (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N) and O5–C2 bonds. The same antiperiplanar orientation is observed for the acyl linkage (OC10–O2) and O4–C1 bonds. A synperiplanar orientation was observed for the dihedral angles ϕ2 and ϕ3 for 5c only. This is reflected in a lowering of the dipole moment shown by this molecule.
N) and O5–C2 bonds. The same antiperiplanar orientation is observed for the acyl linkage (OC10–O2) and O4–C1 bonds. A synperiplanar orientation was observed for the dihedral angles ϕ2 and ϕ3 for 5c only. This is reflected in a lowering of the dipole moment shown by this molecule.
Theoretical calculations are a powerful tool that helps us to understand the observed dependence of the thermal behavior on the length and the parity of the spacer for 5a–d and 9a–d, and even for 7a–d which are definitely not liquid crystals.35 The even–odd effect of the melting point, and less visibly the enthalpy and entropy changes as the length of the spacer increases, can be explained by the shape of the molecules when considering the conformational issues of the flexible spacer.36 Despite the small differences in the energy barriers for the conformers observed in this study it is possible to assume that the conformers shown in Fig. 3 are at least responsible for the observation of the odd–even effects or partially responsible for the observed behavior. We are assuming that, for example, compounds that have one and three carbon atoms in the flexible spacer (odd-numbered members) are more anisotropic in their V-shape than the even-numbered members, and therefore their enthalpy and entropy values are higher than the even-numbered members.37 Under these circumstances, the melting points of the odd-numbered members are higher than the even-numbered members for all of the compounds listed in Table 1 as a consequence of the better packing for the odd-numbered members. We consider that the molecular packing for the odd-numbered members in an intermolecular V-fashion is face to face where the two molecular planes are nearly flattened to the normal. Even-numbered members may be packed one by one in V-fashion similar to a chevron structure (see Fig. S44, ESI†) considering that the planes are tilted to normal. So the odd-numbered members in this study can absorb more energy without causing disintegration of the crystal lattice until the melting point is reached.
The dependence of the transitional properties of LCs 5a–d and 9a–d in relation to the flexible spacer is better seen when observing the melting point. The irregular behavior of the mesophase makes the analysis more complex due to the enantiotropic or monotropic behavior observed for these LCs (Table 1). The enthalpy values also show a similar effect being more pronounced for the 5a–d series. The entropy values follow the same tendency as observed for compounds 5a–d and 9a–d. However, the values for 5a–d are higher due to transitions occuring from the ordered crystalline state to the directly disordered liquid state. LCs which have an enantiotropic mesophase such as 9a or 9c have an enhanced anisotropic-shape which allows molecules to pack more efficiently in the mesophase resulting in higher transition temperatures and entropy changes.2 It is possible to associate to these LCs the synergy between the conformational distribution and the orientational order of the nematic phase.33 The mesomorphic behavior found for 9a–d in this work is due to the presence of the long aromatic moiety terminally bonded to the isoxazoline ring. However, in some cases such as 5a–d or 7a–d the molecular dimensions (length-to-breadth ratio) of the aromatic moiety are not sufficient to overcome the non-coplanarity of the isoxazoline ring and the conformational issues of the flexible spacer. In this situation no mesophase or unstable mesophase (i.e., monotropic behavior) appears.
X-ray experiments
In Fig. 4 we present the X-ray results obtained for compound 5a through varying the temperature of the sample. The spectra were collected during cooling from the isotropic phase, where a broad halo is observed in the isotropic phase at around 2θ ≈ 20°, which according to Bragg's law corresponds to a distance of about 4.5 Å. This distance is related to the short length correlations between neighboring molecules. It is worth emphasizing that the SmA and SmC phases are almost indistinguishable from X-ray experiments, where in both cases an intense peak appears in the low angle region as a result of the X-ray beam diffraction by the smectic layers. In this case, the assignment is possible with additional techniques such as polarizing optical microscopy.38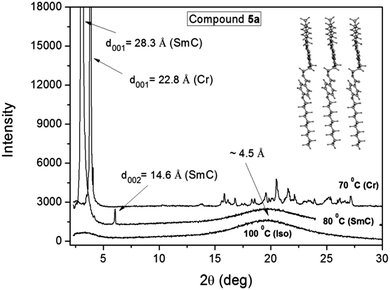 | ||
| Fig. 4 X-ray spectra of compound 5a for different temperatures. The inset shows a schematic representation of the molecules in the layered structure. | ||
By applying Bragg's law to the position of the first intense peak in the SmC phase at 80 °C it is possible to obtain an interlayer spacing of 28.3 Å, as well as, the second ordered peak at 14.6 Å. The ratio of d001/d002 ≈ 2 confirms the smectic character of the phase. The calculated molecular length (L) for compound 5a in the lower energetic conformation between the external H atoms is 29.95 Å. Considering that the molecules adopt the most extended form of the aliphatic chains in the mesophase, the tilt angle (θ) of the molecules in the SmC phase can be determined using the expression θ = cos−1(d001/L) = 19 degrees. Despite the fact that this value is relatively low, the same has been previously obtained for another SmC compound.36 The inset in Fig. 4 shows a schematic representation of the molecular packing according to the optimized molecular structure obtained from the theoretical analysis. Below the SmC–Cr transition temperature at 70 °C, additional peaks appear at the high angle region between 15 and 27 degrees, which are characteristic of the sample crystallization. However, in the low angle region an intense peak is still observed with an associated distance of 22.8 Å. It suggests that the smectic order is preserved, where the reduction of the interlayer distance compared to the one in the SmC phase can be associated to an increase of the tilt angle, to a reduction of the molecular length, or both.
For compound 5b it was not possible to obtain a clear spectrum of the SmC phase, where the crystallization and the mesophase occur simultaneously for the sample, which was observed right below the isotropic transition. This was due to the narrow temperature region of the SmC phase, but it was also an indication that the SmC phase is very unstable.
Conclusion
Two new series of non-symmetric liquid-crystalline dimers with 3,5-disubstituted 4,5-dihydroisoxazole benzoates and non symmetric isoxazoline derivatives, 5a–d and 9a–d, have been synthesized. 5a and 5b displayed a monotropic SmC phase whereas 9a–d displayed an enantiotropic nematic phase for 9a and 9c. Monotropic behaviour was observed for 9b and 9d. The mesomorphic behavior observed for 9a–d in this work is due to the presence of the naphthyl aromatic moiety laterally bonded to the isoxazoline ring. A dependence of the melting point thermal behavior on the length and the parity of the spacer was observed for 5a–d and 9a–d, and even to 7a–d which are not definitely not liquid crystals. Transition temperatures, and enthalpy and entropy values for odd-numbered members were higher than those for even-numbered members, reflecting that they are more shape-anisotropic. Density functional theory calculations were performed to evaluate the conformational issues of the flexible spacers and how these influence the mesomorphic behaviour of the dimers. An antiperiplanar arrangement was found for all of the carbon atoms of the flexible spacer including the C4 carbon atom of the isoxazoline ring, except for 5a. For 5a, an antiperiplanar arrangement was observed when considering the oxygen atom O1 of the isoxazoline ring. Otherwise, a less stable gauche rotamer for 5a could be observed taking into account the alignment of the carbon atom of the flexible spacer with the heterocyclic C4 carbon atom. Compounds that have one and three carbon atoms in the flexible spacer (odd-numbered members) are more anisotropic in their V-shape than the even-numbered members. Melting points for both of the series 5a–d and 9a–d displayed a regular behaviour concerning the length and parity of the flexible spacer. Enthalpy and entropy values for the 5a–d esters followed the tendency observed for the melting point. However, for 9a–d the behaviour was irregular, and therefore their enthalpy and entropy values are in general higher than the even-numbered members. Under these circumstances the melting points for the odd-numbered members are higher than the even-numbered members for all of the compounds in this work as a consequence of the better packing of the odd-numbered members.Acknowledgements
This work was supported by MCT/CNPq, Fapergs-Edital PqG 002/2014. A. A. M. thanks MCT/CNPq for his postdoctoral studies at the University of Hull, Hull, UK (grant no. 201116/2011-1). Thanks to FAPESC, Laboratório de Difração de Raios-X (LDRX-DF/UFSC) for the X-ray diffraction experiments and the Department of Chemistry, University of Hull, Hull, UK for the use of NMR facilities.References
- C. T. Imrie and G. R. Luckhurst, in Handbook of Liquid Crystals, ed. D. Demus, J. Goodby, G. W. Gray, H.-W. Spiess and V. Vill, Wiley-VCH, Weinheim, 1998, vol. 2B, pp. 801–833 Search PubMed.
- C. T. Imrie and P. A. Henderson, Chem. Soc. Rev., 2007, 36, 2096 RSC.
- D. Vorlander, J. Phys. Chem., 1927, 126, 449 Search PubMed; D. W. Bruce, K. Heyns and V. Vill, Liq. Cryst., 1997, 23, 813 CrossRef CAS.
- J. Rault, L. Liebert and L. Strzelecki, Bull. Soc. Chim. Fr., 1975, 1175 CAS.
- S. Kumar, Liq. Cryst., 2005, 32, 1089 CrossRef CAS; J. H. Wild, K. Bartle, N. T. Kirkman, S. M. Kelly, M. O'Neill, T. Stirner and R. P. Tuffin, Chem. Mater., 2005, 17, 6354 CrossRef; H. Wang, B. Bai, P. Zhang, B. Long, W. Tian and M. Li, Liq. Cryst., 2006, 33, 445 CrossRef; M. P. Aldred, R. Hudson, S. P. Kitney, P. Vlachos, A. Liedtke, K. L. Woon, M. O'Neill and S. M. Kelly, Liq. Cryst., 2008, 35, 413 CrossRef.
- B. Kosata, G. M. Tamba, U. Baumeister, K. Pelz, S. Diele, G. Pelzl, G. Galli, S. Samaritani, E. V. Agina, N. I. Boiko, V. P. Shibaev and W. Weissflog, Chem. Mater., 2006, 18, 691 CrossRef CAS.
- M. G. Tamba, B. Kosata, K. Pelz, S. Diele, G. Pelzl, Z. Vakhovskaya, H. Kresse and W. Weissflog, Soft Matter, 2006, 2, 60 RSC.
- I. Sledzinska, E. Bialecka-Florjanczyk and A. Oresko, Eur. Polym. J., 1996, 32, 1345 CrossRef CAS.
- M. Ibn-Elhaj, A. Skoulios, D. Guillon, J. Newton, P. Hodge and H. J. Coles, Macromolecules, 1995, 19, 1264 Search PubMed.
- H. C. Lee, Z. B. Lu, P. A. Henderson, M. F. Achard, W. A. K. Mahmood, G. Y. Yeap and C. T. Imrie, Liq. Cryst., 2012, 39, 259 CrossRef CAS.
- A. Blumstein and O. Thomas, Macromolecules, 1982, 15, 1264 CrossRef CAS.
- C. V. Yelamaggad, I. S. Shashikala and Q. Li, Chem. Mater., 2007, 19, 6561 CrossRef CAS.
- I. Nishiyama, J. Yamamoto, J. W. Goodby and H. Yokoyama, J. Mater. Chem., 2003, 13, 2429 RSC.
- C. V. Yelamaggad, U. S. Hiremath, D. S. S. Rao and S. K. Prasad, Chem. Commun., 2000, 57 RSC; A. S. Achalkumar, D. S. S. Rao and C. V. Yelamaggad, New J. Chem., 2014, 38, 4235 RSC.
- T. Donaldson, P. A. Henderson, M. F. Achard and C. T. Imrie, J. Mater. Chem., 2011, 21, 10935 RSC.
- C. V. Yelamaggad, U. S. Hiremath, D. S. S. Rao and S. K. Prasad, Chem. Commun., 2000, 57 RSC.
- A. C. Griffin and T. R. Britt, J. Am. Chem. Soc., 1981, 103, 4957 CrossRef CAS.
- C. K. Ober, J. I. Jin and R. W. Lenz, Adv. Polym. Sci., 1984, 59, 103 CrossRef CAS.
- A. Ferrarini, C. Greco and G. R. Luckhurst, J. Mater. Chem., 2007, 17, 1039 RSC.
- H. Wang, R. Shao, C. Zhu, B. Bai, C. Gong, P. Zhang, F. Li, M. Li and N. A. Clark, Liq. Cryst., 2008, 35, 967 CrossRef CAS.
- R. M. Srivastava, R. A. W. N. Filho, R. Schneider, A. A. Vieira and H. Gallardo, Liq. Cryst., 2008, 35, 737 CrossRef CAS; B. L. Bai, H. T. Wang, X. L. Lin, X. Ran, C. X. Zhao and M. Li, Lett. Org. Chem., 2012, 9, 76 CrossRef.
- M. J. Wallage and C. T. Imrie, J. Mater. Chem., 1997, 7, 1163 RSC.
- V. Bezborodov, N. Kauhanka and V. Lapanik, Mol. Cryst. Liq. Cryst., 2004, 411, 103 CrossRef CAS; V. N. Kovganko and N. N. Kovganko, Russ. J. Org. Chem., 2006, 42, 696 CrossRef; O. M. S. Ritter, F. C. Giacomelli, J. A. Passo, N. P. Silveira and A. A. Merlo, Polym. Bull., 2006, 56, 549 CrossRef; J. A. Passo, G. D. Vilela, P. H. Schneider, O. M. S. Ritter and A. A. Merlo, Liq. Cryst., 2008, 35, 833 CrossRef.
- A. Tavares, P. H. Schneider and A. A. Merlo, Eur. J. Org. Chem., 2009, 889 CrossRef CAS; A. Tavares, P. R. Livotto, P. F. B. Gonalves and A. A. Merlo, J. Braz. Chem. Soc., 2009, 9, 1742 Search PubMed.
- M. A. Weidner-Wells, S. A. Fraga-Spano and I. J. Turchi, J. Org. Chem., 2010, 63, 6319 CrossRef.
- F. A. Carey and R. J. Sundberg, Advanced Organic Chemistry, Part B: Reactions and Synthesis, Plenum Press, 2008 CrossRef; R. Huisgen, in 1,3-Dipolar Cycloadditon Chemistry, ed. A. Padwa, Wiley, New York, 1984, vol. 1 CrossRef; C. Nájera, J. M. Sansano and M. Yus, J. Braz. Chem. Soc., 2010, 21, 377 CrossRef.
- U. B. Vasconcelos and A. A. Merlo, Synthesis, 2006, 1141 CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery Jr., T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian 03, Revision A.1, Gaussian, Inc., Wallingford CT, 2003 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS; C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999 CrossRef CAS PubMed.
- F. A. Carey and R. J. Sundberg, Advanced Organic Chemistry, Part A, Plenum Press, New York, 3rd edn, 1990, pp. 117 Search PubMed.
- R. W. Hoffmann, Angew. Chem., Int. Ed., 2000, 39, 2054 CrossRef PubMed.
- J. B. Klauda, R. W. Pastor and B. R. Brooks, J. Phys. Chem. B, 2005, 109, 15684 CrossRef CAS PubMed.
- P. J. Flory, Statistical Physics of Chain Molecules, Wiley, New York, 1969 Search PubMed.
- Unfortunately we were not able to get a single crystal of 5a–d or 9a–d to be analyzed using X-ray experiments and compare to our DFT studies.
- D. Demus, J. Goodby, G. W. Gray, H. W. Spiess and V. Vill, Handbook of Liquid Crystals, Wiley-VCH, Weinheim, New York, Chichester, Brisbane, Singapore, Toronto, 1998, p. 72 Search PubMed.
- D. P. Pink, J. Chem. Phys., 1975, 63, 2533 CrossRef CAS; T. Carnelley, Philos. Mag., 1882, 13, 112 Search PubMed.
- H. Gallardo, F. R. Bryk, A. A. Vieira, T. E. Frizon, G. Conte, B. S. Souza, J. Eccher and I. H. Bechtold, Liq. Cryst., 2009, 36, 839 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental procedure, 1H and 13C NMR spectrum and spectroscopic data final compounds, modeling pictures of the rotamers. See DOI: 10.1039/c5nj02199e |
| This journal is © The Royal Society of Chemistry and the Centre National de la Recherche Scientifique 2016 |