Precise analysis of calcium stable isotope variations in biological apatites using laser ablation MC-ICPMS†
Théo
Tacail
*,
Philippe
Télouk
and
Vincent
Balter
Laboratoire de Géologie de Lyon: Terre, Planète, Environnement, UMR CNRS 5276 (CNRS, ENSL, Université Lyon 1), Ecole Normale Supérieure de Lyon, 69364 Lyon cedex 07, France. E-mail: theo.tacail@ens-lyon.fr
First published on 7th August 2015
Abstract
Laser ablation (LA) is potentially an interesting technique to measure natural variations (δ44/42Ca) of calcium isotopes in calcium-rich minerals because it allows spatial resolution and avoids micro-sampling and consecutive wet chemistry. We developed a matrix-match sample/standard normalization method and used an Excite 193 nm Photon Machines LA system coupled to a Neptune plus MC-ICPMS to measure δ44/42Ca variations in enamel apatite. First, high precision δ44/42Ca solution mode (SOL) analyses were performed on a series of 5 crystalline igneous apatite and 6 modern tooth enamel samples, which were micro-sampled using a MicroMill device. The δ44/42Ca isotopic values ranged evenly between −0.60 and +0.60‰ (per amu). Second, we sintered by means of a spark plasma sintering technique the bone ash SRM1400 standard and two synthetic apatites (doped or not with Sr). The Ca isotope compositions using LA were measured in the samples in the raster mode along 600 × 85 μm profiles and bracketed with the SRM1400 standard. We obtained very good agreement between SOL and LA measurements, i.e. δ44/42CaLAvs. δ44/42CaSOL slope of 0.960 ± 0.091 (2SE, R2 = 0.971) and null offset at origin (0.012 ± 0.084, 2SE). For all samples, residual values to the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 slope were ≤0.1‰ (per amu). However, an unexplained and constant 0.13‰ offset occurred when considering the 43/42Ca ratio, suggesting an uncorrected isobaric interference on 43Ca in the LA mode. We also noticed that the doubly charged strontium (Sr) interference correction is of crucial importance for accurate matching between LA and SOL measurements. In the SOL mode, Sr is discarded by ion chromatography leading to typical 87Sr2+/44Ca+ ratios of 10−5 to 10−6. In the LA mode, this ratio can exceed 10−3. We show that the value set for the 87Sr/86Sr ratio is of importance to correct the Sr interference, and that optimized residuals to the 1
1 slope were ≤0.1‰ (per amu). However, an unexplained and constant 0.13‰ offset occurred when considering the 43/42Ca ratio, suggesting an uncorrected isobaric interference on 43Ca in the LA mode. We also noticed that the doubly charged strontium (Sr) interference correction is of crucial importance for accurate matching between LA and SOL measurements. In the SOL mode, Sr is discarded by ion chromatography leading to typical 87Sr2+/44Ca+ ratios of 10−5 to 10−6. In the LA mode, this ratio can exceed 10−3. We show that the value set for the 87Sr/86Sr ratio is of importance to correct the Sr interference, and that optimized residuals to the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 slope are obtained using a Sr correction that takes into account a mass fractionation factor for doubly charged Sr distinct from that of Ca. We found that deciduous teeth enamel is depleted of Ca heavy isotopes by about 0.35–0.40‰ (per amu) compared to wisdom teeth enamel, a shift compatible with a transition from a milk based diet to a plant and meat based diet.
1 slope are obtained using a Sr correction that takes into account a mass fractionation factor for doubly charged Sr distinct from that of Ca. We found that deciduous teeth enamel is depleted of Ca heavy isotopes by about 0.35–0.40‰ (per amu) compared to wisdom teeth enamel, a shift compatible with a transition from a milk based diet to a plant and meat based diet.
1. Introduction
The Ca stable isotope compositions of biological hydroxylapatites (bioapatite) and especially of fossil teeth enamel constitute a promising tool for paleodietary studies, because a stepwise trophic level effect has been described in marine, and to a lesser extent, in continental environments.1–7 In addition, the Ca isotope composition of milk is one of the most 44Ca-depleted materials reported so far.5,8 Although not demonstrated yet, physiological stresses or early-life dietary transitions can influence the body Ca isotope burden, the resulting variations of which are potentially recorded spatially in the enamel. This suggests that the weaning period could be defined by a shift towards heavier Ca isotopic values along enamel growth prisms. These applications would notably benefit from the development of a quasi non-destructive in situ method, adapted to the analysis of precious fossils, whilst allowing an increased spatial resolution and without compromising analytical precision.In situ measurements of stable isotope ratios by laser ablation multi-collector inductively coupled plasma mass spectrometry (LA-MC-ICPMS) have been restricted to a few elements so far, mainly iron,9–18 magnesium,15,18–20 silicon,20,21 copper,9,22 sulphur23 and boron,24 and have mainly been applied to the characterization of silicate glasses and minerals, oxides, metals, allies and sulphides. The laser ablation (LA) technique faces a series of technical hindrances to the measurements of accurate and precise stable isotope ratios, including LA induced fractionation, unresolved isobaric interferences and a serious lack of solid matrix-matched homogeneous standards certified for isotopic compositions. The multiple elemental and isotopic fractionation effects associated with the LA technique take place during vaporization and condensation at the ablation site, during transport of resulting heterogeneously sized particles and in the plasma during incomplete atomization and ionization of particles.11,12,14,22 These effects strongly depend on the nature of the ablated material and thus require matching of matrices between standards and samples in terms of the chemical composition and mineralogy, especially when considering nanosecond LA systems.9,13,20,24,25
We present here the first method described for Ca isotope determination by LA-MC-ICPMS on enamel bioapatite that solves these problems and fulfils mass-dependent fractionation, accuracy and precision requirements. We developed a strategy based on a matrix-matched standard-bracketing normalization and an extensive doubly charged Sr interference correction. This strategy is applied to a series of macrocrystalline igneous fluorapatites (FAPs) as well as synthetic and biogenic microcrystalline hydroxylapatites (HAPs), previously measured for their Ca isotope composition using classical wet chemistry (hereafter referred to as solution or SOL mode).
2. Materials
We selected various natural geological and biological apatites, with various crystallite sizes and isotopic compositions, as described in Table 1A. Standards for LA measurements were prepared in order to achieve matching of matrices between standards and samples in terms of mineralogy and Sr contents.| Sample abbreviation | Description |
|---|---|
| a 1Described by Tacail et al.,342described by Balter and Reynard,32 Balter et al.31 and Balter et al.,33 *used as the LA mode bracketing standard, **used as the SOL mode bracketing standard, ***sample obtained using MicroMill. | |
| A-samples | |
| BRM | Natural igneous monocrystalline FAP, Burma |
| BRZa | Natural igneous monocrystalline FAP, Brazil |
| DUR | Natural igneous monocrystalline FAP Durango, Mexico |
| MD1 | Natural igneous monocrystalline FAP, Madagascar |
| MRCa | Natural igneous monocrystalline FAP, Morocco |
| BMM3 | Female wisdom 3d molar tooth enamel*** |
| HPME | Female wisdom 3d molar tooth enamel |
| BME1 | Female deciduous canine tooth enamel |
| BMC | Female deciduous canine tooth enamel*** |
| PBC | Male deciduous canine tooth enamel*** |
| VBI | Male deciduous incisor tooth enamel*** |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|
| B-SOL mode standards | |
| ICP Ca Lyon** | ICP Alfa Aesar 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 μg L−1 Ca solution1 000 μg L−1 Ca solution1 |
| SRM915b | Clinical grade carbonate NIST standard reference material |
| SRM1486 | Bone meal NIST standard reference material |
| Seawater | Seawater sample from Belize near the shore |
| CBE | Cave bear enamel powder in-house standard1 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|
| C-LA mode standards | |
| SRM1400 | Bone ash hydroxyapatite NIST SRM powder |
| SRM1400-SPS | Bone ash hydroxyapatite NIST SRM sintered using the SPS technique |
| SRM1400-gold | Bone ash hydroxyapatite NIST SRM belt sintered using the belt technique2 |
| HAPp1-SPS | SPS sintered powder synthetic hydroxyapatite |
| HAPp2-SPS | SPS sintered powder synthetic hydroxyapatite doped with Sr |
2.1. Samples
A series of five igneous centimetre long monocrystalline FAPs from various locations (Burma, Brazil, Mexico, Madagascar and Morocco, Table 1A) were selected. These igneous materials are expected to have quite high δ44/42Ca values1,4 and to be isotopically homogeneous at the crystal scale. Igneous apatites were cut into thin slices and small chips of approximately 1 mg were sampled for analysis in the SOL mode. Remaining FAP crystals were included in araldite and resulting mounts were cleaned using wet fine-grained sandpapers.Two wisdom and four deciduous human teeth from four different living individuals (Table 1A) were also selected. Tooth enamel samples are expected to have quite low δ44/42Ca values (e.g.ref. 2, 3, 5 and 7) together with possible individual or tooth type specificities. Once included in araldite, the resulting mounts were cut and polished across the tooth vertical bucco-lingual plane for LA mode analyses. Chips of HPME and BMM3 enamel were sampled for analysis in the SOL mode on the other halves of teeth. For the 4 other teeth, a MicroMill device was used for precise position drilling with a 400 μm diameter tungsten carbide drill. Drill holes were approximately 400 μm in diameter and 300 μm in depth. Small powder heaps were collected using two clean razorblades and introduced into 7 mL Teflon beakers. Enamel surface, drill bit and razorblades were washed with 99% pure ethanol and blown off using a compressed air duster between each drilling. A single drilling allowed recovery of approximately 80 μg HAP corresponding to about 30 μg Ca.
2.2. SOL mode standards
The precision and accuracy of solution mode measurements were estimated by measuring isotopic compositions of several international and in-house Ca isotope standards listed in Table 1B.2.3. LA mode standards
The standards used in the LA mode are listed and described in Table 1C. The SRM1400 standard was used as the main reference standard for the LA mode. It is a cattle bone ash NIST Standard Reference Material powder certified or well described for major and trace element concentrations and for Pb and Sr radiogenic ratios26–28 but for which no Ca isotopic composition has been proposed yet. This standard, which contains no or very little organic matter, consists of nano- to microcrystalline HAP that resembles enamel crystallites.In order to better control the Sr double charge effects on the Ca isotope composition, we carried out two experiments of apatite precipitation following the procedure described by Balter and Lécuyer.29 Briefly, HAPp1 was synthesized by mixing 1 L of CaCl2·4H2O at 2.6 × 10−2 mol L−1 and 1 L of Na2HPO4·2H2O at 2.5 × 10−2 mol L−1. For both initial solutions, the pH was set at 10.8 by adding 1 M NaOH. For the second precipitation experiment (HAPp2), 4 mg Sr from Alfa Aesar ICP 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ppm solution were added to the CaCl2·4H2O prior to pH adjustment. The resulting precipitates were constantly agitated in reaction vessels and kept at 25 °C for 96 h for maturation of crystals. At the end of the experiments the supernatant was discarded after centrifugation in 500 mL centrifugation vials. Precipitates were freeze-dried to avoid subsequent modification of crystallites and finally homogenized in an agate mortar.
000 ppm solution were added to the CaCl2·4H2O prior to pH adjustment. The resulting precipitates were constantly agitated in reaction vessels and kept at 25 °C for 96 h for maturation of crystals. At the end of the experiments the supernatant was discarded after centrifugation in 500 mL centrifugation vials. Precipitates were freeze-dried to avoid subsequent modification of crystallites and finally homogenized in an agate mortar.
Powders of SRM1400, HAPp1 and HAPp2 were sintered using the Spark Plasma Sintering technique (SPS), which consists in applying a pulsed electric current simultaneously with compressive stress to a die containing the initial powder sample.30 The rapid and efficient heating enabled by the current applied to the powder allows coalescence of grains without major phase changes at temperatures up to 1200 °C and pressure less than 100 MPa.30 The SPS technique allows drastic reduction of porosity and thus leads to sintered materials yielding more than 98% of theoretical maximal density. The sintering of SRM1400, HAPp1 and HAPp2 powders was carried out at the INSA Lyon MATEIS Laboratory using a FCT system HP D 25 SPS apparatus (Germany). The SPS runs were carried out in a vacuum sintering atmosphere (3 × 10−1 mbar) at the following operating conditions:30 compressive stress was set at 75 MPa, temperature was increased at a rate of 100 °C min−1 and plateaued at 900 °C for 3 to 4 min until the shrinkage rate was null. The SRM1400 standard used in previous studies by Balter31–33 was also analysed in the LA mode to test for the possible effect of the sintering technique. This standard, labelled here as “SRM1400-gold”, was sintered at 2 GPa and 700 °C in a belt apparatus at the Centre des Hautes Pressions of the Claude Bernard Lyon 1 University. Prior to LA analysis, all sintered standards were included in araldite resin and polished to obtain flat surfaces and remove superficial impurities such as graphite from SPS dies.
In parallel with the preparation of the SPS standards (written with “-SPS” suffix hereafter), SRM1400, HAPp1 and HAPp2 powders were sampled for precise analysis in the SOL mode. The SRM1400-SPS sintered standard was also micro-sampled for precise SOL mode analysis using MicroMill in order to check for any influence of the sintering process on the Ca isotope composition.
3. Analytical methods
3.1. SOL mode analysis
A two-step chemical purification of samples was performed following the method described by Tacail et al.34 Briefly, once digested, samples were processed through AG50W-X12 cationic resins in 1 N HCl medium for matrix discard. Calcium was recovered together with Sr in 6 N HCl and processed through Sr specific resins (Sr Spec) in 2 N HNO3 medium for Sr elimination. The measurements of Ca isotope ratios in the SOL mode were carried out at the ENS-Lyon using a Neptune plus MC-ICPMS (Thermo Scientific, Bremen, Germany) following the method described by Tacail et al.34 Optimized operating parameters for SOL mode analyses are summarized in Table 2A. Each analysis was preceded by a washout pumping in 0.5 N HNO3 using the Aridus quickwash module. A second washout pumping was carried out in 0.05 N HNO3 and measured as the blank, this background being subtracted online before calculation of isotope ratios. The ICP Ca Lyon standard34 was used as the SOL mode bracketing standard. All Ca isotope compositions are expressed using the delta notation defined as follows for δ44/42Ca: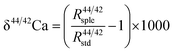 | (1) |
| Settings | A-SOL mode | B-LA mode |
|---|---|---|
| Aridus II | ||
| Sweep gas flow (Ar) [L min−1] | 7–9 | 7–8 |
| Nitrogen gas flow [mL min−1] | 5–8 | 4–6 |
| Spray chamber temp. [°C] | 110 | |
| Desolvator temp. [°C] | 160 | |
| Aspiration type | Free | |
| Uptake rate [μL min−1] | 120 | |
| Ca concentration [mg L−1] | 1.5–3.0 | — |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||
| Thermo Neptune plus | ||
| RF power [W] | 1200 | |
| Cool gas [L min−1] | 15 | |
| Aux gas [L min−1] | 0.7 | |
| Sample gas [L min−1] | 0.95–1.20 | |
| Extraction [V] | −2000 | |
| Acceleration potential [V] | −10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
|
| Sampler cone | Jet | Standard |
| Skimmer cone | X | H |
| Resolution slit | MR | HR |
| Faraday cup configuration and resistances [Ω] | L4 – 42Ca+ – 1011 Ω | |
| L2 – 43Ca+ – 1012 Ω | ||
| L1 – 87Sr2+ – 1011 Ω | ||
| C – 44Ca+ – 1011 Ω | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||
| Excite 193 nm LA system | ||
| Cell type | — | Helex chamber |
| LA pulse width | — | <4 ns |
| He carrier MFC1 flow [L min−1] | — | 0.900 |
| He carrier MFC2 flow [L min−1] | — | 0.400 |
| Maximal fluence [J cm−1] | — | 15.2 |
| Delivered fl. [% of max. fl.] | — | 70–100 |
| Raster scan lengths [μm] | — | 500–600 |
| Scan speed [μm s−1] | — | 10 |
| Spot size (diameter) [μm] | — | 85 |
| Repetition rate [Hz] | — | 15 |
| Washout time [s] | — | 30 |
3.2. LA mode analysis
Analyses in the LA mode were carried out using an Excite 193 nm ArF Excimer laser system (Photon Machines, MT, USA) delivering 4 ns pulses at a maximal fluence of 15.2 J cm−1. The mounted HeLex cell allowed ablation of samples in an ultra-pure He atmosphere with efficient recovery of the ablated material. The LA system was connected to the plasma torch via Teflon tubing in series with a “squid” signal-smoothing device. A T-piece adapter allowed mixing of the He carrier gas with an Ar makeup gas flow from Aridus II in order to ensure plasma ignition and stability. Although this desolvating system drastically reduces the amount of transmitted water, it allows either moderate addition of water from freely aspirated and nebulized distilled 0.05 N HNO3 during LA mode analyses, or introduction of Ca from ICP Ca Lyon solution for daily pre-tuning of MC-ICPMS.The optimized LA mode operating parameters of MC-ICPMS and LA systems are summarized in Table 2B. Faraday cup configurations were identical to SOL mode. As doubly charged Sr isotopes constitute unresolvable interfering species on all three measured Ca isotope beams,34 L1 faraday cup was also set for the collection of m/z = 43.5 beams, corresponding to the measurement of 87Sr2+ signal. In contrast to SOL mode, where a nickel Jet-X sampler and skimmer cones were used,34,35 LA mode analyses were performed with a standard-H pair, although jet interface allows an average 5-fold transmission increase. This combination permitted reduction of polyatomic species formation at the cone interface, such as molecular oxides, hence reducing potential isobaric interferences or instabilities (e.g.ref. 36).
As described elsewhere,34,37 measurements of 42Ca+, 43Ca+ and 44Ca+ signals are hindered by numerous polyatomic isobaric interferences, largely caused by Ar from the introduction gas, O2 and N2 from air and H2O from dilute acids. These interferents constrain the measurement of Ca isotopic ratios to the left shoulder of the Ca peak, especially because of the interference of 40Ar1H2+ with 42Ca+. Calcium isotopes measurement by MC-ICPMS requires a minimal resolving power of 2200 in order to perform measurement in a 10−2 amu wide window,37 which is achieved by the use of the Medium Resolution mode (MR mode). Concerning analyses in the LA mode, polyatomic interferences induced by introduction gases and water are apparently unchanged despite addition of He flow. Mass scan of blanks in the LA mode, i.e. with gas only and unfocused firing laser, was similar to those performed in the SOL mode using 0.05 N HNO3 (Fig. S1†). Analyses in the LA mode were performed using the High Resolution slit (HR mode) to ensure maximal resolution and stability of the central mass position.
Daily tuning of MC-ICPMS consisted in a primary gross tuning of transmission, peak shape and peak centering using an ICP Ca Lyon introduced via Aridus II and in a second refined tuning performed by ablating SRM1400-SPS along a continuous raster. This allowed optimization of Aridus II and He gas flows, torch position, source lenses and zoom optics.
Laser ablation scan speed, repetition rate and effective fluence were optimized for Ca transmission and signal stability, but were not found to have a specific impact on the measured Ca isotope ratios. Spot diameter was set at 85 μm in order to ensure sufficient Ca transmission, notably in order to overcome the influence of potentially unresolved constant polyatomic isobaric interferences induced by introduction gases.
In this study, scan line ablations were preferred to spot ablation because of the strong transient laser induced fractionation described for spot ablation on several isotopic systems, especially regarding nanosecond UV LA when compared to femtosecond UV LA.11,22–25 Although it is uncertain whether these transient isotopic effects are linked to heterogeneous particle sizes or to fractionation effects occurring at the ablation site and/or in the plasma, scan lines allow reaching a steady state in both transport of different particle types and fractionation effects. Ablation lines of about 500 to 600 μm were thus performed in order to quickly obtain intensities and measured ratios as steady as possible.
The ablation and acquisition procedure was performed as follows. An ablation sequence was prepared using the LA system software (Chromium 2) and consisted in a fine optical focus on the sample surface together with a precise positioning of scan lines. An acquisition method was set to acquire an infinite number of 1.049 s lasting integration cycles. Sample ablations were preceded by blank acquisition, implying unchanged Ar and He gas flows combined with unfocused laser firing on a sample-free zone. Sequences consisted in series of 15 to 25 ablation scans in which ablations of samples were bracketed by analyses of the SRM1400-SPS standard. Each ablation was followed by 30 s of washout, necessary to reach average blank levels. The HAPp2-SPS standard was regularly analysed as a sample in order to check for the influence of the doubly charged Sr interference on the accuracy of the measurements on a Ca-fractionated and Sr-doped material.
All ablated materials displayed intensities within 10% of the SRM1400-SPS typical signal, even when considering macro- vs. microcrystalline apatites (i.e. igneous FAP vs. synthetic or biological HAP). Typical signal intensities in these conditions are about 1.2 V, 0.3 V and 4.2 V for the 42Ca+, 43Ca+ and 44Ca+ signals respectively, while blanks were yielding average values of 1 × 10−3 V, 2 × 10−4 V and 3 × 10−3 V for 42, 43 and 44 m/z ratio signals respectively.
Data were processed offline using an in-house python code. This program allowed isolating initial blank sections and cutting sample ablation plateaus with systematic rejection of instabilities at the signal onset. After blank subtraction, Ca isotope signals were corrected for doubly charged Sr interferences, i.e.84Sr2+, 86Sr2+ and 88Sr2+ on 42Ca+, 43Ca+ and 44Ca+ respectively. As described by Tacail et al.,34 the correction consisted in subtracting inferred doubly charged 2xSr2+ contribution on xCa+ signals. This contribution was calculated by considering that Sr isotopes are fractionated in the instrument following a mass-dependent exponential fractionation law.38,39 The equation for correction of a given xCa+ signal gives:
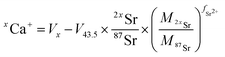 | (2) |
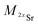 and
and 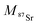 the atomic masses of 2xSr and 87Sr isotopes in atomic mass units (amu) and fSr2+ the doubly charged Sr exponential-law mass fractionation coefficient (see Section 5.2.). This correction relies on two main parameters, namely the true Sr isotopic ratio and the mass-fractionation coefficient. True 2xSr/87Sr isotopic ratios were calculated on the basis of a radiogenic 87Sr/86Sr ratio of 0.7103, corresponding to a rounded 87Sr/86Sr ratio in NBS987.40–44 This ratio allows calculation of the true ratios of 0.0796, 1.4079 and 11.7959 for 84Sr/87Sr, 86Sr/87Sr and 88Sr/87Sr, respectively, considering average natural abundances of Sr stable isotopes. The doubly charged Sr mass fractionation coefficient, fSr2+, was estimated on the basis of accuracy optimization on the 44Ca/42Ca ratio of repeated analyses of the HAPp2-SPS standard measured as the sample. This sample was chosen because it had the highest Sr content of all samples and standards. Both of these parameters were used to correct for doubly charged interferences of all measured samples and standards. All 44Ca/42Ca and 43Ca/42Ca corrected ratios were then calculated for each cycle of each scan, and values deviating by more than 1SD from the mean were discarded. Average ratios of each ablation scan were then used for the calculation of δ44/42CaSRM and δ43/42CaSRM of the sample or standard.
the atomic masses of 2xSr and 87Sr isotopes in atomic mass units (amu) and fSr2+ the doubly charged Sr exponential-law mass fractionation coefficient (see Section 5.2.). This correction relies on two main parameters, namely the true Sr isotopic ratio and the mass-fractionation coefficient. True 2xSr/87Sr isotopic ratios were calculated on the basis of a radiogenic 87Sr/86Sr ratio of 0.7103, corresponding to a rounded 87Sr/86Sr ratio in NBS987.40–44 This ratio allows calculation of the true ratios of 0.0796, 1.4079 and 11.7959 for 84Sr/87Sr, 86Sr/87Sr and 88Sr/87Sr, respectively, considering average natural abundances of Sr stable isotopes. The doubly charged Sr mass fractionation coefficient, fSr2+, was estimated on the basis of accuracy optimization on the 44Ca/42Ca ratio of repeated analyses of the HAPp2-SPS standard measured as the sample. This sample was chosen because it had the highest Sr content of all samples and standards. Both of these parameters were used to correct for doubly charged interferences of all measured samples and standards. All 44Ca/42Ca and 43Ca/42Ca corrected ratios were then calculated for each cycle of each scan, and values deviating by more than 1SD from the mean were discarded. Average ratios of each ablation scan were then used for the calculation of δ44/42CaSRM and δ43/42CaSRM of the sample or standard.
4. Results
4.1. SOL mode results
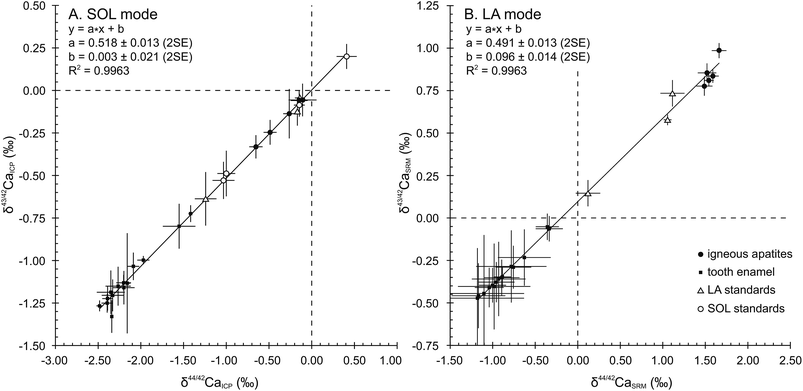
When plotted in a δ43/42CaICPvs. δ44/42CaICP diagram (Fig. 1A), all samples and standards measured in the SOL mode fall on a line displaying a strong correlation (R2 = 0.9963), a null offset at origin (0.003 ± 0.021, 2SE) and a slope of 0.518 ± 0.013 (2SE), which is in general agreement with the value of 0.507 predicted by the linear approximation of the exponential mass-dependent fractionation law.The δ44/42CaICP values of the standards are given in Table 3 together with converted literature values. All measured standards – namely SRM915b, Seawater, SRM1486 and CBE – display values in good agreement with literature data and with previously published values. Long-term external reproducibility (2SD), estimated using SRM1486, yields 0.13‰ for δ44/42Ca (n = 120). The SRM1400 standard displays a δ44/42CaICP value of −1.24 ± 0.13‰ (2SD, n = 26). This first published SRM1400 Ca isotope composition falls within the domain of previously described isotopic compositions of cattle bones,5 which yield an average δ44/42CaICP value of −1.00 ± 0.34‰ (2SD, n = 25). When expressed relative to SRM915b, the δ44/42Ca915b value of SRM1400 is −1.10 ± 0.14‰ (2SD, n = 26). The δ44/42CaICP value remains unchanged after sintering and micro-sampling of SRM1400-SPS (−1.18 ± 0.16‰, 2SD, n = 11) showing that these treatments have no effect on the Ca isotope compositions.
| Study | SRM915a | SRM915b | Seawater | SRM1486 | CBE | SRM1400 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| This study | Used for conversion | −0.14 ± 0.06 | (4) | 0.41 ± 0.12 | (5) | −1.03 ± 0.13 | (120) | −1.00 ± 0.10 | (21) | −1.24 ± 0.13 | (26) | |
| Ref. 34 | −0.12 ± 0.07 | (11) | 0.41 ± 0.06 | (2) | −0.96 ± 0.14 | (17) | −1.05 ± 0.07 | (9) | ||||
| Ref. 50 | −0.49 ± 0.02 | (2) | ||||||||||
| Ref. 48 | −0.50 ± 0.15 | (56) | −1.02 ± 0.12 | (142) | ||||||||
| Ref. 6 | −1.03 ± 0.04 | (n.a.) | ||||||||||
| Ref. 6 | −0.98 ± 0.04 | (n.a.) | ||||||||||
| Ref. 49 | −0.49 ± 0.14 | (46) | ||||||||||
| Ref. 51 | 0.42 ± 0.07 | (n.a.) | ||||||||||
| Ref. 52 | 0.41 ± 0.03 | (13) | ||||||||||
| Ref. 7 | 0.41 ± 0.02 | (55) | ||||||||||
| Ref. 53 | 0.49 ± 0.09 | (15) | ||||||||||
| Ref. 5 | −0.57 ± 0.18 | (38) | 0.44 ± 0.16 | (13) | ||||||||
| Ref. 54 | 0.49 ± 0.08 | (10) | ||||||||||
| Ref. 37 | 0.36 ± 0.11 | (54) | ||||||||||
| Average of literature data | −0.52 ± 0.08 | (2SD) | −0.12 ± 0.07 | (2SD) | 0.43 ± 0.08 | (2SD) | −1.00 ± 0.07 | (2SD) | −1.05 ± 0.07 | (2SD) | ||
Results obtained in the SOL mode for samples and standards are given in Table 4 relative to ICP and to SRM1400 for convenient comparisons with results obtained in the LA mode. The δ44/42Ca dataset displays values spanning a range of 2.50‰, which is almost the entire natural variability described so far. The four deciduous teeth exhibit the most 44Ca-depleted compositions of the dataset, with an average δ44/42CaICP of −2.22 ± 0.21‰ (2SD, n = 4) while the two wisdom teeth have less 44Ca-depleted values (−1.48 ± 0.19‰, 2SD). Igneous FAPs represent the most 44Ca-enriched apatites, with notably MD1 yielding a value of −0.11 ± 0.16‰ (2SD, n = 6). Synthetic apatites HAPp1 and HAPp2 display quite 44Ca-enriched compositions as well, with δ44/42CaICP values of −0.14 ± 0.06‰ (n = 2) and −0.17 ± 0.01‰ (n = 2) respectively, corresponding to −1.10 ± 0.06‰ (n = 2) and −1.07 ± 0.01‰ (n = 2) when expressed relative to SRM1400.
| Sample ID | A-solution mode | B-LA mode | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| d-cusp mm | n | δ44/42Ca | δ43/42Ca | d-cusp mm | n | δ44/42Ca | δ43/42Ca | 87Sr2+/44Ca+ | |||||||||||
| ‰ SRM | ‰ ICP | 2SD | ‰ SRM | ‰ ICP | 2SD | ‰ SRM | 2SD | 2SE | ‰ SRM | 2SD | 2SE | ||||||||
| Igneous apatites | BRM | — | 4 | 0.98 | −0.26 | ±0.07 | 0.50 | −0.14 | ±0.15 | 36 | 1.49 | ±0.56 | 0.10 | 0.78 | ±0.33 | 0.06 | 1.1 × 10−03 | ||
| BRZa | — | 6 | 1.09 | −0.15 | ±0.10 | 0.58 | −0.06 | ±0.06 | 65 | 1.52 | ±0.88 | 0.11 | 0.85 | ±0.45 | 0.06 | 9.0 × 10−04 | |||
| DUR | — | 11 | 0.75 | −0.49 | ±0.08 | 0.39 | −0.25 | ±0.07 | 65 | 1.66 | ±0.69 | 0.09 | 0.99 | ±0.36 | 0.04 | 1.4 × 10−03 | |||
| MD1 | — | 6 | 1.13 | −0.11 | ±0.16 | 0.58 | −0.06 | ±0.10 | 90 | 1.59 | ±0.66 | 0.07 | 0.84 | ±0.38 | 0.04 | 1.0 × 10−03 | |||
| MRCa | — | 4 | 0.59 | −0.65 | ±0.08 | 0.31 | −0.33 | ±0.07 | 95 | 1.54 | ±0.56 | 0.06 | 0.81 | ±0.33 | 0.03 | 2.1 × 10−03 | |||
| Tooth enamel | BMM3 | 0.60 | 9 | −0.31 | −1.55 | ±0.19 | −0.16 | −0.80 | ±0.13 | 0.60 | 27 | −0.34 | ±0.81 | 0.16 | −0.06 | ±0.38 | 0.07 | 5.3 × 10−04 | |
| HPME | — | 4 | −0.18 | −1.42 | ±0.02 | −0.09 | −0.72 | ±0.05 | — | 32 | −0.36 | ±0.76 | 0.14 | −0.05 | ±0.43 | 0.08 | 2.9 × 10−04 | ||
| BME1 | — | 3 | −0.85 | −2.09 | ±0.07 | −0.40 | −1.03 | ±0.08 | — | 16 | −0.63 | ±1.16 | 0.31 | −0.23 | ±0.62 | 0.17 | 2.2 × 10−04 | ||
| BMC | BMCa 5sx | 1.06 | 4 | −1.09 | −2.33 | ±0.13 | −0.57 | −1.21 | ±0.09 | 1.20 | 9 | −0.93 | ±0.82 | 0.32 | −0.36 | ±0.57 | 0.22 | 2.3 × 10−04 | |
| BMCa 6sx | 1.33 | 4 | −1.15 | −2.39 | ±0.06 | −0.59 | −1.22 | ±0.07 | |||||||||||
| BMCa 7sx | 2.15 | 2 | −1.15 | −2.39 | ±0.07 | −0.61 | −1.25 | ±0.06 | 2.31 | 6 | −1.10 | ±0.90 | 0.47 | −0.44 | ±0.66 | 0.34 | 2.6 × 10−04 | ||
| BMCa 8sx | 2.47 | 4 | −1.11 | −2.35 | ±0.16 | −0.55 | −1.19 | ±0.13 | |||||||||||
| BMCa 9sx | 3.62 | 4 | −1.02 | −2.27 | ±0.15 | −0.51 | −1.15 | ±0.11 | 3.62 | 5 | −1.17 | ±0.51 | 0.32 | −0.46 | ±0.31 | 0.19 | 2.7 × 10−04 | ||
| BMC average | −1.11 | −2.35 | ±0.10 | −0.57 | −1.20 | ±0.08 | — | 20 | −1.04 | ±0.72 | 0.17 | −0.41 | ±0.50 | 0.12 | |||||
| PBC | PBCa 1sx | 0.65 | 4 | −0.96 | −2.20 | ±0.13 | −0.52 | −1.16 | ±0.10 | 0.65 | 7 | −0.98 | ±0.92 | 0.43 | −0.40 | ±0.55 | 0.25 | 2.4 × 10−04 | |
| PBCa 3sx | 1.99 | 3 | −1.10 | −2.34 | ±0.01 | −0.69 | −1.33 | ±0.10 | 1.99 | 4 | −1.18 | ±0.69 | 0.55 | −0.47 | ±0.37 | 0.30 | 2.4 × 10−04 | ||
| PBCa 4sx | 3.27 | 5 | −0.96 | −2.20 | ±0.09 | −0.49 | −1.13 | ±0.05 | 3.27 | 6 | −0.78 | ±0.79 | 0.41 | −0.29 | ±0.41 | 0.21 | 2.4 × 10−04 | ||
| PBC average | −1.01 | −2.25 | ±0.16 | −0.57 | −1.21 | ±0.21 | — | 17 | −0.96 | ±0.84 | 0.21 | −0.38 | ±0.46 | 0.12 | |||||
| VBI | VBIa 10sx | 2.33 | 2 | −0.92 | −2.16 | ±0.04 | −0.50 | −1.13 | ±0.29 | 2.33 | 18 | −0.89 | ±0.84 | 0.21 | −0.35 | ±0.43 | 0.11 | 2.9 × 10−04 | |
| VBIa 11sx | 1.24 | 3 | −0.73 | −1.97 | ±0.07 | −0.36 | −1.00 | ±0.02 | 1.24 | 18 | −0.76 | ±0.84 | 0.21 | −0.29 | ±0.51 | 0.13 | 2.9 × 10−04 | ||
| VBIa 12sx | 0.25 | 3 | −1.24 | −2.48 | ±0.04 | −0.63 | −1.27 | ±0.03 | 0.45 | 18 | −1.00 | ±0.64 | 0.16 | −0.40 | ±0.41 | 0.10 | 2.9 × 10−04 | ||
| VBI average | −0.96 | −2.20 | ±0.52 | −0.50 | −1.13 | ±0.27 | — | 56 | −0.89 | ±0.78 | 0.10 | −0.35 | ±0.44 | 0.06 | |||||
| LA stds | SRM1400 powder | 26 | 0* | −1.24 | ±0.13 | 0* | −0.64 | ±0.16 | — | — | — | — | — | — | — | — | |||
| SRM1400-SPS | 11 | 0* | −1.18 | ±0.16 | 0* | −0.57 | ±0.10 | — | — | — | — | — | — | — | — | ||||
| SRM1400-gold | — | 0* | — | — | 0* | — | — | 24 | 0.12 | ±0.68 | 0.14 | 0.15 | ±0.37 | 0.08 | 8.7 × 10−04 | ||||
| HAPp1-SPS | 2 | 1.10 | −0.14 | ±0.06 | 0.59 | −0.04 | ±0.00 | 31 | 1.11 | ±0.77 | 0.14 | 0.73 | ±0.42 | 0.08 | 2.7 × 10−04 | ||||
| HAPp2-SPS | 2 | 1.07 | −0.17 | ±0.01 | 0.51 | −0.12 | ±0.08 | 192 | 1.06 | ±0.64 | 0.05 | 0.58 | ±0.45 | 0.03 | 3.8 × 10−03 | ||||
4.2. LA mode results
A total of 857 laser ablation analyses were carried out throughout 3 sessions, lasting 3 to 5 days each. As explained in Section 3.2., the 87Sr/86Sr radiogenic ratio used for the correction of Sr interferences was set at 0.7103. HAPp2-SPS, analysed 192 times, is the material with the highest Sr levels of the dataset (87Sr2+/44Ca+ of about 3.8 × 10−3). Its δ44/42CaSRM value was better corrected for (i.e. minimized difference between LA and SOL δ44/42CaSRM values) when using a fSr2+ mass discrimination coefficient of 1.1, which was set as the default value for the entire dataset. HAPp2-SPS displayed a δ44/42CaSRM value of 1.06 ± 0.05‰ (2SE, n = 192) in the LA mode and yielded a value of 1.07 ± 0.01‰ (2SD, n = 2) in the SOL mode. The exponential mass discrimination coefficient for corrected Ca isotope ratios in the instrument (fCa) yielded an average value of 1.70 and was stable through time. Machine induced mass fractionation displayed a mean value of 4% per amu.38 These observations were identical to the measured values in the SOL mode and indicate a similar instrumental isotopic fractionation of Ca in both modes.In order to verify the absence of major isobaric interferences, results in the LA mode were plotted in ln(43Ca/42Ca) vs. ln(44Ca/42Ca) diagrams after each sequence allowing the verification of the correct mass-dependent fractionation. When summarized in a δ43/42CaSRMvs. δ44/42CaSRM diagram (Fig. 1B), averaged results in the LA mode fall on a line displaying a strong correlation (R2 = 0.9963) and a 0.491 ± 0.013 (2SE) slope, in good agreement with the predicted slope of 0.507, according to the mass dependent fractionation exponential law. However, a 0.096 ± 0.014 (2SE) offset at origin reveals a systematic limited bias most probably due to an uncorrected isobaric interference affecting the 43Ca+ beam. All analyses obtained in the LA mode are presented along with their corresponding values obtained in the SOL mode in Table 4.
5. Discussion
5.1. LA–SOL mode correlations
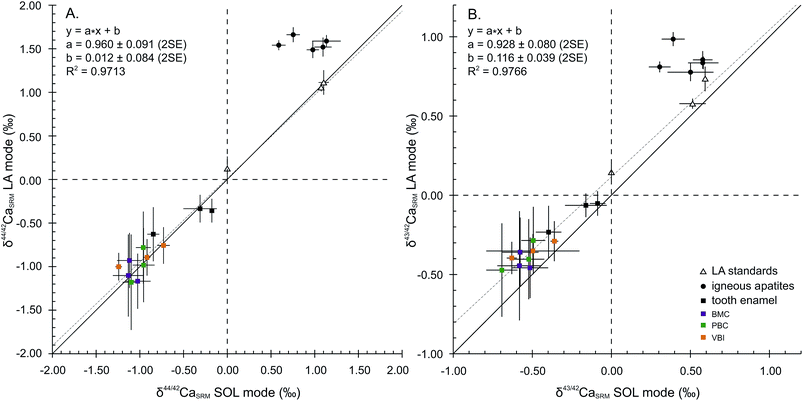
Considering the 44Ca/42Ca ratio, the values in the LA mode for all samples except FAPs compare well with those in the SOL mode (Fig. 2A), resulting in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 correlation and demonstrating global agreement between SOL and LA mode analyses. The regression line displays a squared correlation coefficient of 0.9713, a null offset at origin (0.012 ± 0.084‰, 2SE) and a slope of 0.960 ± 0.091 (2SE), statistically identical to 1. Isotopic analyses in the LA mode of the sintered standards HAPp1-SPS and SRM1400-gold yield values in agreement with those in the SOL mode. The δ44/42CaSRM value of HAPp1 is 1.11 ± 0.14‰ (2SE, n = 31) in the LA mode and 1.10 ± 0.06‰ (2SD, n = 2) in the SOL mode. This standard contains more than 10 times less Sr than HAPp2 (87Sr2+/44Ca+ ratio of 2.7 × 10−4 and 3.8 × 10−3 for HAPp1 and HAPp2, respectively). The δ44/42CaSRM value of HAPp2 is 1.07 ± 0.01‰ (2SD, n = 2) in the SOL mode and 1.06 ± 0.05 (2SE, n = 192) in the LA mode. The fact that HAPp1 and HAPp2 display the same Ca isotopic ratio in both the SOL and LA modes suggests that the doubly charged Sr interference correction is efficient in this range of Sr levels. The belt sintered SRM1400-gold secondary standard, which must have the same Ca isotopic composition as SRM1400-SPS, displayed the expected null δ44/42CaSRM composition when measured in the LA mode (0.12 ± 0.14‰, 2SE, n = 24).
1 correlation and demonstrating global agreement between SOL and LA mode analyses. The regression line displays a squared correlation coefficient of 0.9713, a null offset at origin (0.012 ± 0.084‰, 2SE) and a slope of 0.960 ± 0.091 (2SE), statistically identical to 1. Isotopic analyses in the LA mode of the sintered standards HAPp1-SPS and SRM1400-gold yield values in agreement with those in the SOL mode. The δ44/42CaSRM value of HAPp1 is 1.11 ± 0.14‰ (2SE, n = 31) in the LA mode and 1.10 ± 0.06‰ (2SD, n = 2) in the SOL mode. This standard contains more than 10 times less Sr than HAPp2 (87Sr2+/44Ca+ ratio of 2.7 × 10−4 and 3.8 × 10−3 for HAPp1 and HAPp2, respectively). The δ44/42CaSRM value of HAPp2 is 1.07 ± 0.01‰ (2SD, n = 2) in the SOL mode and 1.06 ± 0.05 (2SE, n = 192) in the LA mode. The fact that HAPp1 and HAPp2 display the same Ca isotopic ratio in both the SOL and LA modes suggests that the doubly charged Sr interference correction is efficient in this range of Sr levels. The belt sintered SRM1400-gold secondary standard, which must have the same Ca isotopic composition as SRM1400-SPS, displayed the expected null δ44/42CaSRM composition when measured in the LA mode (0.12 ± 0.14‰, 2SE, n = 24).
Igneous fluorapatites are tightly clustered and shifted from the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
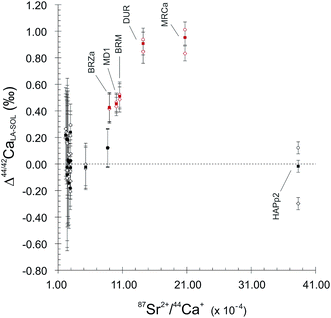
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 line, both for 44Ca/42Ca and 43Ca/42Ca ratios (Fig. 2). This reveals a difference of behaviour between igneous apatites on the one hand and enamel and sintered apatites on the other hand. Igneous apatites, which have false δ44/42CaSRM values by about 0.40 to 1.00‰, do not display any correlation when plotted in the LA–SOL diagrams (Fig. 2A and B). This group is entirely composed of igneous centimetric monocrystalline FAPs, all of which are richer in Sr than the rest of the dataset, with the exception of HAPp2. An inadequacy in the calculation of the Sr correction could be at the source of the discrepancies between the results obtained in the SOL and the LA modes.
1 line, both for 44Ca/42Ca and 43Ca/42Ca ratios (Fig. 2). This reveals a difference of behaviour between igneous apatites on the one hand and enamel and sintered apatites on the other hand. Igneous apatites, which have false δ44/42CaSRM values by about 0.40 to 1.00‰, do not display any correlation when plotted in the LA–SOL diagrams (Fig. 2A and B). This group is entirely composed of igneous centimetric monocrystalline FAPs, all of which are richer in Sr than the rest of the dataset, with the exception of HAPp2. An inadequacy in the calculation of the Sr correction could be at the source of the discrepancies between the results obtained in the SOL and the LA modes.
Considering now the 43Ca/42Ca ratio, the values in the LA mode of all samples except FAPs compare well with those in the SOL mode but are systematically offset by about +0.1‰ (Fig. 2B). Precisely, the regression line displays a squared correlation coefficient of 0.9766, an offset at origin of 0.116 ± 0.039‰ (2SE) and a slope of 0.928 ± 0.080 (2SE). The systematic offset between the SOL and the LA modes suggests that an uncorrected interference, probably linked to Sr double charge, permanently affects the 43Ca/42Ca ratio in the LA mode.
5.2. Doubly charged Sr interference corrections
Mass fractionation is the process by which isotopes are transmitted in the mass spectrometer according to their mass, given the exponential law relationship:| f = ln(r/R)/ln(M1/M2) | (3) |
5.3. Variations of Ca isotopic compositions in enamel
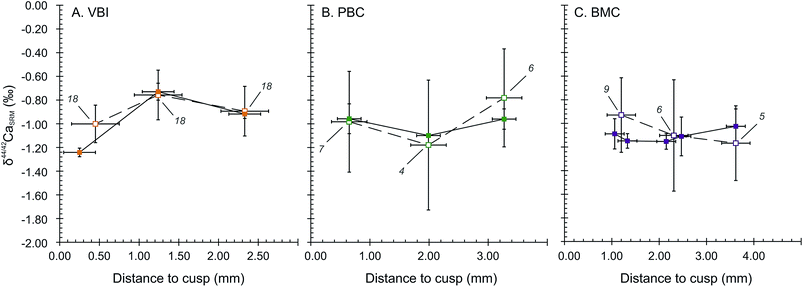
The wisdom and deciduous teeth analysed for Ca isotope compositions exhibit significantly different bulk δ44/42Ca values in the SOL mode. Deciduous teeth are depleted in Ca heavy isotopes, with an average δ44/42CaSRM of −0.98 ± 0.21‰ (2SD, 4 teeth). These are significantly different from the two wisdom teeth (−0.24 ± 0.19‰, 2SD), corresponding to a shift of about +0.74 ± 0.29‰ from deciduous to wisdom teeth. The LA mode also accounts for an average shift of +0.53 ± 0.36‰ between deciduous and wisdom teeth, respectively being −0.88 ± 0.36‰ (2SD, 4 teeth) and −0.35 ± 0.03‰ (2SD, 2 teeth). The significantly 44Ca-depleted compositions of deciduous teeth are likely to be the result of the influence of milk in the early life diet because the Ca isotope composition of human milk has a particularly 44Ca-depleted composition, with δ44/42CaICP values around −1.68 ± 0.43‰ (2SD, n = 4)8 while the European diet is thought to lie around −1.08‰ in average.46 The observed shift between the δ44/42Ca values of deciduous and wisdom teeth is thus likely to be induced by a transition from a milk based diet to a plant and meat based diet.The results of micro-sampled deciduous tooth enamel are presented in Fig. 4, where the δ44/42CaSRM values acquired in the SOL and LA modes are plotted with respect to the distance to the tip of the tooth cusp. The results obtained in the SOL mode reveal no distinguishable variation within the tooth enamel for the PBC and BMC canines (Fig. 4B and C), while the VBI incisor displays a strong variation in δ44/42CaSRM values, with a shift from −1.24 ± 0.04‰ to −0.73 ± 0.07‰ from 0.25 to 1.24 mm distance to the cusp (Fig. 4A). The δ44/42CaSRM results in the LA mode are consistent with those in the SOL mode, although the reduced number of analyses per point (4 to 9) is responsible for some apparent discrepancies between the two modes for the PBC and BMC canines. For all tooth samples, discrepancy in the results between the SOL and LA modes can also be explained by local variations, because all laser rasters could not be processed exactly where the associated micro-samplings have been. The δ44/42CaSRM variations in VBI along the enamel growth axis are most probably linked to dietary or physiological transitions during the formation of deciduous incisors. The mineralisation of human deciduous incisors is achieved at least 6 months before the complete formation of canine crowns, after birth.47 This early formation of incisors could explain the recording of early transitions in Ca sources.
6. Conclusion
We demonstrate in the article that the laser ablation technique can be used to measure Ca isotope compositions in biological, but not igneous, apatites. However, only the δ44/42Ca ratio yields accurate values, the δ43/42Ca ratio being systematically offset by about 0.1‰. We stress that appropriate correction of Sr double charge interferences and use of matrix-matched standards are of crucial importance to obtain accurate δ44/42Ca values. We also show using calculations that the offset at origin of the δ43/42Ca vs. δ44/42Ca regression line is the most sensible outcome when optimizing the correction of Sr double charge interferences. Despite the use of an extensive correction of the interferences due to Sr double charges, which considers the fractionation factor of Sr2+ and the value of the 87Sr/86Sr as variables, we were not able to find accurate δ44/42Ca values for the igneous apatites. We hypothesize that the mismatch is probably due to different matrix textures and compositions between the sintered microcrystalline fluorine-free standards and the macrocrystalline fluorine-rich samples.The present study opens up perspectives for the measurements of Ca isotopes in fossil vertebrates with a minimum of sample preparation and destruction. However, providing an adapted matrix-matched strategy, the technique can also be applied to carbonate Ca calcified tissues, such as shells, tests and otoliths.
Acknowledgements
The laser ablation device was funded by the Fonds Recherche of the Ecole Normale Supérieure de Lyon and this study was supported by the Bullukian and the Mérieux foundations. The authors are grateful to B. Reynard and G. Bonnefont for SPS sintering experiments. F. Albarède and E. Albalat are thanked for their help and advice on MC-ICPMS theory.References
- J. Skulan, D. J. DePaolo and T. L. Owens, Geochim. Cosmochim. Acta, 1997, 61, 2505–2510 CrossRef CAS.
- J. Skulan and D. DePaolo, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 13709–13713 CrossRef CAS.
- M. T. Clementz, P. Holden and P. L. Koch, Int. J. Osteoarchaeol., 2003, 13, 29–36 CrossRef PubMed.
- D. DePaolo, Rev. Mineral. Geochem., 2004, 55, 255–288 CrossRef CAS.
- L. M. Reynard, G. M. Henderson and R. E. M. Hedges, Geochim. Cosmochim. Acta, 2010, 74, 3735–3750 CrossRef CAS PubMed.
- A. Heuser, T. Tütken, N. Gussone and S. J. G. Galer, Geochim. Cosmochim. Acta, 2011, 75, 3419–3433 CrossRef CAS PubMed.
- A. D. Melin, B. E. Crowley, S. T. Brown, P. V. Wheatley, G. L. Moritz, F. T. Yit Yu, H. Bernard, D. J. DePaolo, A. D. Jacobson and N. J. Dominy, Am. J. Phys. Anthropol., 2014, 154, 633–643 CrossRef PubMed.
- N.-C. Chu, G. M. Henderson, N. S. Belshaw and R. E. M. Hedges, Appl. Geochem., 2006, 21, 1656–1667 CrossRef CAS PubMed.
- S. Graham, N. Pearson, S. Jackson, W. Griffin and S. Y. O'Reilly, Chem. Geol., 2004, 207, 147–169 CrossRef CAS PubMed.
- I. Horn, R. Schoenberg and F. von Blanckenburg, J. Anal. At. Spectrom., 2006, 21, 211 RSC.
- J. Košler, R. Pedersen, C. Kruber and P. Sylvester, J. Anal. At. Spectrom., 2006, 21, 214 RSC.
- I. Horn, F. von Blanckenburg, R. Schoenberg, G. Steinhoefel and G. Markl, Geochim. Cosmochim. Acta, 2006, 70, 3677–3688 CrossRef CAS PubMed.
- I. Horn and F. von Blanckenburg, Spectrochim. Acta, Part B, 2007, 62, 410–422 CrossRef PubMed.
- F.-X. D'Abzac, A.-M. Seydoux-Guillaume, J. Chmeleff, L. Datas and F. Poitrasson, J. Anal. At. Spectrom., 2012, 27, 108 RSC.
- C. K. I. Sio, N. Dauphas, F.-Z. Teng, M. Chaussidon, R. T. Helz and M. Roskosz, Geochim. Cosmochim. Acta, 2013, 123, 302–321 CrossRef CAS PubMed.
- W. Dziony, I. Horn, D. Lattard, J. Koepke, G. Steinhoefel, J. a. Schuessler and F. Holtz, Chem. Geol., 2014, 363, 101–113 CrossRef CAS PubMed.
- F.-X. d'Abzac, A. D. Czaja, B. L. Beard, J. J. Schauer and C. M. Johnson, Geostand. Geoanal. Res., 2014, 38, 293–309 CrossRef PubMed.
- M. Oeser, S. Weyer, I. Horn and S. Schuth, Geostand. Geoanal. Res., 2014, 38, 311–328 CrossRef CAS PubMed.
- E. D. Young, R. D. Ash, A. Galy and N. S. Belshaw, Geochim. Cosmochim. Acta, 2002, 66, 683–698 CrossRef CAS.
- P. E. Janney, F. M. Richter, R. A. Mendybaev, M. Wadhwa, R. B. Georg, E. B. Watson and R. R. Hines, Chem. Geol., 2011, 281, 26–40 CrossRef CAS PubMed.
- J. A. Schuessler and F. von Blanckenburg, Spectrochim. Acta, Part B, 2014, 98, 1–18 CrossRef CAS PubMed.
- S. E. Jackson and D. Günther, J. Anal. At. Spectrom., 2003, 18, 205–212 RSC.
- P. R. Craddock, O. J. Rouxel, L. A. Ball and W. Bach, Chem. Geol., 2008, 253, 102–113 CrossRef CAS PubMed.
- J. Míková, J. Košler and M. Wiedenbeck, J. Anal. At. Spectrom., 2014, 29, 903 RSC.
- M. D. Norman, M. T. McCulloch, H. S. C. O'Neill and G. M. Yaxley, J. Anal. At. Spectrom., 2006, 21, 50 RSC.
- T. Hinners, R. Hughes, P. Outridge, W. J. Davis, K. Simon and D. R. Woolard, J. Anal. At. Spectrom., 1998, 13, 963–970 RSC.
- M. M. Schweissing and G. Grupe, J. Archaeol. Sci., 2003, 30, 1373–1383 CrossRef.
- A. Ugarte, N. Unceta, C. Pécheyran, M. A. Goicolea and R. J. Barrio, J. Anal. At. Spectrom., 2011, 26, 1421 RSC.
- V. Balter and C. Lécuyer, Geochim. Cosmochim. Acta, 2004, 68, 423–432 CrossRef CAS.
- E. Champion, Acta Biomater., 2013, 9, 5855–5875 CrossRef CAS PubMed.
- V. Balter, P. Telouk, B. Reynard, J. Braga, F. Thackeray and F. Albarède, Geochim. Cosmochim. Acta, 2008, 72, 3980–3990 CrossRef CAS PubMed.
- V. Balter and B. Reynard, Bone, 2008, 42, 229–234 CrossRef CAS PubMed.
- V. Balter, J. Braga, P. Télouk and J. F. Thackeray, Nature, 2012, 10–12 Search PubMed.
- T. Tacail, E. Albalat, P. Télouk and V. Balter, J. Anal. At. Spectrom., 2014, 29, 529 RSC.
- M. Schiller, C. Paton and M. Bizzarro, J. Anal. At. Spectrom., 2012, 27, 38 RSC.
- J.-I. Kimura, T. Takahashi and Q. Chang, J. Anal. At. Spectrom., 2013, 28, 945–957 RSC.
- M. E. Wieser, D. Buhl, C. Bouman and J. Schwieters, J. Anal. At. Spectrom., 2004, 19, 844 RSC.
- C. Maréchal, P. Télouk and F. Albarède, Chem. Geol., 1999, 156, 251–273 CrossRef.
- F. Albarède, P. Telouk, J. Blichert-Toft, M. Boyet, A. Agranier and B. Nelson, Geochim. Cosmochim. Acta, 2004, 68, 2725–2744 CrossRef PubMed.
- Y. Asahara, T. Tanaka and H. Kamioka, Earth Planet. Sci. Lett., 1995, 133, 105–116 CrossRef CAS.
- M. S. A. Horstwood, J. A. Evans and J. Montgomery, Geochim. Cosmochim. Acta, 2008, 72, 5659–5674 CrossRef CAS PubMed.
- P. Stille, A. D. Schmitt, F. Labolle, M. C. Pierret, S. Gangloff, F. Cobert, E. Lucot, F. Guéguen, L. Brioschi, M. Steinmann and F. Chabaux, C. R. Geosci., 2012, 344, 297–311 CrossRef CAS PubMed.
- R. S. Hindshaw, B. Bourdon, P. A. E. Pogge von Strandmann, N. Vigier and K. W. Burton, Earth Planet. Sci. Lett., 2013, 374, 173–184 CrossRef CAS PubMed.
- M. S. Fantle, Geochim. Cosmochim. Acta, 2015, 148, 378–401 CrossRef CAS PubMed.
- P. L. Roeder, D. Macarthur, X. D. Ma, G. R. Palmer and A. N. Mariano, Am. Mineral., 1987, 72, 801–811 CAS.
- A. Heuser and A. Eisenhauer, Bone, 2010, 46, 889–896 CrossRef CAS PubMed.
- S. Hillson, Dental Anthropology, Cambridge University Press, Cambridge, 1996 Search PubMed.
- A. Heuser and A. Eisenhauer, in Geostandards and Geoanalytical Research, 2008, vol. 32, pp. 311–315 Search PubMed.
- R. S. Hindshaw, B. C. Reynolds, J. G. Wiederhold, R. Kretzschmar and B. Bourdon, Geochim. Cosmochim. Acta, 2011, 75, 106–118 CrossRef CAS PubMed.
- C. A. Colla, J. Wimpenny, Q.-Z. Yin, J. R. Rustad and W. H. Casey, Geochim. Cosmochim. Acta, 2013, 121, 363–373 CrossRef CAS PubMed.
- D. Hippler, A.-D. Schmitt, N. Gussone, A. Heuser, P. Stille, A. Eisenhauer and T. F. Nägler, Geostand. Geoanal. Res., 2003, 27, 13–19 CrossRef CAS PubMed.
- C. Holmden and N. Bélanger, Geochim. Cosmochim. Acta, 2010, 74, 995–1015 CrossRef CAS PubMed.
- B. Page, T. Bullen and M. Mitchell, Biogeochemistry, 2008, 88, 1–13 CrossRef CAS.
- J. L. Skulan, T. D. Bullen, A. D. Anbar, J. E. Puzas, L. C. Shackelford, A. LeBlanc and S. M. Smith, Clin. Chem., 2007, 53, 1153–1155 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ja00239g |
| This journal is © The Royal Society of Chemistry 2016 |