Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Cost-effectiveness and community impacts of two urine-collection programs in rural South Africa†
Elizabeth
Tilley

ETH Zurich, NADEL, Clausiusstrasse 37, Zurich, Switzerland. E-mail: elizabeth.tilley@eawag.ch
First published on 6th January 2016
Abstract
As the number of technologies and programming approaches for improving global sanitation grows, there is an increasing need to evaluate the cost-effectiveness of each so that policy can be driven by informed decisions that consider cost as well as impact. I use data from two different urine-collection programs that were implemented in rural South Africa to model the cost-effectiveness of each in terms of the cost per litre of urine collected and the cost per household, over a range of operational values. One program was based on conditional cash transfers with the aim of increasing toilet use, while the second program was centrally managed and designed to be logistically simple for the municipality. In comparing the results of the two models I find a paradox. Urine that is collected from households by the municipality is less expensive than incentivized urine collection on both a volumetric and household basis, but only at urine collection rates that cannot be achieved without incentives. Conversely, the incentivized collection is more cost effective when the collection rates are low, but at rates that would correspond to very low incentive prices, rendering the incentive scheme useless. My results illustrate the importance of cost-effectiveness analysis as a tool in sanitation programming but I also highlight the need to view the data with a more nuanced approach that considers the complexities of program implementation in poor, rural communities as the mathematical optimal may not correspond to a realistic, or socially desirable one.
Water impactThe cost-effectiveness of two different urine-collection models are compared in terms of households served and the volume of urine collected. Results show that conditional-cash transfers are generally more expensive, but increase toilet use, the quantity of urine available for nutrient recovery and generate a multitude of financial benefits for communities. This work shows the importance of cost-effectiveness analysis for novel approaches to sanitation programming. |
1 Introduction
Although there have been regional successes, the Millennium Development Goal (MDG) to halve the number of people without access to sanitation has not been met: 2.5 billion people still lack access to improved sanitation.1 Apart from being culturally, geographically and technically challenging, solving the sanitation problem will be expensive. The cost of meeting the target has been estimated to be about $332 billion2 and although benefit-cost ratios are generally greater than one, and sometimes significantly higher3–5 sufficient funds have not been mobilized.More than a century ago, the industrialized world achieved near-universal sanitation because, faced with huge, looming public health catastrophes, governments invested massively to install sewers and treatment plants for their relatively small, but growing cities.6 Now, governments in low-income countries, faced with fast growing cities and mega-slums, already at unprecedented densities7 are too poor, water-stressed and over-burdened to take on similar sewerage projects. Instead of providing sewers, the focus has mostly shifted towards providing onsite sanitation technologies, like pit latrines or septic tanks. Indeed, sanitation progress is measured by counting the number of toilet facilities that have been installed.1
Although sewers are exorbitantly expensive to build and operate, they are financed with government money and generally subsidized for those who are permitted a connection. Conversely, the costs for constructing, maintaining, and emptying onsite toilet technologies are borne by the households themselves. The result is that the poor end up paying significantly more for sanitation than the (mostly) rich customers connected to sewers.8 In Bangladesh and Peru, onsite sanitation options were found to cost between 3–7% of the annual income of poor households, respectively.9 However, households delay purchasing an adequate solution because they aspire to something that they cannot afford (usually a flush toilet), or that which may not even be possible in water-stressed areas (ibid). Perhaps unsurprisingly, the poor, with limited resources to get what they want, make do with what is available, which may be nothing: open defecation persists at alarming rates and is increasing in some regions.10
To compensate for the lack of centralized technology, much effort has therefore focused on increasing demand, both by trying to lift budget constraints and by changing preferences. Subsidies, in the form of money and/or materials, have been used to increase demand and encourage households to build a toilet of their choosing. Unfortunately, subsidies are difficult to target (get the money to the right person), monitor (ensure that a toilet was actually built) or induce behaviour change (motivate the family to use it).11 Even if families have a facility, and are motivated to use it, maintenance can be expensive; one study found that the cost of sustaining a facility over 20 years, can cost 5–20 times as much as the purchase price.12
In response to the realization that millions of dollars had been spent on constructing facilities, but that open defecation was still being practiced, the Nirmal Gram Puraskar (NGP) program in India was launched in 2003. The NGP was innovative in that it offered cash incentives to communities for not only having sanitation facilities, but for remaining open-defecation-free (ODF).13 However, questions about the quality and transparency of the monitoring required to deem a community ODF have been raised.14 The impact of this program, especially in terms of cost effectiveness (e.g. dollars per new toilet user) has not been determined. Only recently was the cost effectiveness of CLTS (a much older program) in 3 countries analysed; the results were surprisingly poor. In Mozambique, an investment of $5 per person per year, resulted in a 5% increase in “basic faecal containment and latrine use”‡.15 This is not a huge sum of money, but the results are poor regardless, and indicate that constant, universal use cannot be accomplished with one-time interventions. One alternative would be sustained transfers, after construction, to incentivize continued use, i.e. conditional cash transfers (CCTs).
Therefore, in an effort to understand if and how conditional cash transfers could be used to increase and sustain toilet use at the household level, I conducted a field experiment in rural eThekwini, South Africa where a large number of Urine-Diverting Dry Toilets (UDDTs) had been installed. Specifically, I offered cash payments to toilet owners based on the volume of urine delivered to the collection point, and tested the impact of varying the payment on toilet use. The results of this Community-Delivered Urine (CDU) experiment showed that payments of 1 South African Rand per L (about 0.1 € L−1) resulted in a significant increase in toilet use and also, because the urine that was collected was transported away, a decrease in the volume of urine that was discharged to the environment.
I also tested an alternative to this program, specifically household collection of urine by the municipality: the Municipal Collected Urine (MCU) program. In this program, employees from the eThekwini municipality went house to house to collect the urine that accumulated in storage tanks. The service was free to the households but they did not receive any compensation for their urine. This system was simple, but labour-intensive for the Municipality, and most importantly, offered no reason for toilet owners to use the toilet more.
Using the empirical data collected from these two interventions, I develop models that are used to predict several metrics of cost-effectiveness over a range of operational parameters for both the Community-Delivered and Municipal Collection programs. Specifically, I determine if, and over what range of use (i.e. urine production) one program is more cost efficient than the other on a volumetric (cost per litre of urine) or household basis. Furthermore, I investigate whether the findings are realistic and achievable in the context and examine the implications of each program on community welfare. This research addresses recent calls for increased cost-effectiveness studies that are both contextual and comparable,16 and contributes to the limited body of evidence about the most efficient ways to increase and maintain sanitation services in low-income countries.
The structure of the paper is as follows: the two experimental programs are explained in more detail in section 2. The data collected and the model construction are explained in section 3. The model results are presented in section 4. The conclusions and recommendations about how these models can be used in future applications are discussed in section 5.
2 Background and program description
2.1 Urine-diversion toilet program
Faced with a massive sanitation backlog at the end of apartheid, the authority responsible for water and sanitation in the municipality around Durban—eThekwini Water and Sanitation (EWS)—decided not to extend the water-intensive sewer network into the dispersed peri-urban and rural areas, and instead installed Urine-Diverting Dry Toilets (UDDT).17 By the end of 2010, over 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 UDDTs had been installed.18
000 UDDTs had been installed.18
The UDDT works on the principle of separation: a specially designed toilet separates the urine from the faeces at the point of generation. The urine can be infiltrated into the ground or collected for later use while the faeces fall into one of two dehydration chambers. One chamber is filled while the faeces in the second chamber are allowed to dehydrate, reduce in volume, become hygienized and eventually, discarded safely.19
Urine, on the other hand contains all of the nutrients that are needed by plants: nitrogen, phosphorus, potassium, and sulphur, among others.20 For that reason, urine can easily be applied as a type of liquid fertilizer and although effective, the work is labour-intensive and unpleasant.21,22 Recovering nutrients from urine in the form of a dry, powered fertilizer not only makes it easier to store and apply, but is an important treatment step to prevent the transmission of persistent pathogens.23 The VUNA project, in which this research was embedded (http://www.vuna.ch), was an interdisciplinary project that examined a variety of technologies to convert urine-derived nutrients into safe, useable products24,25
Therefore, the goal of the two urine collection programs (detailed below) was to not only generate a large quantity of urine to use for fertilizer production, but to increase sanitation coverage and use of the not always intuitive UDDTs.
2.2 Community-Delivered Urine (CDU)
The Community-Delivered Urine program was designed to determine if and how the use of Urine-Diverting Dry Toilets (UDDTs) could be increased using conditional cash transfers. Cash transfers were made to participant households based on the volume of urine collected from the UDDT and brought to a collection point (i.e. a centrally located drop-off point). In a first phase, I offered 0.5 Rand per litre (R L−1) of urine delivered to a community collection point, and in a second phase (about 4 months later), I offered 1 R L−1. The urine tanks provided to households were 20 L (the same as in the MCU model) so the total value for a full tank was either 10 R or 20 R though any quantity of urine could be delivered for payment. The number of participating households as well as the volume of urine delivered was recorded for each incentive price. Therefore, I was able to quantify the effect of the changing incentive price on both the quantity of urine collected and household participation (147 households were invited to participate). These data were used to predict the elasticity of the incentive price with respect to household participation and urine collection in the CDU model. The experimental data were collected in a single, rural community of eThekwini between 2012–2013.All work was approved by the local utility (eThekwini Water and Sanitation Unit: EWS) that is responsible for providing water and sanitation services to the area. Furthermore, the research was approved by the local Ward councilors (elected), and local chiefs (traditional). Prior to the intervention, respondents were read a text informing them about the nature of the research; given that many of the area residents were illiterate or had poor reading skills, the enumerators read the document to the respondent, although the document was also left at the household for future reference. All participating households were asked if they were willing to have their urine pipe retrofitted and told that they were a) not obliged to participate and b) could have it connected back at any time. None of the participating households requested a pipe disconnection.
A schematic of the CDU program is presented in Fig. 1. In the CDU program, participants brought their urine to a Collection Point (CP) during opening hours. There was always a fieldworker waiting at the CP who would weigh the urine tank, test the quality of the urine (as measured by conductivity (mS cm−1)), record the data and determine the correct payment. Urine was exchanged for tokens, which were then exchanged by the participant at local participating shops for cash. Local shop owners were paid a 10% commission for every token they exchanged, as a way of incentivizing them to participate and to maintain a supply of small change for urine-token customers. The token system ensured a high-degree of accountability, and was also convenient because transport from rural areas to formal cash points is expensive and would have been too burdensome for participants (if, for example, they were required to exchange vouchers at city banks).
Fieldworkers managed all of the data, the payments, and additionally, monitored the urine levels in the tanks used for storage at the collection points (1000 L plastic “Jojo” tanks, that are traditionally used for water storage). When the storage tanks were full, a team from the municipality (likely the same team that was responsible for the MCU) came to pump out the urine. The municipal team would arrive with a pump, a hose and an equivalent-sized storage tank on the back of a truck. Depending on the quantity of urine in the community and their other commitments and the time of day, the municipal team may have returned several times to repeat the emptying process. The fieldworkers (who manage the CPs) were from the communities in which they worked, and did not require transport to or from the site.
2.3 Municipal Collected Urine (MCU)
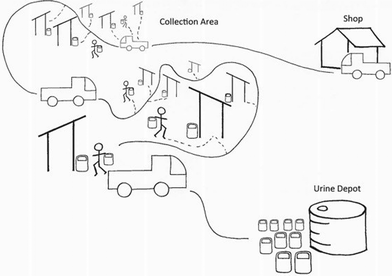
Normally, urine that is separated within the UDDTs drains into the ground, while faeces are stored in a dry, concrete chamber and allowed to dehydrate. In order to collect urine for this project, the urine pipes were diverted so that the urine could be collected in 20 L tanks. The Municipal Collected Urine (MCU) program is a centrally managed program that is relatively easy to operate, but does not offer an incentive to toilet owners to maintain or increase their use.The areas in which the MCU operates are rural: about 40 km away from central Durban. Collected urine is transported from the households and stored at a research facility (urine depot) until it can be used for fertilizer production and related research. A schematic of the MCU is presented in Fig. 2. There is a significant amount of driving and urine transport required in the MCU model: municipal workers start their day at the truck storage site (the “shop”). The team (1 driver and two labourers) drives to the field site and then begins the collection. The driver parks on the road, and the 2 labourers walk to the house (either together or separately), replace the full household tank with an empty one that the labourers bring, walk back to the truck, and put the full tank in the back of the truck. For safety and efficiency reasons, it is not possible for the driver to get out the vehicle to help; locking, unlocking and re-starting the vehicle after each collection would slow the process down considerably. The labourers have no way of knowing how much is in each tank and the number of tanks that can be emptied in a day is dictated by the distance between the house and the road, and the speed of the worker (which is a function of her fitness, the difficulty of the terrain, the temperature, etc.). An optimized system is under development26 but the case considered here is one in which the driving and walking routes, and the prioritization of houses is not optimized. When the day is finished the team drives to the urine depot; this is the site where all urine, from all sources is stored and processed into fertilizer. The municipal team dumps all the urine into large storage tanks, cleans all the household urine tanks and then returns to the shop before the end of the day.
3 Methodology
3.1 Model data
A cost-effectiveness model for both of the urine transport systems (MCU and CDU) was constructed to determine two outcome values: the cost per litre of urine collected, and the cost per household (cost per L and cost per HH, as above). Each model was built using five types of data: master variables, measured values, assumed values, literature values and calculated values. Most of the calculated values are used in subsequent calculations but the outcome values are also calculated values. All of the values and variables that were used in the construction of the models are presented in appendices A and B. Each type of data is discussed below.The master variables were manipulated in order to control the model output. The incentive price is the master variable in the CDU model; as it was changed, all calculated variables in the model were affected and the total cost of the program, for example could be modelled.
Measured values are those values that were measured in the field during the interventions. For example, the price of the 20 L Jerry Can was set to 65 R, as this was the actual price paid. When measured values were not available, values from the literature were used.
When no field or reference values were available or possible, assumptions were made. For example, I assumed a safety factor of 1.1 in the calculation of how many tanks the collection team should have when they go on a collection trip (i.e. 10% more storage space than necessary).
Calculated values are those intermediary values that were necessary to determine, in order to calculate the outcome variables. For example, the total cost per week was a calculated value that was then used in the determination of the outcome variables. The calculated values were determined using the equations that I developed and which I believe represent the way in which the variables interact and describe the experimental programs, with the fewest, and most probable assumptions.
Common to both models was the calculation of the volume produced. The volume produced refers to how much urine a household produces, irrespective of whether or not they participate in the collection program. The volume produced is simply the maximum amount of urine that could theoretically be collected, but the volume produced and the volume collected are not necessarily the same. The volume produced takes into account the number of adults in the family and the time that they spend at home. To estimate the volume produced, an average family size of 7 (3 adults, 4 children) in which 25% of the adults are employed full time (and spend 50% of their time away from home) and 50% of the children are in school full time (and spend 33% of their time away from home) is assumed. Using average urine production values of 1 litres per adult per day and 0.7 litres per child per day, the volumes are weighted according to the time spent at the home, and a family total is generated (4.95 litres per household per day) or 2475 L for the whole community per day. The calculations and variables for determining the volume produced are presented in appendix C.
Each model is run using a standard community size of households. Any size of community could be chosen, but this size was chosen to represent a realistic project area, and one that could be reasonably managed. The experimental areas for the different MCU and CDU programs included between 100–150 households but these were interspersed with non-participant households, because of the experimental nature of the programs (i.e. I took a random sample). By increasing the density (i.e., including all households within one area), 500 households represent what a full-scale program would look like in a standard rural community.
3.2 Community-Delivered Urine (CDU) model
The CDU model is constructed of several modules, which are composed of the relevant values and variables. The modules included in each of the models are: Volume collected, Labour, Transport, Materials and Capital costs. By grouping the values and variables into modules, disaggregated costs (e.g. for labour) can be more clearly calculated and understood. Fig. 3 shows the module linkages for the CDU model.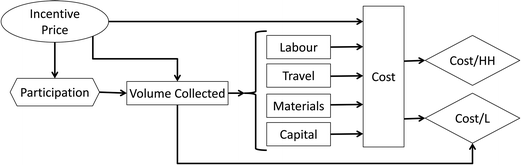 | ||
| Fig. 3 CDU model modules and linkages. Ovals represent master variables, hexagons represent calculated variables, rectangles are calculated modules, and diamonds are outcome variables. | ||
The master variable in the CDU model is the incentive price: it directly controls the participation rate, the volume collected, and the overall cost of the program (because an increase in the incentive price influences the total program cost). The participation rate is one of many calculated variables, but because of it's importance in determining the volume collected it is shown in the schematic for the sake of clarity. The volume collected directly influences the amount of labour, travel, materials and capital costs that in turn, contribute to the total cost of the program. The total volume of urine collected influences the cost per litre of urine; since the number of households is fixed, the cost per household is only indirectly influenced by the total cost, and not by the volume collected. Using this diagram as a basis for understanding the basic model structure, all of these modules and the key parameters and assumptions within each module are described in the following sections.
The volume that is collected at the collection points is calculated based on the data that were collected from the field experiment. The incentive price affects the quantity delivered through two mechanisms: the participation (i.e. the number of families who brought their urine tanks to the collection point) and the amount of volume that was collected from each family (as illustrated in Fig. 3). In other words, as the price offered increased, more people came to the collection points, and additionally, each person who came, brought more.
Participation and average volume collected data (per household per day) were measured at two different incentive prices: 0.5 R L−1 and 1 R L−1. At the time of the experiment, the minimum wage at EWS was 162 Rand per day, or about 20 R per hour. The incentive values were selected based on these hourly rates, assuming an average walking time of 30 minutes. Specifically, if 20 L were delivered at 0.5 R L−1, the payment would be 10 R for 30 minutes of work, which is equivalent to an hourly salary at minimum wage. The 1 R L−1 payment would correspond to double the minimum wage (40 R per hour). In reality, variations in walking time and volumes would affect the hourly rate for each participant, but as a foundation for determining a range of incentive values, it was useful.
I measured a 48% participation rate when 0.5 R L−1 was offered and a 74% participation rate when 1 R L−1 was offered. These participation rates correspond to a collected volume of 0.83 and 2.09 litres per household per day (L HH−1 day−1), respectively. When the participation and volume measurements are plotted against the incentive values, the slope, i.e. a coefficient relating of the incentive value to the measured parameters, can be determined. The participation constant (i.e. participation vs. incentive value) was determined to be 0.78 and the collected volume constant was 2.00. Certainly, a greater range of experimental values would be useful for developing a more robust model, but I have no option but to extrapolate and therefore the modelled results estimated beyond these points are theoretical.
Indeed, there is reason to believe that the relationship between participation and the incentive price may not be linear; as trust increases and information spreads, 100% participation may be achieved with only marginal increases in payment. However, due to time and financial limitations, only 4 months per intervention were possible. The results generated by the model are therefore, likely conservative and so represent even more costly estimates than would likely be achieved if the intervention had been run for an increased period of time, and beyond the highest payment values offered. An equation to predict the amount of urine delivered in a day must take into account both how much is delivered by each household, but also how many households are participating. In the model, the participation constant and the volume increase constant are included as measured values. The two empirical relationships can be combined into a single function to predict the volume collected through the following equation:
| Vol = HH × (volconst × incvalue) × (participconst × incvalue) | (1) |
| Vol = HH × volconst × participconst × incvalue2 | (2) |
| Vol = HH × 0.78 × 2 × incvalue2 | (3) |
However, if used directly, eqn (3) would pose two problems. As the incentive price increases, both the calculated percent participation and the calculated volume collected could theoretically exceed possible values (i.e. 100% participation, and the volume produced, respectively). To correct for this, the equation is adjusted in the model so that the calculated participation is forced to remain constant at calculated percentages that exceed 100% and the volume collected is forced to remain at the maximum produced per household (4.95 L HH−1 day−1). The relationship between the incentive price, volume produced, and participation is shown in Fig. 4.
The quantity of urine collected increases exponentially as a function of the incentive payment, until maximum participation is achieved (this occurs at an incentive payment of 1.285 R L−1). After this point, the urine collected increases linearly until the volume collected reaches the maximum possible value, i.e. the urine produced. After the point of maximum urine production (2.5 R L−1), no increase in the incentive price can increase the volume collected (assuming that people do not increase their intake of liquids unnaturally to push their production beyond normal levels). By manipulating the incentive price, this set of equations governs the amount of urine that is collected, and therefore the associated staff and infrastructure costs that are required to manage its collection. The volume of wasted urine is simply the difference between the volume of urine that is produced and the volume that is collected. The volume of wasted urine is the quantity of urine that is either collected in a different toilet, lost to the environment, or that overflows from the urine tank.
Fieldworkers are those community members who work at the collection points measuring urine and exchanging it for tokens. The number of participant visits that occur in a week dictates the amount of field staff; a single fieldworker can only handle a maximum of 60 visits a day (based on field experience). For every 60 visits (a function of the participation), an extra fieldworker day is added. Given the variability of participant visits, the model does not allow fieldworkers to work partial days.
A supervisor is required to come to the site to exchange tokens for cash at the token exchange points (shops), pay the rent on the storage rental sites, and generally supervise the program. The supervisor days are calculated to be 20% of the total number of field staff days, again, based on the field experience.
Supervisors are assumed to have other work and the model allows them to work partial days (i.e. full days are not charged).
The EWS staff component includes those who work for the municipality and who are responsible for coming to the site, emptying the urine from the collection points and then dropping it at the urine depot. EWS staff works in teams that includes 1 driver and 2 labourers, though depending on the requirements, several teams may work in parallel. The number of municipal staff days is based on the volume of urine that has to emptied, under the assumption that all urine is emptied from the site every week, i.e. urine generated one week can not be collected in the next one. This key assumption forces some inefficiency in the model, e.g. an extra team may need to be added to remove the last few hundred litres of urine if the entire team is occupied for 5 full days, but it also ensures a conservative estimate of emptying costs. For community relations and health, it is important that urine is not stored indefinitely on site with continuous carry overs; at a certain point, the storage tanks required would cover a significant portion of the town. Furthermore, a municipal presence helps to promote community acceptance.
The labour costs for municipal staff include partial days, based on the assumption that they can, and will work on other municipal projects (i.e. if emptying the CPs takes 3.5 days, 3.5 days of the teams' labour will be charged to this project).
Referring back to Fig. 3, the labour costs are directly influenced by the volume collected, i.e. the more urine that is collected at the collection points, the more staff, of all types, is required.
Field staff are recruited from the community in which the incentive program is operated and therefore do not require transport. Additionally, the benefit of hiring community members is an increase in rural employment and cohesion (i.e. problem resolution is more direct, etc.).
The transport module also includes transport for the supervisor. The supervisor only comes to do administration and management and drives a (1 tonne) pick-up truck. The supervisor only drives between the shop and the site; the distances and transport costs (e.g. related to fuel, oil, etc.) are calculated accordingly.
The number of 1000 L storage containers (“Jojo tanks”) is calculated based on the volume of urine that is collected and multiplied by a safety factor (i.e. a conservative multiplier) to account for variation, safety, and hygiene.
Included in this module are the costs associated with administering the incentive payments, specifically, the payments that are made to the shop owners for exchanging the tokens for cash, and the rent paid for the collection point space. Both of these values are based on the field values that were used during the actual interventions.
Working with urine requires proper personal protection equipment (PPE): gloves, boots, face masks and uniforms are required for each of the fieldworkers and for each member of the EWS emptying team. The model assumes that all PPE is replaced each year.
3.3 Municipal collected urine
The Municipal Collected Urine (MCU) model has a different structure than the CDU as shown in Fig. 5. This model has two master variables: the visit rate and the volume collected. The visit rate does not influence the volume collected, since the total amount of urine generated by toilet use is collected, regardless of the rate at which it can be collected. The volume collected is fixed (based on the average per household volumes measured during baseline measurements) and the cost is controlled by the speed at which that fixed volume can be collected. Each of the key variables, modules and assumptions are explained in detail below. | ||
| Fig. 5 CDU model modules and linkages. Ovals represent master variables, rectangles are calculated modules, and diamonds are outcome variables. | ||
The second master variable (which does not directly affect the volume collected, but is important for the calculation of the output variable cost per L) is the number of tanks that a team can collect in a day: the visit rate. To determine this field value, a time-motion study was conducted in the three different areas where the MCU was conducted. This was done to generate data about the time needed to arrive at, and transport the urine away from, each household. The time spent by each team doing one of the following activities was recorded: walking/carrying urine, driving, idle (breaks), and emptying (at the depot at the end of the day). Based on 3 days of measurements, I determined that a single collection team (1 driver with 2 collectors) could visit an average of 36 households in a day. The team had no information about the toilet usage and therefore, went to each house regardless of how much urine was in the tank. The variation in the number of households that a team could visit in a day is small (31–41) and most of the variation can be accounted for due to the density of houses, the difficulty of the terrain and the distance between the site and the depot. These values are used to inform the range of visit rates over which the model is run. The model assumes that the municipal team collects the same volume from every household (i.e. the volume collected does not vary between households).
Given the variability of urine production and the risk of overflow, as well as the benefits of customer interaction, the frequency of emptying is set so that collection must happen weekly. Variables such as tank size, optimized collection routes, etc., could be varied to reduce the need for weekly visits, but as the CDU model requires that the collection points are emptied weekly, the same requirement is set here (also out of consideration for the households who appreciate weekly collection). If more than 2.85 L per household per day is produced (i.e. a full 20 L container per week) additional collection days are not added; instead the model simply adds additional household storage tanks and assumes that weekly collection removes whatever volume is present at each household. It may seem excessive to collect weekly when urine production is low, at say, less than 1 L HH−1 day−1, but there are at least three good reasons to do so. First, even at such a low level, there would still be 14 L after two weeks, which, without taking in any sort of variation, is precariously close to be being full. It would only require a few weekend visitors during a two week time period to cause a potential overflow. Second, visiting every week ensures good community interaction, and maintains a municipal presence; leaks, broken or missing tanks, etc. can be reported and quickly repaired. The financial and opportunity costs of contacting the municipal help desk is often too high and many problems go unreported. Third, if residents see that there is a regular, consistent pick-up, families may be motivated by community norms to increase their toilet usage, despite the fact that there is no actual cash incentive
4 Results
The goal of comparing the Municipal Collected Urine (MCU) model and the Community Delivered Urine (CDU) model is to determine the points at which the household cost (R HH−1) and volumetric cost (R L−1) of urine collection for each model are equal and to determine which model is more or less cost-effective on either side of that point. In this way, the range over which each model is more cost effective, for a given outcome, can be examined and compared to the alternative model in the regions before and after the equivalence points. It is important to note that the results are purely cost based: the models do not take into account any associated benefits. For example I do not allocate financial values to the environmental impacts or health effects of open defecation, etc., but instead focus on the cost per desired outcome. The field experiment provided information about the likely values and ranges of volume collection, so the calculated optimums for each of the outcome values must be viewed in the context of what could realistically be expected or achieved.4.1 Cost per household
The cost per household was determined over a range of urine collection values using both the MCU and the CDU models.In the MCU model, the variable that controls the total volume of urine collected per week is the number of households that each collection team can visit in a day. Therefore three different visit rates: 30, 45 and 60 households per day were selected. The recorded visit rates ranged between 31 and 41, therefore the model range represents the slowest recorded rate, an improved rate, and an optimized rate.
Conversely, the volume of urine collected in the CDU is based on the incentive price, which in turn influences both the number of participants and the volume of urine that is collected from each of the participants. These relationships were developed in eqn (1)–(3) and shown graphically in Fig. 4.
The total weekly volume collected in the CDU was calculated over a range of incentive values from 0.2–3.5 R L−1 and the corresponding household collection (L HH−1 per day) values were determined. These daily collection volumes were then used in both the CDU and the MCU models to determine the weekly costs on a household basis (R HH−1 per week). The results are presented in Fig. 6.
The predicted weekly costs for each of the collection rates (30, 45 or 60 households per day) using the MCU model are flat, i.e. the amount of urine that the household produces does not affect the cost to collect it, since the collection team must visit each house weekly and remove whatever quantity of urine has been generated during that week. The predicted costs per household per week for operating the MCU at a collection rate of 30, 45 or 60 households per day are 20, 26, or 39 R per household per week, respectively. Note that the costs per household are calculated for the whole area (i.e. 500 households).
The predicted weekly costs for the CDU model increases in a non-linear form as a function of the urine collected per household per day. Note that the urine volumes collected per household are for those households that are participants as non-participants do not visit collection points, and only urine that is delivered to collection points is measured as being collected. However, the weekly costs are calculated for the full area of intervention. This is done both to standardize the models and to reflect the expected costs for a community-scale intervention, regardless of how many households participate (furthermore, the cost per participant household would not be meaningful at very low participation rates).
The equivalence points where the CDU program is equal to the MCU program are labelled (A–C) and the corresponding values are summarized in Table 1.
| Equivalence points | CDU values | |||
|---|---|---|---|---|
| Point | Weekly cost (R HH−1 week−1) | Volume collected (L HH−1 day−1) | Incentive price (R L−1) | Participation (%) |
| A | 20 | 1.8 | 0.9 | 70% |
| B | 27 | 2 | 1 | 78% |
| C | 39 | 2.41 | 1.21 | 94% |
The points A, B, and C correspond to the points where the CDU model results intersect with the MCU model results for visit rates of 60, 45 and 30 households per day, respectively. The CDU values were back-calculated from the CDU model based on the corresponding volume collected values. Referring to point A, the incentive price of 0.9 R L−1 would be required to generate a collected volume of 1.8 litres per household per day.
If the municipality could only achieve a visit rate of 60 households per day (MCU-60) the weekly costs per household would be 20 R HH−1 per week; operating the MCU with a visit rate of only 30 households per day would cost 39 R HH−1 per week.
On a household basis, the MCU-60 program would be more expensive to operate than the CDU program until the incentive price reaches 0.9 R L−1 (point A), after which point the CDU program would be more expensive on a household basis.
However, if the visit rate was only 30 households per day, the CDU program could be operated at any incentive price below 1.2 R L−1 and still be less expensive on a cost per household basis (point C). Referring back to Table 1, an incentive payment of 2.12 R L−1 would also correspond to a collection rate of 2.41 L HH−1 day−1 and would achieve a participation rate of 94%.
Though descriptive, the results must be carefully considered within the context of what could be possibly achieved or expected in a real-life setting. Since there is no reason for households that are part of the MCU program to alter their toilet use, the range over which the model was plotted is hypothetical at all values above the baseline measurements. The CDU urine program was tested specifically to determine if and how urine collection rates could be increased, and the experimental results proved that they could. Considering that the average daily urine collection rate was 1.34 L HH−1 day−1, one must consider whether the modelled results are realistic or meaningful past these observed values. The equivalence point A occurs at a collection rate of 1.8 L HH−1 day−1; this and every other equivalence point could be considered beyond the range of fair comparison with the MCU models, which realistically, could never generate the volumes required for a genuine comparison. However, the trends and equivalence points are important to understand and visualize as they describe the general behaviour of each model, regardless of how realistic the range of collection volumes is.
4.2 Volumetric cost
In order to determine the equivalence points for volumetric cost, the four models were run over a range of collection volumes (0–4.95 L HH−1 day−1). The volumetric cost of urine, i.e. the cost per volume of urine (Rand per litre) was calculated by dividing the total calculated costs (operating and capital) by the total volume of urine collected (all calculations were done on a weekly basis). Fig. 7 shows the relationship between the volume collected per household and the volumetric cost for each of the MCU and CDU models.As the household collection rate for the MCU increases from 30–60 HH per day the curve drops down, i.e. at the same daily collection rate, the volumetric cost decreases when more volume can be collected in a shorter amount of time. The difference is most significant at very low volumes. Salaries, driving, and capital costs all remain fixed, regardless of how much urine is collected in a day, so the volumetric cost reduces quickly for all additional volume that can be collected at a given collection rate. In the extreme case that the municipal workers collect less than 0.5 L per household, the volumetric costs are very high compared to the case when full tanks are collected, using the same amount of labour and materials.
While the volume of household urine collected and the visit rate control the MCU models, the CDU models are controlled only by the incentive price, which in turns controls the participation rate and the volume collected per household.
At very low incentive prices, the cost to collect the urine is very high. This is due to the fact that the fixed costs like the storage tanks, salaries, etc. are set at a minimum value, regardless of how much urine is collected (i.e. the field staff must sit at the collection point for a full day, even if only 1 person visits). As the incentive price increases, more households participate, and the urine volume collected increases.
Although the trend for the CDU models is generally decreasing until a minimum point after which it increases again, the curve is not smooth. This variation is due to the way the model forces the addition of extra staff, infrastructure or emptying trips when a certain quantity of urine is exceeded. For example, a fieldworker is limited to serving only 60 customers in a day, for a 5 day week; once the volume of urine generated requires more than 300 visits (60 × 5), the model requires that an extra fieldworker is added to the staff, and so forth.
The increasing slope that is visible at higher collection volumes (e.g. after about 2.5 L HH−1 day−1) is due to the cumulative effect of the incentives required to pay for the increasing volumes of collected urine, while the other costs remain relatively unresponsive to increased volume.
Comparing the CDU and MCU models on a volumetric cost basis is less straightforward than on a household basis because the CDU models do not produce smooth results as before. To simplify the comparison, a flat line is fitted for the CDU results between collection volumes of 1–2.5 L HH−1 day−1 and is assumed to be flat at 2.4 R L−1, which means that the CDU curve only crosses each of the MCU curves once (marked by points D, E and F).
The equivalence points where the CDU model is the same as MCU models on a volumetric basis, for a given household collection rate are summarized in Table 2.
| Equivalence points | CDU values | |||
|---|---|---|---|---|
| Point | Volumetric price (R L−1) | Volume collected (L HH−1 day−1) | Incentive price (R L−1) | Participation (%) |
| D | 2.4 | 1.19 | 0.6 | 47% |
| E | 2.4 | 1.58 | 0.8 | 62% |
| F | 2.4 | 2.3 | 1.15 | 90% |
The MCU-60 program is the least expensive on a volumetric cost basis after Point D, or at any collection rate greater than 1.19 L HH−1 day−1. Indeed the volumetric cost drops quickly and drops below 1 R L−1 after a collection rate of 3 L HH−1 day−1. At daily collection rates higher than 1.58 L HH−1 day−1 (point E) MCU becomes increasingly less expensive on volumetric basis, though up until this point, the CDU model was the most cost-efficient program. Achieving the collection rate that corresponds to point E through the CDU could be achieved by offering an incentive of 0.8 R L−1, and this would also result in about 62% participation. Similarly, assuming a visit rate of 30 households per day, the CDU program is expected to be less expensive than the MCU program until a collection rate of 2.3 L HH−1 day−1, after which the volumetric cost increases steadily.
In the previous section, when the cost-effectiveness of each model was compared on a household basis, the equivalence points occurred at collection rates beyond what could be expected from households who were not incentivized to use their toilets more. In this comparison however, the equivalence points for the MCU model at visit rates of 45 and 60 fall within the realistic range of baseline collection rates. Between equivalence points D and E, the exact collection and visit rate would need to be specified to determine the most cost-effective model, as the models intersect within such a small, and parameter-specific range. However, after equivalence point E, the collection rate for the MCU models become increasingly unrealistic, despite the fact that the MCU models become increasingly cost-effective on a volumetric basis. The most relevant information that can be gleaned from Fig. 7 after point E are the volumetric costs for implementing the CDU-P program, and the hypothetical volumetric costs for the MCU programs, assuming a no-cost method of increasing the collection rates (beyond 1.34 L HH−1 day−1) in the MCU areas was implemented.
4.3 Sensitivity analysis
In order to determine the robustness of the modelled results, a sensitivity analysis is presented. Two different equivalence points from the previous analyses are subjected to variations in four of the most important variables, and the impact on the two outcome variables is estimated.Equivalence point A from Fig. 6 represents the point where the weekly household costs for the CDU and MCU-60 models are equal (for a collection rate of 1.8 L HH−1 day−1, the cost is 20 R HH−1). Similarly, equivalence point E is the point at which the volumetric cost for the CDU and MCU-45 models are (roughly) equal (at 2.4 R L−1). Since the exact point of intersection was estimated earlier using a straight-line method, and the two models do not precisely intersect at 2.4 R L−1, the exact points for each of the curves at the collection rate of 1.8 L HH−1 day−1 are selected. These points are slightly away from equivalence point E, but, by setting the collection rate to the same as Equivalence point A, the comparison is simplified between models and across outcome variables. These points were selected to analyse because they occur at a realistic incentive price (0.9 R L−1) and are at realistic collection rates for the MCU (though the visit rate of 60 households per day represents the most optimized visiting scheme possible). As discussed before, equivalence points that occur at higher collection volumes are purely theoretical and have little practical meaning since collection volumes beyond 1.34 litres per household per day are rare.
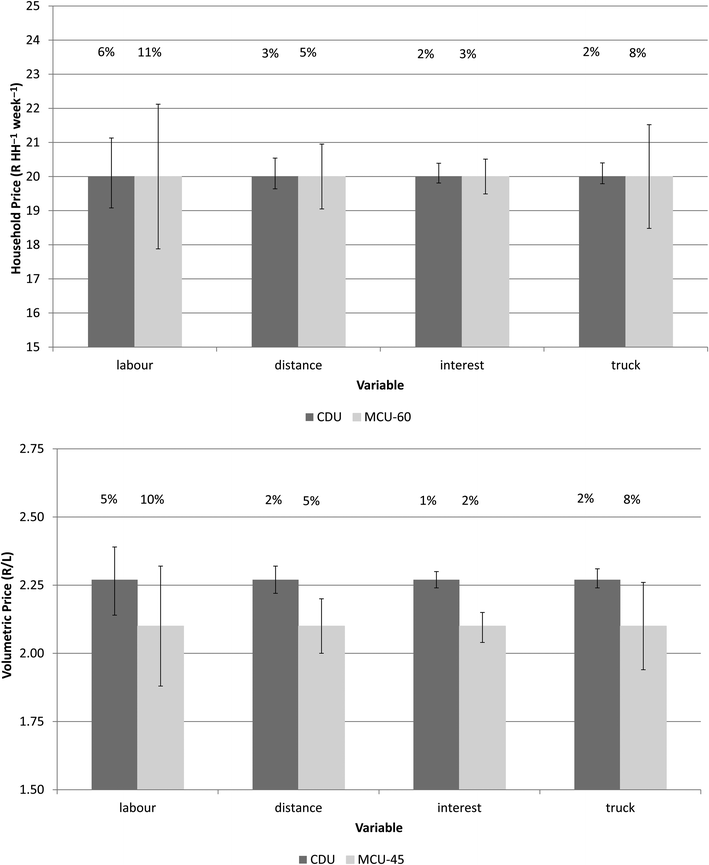
The four variables identified for the analysis were a) the cost of labour b) the distance between the shop and the site, c) the interest rate and d) the purchase price of the 3–5 tonne truck. These variables were chosen because they affect all or many of the modules and would, in a different context, or in the future, be set to significantly different values. All variables were adjusted by 25% with respect to model values.
Salaries contribute substantially to program costs, especially when urine volumes require multiple fieldworkers and EWS staff to manage the collection and transport. Furthermore, a long-term project should account for the annual increase in wages. The models were tested using wages that were increased and decreased by 25% over their base value (e.g. the normal fieldworker wage of 162 is tested at 122 and 203 R per day).
Both urine and workers require a significant amount of transport, and since the site is nearly 40 km from the shop, and the site is 45 km from the depot, transport is not only a significant cost, but potentially one that could be reduced in eThekwini. The effects of moving the shop 10 km closer to and further from the site were tested. The area was assumed to move along a straight line towards or away from the shop, and the distance to the depot was corrected accordingly (assuming the three locations form a right angle triangle and using Pythagorean theorem).
The interest rate influences all of the annualized capital costs, and could have a potentially large effect on the weight that the capital costs assume in the total cost calculations. The original models were run based on an interest rate of 9%; I test the models using rates of 6.75% and 11.25%.
Finally, the sensitivity of the purchase price of the 3–5 tonne truck is tested. At high urine volumes, both models require several trucks to be working in parallel in order to transport all of the urine. Given the need to purchase multiple trucks (at a purchase price set to 350![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 R), small changes in the purchase price could have a significant effect on the cost effectiveness of either program.
000 R), small changes in the purchase price could have a significant effect on the cost effectiveness of either program.
The predicted range of outcome values (household cost and the volumetric cost) for each of the modified variables is plotted in Fig. 8. The results show that, in general, the CDU model is less sensitive to changes in the parameters tested, that labour and the purchase price of the 5 tonne truck are highly sensitive to price changes within the MCU-models, and that the models respond similarly regardless of whether the results are estimated in terms of household or volumetric price (at the collection volumes tested).
Looking first at the values plotted for the household costs, a 25% increase in labour costs results in a 6% increase in per household costs for the CDU model and a 11% increase in the MCU-60 model (top figure). The relatively large increase for the MCU-60 is due to the fact that, although there are not many types of staff (only drivers and collectors), there are multiple teams who must work in parallel to visit every house, every week. This is in contrast to the CDU model which has a variety of workers (including a supervisor and field staff), but only the field staff is required to work daily, while the other staff only visits the area periodically.
Considering that the transport and driving distance has an effect on a variety of parameters (fuel, oil, tires, etc.) a 25% change has a surprisingly small effect on the household or volumetric costs. Minimum costs could be achieved if the urine-depot was moved into the community (so that the driving distance was as close to 0 as possible), but this would require trucks to also move the urine within the community, i.e. from the collection points to the processing facility. A truck would still need to drive from the shop to the field, since it would be inefficient to leave a truck in each community just for transporting the urine from collection points to the processing facility. More pressing than the question of truck storage is that of actually processing the urine on site. Even if a processing facility could be installed in each community to convert the urine into a useable nutrient product, trained field staff, chemicals, and waste processing facilities would also be needed. It is unclear whether, and/or at what scale, decentralized processing would be financially feasible and it is beyond the scope of this paper to determine.
Given its control over all capital costs, the low sensitivity of the models with respect to a change in the interest rate means that I need not worry about the accuracy of the chosen interest rate value in these models as it does not have a significant impact on the estimated results. However, the capital cost of the 3–5 tonne truck, which is set to 350![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 R in the baseline model, is quite sensitive to change. This model assumes that the truck is purchased new at the start of the project, which would not normally be the case. However, the analysis points to the importance of the purchase price of new trucks, which could, if minimized, have a significant impact on the long-term program costs. The CDU is more heavily dependent on the incentive price, while the MCU is sensitive to the labour and transport aspects of the operation, and could become substantially more expensive on a household basis if the capital costs were to increase.
000 R in the baseline model, is quite sensitive to change. This model assumes that the truck is purchased new at the start of the project, which would not normally be the case. However, the analysis points to the importance of the purchase price of new trucks, which could, if minimized, have a significant impact on the long-term program costs. The CDU is more heavily dependent on the incentive price, while the MCU is sensitive to the labour and transport aspects of the operation, and could become substantially more expensive on a household basis if the capital costs were to increase.
In terms of the volumetric cost (bottom figure), the estimated model values for the CDU model are slightly lower than the MCU-45 at the volume collection rate of 1.8 L HH−1 day−1. Except for labour, the range of values predicted for the MCU-45 model are, at the highest predicted values, lower than the baseline values of the CDU. This means that already by a volume collection rate of 1.8 L HH−1 day−1, the gap between the two models is so wide that increases in volumetric cost predicted the MCU-45 model are still lower than the CDU-model costs, which continue to increase upward from this point.
The sensitivity analyses shows that variation in some baseline values can move the estimated equivalence points significantly, and therefore change which model is most cost-effective at a given collection rate. However, as before the results must be viewed within the context of the visit rates and the collection rates that are possible. The equivalence points examined (A and E) assumed visit rates of 60 and 45 houses, respectively, and a collection rate of 1.8 L HH−1 day−1; these are all higher than recorded values, though not unrealistic.
4.4 Community welfare
In the previous sections, I have compared the different collection programs from the financial perspective of the program operator, i.e. the municipality. In this section on community welfare I examine the program impacts from the perspective of the community residents.In South Africa, the national unemployment rate is high and in KwaZulu Natal (the province where the study took place) it is over 35%.27 Although South Africa has an extensive social welfare program that includes benefit payments for children and the elderly, communities, especially rural communities, struggle to survive with the small amounts of cash they receive. As of January 2014, the Child Care Grant was worth 300 R per month (for every child under 18) while the Older Persons Grant was worth a maximum of 1270 R per month (for persons older than 60 years). There is no national minimum wage, but there are different standards across professions: the minimum wage for a fieldworker that is employed at EWS is 162 R per day (about 20 R per hour).
It is important to note also that, even if a job is available, transport to and from peri-urban or rural areas either consume a substantial part of the salary or make it so expensive that it is not even worthwhile to work. Given the size of government benefits, the scarcity of employment, low salaries, and the cost of transport, any source of cash would likely be a welcome addition to peri-urban and rural communities.
As part of the CDU model there were several ways in which cash was directed towards various community members. Incentive payments were given directly to the person who delivered the urine; shops that performed this service were paid a 10% commission on every token they exchanged. The collection points (1000 L storage tanks) were located on private property, and the landowners were paid a monthly fee of 100 R to compensate them for the traffic and nuisance. The field staff was recruited from the communities; depending on community participation and local arrangements, part or full-time employment was created for one or several community members. All of these cash flows were frequent (daily, weekly, or monthly) and consistent. Together, fieldworker salaries, rent, commissions, and incentives are referred to as community-directed funds (CDF), i.e. all program funds that directly reach community members in the form of cash. Program costs that are not community-directed could be considered as overhead costs and are paid out to private companies or municipal employees. The impacts of the different collection programs on community welfare, predicted by the models at different collection rates, are summarized in Table 3.
| CDU | MCU-30 | MCU-45 | MCU-60 | |||
|---|---|---|---|---|---|---|
| Incentive (R L−1) | 0.9 | 1.25 | 2 | — | — | |
| Vol. collected (L HH−1 day−1) | 1.8 | 2.5 | 4.95 | Any | Any | Any |
| Cash payment to family (R week−1) | 11 | 22 | 56 | 0 | 0 | 0 |
| Cash payment as a % of child grant | 15% | 29% | 75% | 0 | 0 | 0 |
| Equivalent hours | 0.6 | 1.1 | 2.8 | 0 | 0 | 0 |
| Total cost (R week−1) | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 047 047 |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 568 568 |
45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 890 890 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 380 380 |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 221 221 |
9992 |
| CDF (R week−1) | 5313 | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 600 |
33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 792 792 |
0 | 0 | 0 |
| CDF as a % of total costs | 53% | 63% | 74% | 0 | 0 | 0 |
The total cost of the CDU increases on both a household and volumetric basis as the urine volume collected increases. However, as shown in Table 3, the percentage of that cost that is community directed, also increases. At a reasonable incentive value of 1.25, the average weekly cash directed towards family would be approximately 22 R (this does not include other community-directed funds). This is equivalent to 29% of the money received through the government child grant, or the equivalent of just over 1 hour of paid labour.
The MCU costs are not dependent on the quantity of urine collected, only the visit rate. On a total cost basis, the MCU is less expensive than the CDU with an incentive offer of 1.25 for all visit rates. As the collection rate increases for the CDU, so does the total cost. However, since the total cost increase is driven by the incentive payments, the CDF, as a percentage of the total costs, also increases; at an incentive payment of 2 R L−1, 74% of the total CDU costs are spent in the community, meaning that only 26% is spent on overhead, as opposed to 100% for the MCU programs.
In the area that the model is based on, an incentive payment of 1 R L−1 was offered for 13 weeks. During that time, the average participating household earned 215 R, or about 16 R per week, which is slightly above the model-predicted value of 14 R per week. Following the incentive program, a follow-up survey was conducted to determine the views of the participants and non-participants. Out of 112 participants from the study area, 72% stated that the incentive program made a “very big impact” on their family budget, and over 95% of participants said that the program made a “big” or “very big” impact.
What is important however, more than the individual, self-reported impacts, are the sum total of the community-directed funds, and the fact that as the program costs increase, the ratio of the costs that actual go into the community increases as well. While the individual impacts may not be significant at first glance, the cumulative effects, i.e. the injection of a large, but dispersed amount of cash, could have large and positive impact on the community as a whole.
5 Conclusions and recommendations
The goal of this paper was to determine the point or range of urine collection volumes over which each model is most cost effective, and then to assess whether those values are realistic or achievable in a real-world context. Additionally, I was interested in the impacts of each program on the communities in question.The speed at which the workers collect the household tanks in the MCU, i.e. the visit rate, has a strong effect on both the volumetric cost (R L−1), and on the cost per household (R HH−1). The best way to lower costs for the MCU would be to improve efficiency and increase the number of tanks that can be collected per day. However, the MCU does not encourage UDDT use, which is currently low at only 1.34 L per household per day of urine, out of a (theoretical average) maximum of almost 5 L HH−1 day−1. Until use is increased and higher volumes can be collected, the cost of municipal household collection will remain high.
The CDU program is highly sensitive to, and correlated with incentive price: the model predicts that participation is maximized at 1.285 R L−1 and the point at which all volume was collected (without waste) was 2.5 R L−1; the model was based on limited empirical data and therefore the results should be viewed as conservative estimates.
Depending on the objective of the program, either the CDU or the MCU could be preferable. If the objective were to collect urine for nutrient processing at the lowest cost possible, it would be easiest, and least expensive to have the municipality collect the urine. Since there is no incentive for the households to increase or change their rates of toilet use, it is unlikely that the volumes would increase or change noticeably over time.
If however, the objective is to encourage UDDT use and limit environmental pollution while simultaneously transferring much-needed cash into poor communities, then the CDU program should be implemented. The paradox I have illustrated is that the CDU becomes increasingly expensive on a volumetric and household basis as the volume of urine collected increases. If the program is operated with low incentives, the total costs could be lowered, but the program would have little impact on toilet use in the community, and so would be senseless. On the other hand, the MCU is very expensive at low collection volumes, though these collection volumes are realistic. Although the MCU becomes increasingly inexpensive at higher collection volumes, there is no way to achieve these values.
Conditional cash transfers should be seen as a temporary behaviour-change tool, though the definition of “temporary” is best left open to interpretation. Further studies should be conducted in order to determine how long an incentivized program would have to last before behaviour change became so ingrained that it was irreversible (i.e. UDDT use became the norm and no one reverted to open defecation/urination). Though the model values have been set to reflect the reality of eThekwini, the model itself could easily be used and adapted for a different context, and even without experimental values would be particularly useful for planning potential urine-collection projects.
Incentivized urine collection brings jobs, money, and improved sanitation to the community, and frees up municipal staff to focus on other, more technical problems. If the goal is really to increase toilet use, acceptance, and strive towards 100% sanitation coverage, incentivized toilet use should be considered, not only at the equivalence points identified, but, in contexts where the program may be more expensive than the MCU, but where the benefits are clear and perhaps, unquantifiable.
Acknowledgements
I am grateful to Teddy Gounden, Neil McLeod, Scelo Xulu and the staff at EWS for their commitment and support; to the enumerators for their diligent work and dedication; and to the women and men in eThekwini who gave their time and energy generously.References
- WHO and UNICEF, Progress on Drinking Water and Sanitation, World Health Organization, Geneva, 2014 Search PubMed.
- G. Hutton, Global costs and benefits of drinking-water supply and sanitation interventions to reach the MDG target and universal coverage, World Health Organization, Geneva, WHO/HSE/WSH/12.01, 2012 Search PubMed.
- G. Hutton, L. Haller and J. Bartram, Global cost-benefit analysis of water supply and sanitation interventions, J. Water Health, 2007, 4, 481–502 CrossRef PubMed.
- A. Prüss-Üstün, R. Bos, F. Gore and J. Bartram, Safer water, better health: costs, benefits and sustainability of interventions to protect and promote health, World Health Organization, Geneva, 2008 Search PubMed.
- D. Whittington, M. A. Jeuland, K. Barker and Y. Yuen, Setting Priorities, Targeting Subsidies among Water, Sanitation, and Preventive Health Interventions in Developing Countries, World Dev., 2012, 40(8), 1546–1568 CrossRef.
- C. Hamlin and S. Sheard, Revolutions in public health: 1848 and 1998?, BMJ [Br. Med. J.], 1998, 317(7158), 587–598 CrossRef CAS.
- B. Marx, T. Stoker and T. Suri, The Economics of Slums in the Developing World, J. Econ. Perspect., 2013, 27(4), 187–210 CrossRef.
- P.-H. Dodane, M. Mbéguéré, M. O. Sow and L. Strande, Capital and Operating Costs of Full-Scale Fecal Sludge Management and Wastewater Treatment Systems in Dakar, Senegal, Environ. Sci. Technol., 2012, 46(7), 3705–3711 CrossRef CAS PubMed.
- J. Sy, R. Warner and J. Jamieson, Tapping the Markets: Opportunities for Domestic Investments in Water and Sanitation for the Poor, Directions in Development, The World Bank, Washington, DC, 2014, DOI:10.1596/978-1-4648-0134-1.
- M. R. Hopewell and J. P. Graham, Trends in access to water supply and sanitation in 31 major sub-Saharan African cities: an analysis of DHS data from 2000 to 2012, BMC Public Health, 2014, 14(1), 1–12 CrossRef PubMed.
- B. Evans, C. van der Voorden and A. Peal, Public Funding for Sanitation-The Many Faces of Sanitation Subsidies, Water Supply & Sanitation Collaborative Council, Geneva, Switzerland, 2009 Search PubMed.
- WASHCost, WASHCost Infosheet 2: The cost of sustaining sanitation services for 20 years can be 5–20 times the cost of building a latrine, 2012, pp. 1–6 Search PubMed.
- M. Snehalatha, P. Busenna, V. A. Raj and M. Vnkataswamy, 7 Nirmal Gram Puraskar and Sanitation Service Levels: the Curse of Slippage in Sustainable Water and Sanitation Services: The Life-Cycle Cost Approach to Planning and Management, Routledge, 2014 Search PubMed.
- A. Hueso and B. Bell, An untold story of policy failure: the Total Sanitation Campaign in India, Water Policy, 2013, 15(6), 1001–1018 CrossRef.
- A. Potter, M. van de Reep, P. Burr and A. Dube, Working Paper 6: Assessing hygiene cost-effectiveness, IRC International Water and Sanitation Centre, 2011 Search PubMed.
- D. K. Evans and A. Popova, Cash Transfers and Temptation Goods: A Review of Global Evidence, Policy Research Working Paper 6886, The World Bank, 2014 Search PubMed.
- T. Gounden, B. Pfaff, N. Macleod and C. Buckley, Sustainable Development of Water Resoures, Water Supply and Environmental Sanitation- Provision of Free Sustainable Basic Sanitation: The Durban Experience, 32nd WEDC International Conference, Colombo, Sri Lanka, 2006 Search PubMed.
- A. E. Okem, S. Xulu, E. Tilley, C. Buckley and E. Roma, Assessing perceptions and willingness to use urine in agriculture: A case study from rural areas of eThekwini Municipality, South Africa, J. Water, Sanit. Hyg. Dev., 2013, 3(4), 582–591 CrossRef.
- E. Tilley, L. Ulrich, C. Lüthi, P. Reymond and C. Zurbrügg, Compendium of Sanitation Systems and Technologies, Eawag, Duebendorf, Switzerland, 2014 Search PubMed.
- WissenschaftlicheTabellen Geigy, Teilband Körperflüssigkeiten (Scientific tables Geigy. Volume body fluids), Ciba-Geigy, Basel, Switzerland, 1977 Search PubMed.
- P. Bracken, E. V. Münch and A. Panesar, Tackling the urban waste and food crises simultaneously and sustainably – examples from the Philippines and Burkina Faso, 34th WEDC International Conference: Water, Sanitation and Hygiene: Sustainable Development and Multisectoral Approaches, Addis Ababa, Ethiopia, 2009 Search PubMed.
- K. Kassa, F. Meinzinger and W. Zewdie, Experiences from the use of urine in Arba Minch, Ethiopia, Sustainable Sanitation Practice, 2010, 3, 12–17 Search PubMed.
- H. N. Bischel, B. D. Duygan, L. Strande, C. S. McArdell, K. M. Udert and T. Kohn, Pathogens and Pharmaceuticals in Source-Separated Urine in eThekwini, Water Res., 2015, 85, 57–65 CrossRef CAS PubMed.
- K. M. Udert and M. Wächter, Complete nutrient recovery from source-separated urine by nitrification and distillation, Water Res., 2012, 46(2), 453–464 CrossRef CAS PubMed.
- M. G. Grau, S. L. Rhoton, C. J. Brouckaert and C. A. Buckley, Evaluation of an automated struvite reactor to recover phosphorus from source-separated urine collected at urine diversion toilets in eThekwini, Water SA, 2015, 41(3), 383–389 CrossRef CAS.
- Valorisation of Urine Nutrients: Promoting Sanitation & Nutrient Recovery through Urine Separation, Final Project Report 2015, Eawag, Duebendorf, Switzerland, 2015, pp. 1–40 Search PubMed.
- Statistics South Africa, Census 2011 Statistical release, Pretoria, South Africa, 2012.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ew00237k |
| ‡ Defined as: “all or some household members use a latrine some or most of the time; where there is no access to a latrine, faeces are generally buried; the latrine separates users from faecal waste”. |
| This journal is © The Royal Society of Chemistry 2016 |