Much ado about α: reframing the debate over appropriate fate descriptors in nanoparticle environmental risk modeling
Amy L.
Dale
*abc,
Gregory V.
Lowry
 bc and
Elizabeth A.
Casman
ac
bc and
Elizabeth A.
Casman
ac
aEngineering and Public Policy, Carnegie Mellon University, Pittsburgh, Pennsylvania, USA. E-mail: adale4552@gmail.com; Tel: +1 (412) 689 7245
bCivil and Environmental Engineering, Carnegie Mellon University, Pittsburgh, Pennsylvania, USA
cCenter for Environmental Implications of NanoTechnology, Duke University, Durham, North Carolina, USA
First published on 11th December 2014
Abstract
Large-scale fate and transport models have used different approaches to account for engineered nanoparticle (ENP) heteroaggregation and its effects on fate. Praetorius et al. and Cornelis, in recent Perspectives in this journal, favor the use of particle number-based kinetic models and attachment efficiency, α, in place of mass-based approaches relying on partition coefficients, or Kd values, because the former is more theoretically faithful to the particulate nature of ENPs. Here, we provide perspective on these two popular modeling frameworks, particle balance and mass balance, with regards to their ability to capture ENP fate processes at large scales. We show that particle balance using α is not unique in its ability to describe ENP heteroaggregation kinetically, since mathematically equivalent rates can be created for mass balance, and that the ability of particle balance to accurately describe particle behaviors is still severely hindered by evolving scientific understanding of ENP heteroaggregation. Ultimately, we find that models at this scale are relatively insensitive to the particulate nature of ENPs. In the short term, mass-based models that rely on simple heuristics can be more practical, and less error-prone, than particle balance alternatives using α.
Nano impactA recent Perspective in this journal (Praetorius et al., 2014) favors engineered nanoparticle (ENP) fate models based on colloid science (particle balance) over mass-based alternatives because the latter often incorrectly assume that contaminant distribution between solid phases and water is at equilibrium. We show that mass-based models need not assume equilibrium. Further, we show they can be as effective as particle balance for risk assessment at large scales even when they apply simple heuristics. This paper broadens the current debate over appropriate fate descriptors for ENPs and cautions against the premature censure of alternative modeling approaches until understanding of ENP heteroaggregation improves, model validation can be performed, and model error can be systematically evaluated and compared across alternative frameworks. |
Introduction
Large-scale (e.g., watershed, regional, national, and global) models have been used for decades to study the environmental fate and transport of ionic and molecular contaminants.1 Many such models have been adapted for use with, or specifically developed for, engineered nanoparticles (ENPs),2–15 but recently a debate has surfaced over the best modeling approach for ENP heteroaggreation, or the attachment of ENPs to naturally-occurring solids such as soil particles or suspended sediments.16,17 Indeed, heteroaggregation strongly influences ENP bioavailability and mobility in the environment,17 and accounting for it in environmental models is essential to their usefulness as a scientific or decision-making tool. However, relatively little attention has been paid thus far to practical considerations affecting model selection, such as data limitations, model scale, and study objectives.Cerco (2003) distinguished between “scientific” and “engineering” models, where scientific models are designed to enhance scientific understanding of processes and guide research efforts, and engineering models are designed with an application in mind—often to facilitate “real-time” decision-making by regulators and risk managers. He remarked that, “scientific models, as a class, tend to be limited in scope. They tend to examine at most a few processes on a local spatial scale. Engineering models, on the other hand, are usually system wide and attempt to incorporate an entire universe of transport, chemical, and biological processes”.18 Scientific models are typically mechanistic, whereas engineering models often rely on empirical relations. Most large-scale ENP fate and transport models developed to date are engineering models (e.g., ref. 2–15).
Mechanistic heteroaggregation models based on DLVO theory and coagulation theory have recently been simplified for inclusion in the type of large-scale engineering models intended for decision-making.14,15 In their recent Perspective in this journal, Praetorius et al. argue that this is the most appropriate approach because it explicitly accounts for the colloidal nature of ENPs, unlike the mass-based alternatives developed for ionic and molecular contaminants. We examine this claim in light of ongoing practical challenges in model formulation, parameterization, and calibration for ENPs.
Mass balance and population balance in ENP fate models
Most early successes in ENP fate modeling were achieved with the mass balance framework developed to describe molecular contaminants, in which the inflow and outflow of total contaminant mass is balanced over time or at steady state (e.g., ref. 1, 3–6, 8–13). Partition coefficients, or Kd values, are commonly used in mass balance to describe the solid–water distribution of contaminants. Kd (L kg−1) is experimentally derived from Cs/Caq, where Cs is the sorbed mass concentration (mg kg−1) and Caq is the aqueous mass concentration (mg L−1).19 Using Kd in a model implies that sorption is reversible and occurs so quickly relative to other processes that its time dependence can be safely ignored. In fact, a rigorous theoretical derivation of Kd requires that equilibrium has been achieved locally.1,20Recent Perspectives argued that, since colloidal suspensions never reach an equilibrium state, kinetic models based on colloid transport theory (“coagulation models”) are a better alternative than Kd for ENPs.16,17 The authors describe the decrease in the number concentration of unaggregated particles over time (dNNP/dt) as the product of the collision frequency, K, the attachment efficiency, α, and the number concentrations of the colliding species, NNP (nanoparticles) and NNC (natural colloids):21
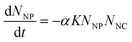 | (1) |
Terms for advection, settling, reaction, and so on are added to eqn (1) to provide a complete description of ENP fate. This framework typifies particle balance (a type of population balance), which splits a population of particles into discrete bins based on (e.g.) geochemical identity, size, and heteroaggregation state and then performs a balance on the number concentration in each bin at each model time step.22 For example, aggregation of ENPs in size class i to natural colloids in size class j is expressed as a loss in the number concentration of unaggregated ENPs and a gain in the number concentration of the size class combination (i, j).15
Particle balance has been successfully applied in a large-scale engineering ENP fate model that includes heteroaggregation.15 It has not yet been applied at large scales to a dynamic system or to systems with reactive ENPs. In support of this approach, there has been a recent spike in the publication of empirically-determined α's or related parameters (e.g., Debye length) for use in such models.21,23,24
The two approaches are not entirely interchangeable. Error can arise when converting number concentrations to mass concentrations because particle balance models discretize mass by discretizing size. Similarly, mass concentrations cannot be converted to number concentrations unless the size distribution is known or estimated. Conversion between mass and number concentrations is most error-prone when the nanoparticle sizes are changing over time. For example, numerical dispersion can occur when modeling highly reactive particles using particle balance. To avoid these errors, some coagulation models balance both mass and particle number.25
The most important difference between particle balance and mass balance is not what they balance, but rather their approach to scale-up. Mass balance tends to simplify. For example, Kd allows modelers to express free and solid-associated mass concentrations using a single state variable. In particle balance, each particle and heteroaggregate size and type is assigned its own state variable. Particle balance typically uses binning to scale up process-based descriptions of individual particle behaviors (collisions, surface area-dependent reactions) to the entire population. Mass balance typically neglects differences between ENPs in the population, averaging them through the choice of parameters. This approach implies differences are irrelevant at the scale of interest to the modeler.
Challenges in population balance modeling of ENPs
Of the two approaches, population balance is more faithful to nanoparticle-specific properties and processes. However, this strength for scientific models can be a weakness in large-scale engineering models.Because of the need to assign a separate continuity equation to each particle type and size, computational burden is an oft-cited weakness of particle balance at large scales,22,26 Certainly, it is more computational demanding than mass balance. However, analytical solutions to the coagulation equation do exist for simplified systems, including monodisperse primary particles heteroaggregating with a constant collision rate, K,22 and steady-state solutions assuming pseudo-first-order heteroaggregation (i.e., that NNC in eqn (1) is constant).15 Since the publication of the coagulation equation in 1917, several iterative and noniterative numerical solutions have also been developed. Thus computational complexity need not be limiting; a typical atmospheric model using this approach can contain as many as 104 state variables solved for each of 105 grid cells.25
Model parameterization is more problematic. Many α's are needed to describe the diversity of ENPs and natural colloids in the environment (e.g., inorganic and organic particles with highly variable compositions and sizes, bacteria, algae, and macromolecules), the effects of engineered surface coatings, the complex interactions of ENPs with organic matter, and solution chemistry including ionic strength.14,22,26 Because error results from both uncertainty in model structure and in model parameters, increasing a model's faithfulness to process (beyond a certain point) can actually decrease performance by increasing the number of uncertain parameters.27,28 Additionally, models with a large number of parameters (especially those that are highly correlated) often suffer from overparameterization. Such models will perform well during calibration but exhibit poor predictive performance.1
Simplifying assumptions are thus necessary to reduce model error and complexity, especially in light of the scientific uncertainty surrounding ENP heteroaggregation.13–15,22,26 However, the scientific validity of particle balance, or at least its superiority over mass balance, is undermined at present by its reliance on the following common assumptions: (1) unaggregated NPs and NCs are monodisperse, (2) all but one “typical” NC type can be ignored, (3) NC concentrations do not vary over time (pseudo-first-order kinetics apply), (4) the collision rate is constant and collisions are rectilinear (i.e., particles and heteroaggregates do not affect the flow field as they approach one another), (5) heteroaggregation events other than single NP/single NC collisions can be ignored (where the NC can represent a homoaggregate of primary NCs but higher-order NC/NC collisions are not considered), (6) variation in α due to the effects of organic matter, engineered surface coatings, and solution chemistry can be ignored, and (8) no aggregate break-up is considered. With respect to the last assumption, neither complete reversibility of aggregation (assumed for Kd) nor complete irreversibility (assumed for α) are likely to occur in natural environments. Break-up has been repeatedly observed in soil systems for colloids such as bacteria and viruses, and is often accounted for in such models by assuming the presence of a non-sorbing fraction.29
Finally, some methodological problems with α should be noted. Theoretical determinations of α (via classic and extended DLVO theory) have consistently failed to show quantitative or even qualitative agreement with experimental results,30–34 so α must (like Kd) be determined empirically.17,26 Although the experimental setup for determining α (column studies) is less operationally defined than that of Kd (batch studies), significant differences do still remain between column studies and the natural environment.17 For example, comparisons of field-scale studies to column studies on the mobility of bacteria, protozoa, and viruses suggest that estimates of α for these colloidal organisms decrease as the scale of the study increases.29
The case for mass balance
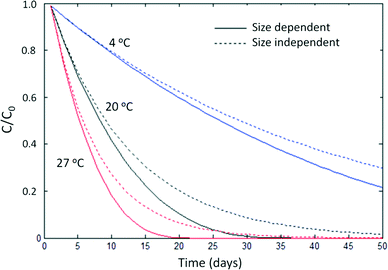
Because mass balance models do not track the particle size distribution over time, they are generally unable to describe size-dependent processes that may affect ENP behavior, e.g. the reaction rate increases that occur as ENPs dissolve. However, these effects can be minor and large-scale models may not be sensitive to these differences. Reactive ENP dissolution rates and solubilities vary less than an order of magnitude for silver ENPs of different sizes (4 vs. 60 nm)35 and ZnO NPs (4 vs. 241 nm),36 and several studies suggest size may play a relatively minor role in ENP speciation and toxicity, especially when compared to environmental factors such as pH, soil type, and redox conditions.36–38Fig. 1 compares a mass-based shrinking particle model39 of the dissolution of spherical silver ENPs to an alternative which assumes a size-independent reaction rate19 (in the standard units of d−1) at three temperatures. Particle shrinkage has a relatively small effect compared to temperature. Note that this model assumes the dissolution rate increases proportionately to the increase in specific surface area. Non-proportional rate behavior is theoretically possible for ENPs but has not been reported in kinetic studies of silver NP dissolution.35,40,41K d values are not strictly appropriate for ENPs because the equilibrium assumption is invalid for colloidal suspensions.16,17 However, in spite of this, partition coefficients and their operationally-defined, experimentally determined counterparts, retention coefficients (Kr),17 have long been used as screening-level heuristics for species that do not follow the equilibrium assumption such as metal ions.20,42 Ramaswami et al. state “equilibrium conditions are often not attained in the environment…. However, equilibrium calculations are relatively straightforward to make and provide a good first estimate of the overall distribution of a chemical in the different media…(72)”1
Of course, rather than relying on the equilibrium assumption, kinetic rates of formation and break-up of heteroaggregates of different sizes or types can also easily be incorporated into mass balance. Consider eqn (2), a mass-based analog to eqn (1) where the product of α and K is replaced with a second-order (mass-based) rate of heteroaggregation, khet,mass:
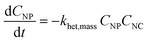 | (2) |
Unlike Kd, this formulation requires at least two state variables, one for the unaggregated NPs and one for the aggregates. However, it is still simple to implement and can be made pseudo-first-order if CNC is constant. Limousin et al. (2007) reviewed sixteen equilibrium approaches and eight kinetic approaches to sorption developed for mass balance modeling of “conventional” (non-nano) contaminants. They note that partition coefficients are the simplest of all available approaches.43
The kinetic mass-based approach that uses one state variable to represent unaggregated NPs and another to represent aggregates is in fact equivalent to a population balance approach in which only a single size class is considered for each particle type and aggregation events other than those between single NPs and single NCs are ignored. More complex formulations, such as multiple size classes, also have direct analogs. In fact, the interchangeability of kinetic mass-based models and particle number balance models reduced for use at large scales (minus some conversion error, discussed previously) has already been noted and applied for ENPs.13,26 Quik et al. (2014) showed that the population balance model for aggregation and sedimentation can be reliably replaced with a mass balance equivalent that follows a first-order loss rate to a non-sorbing fraction.26
The choice of simulation method for ENP heteroaggregation will only be relevant if the model under consideration is sensitive to that choice with respect to the output of interest. Using a “complete removal” case for surface water segments as compared to a “no removal” case resulted in only a factor of three difference between predicted median surface water concentrations (0.43 μg L−1versus 0.14) of nano-TiO2 in a spatially resolved model of Swiss rivers.8 Out of seven tested parameters, Blaser et al. (2008) found that their model was less sensitive to Kd than to two other parameters in the water column (water velocity and the settling velocity of solids) and five others in the sediment.3 In contrast, Liu and Cohen find that the percent removal of ENPs from the water column by sedimentation as opposed to outflow will increase rapidly (from 0 to ~40%) for “attachment factors” above approximately 0.95.12 This fate descriptor equals Cs/(Cs + Caq) and corresponds to a Kd of 19, which is small compared to Kd values reported for some NPs but may be realistic for others (Kd or Kr = 0.9 to 250 for C60;44,45 590 (median)46 and 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 (mean)47 for Ag NPs; 9.2 (median) for CeO2 NPs48). Praetorius et al. (2012) found relatively small differences in ENP mobility between an α = 0.1 and α = 1.0 case, although more significant differences were observed for α < 0.1.15 Therezien et al. (2014) showed that complete heteroaggregation occurs in at most several weeks in a box model of nanosilver and NC homo- and heteroaggregation under a wide range of conditions (20 nm or 100 nm silver NPs, NC diameters prior to aggregation between 50 and 2000 nm, background NC concentrations between 0 and 100 mg L−1, and α's between 0.005 and 1). The half-life of a dose of 0.25 ppm unaggregated NPs is less than a day when α > 0.05 and the background NC concentration is above ~15 mg L−1, which seems likely in natural systems.22
000 (mean)47 for Ag NPs; 9.2 (median) for CeO2 NPs48). Praetorius et al. (2012) found relatively small differences in ENP mobility between an α = 0.1 and α = 1.0 case, although more significant differences were observed for α < 0.1.15 Therezien et al. (2014) showed that complete heteroaggregation occurs in at most several weeks in a box model of nanosilver and NC homo- and heteroaggregation under a wide range of conditions (20 nm or 100 nm silver NPs, NC diameters prior to aggregation between 50 and 2000 nm, background NC concentrations between 0 and 100 mg L−1, and α's between 0.005 and 1). The half-life of a dose of 0.25 ppm unaggregated NPs is less than a day when α > 0.05 and the background NC concentration is above ~15 mg L−1, which seems likely in natural systems.22
Rapid aggregation and settling of ENPs has been observed in quiescent49 and turbulent50 experimental systems. Eqn (1) reveals that even low α's can result in high attachment when K is high (e.g., when colloids are abundant). In systems with long residence times (>1 day) and those in which ENPs heteroaggregate prior to entering the system, even the simple assumption of 100% ENP association with the solid phase should yield results similar to that of a particle balance model assuming irreversible heteroaggregation.
Ultimately, at large scales, model error arising from ignoring nanoparticle-specific properties is likely to be overshadowed by variation in model output due to either uncertainty or natural variation in other input parameters or process descriptions, such as ENM production estimates and the speciation of ENPs within sewage treatment plants and biosolids.11
No matter which framework is employed, one important consideration is how best to subdivide the solid phase in order to ensure that mobile fractions are distinguished from immobile fractions and high-sorbing fractions are distinguished from low-sorbing fractions at the level of detail appropriate to the analysis. For example, many models designed to capture sediment movement in rivers and river beds (e.g., surface runoff, bank erosion, settling, resuspension, bed load shift, and burial) as a function of time-variable stream flow break sediment into size classes (e.g., clay, sand, and silt) with diameter-dependent parameter values.51
Conclusion
Scientific models are testable mathematical hypotheses of how a phenomenon works, usually under simple and controlled conditions. Engineering models, in contrast, are designed to describe the essential features of a phenomenon at large scales for decision-making purposes. There is no question that α is the appropriate fate descriptor for small-scale scientific models, but this is not necessarily the case for large-scale engineering models, which must abstract greatly from first principles and thus cannot be judged solely on the theoretical purity of their assumptions. As Dominic DiToro noted, engineering models must compromise between simplicity and realism. “The best solution emphasizes the former without undue violence to the latter”.52 Particle balance models for ENPs are more complex and difficult to parameterize, and at present they do not appear to add appreciably to the realism of large-scale ENP fate models. Concerns about the equilibrium assumption behind Kd can be easily put to rest by developing mass balance models that rely instead on overall rates of sorption and desorption. However, these models ultimately appear relatively insensitive to the choice of ENP heteroaggregation fate descriptor, and simple approaches such as assuming 100% sorption of ENPs to a solid phase may be appropriate for engineering models of most systems, at least until scientific understanding of ENP heteroaggregation substantially improves.Because the ultimate test of an engineering model is its ability to match and predict experimental observations during calibration or validation, and because challenges in detecting and characterizing ENPs in environmental matrices are significant and ongoing,53 neither mass-based nor population-based frameworks can yet be decisively shown to be better than the other. However, we can perform sensitivity analyses to determine whether the particulate nature of ENPs strongly influences their environmental fate. For example, Fig. 1 shows that the dissolution rate of an aqueous suspension of pristine silver nanoparticles is more sensitive to temperature than to particle shrinkage. While, with increasing computational power and improving environmental measurement capabilities, process-based scientific models and “big picture” engineering models may someday converge, they presently occupy valid, but distinct, practical niches. In the short term, the desire for theoretical purity should not outweigh the practical utility of mass balance for risk assessment purposes.
References
- A. Ramaswami, J. B. Milford and M. J. Small, Integrated environmental modeling: pollutant transport, fate, and risk in the environment, John Wiley & Sons, New York, NY, 1st edn, 2005 Search PubMed.
- A. Boxall, Q. Chaudhry, C. Sinclair, A. Jones, R. Aitken, B. Jefferson and C. Watts, Current and Future Predicted Environmental Exposure to Engineered Nanoparticles, Report by the Central Science Laboratory, Department of the Environment and Rural Affairs, London, UK, 2007 Search PubMed.
- S. A. Blaser, M. Scheringer, M. MacLeod and K. Hungerbühler, Sci. Total Environ., 2008, 390, 396–409 CrossRef CAS PubMed.
- N. C. Mueller and B. Nowack, Environ. Sci. Technol., 2008, 42, 4447–4453 CrossRef CAS.
- F. Gottschalk, T. Sonderer, R. W. Scholz and B. Nowack, Environ. Sci. Technol., 2009, 43, 9216–9222 CrossRef CAS PubMed.
- F. Gottschalk, R. W. Scholz and B. Nowack, Environ. Modell. Softw., 2010, 25, 320–332 CrossRef PubMed.
- N. O'Brien and E. Cummins, Hum. Ecol. Risk Assess., 2010, 16, 847–872 CrossRef.
- F. Gottschalk, C. Ort, R. Scholz and B. Nowack, Environ. Pollut., 2011, 159, 3439–3445 CrossRef CAS PubMed.
- A. A. Keller, S. McFerran, A. Lazareva and S. Suh, J. Nanopart. Res., 2013, 15, 1–17 CrossRef.
- A. A. Keller and A. Lazareva, Environ. Sci. Technol. Lett., 2013, 1, 65–70 CrossRef.
- T. Y. Sun, F. Gottschalk, K. Hungerbühler and B. Nowack, Environ. Pollut., 2014, 185, 69–76 CrossRef CAS PubMed.
- H. H. Liu and Y. Cohen, Environ. Sci. Technol., 2014, 48, 3281–3292 CrossRef CAS PubMed.
- J. Meesters, A. A. Koelmans, J. T. Quik, A. J. Hendriks and D. Van de Meent, Environ. Sci. Technol., 2014, 48, 5726–5736 CrossRef CAS PubMed.
- R. Arvidsson, S. Molander, B. A. Sandén and M. Hassellöv, Hum. Ecol. Risk Assess., 2011, 17, 245–262 CrossRef CAS.
- A. Praetorius, M. Scheringer and K. Hungerbühler, Environ. Sci. Technol., 2012, 46, 6705–6713 CrossRef CAS PubMed.
- A. Praetorius, N. Tufenkji, K.-U. Goss, M. Scheringer, F. von der Kammer and M. Elimelech, Environ. Sci.: Nano, 2014, 1, 317–323 RSC.
- G. Cornelis, Environ. Sci.: Nano, 2015 10.1039/C4EN00122B.
- C. F. Cerco, J. Environ. Eng., 2003, 129, 681–682 CrossRef CAS.
- R. P. Schwarzenbach, P. M. Gschwend and D. M. Imboden, Environmental organic chemistry, Wiley-Interscience, 2005 Search PubMed.
- B. D. Honeyman and P. H. Santschi, Environ. Sci. Technol., 1988, 22, 862–871 CrossRef CAS PubMed.
- J. Quik, I. Velzeboer, M. Wouterse, A. Koelmans and D. van de Meent, Water Res., 2014, 48, 269–279 CrossRef CAS PubMed.
- M. Therezien, A. Thill and M. R. Wiesner, Sci. Total Environ., 2014, 485, 309–318 CrossRef PubMed.
- J. Hammes, J. A. Gallego-Urrea and M. Hassellöv, Water Res., 2013, 47, 5350–5361 CrossRef CAS PubMed.
- L. E. Barton, M. Therezien, M. Auffan, J.-Y. Bottero and M. R. Wiesner, Environ. Eng. Sci., 2014, 31, 421–427 CrossRef CAS.
- M. Z. Jacobson, Fundamentals of Atmospheric Modeling, Cambridge University Press, 2005 Search PubMed.
- J. T. Quik, D. van De Meent and A. A. Koelmans, Water Res., 2014, 62, 193–201 CrossRef CAS PubMed.
- R. Silberstein, Environ. Modell. Softw., 2006, 21, 1340–1352 CrossRef PubMed.
- E. A. Casman, M. G. Morgan and H. Dowlatabadi, Risk Anal., 1999, 19, 33–42 Search PubMed.
- T. R. Ginn, B. D. Wood, K. E. Nelson, T. D. Scheibe, E. M. Murphy and T. P. Clement, Adv. Water Resour., 2002, 25, 1017–1042 CrossRef CAS.
- A. J. Pelley and N. Tufenkji, J. Colloid Interface Sci., 2008, 321, 74–83 CrossRef CAS PubMed.
- Y. Tian, B. Gao, C. Silvera-Batista and K. J. Ziegler, J. Nanopart. Res., 2010, 12, 2371–2380 CrossRef CAS.
- J. E. Song, T. Phenrat, S. Marinakos, Y. Xiao, J. Liu, M. R. Wiesner, R. D. Tilton and G. V. Lowry, Environ. Sci. Technol., 2011, 45, 5988–5995 CrossRef CAS PubMed.
- R. N. Lerner, Q. Lu, H. Zeng and Y. Liu, Water Res., 2012, 46, 975–985 CrossRef CAS PubMed.
- S. Treumann, S. Torkzaban, S. A. Bradford, R. M. Visalakshan and D. Page, J. Contam. Hydrol., 2014, 164, 219–229 CrossRef CAS PubMed.
- J. Liu, D. A. Sonshine, S. Shervani and R. H. Hurt, ACS Nano, 2010, 4, 6903–6913 CrossRef CAS PubMed.
- S.-W. Bian, I. A. Mudunkotuwa, T. Rupasinghe and V. H. Grassian, Langmuir, 2011, 27, 6059–6068 CrossRef CAS PubMed.
- W. A. Shoults-Wilson, B. C. Reinsch, O. V. Tsyusko, P. M. Bertsch, G. V. Lowry and J. M. Unrine, Soil Sci. Soc. Am. J., 2011, 75, 365–377 CrossRef CAS.
- A. L. Dale, G. V. Lowry and E. A. Casman, Environ. Sci. Technol., 2013, 47, 12920–12928 CrossRef CAS PubMed.
- D. M. Di Toro, J. D. Mahony and A. M. Gonzalez, Environ. Toxicol. Chem., 1996, 15, 2156–2167 CrossRef CAS.
- R. D. Kent and P. J. Vikesland, Environ. Sci. Technol., 2012, 46, 6977–6984 CrossRef CAS PubMed.
- J. Liu, K. G. Pennell and R. H. Hurt, Environ. Sci. Technol., 2011, 45, 7345–7353 CrossRef CAS PubMed.
- J. D. Allison and T. L. Allison, Partition Coefficients for Metals in Surface Water, Soil, and Waste. United States Environmental Protection Agency Report EPA/600/R-05, 2005 Search PubMed.
- G. Limousin, J.-P. Gaudet, L. Charlet, S. Szenknect, V. Barthes and M. Krimissa, Appl. Geochem., 2007, 22, 249–275 CrossRef CAS PubMed.
- C.-Y. Chen and C. T. Jafvert, Environ. Sci. Technol., 2009, 43, 7370–7375 CrossRef CAS.
- R. Avanasi, W. A. Jackson, B. Sherwin, J. F. Mudge and T. A. Anderson, Environ. Sci. Technol., 2014, 48, 2792–2797 CrossRef CAS PubMed.
- G. Cornelis, C. Doolette, M. Thomas, M. J. McLaughlin, J. K. Kirby, D. G. Beak and D. Chittleborough, Soil Sci. Soc. Am. J., 2012, 76, 891–902 CrossRef CAS.
- C. O. Hendren, A. R. Badireddy, E. Casman and M. R. Wiesner, Sci. Total Environ., 2013, 449, 418–425 CrossRef CAS PubMed.
- G. Cornelis, B. Ryan, M. J. McLaughlin, J. K. Kirby, D. Beak and D. Chittleborough, Environ. Sci. Technol., 2011, 45, 2777–2782 CrossRef CAS PubMed.
- G. V. Lowry, B. P. Espinasse, A. R. Badireddy, C. J. Richardson, B. C. Reinsch, L. D. Bryant, A. J. Bone, A. Deonarine, S. Chae and M. Therezien, Environ. Sci. Technol., 2012, 46, 7027–7036 CrossRef CAS PubMed.
- I. Velzeboer, J. Quik, D. van de Meent and A. Koelmans, Environ. Toxicol. Chem., 2014, 33, 1766–1773 CrossRef CAS PubMed.
- D. Borah and M. Bera, Trans. ASAE, 2003, 46, 1553–1566 CrossRef.
- D. M. Di Toro, Sediment flux modeling, Wiley-Interscience, New York, 2001 Search PubMed.
- F. Von der Kammer, P. L. Ferguson, P. A. Holden, A. Masion, K. R. Rogers, S. J. Klaine, A. A. Koelmans, N. Horne and J. M. Unrine, Environ. Toxicol. Chem., 2012, 31, 32–49 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2015 |