From regular solutions to microemulsions

Abstract

We address the structure of homogeneous mixtures of equal volumes of water and oil rendered miscible by the addition of amphiphilic molecules. Specifically, we study the pathway from regular ternary solutions to structured microemulsions with increasing amphiphilic chain length, i.e., increasing i and j for alkyl polyglycol ether surfactants (C_iE_j) from C₃E₀ (i.e., propanol) to C₅E₂, using contrast variation small angle neutron scattering (SANS). The bulk-contrast SANS pattern of the symmetric system water–cyclohexane–(2-propanol/1-propanol) with nearly horizontal tie-lines matches Ornstein–Zernike behavior with characteristic q⁻² decay, implying critical composition fluctuations occurring predominantly in the water–oil ratio. Weak scattering signals were detected in film-contrast SANS possibly due to the existence of the nearby tricritical point (TCP). After passing the TCP, the increasing amphiphilic strength leads to the gradual build-up of well-defined amphiphilic interfaces stabilizing water- and oil-rich domains of colloidal dimensions, as evidenced by the well-known q⁻⁴ behavior observed in bulk-contrast SANS pattern at large q. The amphiphilicity factor f_a ranging from +1.15 to −0.60 reveals the crossing of the disorder line, the Lifshitz line, and the wetting to non-wetting transition. Precursors of structuring in those mixtures with compositions, where the lamellar phase appears for even longer-chain amphiphiles, are also borne out by the experiments.

---

Introduction

It is well known that water and oil do not mix. However, equal volumes of water and oil may form a homogeneous stable single phase upon the addition of a third component, being miscible with both the water and the oil, a fact that has been known for over a hundred years. A classic example of such a third component, having the capability of mixing water and oil, is the simple short chain alcohol ethanol, which was also used in the pioneering studies of the ternary phase diagram of water, benzene, and ethanol by Bancroft and Taylor.^1,2 Such ternary systems are typically governed by short range (nearest neighbour) intermolecular interactions, and can thus to a good approximation be described using the concepts of regular solution theory.³ At sufficiently large concentrations of the third component, it becomes the solvent for water and oil, with water and oil molecules being mainly surrounded by solvent molecules.

The solubilization mechanism described above requires relatively large amounts of the third component. A more efficient additive is a surfactant that has a strong affinity for the water–oil interface.^4–6 In these systems, termed microemulsions,^7,8 water and oil do not mix on the molecular length scale but form different domains of colloidal dimensions separated by a dense surfactant film, stabilizing the water–oil interface.⁹ The microemulsion structure may be water or oil continuous, or bicontinuous.^10,11 In the latter case both water and oil form sample spanning domains, again separated by a dense surfactant film.^12–14 With focus on the surfactant-rich dividing surface between water and oil, microemulsions have been identified as interesting experimental model systems to study the thermodynamics of flexible two-dimensional fluid surfaces in three-dimensional space.^15–17 With a fluid surface we here mean a surface that is flexible with a low bending rigidity, and has the ability to undergo topology transformations.^9,15–18

Kahlweit and Strey have in a number of publications addressed the pathway from ternary molecular mixtures to microemulsions.^5,19–23 They clearly described how the three-phase body, a signature of microemulsions, is born in a tricritical point (TCP) with increasing amphiphilicity (increasing i and j in a balanced fashion) of nonionic alkyl polyglycol ether surfactants, CH₃(CH₂)_i−1(OCH₂CH₂)_jOH (C_iE_j).^20,21 They also demonstrated that the regular solution as a simple model is sufficient to generate the TCP even without imposing any structuring by increasing the enthalpic interactions compared to the ideal entropy of mixing.¹⁹ The gradual build-up of water- and oil-rich domains was demonstrated by bulk-contrast small angle neutron scattering (SANS) that showed a gradual transition from Lorentzian Ornstein–Zernike (OZ) scattering²⁴ to a scattering curve exhibiting a well-defined structure factor peak.^22,23 The q⁻⁴ Porod regime observed at higher q-values confirmed the presence of a dense surfactant film separating water- and oil-rich domains. It was also concluded that structured solutions, as defined by the first sign of deviation from simple OZ scattering in bulk-contrast SANS, appear approximately at the wetting to non-wetting transition of the middle-phase microemulsion at the water–oil interface.^25,26 This is also suggested by theory.^27,28 The transition occurs as the spreading coefficient, S = σ_ab − (σ_ac + σ_bc), changes its sign from positive to negative with increasing amphiphilicity. Here, σ_ab is the interfacial tension between the water- (a) and oil-rich (b) phase in the presence of the middle-phase (c), while σ_ac and σ_bc are the water/middle-phase and oil/middle-phase interfacial tensions, respectively. The wetting to non-wetting transition implies the formation of a stable water–oil interface with a low σ_ab. With high amphiphilicity surfactants, σ_ab even becomes ultra-low,^29–31 which has attracted significant attention from e.g., the field of enhanced oil recovery.^32,33 Fig. 1 illustrates the evolution of the isothermal ternary phase behavior when increasing the amphiphilicity of the “third component”. We identify three regimes and refer to them as regular solution, intermediate solution and microemulsion, respectively, where the intermediate solution regime refers to the region between the tricritical point and the wetting to non-wetting transition.

Fig. 1 Schematic phase diagrams illustrating the evolution in phase behavior from regular solutions, via intermediate solutions, to microemulsions, with increasing amphiphilicity of the “third component”. Here, A represents water, B the oil, and C the “third component”. 1 refers to a one phase region, while 2 and 3 refer to regions with two or three coexisting phases, respectively. 2̄ refers to a coexistence of phases rich in water and in the “third component”. In the 2̲ phase region, phases rich in oil and in the “third component” coexist. Dashed lines illustrate tie-lines, and critical plait points are indicated by filled circles.

More recently, microemulsions, referred to as “surfactant-free microemulsions”, or “highly flexible microemulsions” have been proposed to exist also in the regular solution regime^34–42 (see also references therein). Arguments for being microemulsions mainly come from small angle X-ray or neutron scattering data, showing scattering length density (SLD) fluctuations on the nanometer length scale. However, these SLD fluctuations are generally found in the vicinity of critical plait points, pointing to the likelihood that the scattering rather are consequences of critical composition fluctuations.

It is in principle possible to determine whether the observed scattering pattern, I(q), reports mainly on critical composition fluctuations or non-critical solution (i.e., microemulsion) structure.²³ The observation of a Lorentzian OZ scattering pattern, characterized by a forward (q = 0) scattering intensity, I₀, and a real space correlation length of the fluctuations, ξ, is indicative of critical fluctuations.²⁴ But more importantly, if critical composition fluctuations represent the dominating contribution to the scattered intensity, one expects both parameters to diverge at the critical plait point.⁴³ This is something that can be easily verified experimentally, and something that is not expected for a microemulsion structure.^9–14

Another way to address the question of critical composition fluctuation versus microemulsion structure is offered by contrast variation SANS.⁴⁴ Using selectively deuterium labelled components allows for highlighting individual components in the mixture. In the vicinity of a critical plait point, composition fluctuations mainly occur in the direction of the critical tie-line.⁴⁵ For a ternary system, critical fluctuations generally occur in both composition variables,⁴⁶ which complicates the contrast variation analysis. In this paper we define these two variables as ϕ = ϕ_B/(ϕ_A + ϕ_B) and ϕ_C, respectively, where ϕ_I denotes the volume fraction of component I. The exception being the symmetric system, which is schematically illustrated on the left side of Fig. 1. When the third component (C) has the same affinity for the two immiscible components A and B, the critical point is located at equal volumes of A and B and the tie-lines are horizontal, i.e., defined by a constant ϕ_C. In this case, critical composition fluctuations are limited to fluctuations in ϕ.⁴⁷ Then, by contrast matching A and B in a SANS experiment these fluctuations will not be visible and only a low scattering intensity is expected in the absence of a microemulsion structure. With strong contrast between A and B, on the other hand, (critical) fluctuations in ϕ can be evaluated. This is an important approach of the present study.

Non-ionic C_iE_j surfactants are particularly useful model surfactants for systematic studies of microemulsion structure and phase behavior.^5,47,48 They do not require co-surfactants, and the amphiphilicity can be tuned by i and j. Moreover, it is also possible to tune the spontaneous curvature, H₀, of surfactant monolayer films by varying the temperature.^5,47–49 In this paper we particularly address the question of microemulsion structure versus critical composition fluctuations, by comparing three different systems having a different amphiphilicity of the “third component”. The first system is in the regular solution regime close to the TCP, while the two other systems are located on the opposite side of the TCP.

Results and discussion

We have investigated three different experimental systems, in which the degree of amphiphilicity of the “third component” (C) was varied from C₃E₀, via C₄E₁ to C₅E₂. All three systems being in the vicinity of the TCP, with the C₃E₀ system is located on the regular solution side, while the other two are on the microemulsion side. Below we will present and discuss results from the different systems, starting with the C₃E₀ system. For this particular system, we also address the question of “surfactant-free microemulsions”.

Regular solutions – finding the balanced model system

Finding a suitable balanced ternary system in which the “third component” (C) has equal solubility in the A-rich and B-rich phases of the miscibility gap so that the critical composition fluctuations will predominantly involve fluctuations in the A/B-ratio⁴³ with only minor fluctuations in ϕ_C is difficult. Our compromise has been to tune a quasi-ternary system having a mixture of a weakly hydrophilic and a weakly hydrophobic alcohol as the third component. Here, a mixture of 2-propanol (2-C₃E₀) and 1-propanol (1-C₃E₀) was used. Other components (A and B) being water and cyclohexane, respectively. Temperature was kept at T = 25.0 °C. At this temperature the ternary system H₂O–cyclohexane–2-C₃E₀ exhibits the critical plait point on the oil-rich side of the miscibility gap, at ϕ ≈ 0.84. The corresponding system with 1-C₃E₀, on the other hand, has the critical plait point located on the water-rich side, at ϕ ≈ 0.08. Thus, by using a mixture of 2-C₃E₀ and 1-C₃E₀ it is possible to obtain a near-balanced quasi-ternary system for which the critical point is located at ϕ = 0.50 and the critical tie-line has an approximately constant ϕ_C. The two purely ternary phase diagrams with the two different alcohols are presented in the ESI‡ (Fig. S1), together with a schematic illustration of the quaternary phase tetrahedron with the line of critical points.

For SANS experiments performed in the vicinity of the critical point, we are here focusing on two different scattering contrasts. One corresponding to the maximum contrast between water and oil, which is obtained by simply using heavy water (D₂O) and normal cyclohexane. This contrast highlights the fluctuations in ϕ. We refer to this as A/B-contrast. In the second contrast we match the scattering length densities of water and oil by using D₂O and deuterated cyclohexane containing a small amount of protonated cyclohexane. This contrast highlights possible fluctuations in ϕ_C, and we refer to this as C-contrast. In both cases the alcohols had their hydrogen exchanged for deuterium, being 2-propanol-OD and 1-propanol-OD, respectively, in order to avoid the hydrogen exchange with D₂O.

Phase diagram studies were performed (see Methods section and Fig. S2, ESI‡) to find the particular 1-C₃E₀ fraction δ, for which the critical point is located at ϕ = 0.50. δ was found to be slightly different for the two contrasts, with the values δ = 0.24 for the A/B-contrast and δ = 0.18 for the C-contrast. The two corresponding quasi-ternary phase diagrams are presented in Fig. 2.

Fig. 2 Gibbs triangles (volume fraction) of the quasi-ternary systems (a) D₂O–cyclohexane–2-propanol-OD/1-propanol-OD at δ = 0.24 and (b) D₂O–cyclohexane-D₁₂/cyclohexane (96/4)–2-propanol-OD/1-propanol-OD at δ = 0.18, and T = 25.0 °C showing almost symmetric miscibility gaps, which can be described quantitively (red line) by eqn (1) taken from Guggenheim's equation using the predicted critical exponent β = 1/3. The critical points are located at ϕ* = 0.50 ± 0.01 (red filled circles), which are the end points of the lines (red) passing through the center of each tie-line (red open circles) determined from NMR. The SANS measurements were later performed as a function of the total alcohol volume fraction ϕ_C as well as varying the water/oil ratio ϕ (black crosses).

The critical points, located at ϕ* = 0.50 ± 0.01, are marked by red filled circles. The critical C concentrations, are 0.559 ± 0.003 and 0.565 ± 0.003 for the A/B-contrast and the C-contrast, respectively. With the help of ¹H NMR we determined how the two alcohols distribute between the oil-rich phase and water-rich phase and thus the slope of the tie line (ESI,‡ Section S4). Together with the composition of the respective NMR sample and the phase boundary, this gives the tie lines, which are shown as black lines with open red circles marking the middle points where the two coexisting phases have equal volumes. According to the rectilinear diameter method,⁵⁰ the line of open red circles shows the path to the critical point, which can be extrapolated by the intersection with the experimental binodal curve. Note that ϕ_C is close to, but not completely constant along the tie-lines. The experimentally determined binodal data (open circles) are well described by

shown as red lines. Eqn (1) is derived^51–54 from Guggenheim's empirical formula

ρ − ρ_c ∝ (1 − T/T_c)^β (2)

for the phase transition.⁵⁵ The critical exponent β = 0.33 agrees with the predicted value of 1/3, however the determined value of ϕ* = 0.42 ± 0.01 deviates somewhat from 0.5 due to the slight asymmetry of the miscibility gaps.

Regular solutions – small-angle neutron scattering

The two contrast systems were investigated by SANS. The sample compositions measured are indicated as black crosses in Fig. 2(a) and (b). In both systems ϕ_C was varied at constant ϕ = 0.50 approaching the critical point. In the A/B-contrast system we also varied ϕ at constant ϕ_C = 0.565, passing near the critical point.

Fig. 3(a) shows the SANS patterns obtained when varying ϕ_C at constant ϕ = 0.50. As can be seen, the scattered intensity, I(q), increases strongly with decreasing ϕ_C while approaching the critical point. In the studied interval ϕ_C = 0.563–0.645, the low q intensity varies by approximately three orders of magnitude. All curves are well described by the Ornstein–Zernike (OZ) relation²⁴

I(q) = I₀/(1 + ξ²q²) + I_inc, (3)

which implies that critical fluctuations are dominating the scattering. Here I₀ is the forward scattering intensity (at q = 0), ξ is the correlation length and I_inc the incoherent background mainly coming from protons.

Fig. 3 (a) A/B-contrast SANS curves obtained at ϕ = 0.50 and T = 25.0 °C, along a line varying ϕ_C. (b) 1/I₀ and 1/ξ, obtained from the fits, plotted versus ϕ_C. Both 1/I₀ and 1/ξ go to zero at . (c) A/B-contrast SANS curves obtained at ϕ_C = 0.565 ± 0.003, along a line varying ϕ. Solid lines are best fits of eqn (3) to the data shown in (a) and (c).

Best fits of eqn (3) to the data are shown as solid lines. The fitting parameters I₀ and ξ are summarized in the ESI‡ (Table S2). Both parameters diverge at the same critical ϕ_C-value , confirming the presence of the critical point and the fact that the scattering is dominated by critical composition fluctuations. This can be seen in Fig. 3(b) where we have plotted 1/I₀ and 1/ξ versus ϕ_C. Both 1/I₀ and 1/ξ go to zero at .

SANS data were also collected along the line of constant ϕ_C = 0.565 ± 0.003 varying ϕ, passing near the critical point. The collected scattering patterns at selected values of ϕ are presented in Fig. 3(c). Also, along this line, the SANS patterns are well described by the OZ relation (eqn (3)). The values of I₀ and ξ are also presented in the ESI‡ (Table S2). Both parameters show a maximum at the critical ϕ* ≈ 0.50, again consistent with the scattering being dominated by critical composition fluctuations.

Furthermore, SANS measurements in C-contrast were applied to probe any possible solution structure beneath the critical fluctuations. The phase diagram shown in Fig. 2(b) shows that the concentration of the alcohol mixture in the water-rich phase was slightly larger than in the oil-rich phase. Thus, to obtain an exact film contrast, contrast variation experiments (see Fig. S3, ESI‡) were performed to determine the cyclohexane-D₁₂/cyclohexane ratio, at which the total scattering length density of water- and oil-rich domains are fully matched. The obtained 85/15 ratio was used in the C-contrast SANS measurements.

SANS patterns measured in the quasi-ternary system D₂O–cyclohexane-D₁₂/cyclohexane (85/15)–2-propanol-OD/1-propanol-OD (δ = 0.18) at ϕ = 0.50, varying the total alcohol volume fraction ϕ_C are shown in Fig. 4(a). As can be seen, the scattered intensities for this contrast are very low, approximately of the same low magnitude as for the quasi-binary alcohol–D₂O (ϕ = 0) sample (Fig. 3(c)). I₀ is of the order of 1 cm⁻¹, to be compared with A/B-contrast where intensities are three orders of magnitude higher. The question then arises, what is the origin of the weak scattering that increases when ϕ_C decreases towards the critical point? A plausible explanation is that there are small critical fluctuations also in ϕ_C, due to being close to the TCP. As will be further addressed below and in the ESI,‡ the present mixture is in fact close to the TCP, that marks the “birth” of the three-phase triangle, when approaching it from the regular solution side. The three-phase triangle represents an area in the quasi-ternary phase diagram, with variations both in the water–oil ratio ϕ_A/ϕ_B and ϕ_C. Hence, we expect to see fluctuations also in ϕ_C, near the TCP. The observed scattering is weak, and at present we are unable to completely rule out contributions from tie-lines deviating slightly from constant ϕ_C, (Fig. 2(b)). The SANS patterns in Fig. 4(a) do not follow the OZ prediction. Instead of an asymptotic 1/q² dependence, I(q) ∼ 1/q at large q-values. A reasonable description of the data is provided by

I(q) = I₀/(1 + ξq) + I_inc, (4)

where ξ has the dimension of length. However, its true meaning is at present not clear.

Fig. 4 (a) C-contrast SANS curves plotted on a double logarithm scale and (b) [I₀/(I(q) − I_inc)] − 1 plotted versus q for the quasi-ternary system D₂O–cyclohexane–D₁₂/cyclohexane (85/15)–2-propanol-OD/1-propanol-OD measured as a function of the total alcohol volume fraction ϕ_C at δ = 0.18, ϕ = 0.50, and T = 25.0 °C. ξ-Values were obtained from the slope of the plot.

Best fits using eqn (4) are presented in Fig. 4(a) by solid lines. Parameter values are listed in the ESI‡ (Table S3). This unusual functional form of I(q) is further confirmed in Fig. 4(b) where the data are plotted as [I₀/(I(q) − I_inc)] − 1 versus q. The straight lines confirm the functional form of eqn (4). The data set here is limited, but we note that a very similar functional form for I(q) was derived for a model with two coupled fluctuating order parameters,⁵⁶ that also can be traced back to a four-point correlation function.⁵⁷

Regular solutions – analysis of critical fluctuations

Having established above that the scattered intensity in A/B-contrast is governed by critical composition fluctuations, we now proceed and investigate the scaling laws for the correlation length ξ and the forward scattering intensity I₀. As the total alcohol volume fraction ϕ_C is the main tuning parameter used to approach the critical point at a constant temperature and water/oil ratio, we use the chemical potential difference to define the scaling variableequivalently to the reduced temperature⁵⁸ with representing the critical alcohol volume fraction. In Fig. 5(a), ξ and I₀ are plotted versus ε on a double logarithmic scale. Both parameters appear to follow power laws

ξ = [small xi, Greek, circumflex]ε^−ν (6)

and

I₀ = Îε^−γ, (7)

with ν and γ being the critical exponents, and [small xi, Greek, circumflex] and Î the critical amplitudes.⁴⁶

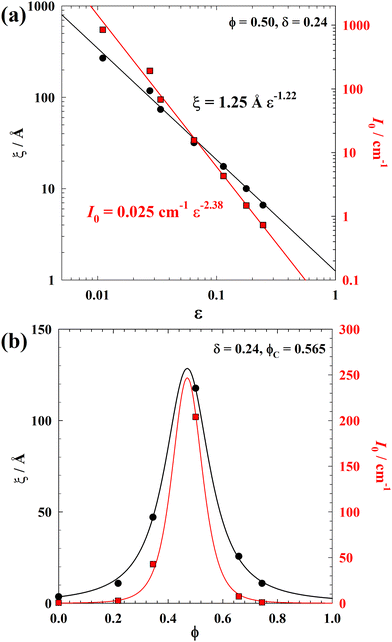Fig. 5 (a) ξ (black circles) and I₀ (red squares) plotted as a function of the reduced logarithm volume fraction of alcohol mixture of the quasi-ternary system D₂O–cyclohexane–2-propanol-OD/1-propanol-OD at δ = 0.24, ϕ = 0.50, and T = 25.0 °C. Critical exponents were determined to be ν = 1.22 and γ = 2.38, which indicates a doubling of the exponents. (b) ξ and I₀ along the line of constant ϕ_C = 0.565 ± 0.003, plotted as a function of ϕ. Both parameters show a maximum in the vicinity of the critical point at ϕ = 0.50. Solid lines are calculated using eqn (9) and (10).⁵⁹

The best fits of eqn (6) and (7) to the ξ- and I₀-data are obtained when the critical volume fraction was set to , which quantitatively agrees with the value determined from the phase behavior within the measurement error. For ξ, the corresponding parameter values are [small xi, Greek, circumflex] = 1.25 ± 0.04 Å and the critical exponent ν = 1.22 ± 0.04. The latter is noticeably larger than the exponents predicted by the mean-field theory and the 3D Ising model, i.e., ν = 0.50 and ν = 0.63, respectively.^46,60–62 For I₀, the best fit of eqn (7) to the data yields Î = 0.025 ± 0.008 cm⁻¹ and γ = 2.38 ± 0.08. Again, the determined value for the critical exponent γ is larger than the predicted values from the mean-field theory and the 3D Ising model, i.e., γ = 1 and γ = 1.24, respectively.^46,58 Nevertheless, the crucial scaling law⁶³

is fulfilled within the experimental error using η = 0.04 and the experimental values, i.e. 2.38/1.22 = 1.95.

In Fig. 5(b) we also analyze the variation of ξ and I₀ along the line of constant ϕ_C = 0.565 ± 0.003, varying ϕ, adapting the approach of Kortan et al.⁵⁹

andwith the constant b_1,ξ, b_2,ξ, b_1,I, and b_2,I.

For the correlation length, the best fit with eqn (9) yields b_1,ξ = 0.60 Å, b_2,ξ = 0.03, ϕ* = 0.47 ± 0.01, , and ν = 1.22 ± 0.01. For the forward scattering we obtain b_1,I = 0.007 cm⁻¹, b_2,I = 0.03, ϕ* = 0.47 ± 0.01, , and γ = 2.38 ± 0.02 using eqn (10).

To sum up, the obtained values of the critical volume fraction of total alcohol and oil ϕ* in the water/oil mixture are consistent with the values found in the phase behavior (Fig. 2(a)) and in the 1/ξ versus ϕ_C plot (Fig. 3(b)). Most importantly, same values of the critical exponents ν and γ were found approaching the critical point by keeping either ϕ or ϕ_C constant. A doubling of the exponents was found, but still keeping the scaling law γ/ν = 2 − η.

The critical exponents obtained here are about two times larger than the values generally found in the literature of microemulsion and micelle systems.^64,65 This exponent doubling phenomenon has been explained with the model of Leung–Griffiths,^58,66 in which the observed behavior was attributed to approaching the line of critical points that bounds the closed-loop coexistence in a direction that becomes tangential to this line.⁶⁷ Sorensen⁶⁸ also explained the exponent doubling observed in microemulsion systems^69,70 with the same argument. Likewise, the exponent doubling observed here might be related to the fact that the critical point of the quasi-ternary system studied is part of the critical line connecting two critical points of the two ternary side systems. However, it should be noted that the critical point is not approached tangentially to the critical line here.

Regular solutions – searching for the tricritical point (TCP)

The weak q⁻¹-scattering observed in the C-contrast SANS data suggested searching for a nearby tricritical point. To prove that a TCP is indeed present in the studied quasi-ternary system by examining the volumes of the water-rich (a) and oil-rich (b) phases with increasing volume fraction δ of 1-propanol in the 2-propanol/1-propanol mixture at ϕ = 0.50, ϕ_C = 0.40. As shown in ESI‡ (Fig. S4), the “bending stress” (as Kahlweit put it) of the sigmoidal curve describing the change in phase volumes with δ increases towards the inflection point when the temperature is lowered from T = 25.0 °C to T = 5.0 °C, in analogy to the concept of Kahlweit et al., according to which the shape of the critical line is an essential measure of the distance to a TCP.^5,19–21 By then increasing the hydrophobicity of the alcohol mixture using a larger 1-C₃E₀ fraction δ, we were able to convert the unbroken critical line into a broken line and thus pass the TCP. Thus, three phases were observed at T = 1.5 °C, confirming that the quasi-ternary system is now located on the other side of the TCP (Fig. 1, center).

To locate the position of the TCP, the point U, characterized by the intersection of the lower (at T_l) and upper (at T_u) critical lines when projected onto the base of a phase prism,^5,20 was determined for different δ through variation of both the volume fraction (ϕ) of cyclohexane in the water/cyclohexane mixture and of the two propanol's in the overall mixture (ϕ_C). Note that, at the point U, two critical lower phases coexist with an oil-rich excess phase at T_l, while at T_u two critical upper phases coexist with a water-rich excess phase, as shown by the photos of the sample closest to the TCP in Fig. 6. It was found that at δ = 0.45, only T_u could be determined, while T_l was below 0 °C. By decreasing δ to δ = 0.435, both T_l = 9.5 °C and T_u = 11.9 °C and could be detected, with three phases forming at temperatures in between. Thus, a phase sequence 2̲ → 3 → 2̄, as observed in classical non-ionic microemulsions, was found. Accordingly, the T(ϕ_C) section taken through the phase prism at this δ and ϕ shown in the ESI‡ (Fig. S5) demonstrates a fish-like phase diagram with a three-phase and a one-phase region.

Fig. 6 Lower (T_l (blue)), mean (T̃ (green)) and upper (T_u (red)) temperature of the three-phase body as a function of the 1-propanol volume fraction δ in the 2-propanol/1-propanol mixture, obtained by varying the volume fractions ϕ and ϕ_C, i.e., of cyclohexane in the water/cyclohexane mixture and of the two propanol's in the overall mixture, respectively. The intersection of the T_u and T_l trajectories gives the tricritical point (TCP) at ϕ = 0.63 ± 0.01, ϕ_C = 0.545 ± 0.002, δ = 0.406 ± 0.005 and T = 15.2 ± 0.1 °C. Photos of the sample located the closest to the TCP were taken at T_u = 14.3 °C, T_l = 13.9 °C, and T̃ = 14.1 °C to show the critical scattering of the phases by green laser light.

The TCP of the quasi-ternary system water–cyclohexane–2-propanol/1-propanol was then successfully determined at δ = 0.406 ± 0.005 and T = 15.2 ± 0.1 °C via the intersection of the trajectories T_l(δ) and T_u(δ) at the point U(δ).

In conclusion, this study shows clearly that the studied quasi-ternary system is located close to a TCP, which is indeed passed when the temperature and the composition are adjusted accordingly. This proximity of a TCP therefore supports our hypothesis that the weak fluctuations detected in the C-contrast SANS measurements originate from fluctuations in ϕ_C.

Microemulsions

To prove the formation of the amphiphilic film in systems after passing the TCP, two systems water–n-octane–C_iE_j were studied with SANS measurements in bulk (A/B) – contrast. In the balanced state, there is now a three-phase triangle where the middle phase contains equal amounts of water and oil in the system. With increasing amphiphilicity (i, j), the evolution from weakly to strongly structured microemulsions with a three-phase triangle is expected.^5,19–23

Microemulsions – phase behavior

The isothermal ternary phase diagram (Gibbs triangle) of the system water–n-octane–C₄E₁, determined at the phase inversion temperature T̃ = 19.5 °C, is shown in Fig. 7(a). Within this system, the monomeric solubility γ₀ of C₄E₁ in water and oil is 0.152 and the minimum mass fraction [small gamma, Greek, tilde] of C₄E₁ to solubilize water and oil into each other is 0.533, which is also known from a previous study.¹⁹

Fig. 7 Gibbs triangles (volume fraction) of the ternary systems (a) H₂O–n-octane–C₄E₁ measured at T = 19.5 °C and (b) H₂O–n-octane–C₅E₂ measured at T = 33.7 °C. Black crosses illustrate the SANS study measured as a function of ϕ_C in bulk-contrast at equal volumes of water and oil, i.e., ϕ = 0.50.

After passing the wetting–nonwetting transition, a more amphiphilic C₅E₂ was used in the system water–n-octane–C₅E₂ to characterize microemulsions dominated by the properties of the amphiphilic surfactant film. The ternary phase diagram measured at T̃ = 33.7 °C in Fig. 7(b) shows a larger three-phase triangle compared to the C₄E₁ microemulsion system. It is already known that the three-phase body evolves from the tricritical point upon increasing amphiphilicity (i, j) of C_iE_j and reaches a maximum in the range of rather short medium chain amphiphiles.¹⁹ However, with stronger amphiphilicity, a more efficient solubilization of water and n-octane, i.e., smaller [small gamma, Greek, tilde] as 0.474, with a much smaller monomeric solubility γ₀ compared to C₄E₁ was observed here.

Microemulsions – small-angle neutron scattering

The SANS spectra of the ternary system D₂O–n-octane–C₄E₁ measured in bulk (A/B) – contrast varying the volume fraction of amphiphile ϕ_C at ϕ = 0.50 and T = 14.8 °C are presented in Fig. 8(a). One can see that, a decrease in the scattering intensity at low q and a gradual development of the peak at high q while increasing ϕ_C. There is no obvious peak in samples with low ϕ_C, which agrees to the findings in previous works.^22,23 At high q, an asymptotic Porod regime (I(q) ∼ q⁻⁴) is observed indicating the birth of a structure of separated water-rich and oil-rich domains with a sharp interface between them. These curves can be well described with the Teubner–Strey model for bicontinuous microemulsions⁷¹

I_TS(q) = (a₂ + c₁q² + c₂q⁴)⁻¹. (11)

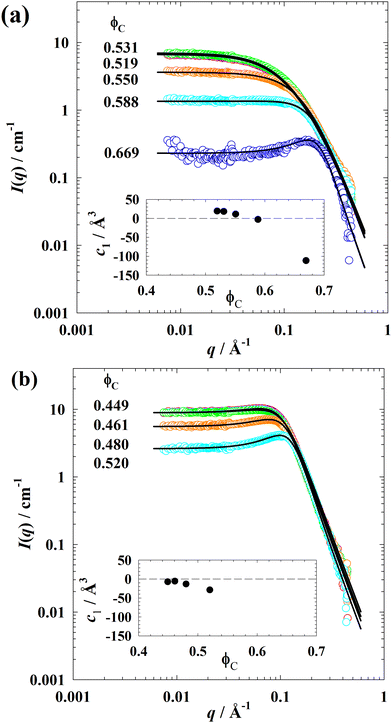Fig. 8 SANS curves of (a) the ternary system D₂O–n-octane–C₄E₁ at T = 14.8 °C and (b) the ternary system D₂O–n-octane–C₅E₂ at T = 30.3 °C measured as a function of the volume fraction ϕ_C of amphiphile in bulk-contrast at equal volumes of water and oil, i.e., ϕ = 0.50. The insets show the parameter c₁ of the Teubner–Strey structure factor (eqn (11)) as a function of ϕ_C for both ternary systems. Note that we have added a plot of 1/I(q) versus (q − q_max)² in the ESI‡ (Fig. S6) exemplarily for the system D₂O–n-octane–C₅E₂, including the fits with the TS model.

Here a₂ = 1/I₀, c₁ and c₂ are the coefficients of the order parameter expansion defining the periodicity d_TS, the correlation length ξ_TS, and the amphiphilicity factor f_a according to

As can be seen, the Teubner–Strey model allows for a quantitative description of the scattering data. The fitting results are listed in the ESI‡ (Table S4). It was found that the periodicity d_TS decreases with increasing volume fraction ϕ_C of amphiphile, whereas the correlation length ξ_TS slightly increases from 7.24 Å to 10.33 Å. Note that, no d_TS values can be obtained when the f_a values are bigger than 1 in the first two samples with low ϕ_C, which is already revealed by the monotonically drop in I(q) curves. It is noteworthy that the amphiphilicity factor f_a is an important parameter, which changes from positive to negative when c₁ becomes negative, to quantify the degree of order in bicontinuous microemulsions.^72,73 For f_a > 1 the water–water correlation function (being the Fourier transform of the structure factor eqn (11)), decays monotonically. For f_a < 1, the correlation function also contains oscillations, indicative of solution structure. The so-called disorder line (f_a = 1) marks the boundary between these two cases. As c₁ and f_a becomes negative, passing the Lifshitz line (f_a = 0), a structure factor peak gradually appears at q > 0. Accordingly, well-structured bicontinuous microemulsions show correlation peaks in the scattering spectra and have negative values of f_a.

The analysis of the SANS spectra of the ternary system D₂O–n-octane–C₄E₁ revealed that f_a decreases from 1.15 to −0.60 with increasing ϕ_C (ESI,‡ Table S4) implies a transition passing the disorder line and Lifshitz line. Values of c₁ are reported as insets in Fig. 8(a) and (b). These results agree to the previous studies of Gompper and Schick^72,73 that the disorder line and/or the Lifshitz line can be passed by increasing the amphiphile concentration even with weak amphiphiles. Further increasing amphiphile concentration will lead to more negative f_a values and closer to −1, which implies more structured microemulsions or even lamellar phase.

Afterwards, the structure of the D₂O–n-octane–C₅E₂ system was also studied as a function of ϕ_C at ϕ = 0.50 and T = 30.3 °C. The SANS curves in Fig. 8(b) show that increasing the C₅E₂ volume fraction leads to a more distinct scattering peak moving towards higher q-values. In other words, a classical microemulsion behavior was presented and can thus be well described with the TS model. The results of the analysis are listed in the ESI‡ (Table S4). As one can see, the correlation length ξ_TS in the mixture D₂O–n-octane–C₅E₂ varies from 16.9 Å to 17.7 Å while in the mixture D₂O–n-octane–C₄E₁ the ξ_TS varies from 7.24 Å to 10.3 Å. In addition, the decrease of periodicity d_TS and amphiphilicity factor f_a with increasing amphiphile concentration ϕ_C indicates the evolution of a more defined structure.^22,23 The fact that more negative values of f_a at low ϕ_C also points out that more defined structures exist in the mixtures with C₅E₂ than with C₄E₁.

Finally, the insets of Fig. 8(a) and (b) show that with increasing amphiphile concentration ϕ_C, the c₁ value obtained from the TS model decreases strongly for both systems, i.e., more structured mixtures are developed with increasing ϕ_C. Especially, at low ϕ_C, the system formulated with C₅E₂ already exhibits negative c₁ values, while the system formulated with C₄E₁ shows positive ones, indicating a higher structural ordering formed with a more amphiphilic C₅E₂.

Critical composition fluctuations versus “surfactant-free microemulsions”

Above, we have characterized the transition from regular solutions to microemulsions by gradually increasing the amphiphilicity of the “third component”, including the birth of the microemulsion phase, as a “middle phase” from a tricritical point. In the regular solution regime, we have paid particular attention to the critical composition fluctuations that occur not only near the critical plait point, and characterized these fluctuations quantitatively. The results from this work suggest that the mixtures containing propanol as “third component”, showing only a simple miscibility gap, behave to a good approximation as regular solutions, while with C₄E₁ and C₅E₂ the SANS data clearly indicate structure on the colloidal length scale and the presence of relatively sharp water–oil interfaces. This crucial difference between regular solutions and microemulsions manifests itself through the different power law behavior of the bulk contrast SANS at large q. While the former exhibit I(q) ∼ q⁻² behavior that results from a diverging correlation function,⁶³ microemulsions show Porod scattering (I(q) ∼ q⁻⁴). These results are perfectly in line with the overall picture outlined by Kahlweit, Strey and coworkers in their pioneering work approximately three decades ago.^19–21

Several works have claimed that also solutions in the regular solution regime can be structured microemulsions, referring this to “surfactant-free microemulsions”.^34–41 In the early works of Barden and coworkers,^74,75 the system water–n-hexane–2-propanol was investigated, and a large part of the one phase region near the binodal was claimed to be an oil continuous microemulsion. More recently, the system water–1-octanol–ethanol has been extensively studied^35–38 in particular using small angle scattering, interpreting the scattering data in terms of oil-in-water, bicontinuous and water-in-oil structures.

Obviously, the molecular mixing in these ternary regular solutions is not completely random, as shown by the presence of a miscibility gap. However, referring to these solutions as microemulsions is somewhat misleading and may be a source of confusion as this term normally is reserved for surfactant stabilized oil–water solutions, having structure on the colloidal length scale where essentially pure oil and water domains are separated by a dense surfactant film. Clearly there is a gradual, although non-trivial, transition from regular solutions to microemulsions as illustrated in this work, and first demonstrated by Kahlweit and coworkers.^19–21 There is a vast structural difference between the solutions situated on the opposite sides of the tricritical point and the wetting to non-wetting transition. Calling everything microemulsion seems less useful. It is probably better to stay with the suggestions of Danielsson and Lindman,⁸ including that the concept of microemulsion does not cover surfactant-free systems of any kind.

If small angle scattering data in the regular solution regime essentially show a Lorentzian q-dependence (Ornstein–Zernike), this should most likely best be interpreted in terms of simple composition fluctuations. In particular if the forward scattering, I(0), and the correlation length monotonically increases and appear to diverge as one approaches the critical plait point. Claiming microemulsion structure from such data would require that one first clearly demonstrate that they are not resulting from critical composition fluctuations.

Conclusions

The present study deals with water–oil mixtures stabilized by a third component of varying amphiphilicity. Particular focus is on the transition between essentially disordered molecular mixtures, i.e., regular solutions, and structured microemulsions containing distinct water-rich and oil-rich domains of colloidal dimensions, separated by a surfactant loaded interface. With C₃E₀ (propanol) as third component, the quasi-ternary system forms regular solutions. In contrast variation SANS the observed scattering is dominated by diverging composition fluctuations as the critical plait point is approached. By carefully tuning a mixture of 1-propanol and 2-proponol it was possible to obtain an approximately symmetric system with fluctuations only in the local water–oil ratio. No signs of any significant solution structure on the nanometer length scale were observed. In oil–water contrast, the SANS patterns, showing the typical q⁻² decay, are well described by the classical Ornstein–Zernike scattering function. The critical fluctuations were quantitatively analyzed in terms of critical exponents for the correlation length and the effective compressibility, that showed a doubling of the exponents compared to classical mean-field and 3D Ising models. Such doubling has been explained by the presence of a line of critical points^58,66–68 that here may be associated with the use of an alcohol mixture as a quasi third component.

The regular solution regime and microemulsions are essentially separated by a tricritical point (TCP), that thus marks the birth of the middle phase microemulsions. The propanol system is close to the TCP and a minor increase in molecular amphiphilicity to C₄E₁ results in a crossing of the TCP and the formation of microemulsions. Here, the observation of an asymptotic Porod regime (I(q) ∼ q⁻⁴) in water–oil contrast strongly indicates a structure of separate water-rich and oil-rich domains with a sharp interface in between. Increasing the amphiphilicity of the third component further to C₅E₂, results in a further swelling of the middle phase microemulsion and an increasingly well-defined structure as seen by the appearance of a peak in the SANS pattern. We conclude from this that C₃E₀ (propanol) is not sufficiently amphiphilic to form a dense film at the oil–water interface and stabilize a microemulsion structure, while C₄E₁ and subsequently C₅E₂ are.

It has been suggested in the literature that also ternary mixtures in the regular solution regime may be structured into separate water-rich and oil-rich domains, and have referred to the solutions as “surfactant-free microemulsions”.^{34–42,74,75} The results of the present study, however, where our propanol system is close to the TCP, on the contrary suggest that microemulsions, as defined by being structured into water-rich and oil-rich domains separated by a surfactant loaded interface, are first formed after the TCP. We note also that the ability to form microemulsions with surfactant stabilized oil–water interfaces is also manifested by the wetting-to-nonwetting transition of the middle phase microemulsion.^25,26

Data availability

The authors declare that the data supporting the findings of this study are available within the article and its ESI.‡ Should any raw data files be needed in another format they are available from the corresponding author upon reasonable request.

Conflicts of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this article.

Acknowledgements

The authors thank Karl-Erik Bergquist (Lund University) for NMR measurements and the SANS teams consisting of K. Abitaev, K. Schneider, D. Sottmann, S. Lülsdorf, J. Fischer and M. Krappel (Institute of Physical Chemistry, University of Stuttgart) for their help during the SANS measurements. We acknowledge the support of the National Institute of Standards and Technology, U.S. Department of Commerce, in providing the neutron research facilities used in this work. The authors particularly thank the local contact Yun Liu for his expert help during the two beam-times under the proposal numbers S37-87 and S39-47. This work is furthermore based upon experiments (proposal number 14021) performed at the KWS-1 instrument operated by Henrich Frielinghaus at the Heinz Maier-Leibnitz Zentrum (MLZ), Garching, Germany. The authors gratefully acknowledge the financial support provided by the Jülich Centre for Neutron Science (JCNS) to perform the neutron scattering measurements at the MLZ. We thank the Institut Laue Langevin (ILL) in Grenoble (France) for additional SANS measurements performed at the D11 instrument and the valuable support of our local contact Ralf Schweins also for DLS measurements performed at the Partnership for Soft Condensed Matter (PSCM). S.-Y. Tseng acknowledges support from the European Union's Horizon 2020 research and innovation program under grant agreement no. 731019 (EUSMI). U. Olsson acknowledges funding from the Swedish Research Council (grant no. 2020-04633).

References

1. S. F. Taylor, J. Phys. Chem., 1897, 1, 301.
2. W. D. Bancroft and S. S. Hubard, J. Am. Chem. Soc., 1942, 64, 347.
3. J. H. Hildebrandt, Proc. Natl. Acad. Sci. U. S. A., 1927, 13, 267.
4. K. Shinoda, H. Kunieda, T. Arai and H. Saijo, J. Phys. Chem., 1984, 88, 5126.
5. M. Kahlweit and R. Strey, Angew. Chem., Int. Ed. Engl., 1985, 24, 654.
6. K. Ishikawa, M. Behrens, S. Eriksson, D. Topgaard, U. Olsson and H. Wennerström, J. Phys. Chem. B, 2016, 120, 6074.
7. J. H. Schulman and T. P. Hoar, Nature, 1943, 152, 102.
8. I. Danielsson and B. Lindman, Colloids Surf., 1981, 3, 391.
9. P. G. De Gennes and C. Taupin, J. Phys. Chem., 1982, 86, 2294.
10. D. Langevin, Acc. Chem. Res., 1988, 21, 255.
11. R. Strey, Colloid Polym. Sci., 1994, 272, 1005.
12. J. F. Bodet, J. R. Bellare, H. T. Davis, L. E. Scriven and W. G. Miller, J. Phys. Chem., 1988, 92, 1898.
13. W. Jahn and R. Strey, J. Phys. Chem., 1988, 92, 2294.
14. B. Lindman, K. Shinoda, U. Olsson, D. Anderson, G. Karlström and H. Wennerström, Colloids Surf., 1989, 38, 205.
15. S. A. Safran, Statistical Thermodynamics of Surfaces, Interfaces, and Membranes, Addison-Wesley, Reading, MA, 1994.
16. H. Wennerström and U. Olsson, Langmuir, 1993, 9, 365.
17. G. Gompper and M. Schick, Self-assembling Amphlphilic Systems, Academic Press, 1994.
18. D. C. Morse, Curr. Opin. Colloid Interface Sci., 1997, 2, 365.
19. M. Kahlweit, R. Strey, P. Firman, D. Haase, J. Jen and R. Schomaecker, Langmuir, 1988, 4, 499.
20. M. Kahlweit, R. Strey, M. Aratono, G. Busse, J. Jen and K. V. Schubert, J. Chem. Phys., 1991, 95, 2842.
21. M. Kahlweit, R. Strey and G. Busse, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1993, 47, 4197.
22. K. V. Schubert, R. Strey, S. R. Kline and E. W. Kaler, J. Chem. Phys., 1994, 101, 5343.
23. K. V. Schubert and R. Strey, J. Chem. Phys., 1991, 95, 8532.
24. L. S. Ornstein and F. Zernike, Proc. Akad. Sci., 1914, 17, 793.
25. O. Abillon, L. T. Lee, D. Langevin and K. Wong, Phys. A, 1991, 172, 209.
26. M. Gradzielski, D. Langevin, T. Sottmann and R. Strey, J. Chem. Phys., 1996, 104, 3782.
27. B. Widom, Langmuir, 1987, 3, 12.
28. G. Gompper and M. Schick, Phys. Rev. Lett., 1990, 65, 1116.
29. R. Aveyard, B. P. Binks, S. Clark and J. Mead, J. Chem. Soc., Faraday Trans. 1, 1986, 82, 125.
30. T. Sottmann and R. Strey, Ber. Bunsen-Ges. Phys. Chem., 1997, 100, 237.
31. T. Sottmann and R. Strey, J. Chem. Phys., 1997, 106, 8606.
32. D. O. Shah and R. S. Schechter, Improved oil recovery by surfactant and polymer flooding: AIChE symposium on improved oil recovery by surfactant and polymer flooding, 1976, Elsevier, New York, 1977.
33. A. Bera and A. Mandal, J. Pet. Explor. Prod. Technol., 2015, 5, 255.
34. W. Hou and J. Xu, Curr. Opin. Colloid Interface Sci., 2016, 25, 67.
35. T. N. Zemb, M. Klossek, T. Lopian, J. Marcus, S. Schöettl, D. Horinek, S. F. Prevost, D. Touraud, O. Diat, S. Marčelja and W. Kunz, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 4260.
36. M. L. Klossek, D. Touraud, T. Zemb and W. Kunz, ChemPhysChem, 2012, 13, 4116.
37. O. Diat, M. L. Klossek, D. Touraud, B. Deme, I. Grillo, W. Kunz and T. Zemb, J. Appl. Crystallogr., 2013, 46, 1665.
38. S. Schöttl, T. Lopian, S. Prévost, D. Touraud, I. Grillo, O. Diat, T. Zemb and D. Horinek, J. Colloid Interface Sci., 2019, 540, 623.
39. J. Xu, J. Song, H. Deng and W. Hou, Langmuir, 2018, 34, 7776.
40. V. Fischer, J. Marcus, D. Touraud, O. Diat and W. Kunz, J. Colloid Interface Sci., 2015, 453, 186.
41. S. Krickl, L. Jurko, K. Wolos, D. Touraud and W. Kunz, J. Mol. Liq., 2018, 271, 112.
42. Y. Han, N. Pan, D. Li, S. Liu, B. Sun, J. Chai and D. Li, Chem. Eng. J., 2022, 437, 135385.
43. B. Widom, Physica, 1974, 73, 107.
44. H. B. Stuhrmann, J. Appl. Crystallogr., 1974, 7, 173–178.
45. J. C. Wheeler and B. Widom, J. Am. Chem. Soc., 1968, 90, 3064.
46. H. E. Stanley, Introduction to phase transitions and critical phenomena, Oxford University Press, 1971.
47. H. Kunieda and K. Shinoda, J. Dispersion Sci. Technol., 1982, 3, 233.
48. U. Olsson and H. Wennerström, Adv. Colloid Interface Sci., 1994, 49, 113.
49. R. Strey, Curr. Opin. Colloid Interface Sci., 1996, 1, 402.
50. L. Cailletet and E. Mathias, J. Phys. Theor. Appl., 1886, 5, 549.
51. W. Schröer, J. Mol. Liq., 2006, 125, 164.
52. V. R. Vale, B. Rathke, S. Will and W. Schröer, J. Chem. Eng. Data, 2010, 55, 4195.
53. X. Shao, W. Schröer and B. Rathke, J. Chem. Eng. Data, 2014, 59, 225.
54. S. Diekmann, E. Dederer, S. Charmeteau, S. Wagenfeld, J. Kiefer, W. Schröer and B. Rathke, J. Phys. Chem. B, 2020, 124, 156.
55. E. A. Guggenheim, J. Chem. Phys., 1945, 13, 253.
56. D. Roux, M. E. Cates, U. Olsson, R. C. Ball, F. Nallet and A. M. Belloq, Europhys. Lett., 1990, 11, 229.
57. S. Davatolhagh, Am. J. Phys., 2006, 74, 441.
58. R. B. Griffiths and J. C. Wheeler, Phys. Rev. A:At., Mol., Opt. Phys., 1970, 2, 1047.
59. A. R. Kortan, H. v Känel, R. J. Birgeneau and J. D. Litster, Phys. Rev. Lett., 1981, 47, 1206.
60. J. C. le Guillou and J. Zinn-Justin, Phys. Rev. B:Condens. Matter Mater. Phys., 1980, 21, 3976.
61. A. Sariban and K. Binder, J. Chem. Phys., 1987, 86, 5859.
62. R. Guida and J. Zinn-Justin, J. Phys. A: Math. Gen., 1998, 31, 8103.
63. M. E. Fisher, J. Math. Phys., 1964, 5, 944.
64. J. S. Huang and M. W. Kim, Phys. Rev. Lett., 1981, 47, 1462.
65. M. Corti and V. Degiorgio, J. Phys. Chem., 1981, 85, 1442.
66. S. S. Leung and R. B. Griffiths, Phys. Rev. A:At., Mol., Opt. Phys., 1973, 8, 2670.
67. R. G. Johnston, N. A. Clark, P. Wiltzius and D. S. Cannell, Phys. Rev. Lett., 1985, 54, 49.
68. C. M. Sorensen, Chem. Phys. Lett., 1985, 117, 606.
69. R. Dorshow, F. de Buzzaccarini, C. A. Bunton and D. F. Nicoli, Phys. Rev. Lett., 1981, 47, 1336.
70. F. Nicoli, F. de Buzzaccarini, L. S. Romsted and C. A. Bunton, Chem. Phys. Lett., 1981, 80, 422.
71. M. Teubner and R. Strey, J. Chem. Phys., 1987, 87, 3195.
72. J. Lerczak, M. Schick and G. Gompper, Phys. Rev. A:At., Mol., Opt. Phys., 1992, 46, 985.
73. G. Gompper, R. Hołyst and M. Schick, Phys. Rev. A: At., Mol., Opt. Phys., 1991, 43, 3157.
74. G. D. Smith, C. E. Donelan and R. E. Barden, J. Colloid Interface Sci., 1977, 60, 488.
75. B. A. Keiser, D. Varie, R. E. Barden and S. L. Holt, J. Phys. Chem., 1979, 83, 1276.

---

Footnotes

† This article is dedicated to the memory of Professor Stefan Egelhaaf, an outstanding scientist and inspiring academic teacher. To have known and worked with Stefan personally has been a privilege and an honour.

‡ Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm01258e

---