Effects of removing boron from subphthalocyanines: a theoretical perspective

Abstract

The element hosted within the inner cavity of phthalocyanines (Pcs) dictates the wide functional versatility of these well-known macrocycles. Subphthalocyanines (SubPcs), by contrast, are only known as boron complexes, yet they exhibit a range of emerging properties unattainable with other compounds. The effects of replacing the boron atom in these macrocycles, however, remain unclear. Herein, we present a comprehensive theoretical investigation of non-boron SubPc complexes incorporating various metal and non-metal elements. Specifically, we use density functional theory (DFT) to assess the impact of boron replacement on bowl depth, dipole moment, charge distribution, key frontier molecular orbitals, UV-vis absorption properties, ionization potential, and electron affinity of SubPcs. Our findings reveal that substituting the boron atom induces significant alterations across these properties, with pronounced variability depending on the group, atomic size, and oxidation state of the central element. Altogether, this study underscores the functional versatility that non-boron SubPcs could introduce within the broader field of porphyrinoid chemistry, paving the way for disruptive materials with tailored electronic and photophysical properties.

---

1. Introduction

Porphyrinoids, first recognized for their pivotal roles in biological processes such as photosynthesis and cellular respiration, hold a privileged position among the most employed electroactive dyes.^1–3 Among them, phthalocyanines (Pcs; Fig. 1), well-known for their 18π-electron aromaticity, stand out due to their remarkable chemical robustness and extensive functional landscape, spanning applications from molecular photovoltaics,^4–6 optoelectronics,⁷ and spintronics⁸ to photodynamic therapy,⁹ artificial photosynthesis,¹⁰ and catalysis.¹¹ This versatility arises from the ability to finely tune the properties of these macrocycles through a variety of chemical modifications, allowing precise control over critical aspects such as absorption–emission characteristics,^12,13 excited-state dynamics,¹⁴ and supramolecular organization.¹⁵ In this regard, a key design strategy has been the selection of the central atom complexed within the tetrapyrrolic core. The central element in Pcs exerts a profound influence on their physical and electronic properties and may even endow them with novel features, such as magnetism or potential for exotic post-functionalization.^14,16 Indeed, more than 70 elements have been successfully complexed within Pcs, each inducing distinct electronic and structural perturbations, ultimately leading to different functional behaviors.

Fig. 1 Molecular structure of metalated Pcs and boron–SubPcs.

In sharp contrast, subphthalocyanines (SubPcs), the contracted homologues of Pcs, are known only as boron complexes.^17,18 This intriguing class of porphyrinoids consists of three isoindole rings linked by nitrogen bridges, forming tridentate ligands. Notably, SubPcs exhibit a characteristic bowl-shaped topology, comprising a non-planar 14π-electron system, which imparts unique properties not attainable in their planar counterparts (e.g., shape-assisted self-assembly, polarization, and chirality).¹⁹ These features make SubPcs particularly valuable in the quest for next-generation materials. Consequently, SubPcs have garnered significant attention in recent years, finding applications in cutting-edge technologies, including ferroelectricity,²⁰ spin-filtering,²¹ and on-surface chemistry.²²

Inspired by the precedent set by Pcs, numerous efforts have been devoted over the decades to preparing “boron-free” SubPcs, though without success. The boron atom in SubPcs is integral to their synthesis, which involves the cyclotrimerization of phthalonitriles in the presence of a boron trihalide, typically BCl₃, which acts as a templating Lewis acid.^23,24 This templation is driven by the tendency of boron to form four bonds and adopt a tetrahedral geometry—an arrangement not possible with Pc ligands. Consequently, the boron atom in SubPcs is coordinated to a fourth substituent, referred to as the axial ligand. Thus, the energy lost by curving the π-system is compensated by the stabilization provided through complexation with the B³⁺ atom. It is not surprising therefore that attempts to use Lewis acids other than BX₃ reagents have either led to the formation of Pcs—due to their less strained π-skeleton—or have simply prevented cyclization. Another proposed approach to obtaining boron-free SubPcs has involved post-synthesis removal of the boron atom using external nucleophiles. However, the high affinity of the tridentate ligand for boron, due to its ideal size and hybridization, combined with the macrocycle's sensitivity to ring-opening reactions, has rendered this strategy unsuccessful. Although promising studies on boron-free subporphyrins (SubPs) have been reported by Kim, Osuka, Song and coworkers,²⁵ the preparation of boron-free SubPcs remains an unexplored territory.

This challenging synthetic endeavor would only be meaningful if significant electronic, structural, and physical perturbations are introduced by the removal of boron. At this juncture, despite the well-established precedent of Pcs, theoretical predictions regarding the impact of boron removal in SubPcs are crucial to guide future synthetic efforts. While a few elegant studies using DFT have been described in recent years,^26–33 a comprehensive theoretical investigation of boron-free SubPcs from the perspective of organic chemistry and materials science remains absent.

In this work, we aim to shed light on this issue by modeling, through DFT calculations, a series of SubPcs complexed with elements—both metals and non-metals—different from boron. Our study reveals how the choice of central element would significantly modulate fundamental single-molecule properties, including molecular structure, electronic distribution, orbital alignment, and the optical and redox properties of these macrocycles. A direct comparison with boron SubPcs is established, and the properties of free-base SubPcs are also discussed. Altogether, this work provides a solid proof of concept that the replacement of boron in SubPcs by other atoms is a milestone that would open new functional dimensions within porphyrinoid chemistry.

2. Results and discussion

The molecules selected for this study are summarized in Fig. 2. We have proposed a series of SubPc complexes based on both metals and non-metals. The coordination index, geometry, and electronic configuration were chosen according to the common chemical behavior of the element, its oxidation state, and the dianionic nature of the SubPc tridentate ligand. Among the main group elements, Al³⁺, Ga³⁺, and In³⁺-based complexes were considered due to their chemical similarity to boron, making them plausible candidates for complexation. Additionally, group 14 elements—C, Si, Ge, Sn, and Pb—as well as P³⁺ and P⁵⁺, were included, given their ability to form stable complexes with nitrogen-based ligands. For transition metal complexes, all first-row elements were considered, with oxidation states selected based on their common redox behavior. To enable a meaningful comparison, second- and third-row elements from groups 6 to 8 were also included. In all cases, neutral species were prioritized, with the exception of C⁴⁺, P³⁺, and P⁵⁺, which were modeled as cationic due to their inherent charge requirements. Other charged species are the deprotonated versions (H₁⁻– and 2⁻–Td) of SubPc free base (H₂–Td) which are mono and dianionic. Complexes with elements in the oxidation state +3 were modeled as tetrahedral (Td) complexes, with a chlorine atom occupying the axial position (M–TdCl), following the standard reference structure of B-SubPc (B–TdCl). For elements in the oxidation state +4, octahedral “hourglass” geometries were adopted (M–Oc). Complexes in the +2 oxidation state were modeled also as tetrahedral complexes, but with a neutral pyridine ligand that stabilizes the axial position (M–Tdpy). Furthermore, oxo-complexes (M–Td=O) were considered for elements that typically form them, such as V⁴⁺, Mn⁴⁺, and P⁵⁺. For transition metals, both low-spin and high-spin configurations were investigated – in the case of tetrahedral complexes, the electronic distribution over e and t₂ orbitals was analyzed, while for octahedral complexes, the distribution between t_2g and e_g orbitals was studied. These configurations are expected for d-block transition metals in tetrahedral and octahedral geometries, respectively. Moreover, the SubPc free base was also analyzed. All optimizations were performed using DFT at the B3LYP level of theory. The 6-31G+(d,p) basis set was used for lighter elements, while LANL2DZ was applied for elements beyond the first-row transition metals.

Fig. 2 Molecular structure of the M–SubPcs considered in this study.

Our analysis focuses on four key aspects that we consider critical for determining the potential applications of SubPcs. (1) Bowl depth (BD): this parameter refers to the “deepness” of the bowl-shaped geometry in SubPcs. BD has a significant impact on how SubPc molecules interact with one another and also with other electroactive partners. In essence, bowl depth plays a crucial role in the shape-assisted supramolecular chemistry of SubPcs, which is fundamental for instance, for forming 1D arrays for efficient light harvesting and charge transport, as well as for preparing multicomponent systems with shape- and electron-complementary molecules, such as fullerenes.¹⁹ (2) Dipole moment (DM) and charge distribution: the DM is an essential property of SubPcs given its potential in the development of polarized materials, which is a differential feature of these compounds. This would anticipate utility in state-of-the art technologies, such as bulk-photovoltaic effect or nonlinear optics.³⁴ (3) Impact on molecular orbitals: the main absorption band of SubPcs, known as the Q-band, brings the molecule to the excited state, initiating various photophysical processes that form the basis for their applicability. In boron-based SubPcs, the Q-band typically results from transitions between the HOMO, LUMO, and LUMO+1 orbitals. These orbitals are also involved in charge transport and electron transfer processes. Therefore, understanding how these orbitals are affected by different complexation is crucial for predicting the electronic behavior of SubPcs. (4) Electron Affinity (EA) and ionization potential (IP): these parameters relate to the addition or removal of an electron from the molecule, i.e., the redox properties of the system. Since redox behavior is pivotal for applications in semiconducting materials, examining these aspects will provide insight into the electron-donating and electron-accepting capabilities of the proposed SubPcs.

2.1. Structural variations and bowl-depth

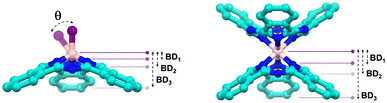
BD, typically measured in angstroms (Å), corresponds to the distance between the maximum curvature of the “bowl” and the plane formed by specific atoms. In SubPcs, three distinct BDs can be identified, as illustrated in the representation of Table 1. BD₁ corresponds to the distance between the maximum of the bowl and the plane formed by the three coordinating pyrrolic nitrogen atoms; BD₂ involves the plane formed by the three meso-nitrogen atoms; and BD₃, the most commonly referenced BD in SubPcs, is defined by the plane formed by the six outer carbon atoms of the fused benzene rings. All three bowl depths—BD₁, BD₂, and BD₃—have been calculated for all compounds, and the corresponding values are summarized in Table 1. For reference, the values of B–TdCl are 0.597 Å, 1.150 Å, and 2.578 Å.

Table 1 BD_1–3 values of the M–TdCl, M–Tdpy, M–Oc, M–Td=O and M–Td complexes

Entry	Complex	BD1	BD2	BD3	Entry	Complex	BD1	BD2	BD3
1	B–TdCl	0.597	1.150	2.578	26	Ru(5)–Tdpy	1.323	2.148	4.194
2	Al–TdCl	1.048	1.815	3.884	27	Os(3)–Tdpy	1.328	2.090	4.069
3	Ga–TdCl	1.099	1.856	3.956	28	Os(5)–Tdpy	1.299	2.115	4.101
4	In–TdCl	1.320	2.118	3.355	29	Co–Tdpy	1.120	1.906	4.031
5	C–TdCl	0.492	0.879	1.912	30	Rh–Tdpy	1.442	2.201	4.233
6	Sc–TdCl	1.394	2.158	4.177	31	Ir–Tdpy	1.416	2.185	4.226
7	Cr(2)–TdCl	1.111	1.873	3.730	32	Zn–Tdpy	1.122	1.917	4.152
8	Cr(4)–TdCl	1.226	1.934	3.781	33	P–Td=O	0.865	1.536	3.197
9	Fe(2)–TdCl	1.065	1.778	3.561	34	Mn(2)–Td=O	1.115	1.849	3.698
10	Fe(6)–TdCl	1.207	1.970	3.972	35	Mn(4)–Td=O	1.206	1.923	3.808
11	Ru(2)–TdCl	1.274	2.004	3.872	36	V–Td=O	1.243	2.001	3.990
12	Ru(6)–TdCl	1.660	2.432	4.483	37	P–Td	0.980	1.624	3.370
13	Os(2)–TdCl	1.291	2.033	3.927	38	H2–Td	—	0.669	2.431
14	Os(6)–TdCl	1.362	2.174	4.127	39	H1^−–Td	—	0.67	2.404
15	Co(3)–TdCl	1.219	2.024	4.128	40	2^−–Td	—	0.732	2.653
16	Co(5)–TdCl	1.218	2.024	4.143	41	Si–Oc	1.154	1.859–1.860	3.737–3.738
17	Rh(3)–TdCl	1.419	2.186	4.232	42	Ge–Oc	1.214–1.215	1.944	3.957–3.958
18	Rh(5)–TdCl	1.557	2.338	4.391	43	Sn–Oc	1.409	2.179	4.320
19	Ir(3)–TdCl	1.342	2.094	4.032	44	Pb–Oc	1.489–1.490	2.261	4.434–4.435
20	Ir(5)–TdCl	1.551	2.334	4.383	45	Ti–Oc	1.370–1.376	2.120–2.125	4.092–4.093
21	Ni–TdCl	1.107	1.854	3.762	46	V–Oc	1.318	2.057	3.979
22	Cu–TdCl	1.188	1.905	3.683	47	Mn–Oc	1.251–1.252	1.963	3.847–3.850
23	Fe(3)–Tdpy	1.092	1.875	3.625	48	Tc–Oc	1.413	2.158	4.156
24	Fe(5)–Tdpy	1.226	2.001	4.105	49	Re–Oc	1.413	2.161	4.173
25	Ru(3)–Tdpy	1.360	2.117	4.119

---

As expected, all complexes feature a concave structure, but a broad variability in the BD_1–3 values, ranging from 0.492 to 1.660 Å, 0.879 to 4.432 Å, and 1.912 to 4.483 Å, respectively, were observed. Nevertheless, no significant alterations of the π-skeleton were noticed, suggesting structural stability of the proposed systems. Interestingly, the free H₂–Td also exhibits a concave structure (BD₂ and BD₃ of 0.669 Å and 2.431 Å), despite the absence of the boron atom, which is typically the main origin of pyramidalization. This is in accordance with the non-planarity reported for the borenium cation of SubPcs,³⁵ which is likely due to the lower size of macrocycle's cavity compared to that of non-aza-bridged subporphyrinoids. In these cases, the borenium cation is totally planar.³⁶ Notably, in its free base form, SubPc display the inner hydrogen atoms adopting an up–down conformation, with one bridging two nitrogen atoms (Fig. 3). Upon deprotonation, the BDs are not significantly altered, whereas the second deprotonation increases the depth, likely to alleviate electronic repulsion.

Fig. 3 DFT optimized structures of selected examples of M–TdCl, M–Tdpy, M–Oc, M–Td=O and M–Td.

In the case of M–TdCl complexes, an intuitive trend is observed in elements within the same group, as exceptionally illustrated in group 13: the bowl depth increases as descending in the group (Fig. 4a). This is due to the larger atomic size, which forces the complexation into a more pyramidal, out-of-plane geometry. This trend is also observed with carbon atom (C–TdCl), where its smaller size allows it to embed more deeply into the macrocycle, resulting in a more planar structure with BD_1–3 values of 0.492 Å, 0.879 Å, and 1.912 Å, respectively. In the case of P–SubPc, the structure is narrower than that of the P=O complex, likely due to the lone pair on the phosphorus atom. The bowl depths for P–Td are 0.980 Å, 1.624 Å, and 3.370 Å, compared to 0.865 Å, 1.536 Å, and 3.197 Å for P–Td=O, both of which are significantly more pronounced than in boron SubPc. For transition metal complexes, the correlation between larger atomic radius and greater bowl depth is also noted in groups 8 and 9 when the multiplicity is 2 and 5, respectively. However, for complexes with multiplicities of 6 and 3, the M–Cl bonds in second- and third-row transition metal complexes show a binding which is not coaxial with molecular axis, leading to deviation angles of 11° in Ru, 29° in Os, 41° in Rh, 16° in Ir, (see example of Fig. 3). This points out to less effective complexation as a result of the electronic repulsion between the ligand and the d-electrons of the metal center. In such cases, the atomic radius-BD direct correlation is not maintained; likewise, this trend is neither strictly followed when moving from left to right across the first-row transition metals, likely due to the combined effects of atomic size, oxidation state, and electronic configuration. Nevertheless, Sc³⁺, with its larger size, leads to the highest BD values, reaching 1.394 Å, 2.158 Å, and 4.177 Å for BD_1–3, respectively.

Fig. 4 Evolution of the BD_1–3 in (a) M–TdCl and (b) M–Oc complexes based on groups 13 and 14 elements, respectively. Hydrogen atoms are omitted for clarity. Atom's colour code: carbon in grey, nitrogen in blue, chlorine in green. The central element is indicated in each case.

For the “hourglass” complexes M–Oc, all cases exhibit a highly symmetric distribution, characterized by a staggered orientation of the SubPc units. Similar to M–TdCl complexes, the trend of increasing BD with larger atomic size is observed, as clearly demonstrated in the group 14 complexes (Fig. 4b). An increase in BD within these octahedral complexes leads to a larger array and a less accessible bowl-shaped π-surface (Fig. 4). In this case, the BD_1–3 values show less variability, ranging between 1.154–1.490 Å, 1.860–2.261 Å, and 3.380–4.435 Å, respectively. This trend is also consistent when progressing from Ti⁴⁺ to V⁴⁺ to Mn⁴⁺, as well as in M–Td=O complexes. By contrast, this trend is reversed in group 7 metal-based complexes. In all cases, these hourglass species exhibit a sharpener concavity than reference B–TdCl.

The M–Tdpy species exhibit also narrower BD_1–3 values compared to B–TdCl, ranging from 1.092–1.442 Å, 1.875–2.201 Å, and 3.625–4.233 Å, respectively. In this case, no clear correlation between inner element size and BD is observed; rather, the combined effects of oxidation state and multiplicity appear to play a more significant role. As expected, the M–N bond lengths between the metal and the nitrogen atom of the pyridine ligand are slightly longer than those between the metal and the nitrogen atoms of the tridentate ligand, indicating a more labile coordination to the central element.

2.2. Dipole moment and charge distribution

The DM values as well as the electrostatic potential (ESP) maps of all complexes are illustrated in Fig. 5. The reference B–TdCl exhibits a dipole moment of 4.8 D, oriented along the direction of the axial ligand, which is considered positive. It should be noted that both the magnitude and direction of the DM depend on the coordination structure. M–TdCl and M–Td=O complexes display a wide range of DM values, all oriented toward the axial ligand (positive values), with a minimum of 2.8 D in Ga–TdCl and a maximum of 10.1 D in Ni–TdCl. In contrast, M–Tdpy exhibit DMs ranging from −1.4 D to −10.0 D, where the negative values indicate a DM direction opposite to the axial ligand. On the other hand, the hourglass M–Oc systems show either zero or near-zero dipole moments, as expected given their symmetrical geometries. Interestingly, the free base SubPc has a modest DM of 1.35 D, which increases to 2.4 D and 3.0 D upon mono- and di-deprotonation, respectively, resulting from the generation negatively charged nitrogen atoms. Regarding the positively charged C–TdCl, P–Td, and P–Td=O SubPcs, the dipole moments are 3.3 D, −1.3 D, and 5.4 D, respectively. Notably, the oxidation of the phosphorus atom results in a reversal of the dipole moment. Additionally, it is worth mentioning that the C–TdCl, despite being positively charged, still exhibits strong polarization toward the axial chlorine ligand.

Fig. 5 DFT ESP maps of M–TdCl, M–Tdpy, M–Oc, M–Td=O and M–Td complexes. Red color corresponds to a charge of −3.7 × 10⁻², for neutral complexes, 0.075 for cationic complexes, −0.15 for H₁⁻–Td, −0.25 for 2⁻–Td; and the blue colour corresponds to a charge of 3.7 × 10⁻², for neutral complexes, 0.11 for cationic complexes, 0.10 for H₁⁻–Td, 0 for 2⁻–Td.

In bowl-shaped aromatics, the dipole moment is typically correlated with the BD, where a more curved structure results in greater asymmetry in charge distribution, thereby increasing the DM. To determine if this general behavior applies to SubPcs, we analyzed the correlation between BD and DM. Interestingly, an inverse correlation was observed in group 13 M–TdCl structures (Fig. 6); the more pronounced the pyramidalization of the molecule, the lower the dipole moment. Thus, B–TdCl, which has the flattest structure within the group, exhibits the highest dipole moment (4.8 D), vs. that of In–TdCl (2.9 D). This result seems counterintuitive, as one would expect a more conical structure to induce stronger dipole moments. We hypothesize that this inverse behavior in SubPcs is due to the nature of the bond between the axial ligand and the central element. When the central element is small enough, it can be efficiently embedded within the inner cavity, leading to shorter bond distances with the pyrrolic nitrogen atoms and stronger complexation. As a result, the electronic environment of the central element resembles sp² hybridization, leading to a more ionic and thus more polar bond with the axial ligand. In this scenario, the axial chlorine ligand bonds through a quasi-p orbital, which is less electronegative. However, when the size of the central element increases, a more sp³-like hybridization is adopted, reducing the inherent polarization of the bond with the axial ligand. For transition metal complexes, this tendency is also noted when descending from the second to the third row in groups 8 and 9, specifically with multiplicities 2 and 6 (i.e., those that do not induce axial distortion). However, a clear trend cannot be established when moving further to the fourth row, likely due to multiple factors influencing the outcome simultaneously but not cooperatively. It is noteworthy the strong dipole moment observed in non-axially distorted complexes based on group 9 elements, reaching values as high as 10 D. This is significantly higher compared to the rest of the first-row transition metals, which exhibit dipole moments in the range of 4.6–5.9 D. Importantly, this range is much narrower than that observed for the BD, once again indicating that a clear correlation between BD and dipole moment is not present. For M–Td=O complexes, V–Td=O, with its larger atomic size and greater BD, exhibits a lower DM compared to Mn–Td=O, following the trends observed for group 13 elements. In contrast, for M–Tdpy complexes, the DM significantly decreases as one moves down the group. This trend is also observed in group 9 elements and from Fe to Co to Zn, although the variation range is narrower, with values between 9.3–6.4 D and 8.2–10.39 D, respectively. Similar to the inverse BD–DM correlation seen in group 13 M–TdCl complexes, this may be due to less efficient bonding with the pyridine ligand when the bowl structure becomes less curved. This weaker bond would result in lower stabilization of the positive charge at the central metal, thereby increasing the negative dipole moment.

Fig. 6 Correlation between the BD and the DM in M–TdCl complexes of group 13.

As shown in Fig. 5, the charge distribution morphology strongly depends on the geometry and is significantly influenced by the element complexed. In M–TdCl compounds, positive charge density is generally concentrated on the bowl, particularly at the hydrogen atoms and the central element, while higher electron density is observed over the axial ligand and meso-nitrogen atoms. A similar pattern occurs in M–Td=O complexes. However, in M–Tdpy complexes, the electronic distribution is reversed, with higher electron density residing in the π-conjugated bowl and the positive charges localized on the axial pyridine ligand. In the hourglass structures, despite the absence of a DM, there is a clear asymmetry in the charge distribution. The peripheral hydrogen atoms hold a positive charge, while moving toward the center of the bowl, the electron density gradually increases. As expected, the meso-nitrogen atoms also exhibit the highest electron density.

Turning to a more specific comparison, in M–TdCl compounds from group 13, a notable difference compared to B–TdCl is the lower electron density on the chlorine atom, which accounts for the lower dipole moment. Multiplicity generally does not induce significant charge redistribution, except for complexes made from second- and third-row metals in groups 8 and 9 with multiplicities of 6 and 3, respectively, where axial distortion occurs. The π-cloud shows a homogeneous charge distribution, with the aromatic core and the inner aromatic circuit contributing equally. A clear correlation between the charge located on the axial ligand and the DM is evident. A similar correlation between DM and ESP maps is observed in M–Tdpy complexes, though the differences are more visually apparent. In this case, the positive charge on the pyridine ligand decreases as the DM decreases, while the depletion of the red regions in the bowl's π-fragment becomes evident.

2.3. Impact on molecular orbitals and Q-band

As previously commented, the HOMO, LUMO, and LUMO+1 orbitals of B–TdCl are critical as they govern the Q-band and the main redox behavior of these macrocycles. As shown in Fig. 7, these orbitals—of symmetries a₂, e, and e, respectively—are mainly located over the π-conjugated scaffold, with a node at the central boron atom. Thus, one might expect that substituting the boron atom with other elements would not significantly alter the shape or symmetry of these orbitals, unless effective orbital overlap occurs. To investigate this, we analyzed the shape and energy of these three orbitals in M–TdCl, M–Tdpy, M–Oc, M–Td=O and M–Td complexes. Fig. 7 displays the Kohn–Sham representations and energy evolution of these orbitals across all complexes, with B–TdCl as a reference. At first glance, it is evident that while these three orbitals are identifiable in all species, their shape, distribution, and energy are notably influenced by the central element. Degeneracy can also be significantly perturbed, depending on the nature of the element and the multiplicity, particularly if the central element contributes directly to these orbitals. Importantly, these frontier orbitals may shift from their positions as HOMO or LUMO, becoming either more stable or less stable, particularly in transition metal complexes where unpaired electrons are present. In such cases, the “magic” orbitals can even become singly occupied molecular orbitals (SOMOs). Overall, the electronic impact is more pronounced between elements of different groups than within the same group, although some trends persist. For group 13 M–TdCl complexes, the appearance of these orbitals remains relatively similar to B–TdCl, though they become increasingly unstable when descending the group, likely due to the decreasing electronegativity of the complexed element. Notably, C–TdCl, being positively charged and containing a more electronegative central atom than boron, shows a stabilization of these orbitals. In P–Td and P–Td=O, similar orbital stabilization occurs, with slight participation of the central fragment in the LUMOs. In the free base H₂–Td, the molecule becomes more electron-donating. Due to the negative charge injected to the system, the conjugate bases H₁⁻–TdCl and 2⁻–Td show further orbital destabilization, with some or all of them becoming antibonding.

Fig. 7 Evolution of a₂ and e orbitals of B–TdCl in M–TdCl, M–Tdpy, M–Oc, M–Td=O and M–Td complexes. Orbital's colour code: occupied in blue/red, unoccupied in yellow/turquoise, partially occupied in pink/pale blue.

In general, M–TdCl complexes display these three orbitals similarly to B–TdCl. However, there are some species, such as Cr(4)–TdCl, Sc–TdCl or Ru(6)–TdCl, where strong perturbation due to metal or metal/axial ligand interaction is observed. For hourglass M–Oc complexes, six orbitals (two a₂ and four e) arise, as expected given the presence of two SubPc units. Here, the topology and localization are only slightly affected by the metal. Similar to M–TdCl group 13 complexes, group 14 hourglass systems exhibit increased orbital instability upon descending the group, although this trend is not equally applicable across all six orbitals. M–Tdpy complexes generally display minimal perturbation in orbital shape, with the three key orbitals remaining localized over the π-system, except in Ir(4)–Tdpy, where the LUMO and other orbitals partially extend over the axial ligand. Interestingly, for group 8 M–Tdpy complexes, orbital stability increases as one descends the group, consistent across both multiplicities. The same trend is observed in group 9, where the contribution by central metal is negligible, but multiplicity strongly influences the orbitals energy and order. Regarding V–Td=O and Mn–Td=O complexes, the three orbitals remain relatively unperturbed, though there is minor participation of the oxygen atom in the LUMO+1. Here, as expected, multiplicity affects both the energy and, in some cases, the topology, though only to a minor extent.

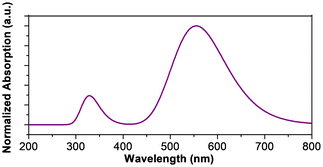
TD-DFT calculations were performed at the CAM-B3LYP/6-31G+(d,p) level of theory on singlet M–TdCl, M–Tdpy, M–Oc, M–Td=O and M–Td complexes to assess whether the central atoms influence the shape and position of the B–TdCl Q-band, which is used as a reference. Selected TD-DFT transition energies, oscillator strengths (f), and molecular orbital configurations are provided in Table 2 and ESI.† Importantly, TD-DFT profiles of the singlet complexes considered closely resemble that of B–TdCl, with the Q-band arising from S₀ → S₁ and S₀ → S₂ excitations, corresponding to transitions from the HOMO (a₂ symmetry) to the LUMO (e symmetry) and LUMO+1 (e symmetry), respectively. Importantly, an increasing red-shift in the Q-band maximum is observed when descending in group 13, peaking at 580 nm in In–TdCl. Notably, Al–, Ga–, and In–TdCl exhibit lower oscillator strengths, which are similar to each other but lower than that of B–TdCl. Further red-shifting is observed in Sc–TdCl. Interestingly, C–TdCl displays a notable red-shift of 32 nm compared to B–TdCl, along with a lower oscillator strength. The most pronounced red-shifts are seen in phosphorus-based compounds, reaching values of 630 nm in P–Td and 611 in P–Td=O SubPc. While P–Td=O shows similar orbital contributions for each transition, P–Td behaves slightly differently, with both the LUMO and LUMO+1 contributing to the S₀ → S₁ and S₀ → S₂ transitions, though to varying extents. In all these cases, the oscillator strengths are lower than that of B–TdCl. For Zn–Tdpy, the Q-band originates from the S₀ → S₂ and S₀ → S₃ transitions, involving transitions from the HOMO to the LUMO and LUMO+1, respectively. In the M–Oc group 14 complexes, the Q-band arises from S₀ → S₃ and S₀ → S₄ transitions, involving mainly five orbitals (HOMO, HOMO−1, LUMO, LUMO+1, and LUMO+3). Due to the presence of two SubPc units, the oscillator strength of this band is approximately double that of single-unit complexes. On the other hand, maximum is slightly red-shifted and they remain almost constant upon descending the group.

Table 2 Transitions involved in the Q-band and selected TD-DFT parameters. The theoretical spectrum of B–TdCl is shown as an example. f = oscillator strength

Entry	Complex	Transition	Energy (nm)	f
1	B–TdCl	S0 → S1	556	0.349
		S0 → S2	556	0.349
2	Al–TdCl	S0 → S1	575	0.291
		S0 → S2	575	0.291
3	Ga–TdCl	S0 → S1	574	0.292
		S0 → S2	574	0.292
4	In–TdCl	S0 → S1	580	0.278
		S0 → S2	580	0.278
5	C–TdCl	S0 → S1	588	0.304
		S0 → S2	588	0.304
6	Sc–TdCl	S0 → S1	592	0.245
		S0 → S2	592	0.245
7	Zn–Tdpy	S0 → S2	568	0.285
		S0 → S3	568	0.292
8	P–Td=O	S0 → S1	611	0.254
		S0 → S2	611	0.254
9	P–Td	S0 → S1	630	0.225
		S0 → S2	630	0.225
10	H2–Td	S0 → S1	575	0.306
		S0 → S2	560	0.329
11	Si–Oc	S0 → S3	567	0.430
		S0 → S4	568	0.430
12	Ge–Oc	S0 → S3	565	0.457
		S0 → S4	565	0.457
13	Sn–Oc	S0 → S3	568	0.472
		S0 → S4	568	0.430
14	Pb–Oc	S0 → S3	570	0.468
		S0 → S4	570	0.468

---

2.4. Electron affinity and ionization potential

The electron affinity (EA) and ionization potential (IP) of each complex were calculated to provide insights into their general redox behavior. Calculations were performed at the CAM-B3LYP/6-31G+(d,p) level, using the energies of the neutral species (E) along with those of the optimized anion (E(M⁻)) and cation (E(M⁺)). The IP and EA values, collected in Table 3, were determined as follows: IP = E(M⁺) − E(M) and EA = E(M) − E(M⁻). In general, the EA and IP values correlate well with the energies of the a₂ and e orbitals previously discussed when these serve as the frontier molecular orbitals. In open-shell complexes, however, the behavior is more variable, as the presence of unpaired electrons comes into play. For M–TdCl group 13 complexes, EA values become more negative and IP values less positive as one moves down the group, indicating a progressively reduced acceptor character (or increased donor character) from B–TdCl to In–TdCl. A similar trend is observed in the hourglass group 14 complexes. For C–TdCl, the EA decreases significantly to −5.10 eV, while the IP increases to 9.95 eV, aligning well with the HOMO–LUMO energy levels, thus suggesting a strong acceptor character for this molecule. Similarly, P–Td and P–Td=O SubPcs exhibit more negative EA values and more positive IP values, reflecting a higher electron-deficient π-system in these complexes.

Table 3 Electron affinity and ionization potential of the M–TdCl, M–Tdpy, M–Oc, M–Td=O and M–Td complexes

Entry	Complex	EA	Ionization potential	Entry	Name	EA	Ionization potential
1	B–TdCl	1.464	6.491	24	Fe(5)–Tdpy	1.174	5.342
2	Al–TdCl	1.372	6.286	25	Ru(3)–Tdpy	1.198	4.496
3	Ga–TdCl	1.365	6.277	26	Ru(5)–Tdpy	2.539	4.126
4	In–TdCl	1.288	6.154	27	Os(3)–Tdpy	1.192	4.664
5	C–TdCl	5.106	9.953	28	Os(5)–Tdpy	2.510	4.484
6	Sc–TdCl	1.454	6.261	29	Co–Tdpy	1.078	5.424
7	Cr(2)–TdCl	1.678	5.977	30	Rh–Tdpy	2.303	4.556
8	Cr(4)–TdCl	1.547	7.011	31	Ir–Tdpy	2.343	4.616
9	Fe(2)–TdCl	2.114	6.444	32	Zn–Tdpy	0.947	5.327
10	Fe(6)–TdCl	2.877	6.786	33	P–Td=O	5.231	10.020
11	Ru(2)–TdCl	1.571	6.432	34	Mn(2)–Td=O	1.677	6.348
12	Ru(6)–TdCl	1.880	5.969	35	Mn(4)–Td=O	2.068	6.132
13	Os(2)–TdCl	1.494	6.361	36	V–Td=O	2.012	7.192
14	Os(6)–TdCl	3.167	5.061	37	P–Td	5.008	9.780
15	Co(3)–TdCl	2.265	6.829	38	Si–Oc	1.440	5.753
16	Co(5)–TdCl	3.023	6.851	39	Ge–Oc	1.422	5.702
17	Rh(3)–TdCl	2.525	6.751	40	Sn–Oc	1.378	5.763
18	Rh(5)–TdCl	3.052	6.224	41	Pb–Oc	1.350	5.368
19	Ir(3)–TdCl	2.104	5.961	42	Ti–Oc	2.643	5.687
20	Ir(5)–TdCl	3.081	5.408	43	V–Oc	3.312	6.559
21	Ni–TdCl	3.764	5.950	44	Mn–Oc	1.366	5.567
22	Cu–TdCl	3.613	6.374	45	Tc–Oc	1.378	5.602
23	Fe(3)–Tdpy	0.756	4.788	46	Re–Oc	1.357	5.443

---

Turning to transition metal SubPcs, group 8 M–TdCl complexes exhibit a stronger acceptor character than B-TdCl, which becomes more pronounced as one descends the group. These complexes also display higher donor character than B–TdCl, with slight variations upon descending the group. Notably, the acceptor character increases with higher multiplicity. In contrast, group 9 complexes tend to be more electron-accepting and less electron-donating than B–TdCl, showing no significant influence of multiplicity and no clear trend upon descending the group. Ni–TdCl and Cu–TdCl are both stronger electron acceptors than B–TdCl; however, Ni–TdCl is more electron-donating, while Cu–TdCl is less donating.

A distinct pattern is observed in Cr–TdCl complexes: with multiplicities of 2 and 4, they are less electron-accepting than B–TdCl; however, the multiplicity 2 complex is more electron-donating, whereas the multiplicity 4 complex is less so. For M–Tdpy systems, Zn–Tdpy and Co–Tdpy show poor acceptor character and higher donor character compared to the reference SubPc. Upon descending group 8, M–Tdpy complexes become more electron-accepting and less electron-donating than B–TdCl, whereas in group 9, they become both more electron-accepting and more electron-donating. In M–Td=O complexes, those based on V and Mn display pronounced acceptor character. Mn–Td=O complexes exhibit greater donor character than B–TdCl and show minimal variation when descending to Re- and Tc-based complexes. Among M–Oc complexes, Ti and V are notable for their highly negative EA values, indicating strong electron-accepting behavior.

3. Conclusions

In summary, we have theoretically evaluated the properties of non-boron SubPcs, focusing on characteristics that are crucial from a materials science viewpoint. Using boron–SubPc as a reference, we have analyzed the impact of the central element on molecular curvature, charge distribution, dipole moment, π-orbitals, absorption pattern, as well as the electron-donor/acceptor (redox) properties. Overall, we found that the central element significantly influences all these properties, detailed as follows:

• The curvature of the macrocycle can be deepened by up to approximately 70% or flattened by up to 25%, depending solely on the choice of central element.

• The DM is strongly affected not only in magnitude, ranging from −10 to 10 D, but also in direction, which can be opposite to the axial ligand. This substantial variability in DM also results in a significant modulation of charge distribution.

• The central element significantly affects HOMO, LUMO, and LUMO+1 orbitals of SubPcs, which govern the Q-band. Although energy variations are observed, the orbital topology remains largely unchanged.

• TD-DFT calculations reveal that the Q-band can be red-shifted by up to 30 nm relative to B–SubPc, or blue-shifted by up to 50 nm upon deprotonation of the free base.

• The EA and IP are also highly dependent on the central element, allowing fine-tuning of the macrocycle's electron-accepting and -donating properties. This adaptability anticipates the design of both n-type and p-type semiconductors, with tunable electrochemical gaps.

In conclusion, this work highlights the potential of boron replacement in SubPcs. Notably, our calculations suggest that SubPc free bases and metalated SubPcs with elements other than boron are expected to be kinetically and thermodynamic stable because: (i) the macrocycle, although it may deepen or flatten, remains largely preserved; and (ii) frontier molecular orbitals, which govern oxidation and reduction, and charge distribution—a factor directly related to reactivity—do not reach extreme values. However, we consider that complexes with a distorted bond to the axial ligand are expected to exhibit lower kinetic stability. We hope this proof of concept will inspire and guide future experimental efforts. To this end, exploring alternative metals for templating cyclotrimerization reactions or employing “boron scavenging” strategies with other ligands appear to be promising avenues for further investigation.

4. Experimental

All reported structures were optimized at DFT level using the B3LYP³⁷ functional and the standard 31+G(d,p) basis set for first-, second- and third-row elements, and LANL2DZ basis set for heavier elements, which includes the relativistic effective core potential (ECP) of Hay and Wadt and employs a split-valence (double-ζ) basis set.^38–42 Although non-covalent interactions were not expected to play a significant role, dispersion interactions were accounted for using Grimme's D3 correction (DFT-D3). Analytical harmonic frequencies were computed at the same level of theory to confirm the nature of the stationary points. All calculations have been performed in the gas phase. This study was also conducted using more computationally expensive basis sets, such as def2-SVP for light atoms and LANL2DZ + f for heavier elements. Nevertheless, the deviations in structural parameters (bowl depths), electronic properties (orbital energies, dipole moments, and ESP maps), and AE/IP values compared to the aforementioned basis sets were negligible, with differences below 1%. TD-DFT were carried out at the CAM-B3LYP/6-31+G(d,p) level of theory. All calculations were carried out by the methods implemented in Gaussian 16 package.⁴³

Data availability

The data supporting the findings of this study is available within the article and its ESI.† XYZ coordinates, as well as additional TD-DFT results are included in the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Financial support from the Spanish MCIN/AEI/10.13039/501100011033 and European Union NextGenerationEU/PRTR TED2021-131255B-C43), MCIU/AEI/10.13039/501100011033/FEDER, UE (PID) (PID2023-151167NB-I00), the Comunidad de Madrid and the Spanish State through the Recovery, Transformation and Resilience Plan [“Materiales Disruptivos Bidimensionales (2D)” (MAD2D-CM) (UAM1)-MRR Materiales Avanzados], and the European Union through the Next Generation EU funds, is fully acknowledged. IMDEA Nanociencia acknowledges support from the “Severo Ochoa” Programme for Centres of Excellence in R&D (MINECO, CEX2020-001039-S). We acknowledge the generous allocation of computer time at the Centro de Computación Científica at the Universidad Autónoma de Madrid (CCC-UAM).

References

1. The Porphyrin Handbook, ed. K. M. Kadish, K. M. Smith and R. Guilard, Academic Press, New York, 1999, vol. 1–10.
2. The Porphyrin Handbook, ed. K. M. Kadish, K. M. Smith and R. Guilard, Academic Press, New York, 2003, vol. 11–20.
3. Handbook of Porphyrin Science, ed. K. M. Kadish, K. M. Smith and R. Guilard, World Scientific Publishing, Singapore, 2010, vol. 1–25.
4. M. V. Martínez-Díaz, G. de la Torre and T. Torres, Chem. Commun., 2010, 46, 7090–7108,  10.1039/C0CC02213F.
5. M. Urbani, M. Ragoussi, M. K. Nazeeruddin and T. Torres, Coord. Chem. Rev., 2019, 381, 1–64,  DOI:10.1016/j.ccr.2018.10.007.
6. M. Urbani, G. de la Torre, M. K. Nazeeruddin and T. Torres, Chem. Soc. Rev., 2019, 48, 2738–2766,  10.1039/C9CS00059C.
7. A. Zampetti, A. Minotto and F. Cacialli, Adv. Funct. Mater., 2019, 29, 1807623,  DOI:10.1002/adfm.201807623.
8. A. G. Martynov, Y. Horii, K. Katoh, Y. Bian, J. Jiang, M. Yamashita and Y. G. Gorbunova, Chem. Soc. Rev., 2022, 51, 9262–9339,  10.1039/D2CS00559J.
9. V. Almeida-Marrero, E. van de Winckel, E. Anaya-Plaza, T. Torres and A. de la Escosura, Chem. Soc. Rev., 2018, 47, 7369–7400,  10.1039/c7cs00554g.
10. G. Bottari, O. Trukhina, M. Ince and T. Torres, Coord. Chem. Rev., 2012, 256, 2453–2477,  DOI:10.1016/j.ccr.2012.03.011.
11. E. Nikoloudakis, I. López-Duarte, G. Charalambidis, K. Ladomenou, M. Ince and A. G. Coutsolelos, Chem. Soc. Rev., 2022, 51, 6965–7045,  10.1039/D2CS00183G.
12. N. Kobayashi, H. Ogata, N. Nonaka and E. A. Lukyanets, Chem. – Eur. J., 2003, 9, 5123–5134,  DOI:10.1002/chem.200304834.
13. J. Mack and N. Kobayashi, Chem. Rev., 2011, 111, 281–321,  DOI:10.1021/cr9003049.
14. G. Bottari, G. de la Torre, D. M. Guldi and T. Torres, Chem. Rev., 2010, 110, 6768–6816,  DOI:10.1021/cr900254z.
15. J. Elemans, R. van Hameren, R. Nolte and A. Rowan, Adv. Mater., 2006, 18, 1251–1266,  DOI:10.1002/adma.200502498.
16. J. M. Van Raden, D. I. Alexandropoulos, M. Slota, S. Sopp, T. Matsuno, A. L. Thompson, H. Isobe, H. L. Anderson and L. Bogani, J. Am. Chem. Soc., 2022, 144, 8693–8706,  DOI:10.1021/jacs.2c02084.
17. C. G. Claessens, D. Gonzalez-Rodriguez, M. S. Rodriguez-Morgade, A. Medina and T. Torres, Chem. Rev., 2014, 114, 2192–2277,  DOI:10.1021/cr400088w.
18. G. Lavarda, J. Labella, M. V. Martínez-Díaz, M. S. Rodríguez-Morgade, A. Osuka and T. Torres, Chem. Soc. Rev., 2022, 51, 9482–9619,  10.1039/D2CS00280A.
19. J. Labella and T. Torres, Trends Chem., 2023, 5, 353–366,  DOI:10.1016/j.trechm.2023.02.003.
20. A. V. Gorbunov, M. G. Iglesias, J. Guilleme, T. D. Cornelissen, W. S. C. Roelofs, T. Torres, D. Gonzalez-Rodriguez, E. W. Meijer and M. Kemerink, Sci. Adv., 2017, 3, e1701017,  DOI:10.1126/sciadv.1701017.
21. J. Labella, D. K. Bhowmick, A. Kumar, R. Naaman and T. Torres, Chem. Sci., 2023, 14, 4273–4277,  10.1039/D3SC01069D.
22. J. Labella, G. Lavarda, L. Hernandez-Lopez, F. Aguilar-Galindo, S. Diaz-Tendero, J. Lobo-Checa and T. Torres, J. Am. Chem. Soc., 2022, 144, 16579–16587,  DOI:10.1021/jacs.2c06377.
23. C. G. Claessens, D. González-Rodríguez, C. M. McCallum, R. S. Nohr, H. Schuchmann and T. Torres, J. Porphyrins Phthalocyanines, 2007, 11, 181–188,  DOI:10.1142/S1088424607000230.
24. C. Wang, X. Chen, D. Qi, S. Bi and J. Jiang, Inorg. Chem. Commun., 2017, 85, 9–15,  DOI:10.1016/j.inoche.2017.04.025.
25. L. Liu, J. Kim, L. Xu, Y. Rao, M. Zhou, B. Yin, J. Oh, D. Kim, A. Osuka and J. Song, Angew. Chem., Int. Ed., 2022, 61, e202214342,  DOI:10.1002/anie.202214342.
26. Y. J. Yang and Z. M. Su, Int. J. Quantum Chem., 2005, 103, 54,  DOI:10.1002/qua.20479.
27. D. Zdravkovski and M. Milletti, J. Mol. Struct., 2005, 717, 85,  DOI:10.1016/j.theochem.2004.08.043.
28. Y. Yang, Polyhedron, 2012, 42, 249,  DOI:10.1016/j.poly.2012.05.022.
29. Y. Yang, Polyhedron, 2012, 33, 310,  DOI:10.1016/j.poly.2011.11.043.
30. M. M. Montero-Campillo, A. M. Lamsabhi, O. Mó and M. Yáñez, ChemPhysChem, 2013, 14, 915,  DOI:10.1002/cphc.201201028.
31. M. M. Montero-Campillo, A. M. Lamsabhi, O. Mó and M. Yáñez, J. Phys. Chem. A, 2016, 120, 4845,  DOI:10.1021/acs.jpca.5b12374.
32. M. J. Waters, D. Hashemi, G. Shi, E. Kioupakis and J. Kieffer, J. Electron. Mater., 2019, 48, 2962,  DOI:10.1007/s11664-019-06961-w.
33. W. Chen, S. Peng and S. Zheng, Spectrochim. Acta, Part A, 2020, 229, 118018,  DOI:10.1016/j.saa.2019.118018.
34. C. Zhang, K. Nakano, M. Nakamura, F. Araoka, K. Tajima and D. Miyajima, J. Am. Chem. Soc., 2020, 142, 3326–3330,  DOI:10.1021/jacs.9b12710.
35. T. Kato, F. S. Tham, P. D. W. Boyd and C. A. Reed, Heteroat. Chem., 2006, 17, 209–216,  DOI:10.1002/hc.20223.
36. E. Tsurumaki, S. Hayashi, F. S. Tham, C. A. Reed and A. Osuka, J. Am. Chem. Soc., 2011, 133, 11956–11959,  DOI:10.1021/ja2056566.
37. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789,  DOI:10.1103/PhysRevB.37.785.
38. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652,  DOI:10.1063/1.464913.
39. W. Kohn, A. D. Becke and R. G. Parr, J. Phys. Chem., 1996, 100, 12974–12980,  DOI:10.1021/jp960669l.
40. P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 270–283,  DOI:10.1063/1.448799.
41. P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 284,  DOI:10.1063/1.448800.
42. P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299–310,  DOI:10.1063/1.448975.
43. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dt03173c

‡ These two authors contributed equally to this work.

---