Open Access Article
Open Access Article4f-Orbital mixing increases the magnetic susceptibility of Cp′3Eu†
S. Olivia
Gunther‡
 a,
Yusen
Qiao‡
a,
Yusen
Qiao‡
 a,
Patrick W.
Smith
a,
Patrick W.
Smith
 a,
Sierra R.
Ciccone
b,
Alexander S.
Ditter
a,
Daniel N.
Huh§
a,
Sierra R.
Ciccone
b,
Alexander S.
Ditter
a,
Daniel N.
Huh§
 b,
Liane M.
Moreau
b,
Liane M.
Moreau
 ac,
David K.
Shuh
ac,
David K.
Shuh
 a,
Taoxiang
Sun
a,
Taoxiang
Sun
 d,
Polly L.
Arnold
d,
Polly L.
Arnold
 ae,
Corwin H.
Booth
a,
Wibe A.
de Jong
ae,
Corwin H.
Booth
a,
Wibe A.
de Jong
 f,
William J.
Evans
f,
William J.
Evans
 b,
Wayne W.
Lukens
Jr
b,
Wayne W.
Lukens
Jr
 a and
Stefan G.
Minasian
a and
Stefan G.
Minasian
 *a
*a
aChemical Sciences Division, Lawrence, Berkeley National Laboratory, Berkeley, CA 94720, USA. E-mail: sgminasian@lbl.gov
bDepartment of Chemistry, University of California, Irvine, CA 92697, USA
cDepartment of Chemistry, Washington State University, Pullman, WA 99164, USA
dInstitute of Nuclear and New Energy Technology, Tsinghua University, Beijing 100084, P. R. China
eDepartment of Chemistry, University of California, Berkeley, CA 94720, USA
fComputational Research Division, Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA
First published on 11th June 2024
Abstract
Traditional models of lanthanide electronic structure suggest that bonding is predominantly ionic, and that covalent orbital mixing is not an important factor in determining magnetic properties. Here, 4f orbital mixing and its impact on the magnetic susceptibility of Cp′3Eu (Cp′ = C5H4SiMe3) was analyzed experimentally using magnetometry and X-ray absorption spectroscopy (XAS) methods at the C K-, Eu M5,4-, and L3-edges. Pre-edge features in the experimental and TDDFT-calculated C K-edge XAS spectra provided unequivocal evidence of C 2p and Eu 4f orbital mixing in the π-antibonding orbital of a′ symmetry. The charge-transfer configurations resulting from 4f orbital mixing were identified spectroscopically by using Eu M5,4-edge and L3-edge XAS. Modeling of variable-temperature magnetic susceptibility data showed excellent agreement with the XAS results and indicated that increased magnetic susceptibility of Cp′3Eu is due to removal of the degeneracy of the 7F1 excited state due to mixing between the ligand and Eu 4f orbitals.
Introduction
The ability to harness the 4f-orbital anisotropies and magnetic susceptibilities of lanthanide (Ln) elements is key to their application in molecular magnetism, including as molecular qubits and single-molecule magnets (SMMs). For example, in the field of SMMs, chemists have developed ligand design principles1–7 that facilitate subtle tuning of the crystal field, which in turn enhances magnetic anisotropy and the blocking temperature in single-ion8–15 magnets. In addition to the 4f crystal field, lanthanide magnetic properties can be influenced by strong electron correlations, generating effects such as homogenous mixed valence with magnetic singlet formation and valence tautomerism.16–22 However, the impact of covalent mixing between metal and ligand orbitals on the magnetic properties of trivalent lanthanide systems is typically small, compared to its more significant effect in actinide complexes23–29 and in certain tetravalent lanthanide complexes.30–36 The Ln 4f orbitals have limited radial extension, such that the effect of overlap between the 4f and ligand orbitals is much weaker than electron repulsion and spin–orbit coupling.37 Covalent interactions between ligands and contracted 4f orbitals have been identified by recent theoretical and spectroscopic studies of Ln(III) compounds.19–21,38–42 Despite this progress, it remains challenging to predict how charge transfer resulting from 4f orbital mixing will be manifested by changes in magnetic behaviour.43Denning and coworkers previously quantified 4f shell covalency in Cp3Yb in terms of charge-transfer from the ligand to the metal center using X-ray photoelectron spectroscopy (XPS), EPR (HYSCORE), and optical spectroscopies.39,40 They hypothesized40 that 4f shell covalency could also be significant in Cp3Eu because, like Yb3+, Eu3+ has a low-energy charge transfer state.44 In fact, Cp′3Eu (Cp′ = trimethylsilylcyclopentadienyl) has a more positive redox potential relative to Cp′3Yb (−1.07 V vs. −1.64 V, respectively),45 and Eu and Yb have the most favourable third ionization potentials of the entire lanthanide series (24.92 ± 0.10 eV and 25.05 ± 0.03 eV, respectively).46 Electron delocalization has been observed in Eu intermetallics; however, evidence of similar effects in molecules is limited.47 4f orbital mixing in an organometallic Eu(III) compound, Cp3Eu(THF), was illustrated by an unprecedentedly negative isomer shift in its 151-Eu Mössbauer spectrum.38 Laboratory XPS has recently been applied to study the electronic structures of Cp′3Ln and [K(crypt)][Cp′3Ln] (Ln = Gd, Eu, Sm, Tb), but spectral signatures for charge transfer were not observed.48 Direct probes of 4f orbital mixing are needed to understand the relationship between charge transfer and magnetism in lanthanide organometallic complexes.
Studies of lanthanide and actinide organometallic compounds have shown that C K-edge XAS provides unique insight into the interactions between π systems and metal orbitals in specific valence orbitals.49–51 We previously used a combination of C K-edge XAS and DFT to provide direct evidence of C 2p and Ce 4f orbital mixing in the δ-antibonding orbitals of (C8H8)2Ce.50 Here, we use C K-edge XAS and time dependent density functional theory (TDDFT) calculations to provide direct evidence of 4f orbital mixing in Cp′3Eu. In addition, Eu L3- and M5,4-edge spectroscopies were used to show how the 4f-orbital mixing results in C 2p → Eu 4f charge transfer. Taken together with variable temperature magnetic susceptibility measurements, these spectroscopic evaluations reveal how 4f-orbital mixing can impact magnetism in lanthanide organometallic complexes.
Results and discussion
Ground state electronic structure
The following discussion of the molecular orbital interactions in Cp′3Eu provides a framework for evaluating the experimental results. Because the electronic structures for Ln(C5R5)3 (R![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) H or alkyl) are well established,40,52–55 this discussion will focus on the metal-based orbitals that are relevant to the XAS experiments. Visual depictions comparing the effects of spin–orbit coupling, ligand field splitting, and coulombic repulsion have been published for f1 systems,7,56 but are not possible for Eu3+ due to the large number of states involved. Hence, an MO model for the interaction between 2p–π orbitals on the [Cp′3]3− framework and the Eu 5d- and 4f-orbitals was constructed in pseudo-C3h symmetry (Fig. 1).40 In C3h, the 5d orbitals on Cp′3Eu transform as a′ (dz2), e′ (dxy and dx2−y2), and e′′ (dxz and dyz), which form σ-, π-, and δ-bonding interactions with the equatorial Cp′ ligands. The Eu 4f orbitals transform as 2a′ + a′′ + e′ + e′′, most of which are best described as non-bonding. However, mixing between appropriate ligand orbitals and one of the 4f orbitals of a′ symmetry gives rise to a weakly π-antibonding MO.58 Such mixing with the 4f orbitals can be described using an MO model by the linear combination of orbitals as:
H or alkyl) are well established,40,52–55 this discussion will focus on the metal-based orbitals that are relevant to the XAS experiments. Visual depictions comparing the effects of spin–orbit coupling, ligand field splitting, and coulombic repulsion have been published for f1 systems,7,56 but are not possible for Eu3+ due to the large number of states involved. Hence, an MO model for the interaction between 2p–π orbitals on the [Cp′3]3− framework and the Eu 5d- and 4f-orbitals was constructed in pseudo-C3h symmetry (Fig. 1).40 In C3h, the 5d orbitals on Cp′3Eu transform as a′ (dz2), e′ (dxy and dx2−y2), and e′′ (dxz and dyz), which form σ-, π-, and δ-bonding interactions with the equatorial Cp′ ligands. The Eu 4f orbitals transform as 2a′ + a′′ + e′ + e′′, most of which are best described as non-bonding. However, mixing between appropriate ligand orbitals and one of the 4f orbitals of a′ symmetry gives rise to a weakly π-antibonding MO.58 Such mixing with the 4f orbitals can be described using an MO model by the linear combination of orbitals as:| Ψ* = N{ψ4f − λψCp′ π*} | (1) |
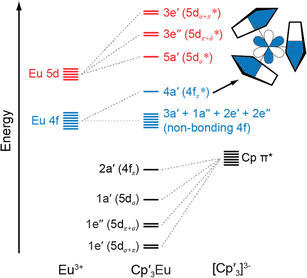 | ||
| Fig. 1 A qualitative MO diagram of Cp3Eu in C3h symmetry. The inset shows the a′ antibonding interaction of metal f and ligand orbitals. The nodal characteristics of the (Cp)33− fragment relative to the metal atom are represented with common short-hand notation.53,57 | ||
The MO model does not account for exchange interactions or core-hole induced charge transfer, among other effects associated with the multi-electron 4f6 configuration of a Eu3+ ion. Hence, the single-determinant MO wavefunction shown in eqn (1) can be rewritten using a many-electron, configuration interaction (CI) model,50,59 where the ground state is expressed by a combination of two terms that differ only by one electron:
Ψ* = N{|4f6〉 + λ|4f7![[L with combining low line]](https://www.rsc.org/images/entities/i_char_004c_0332.gif) 〉} 〉} | (2) |
![[L with combining low line]](https://www.rsc.org/images/entities/i_char_004c_0332.gif) 〉 describes the result of a ligand-to-metal electron transfer leading to reduction to Eu2+ and formation of a ligand hole (
〉 describes the result of a ligand-to-metal electron transfer leading to reduction to Eu2+ and formation of a ligand hole (![[L with combining low line]](https://www.rsc.org/images/entities/i_char_004c_0332.gif) ). Because the electrons are assumed to be fully localized, the CI model is better suited to interpret the metal-based Eu M5,4- and L3-edge XAS and magnetic measurements described below.
). Because the electrons are assumed to be fully localized, the CI model is better suited to interpret the metal-based Eu M5,4- and L3-edge XAS and magnetic measurements described below.
Carbon K-edge XAS
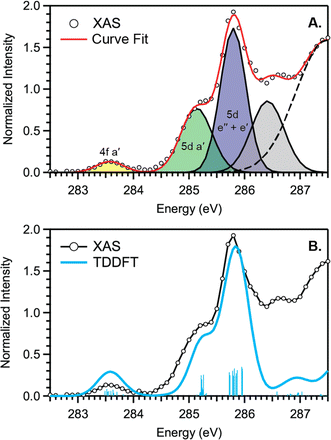
C K-edge XAS spectra were collected with a scanning X-ray transmission microscope (STXM) on micron-scale crystallites of Cp′3Eu (Fig. S4†).58 This approach minimizes the saturation and self-absorption effects that commonly occur when using weakly penetrating incident radiation at low photon energies, and has been applied in the study of metal-carbon bonding for both d- and f-block systems.49,50,60 The background-subtracted and normalized C K-edge spectrum of Cp′3Eu is shown in Fig. 2A together with a curve-fit model. For the pre-edge region of the spectrum above 284 eV, the spectrum was fit using three Gaussian functions (refer to the ESI† for full details). The C K-edge spectrum of Cp′3Eu also exhibited a small peak at low energy, which required a fourth Gaussian function at 283.6 eV. The presence of a transition in this energy range is unusual, since transitions below 284 eV have not been observed previously for a variety of 1st, 2nd, or 3rd row d-block metallocenes.60–63 Because an equivalent low-energy peak was also not resolved in the C K-edge spectrum of 4f7 Cp′3Gd (see Fig. S6†), we hypothesized that the peak at 283.6 eV was associated with transitions into MOs of 4f-parentage.To assign the pre-edge features in the C K-edge XAS of Cp′3Eu, the spectrum was modelled using TDDFT implemented with NWChem and using the long-range corrected LC-PBE0 functional.63Fig. 2B shows that the experimental spectrum for Cp′3Eu was well-reproduced with this computational method. Examination of the acceptor orbitals associated with a group of 15 transitions centered at 283.6 eV confirms that the low-energy feature is associated with transitions from the C 1s orbitals into the Eu–Cp′ π-antibonding 4f-orbital of a′ symmetry. Both the experimental and TDDFT calculated C K-edge spectrum agree regarding the relative location of the 4f and 5d orbitals; each show that the C 1s → a′ (4f–π) transition is 1.6 eV lower in energy than the lowest energy transition into the 5d manifold, C 1s → a′ (5d–σ). Moving to higher energy, the TDDFT calculations indicate that the next feature at 285.8 eV is associated with C 1s transitions into both the e′′ 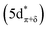 and e′
and e′ 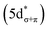 orbitals. These transitions are close in energy and not resolved individually in the experimental spectrum. The fourth feature observed at 286.4 eV was not well reproduced in the calculated spectrum; features in this energy range are likely associated with Rydberg-type orbitals that are not the unoccupied, antibonding counterpart to bonding orbitals that are occupied in the ground-state.60
orbitals. These transitions are close in energy and not resolved individually in the experimental spectrum. The fourth feature observed at 286.4 eV was not well reproduced in the calculated spectrum; features in this energy range are likely associated with Rydberg-type orbitals that are not the unoccupied, antibonding counterpart to bonding orbitals that are occupied in the ground-state.60
The C K-edge pre-edge transitions described above have intensities that are weighted by the amount of C 2p character in the acceptor MO. Hence, the C K-edge XAS and TDDFT calculations provide evidence that C 2p and Eu 4f orbital mixing occurs specifically in the Eu–Cp′ π-antibonding orbitals of a′ symmetry. This assignment is consistent with the MO diagram derived experimentally from magnetometry (see below), which showed that the a′ MO is the most destabilized by the Cp′ ligand field. In this regard, Cp′3Eu is similar to Cp3Yb, which also exhibits significant orbital mixing in the partially occupied a′ orbital as shown by XPS and ADF-DFT calculations.39,40 The consequence of mixing in the a′ MO is Cp′ → Eu charge transfer. In a configuration interaction (CI) model where the orbitals are localized, this mixing is manifested by a greater weight of the Eu2+ configuration, 4f7![[L with combining low line]](https://www.rsc.org/images/entities/i_char_004c_0332.gif) , where
, where ![[L with combining low line]](https://www.rsc.org/images/entities/i_char_004c_0332.gif) represents a hole on one of the Cp′ ligands resulting from Cp′ π → 4f charge transfer.22 Charge transfer is also reflected in the DFT calculation for Cp′3Eu by the Lowdin spin population analysis, which provided a value of 6.32. This value exceeds the prediction of 6 for a Eu3+ ion and suggests that the weight of the Eu2+ CT configuration (4f14
represents a hole on one of the Cp′ ligands resulting from Cp′ π → 4f charge transfer.22 Charge transfer is also reflected in the DFT calculation for Cp′3Eu by the Lowdin spin population analysis, which provided a value of 6.32. This value exceeds the prediction of 6 for a Eu3+ ion and suggests that the weight of the Eu2+ CT configuration (4f14![[L with combining low line]](https://www.rsc.org/images/entities/i_char_004c_0332.gif) ) in the ground state is 32%.
) in the ground state is 32%.
Europium L3- and M5,4-edge XAS
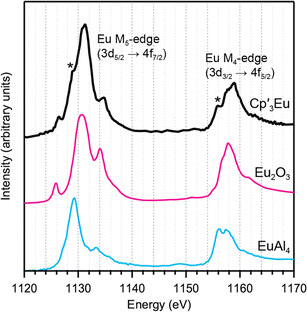
Eu M5,4-edge and L3-edge XAS were obtained to provide further evidence of Cp′ π → 4f charge transfer interactions in Cp′3Eu. Previous work has shown that M5,4-edge and L3-edge XAS are particularly useful techniques for probing 4f orbital mixing and charge transfer in tetravalent Ce, Pr, and Tb systems,59,64–66 and in trivalent Sm, Eu, Tm, and Yb systems.67–69 Both the Eu L3 (2p → 5d) and M5,4-edge (3d → 4f) spectroscopies probe electric-dipole allowed transitions from Eu core orbitals to empty or partially occupied valence orbitals.Fig. 3 shows the background subtracted and normalized Eu M5,4-edge XAS spectra for Cp′3Eu compared to reference compounds for Eu2+ (Eu2O3) and Eu3+ (EuAl4).69 The spectra are split into low-energy M5 (3d5/2 → 4f7/2) and high-energy M4 (3d3/2 → 4f5/2) edges due to spin–orbit coupling with the 3d core hole.70,71 Both the M5- and M4-edges can also exhibit fine structure due to final-state multiplet splitting, with characteristic patterns based on the number of 4f electrons.50,59,72,73 The spectrum of Cp′3Eu consists of main M5 and M4 peaks centered at 1131.3 eV and 1158.9 eV, respectively, and fine structure that most clearly resembles the spectrum of Eu2O3.70,71,74 However, additional features were also observed at 1129.1 and 1155.9 eV, which were not present in the spectrum for Eu2O3 but were coincident with the peak energies of the Eu2+ standard, EuAl4.69 In this regard the M5,4-edge spectrum of Cp′3Eu resembles that of mixed-valent Sm, Eu, and Tm solids, which have been described as superpositions of Ln3+ and Ln2+ subspectra.68 Qualitatively, the presence of features attributable to both Eu2+ and Eu3+ configurations in the M5,4-edge XAS of Cp′3Eu provides further support for the existence of Cp′ π → 4f charge transfer interactions identified by C K-edge spectroscopy. However, the relatively low intensity of the Eu2+ features indicates that the Eu3+ configuration is likely a more dominant component of the ground state for Cp′3Eu The spectrum of Cp′3Eu is also distinct from the M5,4-edge spectra of formally tetravalent Ce and Pr compounds, where the phenomenon of increased charge transfer in the final state causes emergence of satellite features at high energy relative to the main M5 and M4 peaks.75 Theoretical models of M5,4-edge spectra have been developed for certain f-element systems by using CI calculations,50,59,72,76–80 but could not be performed at the time of this study due to challenges with incorporating charge transfer in the calculations.81–83 More detailed theoretical and experimental investigation is needed to determine whether charge transfer satellite peaks are also present, but not resolved, in the M5,4-edge spectra of Cp′3Eu and some other Sm, Eu, and Tm molecules and solids.
Background-subtracted and normalized Eu L3-edge XANES spectra of Cp′3Eu and reference compounds Eu2O3 and 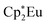 are shown in Fig. 4. The spectra for Cp′3Eu and Eu2O3 were similar in that both had the same white-line energy (6981.7 eV). However, Cp′3Eu also exhibited a lower energy shoulder at ca. 6974 eV, which is similar to the white-line energies for
are shown in Fig. 4. The spectra for Cp′3Eu and Eu2O3 were similar in that both had the same white-line energy (6981.7 eV). However, Cp′3Eu also exhibited a lower energy shoulder at ca. 6974 eV, which is similar to the white-line energies for 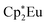 (6975 eV) and other Eu2+ compounds.84,85 The presence of two features in the Eu L3-edge spectrum of Cp′3Eu is reminiscent of the Yb L3-edge spectra of Yb organometallic complexes19–21 and the L3-edge spectra of tetravalent Ce, Pr, and Tb compounds, which show a low-energy feature that is attributable to a charge-transfer configuration.59 In analogy to these studies, we described the ground-state electronic structure of Cp′3Eu with a CI model involving mixing between 4f65d0 and 4f7
(6975 eV) and other Eu2+ compounds.84,85 The presence of two features in the Eu L3-edge spectrum of Cp′3Eu is reminiscent of the Yb L3-edge spectra of Yb organometallic complexes19–21 and the L3-edge spectra of tetravalent Ce, Pr, and Tb compounds, which show a low-energy feature that is attributable to a charge-transfer configuration.59 In analogy to these studies, we described the ground-state electronic structure of Cp′3Eu with a CI model involving mixing between 4f65d0 and 4f7![[L with combining low line]](https://www.rsc.org/images/entities/i_char_004c_0332.gif) 5d0 configurations. Then, at the Eu L3-edge, transitions occur to 4f65d1 and 4f7
5d0 configurations. Then, at the Eu L3-edge, transitions occur to 4f65d1 and 4f7![[L with combining low line]](https://www.rsc.org/images/entities/i_char_004c_0332.gif) 5d1 final states, respectively. Based on this model, the low energy feature in the Eu L3-edge spectrum of Cp′3Eu was attributed to a 4f7
5d1 final states, respectively. Based on this model, the low energy feature in the Eu L3-edge spectrum of Cp′3Eu was attributed to a 4f7![[L with combining low line]](https://www.rsc.org/images/entities/i_char_004c_0332.gif) 5d0 → 4f7
5d0 → 4f7![[L with combining low line]](https://www.rsc.org/images/entities/i_char_004c_0332.gif) 5d1 transition, and the main white-line feature was assigned to a 4f65d0 → 4f65d1. The ca. 6 eV peak separation was attributed to the difference in the number of 4f electrons that are available to screen the 5d electron from the Ln 2p core hole. The relative amount of 4f7
5d1 transition, and the main white-line feature was assigned to a 4f65d0 → 4f65d1. The ca. 6 eV peak separation was attributed to the difference in the number of 4f electrons that are available to screen the 5d electron from the Ln 2p core hole. The relative amount of 4f7![[L with combining low line]](https://www.rsc.org/images/entities/i_char_004c_0332.gif) 5d0 in the ground state was determined at 28(4)% by curve-fitting the spectrum (see Fig. S12 in the ESI†), which indicated that significant charge-transfer interactions are present Cp′3Eu Yb L3-edge XAS for were measured for comparison (see Fig. S13 in the ESI†), which indicated that the relative contribution of the corresponding 4f14
5d0 in the ground state was determined at 28(4)% by curve-fitting the spectrum (see Fig. S12 in the ESI†), which indicated that significant charge-transfer interactions are present Cp′3Eu Yb L3-edge XAS for were measured for comparison (see Fig. S13 in the ESI†), which indicated that the relative contribution of the corresponding 4f14![[L with combining low line]](https://www.rsc.org/images/entities/i_char_004c_0332.gif) 5d0 configuration to the ground-state was 0.11(3). The relative amount of 4f7
5d0 configuration to the ground-state was 0.11(3). The relative amount of 4f7![[L with combining low line]](https://www.rsc.org/images/entities/i_char_004c_0332.gif) 5d0 in the ground state, 0.28(4), is also referred to as nf, the amount of additional 4f character introduced due to covalent bonding.
5d0 in the ground state, 0.28(4), is also referred to as nf, the amount of additional 4f character introduced due to covalent bonding.
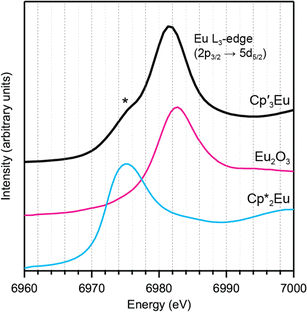 | ||
Fig. 4 L3-edge spectrum for Cp′3Eu (magenta) and references for Eu3+ (Eu2O3, dashed black) and Eu2+ ( dashed blue). A curve fit of the experimental data for Cp′3Eu is provided in the ESI† (Fig. S12†). A shoulder associated with Eu2+ character in the L3-edge spectrum for Cp′3Eu is highlighted with an asterisk. dashed blue). A curve fit of the experimental data for Cp′3Eu is provided in the ESI† (Fig. S12†). A shoulder associated with Eu2+ character in the L3-edge spectrum for Cp′3Eu is highlighted with an asterisk. | ||
Magnetometry
Variable-temperature magnetic susceptibility data for Cp′3Eu reported previously by Meihaus et al. (Fig. 5) was examined for evidence of charge transfer interactions.86 At low temperature, Cp′3Eu displays temperature independent paramagnetism (TIP) with χ equal to 0.13 emu mol−1. At temperatures greater than ∼10 K, the value of χ decreases as the first excited state becomes populated. Qualitatively, the magnetic susceptibility of an isolated Eu3+ ion is straightforward. For a free Eu3+ cation, the term 7F is split by spin–orbit coupling into seven states, 7FJ, with J = 0–6. The energies of the states (EJ)87,88 are: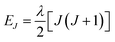 | (3) |
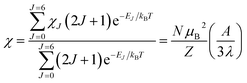 | (4) |
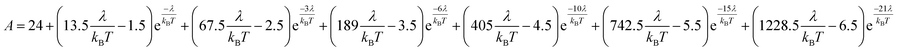 | (5) |
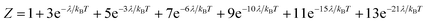 | (6) |
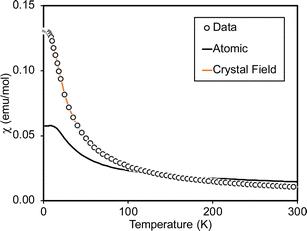 | ||
| Fig. 5 Magnetic susceptibility of Cp′3Eu (open circles). The fit using eqn (4) (free-ion model) is shown as a solid black line. The results of fitting the data using CONDON 3 (crystal field model with k = 0.7) is shown using an orange line. | ||
At low temperature, only the 7F0 orbital-singlet state is populated. This state displays temperature independent magnetism. As the temperature increases, the low-lying 7F1 and 7F2 excited states will be thermally populated, at which point the magnetic susceptibility, χ, becomes temperature dependent and starts to decrease.
However, the details of the magnetic susceptibility of Cp′3Eu are not congruent with this free-ion treatment; both the χ value at 300 K and χTIP at low temperatures are larger than the values for the free Eu3+ cation and reported monomeric Eu(III) compounds. Both observations indicate that the lowest lying excited state is much lower in energy than typical for a Eu(III) complex.87,88,91–96 Attempts to fit these data to a free-ion model using eqn (2) resulted in a very small λ value of 23 K which is an order of magnitude smaller than reported values for Eu(III) compounds (λ = 250–350 K) and is not realistic.87,88,91–96 The free ion model fails due to its implicit assumption that the splitting of the J states by the crystal field is much smaller than the spin orbit coupling constant. The XAS results show that the ground state of Cp′3Eu has a large contribution from a CT state, 4f7![[L with combining low line]](https://www.rsc.org/images/entities/i_char_004c_0332.gif) 5d0, due to mixing between the Eu 4f orbitals and the Cp′ orbitals with a′ symmetry. The magnitude of this interaction suggests that the splitting of the energies of the 4f-orbitals (and the J states) may be large enough to affect the variable temperature magnetic susceptibility of Cp′3Eu
5d0, due to mixing between the Eu 4f orbitals and the Cp′ orbitals with a′ symmetry. The magnitude of this interaction suggests that the splitting of the energies of the 4f-orbitals (and the J states) may be large enough to affect the variable temperature magnetic susceptibility of Cp′3Eu
To examine this possibility, the magnetic susceptibility of Cp′3Eu was modeled with crystal field theory using the program CONDON 3.97 The crystal field parameters B02, B04, B06, and B66 were allowed to vary while spin–orbit coupling (ζ) and Slater repulsion were fixed at their starting values. In comparison to the crystal field parameters, the Slater parameters and ζ are less strongly affected by the ligands. Fits were also performed while allowing ζ to vary, but doing so increased the value of reduced chi-squared, χν2, which indicates that the models with ζ fixed at 1336 cm−1 better reproduced the data. The initial fit of the susceptibility reproduced the data well, but yielded crystal field parameters with values around 104 cm−1, which are not reasonable due to the small overlap between the 4f and ligand orbitals. Since the XAS measurements indicated considerable mixing between the 4f and ligand orbitals, the effect of decreasing the Stevens orbital reduction parameter, k, were examined. This parameter corrects the calculated magnetic susceptibility for the decrease in orbital angular momentum due to mixing of the metal orbital with the ligand orbitals. Allowing k to vary during fits of the magnetic susceptibility provided reasonable quality fits over a large range of k values, from 0.55 to 0.95 – suggesting that k has a relatively flat χν2 profile – but often provided unrealistically large crystal field parameters. Hence, the value of k was set to 0.7 based on the nf value determined by fitting the L3-edge data using the relationship k = 1 − nf. This provided reasonable crystal field parameters with magnitudes on the order of 103 cm−1, which agree well with those reported previously by optical spectroscopy and magnetic measurements (Table 1).98,99
Fig. 6 compares the energies of the low-lying 4f6 states calculated by CONDON 3 during the fit to the energies of the free-ion states, which were determined by setting B02, B04, B06, and B66 to small values. Using Fig. 6, one can understand both the magnetic behavior of Cp′3Eu and why the free ion model fails to reproduce the magnetic susceptibility. In the absence of a crystal field, the energy of the first excited state, 7F1, is 378 cm−1 above the ground state, 7F0. The crystal field splits 7F1. The mJ = ±1 doublet state is destabilized, and the mJ = 0 singlet state is stabilized such that it is only 25 cm−1 above the ground state. Because the first excited state is at low energy, the value of χTIP is much larger than it is in the free ion (χTIP is inversely proportional to the energy gap). In addition, because the first excited state is at low energy, it becomes thermally populated at low temperatures, which results in a rapid decrease in the magnetic susceptibility of Cp′3Eu as the temperature increases above ∼10 K. In the free ion model (eqn (4)–(6)), the only way to decrease the energy of the first excited state is to decrease λ to a small value, which is not physically meaningful. Even this is not sufficient to model the magnetic susceptibility since the first excited state in the free ion model is a triplet while the first excited state is actually a singlet.
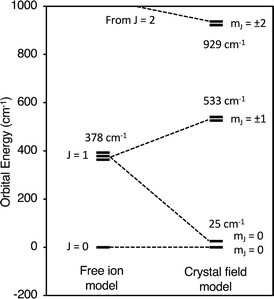 | ||
| Fig. 6 Low lying states of Cp′3Eu described using an atomic model and a crystal field model with k = 0.7. | ||
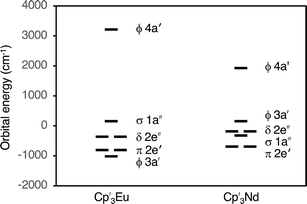
The fact that reasonable values of B02, B04, B06, and B66 could only be obtained when k ≤ 0.75 indicates that a large degree of orbital mixing is present in Cp′3Eu. The nature of this interaction can be evaluated from the experimentally derived MO diagram shown in Fig. 7, which was determined by using the crystal field parameters to calculate the splitting of the 4f orbitals. The MO diagram for Cp′3Eu resembles that previously reported for Cp′3Nd (ref. 100) and the qualitative MO diagram shown in Fig. 1. In these cases, one 4f-orbital is more strongly destabilized due to interaction with the ligands, and the other six 4f orbitals are similar in energy suggesting little interaction with the ligand orbitals.
The results from fitting the magnetic susceptibility also illustrate a drawback of this technique, which is that the crystal field model used by CONDON 3 may have multiple sets of parameters that can fit the data well. For this reason, it is helpful to have results from other physical measurements to better constrain the fit. Ideally, one would like to include the energies of the excited states and fit those along with the magnetic susceptibility. Here, we have adopted a different approach and have used the value of nf determined from XAS measurements to determine the value of k in the crystal field model, 0.7.
Conclusion
In summary, the X-ray spectroscopic and magnetic measurements described above have demonstrated how 4f orbital mixing can increase the magnetic susceptibility of a trivalent Eu organometallic complex, Cp′3Eu Despite inducing very different core-hole potentials, the C K-edge, Eu M5,4-edge, and Eu L3-edge XAS measurements each provided evidence for C 2p and Eu 4f orbital mixing. The C K-edge XAS and TDDFT calculations also showed that C 2p and Eu 4f orbital mixing occurs specifically in the orbitals of a′ symmetry (4f–π). The amount of charge transfer was expressed using a CI model in terms of the relative contribution of the |4f7![[L with combining low line]](https://www.rsc.org/images/entities/i_char_004c_0332.gif) 〉 configuration to the total ground-state wavefunction. The amount of charge transfer determined by fitting of the Eu L3-edge spectrum, 0.28(4), was used to determine the Stevens orbital reduction parameter, k, used in the modeling of the magnetic susceptibility data. The results of crystal field modeling show that the increased magnetic susceptibility of Cp′3Eu at low temperature is due to the presence of a low-lying mJ = 0 excited state resulting from the splitting of the 7F1 term. The qualitative MO diagram produced by modeling the magnetic susceptibility data is in excellent agreement with the results of the XAS studies.
〉 configuration to the total ground-state wavefunction. The amount of charge transfer determined by fitting of the Eu L3-edge spectrum, 0.28(4), was used to determine the Stevens orbital reduction parameter, k, used in the modeling of the magnetic susceptibility data. The results of crystal field modeling show that the increased magnetic susceptibility of Cp′3Eu at low temperature is due to the presence of a low-lying mJ = 0 excited state resulting from the splitting of the 7F1 term. The qualitative MO diagram produced by modeling the magnetic susceptibility data is in excellent agreement with the results of the XAS studies.
In the closely related molecule Cp3Yb, the presence of orbital mixing in Cp3Yb is manifested by a 12% contribution of the Yb2+ charge transfer configuration (4f14![[L with combining low line]](https://www.rsc.org/images/entities/i_char_004c_0332.gif) ) to the ground-state, with the remaining 88% from the ionic, Yb3+ configuration (4f13).39 The enhancement in charge transfer for Cp′3Eu compared to Cp3Yb is consistent with predictions by Denning and coworkers39 based on the 0.44 eV lower energy of the ligand to metal charge transfer transition for Eu3+vs. Yb3+.44 It is also likely to be a general result when comparing isomorphous Eu3+ and Yb3+ complexes owing to the lower reduction potential for Eu3+ (−0.34 V) compared with Yb3+ (−1.05 V) ions.101 To explore the limits of this trend, we are currently studying complexes with the related ions Sm3+ and Tm3+, as well as Nd3+ and Dy3+, which may be able to access either 4fn+1 or 4fn5d1 charge transfer configurations depending on the coordination environment.58,102
) to the ground-state, with the remaining 88% from the ionic, Yb3+ configuration (4f13).39 The enhancement in charge transfer for Cp′3Eu compared to Cp3Yb is consistent with predictions by Denning and coworkers39 based on the 0.44 eV lower energy of the ligand to metal charge transfer transition for Eu3+vs. Yb3+.44 It is also likely to be a general result when comparing isomorphous Eu3+ and Yb3+ complexes owing to the lower reduction potential for Eu3+ (−0.34 V) compared with Yb3+ (−1.05 V) ions.101 To explore the limits of this trend, we are currently studying complexes with the related ions Sm3+ and Tm3+, as well as Nd3+ and Dy3+, which may be able to access either 4fn+1 or 4fn5d1 charge transfer configurations depending on the coordination environment.58,102
Data availability
The data supporting this article have been included as part of the ESI.†Author contributions
Conceptualization and project administration: S. G., Y. Q., P. S., C. B., W. D., W. E., W. L., S. M. Formal analysis: S. G., Y. Q., P. S., L. M., C. B., W. D., W. E., W. L., S. M. Investigation: S. G., Y. Q., P. S., A. D., L. M., T. S., C. B., W. D., W. L., S. M. Resources: S. C., D. H., W. E. Validation: S. G., P. S. Funding acquisition and supervision: P. A., C. B., W. D., W. E., W. L., S. M. Writing – original draft: S. G., Y. Q., P. S., W. L., S. M. Writing – reviewing & editing: all authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We would like to thank the late Prof. Richard A. Andersen for contributing to the conceptualization of this project. This research was supported at LBNL by the Director, Office of Science, Office of Basic Energy Sciences, Division of Chemical Sciences, Geosciences, and Biosciences (CSGB), U.S. Department of Energy (DOE) under contract no. DE-AC02-05CH11231. Ciccone, Huh, and Evans acknowledge the U. S. National Science Foundation for support of this research under CHE-2154255. This research used resources of the ALS, which is a U.S. DOE Office of Science User Facility under contract no. DEAC02-05CH11231 at LBNL. STXM research described in this paper was conducted at Advanced Light Source Beamline 11.0.2, which was supported by the Director, Office of Science, Office of Basic Energy Sciences Division of Chemical Sciences, Geosciences, and Biosciences; and the Condensed Phase and Interfacial Molecular Sciences Program of the aforementioned Division of the U.S. Department of Energy at LBNL under Contract No. DE-AC02-05CH11231. Additional STXM research was conducted at the Canadian Light Source, which is supported by the Canada Foundation for Innovation, Natural Sciences and Engineering Research Council of Canada, the University of Saskatchewan, the Government of Saskatchewan, Western Economic Diversification Canada, the National Research Council Canada, and the Canadian Institutes of Health Research. The Stanford Synchrotron Radiation Lightsource is supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under contract no. DE-AC02-76SF00515.Notes and references
- R. Sessoli and A. K. Powell, Coord. Chem. Rev., 2009, 253, 2328–2341 CrossRef CAS.
- J. D. Rinehart and J. R. Long, Chem. Sci., 2011, 2, 2078–2085 RSC.
- N. F. Chilton, C. A. P. Goodwin, D. P. Mills and R. E. P. Winpenny, Chem. Commun., 2015, 51, 101–103 RSC.
- K. L. M. Harriman and M. Murugesu, Acc. Chem. Res., 2016, 49, 1158–1167 CrossRef CAS PubMed.
- M. Briganti, E. Lucaccini, L. Chelazzi, S. Ciattini, L. Sorace, R. Sessoli, F. Totti and M. Perfetti, J. Am. Chem. Soc., 2021, 143, 8108–8115 CrossRef CAS PubMed.
- N. Mahieu, J. Piatkowski, T. Simler and G. Nocton, Chem. Sci., 2023, 14, 443–457 RSC.
- A. Ramanathan, J. Kaplan, D. C. Sergentu, J. A. Branson, M. Ozerov, A. I. Kolesnikov, S. G. Minasian, J. Autschbach, J. W. Freeland, Z. G. Jiang, M. Mourigal and H. S. La Pierre, Nat. Commun., 2023, 14, 1–11 Search PubMed.
- U. J. Williams, B. D. Mahoney, P. T. DeGregorio, P. J. Carroll, E. Nakamaru-Ogiso, J. M. Kikkawa and E. J. Schelter, Chem. Commun., 2012, 48, 5593–5595 RSC.
- L. Ungur, J. J. Le Roy, I. Korobkov, M. Murugesu and L. F. Chibotaru, Angew. Chem., Int. Ed., 2014, 53, 4413–4417 CrossRef CAS PubMed.
- F. Gendron, B. Pritchard, H. Bolvin and J. Autschbach, Dalton Trans., 2015, 44, 19886–19900 RSC.
- F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, Angew. Chem., Int. Ed., 2017, 56, 11445–11449 CrossRef CAS PubMed.
- C. A. P. Goodwin, F. Ortu, D. Reta, N. F. Chilton and D. P. Mills, Nature, 2017, 548, 439–442 CrossRef CAS PubMed.
- G. M. Risica, V. Vieru, B. O. Wilkins, T. P. Latendresse, J. H. Reibenspies, N. S. Bhuvanesh, G. P. Wylie, L. F. Chibotaru and M. Nippe, Angew. Chem., Int. Ed., 2020, 59, 13335–13340 CrossRef CAS PubMed.
- M. Tricoire, L. Münzfeld, J. Moutet, N. Mahieu, L. La Droitte, E. Moreno-Pineda, F. Gendron, J. D. Hilgar, J. D. Rinehart, M. Ruben, B. Le Guennic, O. Cador, P. W. Roesky and G. Nocton, Chem.–Eur. J., 2021, 27, 13558–13567 CrossRef CAS PubMed.
- L. Münzfeld, M. Dahlen, A. Hauser, N. Mahieu, S. K. Kuppusamy, J. Moutet, M. Tricoire, R. Köppe, L. La Droitte, O. Cador, B. Le Guennic, G. Nocton, E. Moreno-Pineda, M. Ruben and P. W. Roesky, Angew. Chem., Int. Ed., 2023, 62, e202218107 CrossRef PubMed.
- T. Jo and A. Kotani, Phys. Rev. B, 1988, 38, 830–833 CrossRef CAS PubMed.
- J. M. Veauthier, E. J. Schelter, C. J. Kuehl, A. E. Clark, B. L. Scott, D. E. Morris, R. L. Martin, J. D. Thompson, J. L. Kiplinger and K. D. John, Inorg. Chem., 2005, 44, 5911–5920 CrossRef CAS PubMed.
- C. H. Booth, M. D. Walter, M. Daniel, W. W. Lukens and R. A. Andersen, Phys. Rev. Lett., 2005, 95, 267202 CrossRef CAS PubMed.
- C. H. Booth, M. D. Walter, D. Kazhdan, Y.-J. Hu, W. W. Lukens, E. D. Bauer, L. Maron, O. Eisenstein and R. A. Andersen, J. Am. Chem. Soc., 2009, 131, 6480–6491 CrossRef CAS PubMed.
- C. H. Booth, D. Kazhdan, E. L. Werkema, M. D. Walter, W. W. Lukens, E. D. Bauer, Y.-J. Hu, L. Maron, O. Eisenstein, M. Head-Gordon and R. A. Andersen, J. Am. Chem. Soc., 2010, 132, 17537–17549 CrossRef CAS PubMed.
- G. Nocton, C. H. Booth, L. Maron and R. A. Andersen, Organometallics, 2013, 32, 5305–5312 CrossRef CAS.
- D. Sergentu, C. Booth and J. Autschbach, Chem.–Eur. J., 2021, 27, 7239–7251 CrossRef CAS PubMed.
- N. Magnani, Int. J. Quantum Chem., 2014, 114, 755–759 CrossRef CAS.
- S. C. Bart, F. W. Heinemann, C. Anthon, C. Hauser and K. Meyer, Inorg. Chem., 2009, 48, 9419–9426 CrossRef CAS PubMed.
- I. Castro-Rodriguez, K. Olsen, P. Gantzel and K. Meyer, J. Am. Chem. Soc., 2003, 125, 4565–4571 CrossRef CAS PubMed.
- D. P. Mills, F. Moro, J. McMaster, J. van Slageren, W. Lewis, A. J. Blake and S. T. Liddle, Nat. Chem., 2011, 3, 454–460 CrossRef CAS PubMed.
- D. M. King, F. Tuna, J. McMaster, W. Lewis, A. J. Blake, E. J. L. McInnes and S. T. Liddle, Angew. Chem., Int. Ed., 2013, 52, 4921–4924 CrossRef CAS PubMed.
- K. R. Meihaus and J. R. Long, Dalton Trans., 2015, 44, 2517–2528 RSC.
- V. Mougel, L. Chatelain, J. Pécaut, R. Caciuffo, E. Colineau, J.-C. Griveau and M. Mazzanti, Nat. Chem., 2012, 4, 1011–1017 CrossRef CAS PubMed.
- Y. Hinatsu, M. Itoh and N. Edelstein, J. Solid State Chem., 1997, 132, 337–341 CrossRef CAS.
- Y. Hinatsu, M. Wakeshima, N. Edelstein and I. Craig, J. Solid State Chem., 1999, 144, 20–24 CrossRef CAS.
- L. A. Solola, A. V. Zabula, W. L. Dorfner, B. C. Manor, P. J. Carroll and E. J. Schelter, J. Am. Chem. Soc., 2017, 139, 2435–2442 CrossRef CAS PubMed.
- A. R. Willauer, C. T. Palumbo, F. Fadaei-Tirani, I. Zivkovic, I. Douair, L. Maron and M. Mazzanti, J. Am. Chem. Soc., 2020, 142, 5538–5542 CrossRef CAS PubMed.
- M. J. Daum, A. Ramanathan, A. I. Kolesnikov, S. Calder, M. Mourigal and H. S. La Pierre, Phys. Rev. B, 2021, 103, L121109 CrossRef CAS.
- Y. S. Qiao, H. L. Yin, L. M. Moreau, R. L. Feng, R. F. Higgins, B. C. Manor, P. J. Carroll, C. H. Booth, J. Autschbach and E. J. Schelter, Chem. Sci., 2021, 12, 3558–3567 RSC.
- A. Ramanathan, E. D. Walter, M. Mourigal and H. S. La Pierre, J. Am. Chem. Soc., 2023, 145, 17603–17612 CrossRef CAS PubMed.
- W. W. Lukens, Jr., S. G. Minasian and C. H. Booth, Chem. Sci., 2023, 14, 12784–12795 RSC.
- G. Depaoli, U. Russo, G. Valle, F. Grandjean, A. F. Williams and G. J. Long, J. Am. Chem. Soc., 1994, 116, 5999–6000 CrossRef CAS.
- M. Coreno, M. de Simone, R. Coates, M. S. Denning, R. G. Denning, J. C. Green, C. Hunston, N. Kaltsoyannis and A. Sella, Organometallics, 2010, 29, 4752–4755 CrossRef CAS.
- R. G. Denning, J. Harmer, J. C. Green and M. Irwin, J. Am. Chem. Soc., 2011, 133, 20644–20660 CrossRef CAS PubMed.
- W. W. Lukens, N. Magnani and C. H. Booth, Inorg. Chem., 2012, 51, 10105–10110 CrossRef CAS PubMed.
- G. Nocton, W. W. Lukens, C. H. Booth, S. S. Rozenel, S. A. Medling, L. Maron and R. A. Andersen, J. Am. Chem. Soc., 2014, 136, 8626–8641 CrossRef CAS PubMed.
- B. M. Day, F.-S. Guo and R. A. Layfield, Acc. Chem. Res., 2018, 51, 1880–1889 CrossRef CAS PubMed.
- P. Dorenbos, J. Phys.: Condens. Matter, 2003, 15, 8417 CrossRef CAS.
- M. T. Trinh, J. C. Wedal and W. J. Evans, Dalton Trans., 2021, 50, 14384–14389 RSC.
- X. Cao and M. Dolg, J. Mol. Struct., 2002, 581, 139–147 CrossRef CAS.
- S. D. Ramarao, A. K. Singh, U. Subbarao and S. C. Peter, J. Solid State Chem., 2020, 281, 121048 CrossRef CAS.
- D. N. Huh, J. P. Bruce, S. Ganesh Balasubramani, S. R. Ciccone, F. Furche, J. C. Hemminger and W. J. Evans, J. Am. Chem. Soc., 2021, 143, 16610–16620 CrossRef CAS PubMed.
- S. G. Minasian, J. M. Keith, E. R. Batista, K. S. Boland, D. L. Clark, S. A. Kozimor, R. L. Martin, D. K. Shuh and T. Tyliszczak, Chem. Sci., 2014, 5, 351–359 RSC.
- D. E. Smiles, E. R. Batista, C. H. Booth, D. L. Clark, J. M. Keith, S. A. Kozimor, R. L. Martin, S. G. Minasian, D. K. Shuh, S. C. E. Stieber and T. Tyliszczak, Chem. Sci., 2020, 11, 2796–2809 RSC.
- Y. Qiao, G. Ganguly, C. H. Booth, J. A. Branson, A. S. Ditter, D. J. Lussier, L. M. Moreau, D. R. Russo, D.-C. Sergentu, D. K. Shuh, T. Sun, J. Autschbach and S. G. Minasian, Chem. Commun., 2021, 57, 9562–9565 RSC.
- M. E. Fieser, M. G. Ferrier, J. Su, E. Batista, S. K. Cary, J. W. Engle, W. J. Evans, J. S. Lezama Pacheco, S. A. Kozimor, A. C. Olson, A. J. Ryan, B. W. Stein, G. L. Wagner, D. H. Woen, T. Vitova and P. Yang, Chem. Sci., 2017, 8, 6076–6091 RSC.
- J. W. Lauher and R. Hoffmann, J. Am. Chem. Soc., 1976, 98, 1729–1742 CrossRef CAS.
- B. E. Bursten and R. J. Strittmatter, Angew. Chem., Int. Ed., 1991, 30, 1069–1085 CrossRef.
- L. Maron, O. Eisenstein and R. A. Andersen, Organometallics, 2009, 28, 3629–3635 CrossRef CAS.
- W. W. Lukens, N. M. Edelstein, N. Magnani, T. W. Hayton, S. Fortier and L. A. Seaman, J. Am. Chem. Soc., 2013, 135, 10742–10754 CrossRef CAS PubMed.
- T. A. Albright, J. K. Burdett and M. Whangbo, Orbital Interactions in Chemistry, John Wiley and Sons, New York, 1985 Search PubMed.
- M. E. Fieser, M. R. MacDonald, B. T. Krull, J. E. Bates, J. W. Ziller, F. Furche and W. J. Evans, J. Am. Chem. Soc., 2015, 137, 369–382 CrossRef CAS PubMed.
- S. G. Minasian, E. R. Batista, C. H. Booth, D. L. Clark, J. M. Keith, S. A. Kozimor, W. W. Lukens, R. L. Martin, D. K. Shuh, S. C. E. Stieber, T. Tylisczcak and X.-d. Wen, J. Am. Chem. Soc., 2017, 139, 18052–18064 CrossRef CAS PubMed.
- S. G. Minasian, J. M. Keith, E. R. Batista, K. S. Boland, S. A. Kozimor, R. L. Martin, D. K. Shuh, T. Tyliszczak and L. J. Vernon, J. Am. Chem. Soc., 2013, 135, 14731–14740 CrossRef CAS PubMed.
- E. Ruhl and A. P. Hitchcock, J. Am. Chem. Soc., 1989, 111, 5069–5075 CrossRef.
- A. T. Wen and A. P. Hitchcock, Can. J. Chem., 1993, 71, 1632–1644 CrossRef CAS.
- A. T. Wen, E. Ruhl and A. P. Hitchcock, Organometallics, 1992, 11, 2559–2569 CrossRef CAS.
- A. Bianconi, A. Marcelli, H. Dexpert, R. Karnatak, A. Kotani, T. Jo and J. Petiau, Phys. Rev. B, 1987, 35, 806–812 CrossRef CAS PubMed.
- H. Dexpert, R. C. Karnatak, J. M. Esteva, J. P. Connerade, M. Gasgnier, P. E. Caro and L. Albert, Phys. Rev. B, 1987, 36, 1750–1753 CrossRef CAS PubMed.
- G. Kaindl, G. Schmiester, E. V. Sampathkumaran and P. Wachter, Phys. Rev. B, 1988, 38, 10174–10177 CrossRef CAS PubMed.
- B. T. Thole, G. van der Laan, J. C. Fuggle, G. A. Sawatzky, R. C. Karnatak and J. M. Esteva, Phys. Rev. B, 1985, 32, 5107–5118 CrossRef CAS.
- G. Kaindl, G. Kalkowski, W. D. Brewer, B. Perscheid and F. Holtzberg, J. Appl. Phys., 1984, 55, 1910–1915 CrossRef CAS.
- M. Stavinoha, J. A. Cooley, S. G. Minasian, T. M. McQueen, S. M. Kauzlarich, C. L. Huang and E. Morosan, Phys. Rev. B, 2018, 97, 195146 CrossRef CAS.
- B. T. Thole, G. Vanderlaan, J. C. Fuggle, G. A. Sawatzky, R. C. Karnatak and J. M. Esteva, Phys. Rev. B, 1985, 32, 5107–5118 CrossRef CAS PubMed.
- J. B. Goedkoop, B. T. Thole, G. van der Laan, G. A. Sawatzky, F. M. F. de Groot and J. C. Fuggle, Phys. Rev. B, 1988, 37, 2086–2093 CrossRef CAS PubMed.
- M. W. Löble, J. M. Keith, A. B. Altman, S. C. E. Stieber, E. R. Batista, K. S. Boland, S. D. Conradson, D. L. Clark, J. Lezama Pacheco, S. A. Kozimor, R. L. Martin, S. G. Minasian, A. C. Olson, B. L. Scott, D. K. Shuh, T. Tyliszczak, M. P. Wilkerson and R. A. Zehnder, J. Am. Chem. Soc., 2015, 137, 2506–2523 CrossRef PubMed.
- T. A. Pham, A. B. Altman, S. C. E. Stieber, C. H. Booth, S. A. Kozimor, W. W. Lukens, D. T. Olive, T. Tyliszczak, J. Wang, S. G. Minasian and K. N. Raymond, Inorg. Chem., 2016, 55, 9989–10002 CrossRef CAS PubMed.
- M. G. Silly, S. Blanchandin, F. Sirotti, F. Lux, S. Chevreux, G. Lemercier and F. Charra, J. Phys. Chem. C, 2013, 117, 9766–9771 CrossRef CAS.
- A. Kotani and H. Ogasawara, J. Electron Spectrosc. Relat. Phenom., 1992, 60, 257–299 CrossRef CAS.
- C. Dallera, K. Giarda, G. Ghiringhelli, A. Tagliaferri, L. Braicovich and N. B. Brookes, Phys. Rev. B, 2001, 64, 153104 CrossRef.
- C. Dallera, M. Grioni, A. Shukla, G. Vankó, J. L. Sarrao, J. P. Rueff and D. L. Cox, Phys. Rev. Lett., 2002, 88, 196403 CrossRef CAS PubMed.
- S. M. Butorin, A. Modin, J. R. Vegelius, K. O. Kvashnina and D. K. Shuh, J. Phys. Chem. C, 2016, 120, 29397–29404 CrossRef CAS.
- K. O. Kvashnina, P. M. Kowalski, S. M. Butorin, G. Leinders, J. Pakarinen, R. Bès, H. J. Li and M. Verwerft, Chem. Commun., 2018, 54, 9757–9760 RSC.
- K. O. Kvashnina and S. M. Butorin, Chem. Commun., 2022, 58, 327–342 RSC.
- E. Stavitski and F. M. F. de Groot, Micron, 2010, 41, 687–694 CrossRef CAS PubMed.
- R. D. Cowan, Theory of Atomic Structure and Spectra, University of California Press, 1981 Search PubMed.
- F. M. F. de Groot and A. Kotani, Core Level Spectroscopy of Solids, Taylor and Francis, New York, 2008 Search PubMed.
- S. Harder, D. Naglav, C. Ruspic, C. Wickleder, M. Adlung, W. Hermes, M. Eul, R. Pottgen, D. Rego, F. Poineau, K. Czerwinski, R. Herber and I. Nowik, Chem.–Eur. J., 2013, 19, 12272–12280 CrossRef CAS PubMed.
- W. Liu, L. Liu, Y. Wang, L. Chen, J. A. McLeod, L. Yang, J. Zhao, Z. Liu, J. Diwu, Z. Chai, T. E. Albrecht-Schmitt, G. Liu and S. Wang, Chem.–Eur. J., 2016, 22, 11170–11175 CrossRef CAS PubMed.
- K. R. Meihaus, M. E. Fieser, J. F. Corbey, W. J. Evans and J. R. Long, J. Am. Chem. Soc., 2015, 137, 9855–9860 CrossRef CAS PubMed.
- Y. Takikawa, S. Ebisu and S. Nagata, J. Phys. Chem. Solids, 2010, 71, 1592–1598 CrossRef CAS.
- M. Andruh, E. Bakalbassis, O. Kahn, J. C. Trombe and P. Porcher, Inorg. Chem., 1993, 32, 1616–1622 CrossRef CAS.
- G. S. Ofelt, J. Chem. Phys., 1963, 38, 2171–2180 CrossRef CAS.
- J. H. Van Vleck, The Theory of Electric and Magnetic Susceptibilities, Oxford University Press, 1932 Search PubMed.
- M.-L. Sun, J. Zhang, Q.-P. Lin, P.-X. Yin and Y.-G. Yao, Inorg. Chem., 2010, 49, 9257–9264 CrossRef CAS PubMed.
- Y. Wan, L. Zhang, L. Jin, S. Gao and S. Lu, Inorg. Chem., 2003, 42, 4985–4994 CrossRef CAS PubMed.
- J. Lhoste, A. Pérez-Campos, N. Henry, T. Loiseau, P. Rabu and F. Abraham, Dalton Trans., 2011, 40, 9136–9144 RSC.
- J. Legendziewicz, V. Tsaryuk, V. Zolin, E. Lebedeva, M. Borzechowska and M. Karbowiak, New J. Chem., 2001, 25, 1037–1042 RSC.
- C. Benelli, A. Caneschi, D. Gatteschi, L. Pardi, P. Rey, D. P. Shum and R. L. Carlin, Inorg. Chem., 1989, 28, 272–275 CrossRef.
- X.-J. Wang, Z.-M. Cen, Q.-L. Ni, X.-F. Jiang, H.-C. Lian, L.-C. Gui, H.-H. Zuo and Z.-Y. Wang, Cryst. Growth Des., 2010, 10, 2960–2968 CrossRef CAS.
- M. Speldrich, J. van Leusen and P. Kögerler, J. Comput. Chem., 2018, 39, 2133–2145 CrossRef CAS PubMed.
- S. Jank, H. Reddmann and H. D. Amberger, J. Alloys Compd., 1997, 250, 387–390 CrossRef CAS.
- P. W. Smith, J. Hrubý, W. J. Evans, S. Hill and S. G. Minasian, J. Am. Chem. Soc., 2024, 146(9), 5781–5785 CrossRef CAS PubMed.
- W. W. Lukens, M. Speldrich, P. Yang, T. J. Duignan, J. Autschbach and P. Kögerler, Dalton Trans., 2016, 45, 11508–11521 RSC.
- S. Cotton, Lanthanide and Actinide Chemistry, John Wiley and Sons, West Sussex, UK, 2006 Search PubMed.
- M. E. Fieser, C. T. Palumbo, H. S. La Pierre, D. P. Halter, V. K. Voora, J. W. Ziller, F. Furche, K. Meyer and W. J. Evans, Chem. Sci., 2017, 8, 7424–7433 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available: Experimental and computational methods, additional plots of XAS data for Cp′3Eu (Ln = Eu, Gd, Yb). See DOI: https://doi.org/10.1039/d4sc01300j |
| ‡ These authors contributed equally. |
| § Present address: Department of Chemistry, University of Rhode Island, Kingston, RI 02881, USA. |
| This journal is © The Royal Society of Chemistry 2024 |