Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
First principles study on the structural stability, mechanical stability and optoelectronic properties of alkali-based single halide perovskite compounds XMgI3 (X = Li/Na): DFT insight
Kefyalew Wagari
Guji
*a,
Tesfaye Abebe
Geleta
 *b,
Nabil
Bouri
c and
Victor José
Ramirez Rivera
d
*b,
Nabil
Bouri
c and
Victor José
Ramirez Rivera
d
aPhysics Department, Bule Hora University, P. O. BOX 144, Bule Hora, Ethiopia. E-mail: gujikefyalew@gmail.com
bDepartment of Agricultural Chemistry, National Taiwan University, Taipei, 10617, Taiwan. E-mail: tesfaye867@gmail.com
cLaboratory of Materials Physics and Subatomic, Faculty of Science, University Ibn Tofail, BP. 133, 14000, Kénitra, Morocco
dDepartment of Physics, Jorge Basadre Grohmann National University, Tacna, Peru
First published on 24th July 2024
Abstract
Metal-halide perovskites are recognized as cutting-edge solar energy technology, boasting remarkable absorption capabilities, minimal environmental impact, and cost-effectiveness. This study delves into the structural stability, mechanical stability, and optoelectronic properties of lead-free halide perovskites, specifically XMgI3 (X = Li/Na), by utilizing the CASTEP and WIEN2k software along with the GGA-PBE and Tran–Blaha modified Becke–Johnson (TB-mBJ) exchange–correlation functions to compare their electronic properties. The structural and mechanical stabilities were confirmed by assessing their tolerance factor and formation energy and by evaluating their elastic constants, respectively. Using the TB-mBJ exchange–correlation potential function, the calculated indirect band gap values for LiMgI3 and NaMgI3 were 2.474 and 2.556 eV, respectively. These band gaps are suitable for solar energy harvesting due to their broad optical absorption ranging from infrared to visible light. The partial density of states and the total density of states were determined to investigate the contribution of individual atoms. Consequently, this study can guide researchers focusing on the experimental synthesis of these materials at the laboratory scale for in-depth exploration, particularly in applications such as photovoltaics and various optoelectronic devices.
1. Introduction
With the increase in the world's population and economy, the demand for energy is growing.1 However, non-renewable energy sources such as fossil fuels employed to meet this demand are being depleted,2,3 and the energy generated from non-renewable energy sources is harmful to the surrounding environment due to CO2 emissions.4 Therefore, it is necessary to discover safe and reliable new energy technologies. To solve this kind of problem, perovskite materials (ABX3)5 have the characteristics of photovoltaics (PV), the most common type of solar technology,6,7 due to their significant properties6,8–10 that contribute to the production of clean energy from pollution.11–13 The most promising solar energy in recent years has been organic–inorganic halide perovskite (OIHP)-based PV technology, which is efficient, inexpensive, and has special optoelectronic effects.However, the low stability of OIHPs hinders their application in the production of solar cells. For example, conventional OIHPs such as MAPbI3 (ref. 14) and MAPbX3 (X = Cl, Br, and I)15 have attracted considerable interest due to their high efficiency and suitability for optoelectronic applications, despite concerns regarding their instability and the toxicity associated with the presence of lead (Pb). Most of the metal halide Pb-free materials such as ZYbI3 (Z = Rb, Cs) have been used as perovskite materials as a result of their high efficiency.16 Mahmood et al.16 reported the preparation of RbYbI3 and CsYbI3 with a narrow direct band of 1.22 eV and 1.12 eV, respectively, which are considered suitable for the fabrication of solar cells.
Interestingly, Ray et al.17 proposed substituting divalent atoms (such as Ge, Sn, Pb, Mg, Ca, Sr, and Ba) for Pb to address the toxicity concerns associated with perovskite materials in photovoltaic applications. They found that Mg and Ba perovskites are unlikely to form in the cubic, tetragonal, and orthorhombic phases due to their positive formation energies. Alternatively, Ca and Sr perovskites exhibit negative formation energies with respect to the metal-iodide precursors and they possess wide band gaps, making them less favorable candidates for use in photovoltaic devices. They additionally reported that the predictive capability of a local density functional with a non-separable gradient approximation (NGA) closely resembles that of hybrid functionals in terms of band gap predictions, particularly when M in CsMI3 represents a p-block element such as Pb, Sn, and Ge.
The stability of perovskite materials was identified to be enhanced by introducing K and Rb atoms,18–21 specifically KGeX3 and RbGX3 (where X = Cl or Br). Due to their exceptional optoelectronic properties, which include a high static refractive index, low reflectivity, high absorption coefficient, and excellent stability, they have been thoroughly investigated for their possible uses in solar energy and photoelectric systems. Furthermore, they exhibit relatively low levels of toxicity. Additionally, CsGeX3 (X = F, Cl, and Br) perovskite has been identified as a promising candidate for optoelectronic applications owing to its exceptional electronic, optical, thermoelectric, and tunable band gap properties.5,22,23 Lead-free metal halide compounds XBeCl3 (X = Ga/Ag)24,25 and NaXCl3 (X = Be/Mg)26 have been investigated for application in optoelectronic devices due to their unique structural, optical, electronic, and elastic properties. GaBeCl3 and AgBeCl3 have band gaps of 3.03 eV and 3.25 eV, while NaBeCl3 and NaMgCl3 show band gaps of 4.15 eV and 4.16 eV, respectively. An increase in atomic radii corresponds to a decrease in band gap. These materials also exhibit ductility, enhancing their suitability for use in optoelectronic devices. First-principle calculations were used to comprehensively evaluate these properties.
The electrical and optical properties of different cubic lead-free halide perovskites, CsMgX3 (X = Cl and Br) compounds, were studied.27 Similar to these compounds, the cubic halide perovskite CsBX3 (B = Sn, Ge, X = I, Br, and Cl) compounds were reported to be suitable for optoelectronic energy devices.28 Furthermore, recently narrow band gap perovskite materials such as BaZrS3 (ref. 6) and CsYbI3 (ref. 16) were reported. Owing to their narrow band gap, the reported materials are highly recommended for perovskite solar cell applications due to their wide absorption spectrum, primarily covering the visible and infrared regions. However, their elements are categorized as transition metals and lanthanides, which are computationally expensive and result in the formation of compounds with a relatively high density. In the calculation of the electronic structure of transition metals, standard density functional theory (DFT) underestimates the results. Therefore, it is essential to consider additional methods such as incorporating the Hubbard–U function or hybrid function.
Caid et al.29 introduced Cs2CdZnCl6, a lead-free halide double perovskite, via DFT calculations. This compound exhibits mechanical stability in the cubic nonmagnetic phase and has a direct band gap of 1.43 eV. Its optical conductivity was determined to be up to 13.0 eV, showing a significant ultraviolet photoresponse. These characteristics suggest that Cs2CdZnCl6 is promising for optoelectronic applications, making it a valuable addition to materials science and technology. In another study, Caid et al.30 extensively investigated Cs2B′B′′Br6 double perovskites, revealing their potential in various technological fields. These compounds demonstrated robust stability with negative formation energies and favorable elastic constants. In the case of both BeMg and CdBe, Cs2B′B′′Br6 exhibited direct band gaps, whereas indirect band gaps were observed with CdGe, GeMg, GeZn, and MgZn. The optical property assessments highlighted the exceptional dielectric characteristics and strong light absorption in visible and UV spectra of these perovskites, making them promising candidates for solar cells and energy harvesting technologies, indicating significant potential for future energy and optoelectronic advancements.
Therefore, to address these issues, we were motivated to develop transition metal-free and lightweight compounds within alkali and alkaline-based halide perovskite materials (XMgI3, X = Li/Na). Our proposed materials exhibit superior optoelectronic properties compared to previous reports, particularly maintaining a narrow band gap, which enhances the photon absorption region. To the authors' knowledge, there are currently no reports available on alkali metal-based iodide perovskite compounds, namely LiMgI3 and NaMgI3, based on either DFT simulations or experimental studies. Thus, this study aimed to thoroughly investigate the mechanical stability, optoelectronic characteristics, and atomic population analysis of XMgI3 (X = Li/Na) using DFT and the CASTEP and WIEN2k software. This article presents XMgI3 (X = Li and Na) perovskite compounds as novel and inventive materials for solar cell applications that outperforms all previously investigated metal-halide perovskites.
2. Computational analysis
In this investigation, we applied the plane wave pseudopotential approach utilizing CASTEP software31–34 based on DFT principles. The electron exchange-correlation energy was computed following the Perdew–Burke–Ernzerhof (PBE) scheme within the framework of the generalized gradient approximation (GGA).35 We used an ultrasoft pseudopotential36 to describe the atomic potential. The electron configurations of the Li, Na, Mg, and I atoms are 1s22s1, [Ne] 3s1, [Ne] 3s2, and [Kr] 5s24d105p5, respectively. For optimizing the crystal structure, we employed a plane wave cutoff energy of 700 eV and a 6 × 6 × 6 k-point grid in the Brillouin zone37 for both XMgI3 (X = Li/Na) compounds. Structure optimization and lattice parameter calculations were carried out using the BFGS method. The specific tolerances included a total energy of 5.0 × 10−6 eV per atom, self-consistent field (scf) of 5.0 × 10−7 eV per atom, maximum force of 0.01 eV Å−1, maximum stress of 0.02 GP, and maximum displacement of 5.0 × 10−4 Å. The elastic constants, electron localization function, and Mulliken population analysis were performed using CASTEP software. The Bader change analysis was performed using Quantum ESPRESSO.To precisely assess the ground-state characteristics and optoelectronic properties of the materials, the full-potential linearized augmented plane wave (FP-LAPW)38 method within the WIEN2k code was used.39 The Trans–Blaha (TB-mBJ) exchange–correlation approximations were employed. Implementing the TB-mBJ function yielded a highly accurate band gap value.40,41 For the specified objective, the adjusted fundamental parameters were chosen as the standard configuration in the computational software, incorporating RMT × Kmax = 8, with Kmax denoting the wave vector and RMT representing the muffin-tin sphere radius. A k-mesh of 15 × 15 × 15 was chosen to ensure precise energy calculations. The self-consistent field method with an energy convergence threshold of 10−4 Ry was employed in the iteration process. The comparison of the GGA-PBE function employed in CASTEP and WIEN2k was conducted comprehensively in this study.
Moreover, to validate the significance of FP-LPAW in conjunction with the mBJ hybrid function, an analysis employing the Heyd–Scuseria–Ernzerhof 2006 functional (HSE06) within the framework of Quantum ESPRESSO (QE) was conducted.42 In the process of the scf calculation, a convergence threshold of 60 Ry was established for the Ecutoff wave function, and a denser k-mesh of 14 × 14 × 14 in the Brillouin zone was utilized. The phonon dispersion analysis was conducted through the utilization of the phonopy module integrated in the WIEN2k software. Moreover, ab initio molecular dynamics (AIMD) simulations were executed using the Forcite tools, wherein the NVE thermodynamic ensemble was designated to assess the thermal stability of the compounds under investigation at room temperature.
3. Results and discussion
3.1 Structural analysis
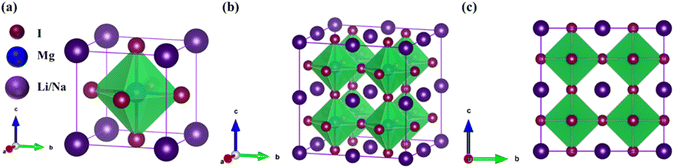
The investigated alkali-based single halide perovskite compounds, denoted as XMgI3 (X = Li/Na), exhibit a cubic ABX3 structure, conforming to the Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m crystallographic space group (no. 221). The cubic primitive unit cell of XMgI3 (where X = Li/Na) comprises five atoms. Specifically, the X atoms are positioned at the corners in the 1a Wyckoff position (0, 0, 0), the Mg atom occupies the body center in the 1b Wyckoff position (0.5, 0.5, 0.5), and the I atoms are positioned at the face center in the Wyckoff position (0.5, 0.5, 0.0). The optimized bulk crystal structure of XMgI3 (X = Li/Na) is given in Fig. 1. Table 1 displays the computed the lattice parameters (a = b = c), band gap (Eg), cell volume (V), tolerance factor (τ), and formation energy (Ef) values for the investigated compounds. To further confirm the structural stability, specifically the lattice parameters, of the cubic perovskite materials, we performed the optimization utilizing the CASTEP and WIEN2k code tools. The optimized lattice constants for LiMgI3 and NaMgI3 were calculated to be 5.8022/5.8297 Å and 5.8207/5.8408 Å utilizing CASTEP and WIEN2k with the corresponding cell volumes of 194.2461/198.0969 Å3 and 195.3316/199.2664 Å3, respectively, as indicated in Table 1 and Fig. 2A. The lattice parameters increased by approximately 0.47% and 0.34% for LiMgI3 and NaMgI3, respectively, while the volume increased by nearly 2% for both materials. These results indicate that their cubic structures remain stable even when optimized with different tools. Due to ionic differences between the Li and Na atoms, variations in both their lattice constants and cell volume were observed when utilizing the same tool (either CASTEP or WIEN2k).
m crystallographic space group (no. 221). The cubic primitive unit cell of XMgI3 (where X = Li/Na) comprises five atoms. Specifically, the X atoms are positioned at the corners in the 1a Wyckoff position (0, 0, 0), the Mg atom occupies the body center in the 1b Wyckoff position (0.5, 0.5, 0.5), and the I atoms are positioned at the face center in the Wyckoff position (0.5, 0.5, 0.0). The optimized bulk crystal structure of XMgI3 (X = Li/Na) is given in Fig. 1. Table 1 displays the computed the lattice parameters (a = b = c), band gap (Eg), cell volume (V), tolerance factor (τ), and formation energy (Ef) values for the investigated compounds. To further confirm the structural stability, specifically the lattice parameters, of the cubic perovskite materials, we performed the optimization utilizing the CASTEP and WIEN2k code tools. The optimized lattice constants for LiMgI3 and NaMgI3 were calculated to be 5.8022/5.8297 Å and 5.8207/5.8408 Å utilizing CASTEP and WIEN2k with the corresponding cell volumes of 194.2461/198.0969 Å3 and 195.3316/199.2664 Å3, respectively, as indicated in Table 1 and Fig. 2A. The lattice parameters increased by approximately 0.47% and 0.34% for LiMgI3 and NaMgI3, respectively, while the volume increased by nearly 2% for both materials. These results indicate that their cubic structures remain stable even when optimized with different tools. Due to ionic differences between the Li and Na atoms, variations in both their lattice constants and cell volume were observed when utilizing the same tool (either CASTEP or WIEN2k).
| Compounds | Lattice constants, a = b = c (Å) | E g (eV) | V (Å3) | E f (eV) | τ | Ref. | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CASTEP | WIEN2k | PBE-CASTEP | PBE-WIEN2k | mBJ-WIEN2k | HSE06-QE | CASTEP | WIEN2k | ΔV (%) | ||||
| LiMgI3 | 5.8022 | 5.8297 | 1.174 | 1.181 | 2.474 | 2.219 | 194.246 | 198.097 | 1.98 | −1.8864 | 0.81 | This study |
| NaMgI3 | 5.8207 | 5.8408 | 1.176 | 1.185 | 2.556 | 2.239 | 195.332 | 199.266 | 2.01 | −1.9021 | 0.87 | This study |
| LiMgI3 | — | 5.805 | — | 1.132 | 2.586 | — | — | — | — | — | 43 | |
| LiCaI3 | — | 6.1382 | — | 2.457 | 4.525 | — | — | — | — | — | 43 | |
| NaCaI3 | — | 6.146 | — | 2.527 | 4.600 | — | — | — | — | — | 43 | |
| NaMgCl3 | — | 4.940 | — | — | 4.16 | — | — | — | — | −0.923 | 26 | |
| NaBeCl3 | — | 4.550 | — | — | 4.16 | — | — | — | — | −1.023 | 26 | |
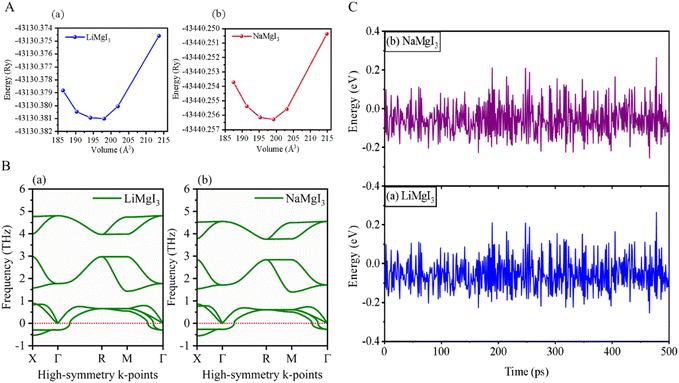 | ||
| Fig. 2 (A) Total energy with volume optimization curves, (B) phonon dispersion, and (C) thermal stability of LiMgI3 and the NaMgI3, respectively. | ||
The Goldschmidt tolerance factor, denoted as “τ”, is widely used to investigate the structural stability of ABX3 perovskites, giving insight to determine the compatibility of the cations within their structure, which is defined as follows:44
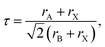 | (1) |
Furthermore, the formation energy (ΔEf) of the compounds was calculated to confirm their thermodynamic stability at room temperature using eqn (2), as follows:50
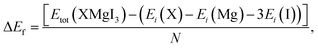 | (2) |
Furthermore, phonon dispersion calculations offers valuable insights into the dynamical stability of the materials being studied.51 The phonon dispersion curves were obtained by computing the phonon frequencies along the high symmetry directions (X → Γ → R → M → Γ) of the Brillouin zone, as illustrated in Fig. 2B. Typically, stable phonon structures exhibit real frequencies, as denoted by positive signs, whereas unstable structures are characterized by imaginary frequencies, which are indicated by negative signs. The computed phonon spectra revealed that both the LiMgI3 and NaMgI3 perovskite materials exhibit real frequencies at the gamma (Γ) point, confirming their dynamic stability. However, at the X-point in the first Brillouin zone, a less negative phonon frequency (∼−0.54 THz) was observed, suggesting localized instabilities or specific vibrational modes affecting certain directions or regions within the crystal lattice.52,53 Positive phonon frequencies at the Γ-point indicate stable vibrational modes at the center of the Brillouin zone, typically corresponding to the collective motions of the entire crystal lattice or large-scale atomic displacements. These stable modes contribute to the overall stability of the material by ensuring well-defined lattice vibrations without leading to global instabilities.
To evaluate the thermal stability of LiMgI3 and NaMgI3, ab initio molecular dynamics simulations (AIMD) were carried out at room temperature over a period of 500 ps, utilizing a time step of 1 fs. The results, as depicted in Fig. 2C, reveal that minimal energy fluctuations occurred during the simulation. Furthermore, both perovskite frameworks preserved their original configurations without exhibiting any discernible structural deformities. Thus, these findings undeniably confirm the stability of LiMgI3 and NaMgI3 at room temperature.26
3.2 Atomic populations analysis
Mulliken atomic population (MAP) is suitable for gaining insight into the atomic bonding (such as chemical bonds, bond overlap, and movement of charge between atoms) in compounds.54,55 The calculated bond populations, charges, and bond lengths are summarized in Table 2 for the XMgI3 (X = Li/Na) compounds. The determined positive (Li, Mg, and Na) and negative (I) charges in the XMgI3 (X = Li/Na) compounds, as shown in Table 2, suggest that charge is transferred from the alkali metals (Li and Na) and alkaline earth metallic (Mg) atoms to the halogen (I). In both the LiMgI3 and NaMgI3 compounds, charge transfer of 0.46 e and 0.28 e to iodine (I), respectively, was observed. Moreover, we conducted theoretical investigations into the charge-transfer mechanism utilizing Bader analysis,56 as depicted in Table 2. The Bader charge analysis utilizes electron density to determine the electronic charges associated with individual atoms.57 It helps in understanding the nature of chemical bonding and intermolecular interactions. The ability of the I atom to accept electrons from Li/Na and Mg suggests its ionization nature. Substituting Li with Na resulted in slight alterations in the Bader charges, as shown in Table 2. In the LiMgI3 structure, the average Bader charge on the I atoms was −0.816 e, while that in the NaMgI3 structure was −0.784 e. The variation observed in the charge distribution computed using Mulliken and Bader analyses likely stems from their differing methodologies. Bader analysis emphasizes the topological aspects of electron density, whereas Mulliken analysis relies on population analysis.| Compound | Species | Charge spilling (%) | Atom population | Mulliken charge (e) | Bader charge (e) | Bond | Bond population | Bond length (Å) | ||
|---|---|---|---|---|---|---|---|---|---|---|
| s | p | Total | ||||||||
| LiMgI3 | Li | 0.34 | 2.15 | 0.00 | 2.15 | +0.850 | +0.959 | I–Li | 0.04 | 4.095 |
| Mg | 0.67 | 6.81 | 7.48 | +0.520 | +1.488 | I–Mg | 0.10 | 2.896 | ||
| I | 1.88 | 5.58 | 7.46 | −0.460 | −0.816 | I–I | −1.84 | 4.095 | ||
| NaMgI3 | Na | 0.22 | 2.18 | 6.40 | 8.59 | +0.410 | +0.928 | I–Na | 0.04 | 4.103 |
| Mg | 0.73 | 6.86 | 7.58 | +0.420 | +1.424 | I–Mg | 0.02 | 2.901 | ||
| I | 1.74 | 5.53 | 7.28 | −0.280 | −0.784 | I–I | −1.50 | 4.103 | ||
Additionally, Table 2 provides data on the bond populations, population ionicity, and bond lengths for the Li–I, Mg–I, Na–I, and I–I bonds within the XMgI3 (X = Li/Na) perovskite structure. Positive and negative values signify bonding and antibonding states, respectively, with a higher positive bond population denoting increased covalency in the bond.58 For example, the lower positive bond population in Li/Na–I (associated with longer bond lengths) and Mg–I (associated with shorter bond lengths) in Table 2 suggests a high level of ionic character and insignificant covalent bonding in both compounds. Additionally, the negative bond population of I–I indicates the formation of antibonding interactions.
3.3 Electron localization function
The electron localization function (ELF) serves as a valuable tool for analyzing the electron distribution and localization during the formation of a crystalline structure.59 ELF quantifies the probability of finding electrons with identical spins and fixed positions within a reference electron field, offering insights into the electron localization within the lattice space and revealing the bonding characteristics in materials. Fig. 3 shows the 3D and 110 crystal dimension ELF maps for the XMgI3 compounds (X = Li/Na). The right side of the ELF maps illustrates the ELF scaling, including the coordination scaling, where regions with lower electron density are depicted in blue and that with higher electron density in red. The examination of the ELF maps for the XMgI3 compounds revealed a heightened degree of electron localization around the I ions, which is attributed to their significant electronegativity. This observation is consistent with the findings from the Mulliken population analysis and the Bader charge analysis.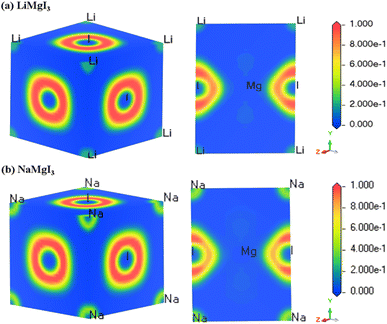 | ||
| Fig. 3 DFT-computed electron localization function (ELF) in the 3D and 110 crystal direction of (a) LiMgI3 and (b) NaMgI3 single perovskite compounds, respectively. | ||
3.4 Elastic constants and mechanical properties
The mechanical and structural stability of materials can be determined by measuring their elastic constant (Cij). These measurements indicate that materials deform under stress but return to their original shape once the stress is removed.60 Thus, to ensure the materials' mechanical stability, we calculated Cij using the finite strain theory, providing insights into their strength and response to external forces. In this investigation, we first performed elastic constant calculations, followed by determining the mechanical and structural stability parameters, as listed in Table 3. The mechanical properties of these materials include hardness, softness, compressibility, ductility, brittleness, and strength, which are vital for industrial applications. In cubical crystals, there are three independent elastic constants, C11, C12, and C44,61 which were calculated using the finite strain theory.62 According to the symmetry results, C11 = C22 = C33, C12 = C23 = C13, and C44 = C55 = C66.63 Alternatively, it is feasible to determine the Young's modulus (E), shear modulus (G), bulk modulus (B), anisotropy modulus (A), and Poisson's ratio (σ) using the elastic constants.64–66 In addition, the elastic constant is used to determine the mechanical stability of the compounds according to the Born stability criterion,67 where the crystal deformations in a compound depends on a specific criterion.68 In the case of the cubic phase, three independent elastic constants are required to fulfill the Born stability criterion, as given in eqn (3), to determine the stability of a compound:69| C11 > 0, C44 > 0, C11 − C12, C11 − 2C12 > 0 | (3) |
| Material property | LiMgI3 | NaMgI3 |
|---|---|---|
| C 11 (GPa) | 43.10 | 43.38 |
| C 12 (GPa) | 16.06 | 15.93 |
| C 44 (GPa) | 10.97 | 11.53 |
| Bulk modulus, B (GPa) | 25.08 | 25.08 |
| Shear modulus, G (GPa) | 11.93 | 12.36 |
| Young's modulus, E (GPa) | 30.88 | 31.85 |
| Poisson's ratio, σ | 0.29 | 0.29 |
| Pugh ratio, B/G | 2.10 | 2.03 |
| Cauchy pressure, CP (GPa) | 5.09 | 4.40 |
| Anisotropy factor (A) | 0.81 | 0.84 |
| Transverse sound velocity, vt (m s−1) | 1839.41 | 1843.22 |
| Longitudinal sound velocity, vl (m s−1) | 3409.56 | 3379.92 |
| Average sound velocity, vm (m s−1) | 2051.79 | 2053.93 |
| Debye temperature, θD (K) | 180.37 | 180.22 |
| Melting temperature, Tm (K) | 807.72 | 809.38 |
The elasticity of length and shape is related to the C11 and C12 constants, respectively. For a cubic structure, C11 must be considerably larger than C12.61 Interestingly, the estimated elastic constants for both the LiMgI3 and NaMgI3 compounds listed in Table 3 confirm they satisfy the Born stability criteria, indicating their mechanical stability. The Pugh ratio (B/G) and Cauchy pressure are useful parameters to assess a material's brittleness and ductility.60 In this case, a material is determined to be ductile when B/G is equal to or greater than 1.75, whereas when it is less than 1.75, the material is brittle.70 According to this study, the (B/G) ratios for LiMgI3(2.1) and NaMgI3(2.03) are higher than 1.75, suggesting that these materials exhibit ductile behavior, as shown in Table 3.
The Cauchy pressure for the cubic LiMgI3 and NaMgI3 determines their ductility and brittleness based on the negative and positive values of C12 − C44, as previously reported.71 A positive value indicates ductility, whereas a negative value suggests brittleness. In this study, the difference between C12 and C44 (Table 3) for both compounds are positive values, resulting in indicating ductility. Alternatively, the Voigt–Reuss–Hill (VRH) method is an approach used to calculate the B, G, E, and σ of the materials. The Voigt and Reuss methods are used to determine the bulk72 and shear73 moduli of materials, respectively, while Hill's64 method is used to calculate the average values of these properties. The Reuss bulk modulus (BR) and Voigt bulk modulus (BV) are given by eqn (4):
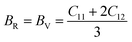 | (4) |
The shear modulus (GV) of a material according to Voigt72 is presented in eqn (5):
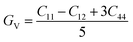 | (5) |
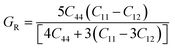 | (6) |
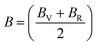 | (7) |
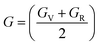 | (8) |
The values for B, G, and E are presented in Table 3. The B (25.08, 25.08), G (11.93, 12.36), and E (30.88, 31.85) of LiMgI3 and NaMgI3, respectively, indicate that both materials exhibit comparable resistance to changes in volume and shape.
Moreover, the observed E and σ listed in Table 3 can be calculated using the following expression, respectively:69
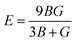 | (9) |
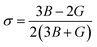 | (10) |
The resistance of a material, which is indicated by its stiffness, is quantified by E, where materials with high E values exhibit increased resistance. Therefore, as shown in Table 3, LiMgI3 and NaMgI3 exhibit identical and high E values, suggesting that they possess a significant level of stiffness. Alternatively, σ, which is limited to values between 0.25 and 0.50, determines the behavior of bond forces. A σ value greater than 0.26 indicates that the material is ductile, whereas a value less than 0.26 indicates that it is brittle.74 Hence, as indicated in Table 3, the bond force of the LiMgI3 and NaMgI3 compounds is close to the center of the above-mentioned range (0.29). As a result, both compounds exhibit a characteristic of ductility that agrees well with the results of the B/G ratio and Cauchy's pressure equation.
Moreover, the elastic anisotropy factor (A), which is used to determine the direction-dependent properties of a system, was computed by using eqn (11):69
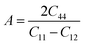 | (11) |
For isotropic compounds, A is ideally 1, indicating uniformity, whereas any deviation from 1 indicates the presence of anisotropy.75,76 As shown in Table 3, the computed anisotropy factors for both compounds deviated from unity (0.81 for LiMgI3 and 0.84 for NaMgI3), indicating the presence of anisotropy in these materials.
The calculation of G and B enables the determination of the transverse sound velocity, vt (eqn (12)), and longitudinal sound velocity, vl (eqn (13)), of XMgI3 (X = Li/Na) crystals, where ρ refers to the density of the investigated compounds as follows:77–80
 | (12) |
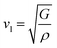 | (13) |
Moreover, utilizing eqn (10) and (11), eqn (12) allows the calculation of the mean sound velocity (vm), as follows:
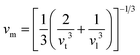 | (14) |
The Debye temperature (θD) is used to determine the thermal characteristics of a material including its melting temperature and thermal expansion. Employing eqn (14), θD of LiMgI3 and NaMgI3 can be obtained, as expressed in eqn (15):
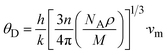 | (15) |
The calculated values (vt, vl, and vm) and θD for the LiMgI3 and NaMgI3 compounds are shown in Table 3. The calculated parameters for LiMgI3 and NaMgI3 compounds approximately show similar θD, making both compounds have similar thermal conductivity and melting temperature. The melting temperature (Tm) is a crucial parameter for determining the bond characteristics and thermal conductivity of XMgI3 (X = Li/Na). The melting temperatures of these cubic materials, as listed in Table 3, were calculated using eqn (16):81–83
| Tm = 553 + 5.91C11 | (16) |
As illustrated in Table 3, both LiMgI3 and NaMgI3 exhibit high and comparable melting temperatures (Tm), indicating their suitability for high-temperature optoelectronic applications. Thus, the high computed melting temperatures for these compounds imply their strong bonding characteristics and excellent thermal conductivity.
3.5 Electronic properties
In this section, we present the analysis of the energy dispersion and electronic states of the compounds, which determine their electronic properties. The electronic bandgap (Eg) of the materials was obtained through band structure analysis, while their partial density of states (PDOS) and total density of states (TDOS) were determined, which describe the distribution of electronics at different energy levels. The electronic properties of the XMgI3 (X = Li/Na) single perovskite materials were investigated using the CASTEP and WIEN2k codes. Fig. 4 and Table 1 demonstrate the narrow indirect band gaps of 1.174/1.176 eV, 1.181/1.185 eV, 2.474/2.556 eV, and 2.219/2.239 eV for LiMgI3/NaMgI3, which were calculated employing PBE-CASTEP, PBE-WIEN2k, mBJ-WIEN2k, and HSE06-QE, respectively. It is clear that the standard DFT PBE function consistently underestimated the electronic structure, particularly the band gap, in both CASTEP and WIEN2k, as shown in Fig. 4a and b, respectively. However, despite this underestimation, the results suggest that the proposed compounds exhibit sufficient stability, given that they yielded similar outcomes across different computational codes. Furthermore, the mBJ correlation function (Fig. 4c) accurately predicted the band gap, which correlates well with the experimental values. This suggests that LiMgI3 and NaMgI3 have a favorable band gap, which shows their potential for use as semiconductor materials in PV devices and other optoelectronic applications. Further examination was conducted to validate the prediction by the mBJ correlation function employing the alternative robust HSE06 hybrid functional (Fig. 4d), leading to the sustained accurate correlation with the mBJ prediction. The stability and reliability of both LiMgI3 and NaMgI3 are evident from the predictions by the mBJ and HSE06 correlation functions, suggesting their suitability for future empirical investigations.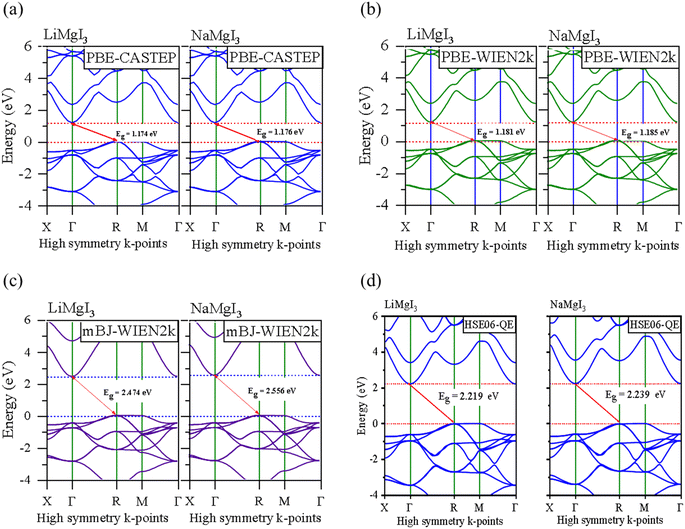 | ||
| Fig. 4 Band structures computed using (a) GGA-PBE-CASTEP, (b) GGA-PBE-WIEN2k, (c) mBJ-WIEN2k, and (d) HSE06-QE for LiMgI3 and NaMgI3, respectively. The Fermi level is set to zero. | ||
Fig. 4a–d show that both the conduction band minimum (CBM) and valence band maximum (VBM) of the LiMgI3 and NaMgI3 compounds are located at Γ and R, respectively, in the first Brillion zone, which agrees with the previous finding.84 The s-block VB metals are flat between the R and M points, suggesting the presence of heavy holes, whereas the p-block metals have a greater dispersed CB at the Γ-point.85
Fig. 5 and 6 show the analysis of the partial density of states (PDOS) and total partial density of states (TDOS) of the LiMgI3 and NaMgI3 compounds, respectively. In these figures, the TDOS and PDOS were analyzed to identify their effects on the VB to CB electronic characteristics. Fig. 5a illustrates the dominance of the Li p-state in the VB due to its high intensity near to the Fermi level. The proximity of the peak intensity to the Fermi level is crucial for electron transitions from the VB to the CB. Therefore, the Li p-state is the dominant peak in the electron transfer from VB to CB. In the case of the Mg atom, the p-state contributes to the VB, while the s-state contributes to the CB, as depicted in Fig. 5b. Moreover, Fig. 5c clearly shows that the prominent peak near the Fermi level within the VB primarily originates from the I p-state. In summary, the TDOS in Fig. 5d shows that the VB is mainly contributed by the p-states of Li, Mg, and I, while the s-states of Li and Mg contribute to the CB with a smaller contribution from the I p-states in the LiMgI3 compound.
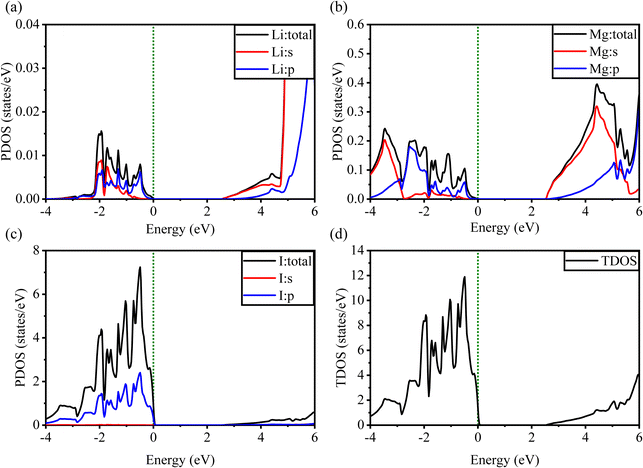 | ||
| Fig. 5 Calculated PDOS of individual atoms in LiMgI3 including (a) Li, (b) Mg, and (c) I and (d) TDOS of the LiMgI3 perovskite compound. | ||
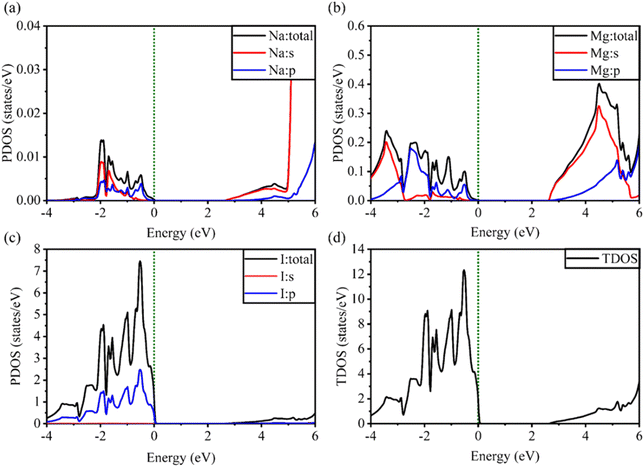 | ||
| Fig. 6 Calculated PDOS of individual atoms in the NaMgI3 compound including (a) Na, (b) Mg, and (c) I and (d) TDOS of the NaMgI3 perovskite structure. | ||
Notably, when replacing the Li atom with Na, similar trends were observed, as depicted in Fig. 6. These similarities arise from the shared properties of Li and Na as elements within the same family. Our investigation is supported by the previous reports on similar families.20,86
3.6 Optical properties
Details on the optical properties of perovskite compounds can be obtained by calculating various parameters, including the dielectric constant, absorption coefficient, extinction coefficient, refractive index, reflectance, transmission, and loss function. The expression for the complex dielectric function, ε(ω), with respect to angular frequency is provided as follows:77–80| ε(ω) = ε1(ω) + iε2(ω) | (17) |
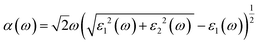 | (18) |
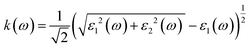 | (19) |
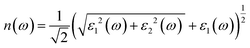 | (20) |
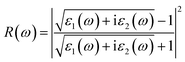 | (21) |
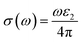 | (22) |
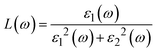 | (23) |
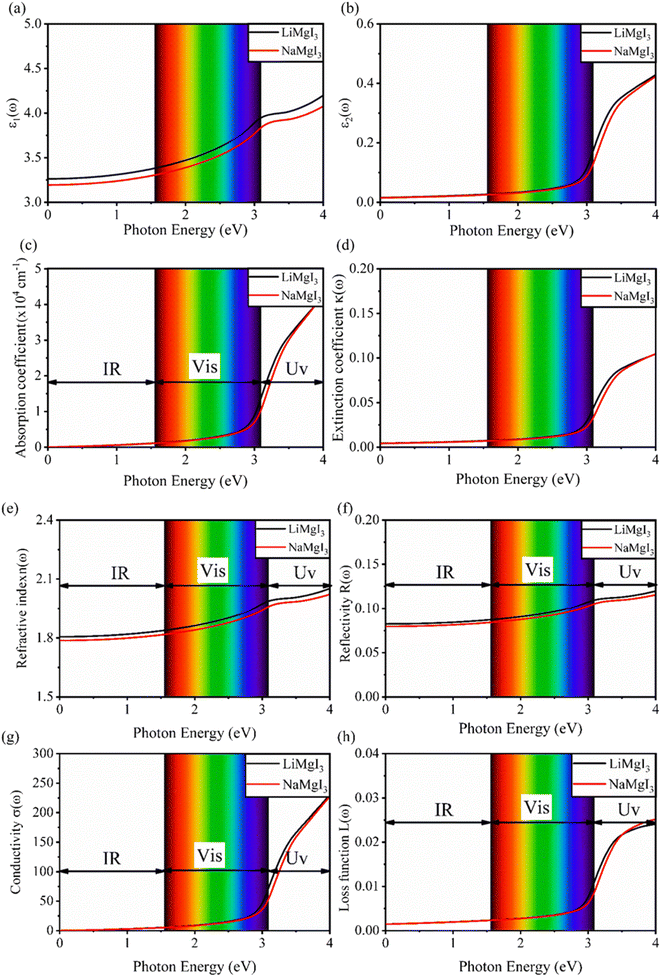
Fig. 7 shows the optical properties of the investigated LiMgI3 and NaMgI3 compounds. Based on the photon radiation on the surface of the compounds, the dielectric function determines their optical properties. Fig. 7a and b show the dielectric functions of the real and imaginary parts of XMgI3 (X = Li/Na), respectively. As shown in Fig. 7a, according to the static frequency of ε1(0), the real dielectric constant is 3.26 for LiMgI3 and 3.19 for NaMgI3. The ε1(ω) of LiMgI3 and NaMgI3 reached the maximum peak intensities of 3.96 and 3.86 at the 3.10 eV edge of the visible light region, respectively. However, as shown in Fig. 7b, LiMgI3 and NaMgI3 revealed 0 eV at ε2(0), indicating the absence of dissipated energy. The imaginary part of a dielectric material, ε2(ω), increases until energy dissipation occurs in the photon energy absorption region. Thus, the imaginary parts of a dielectric material reflect the behavior of its absorption coefficient.
Fig. 7c shows the absorption coefficient of the cubic structure of LiMgI3 and NaMgI3. In Fig. 7c, it is evident that both the LiMgI3 and NaMgI3 compounds initiate photon absorption at 1.3 eV and display a wide absorption peak spanning the infrared (IR) to ultraviolet (UV) region. Therefore, the proposed materials are highly suitable as novel lead-free halide perovskite materials for solar energy harvesting applications. The extinction coefficient demonstrates how the light intensity attenuated on the investigated compounds, LiMgI3 and NaMgI3, as displayed in Fig. 7d, where both compounds exhibit similar behavior. Thus, the light-absorbing properties of both compounds are similar and consistent with the discussion in Fig. 7c.
Fig. 7e shows the evaluation of the optical characteristics of the refractive index, which explains the bending or refracting behavior of light in a medium. The static refractive indices of LiMgI3 and NaMgI3 were determined to be 1.81 and 1.78, respectively. This suggests that the square of the refractive index (n(ω))2 corresponds to ε1(ω) at a static frequency, as represented in Fig. 7a. Additionally, both compounds reached their maximum at the edge of higher energy of visible light (3.1 eV). The detection of the refractive index peaks within the low-energy segment of the spectrum is a crucial aspect, especially in the visible region, providing valuable insights for applications in optoelectronic devices. Thus, examining the reflectivity of perovskites offers insights into their surface attributes. Fig. 7f illustrates the reflectance spectra of the LiMgI3 and NaMgI3 perovskite compounds as a function of photon energy. Both compounds consistently demonstrate low reflectivity (less than 0.10) across the infrared to visible region spectrum, which is negligible. Remarkably, their reflectivity remains consistently low in the visible to infrared range, making these materials well-suited for solar cell applications.
Fig. 7g shows how electromagnetic (EM) radiation induces optical excitation in the compounds, displaying the conductivity σ(ω) of XMgI3 (X = Li and Na). In the case of LiMgI3 and NaMgI3, their σ(ω) remains zero in the photon energy range of 0 eV to 0.98 eV due to the absence of optical excitation, indicating the absence of interaction between incident EM radiation and the electrons in these materials in this energy range. As LiMgI3 and NaMgI3 absorb energy, their electrons shift from the VB to the CB. The consistency of their spectra with the absorption coefficient analysis (Fig. 7c) suggests that absorbing light within the visible part of the electromagnetic spectrum is particularly beneficial for solar cell applications. Another significant consideration involves measuring the energy loss function, denoted as L(ω), which accounts for inter-band, intra-band, and plasmonic interactions. Additionally, the optical loss serves as an indicator of energy dissipation through scattering, dispersion, and thermal effects, as depicted in Fig. 7h. Fascinatingly, for both LiMgI3 and NaMgI3, their optical loss in the visible region (1.55–3.10 eV) is nearly insignificant compared to that in the ultraviolet region (3.10–4.0 eV), confirming the suitability of these materials to realize an excellent optoelectronic performance within the visible range of the electromagnetic spectrum.
4. Conclusion
This investigation explored the structural, electronic, optical, and mechanical attributes of cubic XMgI3 (X = Li/Na) through first-principle calculations by employing CASTEP and the GGA-PBE exchange-correlation function. Our examination of the elastic constants and mechanical properties indicated the notable stability and ductile nature of each perovskite material. Additionally, we investigated the electron charge distribution using Mulliken atomic population analysis and the electron localization function. The developed compounds exhibited advantageous indirect narrow band gaps (2.474 eV for LiMgI3 and 2.556 eV for NaMgI3) and a broad-spectrum absorption coefficient using the mBJ correlation function in WIEN2k. Based on our findings, especially the band gap and optical properties, these alkali-based halide perovskite materials are suitable for several applications, such as photovoltaics, photocatalysts, and optoelectronic devices. DFT analysis suggested their highly favorable band gap for photovoltaic applications. Consequently, further efforts are required for the synthesis and exploration of these alkali-based halide perovskite materials for realistic applications and future advancements.Data availability
This manuscript has associated data in a data repository. The raw/processed data can be made available with a reasonable request to the corresponding author.Author contributions
Kefyalew Wagari Guji: conceptualization, methodology, writing-original draft preparation writing-reviewing and editing. Tesfaye Abebe Geleta: conceptualization, methodology, software, writing-reviewing and editing, supervising. Nabil Bouri: methodology, software, writing-reviewing and editing. Victor José Ramirez Rivera: methodology, conceptualization, software, writing-reviewing.Conflicts of interest
The authors declare that they have no known competing financial interests.References
- K. Dedecker and G. Grancini, Adv. Energy Mater., 2020, 10(31), 2001471 CrossRef CAS.
- I. Hamideddine, H. Jebari, N. Tahiri, O. El Bounagui and H. Ez-Zahraouy, Int. J. Energy Res., 2022, 46(14), 20755–20765 CrossRef CAS.
- T. A. Geleta and T. Imae, ACS Appl. Nano Mater., 2021, 4(1), 236–249 CrossRef CAS.
- F. Perera, Int. J. Environ. Res. Public Health, 2018, 15(1), 16 CrossRef PubMed.
- S. Bouhmaidi, A. Marjaoui, A. Talbi, M. Zanouni, K. Nouneh and L. Setti, Comput. Condens. Matter, 2022, 31, e00663 CrossRef.
- H. I. Eya and N. Y. Dzade, ACS Appl. Energy Mater., 2023, 5729–5738 CrossRef CAS.
- T. A. Geleta and T. Imae, Bull. Chem. Soc. Jpn., 2020, 93, 611 CrossRef CAS.
- S. Körbel, M. A. Marques and S. Botti, J. Mater. Chem. C, 2016, 4(15), 3157–3167 RSC.
- I. Hamideddine, H. Zitouni, N. Tahiri, O. El Bounagui and H. Ez-Zahraouy, Appl. Phys. A, 2021, 127, 1–7 CrossRef.
- T. A. Geleta, D. Behera, R. Sharma, M. m. Al-Anazy, E. S. Yousef, V. Srivastava and A. J. A. Moayad, RSC Adv., 2024, 14(6), 4165–4178 RSC.
- Q. A. Akkerman, M. Gandini, F. Di Stasio, P. Rastogi, F. Palazon, G. Bertoni, J. M. Ball, M. Prato, A. Petrozza and L. Manna, Nat. Energy, 2016, 2(2), 1–7 CrossRef.
- G. E. Eperon, G. M. Paternò, R. J. Sutton, A. Zampetti, A. A. Haghighirad, F. Cacialli and H. J. Snaith, J. Mater. Chem. A, 2015, 3(39), 19688–19695 RSC.
- P. Ramasamy, D.-H. Lim, B. Kim, S.-H. Lee, M.-S. Lee and J.-S. Lee, Chem. Commun., 2016, 52(10), 2067–2070 RSC.
- J.-H. Im, C.-R. Lee, J.-W. Lee, S.-W. Park and N.-G. Park, Nanoscale, 2011, 3(10), 4088–4093 RSC.
- E. Mosconi, P. Umari and F. De Angelis, Phys. Chem. Chem. Phys., 2016, 18(39), 27158–27164 RSC.
- Q. Mahmood, U.-e. Hani, T. I. Al-Muhimeed, A. A. AlObaid, B. U. Haq, G. Murtaza, T. H. Flemban and H. Althib, J. Phys. Chem. Solids, 2021, 155, 110117 CrossRef CAS.
- D. Ray, C. Clark, H. Q. Pham, J. Borycz, R. J. Holmes, E. S. Aydil and L. Gagliardi, J. Phys. Chem. C, 2018, 122(14), 7838–7848 CrossRef CAS.
- S. Mitro, M. Saiduzzaman, A. Biswas, A. Sultana and K. M. Hossain, Mater. Today Commun., 2022, 31, 103532 CrossRef CAS.
- S. Mitro, M. Saiduzzaman, T. I. Asif and K. M. Hossain, J. Mater. Sci.: Mater. Electron., 2022, 33(17), 13860–13875 CrossRef CAS.
- D. Behera, B. Akila, S. K. Mukherjee, T. A. Geleta, A. Shaker and M. M. Salah, Crystals, 2023, 13(10), 1437 CAS.
- M. M. Namisi, R. J. Musembi, W. M. Mulwa and B. O. Aduda, Comput. Condens. Matter, 2023, 34, e00772 Search PubMed.
- L.-C. Tang, Y.-C. Chang, J.-Y. Huang, M.-H. Lee and C.-S. Chang, Jpn. J. Appl. Phys., 2009, 48(11R), 112402 CrossRef.
- S. Idrissi, S. Ziti, H. Labrim and L. Bahmad, Mater. Sci. Semicond. Process., 2021, 122, 105484 CrossRef CAS.
- M. Husain, N. Rahman, N. Sfina, N. H. Al-Shaalan, S. Alharthi, S. A. Alharthy, M. A. Amin, V. Tirth, R. Khan and M. Sohail, Opt. Quantum Electron., 2023, 55(10), 920 CrossRef CAS.
- Z. Khan, S. N. Khan, M. Husain, N. Rahman, V. Tirth, M. Elhadi, A. Azzouz-Rached, W. Ullah, M. Uzair and S. Al-Qaisi, Opt. Quantum Electron., 2024, 56(5), 836 CrossRef CAS.
- A. Jehan, M. Husain, V. Tirth, A. Algahtani, M. Uzair, N. Rahman, A. Khan and S. N. Khan, RSC Adv., 2023, 13(41), 28395–28406 RSC.
- R. Sharma, A. Dey, S. A. Dar and V. Srivastava, Comput. Theor. Chem., 2021, 1204, 113415 CrossRef CAS.
- Y. Nassah, A. Benmakhlouf, L. Hadjeris, T. Helaimia, R. Khenata, A. Bouhemadou, S. Bin Omran, R. Sharma, S. Goumri Said and V. Srivastava, Bull. Mater. Sci., 2023, 46(2), 55 CrossRef CAS.
- M. Caid, D. Rached, S. Al-Qaisi, Y. Rached and H. Rached, Solid State Commun., 2023, 369, 115216 CrossRef CAS.
- M. Caid, D. Rached, H. Rached and Y. Rached, J. Mol. Model., 2024, 30(3), 59 CrossRef CAS PubMed.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr. Cryst. Mater., 2005, 220(5–6), 567–570 CrossRef CAS.
- M. D. Segall, P. J. D. Lindan, M. J. a. Probert, C. J. Pickard, P. J. Hasnip, S. J. Clark and M. C. Payne, J. Phys.: Condens. Matter, 2002, 14(11), 2717 CrossRef CAS.
- I. Zeba, M. Ramzan, R. Ahmad, M. Shakil, M. Rizwan, M. Rafique, M. Sarfraz, M. Ajmal and S. S. A. Gillani, Solid State Commun., 2020, 313, 113907 CrossRef CAS.
- X. Liu and J. Fu, Vacuum, 2020, 179, 109504 CrossRef CAS.
- H. Chen, X. Li, R. Wan, S. Kao-Walter and Y. Lei, Chem. Phys., 2018, 501, 60–67 CrossRef CAS.
- R. J. Meier, J. Mol. Struct.: THEOCHEM, 1999, 467(1), 79–83 CrossRef CAS.
- P. Wisesa, K. A. McGill and T. Mueller, Phys. Rev. B, 2016, 93(15), 155109 CrossRef.
- P. Blaha, K. Schwarz, G. K. H. Madsen, D. Kvasnicka and J. Luitz, An Augmented Plane Wave+ Local Orbitals Program for Calculating Crystal Properties, 2001, 60(1) Search PubMed.
- K. Schwarz and P. Blaha, Comput. Mater. Sci., 2003, 28(2), 259–273 CrossRef CAS.
- M. A. Amin, G. Nazir, Q. Mahmood, J. Alzahrani, N. A. Kattan, A. Mera, H. Mirza, A. Mezni, M. S. Refat and A. A. Gobouri, J. Mater. Res. Technol., 2022, 18, 4403–4412 CrossRef CAS.
- M. A. Ali, A. A. Alothman, M. Mushab, A. Khan and M. Faizan, J. Inorg. Organomet. Polym., 2023, 33(11), 3402–3412 CrossRef CAS.
- U. Shahzadi, D. Yang, K. Fatima and F. Wang, J. Phys. Chem. A, 2024, 1173–1180 CrossRef CAS PubMed.
- N. S. Kaleemullah, M. S. Hussain, V. Ashwin, G. Ajay and M. M. S. Sirajuddeen, Chem. Phys. Impact, 2024, 100545 CrossRef.
- W. Rahim, A. Cheng, C. Lyu, T. Shi, Z. Wang, D. O. Scanlon and R. G. Palgrave, Chem. Mater., 2020, 32(22), 9573–9583 CrossRef CAS.
- M. Talebi and A. Mokhtari, arXiv, 2023, preprint, arXiv:230212494, DOI:10.48550/arXiv.2302.12494.
- W. Travis, E. Glover, H. Bronstein, D. Scanlon and R. Palgrave, Chem. Sci., 2016, 7(7), 4548–4556 RSC.
- H. Tanaka, T. Oku and N. Ueoka, Jpn. J. Appl. Phys., 2018, 57(8S3), 08RE12 CrossRef.
- M. A. Rahman, F. Mostari, M. Z. Hasan, A. Irfan, M. F. Rahman, M. J. Hosain, S. C. Mouna, I. A. Chowdhury, M. Rasheduzzaman and M. S. H. Choudhury, Phys. B, 2023, 669, 415260 CrossRef CAS.
- H. Louis, C. A. Anyama, U. G. Chukwu, A. A. Ayi and A. S. Adeyinka, Results Opt., 2023, 13, 100506 CrossRef.
- J. K. Rony, M. Islam, M. Saiduzzaman, K. M. Hossain, S. Alam, A. Biswas, M. H. Mia, S. Ahmad and S. K. Mitro, J. Mater. Res. Technol., 2024, 29, 897–909 CrossRef CAS.
- N. Xu, Y. Chen, S. Chen, S. Li and W. Zhang, Int. J. Hydrogen Energy, 2024, 50, 114–122 CrossRef CAS.
- R. Padmavathy, A. Amudhavalli, M. Manikandan, R. Rajeswarapalanichamy, K. Iyakutti and A. K. Kushwaha, J. Electron. Mater., 2019, 48, 1243–1251 CrossRef CAS.
- L.-y. Huang and W. R. L. Lambrecht, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90(19), 195201 CrossRef.
- R. S. Mulliken, J. Chem. Phys., 1955, 23(10), 1833–1840 CrossRef CAS.
- M. Segall, R. Shah, C. J. Pickard and M. Payne, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(23), 16317 CrossRef CAS PubMed.
- T. Watcharatharapong, M. Minakshi Sundaram, S. Chakraborty, D. Li, G. M. Shafiullah, R. D. Aughterson and R. Ahuja, ACS Appl. Mater. Interfaces, 2017, 9(21), 17977–17991 CrossRef CAS PubMed.
- W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21(8), 084204 CrossRef CAS PubMed.
- F. M. Hossain, B. Z. Dlugogorski, E. M. Kennedy, I. V. Belova and G. E. Murch, Solid State Commun., 2010, 150(17–18), 848–851 CrossRef CAS.
- K. Artmann, Z. Naturforsch. A, 1946, 1(8), 426–432 CrossRef CAS.
- M. Khan, M. Z. Rahaman and M. L. Ali, ACS Omega, 2023, 8(28), 24942–24951 CrossRef CAS PubMed.
- M. Jamal, S. J. Asadabadi, I. Ahmad and H. R. Aliabad, Comput. Mater. Sci., 2014, 95, 592–599 CrossRef CAS.
- F. D. Murnaghan, Am. J. Math., 1937, 59(2), 235–260 CrossRef.
- R. Majumder, S. K. Mitro and B. Bairagi, J. Alloys Compd., 2020, 836, 155395 CrossRef CAS.
- R. Hill, Proc. Phys. Soc., London, Sect. A, 1952, 65(5), 349 CrossRef.
- X. Tao, J. Yang, L. Xi and Y. Ouyang, J. Solid State Chem., 2012, 194, 179–187 CrossRef CAS.
- P. Mao, B. Yu, Z. Liu, F. Wang and Y. Ju, J. Appl. Phys., 2015, 117(11), 115903 CrossRef.
- F. Mouhat and F.-X. Coudert, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90(22), 224104 CrossRef.
- On the stability of crystal lattices. I, Mathematical Proceedings of the Cambridge Philosophical Society, ed. M. Born, Cambridge University Press, 1940 Search PubMed.
- S. A. Dar, S. A. Khandy, I. Islam, D. C. Gupta, U. K. Sakalle, V. Srivastava and K. Parrey, Chin. J. Phys., 2017, 55(5), 1769–1779 CrossRef CAS.
- S. Pugh, London, Edinburgh Dublin Philos. Mag. J. Sci., 1954, 45(367), 823–843 CrossRef CAS.
- M. I. Kholil and M. T. H. Bhuiyan, J. Phys. Chem. Solids, 2021, 154, 110083 CrossRef CAS.
- Q.-J. Liu, H. Qin, Z. Jiao, F.-S. Liu and Z.-T. Liu, Mater. Chem. Phys., 2016, 180, 75–81 CrossRef CAS.
- S. Kuma and M. M. Woldemariam, Adv. Condens. Matter Phys., 2019, 2019, 1–12 CrossRef.
- E. D. Bauer, F. Ronning, B. L. Scott and J. D. Thompson, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78(17), 172504 CrossRef.
- H. Y. Wu, Y. H. Chen, C. R. Deng, X. Y. Han and Z. J. Liu, J. Solid State Chem., 2015, 231, 1–6 CrossRef CAS.
- Q. Fu, L. Si, J. Liu, H. Shi and Y. Li, Appl. Opt., 2022, 61(21), 6330–6338 CrossRef CAS PubMed.
- A. Settouf, H. Rached, N. Benkhettou and D. Rached, Comput. Condens. Matter, 2019, 19, e00377 CrossRef.
- A. Benslimane, S. Kouidri, H. Rached, M. El Keurti, S. Meliani and M. Ould Moussa, Indian J. Phys., 2024, 98(3), 955–966 CrossRef CAS.
- S. Meliani, S. Kouidri, H. Rached, M. El Keurti, M. Ould Moussa and A. Ben Slimane, Solid State Commun., 2022, 357, 114973 CrossRef CAS.
- T. A. Geleta, D. Behera, N. Bouri, V. J. R. Rivera and F. M. Gonzalo, J. Comput. Chem., 2024, 1 Search PubMed.
- Y. Shen, D. R. Clarke and P. A. Fuierer, Appl. Phys. Lett., 2008, 93(10), 102907 CrossRef.
- G. Ajay, V. Ashwin, M. M. S. Sirajuddeen and A. Alam, Phys. B, 2024, 682, 415858 CrossRef.
- M. Rahman, M. R. U. Akhand, M. M. Ali, P. Barman, M. F. Rahman, M. Rasheduzzaman, M. M. Hossen, M. S. H. Choudhury, S. Nasrin and M. Z. Hasan, Phys. B, 2024, 685, 415997 CrossRef CAS.
- M. R. Filip and F. Giustino, J. Phys. Chem. C, 2016, 120(1), 166–173 CAS.
- D. Ray, C. Clark, H. Q. Pham, J. Borycz, R. J. Holmes, E. S. Aydil and L. Gagliardi, J. Phys. Chem. C, 2018, 122(14), 7838–7848 CrossRef CAS.
- D. Behera, T. A. Geleta, I. Allaoui, M. Khuili, S. K. Mukherjee, B. Akila and S. Al-Qaisi, Eur. Phys. J. Plus, 2024, 139(2), 127 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2024 |