Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Fluorite-based proton conducting oxides: structures, materials and applications
Pan
Xiang†
a,
Sara Adeeba
Ismail†
a,
Shihang
Guo
a,
Lulu
Jiang
a and
Donglin
Han
 *abc
*abc
aCollege of Energy, Soochow University, No 1 Shizi Street, Gusu District, Suzhou 215006, China. E-mail: dlhan@suda.edu.cn
bProvincial Key Laboratory for Advanced Carbon Materials and Wearable Energy Technologies, Soochow University, No 1 Shizi Street, Gusu District, Suzhou 215006, China
cLight Industry Institute of Electrochemical Power Sources, Shahu Science & Technology Innovation Park, Suzhou 215638, China
First published on 8th September 2023
Abstract
Proton conducting oxides have promising potential for application in solid-state electrochemical devices and have seen significant progress in recent years. At present, perovskite-type proton conductors (e.g., Y-doped Ba(Zr, Ce)O3) attract much attention. However, in fact, those with a fluorite-based structure constitute another interesting category, including doped zirconia and ceria with a fluorite structure, and lanthanide zirconates, stannates, and titanates with a pyrochlore structure. In this work, we focus on the volume transport of protons in fluorite and pyrochlore oxides, summarize the progress on the development of materials and their applications, and discuss the present problems and challenges ahead.
 Pan Xiang | Pan Xiang is currently an undergraduate student at the College of Energy, Soochow University under the supervision of Prof. Donglin Han. His research interest is proton conducting oxides. |
1. Introduction
Proton conducting oxide ceramics are attracting increasing attention due to their promising applications as electrolyte materials in fuel cells,1 electrolysis cells,2 hydrogen sensors,3 hydrogen pumps,4 hydrogen permeation membranes,5 and membrane reactors.6 The most successful proton conducting oxide ceramics have an ABO3 perovskite structure, including acceptor-doped BaZrO3, BaCeO3 and Ba(Zr, Ce)O3 solid solutions,7–9 which contain oxygen vacancies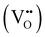 favoring hydration reactions to introduce protons:
favoring hydration reactions to introduce protons: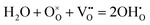 | (1) |
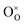 is the Kröger–Vink notation for oxide ions, and
is the Kröger–Vink notation for oxide ions, and 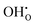 represents protons, which are associated with oxide ions. Protons rotate around and hop between lattice oxide ions to facilitate proton conduction, which is commonly known as the Grotthuss mechanism.
represents protons, which are associated with oxide ions. Protons rotate around and hop between lattice oxide ions to facilitate proton conduction, which is commonly known as the Grotthuss mechanism.
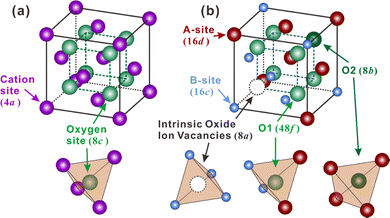
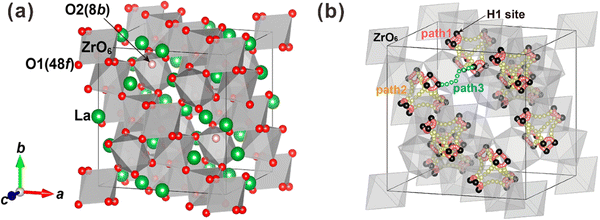
Besides, some other oxides with crystal structures of fluorite and pyrochlore, which can be regarded as an ordered fluorite structure, are also known to demonstrate proton conduction. As shown in Fig. 1(a), in the fluorite structure taking an AO2 formula, cations occupy the corners and face centers (Wyckoff 4a site) of the unit cell, and oxide ions occupy the center of the tetrahedrons (8c site) composing four cations. All the cations and oxide ions (also oxygen vacancies) are randomly distributed. The pyrochlore structure, which takes an A2B2O7 formula, is derived from the fluorite structure with both the cations and oxide ions arranged in order. A unit cell of the pyrochlore structure is composed of eight octants, one of which is shown in Fig. 1(b) to facilitate the explanation. Large cations occupy the A-site (16d), and small cations occupy the B-site (16c). Besides the intrinsic oxygen vacancies (8a site), there are two types of oxide ion sites; one is the 48f site in the center of tetrahedrons composed of two A and two B cations – named the O1 site hereafter – another is the 8b site in the center of tetrahedrons containing four A cations – named the O2 site hereafter.
The stability of the A2B2O7 pyrochlore structure depends on the size of the A and B cations. A study from Minervini et al. using energy-minimization-based atomistic simulation calculations revealed that the ordering of the pyrochlore structure was enhanced with the increasing size of the A-site cations and decreasing size of the B-site cations.10 Subramanian et al. reported a relationship between the structural ordering and the radius ratio of rA3+/rB4+,11 and suggested a stable range of 1.46 < rA3+/rB4+ < 1.8 for the pyrochlore structure.12 Blanchard et al.13 and Yamamura et al.14 conducted a combined study using X-ray absorption near edge structure (XANES) and X-ray diffraction (XRD) techniques to study the structure of Ln2Zr2O7 (Ln = lanthanide elements), leading to the finding that when the Ln3+ cation is larger than Gd3+, the samples take the pyrochlore structure, and when Ln3+ is smaller than Gd3+, the fluorite structure is stable.13 Moreover, a higher temperature appears to favor the structural disordering. Moriga et al. observed that Gd2Zr2O7 had a pyrochlore structure between 1400 and 1900 °C, and a fluorite structure at higher temperature.15 Nd2Zr2O7 and Sm2Zr2O7 undergo a phase transition from pyrochlore to fluorite at 2000 and 1530 °C, respectively.16
This review mainly focuses on the fluorite and pyrochlore-type proton conducting oxides attracting most of the interest, including acceptor-doped ZrO2, CeO2, La2Ce2O7, and La2Zr2O7. The progress of some other materials of lanthanide ziconates, stannates and titanates, and La2(Nb1−xMx)2O7−δ (M = Y, Yb) – a recently discovered new proton conductor – was also summarized. Although nanocrystalline or porous ZrO2 and CeO2 are also known for their surface proton conduction at low temperature, detailed information can be found in a recent review paper,17 and only the volume transport is discussed in this review paper.
2. Fluorite oxides
2.1 ZrO2
Zirconia (ZrO2) partly substituted by acceptor dopants is currently the most successful oxide ion-conducting electrolyte in high temperature solid-state electrochemical devices, such as solid oxide fuel cells (SOFCs).18,19 Pure ZrO2 has a monoclinic structure between room temperature and 1170 °C, and becomes tetragonal between 1170 and 2370 °C. The cubic fluorite phase ZrO2 exists between 2370 °C and the melting point (2830 °C).20 Besides, pure ZrO2 has no oxygen vacancy, asking for doping with lower valence elements to form oxygen vacancies and generate oxide ion conduction. Moreover, the temperature range for the cubic fluorite phase can be lowered by using appropriate doping strategies.21 By doping 8–17 mol% Sc2O3, the temperature to form the cubic fluorite phase can be lowered to 1000 °C.22 When Y (10–20 mol% Y2O3),23 Gd (14–20 mol% Gd2O3)24 and Sm (9–19 mol% Sm2O3)25 are doped, the cubic fluorite phase can be stable even at room temperature.Y-doped ZrO2 – commonly known as yttria-stabilized zirconia (YSZ) – is the most widely used composition of doped ZrO2, due to its excellent chemical stability and high oxide ion conductivity.26–28 Replacing tetravalent Zr cations with trivalent Y cations results in the formation of oxygen vacancies following eqn (2) to preserve the electroneutrality:
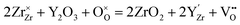 | (2) |
In addition, the solubility of protons in the intra-grain (bulk) and inter-grain (grain boundary) of YSZ appears to be different. The proton concentration of 8YSZ (8YSZ-poly) is higher than that of 8YSZ-SC under the same test conditions. After annealing at 600 °C under pH2O = 0.017 atm and at 950 °C under pH2O = 0.066 atm, the proton concentrations of 8YSZ-poly are 9.1 × 10−7 and 2.3 × 10−6 mol cm−3, respectively, higher than those of the grain boundary-free single crystal 8YSZ (8YSZ-SC), implying that the proton concentration at the grain boundary of YSZ is higher than that in the bulk.
Dawson et al. investigated the crystal structure of YSZ and its potential as a proton-conducting material using combined classical and quantum mechanical computational techniques.40,41 The redox stability of proton conductors is crucial as they must remain stable under both the oxidizing and reducing conditions. The reduction reaction involves the formation of oxygen vacancies which are compensated by electrons:
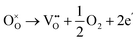 | (3) |
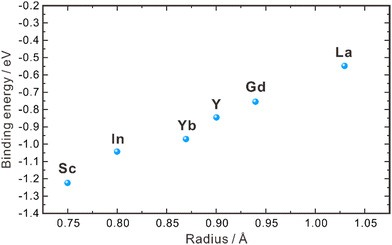 | ||
| Fig. 2 Binding energies between dopants with different ionic radii and protons in the grain interior of ZrO2.40 | ||
As aforementioned, the proton concentration of doped ZrO2 is very low, in comparison with the concentration of oxygen vacancies. For example, the concentration of oxygen vacancies in 8YSZ is about 1.03 × 10−4 mol cm−3, but its proton concentration reported in the literature varies within 10−6–10−8 mol cm−3,30,31,35,36 indicating that only a very limited amount of oxygen vacancies participates in the hydration reaction. Empirically, oxides with higher basicity favor the hydration reaction, facilitating the introduction of protons. However, ZrO2 exhibits weak basicity,43 resulting in only a small portion of oxygen vacancies participating in the hydration reaction. Furthermore, Bjørheim et al. discovered that among oxides with the same structure, the material with lower ionization potential (the difference between the valence band (VB) maximum and the vacuum level) exhibits a more negative hydration enthalpy.42,44 In the case of ZrO2, its ionization potential is approximately 6.86 eV,45 indicating that the hydration reaction does not occur easily. This low proton concentration thereby leads to low proton conductivity. In 2004, Nigara et al. used the gas permeation method to measure the proton conductivity of 10 mol% Y2O3-doped ZrO2 single crystal at 777–1527 °C, which was 1.5 × 10−8–2.4 × 10−6 S cm−1, far lower than the oxide ion conductivity.46 Based on the results of both experimental investigations and theoretical calculations, it is clear that the proton concentration in the ZrO2 system is low and the activation energy of proton diffusion is high. As a result, the bulk conductivity of protons is too low to give a significant contribution to the performance of the electrochemical devices using the ZrO2-based electrolytes.
2.2 CeO2
Ceria (CeO2) has high thermal stability, and only undergoes phase transition to an orthorhombic α-PbCl2 type structure (Pnma) under high pressure (e.g., 31 GPa).47,48 Doping low valence elements makes CeO2 show high oxide ion conductivity, leading to the application of doped CeO2 as an electrolyte for intermediate temperature solid oxide fuel cells (IT-SOFC).22,49,50 Sm3+ was found to be one of the most effective dopants for CeO2, and the conductivity of Ce0.8Sm0.2O2−δ is as high as 1.0 × 10−2 S cm−1 at 500 °C.51,52 Besides, some other dopants also impart CeO2 with considerably high oxide ion conductivity at an intermediate temperature. For example, the conductivities of Ce0.85Gd0.15O2−δ and Ce0.95La0.05O2−δ at 500 °C are 3.0 × 10−3 and 4.2 × 10−3 S cm−1, respectively.53,54 In 1999, Doshi et al. fabricated a fuel cell with a 30 μm-thick Gd0.2Ce0.8O2−δ electrolyte using a multilayer belt casting technique, showing Pmax of 140 mW cm−2 at 450 °C.55 Later, Ai et al. reported a fuel cell with a 15 μm-thick Sm0.2Ce0.8O2−δ electrolyte deposited by a spin coating method, showing Pmax of 103 mW cm−2 at 450 °C.56The ionic conductivity in CeO2 correlates with the oxygen vacancies, which are introduced by doping low valence elements. For example, the reaction of doping trivalent Sm is given as:
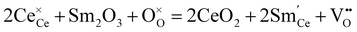 | (4) |
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) ) phase forms.57,58,60,61 The C-type structure can be described as a cubic fluorite superstructure resulted from the ordering of vacancies in the anion sub-lattice, and is commonly seen for rare earth oxides. This structure is also known as a double fluorite structure, and the lattice constant is twice as large as that of a simple fluorite one.8,16
) phase forms.57,58,60,61 The C-type structure can be described as a cubic fluorite superstructure resulted from the ordering of vacancies in the anion sub-lattice, and is commonly seen for rare earth oxides. This structure is also known as a double fluorite structure, and the lattice constant is twice as large as that of a simple fluorite one.8,16
CeO2 allows higher acceptor solubility, leading to the presence of a significant number of oxygen vacancies. Nevertheless, the high stability of these vacancies makes it challenging to hydrate and introduce protons, resulting in a low concentration of protons.44 In 1999, Sakai et al. utilized the SIMS method to determine the proton concentration of pure polycrystalline CeO2 and that doped with rare earth elements (Ce0.8M0.2O2−δ, M = Y, La, Nd, Sm, Gd, Yb), which were annealed at 880 and 990 °C under pH2O = 0.03 atm, as shown in Fig. 3.62 The proton concentration of pure CeO2 is low (∼1.7 × 10−6 mol cm−3) and increases by 10–100 times by doping the trivalent rare earth elements. From Fig. 3, one can see that the proton concentration decreases with increasing lattice constants of Ce0.8M0.2O2−δ containing larger dopants. By doping the smallest dopant Yb, the highest proton concentration of 3.3 × 10−4 mol cm−3 was obtained at 990 °C, while doping the largest La leads to the lowest proton concentration of 1.2 × 10−5 mol cm−3.62 The reason is not clear, but enhanced mismatch between the size of dopants and host cations (Ce4+) may hamper the hydration reaction. It should be noted that the proton concentration of all the aforementioned doped CeO2 is higher than that of the single crystal 8YSZ (namely, 8YSZ-SC),36 and Ce0.8Yb0.2O2−δ has a proton concentration two orders of magnitude higher than that of 8YSZ-SC, attributed possibly to the difference in thermodynamic and chemical properties of the defects.63
 | ||
| Fig. 3 Proton concentration in undoped CeO2 and Ce0.8M0.2O2−δ (M = Y, La, Nd, Sm, Gd, Yb) after annealing at 880 and 990 °C in a wet atmosphere (pH2O = 0.03 atm).62 | ||
In a reducing atmosphere, CeO2 exhibits electron conduction as Ce4+ is reduced to Ce3+,28,64 leading to the ability of CeO2 to permeate hydrogen when protons conduct simultaneously. Nigara et al. studied the permeability of hydrogen in pure and doped CeO2 at high temperatures, and confirmed the presence of proton conductivity.65–68 Assuming that hydrogen atoms are dissociated into protons and electrons, the proton conductivity can be roughly calculated based on the gradient of chemical potential of hydrogen. The proton conductivity of undoped CeO2 is 8.5 × 10−6 S cm−1 at 1050 K, which increases to 1.6 × 10−4 S cm−1 at 1800 K.65 The proton conductivity of Ce0.9Gd0.1O2−δ is 1.2 × 10−6 S cm−1 at 1070 K, and increases to 1.4 × 10−4 S cm−1 at 1800 K.66 The proton conductivity of Ce0.8Yb0.2O2−δ is 1.0 × 10−6 S cm−1 at 1000 K, and increases to 1.0 × 10−4 S cm−1 at 1800 K.67 Among the compositions studied, Ce0.85Ca0.15O2−δ shows the highest proton conductivity, which is 1.4 × 10−6 and 5.0 × 10−5 S cm−1 at 1050 and 1800 K, respectively.68 The permeability of hydrogen is not solely determined by proton conductivity, but is also influenced by electronic conductivity. Therefore, the estimation of proton conductivity using hydrogen permeability can only be a rough approximation.
Although proton incorporation and conduction were confirmed in both pure and doped CeO2 at high temperatures, the proton conductivity is quite low, far lower than the required level (∼0.01 S cm−1) for application as a proton-conducting electrolyte. Therefore, similar to the case of doped ZrO2, the application of doped CeO2 as the electrolyte is mainly based on its oxide ion conduction, and the contribution from volume proton conduction is negligibly small.
2.3 La2Ce2O7
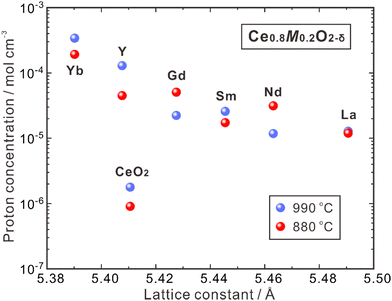
CeO2 doped with lanthanide elements exhibits a sharp decline in oxide ion conductivity as doping levels rise over 10–20 mol%,69–71 but CeO2 heavily doped with some large lanthanides (e.g., La) can be hydrated and exhibits proton conduction in wet atmospheres.72 50 at% La-doped CeO2 – namely Ce0.5La0.5O2−δ, and is generally depicted in the literature as La2Ce2O7 – takes a disordered fluorite structure and has high oxide ion conductivity and moderate proton conductivity, depending on the temperature and atmosphere. Kalland et al. measured water uptake and hydration enthalpy in La2Ce2O7 using combined thermogravimetry (TG) and differential scanning calorimetry (DSC) techniques,73 and determined the change of standard hydration enthalpy (ΔhydrH°) of −74 kJ mol−1, which was independent on the water uptake. They also prepared the solid solution of (La1−xNdx)2Zr2O7−δ with La2Ce2O7 and Nd2Ce2O7 as the end compositions and found that the water uptake increased with the increasing La concentration. They thereby proposed a model explaining that in La2Ce2O7, the oxide ions and oxygen vacancies coordinated with four La3+ cations have the strongest hydration ability, and those coordinated with less La3+ cations are less prone to be hydrated.73 Ismail et al. recently reported that both the proton concentration and conductivity increased by doping divalent alkaline earth elements to replace La and trivalent earth elements to replace Ce. Besides the increasing oxygen vacancies by these doping strategies, which benefits the hydration reaction, another reason is suggested to be the formation of new coordination types, including the oxide ions and oxygen vacancies coordinated with three La3+ and one A2+ (A = Ca, Sr and Ba) cations,74 and three La3+ and one B3+ (B = Y, Ho, Er, Tm and Yb) cations.75 Following the model proposed by Kalland et al., these new coordination types containing lower valence dopants benefit the hydration reaction, leading to higher proton concentration and conductivity.73–75 It should be noted that increasing the concentration of oxygen vacancies is the strategy commonly taken to increase the proton conductivity, but the model proposed by Kalland et al. in the La2Ce2O7 system emphasizes the importance to pay attention on the coordination environment surrounding the oxide ions and oxygen vacancies.La2Ce2O7 is, in most conditions, a mixed conductor with protons and oxide ions as the ionic charge carriers, and also shows partial electron conduction in a reducing atmosphere, due to the reduction of a part of Ce4+ to Ce3+.69,74 Sun et al. studied the effect of pH2O and temperature on the conduction behavior of La2Ce2O7, and found that the total conductivity increased significantly with increasing pH2O, due to the enhancement in proton conduction, as shown in Fig. 4(a).76 For example, the proton conductivity (σH+) of La2Ce2O7 increases from 2.44 × 10−5 S cm−1 to 6.68 × 10−5 S cm−1 with pH2O increasing from 0.0025 atm to 0.03 atm at 550 °C, and the transport number of protons (tH+) – reflecting the contribution of proton conduction to the total conduction – also increases. Since higher temperature activates the oxide ion conduction and promotes dehydration, tH+ decreases with the elevating temperature. tH+ of La2Ce2O7 is 0.90 at 250 °C under pH2O = 0.03 atm, and decreases to 0.13 at 550 °C.76 Therefore, the contribution of proton conduction in pristine La2Ce2O7 at the intermediate temperature range (450–700 °C) is quite small. Later on, Ismail et al. doped trivalent rare earth elements (Y, Ho, Er, Tm and Yb) to substitute Ce and studied the conduction behavior in the atmosphere with pH2O varying within 0.03–0.40 atm.75 Among the compositions studied, they found that La2(Ce0.95Y0.05)2O7−δ showed the highest σH+, which was 8.0 × 10−5 S cm−1 at 600 °C under pH2O = 0.03 atm, four times higher than that of pristine La2Ce2O7 (2.0 × 10−5 S cm−1), as shown in Fig. 4(b).75 Moreover, by increasing pH2O to 0.40 atm, σH+ of La2(Ce0.95Y0.05)2O7−δ further increased by more than four times to 3.3 × 10−4 S cm−1, and tH+ was kept at a moderate value of 0.22.75 These results indicate that by optimizing the composition and environmental atmosphere (e.g., increasing pH2O), the proton conduction in La2Ce2O7 can be enhanced efficiently. However, it should be noted that the majority charge carriers in La2Ce2O7 in the intermediate temperature range are oxide ions, and tH+ is much smaller than tO2−. Therefore, the fuel cells and electrolyzers using the La2Ce2O7-based electrolytes should not be classified into the category of protonic ceramic electrochemical devices.
 | ||
| Fig. 4 Proton conductivity and proton transport number of (a) La2Ce2O7 in wet air,76 and (b) La2(Ce0.95B0.05)2O7−δ (B = Y, Ho, Er, Tm and Yb) at 600 °C in wet oxygen plotted against pH2O.75 | ||
3. Pyrochlore oxides
3.1 La2Zr2O7
As a pyrochlore-type proton conductor, lanthanum zirconate (La2Zr2O7) attracts a lot of interest and has been studied profoundly. Pristine La2Zr2O7 has low electrical conductivity (e.g., 1.0 × 10−5 S cm−1 in a humidified H2 atmosphere at 900 °C),77 so it is commonly doped with acceptor dopants to increase the concentration of oxygen vacancies, which is beneficial for both the proton and oxide ion conduction. In this section, a summarization of the information of the solubility of dopants, electrical conduction behavior, and conduction mechanism of protons in the crystal structure of La2Zr2O7 is provided.In addition, the Zr-site can also be used for doping trivalent rare earth elements (e.g., Y, Nd, Sm, Gd) and divalent alkaline earth elements (e.g., Ca) to introduce oxygen vacancies. Omata et al. prepared La2(Zr1−yCay)2O7−δ with the doping limit of Y to be y = 0.0075.81 Han et al. found that the doping limit of Y in La2(Zr1−yYy)2O7−δ reached above y = 0.15 using the solid state reaction method, but the doping limits of Nd, Sm and Gd elements were only around y = 0.05.84
Furthermore, the difference in doping the same dopants into the La and Zr-sites was compared. The proton concentration in (La0.99Sr0.01)2Zr2O7−δ annealed at 800 °C under pH2O ∼ 0.30 atm was reported to be 2.0 × 10−5 mol cm−3, higher than that in La2(Zr0.99Sr0.01)2O7−δ (1.5 × 10−5 mol cm−3).78 Omata et al. suggested that oxygen vacancies form in the 48f and 8b sites, when doping into the La-site, and only form in the 48f site, when doping into the Zr-site.85 The authors speculated that the oxygen vacancies in different sites resulted in the differences in hydration ability to introduce protons with different mobilities.85 However, theoretical calculations indicate that oxygen vacancies mainly formed at the 48f site in La2Zr2O7 by acceptor-doping and are energetically unfavorable in the 8b site.87–91 The appropriateness of the aforementioned viewpoint needs further verification. We suggest that the discrepancy is due to the fact that the eight-coordinated radius of Ca2+ (1.120 Å11) is closer to that of La3+ (1.160 Å11), but the six-coordinated radius of Ca2+ (1.000 Å11) is obviously larger than that of Zr4+ (0. 720 Å11). This mismatch in cation radii induces local distortions, which is unfavorable for the hydration reaction.
Interestingly, it seems that not all the oxygen vacancies generated by doping participate the hydration reaction. Björketun et al. reported that only 59% of the oxygen vacancies in (La0.975Ca0.025)2Zr2O7−δ and (La0.955Ca0.045)2Zr2O7−δ participated into the hydration reaction.88 Omata et al. found that the ratio of hydratable oxygen vacancies in (La0.975Ca0.025)2Zr2O7−δ and (La0.96Ca0.04)2Zr2O7−δ were 30%78 and 38%,85 respectively. Antonova et al. reported that 36%83 and 45%86 of the oxygen vacancies in (La0.975Ca0.025)2Zr2O7−δ and (La0.95Ca0.05)2Zr2O7−δ, respectively, were active for the hydration reaction. The reason is still unclear, but a possible explanation is that the hydration ability of the oxygen vacancies and oxide ions strongly depends on their coordination environment. Analogous to the case in the La2Ce2O7, the oxygen vacancies and oxide ions surrounded by trivalent La and the dopants with lower valence might be prone to participate into the hydration reaction, and those in the vicinity of tetravalent cations (Ce4+, Zr4+) are difficult to be hydrated, making the system unable to be fully hydrated.
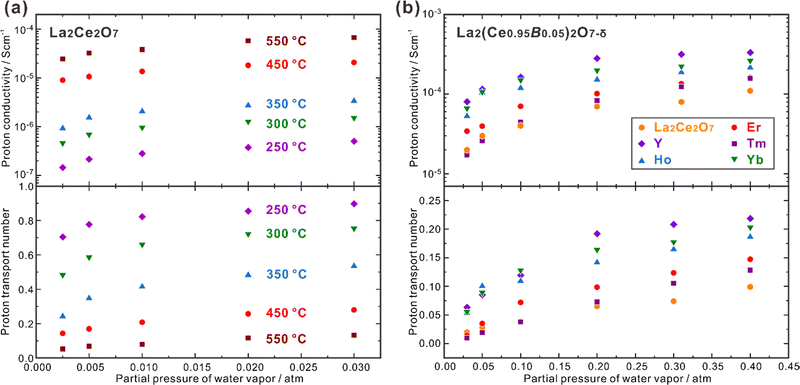
Besides, the site for doping was also suggested to play an effective role in influencing the proton concentration and conductivity. Omata et al. found that (La0.96Ca0.04)2Zr2O7−δ has a proton concentration about three times higher than that in La2(Zr0.98Ca0.02)2O7−δ, although these two samples have the same concentration of extrinsic oxygen vacancies (δ = 0.04).85 They further separated the partial conductivities of protons and oxide ions in (La0.975Ca0.025)2Zr2O7−δ and La2(Zr0.9925Ca0.0075)2O7−δ, and found that as shown in Fig. 5, the proton conductivity of (La0.975Ca0.025)2Zr2O7−δ (6.8 × 10−4 S cm−1) is nearly 7 times higher than that of La2(Zr0.9925Ca0.0075)2O7−δ (1.0 × 10−4 S cm−1) at 600 °C, although the concentration of oxygen vacancies in (La0.975Ca0.025)2Zr2O7−δ (δ = 0.025) is less than twice as high as that in La2(Zr0.9925Ca0.0075)2O7−δ (δ = 0.015).85 The proton conductivity in (La0.985Ca0.015)2Zr2O7−δ, which has the same concentration of oxygen vacancies as La2(Zr0.9925Ca0.0075)2O7−δ, is 3.9 × 10−4 S cm−1 at 600 °C.85
 | ||
| Fig. 5 Temperature dependence of partial conductivities of proton, oxide ion in (La0.975Ca0.025)2Zr2O7−δ (0.025 Ca–La) and (La0.95Ca0.05)2Zr2O7−δ (0.052 Ca–La) in wet H2 (pH2O ∼ 0.028 atm),92 and (La0.975Ca0.025)2Zr2O7−δ (0.025 Ca–La) and (b) La2(Zr0.9925Ca0.0075)2O7−δ (0.0075 Ca–Zr) in wet H2 (pH2O: 0.017–0.25 atm).81 The samples are polycrystalline, and the conductivities comprise the contributions from both bulk (intra-grain) and grain boundaries (inter-grain). | ||
As shown in Fig. 5, when the temperature is not high enough (typically < 600 °C), Ca-doped La2Zr2O7 is almost a pure proton conductor in wet H2, since the partial conductivity of protons is higher by more than one order of magnitude than that of oxide ions. However, with the increasing temperature, the proton conductivity decreases due to dehydration, and the contribution from oxide ions increases. In the case of (La0.975Ca0.025)2Zr2O7−δ, when the temperature is around 835 °C, the partial conductivities of protons and oxide ions are close. When the temperature is elevated to 900 °C, the partial conductivity of oxide ions is higher than that of protons by one order of magnitude, making the material become nearly a pure oxide ion conductor.
Besides doping alkaline earth elements, substituting Zr with trivalent rare earth elements (e.g., Y) also effectively enhances the proton conduction. Y3+ has the same valence state as La3+ and cannot be used as an acceptor dopant for the A-site. However, doping at the tetravalent B-site can introduce oxygen vacancies, which in turn increases the concentration and partial conductivity of protons. Labrincha et al. reported that La2Zr2O7 and La2(Zr0.84Y0.16)2O7−δ exhibited proton conduction at temperatures lower than 1000 °C,93 and the conductivities at 900 °C were 3.3 × 10−5 and 1.0 × 10−4 S cm−1 for La2Zr2O7 and La2(Zr0.84Y0.16)2O7−δ, respectively. Shimura et al. measured the conduction behavior of La2(Zr0.9Y0.1)2O7−δ, whose tH+ was 0.45 and 0.10 at 600 and 900 °C, respectively, corresponding to σH+ of 1.1 × 10−4 and 1.5 × 10−4 S cm−1, respectively.77 Han et al. measured the conductivities of La2Zr2O7 doped with various concentrations of Y, and found that the bulk conductivity of La2(Zr0.9Y0.1)2O7−δ was 3.68 × 10−4 S cm−1 at 600 °C in wet H2, which was the highest among the compositions studied in their work.84
 | ||
| Fig. 6 (a) Pyrochlore crystal structure of La2Zr2O7, where the green and red balls are La and O ions, and the grey octahedrons are ZrO6 units. (b) Conduction route of protons in La2Zr2O7. Reprinted with permission,90 Copyright [2015] American Chemical Society. | ||
3.2 La2(Nb1−xMx)2O7−δ
La2(Nb1−xMx)2O7−δ (M = rare earth elements) is a new class of fluorite/pyrochlore proton conductor. Although it contains neither Zr nor Ce, the idea of this composition was inspired from La2Zr2O7. The design strategy of La2(Nb1−xMx)2O7−δ is to use a mixture of pentavalent Nb and trivalent rare earth elements (M) to occupy the tetravalent B-site. When the atomic ratio between Nb and rare earth elements is 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, the average positive charge of the B-site is four. Furthermore, interestingly, if the ratio between Nb and rare earth elements is increased over unity, oxygen vacancies form following
1, the average positive charge of the B-site is four. Furthermore, interestingly, if the ratio between Nb and rare earth elements is increased over unity, oxygen vacancies form following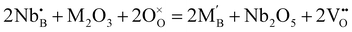 | (5) |
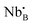 and
and 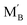 are the Nb and rare earth cations occupying the B-site. Therefore, by simply changing the concentration of the domestic cations in the B-site, oxygen vacancies can be created, favoring the hydration reaction. Firstly, dopant candidates of rare earth elements were screened, including Sc, Y, Nd, Sm, Gd, Ho, Er, Tm and Yb, but only limited compositions showed single phase: La2(Nb0.5Sc0.5)2O7−δ, La2(Nb1−xYx)2O7−δ (LNY, x = 0.60, 0.65, 0.70),94 and La2(Nb0.45Yb0.55)2O7−δ (LNYb55).95 Since there are no extrinsic oxygen vacancies in La2(Nb0.5Sc0.5)2O7−δ, the conductivity of this sample showed no response to moisture, indicating that there is no proton conduction. The crystal structure of La2(Nb1−xYx)2O7−δ (LNY) depends on the composition, and is pyrochlore and fluorite, when x = 0.60 and 0.65 and x = 0.70, respectively.94 A clear H2O/D2O isotope effect was confirmed for these compositions, indicating that protons are the majority charge carriers.
are the Nb and rare earth cations occupying the B-site. Therefore, by simply changing the concentration of the domestic cations in the B-site, oxygen vacancies can be created, favoring the hydration reaction. Firstly, dopant candidates of rare earth elements were screened, including Sc, Y, Nd, Sm, Gd, Ho, Er, Tm and Yb, but only limited compositions showed single phase: La2(Nb0.5Sc0.5)2O7−δ, La2(Nb1−xYx)2O7−δ (LNY, x = 0.60, 0.65, 0.70),94 and La2(Nb0.45Yb0.55)2O7−δ (LNYb55).95 Since there are no extrinsic oxygen vacancies in La2(Nb0.5Sc0.5)2O7−δ, the conductivity of this sample showed no response to moisture, indicating that there is no proton conduction. The crystal structure of La2(Nb1−xYx)2O7−δ (LNY) depends on the composition, and is pyrochlore and fluorite, when x = 0.60 and 0.65 and x = 0.70, respectively.94 A clear H2O/D2O isotope effect was confirmed for these compositions, indicating that protons are the majority charge carriers.
Besides increasing the atomic ratio between the rare earth elements and Nb in the B-site, oxygen vacancies can also be introduced by acceptor-doping into the A-site, and divalent Ca, Sr and Ba are common dopants to partially substitute trivalent La. A comparison of the conductivities of the LNY system and those of some state-of-the-art proton conductors are summarized in Fig. 7. The conductivity of La2(Nb0.4Y0.6)2O7−δ (LNY60) is 3.17 × 10−4 S cm−1 at 700 °C in wet hydrogen (pH2O = 0.05 atm), and increases by nearly four times to 1.16 × 10−3 S cm−1 by doping 2.54 at% Ca (La + Ca = 100 at%).96 Similarly, the conductivity of La2(Nb0.35Y0.65)2O7−δ (LNY65) increases from 2.88 × 10−4 S cm−1 to 1.16 × 10−3 S cm−1 by doping 0.98 at% Sr (La + Sr = 100 at%),95 and the conductivity of LNYb55 increases from 2.78 × 10−4 S cm−1 to 4.51 × 10−4 S cm−1 by doping 3 at% Ca (La + Ca = 100 at%).94 Anyhow, the conductivity of this system is still too low to be directly used as the electrolyte, but it may be potentially applicable as a buffer layer between the electrode and electrolyte of acceptor-doped BaZrO3 and Ba(Zr, Ce)O3, based on the superior chemical stability of LNY and LNYb55.
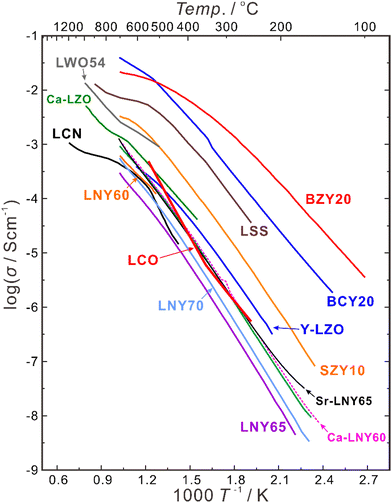 | ||
| Fig. 7 Total conductivities of BaZr0.8Y0.2O3−δ (BZY20),94 BaCe0.8Y0.2O3−δ (BCY20),94 SrZr0.9Y0.1O3−δ (SZY10),94 La2(Zr0.9Y0.1)2O7−δ (Y-LZO),84 La2(Nb0.40Y0.60)2O7−δ (LNY60),94 La2(Nb0.35Y0.65)2O7−δ (LNY65),94 La2(Nb0.30Y0.70)2O7−δ (LNY70),94 (La0.95Ca0.05)2(Nb0.40Y0.60)2O7−δ (Ca-LNY60),96 (La0.95Sr0.05)2(Nb0.35Y0.65)2O7−δ (Sr-LNY65)96 in wet H2 (pH2O = 0.05 atm), (La0.975Ca0.025)2Zr2O7−δ (Ca-LZO) in wet H2 (pH2O ∼ 0.02 atm),81 La2Ce2O7 in wet air (pH2O = 0.03 atm),76 La0.9Sr0.1ScO3−δ (LSS) in wet Ar-1% H2 (pH2O = 0.02 atm),97 La27W5O54+δ (LWO54) in wet Ar-5% H2O (pH2O ∼ 0.025 atm),98 and La0.99Ca0.01NbO4−δ (LCN) in wet H2 (pH2O ∼ 0.02 atm).99 | ||
In addition, the generation of electron hole conduction in an oxidizing atmosphere is a problem for the acceptor-doped BaZrO3 and Ba(Zr, Ce)O3 electrolytes. For example, the state-of-the art BaZr0.8Y0.2O3−δ electrolyte has the transport number of ionic conduction (tion) of 0.79 and 0.43 in wet oxygen (pH2O = 0.05 atm) at 600 and 700 °C, respectively. Remarkably, LNY and LNYb55 have higher tion, which is 0.92 and 0.80 at 600 and 700 °C, respectively, for LNY65,96 and 0.95 and 0.90 at 600 and 700 °C, respectively, for (La0.99Ca0.01)2(Nb0.45Yb0.55)2O7−δ.95 Therefore, depositing the LNY/LNYb55 electrolyte onto the Ba-based perovskite electrolytes will be a feasible strategy to improve the chemical stability and transport properties of the electrolyte.
The long-range and local crystal structures were also analyzed. Based on Rietveld refinement of powder XRD patterns of pristine and alkaline earth element-doped LNYb55, it was found that the 8b O2 site – in the center of the tetrahedrons containing four La cations – was fully occupied by oxide ions. The oxygen vacancies which were introduced by elevating the atomic ratio between Yb and Nb over unity and partially substituting trivalent La with divalent Ca, Sr and Ba cations located solely in the 48f O1 site, which is in the center of the tetrahedrons composed of two La and two Nb/Yb cations.95 Furthermore, the results of extended X-ray absorption fine structure (EXAFS) analysis indicated that the coordination number of oxide ions in the vicinity of Y in the hydrated La2(Nb1−xYx)2O7−δ (x = 0.60, 0.65) samples is higher than those of the dried samples,96 indicating that only the oxide ions/oxygen vacancies close to Y are active for the hydration reaction, and the oxygen vacancies formed by acceptor-doping prefer to be located in the vicinity of Y than Nb. Thereby, it is reasonable to conclude that even in the tetrahedrons composed of two La and two Nb/Yb or Y cations, oxygen vacancies prefer to form in the tetrahedrons containing La and Y or Yb, rather than those with Nb, suggesting a potential strategy to further improve the hydration ability and proton conduction by regulating the coordination of the local tetrahedrons in this class of materials.
3.3 Other materials
3.4 Dependence of hydration ability on cation radius
One interesting conclusion from the 3.3 section is that in the system with the same B-site cation, the proton conductivity increases with the increasing size of the A-site cation. In addition, a relationship can also be found between the B-site cation and the proton conduction of the pyrochlore oxides. Eurenius et al. found that the conductivities of pre-hydrated (Sm0.96Ca0.04)2B2O7−δ (B = Ti, Zr, Sn) decreased when the samples were exposed to dry Ar due to the loss of protons resulting from dehydration.107 By assuming the decrement in conductivity caused by dehydration to the proton conductivity, the proton conductivities of (Sm0.96Ca0.04)2Ti2O7−δ, (Sm0.96Ca0.04)2Sn2O7−δ and (Sm0.96Ca0.04)2Zr2O7−δ at 300 °C can be estimated to be 3.12 × 10−5, 1.68 × 10−6 and 9.39 × 10−8 S cm−1, respectively, decreasing with the increasing radius of the B-site cation (Ti4+(0.605 Å) < Sn4+(0.690 Å) < Zr4+ (0.72 Å)11). Therefore, the proton conduction in pyrochlore oxides can be expected to be dependent on the size of cations in the A and B-sites, which were revealed to influence the hydration ability and thereby the proton concentration significantly.Eurenius et al. measured the proton concentration of (A0.98Ca0.02)2Sn2O7−δ (A = La, Sm, Yb) after annealing at 300 °C in wet nitrogen (pH2O = 0.37 atm), which was 2.85 × 10−5, 2.10 × 10−5 and 1.62 × 10−5 mol cm−3 for (La0.98Ca0.02)2Sn2O7−δ, (Sm0.98Ca0.02)2Sn2O7−δ and (Yb0.98Ca0.02)2Sn2O7−δ, respectively, and decreased with the decreasing size of the A-site cations (La3+ (1.160 Å) > Sm3+ (1.079 Å) > Yb3+ (0.985 Å)11).102 This finding is consistent with the results of Bjørheim et al. that the proton concentration decreased in the sequence of La1.8Ca0.2Sn2O7−δ > Sm1.8Ca0.2Sn2O7−δ > Er1.8Ca0.2Sn2O7−δ with Er3+ (1.004 Å11) to be the smallest A-site cation in their study.108 Since the protons are introduced through the hydration reaction (eqn (1)), the equilibrium constant can be given as
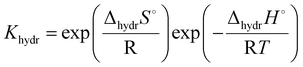 | (6) |
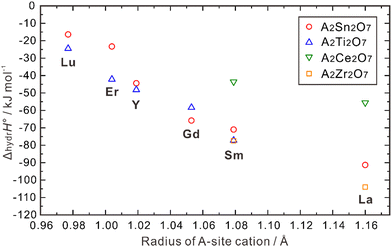 | ||
| Fig. 8 Calculated hydration enthalpies for pyrochlore structured A2B2O7 (B = Ti, Sn, Zr, Ce).108 | ||
ΔhydrH° also correlates with the radii of the B-site cations. As shown in Fig. 8, when the A-site is occupied by Lu, Er, Y and Sm, a larger absolute value of ΔhydrH° is obtained when the B-site is occupied by a small cation (e.g., Ti4+) compared with a large cation (e.g., Sn4+). However, when Gd and La occupy the A-site, the absolute value of ΔhydrH° is larger when the B-site is occupied by Zr4+, which is larger than Sn4+. Eurenius et al. also measured the proton concentration of (Sm0.96Ca0.04)2B2O7−δ (B = Ti, Sn, Zr) hydrated at 300 °C in wet nitrogen (pH2O = 0.37 atm), which were 4.76 × 10−4, 4.97 × 10−4 and 8.69 × 10−5 mol cm−3 for (Sm0.96Ca0.04)2Ti2O7−δ, (Sm0.96Ca0.04)2Sn2O7−δ, and Sm1.92Ca0.08Zr2O7−δ, respectively.107 These results indicate that although there are some exceptions, small cations in the B-site in general favors the hydration reaction in the pyrochlore oxides. The ordering and stability of the pyrochlore structure seem to correlate with the ratio of cation radii (rA3+/rB4+). As this ratio increases, the stability and ordering of the pyrochlore increase.12 Consequently, when the size of A3+ ions increase and that of B4+ ions decrease, the degree of ordering in the pyrochlore structure is likely to increase, potentially leading to a more negative hydration enthalpy, which in turn benefits proton incorporation.
4. Applications
4.1 Intermediate temperature fuel cells
La2Ce2O7-based materials have already been used as electrolytes in fuel cells,109–113 which were demonstrated as protonic ceramic fuel cells (PCFCs, Fig. 9(a)) where the main charge carriers in the electrolyte are protons. However, since the La2Ce2O7-based materials exhibit mixing ionic conduction of protons and oxides in the intermediate temperature range (450–700 °C), and oxide ions are in fact the majority charge carriers at relatively high temperature (e.g., 700 °C), it is not appropriate to claim them as PCFCs. Anyway, we summarize the performance of the reported fuel cells using the La2Ce2O7-based electrolytes in Table 1 for information, from which one can see that compared with pure La2Ce2O7, the fuel cells using the doped La2Ce2O7 electrolyte show higher performance. Besides, by regulating the compositions of the electrolyte, the performance of the fuel cells can be optimized. For example, as shown in Fig. 10, the fuel cell using a (La0.925Mg0.075)2Ce2O7−δ electrolyte exhibits the highest Pmax of 897 mW cm−2 at 700 °C, due to the highest ionic conductivity of the electrolyte among the compositions studied.110 This fuel cell also shows Pmax of 223 mW cm−2 at 550 °C, which is consistent with the trend of conductivity.110 Similarly, the fuel cell utilizing a (Nd0.925Mg0.075)2Ce2O7−δ electrolyte demonstrates Pmax of 483 mW cm−2 and an open circuit voltage (OCV) of 0.890 V at 700 °C, which are the highest value for the fuel cells using the (Nd, Mg)2Ce2O7−δ-based electrolytes.113 It deserves noting that these fluorite-based oxides exhibit excellent chemical stability in CO2 and H2O atmospheres, and a much longer lifetime is thereby expected compared with the case using some Ba-based perovskite electrolytes.9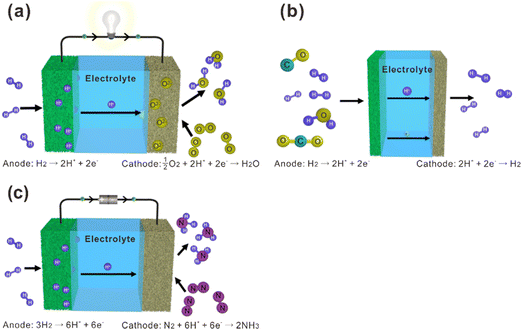 | ||
| Fig. 9 Schematic diagrams of (a) fuel cells, (b) hydrogen separation membranes, and (c) ammonia synthesis based on proton-conducting electrolytes. | ||
| Electrolyte | Anode | Cathode | Electrolyte thickness/μm | Operating temperature/°C | P max/mW cm−2 | OCV/V | Ref. |
|---|---|---|---|---|---|---|---|
| La2Ce2O7 | Ni-BaZr0.1Ce0.7Y0.2O3−δ | La0.6Sr0.4Co0.2Fe0.8O3−δ–Sm0.2Ce0.8O2−δ | 40 | 550 | 80 | 1.07 | 109 |
| (La0.925Mg0.075)2Ce2O7−δ | Ni-La1.85Mg0.15Ce2O7−δ | Sm0.5Sr0.5CoO3−δ–Ce0.8Sm0.2O2−δ | 15 | 550 | 223 | 0.95 | 110 |
| (La0.925Na0.075)2Ce2O7−δ | Ni-La1.85Na0.15Ce2O7−δ | Ba0.5Sr0.5Co0.8Fe0.2O3−δ–La1.85Na0.15Ce2O7−δ | 53 | 600 | 154 | 0.95 | 111 |
| (La0.975Ca0.025)2Ce2O7−δ | Ni-La1.95Ca0.05Ce2O7−δ | LaSr3Co1.5Fe1.5O10−δ–La1.95Ca0.05Ce2O7−δ | 15 | 600 | 149 | 0.86 | 114 |
| (La0.925Mo0.075)2Ce2O7−δ | Ni-La1.85Mo0.15Ce2O7−δ | Ba0.5Sr0.5Co0.8Fe0.2O3−δ–La1.85Mo0.15Ce2O7−δ | 52 | 600 | 290 | 0.90 | 115 |
| (La0.95In0.05)2Ce2O7−δ | Ni-BaCe0.5Zr0.3Dy0.2O3−δ | Ba0.5Sr0.5Co0.8Fe0.2O3−δ–La1.90In0.10Ce2O7−δ | 46 | 550 | 179 | 0.94 | 116 |
| (La0.95In0.05)2Ce2O7−δ | Ni-La1.90In0.10Ce2O7−δ | Ba0.5Sr0.5Co0.8Fe0.2O3−δ–La1.90In0.10Ce2O7−δ | 40 | 550 | 121 | 1.09 | 116 |
| (La0.925Rb0.075)2Ce2O7−δ | Ni-La1.85Rb0.15Ce2O7−δ | Sm0.5Sr0.5Co3−δ–Ce0.8Sm0.2O2−δ | 15 | 700 | 1065 | 0.88 | 117 |
| (Nd0.925In0.075)2Ce2O7−δ | Ni–Nd1.85In0.15Ce2O7−δ | Ba0.5Sr0.5Co0.8Fe0.2O3−δ–Nd1.85In0.15Ce2O7−δ | 46 | 550 | 165 | 0.93 | 112 |
| Nd2Ce2O7 | Ni–Nd2Ce2O7 | Ba0.5Sr0.5Co0.8Fe0.2O3−δ–Nd2Ce2O7 | 50 | 700 | 397 | 0.859 | 113 |
| Nd1.85Mg0.15Ce2O7−δ | Ni–Nd2Ce2O7 | Ba0.5Sr0.5Co0.8Fe0.2O3−δ–Nd2Ce2O7 | 50 | 700 | 483 | 0.890 | 113 |
| Nd1.85Ca0.15Ce2O7−δ | Ni–Nd2Ce2O7 | Ba0.5Sr0.5Co0.8Fe0.2O3−δ–Nd2Ce2O7 | 50 | 700 | 428 | 0.864 | 113 |
| Nd1.85Sr0.15Ce2O7−δ | Ni–Nd2Ce2O7 | Ba0.5Sr0.5Co0.8Fe0.2O3−δ–Nd2Ce2O7 | 50 | 700 | 441 | 0.873 | 113 |
| Nd1.85Ba0.15Ce2O7−δ | Ni–Nd2Ce2O7 | Ba0.5Sr0.5Co0.8Fe0.2O3−δ–Nd2Ce2O7 | 50 | 700 | 418 | 0.878 | 113 |
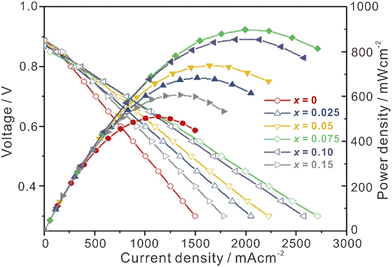 | ||
| Fig. 10 Performance of fuel cells at 700 °C using (La1−xMgx)2Ce2O7−δ as the electrolyte. Reprinted with permission,110 Copyright [2019] Elsevier. | ||
4.2 Hydrogen separation membrane
Proton and electron mixed conducting ceramic membranes are an ideal solution for separating H2 due to its excellent stability, high hydrogen selectivity and low cost.118 As shown in Fig. 9(b), H2 molecules are firstly adsorbed on the surface of the membrane and dissociated into protons and electrons. Then, protons move across the electrolyte to the other side of the membrane, where they recombine with electrons to form H2 molecules. The current technologies for ceramic separation membranes can be classified into two types. One is metal-ceramic composite membranes, where the metal and ceramic phases conduct electrons and protons, respectively. The other is single-phase ceramics, which are mixed conductors of protons and electrons. Some state-of-the art proton conductors – such as SrCeO3 and BaCeO3 – have been doped with multivalent dopants to make them conduct electrons simultaneously. However, BaCeO3 and SrCeO3 are chemically unstable and easily react with CO2 and H2O.119,120 On the other hand, fluorite-based oxide membranes exhibit excellent stability in H2O and CO2, making them a promising option for hydrogen separation, and the progresses are summarized in Table 2. Fig. 11 shows the hydrogen permeation flux across the membrane of La2Ce2O7 doped with various concentrations of Sm, and (La0.975Sm0.025)2Ce2O7−δ is the optimical composition, showing the highest hydrogen permeation flux.121 Besides, the hydrogen permeation flux is influenced not only by the conduction properties (e.g., electron conductivity and proton conductivity) of the material, but also by temperature, hydrogen gradient, and film thickness. The hydrogen permeation flux increases with the increasing temperature, decreasing film thickness and increasing hydrogen gradient.| Material | Feed gas/sweep gas | Film thickness/μm | Operating temperature/°C | Hydrogen permeation flux/mol cm−2 s−1 | Ref. |
|---|---|---|---|---|---|
| Ni-La2Ce2O7 | wet 20% H2 in N2 (3% H2O)/Ar | 600 | 900 | 1.6 × 10−8 | 123 |
| Ni-(La0.975Ca0.025)2Ce2O7−δ | wet 20% H2 in N2 (3% H2O)/Ar | 600 | 900 | 1.9 × 10−8 | 123 |
| Ni-(La0.95Ca0.05)2Ce2O7−δ | wet 20% H2 in N2 (3% H2O)/Ar | 600 | 900 | 1.4 × 10−8 | 123 |
| Ni-La2Ce2O7 | wet 20% H2 in N2 (3% H2O)/Ar | 48 | 900 | 6.83 × 10−8 | 124 |
| La2Ce2O7 | wet 20% H2 in N2 (3% H2O)/Ar | 30 | 900 | 2.6 × 10−8 | 125 |
| Ni-Ce0.8Sm0.2O2−δ | 40% H2 in N2/Ar | 35 | 900 | 1.5 × 10−9 | 126 |
| Ni-Ce0.8Sm0.2O2−δ | 40% H2 in N2/Ar | 21 | 900 | 3.0 × 10−9 | 126 |
| Ni-(La0.975Sm0.025)2Ce2O7−δ | wet 20% H2 in N2 (3% H2O)/Ar | 600 | 900 | 2.86 × 10−8 | 121 |
| Ni-(La0.975Sm0.025)2Ce2O7−δ | wet 20% H2 in N2 (3% H2O)/Ar | 600 | 900 | 2.30 × 10−8 | 121 |
| CeO2 | wet 7.9% H2 in N2 (2.5% H2O)/Ar | 3930 | 777 | 9.44 × 10−11 | 65 |
| Ce0.9Ca0.1O2−δ | wet 7.6% H2 in N2 (2.2% H2O)/Ar | 3800 | 800 | 6.67 × 10−11 | 127 |
| Ce0.85Ca0.15O2−δ | wet 7.6% H2 in N2 (2.3% H2O)/Ar | 3500 | 777 | 9.76 × 10−12 | 68 |
| Ce0.9Gd0.1O2−δ | wet 7.2% H2 in N2 (2.3% H2O)/Ar | 3500 | 780 | 8.06 × 10−12 | 66 |
| Ce0.8Yb0.2O2−δ | wet 7.9% H2 in N2 (2.6% H2O)/Ar | 3920 | 777 | 9.26 × 10−12 | 67 |
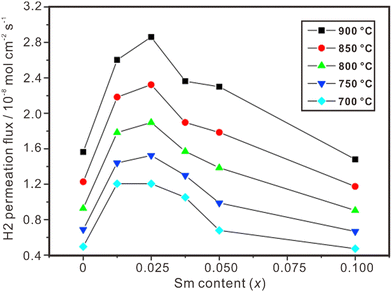 | ||
| Fig. 11 Hydrogen permeation flux through Ni-(La1−xSmx)2Ce2O7−δ membranes. Reprinted with permission,121 Copyright [2010] Elsevier. | ||
Generally, for H2 separation at an industrial level, the ceramic membrane must have partial conductivities of protons and electrons both higher than 0.1 S cm−1, leading to the hydrogen permeation flux exceeding 3.7 × 10−5 mol cm−2 s−1.122 Unfortunately, at present, the conductivity of the fluorite-based oxide membranes is still too low to satisfy the requirements. Nonetheless, this technology is still considered to be a promising alternative for H2 separation due to the excellent H2 selectivity, high energy efficiency, low cost and excellent long-term stability, demanding continuous effort for development in the future.
4.3 Ammonia synthesis
Ammonia (NH3) is an important raw material for the chemical industry and a convenient medium for energy storage.128,129 The Haber–Bosch method is a conventional approach toward NH3 synthesis, involving the reaction of gaseous hydrogen and nitrogen on a catalyst at high temperature (450–500 °C) and high pressure (15–30 MPa),130,131 following| N2 + 3H2 = 2NH3 | (7) |
| 3H2 → 6H+ + 6e− | (8) |
| N2 + 6H+ + 6e− → 2NH3 | (9) |
| Material | Flow rate at cathode (dry N2)/m3 s−1 | Flow rate at anode (wet H2)/m3 s−1 | Voltage/V | Operating temperature/°C | NH3 production rate/mol cm−2 s−1 | Ref. |
|---|---|---|---|---|---|---|
| La1.9Ca0.1Zr2O7−δ | 3.0 × 10−4 | 1.0 × 10−4 | 0.6 | 520 | 1.756 × 10−9 | 138 |
| La1.95Ca0.05Zr2O7−δ | 3.0 × 10−10 | 1.0 × 10−10 | 0.6 | 520 | 1.965 × 10−9 | 139 |
| La1.95Ca0.05Ce2O7−δ | 3.0 × 10−10 | 1.0 × 10−10 | 0.6 | 520 | 1.300 × 10−9 | 139 |
| Ce0.8La0.2O2−δ | 3.0 × 10−4 | 1.0 × 10−4 | 0.6 | 650 | 7.061 × 10−9 | 140 |
| Ce0.8Y0.2O2−δ | 3.0 × 10−4 | 1.0 × 10−4 | 0.6 | 650 | 7.319 × 10−9 | 140 |
| Ce0.8Gd0.2O2−δ | 3.0 × 10−4 | 1.0 × 10−4 | 0.6 | 650 | 7.552 × 10−9 | 140 |
| Ce0.8Sm0.2O2−δ | 3.0 × 10−4 | 1.0 × 10−4 | 0.6 | 650 | 7.955 × 10−9 | 140 |
The electrochemical synthesis of NH3 is influenced significantly by the operating environment, including current density, temperature, materials for electrodes, electrolytes and catalysts. These factors greatly affect the production rate, selectivity, and energy utilization of NH3. While it is true that increasing the current density can enhance the ammonia production rate, it does not always lead to a consistent increase, since high current density promotes the side reaction of hydrogen evolution at the cathode following eqn (10), which reduces the selectivity of ammonia.132
| 2H+ + 2e− → H2 | (10) |
The electrochemical synthesis of ammonia faces several challenges, particularly in the development of materials that are highly active, selective and durable. In order to improve the selectivity of ammonia, it is vital to design the cathode which can effectively suppress the hydrogen evolution reaction. A key factor to increase the ammonia yield is to regulate and optimize the chemical adsorption of nitrogen on the cathode and the binding energy between nitrogen and catalyst. It is important to find a balanced binding energy, as weaker binding energy makes it difficult to reduce nitrogen and decreases ammonia yield, while a stronger binding energy leads to higher desorption energy and potential catalyst poisoning. It is reported that increasing the concentration of oxygen vacancies on the electrode surface can enhance the catalytic activity of nitrogen reduction and also inhibit the hydrogen evolution reaction.135 Therefore, materials with a high concentration of oxygen vacancies can potentially be appropriate cathode candidates. Besides, the production rate and selectivity of ammonia can be influenced by current density and temperature, so it is also important to determine the optimal operating conditions to achieve a high production rate and selectivity. In addition, the proton conductivity of the electrolyte plays a crucial role in facilitating the transport of protons to the cathode for nitrogen reduction. Therefore, it is imperative to enhance the proton conductivity of the electrolyte in order to minimize ohmic loss. The electrolytes should also exhibit good chemical stability, mechanical strength, and negligible electronic conductivity. Additionally, reducing the thickness of the electrolyte further help in reducing ohmic loss.136 Since the hydrogen evolution reaction is unavoidable, unreacted H2 can be recycled back to the cathode to increase the utilization of hydrogen.137 Moreover, in order to consistently achieve the electrochemical synthesis of NH3 with optimal efficiency, the reactor should possess flexibility and be capable of operating across a wide range of conditions.
5. Conclusion remarks
In this work, we reviewed the material systems with a fluorite or pyrochlore crystal structure which show the volume conduction of protons, and described their potential applications in intermediate fuel cells, hydrogen separation membranes, and ammonia synthesis. However, it should be admitted that the fluorite structure-based proton conductors are presently not as successful as those with the perovskite structure for their application in the solid-state electrochemical devices, restricted by their low proton conductivity. To improve the proton conduction, increasing the concentration of oxygen vacancies is a common strategy taken in the system of perovskite oxides, but it does not work well in the fluorite-based oxides. For example, the proton conductivity of Zr0.82Y0.18O2−δ (δ = 0.09) is only 1.5 × 10−8 S cm−1 at 777 °C,46 and that of Ce0.8Yb0.2O2−δ (δ = 0.1) is 1.0 × 10−6 S cm−1 at 727 °C.67 In comparison, BaZr0.8Y0.2O3−δ (δ = 0.1) with a similar concentration of oxygen vacancies (δ) has a proton conductivity of 2.45 × 10−2 S cm−1 at 700 °C,141 more than four orders of magnitude higher than that of the doped ZrO2 and CeO2. Therefore, simply increasing the concentration of oxygen vacancies appears to have little chance to increase the proton conductivity of the fluorite oxides significantly. Based on the model suggested by Kalland et al., the coordination environment directly impacts the ability of the oxide ions and oxygen vacancies to participate in the hydration reaction.73 The oxide ions and oxygen vacancies surrounded by four relatively low valent cations (La3+ in the case of La2Ce2O7) are active for the hydration reaction, but those surrounded by the cations with high oxidation state (Ce4+ in the case of La2Ce2O7) appear to be resistive to the hydration reaction. A similar conclusion was also drawn by an EXAFS study on the local structure of La2(Nb1−xYx)2O7−δ. The coordination number of oxide ions surrounding Y3+ and La3+ increased after hydration, but negligibly small change occurred in that surrounding the Nb5+ cations. Therefore, adjusting the coordination environment surrounding the oxide ions and oxygen vacancies is likely to be a more effective strategy, which can potentially improve the hydration ability and proton conduction of the oxides with the fluorite-based crystal structure.Although the proton conductivity is still low, the chemical stability of the proton conducting fluorite structure-based oxides is excellent. Different from the state-of-the-art perovskite oxides with high proton conductivity (e.g., Y-doped Ba(Zr, Ce)O3), the proton conducting fluorite/pyrochlore oxides contain no main components of alkaline earth elements (e.g., Ba). Even Ca, Sr and Ba are doped to improve the proton conduction, their solubility is very low (<3 at% (cation ratio)). Although at the present stage, it is difficult to directly apply the proton conducting fluorite/pyrochlore oxides as the electrolyte in protonic ceramic cells (PCCs), they can be used as a buffer layer – for example, between the Y-doped Ba(Zr, Ce)O3 electrolyte and the electrodes – to avoid the direct contact of the electrolyte with the atmosphere containing water vapor and/or carbon dioxide. Besides, some pyrochlore oxides (e.g., La2(Nb1−xBx)2O7−δ (B = Y, Yb)) have a higher transport number than Y-doped Ba(Zr, Ce)O3 in wet oxygen, so by inserting such a buffer layer between the Y-doped Ba(Zr, Ce)O3 electrolyte and the oxygen electrode, the transport number of ionic conduction can be improved, leading to decreased leakage current and improved cell efficiency. However, the conventional co-sintering process results in interdiffusion between the buffer layer and electrolyte layer, and some other techniques which are free of high temperature heat-treatment (e.g., pulsed layer deposition) are high in cost and not suitable for depositing large-area thin films. Therefore, breakthrough on the techniques to deposit high quality large-area thin films without high temperature heat-treatment is important towards the practical application of proton conducting ceramics in solid-state electrochemical devices.
Author contributions
Pan Xiang: formal analysis; writing – original draft; writing – review & editing. Sara Adeeba Ismail: formal analysis; writing – original draft. Shihang Guo: writing – original draft. Lulu Jiang: writing – original draft. Donglin Han: conceptualization; formal analysis; supervision; funding acquisition; writing – original draft; writing – review & editing.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
This work was supported by the Natural Science Foundation of Jiangsu Province (Grant No. BK20211071), the Natural Science Research Project of Jiangsu Higher Education Institutions (Grant No. 23KJA150009), the Key Technology Initiative of Suzhou Municipal Science and Technology Bureau (Grant No. SYG202011), the Project of Innovation and Entrepreneurship of Jiangsu Province (Grant No. JSSCRC2021526), and Soochow Municipal Laboratory for Low Carbon Technologies and Industries.References
- C. C. Duan, J. H. Tong, M. Shang, S. Nikodemski, M. Sanders, S. Ricote, A. Almansoori and R. O'Hayre, Science, 2015, 349, 1321–1326 CrossRef PubMed.
- C. C. Duan, R. Kee, H. Y. Zhu, N. Sullivan, L. Z. Zhu, L. Z. Bian, D. Jennings and R. O'Hayre, Nat. Energy, 2019, 4, 230–240 CrossRef.
- N. Taniguchi, T. Kuroha, C. Nishimura and K. Iijima, Solid State Ionics, 2005, 176, 2979–2983 CrossRef.
- S. Robinson, A. Manerbino and W. G. Coors, J. Membr. Sci., 2013, 446, 99–105 CrossRef.
- S. Escolastico, C. Solis, C. Kjolseth and J. M. Serra, Energy Environ. Sci., 2014, 7, 3736–3746 RSC.
- D. Clark, H. Malerod-Fjeld, M. Budd, I. Yuste-Tirados, D. Beeaff, S. Aamodt, K. Nguyen, L. Ansaloni, T. Peters, P. K. Vestre, D. K. Pappas, M. I. Valls, S. Remiro-Buenamanana, T. Norby, T. S. Bjorheim, J. M. Serra and C. Kjolseth, Science, 2022, 376, 390–393 CrossRef PubMed.
- C. Duan, R. J. Kee, H. Zhu, C. Karakaya, Y. Chen, S. Ricote, A. Jarry, E. J. Crumlin, D. Hook, R. Braun, N. P. Sullivan and R. O'Hayre, Nature, 2018, 557, 217–222 CrossRef.
- C. Zuo, S. Zha, M. Liu, M. Hatano and M. Uchiyama, Adv. Mater., 2006, 18, 3318–3320 CrossRef.
- N. Zakowsky, S. Williamson and J. T. S. Irvine, Solid State Ionics, 2005, 176, 3019–3026 CrossRef.
- L. Minervini, R. W. Grimes and K. E. Sickafus, J. Am. Ceram. Soc., 2000, 83, 1873–1878 CrossRef.
- R. D. Shannon, Acta Crystallogr., Sect. A: Found. Crystallogr., 1976, 32, 751–767 CrossRef.
- M. A. Subramanian, G. Aravamudan and G. V. S. Rao, Prog. Solid State Chem., 1983, 15, 55–143 CrossRef.
- P. E. Blanchard, R. Clements, B. J. Kennedy, C. D. Ling, E. Reynolds, M. Avdeev, A. P. Stampfl, Z. Zhang and L. Y. Jang, Inorg. Chem., 2012, 51, 13237–13244 CrossRef CAS.
- H. Yamamura, H. Nishino, K. Kakinuma and K. Nomura, Solid State Ionics, 2003, 158, 359–365 CrossRef CAS.
- T. Moriga, A. Yoshiasa, F. Kanamaru, K. Koto, M. Yoshimura and S. Somiya, Solid State Ionics, 1989, 31, 319–328 CrossRef CAS.
- D. Michel, M. Perezyjorba and R. Collongues, J. Raman Spectrosc., 1976, 5, 163–180 CrossRef CAS.
- J. Gu, L. Jiang, S. A. Ismail, H. Guo and D. Han, Adv. Mater. Interfaces, 2022, 10, 2201764 CrossRef.
- S. P. S. Badwal, Solid State Ionics, 1992, 52, 23–32 CrossRef CAS.
- N. Q. Minh, J. Am. Ceram. Soc., 1993, 76, 563–588 CrossRef CAS.
- R. Khanna, T. R. Welberry and R. L. Withers, J. Phys.: Condens. Matter, 1993, 5, 4251–4262 CrossRef CAS.
- M. O. Zacate, L. Minervini, D. J. Bradfield, R. W. Grimes and K. E. Sickafus, Solid State Ionics, 2000, 128, 243–254 CrossRef CAS.
- T. H. Etsell and S. N. Flengas, Chem. Rev., 1970, 70, 339–376 CrossRef CAS.
- P. Li, I. W. Chen and J. E. Penner-Hahn, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 10074–10081 CrossRef CAS.
- E. A. Agarkova, M. A. Borik, T. V. Volkova, A. V. Kulebyakin, I. E. Kuritsyna, E. E. Lomonova, F. O. Milovich, V. A. Myzina, P. A. Ryabochkina and N. Y. Tabachkova, J. Solid State Electrochem., 2019, 23, 2619–2626 CrossRef CAS.
- M. Hartmanova, F. Kubel, V. Burskova, M. Jergel, V. Navratil, E. E. Lomonova, K. Navratil, F. Kundracik and I. Kosti, Russ. J. Electrochem., 2007, 43, 381–389 CrossRef CAS.
- S. Kim, H. J. Avila-Paredes, S. Z. Wang, C. T. Chen, R. A. De Souza, M. Martin and Z. A. Munir, Phys. Chem. Chem. Phys., 2009, 11, 3035–3038 RSC.
- B. C. H. Steele, Solid State Ionics, 2000, 134, 3–20 CrossRef CAS.
- J. B. Goodenough, Annu. Rev. Mater. Res., 2003, 33, 91–128 CrossRef CAS.
- S. Stotz and C. Wagner, Ber. Bunsen. Phys. Chem., 1966, 70, 781–788 CrossRef CAS.
- C. Wagner, Ber. Bunsen. Phys. Chem., 1968, 72, 778–781 CrossRef CAS.
- T. Yamaguchi, T. Ishiyama, H. Kishimoto, K. Develos-Bagarinao and K. Yamaji, Solid State Ionics, 2020, 354, 115414 CrossRef CAS.
- T. Ishigaki, S. Yamauchi, K. Kishio, K. Fueki and H. Iwahara, Solid State Ionics, 1986, 21, 239–241 CrossRef CAS.
- Y. Aboura and K. L. Moore, Appl. Surf. Sci., 2021, 557, 149736 CrossRef CAS.
- T. Yamaguchi, T. Ishiyama, H. Kishimoto, K. Develos-Bagarinao and K. Yamaji, Solid State Ionics, 2022, 374, 115819 CrossRef CAS.
- N. Sakai, K. Yamaji, T. Horita, H. Kishimoto, Y. P. Xiong and H. Yokokawa, Solid State Ionics, 2004, 175, 387–391 CrossRef CAS.
- L. Bay, T. Horita, N. Sakai, M. Ishikawa, K. Yamaji and H. Yokokawa, Solid State Ionics, 1998, 113, 363–367 CrossRef.
- A. G. Marinopoulos, Solid State Ionics, 2018, 315, 116–125 CrossRef CAS.
- W. Munch, K. D. Kreuer, G. Seifertli and J. Majer, Solid State Ionics, 1999, 125, 39–45 CrossRef CAS.
- W. Munch, K. D. Kreuer, G. Seifert and J. Maier, Solid State Ionics, 2000, 136, 183–189 CrossRef.
- J. A. Dawson and I. Tanaka, J. Mater. Chem. A, 2014, 2, 1400–1408 RSC.
- J. A. Dawson, H. Chen and I. Tanaka, Phys. Chem. Chem. Phys., 2014, 16, 4814–4822 RSC.
- R. Merkle, M. F. Hoedl, G. Raimondi, R. Zohourian and J. Maier, Annu. Rev. Mater. Res., 2021, 51, 461–493 CrossRef CAS.
- M. Miyamoto, A. Hamajima, Y. Oumi and S. Uemiya, Int. J. Hydrogen Energy, 2018, 43, 730–738 CrossRef CAS.
- T. S. Bjørheim, M. F. Hoedl, R. Merkle, E. A. Kotomin and J. Maier, J. Phys. Chem. C, 2019, 124, 1277–1284 CrossRef.
- Y. Hinuma, T. Toyao, T. Kamachi, Z. Maeno, S. Takakusagi, S. Furukawa, I. Takigawa and K. Shimizu, J. Phys. Chem. C, 2018, 122, 29435–29444 CrossRef CAS.
- Y. Nigara, Solid State Ionics, 2004, 171, 61–67 CrossRef CAS.
- L. Gerward, J. Staun Olsen, L. Petit, G. Vaitheeswaran, V. Kanchana and A. Svane, J. Alloys Compd., 2005, 400, 56–61 CrossRef CAS.
- G. A. Kourouklis, A. Jayaraman and G. P. Espinosa, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 4250–4253 CrossRef CAS.
- K. Wincewicz and J. Cooper, J. Power Sources, 2005, 140, 280–296 CrossRef CAS.
- J. W. Fergus, J. Power Sources, 2006, 162, 30–40 CrossRef CAS.
- S. Ramesh, V. P. Kumar, P. Kistaiah and C. V. Reddy, Solid State Ionics, 2010, 181, 86–91 CrossRef CAS.
- Y. Zheng, M. Zhou, L. Ge, S. Li, H. Chen and L. Guo, J. Alloys Compd., 2011, 509, 546–550 CrossRef CAS.
- N. K. Singh, P. Singh, M. K. Singh, D. Kumar and O. Parkash, Solid State Ionics, 2011, 192, 431–434 CrossRef CAS.
- N. Singh, O. Parkash and D. Kumar, Ionics, 2012, 19, 165–170 CrossRef.
- R. Doshi, V. L. Richards, J. D. Carter, X. P. Wang and M. Krumpelt, J. Electrochem. Soc., 1999, 146, 1273–1278 CrossRef CAS.
- N. Ai, Z. Lü, K. Chen, X. Huang, B. Wei, Y. Zhang, S. Li, X. Xin, X. Sha and W. Su, J. Power Sources, 2006, 159, 637–640 CrossRef CAS.
- M. Coduri, P. Masala, M. Allieta, I. Peral, M. Brunelli, C. A. Biffi and M. Scavini, Inorg. Chem., 2018, 57, 879–891 CrossRef CAS.
- M. Coduri, M. Scavini, M. Allieta, M. Brunelli and C. Ferrero, Chem. Mater., 2013, 25, 4278–4289 CrossRef CAS.
- A. Kossoy, Q. Wang, R. Korobko, V. Grover, Y. Feldman, E. Wachtel, A. K. Tyagi, A. I. Frenkel and I. Lubomirsky, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 054101 CrossRef.
- A. Banerji, V. Grover, V. Sathe, S. K. Deb and A. K. Tyagi, Solid State Commun., 2009, 149, 1689–1692 CrossRef CAS.
- E. R. Andrievskaya, O. A. Kornienko, O. I. Bykov, A. V. Sameliuk and Z. D. Bohatyriova, J. Eur. Ceram. Soc., 2019, 39, 2930–2935 CrossRef CAS.
- N. Sakai, K. Yamaji, T. Horita, H. Yokokawa, Y. Hirata, S. Sameshima, Y. Nigara and J. Mizusaki, Solid State Ionics, 1999, 125, 325–331 CrossRef CAS.
- H. Yokokawa, T. Horita, N. Sakai, K. Yamaji, M. Brito, Y. Xiong and H. Kishimoto, Solid State Ionics, 2004, 174, 205–221 CrossRef CAS.
- Y. P. Xiong, K. Yamaji, T. Horita, N. Sakai and H. Yokokawa, J. Electrochem. Soc., 2002, 149, E450–E454 CrossRef CAS.
- Y. Nigara, K. Kawamura, T. Kawada, J. Mizusaki and M. Ishigame, J. Electrochem. Soc., 1999, 146, 2948–2953 CrossRef CAS.
- Y. Nigara, Solid State Ionics, 2003, 159, 135–141 CrossRef CAS.
- Y. Nigara, K. Kawamura, T. Kawada and J. Mizusaki, Solid State Ionics, 2000, 136, 215–221 CrossRef.
- Y. Nigara, K. Yashiro, T. Kawada and J. Mizusaki, Solid State Ionics, 2001, 145, 365–370 CrossRef CAS.
- V. Besikiotis, C. S. Knee, I. Ahmed, R. Haugsrud and T. Norby, Solid State Ionics, 2012, 228, 1–7 CrossRef CAS.
- D. Y. Wang, D. S. Park, J. Griffith and A. S. Nowick, Solid State Ionics, 1981, 2, 95–105 CrossRef CAS.
- J. Faber, C. Geoffroy, A. Roux, A. Sylvestre and P. Abelard, Appl. Phys. A: Mater. Sci. Process., 1989, 49, 225–232 CrossRef.
- T. Norby, M. Wideroe, R. Glockner and Y. Larring, Dalton Trans., 2004, 3012–3018 RSC.
- L. E. Kalland, A. Loken, T. S. Bjorheim, R. Haugsrud and T. Norby, Solid State Ionics, 2020, 354, 115401 CrossRef CAS.
- S. A. Ismail, L. L. Jiang, P. Zhong, T. Norby and D. L. Han, J. Alloys Compd., 2022, 899, 163306 CrossRef CAS.
- S. A. Ismail and D. L. Han, J. Am. Ceram. Soc., 2022, 105, 7548–7557 CrossRef CAS.
- W. Sun, S. Fang, L. Yan and W. Liu, Fuel Cells, 2012, 12, 457–463 CrossRef CAS.
- T. Shimura, M. Komori and H. Iwahara, Solid State Ionics, 1996, 86–88, 685–689 CrossRef CAS.
- T. Omata, Solid State Ionics, 2004, 167, 389–397 CrossRef CAS.
- G. B. D. Huo, D. Siméone, H. Khodja and S. Surblé, ECS Meeting Abstracts, 2015, MA2015-03, 405 CrossRef.
- E. Antonova, E. Tropin and A. Khodimchuk, Ionics, 2022, 28, 5181–5188 CrossRef CAS.
- T. Omata and S. Otsuka-Yao-Matsuo, J. Electrochem. Soc., 2001, 148, E252–E261 CrossRef CAS.
- Q. A. Islam, S. Nag and R. N. Basu, Mater. Res. Bull., 2013, 48, 3103–3107 CrossRef CAS.
- E. P. Antonova, M. V. Ananyev, A. S. Farlenkov, E. S. Tropin, A. V. Khodimchuk and N. M. Porotnikova, Russ. J. Electrochem., 2017, 53, 651–657 CrossRef CAS.
- D. Han, K. Kojima, M. Majima and T. Uda, J. Electrochem. Soc., 2014, 161, F977–F982 CrossRef CAS.
- T. Omata, K. Okuda, S. Tsugimoto and S. Otsuka-Matsuo-Yao, Solid State Ionics, 1997, 104, 249–258 CrossRef CAS.
- E. P. Antonova, A. S. Farlenkov, E. S. Tropin, V. A. Eremin, A. V. Khodimchuk and M. V. Ananyev, Solid State Ionics, 2017, 306, 112–117 CrossRef CAS.
- M. Pirzada, R. W. Grimes, L. Minervini, J. F. Maguire and K. E. Sickafus, Solid State Ionics, 2001, 140, 201–208 CrossRef CAS.
- M. E. Björketun, C. S. Knee, B. J. Nyman and G. Wahnström, Solid State Ionics, 2008, 178, 1642–1647 CrossRef.
- B. J. Nyman, M. E. Björketun and G. Wahnström, Solid State Ionics, 2011, 189, 19–28 CrossRef CAS.
- K. Toyoura, A. Nakamura and K. Matsunaga, J. Phys. Chem. C, 2015, 119, 8480–8487 CrossRef CAS.
- M. P. Vandijk, K. J. Devries and A. J. Burggraaf, Solid State Ionics, 1983, 9–10, 913–919 CrossRef CAS.
- V. A. Vorotnikov, S. A. Belyakov, M. S. Plekhanov, A. Y. Stroeva, A. S. Lesnichyova, O. M. Zhigalina, D. N. Khmelenin, A. V. Atanova, V. G. Basu and A. V. Kuzmin, Ceram. Int., 2022, 48, 35166–35175 CrossRef CAS.
- J. A. Labrincha, J. R. Frade and F. M. B. Marques, Solid State Ionics, 1997, 99, 33–40 CrossRef CAS.
- D. L. Han, K. Kato and T. Uda, Chem. Commun., 2017, 53, 12684–12687 RSC.
- X. R. Zhang, L. L. Jiang, S. H. Guo and D. L. Han, ChemSusChem, 2022, 15, e202201879 CrossRef CAS PubMed.
- D. L. Han, P. Zhong, X. R. Zhang and L. L. Jiang, J. Mater. Chem. A, 2022, 10, 8887–8897 RSC.
- Y. Okuyama, T. Kozai, S. Ikeda, M. Matsuka, T. Sakai and H. Matsumoto, Electrochim. Acta, 2014, 125, 443–449 CrossRef CAS.
- A. Magraso, J. Power Sources, 2013, 240, 583–588 CrossRef CAS.
- R. Haugsrud and T. Norby, Nat. Mater., 2006, 5, 193–196 CrossRef CAS.
- A. V. Shlyakhtina, J. C. C. Abrantes, E. Gomes, N. V. Lyskov, E. Y. Konysheva, S. A. Chernyak, E. P. Kharitonova, O. K. Karyagina, I. V. Kolbanev and L. G. Shcherbakova, Materials, 2019, 12, 2452 CrossRef CAS.
- A. V. Shlyakhtina, N. V. Lyskov, E. Y. Konysheva, S. A. Chernyak, I. V. Kolbanev, G. A. Vorobieva and L. G. Shcherbakova, J. Solid State Electrochem., 2020, 24, 1475–1486 CrossRef CAS.
- K. E. J. Eurenius, E. Ahlberg and C. S. Knee, Solid State Ionics, 2010, 181, 1258–1263 CrossRef CAS.
- K. E. J. Eurenius, E. Ahlberg and C. S. Knee, Solid State Ionics, 2010, 181, 1577–1585 CrossRef CAS.
- H. Fjeld, R. Haugsrud, A. Gunnas and T. Norby, Solid State Ionics, 2008, 179, 1849–1853 CrossRef CAS.
- K. E. J. Eurenius, E. Ahlberg, I. Ahmed, S. G. Eriksson and C. S. Knee, Solid State Ionics, 2010, 181, 148–153 CrossRef CAS.
- K. E. J. Eurenius, H. K. Bentzer, N. Bonanos, E. Ahlberg and C. S. Knee, J. Solid State Electrochem., 2010, 15, 2571–2579 CrossRef.
- K. E. J. Eurenius, E. Ahlberg and C. S. Knee, Dalton Trans., 2011, 40, 3946–3954 RSC.
- T. S. Bjorheim, V. Besikiotis and R. Haugsrud, Dalton Trans., 2012, 41, 13343–13351 RSC.
- Y. Ling, J. Chen, Z. Wang, C. Xia, R. Peng and Y. Lu, Int. J. Hydrogen Energy, 2013, 38, 7430–7437 CrossRef CAS.
- Y. Wu, Z. Gong, J. Hou, L. Miao, H. Tang and W. Liu, Int. J. Hydrogen Energy, 2019, 44, 13835–13842 CrossRef CAS.
- T. Tu, J. Liu and K. Peng, Ceram. Int., 2017, 43, 16384–16390 CrossRef CAS.
- B. Zhang, K. Wu and K. Peng, J. Power Sources, 2018, 399, 157–165 CrossRef CAS.
- Z. Zhong, Y. Jiang, Z. Lian, X. Song and K. Peng, Ceram. Int., 2020, 46, 12675–12685 CrossRef CAS.
- Z. Tao, L. Bi, S. Fang and W. Liu, J. Power Sources, 2011, 196, 5840–5843 CrossRef CAS.
- T. Tu, B. Zhang, J. Liu, K. Wu and K. Peng, Electrochim. Acta, 2018, 283, 1366–1374 CrossRef CAS.
- B. Zhang, Z. Zhong, T. Tu, K. Wu and K. Peng, J. Power Sources, 2019, 412, 631–639 CrossRef CAS.
- M. Zhang, D. Wang, L. Miao, Z. Jin, K. Dong and W. Liu, Electrochem. Commun., 2021, 126, 107026 CrossRef CAS.
- Z. Tao, L. Yan, J. Qiao, B. Wang, L. Zhang and J. Zhang, Prog. Mater. Sci., 2015, 74, 1–50 CrossRef CAS.
- H. Matsumoto, S. Okada, S. Hashimoto, K. Sasaki, R. Yamamoto, M. Enoki and T. Ishihara, Ionics, 2007, 13, 93–99 CrossRef CAS.
- S. Fang, L. Bi, C. Yang, L. Yan, C. Chen and W. Liu, J. Alloys Compd., 2009, 475, 935–939 CrossRef CAS.
- L. Yan, W. Sun, L. Bi, S. Fang, Z. Tao and W. Liu, Int. J. Hydrogen Energy, 2010, 35, 4508–4511 CrossRef CAS.
- J. W. Phair and S. P. S. Badwal, Ionics, 2006, 12, 103–115 CrossRef CAS.
- S. Fang, L. Bi, L. Yan, W. Sun, C. Chen and W. Liu, J. Phys. Chem. C, 2010, 114, 10986–10991 CrossRef CAS.
- Z. Zhu, W. Sun, Z. Wang, J. Cao, Y. Dong and W. Liu, J. Power Sources, 2015, 281, 417–424 CrossRef CAS.
- Z. Zhu, L. Yan, H. Liu, W. Sun, Q. Zhang and W. Liu, Int. J. Hydrogen Energy, 2012, 37, 12708–12713 CrossRef CAS.
- W. Sun, Z. Shi and W. Liu, J. Electrochem. Soc., 2013, 160, F585–F590 CrossRef CAS.
- Y. Nigara, J. Mizusaki, K. Kawamura, T. Kawada and M. Ishigame, Solid State Ionics, 1998, 113, 347–354 CrossRef.
- F. Liu, D. Ding and C. Duan, Adv. Sci., 2023, 10, e2206478 CrossRef PubMed.
- I. A. Amar, R. Lan, C. T. G. Petit and S. Tao, J. Solid State Electrochem., 2011, 15, 1845–1860 CrossRef CAS.
- G. Marnellos, S. Zisekas and M. Stoukides, J. Catal., 2000, 193, 80–87 CrossRef CAS.
- G. Marnellos and M. Stoukides, Science, 1998, 282, 98–100 CrossRef CAS.
- L. Zhu, C. Cadigan, C. Duan, J. Huang, L. Bian, L. Le, C. H. Hernandez, V. Avance, R. O'Hayre and N. P. Sullivan, Commun. Chem., 2021, 4, 121 CrossRef CAS PubMed.
- C. Chen and G. L. Ma, J. Alloys Compd., 2009, 485, 69–72 CrossRef CAS.
- W. B. Wang, X. B. Cao, W. J. Gao, F. Zhang, H. T. Wang and G. L. Ma, J. Membr. Sci., 2010, 360, 397–403 CrossRef CAS.
- T. N. Ye, S. W. Park, Y. F. Lu, J. Li, M. Sasase, M. Kitano and H. Hosono, J. Am. Chem. Soc., 2020, 142, 14374–14383 CrossRef CAS PubMed.
- J. Will, A. Mitterdorfer, C. Kleinlogel, D. Perednis and L. J. Gauckler, Solid State Ionics, 2000, 131, 79–96 CrossRef CAS.
- P. Kuntke, M. R. Arredondo, L. Widyakristi, A. ter Heijne, T. H. J. A. Sleutels, H. V. M. Hamelers and C. J. N. Buisman, Environ. Sci. Technol., 2017, 51, 3110–3116 CrossRef CAS.
- Y. Xie, Solid State Ionics, 2004, 168, 117–121 CrossRef CAS.
- J.-D. Wang, Y.-H. Xie, Z.-F. Zhang, R.-Q. Liu and Z.-J. Li, Mater. Res. Bull., 2005, 40, 1294–1302 CrossRef CAS.
- R. Liu, Y. Xie, J. Wang, Z. Li and B. Wang, Solid State Ionics, 2006, 177, 73–76 CrossRef CAS.
- D. L. Han and T. Uda, J. Mater. Chem. A, 2018, 6, 18571–18582 RSC.
Footnote |
| † These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2024 |