First-principles calculations of strain engineering in NaYF4-based nanocrystals with hydroxyl impurities†
Xian
Qin
 * and
Xiaogang
Liu
* and
Xiaogang
Liu

Department of Chemistry, National University of Singapore, Singapore 117543. E-mail: chmqinx@nus.edu.sg
First published on 16th November 2021
Abstract
Lanthanide-based nanocrystals with heterogeneous core–shell structures possess elastic strain due to lattice mismatch and volumetric expansion or shrinkage. Strain relaxation is usually accompanied by lattice defects, especially those point defects and small defect clusters. However, the influence of strain on the formation of lattice defects remains unclear. Using OH− ions as a representative lattice impurity, first-principles calculations can be used to address the correlation between the thermodynamic stability of OH-based substitutional defects and elastic strain. Moreover, the concentration of OH− impurities in both strained and relaxed sodium yttrium fluoride lattices can be greatly reduced by increasing the concentration of fluoride-containing precursors. These findings suggest that minimal incorporation of OH− ions effectively suppresses multiphonon nonradiative relaxation and thus boost the efficiency of upconversion conversion.
Introduction
Heteroepitaxial growth techniques have proven effective in regulating the electrical, optical, magnetic, and mechanical properties of given materials, mainly due to subtle interactions and cooperative efforts of individual constituents.1–3 Although epitaxial growth of high-quality, coherent heterostructures requires small lattice mismatches (∼1%), epitaxial growth for systems with large lattice mismatches (>8%) can be achieved by matching integral multiples of the main crystal facets between the epitaxial layer and the matrix.4Given the slight differences in the cationic radii of the lanthanide series, the epitaxial growth approach has been extensively used to prepare lanthanide-doped core–shell nanocrystals with controlled shell thickness.5–9 The core–shell engineering not only enhances upconversion efficiency by suppressing surface quenching but also endows nanocrystals with new functionalities that are not available in their bulk counterparts.10–14
Lattice mismatch between core and shell components plays a central role in dictating the optical response of upconversion nanocrystals.15–17 This is because the interfacial tension caused by the mismatch contributes to changes in the free energy during heterogeneous nucleation, thereby affecting the quality and crystalline integrity of epitaxial layers. Notably, it has been shown that the mode (compressive or tensile) rather than the magnitude of the mismatch strain determines the growth coherence of shell layers.18
Apart from lattice mismatch-induced strains, nanocrystals are also subject to lattice expansion or shrinkage during hydrothermal synthesis. To reach a steady state, elastic strain in nanocrystals may relax to some extent and form lattice defects, especially point defects in small nanocrystals. The formation of defects facilitates ion diffusion between core and shell constituents, thereby resulting in cation mixing in core–shell nanocrystals.19–21 Although various core–shell structures have been constructed using different lanthanide-containing materials, it remains unclear how elastic strain affects lattice integrity and upconversion emission.
Here, we systematically study the influence of elastic strain on the formation and stability of hydroxyl (OH−) impurities in cubic-phase NaYF4 core–shell nanocrystals by first-principles calculations based on density functional theory (DFT). The OH− ion was chosen as a model impurity because of its capacity for mediating nonradiative multiphonon relaxation in upconversion nanosystems. We show that OH− is incorporated into host lattices with high probability by substituting F− ions (OHF). Moreover, its concentration increases with the magnitude of elastic tensile loading. In contrast, compressive strain mitigates the formation of such lattice defects. Under fluoride-rich conditions, core–shell nanoparticles with compressive shells can accommodate minimal OHF defects, reduce vibrational coupling, and improve excitation energy harvesting for enhanced upconversion luminescence.
Computational details
First-principles calculations were performed based on DFT implemented in the Vienna ab initio package (VASP) with pseudopotentials constructed by the projector-augmented wave methods.22,23 We used the semi-local generalized gradient approximation in the form of Perdew–Burke–Ernzerhof (GGA-PBE) to characterize electron exchange–correlation interactions.24 To optimize electronic calculations, 15% of the Hartree–Fock exchange interaction was incorporated into the GGA-PBE functional using the screened-exchange hybrid density functional HSE06.25A 97-atom supercell model was employed to investigate the thermodynamic stability of OHF defects in the inner region of a given nanocrystal. Our previous study showed that changes in formation energies of point defects are negligible when the supercell atom increases to 144.26K-Point samplings of 4 × 4 × 2 and 2 × 2 × 2 Monkhorst–Pack meshes were used for the unit cell and supercell, respectively. A slab model containing 218 atoms was constructed to calculate the formation energy of OHF defects on nanocrystal surfaces. Each slab was separated by a 15 Å-thick vacuum layer. A 2 × 2 × 1 Monkhorst–Pack mesh was used for the integrations in the Brillouin zone. For all calculations, the energy cutoff of the plane-wave basis set was set to 520 eV and the energy convergence criterion was set to 1 × 10−6 eV. Note that lattice constants were fixed during geometry optimization and only atoms were allowed to relax. The optimization was terminated when the maximum residual force at each atom was less than 0.01 eV Å−1.
The formation energy of OHF defects was given as:27
| Ef = EqD − EP + nμF − nμOH + q(εF + EV + ΔV), | (1) |
Results and discussion
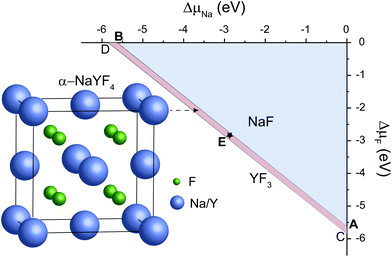
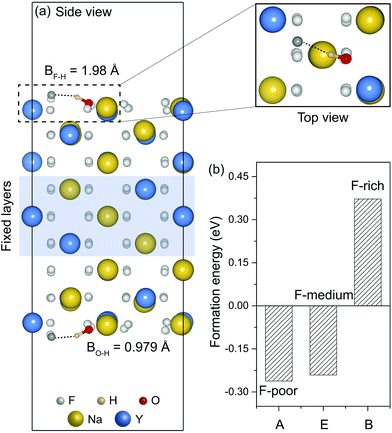
As representative lattice defects, hydroxyl impurities have been observed in both core and shell regions of NaYF4-based nanocrystals.28–31 Given their chemical similarity, the substitution of host F− ions by OH− likely requires low activation energy.32 To explore the atomic and energetic implications of such substitution, we first estimated a thermodynamic stability diagram of α-NaYF4 as a function of the relative chemical potentials of sodium (ΔμNa) and fluoride (ΔμF), relative to their elemental substances (ESI and Table S1†). The plotted phase diagram indicates that α-NaYF4 is stable only in a narrow range (Fig. 1, pink region). Three representative conditions, namely fluoride-poor (point A), fluoride-medium (point E), and fluoride-rich (point B), are selected to calculate the formation energy of OHF.We first studied the OHF formation in the inner region of an unstrained nanocrystal. Optimized atomic structures showed that Na+ and F− ions in the first coordination shell of OH− are slightly relaxed outward, except for Y3+ and F−, which forms a hydrogen bond with H+, as manifested by the change in bond length (Fig. 2a and Table S2†). Additionally, the O−H bond length shows a minor change compared to that of a free OH− ion, suggesting negligible lattice distortion. Plotting the formation energy as a function of chemical potential and Fermi level revealed that the formation energy increases as the synthetic conditions change from F-poor to F-rich (Fig. 2b–d). Notably, neutral OHF is stable over a wide range of εF, while the single positive charge state of OHF becomes more stable when εF is close to the host VBM. More specifically, formation energies of neutral OHF are 0.264, 0.285, and 0.898 eV, calculated under F-poor, F-medium, and F-rich conditions, respectively. This suggests a facile substitution of OH− for F− ions under F-poor or F-medium conditions. It is noteworthy that OHF can form under F-rich conditions because of its moderate formation energy. On the other hand, conventional synthetic methods for lanthanide-doped fluoride nanocrystals generally require a reaction temperature of ∼300 °C, which facilitates the replacement of F− by OH−.33
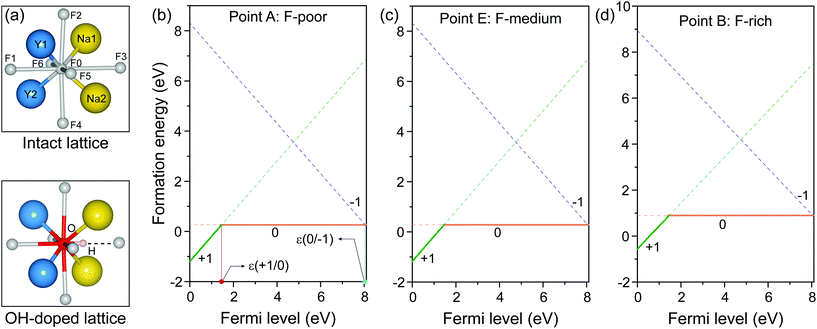 | ||
| Fig. 2 (a) Optimized first coordination shell of F− (upper panel) and OH− (lower panel) ions. (b–d) Formation energies of OHF defects as a function of Fermi energy under F-poor, F-medium, and F-rich conditions (points A, E, and B in Fig. 1). OHF denotes the substitution of F− by OH−, and ε is the corresponding thermodynamic transition level. | ||
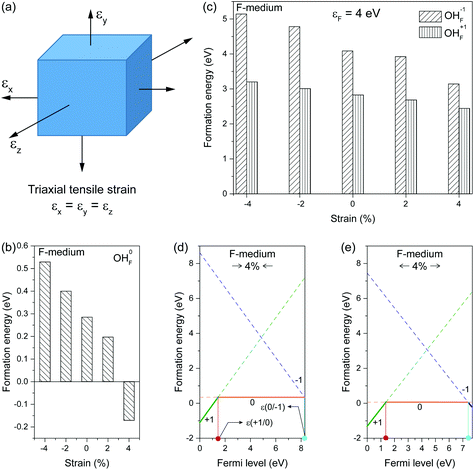
With changes in temperature during synthesis, fluoride nanocrystals can undergo thermal expansion or shrinkage. The mode and magnitude of the corresponding hydrostatic strains depend on the thermal response of host materials. For example, the lattice constant of NaF increases with increasing temperature.34,35 By comparison, the cubic SrF3 lattice contracts with increasing temperature.36 Additionally, the pressure-induced hydrostatic strain has been deliberately applied to lanthanide-containing fluorides, garnets, and oxides for optical modulation.37–40 To probe the influence of hydrostatic elastic strain on OHF formation, we employed a triaxial strain scheme to mimic the expansion and contraction of fluoride lattices (Fig. 3a). Considering that the precursors for NaYF4 nanocrystal synthesis usually follow the stoichiometry 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4, we investigated the formation of OHF in strained lattices under F-medium conditions unless otherwise stated.
4, we investigated the formation of OHF in strained lattices under F-medium conditions unless otherwise stated.
By applying triaxial strain to fluoride crystals, we found that the formation energy of neutral OHF increased with increasing compressive loading (Fig. 3b). In contrast, the formation energy decreased when tensile loading was applied. The same trend was observed for both positively and negatively charged OHF (Fig. 3c). In addition to changes in formation energy, the position of the thermodynamical transition level ε(q/q′) shifted in strained lattices. Note that the transition level is defined as the Fermi level at which formation energies of charge states q and q′ are equal. For illustration, let us consider lattices with 4% compressive and tensile strains. For the compressed lattice, the transition level ε(+1/0) shifted 0.131 eV toward the host VBM relative to the unconstrained lattice (Fig. 3d). In contrast, the position of ε(0/−1) remained unchanged. Upon tensile strain, the system exhibited a slight change in ε(+1/0) (Fig. 3e). Notably, ε(0/−1) shifted away from the host CBM by 0.164 eV relative to the relaxed lattice, indicative of a negative charge state of OHF stabilized by tensile strain. Given the presence of a charge state transition level at ∼1.4 eV above the host VBM, it is likely that OHF defects in rigid fluoride lattice act as nonradiative recombination centers.41
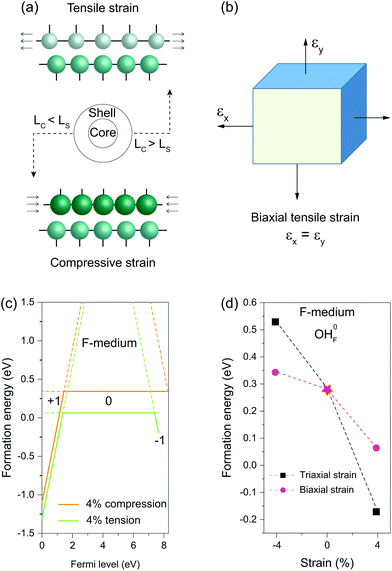
When a nanocrystal is epitaxially coated with a thin shell, the shell layer usually adopts a lattice structure commensurate with the core, thereby sustaining either in-plane tensile or compressive strain (Fig. 4a). Unlike hydrostatic strain, strain along the norm of the shell can relax due to the Poisson effect. We thus used a biaxial strain scheme to study the influence of the misfit-induced strain on OHF formation (Fig. 4b). Similarly, we found that compressive strain increases formation energy, while tensile stress reduces the formation energy (Fig. 4c). It is worth noting that the influence of biaxial strain on formation energy is less pronunced than the influence of triaxial strain. By way of illustration, formation energies of neutral OHF are 0.529, 0.343, and 0.285 eV in fluoride lattices with 4% triaxial tension, biaxial compression, and no strain, respectively. By comparison, formation energies decreased and increased with biaxial compression and tensile strain, respectively. When the tensile strain was applied to shells, the lattice spacing decreased due to lattice contraction along the normal direction, making it difficult to replace F− with large OH− ions. Given the large interface of a typical 20 nm core–shell nanocrystal, the conclusions drawn from the calculations apply not only to the coherent shell but also to the region of the anisotropic shell far from core–shell boundaries.
Considering that neutral OHF is stable over a wide range of εF, we next estimate its concentration as a function of temperature in biaxially strained and unstrained lattices using the calculated formation energy Ef by:
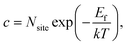 | (2) |
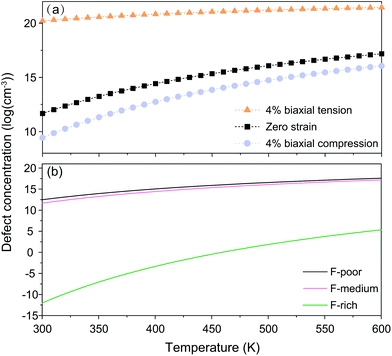
For nanocrystals synthesized under F-medium conditions, the OHF concentration increased with increasing temperature. Compared with an unstrained lattice, thin shells subjected to biaxial tensile strain contain more OHF defects, while biaxially compressed shells contain fewer OHF defects (Fig. 5a). For example, the calculated OHF concentrations at 300 °C are 3.6 × 1018, 1.2 × 1020, and 1.3 × 1022 cm−3 in 4% compressed, unstrained, and stretched lattices, respectively. Analogously, the synthetic condition has a great utility for determining the concentration of OHF defects. If we take neutral OHF in the relaxed lattice for illustration, the OHF concentration increased by six orders of magnitude when the F-poor or F-medium to F-rich conditions were varied (Fig. 5b). Specifically, the calculated OHF concentrations at 300 °C are 1.9 × 1020, 1.2 × 1020, and 3.2 × 1014 cm−3 under F-poor, F-medium, and F-rich conditions, respectively. For an unstrained 25 nm nanocrystal synthesized under F-medium conditions, the number of incorporated OH− ions is ∼980. This estimated OHF concentration could be used to generate geometric descriptors for crystal structures, enabling defect-bound theoretical estimation of intensity parameters associated with 4f–4f transitions.42,43
Using slab models, we investigated the stability of neutral OHF on α-NaYF4 nanocrystal surfaces. The (110) surface was chosen for its high stability, which is enabled by a stoichiometric arrangement of anions and cations in each plane.44 Optimized atomic structures showed a tilted O–H bond pointing toward a neighbouring F− ion, due to the formation of hydrogen bonds (Fig. 6a). The calculated formation energies of OHF at the surface under three representative conditions are much smaller than those of OHF in the interior, suggesting that OH− ions are more prone to substitute F− on the surface. Notably, we obtained negative formation energies for OHF under F-poor and F-medium conditions (Fig. 6b). This implies a spontaneous formation of OHF on nanocrystal surfaces, and nanocrystals might be unstable in the presence of such defects. As such, tensile loading of the surface may lead to a high concentration of OHF on the surface.
OH− is often considered detrimental to upconversion luminescence because it can effectively deactivate excited lanthanide ions through nonradiative multiphonon decay via electronic-to-vibrational energy transfer. The probability of multiphonon relaxation between two states of a lanthanide ion can be estimated by:45,46
| WMR = B × e−αP, | (3) |
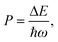 | (4) |
For NaYF4 nanocrystals with high Yb3+ dopant contents, the average distance between OH− and Yb3+ is shorter than that between OH− and lanthanide activators. We thereby use Yb3+ as a model ion to calculate the multiphonon relaxation probability. Given the high-energy stretching vibration of the O–H bonds (∼3500 cm−1), the energy gap between the 2F5/2 and 2F7/2 states of Yb3+ (∼10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 204 cm−1) can be bridged by three phonons. Considering that multiphonon relaxation, in which less than five phonons are emitted, can effectively compete with radiative decays, OH− can largely quench the neighboring excited Yb3+ ions and reduce upconversion efficiency. For the intact NaYF4 lattice with a phonon energy of ∼350 cm−1, multiphonon-induced deactivation of Yb3+ ions hardly occurs because of the emission of 29 phonons.47 Specifically, the presence of OH− enhances the probability of nonradiative multiphonon relaxation by a factor of 2.0 × 1011. Note that OH-induced deactivation of Yb3+ ions has been demonstrated to be responsible for water-associated luminescence quenching in Yb-sensitized upconversion nanocrystals.48
204 cm−1) can be bridged by three phonons. Considering that multiphonon relaxation, in which less than five phonons are emitted, can effectively compete with radiative decays, OH− can largely quench the neighboring excited Yb3+ ions and reduce upconversion efficiency. For the intact NaYF4 lattice with a phonon energy of ∼350 cm−1, multiphonon-induced deactivation of Yb3+ ions hardly occurs because of the emission of 29 phonons.47 Specifically, the presence of OH− enhances the probability of nonradiative multiphonon relaxation by a factor of 2.0 × 1011. Note that OH-induced deactivation of Yb3+ ions has been demonstrated to be responsible for water-associated luminescence quenching in Yb-sensitized upconversion nanocrystals.48
Although OH-mediated surface quenching can be effectively suppressed by shell passivation, the calculated moderate formation energy suggests that internal OHF can be readily formed, especially under F-poor conditions. The presence of internal OH− ions has also been experimentally observed, as manifested by the Fourier-transform infrared spectroscopy signal near 3400 cm−1.29 In that regard, OH− ions can be incorporated into the shell lattice. It has been shown that coherent growth of lanthanide-based core–shell nanocrystals results in a tensile-strained shell.18 Taken together, the OHF concentration in the shell is expected to be higher than that in the core region because biaxial tensile strain reduces the formation energy of OHF. Although lanthanides are spatially confined in the core, the vibronic coupling between the lanthanides in the core and the OHF in the shell could remain strong, mainly due to the small shell thickness (∼2 nm) and long-range electronic-to-vibrational energy transfer.49
Conversely, compressive strain in the shell may reduce OHF concentration due to increased formation energy. However, shell growth under compression are neither coherent nor complete, which severely limits the effectiveness of shell passivation.18 For instance, epitaxial coating of β-NaYbF4 could only be achieved with NaLuF4 and NaYF4.50 This is because other NaLnF4 (Ln = lanthanide) compositions can induce compressive strain when applied to NaYbF4 surfaces. On the other hand, the OHF concentration in both core and shell lattices can be greatly reduced when synthesized under F-rich conditions. Hence, it is believed that the OHF concentration in the core–shell nanocrystals with low-compression mismatch can reach a minimum when the fluoride content is increased during preparation.
It is noteworthy that the Gibbs free energies of the systems under study were approximated to the total energies obtained directly from DFT-based electronic calculations. Consequently, the calculated formation energy does not take into account the contribution of configurational entropy, vibrational entropy, and volume of formation. A simple dimensional analysis indicates a negligible contribution (∼0.1 meV Å−3) from the volume term, even at pressures up to 100 atm. Given the low concentration of OH− and the well-ordered supercells, the estimated contribution of configurational entropy is less than 0.1 meV per substitution site when the temperature falls in the range between 300 and 570 K. Moreover, the contribution of vibrational entropy has reportedly become significant at high temperatures (e.g., 1000 K).51 Taken together, the total energy obtained from the DFT calculation is a dominant term, and the atomistic thermodynamics approach can offer a rapid prediction of the trend of defect formation in certain materials.52,53
Conclusions
In summary, we have systematically investigated the influence of elastic strain on the formation of OHF defects in fluoride-based nanocrystals using first-principles calculations. The calculations show that both the mode and the magnitude of the strain determine the formation of OHF. For a lattice under tensile strain, the concentration of OHF defects is likely higher than that of the relaxed counterparts because of lower formation energies. In contrast, the formation of OHF can be suppressed by compressive strain. The OHF concentration can be greatly reduced when lanthanide-doped nanocrystals are prepared under F-rich conditions instead of F-poor or F-medium conditions. These findings not only provide insights into the thermodynamic stability of OHF defects in fluoride-based nanocrystals but also offer guidance for the fabrication of bright upconversion nanocrystals through strain engineering.Author contributions
X. Q. and X. L. conceived the project, discussed the results, and wrote the manuscript. X. Q. conducted the quantum mechanical calculations.Conflicts of interest
The authors declare no competing interests.Acknowledgements
This work was supported by the National Research Foundation, Prime Minister's Office, Singapore under the NRF Investigatorship program (award no. NRF-NRFI05-2019-0003). The computational work for this article was supported by resources of the High Performance Computing System at National University of Singapore.References
- K. D. Gilroy, X. Yang, S. Xie, M. Zhao, D. Qin and Y. Xia, Adv. Mater., 2018, 30, 1706312 CrossRef PubMed.
- Z. Xia and S. Guo, Chem. Soc. Rev., 2019, 48, 3265–3278 RSC.
- J. Liu and J. Zhang, Chem. Rev., 2020, 120, 2123–2170 CrossRef CAS PubMed.
- J. Narayan and B. C. Larson, J. Appl. Phys., 2003, 93, 278 CrossRef CAS.
- N. J. J. Johnson and F. C. J. M. van Veggel, Nano Res., 2013, 6, 547–561 CrossRef CAS.
- Y. Zhang, L. Huang and X. Liu, Angew. Chem., Int. Ed., 2016, 55, 5718–5722 CrossRef CAS PubMed.
- H. Dong, L. D. Sun, L. D. Li, R. Si, R. Liu and C. H. Yan, J. Am. Chem. Soc., 2017, 139, 18492–18495 CrossRef CAS PubMed.
- P. Z. Zhang, R. Liu, L. D. Sun, H. Dong, L. D. Li, X. Y. Zheng, K. Wu and C. H. Yan, Inorg. Chem. Front., 2018, 5, 1800–1804 RSC.
- D. Liu, Y. Jin, X. Dong, L. Liu, D. Jin, J. A. Capobianco and D. Shen, Nanomaterials, 2021, 11, 654 CrossRef CAS PubMed.
- X. Chen, D. Peng, Q. Ju and F. Wang, Chem. Soc. Rev., 2015, 44, 1318–1330 RSC.
- A. Pilch, C. Würth, M. Kaiser, D. Wawrzyńczyk, M. Kurnatowska, S. Arabasz, K. Prorok, M. Samoć, W. Strek, U. Resch-Genger and A. Bednarkiewicz, Small, 2017, 13, 1701635 Search PubMed.
- B. Zhou, L. Yan, J. Huang, X. Liu, L. Tao and Q. Zhang, Nat. Photonics, 2020, 14, 760–766 CrossRef CAS.
- D. Hudry, I. A. Howard, R. Popescu, D. Gerthsen and B. S. Richards, Adv. Mater., 2019, 31, 1900623 CrossRef PubMed.
- R. A. Janjua, O. Iqbal, M. A. Ahmed, A. A. Al-Kahtani, S. Saeed, M. Imran and A. G. Wattoo, RSC Adv., 2021, 11, 20746–20751 RSC.
- A. Kar and A. Patra, Nanoscale, 2012, 4, 3608–3619 RSC.
- J. Zhao, X. Chen, B. Chen, X. Luo, T. Sun, W. Zhang, C. Wang, J. Lin, D. Su, X. Qiao and F. Wang, Adv. Funct. Mater., 2019, 29, 1903295 CrossRef CAS.
- J. Zhao, B. Chen and F. Wang, Adv. Mater., 2020, 32, 2004142 CrossRef CAS PubMed.
- N. J. J. Johnson and F. C. J. M. van Veggel, ACS Nano, 2014, 8, 10517–10527 CrossRef CAS PubMed.
- J. DiMaio, B. Kokuoz, T. L. James, T. Harkey, D. Monofsky and J. Ballato, Opt. Express, 2008, 16, 11769–11775 CrossRef CAS PubMed.
- D. Hudry, D. Busko, R. Popescu, D. Gerthsen, A. M. M. Abeykoon, C. Kübel, T. Bergfeldt and B. S. Richards, Chem. Mater., 2017, 29, 9238–9246 CrossRef CAS.
- P. U. Bastian, S. Nacak, V. Roddatis and M. U. Kumke, J. Phys. Chem. C, 2020, 124, 11229–11238 CrossRef CAS.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed . Erratum: Phys. Rev. Lett., 1997, 78, 1396.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207 CrossRef CAS . Erratum: J. Chem. Phys., 2006, 124, 219906.
- X. Qin, L. Shen, L. Liang, S. Han, Z. Yi and X. Liu, J. Phys. Chem. C, 2019, 123, 11151–11161 CrossRef CAS.
- C. G. Van De Walle and J. Neugebauer, J. Appl. Phys., 2004, 95, 3851 CrossRef CAS.
- F. T. Rabouw, P. T. Prins, P. Villanueva-Delgado, M. Castelijns, R. G. Geitenbeek and A. Meijerink, ACS Nano, 2018, 12, 4812–4823 CrossRef CAS PubMed.
- Y. Feng, Z. Li, Q. Li, J. Yuan, L. Tu, L. Ning and H. Zhang, Light: Sci. Appl., 2021, 10, 105 CrossRef CAS PubMed.
- A. Skripka, A. Benayas, C. D. S. Brites, I. R. Martín, L. D. Carlos and F. Vetrone, Nano Lett., 2020, 20, 7648–7654 CrossRef CAS PubMed.
- S. Mei, J. Zhou, H. T. Sun, Y. Cai, L. D. Sun, D. Jin and C. H. Yan, Adv. Sci., 2021, 8, 2003325 CrossRef CAS PubMed.
- C. Homann, L. Krukewitt, F. Frenzel, B. Grauel, C. Würth, U. Resch-Genger and M. Haase, Angew. Chem., Int. Ed., 2018, 57, 8765–8769 CrossRef CAS PubMed.
- Y. Liu, D. Tu, H. Zhu and X. Chen, Chem. Soc. Rev., 2013, 42, 6924–6958 RSC.
- B. W. James and B. Yates, Philos. Mag., 2006, 12, 253–259 CrossRef.
- A. S. M. Rao, K. Narender, K. G. K. Rao and N. G. Krishna, J. Mod. Phys., 2013, 4, 208–214 CrossRef.
- B. K. Greve, K. L. Martin, P. L. Lee, P. J. Chupas, K. W. Chapman and A. P. Wilkinson, J. Am. Chem. Soc., 2010, 132, 15496–15498 CrossRef CAS PubMed.
- U. R. Rodríguez-Mendoza, S. F. León-Luis, J. E. Muñoz-Santiuste, D. Jaque and V. Lavín, J. Appl. Phys., 2013, 113, 213517 CrossRef.
- M. D. Wisser, M. Chea, Y. Lin, D. M. Wu, W. L. Mao, A. Salleo and J. A. Dionne, Nano Lett., 2015, 15, 1891–1897 CrossRef CAS PubMed.
- E. Bandiello, C. Popescu, E. L. Da Silva, J. Á. Sans, D. Errandonea and M. Bettinelli, Inorg. Chem., 2020, 59(24), 18325–18337 CrossRef CAS PubMed.
- M. A. Antoniak, S. J. Zelewski, R. Oliva, A. Żak, R. Kudrawiec and M. Nyk, ACS Appl. Nano Mater., 2020, 3, 4209–4217 CrossRef CAS.
- X. Zhang, J. X. Shen, M. E. Turiansky and C. G. Van de Walle, Nat. Mater., 2021, 20, 971–976 CrossRef CAS PubMed.
- R. T. Moura, A. N. Carneiro Neto, E. C. Aguiar, C. V. Santos, E. M. de Lima, W. M. Faustino, E. E. S. Teotonio, H. F. Brito, M. C. F. C. Felinto, R. A. S. Ferreira, L. D. Carlos, R. L. Longo and O. L. Malta, Opt. Mater.: X, 2021, 11, 100080 Search PubMed.
- A. N. Carneiro Neto and R. T. Moura, Chem. Phys. Lett., 2020, 757, 137884 CrossRef CAS.
- P. W. Tasker, J. Phys. C: Solid State Phys., 1979, 12, 4977 CrossRef CAS.
- L. A. Riseberg and H. W. Moos, Phys. Rev., 1968, 174, 429 CrossRef CAS.
- M. J. Weber, Phys. Rev., 1968, 171, 283 CrossRef CAS.
- J. F. Suyver, J. Grimm, M. K. Van Veen, D. Biner, K. W. Krämer and H. U. Güdel, J. Lumin., 2006, 117, 1–12 CrossRef CAS.
- R. Arppe, I. Hyppänen, N. Perälä, R. Peltomaa, M. Kaiser, C. Würth, S. Christ, U. Resch-Genger, M. Schäferling and T. Soukka, Nanoscale, 2015, 7, 11746–11757 RSC.
- A. Aharoni, D. Oron, U. Banin, E. Rabani and J. Jortner, Phys. Rev. Lett., 2008, 100, 057404 CrossRef PubMed.
- J. Zhao, B. Chen, X. Chen, X. Zhang, T. Sun, D. Su and F. Wang, Nanoscale, 2020, 12, 13973–13979 RSC.
- D. Gryaznov, M. W. Finnis, R. A. Evarestov and J. Maier, Solid State Ionics, 2014, 254, 11–16 CrossRef CAS.
- M. Lan, R. Wang, Z.-H. Yang, X. Wang, S. Sun and S.-H. Wei, Phys. Rev. B, 2021, 103, 245201 CrossRef CAS.
- B. Lou, J. Wen, L. Ning, M. Yin, C.-G. Ma and C.-K. Duan, Phys. Rev. B, 2021, 104, 115101 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1nr06904g |
| This journal is © The Royal Society of Chemistry 2021 |