Transition from isolated to interacting copper(II) pairs in extended lattices evaluated by single crystal EPR spectroscopy†
Nicolás I.
Neuman
a,
Emerson
Burna
a,
Ricardo
Baggio
b,
Mario C. G.
Passeggi
a,
Alberto C.
Rizzi
a and
Carlos D.
Brondino
*a
aDepartamento de Física, Facultad de Bioquímica y Ciencias Biológicas, Universidad Nacional del Litoral, S3000ZAA Santa Fe, Argentina. E-mail: brondino@fbcb.unl.edu.ar
bGerencia de Investigación y Aplicaciones, Comisión Nacional de Energía Atómica, Avenida Gral Paz y Constituyentes, San Martín, Buenos Aires, Argentina
First published on 7th July 2015
Abstract
We report the synthesis and X-ray structure of the dimeric zinc(II) compound [Zn(tda)(phen)]2·H2tda, (tda = thiodiacetic acid, phen = 1,10-phenanthroline) hereafter Zn(tda)(phen), and a single crystal EPR study of Zn(tda)(phen) doped with Cu(II) ions. Zn(tda)(phen) is isomorphous to its Cu(II) analogue. The EPR spectra show a central signal composed of one to four resonances assigned to Cu–Zn heterodimers, flanked by less intense satellite signals assigned to Cu–Cu homodimers. Analysis of single crystal EPR data allowed us to determine the g- and A-matrices of the Cu(II) ion and the anisotropic ZFS parameters of the homodimer. Within the experimental error, the Cu(II) g-matrix obtained for the diluted compound was identical to that previously determined by us in pure Cu(tda)(phen). The ZFS is shown to be dominated by magnetic dipolar coupling between the unpaired electrons mainly centered around the Cu(II) ions, although partially delocalized over the equatorial copper ligands. DFT calculations yielded spin population values compatible with those determined from the analysis of the anisotropic ZFS assuming a distributed dipole model. The information obtained from the diluted compound was used to evaluate the interdimeric exchange interaction between dimeric units in pure Cu(tda)(phen). The comparison between both point and distributed dipole approximations is discussed with reference to the analysis of the EPR data.
Introduction
The study of exchange-coupled transition metal ion complexes has played an important role in the development of the field of molecular magnetism.1–4 The information gained with these studies has been essential to establish the underlying molecular bases to design not only paramagnetic materials with predictable magnetic properties5,6 but also to design materials such as molecular-based and single-molecule magnets.7–11 These studies have also been relevant in biology because exchange-coupled transition metal ion systems occur in proteins in which the superexchange pathways are involved in electron-transfer reactions.12–16 Thus, the characterization of exchange coupled systems is nowadays a multidisciplinary research field owing to their applications in chemistry, biology, and physics.Among the vast number of studies on paramagnetic transition metal ion complexes, the study of dinuclear Cu(II) compounds (S = 1/2 spin pair) has been essential in the development of molecular magnetism.4,17–19 The electronic properties of these metal systems are determined by the isotropic exchange interaction, which couples the two individual electron spins (S = 1/2) to yield singlet (S = 0) and triplet (S = 1) states, and other interactions such as anisotropic and antisymmetric exchange and dipolar magnetic coupling.20 The isotropic exchange interaction (Hex = −JS1·S2) splits the singlet from the triplet state of the dimer by an energy amount J, whereas the remaining interactions can remove the three-fold degeneration of the triplet state even in zero magnetic field (ZFS). Additional splitting of the energy levels can be produced by hyperfine interactions with the copper nucleus (I = 3/2). Furthermore, in weakly exchange-coupled dimers the anisotropic interactions can appreciably mix the singlet and triplet states, in which case these states cannot be considered pure. However, the singlet–triplet nomenclature will be used throughout the text for simplicity.
In undiluted magnetic systems, the dimeric units of the crystal lattice may interact with their neighbors through different kinds of chemical paths that may transmit weak exchange interactions, hereafter designated as J′. This interaction modulates the magnetic behavior of the dimer leading to situations called weak (J′ < ZFS), intermediate (J′ ∼ ZFS), or strong (J′ > ZFS) exchange, which can be visualized by single crystal EPR spectroscopy due to the dependence of ZFS with the magnetic field orientation.20,21 For weak exchange, some features of the dimeric behavior can be detected, as EPR may show, besides the forbidden half field transition corresponding to ΔMS = 2, two resonance lines of the triplet state, as expected for a dinuclear unit, but shifted to the center of the spectra and broadened; the larger J′, the larger the shift and broadening. Particularly, for J′ > A, where A is the hyperfine constant with the copper nuclei (I = 3/2), no hyperfine structure is observed although it can be partially solved for situations with J′ < A.22,23 In contrast, for strong exchange, the two triplet lines coming from each dimeric unit merge into one absorption line.
The compound [Cu(tda)(phen)]2·H2tda (tda = thiodiacetate, phen = 1,10-phenanthroline), hereafter Cu(tda)(phen), is a ferromagnetically exchange coupled dimer (J = +3.2 cm−1), in which we determined that very weak interdimeric exchange interactions mediated by hydrophobic chemical paths modulate the dimer EPR resonances giving rise to situations of strong, intermediate, and weak exchange.24,25 Single crystal EPR spectroscopy of Cu(tda)(phen), analyzed on the basis of Anderson's exchange narrowing model26,27 together with statistical arguments, showed that the transition from a weak exchange to a strong exchange situation provoked by the interdimer interaction J′ depends also on the number of neighboring dimers in triplet states surrounding each dimeric unit.25 However, the lack of a suitable diluted Cu(II) system isomorphous to pure Cu(tda)(phen) precluded us to determine the hyperfine interaction parameters associated with the copper nuclei and the ZFS. These inconveniences were overcome by proposing a simplified model that neglected the hyperfine interaction and assumed the ZFS as entirely determined by a dipole–dipole interaction under the point dipole approximation. Although these assumptions reproduced fairly well the experimental data, some discrepancies between the experimental and simulated EPR spectra still remain, likely due to the distinct approximations used in our model.
We report here the synthesis and X-ray characterization of the dimeric zinc(II) compound [Zn(tda)(phen)]2·H2tda, hereafter Zn(tda)(phen), isomorphous to Cu(tda)(phen), and single crystal EPR spectroscopy of Zn(tda)(phen) doped with Cu(II) ions, hereafter Cu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Zn(tda)(phen). The doping of Zn(tda)(phen) was performed at high Cu
Zn(tda)(phen). The doping of Zn(tda)(phen) was performed at high Cu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Zn ratios (1
Zn ratios (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5) so as to enable the observation of EPR spectra associated with mononuclear and dinuclear Cu(II) species. This allowed us to completely determine the magnitudes associated with all the interactions contributing to the energy of the system as well as the subtle effects caused by covalency on the ZFS of the dinuclear units. The new data are used to propose a theoretical model that includes now the hyperfine interaction and covalency effects that explain the transition occurring when a copper pair is sensitive to interdimeric exchange interactions in an extended lattice.
5) so as to enable the observation of EPR spectra associated with mononuclear and dinuclear Cu(II) species. This allowed us to completely determine the magnitudes associated with all the interactions contributing to the energy of the system as well as the subtle effects caused by covalency on the ZFS of the dinuclear units. The new data are used to propose a theoretical model that includes now the hyperfine interaction and covalency effects that explain the transition occurring when a copper pair is sensitive to interdimeric exchange interactions in an extended lattice.
Experimental section
Materials
All chemicals, of commercially available reagent grade, were used as received. Water was purified by a Millipore Milli-Q system.Preparation of Zn(tda)(phen)
Single crystals of Zn(tda)(phen) were prepared as reported previously for the isomorphous Cu(tda)(phen) but using half the reported concentrations in order to slow down crystallization, which otherwise occurred within one to two hours.24 This procedure yielded suitable single crystals for X-ray diffraction.Preparation of Cu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) Zn(tda)(phen)
Zn(tda)(phen)
Single crystals of Zn(tda)(phen) doped with copper(II) impurities were prepared by mixing solutions of Cu(tda)(phen) and Zn(tda)(phen), both prepared as described above for Zn(tda)(phen), in a Cu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Zn ratio of 1
Zn ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5. This procedure yielded single crystals of ∼0.2 × 0.2 × 0.5 mm, which were suitable for the single crystal EPR experiment.
5. This procedure yielded single crystals of ∼0.2 × 0.2 × 0.5 mm, which were suitable for the single crystal EPR experiment.
Crystallography
Single crystal XRD data were collected using a Bruker Smart CCD area detector using Mo Kα radiation (λ = 0.71073 Å) (Diffractometer control: SMART; Data reduction: SAINT; Absorption correction: SADABS).28The structure was solved by direct methods (SHELXS-97)29 and refined by full-matrix least-squares on F2 (SHELXL-2015).30 Graphic material was produced using SHELXTL.28 The acidic hydrogen bonded to oxygen in the thiodiacetic acid molecule was found using a Fourier-difference map and refined isotropically with the restrained O–H distance (0.85(1) Å); those attached to carbon were positioned theoretically and allowed to ride during refinement, with Uiso(H) = 1.2 × Ueq(Host). The H2tda molecule presents the C2 symmetry, being bisected by a twofold axis through its central sulfur atom, thus rendering only one-half of the molecule independent.
A complete set of the results of the XRD crystallographic structural data has been deposited at the Cambridge Structural Database, CSD, in CIF format (deposition number CCDC 1055076). Details on the data collection procedures, structural determination methods, and structure refinement are given in the ESI, Table S1.†
The morphology of the single crystals, required to orient the sample for the single crystal EPR experiment, was determined by measuring the angles between the crystal faces using a Carl Zeiss Axiolab goniometric microscope. The monoclinic crystals are elongated prisms that grow along the c-axis and have lateral faces (110) and (1−10), with the angle between the ca* plane (a* = b × c) and the (110) plane being 36.9°.
EPR measurements
X-band CW-EPR spectra of oriented single crystals of Cu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Zn(tda)(phen) were recorded at room temperature on a Bruker EMX-Plus spectrometer equipped with a rectangular cavity with 100 kHz field modulation. Spectra were recorded in the a*b (a* = b × c), ca* and cb crystal planes by gluing the (110) face of a single crystal to a specially designed triangular-prismatic Rexolite sample holder (see Fig. S1†) with an angle of 36.9° (see above). The sample holder was glued to the tip of a 4 mm quartz EPR tube which was previously flattened by careful sanding, and the tube was introduced into the resonant cavity of the spectrometer attached to a goniometer which allowed rotating the crystal in 5° intervals in the three crystal planes.31 EPR spectra were analyzed with the EasySpin toolbox and home-made programs based on MATLAB®.32
Zn(tda)(phen) were recorded at room temperature on a Bruker EMX-Plus spectrometer equipped with a rectangular cavity with 100 kHz field modulation. Spectra were recorded in the a*b (a* = b × c), ca* and cb crystal planes by gluing the (110) face of a single crystal to a specially designed triangular-prismatic Rexolite sample holder (see Fig. S1†) with an angle of 36.9° (see above). The sample holder was glued to the tip of a 4 mm quartz EPR tube which was previously flattened by careful sanding, and the tube was introduced into the resonant cavity of the spectrometer attached to a goniometer which allowed rotating the crystal in 5° intervals in the three crystal planes.31 EPR spectra were analyzed with the EasySpin toolbox and home-made programs based on MATLAB®.32
Electronic structure calculations
Density functional theory calculations were performed based on the structure of a single complete [Cu(tda)(phen)]2 dimer.24 Calculations were performed with the ORCA program33 using the B3LYP (20% exact Hartree–Fock exchange, HFX),34–36 TPSSh (10% exact HFX),37,38 TPSS0 (25% exact HFX), ωB97x (range-separated functional with 15.77% HFX at a short range and 100% at a long-range)39 and B2PLYP (a perturbatively corrected double-hybrid with 53% HFX)40 functionals. The relativistic effects were included within the ZORA approximation41,42 for which specially recontracted basis sets were used (SV_ZORA, TZV_ZORA or QZV_ZORA, as implemented in ORCA)43 with polarization functions taken from the TZVP basis set.44Results and discussion
Crystal and molecular structures
Crystals of Zn(tda)(phen) consist of dimeric units of [Zn(II)(tda)(phen)]2, connected by H2tda molecules into chains parallel to [103]. The structure is isomorphous to its Cu(II) analogue,24 sharing most of the general structural aspects, with the obvious metric differences in the cation environment. Fig. 1 shows the structure of the dinuclear unit and Table S2† gives some selected coordination bond lengths. The dinuclear unit displays a crystallographic center of symmetry linking the two constituent moieties with each zinc atom residing in a distorted N2O3S octahedral environment. The equatorial positions are occupied by the phen nitrogen atoms (N1 and N2), and by two oxygen atoms of the tda ligand (O2A and O4A) defining some kind of a flat tetrahedron (∠N1–Zn1–O2A: 173.4(2)°, ∠N2–Zn1–O4A: 164.2(2)°), with a maximum deviation from the mean plane of 0.09(1) Å for N2, and 0.16(1) Å for the Zn1 cation. The axial positions are occupied by the thioether sulfur atom (S1A) and a bridging carboxylate oxygen (O2A) of the neighboring ligand bonded to Zn1 [0.5 − x, 0.5 − y, −z], both atoms being fairly away from the normal plane (∠S1A–Zn1–O2A′: 155.5(2)°). The dimeric structure shows two Zn(II) centers bridged by two O-atoms of carboxylate groups in a bi-bridging mode, with C1A–O2A [1.284(2) Å] significantly longer than C1A–O1A [1.216(2) Å] as expected for this type of bonding. The dimer exhibits a (μ2-oxo) Zn1–O2–Zn1[0.5 − x, 0.5 − y, −z] ring which includes the center of symmetry at [0.25, 0.25, 0] with a Zn⋯Zn separation of 3.235(1) Å and a Zn–O–Zn bridging angle of 101.3(1)°. The two five-membered chelate rings with a common Zn–S bond in each tda are roughly planar, in a “butterfly” conformation with a dihedral angle between the least-squares planes of 93.3(1)°.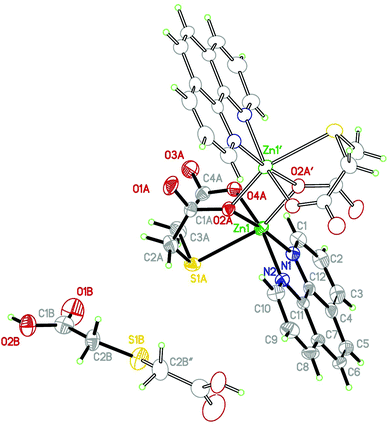 | ||
| Fig. 1 Asymmetric units in Zn(tda)(phen). Displacement ellipsoids drawn at a 40%. Symmetry codes: ′: −x + 1/2, −y + 1/2, −z; ′′: −x, y, −z + 1/2. | ||
To understand the single crystal EPR experiment of the doped compound, it is important to note that Cu(tda)(phen) and Zn(tda)(phen) show four chemically identical dimers in the unit cell related to the symmetry operation of the space group C2/c labeled as A, A′,B and B′. The copper dimers that are related to a translation (A–A′, or B–B′) are magnetically equivalent. In contrast, dimers A and B related to a 180° rotation around the b crystal axis plus a translation (0, 0, 1/2) are magnetically inequivalent. However, as described below, the phen planes of A- and B-type dimers, and therefore the equatorial ligand planes on each Zn and Cu atoms, are nearly parallel, making the g- and A-matrices of the copper dimers A and B indistinguishable within spectral resolution in the EPR experiment.
The phenanthroline planes between molecules of the same dimer type (A or B) are 3.389 Å apart in Zn(tda)(phen) (3.431 Å for Cu(tda)(phen)), whereas the phenanthroline planes of different dimer types (A–B) deviate by 3.70° (4.32° for Cu(tda)(phen)), with the shortest distance between them being 3.226 Å (3.482 Å for Cu(tda)(phen)). These distances strongly suggest delocalized π–π interactions between the aromatic planes. Thus, the dimer A(B) may interact with two type A(B) dimers and two type B(A) dimers (Fig. 2), with distances between dimers (measured from their inversion centers) being 9.932 and 10.200 Å for A–A(B–B) and A–B dimers, respectively (10.291 and 12.040 Å for Cu(tda)(phen)). Similarly to Cu(tda)(phen), nonadjacent A and B dimers in Zn(tda)(phen) are also bridged by a long mixed chemical path involving two hydrogen bonds (O–H⋯O distance = 2.58(6) Å, O–H⋯O angle = 177(6)°) and a thiodiacetic acid molecule (Fig. S2†), forming chains along the [103] direction, which interact with each other via a number of short contacts of the C–H⋯O type (see Table S3† for details). This chemical path of 15 diamagnetic atoms was discarded as the superexchange path in Cu(tda)(phen).25
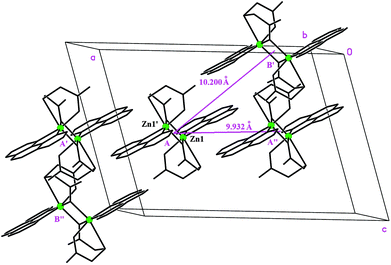 | ||
| Fig. 2 Perspective of the crystal unit cell showing a Zn(tda)(phen) dimer with its four nearest neighbors interacting through hydrophobic interactions. | ||
An extremely similar [Zn(phen)(tda)]2 dimeric unit has been reported by Grirrane et al. (Fig. S3†),45 a structure where the dimers are linked by 5 disordered water molecules filling the interdimeric voids and providing multiple H-bonds to end up in a 3D H-bonded structure.
Single crystal EPR measurements
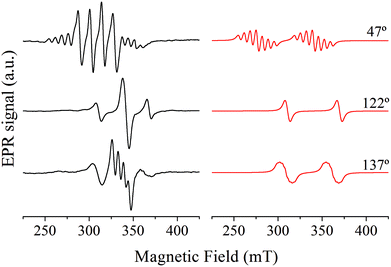
The representative single crystal EPR spectra of Cu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Zn(tda)(phen) recorded in the ca* plane are shown in Fig. 3, left panel. The spectra show a central signal composed of one to four resonances with equal intensities, as expected for isolated mononuclear Cu(II) ions (S = 1/2, I = 3/2), flanked by less intense satellite signals. The latter are composed of one to seven resonances – although not all are observed due to overlapping with the central quartet – with a 1
Zn(tda)(phen) recorded in the ca* plane are shown in Fig. 3, left panel. The spectra show a central signal composed of one to four resonances with equal intensities, as expected for isolated mononuclear Cu(II) ions (S = 1/2, I = 3/2), flanked by less intense satellite signals. The latter are composed of one to seven resonances – although not all are observed due to overlapping with the central quartet – with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4
4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 intensity pattern, typical of a S = 1 electron spin coupled with two equivalent Cu(II) nuclei.20 The central quartets and the satellite lines correspond to Cu–Zn heterodimers and to Cu–Cu homodimers, respectively.
1 intensity pattern, typical of a S = 1 electron spin coupled with two equivalent Cu(II) nuclei.20 The central quartets and the satellite lines correspond to Cu–Zn heterodimers and to Cu–Cu homodimers, respectively.
The EPR spectra in the cb and a*b crystal planes (not shown), where the copper centers are magnetically inequivalent, showed only one central quartet for every magnetic field orientation as in the ca* crystal plane, indicating that the EPR experiment cannot resolve the resonance lines corresponding to magnetically inequivalent copper ions. The reasons for this are explained in the Crystal and molecular structure section.
The central quartets corresponding to Cu–Zn heterodimers were analyzed assuming a Hamiltonian including Zeeman term and hyperfine interaction with the copper nucleus
| H = μBS1·g1·B + S1·A1·I1 | (1) |
The least-squares fitting of four equidistant Gaussian-shaped resonance lines to the central quartet spectra indicated that the experimental resonance positions are well simulated assuming eqn (1) up to the first order approximation, in which case the positions of the quartet resonance lines are given by B0 + aMI, (MI = ±3/2, ±1/2), where B0 and a are the gravity center and the hyperfine spacing of the quartet, respectively. The angular variations of the g2-factor (g = hν/μBB0) and the g2K2-factor (K = agμB/h) obtained by this procedure are shown in Fig. 4 and S4,† respectively.
The components of the g2-matrix were obtained by least-squares fitting a second-rank tensor to the data in Fig. 4
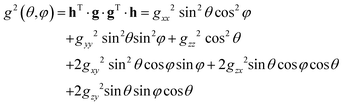 | (2) |
| g 1 = 2.055(4) | g 1 = [0.912, 0.02, −0.408] |
| g 2 = 2.073(4) | g 2 = [0.01, −0.999, −0.00] |
| g 3 = 2.307(5) | g 3 = [0.408, 0.012, 0.912] |
| A 1 = 19(10) MHz | a 1 = [−0.932, −0.009, 0.3625] |
| A 2 = 15(10) MHz | a 2 = [−0.008, 1.00, 0.005] |
| A 3 = 442(5) MHz | a 3 = [0.3625, −0.001, 0.932] |
| D 1 = 562(50) MHz | d 1 = [−0.8760, −0.2204, 0.4290] |
| D 2 = 753(60) MHz | d 2 = [−0.0629, −0.8297, −0.5546] |
| D 3 = −1315(60) MHz | d 3 = [0.4782, −0.5128, 0.7129] |
| D = −1973 MHz (−0.0658 cm−1) | |
| E = −96 MHz (−0.0032 cm−1) | |
| E/D = 0.048 | |
The satellite signals corresponding to the Cu–Cu homodimer present in Cu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Zn(tda)(phen) were analyzed assuming the spin Hamiltonian
Zn(tda)(phen) were analyzed assuming the spin Hamiltonian
| H = μBS·g·B + S·A/2·I1 + S·A/2·I1′ + S·D·S | (3) |
ZFS: point dipole approximation and distributed dipole model
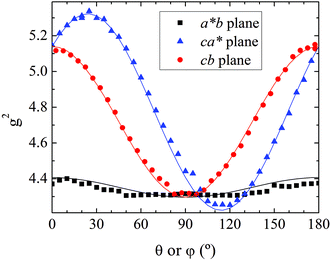
As previously analyzed,25 the ZFS of [Cu(tda)(phen)]2 was assumed to be determined by dipole–dipole interaction under the point dipole approximation. Fig. 5 shows the angular variation of the D-matrix expected for [Cu(tda)(phen)]2 under the point dipole approximation (blue line) together with that obtained from the experimental data (black line). As shown, the point dipole approximation predicts an order of magnitude of the ZFS along with a reasonable angular variation, but clearly other factors should be taken into consideration for a full interpretation of the experimental data. We considered that these discrepancies were due to spin delocalization onto the copper ligands; g- and A-matrices results indicate that the unpaired spin is in a d(x2 − y2) type orbital, and therefore only delocalization onto copper equatorial ligands was considered. With this in mind, we simulated the angular variation of the experimental D-matrix (Fig. 5, black line) assuming the so-called distributed dipole model46–49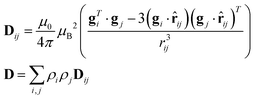 | (4) |
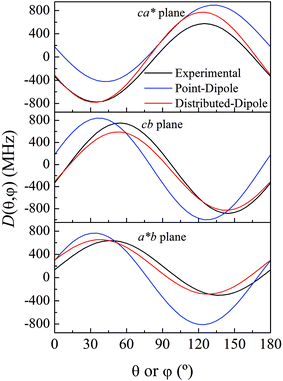 | ||
| Fig. 5 Experimental angular variations (black lines) of D (D(θ,φ)) in the ca*, cb and a*b crystal planes, and simulations performed using the point-dipole approximation (blue) or a distributed dipole approximation (red) with best-fit spin populations shown in Table 2. | ||
| TPSSh | ωB97x | Fit to experimental D-matrix | |
|---|---|---|---|
| Atom | ρ S | ρ S | ρ S |
| Cu | 0.686 | 0.691 | 0.657 |
| N1 | 0.069 | 0.070 | 0.066 |
| N2 | 0.064 | 0.065 | 0.066 |
| O2 | 0.068 | 0.067 | 0.100 |
| O4 | 0.085 | 0.084 | 0.110 |
Calculations given in Table S5† show that all the functionals underestimate the D parameter, likely because the ORCA program calculates the dipolar matrix using the free electron ge value,47 instead of the anisotropic g-matrix associated with each spin (see eqn (4)). In our case we obtained a good agreement between the experiment and theory using anisotropic g-matrices, as proposed by other authors.20,50 In any case, the spin populations calculated using the functionals listed in Tables 2 and S4† are in good agreement with the values obtained from fitting eqn (4) to the data shown in Fig. 5. Our results suggest that in cases where the experimental data allow such details, it is more accurate to calculate the dipolar interaction using the distributed dipole approximation with accurate spin populations predicted by DFT than to rely on the DFT calculated dipolar interaction. Other authors have also used the distributed dipole model, but for the analysis of powder EPR spectra, in which certain subtle effects may not be noticeable, or single crystal EPR spectra in highly symmetrical crystal environments, relying on analytical formulae possibly only due to the high symmetry.46–49 Furthermore in the work of Smith et al. and Harris, only the ZFS parameter D was evaluated. In this work we show a complete analysis of the full angular variation of the dipolar interaction using the distributed dipole model, which allowed us to obtain the contribution to the D-matrix from spin populations on several atoms. Note that this information cannot be obtained only from the D-parameter.
Interdimeric exchange interaction
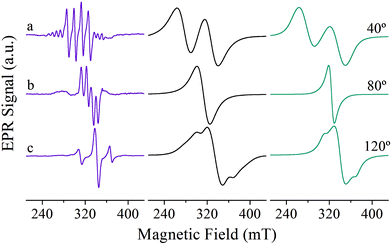
Fig. 6 shows representative single crystal EPR spectra obtained in the ca* crystal plane of Cu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Zn(tda)(phen) (left) and [Cu(tda)(phen)]2 (middle) for nearly the same magnetic field orientation. The changes in the EPR behavior that occur while moving from the magnetically diluted Cu
Zn(tda)(phen) (left) and [Cu(tda)(phen)]2 (middle) for nearly the same magnetic field orientation. The changes in the EPR behavior that occur while moving from the magnetically diluted Cu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Zn(tda)(phen) (Fig. 6, left panel) to pure [Cu(tda)(phen)]2 (Fig. 6, middle panel) are the results of the different spin concentrations of both systems. The spin states are well defined for Cu–Zn heterodimer (S = 1/2, central spectra in Fig. 6, left panel) and for Cu–Cu homodimer but with negligible interdimeric exchange interactions (S = 1, satellite lines in Fig. 6, left panel). The transition from S = 1/2 to S = 1 is caused solely by the intradimer exchange interaction (J = +3.2 cm−1). The Cu–Cu homodimers with the non-negligible interdimeric exchange interaction J′ (Fig. 6, middle panel) can show two-line spectra for those situations with J′ < ZFS (spectrum a), a single line for J′ > ZFS (spectrum b) typical of an exchange-collapsed extended system,31,51 or a mixture of the two previous situations (spectrum c).25
Zn(tda)(phen) (Fig. 6, left panel) to pure [Cu(tda)(phen)]2 (Fig. 6, middle panel) are the results of the different spin concentrations of both systems. The spin states are well defined for Cu–Zn heterodimer (S = 1/2, central spectra in Fig. 6, left panel) and for Cu–Cu homodimer but with negligible interdimeric exchange interactions (S = 1, satellite lines in Fig. 6, left panel). The transition from S = 1/2 to S = 1 is caused solely by the intradimer exchange interaction (J = +3.2 cm−1). The Cu–Cu homodimers with the non-negligible interdimeric exchange interaction J′ (Fig. 6, middle panel) can show two-line spectra for those situations with J′ < ZFS (spectrum a), a single line for J′ > ZFS (spectrum b) typical of an exchange-collapsed extended system,31,51 or a mixture of the two previous situations (spectrum c).25
The changes experienced by the dimer EPR spectra when the dinuclear units are coupled by the interdimeric exchange interaction J′ can be rationalized by computing the EPR spectrum within the linear response theory on the basis of the exchange narrowing model proposed by Anderson.26,27 In this theory, the absorption spectrum in the frequency domain for an extended lattice of paramagnetic centers coupled by an unique exchange interaction is given by52
| I(ω,ωe) = Re{W·[i(ω − ωE + iΓ)+π]−1·1} | (5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Zn(tda)(phen).
Zn(tda)(phen).
Eqn (5) has an analytical solution for the case of spectra showing two resonances which may arise from two interacting dissimilar S = 1/2 spins53 or from interacting S = 1 dimers, both without an explicit hyperfine structure.25 This simplest case can alternatively be obtained from generalized Bloch equations.54 However, as the number of resonances increases, as is the case we are dealing with, an analytical solution first becomes impractical and soon impossible, and a numerical solution of eqn (5) is needed.
As said above, spectral simulation with eqn (5) accounts for the exchange narrowing phenomenon in the case of a dimer interacting with its neighbors through an unique exchange interaction.23,53 However, in the case of [Cu(tda)(phen)]2, eqn (5) fails to explain the angular variation of spectra such as the one shown in Fig. 6c, middle panel. This discrepancy between the experiment and simulation is due to the fact that the exchange interaction coupling of each dinuclear unit is not unique, which occurs when the S = 0 state is thermally accessible. Assuming no interdimeric exchange interactions, [Cu(tda)(phen)]2 is a spin system in which the dimers can be either in singlet (S = 0) or in triplet (S = 1) states, with probabilities given by a Boltzmann distribution. As the singlet–triplet separation J in [Cu(tda)(phen)]2 is 3.2 cm−1,24 the Boltzmann distribution at room temperature gives approximately the same population for all the levels, and hence the probability of a dimer being in one of the triplet states is ρ = 0.75. Taking this into account, a central dimer in the triplet state (only in this state it will have an EPR signal), which is surrounded by four structural first neighbors connected by the superexchange paths (Fig. 2), will have a different number n of neighbors in the triplet state (0 ≤ n ≤ 4) with the probability pn given by
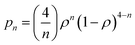 | (6) |
This equation yields p0 = 0.39%, p1 = 4.69%, p2 = 21.09%, p3 = 42.19% and p4 = 31.64% for ρ = 0.75. This means that most of the centers in a triplet state are surrounded by 3 dinuclear centers in a triplet state, but there are also triplet centers surrounded by 1, 2 and 4 dimers in the triplet state, and the exchange interaction between them is different, i.e., ωe,n = nJ′/ħ. In summary, eqn (5) describes the shape of the spectrum of an extended system in the presence of an unique exchange frequency ωe, but if the system is composed of subsystems with different values of ωe (i.e. ωe,n), given by populations of dimers with different number of triplet neighbors, then the spectrum becomes a sum of the spectra of each subsystem.
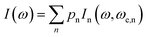 | (7) |
Simulations of the spectra of [Cu(tda)(phen)]2 using eqn (7) are presented in Fig. 6, right panel. This simulation yielded J′ = 0.010(1) cm−1, slightly larger than the one reported in our previous work (J′ = 0.0070(3)) cm−1,25 with the difference being due to the previous use of the point dipole approximation. Our present data show that the point dipole approximation may fail not only in the estimation of distances47 but also in the determination of exchange coupling constants by single crystal EPR spectroscopy using the exchange narrowing phenomenon. Exchange narrowing in EPR is the usual way to estimate very weak intercenter exchange interactions (<0.1 cm−1) in undiluted magnetic systems. As shown in previous studies,23,25,53,55 π–π interactions transmit weak exchange interactions which modulate the magnetic properties of individual paramagnetic centers in extended lattices, and also, as evidenced for [Cu(tda)(phen)]2, can transmit information about the spin-states of dimers, as the magnetic properties of a central dinuclear unit depend on the average number of neighbors in a triplet state. π–π interactions have been shown to play an important role in molecular spintronics, as reported for different magnetic molecules positioned on graphene or carbon nanotubes, and can also be used to design new magnetic materials with unprecedented physical properties.6,56–59
Conclusion
The single crystal EPR study of Cu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Zn(tda)(phen) has revealed the formation of Cu–Zn heterodimers and Cu–Cu homodimers in the diamagnetic zinc(II) host. The experiment allowed us to determine the anisotropic magnitudes g, A, and D. The information obtained from the diluted compound was used to evaluate the interdimeric exchange interaction J′ between the dimeric units in [Cu(tda)(phen)]2. This analysis yielded J′ = 0.010(1) cm−1, slightly larger than that reported previously by us, J′ = 0.0070(3) cm−1, which is ascribed undoubtedly to the use of the point dipole approximation in our previous calculations. Best simulation results were obtained using the distributed dipole model, which takes into account spin delocalization on the copper ligands due to covalency, showing clearly that the point dipole approximation can be used only to estimate an order of magnitude of exchange coupling constants by single crystal EPR spectroscopy. These results are relevant as they allow one to understand the influence of intercluster exchange interactions in the magnetic behavior of metal clusters synthesized as potential molecular magnets and in spintronics.
Zn(tda)(phen) has revealed the formation of Cu–Zn heterodimers and Cu–Cu homodimers in the diamagnetic zinc(II) host. The experiment allowed us to determine the anisotropic magnitudes g, A, and D. The information obtained from the diluted compound was used to evaluate the interdimeric exchange interaction J′ between the dimeric units in [Cu(tda)(phen)]2. This analysis yielded J′ = 0.010(1) cm−1, slightly larger than that reported previously by us, J′ = 0.0070(3) cm−1, which is ascribed undoubtedly to the use of the point dipole approximation in our previous calculations. Best simulation results were obtained using the distributed dipole model, which takes into account spin delocalization on the copper ligands due to covalency, showing clearly that the point dipole approximation can be used only to estimate an order of magnitude of exchange coupling constants by single crystal EPR spectroscopy. These results are relevant as they allow one to understand the influence of intercluster exchange interactions in the magnetic behavior of metal clusters synthesized as potential molecular magnets and in spintronics.
Acknowledgements
We thank FONCyT, CONICET, and CAI+D-UNL for financial support. N.I.N. and C.D.B. are members of CONICET-Argentina.References
- O. Kahn, Molecular Magnetism, VCH Publishers, New York, 1993 Search PubMed.
- A. Bencini and D. Gatteschi, Electron Paramagnetic Resonance of Exchange Coupled Systems, Springer-Verlag, Berlin, Germany, 1990 Search PubMed.
- D. Gatteschi, Adv. Mater., 1994, 6, 635–645 CrossRef CAS PubMed.
- J. Mroziński, Coord. Chem. Rev., 2005, 249, 2534–2548 CrossRef PubMed.
- O. Kahn, Angew. Chem., Int. Ed. Engl., 1985, 24, 834–850 CrossRef PubMed.
- M. Atzori, A. Serpe, P. Deplano, J. A. Schlueter and M. Laura Mercuri, Inorg. Chem. Front., 2015, 2, 108–115 RSC.
- M. Castellano, R. Ruiz-García, J. Cano, J. Ferrando-Soria, E. Pardo, F. R. Fortea-Pérez, S. E. Stiriba, M. Julve and F. Lloret, Acc. Chem. Res., 2015, 48, 510–520 CrossRef CAS PubMed.
- F. Meyer, S. Demeshko, G. Leibeling, B. Kersting, E. Kaifer and H. Pritzkow, Chem. – Eur. J., 2005, 11, 1518–1526 CrossRef CAS PubMed.
- E. Moreno Pineda, N. F. Chilton, R. Marx, M. Dörfel, D. O. Sells, P. Neugebauer, S.-D. Jiang, D. Collison, J. van Slageren, E. J. L. McInnes and R. E. P. Winpenny, Nat. Commun., 2014, 5, 5243 CrossRef CAS PubMed.
- J. Camarero and E. Coronado, J. Mater. Chem., 2009, 19, 1678–1684 RSC.
- D. Cangussu, E. Pardo, M.-C. Dul, R. Lescouëzec, P. Herson, Y. Journaux, E. F. Pedroso, C. L. M. Pereira, H. O. Stumpf, M. Carmen Muñoz, R. Ruiz-García, J. Cano, M. Julve and F. Lloret, Inorg. Chim. Acta, 2008, 361, 3394–3402 CrossRef CAS PubMed.
- A. V. Astashkin, B. O. Elmore, W. Fan, J. G. Guillemette and C. Feng, J. Am. Chem. Soc., 2010, 132, 12059–12067 CrossRef CAS PubMed.
- A. K. Upadhyay, D. T. Petasis, D. M. Arciero, A. B. Hooper and M. P. Hendrich, J. Am. Chem. Soc., 2003, 125, 1738–1747 CrossRef CAS PubMed.
- C. D. Brondino, M. G. Rivas, M. J. Romão, J. J. G. Moura and I. Moura, Acc. Chem. Res., 2006, 39, 788–796 CrossRef CAS PubMed.
- J. H. Van Wonderen, V. S. Oganesyan, N. J. Watmough, D. J. Richardson, A. J. Thomson and M. R. Cheesman, Biochem. J., 2013, 451, 389–394 CrossRef CAS PubMed.
- M. C. Gómez, N. I. Neuman, S. D. Dalosto, P. J. González, J. G. Moura, A. C. Rizzi and C. D. Brondino, J. Biol. Inorg. Chem., 2015, 20, 233–242 CrossRef PubMed.
- D. L. Reger, A. E. Pascui, M. D. Smith, J. Jezierska and A. Ozarowski, Inorg. Chem., 2012, 51, 7966–7968 CrossRef CAS PubMed.
- B. Bleaney and K. D. Bowers, Proc. R. Soc. London, Ser. A, 1952, 214, 451–465 CrossRef CAS.
- C. Núñez, R. Bastida, A. Macías, L. Valencia, N. I. Neuman, A. C. Rizzi, C. D. Brondino, P. J. González, J. L. Capelo and C. Lodeiro, Dalton Trans., 2010, 39, 11654–11663 RSC.
- T. D. Smith and J. R. Pilbrow, Coord. Chem. Rev., 1974, 13, 173–278 CrossRef CAS.
- R. Calvo, J. E. Abud, R. P. Sartoris and R. C. Santana, Phys. Rev. B: Condens. Matter, 2011, 84, 104433–104445 CrossRef.
- C. D. Brondino, R. Calvo and E. J. Baran, Chem. Phys. Lett., 1997, 271, 51–54 CrossRef CAS.
- N. I. Neuman, V. G. Franco, F. M. Ferroni, R. Baggio, M. C. G. Passeggi, A. C. Rizzi and C. D. Brondino, J. Phys. Chem. A, 2012, 116, 12314–12320 CrossRef CAS PubMed.
- R. Baggio, M. T. Garland, J. Manzur, O. Peña, M. Perec, E. Spodine and A. Vega, Inorg. Chim. Acta, 1999, 286, 74–79 CrossRef CAS.
- N. I. Neuman, M. Perec, P. J. González, M. C. G. Passeggi, A. C. Rizzi and C. D. Brondino, J. Phys. Chem. A, 2010, 114, 13069–13075 CrossRef CAS PubMed.
- P. W. Anderson, J. Phys. Soc. Jpn., 1954, 9, 316–339 CrossRef.
- P. W. Anderson and P. R. Weiss, Rev. Mod. Phys., 1953, 25, 269–276 CrossRef CAS.
- Bruker, SMART-NT, SAINT-NT, SADABS, SHELXTL, Bruker AXS Inc., Wisconsin, USA, 2001 Search PubMed.
- G. Sheldrick, Acta Crystallogr., Sect. A: Fundam. Crystallogr., 2008, 64, 112–122 CrossRef CAS PubMed.
- G. Sheldrick, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2015, 71, 3–8 CrossRef PubMed.
- J. M. Schveigkardt, A. C. Rizzi, O. E. Piro, E. E. Castellano, R. C. De Santana, R. Calvo and C. D. Brondino, Eur. J. Inorg. Chem., 2002, 2913–2919 CrossRef CAS.
- S. Stoll and A. Schweiger, J. Magn. Reson., 2006, 178, 42–55 CrossRef CAS PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter, 1988, 37, 785–789 CrossRef CAS.
- B. Miehlich, A. Savin, H. Stoll and H. Preuss, Chem. Phys. Lett., 1989, 157, 200–206 CrossRef CAS.
- V. N. Staroverov, G. E. Scuseria, J. Tao and J. P. Perdew, J. Chem. Phys., 2003, 119, 12129–12137 CrossRef CAS PubMed.
- V. N. Staroverov, G. E. Scuseria, J. Tao and J. P. Perdew, J. Chem. Phys., 2004, 121, 11507–11507 CrossRef CAS PubMed.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- S. Grimme, J. Chem. Phys., 2006, 124, 034108 CrossRef PubMed.
- E. v. Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597–4610 CrossRef PubMed.
- C. van Wüllen, J. Chem. Phys., 1998, 109, 392–399 CrossRef PubMed.
- D. A. Pantazis, X.-Y. Chen, C. R. Landis and F. Neese, J. Chem. Theory Comput., 2008, 4, 908–919 CrossRef CAS.
- A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571–2577 CrossRef PubMed.
- A. Grirrane, A. Pastor, E. Álvarez, C. Mealli, A. Ienco and A. Galindo, Inorg. Chem. Commun., 2006, 9, 160–163 CrossRef CAS PubMed.
- P. Bertrand, P. Camensuli, C. More and B. Guigliarelli, J. Am. Chem. Soc., 1996, 118, 1426–1434 CrossRef CAS.
- C. Riplinger, J. P. Y. Kao, G. M. Rosen, V. Kathirvelu, G. R. Eaton, S. S. Eaton, A. Kutateladze and F. Neese, J. Am. Chem. Soc., 2009, 131, 10092–10106 CrossRef CAS PubMed.
- S. R. P. Smith and J. Owen, J. Phys. C: Solid State Phys., 1971, 4, 1399 CrossRef CAS PubMed.
- E. A. Harris, J. Phys. C: Solid State Phys., 1972, 5, 338 CrossRef CAS PubMed.
- A. Abragam and B. Bleaney, Electron paramagnetic resonance of transition ions, Dover Publications, New York, 1986 Search PubMed.
- A. C. Rizzi, O. E. Piro, E. E. Castellano, O. R. Nascimento and C. D. Brondino, Inorg. Chim. Acta, 2000, 305, 19–25 CrossRef CAS.
- R. A. Sack, Mol. Phys., 1958, 1, 163–167 CrossRef CAS PubMed.
- C. D. Brondino, R. Calvo, A. M. Atria, E. Spodine, O. R. Nascimento and O. Peña, Inorg. Chem., 1997, 36, 3183–3189 CrossRef CAS PubMed.
- S. K. Hoffmann, A. Waśkowska and W. Hilczer, Solid State Commun., 1990, 74, 1359–1361 CrossRef CAS.
- C. D. Brondino, R. Calvo, A. M. Atria, E. Spodine and O. Peña, Inorg. Chim. Acta, 1995, 228, 261–266 CrossRef CAS.
- S. M. Avdoshenko, I. N. Ioffe, G. Cuniberti, L. Dunsch and A. A. Popov, ACS Nano, 2011, 5, 9939–9949 CrossRef CAS PubMed.
- M. Urdampilleta, S. Klayatskaya, M. Ruben and W. Wernsdorfer, ACS Nano, 2015, 9, 4458–4464 CrossRef CAS PubMed.
- M. Urdampilleta, N.-V. Nguyen, J.-P. Cleuziou, S. Klyatskaya, M. Ruben and W. Wernsdorfer, Int. J. Mol. Sci., 2011, 12, 6656 CrossRef CAS PubMed.
- W. Wernsdorfer, N. Aliaga-Alcalde, D. N. Hendrickson and G. Christou, Nature, 2002, 416, 406–409 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Single crystal mounting details for the EPR experiment, additional structural data together with structural figures for Zn(tda)(phen), electronic structure calculation results, and figures containing the angular variation of the A- and D-matrices. CCDC 1055076. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c5qi00086f |
| This journal is © the Partner Organisations 2015 |