Structural and magnetic tuning from a field-induced single-ion magnet to a single-chain magnet by anions†
Dong
Shao
,
Xin-Hua
Zhao
,
Shao-Liang
Zhang
,
Dong-Qing
Wu
,
Xiao-Qin
Wei
and
Xin-Yi
Wang
*
State Key Laboratory of Coordination Chemistry, Collaborative Innovation Center of Advanced Microstructures, School of Chemistry and Chemical Engineering, Nanjing University, Nanjing, 210093, China. E-mail: wangxy66@nju.edu.cn; Fax: +86-25-83314502
First published on 17th July 2015
Abstract
We herein report the syntheses, crystal structures, and magnetic properties of two complexes based on the anisotropic pentagonal bipyramidal FeII starting material [Fe(LN3O2)]2+, namely [Fe(LN3O2)(H2O)2][MQ]2·H2O (1) and [Fe(LN3O2)(CN)][ABSA]·3H2O (2) (LN3O2 = 2,13-dimethyl-6,9-dioxa-3,12,18-triazabicyclo[12.3.1]octadeca-1(18),2,12,14,16-pentaene; MQ− = methyl orange anion; ABSA− = 4-aminoazobenzene-4′-sulfonic anion). Compound 1 is a mononuclear material where the [Fe(LN3O2)(H2O)2]2+ cations form a one-dimensional (1D) chain by the hydrogen bonds between the bulky MQ− anions and the coordinated water molecules. With a slightly different anion, ABSA−, a cyano-bridged FeII chain is formed for compound 2. This chain has a similar structure as that in our recently reported compound [Fe(LN5)(CN)][BF4] (Chem. Commun., 2015, 51, 4360). However, compared with the reported result where the chains interact with each other through the π⋯π interactions, the chains in 2 are well isolated by the bulky ABSA− anions with the shortest interchain Fe⋯Fe distances around 12.0 Å. Magnetic investigation on 1 reveals the easy-axis magnetic anisotropy of the mononuclear FeII centre (zero-field splitting parameter D = −3.7 cm−1), which leads to the field-induced slow magnetic relaxation. For compound 2, the Fe2+ spins are antiferromagnetically coupled through the cyano bridges with a coupling constant of J = −4.13(2) cm−1 with the Hamiltonian H = −J∑Si·Si+1. AC magnetic measurements revealed the pure single-chain magnetic (SCM) behaviour of these isolated chains with an effective energy barrier of 26.1(5) K. This system represents a good example showing that the structures and magnetic properties, such as field-induced single-ion magnets, SCMs, and SCM-based magnets, can be selectively prepared by anion modification.
Introduction
Molecular nanomagnets with a slow magnetic relaxation below their blocking temperatures, such as the single-molecule magnets (SMMs), single-ion magnets (SIMs) and single-chain magnets (SCMs), are of great interest in the field of molecular magnetism.1 Among them, SCMs have received great attention ever since their first observation in a CoII-nitroxide radical chain in 2001.2,3 Theoretically, because of the additional energy component known as the correlation energy (Δξ) stemming from the exchange coupling (J) between the spin centres along the chain, SCMs might display higher relaxation barriers than their counterpart single-molecule magnets (SMMs).4–10For the construction of SCMs, the magnetic anisotropy of the spin unit, the intrachain exchange interaction and the interchain interaction are the three most important factors. However, compared with the former two ingredients for which the stronger the better, the interchain interactions require more careful consideration. Initially, it was believed that negligible interchain coupling is necessary to prevent the three-dimensional magnetic ordering and to achieve the SCM behaviour. Later, it was found that the SCM behaviour can be retained in the antiferromagnetic (AF)4a or ferromagnetic (F)4b,c ordered phases. By taking advantage of the magnetic ordering, new types of high temperature SCM-based magnets can be achieved.5 Following the experimental and theoretical work of Coulon and Clérac et al.,4a,5 a number of SCM-based antiferromagnets have been reported.6–8 These SCM-based antiferromagnets suggest a possible strategy for high temperature SCM-based magnets.
Synthetically, the magnetic anisotropy and intrachain magnetic coupling can be manipulated by using anisotropic spin carriers4–10 and bridging ligands as efficient magnetic couplers such as the cyanide,6,7a,c,h radicals2a,4b,10 or other short bridges.7b–h,8 On the other hand, the design and control of the interchain interaction seems rather difficult. Several parameters can be manipulated to finely tune the interchain distances (and thus the interchain magnetic coupling), such as using counter ions or chelating ligands of a different size,3d,9a,10b,g different bismonodentate bridging ligands of different lengths,9b–d the interchain hydrogen bonds9e and the interchain π–π interactions.6,7b For now, it still remains a synthetic challenge for chemists to tune the interchain distances and also the magnetic properties at will for a specific chain compound. As an illustrative example, Clérac et al. reported the compound [Mn(3,5-Cl2saltmen)Ni(pao)2(phen)][PF6] in 2010,5 where the anion can be replaced from PF6− to the bulky BPh4−, leading to the modification of the magnetic properties from the SCM-based antiferromagnet to the pure SCM.
Very recently, using an anisotropic pentagonal bipyramidal FeII starting material, we prepared a cyano-bridged homospin compound [Fe(LN5)(CN)][BF4], which exhibited the rare coexistence of spin-canting, AF ordering, metamagnetism and SCM behaviour.6 Its strong magnetic anisotropy arises from the pentagonal bipyramidal FeII center, as has been shown by Sutter, Mallah and Gao et al. in the field-induced SIMs,11 and cyano-bridged SMM12a and SCM compounds.12b Because of the small size of the BF4− anion, the chains in [Fe(LN5)(CN)][BF4] are not well isolated and interact with each other by π–π interactions. These weak interactions are believed to be responsible for the weak interchain magnetic coupling and the long-range magnetic ordering. Since this compound is synthesized in the presence of excessive BF4− anions, this system provides a good opportunity to tune the interchain distances with anions of different sizes. Along this line, we performed the reaction using a similar starting material [Fe(LN3O2)(CN)2] with the bulky anions MQ− and ABSA− (LN3O2 = 2,13-dimethyl-6,9-dioxa-3,12,18-triazabicyclo[12.3.1]octadeca-1(18),2,12,14,16-pentaene; MQ− = methyl orange anion; ABSA− = 4-aminoazobenzene-4′-sulfonic anion, Fig. 1). Interestingly, a mononuclear FeII compound [Fe(LN3O2)(H2O)2][MQ]2·H2O (1) and a cyano-bridged 1D chain compound [Fe(LN3O2)(CN)][ABSA]·3H2O (2) were obtained. The chains in 2 are well isolated by the large ABSA− anions. Magnetic studies revealed that 1 exhibits a field-induced slow magnetic relaxation and that 2 is a pure SCM with an effective energy barrier of 26.1(5) K.
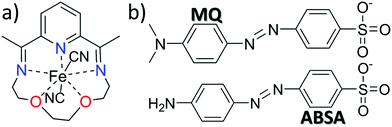 | ||
| Fig. 1 View of the structures of the [Fe(LN3O2)(CN)2] starting material (a) and the bulky anions MQ− and ABSA− (b). | ||
Experimental section
Physical measurements
The infrared spectral data were measured with KBr pellets using a Nexus 870 FT-IR spectrometer in the 4000–400 cm−1 range. Elemental analyses of C, H, and N were performed on an Elementar Vario MICRO analyzer. The powder X-ray diffraction data (PXRD) were recorded at 298 K on a Bruker D8 Advance diffractometer with a Cu Kα X-ray source operated at 40 kV and 40 mA. Thermal gravimetric analysis (TGA) was performed using a STA 449 F3 Jupiter analyzer in the temperature range of 40–800 °C. Magnetic measurements from 2 to 300 K with a DC field of up to 70 kOe were performed using a Quantum Design SQUID VSM magnetometer on the grounded powders from the single crystals of the compounds. Alternating current (AC) magnetic susceptibility data were collected in a zero DC field or a 2000 Oe DC field in the temperature range of 2.0–10 K, under an AC field of 2 Oe, oscillating at frequencies in the range of 1–950 Hz. All magnetic data were corrected for the diamagnetism of the sample holder and of the diamagnetic contribution of the sample (−0.5 × 10−6 × molecular weight).Materials and synthesis
All reagents were obtained from commercially available sources and were used as received unless otherwise noted. Solvents were distilled before use under a N2 atmosphere. The synthesis and crystal growth procedures were performed under a N2 atmosphere using Schlenk techniques or in a N2 atmosphere glovebox. [Fe(LN3O2)(CN)2] was synthesized according to the literature method.13Caution!
Cyanides are highly toxic and they should be handled in small quantities with care.
X-ray crystallography
Single crystal X-ray crystallographic data were collected on a Bruker APEX II diffractometer with a CCD area detector (Mo-Kα radiation, λ = 0.71073 Å) at room temperature. The APEXII program was used to determine the unit cell parameters and for data collection. The data were integrated and corrected for Lorentz and polarization effects using SAINT.14 The absorption corrections were applied with SADABS.15 The structures were solved by direct methods and were refined by the full-matrix least-squares method on F2 using the SHELXTL crystallographic software package.16 All the non-hydrogen atoms were refined anisotropically. The hydrogen atoms of the organic ligands were refined as riding on the corresponding non-hydrogen atoms. Additional details of the data collections and structural refinement parameters are provided in Table 1. Selected bond lengths and angles of 1 and 2 are listed in Table S1 (ESI†).| 1 | 2 | |
|---|---|---|
| a R 1 = ∑||Fo| − |Fc||/∑|Fo|. b wR2 = {∑[w(Fo2 − Fc2)2]/∑[w(Fo2)2]}1/2. | ||
| Formula | C43H55FeN9O11S2 | C28H37FeN7O8S |
| Formula weight [g mol−1] | 993.93 | 687.56 |
| Crystal size [mm3] | 0.56 × 0.15 × 0.08 | 0.63 × 0.22 × 0.15 |
| Crystal system | Triclinic | Monoclinic |
| Space group |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
P21/c |
| a [Å] | 8.5081(2) | 12.7854(1) |
| b [Å] | 11.345(2) | 10.5316(9) |
| c [Å] | 24.713(5) | 24.534(2) |
| α [°] | 76.947(3) | 90 |
| β [°] | 87.749(3) | 97.8160(1) |
| γ [°] | 85.552(3) | 90 |
| V [Å3] | 2316.3(8) | 3272.8(5) |
| Z | 2 | 4 |
| T [K] | 293(2) | 293(2) |
| ρ calcd [g cm−3] | 1.425 | 1.395 |
| μ(Mo-Kα) [mm−1] | 0.485 | 0.582 |
| F (000) | 1044 | 1440 |
| R int | 0.0209 | 0.0532 |
| R 1 /wR2b (I > 2σ(I)) | 0.0688/0.1836 | 0.0488/0.1272 |
| R 1/wR2 (all data) | 0.0846/0.1959 | 0.0565/0.1381 |
| GOF on F2 | 1.010 | 1.062 |
Results and discussion
Synthesis
As reported for the synthesis of compound [Fe(LN5)(CN)][BF4], compounds 1 and 2 were prepared by the recrystallization of the [Fe(LN3O2)(CN)2] starting material in the presence of the bulky anions. The stability of the [Fe(LN3O2)(CN)2] compound in solution seems even lower than that of [Fe(LN5)(CN)2]. Both of the CN groups were replaced by the water molecules to form the isolated mononuclear compound 1; and one of the CN groups was disassociated to from the 1D compound 2 as observed in [Fe(LN5)(CN)][BF4].6 Although the difference between the MQ− and the ABSA− anions is very minor (Fig. 1), attempts to isolate the 1D structure using the MQ− anion failed. The purity of 1 and 2 was confirmed by the powder XRD spectra and the elemental analysis (Fig. S1 and S2, ESI†). Thermal gravimetric analysis (TGA) on 2 shows an 8.3% weight loss in the temperature range of 40–110 °C, corresponding to the removal of three crystallized water molecules (calc. 7.9%, Fig. S3, ESI†).Crystal structure descriptions
Single-crystal X-ray diffraction analyses for 1 and 2 reveal that 1 crystallized in the triclinic space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) and 2 in the monoclinic space group P21/c (Table 1). The asymmetric unit of 1 contains a mononuclear FeII cation chelated by one LN3O2 ligand, two water molecules axially coordinated to the Fe2+, two MQ− anions for the charge balance, and one lattice water molecule (Fig. 2a, Table S1, ESI†). Of the two MQ− anions, one of them contains the disordered N
and 2 in the monoclinic space group P21/c (Table 1). The asymmetric unit of 1 contains a mononuclear FeII cation chelated by one LN3O2 ligand, two water molecules axially coordinated to the Fe2+, two MQ− anions for the charge balance, and one lattice water molecule (Fig. 2a, Table S1, ESI†). Of the two MQ− anions, one of them contains the disordered N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N group. Each FeII centre resides in a N3O4 pentagonal bipyramid environment with a continuous shape measure (CShM)17 calculated to be 0.208 relative to the ideal D5h geometry. The Oaxial–Fe–Oaxial angle of 174.7(8)° is close to linearity and the axial bonds (Fe–O3 = 2.142(3) Å and Fe–O4 = 2.125(3) Å) are slightly shorter than the average bonds of 2.212(6) Å in the equatorial plane. Hydrogen bonds were found between the coordinated water molecules and the oxygen atoms from the SO3 groups of the MQ− anion (O3⋯O6 = 2.740, O3⋯O9 = 2.740 Å, O4⋯O7 = 2.733, O4⋯O11 = 2.684). Bridged by these effective hydrogen bond interactions, a 1D supramolecular chain structure is formed along the a axis (Fig. 2b). These chains are further connected by the hydrogen bonds between the SO3 groups and the lattice water molecules (O5⋯O8 = 2.812, O5⋯O10 = 3.049 Å), forming a 2D layer along the ab plane, which is further separated by the bulky MQ− anions along the c direction (Fig. S4, ESI†). The shortest Fe⋯Fe distance in 1 is 7.85 Å.
N group. Each FeII centre resides in a N3O4 pentagonal bipyramid environment with a continuous shape measure (CShM)17 calculated to be 0.208 relative to the ideal D5h geometry. The Oaxial–Fe–Oaxial angle of 174.7(8)° is close to linearity and the axial bonds (Fe–O3 = 2.142(3) Å and Fe–O4 = 2.125(3) Å) are slightly shorter than the average bonds of 2.212(6) Å in the equatorial plane. Hydrogen bonds were found between the coordinated water molecules and the oxygen atoms from the SO3 groups of the MQ− anion (O3⋯O6 = 2.740, O3⋯O9 = 2.740 Å, O4⋯O7 = 2.733, O4⋯O11 = 2.684). Bridged by these effective hydrogen bond interactions, a 1D supramolecular chain structure is formed along the a axis (Fig. 2b). These chains are further connected by the hydrogen bonds between the SO3 groups and the lattice water molecules (O5⋯O8 = 2.812, O5⋯O10 = 3.049 Å), forming a 2D layer along the ab plane, which is further separated by the bulky MQ− anions along the c direction (Fig. S4, ESI†). The shortest Fe⋯Fe distance in 1 is 7.85 Å.
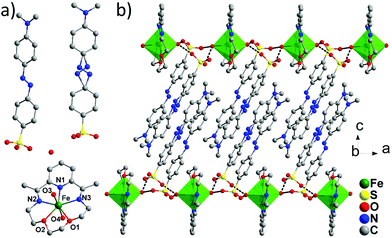 | ||
| Fig. 2 View of the asymmetric unit (a) and the hydrogen bonded 1D chain (b) of 1. Hydrogen atoms were omitted for clarity. | ||
The structure of 2 is very similar to that of the reported [Fe(LN5)(CN)][BF4] compound, with the 1D cyano-bridged FeII chains separated by the bulky ABSA− anions (Fig. 3c and S5, ESI†). The FeII centre is also in a pentagonal bipyramid geometry with a N4O2C1 coordination environment and the CShM parameter is 0.295 to an ideal D5h symmetry (Fig. 3a). Bridged by the cyano groups, regular chains along the b axis are formed with a shortest Fe–Fe distance of 5.30 Å (Fig. 3b). As in [Fe(LN5)(CN)][BF4], the pseudo 5-fold axis of the FeII centre (Ccyano–Fe–Ncyano axis) is tilted away from the b axis with an angle of ∼6° (Fig. 3b). The ABSA− counter anions lie in between the chains and form abundant hydrogen bonds among themselves (NH2–SO3) and between the lattice water molecules (Fig. S6, ESI†). Interestingly, these bulky organic anions efficiently separate the 1D chains away from each other and prevent any supramolecular interactions between the chains, such as the π–π interactions found in [Fe(LN5)(CN)][BF4]. As a result, the shortest interchain Fe⋯Fe distance increases to 12.0 Å along the a direction and to 12.8 Å along the c direction (Fig. 3c), compared to the 9.73 Å in [Fe(LN5)(CN)][BF4]. The increased isolation of the 1D chains efficiently decreases the interchain magnetic interaction and leads to the pure SCM behaviour in 2, as can be seen from the magnetic measurements below.
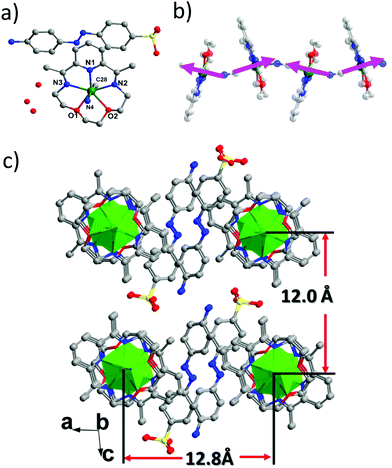 | ||
| Fig. 3 View of the asymmetric unit (a), the chain structure along the b axis (b), and the packing diagram (c) of 2. | ||
Magnetic properties
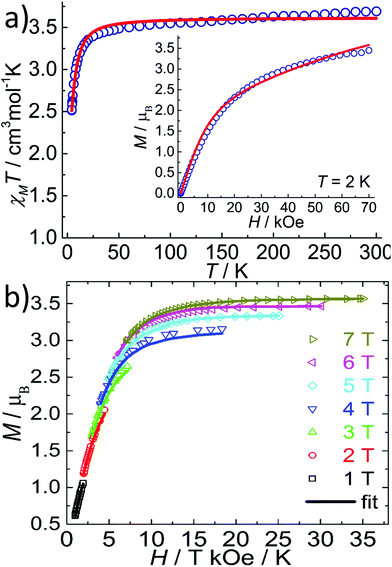
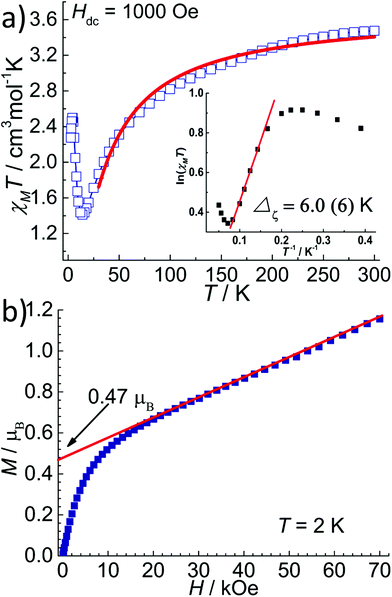
The temperature dependent magnetic susceptibility data of 1 and 2 in the temperature range of 2–300 K were measured under a DC field of 1 kOe. The χMT value at 300 K for 1 was 3.70 cm3 mol−1 K (Fig. 4a), which is larger than the spin-only value of 3.00 cm3 mol−1 K for a high-spin FeII ion (S = 2, g = 2), indicating the magnetic anisotropy of FeII in a near D5h ligand field.11,12 Upon cooling, the χMT values decreased monotonously down to a minimum of 2.50 cm3 mol−1 K at 2 K. The field-dependent magnetization measured at 2 K shows typical paramagnetic behaviour with the largest M value of 3.4μB at 70 kOe (Fig. 4a, insert), which is less than the saturation value of 4μB for a spin-only FeII with S = 2. The χMT(T) and M(H) curves of 1 can be simultaneously fitted with the following Hamiltonian by the software PHI:18| H = D[Sz2 − S(S + 1)/3] + E(Sx2 − Sy2) + μBg·S·B |
The best fit gives D = −3.7 cm−1, E = 0.02 cm−1, gX = gY = 2.32 and gZ = 1.92. Also, the magnetic anisotropy of the FeII ion in the pentagonal bipyramid geometry was further confirmed by the reduced magnetization of 1 as measured at low temperatures. As can be seen in Fig. 4b, these magnetization plots exhibit significant separation between the isofield curves and can be well fitted using Anisofit 2.0,19 giving D = −3.7 cm−1, E = 0.02 cm−1, and g = 2.21. These values agree very well with the parameters obtained above. Although the D value obtained for 1 is significantly smaller than that of the reported compounds of the similar pentagonal bipyramid geometry (around −10 to −16 cm−1) by Sutter et al.,11a,12 the negative D value indicates the easy-axis magnetic anisotropy and suggests the possibility of observing the slow magnetic relaxation behaviour. Indeed, FeII compounds with pentagonal bipyramid geometry can exhibit very strong magnetic anisotropy with a large negative D value, as supported by theoretical and high-field EPR studies.11,20 A recent result illustrates that not only the oxo-ligands from the axial coordination sites, but also the supramolecular organization has a strong impact on the magnetic properties, including the anisotropy parameter D.11
Temperature dependent AC susceptibility measurements of 1 have been carried out under a zero or 2 kOe DC field. Although no out-of-phase signals were detected under the zero DC field, frequency dependent χ′′ signals were observed under the 2 kOe DC field, indicating the field-induced slow magnetic relaxation behaviour of 1 (Fig. S7, ESI†). However, no peaks were observed down to 2 K, in accordance with the small energy barrier of 1 due to the small D value.
As compound 2 has a very similar 1D chain structure to [Fe(LN5)(CN)][BF4], its magnetic properties are also very similar. First of all, the plot of χMT versus T is indicative of spin canting in an antiferromagnetic array (Fig. 5a).6,9e,21 Upon cooling, the χMT value decreased gradually from the room temperature value of 3.47 cm3 mol−1 K to a minimum of 1.41 cm3 mol−1 K at 14 K. Below 14 K, the χMT value increased sharply to a maximum of 2.49 cm3 mol−1 K at 4 K, and then decreased down to 2 K. A Curie–Weiss fit of the data above 50 K gave a Curie constant of 3.92 cm3 mol−1 K and a negative Weiss constant of −39.6 K (Fig. S8, ESI†). The large and negative Weiss constant indicates that the dominant antiferromagnetic interaction is between the FeII centres, although it might also partly come from the spin–orbit coupling. The intrachain AF interaction was also estimated to be J = −4.13(2) cm−1 (g = 2.13(3)) by fitting the susceptibility data above 30 K using the same Fisher model (H = −J∑Si·Si+1) as we have previously employed for the compound [Fe(LN5)(CN)][BF4].6 The intrachain magnetic interaction is almost the same as that for the [Fe(LN5)(CN)][BF4], consistent with their similar 1D structures. Thus, the different magnetic behaviour at low temperature (vide post) can be mainly ascribed to the different interchain magnetic interactions.
 | ||
| Fig. 5 (a) Temperature dependent magnetic susceptibility of 2 measured at 1 kOe. Inset: ln(χMT) vs. 1/T plot; (b) field dependent magnetization curve for 2. | ||
The field dependent magnetization of 2 was measured at 2 K. As displayed in Fig. 5b, the magnetization increases quickly to 0.66 μB at 20 kOe and then increases linearly up to 1.15 μB at 70 kOe, which is far from the saturation value of 4 μB for a high spin FeII with S = 2. This magnetization curve is similar to that of [Fe(LN5)(CN)][BF4] and suggests spin canting of the FeII spins, although the strong magnetic anisotropy might also play a role. The canting angle was estimated as 7.5° from the magnetization value of 0.47 μB, obtained by extrapolating the M(H) curve in the high field region down to zero. Importantly, at the low field region of the M(H) curve, there is no S-shaped transition, ruling out the metamagnetic transition found for [Fe(LN5)(CN)][BF4].6 This is probably a result of the weaker interchain magnetic coupling in 2.
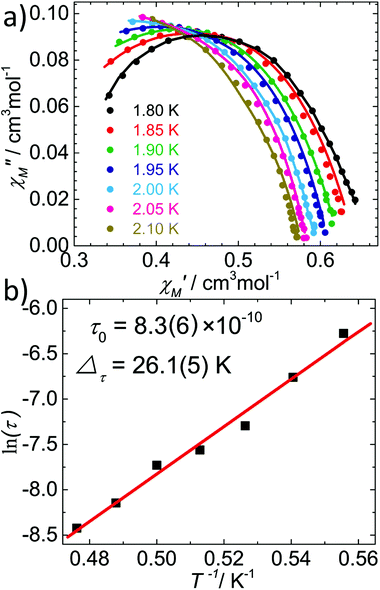
Because of the similar 1D structure and the weaker interchain magnetic coupling, 2 should behave as a pure SCM, as confirmed by the AC susceptibility measurements performed under a zero DC field. As depicted in Fig. 6a, both the in-phase and the out-of-phase temperature dependent AC signals were found to be strongly frequency dependent below 4 K, reflecting the slow magnetic relaxation. The Mydosh parameter ϕ = (ΔTP/TP)/(Δ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) f), where TP is the temperature of the peaks in χ′ and f is the frequency, was found to be 0.3, which falls in the range (0.1 < ϕ < 0.3) expected for a superparamagnetic system.22 Most importantly, the frequency-independent peak at 5.4 K observed in [Fe(LN5)(CN)][BF4] disappeared in the AC data of 2, even under a zero DC field. Furthermore, the variable-frequency AC susceptibility data collected from 1.8–2.4 K are also highly temperature dependent (Fig. 6b). The resulting Cole–Cole plots below 2.1 K can be fitted using a generalized Debye model23 (Fig. 7a) with the parameter α in the range of 0.38–0.44 (Table S2†), which suggests a moderate distribution of the relaxation time of 2.24 Fitting the relaxation time data to the Arrhenius equation τ = τ0
f), where TP is the temperature of the peaks in χ′ and f is the frequency, was found to be 0.3, which falls in the range (0.1 < ϕ < 0.3) expected for a superparamagnetic system.22 Most importantly, the frequency-independent peak at 5.4 K observed in [Fe(LN5)(CN)][BF4] disappeared in the AC data of 2, even under a zero DC field. Furthermore, the variable-frequency AC susceptibility data collected from 1.8–2.4 K are also highly temperature dependent (Fig. 6b). The resulting Cole–Cole plots below 2.1 K can be fitted using a generalized Debye model23 (Fig. 7a) with the parameter α in the range of 0.38–0.44 (Table S2†), which suggests a moderate distribution of the relaxation time of 2.24 Fitting the relaxation time data to the Arrhenius equation τ = τ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(Δτ/T) gives the effective energy barrier Δτ = 26.1(5) K with the pre-exponential factor τ0 = 8.3(6) × 10−10 s (Fig. 7b).
exp(Δτ/T) gives the effective energy barrier Δτ = 26.1(5) K with the pre-exponential factor τ0 = 8.3(6) × 10−10 s (Fig. 7b).
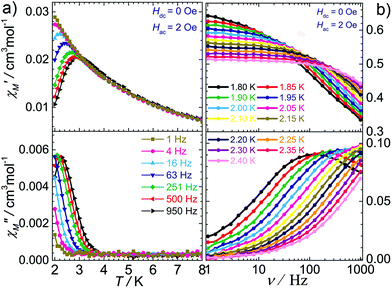 | ||
| Fig. 6 Variable-temperature (a) and variable-frequency (b) AC magnetic susceptibility data for 2 measured in a zero DC field. | ||
For an anisotropic Heisenberg or Ising-like 1D system, it is well known that the χMT value is proportional to the correlation length (ξ) and that it increases exponentially with decreasing temperature, following the equation χMT = Ceff![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(Δξ/T). The Ceff is the effective Curie constant and Δξ gives an estimation of the intrachain exchange energy needed to create a domain wall within the chain. The resulting ln(χMT) versus 1/T plot of 2 features a linear region in the temperature range of 6–12 K, yielding Ceff = 0.85 cm3 mol−1 K and Δξ = 6.06 K (Fig. 5a). As the relaxation time of 2, which was used to estimate the effective energy barrier Δτ, was determined at a very low temperature (below 3 K), the slow relaxation is considered to be within the “finite-size chain” regime and the energy barrier should be given as Δτ = Δξ + ΔA. According to this relationship, the magnetic anisotropy energy ΔA for the individual Fe2+ centres can be estimated as 20.0 K, which is almost equal to the value (20.1 K) for compound [Fe(LN5)(CN)][BF4]. On the other hand, the correlation energy (Δξ) in 2 is about one third of the value for [Fe(LN5)(CN)][BF4], and the blocking temperature of 2 is significantly lower than that of [Fe(LN5)(CN)][BF4] (for example, the peak temperature of the χ′′ at 950 Hz is around 2.2 K for 2, compared with 3.4 K for [Fe(LN5)(CN)][BF4]). These observations indicate that the AF ordering is a potential advantage for the properties of SCM-based magnets.
exp(Δξ/T). The Ceff is the effective Curie constant and Δξ gives an estimation of the intrachain exchange energy needed to create a domain wall within the chain. The resulting ln(χMT) versus 1/T plot of 2 features a linear region in the temperature range of 6–12 K, yielding Ceff = 0.85 cm3 mol−1 K and Δξ = 6.06 K (Fig. 5a). As the relaxation time of 2, which was used to estimate the effective energy barrier Δτ, was determined at a very low temperature (below 3 K), the slow relaxation is considered to be within the “finite-size chain” regime and the energy barrier should be given as Δτ = Δξ + ΔA. According to this relationship, the magnetic anisotropy energy ΔA for the individual Fe2+ centres can be estimated as 20.0 K, which is almost equal to the value (20.1 K) for compound [Fe(LN5)(CN)][BF4]. On the other hand, the correlation energy (Δξ) in 2 is about one third of the value for [Fe(LN5)(CN)][BF4], and the blocking temperature of 2 is significantly lower than that of [Fe(LN5)(CN)][BF4] (for example, the peak temperature of the χ′′ at 950 Hz is around 2.2 K for 2, compared with 3.4 K for [Fe(LN5)(CN)][BF4]). These observations indicate that the AF ordering is a potential advantage for the properties of SCM-based magnets.
Conclusions
In conclusion, the reaction of a pentagonal bipyramidal FeII starting material of D5h symmetry with excessive bulky anions results in two new magnetic materials of significant magnetic anisotropy and slow magnetic relaxation. Because of the terminal coordinated water molecules, compound 1 contains a mononuclear FeII centre, which is further connected by the hydrogen bonds to form an extended structure. Easy-axis magnetic anisotropy with a negative D value of about −3.7 cm−1 was obtained from the analysis of the DC magnetic data, which leads to the field-induced slow magnetic relaxation at low temperatures. Interestingly, a very minor change in the anion results in the 1D cyano-bridged chain structure of compound 2. These 1D chains in 2 are well isolated by the bulky anions preventing any efficient interchain magnetic interactions. Because of the easy-axis magnetic anisotropy, the AF magnetic coupling and spin canting, and the negligible magnetic interactions, pure SCM behaviour with an effective energy barrier of 26.1(5) K is established in 2. Both of these compounds and the formerly reported system with a smaller anion clearly demonstrate the importance of the anions on the fine tuning of the structures and thus on the magnetic properties of the resulting materials. Efforts to introduce functional anions and to extend this chain architecture to other metal centres are under way.Acknowledgements
We thank the Major State Basic Research Development Program (2013CB922102), NSFC (91022031, 21101093, 21471077). This work was also supported by a Project Funded by the Priority Academic Program Development of Jiangsu Higher Education Institutions and the Fundamental Research Funds for the Central Universities (020514380006).Notes and references
- (a) D. Gatteschi, R. Sessoli and J. Villain, Molecular Nanomagnets, Oxford University Press, Oxford, 2006 Search PubMed; (b) R. E. P. Winpenny, Molecular Cluster Magnets, World Scientific, London, 2012 Search PubMed; (c) G. A. Craig and M. Murrie, Chem. Soc. Rev., 2015, 44, 2135 RSC.
- (a) A. Caneschi, D. Gatteschi, N. Lalioti, C. Sangregorio, R. Sessoli, G. Venturi, A. Vindigni, A. Rettori, M. G. Pini and M. A. Novak, Angew. Chem., Int. Ed., 2001, 40, 1760 CrossRef CAS; (b) R. Clérac, H. Miyasaka, M. Yamashita and C. Coulon, J. Am. Chem. Soc., 2002, 124, 12837 CrossRef PubMed.
- (a) S. Dhers, H. L. C. Feltham and S. Brooker, Coord. Chem. Rev., 2015, 296, 24 CrossRef CAS PubMed; (b) W.-X. Zhang, R. Ishikawa, B. Breedlove and M. Yamashita, RSC Adv., 2013, 3, 3772 RSC; (c) H.-L. Sun, Z.-M. Wang and S. Gao, Coord. Chem. Rev., 2010, 254, 1081 CrossRef CAS PubMed; (d) H. Miyasaka, M. Julve, M. Yamashita and R. Clérac, Inorg. Chem., 2009, 48, 3420 CrossRef CAS PubMed; (e) L. Bogani, A. Vindigni, R. Sessoli and D. Gatteschi, J. Mater. Chem., 2008, 18, 4750 RSC; (f) R. Lescouezec, L. M. Toma, J. Vaissermann, M. Verdaguer, F. S. Delgado, C. Ruiz-Pérez, F. Lloret and M. Julve, Coord. Chem. Rev., 2005, 249, 2691 CrossRef CAS PubMed.
- (a) C. Coulon, R. Clérac, W. Wernsdorfer, T. Colin and H. Miyasaka, Phys. Rev. Lett., 2009, 102, 167204 CrossRef; (b) N. Ishii, Y. Okamura, S. Chiba, T. Nogami and T. Ishida, J. Am. Chem. Soc., 2008, 130, 24 CrossRef CAS PubMed; (c) R. Sessoli, Angew. Chem., Int. Ed., 2008, 47, 5508 CrossRef CAS PubMed.
- H. Miyasaka, K. Takayama, A. S. Saytoh, S. Furukawa, M. Yamashita and R. Clérac, Chem. – Eur. J., 2010, 16, 3656 CrossRef CAS PubMed.
- D. Shao, S.-L. Zhang, X.-H. Zhao and X.-Y. Wang, Chem. Commun., 2015, 51, 4360 RSC.
- (a) Y.-Z. Zhang, H.-H. Zhao, E. Funck and K. R. Dunbar, Angew. Chem., Int. Ed., 2015, 54, 1 CrossRef PubMed; (b) L. Qin, Z. Zhang, Z.-P. Zheng, M. Speldrich, P. Kögerler, W. Xue, B.-Y. Wang, X.-M. Chen and Y.-Z. Zheng, Dalton Trans., 2015, 44, 1456 RSC; (c) I. Bhowmick, E. A. Hillard, P. Dechambenoit, C. Coulon, T. D. Harris and R. Clérac, Chem. Commun., 2012, 48, 9717 RSC; (d) X.-M. Liu, B.-Y. Wang, W. Xue, L.-H. Xie, W.-X. Zhang, X.-N. Cheng and X.-M. Chen, Dalton Trans., 2012, 41, 13741 RSC; (e) J. Boeckmann, M. Wriedt and C. Nather, Chem. – Eur. J., 2012, 18, 5284 CrossRef CAS PubMed; (f) J. H. Yoon, J. W. Lee, D. W. Ryu, S. W. Yoon, B. J. Suh, H. C. Kim and C. S. Hong, Chem. – Eur. J., 2011, 17, 3028 CrossRef CAS PubMed; (g) C.-I. Yang, P.-H. Chuang and K.-L. Lu, Chem. Commun., 2011, 47, 4445 RSC; (h) T. Liu, Y.-J. Zhang, S. Kanegawa and O. Sato, J. Am. Chem. Soc., 2010, 132, 8250 CrossRef CAS PubMed.
- (a) X.-B. Li, G.-M. Zhuang, X. Wang, K. Wang and E.-Q. Gao, Chem. Commun., 2013, 49, 1814 RSC; (b) Y.-Q. Wang, Q. Yue, Y. Qi, K. Wang, Q. Sun and E.-Q. Gao, Inorg. Chem., 2013, 52, 4259 CrossRef CAS PubMed; (c) X.-B. Li, G.-M. Zhuang, X. Wang, K. Wang and E.-Q. Gao, Chem. Commun., 2013, 49, 1814 RSC; (d) X.-M. Zhang, Y.-Q. Wang, K. Wang, E.-Q. Gao and C.-M. Liu, Chem. Commun., 2011, 47, 1815 RSC; (e) X.-M. Zhang, K. Wang, Y.-Q. Wang and E.-Q. Gao, Dalton Trans., 2011, 40, 12742 RSC; (f) Y.-Q. Wang, W.-W. Sun, Z.-D. Wang, Q.-X. Jia, E.-Q. Gao and Y. Song, Chem. Commun., 2011, 47, 6386 RSC.
- (a) L. M. Toma, C. Ruiz-Pérez, F. Lloret and M. Julve, Inorg. Chem., 2012, 51, 1216 CrossRef CAS PubMed; (b) L. M. Toma, C. Ruiz-Pérez, J. Pasán, W. Wernsdorfer, F. Lloret and M. Julve, J. Am. Chem. Soc., 2012, 134, 15265 CrossRef CAS PubMed; (c) Z.-X. Li, Y.-F. Zeng, H. Ma and X.-H. Bu, Chem. Commun., 2010, 46, 8540 RSC; (d) Y.-Z. Zheng, M.-L. Tong, W.-X. Zhang and X.-M. Chen, Angew. Chem., Int. Ed., 2006, 45, 6310 CrossRef CAS PubMed; (e) W. X. Zhang, T. Shiga, H. Miyasaka and M. Yamashita, J. Am. Chem. Soc., 2012, 134, 6908 CrossRef CAS PubMed.
- (a) M. Zhu, J.-J. Wang, M. Yang, Y. Ma and L.-C. Li, Dalton Trans., 2015, 44, 9815 RSC; (b) Z.-X. Wang, X. Zhang, Y.-Z. Zhang, M.-X. Li, H.-H. Zhao, M. Andruh and K. R. Dunbar, Angew. Chem., Int. Ed., 2014, 53, 11567 CrossRef CAS PubMed; (c) M. G. F. Vaz, P. M. Lahti, R. A. A. Cassaro and M. A. Novak, Chem. – Eur. J., 2014, 20, 1 CrossRef PubMed; (d) R. Ishikawa, K. Katoh, B. K. Breedlove and M. Yamashita, Inorg. Chem., 2012, 51, 9123 CrossRef CAS PubMed; (e) K. Bernot, L. Bogani, R. Sessoli and D. Gatteschi, Inorg. Chim. Acta, 2007, 360, 3807 CrossRef CAS PubMed; (f) K. Bernot, L. Bogani, A. Caneschi, D. Gatteschi and R. Sessoli, J. Am. Chem. Soc., 2006, 128, 7947 CrossRef CAS PubMed; (g) H. Miyasaka, T. Madanbashi, K. Sugimoto, Y. Nakazawa, W. Wernsdorfer, K. Sugiura, M. Yamashita, C. Coulon and R. Clérac, Chem. – Eur. J., 2006, 12, 7028 CrossRef CAS PubMed; (h) N. Ishii, T. Ishida and T. Nogami, Inorg. Chem., 2006, 45, 3837 CrossRef CAS PubMed; (i) L. Bogani, C. Sangregorio, R. Sessoli and D. Gatteschi, Angew. Chem., Int. Ed., 2005, 44, 5187 CrossRef PubMed.
- (a) A. K. Bar, C. Pichon, N. Gogoi, C. Duhayon, S. Ramasesha and J. P. Sutter, Chem. Commun., 2015, 51, 3616 RSC; (b) R. Ruamps, L. J. Batchelor, R. Maurice, N. Gogoi, J. L. Pablo, N. Guihry, C. Graaf, A. L. Barra, J. P. Sutter and T. Mallah, Chem. – Eur. J., 2013, 19, 950 CrossRef CAS PubMed.
- (a) Y.-Z. Zhang, B.-W. Wang, O. Sato and S. Gao, Chem. Commun., 2010, 46, 6959 RSC; (b) T. S. Venkatakrishnan, S. Sahoo, N. Bréfuel, C. Paulsen, C. Duhayon, A. L. Barra, S. Ramasesha and J. P. Sutter, J. Am. Chem. Soc., 2010, 132, 6047 CrossRef CAS PubMed.
- S. M. Nelson, P. D. A. Mcllroy, C. S. Stevenson, E. Konig, G. Ritter and J. Waigel, J. Chem. Soc., Dalton Trans., 1986, 991 RSC.
- SAINT Software Users Guide, version 7.0, Bruker Analytical X-Ray Systems, Madison, WI, 1999 Search PubMed.
- G. M. Sheldrick, SADABS, version 2.03, Bruker Analytical X-Ray Systems, Madison, WI, 2000 Search PubMed.
- G. M. Sheldrick, SHELXTL, Version 6.14, Bruker AXS, Inc., Madison, WI, 2000–2003 Search PubMed.
- M. Llunell, D. Casanova, J. Cirera, P. Alemany and S. Alvarez, SHAPE, Version 2.1, Universitat de Barcelona, 2013 Search PubMed.
- N. F. Chilton, R. P. Anderson, L. D. Turner, A. Soncini and K. S. Murray, J. Comput. Chem., 2013, 34, 1164 CrossRef CAS PubMed.
- M. P. Shores, J. J. Sokol and J. R. Long, J. Am. Chem. Soc., 2002, 124, 2279 CrossRef CAS PubMed.
- S. Gomez-Coca, E. Cremades, N. Aliaga-Alcalde and E. Ruiz, J. Am. Chem. Soc., 2013, 135, 7010 CrossRef CAS PubMed.
- (a) A. V. Palii, O. S. Reu, S. M. Ostrovsky, S. I. Klokishner, B. S. Tsukerblat, Z.-M. Sun, J.-G. Mao, A. V. Prosvirin, H.-H. Zhao and K. R. Dunbar, J. Am. Chem. Soc., 2008, 130, 14729 CrossRef CAS PubMed; (b) K. Bernot, J. Luzon, R. Sessoli, A. Vindigni, J. Thion, S. Richeter, D. Leclercq, J. Larionova and A. Lee, J. Am. Chem. Soc., 2008, 130, 1619 CrossRef CAS PubMed; (c) H.-L. Sun, Z.-M. Wang and S. Gao, Chem. – Eur. J., 2009, 15, 1757 CrossRef CAS PubMed.
- J. A. Mydosh, Spin Glasses: An Experimental Introduction, Taylor & Francis, London, 1993 Search PubMed.
- K. S. Cole and R. H. Cole, J. Chem. Phys., 1941, 9, 341 CrossRef CAS PubMed.
- S. M. Aubin, Z. Sun, L. Pardi, J. Krzysteck, K. Folting, L. J. Brunel, A. L. Rheingold and D. N. Hendrickson, Inorg. Chem., 1999, 38, 5329 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Structure information in detail and additional magnetic data. CCDC 1403677 (1) and 1403678 (2). For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c5qi00089k |
| This journal is © the Partner Organisations 2015 |