Open Access Article
Open Access ArticleInfluence of bacterial swimming and hydrodynamics on attachment of phages†
Christoph
Lohrmann
 a,
Christian
Holm
a,
Christian
Holm
 b and
Sujit S.
Datta
b and
Sujit S.
Datta
 *c
*c
aInstitute for Computational Physics, University of Stuttgart, 70569 Stuttgart, Germany. E-mail: clohrmann@icp.uni-stuttgart.de
bInstitute for Computational Physics, University of Stuttgart, 70569 Stuttgart, Germany. E-mail: holm@icp.uni-stuttgart.de
cDepartment of Chemical and Biological Engineering, Princeton University, Princeton, New Jersey 08544, USA. E-mail: ssdatta@princeton.edu
First published on 6th June 2024
Abstract
Bacteriophages (“phages”) are viruses that infect bacteria. Since they do not actively self-propel, phages rely on thermal diffusion to find target cells—but can also be advected by fluid flows, such as those generated by motile bacteria themselves in bulk fluids. How does the flow field generated by a swimming bacterium influence how it encounters phages? Here, we address this question using coupled molecular dynamics and lattice Boltzmann simulations of flagellated bacteria swimming through a bulk fluid containing uniformly-dispersed phages. We find that while swimming increases the rate at which phages attach to both the cell body and flagellar propeller, hydrodynamic interactions strongly suppress this increase at the cell body, but conversely enhance this increase at the flagellar bundle. Our results highlight the pivotal influence of hydrodynamics on the interactions between bacteria and phages, as well as other diffusible species, in microbial environments.
1 Introduction
More than 1031 bacteriophages (“phages” for short) are estimated to exist on Earth, more than every other organism on the planet combined.1,2 Indeed, on average, phages—viruses that infect bacteria—outnumber bacterial cells by a factor of ten.3 Thus, their interactions with phages regulate how bacteria function in natural environments, with critical implications for agriculture, ecology, and medicine.4–8 Extensive research has focused on documenting various biological and chemical factors that influence these interactions; nevertheless, the basic physical processes underlying how bacteria encounter and ultimately become infected by phages in the first place remain poorly understood.For example: while phages do not actively self-propel, many bacteria do using, e.g., flagella-driven swimming through fluids. We therefore focus on this mode of motility here. How does swimming influence the rate at which bacteria encounter and eventually become infected by phages, if at all? Despite its apparent simplicity, this question still does not have a clear answer9—even for the illustrative, idealized case of a cell swimming at a constant velocity vswim in an unbounded, uniform, Newtonian fluid at low Reynolds number. One might expect that the rate at which phages encounter and attach to the cell simply increases proportionately with its swimming speed as it explores more space;10 however, this expectation does not consider the complex flow field generated by the bacterium around itself as it swims,11 which can advect and entrain surrounding phages in a non-trivial manner.11,12 The importance of these hydrodynamics is highlighted by examining the Péclet number comparing the characteristic rates of phage transport by fluid advection and thermal diffusion, Pephage ≡ vswimrbody/DP, which exceeds unity for typical values of the bacterial swimming speed vswim ∼ 10–100 μm s−1, size rbody ∼ 1 μm, and phage diffusivity DP ∼ 1–10 μm2 s−1. Hence, the rate at which phages encounter, attach to, and ultimately infect a bacterium is likely highly sensitive to the nature of the flow field it generates by swimming.
In a classic study,13 Berg and Purcell examined the influence of these hydrodynamics by treating the swimming bacterium as an externally-driven sphere. Building on prior calculations,14,15 the authors concluded that because the cell pushes fluid around it as it moves, “motility cannot significantly increase the cell's acquisition of material”. While this study focused on cellular interactions with chemical species like nutrients, the authors considered interactions with phages as a specific application of their results—concluding that the phage attachment rate only increases sublinearly with swimming speed. However, while instructive, this analysis neglects two crucial features of flagellated bacteria—which are not uniform spheres, but are typically comprised of an elongated cell body driven by an adjoined elongated flagellar propeller. First, it is now well known that many such bacteria (including Escherichia coli, Bacillus subtilis, and Salmonella enterica) are force-free “pushers”: each cell pushes on surrounding fluid with an equal and opposite force to the one generated by its flagella as it swims.11,16,17 As a result, the fluid boundary conditions are distinct for the cell body and the flagella, and phage attachment rates may thus differ considerably between the two. Second, the flow field away from such a swimming bacterium has a dipolar shape with a fluid velocity magnitude v that decays with distance r away from the cell as ∼1/r2, unlike the longer-ranged v(r) ∼ 1/r decay characteristic of a driven sphere. How these two features influence the manner in which phages encounter and attach to swimming bacteria is, to the best of our knowledge, still unknown.
Here, we address this gap in knowledge using simulations of a bacterium swimming through a fluid containing uniformly-dispersed phages. We focus on the case of “pusher”-type bacteria in the main text; we find qualitatively similar results for the opposite case of “pullers”, as detailed in the ESI.† We use particle-resolved molecular dynamics to explicitly treat the cell body, flagellar propeller (hereafter referred to as the flagellum for convenience), and individual phages, all of which are coupled to and interact via an underlying fluid which we simulate using a lattice Boltzmann algorithm. We find that while bacterial swimming increases the rate at which the phages attach to the cell body, the dipolar flow thereby generated advects phages away from the forward-facing “head” of the cell body, thereby suppressing this increase by as much as twofold—as suggested by Berg and Purcell. However, this dipolar flow field also pumps phage-containing fluid to the flagellum. As a result, the phage attachment rate at the flagellum is appreciable and increases nearly linearly with swimming speed, in stark contrast to the findings of Berg and Purcell. Altogether, our work suggests that while the fluid flow generated by swimming helps to protect the bacterial cell body from phages, it promotes phage attachment at the flagellum—an effect that, to the best of our knowledge, has been overlooked in previous work. This effect may be exploited by flagellotropic phages, i.e., phages that initiate infection by attaching to the host flagellum, which are increasingly being recognized as key constituents of natural microbial communities and potentially useful therapeutics against pathogenic bacteria.18,19 More broadly, our findings highlight the pivotal influence of hydrodynamics on the interactions between bacteria and phages, as well as other diffusible species, in microbial environments.
2 Methods
2.1 Molecular dynamics model of phages and bacterium
We use a particle-resolved, coarse-grained molecular dynamics algorithm to represent the phages and bacterium. Particles of each are coupled to and interact with each other via an underlying lattice Boltzmann fluid through friction forces, as detailed below. This approach enables us to simulate the coupling between short-range interactions between phage and bacteria and larger-range hydrodynamic interactions associated with bacterial swimming. While here we focus on the case of a Newtonian fluid, which is relevant to many aquatic microbial habitats, studying the case of a more complex non-Newtonian fluid10,20–31 will be a useful extension of our work.mP![[r with combining umlaut]](https://www.rsc.org/images/entities/b_char_0072_0308.gif) Pi = Fphage–fluidi + Fbact–phagei, Pi = Fphage–fluidi + Fbact–phagei, | (1) |
 | (2) |
We treat hydrodynamics at a continuum level by solving the Navier–Stokes equations using a standard two-relaxation time lattice Boltzmann algorithm with “magic” parameter Λ = 3/16 and Guo forcing.32 Thermal fluctuations of the fluid are included following the approach of ref. 33. To obtain the fluid velocity vfl at the particle positions rPi, we interpolate between the nearest lattice nodes according to ref. 34. The coupling force Fphage–fluid reflects the microscopic interactions between the fluid and the phage particles. These interactions obey Newton's third law, so the coupling force is also applied to the fluid, but with opposite sign. We thus extrapolate −Fphage–fluid to the nearest lattice node as detailed in ref. 34.
More specifically, the cell body comprises Nbody particles of type one arranged in a line along ê, evenly spaced over the length lbody, along with Ncoupl additional coupling points of type two on the surface of the cell body. The dynamics of the central particle of the cell body in three spatial dimensions are described by the equations of motion
 | (3) |
 | (4) |
 | (5) |
 | (6) |
 | (7) |
![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) B the bare friction coefficient, and ηBj a noise term with the same properties as ηP. As for the phages, all coupling forces Fbact-fluidj are also applied to the fluid in the opposite direction to ensure net momentum conservation. The coupling forces also lead to the torque
B the bare friction coefficient, and ηBj a noise term with the same properties as ηP. As for the phages, all coupling forces Fbact-fluidj are also applied to the fluid in the opposite direction to ensure net momentum conservation. The coupling forces also lead to the torque | (8) |
The flagellum is modelled by Nflagellum particles of type three arranged in a line along ê and evenly spaced over a length lflag, with the central particle of the flagellum at a distance ldipole behind the central particle of the cell body. Flagellum particles do not experience friction or noise as the other particles in the system. Instead, each of them applies a force
 | (9) |
Cell body particles of type one and flagellum particles interact with phages via the short-ranged, purely-repulsive, almost-hard-sphere Weeks–Chandler–Anderson potential39
 | (10) |
 | (11) |
 | (12) |
In our simulations, we solve eqn (1)–(12) numerically using the development version of the ESPResSo simulation package40 with the waLBerla41,42 library for lattice Boltzmann hydrodynamics. Exact software versions as well as our custom code are freely available; details are provided in ref. 43.
 and
and 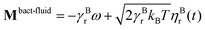 , where γBt and γBr are the translational and rotational friction coefficients, respectively.
, where γBt and γBr are the translational and rotational friction coefficients, respectively.
2.2 Model of phage attachment
We consider a phage as being in contact with the bacterium (either the cell body or flagellum) if the surface-to-surface distance is smaller than a prescribed encounter distance denc. Once it contacts the bacterium, the phage attaches to the cell at a rate katt, which is a lumped parameter that reflects the influence of short-ranged microscopic interactions mediating the complex process of binding to specific receptors to complete the process of attachment.44,45 As we show below, the overall qualitative insights that result from our simulations are insensitive to the specific choice of katt. Because our focus is on the purely physical processes underlying phage encounter and attachment, we do not consider the subsequent biological steps needed for the phage to actually insert its genetic material into the cell and complete the process of infection.In our time-discretised numerical implementation, we check for phages in contact with the bacterium after every successive time interval Δt. For such contacting phages, we calculate the attachment probability patt = Δtkatt. Based on this probability, using a random number generator, we choose whether the phage remains free or it successfully attaches to the cell. If attachment happens, we register the time and relative position of the phage encounter on the bacterium surface. We then move the phage to a random position outside the encounter region defined by denc to prevent double-counting; this procedure mimics the case of a bacterium swimming in an infinite fluid reservoir with constant phage number density.
We apply the same model for phage attachment to both the cell body and the flagellar bundle. We thus use contact with the flagellar bundle as the criterion for attachment instead of contact to individual flagella, which are not explicitly resolved in our coarse-grained approach. This simplifying assumption is justified because the fast motion of individual flagella, the complex flow field inside the bundle and the large surface-to-volume ratio of flagella all promote contact with phages once they have entered the bundle, making the approach to the bundle the limiting step.
We determine the overall attachment rate  from a linear fit to the computed number of phages that have attached to the cell at time t, Natt(t) (ESI†). For the case of katt → 0 (patt → 0), the number density of phages in the encounter region is asymptotically independent of katt. Hence, J scales linearly with katt, and we only need to determine the number density of phages in the encounter region. Therefore, for simulations of katt → 0, we compute J by tracking the trajectories of phages in the contact region to obtain their number density.
from a linear fit to the computed number of phages that have attached to the cell at time t, Natt(t) (ESI†). For the case of katt → 0 (patt → 0), the number density of phages in the encounter region is asymptotically independent of katt. Hence, J scales linearly with katt, and we only need to determine the number density of phages in the encounter region. Therefore, for simulations of katt → 0, we compute J by tracking the trajectories of phages in the contact region to obtain their number density.
2.3 Continuum modelling
To compare the results of our particle-based simulations to those of Berg and Purcell,13 we follow their approach and solve the continuum advection-diffusion equation| DP∇2c(r) + vStokes(r)·∇c(r) = 0 | (13) |
 in an infinite reservoir of phages, with boundary conditions c(|r| = req) = 0 and c(|r| → ∞) = c∞. The Stokes flow field is given by
in an infinite reservoir of phages, with boundary conditions c(|r| = req) = 0 and c(|r| → ∞) = c∞. The Stokes flow field is given by| vStokes(r) = vrer + vΘeΘ, | (14) |
 | (15) |
 | (16) |
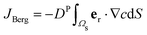 .
.
In practice, we solve eqn (13)–(16) using a finite element algorithm46 with the boundary condition c(|r| = R) = c0 with R = 50 μm ≫ req. The finite size effects from restricting the simulation domain to this radius are negligible, and the attachment rate for vswim = 0 obtained with finite R deviates from the analytical solution for R → ∞ only by ≈1%.
2.4 Choice of numerical parameters
For the phages, we choose rP = 50 nm, which is comparable to the size of many commonly-studied phages, including T447 and the flagellotropic phages χ and PBS1.19 We calculate the phage friction coefficient from Stokes’ law as γP = 6πμwaterrP, where μwater = 1 × 10−3 Pa s is the dynamic shear viscosity of water; the numerical friction coefficient then follows from a lattice correction given by γP* = [(γP)−1 − (25μwateragrid)−1]−1, where agrid is the lattice Boltzmann grid constant.34 The phage diffusion coefficient is given by the Einstein–Smoluchowski relation DP = kBT/γP ≈ 4.4 μm2 s−1 at our choice of T = 300 K, which is in good agreement with experimental measurements.10,48We calculate the phage mass as mP = ρP4/3π(rP)3, where ρP is the mass density of the phage. At the low Reynolds numbers (<1) relevant to this study, inertia should not play a role. However, we use the underdamped, Langevin equations of motion eqn (1)–(12) to facilitate coupling to the fluid in our coupled molecular dynamics-lattice Boltzmann framework. Therefore, we must still include inertia while both ensuring that it does not influence the results of the simulations and does not make the simulations too computationally intensive. Our choices of density accomplish this balance. First, we note that the time scale over which momentum relaxes for phage particles of size r = 50 nm with a density equal to that of water, ρwater = 1000 kg m−3, is τPdiff = mP/γP ≈ 5.6 × 10−10 s—much smaller than the relevant time scales of our system, again reflecting the fact that inertia is not relevant. Indeed, as long as this momentum dissipation time scale is smaller that any other time scales of the system, inertia does not play a role in the physics of the system. Therefore, we instead choose ρP = 105ρwater such that the momentum dissipation time scale is τPdiff ≈ 5.6 × 10−5 s—still small compared to the time scales we are interested in, ensuring that the resulting physics remain unchanged, but large enough to enable us to choose time steps that are 105 times larger, δt = 3.33 × 10−5 s, rendering the simulations computationally tractable. We confirm this expectation by directly verifying that changing the phage mass density does not affect our results, as shown in the ESI.†
To mimic the commonly-studied flagellated bacterial species E. coli49 and S. enterica,50 we choose lbody = 3 μm and rbody = 0.5 μm, with Nbody = 9 and Ncoupl = 62 to obtain a sufficiently well-resolved cell surface. The bacterial mass is approximated by mB = ρBπrbody2lbody; as detailed above for the phages, the diffusive time scale for bacteria is very small and the dynamics are overdamped, so we choose ρB = 5 × 103ρwater. For simulations without hydrodynamics, we use a spheroidal approximation, with the translational and rotational friction coefficients γBt and γBr calculated following, ref. 51 and 52 respectively. The force needed to propel the bacterium with the desired velocity is then given by Fswim = γBtvswim. For simulations with hydrodynamics, we set ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) B = 2.4 × 10−9 kg s−1, which represents the largest value that we can use without impeding numerical stability to most closely approximate a no-slip boundary condition. The relation between Fswim and vswim is nontrivial because of the complex flow field and the many coupling points; however, empirically, we find that using Fswim = γeffvswim with an effective friction coefficient γeff = Nbody
B = 2.4 × 10−9 kg s−1, which represents the largest value that we can use without impeding numerical stability to most closely approximate a no-slip boundary condition. The relation between Fswim and vswim is nontrivial because of the complex flow field and the many coupling points; however, empirically, we find that using Fswim = γeffvswim with an effective friction coefficient γeff = Nbody![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) B/0.825 yields good agreement between the desired and actual swimming velocity, as detailed further in ESI.† The flagellum is lflag = 5 μm long with a radius of rflag = 0.25 μm at a distance ldipole = 5 μm, and we take Nflagellum = 41.
B/0.825 yields good agreement between the desired and actual swimming velocity, as detailed further in ESI.† The flagellum is lflag = 5 μm long with a radius of rflag = 0.25 μm at a distance ldipole = 5 μm, and we take Nflagellum = 41.
The lattice Boltzmann fluid has a dynamic viscosity μ = μwater and is discretised on a grid with lattice spacing agrid = rbody. Since the typical size of flow field variations is larger than the cell size and all velocities are interpolated between lattice nodes, this resolution is fine enough to resolve the flow near the bacterium surface. To keep simulations stable, we choose a fluid mass density of ρfluid = 1200ρwater. This choice does not change the flow behaviour with respect to water since the Reynolds number Re ≡ ρfluidvswimrbody/μ ≈ 0.017 for a typical swimming velocity vswim = 25 μm s−1 is much smaller than unity, even for this increased density. We confirm this expectation by directly verifying that changing the fluid mass density does not affect our results, as shown in the ESI.†
Our simulations consider one bacterium and NP = 1000 phage particles in a fully periodic, cubic simulation domain with box length L = 16 μm. Since all forces of our fluid–particle coupling scheme add to zero, the total momentum of the system remains at zero and no boundaries are necessary to keep the fluid at rest. When the bacterium moves forward, the fluid moves in the opposite direction with the same momentum—but since there is much more fluid mass than bacterium mass in the simulation box, the fluid center of mass remains nearly at rest. The volume fraction of phages ϕ = NP4π(rP)3/3L3 ≈ 10−4, is very low, so we expect any hydrodynamic interactions between them to be negligible. Moreover, in the ESI† we present evidence that there are no appreciable finite-size effects associated with the size of the simulation domain. We set the encounter distance denc = rP = 50 nm; the time scale for phage diffusion across this distance is τcross ∼ denc2/DP ≈ 6 × 10−4 s, so we choose the Δt = 1 × 10−4 s to adequately register phage encounters.
Each simulation is repeated Nensemble times with different seeds, i.e., different initial conditions and noise realisations, to obtain the standard error of the mean of the quantities reported below. We choose Nensemble ≥ 5, the exact numbers for each reported result can be found in the data set43 that accompanies this work.
3 Results
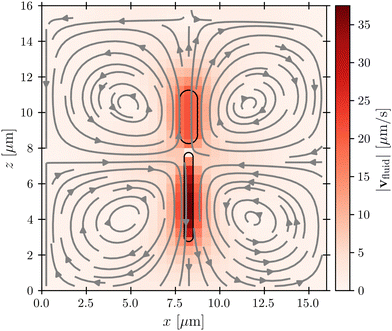
Before considering interactions with phages, we first verify that our simulation approach recapitulates the far-field dipolar flow field characteristic of swimming flagellated bacteria.11,16 This is indeed the case, as shown in Fig. 2, which shows the fluid flow field in the laboratory frame of reference; furthermore, as shown in the ESI,† the fluid velocity magnitude v decays with distance r away from the cell as ∼1/r2, as predicted by theory. Importantly, while the bacterium moves in the positive z-direction, our model for the flagellum–fluid interaction leads to fluid motion in the negative z-direction inside the flagellum, with swimming being force-free overall.Having established that our simulations reproduce this characteristic dipolar flow field, we next investigate what its implications are for attachment by phages. We emphasize that while the physics of direct phage–bacterium interactions happens on the scale of the phages, smaller than the grid size used for modeling the fluid flows, a key strength of our coupled molecular dynamics and lattice Boltzmann approach is that these direct phage–bacterium interactions are not influenced by the fluid simulation; instead, they are explicitly treated by our molecular dynamics approach over the encounter distance denc = rP = 50 nm, much smaller than the lattice Boltzmann grid size. Thus, our approach treats both the large-scale features of fluid flows that advect phages—which vary on a much larger scale that is comparable to the size of the bacterium and much larger than the lattice Boltzmann grid cell—as well as the small-scale features of phage–bacteria interactions. As described below, we use these simulations to examine phage interactions first with the cell body, then with the flagellum.
3.1 Phage attachment to the cell body
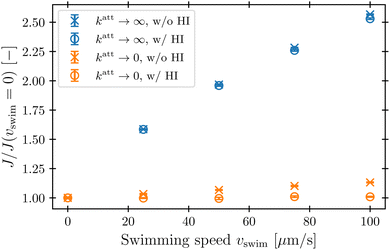
To characterize how bacterial swimming and the associated hydrodynamic interactions (HI) influence how phages attach to the cell body, we compute the attachment rate J over a broad range of representative swimming speeds vswim, for a broad range of katt, with or without HI included. Our results are presented in Fig. 3 for the limiting cases of katt → 0 and katt → ∞ for clarity; the intermediate values of katt monotonically interpolate between these cases, as shown in the ESI.†We first consider the case of katt → ∞. In the absence of HI, J increases approximately linearly with vswim (blue ×, Fig. 3), as suggested previously.10 Indeed, without HI, we expect that J/c0 ≈ 4πDPreq + πreq2vswim; here, the first term on the right hand side describes the flux of a diffusive species into a spherical, stationary, perfect absorber53 and is given by the solution of eqn (13) with vswim = 0, and the second term takes the motion of the absorber into account by calculating the rate at which its cross section explores the volume filled with a constant number density of phages that are absorbed upon contact. As shown by the dashed green line in Fig. 3, this prediction agrees well with our simulation results.
Incorporating HI strongly suppresses attachment by phages, however. While J still increases monotonically with vswim, the magnitude of this increase is considerably lessened by hydrodynamics (blue ○, Fig. 3)—indeed, by as much as twofold at the largest swimming speed tested. Why is this the case?
Close inspection of the flow field around the cell body provides a clue: as shown in Fig. 2, the no-slip boundary condition on the cell body surface causes a region of fluid in its immediate vicinity to be dragged along with it as it swims. We expect that this region also advects surrounding phages along with the cell, pushing them away from its forward-facing “head”; consequently, these phages must rely primarily on passive thermal diffusion to cross this region and successfully attach to the cell, independent of the bacterial swimming speed.
This effect is more clearly visualized in the reference frame that moves along with the bacterium. The relative flow field given by 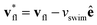 , where the asterisk denotes quantities measured in this comoving frame, is shown in Fig. 4. We quantify the relative importance of phage advection and diffusion using the local Péclet number
, where the asterisk denotes quantities measured in this comoving frame, is shown in Fig. 4. We quantify the relative importance of phage advection and diffusion using the local Péclet number 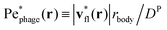 defined in this comoving frame; the iso-line of
defined in this comoving frame; the iso-line of  is shown by the dashed line. As expected, within the region bordered by the dashed line, the fluid is nearly at relative rest and
is shown by the dashed line. As expected, within the region bordered by the dashed line, the fluid is nearly at relative rest and  —confirming that any phages contained therein must rely primarily on thermal diffusion to attach to the cell body. Any enhancement in the phage attachment rate arising from bacterial swimming is therefore suppressed by this “protective shield” of fluid that surrounds the cell body.
—confirming that any phages contained therein must rely primarily on thermal diffusion to attach to the cell body. Any enhancement in the phage attachment rate arising from bacterial swimming is therefore suppressed by this “protective shield” of fluid that surrounds the cell body.
 | ||
Fig. 4 Cross-section through the dipolar flow field generated by a swimming bacterium, in the cell's moving frame of reference. The image shows the same flow field as in Fig. 2, but in the comoving frame. The cell is swimming in the +z direction. The blue dashed line marks  . . | ||
This hydrodynamic effect manifests as katt → 0, as well. When HI are not included, the swimming bacterium is not protected by the “shield” of quiescent fluid discussed above. Instead, as it swims, the cell collects and accumulates phages at its head, and J again increases approximately linearly with vswim, as shown by the orange × in Fig. 3. In this case, the swimming bacterium does not appreciably remove contacting phages from the fluid, whereas in the case of katt → ∞, phages are locally depleted from the vicinity of the cell upon contact and attachment. Therefore, the dependence of J on vswim is more modest for phages with katt → 0; indeed, when HI are included, there is no measurable dependence of J on vswim (orange ○, Fig. 3).
The protective influence of the hydrodynamic “shield” is also apparent in the spatial distribution of phage attachment over the cell body, shown for the example of vswim = 100 μm s−1 and katt → 0 in Fig. 5; the corresponding distributions for a range of other swimming speeds are shown in the ESI.† As expected, without HI (left panel), phage attachment occurs preferentially at the head of the cell. However, HI push phages away from the head of the cell, causing attachment to be distributed more uniformly around the cell body (right panel). Fig. 6 quantifies this difference for all the simulation conditions tested using the average z-position of phage attachment relative to the cell body center of mass, i.e., the first moment of the attachment probability density. Again, as shown by the difference between × and ○ symbols, HI reduce the asymmetry of phage attachment for both katt → 0 and katt → ∞ over all swimming speeds tested.
In their classic paper,13 Berg and Purcell did not consider the elongated shape of a swimming bacterium, the distinction between the cell body and flagellum, or the dipolar flow field established by swimming. Nevertheless, using a more simplified continuum model of an externally-forced sphere, they intuited the protective hydrodynamic effect uncovered by our simulations, noting that “The molecules [or in our case, phages] in front of the cell are carried out of its way along with the fluid it must push aside to move. The cell carries with it a layer of liquid that is practically stationary in its frame of reference. Every molecule [or phage] that reaches the surface of the cell must cross this layer by diffusion.” Remarkably, despite the simplifications made in their work, Berg and Purcell's prediction for the attachment rate (solid green curve, Fig. 3) shows excellent agreement with the results of our more detailed simulations (blue ○). One may not expect this agreement a priori given the marked difference between the actual dipolar flow field established by the swimming cell and the approximation used by Berg and Purcell. However, our results show that the essential qualitative feature of the low  region is independent of the shape and propulsion mechanism of the bacterium, justifying their simplifying assumptions a posteriori—but only for the case of the cell body. As we show in the next section, we find dramatically different behavior for the bacterial flagellum.
region is independent of the shape and propulsion mechanism of the bacterium, justifying their simplifying assumptions a posteriori—but only for the case of the cell body. As we show in the next section, we find dramatically different behavior for the bacterial flagellum.
3.2 Phage attachment to the flagellum
While the cell body drags a protective region of fluid with it, the flagellum does not. Instead, because it is permeable to and exerts a force on the fluid,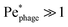 especially in the immediate vicinity of the flagellum, as seen by the dark red region of Fig. 4. As a result, we expect that hydrodynamic interactions are not protective as for the cell body, but instead, promote attachment to the flagellum. Our simulations confirm this expectation, as shown in Fig. 7.
especially in the immediate vicinity of the flagellum, as seen by the dark red region of Fig. 4. As a result, we expect that hydrodynamic interactions are not protective as for the cell body, but instead, promote attachment to the flagellum. Our simulations confirm this expectation, as shown in Fig. 7.
Unlike the case of the cell body, HI greatly increase the flagellar attachment rate, as seen by comparing the ○ and × points in Fig. 7(A)—indeed, by nearly twofold at the largest swimming speed tested. In the absence of HI, J only increases marginally with vswim for katt → ∞. It even decreases with vswim for katt → 0, due to the cell body pushing phages radially outward upon contact. However, when HI are taken into account, the flagellum pumps in phage-laden fluid from the sides of the cell body and moves it through the space occupied by the flagellar bundle. Therefore, the volume of fluid coming in contact with the flagellum, and thus phage attachment, increases with vswim. Moreover, because the fluid is pumped along the −ê direction, we expect that phage attachment is more likely to occur at the forward end of the flagellum with increasing vswim. Inspecting the spatial distribution of phage attachment along the flagellum confirms this expectation, as shown for the example of vswim = 100 μm s−1 and katt → 0 in Fig. 7(B), and quantified for all the simulation conditions tested in Fig. 7(C).
3.3 Overall attachment rate
Our simulations have revealed that hydrodynamic interactions suppress phage attachment to the cell body and conversely promote attachment to the flagellum. How do these effects compete in determining the overall phage attachment rate integrated over the entire cell body and flagellum? Inspecting the flow field in the reference frame that moves along with the bacterium (Fig. 4) suggests that these effects should nearly cancel each other out, since the fluid streamlines immediately in front of the cell body bend around it and then become re-focused within the flagellum. Therefore, phages that would have attached to the cell body in the absence of HI are instead advected by the fluid to later attach to the flagellum, instead—causing the overall attachment rate to be unaffected. This expectation is borne out by the simulations, as shown in Fig. 8: hydrodynamic interactions do not appreciably influence the overall attachment rate, just the position of phage attachment. Taken together, these results highlight the importance of considering spatial variations of attachment fluxes along the surface of the cell, not just their overall sum, which masks these variations.4 Conclusions
Using coarse-grained molecular dynamics simulations of a swimming bacterium that explicitly treat its cell body and flagellum separately, with hydrodynamic interactions incorporated via coupling to a lattice Boltzmann fluid, our work has shed new light on the influence of swimming on attachment by phages. We find that while swimming increases the rate at which phages attach to both the cell body and flagellar propeller, hydrodynamic interactions strongly suppress this increase at the cell body, but conversely enhance this increase at the flagellar bundle. This difference in attachment arises from the characteristic dipolar flow field generated by a swimming bacterium, which advects phages away from the cell body, but pumps phage-laden fluid into the flagellum. Hence, while our results corroborate the findings of Berg and Purcell for the cell body, our work provides a counterpoint to their conclusion that “in a uniform medium motility cannot significantly increase the cell's acquisition of material.” (In our case, “material” refers to external phages, although our results may also apply to cellular uptake of chemical species like nutrients and antibiotics54). Experimentally testing these predictions—e.g., by combining direct visualization of phage attachment55 with optical trapping of swimming cells56—will be an important direction for future work.While in the main text we focused on the case of pusher-type bacteria, many other microswimmers (e.g., Chlamydomonas reinhardtii) are pullers: their flagellum is at the front of the cell body, not the rear, and as a result, they generate a similar flow field to that of a pusher, but with opposite flow directions.57 To explore the generality of our findings, we also perform all our simulations with a puller-type swimmer with ldipole = 5 μm, which is equivalent to reversing the swim force Fswim and correspondingly redefining the notions of “forward” and “backward”. In this case, our results (shown in the ESI†) point to a similar overall conclusion as for pushers: while the fluid flow generated by swimming helps to protect the cell body from phages, it promotes phage attachment at the flagellum. Building on our work, it will be interesting to investigate how hydrodynamics influence interactions with phages for microswimmers that use other forms of swimming. Another related direction for future inquiry will be to investigate how the flows generated by collectives of microswimmers,58versus the individuals considered here, influence interactions with phages.
Our model takes a step toward capturing the essential biophysical processes underlying the interactions between phage and swimming bacteria, and necessarily involved some simplifying assumptions and approximations. For example, in reality, the surfaces of individual flagella in a bundle are no-slip boundaries; therefore, a region of small Péclet number surrounds each flagellum over which phages must diffuse, following a similar argument to that we made for the cell body. However, because the flagellar bundle consists of many individual flagella moving at large speeds compared to the swim speed of the cell body, the small-Pe region around each flagellum is much smaller than that around the cell body. The flows inside the bundle are also highly complex and time-dependent, potentially increasing the mixing of phages that enter the bundle and the likelihood of contact. Our modelling approach simplifies these complex interactions by coarse-graining the fast moving, small flagella into a larger solid, permeable object representing the entire bundle. Importantly, because inside the bundle the aforementioned factors increase the likelihood of phage attachment, the rate-limiting step to attachment is the approach of a phage from the exterior to the bundle itself, mediated by larger-scale hydrodynamics—which are captured by our coarse-grained model. Therefore, while a model with explicitly-resolved flagella could yield attachment rates that are slightly different from ours, because the rate-limiting step to attachment is phage transport from the exterior of the cell to the surface of the flagella—versus the subsequent step of contacting an individual flagellum—we expect that our central findings would be the same in such an explicitly-resolved model. Exploring these details will be a useful direction for future work.
Another simplification we made is to model phage–bacterium interactions as being short-ranged and purely-repulsive; exploring the influence of more sophisticated microscopic interactions will be another useful direction for further research. We do not expect that our central findings will change in this case, however: our coarse-grained treatment subsumes all these complex microscopic interactions into the lumped rate katt, and as shown in the ESI,† the conclusions of our work are robust to changes in the exact value of this parameter.
Altogether, our findings highlight the pivotal influence of hydrodynamics on the interactions between bacteria and phages, as well as other diffusible species—e.g., nutrients, toxins, or signalling molecules—in microbial environments. They also provide a new perspective on the biophysical tradeoffs associated with bacterial swimming. While swimming can be beneficial by enabling bacteria to escape from harmful environments, find new resources, and colonize new terrain, it can also be costly—not only because of the additional energy it requires of the cell, but also because it is often thought to increase the probability of encountering surrounding phages. Our results demonstrate that this latter cost is not appreciable for the cell body, due to the protective “shield” of fluid established by hydrodynamics, but is appreciable for the flagellar bundle, which pumps surrounding phages in. We conjecture that this may in part be why many phages have, over billions of years of evolution, developed ways to exploit bacterial swimming for their benefit by targeting the flagellum.18,19 Swimming bacteria may, in turn, have evolved localised defence countermeasures against phage infection such as through modification of specific surface receptors or production of outer membrane vesicles as decoys.59 Investigating how these biological and chemical processes, combined with the hydrodynamic effects illuminated by our work, influence phage–bacteria interactions will be a useful avenue for future research.
Data and code availability
The data that support the findings of this study as well as the source code are available in ref. 43.Author contributions
C. L. performed all simulations and theoretical calculations; C. L., C. H., and S. S. D. designed the simulations, analyzed the data, discussed the results and implications, and wrote the manuscript; S. S. D. designed and supervised the overall project.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the Visiting Student Research Collaborator (VSRC) program of the Graduate School at Princeton for enabling C. L. to visit the Datta Lab and conduct this research, as well as funding support by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under project number 327154368-SFB 1313 and under Germany's Excellence Strategy EXC 2075 – 390740016. The simulations were performed on computational resources managed and supported by Princeton Research Computing, a consortium of groups including the Princeton Institute for Computational Science and Engineering (PICSciE) and the Office of Information Technology's High Performance Computing Center and Visualization Laboratory at Princeton University. It is a pleasure to thank Ido Golding and Ned Wingreen for useful discussions, and Chris Browne for helpful comments on the manuscript.Notes and references
- R. W. Hendrix, M. C. M. Smith, R. N. Burns, M. E. Ford and G. F. Hatfull, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 2192–2197 CrossRef CAS PubMed.
- A. Mushegian, J. Bacteriol., 2020, 202, 10–1128 CrossRef PubMed.
- C. A. Suttle, Nature, 2005, 437, 356–361 CrossRef CAS PubMed.
- A. Chevallereau, B. J. Pons, S. van Houte and E. R. Westra, Nat. Rev. Microbiol., 2022, 20, 49–62 CrossRef CAS PubMed.
- B. Koskella, C. A. Hernandez and R. M. Wheatley, Annu. Rev. Virol., 2022, 9, 57–78 CrossRef CAS PubMed.
- M. Breitbart, C. Bonnain, K. Malki and N. Sawaya, Nat. Microbiol., 2018, 3, 754–766 CrossRef CAS PubMed.
- S. A. Strathdee, G. F. Hatfull, V. K. Mutalik and R. T. Schooley, Cell, 2023, 186, 17–31 CrossRef CAS PubMed.
- H. G. Hampton, B. N. Watson and P. C. Fineran, Nature, 2020, 577, 327–336 CrossRef CAS PubMed.
- S. T. Abedon, Antibiotics, 2023, 12, 723 CrossRef PubMed.
- K. L. Joiner, A. Baljon, J. Barr, F. Rohwer and A. Luque, Sci. Rep., 2019, 9, 1–12 CrossRef CAS PubMed.
- K. Drescher, J. Dunkel, L. H. Cisneros, S. Ganguly and R. E. Goldstein, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 10940–10945 CrossRef CAS PubMed.
- A. J. Mathijssen, R. Jeanneret and M. Polin, Phys. Rev. Fluids, 2018, 3, 033103 CrossRef.
- H. Berg and E. Purcell, Biophys. J., 1977, 20, 193–219 CrossRef CAS PubMed.
- S. Friedlander, AIChE J., 1957, 3, 43–48 CrossRef CAS.
- A. Acrivos and T. D. Taylor, Phys. Fluids, 1962, 5, 387–394 CrossRef.
- E. Lauga, Annu. Rev. Fluid Mech., 2016, 48, 105–130 CrossRef.
- S. E. Spagnolie and E. Lauga, J. Fluid Mech., 2012, 700, 105–147 CrossRef.
- P. Katsamba and E. Lauga, Phys. Rev. Fluids, 2019, 4, 013101 CrossRef.
- N. C. Esteves and B. E. Scharf, Int. J. Mol. Sci., 2022, 23, 7084 CrossRef CAS PubMed.
- A. Patteson, A. Gopinath, M. Goulian and P. Arratia, Sci. Rep., 2015, 5, 15761 CrossRef CAS PubMed.
- J. P. Binagia and E. S. Shaqfeh, Phys. Rev. Fluids, 2021, 6, 053301 CrossRef.
- K. D. Housiadas, J. P. Binagia and E. S. Shaqfeh, J. Fluid Mech., 2021, 911, A16 CrossRef CAS.
- J. P. Binagia, A. Phoa, K. D. Housiadas and E. S. Shaqfeh, J. Fluid Mech., 2020, 900, A4 CrossRef CAS.
- J. A. Puente-Velázquez, F. A. Godnez, E. Lauga and R. Zenit, Microfluid. Nanofluid., 2019, 23, 1–7 CrossRef.
- L. Zhu, E. Lauga and L. Brandt, Phys. Fluids, 2012, 24, 051902 CrossRef.
- L. W. Rogowski, J. Ali, X. Zhang, J. N. Wilking, H. C. Fu and M. J. Kim, Nat. Commun., 2021, 12, 1116 CrossRef CAS PubMed.
- V. A. Martinez, J. Schwarz-Linek, M. Reufer, L. G. Wilson, A. N. Morozov and W. C. Poon, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 17771–17776 CrossRef CAS PubMed.
- Z. Qu and K. S. Breuer, Phys. Rev. Fluids, 2020, 5, 073103 CrossRef.
- Y. Zhang, G. Li and A. M. Ardekani, Phys. Rev. Fluids, 2018, 3, 023101 CrossRef.
- S. Kamdar, S. Shin, P. Leishangthem, L. F. Francis, X. Xu and X. Cheng, Nature, 2022, 603, 819–823 CrossRef CAS PubMed.
- A. Martínez-Calvo, C. Trenado-Yuste and S. S. Datta, Out-of-equilibrium Soft Matter, The Royal Society of Chemistry, 2023, ch. 5, pp. 151–218 Search PubMed.
- T. Krüger, H. Kusumaatmaja, A. Kuzmin, O. Shardt, G. Silva and E. M. Viggen, The Lattice Boltzmann Method: Principles and Practice, Springer International Publishing, 2017 Search PubMed.
- B. Dünweg, U. D. Schiller and A. J. Ladd, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 036704 CrossRef PubMed.
- P. Ahlrichs and B. Dünweg, J. Chem. Phys., 1999, 111, 8225–8239 CrossRef CAS.
- J. de Graaf, H. Menke, A. J. Mathijssen, M. Fabritius, C. Holm and T. N. Shendruk, J. Chem. Phys., 2016, 144, 134106 CrossRef PubMed.
- M. Lee, K. Szuttor and C. Holm, J. Chem. Phys., 2019, 150, 174111 CrossRef PubMed.
- M. Lee, C. Lohrmann, K. Szuttor, H. Auradou and C. Holm, Soft Matter, 2021, 17, 893–902 RSC.
- C. Lohrmann and C. Holm, Phys. Rev. E, 2023, 108, 054401 CrossRef CAS PubMed.
- J. D. Weeks, D. Chandler and H. C. Andersen, J. Chem. Phys., 1971, 54, 5237–5247 CrossRef CAS.
- F. Weik, R. Weeber, K. Szuttor, K. Breitsprecher, J. de Graaf, M. Kuron, J. Landsgesell, H. Menke, D. Sean and C. Holm, Eur. Phys. J.: Spec. Top., 2019, 227, 1789–1816 Search PubMed.
- M. Bauer, S. Eibl, C. Godenschwager, N. Kohl, M. Kuron, C. Rettinger, F. Schornbaum, C. Schwarzmeier, D. Thönnes and H. Köstler, et al. , Comput. Math. Phys., 2021, 81, 478–501 Search PubMed.
- C. Godenschwager, F. Schornbaum, M. Bauer, H. Köstler and U. Rüde, Proceedings of the International Conference on High Performance Computing, Networking, Storage and Analysis, 2013, pp. 1–12 Search PubMed.
- C. Lohrmann and C. Holm, Replication Data for: Lohrmann, Holm, Datta: Influence of bacterial motility and hydrodynamics on phage bacteria encounters, 2023 DOI:10.18419/darus-3836.
- M. Schwartz, J. Mol. Biol., 1976, 103, 521–536 CrossRef CAS PubMed.
- Z. J. Storms and D. Sauvageau, Virology, 2015, 485, 355–362 CrossRef CAS PubMed.
- A. Logg and G. N. Wells, ACM Trans. Math. Software, 2010, 37, 1–28 CrossRef.
- H.-W. Ackermann and H. Krisch, Arch. Virol., 1997, 142, 2329–2345 CrossRef CAS PubMed.
- J. J. Barr, R. Auro, N. Sam-Soon, S. Kassegne, G. Peters, N. Bonilla, M. Hatay, S. Mourtada, B. Bailey, M. Youle, B. Felts, A. Baljon, J. Nulton, P. Salamon and F. Rohwer, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 13675–13680 CrossRef CAS PubMed.
- J. Schwarz-Linek, J. Arlt, A. Jepson, A. Dawson, T. Vissers, D. Miroli, T. Pilizota, V. A. Martinez and W. C. Poon, Colloids Surf., B, 2016, 137, 2–16 CrossRef CAS PubMed.
- A. Andino and I. Hanning, et al. , Sci. World J., 2015, 2015, 520179 CAS.
- S. Datta and D. K. Srivastava, Proc. Math. Sci., 1999, 109, 441–452 CrossRef.
- F. Perrin, J. Phys. Radium, 1934, 5, 497–511 CrossRef CAS.
- M. v Smoluchowski, Z. Phys. Chem., 1918, 92, 129–168 CrossRef.
- R. C. Coelho, N. A. Araújo and M. M. T. da Gama, Soft Matter, 2022, 18, 7642–7653 RSC.
- E. Rothenberg, L. A. Sepúlveda, S. O. Skinner, L. Zeng, P. R. Selvin and I. Golding, Biophys. J., 2011, 100, 2875–2882 CrossRef CAS PubMed.
- T. L. Min, P. J. Mears, L. M. Chubiz, C. V. Rao, I. Golding and Y. R. Chemla, Nat. Methods, 2009, 6, 831–835 CrossRef CAS PubMed.
- J. Elgeti, R. G. Winkler and G. Gompper, Rep. Prog. Phys., 2015, 78, 056601 CrossRef CAS PubMed.
- A. J. Mathijssen, F. Guzmán-Lastra, A. Kaiser and H. Löwen, Phys. Rev. Lett., 2018, 121, 248101 CrossRef CAS PubMed.
- K. D. Seed, PLoS Pathog., 2015, 11, e1004847 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm00060a |
| This journal is © The Royal Society of Chemistry 2024 |