Open Access Article
Open Access ArticleTheoretical study of a derivative of chlorophosphine with aliphatic and aromatic Grignard reagents: SN2@P or the novel SN2@Cl followed by SN2@C?†
Nandini Savooa,
Lydia Rhyman*ab and
Ponnadurai Ramasami *ab
*ab
aComputational Chemistry Group, Department of Chemistry, Faculty of Science, University of Mauritius, Réduit 80837, Mauritius. E-mail: p.ramasami@uom.ac.mu
bCentre for Natural Product Research, Department of Chemical Sciences, University of Johannesburg, Doornfontein Campus, Johannesburg 2028, South Africa. E-mail: lyd.rhyman@gmail.com
First published on 23rd March 2022
Abstract
The proposed SN2 reactions of a hindered organophosphorus reactant with aliphatic and aromatic nucleophiles [Ye et al., Org. Lett., 2017, 19, 5384–5387] were studied theoretically in order to explain the observed stereochemistry of the products. Our computations (using B3LYP as the functional) indicate that the reaction with the aliphatic nucleophile occurs through a backside SN2@P pathway while the reaction with the aromatic nucleophile proceeds through a novel SN2@Cl mechanism, followed by a frontside SN2@C mechanism.
Introduction
Organophosphorus derivatives possess significant value in disciplines such as asymmetric metal catalysis,1 pest control,2 medicine3 and bioorganic chemistry.4 An insight into their synthetic routes is thus essential.1,5–8 One of the reactions often encountered in the synthesis of organophosphorus derivatives is the bimolecular nucleophilic substitution (SN2) reaction at the trivalent tricoordinate phosphorus atom.5,8–10 The SN2 reaction at a trivalent phosphorus atom (SN2@P) refers to the replacement of a substituent (leaving group, L) around the phosphorus atom by an electron-rich molecule (nucleophile, Nu−). An SN2@P reaction occurs via the inversion and retention pathways in which molecular configuration around the phosphorus atom is inverted (P-inverted) and retained (P-retained), respectively [Fig. 1(a)].10 The inversion pathway takes place by the attack of the Nu− opposite to L which is synonymous to a backside SN2 pathway (SN2@P-b). Nucleophilic attack can also occur opposite to the lone pair of electrons on the phosphorus atom and on the same side as L in the retention pathway; this is analogous to a frontside SN2 attack (SN2@P-f).10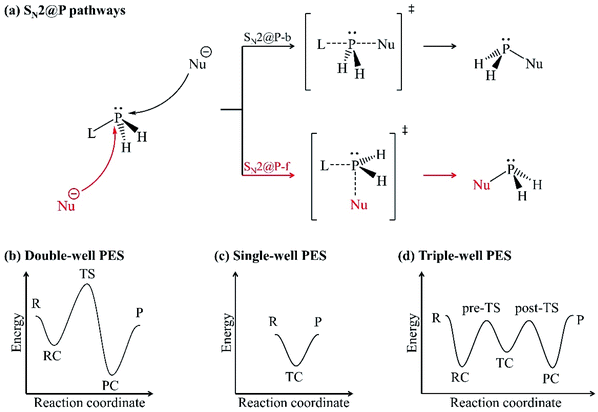 | ||
| Fig. 1 (a) Inversion (SN2@P-b, black) and retention (SN2@P-f, red) pathways; (b) double-well; (c) single-well and; (d) triple-well PESs. | ||
In the inversion and retention pathways of an archetypal SN2@P reaction, the initial interaction of the organophosphorus and the Nu− reactants (R) generates a reactant complex (RC) which forms a pentacoordinate transition state (TS). The TS dissociates to form the product complex (PC) and finally the separate products (P). The R, RC, TS, PC and P make up the typical double-well potential energy surface (PES) [Fig. 1(b)].11 An example is the retention pathway of the PH2Cl + Cl− reaction which occurs through a double-well PES with a Berry pseudorotation about the phosphorus atom.12 Studies also reported atypical PESs for SN2@P reactions when the bulkiness of the substituents around the phosphorus atom is changed.11,13–15 An example is the nucleophilic attack at unhindered trivalent phosphorus atom centres which may result in a single-well PES [Fig. 1(c)] with a relatively stable pentacoordinate intermediate, which is known as the transition complex (TC).12–15 The TC is in accordance with experimental reports.16–19 Such a reaction is spontaneous; the reactants form a stable TC followed by the products without the formation of the RC or PC. An increase in the bulkiness of substituents around the trivalent phosphorus atom separates the TC from the R and P by the pre-TS and the post-TS, respectively. This results in a triple-well PES [Fig. 1(d)] which constitutes a stepwise Walden inversion with favourable energy barriers in an addition-elimination fashion.6,10,11,14,20,21
The bulkiness of substituents around the phosphorus atom is one of several factors governing the stereochemical consequences of SN2@P synthesis of organophosphorus derivatives. Other factors include the effect of neighbouring groups,6,8 solvent6,22 and the choice of nucleophile.9,23–25 Ye et al. carried out an experimental study and they highlight the choice of nucleophile as a factor influencing the stereoselectivity of SN2@P reactions of organophosphorus compounds.25 The study deals with the synthesis of tertiary phosphines from diastereomeric mixtures of secondary phosphine oxides in tetrahydrofuran (THF) in the presence of boron trihydride (BH3) [Fig. 2(a)].25 One of the steps in the synthesis [highlighted in blue in Fig. 2(a)] involves the replacement of a Cl atom bonded to the trivalent tertiary phosphorus atom by an R group from a Grignard reagent. The authors reported diastereomeric ratios (dr) of 98![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and 1
2 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 99 for the P-inverted and P-retained organophosphorus products in the reactions involving an aliphatic and aromatic Grignard reagent, respectively.25 Based on these observations, Ye et al. proposed that the aliphatic Grignard reagent attacks opposite to the leaving group Cl (SN2@P-b) and the aromatic Grignard reagent attacks opposite to the lone pair of electrons on the phosphorus atom (SN2@P-f).25
99 for the P-inverted and P-retained organophosphorus products in the reactions involving an aliphatic and aromatic Grignard reagent, respectively.25 Based on these observations, Ye et al. proposed that the aliphatic Grignard reagent attacks opposite to the leaving group Cl (SN2@P-b) and the aromatic Grignard reagent attacks opposite to the lone pair of electrons on the phosphorus atom (SN2@P-f).25
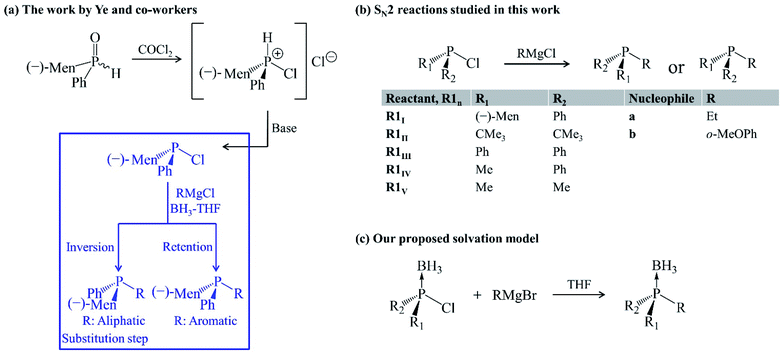 | ||
| Fig. 2 (a) Ye and co-workers' work.25 The substitution step highlighted in blue shows the stereoselectivity of the reaction. (b) Gas-phase SN2 reactions studied in this work. (c) Solvation model employed. | ||
In continuation to our research programme to understand substitution reactions and our reports on the influence of ion-pair nucleophiles on SN2 reactions,26–28 we attempted a computational study of the reaction mechanisms which were proposed by Ye and co-workers.25 The presence of BH3 was considered when investigating the reactions in THF so as to mimic the solvation conditions in the experiment,25 as it is reported that solvent systems constitute a crucial factor in influencing the stereoselectivity of reactions.29 The occurrence of activation barriers was explained using the distortion/interaction–activation strain model (D/I–ASM) of chemical reactivity.30,31 The mechanisms that we determined do not only explain the experimental outcome25 but also constitute a novel synthetic route, via SN2@Cl mechanism, for organophosphorus derivatives which experimentalists may explore in cases where a control over stereoselectivity is required. Such an SN2@Cl mechanism was reported by Zhang et al.32 In addition, we investigated the steric effect on SN2 reactions with Grignard reagents (a and b) as ion-pair nucleophiles in the gas phase and in THF. The results are shown in the ESI document in Fig. S1 and S2.†
Results and discussion
Mechanistic explanation of diastereoselectivity
In this section, we report on the mechanism by which the R1I + a and R1I + b reactions occur in order to explain their diastereoselectivity.25 Depending on the orientation of the nucleophiles, we located several SN2@P-b and SN2@P-f pathways in the gas phase and in THF (see ESI†). Only those with the lowest Gibbs free activation barriers are reported in the manuscript (Fig. 3 and 4).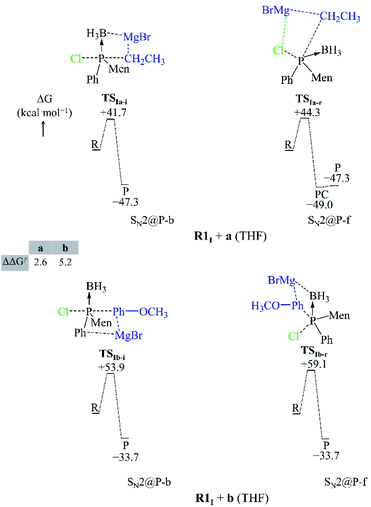 | ||
| Fig. 3 Geometries of the TSs and PESs of the R1I + a and R1I + b SN2@P reactions in the gas phase. The bond lengths/distances are in Å. The ΔG and ΔΔG≠ are in kcal mol−1. | ||
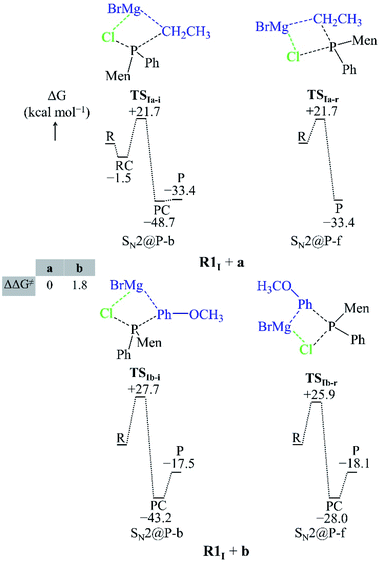 | ||
| Fig. 4 Geometries of the TSs and PESs of the R1I + a and R1I + b SN2@P reactions in THF. The bond lengths/distances are in Å. The ΔG and ΔΔG≠ are in kcal mol−1. | ||
Both the gas-phase SN2@P-b and SN2@P-f pathways occur through a TS in which the Mg2+ cation interacts with both the Cl and C atoms and this causes the Cl–P–C bond angle to bend (Fig. 3). The bent Cl–P–C bond angle of the SN2@P-b pathways is contrary to the typical near-linear TSs which are reported for anionic SN2-b reactions.14,33 This reflects the effect of the presence of the countercation Mg2+. The small relative Gibbs free energy barriers (ΔΔG≠) between the TSs of SN2@P-b and SN2@P-f pathways do not explain the drs (98![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and 1
2 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 99 for the P-inverted and P-retained organophosphorus products, respectively) obtained in the experiment.25 This mismatch between experiment and computations prompted us to consider the solvent effect.
99 for the P-inverted and P-retained organophosphorus products, respectively) obtained in the experiment.25 This mismatch between experiment and computations prompted us to consider the solvent effect.
We studied the solvent effect by incorporating a BH3 molecule in the R1I reactant and performing bulk solvation with THF as the solvent. Under such conditions, the SN2@P-b pathways feature TSs with near-linear Cl–P–C bond angles. The PESs adopt a unimodal or a hill-and-well shape, which differs from anionic reactions.14,15,29 The ΔΔG≠ of 2.6 kcal mol−1 of the R1I + a reaction (Fig. 4) indicates that the SN2@P-b pathway is preferred. Indeed, the P-inverted organophosphorus stereoisomer was obtained in a higher dr (98![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2).25 Hence, the aliphatic nucleophile a prefers to react via the inversion pathway, as proposed by Ye et al.25
2).25 Hence, the aliphatic nucleophile a prefers to react via the inversion pathway, as proposed by Ye et al.25
The ΔΔG≠ (5.2 kcal mol−1) of the R1I + b reaction in THF shows that, similar to the R1I + a reaction, the P-inverted stereoisomer should be obtained. However, the dr, higher for the P-retained stereoisomer (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 99),25 shows that the SN2@P-b mechanism is not at play. Hence, to explain the observations of Ye et al.,25 we went back to the basics of charge distribution in a molecule. We therefore employed ESP maps to determine the possible modes of attack, or approach, of the nucleophile b. Owing to the coulombic nature of molecular interactions, ESP maps serve as good indicators of molecular regions which favour particular interactions; for instance, Bhasi et al. expanded the use of ESP maps to the successful location of TSs for atmospheric reactions which were previously thought to be barrierless.34
99),25 shows that the SN2@P-b mechanism is not at play. Hence, to explain the observations of Ye et al.,25 we went back to the basics of charge distribution in a molecule. We therefore employed ESP maps to determine the possible modes of attack, or approach, of the nucleophile b. Owing to the coulombic nature of molecular interactions, ESP maps serve as good indicators of molecular regions which favour particular interactions; for instance, Bhasi et al. expanded the use of ESP maps to the successful location of TSs for atmospheric reactions which were previously thought to be barrierless.34
The ESP map of the organophosphorus reactant R1I [Fig. 5(a)] shows a σ-hole at the extremity of and a belt of negative potential on the Cl atom. Previous reports related the σ-hole to the anisotropic charge distribution of the Cl atom in the molecule and to the occurrence of halogen-bonded complexes.35–37 In this study, the σ-hole gives rise to a halogen-bonded RC [RC in Fig. 5(c)] with an electronic interaction energy of −1.9 kcal mol−1; this qualifies as a halogen bonding interaction (that is, interaction between a halogen and a base) based on the study by Metrangolo et al.38 Hence, we investigated the possibility of a reaction mechanism which is initiated by a halogen-bonded RC.
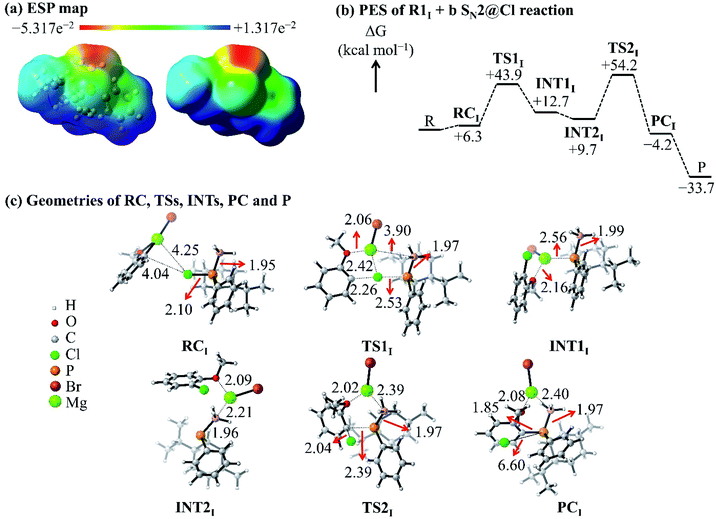 | ||
| Fig. 5 (a) ESP map of the R1I reactant. (b) PES of the R1I + b SN2@Cl reaction in THF. (c) Geometries of the RC, TSs, INTs, PC and P of the R1I + b SN2@Cl reaction in THF. | ||
The C atom and the Mg2+ cation of nucleophile b interacts with the σ-hole and the belt of negative potential on the Cl atom, respectively, which forms RC. This halogen-bonded RC gives rise to a new type of SN2 reaction, namely, an SN2@Cl reaction. The RC [Fig. 5(c)] proceeds through a TS (TS1) where the C atom of the nucleophile b forms a bond with the Cl atom of R1I and simultaneously breaks the P–Cl bond of R1I. As such, in the SN2@Cl pathway, the Cl atom is the reactive centre and the organophosphorus moiety becomes the leaving group. The TS1 leads to an intermediate (INT1) in which the Mg2+ cation is attracted to the negatively-charged P atom of the organophosphorus moiety. The INT1 reorganises to form INT2 where the Mg2+ cation shifts to interact with the electron density of the BH3 moiety. This change in geometry brings the negatively-charged P atom in INT2 in a position where an attack on the C atom of the o-MeOPhCl moiety is possible. This attack occurs through a frontside SN2@C (SN2@C-f) pathway. The INT2 overcomes TS2 [Fig. 5(c)] leading to the PC and finally to the separate products. This mechanism causes no umbrella flip around the P atom of the organophosphorus reactant and thus, the organophosphorus product retains its geometry around the P atom.
The ΔG of TS1 [+43.9 kcal mol−1, Fig. 5(b)] is lower than the Gibbs free activation energy of the inversion pathway of the SN2@P reaction (+53.9 kcal mol−1) by 10 kcal mol−1. Hence, this explains the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 99 dr obtained by Ye et al. for the P-retained product.25 We thus confirmed that the reaction with nucleophile b occurs via an SN2@Cl mechanism followed by an SN2@C-f mechanism.
99 dr obtained by Ye et al. for the P-retained product.25 We thus confirmed that the reaction with nucleophile b occurs via an SN2@Cl mechanism followed by an SN2@C-f mechanism.
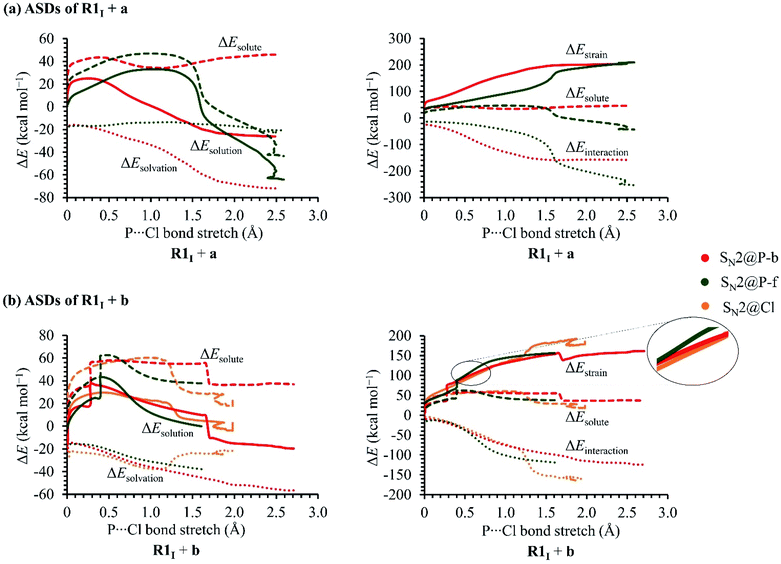
In order to investigate the solvation, strain and interaction factors behind the trend in reactivity of the R1I + a and R1I + b reactions, we employed the D/I–ASM. An analysis of the ASDs in Fig. 6 shows that the SN2@P-b pathways are more stabilised by bulk solvation by THF than the SN2@P-f pathways. This happens because of the change in geometries along the PESs; the reactants along the SN2@P-b pathways deform to generate TSs with near-linear Cl–P–C bond angles (169.4° in TSIa-i and 175.3° in TSIb-i), whereas along the SN2@P-f pathway, the reactants deform and lead to a TS with bent Cl–P–C bond angles (61.7° in TSIa-r and 72.0° in TSIb-r). There is more charge separation along the pathways which form the TSs with linear Cl–P–C bond angles than along pathways which lead to cyclic geometries.26–28 The ΔEsolvation curve for the SN2@Cl reaction indicates that the PES is most stabilised by THF at the start of the reaction (C–Cl–P bond angle is 174.7°). As the INT1 is formed, the drop in charge separation causes less stabilisation by THF.
The R1I + a reaction experiences more strain in the SN2@P-b pathway which we ascribe to the umbrella flip about the phosphorus atom and to more geometrical deformation to reach the linear TSIa-i in THF. However, the SN2@P-b pathway has a lower Gibbs free energy barrier than the SN2@P-f pathway due to more favourable interaction between the deformed reactants and due to more stabilisation by THF. The initial stages of both the SN2@P pathways of the R1I + b reaction have similar strain curves while the SN2@Cl reaction experiences higher strain. However, as TS1 forms, the ΔEstrain lowers slightly [shown in magnified section in Fig. 5(b)] and the ΔEinteraction between the deformed reactants becomes comparable to the SN2@P pathways. As the reaction progresses, the ΔEstrain stays lower than the SN2@P-f pathway and comparable to the SN2@P-b pathway, and eventually becomes the highest due to the extent of deformation of the reactant fragments involved in reaching the INT1I. The interplay between the stabilisation by THF and reduction in strain while the TS forms that causes the SN2@Cl mechanism to be the most preferred. Hence, we confirmed that (i) the R1I + a reaction yields the P-inverted product in higher dr through an SN2@P-b pathway and (ii) the R1I + b reaction prefers the halogen bond-assisted SN2@Cl pathway over the SN2@P-b pathway by a factor of 10 kcal mol−1. The reactions were also investigated using the M06-2X-D3/6-31++G(d,p) method. The ΔG values are listed in Tables 1 and 2 in kcal mol−1.
| R1I + a | R1I + b | |
|---|---|---|
| RC | +1.9 (+1.9) | −2.7 (−1.7) |
| TS | +29.3 (+41.6) | +31.5 (+47.6) |
| PC | −48.7 (−59.0) | −2.9 (−7.6) |
| P | −50.3 (−50.3) | −34.3 (−37.2) |
| SN2@Cl pathway | |
|---|---|
| RC | +2.1 |
| TS1 | +42.2 |
| INT1 | +13.6 |
| SN2@C-f pathway | |
|---|---|
| INT2 | +8.5 |
| TS2 | +34.4 |
| PC | −21.2 |
| P | −38.4 |
A comparison of the energy values shows that the R1I + a reaction has a lower activation barrier of +29.3 kcal mol−1 in the SN2@P-b pathway and thus, the reaction occurs through the SN2@P-b pathway. This explains the formation of the products of inverse geometry in the experiment.25 The R1I + b reaction has activation barriers of +31.5, +47.6 and +42.2 kcal mol−1 in the SN2@P-b, SN2@P-f and SN2@Cl pathways, respectively. Hence, the R1I + b reaction also prefers the SN2@P-b pathway. This differs from the results obtained using the B3LYP functional and does not explain the formation of the products of retained geometry in the experiment.25
The TSs were optimised using the MP2 method to obtain more accurate energy values. Due to the large size of the organophosphorus reactant and due to the computationally-demanding nature of the MP2 method, the ΔG values were computed only for the TSs instead of along the whole PESs. We employed the 6-31G(d) basis set because using any higher basis set causes the TS to converge to the RC. Table 3 shows the ΔG of the TSs of the SN2@P-b, SN2@P-f, SN2@Cl and SN2@C-f pathways. It was observed that the TS of the SN2@P-b pathway has the lowest activation energy. Hence, the SN2@P-b pathway is preferred, similar to the M06-2X-D3 results. This is in contrast to the B3LYP results. It was thus deduced that the product of retained geometry may be obtained through a different reaction mechanism instead of those investigated in this manuscript.
| SN2@P-b | SN2@P-f | SN2@Cl | SN2@C-f | |
|---|---|---|---|---|
| TS | +32.4 | +48.1 | +37.2 | +42.6 |
Conclusions
Ye et al. substituted the chlorine atom in a derivative of chlorophosphine and obtained the P-inverted and P-retained organophosphorus products on using aliphatic and aromatic Grignard reagents, respectively.25 In this manuscript, we determined the reaction mechanisms of these two reactions (R1I + a and R1I + b) using the B3LYP/6-31++G(d,p) method. We also highlighted the use of a model of the THF-solvated reaction system with a dative bond between the P and B atoms to account for the presence of the BH3 molecule. The lower Gibbs free activation barrier of the SN2@P-b pathway of the R1I + a reaction explains the formation of the P-inverted product in THF. Our D/I–ASM analyses attribute the preference of the SN2@P-b pathway to more favourable interaction between the deformed reactants and more stabilisation by THF. In the case of the R1I + b reaction, the SN2@P mechanism fails to explain the formation of the P-retained product. In fact, our computations point to a halogen bond-assisted SN2@Cl mechanism. The SN2@Cl mechanism occurs with a lower free Gibbs activation barrier than the SN2@P pathways and is followed by an SN2@C-f mechanism. The preference of the SN2@Cl mechanism resulted from greater stabilisation by THF and reduction in strain while the TS1I forms.We also investigated the effect of decreasing steric crowding of the phosphorus atom of the R1n organophosphorus reactants. The results are reported in the ESI.† As the bulkiness of the substituents decreases, the R1n + a reactions occur through the SN2@P-b pathways; the decrease in bulkiness lowers the Gibbs free energy barriers of the SN2@P-b pathways on account of more stabilisation by THF and lower deformational strain in the initial stages of the reactions. As the bulkiness of the substituents decreases in the R1n + b reactions, the relative Gibbs free energy barrier of the SN2@P-b pathways becomes lower than that of the SN2@Cl pathway due to the interplay between the strain and interaction components. Hence, a consideration of competing interactions, such as halogen bonding, becomes significant when determining the course of an SN2 reaction, especially in the presence of bulky substituents which hinder the reactive centre.
When the reactions were repeated using the M06-2X-D3/6-31++G(d,p) and MP2/6-31G(d) methods, the preference of the reaction changed to the SN2@P-b pathway. This does not explain the formation of the retention products in the experiment and shows that the computational findings depend on the level of theory used for computations. It is known that different methods give different results due to the different level of approximations.39–42 This may lead to benchmark studies with respect to such organophosphorus reactions.
Methodology
Full optimisation with no symmetry constraints was performed using the B3LYP43–45 hybrid functional and the 6-31++G(d,p) basis set in the gas phase. We selected this method based on previous reports involving SN2@P.20,33,46–48 The stationary points were characterised by frequency computations to verify that the TSs have only one imaginary frequency49 and these were checked by intrinsic reaction coordinate (IRC) computations.The same computational method was employed based on the polarisable continuum model (PCM)50 to perform bulk solvation with THF by incorporating BH3 in the reaction system to mimic the experiment conditions.25 This procedure is reported in the literature.6 All the computations were carried out at 298.15 K and 1 atm. The reactions are reported in terms of the ΔG with respect to the separate reactants, unless otherwise specified.
We performed a non-covalent interaction (NCI) analysis of selected TSs using the Multiwfn program.51–53 The NCI plots, which are shown in the ESI in Fig. S3,† allow for a visualisation of non-covalent interactions between molecular fragments as real-space surfaces. Within the NCI framework, the sign of λ2 enables identification of the interaction type. Attractive interactions are negative, van der Waals interactions occur close to zero and steric repulsions are positive. The Visual Molecular Dynamics program was used to visualise the molecules in 3D.54 The Gnuplot 4.2 program55 and Ghostscript interpreter56 were employed to generate the 2D plots.
Moreover, the D/I–ASM of chemical reactivity was employed to explain the trends in reactivity along the reaction.30,31,57,58 In the D/I–ASM, the energy along the reaction coordinate is decomposed into its strain and interaction energies. Eqn (1) shows how the D/I–ASM relates the relative electronic energy of a reaction (ΔE) to the relative strain (ΔEstrain) and relative interaction (ΔEint) energies of the deformed reactant fragments along the reaction coordinate (ζ).
| ΔE(ζ) = ΔEstrain(ζ) + ΔEint(ζ) | (1) |
The ΔEstrain(ζ) corresponds to the relative electronic energy necessary to distort the reactant fragments throughout the reaction while the ΔEint(ζ) corresponds to the interactions between the deforming reactant fragments.
The D/I–ASM was also applied in THF to investigate the effect of solvation (ΔEsolvation). The solvent-phase PES is described in terms of its components, solute energy and solvation energy, as in eqn (2). The solvation energy englobes the solute–solvent interaction, as well as the formation of the solvent cavity.
| ΔEsolution(ζ) = ΔEsolute(ζ) + ΔEsolvation(ζ) | (2) |
We obtained the ΔEsolute(ζ) from the SP energy values of the reactant fragments in gas phase, computed using their geometry from solvent-phase computations. Eqn (3) shows a further breakdown of the ΔEsolute into ΔEstrain and ΔEint.
| ΔEsolute(ζ) = ΔEstrain(ζ) + ΔEint(ζ) | (3) |
The reaction coordinate was considered as the IRC projected onto P⋯Cl bond stretch, which constitutes the activation strain diagram (ASD).
In another attempt to explain the outcome of the experiment computationally under the experiment conditions employed by Ye et al.,25 the effect of a temperature of 193.15 K was considered on the ΔG; the results are reported in the ESI.† ΔE at both at 298.15 K and 193.15 K are reported in the ESI.† The ExcelAutomat tool59–61 facilitated file manipulation and file extraction. GaussView 6,62 Chemcraft63 and CylView64 were employed to visualise structures. All computations were carried out in Gaussian 09![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 65 and Gaussian 16
65 and Gaussian 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 66 suites using the SEAGrid computing facilities.67–71 Explicit details about the computational methods are found in the ESI.†
66 suites using the SEAGrid computing facilities.67–71 Explicit details about the computational methods are found in the ESI.†
According to several reports, the use of dispersion correction is necessary for the investigation of non-covalent interactions between the nucleophile and the σ-hole of the chlorine atom.29,72–74 Hence, these reactions were studied using the M06-2X functional and dispersion correction was considered; full optimisation computations were performed using the dispersion-corrected M06-2X-D3.72,75–78 Moreover, the second-order Møller–Plesset (MP2)79–83 method was also employed in order to obtain more reliable energy values. The energy values were compared with the results obtained using the B3LYP/6-31++G(d,p) method.
Author contributions
PR was responsible for project administration, conceptualisation, supervision and writing – review & editing.LR was responsible for conceptualisation, supervision and writing – review & editing.
NS was responsible for conceptualisation, investigation, data curation and writing – original draft.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are grateful to the Higher Education Commission (HEC) of Mauritius. The authors are also grateful to SEAGrid and South African CHPC for providing computing facilities.References
- K. Shioji, A. Tashiro, S. Shibata and K. Okuma, Tetrahedron Lett., 2003, 44, 1103 CrossRef CAS
.
- M. Etō, Organophosphorus Pesticides: Organic and Biological Chemistry, CRC Press, Inc., Boca Raton, 1979 Search PubMed
.
- Y. Song, J. J. Vittal, N. Srinivasan, S.-H. Chan and P.-H. Leung, Tetrahedron: Asymmetry, 1999, 10, 1433 CrossRef CAS
.
- K. M. Pietrusiewicz and M. Zablocka, Chem. Rev., 1994, 94, 1375 CrossRef CAS
.
- O. I. Kolodiazhnyi, Tetrahedron: Asymmetry, 2012, 23, 1 CrossRef CAS
.
- H. Zijlstra, T. León, A. de Cózar, C. F. Guerra, D. Byrom, A. Riera, X. Verdaguer and F. M. Bickelhaupt, J. Am. Chem. Soc., 2013, 135, 4483 CrossRef CAS PubMed
.
- G.-Q. Lin, Q.-D. You and J.-F. Cheng, Chiral Drugs: Chemistry and Biological Action, John Wiley & Sons, Inc., New Jersey, 2011 Search PubMed
.
- O. I. Kolodiazhnyi, Asymmetric Synthesis in Organophosphorus Chemistry, Wiley-VCH, Germany, 2017 Search PubMed
.
- J.-L. Montchamp, Topics in Current Chemistry: Phosphorus Chemistry I, Springer International Publishing, Switzerland, 2015 Search PubMed
.
- O. I. Kolodiazhnyi and A. Kolodiazhna, Tetrahedron: Asymmetry, 2017, 28, 1651 CrossRef CAS
.
- M. A. van Bochove, M. Swart and F. M. Bickelhaupt, Phys. Chem. Chem. Phys., 2009, 11, 259 RSC
.
- Y. Ding, J. Mu and L. Gong, J. Chin. Chem. Soc., 2013, 60, 327 CrossRef CAS
.
- M. A. van Bochove and F. M. Bickelhaupt, Eur. J. Org. Chem., 2008, 2008, 649 CrossRef
.
- M. A. van Bochove, M. Swart and F. M. Bickelhaupt, J. Am. Chem. Soc., 2006, 128, 10738 CrossRef CAS PubMed
.
- M. A. van Bochove, M. Swart and F. M. Bickelhaupt, ChemPhysChem, 2007, 8, 2452 CrossRef CAS PubMed
.
- I. Granoth and J. C. Martin, J. Am. Chem. Soc., 1978, 100, 7434 CrossRef CAS
.
- K. B. Dillon and T. C. Waddington, J. Chem. Soc., Chem. Commun., 1969, 1317a RSC
.
- W. S. Sheldrick, A. Schmidpeter, F. Zwaschka, K. B. Dillon, A. W. G. Platt and T. C. Waddington, J. Chem. Soc., Dalton Trans., 1981, 413 RSC
.
- A. P. Marchenko, G. N. Koidan, A. N. Hurieva, A. B. Rozhenko and A. N. Kostyuk, Heteroat. Chem., 2016, 27, 12 CrossRef CAS
.
- O. Dmitrenko, C. Thorpe and R. D. Bach, J. Org. Chem., 2007, 72, 8298 CrossRef CAS PubMed
.
- O. I. Kolodiazhnyi and A. O. Kolodiazhna, Phosphorus, Sulfur Silicon Relat. Elem., 2017, 192, 621 CrossRef CAS
.
- O. I. Kolodiazhnyi, Pure Appl. Chem., 2019, 91, 43 CrossRef CAS
.
- O. I. Kolodiazhnyi, S. Sheiko and E. V. Grishkun, Heteroat. Chem., 2000, 11, 138 CrossRef CAS
.
- M. Oliana, F. King, P. N. Horton, M. B. Hursthouse and K. K. Hii, J. Org. Chem., 2006, 71, 2472 CrossRef CAS PubMed
.
- J.-J. Ye, S.-Z. Nie, J.-P. Wang, J.-H. Wen, Y. Zhang, M.-R. Qiu and C.-Q. Zhao, Org. Lett., 2017, 19, 5384 CrossRef CAS PubMed
.
- J. Z. A. Laloo, L. Rhyman, P. Ramasami, F. M. Bickelhaupt and A. de Cózar, Chem.–Eur. J., 2016, 22, 4431 CrossRef CAS PubMed
.
- J. Z. A. Laloo, L. Rhyman, O. Larrañaga, P. Ramasami, F. M. Bickelhaupt and A. de Cózar, Chem.–Asian J., 2018, 13, 1138 CrossRef CAS PubMed
.
- N. Savoo, J. Z. A. Laloo, L. Rhyman, P. Ramasami, F. M. Bickelhaupt and J. Poater, J. Comput. Chem., 2020, 41, 317 CrossRef CAS PubMed
.
- S. Jain and K. Vanka, J. Am. Chem. Soc., 2020, 124, 8019 CAS
.
- W.-J. van Zeist and F. M. Bickelhaupt, Org. Biomol. Chem., 2010, 8, 3118 RSC
.
- P. Vermeeren, S. C. C. van der Lubbe, C. F. Guerra, F. M. Bickelhaupt and T. A. Hamlin, Nat. Protoc., 2020, 15, 649 CrossRef CAS PubMed
.
- X. Zhang, J. Ren, S. M. Tan, D. Tan, R. Lee and C.-H. Tan, Science, 2019, 363, 400 CrossRef CAS PubMed
.
- P. Farahani, M. Lundberg and H. O. Karlsson, Chem. Phys., 2013, 425, 134 CrossRef CAS
.
- P. Bhasi, Z. P. Nhlabatsi and S. Sitha, Phys. Chem. Chem. Phys., 2016, 18, 13002 RSC
.
- T. Clark, M. Hennemann, J. S. Murray and P. Politzer, J. Mol. Model., 2007, 13, 291 CrossRef CAS PubMed
.
- P. Politzer, J. S. Murray and T. Clark, Phys. Chem. Chem. Phys., 2010, 12, 7748 RSC
.
- P. Politzer, J. S. Murray and T. Clark, Phys. Chem. Chem. Phys., 2013, 15, 11178 RSC
.
- P. Metrangolo, H. Neukirch, T. Pilati and G. Resnati, Acc. Chem. Res., 2005, 38, 386 CrossRef CAS PubMed
.
- M. Linder and T. Brinck, Phys. Chem. Chem. Phys., 2013, 15, 5108 RSC
.
- X. Xu and W. A. Goddard, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 2673 CrossRef CAS PubMed
.
- G. S. J. Armstrong, M. A. Khokhlova, M. Labeye, A. S. Maxwell, E. Pisanty and M. Ruberti, Eur. Phys. J. D, 2021, 75, 209 CrossRef CAS
.
- M. D. Hack, R. G. A. R. Maclagan, G. E. Scuseria and M. S. Gordon, J. Chem. Phys., 1996, 104, 6628 CrossRef CAS
.
- A. D. Becke, Phys. Rev. A, 1988, 38, 3098 CrossRef CAS PubMed
.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS PubMed
.
- B. Miehlich, A. Savin, H. Stoll and H. Preuss, Chem. Phys. Lett., 1989, 157, 200 CrossRef CAS
.
- C. Fish, M. Green, R. J. Kilby, J. M. Lynam, J. E. McGrady, D. A. Pantazis, C. A. Russell, A. C. Whitwood and C. E. Willans, Angew. Chem., Int. Ed., 2006, 45, 3628 CrossRef CAS PubMed
.
- D. Mandal, B. Mondal and A. K. Das, J. Phys. Chem. A, 2012, 116, 2536 CrossRef CAS PubMed
.
- E. V. Jennings, K. Nikitin, Y. Ortin and D. G. Gilheany, J. Am. Chem. Soc., 2014, 136, 16217 CrossRef CAS PubMed
.
- L. Fan, L. Versluis, T. Ziegler, E. J. Baerends and W. Ravenek, Int. J. Quantum Chem., 1988, 34, 173 CrossRef
.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999 CrossRef CAS PubMed
.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580 CrossRef CAS PubMed
.
- E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498 CrossRef CAS PubMed
.
- A. Otero-de-la-Roza, E. R. Johnson and J. Contreras-García, Phys. Chem. Chem. Phys., 2012, 14, 12165 RSC
.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33 CrossRef CAS PubMed
.
- T. Williams and C. Kelley, Gnuplot, Version 4.2: An interactive plotting program, 2007, http://www.gnuplot.info/ Search PubMed
.
- Ghostscript, Version 9.53.3, http://www.artifex.com Search PubMed
.
- I. Fernandez and F. M. Bickelhaupt, Chem. Soc. Rev., 2014, 43, 4953 RSC
.
- T. A. Hamlin, B. van Beek, L. P. Wolters and F. M. Bickelhaupt, Chem.–Eur. J., 2018, 24, 5927 CrossRef CAS PubMed
.
- J. Z. A. Laloo, N. Laloo, L. Rhyman and P. Ramasami, J. Comput.-Aided Mol. Des., 2017, 31, 667 CrossRef CAS PubMed
.
- J. Z. A. Laloo, N. Savoo, N. Laloo, L. Rhyman and P. Ramasami, ExcelAutomat 1.2: Automation of natural bond order analysis and extraction of electronic energies from quantum chemical calculations, Global Science & Technology Forum (GSTF), 2018, pp. 72–76 Search PubMed
.
- J. Z. A. Laloo, N. Savoo, N. Laloo, L. Rhyman and P. Ramasami, J. Comput. Chem., 2019, 40, 619 CrossRef CAS PubMed
.
- R. Dennington, T. A. Keith and J. M. Millam, GaussView, Version 6, 2016 Search PubMed
.
- G. A. Zhurko and D. A. Zhurko, ChemCraft, Version 1.7, 2013. http://www.chemcraftprog.com Search PubMed
.
- C. Y. Legault, CYLview 1.0b, Université de Sherbrooke, 2009 Search PubMed
.
- M. J. Frischet al., Gaussian 09, Revision D.01, Gaussian, Inc.Wallingford CT, 2009 Search PubMed
.
- M. J. Frischet al., Gaussian 16, Revision B.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed
.
- S. Pamidighantam, S. Nakandala, E. Abeysinghe, C. Wimalasena, S. R. Yodage, S. Marru and M. Pierce, Procedia Comput. Sci., 2016, 80, 1927 CrossRef
.
- N. Shen, Y. Fan and S. Pamidighantam, J. Comput. Sci., 2014, 5, 576 CrossRef
.
- R. Dooley, K. Milfeld, C. Guiang, S. Pamidighantam and G. Allen, J. Grid Comput., 2006, 4, 195 CrossRef
.
- K. Milfeld, C. Guiang, S. Pamidighantam and J. Giuliani, Cluster Computing through an Application-oriented Computational Chemistry Grid. Proceedings of the 2005 Linux Clusters: The HPC Revolution, 2005 Search PubMed
.
- This work used the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation grant number OCI-1053575.
- L. Goerigk and S. Grimme, Phys. Chem. Chem. Phys., 2011, 13, 6670 RSC
.
- R. Sedlak, T. Janowskic, M. Pitoňákd, J. Řezáča, P. Pulayc and P. Hobza, J. Chem. Theory Comput., 2013, 9, 3364 CrossRef CAS PubMed
.
- M. Breugst and J. J. Koenig, Eur. J. Org. Chem., 2020, 2020, 5473 CrossRef CAS
.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215 Search PubMed
.
- L. Goerigk, A. Hansen, C. Bauer, S. Ehrlich, A. Najibi and S. Grimme, Phys. Chem. Chem. Phys., 2017, 19, 32184 RSC
.
- M. Walker, A. J. A. Harvey, A. Sen and C. E. H. Dessent, J. Phys. Chem. A, 2013, 117, 12590 CrossRef CAS PubMed
.
- I. Singh, A. A. El-Emam, S. K. Pathak, R. Srivastava, V. K. Shukla, O. Prasad and L. Sinha, Mol. Simul., 2019, 45, 1029 CrossRef CAS
.
- M. J. Frisch, M. Head-Gordon and J. A. Pople, Chem. Phys. Lett., 1990, 166, 275 CrossRef CAS
.
- M. J. Frisch, M. Head-Gordon and J. A. Pople, Chem. Phys. Lett., 1990, 166, 281 CrossRef CAS
.
- M. Head-Gordon, J. A. Pople and M. J. Frisch, Chem. Phys. Lett., 1988, 153, 503 CrossRef CAS
.
- S. Sæbø and J. Almlöf, Chem. Phys. Lett., 1989, 154, 83 CrossRef
.
- M. Head-Gordon and T. Head-Gordon, Chem. Phys. Lett., 1994, 220, 122 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d2ra00258b |
| This journal is © The Royal Society of Chemistry 2022 |