Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Solubility of Ca(II), Ni(II), Nd(III) and Pu(IV) in the presence of proxy ligands for the degradation of polyacrylonitrile in cementitious systems†
P. G.
Szabo
a,
A. G.
Tasi
 *a,
X.
Gaona
*a,
X.
Gaona
 *a,
R.
Polly
a,
A. C
Maier
*a,
R.
Polly
a,
A. C
Maier
 b,
S.
Hedström
b,
S.
Hedström
 b,
M.
Altmaier
a and
H.
Geckeis
a
b,
M.
Altmaier
a and
H.
Geckeis
a
aKarlsruhe Institute of Technology, Institute for Nuclear Waste Disposal, P. O. Box 3640, 76021 Karlsruhe, Germany. E-mail: agost.tasi@kit.edu; xavier.gaona@kit.edu
bSvensk Kärnbränslehantering AB, Evenemangsgatan 13, Box 3091, 169 03, Solna, Sweden
First published on 30th May 2022
Abstract
The solubility of Ca(OH)2(cr), β-Ni(OH)2(cr), Nd(OH)3(s) and PuO2(ncr, hyd) was investigated in cement porewater solutions containing glutarate (GTA), α-hydroxyisobutarate (HIBA) and 3-hydroxybutarate (HBA). These ligands were proposed as probable degradation products of UP2W, a polyacrylonitrile-based filter aid used in nuclear power plants. Results obtained in this work are compared with reported solubility data in the presence of iso-saccharinic acid (ISA), a polyhydroxocarboxylic acid resulting from cellulose degradation. None of the investigated proxy ligands shows any significant impact on the solubility of Ca(II), Nd(III) or Pu(IV) in cement porewater solutions. Although the formation of binary complexes M–L (M = Ca(II), Nd(III), An(IV); L = GTA, HIBA, HBA) under acidic conditions is described in the literature, these organic ligands cannot outcompete hydrolysis under hyperalkaline conditions. GTA, HIBA and HBA induce a slight increase in the solubility of β-Ni(OH)2(cr) at [L]tot = 0.1 M. This observation supports the formation of stable Ni(II)–GTA, –HIBA and –HBA complexes in hyperalkaline conditions, although the exact stoichiometry of these complexes remains unknown. The comparison of these results with solubility data in the presence of ISA confirms the stronger complexation properties of the latter ligand. Even though HIBA and HBA are carboxylic acids containing one alcohol group, this comparison shows that additional alcohol groups are required to efficiently chelate the metal ion and outcompete hydrolysis. This conclusion is supported by DFT calculations on the Pu(IV)-OH–L systems (L = GTA, HIBA and HBA), which indicate that the complexation with the proxy ligands takes places through the carboxylate group. XRD of selected solid phases after equilibration with proxy ligands at [L]tot = 0.1 M confirms that Ca(II), Ni(II), Nd(III) and Pu(IV) starting solid materials remained mostly unaltered in the course of the experiments. However, the presence of new XRD features suggests the possible formation of secondary phases. These results allow assessment of the effect of the proposed proxy ligands on the solubility of key radionuclides and metal ions in cementitious systems relevant for low and intermediate level waste, and feed into on-going sorption studies evaluating the impact of UP2W degradation products on the uptake of radionuclides by cement.
1. Introduction
The most commonly accepted safety concept for underground repositories for nuclear waste disposal relies on the combination of engineered and geological barriers, which retard the release of radionuclides into the biosphere. Cementitious materials are often used for the stabilization of the waste and for construction purposes, especially in the context of low and intermediate level wastes (L/ILW). In contact with groundwaters, cementitious materials are known to degrade over time, resulting in the buffering of the porewater at 10 ≤ pH ≤ 13.3 and 10−4 M ≤ [Ca] ≤ 0.02 M according to the different degradation stages.1,2 The relatively high concentration of dissolved Ca can play an important role in the solution chemistry of the radionuclides originating from the waste, e.g. Ca participating in the formation of new solid phases and aqueous complexes or Ca competing for complexation with organic ligands, etc.3–11Different types of organic materials are often disposed together with radioactive waste, in particular in L/ILW repositories. One of these organic materials is UP2W, a polyacrylonitrile-based (PAN) filter aid used both in nuclear and in fossil-fuelled power plants (see Fig. 1). Significant amounts of used UP2W are disposed of in SFR, the final repository for short-lived radioactive waste in Sweden.12–15 The exposure of UP2W to slightly oxidizing conditions in nuclear power plants and its later disposal under the strongly alkaline conditions prevailing in cementitious systems can result in the degradation of the polymeric material and the consequent release of organic ligands able to complex radionuclides.12,13 The presence of such degradation products can accordingly affect the solubility and sorption of radionuclides in the cementitious system of a repository.
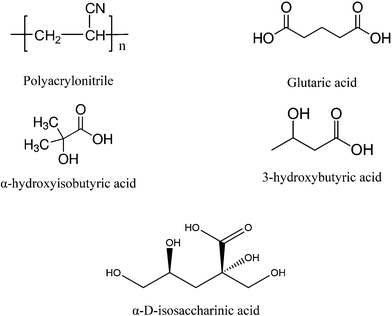 | ||
| Fig. 1 Chemical structures of polyacrylonitrile (PAN), glutaric acid (GTA), α-hydroxyisobutyric acid (HIBA), 3-hydroxybutyric acid (HBA) and α-D-isosaccharinic acid. | ||
An on-going collaborative project between Karlsruhe Institute for Technology – Institute for Nuclear Energy (KIT-INE) and the Swedish Nuclear Fuel and Waste Management Co. (SKB) is dedicated to evaluate the impact of the UP2W degradation products on the retention of radionuclides by cement. Within the project, the organic compounds glutarate (GTA), α-hydroxyisobutarate (HIBA) and 3-hydroxybutarate (HBA) were proposed as possible degradation products of PAN, based on the characterization by 13C-NMR of the supernatant solution in degradation experiments under hyperalkaline conditions (see Fig. 1).16 GTA was considered as representative of the bulk chain of the generated PAN-polymer fragments, whilst HIBA and HBA were proposed to simulate the effect of the end groups. Fig. 1 shows also the chemical structure of α-D-isosaccharinic acid (ISA), a polyhydroxocarboxylic acid resulting from the alkaline degradation of cellulose, which like UP2W is a common waste material in L/ILW. ISA is considered as representative of a family of ligands forming strong complexes with metal ions under hyperalkaline conditions, and is used throughout this work for comparative purposes. Note however that several of the alcohol groups in ISA are characterized by a stronger acidity than those in HIBA and HBA due to the presence of several electron-withdrawing hydroxy groups in the former.
In this overall research context, the present contribution evaluates the impact of the aforementioned proxy ligands on the solubility of key elements and radionuclides in porewater conditions representative of the degradation stage II of cement, i.e. pH ≈ 12.5 and [Ca] ≈ 0.02 M. Calcium has been selected as one of the main elements in cement systems, whereas nickel (as 59Ni and 63Ni) and plutonium (as 239Pu) are considered in this study as important contributors to the radiotoxicity of the waste in L/ILW.17 Neodymium is taken as inactive and redox-stable analogue of key trivalent actinides, e.g. Am(III) and Pu(III). This analogy relies on the similar ionic radii of these metal ions (rNd3+ = 1.11 Å, rAm3+ = 1.10 Å and rPu3+ = 1.12 Å, all with coordination numbers CN = 8)18,19 and accordingly similar aqueous speciation. Although the interaction of Ca(II), Ni(II), Ln(III) and An(IV) with the proxy ligands considered in this work has been previously investigated under acidic conditions (see discussion in Sections 4.1 to 4.4), data on the complex formation in the hyperalkaline conditions relevant for cementitious systems is so far lacking. In these conditions, the presence of elevated hydroxide concentrations may compete with organic ligands for the interaction with these metal ions.
2. Experimental
2.1. Chemicals and cement porewater
All samples were prepared and stored at T = (22 ± 2) °C in Ar-gloveboxes with O2 < 2 ppm. Purified water (Millipore Milli-Q Advantage A10 (18.2 MΩ cm at 22 °C, 4 ppb TOC) with Millipore Millipak® 40 0.22 μm) was used for sample preparation. Milli-Q water was purged with Ar for >1 hour to remove traces of oxygen and CO2. Ni(OH)2(cr) was obtained from Acros Organics. Ca(OH)2(cr) (96%), glutaric acid (C5H8O4, 99%), α-isobutyric acid (C4H8O3, 99%), 3-hydroxybutyric acid (C4H8O3, 99%) and tin(II) chloride (SnCl2, p.a.) were purchased from Sigma-Aldrich. Sodium hydroxide (Titrisol®) and hydroquinone (C6H6O2, HQ, p.a.) were obtained from Merck. Nd(OH)3(s) was prepared by hydration of Nd2O3(cr) (Merck, 99%).20,21A PuO2(ncr, hyd) synthesized in a previous study and with an isotopic composition of 99.4 wt% 242Pu, 0.58 wt% 239Pu, 0.005 wt% 238Pu and 0.005 wt% 241Pu was used in the solubility experiments with Pu(IV). Because of the predominance of the long-lived isotope 242Pu, radiolysis effects in the solubility experiments are negligible. Details on the synthesis and characterization of the PuO2(ncr, hyd) solid phase are reported by Tasi et al. (2018).22 By the initialization of these experiments, the PuO2(ncr, hyd) phase had aged ca. 12 years in 0.10 M NaCl–HCl (pH ≈ 4).
All solubility experiments were performed using a cement porewater representative of the degradation stage II, with pH ≈ 12.5, [Ca] ≈ 0.02 M and low content of Na and K (≤3 × 10−4 M). The cement porewater was prepared using the protocol described in (Tasi et al., 2021) and the solution composition is also found there. The hardened cement paste (HCP) used for the preparation of the porewater (with CEM I 42.5N BV/SR/LA) was provided by the SKB. It was conditioned (grinded, milled and sieved to <100 μm) and characterized in a previous study.23
2.2. pH and Eh measurements
The pH was measured using a ROSS combination pH electrode (Thermo Scientific, OrionTM) calibrated against standard buffer solutions (pH = 2 to 12, Merck). Measurements of the redox potential were conducted using a Pt combination electrode (Metrohm) with Ag/AgCl as a reference system. Measurements were performed only for the plutonium system following the protocol described in Altmaier et al. (2010).24 The measured potentials were converted to Eh (values referred to the standard hydrogen electrode, SHE) by correcting for the potential of the Ag/AgCl reference in 3.0 M KCl at T = 22 °C, i.e. +207 mV. Eh values were converted to pe (with pe = −log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ae−) as Eh = −RT
ae−) as Eh = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(10)F−1
ln(10)F−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ae−, where R is the ideal gas constant (8.3144 J mol−1 K−1) and F is the Faraday constant (96485.3 C mol−1).
ae−, where R is the ideal gas constant (8.3144 J mol−1 K−1) and F is the Faraday constant (96485.3 C mol−1).
Redox conditions along this work are referred to in terms of (pe + pH) values, which allow a more generalized description of the reducing character of a given system. The lower stability line of water is defined for p(H2(g)) = 1 bar, thus with (pe + pH) = 0.25,26
2.3. Solubility experiments and solid phase characterization
Solubility experiments were performed from undersaturation conditions. A well-defined solid phase (Ca(OH)2(cr), β-Ni(OH)2(cr), Nd(OH)3(s) or PuO2(ncr, hyd)) was contacted with the cement porewater containing the proxy ligands, and the metal concentration was followed with time until attaining equilibrium. Equilibrium conditions were assumed after repeated measurements with constant metal concentration. This approach avoids the shortcomings related with the use of oversaturation conditions, especially regarding the formation of stable colloidal species described for Ln(III)/An(III) and An(IV).20,22,25,27,28Experiments were performed in 15 mL centrifuge vessels (PP, Sarstedt AG) containing 10 mL of cement porewater and the given proxy ligand concentration. A small amount of solid phases was then added to the solution, i.e. 10–20 mg in the Ca, Ni and Nd systems, or 0.5–1 mg in the Pu system. These amounts provide sufficient metal inventory to reach the solubility limit in each system. Total ligand concentrations in the cement porewater were varied between 10−6 M ≤ [L]tot ≤ 0.1 M (with L = GTA, HIBA and HBA), except in the Pu system where [L]tot = 10−3 and 0.1 M. Redox conditions in the solubility experiments with PuO2(ncr, hyd) were buffered with 2 mM of either HQ or SnCl2. Hydroquinone defines slightly reducing conditions (pe + pH ≈ 9) where Pu(IV) is known to prevail, whereas Sn(II) sets very strongly reducing conditions (pe + pH ≈ 2) in which both Pu(III) and Pu(IV) may form.22,23,29 The values of pH, Eh and metal concentration were regularly measured up to t ≤ 320 days (Ca-system), t ≤ 359 days (Ni-system), t ≤ 358 days (Nd-system) and t ≤ 223 days (Pu-system). Metal concentrations were measured after ultrafiltration with 10 kDa filters (2–3 nm cut-off, Nanosep® centrifuge tubes, Pall Life Sciences) by inductively coupled plasma atomic emission spectroscopy (ICP-OES, for Ca), inductively coupled plasma mass spectrometry (ICP-MS, for Ni and Nd) and sector field inductively coupled plasma mass spectrometry (SF-ICP-MS, for Pu). Solid phases of the respective Ca(II), Ni(II), Nd(III) and Pu(IV) systems were characterized by X-ray diffraction (XRD): (i) starting materials, and (ii) solid phases collected after attaining equilibrium conditions from the solubility experiments with [L]tot = 0.1 M (L = GTA, HIBA and HBA).
Aliquots of approximately 1–2 mg of the selected solid phases were separated from the solution by centrifugation inside an Ar-glovebox. Solid samples were not washed because of the dilute background electrolyte concentration used in the solubility experiments, and to avoid the washing out of potentially forming secondary phases with the organic ligands. After drying, the solid samples were transferred to a capped silicon single crystal sample holder (Dome, Bruker). The samples were taken out of the glovebox and the XRD patterns were collected on a Bruker AXS D Advance X-ray powder diffractometer. Measurements were performed at angles 2Θ = 5–80° with incremental steps of 0.02–0.04° and accumulation time of one second per step. The resulting diffraction patterns were compared with powder diffraction files (PDF) provided by the JCPDS-ICDD database.
3. Theoretical methods
Tentative structures for ternary complexes Pu(IV)-OH–L (with L = GTA, HIBA and HBA) were investigated by means of DFT calculations.30,31 Calculations were performed using TURBOMOLE (version 7.0, 2015)32–38 with the same functional and basis set as in our previous studies (DFT-BP86,39 def2-SVP![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 32).8,40 For Pu(IV),41 we used the 5f-in core pseudo potentials (PP) which considerably simplified the DFT calculations and the corresponding basis set of double zeta (ecpIVmwb-avdz) quality.8,40 We checked the accuracy of the applied basis sets by comparing with calculations for Pu(IV)-OH–GTA with the larger def2-TZVPP basis sets for the lighter atoms and the triple zeta (ecpIVmwb-avtz) basis set for Pu.
32).8,40 For Pu(IV),41 we used the 5f-in core pseudo potentials (PP) which considerably simplified the DFT calculations and the corresponding basis set of double zeta (ecpIVmwb-avdz) quality.8,40 We checked the accuracy of the applied basis sets by comparing with calculations for Pu(IV)-OH–GTA with the larger def2-TZVPP basis sets for the lighter atoms and the triple zeta (ecpIVmwb-avtz) basis set for Pu.
In a first step, DFT calculations were performed without the addition of any solvent, corresponding to a calculation in the gas phase. Further calculations including aqueous media with the first shell (six molecules) of H2O explicitly and beyond that approximated with the conductor-like screening model (COSMO)42–44 were also conducted. Considering the first water shell explicitly and dealing with additional solvation effects by means of COSMO provides a reasonable approach to investigate structures of species in aqueous solutions.
4. Results and discussion
4.1. Solubility of Ca(II) in the presence of proxy ligands
Fig. 2 shows the solubility data of Ca(OH)2(cr) determined at pH ≈ 12.5 in the presence of GTA, HBA and HIBA. Red solid and dashed lines in the figure represent the calculated solubility of Ca(OH)2(cr) and corresponding uncertainty in ligand-free systems for the given geochemical boundary conditions using thermodynamic data selected in NEA-TDB and the ThermoChimie databases.5,6,45 Cross symbols in the figure show the concentration of Ca in the cement porewater investigated in this work. Typical to a cement pore water composition of degradation state II, the Ca-concentration is controlled by the dissolution of portlandite (Ca(OH)2). For comparison purposes, the figure includes also the calculated solubility of Ca(OH)2(cr) in the presence of ISA (solid black line in the figure).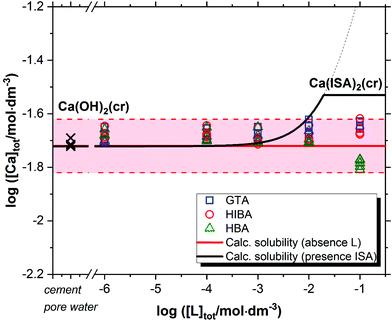 | ||
| Fig. 2 Solubility of Ca(OH)2(cr) in equilibrium with cement porewater at pH = 12.5 with 10−6 M ≤ [L]tot ≤ 0.1 M at t ≤ 320 days. L = glutaric acid (GTA), α-hydroxyisobutyric acid (HIBA) and 3-hydroxybutyric acid (HBA). Cross symbols show the concentration of Ca(II) determined in cement porewater. Red solid and dashed lines in the figure represent the calculated solubility of Ca(OH)2(cr) and corresponding uncertainty at pH = 12.5 in ligand-free systems. Black line correspond to the solubility of Ca(OH)2(cr) in the presence of ISA. All thermodynamic calculations performed using NEA-TDB and ThermoChimie databases.5,6,45 | ||
Fig. 2 shows that GTA, HBA and HIBA have no significant impact on the solubility of Ca(OH)2(cr) within the investigated ligand concentrations. Equilibrium conditions are attained already at t ≈ 8 days. Although still within the uncertainty of the calculated solubility, the concentration of calcium determined for HBA slightly decreases with respect to the calculated value. The decrease in Ca concentration is correlated with a slight increase in pH (from 12.54 ± 0.05 to 12.64 ± 0.05).
Previous thermodynamic studies have investigated the complexation of Ca(II) with GTA, HIBA and HBA under weakly acidic to near-neutral pH conditions. Cannan and Kibrick conducted a comprehensive potentiometric study involving a number of divalent metal ions (Mg, Ca, Sr, Ba and Zn) and mono-/di-carboxylic acids.46 For the equilibrium reactions Ca2+ + GTA2− ⇌ Ca(GTA)(aq) and Ca2+ + HBA− ⇌ Ca(HBA)+, the authors reported the conditional constants log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β′1 = 0.51 and 0.60, respectively, in ∼0.2 M KCl. On the basis of the ion-exchange method, Schubert and Lindenbaum (1952) investigated the complexation of Ca(II) and Sr(II) with a series of mono-, di- and tricarboxylic acids.47 Experiments were performed under near-neutral pH conditions at constant ionic strength, I = 0.16 M NaCl. The authors reported log
β′1 = 0.51 and 0.60, respectively, in ∼0.2 M KCl. On the basis of the ion-exchange method, Schubert and Lindenbaum (1952) investigated the complexation of Ca(II) and Sr(II) with a series of mono-, di- and tricarboxylic acids.47 Experiments were performed under near-neutral pH conditions at constant ionic strength, I = 0.16 M NaCl. The authors reported log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β′1 = 0.55 for the formation of the complex Ca(GTA)(aq), which is in line with the value reported by Cannan and Kibrick. Verbeek and Thun investigated the complexation of lactate and HIBA with alkali-earth elements by means of cation exchange chromatography.48 For the complex Ca(HIBA)+, the authors reported log
β′1 = 0.55 for the formation of the complex Ca(GTA)(aq), which is in line with the value reported by Cannan and Kibrick. Verbeek and Thun investigated the complexation of lactate and HIBA with alkali-earth elements by means of cation exchange chromatography.48 For the complex Ca(HIBA)+, the authors reported log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β′1 = 0.92–1.11, depending upon the method used for the calculation of the equilibrium constant. Piispanen and Lajunen conducted systematic potentiometric titrations to evaluate the complexation of different α-hydroxycarboxylic acids with Ca(II) and Mg(II).49 In 0.5 M NaClO4, the authors determined log
β′1 = 0.92–1.11, depending upon the method used for the calculation of the equilibrium constant. Piispanen and Lajunen conducted systematic potentiometric titrations to evaluate the complexation of different α-hydroxycarboxylic acids with Ca(II) and Mg(II).49 In 0.5 M NaClO4, the authors determined log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β′1 = (1.09 ± 0.03) for the complex Ca(HIBA)+, which is in excellent agreement with the value previously reported by Verbeek and Thun.48 The discussion above highlights the weak character of the complexes of Ca with GTA, HIBA and HBA. Note that although these studies were conducted at lower pH values than those investigated in the present work, the weak character of the complexation is in line with the negligible impact of the proxy ligands on the solubility of Ca(OH)2(cr) at pH ≈ 12.5.
β′1 = (1.09 ± 0.03) for the complex Ca(HIBA)+, which is in excellent agreement with the value previously reported by Verbeek and Thun.48 The discussion above highlights the weak character of the complexes of Ca with GTA, HIBA and HBA. Note that although these studies were conducted at lower pH values than those investigated in the present work, the weak character of the complexation is in line with the negligible impact of the proxy ligands on the solubility of Ca(OH)2(cr) at pH ≈ 12.5.
The calculated solubility of Ca(OH)2(cr) in the presence of ISA is included in Fig. 2 for comparison purposes (solid black line in the figure). In contrast to GTA, HBA and HIBA, ISA is expected to enhance the solubility of Ca(OH)2(cr) above [ISA]tot ≈ 10−3 M. Although the binary complex Ca(ISA)+ is also relatively weak (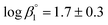 ), the formation of the complex Ca(ISA−H)(aq) involving the deprotonation of an alcohol group of ISA becomes predominant in hyperalkaline pH conditions and is responsible for the calculated increase in the solubility.5,6,45 Above [ISA]tot ≈ 0.02 M, the precipitation of Ca(ISA)2(cr) occurs and the aqueous concentration of ISA remains constant.
), the formation of the complex Ca(ISA−H)(aq) involving the deprotonation of an alcohol group of ISA becomes predominant in hyperalkaline pH conditions and is responsible for the calculated increase in the solubility.5,6,45 Above [ISA]tot ≈ 0.02 M, the precipitation of Ca(ISA)2(cr) occurs and the aqueous concentration of ISA remains constant.
The complexation of Ca2+ with ISA in hyperalkaline systems has been reported to preferentially take place through a 5 membered ring defined by one oxygen of the carboxylate group (C1), the deprotonated alcohol in C2 (α-hydroxyl group) and the Ca atom.50 Although a similar structure can be envisaged for the complex of Ca2+ with the carboxylate and hydroxyl groups of HIBA or HBA, the weaker acidity of the hydroxyl groups of the latter ligands possibly leads to the formation of such complexes only at pH values higher than those investigated in this work, i.e. pH ≈ 12.5.
4.2. Solubility of Ni(II) in the presence of proxy ligands
Fig. 3 shows the impact of GTA, HIBA and HBA on the solubility of β-Ni(OH)2(cr) in cement porewater. Red solid and dashed lines in the figures represent the calculated solubility of β-Ni(OH)2(cr) and corresponding uncertainty in ligand-free systems.51 Cross symbols in the figure show the concentration of Ni in the cement porewater investigated in this work. Black symbols and solid line in Fig. 3 correspond to the experimental and calculated solubility of β-Ni(OH)2(cr) in the presence of increasing ISA concentrations, as reported by González-Siso and co-workers.51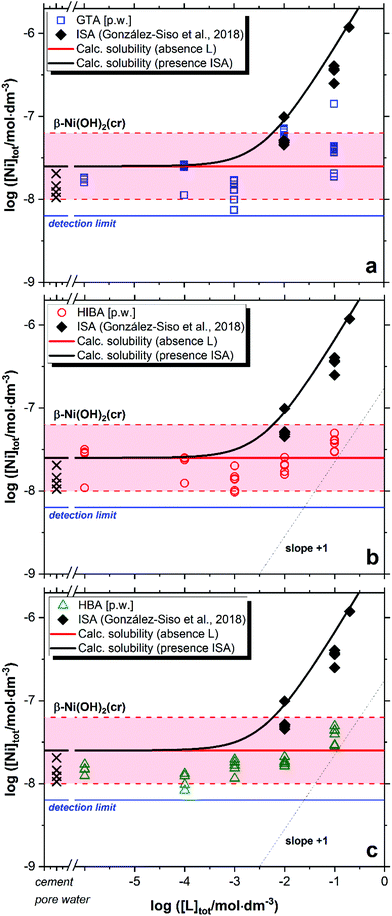 | ||
| Fig. 3 Solubility of β-Ni(OH)2(cr) in equilibrium with cement porewater at pH = 12.5 with 10−6 M ≤ [L]tot ≤ 0.1 M at t ≤ 359 days: (a) glutaric acid (GTA); (b) α-hydroxyisobutyric acid (HIBA); (c) 3-hydroxybutyric acid (HBA). Cross symbols show the concentration of Ni(II) determined in cement porewater. Red solid and dashed lines in the figure represent the calculated solubility of β-Ni(OH)2(cr) and corresponding uncertainty at pH = 12.5 in ligand-free systems. Black lines correspond to the solubility of β-Ni(OH)2(cr) in the presence of ISA. All thermodynamic calculations performed using the chemical and thermodynamic models reported in González-Siso et al. (2018).51 | ||
Nickel concentrations measured in cement porewater in the absence of organic ligands are in excellent agreement with previous observations reported in the literature, i.e. [Ni(II)]aq ≈ 10−8–10−7 M.52,53 These Ni(II) concentrations are in line with solubility data reported for β-Ni(OH)2(cr).51 or determined in this work at low ligand concentration, i.e. [L]tot < 10−2 M. Extensive efforts have been previously dedicated to the identification of the solid phase/s controlling the solubility of Ni(II) in cementitious systems,54–56 which hint towards the incorporation of Ni in layered double hydroxide (LDH) phases. Based on the current knowledge of thermodynamic data for Ni(II) solubility and hydrolysis in hyperalkaline systems, we remark that some of the systems considered to spectroscopically investigate the structure of solid-solution phases incorporating Ni(II) in cementitious systems were oversaturated with respect to β-Ni(OH)2(cr) (10−7–10−6 M, see Fig. 1 in Vespa et al., 2006, with a solubility limit of β-Ni(OH)2(cr) reported as ∼2.5 × 10−8 M in González-Siso et al.51). Conclusions on the solid-solution formation under these oversaturation conditions should be considered with care.
In contrast to the Ca(II)-system, a weak but reproducible increase in the solubility of β-Ni(OH)2(cr) is observed for the three proxy ligands at [L]tot ≥ 10−2 M (Fig. 3). This observation hints to the formation of weak complexes within the investigated chemical boundary conditions. Under analogous pH conditions but absence of Ca, González-Siso and co-workers reported a remarkable impact of ISA on the solubility of Ni(II) due to the predominance of the complexes Ni(OH)2ISA− and Ni(OH)3ISA2− in the aqueous phase.51 The limited effect on the solubility observed for GTA, HIBA and HBA does not allow a sound evaluation of the stoichiometry and stability of the complexes prevailing in solution, although the formation of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes can be speculated based on the moderate increase in solubility. A limited number of experimental studies are available in the literature reporting on the complexation of Ni(II) with GLU, HIBA and HBA.57–60 All these studies were performed in acidic to near-neutral pH conditions, and thus report the formation of 1
1 complexes can be speculated based on the moderate increase in solubility. A limited number of experimental studies are available in the literature reporting on the complexation of Ni(II) with GLU, HIBA and HBA.57–60 All these studies were performed in acidic to near-neutral pH conditions, and thus report the formation of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1
1, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and up to 1
2 and up to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 complexes of the unhydrolyzed Ni2+ cation with these ligands. The incorporation of these complexes and corresponding equilibrium constants to the thermodynamic calculations confirm that in the hyperalkaline conditions of interest in this work, these complexes cannot outcompete Ni(II) hydrolysis and thus cannot explain the slight increase in the solubility of β-Ni(OH)2(cr) observed at [L]tot ≥ 10−2 M. This leads to the assumption that hydroxide participates also in the complexation process, and thus the formation of ternary complexes Ni(OH)xL–x (GTA) or Ni(OH)xL−yH1−x−y (HIBA and HBA, with y = 0 or 1) is proposed on the basis of the observed solubility enhancement. However, an accurate characterization of the stoichiometry and thermodynamic stability of these complexes can be only achieved with systematic solubility experiments under a wide variation of pH and [L]tot, which was out of the scope in this work. Note that the pore water solution before adding solid Ni(OH)2 does already contain Ni(II) originating from the preparation using HCP in a concentration range corresponding to a solution saturated with regard to β-Ni(OH)2(cr) (see cross symbols in Fig. 3).
3 complexes of the unhydrolyzed Ni2+ cation with these ligands. The incorporation of these complexes and corresponding equilibrium constants to the thermodynamic calculations confirm that in the hyperalkaline conditions of interest in this work, these complexes cannot outcompete Ni(II) hydrolysis and thus cannot explain the slight increase in the solubility of β-Ni(OH)2(cr) observed at [L]tot ≥ 10−2 M. This leads to the assumption that hydroxide participates also in the complexation process, and thus the formation of ternary complexes Ni(OH)xL–x (GTA) or Ni(OH)xL−yH1−x−y (HIBA and HBA, with y = 0 or 1) is proposed on the basis of the observed solubility enhancement. However, an accurate characterization of the stoichiometry and thermodynamic stability of these complexes can be only achieved with systematic solubility experiments under a wide variation of pH and [L]tot, which was out of the scope in this work. Note that the pore water solution before adding solid Ni(OH)2 does already contain Ni(II) originating from the preparation using HCP in a concentration range corresponding to a solution saturated with regard to β-Ni(OH)2(cr) (see cross symbols in Fig. 3).
4.3. Solubility of Nd(III) in the presence of proxy ligands
The impact of GTA, HIBA and HBA on the solubility of Nd(OH)3(s) in cement porewater is shown in Fig. 4. Red solid and dashed lines in the figures represent the calculated solubility of Nd(OH)3(s) and corresponding uncertainty in ligand-free systems.20 Black symbols and the solid line in Fig. 4 correspond to the experimental and calculated solubility of Nd(OH)3(s) in the presence of increasing ISA concentrations as reported by Gugau.61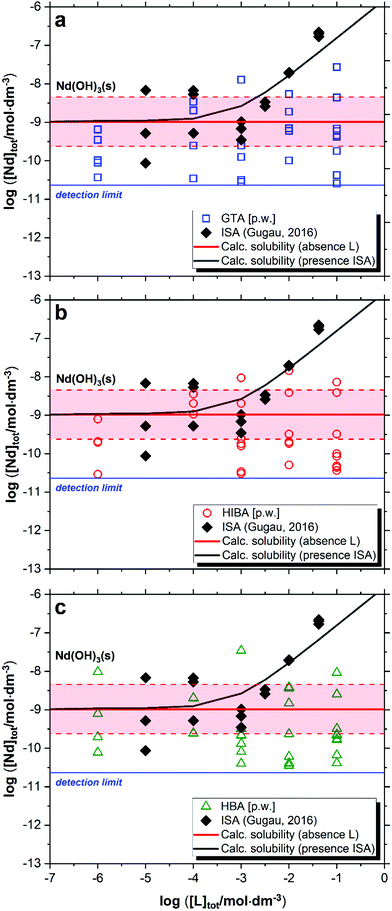 | ||
| Fig. 4 Solubility of Nd(OH)3(s) in equilibrium with cement porewater at pH = 12.5 with 10−6 M ≤ [L]tot ≤ 0.1 M at t ≤ 358 days: (a) glutaric acid (GTA); (b) α-hydroxyisobutyric acid (HIBA); (c) 3-hydroxybutyric acid (HBA). Red solid and dashed lines in the figure represent the calculated solubility of Nd(OH)3(s) and corresponding uncertainty at pH = 12.5 in ligand-free systems as reported in Neck et al., (2009).20 Black symbols and line correspond to the experimental and calculated solubility of Nd(OH)3(s) in the presence of ISA as reported in Gugau (2016).61 | ||
Fig. 4 shows no evident increase in the solubility of Nd(OH)3(s) caused by any of the investigated proxy ligands. A large dispersion in the concentration of neodymium at log[Nd(III)]tot ≈ −(9 ± 1.5) is observed for the three systems. Similar observations are widely reported in the literature for the solubility of An(III)/Ln(III) and An(IV) under alkaline conditions,20,22,28 and are generally attributed to artefacts related to the predominance of the neutral species An/Ln(OH)3(aq) or An(OH)4(aq) in solution, e.g. sorption on the vessel walls and/or filter, presence of small colloidal species that are not filtered out in the phase separation process, etc. The large dispersion in the solubility data observed up to high ligand concentrations can be also attributed to the absence of complexation, which would expectedly result in the formation of negatively charged complexes that can be quantified more accurately. This hypothesis is underpinned by solubility data determined by Gugau for the system Nd(III)–ISA (see Fig. 4), who reported a large dispersion in the Nd(III) concentrations up to log[ISA]tot ≈ −3, whereas above this ligand concentration, precise solubility measurements and systematic increase of log[Nd(III)]tot were obtained.61 These observations were explained by the author with the predominance of the complex Nd(OH)3ISA− at pHm ≥ 12 and log[ISA]tot ≥ −3.
A number of experimental studies are available in the literature investigating the complexation of Nd(III) (or other lanthanides) with GLU, HIBA and HBA.62–67 Most of these studies target only the complexation taking place under acidic conditions with the exception of Giroux and co-workers, who investigated the system Pr(III)–HBA by means of potentiometric titrations in acidic to weakly alkaline conditions.64 Although the formation of stable binary complexes with log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β(1,1) ≈ 2–4 is reported for these systems, none of these studies tackles the complexation under hyperalkaline conditions where a strong competition with hydrolysis is to be expected.
β(1,1) ≈ 2–4 is reported for these systems, none of these studies tackles the complexation under hyperalkaline conditions where a strong competition with hydrolysis is to be expected.
Fig. 5 shows the fraction diagrams indicating the species distribution for the systems Nd(III)–GTA, Nd(III)–HBA and Nd(III)–HIBA calculated for 4 ≤ pH ≤ 13 and [L]tot = 0.1 M using thermodynamic data available in the literature.20,63,64,67 As qualitatively discussed above, Fig. 5 clearly shows that the binary complexes Nd(GTA)+, Nd(HBA)2+ and Nd(HIBA)2+ (all of them with full deprotonated carboxylic groups) prevail only up to pH ≈ 8–9, where hydrolysis takes over dominating the aqueous speciation of Nd(III) up to pH = 13. Although these calculations are based on thermodynamic data determined in acidic to weakly alkaline conditions, our solubility experiments conducted at pH = 12.5 support that complexation is very weak or inexistent in the hyperalkaline conditions of relevance for cementitious systems.
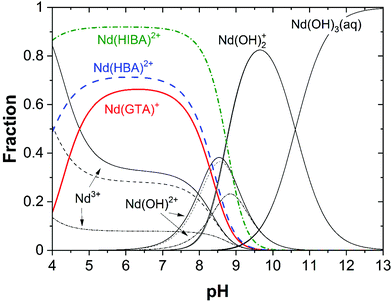 | ||
| Fig. 5 Fraction diagram of Nd(III) calculated for the systems Nd(III)–GTA, Nd(III)–HBA and Nd(III)–HIBA at 4 ≤ pH ≤ 13 and [L]tot = 0.1 M using thermodynamic data reported in Wang et al. (2000)67 (system Nd(III)–GTA), Giroux et al. (2002)64 (system Pr(III)–HBA, considered as analogue of Nd(III)–HBA) and Deelstra and Verbeek (1964)63 (system Nd(III)–HIBA). Underlying hydrolysis calculated using thermodynamic data reported in Neck et al. (2009).20 | ||
4.4. Solubility of Pu(IV) in the presence of proxy ligands
Fig. 6 shows the solubility of PuO2(ncr, hyd) in the presence of GTA, HBA and HIBA in systems buffered with HQ (pe + pH ≈ 9, Fig. 6a) and Sn(II) (pe + pH ≈ 2, Fig. 6b). Red solid and dashed lines in the figures represent the calculated solubility of PuO2(ncr, hyd) and corresponding uncertainty in ligand-free systems.5,25 Black symbols and solid line in Fig. 6 illustrate the experimental and calculated solubility of PuO2(ncr, hyd) in cement porewater with increasing ISA concentrations as reported by Tasi and co-workers.23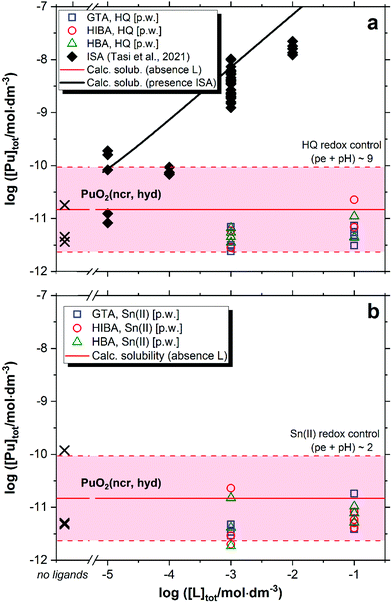 | ||
| Fig. 6 Solubility of PuO2(ncr, hyd) in equilibrium with cement porewater at pH = 12.5 with [L]tot = 10−3 and 0.1 M at t ≤ 223 days. L = glutaric acid (GTA), α-hydroxyisobutyric acid (HIBA) and 3-hydroxybutyric acid (HBA). Redox conditions buffered by HQ (pe + pH ≈ 9, figure (a)) and Sn(II) (pe + pH ≈ 2, figure (b)). Cross symbols show the concentration of Pu determined in the absence of proxy ligands. Red solid and dashed lines in the figure represent the calculated solubility of PuO2(ncr, hyd) and corresponding uncertainty at pH = 12.5 in ligand-free systems.5,25 Black symbols and line correspond to the experimental and calculated solubility of PuO2(ncr, hyd) in the presence of ISA as reported in Tasi et al. (2018).23 | ||
The solubility of PuO2(ncr, hyd) remains unaffected in the presence of proxy ligands, both in HQ- and Sn(II)-buffered systems (Fig. 6). As observed for Nd(III), none of the proxy ligands are able to outcompete the strong hydrolysis of Pu(IV) in HQ-systems. Our results do not allow discerning the oxidation state of Pu in Sn(II) systems, but the constant level of Pu concentration disregards the formation of either Pu(IV)–L or Pu(III)–L complexes in the aqueous phase.
Under exactly the same boundary conditions (HCP porewater in the degradation stage II) but in the presence of ISA, Tasi and co-workers reported a significant increase in the solubility of PuO2(ncr, hyd) at ligand concentrations above ∼10−5 M (black squares in Fig. 6a).23 Based on the thermodynamic model previously derived by the same authors, the increase in solubility was attributed to the formation of the quaternary complex CaPu(IV)(OH)3(ISA−2H)(aq).8 DFT calculations conducted in the latter study confirmed the key role of the deprotonated α- and δ-OH groups of ISA in the formation of a very stable chelate complex with Pu(IV). The presence of only one alcohol group in HIBA and HBA can partly explain the great differences in their complexation behaviour with respect to the Pu(IV)–ISA system. Moreover, the weaker acidity of the alcohol groups in HIBA and HBA compared to ISA is expected to promote also the formation of weaker complexes with hard Lewis acids like Pu(IV).
There are virtually no experimental studies focusing on the complexation of Pu(IV) with GTA, HIBA or HBA. A few studies targeted the complexation of these proxy ligands with Th(IV), which we discuss here as analogue of Pu(IV).60,68,69 The potentiometric titrations conducted by Magon et al. in acidic conditions were fit with the formation of (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), (1
1), (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2), (1
2), (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3) and (1
3) and (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4) complexes for the Th(IV)–HIBA system and (1
4) complexes for the Th(IV)–HIBA system and (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), (1
1), (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) and (1
2) and (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3) for the Th(IV)–HBA system.68 By comparison with other hydroxymonocarboxylate ligands (hydroxyacetic, 2-hydroxypropanoic, 2-phenyl-2-hydroxyacetic, 2-hydroxy-2-methylpropanoic (HIBA), 3-hydroxybutanoic (HBA) and 4-hydroxybutanoic), the authors concluded that only alcohol groups in α-position participate in the chelate formation with Th(IV).
3) for the Th(IV)–HBA system.68 By comparison with other hydroxymonocarboxylate ligands (hydroxyacetic, 2-hydroxypropanoic, 2-phenyl-2-hydroxyacetic, 2-hydroxy-2-methylpropanoic (HIBA), 3-hydroxybutanoic (HBA) and 4-hydroxybutanoic), the authors concluded that only alcohol groups in α-position participate in the chelate formation with Th(IV).
Tomat and co-workers investigated also by potentiometric means the complexation of Th(IV) with the dicarboxylate ligands malonic, succinic, phthalic, maleic and glutaric acids.69 All experiments were performed in strongly acidic conditions defined by 1.0 M (H, Na)ClO4, with −log[H+] < 3. In contrast to all other ligands, glutaric acid resulted in complexes with Th(IV) in the protonated form, i.e. Th(HGTA)3+ and Th(HGTA)22+. We hypothesize that complexes with the fully deprotonated ligand will form at pH values higher than those considered by Tomat and co-workers. The so far reported complexes of Th(IV) with GTA, HIBA and HBA are predominant under acidic conditions, but cannot outcompete hydrolysis in alkaline to hyperalkaline conditions. Although the formation of ternary complexes of the type An(IV)-OH–L (with L = GTA, HIBA or HBA) can be speculated, our results with Pu(IV) disregard their predominance in hyperalkaline systems with [L]tot ≤ 0.1 M.
4.5. Solid phase characterization
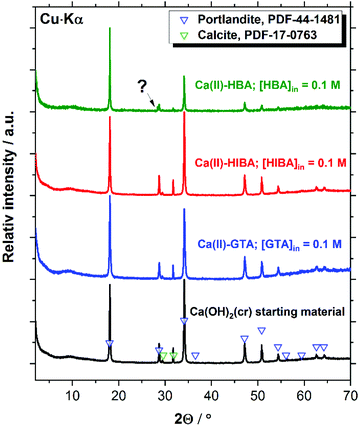
X-ray diffractograms collected for Ca(OH)2(cr), β-Ni(OH)2(cr), Nd(OH)3(s) and PuO2(ncr, hyd) before and after the equilibration with cement porewater solutions containing [L]tot = 0.1 M are displayed in Fig. 7–10. These measurements are mainly intended to support the interpretation of the solution-phase chemistry; a thorough characterisation of the solid phase is beyond the scope of the study.Fig. 7 shows that the XRD patterns of the starting Ca(II) material are in excellent agreement with reference data reported for Ca(OH)2(cr), although the starting material contains also a small impurity of calcite, CaCO3(cr). Both solid phases remain unaltered after the solubility experiments with GTA, HIBA and HBA at the highest ligand concentration. A small new feature at 2Θ ≈ 28.3 degree appears in the diffractogram of the Ca(II)–HBA system. Although this peak appears close to one of the main reflections of Ca(OH)2(cr) at 2Θ ≈ 28.6 degree, it may hint towards the formation of a secondary solid phase “Ca(II)–HBA”. This hypothesis is in line with the slight decrease in solubility observed at [HBA]tot = 0.1 M (see Fig. 2).
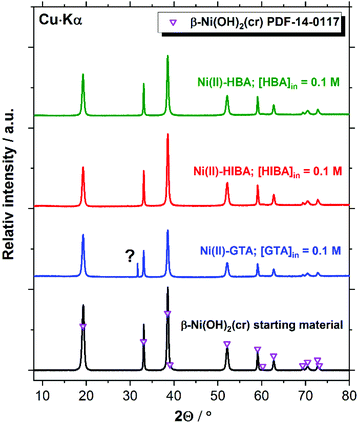
XRD patterns of the Ni(II) solid phases before and after equilibration with cement porewater containing the proxy ligands are in excellent agreement with reference data for β-Ni(OH)2(cr) (PDF 14-0117, see Fig. 8). The feature at 2Θ ≈ 31.7 degree observed in the diffractogram of the Ni(II)–GTA system does not belong to β-Ni(OH)2(cr) and could not be assigned to any previously reported Ni(II) compound. The formation of crystalline Ni(II) compounds with linear dicarboxylic acids is reported in the literature for the series oxalic, malonic, succinic and glutaric acids.70–78 However, the synthetic routes used for the preparation of these solid phases usually rely on hydrothermal conditions and acidic environments to avoid the precipitation of Ni(II) hydroxide or oxide phases, and thus are not expected to form in the aqueous alkaline systems investigate in the present work at T = 22 °C. The peak at 2Θ ≈ 31.7 degree may thus correspond to a solid phase containing the ligand but not Ni(II).
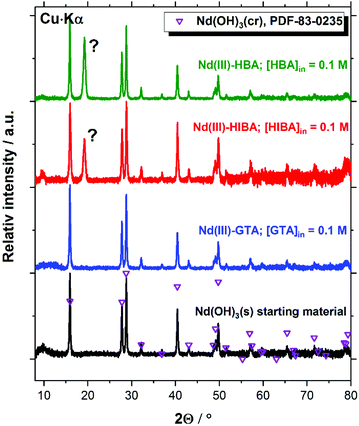
Fig. 9 confirms that the Nd(III) starting material exclusively corresponds to Nd(OH)3(s) (PDF 83-0235). The patterns of this solid phase remain unaltered after completing the solubility experiments in the presence of proxy ligands at [L]tot = 0.1 M. A new intense reflection at 2Θ ≈ 19.2 degree appears in both Nd(III)–HBA and Nd(III)–HIBA systems, which however cannot be assigned to any reported Nd(III) compound. Cheng and Zhao-ai synthesized the solid phases Ln(HIBA)2NO3·2H2O(cr) (Ln = Ce–Nd) and Ln(HIBA)2NO3·3H2O(cr) (Ln = La, Sm–Lu, Y) in acidic systems containing nitrate,79,80 which however are not expected to form in the hyperalkaline conditions of this study. Böszörményi and co-workers recently reported the formation of Nd(III)-gluconate solid phases Nd(GLU−H)(OH)·2H2O(cr) and CaNd(GLU−H)(OH)3·2H2O(cr) in alkaline systems at room temperature.81 These observations cannot be directly extrapolated to the proxy ligands investigated in this work because of (i) the stronger interaction of Nd(III) and gluconate in alkaline systems,21,82 expectedly due to the presence of several alcohol groups in gluconate as opposed to HIBA and HBA (with only one OH-group each), and (ii) the large oversaturation conditions used by Böszörményi et al., i.e. [NdCl3]0 = [NaGLU]0 = 0.5 M.
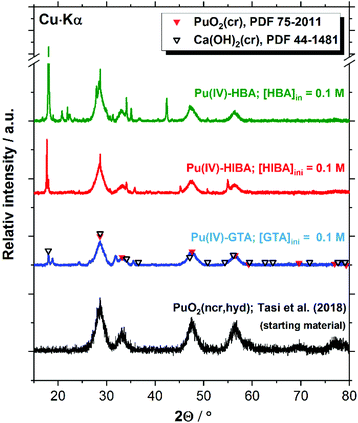
The XRD patterns shown in Fig. 10 for the Pu system confirm the presence of PuO2(ncr, hyd) in the investigated solubility samples containing HQ and proxy ligands at [L]tot = 0.1 M. Given the analogous solubility behaviour observed for HQ- and Sn(II)-buffered systems (see Section 4.4), the same Pu solid phase identified for HQ is expected in Sn(II) systems. Patterns belonging to portlandite (Ca(OH)2(cr)) are obtained for the three proxy ligands systems. This observation is not unexpected, considering that solubility experiments are conducted in cement porewater in the degradation stage II, i.e. in equilibrium with portlandite (saturation index (SI) ≈ 0). Hence, minor changes in the boundary conditions (e.g. pH, temperature, etc.) may trigger the precipitation of this solid phase under close to equilibrium conditions. In addition to PuO2(ncr, hyd) and Ca(OH)2(cr), a number of additional reflections arise in all investigated systems, which could not be assigned to any Pu- or Ca-solid phase included in the JCPDS-ICDD database. The characterization of the residue obtained after drying 5 mL of supernatant under Ar atmosphere resulted in virtually the same patterns (see Fig. S1–S3 in the ESI†). Provided the Ca and Pu concentrations in the supernatant (∼0.02 M and ∼10−11 M, respectively), we propose that the patterns correspond to binary solid phases containing Ca and proxy ligands. The formation of potential new solid phases containing the proxy ligands investigated in this work is a topic of fundamental scientific interest, but does not impact the main outcome of this study obtained in terms of robust solubility limits for radionuclides under conditions relevant for nuclear waste disposal.
4.6. Theoretical calculations for the system Pu(IV)/proxy ligands. Comparison with the ISA case
In contrast to other hydroxocarboxylic acids (e.g. ISA, gluconate), none of the investigated proxy ligands has shown any significant impact on the solubility of Pu(IV) in the porewater representative of the degradation stage II of cement (see Section 4.4). In order to further understand the weak complexation character of these ligands, DFT calculations were performed providing tentative structures for the ternary complexes Pu(IV)-OH–L, with L = GTA, HIBA and HBA. Structural information obtained with corresponding computational methods for the system Pu(IV)-OH–ISA is also discussed in this section for comparative purposes.40Due to the lack of evidence with respect to the stoichiometry of the hypothetical Pu(IV)-OH–L complexes forming, the assumption of complex formation involving the individual aqueous species prevailing within the investigated boundary conditions was made, i.e. [Pu(OH)4L]n/m (with n = −2 for GTA and m = −1 for HIBA and HBA). The attempt to include HIBA and HBA with deprotonated alcohol groups coordinating Pu(IV) led during the structural optimization to spontaneous protonation of the alcohol by an adjacent water molecule which then became a hydroxide. This sets clear differences with respect to ISA, for which up to two deprotonated alcohol groups could be stabilized by the complexation with Pu(IV).40 The optimized structures obtained for the Pu(IV)-OH–L complexes are shown in Fig. 11, whereas Table 1 summarizes the Pu–O distances optimized by DFT in this work or in Tasi et al. (2018).40 We tested the accuracy of the def2-SVP/ecpIVmwb-avdz basis sets for [Pu(OH)4GTA]2− with the def2-TZVPP/ecpIVmwb-avtz basis sets and found hardly any difference. Hence the optimized structures with the smaller basis sets are already reasonably converged.
| [Pu(OH)4GTA]2− | [Pu(OH)4HBA]− | [Pu(OH)4HIBA]− | [Pu(OH)3ISA−H]− | ||||
|---|---|---|---|---|---|---|---|
| Bond | DFT/DFT + COSMO | Bond | DFT/DFT + COSMO | Bond | DFT/DFT + COSMO | Bond | DFT + COSMO |
| Pu-OH− | 223 (223)/225 | Pu-OH− | 219/222 | Pu-OH− | 225/225 | Pu-OH− | 226/227 |
| Pu-OH− | 231 (231)/230 | Pu-OH− | 225/224 | Pu-OH− | 225/227 | Pu–ISA(–C2O−) | 231/230 |
| Pu-OH− | 233 (233)/234 | Pu-OH− | 229/226 | Pu-OH− | 228/228 | Pu-OH− | 233/233 |
| Pu-OH− | 240 (239)/238 | Pu-OH− | 229/231 | Pu-OH− | 228/229 | Pu-OH− | 236/234 |
| Pu–GTA(–COO−) | 247 (247)/243 | Pu–HBA(–COO−) | 255/252 | Pu–HIBA(–COO−) | 248/253 | Pu–ISA(–COO−) | 239/240 |
| Pu-OH2 | 259 (259)/253 | Pu–HBA(–COO−) | 263/259 | Pu–HBA(–COO−) | 266/257 | Pu-OH2 | 250/251 |
| Pu-OH2 | 259 (261)/263 | Pu-OH2 | 274/266 | Pu-OH2 | 268/258 | Pu-OH2 | 260/259 |
| Pu-OH2 | 275 (268)/269 | Pu-OH2 | 377/378 | Pu-OH2 | 369/369 | Pu-OH2 | 267/267 |
Optimized structures and distances shown in Table 1 confirm that the bonding of GTA, HBA and HIBA to Pu(IV) takes place exclusively through one carboxylate group, and that the alcohol groups of HBA and HIBA do not participate in the coordination to plutonium, neither deprotonated nor as protonated functional groups. This is correlated with the weaker acidity of the hydroxide groups in H(I)BA compared to those in ISA. Significantly shorter Pu–L(–COO–) distances were calculated by Tasi and co-workers for L = ISA, as compared to the systems L = GTA, HBA and HIBA investigated in this work. All evidences obtained from DFT calculations further support the weak complexation properties of the proxy ligands investigated in this work, in contrast to the case of ISA.
5. Summary and conclusions
The impact of glutarate (GTA), α-hydroxyisobutarate (HIBA) and 3-hydroxybutarate (HBA) on the solubility of Ca(OH)2(cr), β-Ni(OH)2(cr), Nd(OH)3(s) and PuO2(ncr, hyd) was systematically investigated in cement porewater solutions representative for a repository for L/ILW after an early stage in which the alkalis (Na, K) are washed out of cement, i.e. degradation stage II (pH ≈ 12.5, [Ca] ≈ 0.02 M). Within the EURAD-CORI EU project, the selected ligands were previously proposed by KIT-INE as possible degradation products of the filter aid UP2W. Solubility data obtained in this work are compared with experimental results and thermodynamic calculations for the systems Ca(II)–, Ni(II)–, Nd(III)– and Pu(IV)–ISA systems under analogous boundary conditions, as previously reported in the literature.The solubility of Ca(OH)2(cr), β-Ni(OH)2(cr) and PuO2(ncr, hyd) remain mostly unaffected in cement porewater solutions containing [L]tot ≤ 0.1 M (L = GTA, HIBA and HBA). The slight increase in solubility observed for β-Ni(OH)2(cr) in the presence of GTA, HIBA and HBA at [L]tot = 0.1 M suggests the formation of stable complexes in the hyperalkaline conditions investigated in this work, most likely in the form of ternary species Ni(II)-OH–L. The formation of binary complexes M–L (M = Ca(II), Ni(II), Nd(III), An(IV); L = GTA, HIBA, HBA) in acidic to near-neutral conditions is described in the literature, and thermodynamic data are reported. However, speciation calculations performed for these systems show that these binary complexes cannot outcompete hydrolysis under the high pH conditions defined by cementitious systems.
The comparison of solubility data determined in this work for GTA, HIBA and HBA ligands with previously reported data for the systems Ca(II)–, Ni(II)–, Nd(III)– and Pu(IV)–ISA under analogous boundary conditions confirms the systematically stronger complexation properties of the latter ligand, at least in the pH conditions investigated in this work. In spite of the similar functional groups present in HIBA (1 –COOH + 1 –C-OH in α-position), HBA (1 –COOH + 1 –C-OH in β-position) and ISA (1 –COOH + 4 –C-OH), this comparison makes evident that the presence of several alcohol groups is required for the formation of stable chelated complexes in hyperalkaline systems. This is expectedly due to the need of deprotonating one or more OH-groups of the ligand, which readily occurs in the case of ISA due to the higher acidity of its alcohol groups. This hypothesis is further supported by DFT calculations conducted on the system Pu(IV)–L (with L = GTA, HBA and HIBA), which show that the alcohol groups of HBA and HIBA do not participate in the complexation with plutonium, neither as deprotonated nor as protonated functional groups.
Solid phase characterization by XRD confirms the predominance of Ca(OH)2(cr), β-Ni(OH)2(cr), Nd(OH)3(s) and PuO2(ncr, hyd) after completing the solubility experiments in the presence of [L]tot = 0.1 M, although the observation of new XRD patterns indicates that secondary phases M–L may have formed in some of the investigated systems.
These results highlight the minor impact of the proposed proxy ligands on the solubility of key radionuclides and metal ions in cementitious systems relevant in the context of L/ILW final disposal. Future studies will target the impact on solubility of UP2W complex degradation leachates simulating close-to-real systems under repository conditions. These solubility data represent a key input in the design and interpretation of sorption studies evaluating the impact of UP2W degradation products on the uptake of radionuclides by cement under conditions relevant for the safety assessment of a repository.
Glossary of abbreviations and acronyms
| aq | Aqueous |
| An | Actinides |
| COSMO | Conductor-like screening model |
| cr | Crystalline |
| DFT | Density functional theory |
| GTA | Glutarate |
| HBA | 3-Hydroxybutarate |
| HIBA | α-Hydroxyisobutarate |
| hyd | Hydrated |
| ICP-OES | Inductively coupled plasma atomic emission spectroscopy |
| ICP-MS | Inductively coupled plasma mass spectrometry |
| ISA | α-D-Isosaccharinic acid |
| L/ILW | Low and intermediate level waste |
| Ln | Lanthanides |
| ncr | Nano-crystalline |
| p.a. | Per analysis |
| PAN | Polyacrylonitrile |
| s | Solid |
| SF-ICP-MS | Sector field inductively coupled plasma mass spectrometry |
| XRD | X-ray diffraction |
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was partially funded by SKB. The EURAD project leading to this application has received funding from the European Union's Horizon 2020 research and innovation programme under grant agreement no. 847593. The work was performed as part of the WP CORI. Frank Geyer, Annika Fried, Cornelia Walschburger, Stephanie Kraft and Melanie Böttle (all KIT-INE) are gratefully acknowledged for the ICP-MS/OES measurements and technical support.References
- H. F. W. Taylor, Cement chemistry, T. Telford, London, 2nd edn, 1997 Search PubMed.
- M. Ochs, D. Mallants and L. Wang, Radionuclide and Metal Sorption on Cement and Concrete, in Topics in Safety, Risk, Reliability and Quality, Springer International Publishing: Imprint: Springer, Cham, 1st edn, 2016, p. 1, online resource (XXX, 301 pages) Search PubMed.
- D. Fellhauer, J. Rothe, M. Altmaier, V. Neck, J. Runke, T. Wiss and T. Fanghänel, Radiochim. Acta, 2016104355–379. DOI:10.1515/ract-2015-2489.
- D. Fellhauer, M. Altmaier, X. Gaona, J. Lützenkirchen and T. Fanghänel, Radiochim. Acta, 2016104381–397. DOI:10.1515/ract-2015-2490.
- I. Grenthe, X. Gaona, A. V. Plyasunov, L. Rao, W. H. Runde, B. Grambow, R. J. M. Konings, A. L. Smith and E. E. Moore, Second Update on the Chemical Thermodynymics of Uranium, Neptunium, Plutonium, Americium and Technetium, 2020, vol. 14 Search PubMed.
- W. Hummel, G. Anderegg, L. Rao, I. Puigdomènech and O. Tochiyama, Chemical Thermodynamics of Compounds and Complexes of U, Np, Pu, Am, Tc, Se, Ni and Zr with Selected Organic Ligands, Elsevier, North Holland, Amsterdam, 2005, vol. 9 Search PubMed.
- B. Kutus, X. Gaona, A. Pallagi, I. Palinko, M. Altmaier and P. Sipos, Coord. Chem. Rev., 2020, 417, 213337 CrossRef CAS.
- A. Tasi, X. Gaona, D. Fellhauer, M. Bottle, J. Rothe, K. Dardenne, R. Polly, M. Grive, E. Colas, J. Bruno, K. Kallstrom, M. Altmaier and H. Geckeis, Appl. Geochem., 2018, 98, 351–366 CrossRef CAS.
- J. Tits, X. Gaona, A. Laube and E. Wieland, Radiochim. Acta, 2014, 102, 385–400 CrossRef CAS.
- J. Tits, E. Wieland and M. H. Bradbury, Appl. Geochem., 2005, 20, 2082–2096 CrossRef CAS.
- K. Vercammen, M. A. Glaus and L. R. Van Loon, Radiochim. Acta, 2001, 89, 393–401 CrossRef CAS.
- M. Dario, M. Molera and B. Allard, Effect of organic ligands on the sorption of europium on TiO2 and cement at high pH, SKB, 2004 Search PubMed.
- L. Duro, M. Grive, X. Gaona, J. Bruno, T. Andersson, H. Boren, M. Dario, B. Allard, J. Hagberg and K. Källström, Study of the effect of the fibre mass UP2 degradation products on radionuclide mobilisation, 2012 Search PubMed.
- M. J. Keith-Roach, M. Lindgren and K. Källström, Assessment of complexing agent concentrations in SFR, SKB, 2014 Search PubMed.
- M. Keith-Roach, M. Lindgren and K. Källström, Assessment of complexing agent concentrations for the post-closure safety assessment in PSAR SFR, SKB, 2021 Search PubMed.
- A. Tasi, P. Szabo, X. Gaona, M. Altmaier and H. Geckeis, Contribution by KIT-INE to CORI Task 2, in Eurad European Joint Programme on Radiaoactive waste management, Milestone DMS97 – CORI Technical Report – Task 2 Hydrolytic/radiolytic degradation of organics: description of first results on hydrolytic and radiolytic organic degradation and identification of released species, ed. D. Ricard and J. Vandenborre, 2021 Search PubMed.
- SKB, Safety Analysis SFR 1. Long-term safety, 2008 Search PubMed.
- V. Neck and J. I. Kim, Radiochim. Acta, 2001, 89, 1–16 CrossRef CAS.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef.
- V. Neck, M. Altmaier, T. Rabung, J. Lutzenkirchen and T. Fanghanel, Pure Appl. Chem., 2009, 81, 1555–1568 CrossRef CAS.
- H. Rojo, X. Gaona, T. Rabung, R. Polly, M. Garcia-Gutierrez, T. Missana and M. Altmaier, Appl. Geochem., 2021, 126, 104864 CrossRef CAS.
- A. Tasi, X. Gaona, D. Fellhauer, M. Bottle, J. Rothe, K. Dardenne, D. Schild, M. Grive, E. Colas, J. Bruno, K. Kallstrom, M. Altmaier and H. Geckeis, Radiochim. Acta, 2018, 106, 259–279 CrossRef CAS.
- A. Tasi, X. Gaona, T. Rabung, D. Fellhauer, J. Rothe, K. Dardenne, J. Lutzenkirchen, M. Grive, E. Colas, J. Bruno, K. Kallstrom, M. Altmaier and H. Geckeis, Appl. Geochem., 2021, 126, 104862 CrossRef CAS.
- M. Altmaier, X. Gaona, D. Fellhauer and G. Buckau, Intercomparison of redox determination methods on designed and near-neutral aqueous systems, KIT-SR 7572, Karlsruhe Institute of Technology, Karlsruhe, 2010, p. 34 Search PubMed.
- V. Neck, M. Altmaier and T. Fanghänel, C. R. Chim., 2007, 10, 959–977 CrossRef CAS.
- X. Gaona, D. Fellhauer and M. Altmaier, Pure Appl. Chem., 2013, 85, 2027–2049 CrossRef CAS.
- M. Altmaier, X. Gaona and T. Fanghänel, Chem. Rev., 2013, 113, 901–943 CrossRef CAS PubMed.
- M. Altmaier, V. Neck and T. Fanghanel, Radiochim. Acta, 2004, 92, 537–543 CrossRef CAS.
- D. Fellhauer, Untersuchungen zur Löslichkeit und Redoxchemie von Plutonium und Neptunium, PhD thesis, Universität Heidelberg, 2013 Search PubMed.
- P. Hohenberg and W. Kohn, Phys. Rev. [Sect.] B, 1964, 136, B864 CrossRef –B871.
- W. Kohn and L. J. Sham, Phys. Rev. [Sect.] A, 1965, 140, 1133 CrossRef –1138.
- A. Schafer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571–2577 CrossRef.
- K. Eichkorn, O. Treutler, H. Ohm, M. Haser and R. Ahlrichs, Chem. Phys. Lett., 1995, 240, 283–289 CrossRef CAS.
- K. Eichkorn, F. Weigend, O. Treutler and R. Ahlrichs, Theor. Chem. Acc., 1997, 97, 119–124 Search PubMed.
- R. Ahlrichs, F. Furche, C. Hättig, W. M. Klopper, M. Sierka and F. Weigend, TURBOMOLE v7.0, University of Karlsruhe and Forchungszentrum Karslruhe GmbH, 2015 Search PubMed.
- P. Deglmann, K. May, F. Furche and R. Ahlrichs, Chem. Phys. Lett., 2004, 384, 103–107 CrossRef CAS.
- O. Treutler and R. Ahlrichs, J. Chem. Phys., 1995, 102, 346–354 CrossRef CAS.
- M. von Arnim and R. Ahlrichs, J. Chem. Phys., 1999, 111, 9183–9190 CrossRef CAS.
- R. Ahlrichs, F. Furche and S. Grimme, Chem. Phys. Lett., 2000, 325, 317–321 CrossRef CAS.
- A. Tasi, X. Gaona, D. Fellhauer, M. Bottle, J. Rothe, K. Dardenne, R. Polly, M. Grive, E. Colas, J. Bruno, K. Kallstrom, M. Altmaier and H. Geckeis, Appl. Geochem., 2018, 98, 247–264 CrossRef CAS.
- A. Moritz, X. Y. Cao and M. Dolg, Theor. Chem. Acc., 2007, 117, 473–481 Search PubMed.
- K. Baldridge and A. Klamt, J. Chem. Phys., 1997, 106, 6622–6633 CrossRef.
- A. Klamt, J. Phys. Chem., 1995, 99, 2224–2235 CrossRef CAS.
- A. Klamt and G. Schuurmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805 RSC.
- E. Giffaut, M. Grive, P. Blanc, P. Vieillard, E. Colas, H. Gailhanou, S. Gaboreau, N. Marty, B. Made and L. Duro, Appl. Geochem., 2014, 49, 225–236 CrossRef CAS.
- R. K. Cannan and A. Kibrick, J. Am. Chem. Soc., 1938, 60, 2314–2320 CrossRef CAS.
- J. Schubert and A. Lindenbaum, J. Am. Chem. Soc., 1952, 74, 3529–3532 CrossRef CAS.
- F. Verbeek and H. Thun, Anal. Chim. Acta, 1965, 33, 378 CrossRef CAS –383.
- J. Piispanen and L. H. J. Lajunen, Acta Chem. Scand., 1995, 49, 235–240 CrossRef CAS.
- C. Dudas, B. Kutus, I. Palinko and P. Sipos, Abstr. Pap. Am. Chem. Soc., 2017, 253, 1155 Search PubMed.
- M. R. González-Siso, X. Gaona, L. Duro, M. Altmaier and J. Bruno, Radiochim. Acta, 2018, 106, 31–45 CrossRef.
- C. J. Engelsen, H. A. van der Sloot, G. Wibetoe, H. Justnes, W. Lund and E. Stoltenberg-Hansson, Cem. Concr. Res., 2010, 40, 1639–1649 CrossRef CAS.
- E. Wieland, J. Tits, A. Ulrich and M. H. Bradbury, Radiochim. Acta, 2006, 94, 29–36 CrossRef CAS.
- M. Vespa, R. Dahn, E. Gallucci, D. Grolimund, E. Wieland and A. M. Scheidegger, Environ. Sci. Technol., 2006, 40, 7702–7709 CrossRef CAS PubMed.
- A. M. Scheidegger, E. Wieland, A. C. Scheinost, R. Dahn, J. Tits and P. Spieler, J. Synchrotron Radiat., 2001, 8, 916–918 CrossRef CAS PubMed.
- A. M. Scheidegger, E. Wieland, A. C. Scheinost, R. Dahn and P. Spieler, Environ. Sci. Technol., 2000, 34, 4545–4548 CrossRef CAS.
- N. d. R. Aruga, Atti Accad. Sci. Torino, Cl. Sci. Fis., Mat. Nat., 1977, 111, 193–201 Search PubMed.
- I. Filipovic, M. Tkalcec and B. S. Grabaric, Inorg. Chem., 1990, 29, 1092–1097 CrossRef CAS.
- B. Grabaric, B. Mayer, I. Piljac and I. Filipovi, J. Inorg. Nucl. Chem., 1974, 36, 3809–3812 CrossRef CAS.
- P. Prapaipong, E. L. Shock and C. M. Koretsky, Geochim. Cosmochim. Acta, 1999, 63, 2547–2577 CrossRef CAS.
- K. Gugau, Complexation of Nd(III) and Cm(III) with α-D-isosaccharinic acid under repository relevant conditions, KIT, 2016 Search PubMed.
- G. R. Choppin, A. Dadgar and E. N. Rizkalla, Inorg. Chem., 1986, 25, 3581–3584 CrossRef.
- H. Deelstra and F. Verbeek, Anal. Chim. Acta, 1964, 31, 251 CrossRef CAS –257.
- S. Giroux, S. Aury, B. Henry and P. Rubini, Eur. J. Inorg. Chem., 2002, 1162–1168 CrossRef CAS.
- H. K. Kim, K. Jeong, H. R. Cho, K. Kwak, E. C. Jung and W. Cha, Inorg. Chem., 2020, 59, 13912–13922 CrossRef CAS PubMed.
- P. Thakur, P. N. Pathak, T. Gedris and G. R. Choppin, J. Solution Chem., 2009, 38, 265–287 CrossRef CAS.
- Z. M. Wang, L. J. van de Burgt and G. R. Choppin, Inorg. Chim. Acta, 2000, 310, 248–256 CrossRef CAS.
- L. Magon, A. Bismondo, L. Maresca, G. Tomat and R. Portanov, J. Inorg. Nucl. Chem., 1973, 35, 4237–4243 CrossRef CAS.
- G. Tomat, L. Magon, A. Cassol and R. Portanov, Z. Anorg. Allg. Chem., 1972, 393, 184 CrossRef CAS –192.
- A. S. Antsyshkina, G. G. Sadikov, T. V. Koksharova and V. S. Sergienko, Russ. J. Inorg. Chem., 2014, 59, 50–57 CrossRef CAS.
- P. M. Forster and A. K. Cheetham, Angew. Chem., Int. Ed., 2002, 41, 457–459 CrossRef CAS PubMed.
- N. Guillou, C. Livage, M. Drillon and G. Ferey, Angew. Chem., Int. Ed., 2003, 42, 5314–5317 CrossRef CAS PubMed.
- J. D. Hanawalt, H. W. Rinn and L. K. Frevel, Ind. Eng. Chem., 1938, 10, 457–512 CAS.
- J. D. Hanawalt, Appl. Spectrosc., 1967, 21, 382 Search PubMed.
- S. H. Jhung, J. H. Lee, P. M. Forster, G. Ferey, A. K. Cheetham and J. S. Chang, Chem. – Eur. J., 2006, 12, 7899–7905 CrossRef PubMed.
- A. Kolezynski, B. Handke and E. Drozdz-Ciesla, J. Therm. Anal. Calorim., 2013, 113, 319–328 CrossRef CAS.
- M. R. Montney, R. M. Supkowski, R. J. Staples and R. L. LaDuca, J. Solid State Chem., 2009, 182, 8–17 CrossRef CAS.
- C. Ruiz-Perez, M. Hernandez-Molina, J. Sanchiz, T. Lopez, F. Lloret and M. Julve, Inorg. Chim. Acta, 2000, 298, 245–250 CrossRef CAS.
- X. U. Cheng and L. F. N. Zhao-ai, Chem. Res. Chin. Univ., 1992, 13, 10–13 CrossRef.
- X. U. Cheng and L. F. N. Zhao-ai, J. Hangzhou Univ., 1995, 22, 47–51 Search PubMed.
- E. Böszörményi, J. Lado, C. Dudas, B. Kutus, M. Szabados, G. Varga, I. Palinko and P. Sipos, Pure Appl. Chem., 2020, 92, 1709–1715 CrossRef.
- B. Kutus, N. Varga, G. Peintler, A. Lupan, A. A. A. Attia, I. Palinko and P. Sipos, Dalton Trans., 2017, 46, 6049–6058 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2dt01409b |
| This journal is © The Royal Society of Chemistry 2022 |