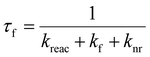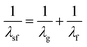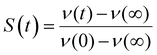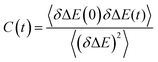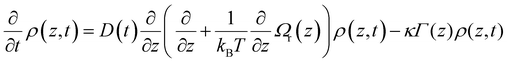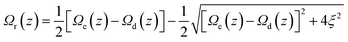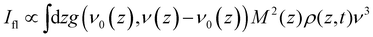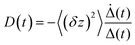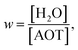Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Altered relaxation dynamics of excited state reactions by confinement in reverse micelles probed by ultrafast fluorescence up-conversion
Ismael A.
Heisler
 a and
Stephen R.
Meech
a and
Stephen R.
Meech
 *b
*b
aDepartamento de Física, Universidade Federal do Paraná, Curitiba, Paraná, CEP 81531-980, Brazil
bSchool of Chemistry, University of East Anglia, Norwich NR4 7TJ, UK. E-mail: s.meech@uea.ac.uk
First published on 19th August 2021
Abstract
Chemical reactions in confined environments are important in areas as diverse as heterogenous catalysis, environmental chemistry and biochemistry, yet they are much less well understood than the equivalent reactions in either the gas phase or in free solution. The understanding of chemical reactions in solution was greatly enhanced by real time studies of model reactions, through ultrafast spectroscopy (especially when supported by molecular dynamics simulation). Here we review some of the efforts that have been made to adapt this approach to the investigation of reactions in confined media. Specifically, we review the application of ultrafast fluorescence spectroscopy to measure reaction dynamics in the nanoconfined water phase of reverse micelles, as a function of the droplet radius and the charge on the interface. Methods of measurement and modelling of the reactions are outlined. In all of the cases studied (which are focused on ultrafast intramolecular reactions) the effect of confinement was to suppress the reaction. Even in the largest micelles the result in the bulk aqueous phase was not usually recovered, suggesting an important role for specific interactions between reactant and environment, for example at the interface. There was no simple one-to-one correspondence with direct measures of the dynamics of the confined phase. Thus, understanding the effect of confinement on reaction rate appears to require not only knowledge of the dynamics of the reaction in solutions and the effect of confinement on the medium, but also of the interaction between reactant and confining medium.
1. Introduction
Developing a detailed microscopic understanding of chemical reactivity in the living cell is a key objective of modern molecular science. Such an understanding will provide new insights into important aspects of cellular function, which will in-turn inform ideas of – for example – the mechanism of operation of pharmaceuticals. Clearly, the living cell presents a very different environment to the isotropic liquid phase, where the most detailed studies of chemical reactivity have been made. In the cell there are multiple interfaces, steep charge gradients, regions of low and high friction and polarity, all in a spatially crowded inhomogeneous environment. To probe reactivity in the cell it is therefore necessary to extend investigations of chemical reactivity from isotropic liquids to more complex and spatially confined media. In this contribution to the themed issue on ‘Nanoconfinement’ we will focus on the real time experimental investigation of reactivity in model confined media – mainly micelles – as an intermediate step to the more challenging case of the biological cell, where spatial as well as temporal resolution will be required.Ultrafast spectroscopy has long been established as a key tool in the investigation of chemical reactions in the condensed phase. The subject has been the topic of a large number of reviews, only a few of which are listed here.1–6 The early review of Hynes was influential in developing an understanding of the role of solvent dynamics in diverse ultrafast chemical reactions.1 Some recent comprehensive reviews of reaction in solution have highlighted how much progress has been made in this field, and also highlighted the role that vibrational relaxation can play in the fastest processes alongside solvent dynamics.5,6 Fleming and Cho2 and de Boeij et al.3 reviewed the considerable level of detail which can be attained in understanding and analysing polar solvation dynamics, which play such a key role in chemical reaction dynamics.1 Much of the progress in understanding reaction dynamics in solution has been driven by progress in ultrafast experimentation, and a top level review of this area has recently been presented, which serves as a useful introduction.7 Progress in theory and calculation methods have also been key, and recent developments were covered by Conti et al.4
Among the numerous ultrafast experimental methods that have been applied to study chemical reactivity in the condensed phase, this review will focus on fluorescence up-conversion. The method is described in more detail below. While limited to the investigation of reactions of fluorescent excited states, it does provide high sensitivity and high temporal resolution and, as an emission technique, is free of interference from the multiple dark states, which complicate interpretation in, for example, ultrafast transient absorption spectroscopy (TA).8–13 The fluorescence up-conversion method has been widely applied to the investigation of chemical reactions in isotropic solution. In most cases these efforts have been focused on unimolecular reactions. In bimolecular reactions the molecular dynamics on the reactive potential energy surface are often obscured by slower diffusive process. This limitation also applies in the present review of ultrafast reactions in confined media. Thus, the many interesting examples where confinement modifies the rates and even products of bimolecular reactions are not addressed here.
This is perhaps a niche topic for a review. However, within the context of this themed issue on nanoconfinement the study of reaction dynamics through ultrafast fluorescence plays an important role. A central issue is the effect of nanoconfinement on reactive potential energy surfaces, and therefore how confinement can modify the outcome of chemical reaction. For reactions in the condensed phase the methods of ultrafast fluorescence spectroscopy (of which up-conversion has the best time resolution) uniquely provides insight into the initial decay of the Franck–Condon state. Further, time resolved fluorescence yields a clear picture of real time molecular dynamics on the excited state potential surface. These features mean that these data are well suited to theoretical modelling. For these reasons, studies of reactive systems by ultrafast up-conversion measured under conditions of confinement represent a unique tool for probing reaction dynamics in confined media. A more widely applied method for probing excited state reactions is femtosecond TA, in which an ultrafast pump pulse initiates the reaction, which is then studied by absorption of a continuum probe pulse arriving a controlled time later.14,15 The TA approach has many advantages. Since it probes the evolution of the absorption spectrum (or more usually the absorption difference spectrum, where the unpumped sample absorbance is subtracted) such that the time evolution of the population of all states is measured. In this way, the decay of the excited state, the formation and decay of any intermediates and the repopulation of the initial ground state are monitored simultaneously. TA is thus an extremely powerful tool for investigating excited state dynamics. It does however present the experimenter with the challenge of separating all of these spectrally distinct contributions. This is usually met by application of one of the established global analysis methods, which fit the evolution of the entire transient spectrum to a kinetic model.14 Despite its obvious power the TA method is less widely applied to the study of reactions in confinement than time resolved fluorescence. The advantages of fluorescence are twofold. First, as stated above, fluorescence focuses on the reactive potential energy surface (at least for a long as fluorescence is maintained) without contributions from changes in product or ground state absorbance. Second, as will be seen below, the spectral evolution on a reactive potential energy surface is often better represented by a continuous spectral evolution rather than a conversion from one state to another with an associated kinetic rate constant. The global analysis programs developed to date do not deal well with this type of evolution, while methods for measuring the temporal evolution of fluorescence spectra are rather well developed. It is for these reasons that time resolved fluorescence has become the method of choice in probing reactive dynamics in confinement. Nevertheless, TA has been used to investigate a number of reactions in confined environments, and where they complement fluorescence data they are included in the discussion.
This review is structured as follows. First, the experimental method of fluorescence up-conversion will be described. Then a simple model of excited state reactivity which incorporates the effects of the medium will be outlined. After that, the dynamics of confined media will be briefly reviewed, as they have a critical influence on reactivity. This will be followed by a detailed look at ultrafast reaction dynamics in some of those confined liquids, with the focus on inverse micelles (inverse and reverse will be used interchangeably in this work) stabilizing water nanodroplets.
2. Ultrafast fluorescence up-conversion
Time resolved fluorescence spectroscopy is an essential tool for understanding excited state relaxation processes.8,16 If one of the mechanisms of fluorescence quenching is an excited state reaction (rate constant kreac) then the fluorescence lifetime, τf, is:where kf is the rate constant for fluorescence (the radiative rate constant) and knr is the sum of all other radiationless decay processes (and for now it is assumed that all decay processes are intramolecular and first order). In the limit that kreac ≫ kf + knr then the fluorescence lifetime directly probes the reaction rate, i. e. τf ≈ 1/kreac. In this way time resolved fluorescence measurements provide a direct measure of a reaction rate constant.
The most popular tool in time resolved fluorescence is certainly time correlated single photon counting, in which a short pulse of light excites a sample and the arrival time between the excitation pulse and a detected photon is measured. Repeated measurements build up a fluorescence decay profile with outstanding signal to noise. However, the requirement that the reaction rate dominates over the (typically) nanosecond radiative decay already suggests the need for temporal resolution in the picosecond time domain. Further, as will be discussed below, reaction rates in solutions are often determined by dynamics in the solute environment, which suggests the requirement for pico- and even sub-picosecond time resolution. Such temporal resolution is beyond what can be attained with conventional time correlated single photon counting, and so more specialist ultrafast methods are required.
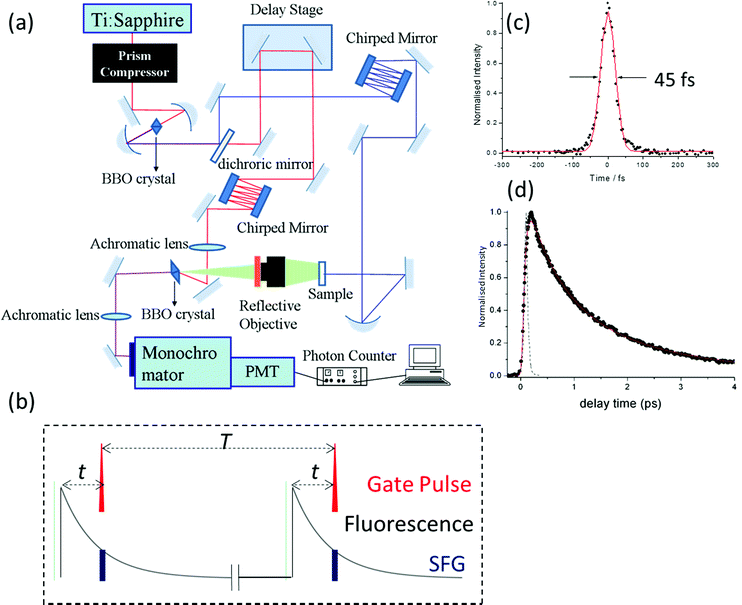
Ultrafast fluorescence up-conversion is one of the oldest methods of ultrafast spectroscopy.17,18 It is essentially a sampling method where fluorescence intensity is sampled through up-conversion by an ultrashort pulse in a nonlinear crystal. The basic experimental layout is shown in Fig. 1a. An ultrafast laser pulse (the pump) excites fluorescence from the sample. The fluorescence is collected and focussed into a nonlinear crystal. A second ultrafast laser pulse (the gate pulse) is temporally synchronised with the pump pulse. The gate and pump pulses have different wavelengths; often the gate is the fundamental and the pump the second harmonic output of a single laser, though both may be generated in independent optical parametric amplifiers (OPAs) pumped by the same laser source. In either case the gate pulse is routed through an optical delay line, such that precise control of the path length difference between pump and gate yields an exactly known interpulse time delay. The gate pulse (wavelength λg) is then mixed with the fluorescence (λf) in the nonlinear crystal to generate a wavelength of light at the sum frequency, λsf:
The intensity of the sum frequency output is linearly proportional to the intensity of the gate beam as well as the instantaneous intensity of the fluorescence when they overlap spatially and temporally (Fig. 1b). In the limit that the ultrafast pulse width is much less than the fluorescence decay time, a scan of the pump – gate delay while measuring the sum-frequency intensity, maps out the fluorescence decay profile. In the case that the pulse width is on the same timescale as the fluorescence, what is measured is a convolution of the fluorescence decay with the cross correlation of the pump and gate pulses. If that cross correlation is determined, the fluorescence decay can be extracted by one of the established deconvolution procedures.19
Modern ultrafast laser sources driving OPAs routinely produce pulses of 20 fs or less, which sets the ultimate time resolution of the up-conversion experiment. As with all ultrafast experiments, one of the challenges in attaining the best time resolution is preventing pulse broadening due to group velocity dispersion in the optics between the laser and sample/nonlinear crystal.20 This is doubly tricky in up-conversion, because there are two different wavelengths to deal with. Experimentally this is achieved by using reflective optics wherever possible, to minimise dispersion problems. Where transmissive optics are required (waveplates to control polarisation, nonlinear crystals, sample cells, etc.) they are selected to be as thin as possible. Still, dispersion is inevitable in these optics, so for the best time resolution dispersion compensation must be introduced independently in both pump and gate pathways. This is usually achieved by using chirped mirrors or prism pairs (or a combination of both) for compression, and through a careful choice of the geometry for sum-frequency generation. In this way Joo and co-workers have shown that the time resolution of fluorescence up-conversion can be reduced to <30 fs and sub 50 fs is routinely achieved.21,22 Experimentally, the instrument response time (the cross correlation of pump and gate pulses) is usually determined by up-converting Raman scattered light from the solvent (Raman being a near instantaneous with the pump pulse), and this measurement can be used in the deconvolution.
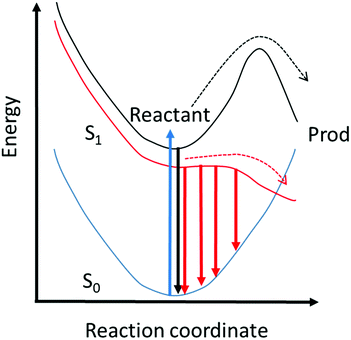
Thus, the up-conversion experiment yields the fluorescence lifetime with excellent time resolution. In simple cases the rate constant for the reaction is recovered directly. This will be the case in reactions for which the barrier is high and the decay of the population in the fluorescent state is a good measure of the reaction rate. However, for ultrafast reactions on barrierless or low barrier potential energy surfaces, the reactive dynamics in the excited state may be directly observed in the fluorescence spectrum. This is illustrated in Fig. 2, where motion along the reactive surface will be observed as temporal evolution in the fluorescence spectrum. Clearly, in the latter case, by time resolving the fluorescence spectrum it is possible to recover more detail concerning dynamics on the reactive potential surface. Extracting this data from TA measurements is more challenging because of the spectral overlap mentioned above.
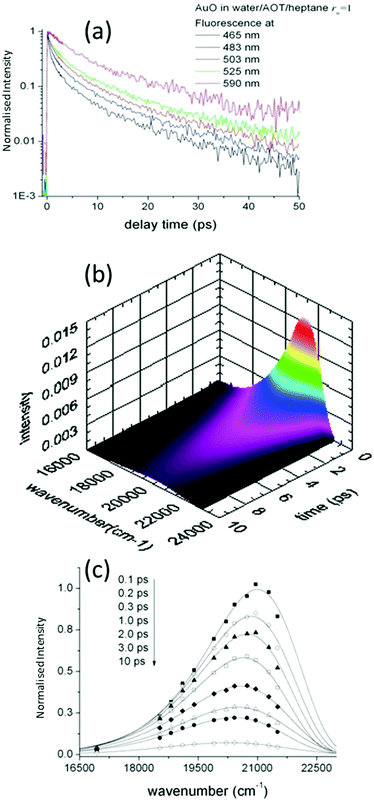
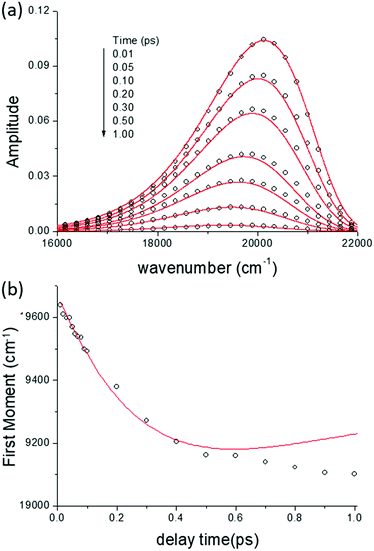
Such time resolved emission spectra (TRES) can be measured with tens of femtosecond time resolution by the simple (though tedious) expedient of recording fluorescence decays at wavelengths spanning the entire emission spectrum (Fig. 3a). The fluorescence wavelength may be selected by both tuning the phase-matching angle of the up-conversion crystal, and selecting the up-converted wavelength with a monochromater. By area normalising the measured time resolved fluorescence profile (or more usually its noise free fit recovered from the deconvolution) to the intensity in the steady state emission, a three dimensional surface (intensity – time – wavelength) is created (Fig. 3b) and the time resolved spectra are recovered from intensity – wavelength slices at any given time (Fig. 3c).23,24 From these TRES it is possible to track the excited state dynamics as the population evolves along the reactive potential energy surface. An extension of the method is time resolved area normalised emission spectra (TRANES) where a second area normalization is used.25 The latter method is especially useful for analysis of reactions with two emissive states (reactant and product).
One difficulty with the TRES measurement is the long data collection times, which can be a severe limitation for photoactive samples. There have been some innovative adaptations to automate the collection of TRES.26 An important recent advance is the development of true broadband detection methods, whereby careful selection of the gate beam wavelength and up-converting crystal, coupled with control of the fluorescence detection pathway, complete TRES can be detected on a CCD.27,28 In this way the spectral resolution is greatly improved and the data collection time dramatically reduced. There is a small penalty to pay with time resolution, which is probably only significant when the objective is to detect high frequency coherences in fluorescence, which may be related to reaction mechanism,29,30 but are not of principle concern in this review.
A key observable in interpreting chemical reactions in the condensed phase is dynamics in the solvent, and in particular how the solvent responds to a change in electric field (such as might occur in an electron transfer reaction for example). A sudden perturbation to the electric field is provided upon electronic excitation if the permanent dipole moment of the ground and excited states of the solute differ. A consequence of this change is that a polar solvent environment will relax in response to the new electric field, stabilising the excited state, leading to a red-shift in the emission spectrum. Analysis of the total spectral shift as a function of solvent polarity yields the excited state dipole moment.31 The shift is not however instantaneous but evolves as the solvent responds to the new dipole moment. TRES measurements time resolve the spectral shift, giving rise to a solvation response, which can be converted to the solvent response function, S(t):
In the limit that solute electronic excitation represents a small perturbation to the solute–solvent interaction, the experimentally determined parameter S(t) can be approximated by its linear-response counterpart, the solvation time correlation function, C(t)33 where33,34
This represents the autocorrelation function of ensemble averaged solute energy gap fluctuations. Importantly this parameter is accessible through molecular dynamics simulation. Further, and as detailed by Maroncelli and Ladanyi, the solvation time correlation function is related to other correlation functions which may be accessed in different experiments.33 For example the polarizability correlation function measured in the optical Kerr effect or the dipole correlation function measured in dielectric relaxation can both be related to C(t) through appropriate power law relations.34 Indeed related correlation functions are accessible from a range of ultrafast multidimensional nonlinear optical experiments (where C(t) is often described as a frequency-frequency correlation function).34–38 These interrelations are important as they connect the observables of numerous time domain experiments to the medium dynamics (for examples see Section 4) which can in-turn have a controlling influence on reactive dynamics (see Section 3) and which are accessible through molecular dynamics simulations. Such multiple means of characterising medium dynamics are important in understanding complex phenomena such as reactions in solution.
In most liquids C(t) reveals quite complex dynamics including an ultrafast (ca 100 fs) impulsive response, which can be connected to librational dynamics in the liquid, as well as slower diffusive solvent reorganisation.39,40 A detailed discussion is beyond the present scope, but it is sufficient to note that solvation dynamics plays an important, and sometimes controlling, role in the dynamics of many reactive systems in the condensed phase. This becomes more apparent in the next section, where the solvation time correlation function is an important input to the theoretical modelling of reaction dynamics. While multiple methods of measuring C(t) mentioned above are useful, they are usually macroscopic measurements. In contrast, TRES yields the solvation response in the local environment of the fluorophore, and is thus particularly useful as a probe of liquid dynamics at nanoscale, and thus in confined and heterogeneous media.
Before closing this section, we note one caveat that applies especially to complex media. Time resolved spectral shifts can be observed in heterogeneous media even in the absence of solvation dynamics, or where the solvation dynamics are fast. For example, TRES measurements on an inhomogeneous system which has the fluorophore localized in short lived blue emitting sites and long lived red emitting sites, will reveal an apparent red shift over time which is unrelated to solvation dynamics.41 Careful analysis is required to resolve such cases, which becomes increasingly difficult when multiple sites are occupied. Thus, it is important to select probes of complex media where the site distribution is as homogeneous as possible. This can often be achieved by inclusion of some kind of anchoring group in the fluorescence probe. In probing protein dynamics it is possible to incorporate reactive fluorophores through unnatural amino acid substitution, which then report site specific data.42,43
3. Modelling medium friction effects on excited state chemical reactions
In this section we outline a theory of excited state reaction dynamics in the condensed phase that has proven useful in modelling a range of experimental data in confined media, and will describe its specific application to a time resolved fluorescence study of a suitable model excited state reaction. While the model is simple, it incorporates the main molecular features required for modelling, specifically a reactive potential energy surface and the viscosity and polarity of the environment, introduced through a time dependent diffusion coefficient which may be calculated from C(t). These and similar models have been widely discussed in connection with ultrafast reactions in solution.1,44–49To model ultrafast TRES we require a calculation of the population distribution dynamics on the reactive excited state surface. This can be obtained from the generalized Smoluchowski equation (GSE):50–53
Concerning this choice of suitable solute with a reactive excited state, we follow Glasbeek and co-workers who used the GSE to model the excited state dynamics of the dye Auramine O (AO, Fig. 4a) in solutions of n-alcohols at reduced temperature.59,61,62 AO has a particularly simple excited state reaction which has been studied in some depth.61–64 The reaction coordinate is a twisting of a phenyl ring following electronic excitation, which leads from the bright Franck Condon active state to a twisted dark state with charge transfer character, at which geometry a conical intersection to the ground state is accessible, quenching the fluorescence. In addition to its simple reaction coordinate, AO has a large transition dipole moment between ground state, S0, and first singlet excited state, S1, which is a key factor in obtaining high signal-to-noise up-conversion data. Thus AO is a well-suited model reaction, to which the simple GSE model can reasonably be applied. We have adopted the approach originally described by Glasbeek and co-workers for AO in free solutions to simulate confinement effects on AO excited state reaction. We note that the GSE model has also been applied in a study of the viscosity sensitive probe Thioflavin T, which has a rather similar reaction coordinate to AO, and also to the ultrafast decay of the green fluorescent protein chromophore.57,65
 | ||
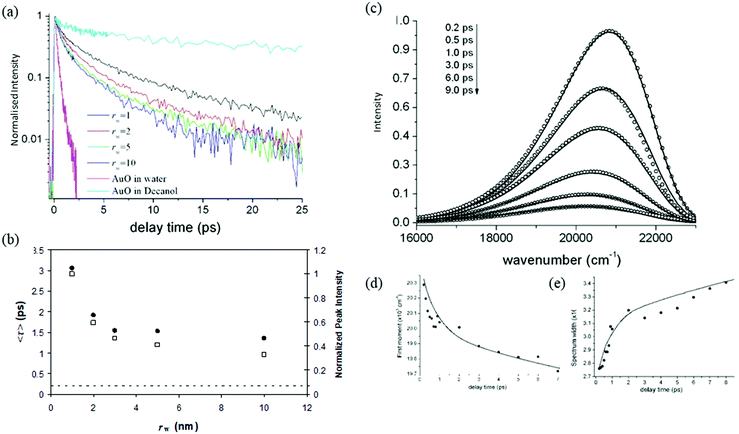
| Fig. 4 (a) Structure of Auramine O, illustrating (arrow) the reaction coordinate, rotation of the dimethylanilino ring – the final angle between the plane of the two rings in the excited state is calculated to be 90°.136,138 (b) The evolution of the excited state distribution, ρ(z, t) on the potential energy surface shown for the normalized reaction coordinate, z (black). | ||
To compare directly the calculated population distribution from the GSE with experimental data requires some further input. In the absence of a known or calculated PES, a model surface for the reaction must be chosen. For AO three harmonic PES's are used: the ground state, Ω0(z); the emissive excited state, Ωe(z); the twisted dark state, Ωd(z), reached along the torsional reaction coordinate, which eventually relaxes to the original ground state through the Gaussian sink representation of a conical intersection. The relative energies of the three harmonic PES's are selected to fit the energies of the absorption and emission spectra. For AO the reaction coordinate z is a normalized torsional coordinate for rotation of the AO phenyl ring about the single bond (Fig. 4a). Coupling the bright and dark states yields the reactive PES53
The objective is to simulate the TRES, which means it is necessary to convert the time dependent population distribution (Fig. 4b) into TRES. The conversion is59
In Fig. 5 we show the data for AO in bulk aqueous solution.66 The TRES are quite well fit by the model (Fig. 5a and b). The key new information extracted from this fit is the form of the time dependent diffusion coefficient. Indeed, what we ultimately wish to recover from these measurements is the effect of confinement on reaction dynamics, and the quantitative information – which could ultimately be reproduced by molecular dynamics simulation for example – is contained in D(t). Glasbeek and co-workers studied AO in low temperature alcohols and found that a time independent D scaled linearly with η/T, i.e. the rate of decay is determined by the Stokes–Einstein-Debye equation, which suggests that hydrodynamic friction opposing the rotation of the phenyl ring is rate determining.59 We investigated AO in aqueous solution and found D(t) to be best modelled by C(t), while macroscopic viscosity was less successful. The connection between these two parameters has been detailed by Hynes and co-workers:45,51
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 66). The switch in AO dynamics between control of D(t) by viscosity in low temperature alcohols to C(t) in fluid polar media has been discussed elsewhere in terms of the nature of the reaction coordinate in media with very different dynamics.66
66). The switch in AO dynamics between control of D(t) by viscosity in low temperature alcohols to C(t) in fluid polar media has been discussed elsewhere in terms of the nature of the reaction coordinate in media with very different dynamics.66
Of course there is still a significant level of curve fitting in the procedure described, and there is clearly a need for more rigorous descriptions of excited state reaction dynamics. The model reaction coordinate obtained from coupling two harmonic surfaces would be better replaced with one obtained from high level quantum chemical calculations (although such calculations remain challenging for large molecules and complex reaction coordinates). Determining population evolution on such surfaces probably requires use of the GLE rather than the GSE. The interpretation of the friction recovered from the analysis, typically based on bulk viscosity measurements or empirical solvation dynamics data, could be better represented by molecular dynamics calculation. Clearly, progress in this area depends critically on developments in computational chemistry to simulate complex media.
4. Dynamics in confined liquids
Dynamics in nanoconfined liquids is a large and diverse topic, ranging across fundamental physics to materials and biology.68–71 Here we focus on those particular measurements of bulk liquid dynamics which inform the modelling of excited state reactions in confined media (with a particular focus on aqueous nanodroplets confined in inverse micelles) and specifically those measurements which either directly or indirectly yield the ultrafast C(t) required to model excited state reactions, as described in Section 3. These methods include the ultrafast optical Kerr effect (OKE),72–75 ultrafast transient infrared (TRIR) and 2D IR spectroscopies76,77 and solvation dynamics through time resolved fluorescence measurements of S(t).3,78–80 More detailed reviews were presented by Levinger81 and Maroncelli and Castner.82 Clearly, only the latter experiment exploits the tool of fluorescence up-conversion. The importance of the others is that they add an independent assessment of the effect of confinement on the dynamics of a confined medium, which is independent of the presence of the reactive molecule. The role of medium friction in determining reactive dynamics was developed in the preceding section, so these data act as important input when modelling the up-conversion results. Further, differences between confined media dynamics determined ‘probe free’ (OKE and 2DIR) and with a probe (time resolved fluorescence) reveal a role for the specific site occupied by the probe.Ultrafast OKE measures the relaxation of transient polarizability anisotropy induced in a fluid by a linearly polarised pump pulse. The induced anisotropy is measured through its effect on the polarisation of a transmitted time delayed probe pulse. The method has been widely applied to record the fastest dynamics of a very broad range of molecular liquids. In the context of these bulk measurements the OKE has been extensively reviewed.74,75,83 A key feature is that it reveals liquid dynamics with high time resolution and excellent signal-to-noise. It is straightforward to convert between the measured polarizability correlation function and C(t).82,84
Since the OKE measures relaxation in the macroscopic sample, its extension to probe nanoconfined liquids requires sufficient contrast between the signal from the confined liquid of interest and that of the confining medium. Effectively this requires a confined liquid comprising molecules with large polarizability anisotropy. Fourkas and co-workers pioneered the study of liquids confined within the nanoscale pores of sol–gel glasses.85–89 They found that the effect of confinement was always to slow the liquid dynamics, but the mechanism of slowing down depended on the details of the interactions at the interface, and the nature of the liquid. Furthermore, they extended their method to specifically investigate relaxation dynamics of nanoconfined water,88 as also studied by others.90,91 The dynamics of liquids in sol–gel glasses was reviewed by Fourkas.87 It would be interesting to study directly molecules with reactive excited states solubilised within liquids in the silica nanopores – there are some papers on the theory and observation of proton transfer reaction in such media.92,93 The OKE method itself has also been applied to the study of micellar solutions where molecular liquids with sufficiently large polarizability anisotropies were solubilised within regular micelles in an aqueous continuous phase.73,94,95 The effect of confinement was again to slow orientational relaxation. For solubilised CS2, which has particularly good contrast, the relaxation dynamics were intermediate between neat liquid CS2 and CS2 dispersed in long chain alkanes.95
A number groups applied ultrafast IR methods to investigate dynamics of water nanodroplets confined in inverse micelles. The steady state IR spectra of water in the charged inverse micelle Aerosol OT (AOT) is already instructive in suggesting multiple environments, and revealing size effects. These early observations were discussed in terms of a core–shell model in which an interface bound population and a bulk like population are in equilibrium.96 The strong IR absorption of the water OH vibrational mode provides a suitable probe, but the complexity associated with multiple types of H-bonding and intermolecular vibrational energy transfer makes interpretation challenging. The problem can be simplified by studying HOD dissolved in H2O, where the isolated OD resonance provides a more localised probe of the H-bond dynamics.
IR pump–probe spectroscopy measures the population and orientational relaxation of excited vibrational states. The vibrational lifetime for OD in water was reported to be extended upon confinement in AOT micelles, and was a function of size of the water pool.97–99 The observed relaxation is inhomogeneous, with relaxation being slower in the charged interfacial region. It is however challenging to relate the vibrational lifetime of the OH/D oscillator to the properties of the confined phase which might then affect the dynamics of a chemical reaction.
A more useful probe of the medium is the orientational relaxation time of the isolated OD oscillator, which can be measured by polarization resolved IR pump–probe spectroscopy. These anisotropy measurements are restricted to probing relaxation on the same timescale as the vibrational population lifetime, which is a limitation when orientational relaxation is slow. Such measurements were undertaken for reverse micellar media by Doktor et al. They studied the two distinct populations (bulk and interface) which could be resolved by their different vibrational frequencies. Orientational relaxation in the interface was slower than for water in the core of the micelle, which was measured to be quite similar to that of bulk water.99,100
A more detailed picture of dynamics in the confined water phase of inverse micelles can be obtained from IR photon echo and two-dimensional IR (2DIR) spectroscopy. For example, Piletic et al. probed vibrational and orientational relaxation and spectral diffusion (the time dependent broadening of the IR linewidth as it samples its possible inhomogeneous distribution of frequencies) in water confined in AOT.101 They found that the observed spectra and vibrational lifetime were well reproduced by a core–shell model, with a 0.4 nm width shell and bulk like core. Cringus et al. showed that the two populations can have different dynamics as they also do not exchange energy by energy transfer (which might otherwise blur the distinction).102 Interestingly the spectral diffusion and orientational relaxation were less well reproduced by a core shell model than were the vibrational spectra and lifetimes, suggesting a more complex picture. Fayer and co-workers found that changing from ionic AOT to an uncharged confining interface (e.g. aqueous nanodroplets in inverse micelles comprised of the Igepal surfactant) modified the local interactions, which changed the spectra and vibrational lifetimes, while the orientational relaxation rather reflected more global relaxation associated with the H-bonding network.103–106 Thus, for this observable, the geometry of the interface is more significant than its nature (ionic or neutral). The topic has been extensively reviewed.107
Hochstrasser and co-workers extended these IR measurements to probe the relaxation dynamics of a solute ion, tricyanomethanide, in the dispersed aqueous phase of AOT reverse micelles by 2DIR. The advantage of extrinsic probes is that they are not limited by the short lifetime of the OD oscillator. IR spectra suggest that the ion occupies two slowly interconverting sites, interface and core. The interfacial dynamics were seen to be size independent, while vibrational lifetime and spectral diffusion in the core were both dependent on micelle radius. The data were modelled by an extended core–shell model which accounted for the radius dependent heterogeneous dynamics of the core phase.108 Sando et al. studied the vibrational lifetime and orientational relaxation of the azide ion in a series of ionic and neutral reverse micelles.109 They were able to correlate azide dynamics with interfacial charge, consistent with a core–shell model, and orientational relaxation was more affected by confinement than vibrational relaxation. Yuan et al. applied IR pump probe measurements to vibrational and orientational dynamics of the SCN− ion, finding core shell behaviour, with the ion either in the bulk phase or in a shell which is transitional between interface and bulk.110 The IR probe SCN− was also studied in AOT reverse micelles by IR pump–probe spectroscopy, as a function of the headgroup counterion.111 Orientational relaxation was slowest for Ca2+ and fastest for Cs+.
Measurements of spectral diffusion by 2DIR can be related to the solvation time correlation function, C(t), required for modelling dynamics on a reactive PES (Section 3). However, the most direct route to C(t) is through TRES measurements of solvation dynamics, as described above. The topic has a long history. Early measurements on confined media were pioneered by Bhattacharyya and co-workers, who reported significant slowing of solvation dynamics in a wide variety of confining media for a range of solute molecules.112,113 The earliest measurements did not have the time resolution to reach the subpicosecond time range required to characterise the bulk water C(t). Levinger was the first to present a systematic study of solvation dynamics in confined media with sub-picosecond time resolution.114,115 They focused on studies using the best characterised fluorescence probe family, the Coumarin dyes,116,117 which were shown by Maroncelli and co-workers to be quite resistant to perturbation by specific solvent–solute interactions, and thus most likely to report accurately on the medium probed.24,32,118 Coumarin 343 was often the probe chosen, as it exists as an anion at reduced pH so is well solvated in the aqueous phase. Both Bhattacharyya and Levinger have provided detailed reviews on this topic.81,119–122 Below the focus is on those results for ultrafast S(t) measurements which overlap with the reaction timescales investigated for AO in micelles.
Riter et al. made a detailed study of S(t) in Na+AOT reverse micelles as a function of the radius of the water phase.115 For very small micelles the S(t) did not reveal any time dependence. As the radius increased, strongly nonexponential solvation dynamics were observed. A sub-picosecond component grew in, indicative of bulk like dynamics, which is consistent with the core–shell modelling of the IR data mentioned above. In addition, both picosecond and much slower dynamics were observed. These inhomogeneous dynamics may indicate both an intrinsic range of relaxation times in the aqueous phase, but may also arise from a distribution of sites where the fluorophore may locate. The very long relaxation times seemed too long to be assigned to relaxation in water, and it was proposed that these reflected a solvation response in the headgroup/double-layer region. Strong evidence for the role of the interface in determining at least some components of S(t) was obtained from changing the headgroup. For example, Na+AOT micelles stabilizing small water droplets showed negligible time dependence, while K+AOT showed significant differences.123 This suggests that the counterions play a significant role in modifying solvation dynamics, at least for probes solvated in the headgroup region. Thus, for S(t) in reverse micelles both the fact of confinement and the nature of the interface play a role in determining relaxation dynamics. Levinger extended these studies to a wide range of inverse micelles.122,124
Molecular dynamics (MD) simulations of the water phase of inverse micelles have been reported. Faeder and Ladanyi identified three characteristic relaxation timescales, associated with trapped water, interface bound water and bulk like water.125–129 These results are broadly consistent with the core–shell model, though provide more detail. The counterion effect was studied, and shown to be significant. In particular, the large effect of exchange of Na+ for K+ in AOT reverse micelles observed experimentally in solvation dynamics was reproduced, with simulations showing that the K+ ion both displaced water from the interface, and immobilized fewer molecules than Na+.127,130 Further structural details were extracted from MD simulations; Berkowitz and co-workers also reproduced the observed counterion effects and showed that formation of water bridges between ions contributed to slowing dynamics in the confined phase.131–134 The topic was reviewed by Thompson.93
5. Confined reaction dynamics AO in inverse micelles
We now have a means of observing reaction dynamics in real time through fluorescence up-conversion, an efficient (though approximate) approach to modelling them through the GSE, and a method for representing the medium dynamics D(t) through the measured solvation time correlation function, C(t). Here we discuss our work and that of others who have brought these together to probe reactions in confined media, initially focusing on inverse micelles. As a suitable reaction in the excited state structural dynamics of AO (Fig. 4a) was selected. AO is suitable because this diphenylmethane dye is ionic, so it will preferentially localise in the aqueous phase of the inverse micelles. Other classical excited state reactions, such as the isomerization of stilbene and azobenzene would not enter the confined medium. Further, the excited state reaction of AO has been very well characterised in solution. The reaction coordinate is an ultrafast friction dependent phenyl ring torsion, which is coupled to a change in electronic structure, such that the population evolution, ρ(z,t), is from a bright state to a dark state (as modelled by transition dipole moment, M(z)).59,61,64 The PES associated with this structural evolution has been represented by a model, Ω(z), where the energies of the ground and coupled excited states are selected to fit the experimental steady state spectra. We note that there are a number of indications that specific solvent solute interactions may modify the energetics, and even mechanism, of reaction in the AO excited state. For example, it is proposed that in some circumstances the ring torsion may be accompanied by changes in the orientation of the dimethylamino group (although recent calculations favour ring torsion as the major pathway).135–138 Because of these complications it is best to compare AO dynamics measured in similar media. For consistency and to avoid effects associated with the specific probe we will focus on AO in this section. In Section 6 other fluorescent reactive probes of confinement will be reviewed.The second choice required for measurements is the model confining medium. Here we focus on inverse micelles, in particular those comprising the surfactants AOT and Igepal. Dispersed in a nonpolar continuous phase these inverse micelles stabilize nanoscale droplets of aqueous solutions. AOT is an ionic surfactant for which the size of the aqueous nanodroplet can be varied from ca 1 nm up to tens of nanometres, by controlling the molar ratio of water to AOT, w:139,140
| rw ∼ 0.18w. |
Importantly AOT allows a degree of experimental control over the interface, at least in the sense that the counterion can be exchanged. The second surfactant, Igepal, is a non-ionic surfactant, in which the size of the aqueous droplet can be modified according to141
| rw ∼ 0.19w + 0.7, |
A detailed study of the rw dependence of the photophyscis of AO in Na+AOT was presented for rw in the range 1–10 nm. The data were compared with AOT in bulk aqueous solution, and in the viscous moderately polar solvent decanol.142–145 The absorption and emission spectra for solvents and micelles were overall similar in all media, although the dependence of the peak wavelength scanned between decanol and aqueous environments, suggesting some evolution in medium-AOT interaction. The fluorescence decays were ultrafast and wavelength dependent, as expected for AO (Fig. 6a). The lifetime measured at the peak wavelength was taken as representative of an average AO fluorescence decay rate, and was seen to increase by about a factor of ca 5 as rw decreased from 10 to 1 nm. Significantly, even for the largest rw the average decay time was always greater than for bulk water, though also markedly faster than for decanol (Fig. 6b).
From these data it is apparent that, although the rw dependence is significant, a simple core–shell analysis is not appropriate, as for even the largest micelle the AO lifetime is much longer than the bulk water value, which would be approached for AO in the core of larger micelles. This indicates that the distribution of the cationic AO dye is not statistical in the nanodroplet. The data could be interpreted as indicating that on average the ‘microviscosity’ of the dispersed nanodroplet is increased compared to bulk water and increases further with decreasing rw. However, that result is also not clear-cut. For example, the decay time of AO in ethanol is longer than in water solvent, although they have a similar viscosity.66,145 This suggests some unique role for water in controlling the AO excited state dynamics.
The GSE analysis was attempted for AO in AOT. As noted above and detailed elsewhere, it was established that for room temperature water and decanol solvents the best fit to the TRES was recovered when a time dependent diffusion coefficient was used.142 The data in Na+AOT also could not be represented by a time independent D. The fit was improved by employing the C(t) recovered from Levinger's study of solvation dynamics in micelles, but was not quantitative. Using a biexponential D(t) as a fitting parameter gave an accurate fit to the data (Fig. 6c and d). By comparing the best fit result with the D(t) predicted from C(t) recovered from solvation dynamics, showed that the slowest components of C(t) appeared to play a less significant role in controlling AO reaction dynamics.142,146 This was interpreted as reflecting the different physical origins of the approximately biphasic C(t), where the faster components come from impulsive relaxation related to librational motions in the bulk liquid, while the slower response reflects diffusive solvent reorientation. Thus one possible explanation for the difference is that the former played a more significant role in controlling the reactive dynamics of AO. While it is possible to speculate how different contributions to C(t) might influence the reactive dynamics of AO, measurements outlined below point to a water specific relaxation pathway. This would not necessarily be represented in the C(t) measurements, since it reflects the AO-water interaction.
The up-conversion measurements were extended to AOT with a variety of counterions, thus modifying the charge or charge density in the interfacial region (Fig. 7). When Na+ was exchanged for K+ the effect on the AO reaction dynamics was negligible.142,146 This further highlights the difference between the C(t) measurements (where the effect was large123) and the D(t) which drives the AO reaction. When the counterion was changed to Ca2+ a further suppression of the AO reaction rate was observed, but again the effect was slight compared to what was seen for C(t). Thus the suppression of the AO reaction in AOT (relative to bulk aqueous solution) is not highly sensitive to the charge of the interface. Evidently the solvation and reaction dynamics of ionic chromophores in AOT inverse micelles are not directly related, at least in the case of the AO reaction. Again, it is possible that only a subset of the dynamics contributing to C(t) are effective in controlling the reactive dynamics. For example, for all samples an ultrafast (sub 100 fs) component is present in the measured C(t), independent of counterion. However, this seems too fast to be rate controlling for the picosecond AO reaction in AOT. This weak counterion dependence is surprising, given that the rw dependent data indicate that AO never has the ultrafast dynamics associated with the bulk aqueous phase, so presumably favours an interface site.
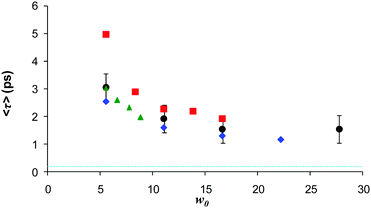 | ||
| Fig. 7 Dependence of the mean decay time for different counterions for AO in AOT, as a function of w. Black Na+, blue K+, Green NH4+ and red Ca2+. Dash blue indicates bulk water lifetime. | ||
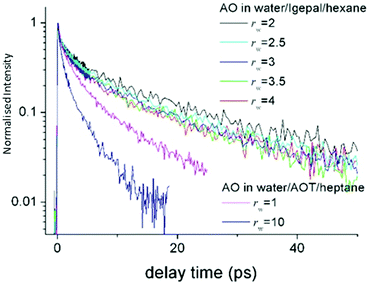 | ||
| Fig. 8 Time resolved fluorescence of AO in Igepal reverse micelles as a function rw, compared to the data in AOT. The AO reaction is suppressed in Igepal compared to any size of AOT micelle. | ||
The same AO reaction was studied in the aqueous nanodroplet stabilized in the non-ionic surfactant Igepal, in which the ionic headgroup has been replaced with an oxyethylene chain.147 Again the AO reaction was studied as a function of rw, between 2 and 4 nm. The reaction dynamics observed were nearly independent of rw, and significantly slower than in even the smallest AOT stabilised aqueous nanodroplet (Fig. 8). That the dynamics are slowed down in the nonionic surfactant is consistent with the observations from transient IR experiments. However, the weak dependence on rw again shows that a statistical distribution over a water like core and an interfacial shell cannot reproduce the AO up-conversion data. It is likely that the AO is localised at the interface, independent of rw. The long lifetime gives rise to the question as to whether the reactive AO is in fact localised in the oxyethylene headgroup. However, spectroscopic measurements in the micelle compared to water/polyethylene glycol mixtures, show that the AO occupies a water like phase. Evidently, the AO reactive dynamics in the aqueous non-ionic surfactant interface location are markedly suppressed compared even to AOT, and dramatically so compared to bulk water.
A further study of the role of the interface in controlling AO reaction dynamics was conducted using the regular micelle, sodium dodecyl sulfate (SDS) which has the same ionic headgroup as AOT.66 Thus, the reactive AO will be located at the ionic interface, but with the opposite curvature to AOT. In this case the excited state dynamics at the SDS interface were found to be slower than in bulk water but faster than in even the largest AOT micelle. These data are significant because they point to the properties of the interface rather than the size of the nanoconfined aqueous phase or the interfacial charge being the controlling influence on the reaction dynamics. Because all of the spectroscopic data point to the AO being located in the aqueous phase for all of the confined systems studied, then the further conclusion can be drawn that the structure of the aqueous phase at the interface is the key controlling element. This therefore suggests a unique role for interfacial water in determining the AO reaction dynamics. Measurements in bulk solvents support this conclusion. The excited state reaction of AO in water is anomalously fast, compared to what is expected from the viscosity, and is quite well modelled by solvation dynamics data.66 In contrast the reaction dynamics for AO in alcohols at reduced temperature are well reproduced by bulk viscosity effects.59 This is consistent with H-bond dynamics in aqueous solution controlling the AO reaction, while in other solvents hydrodynamic friction plays a more important role.
Thus, from the accumulated evidence in a variety of micelle media, the excited state reaction of AO appears to reflect the structure and dynamics of water at the interface of the confining medium, rather than the properties of the entire confined phase (which in the absence of a solute appears to be well reproduced by the core shell model). There is evidence from simulations that the dynamics of the interfacial water varies considerably for different confining interfaces. However, it is not sufficient to consider water interface dynamics separate from the role of the AO solute. For example, the data for different counterions (e.g. the exchange of Na+ for K+) show only a small effect on AO dynamics, while they are known to have a significant effect on interfacial structure and dynamics. Thus, the effect of the reactive probe itself on interface dynamics in the aqueous shell must also be considered.
6. Other excited state reactions in micelles
A plausible alternative to AO as a probe of confinement effects on reaction dynamics would be Thioflavin T. Its ultrafast fluorescence was characterised by Huppert in detail, in a range of solvents and analysed with the GSE approach (Section 3).56,137,148,149 This dye also has a radiationless decay pathway involving phenyl torsion, which gives rise to a degree of internal charge transfer.56,149 It is thus quite similar to AO and has was accurately modelled using the GSE approach. In an early study of confinement effects Singh et al. investigated Thioflavin T in inverse micelles.150 The findings are broadly similar to the AO data, with a significant suppression of the excited state reaction in the smaller micelles, although the bulk water value is not recovered, even for the largest rw.150 The Thioflavin T measurements were extended to the non-ionic inverse micelle Triton X-100.151 Similarly to the Igepal case described above the lifetime was greatly enhanced compared to bulk water, but was only a weak function of rw. Thioflavin T was also studied at the interface of the regular micelle SDS.152 The decay was non-single-exponential and suppressed up to eight times compared to free solution. Chatterjee et al.153 studied thioflavin T in a series of nonaqueous inverse micelles, and again found a longer excited state decay time in the smaller micelles.Other probes of reactions in micelles have been investigated. Rafiq et al. studied the ultrafast fluorescence decay of the triphenyl methane dye malachite green in AOT reverse micelles.154 The coordinate is again a phenyl torsion, as for AO, and the results are qualitatively similar, in that the rw dependence revealed a faster reaction in larger micelles, but the effect was modest, and never reached the bulk limit. Hsu et al. studied the dye stilbene 3 (a pair of linked stilbenes) in AOT and CTAB micelles.155 They also observed a decreasing conformational relaxation in the excited state with decreasing rw, although at w < 2 they observed a sudden shortening of the relaxation time. Lee et al. studied the fluorescence decay reflecting charge transfer state formation in 4-dimethylamino-4′-nitrobiphenyl in AOT, and again observed a slower excited state decay in the smaller micelles.156
These approaches have been extended to the study of reaction dynamics in the cavities of supramolecular complexes. Kondo et al. studied the reaction of AO in a series of cyclodextrin nanocavities. The effect was size dependent, with only β-cyclodextrin providing a significant slowing of the reaction compared to aqueous solution.157 In contrast Singh et al. studied AO absorbed in a chemically modified cyclodextrin cavity and found an enhancement of fluorescence relative to β-cyclodextrin.158 This suggests that the details of the interaction of the dye with the cavity are important in determining the effect on the reaction rate. The same group investigated the torsional dynamics of the related dye, thioflavin T, in the modified cyclodextrin cage, and again reported a significant suppression of the reaction leading to radiationless decay.159 The classical cis–trans isomerization of azobenzene incorporated into the hydrophobic cavity of another supramolecular complex was observed.160 The rate of the excited state reaction was again slowed down, and the photochemical yields modified by the confinement.
There are other important examples of excited state reactions in confined media. Some of these are covered in other reviews70,161,162 and elsewhere in this special issue. Examples closest to the spirit of this review are the excited state isomerization reactions of stilbene and azobenzene dyes, which have been the topic of very detailed study in the solution phase for over fifty years. These have not been much studied in reverse micelles because of the solubility problem, so fall somewhat outside our remit, but their reactions have been studied in a variety of other confining media. One of the most interesting effects found in strongly spatially confining media, such as cyclodextrin cages, is that the nature of the reaction coordinate can be modified by confinement. For example a family of methoxynaphthalenes incorporated in cyclodextrins undergoes a volume conserving isomerization reaction which is not observed in free solution.163,164 This effect thus offers a degree of control over the structure of the photoproduct. Such volume conserving pathways (such as “crankshaft motion” and “hula twist”) which contrast with the solvent displacing “one-bond flip” rotation about a single bond, had earlier been shown to be important for isomerization reactions in glassy media, but are generally thought to proceed over higher activation barriers barriers.165 Similar effects have been reported for cage-confined azobenzenes, where quite small changes in molecular structure can modify the isomerization coordinate, indicating strong coupling with the confining medium.166 In such cases confinement is not simply modifying the rate of the reaction, as for AO and Thioflavin T, but also its mechanism.
Very recently there have been some time resolved transient absorption studies in strongly confining media by Otolski et al.160,167,168 For a series of encapsulated azobenzene and stilbene derivatives they observed both significant lengthening of excited state lifetimes and the opening up of new isomerization pathways. It was suggested that spatial confinement modifies the topology of the conical intersection with the ground electronic states, thus excited state lifetime and the photoproduct yield. These effects were found to be quite dependent on the precise molecular structure of the stilbene derivative.160 Variation of the confining medium in such systems will provide important information on its coupling to the reaction coordinate.
A second class of reaction that has a rather different reaction coordinate, but which has been quite extensively studied in AOT reverse micelles, is excited state proton transfer (ESPT). In early work, an ionic 2-naphthol probe was studied. In the largest micelles the bulk ESPT rate was recovered, while in smaller micelles the reaction was suppressed.169 The result indicated increased friction in the interface. The ESPT reaction of 7-hydroxyquinolone was studied in AOT. For w < 5 the ESPT was suppressed, which was assigned to a size dependence of the H-bond network dynamics in the aqueous phase. The reaction is faster in the larger micelles, but never reaches the bulk water ESPT rate, even for large micelles.170 Sedgwick et al. measured the prototypical ESPT molecule 8-hydroxypyrene trisulfonate in AOT and CTAB reverse micelles using TA and NMR. In w = 10 AOT the ESPT dynamics approach the bulk (smaller micelles were not studied) while in CTAB no ESPT was observed. Data were consistent with the trisulfonate burying itself in the CTAB water interface.171 Khorwal and Sen studied a benzimidazole intramolecular ESPT (ESIPT) in different inverse micelles and found the confing medium influenced the dynamics.172 Basu et al. studied ESIPT for 3-hydroxyflavone (3HF) in AOT reverse micelles. The reaction was suppressed in very small micelles (w = 0) which was suggested to be due to complex formation with the headgroup. As water was introduced the ESPT rate increased markedly, which was proposed to be due to the intermolecular route becoming accessible as the water solvates the headgroup, and displaces the 3HF.173 In a later paper Ghosh et al.174 studied ESIPT in a dimethylamino 3HF, which showed broadly similar behaviour. Some of these aspects were covered in a recent review of supramolecular photochemistry.175
7. Summary
Methods suitable for the rather detailed study of ultrafast reaction dynamics in confined media have been described. Ultrafast time resolved emission spectroscopy provides a convenient route to observing excited state reaction dynamics. It combines excellent time resolution with the ability to record temporal evolution on the reactive PES. Although the focus above was on the reactions of AO, a number of other viable candidates for reactive probes were mentioned. A simple model was outlined which relates reaction dynamics to the effects of the medium on the one hand and to the experimental TRES data on the other. This simple model is based on the GSE, although more accurate (albeit more difficult to use) approaches were noted. Although there are a number of fitting parameters in the model, the main output is the D(t) recovered from the fit. This can be contrasted with either experimental studies of the confined medium (obtained from independent 2DIR, OKE or S(t) measurements) or with MD simulations.In studies of AO confined in inverse micelles, the qualitative effects of confinement on ultrafast reactions were clear. Confinement slows the reaction in all cases studied, and the effect is larger for smaller micelles. In no case was a bulk like relaxation recovered, even in the largest micelles studied. This shows that the core shell model, which successfully describes much of the steady state and transient IR data, is not a good model for reactive dynamics. Evidently, all of the reactive probes studied to date preferentially locate in the interfacial region. Further, there was no one-to-one correspondence between the C(t) recovered from S(t) measurements and that recovered from the GSE analysis, even though both measurements used charged dye molecules which presumably have similar locations. Inevitably, the most interesting confined medium is the aqueous solution, because of its relevance to life sciences. However, there was evidence at least for AO that there is a water specific reaction channel, which will not be reflected in the S(t) data from non-reactive fluorescent probes. These local effects make it difficult for MD simulations for example to reproduce the observed data. To achieve a detailed microscopic picture of the effect of confinement it would be helpful to design reactive molecules (or a series of them) in which the site in the confining medium could be controlled. One approach to this would be site-specific studies of fluorescent probes incorporated into proteins by means of noncanonical amino acid substitution.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The authors are grateful to EPSRC for financial support (EP/E010466/1) and to Dr Minako Kondo for her work on the project.References
- J. T. Hynes, Annu. Rev. Phys. Chem., 1985, 36, 573–597 CrossRef CAS.
- G. R. Fleming and M. H. Cho, Annu. Rev. Phys. Chem., 1996, 47, 109–134 CrossRef CAS.
- W. P. de Boeij, M. S. Pshenichnikov and D. A. Wiersma, Annu. Rev. Phys. Chem., 1998, 49, 99–123 CrossRef CAS PubMed.
- I. Conti, G. Cerullo, A. Nenov and M. Garavelli, J. Am. Chem. Soc., 2020, 142, 16117–16139 CrossRef CAS PubMed.
- T. Kumpulainen, B. Lang, A. Rosspeintner and E. Vauthey, Chem. Rev., 2017, 117, 10826–10939 CrossRef CAS PubMed.
- A. Rosspeintner, B. Lang and E. Vauthey, in Annual Review of Physical Chemistry, ed. M. A. Johnson and T. J. Martinez, 2013, vol. 64, pp. 247–271 Search PubMed.
- M. Maiuri, M. Garavelli and G. Cerullo, J. Am. Chem. Soc., 2020, 142, 3–15 CrossRef CAS.
- H. Lemmetyinen, N. V. Tkachenko, B. Valeur, J. Hotta, M. Ameloot, N. P. Ernsting, T. Gustavsson and N. Boens, Pure Appl. Chem., 2014, 86, 1969–1998 CAS.
- J. Lee, C. H. Kim and T. Joo, J. Phys. Chem. A, 2013, 117, 1400–1405 CrossRef CAS.
- V. Sundstrom, Annu. Rev. Phys. Chem., 2008, 59, 53–77 CrossRef.
- D. C. Todd, J. M. Jean, S. J. Rosenthal, A. J. Ruggiero, D. Yang and G. R. Fleming, J. Chem. Phys., 1990, 93, 8658–8668 CrossRef CAS.
- A. Morandeira, L. Engeli and E. Vauthey, J. Phys. Chem. A, 2002, 106, 4833–4837 CrossRef CAS.
- I. V. Rubtsov and K. Yoshihara, J. Phys. Chem. A, 1999, 103, 10202–10212 CrossRef CAS.
- C. Ruckebusch, M. Sliwa, P. Pernot, A. de Juan and R. Tauler, J. Photochem. Photobiol., C, 2012, 13, 1–27 CrossRef CAS.
- U. Megerle, I. Pugliesi, C. Schriever, C. F. Sailer and E. Riedle, Appl. Phys. B: Lasers Opt., 2009, 96, 215–231 CrossRef CAS.
- J. Lakowitz, Principles of Fluorescence Spectroscopy, Springer, 2006 Search PubMed.
- J. Shah, IEEE J. Quantum Electron., 1988, 24, 276–288 CrossRef.
- H. Mahr and M. D. Hirsch, Opt. Commun., 1975, 13, 96–99 CrossRef.
- D. V. O'Connor, W. R. Ware and J. C. Andre, J. Phys. Chem., 1979, 83, 1333–1343 CrossRef.
- J. C. Diels and W. Rudolpf, Ultrashort Laser Pulse Phenomena, 2006 Search PubMed.
- H. Rhee and T. Joo, Opt. Lett., 2005, 30, 96–98 CrossRef.
- C. H. Kim and T. Joo, Opt. Express, 2008, 16, 20742–20747 CrossRef CAS PubMed.
- S. R. Meech, D. V. Oconnor, A. J. Roberts and D. Phillips, Photochem. Photobiol., 1981, 33, 159–172 CrossRef CAS.
- M. Maroncelli and G. R. Fleming, J. Chem. Phys., 1987, 86, 6221–6239 CrossRef CAS.
- A. S. R. Koti, M. M. G. Krishna and N. Periasamy, J. Phys. Chem. A, 2001, 105, 1767–1771 CrossRef CAS.
- S. Haacke, R. A. Taylor, I. Bar-Joseph, M. Brasil, M. Hartig and B. Deveaud, J. Opt. Soc. Am. B, 1998, 15, 1410–1417 CrossRef CAS.
- L. J. Zhao, J. L. P. Lustres, V. Farztdinov and N. P. Ernsting, Phys. Chem. Chem. Phys., 2005, 7, 1716–1725 RSC.
- M. Sajadi, M. Quick and N. P. Ernsting, Appl. Phys. Lett., 2013, 103, 173514 CrossRef.
- G. Lee, J. Kim, S. Y. Kim, D. E. Kim and T. Joo, Chem. Phys. Chem., 2017, 18, 670–676 CrossRef CAS PubMed.
- J. Conyard, K. Addison, I. A. Heisler, A. Cnossen, W. R. Browne, B. L. Feringa and S. R. Meech, Nat. Chem., 2012, 4, 547–551 CrossRef CAS.
- P. Suppan, J. Photochem. Photobiol., A, 1990, 50, 293–330 CrossRef CAS.
- M. L. Horng, J. A. Gardecki, A. Papazyan and M. Maroncelli, J. Phys. Chem., 1995, 99, 17311–17337 CrossRef CAS.
- B. M. Ladanyi and M. Maroncelli, J. Chem. Phys., 1998, 109, 3204–3221 CrossRef CAS.
- E. W. Castner and M. Maroncelli, J. Mol. Liq., 1998, 77, 1–36 CrossRef CAS.
- K. Kwak, S. Park, I. J. Finkelstein and M. D. Fayer, J. Chem. Phys., 2007, 127, 124503 CrossRef PubMed.
- F. Šanda, V. Perlík, C. N. Lincoln and J. Hauer, J. Phys. Chem. A, 2015, 119, 10893–10909 CrossRef.
- M. Cho and G. R. Fleming, J. Phys. Chem. B, 2020, 124, 11222–11235 CrossRef CAS.
- Z. A. Piskulich, D. Laage and W. H. Thompson, J. Chem. Phys., 2021, 154, 064501 CrossRef CAS PubMed.
- W. P. de Boeij, M. S. Pshenichnikov and D. A. Wiersma, Annu. Rev. Phys. Chem., 1998, 49, 99–123 CrossRef CAS PubMed.
- R. A. Nome, J. Braz. Chem. Soc., 2010, 21, 2189–2204 CrossRef CAS.
- K. P. Ghiggino, A. G. Lee, S. R. Meech, D. V. O'Connor and D. Phillips, Biochemistry, 1981, 20, 5381–5389 CrossRef CAS.
- I. Nikić and E. A. Lemke, Curr. Opin. Chem. Biol., 2015, 28, 164–173 CrossRef PubMed.
- D. Summerer, S. Chen, N. Wu, A. Deiters, J. W. Chin and P. G. Schultz, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 9785–9789 CrossRef CAS.
- G. R. Haynes, G. A. Voth and E. Pollak, J. Chem. Phys., 1994, 101, 7811–7822 CrossRef CAS.
- G. van der zwan and J. T. Hynes, J. Chem. Phys., 1982, 76, 2993–3001 CrossRef CAS.
- J. T. Hynes, J. Phys. Chem., 1986, 90, 3701–3706 CrossRef CAS.
- T. Fonseca, J. Chem. Phys., 1989, 91, 2869–2880 CrossRef CAS.
- R. F. Grote and J. T. Hynes, J. Chem. Phys., 1980, 73, 2715–2732 CrossRef CAS.
- A. Dubey and M. Bandyopadhyay, Phys. A, 2020, 549, 124343 CrossRef.
- S. Okuyama and D. W. Oxtoby, J. Chem. Phys., 1986, 84, 5824–5829 CrossRef CAS.
- R. F. Grote, G. van der Zwan and J. T. Hynes, J. Phys. Chem., 1984, 88, 4676–4684 CrossRef CAS.
- T. J. Kang, W. Jarzeba, P. F. Barbara and T. Fonseca, Chem. Phys., 1990, 149, 81–95 CrossRef CAS.
- K. Tominaga, G. C. Walker, T. J. Kang, P. F. Barbara and T. Fonseca, J. Phys. Chem., 1991, 95, 10485–10492 CrossRef CAS.
- B. Bagchi, G. R. Fleming and D. W. Oxtoby, J. Chem. Phys., 1983, 78, 7375–7385 CrossRef CAS.
- K. Tominaga, G. C. Walker, W. Jarzeba and P. F. Barbara, J. Phys. Chem., 1991, 95, 10475–10485 CrossRef CAS.
- Y. Erez, Y. H. Liu, N. Amdursky and D. Huppert, J. Phys. Chem. A, 2011, 115, 8479–8487 CrossRef CAS.
- K. Addison, I. A. Heisler, J. Conyard, T. Dixon, P. C. B. Page and S. R. Meech, Faraday Discuss., 2013, 163, 277–296 RSC.
- M. Glasbeek, H. Zhang and M. J. van der Meer, J. Mol. Liq., 2000, 86, 123–126 CrossRef CAS.
- M. J. van der Meer, H. Zhang and M. Glasbeek, J. Chem. Phys., 2000, 112, 2878–2887 CrossRef CAS.
- G. Angulo, J. Jedrak, A. Ochab-Marcinek, P. Pasitsuparoad, C. Radzewicz, P. Wnuk and A. Rosspeintner, J. Chem. Phys., 2017, 146, 244505 CrossRef PubMed.
- P. Changenet, H. Zhang, M. J. van der Meer, M. Glasbeek, P. Plaza and M. M. Martin, J. Phys. Chem. A, 1998, 102, 6716–6721 CrossRef CAS.
- P. Changenet, H. Zhang, M. J. van der Meer, M. Glasbeek, P. Plaza and M. M. Martin, J. Fluoresc., 2000, 10, 155–160 CrossRef CAS.
- C. Khurmi and M. A. Berg, J. Phys. Chem. Lett., 2010, 1, 161–164 CrossRef CAS.
- G. Oster and Y. Nishijima, J. Am. Chem. Soc., 1956, 78, 1581–1584 CrossRef CAS.
- Y. Erez, Y. H. Liu, N. Amdursky and D. Huppert, J. Phys. Chem. A, 2011, 115, 8479–8487 CrossRef CAS.
- M. Kondo, I. A. Heisler and S. R. Meech, J. Phys. Chem. B, 2010, 114, 12859–12865 CrossRef CAS PubMed.
- R. Jimenez, G. R. Fleming, P. V. Kumar and M. Maroncelli, Nature, 1994, 369, 471–473 CrossRef CAS.
- W. H. Thompson, J. Chem. Phys., 2018, 149, 170901 CrossRef PubMed.
- D. Muñoz-Santiburcio and D. Marx, Chem. Sci., 2017, 8, 3444–3452 RSC.
- N. Alarcos, B. Cohen, M. Ziółek and A. Douhal, Chem. Rev., 2017, 117, 13639–13720 CrossRef CAS.
- B. Maiti, A. Abramov, R. Pérez-Ruiz and D. Díaz Díaz, Acc. Chem. Res., 2019, 52, 1865–1876 CrossRef CAS PubMed.
- N. A. Smith and S. R. Meech, Int. Rev. Phys. Chem., 2002, 21, 75–100 Search PubMed.
- N. T. Hunt, A. A. Jaye and S. R. Meech, Phys. Chem. Chem. Phys., 2007, 9, 2167–2180 RSC.
- H. Shirota, T. Fujisawa, H. Fukazawa and K. Nishikawa, Bull. Chem. Soc. Jpn., 2009, 82, 1347–1366 CrossRef CAS.
- Q. Zhong and J. T. Fourkas, J. Phys. Chem. B, 2008, 112, 15529–15539 CrossRef CAS.
- P. Hamm and M. Zanni, Concepts and Methods of 2D Infrared Spectroscopy, Cambridge University Press, Cambridge, 2011 Search PubMed.
- J. C. Wright, Int. Rev. Phys. Chem., 2002, 21, 185–255 Search PubMed.
- J. Gardecki, M. L. Horng, A. Papazyan and M. Maroncelli, J. Mol. Liq., 1995, 65-6, 49–57 CrossRef.
- M. Maroncelli, E. W. Castner, B. Bagchi and G. R. Fleming, Faraday Discuss., 1988, 85, 199–210 RSC.
- M. Maroncelli, J. Mol. Liq., 1993, 57, 1–37 CrossRef CAS.
- N. E. Levinger, Curr. Opin. Colloid Interface Sci., 2000, 5, 118–124 CrossRef CAS.
- E. W. Castner and M. Maroncelli, J. Mol. Liq., 1998, 77, 1–36 CrossRef CAS.
- N. A. Smith and S. R. Meech, Int. Rev. Phys. Chem., 2002, 21, 75–100 Search PubMed.
- B. M. Ladanyi and S. Klein, J. Chem. Phys., 1996, 105, 1552–1561 CrossRef CAS.
- X. Zhu, R. A. Farrer and J. T. Fourkas, J. Phys. Chem. B, 2005, 109, 12724–12730 CrossRef CAS.
- A. Scodinu and J. T. Fourkas, Dynamics and Friction in Submicrometer Confining Systems, 2004, vol. 882, pp. 193–204 Search PubMed.
- R. A. Farrer and J. T. Fourkas, Acc. Chem. Res., 2003, 36, 605–612 CrossRef CAS.
- A. Scodinu and J. T. Fourkas, J. Phys. Chem. B, 2002, 106, 10292–10295 CrossRef CAS.
- B. J. Loughnane, R. A. Farrer, A. Scodinu, T. Reilly and J. T. Fourkas, J. Phys. Chem. B, 2000, 104, 5421–5429 CrossRef CAS.
- A. Taschin, P. Bartolini, A. Marcelli, R. Righini and R. Torre, Faraday Discuss., 2013, 167, 293–308 RSC.
- B. Ratajska-Gadomska, B. Bialkowski, W. Gadomski and C. Radzewicz, J. Chem. Phys., 2007, 126, 184708 CrossRef CAS.
- P. Prosposito, D. Marks, H. Zhang and M. Glasbeek, J. Phys. Chem. A, 1998, 102, 8894–8902 CrossRef CAS.
- W. H. Thompson, in Annual Review of Physical Chemistry, ed. S. R. Leone, P. S. Cremer, J. T. Groves and M. A. Johnson, 2011, vol. 62, pp. 599–619 Search PubMed.
- D. Stoner-Ma, A. A. Jaye, P. Matousek, M. Towrie, S. R. Meech and P. J. Tonge, Abstracts of Papers of the American Chemical Society, 2005, 230, U634 Search PubMed.
- N. T. Hunt, A. A. Jaye and S. R. Meech, J. Phys. Chem. B, 2003, 107, 3405–3418 CrossRef CAS.
- G. Onori and A. Santucci, J. Phys. Chem., 1993, 97, 5430–5434 CrossRef CAS.
- A. M. Dokter, S. Woutersen and H. J. Bakker, Phys. Rev. Lett., 2005, 94, 178301 CrossRef PubMed.
- K. J. Tielrooij, M. J. Cox and H. J. Bakker, Chem. Phys. Chem., 2009, 10, 245–251 CrossRef CAS PubMed.
- A. M. Dokter, S. Woutersen and H. J. Bakker, J. Chem. Phys., 2007, 126, 124507 CrossRef PubMed.
- A. M. Dokter, S. Woutersen and H. J. Bakker, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 15355–15358 CrossRef CAS.
- I. R. Piletic, D. E. Moilanen, D. B. Spry, N. E. Levinger and M. D. Fayer, J. Phys. Chem. A, 2006, 110, 4985–4999 CrossRef CAS PubMed.
- D. Cringus, A. Bakulin, J. Lindner, P. Vohringer, M. S. Pshenichnikov and D. A. Wiersma, J. Phys. Chem. B, 2007, 111, 14193–14207 CrossRef CAS PubMed.
- D. E. Moilanen, N. E. Levinger, D. B. Spry and M. D. Fayer, J. Am. Chem. Soc., 2007, 129, 14311–14318 CrossRef CAS PubMed.
- D. E. Moilanen, E. E. Fenn, D. Wong and M. D. Fayer, J. Chem. Phys., 2009, 131, 014704 CrossRef PubMed.
- E. E. Fenn, D. B. Wong and M. D. Fayer, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 15243–15248 CrossRef CAS PubMed.
- E. E. Fenn, D. B. Wong, C. H. Giammanco and M. D. Fayer, J. Phys. Chem. B, 2011, 115, 11658–11670 CrossRef CAS PubMed.
- M. D. Fayer, Acc. Chem. Res., 2012, 45, 3–14 CrossRef CAS.
- P. K. Singh, D. G. Kuroda and R. M. Hochstrasser, J. Phys. Chem. B, 2013, 117, 9775–9784 CrossRef CAS.
- G. M. Sando, K. Dahl and J. C. Owrutsky, J. Phys. Chem. A, 2004, 108, 11209–11217 CrossRef CAS.
- R. F. Yuan, C. Yan, J. Nishida and M. D. Fayer, J. Phys. Chem. B, 2017, 121, 4530–4537 CrossRef CAS.
- D. X. Zhou, Q. S. Wei, S. Y. Wang, X. Q. Li and H. T. Bian, J. Phys. Chem. Lett., 2019, 10, 176–182 CrossRef CAS PubMed.
- N. Sarkar, K. Das, A. Datta, S. Das and K. Bhattacharyya, J. Phys. Chem., 1996, 100, 10523–10527 CrossRef CAS.
- D. Mandal, A. Datta, S. K. Pal and K. Bhattacharyya, J. Phys. Chem. B, 1998, 102, 9070–9073 CrossRef CAS.
- D. Pant, R. E. Riter and N. E. Levinger, J. Chem. Phys., 1998, 109, 9995–10003 CrossRef CAS.
- R. E. Riter, D. M. Willard and N. E. Levinger, J. Phys. Chem. B, 1998, 102, 2705–2714 CrossRef CAS.
- M. A. Kahlow, T. J. Kang and P. F. Barbara, J. Chem. Phys., 1988, 88, 2372–2378 CrossRef CAS.
- W. Jarzeba, G. C. Walker, A. E. Johnson and P. F. Barbara, Chem. Phys., 1991, 152, 57–68 CrossRef CAS.
- J. E. Lewis and M. Maroncelli, Chem. Phys. Lett., 1998, 282, 197–203 CrossRef CAS.
- K. Bhattacharyya, Acc. Chem. Res., 2003, 36, 95–101 CrossRef CAS PubMed.
- K. Sahu, S. K. Mondal, S. Ghosh and K. Bhattacharyya, Bull. Chem. Soc. Jpn., 2007, 80, 1033–1043 CrossRef CAS.
- K. Bhattacharyya, Chem. Commun., 2008, 2848–2857, 10.1039/b800278a.
- N. E. Levinger and L. A. Swafford, Annu. Rev. Phys. Chem., 2009, 60, 385–406 CrossRef CAS PubMed.
- R. E. Riter, E. P. Undiks and N. E. Levinger, J. Am. Chem. Soc., 1998, 120, 6062–6067 CrossRef CAS.
- N. M. Correa and N. E. Levinger, J. Phys. Chem. B, 2006, 110, 13050–13061 CrossRef CAS PubMed.
- J. Faeder and B. M. Ladanyi, J. Phys. Chem. B, 2000, 104, 1033–1046 CrossRef CAS.
- J. Faeder and B. M. Ladanyi, J. Phys. Chem. B, 2001, 105, 11148–11158 CrossRef CAS.
- J. Faeder, M. V. Albert and B. M. Ladanyi, Langmuir, 2003, 19, 2514–2520 CrossRef CAS.
- J. Faeder and B. M. Ladanyi, J. Phys. Chem. B, 2005, 109, 6732–6740 CrossRef CAS PubMed.
- J. Chowdhary and B. M. Ladanyi, J. Phys. Chem. B, 2009, 113, 15029–15039 CrossRef CAS PubMed.
- M. R. Harpham, B. M. Ladanyi and N. E. Levinger, J. Phys. Chem. B, 2005, 109, 16891–16900 CrossRef CAS PubMed.
- S. Senapati and M. L. Berkowitz, J. Phys. Chem. B, 2003, 107, 12906–12916 CrossRef CAS.
- S. Senapati and M. L. Berkowitz, J. Chem. Phys., 2003, 118, 1937–1944 CrossRef CAS.
- L. Y. Lu and M. L. Berkowitz, J. Am. Chem. Soc., 2004, 126, 10254–10255 CrossRef CAS.
- S. Senapati and M. L. Berkowitz, J. Phys. Chem. A, 2004, 108, 9768–9776 CrossRef CAS.
- B. B. Xie, S. H. Xia, X. P. Chang and G. L. Cui, Phys. Chem. Chem. Phys., 2016, 18, 403–413 RSC.
- C. Singh, B. Modak, J. A. Mondal and D. K. Palit, J. Phys. Chem. A, 2011, 115, 8183–8196 CrossRef CAS PubMed.
- Y. Erez, R. Simkovitch, K. Akulov, R. Gepshtein, T. Schwartz and D. Huppert, J. Phys. Chem. C, 2014, 118, 27063–27073 CrossRef CAS.
- S. Rafiq and P. Sen, J. Chem. Phys., 2013, 139, 124302 CrossRef PubMed.
- R. A. Day, B. H. Robinson, J. H. R. Clarke and J. V. Doherty, J. Chem. Soc., Faraday Trans. 1, 1979, 75, 132–139 RSC.
- G. D. Rees and B. H. Robinson, Adv. Mater., 1993, 5, 608–619 CrossRef CAS.
- S. Lipgens, D. Schubel, L. Schlicht, J. H. Spilgies, G. Ilgenfritz, J. Eastoe and R. K. Heenan, Langmuir, 1998, 14, 1041–1049 CrossRef CAS.
- I. A. Heisler, M. Kondo and S. R. Meech, J. Phys. Chem. B, 2009, 113, 1623–1631 CrossRef CAS PubMed.
- N. T. Hunt, A. A. Jaye and S. R. Meech, Chem. Phys. Lett., 2005, 416, 89–93 CrossRef CAS.
- R. Hasegawa, T. Sugimura, Y. Suzaki, Y. Shindo and A. Kitahara, J. Phys. Chem., 1994, 98, 2120–2124 CrossRef.
- Y. Hirose, H. Yui and T. Sawada, J. Phys. Chem. B, 2004, 108, 9070–9076 CrossRef CAS.
- M. Kondo, I. A. Heisler and S. R. Meech, Faraday Discuss., 2010, 145, 185–203 RSC.
- M. Kondo, I. A. Heisler, J. Conyard, J. P. H. Rivett and S. R. Meech, J. Phys. Chem. B, 2009, 113, 1632–1639 CrossRef CAS PubMed.
- N. Amdursky, Y. Erez and D. Huppert, Acc. Chem. Res., 2012, 45, 1548–1557 CrossRef CAS PubMed.
- Y. Erez, N. Amdursky, R. Gepshtein and D. Huppert, J. Phys. Chem. A, 2012, 116, 12056–12064 CrossRef CAS PubMed.
- P. K. Singh, M. Kumbhakar, H. Pal and S. Nath, J. Phys. Chem. B, 2009, 113, 8532–8538 CrossRef CAS PubMed.
- P. K. Singh and S. Nath, J. Photochem. Photobiol., A, 2012, 248, 42–49 CrossRef CAS.
- P. Mukherjee, A. Das and P. Sen, J. Photochem. Photobiol., A, 2017, 348, 287–294 CrossRef CAS.
- A. Chatterjee and D. Seth, Photochem. Photobiol. Sci., 2013, 12, 369–383 CrossRef CAS PubMed.
- S. Rafiq, R. Yadav and P. Sen, J. Phys. Chem. B, 2010, 114, 13988–13994 CrossRef CAS PubMed.
- C.-S. Hsu, K.-L. Liu, K. S. Tan, H.-Y. Yen and I. C. Chen, J. Phys. Chem. B, 2014, 118, 10187–10195 CrossRef CAS PubMed.
- G. Lee, T. Jang, S. Lee, H. Oh, H. Lee and Y. Pang, J. Mol. Liq., 2020, 305, 112873 CrossRef CAS.
- M. Kondo, I. A. Heisler and S. R. Meech, J. Mol. Liq., 2012, 176, 17–21 CrossRef CAS.
- P. K. Singh, A. K. Mora, S. Murudkar and S. Nath, RSC Adv., 2014, 4, 34992–35002 RSC.
- P. K. Singh, S. Murudkar, A. K. Mora and S. Nath, J. Photochem. Photobiol., A, 2015, 298, 40–48 CrossRef CAS.
- C. J. Otolski, A. M. Raj, V. Ramamurthy and C. G. Elles, Chem. Sci., 2020, 11, 9513–9523 RSC.
- V. Ramamurthy and S. Gupta, Chem. Soc. Rev., 2015, 44, 119–135 RSC.
- A. Douhal, Chem. Rev., 2004, 104, 1955–1976 CrossRef CAS PubMed.
- I. Balomenou, A. Kaloudi-Chantzea, N. Karakostas, K. Yannakopoulou, I. M. Mavridis and G. Pistolis, J. Phys. Chem. B, 2011, 115, 10665–10681 CrossRef CAS PubMed.
- I. Balomenou and G. Pistolis, Chem. – Eur. J., 2009, 15, 4228–4232 CrossRef CAS PubMed.
- R. S. H. Liu, Acc. Chem. Res., 2001, 34, 555–562 CrossRef CAS PubMed.
- A. Mohan Raj and V. Ramamurthy, Org. Lett., 2017, 19, 6116–6119 CrossRef CAS PubMed.
- C. J. Otolski, A. M. Raj, G. Sharma, R. Prabhakar, V. Ramamurthy and C. G. Elles, J. Phys. Chem. A, 2019, 123, 5061–5071 CrossRef CAS PubMed.
- C. J. Otolski, A. M. Raj, V. Ramamurthy and C. G. Elles, J. Phys. Chem. Lett., 2019, 10, 121–127 CrossRef CAS PubMed.
- B. Cohen, D. Huppert, K. M. Solntsev, Y. Tsfadia, E. Nachliel and M. Gutman, J. Am. Chem. Soc., 2002, 124, 7539–7547 CrossRef CAS PubMed.
- G. Angulo, J. A. Organero, M. A. Carranza and A. Douhal, J. Phys. Chem. B, 2006, 110, 24231–24237 CrossRef CAS PubMed.
- M. Sedgwick, R. L. Cole, C. D. Rithner, D. C. Crans and N. E. Levinger, J. Am. Chem. Soc., 2012, 134, 11904–11907 CrossRef CAS PubMed.
- V. Khorwal and P. Sen, J. Photochem. Photobiol., A, 2017, 347, 86–92 CrossRef CAS.
- S. Basu, S. Mondal and D. Mandal, J. Chem. Phys., 2010, 132, 034701 CrossRef.
- D. Ghosh, S. Batuta, N. A. Begum and D. Mandal, J. Lumin., 2017, 184, 64–73 CrossRef CAS.
- S. Dutta Choudhury and H. Pal, Phys. Chem. Chem. Phys., 2020, 22, 23433–23463 RSC.
| This journal is © The Royal Society of Chemistry 2021 |