DOI:
10.1039/C3MH00106G
(Review Article)
Mater. Horiz., 2014,
1, 301-313
Protein corona formation around nanoparticles – from the past to the future†
Received
21st September 2013
, Accepted 14th October 2013
First published on 14th October 2013
Abstract
The protein adsorption layer (a.k.a. the “protein corona”) that forms on the surface of colloidal nanoparticles plays an important role in their interaction with living matter. Thus, characterization of the protein corona is of utmost importance for understanding how exposure to nanoparticles affects the biological responses of cells and organisms. Although a lot of experimental studies have been reported in this direction, a comprehensive picture is still missing, in particular due to the multitude of different scenarios under which experiments have been performed. In this review an analysis of existing experimental data about the protein corona, and an outline for required future work will be given. In particular we review how existing simple analytical models such as the adopted Hill model may help to extract quantitative data from such experiments such as equilibrium dissociation and kinetic coefficients. Careful quantitative assessment of equilibrium and kinetic properties would allow for a comparison of protein binding data from the vast array of engineered nanoparticles, so that basic principles could be revealed. This review outlines that the field is in dire need of more quantitative studies to further our understanding of protein corona formation and its biological consequences.
 Pablo del Pino | Pablo del Pino graduated in Physics from Universidad de Sevilla (Spain) in 2002 and obtained his PhD degree from Technische Universität München (Germany) in 2007. After postdoctoral positions at the Ludwig-Maximilians-Universität München (2007–2009, Munich, Germany), and at the Institute of Nanoscience of Aragon (INA) (2009–2013, Zaragoza, Spain), he has recently joined the Biofunctional Nanomaterials Unit at CIC biomaGUNE, San Sebastian, Spain. |
 Beatriz Pelaz | Beatriz Pelaz graduated in Chemistry from Valladolid University (Spain) in 2005 and in Biochemistry from Zaragoza University (Spain) in 2011. She obtained her PhD from Zaragoza University (Spain) in 2012, working in the Institute of Nanoscience of Aragon. Then, she joined the group of Prof. Dr Wolgang Parak as postdoctoral researcher. In 2013, she was awarded a postdoctoral fellowship from the Alexander von Humboldt Foundation. |
 Qian Zhang | Qian Zhang obtained her B.S. in Biological Science in 2008 at the Qingdao Agricultural University (China). She received her M.S. in Biophysics in 2011 at Sichuan Agricultural University (China). Since 2011, she has been a PhD student in the group of Prof. Dr Wolfgang Parak at the Philipps-Universität Marburg (Germany). |
 Pauline Maffre | Pauline Maffre obtained her French-German double diploma with an engineer's degree in 2010 at the National Engineering School of Physics of Grenoble (Phelma, INPG), Grenoble, France, and a physics diploma in 2010 at the Karlsruhe Institute of Technology (KIT), Karlsruhe, Germany. Since 2011, she has been a doctoral student in biophysics in the Nienhaus group at the Institute of Applied Physics, KIT. |
 G. Ulrich Nienhaus | Gerd Ulrich Nienhaus studied Physics and received his PhD degree in Physical Chemistry from the University of Münster, Germany, in 1988. In 1990, he was awarded a Feodor Lynen Fellowship of the Alexander von Humboldt Foundation and joined the Department of Physics of the University of Illinois at Urbana-Champaign, USA, where he became an Assistant Professor (1991), Associate Professor (1996) and Adjunct Professor (1997–present). In 1996, he was appointed as a Chair Professor and Head of the Institute of Biophysics at the University of Ulm, Germany. In 2009, he moved to the Karlsruhe Institute of Technology (KIT), Germany, where he is currently Chair Professor and Head of the Institute of Applied Physics. |
 Wolfgang J. Parak | Wolfgang J. Parak obtained his PhD at the LMU München, Germany (1999) in the group of Prof. Dr Hermann Gaub. After a postdoctoral stay at the University of California, Berkeley, CA, USA in the group of Prof. Dr Paul Alivisatos he returned to Munich as an Assistant Professor in 2002. Since 2007, he has been a Full Professor at the Physics Department of the Philipps Universität Marburg, Marburg, Germany. In addition, he was appointed as Head of the Biofunctional Nanomaterials Unit at CIC biomaGUNE, San Sebastian, Spain in 2013. He is also Associate Editor of ACS Nano. |
Development of new materials demands consistent characterization techniques
The development of new materials always goes hand-in-hand with their characterization. A wide variety of analytical techniques exist that allow materials properties to be assessed in a quantitative fashion. Still, the results often depend on a range of experimental parameters. If these are being varied from experiment to experiment, this may prevent meaningful comparisons of data. Only through reliable, consistent procedures, materials properties can be thoroughly assessed, and further improved in response to feedback from the application side. The interrelation between the physicochemical properties of new materials and their function can then be better understood. Characterization must always include realistic operation conditions. Colloidal nanoparticles (NPs) are an exciting class of “new” materials, which actually go back to ancient times (see the famous Lycurgus cup as an example).1 However, due to impressive advances in the synthesis of colloids, new waves of applications from diverse disciplines ranging from the life sciences to the energy sciences have been initiated only in the last decades. In life science applications, the initial characterization would involve dispersions of the NPs in simple solvents such as water, or the original solution in which the NPs had been synthesized. However, aiming at in vitro and in vivo applications of the NPs, they also need to be studied in biological fluids, which typically contain high amounts of ions and proteins.2 These solution conditions may lead to substantial changes of the physicochemical properties of the NPs as compared to model solutions such as water.
Colloidal nanoparticles have to be characterized in relevant media, especially with respect to colloidal stability and the effect of salt
Many of the original synthesis methods developed in the past yield NPs that are not colloidally stable under conditions present in biological fluids. In particular, inorganic NPs are naturally colloidally instable and prone to agglomeration because they attract each other by van der Waals forces. To stabilize the NPs in a solvent, i.e., to disperse them requires a repulsive force between the NPs. Such an interaction can be introduced by providing the surface of the NPs with charge (which results in repulsion of equally charged NPs) or molecular spacers (which results in steric repulsion as the shields of molecular spacers cannot fully interpenetrate).3,4 Consider a classical example of NPs, CdSe/ZnS quantum dots (QDs), which are often stabilized by a shell of mercaptopropionic acid (MPA). Yet, the MPA-coated NPs will precipitate over the time course of days to weeks if the concentration of salt, a major constituent of most biological fluids, is increased up to the physiological range (150 mM NaCl). The effect is especially pronounced in the presence of divalent ions such as Ca2+. Loss of colloidal stability results from the adsorption of counterions, which screen the negative surface charge provided by the –COO− groups of the MPA. Thus, the electrostatic repulsion between the NPs is drastically reduced.5 In addition, if these NPs are dialyzed against pure water over extended periods of time (days or weeks), they will gradually lose their ligand shell and agglomerate. The bond between the thiol groups (–SH) of MPA and the CdSe/ZnS NPs is subject to photooxidation,6 which ultimately leads to a loss of the MPA ligands. As long as the NPs are in a solution that contains MPA at a sufficiently high concentration, such as the one in which they have been synthesized or modified, there is a dynamic equilibrium of unbinding and rebinding of MPA. However, if the NPs are dialyzed against water, unbound MPA is irreversibly lost to the dialysis bath. Once a certain fraction of MPA ligands have been lost from the NP surface, charge repulsion is no longer sufficient to ensure colloidal stability. A similar process would occur, if these NPs were to be injected into the blood stream. Simply due to the dilution effect, any accidentally detached MPA ligand would eventually be lost. Thus, while MPA-stabilized QDs display sufficient colloidal stability in model solutions, they are typically not well dispersed in more realistic media for biological applications (though protein adsorption from the media might again assist in their dispersion, as will be discussed below). Nowadays, there are myriads of advanced surface coating methods which ensure colloidal stability of NPs even in the presence of high salt concentrations,7–15 and the physicochemical principles of the effects of salt are well understood. Nevertheless, this example illustrates vividly that a meaningful analysis of the performance of NPs requires their characterization in environments that can be considered as realistic for a particular application.
Proteins adsorb onto nanoparticle surfaces
Next to salt, proteins are major constituents of biological fluids. It is a well-established fact that proteins generally adsorb onto the surface of materials. Adsorption of proteins from serum-containing media to surfaces can be easily visualized, for example, by atomic force microscopy (AFM). With the sharp tip of an AFM, proteins adsorbed to a plane surface can be scratched away, leading to a protein free hole.16 Protein adsorption onto surfaces has been investigated vigorously for a long time, in particular, in the biomaterials community, with the aim to develop adsorption-resistant, inert surfaces.17–20 Indeed, the adsorption of proteins onto biomaterials implanted inside the body, and subsequent protein–protein competition and displacement steps (known as the Vroman effect), is an issue of utmost importance.21 Also in bioanalytics, adsorption of the proteins to be analysed onto the surfaces of tubing connected to the detection device is a well-known problem. Traditionally, this problem has been circumvented by flushing the device first with bovine serum albumin (BSA), which blocks the binding sites and thus reduces adsorption of the protein to be analysed. From the large body of work on protein adsorption, it is quite obvious that proteins will also adsorb onto the surfaces of colloidal particles.22–27 For instance, we have observed that the differences in the cellular uptake of colloidal microparticles with different charge were partly suppressed by the presence of serum due to the adsorption of proteins onto the particle surface. At that time, we simply noted that “adsorption of constituents from the medium smears out charge differences”.28 Thus, while the effect was, in principle, known in the nanoparticle community, the role of protein adsorption in modulating the interaction between NPs and cells was not systematically investigated and remained a secondary issue until it was moved centre stage by the pioneering work by Dawson, Linse, and colleagues.29 In this report, a detailed description on protein adsorption onto NPs, then termed “protein corona”, was given, which stimulated a whole field of investigations. Nowadays, there are thousands of manuscripts dedicated to studies of the protein corona. In the meantime, it has been described that the formation of the protein corona depends on the size,30–33 charge,32,34,35 and colloidal stability of NPs,36 as well as on the types of proteins,37 ambient temperature,38,39 incubation conditions and time,37,40–42etc. A lot of details are known for different NPs, however, our knowledge of the protein corona is still not comprehensive.43 The complexity of this topic requires huge datasets (many different combinations of proteins and NPs) to gain sufficiently broad knowledge. Moreover, many studies in the literature were done on very unique systems, and the results can be hardly extrapolated to others, and are too different from each other to allow for comparison among different reports. Having so far reviewed the “past” of protein corona research, we shall discuss the “future” in the following. We will present our opinion about the still missing knowledge, and we will point to characterization techniques that could help advance the field and also discuss potential pitfalls on the way.
Protein adsorption to nanoparticles as described by classical ligand-binding models developed in biochemistry
From the physicochemical point of view, protein adsorption onto NPs resembles ligand binding, which has been discussed above. Proteins can adsorb and desorb to the surface of NPs, they can displace other proteins, or even parts of the original ligand shell around the NPs. We shall start with modelling a solution of inert NPs in contact with only one protein species P. Let us treat protein adsorption according to the following reaction equation,
Thus, each NP has n binding sites for proteins, so that PnNP is a NP fully saturated with n proteins. We emphasize that this “all-or-none” ansatz, which is the basis of the original Hill model for modelling oxygenation of haemoglobin,44 is overly simplistic because it implies that partially saturated species can be neglected. According to the law of mass action, the partitioning between the different species (free NPs ↔ protein-saturated NPs, free proteins ↔ proteins bound to NPs) in thermal equilibrium is described by the dissociation equilibrium coefficient, KD, which is given by the ratio of the off- to on-rates for protein binding to the NPs.45
| | 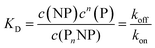 | (2) |
here,
c(NP),
c(P), and
c(P
nNP) represent the concentrations of free NPs, unbound proteins, and protein–NP complexes, respectively. In other words, if we mix two solutions, one containing NPs and the other proteins (with initial concentrations of NPs and proteins,
c0(NP) and
c0(P), respectively), and wait until equilibrium is reached, the concentration of free NPs and proteins will finally be
c(NP) and
c(P), respectively, and protein–NP complexes with concentration
c(P
nNP) will be present in the solution,
cf.Fig. 1. Often, instead of the dissociation coefficient
KD, the concentration at which half of the NPs are saturated with proteins,
K′D, is used.
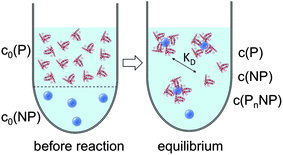 |
| | Fig. 1 Prior to the reaction, free proteins with concentration c0(P), and free NPs with concentration c0(NP) are separated. After the reaction has progressed to equilibrium, according to the law of mass action, eqn (1) and (2), a fraction of proteins is bound to the NP surface, and another fraction of proteins, with concentration c(P), remains free in solution. In this all-or-none model the NPs are either saturated with proteins, with an NP concentration c(PnNP), or they remain free of protein, with an NP concentration c(NP). | |
The Hill model for a single protein species in equilibrium with a nanoparticle surface
According to eqn (1)–(3),44 the ratio of the number of NPs saturated with proteins (N) to the total number of NPs (Nmax) is then given by| | 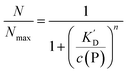 | (4) |
Thus the fraction of NPs which are saturated with proteins (N/Nmax) depends on the concentration of free proteins c(P) and the concentration at which half of the NPs are saturated (K′D), cf.Fig. 2. Even for haemoglobin, which has four oxygen binding sites, the parameter n, the so-called Hill coefficient, was always found to be lower than four, indicating that the restrictive “all-or-none” ansatz is inappropriate. The Hill coefficient is thus treated as an empirical parameter which describes the steepness of the transition from bare to protein-saturated NPs, cf.Fig. 2. The more free protein in solution is required to achieve the midpoint of the protein binding transition, the larger K′D will be. Mathematical details are described in the ESI.† It is clear that an all-or-none scenario, in which all proteins bind simultaneously to the NPs, is entirely unrealistic. Eqn (4) nevertheless provides a useful model for protein binding to NPs, if the involved parameters are suitably reinterpreted.
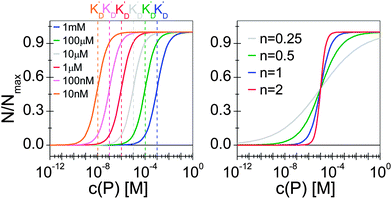 |
| | Fig. 2 Fraction of NPs saturated with proteins (N/Nmax) as a function of the concentration of free protein c(P), calculated with eqn (4) under variation of the concentration at half saturation K′D, and using the Hill coefficient n. At low protein concentrations, almost all NPs are without proteins (N → 0 for c(P) ≪ K′D), whereas at high concentrations, all NPs are saturated with protein (N → Nmax for c(P) ≫ K′D). (a) n = 1, K′D = 10 nM, 100 nM, 1 μM, 10 μM, 100 μM, 1 mM. The concentration at half saturation K′D describes the midpoint of the transition. (b) K′D = 10 μM, n = 0.25, 0.5, 1, 2. The Hill coefficient n describes the steepness of the transition. | |
Eqn (4) and, thus, the curves shown in Fig. 2 can also be reinterpreted as follows (see the ESI† for more details): in equilibrium, the NPs are loaded on average with N proteins, and Nmax is the maximum number of proteins which each NP can bind to, cf.Fig. 3. In this interpretation, the Hill coefficient describes how proteins bound on a NP influence the adsorption of further proteins from the solution onto the same NP. A Hill coefficient n > 1 indicates cooperative binding, i.e., proteins already bound to a NP facilitate the binding of further proteins to the remaining vacant sites. By contrast, n < 1 refers to anti-cooperative binding, so that proteins already adsorbed onto the NP lower the tendency for binding additional ones. This is a very realistic scenario because, upon binding, proteins interact with the NP surface and the proteins already bound to that surface.
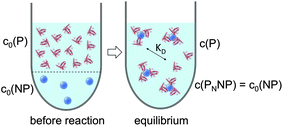 |
| | Fig. 3 Before the reaction, free proteins with concentration c0(P), and free NPs with concentration c0(NP) are separated. After the reaction has progressed to equilibrium, some proteins are bound to the NP surface (which is in general not yet saturated by proteins), and only a fraction of proteins, with concentration c(P), remain free in solution. Technically all NPs are assumed to have the same number N ≤ Nmax of proteins bound per NP. However, please note that N in fact represents the average number of proteins per NP. This is a reinterpretation of the same situation as depicted in Fig. 1 (same values for c0(P), c0(NP), c(P)). As a sufficiently high protein concentration is assumed (c0(P) ≫ c0(NP)), as otherwise there would be no protein corona, there are no bare NPs without adsorbed proteins. | |
It is trivial that the concentration of unbound protein remaining free in solution, c(P), is smaller than the initial concentration of added protein c0(P). Both are related viaeqn (5), which allows for calculation of c(P) from knowing c0(P) and the parameters of the saturation curve. The total protein concentration c0(P) comprises the free proteins c(P), as well as the proteins which are bound to NPs Nc0(NP), as given by eqn (4):
| | 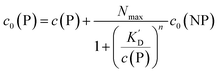 | (5) |
Using eqn (5), the fraction of proteins bound to NPs, 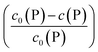 , can be calculated depending on the initial parameters c0(P), c0(NP), cf.Fig. 4. Here, c(P) needs to be derived implicitly from eqn (5). For all steps of the calculation, we refer to the ESI.† If c(P) is much greater than K′D, each NP is saturated with Nmax proteins, and the fraction becomes
, can be calculated depending on the initial parameters c0(P), c0(NP), cf.Fig. 4. Here, c(P) needs to be derived implicitly from eqn (5). For all steps of the calculation, we refer to the ESI.† If c(P) is much greater than K′D, each NP is saturated with Nmax proteins, and the fraction becomes
| | 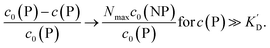 | (6) |
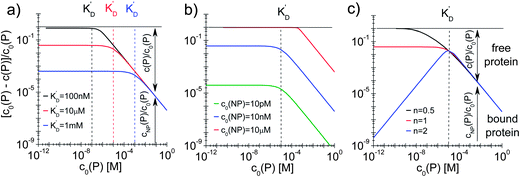 |
| | Fig. 4 Fraction of proteins bound to the NPs (c0(P) − c(P))/(c0(P) = cNP(P)/c0(P)) depending on the total protein concentration c0(P), according to eqn (5), using Nmax = 40 as the maximum number of proteins which each NP can bind to. The total concentration of NPs, c0(NP), the protein concentration at half saturation, K′D, and the Hill coefficient n are varied. (a) c0(NP) = 10 nM, n = 1, K′D = 100 nM, 10 μM, 1 mM. (b) c0(NP) = 10 pM, 10 nM, 10 μM, n = 1, K′D = 10 μM. (c) c0(NP) = 10 nM, n = 0.5, 1, 2, K′D = 10 μM. The dashed lines indicate the respective protein concentrations at half saturation, K′D. The arrows in the graphs indicate how the proteins are divided into a fraction of proteins bound to NPs (cNP(P)/c0(P)) and a fraction of free proteins (c(P)/c0(P)). | |
In this case, even if more and more protein is added, additional protein cannot be bound to the NP surface, as all NPs are already saturated with Nmax proteins. Some examples are displayed in Fig. 4.
With the examples presented in Fig. 4 several effects can be visualized. Fig. 4a illustrates how the fraction of proteins bound depends on the value of K′D in a case without cooperativity, i.e., where proteins do not influence each other upon binding (n = 1). At a total protein concentration c0(P) much lower than K′D, most of the binding sites are vacant and each protein has a certain probability to bind to the NPs that only depends on the ratio of the off- to the on-rate coefficients, i.e., K′D. At low protein concentration, the fraction of proteins bound directly reflects this probability (it corresponds to the range where the fraction is constant). A smaller K′D corresponds to a higher probability for a protein to stay on the NP surface, i.e., a higher fraction of proteins is bound. If the total protein concentration reaches values around K′D, significant amounts of proteins are already bound and the probability for one protein to bind to the surface no longer depends on K′D only, but also on the probability for a binding site to be free. Thus, relatively fewer proteins bind to the NPs and the fraction of bound proteins decreases. Once the NPs are saturated with proteins (c0(P) ≫ K′D), no more proteins can bind anymore and the fraction of proteins bound decreases proportionally to the total protein concentration. Fig. 4b illustrates how the fraction of bound proteins depends on the value of c0(NP) for a case without cooperativity (n = 1). At total protein concentrations much smaller than K′D, the fraction of bound proteins cNP(P) is again directly proportional to the probability for each protein to bind to the surface of one NP. As K′D is the same for all three curves, this probability is the same. However, for a higher NP concentration, the absolute number of bound proteins is higher and thus the fraction of bound proteins is higher for high c0(NP). Thus, under these conditions (c0(NP) ≫ c0(P), K′D ≫ c0(P), n ≤ 1) proteins can be sufficiently removed from solution, which might be interesting for purification applications. The fraction of bound proteins starts to decrease when the total protein concentration reaches the range of K′D. Note that the onset of the decrease shifts to the right in Fig. 4b for high NP concentration because the maximum number of binding sites is higher. Thus, for a fixed total protein concentration, the probability of a binding site to be vacant is also higher. Fig. 4c illustrates the effect of the Hill coefficient n on the fraction of proteins bound. At a total protein concentration smaller than K′D, cooperativity leads to fewer proteins bound than in a reaction without cooperativity. Indeed, in a reaction with cooperativity, it is easier for several proteins to bind jointly than for each protein to bind individually. At low protein concentrations, the probability of several proteins binding to a single NP is low and, consequently, fewer proteins are bound to the NPs compared to that in the non-cooperative case. This probability increases linearly (the blue line has a slope of 1 in Fig. 4c) with the free protein concentration. Thus, at a concentration of free proteins smaller than K′D, cooperativity leads to less overall protein binding onto the NPs. By contrast, if the reaction is anti-cooperative, the probability that a protein binds to a NP is higher if there are no other proteins already bound, i.e., at lower protein concentration. Thus, anti-cooperativity enhances protein binding at low free protein concentration, compared to the non-cooperative case. Naturally, once the NP surface is saturated with proteins (c0(P) ≫ K′D), there is no longer any effect of n, as n is associated only with the binding process and thus has no relevance when all the binding sites are already occupied. Such theoretical considerations/simulations may be useful to choose relevant protein and NP concentration ranges by designing experiments.
The Hill model for two protein species in equilibrium with the nanoparticle surface
We can extend this description to the case in which not only one, but two protein species P(1) and P(2) can bind to the surface of NPs. In analogy to eqn (1) and (2), yet for two protein species, the following equations are considered:| | 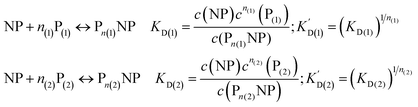 | (7) |
Let us discuss the case that NPs are saturated with proteins of species P(1), which are then brought into contact with free protein of species P(2). Subsequently, a dynamic exchange between proteins of both species can occur:
| | 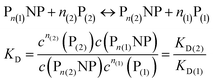 | (8) |
Likewise, if bare NPs are incubated with both protein species simultaneously, NPs can be covered with proteins P(1) or with proteins P(2):
| | | NP + n(1)P(1) + n(2)P(2) ↔ Pn(1)NP + Pn(2)NP | (9) |
In analogy to eqn (4) one can calculate the ratio of NPs saturated with proteins P(1), and P(2) to the total amount of NPs, N(1)/Nmax, and N(2)/Nmax, respectively:
| | 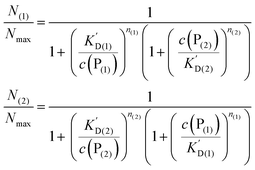 | (10) |
In line with the description of only one protein species (cf.Fig. 1 and 3), eqn (10) describes how many (N(1) and N(2)) of the Nmax binding sites per NP are occupied by proteins of species P(1) and P(2), cf.Fig. 5. With eqn (10), the protein corona formed by the two protein species can be analysed, cf.Fig. 6. The data show that one protein species (P(2)) displaces the other one (P(1)) if it has a much lower half saturation concentration (K′D(2) ≪ K′D(1)) or is present at a much higher concentration (c(P(2)) ≫ c(P(1))). Please note that this “adapted” Hill formalism is appropriate only for describing the binding reaction in the special case Nmax(1) = Nmax(2) = Nmax, and that in eqn (10)N(1) + N(2) ≤ Nmax is supposed. This assumption certainly will not hold true in case two very different protein species (in particular in terms of size) are considered, but it helps understanding the concept of competition of different protein species for the binding sites on the surface of NPs. In this way, concepts like “soft” versus “hard” corona30 could be quantitatively described, as will be discussed in more detail later.
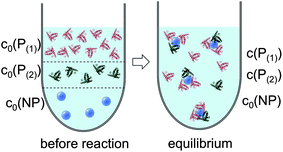 |
| | Fig. 5 Before the reaction, free proteins of species P(1) and P(2) with concentrations c0(P(1)) and c0(P(2)), respectively, and free NPs with concentration c0(NP) are separated. After the reaction has progressed to equilibrium, some proteins are bound to the NP surface (which is in general not yet saturated by proteins), while other proteins, with concentrations c(P(1)) and c(P(2)), are free in solution. All NPs are assumed to have the same average numbers N(1) and N(2) of proteins bound per NP (N(1) + N(2) ≤ Nmax). It should be clearly pointed out, however, that, actually, there will be a statistical distribution of the number of proteins per NP (which we only represent here by the average number). Thus, N(1) and N(2) have to be viewed as average numbers of proteins bound per NP. There also might be interaction between both protein species, which is not included in our simple model. | |
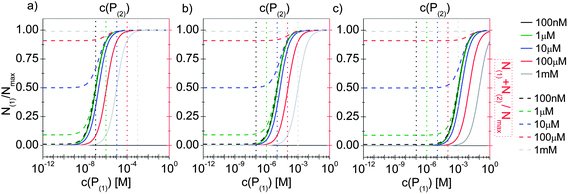 |
| | Fig. 6 The fractions N(1)/Nmax and N(2)/Nmax of proteins of species P(1) and P(2) per NP, are plotted as a function of the concentration c(P(1)) of free protein P(1). N(1) + N(2) ≤ Nmax according to eqn (10). The Hill coefficients of both protein species are assumed to be n(1) = n(2) = 1, and the concentration of half saturation of protein species P(2) is K′D(2) = 10 μM. Different concentrations for protein species P(2) are used: c(P(2)) = 100 nM, 1 μM, 10 μM, 100 μM, 1 mM. Solid and dashed lines represent N(1) and N(1) + N(2)/Nmaxversus the concentration c(P(1)) of free protein P(1), (black and red axes) respectively. (a) K′D(1) = 100 nM. (b) K′D(1) = 10 μM, (c) K′D(1) = 1 mM. The vertical dashed lines indicate c(P(2)). | |
Quantification of the number of proteins bound per nanoparticle and the problem of determining nanoparticle concentrations
Having described protein binding to the surface of NPs with concepts originating from protein biochemistry, we can now try to understand their significance for the experimental determination of the protein corona. An essential parameter that characterizes a protein corona is the average number of proteins N that are bound to the surface of a NP under a given experimental condition. Assuming that virtually all NPs have some proteins bound to their surface (other conditions are not of interest, as then there would be no protein corona), two main parameters are required for a complete characterization of the protein corona, that is, the concentration of NPs in the solution (c0(NP), cf.Fig. 3), and the concentration of proteins bound to the NP surface (cNP(P)):
Though this sounds trivial, unfortunately, the complication lies in the experimental details. Already the NP concentration is hard to determine. First of all, NP concentrations can be quantified differently.2 In our work, we always measure NP concentrations in terms of molarities, i.e., the number of NPs (in [mol]) per volume (in [L]), resulting in the unit M = mol L−1. However, often, NPs are also quantified in terms of mass concentrations in the unit g L−1, or in the overall molar concentration of atoms contained in the NP solution, in mol L−1. Weighing of a dried NP solution can give an estimate for the mass concentration (in g L−1), and the molar concentration of the atoms of dissolved NPs can be determined with element detection techniques such as inductively coupled plasma mass spectrometry (ICP-MS) or atomic absorption spectrometry (AAS), but conversion of these concentration into molar NP concentrations is not straightforward. This is due to the fact that, most often, the molecular mass and the number of atoms per NP, which are the coefficients relating the different concepts of concentration, are not precisely known. We have discussed this problem in a previous review in detail.2
A number of correlation techniques exist with which NP concentrations can be determined directly in solution with high precision, including fluorescence correlation spectroscopy (FCS)46,47 and photothermal absorption correlation spectroscopy (PhACS).48 However, these techniques are very sensitive to agglomeration and, therefore, only suitable for colloidally very stable NPs. For some types of NPs, concentrations can be determined via absorption measurements, in particular, if the NP solution has characteristic absorption peaks. This is, for example, the case for the surface plasmon resonance peak of plasmonic NPs such as Au and Ag, or for the first exciton peak of quantum dots (QDs). In such cases, (more or less precise) estimations for molecular extinction coefficients have been obtained, enabling determination of NP concentrations via determination of the absorption of the NP solution.49–51 However, even if reliable values exist, for example for CdSe NPs, the situation can be complicated if the same NPs are enclosed within an additional shell, e.g., CdSe/ZnS. The shell also changes the optical spectrum of these QDs. In particular, it increases the absorption cross-section and thus the extinction coefficient, which can be observed in the red-shift of the first exciton peak, which indicates an increase in the NP diameter.52 In our experience, determination of the concentration of NPs can easily involve an error of 50% or more. Thus, it is paramount to precisely describe for each experimental study how the concentration of NPs was determined, for example, by stating the molar extinction coefficients used in the calculation. Only in this way, different studies can be compared, taking into account the big experimental error in determining c0(NP). In addition, also the NP dispersion plays a crucial role. Most NPs tend to agglomerate, in particular, in the presence of salt.3 As sketched in Fig. 7, formation of the protein corona around well dispersed NPs is likely to be different compared to a situation in which NPs are highly agglomerated. Thus, experimental studies about the protein corona should always be accompanied by a profound NP characterization, in particular in regard to their colloidal properties. One key parameter in this direction is the hydrodynamic diameter of the NPs (dh), which can, for example, be determined by dynamic light scattering (DLS)35 or by FCS.53,54 In the case that dh is much bigger than the geometric diameter dc of the inorganic core of the NPs, as, for example, determined by transmission electron microscopy (TEM), it is likely that the NPs are not well dispersed but agglomerated.2 Furthermore, absorption spectra are helpful in this direction.35 Extinction at long wavelength (∼1000 nm) is often not due to absorption but scattering of agglomerated NPs, cf.Fig. 7, unless it is due to specific features such as plasmon or exciton peaks, as for example in Au nanorods.
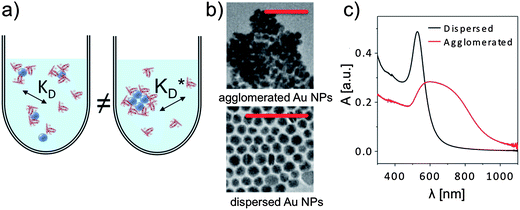 |
| | Fig. 7 (a) Formation of the protein corona is sensitive to the dispersion of the NPs in solution, for example via steric effects. (b) If dried NPs (in this case gold NPs of ca. dc = 15 nm in core diameter) are observed to form agglomerates in TEM imaging (scale bars are 100 nm in both micrographs), they are usually also agglomerated in solution. (c) Agglomeration in solution can be observed with UV/vis absorption spectroscopy, in which the absorption A is plotted versus the wavelength λ. | |
Separation of unbound proteins from nanoparticle–protein conjugates
Not only the NP concentration, but also the concentration of proteins attached to the NPs, cNP(P), is difficult to determine precisely. In situ techniques such as fluorescence correlation spectroscopy (FCS) or analytical ultracentrifugation exist, which do not require separation of the NPs from the solution (in which, in general, unbound proteins are also present). More often, ex situ techniques are employed, in which unbound protein needs to be separated from bound proteins (and NPs). cNP(P) may be determined indirectly ex situ by measuring the concentration of unbound proteins c(P) in the supernatant:| | | cNP(P) = c0(P) − c(P) | (12) |
Alternatively, cNP(P) can also be measured directly ex situ. The required separation step can be quite challenging experimentally. For sufficiently large NPs, they can be precipitated by centrifugation, whereby the NPs with attached proteins are precipitated and the unbound proteins remain in the supernatant.55,56 The supernatant can be separated from the pellet of purified NPs (without excess protein), though, technically it is quite difficult to separate 100% of the supernatant. In particular, all subsequent purification steps (to further remove residual unbound proteins) are associated with complications. Let us assume that the pellet of NPs is redissolved in fresh buffer, precipitated again by centrifugation, followed again by separation of supernatant and NP pellet. Upon removal of free proteins, the equilibrium of eqn (1) and (2) is shifted, and bound proteins will dissociate from the NP surfaces and go into solution. This is relevant for all proteins with mean residence times (inverse koff rates) on the NPs shorter than the duration of the analysis. Consequently, only those proteins that are very strongly (persistently) bound remain on the NPs, and the weakly bound part of the original protein corona is lost. Based on this scenario, Dawson and coworkers have suggested to differentiate between a “hard” and a “soft” corona.57–60 This is a direct consequence of the law of mass action, in which removal of unbound proteins from the solution is compensated by detachment of part of the originally bound proteins. In the case that the protein corona is formed by multiple species P(i), the species with the highest concentration of half saturation K′D(i) will dissociate first. The distinction between proteins forming the “hard” and “soft” corona thus, to first order, is directly related to the half saturation concentrations K′D(i) of the respective protein species P(i). Detachment of bound proteins upon removal of free unbound protein can be clearly visualized with the examples shown in Fig. 4. If NPs are incubated with a protein solution of initial concentration c0(P), the curves shown in Fig. 4 predict the concentration of bound proteins cNP(P). Yet, if the free protein is removed, as aforementioned, the total protein concentration is reduced, c′0(P) < c0(P), and this involves that proteins dissociate from the NP surface. Now the new value c′0(P) has to be used in the curves shown in Fig. 4, leading to a new value of bound protein c′NP(P). We can see from Fig. 4, that if c′0(P) ≫ K′D there will be an increase in the ratio c′NP(P)/c′0(P) > cNP(P)/c0(P) (though c′NP(P) < cNP(P), as, in total, proteins have been removed with the supernatant). This means that due to shortage of protein, a higher percentage of the available proteins are bound to the NP surface. Thus, repetitive purification steps change the equilibrium of the protein corona and do not reflect the original situation. Furthermore, with small NPs (≤10 nm), separation of unbound proteins by centrifugation can be complicated (it may require ultracentrifugation)61 and time-costly due to the very small mass of these NPs. In the case of magnetic NPs, if their magnetic moment is big enough to allow for magnetic precipitation, the NPs can be also trapped in a magnetic field gradient, while unbound proteins can be rinsed away.39 However, according to eqn (1) and (2), this rinsing step again leads to a partial loss of the original protein corona.
Quantification of unbound proteins to deduce the amount of bound proteins
Taking into account the aforementioned technical challenges involved in the separation of unbound proteins from protein–NP conjugates, we continue here with a discussion of methods to determine the concentration of free protein from the separated supernatant. The fraction of protein c(P)/c0(P) remaining free in solution can be derived from Fig. 4. These examples highlight the importance of assessing, at least qualitatively, the strength of the interaction between proteins and NPs (i.e., K′D). Please note that for practical purpose protein concentrations bigger than the NP concentrations (c0(NP) ≪ c0(P)) are desirable, as otherwise no saturated NPs can be obtained. (i) If c0(P) ≫ K′D (and c0(NP) ≪ c0(P)) most of the proteins will remain free in solution, i.e., all NPs are already saturated with proteins and, thus, all additionally added proteins will remain unbound, cf.Fig. 4. Therefore, only a tiny fraction of proteins is removed from the supernatant and attaches to the NP surface, i.e. (c0(P) − c(P))/c0(P) = cNP(P)/c0(P) → 0. The tiny reduction of protein concentration is experimentally very hard to detect, thus prone to error, and absolute quantitative values have to be interpreted with utmost care. In addition, if not all supernatant containing unbound protein has been removed (this is likely due to pipetting errors), then this “contaminates” the solution, and the fraction of proteins attached to the NPs will be wrongfully overestimated. However, there are scenarios in which concentration determination needs to be performed under saturation conditions. One major issue for indirect determination of the fraction of bound proteins is the analysis of competitive binding of proteins to NPs, as it is necessary to analyse the difference between the soft and hard corona.57 In that case, a large excess of protein might be required to displace already bound proteins. (ii) If c0(P) ≈ K′D (and c0(NP) ≪ c0(P)), the NPs are half saturated with proteins on average, and the amounts of free and attached proteins will be in a similar range, cf.Fig. 4. This is the optimum situation in which it is possible to analyse the free proteins as well as the bound proteins. For instance, using ultracentrifugation and chromatography as alternative methods, Lundqvist et al. quantified unbound proteins in the presence of silica NPs (ratio NPs![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) protein = 1
protein = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1).26 It is important to point out that in the mentioned work, the estimation of the attached protein is possible because of the working conditions (c0(P) ≈ K′D). In fact, if the experiments would have been performed at oversaturation (c0(P) ≫ K′D), these methods would not have been reliable.26 (iii) At low protein concentrations (c0(P) ≪ K′D), changes in free protein upon protein binding to NPs can be easily detected in the case of non-cooperative (n = 1) and anti-cooperative binding (n < 1) because a significant fraction of the available proteins is attached to the surface of the NPs, cf.Fig. 4. However, in the case of cooperative binding, almost all proteins are free in solution at very low protein concentrations. Due to the cooperativity of the binding process, significant binding can occur only at higher protein concentrations (c0(P) ≈ K′D), cf.Fig. 4. Thus, the predictions of Fig. 4 help in choosing the experimental conditions under which changes in protein concentration can be determined best.
1).26 It is important to point out that in the mentioned work, the estimation of the attached protein is possible because of the working conditions (c0(P) ≈ K′D). In fact, if the experiments would have been performed at oversaturation (c0(P) ≫ K′D), these methods would not have been reliable.26 (iii) At low protein concentrations (c0(P) ≪ K′D), changes in free protein upon protein binding to NPs can be easily detected in the case of non-cooperative (n = 1) and anti-cooperative binding (n < 1) because a significant fraction of the available proteins is attached to the surface of the NPs, cf.Fig. 4. However, in the case of cooperative binding, almost all proteins are free in solution at very low protein concentrations. Due to the cooperativity of the binding process, significant binding can occur only at higher protein concentrations (c0(P) ≈ K′D), cf.Fig. 4. Thus, the predictions of Fig. 4 help in choosing the experimental conditions under which changes in protein concentration can be determined best.
Direct quantification of proteins bound to nanoparticles
Notwithstanding that, due to the required washing steps, part of the original protein corona has been lost (cf.eqn (1) and (2)), the direct determination of the proteins attached per NP is straightforward. It is not only possible to quantify the amount of attached proteins, but also to specify the species of proteins forming the protein corona. A classical method is enzymatic digestion of the proteins bound to the NP surface, and their subsequent quantification with polyacrylamide gel electrophoresis or with mass spectroscopy.37,39,58,61 Thereby, the attached proteins are sorted by their molecular weight,55 which together with protein databases enables identification of the protein species. As will be demonstrated later, for small NPs (≤10 nm), typically less than Nmax = 100 proteins are bound per NP, and they are statistically distributed. Contributions of hundreds of proteins to the protein corona around NPs have been identified in several reports. It is obvious that not every NP will have the same protein corona.37 Due to a statistical distribution of ≥100 existing protein species (in realistic media which, for example, contain serum) bound to ≤100 protein binding sites per NP, the protein corona of each individual NP can be quite different. Consequently, these details cannot be described with our simplified model.
Indirect quantification of proteins bound to nanoparticles by size measurements
The proteins adsorbed to the NPs can also be quantified indirectly via in situ size measurements. The more proteins are attached per NP, the greater its hydrodynamic radius rh will become. Therefore, the amount of bound proteins can be determined via size measurements of NPs. Obviously, this is only possible for colloidally stable NPs with a narrow size distribution. Such indirect quantification has the huge conceptual advantage that, typically, measurements can be carried out without having to separate unbound excess proteins, and thus, measurements in real equilibrium are possible. There are several standard methods for quantifying hydrodynamic radii, such as dynamic light scattering (DLS59), centrifugation (differential centrifugal sedimentation,59,62 analytical ultracentrifugation63), and fluorescence correlation spectroscopy (FCS53,64). DLS is based on the light scattering from the NPs. To separate the light scattered from the free proteins and the NPs by DLS measurements, the NPs have to be significantly larger (≥10 nm) than the proteins. DLS can then allow for convenient observation of the in situ formation of the protein corona, enabling determination of hydrodynamic radii of protein–NP complexes. For NPs in the size range of proteins, their scattering can no longer be unequivocally separated from the one of unbound proteins.35 FCS is a very attractive alternative to DLS, which however requires fluorescence labelling of the NPs.9 Assuming that fluorescence labelling of the NPs does not interfere with protein corona formation, FCS is only sensitive to the fluorescent protein–NP complexes, provided that the autofluorescence from unbound proteins can be neglected. FCS allows the measurement of hydrodynamic diameters dh = 2rh of small protein–NP complexes (if one assumes spherical NPs; anisotropic shape in general is complicated to analyse39). The measurement of protein corona formation via size determination by FCS or DLS is only possible for smaller NPs. Upon protein adsorption, the hydrodynamic radius of the NPs will increase on the order of the linear dimensions of the protein. While adsorption of 5 nm (diameter) protein may easily be detected on a NP with rh = 5 nm (i.e., a change of 100%), measurement of the size increase of a NP with 100 nm radius (i.e. a change of only 5%) upon protein binding will not be feasible.
Quantification of protein adsorption with fluorescence correlation spectroscopy
Following a simple approximation, we can consider the volume of a protein–NP conjugate as the volume of the NP and N times the volume of one protein VP, given that each NP binds N proteins.54 The hydrodynamic diameter of this conjugate is then| | 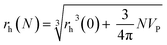 | (13) |
where rNP = rh(0) is the hydrodynamic radius of one plain NP without adsorbed proteins.54 Using eqn (4) for the number of adsorbed proteins per NP, the hydrodynamic radius of protein–NP complexes can be given as a function of the concentration of free protein c(P):54| |  | (14) |
However, as for Fig. 4, where the fraction of bound proteins is represented depending on c0(P), also eqn (14) can be recast in terms of c0(P), by using eqn (5), which transforms c0(P) into c(P). This enables an estimation of the NP radius depending on the amount of added protein, cf.Fig. 8. FCS (and also DLS) allows measurements of rh(c0(P)) as a function of the concentration c0(P) of added protein.54,65,66 Thus, fitting of these experimental data with eqn (14) yields the hydrodynamic radii of the NPs without protein rh(0) and saturated with protein rh(Nmax), respectively. The Hill coefficient n, the concentration of half saturation K′D, and the number of potential binding sites Nmax of proteins per NP remain then as fit parameters. In this way, quantitative data, in particular, K′D, can be extracted. Table 1 summarizes some experimental data extracted in this way for a variety of different NPs and proteins. One of the most striking results from these data is that, under saturation conditions, the corona consists of a single protein monolayer, at least when using highly defined model NPs and only one protein species.54,65,66 The data in Table 1 show, for example, how the surface chemistry of the NPs influences protein adsorption. It has been observed that proteins can preferentially adsorb to surfaces with different charge density by different facets.67 Thus, FCS measurements allow for investigation of protein oriented adsorption to NP surfaces.65
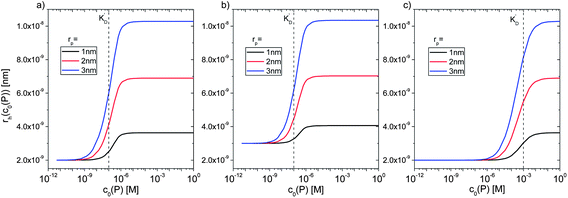 |
| | Fig. 8 Hydrodynamic radius rh of NPs for different protein concentrations c0(P), as calculated according to eqn (14) with the parameters Nmax = 40, n = 1, c0(NP) = 10 nM, 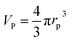 where rP = 1, 2, or 3 nm (idealized globular proteins were considered in these examples). (a) rNP = 2 nm, K′D = 100 nM, (b) rNP = 3 nm, K′D = 100 nM, (c) rNP = 2 nm, K′D = 1 mM. where rP = 1, 2, or 3 nm (idealized globular proteins were considered in these examples). (a) rNP = 2 nm, K′D = 100 nM, (b) rNP = 3 nm, K′D = 100 nM, (c) rNP = 2 nm, K′D = 1 mM. | |
Table 1 Protein adsorption quantified by the Hill model as determined for NPs of different materials (FePt, Au, CdSe/ZnS) and surface coatings (PMA = poly(isobutylene-alt-maleic anhydride),68 P(−) = PMAPHOS-stat-PLMA,35 P(+) = PTMAEMA-stat-PLMA,35 PAA = polyacrylic acid) with different proteins (HSA = human serum albumin, apo-Tf = apo-transferrin, apoA-I = apolipoprotein A-I, apoE4 = apolipoprotein E4) at different temperatures T (RT = room temperature). The radius rc of the (spherical) inorganic cores of the NPs was determined by transmission electron microscopy (TEM). For the FePt NPs reported here,54,65,66 the rc data are taken from Lehmann et al.69 In the case of the CdSe/ZnS NPs, according to the provider (Invitrogen), these NPs are not spherical but ellipsoids with 6 nm and 12 nm axes. rh(0) and rh(Nmax) are the hydrodynamic radii of NPs without adsorbed proteins and upon saturation of the NP surface with proteins (Δrh = rh(Nmax) − rh(0)), respectively, as determined by FCS using the Hill model. The Hill coefficient n controls the steepness of the binding curve, Nmax is the maximum number of proteins adsorbing onto a single NP, and K′D represents the concentration of protein molecules at half coverage
| NP core |
r
c [nm] |
NP coating |
Protein |
T [°C] |
r
h(0) [nm] |
r
h(Nmax) [nm] |
Δrh [nm] |
K
′D [μM] |
n
|
N
max
|
Report |
| FePt |
1.6 ± 0.2 |
PMA |
HSA |
RT |
5.6 ± 0.2 |
8.9 ± 0.3 |
3.3 ± 0.3 |
5.1 ± 1.3 |
0.7 ± 0.1 |
22 ± 4 |
54
|
| FePt |
1.6 ± 0.2 |
PMA |
HSA |
RT |
6.0 ± 0.1 |
9.3 ± 0.3 |
3.3 ± 0.3 |
9.9 ± 4.7 |
0.9 ± 0.2 |
27 ± 3 |
66
|
| FePt |
1.7 ± 0.3 |
PMA |
HSA |
13 |
5.5 ± 0.3 |
9.2 ± 0.4 |
3.7 ± 0.5 |
10 ± 4 |
0.6 ± 0.1 |
31 ± 5 |
39
|
| FePt |
1.7 ± 0.3 |
PMA |
HSA |
23 |
6.0 ± 0.1 |
9.3 ± 0.2 |
3.3 ± 0.2 |
6.3 ± 2.2 |
0.9 ± 0.2 |
30 ± 3 |
39
|
| FePt |
1.7 ± 0.3 |
PMA |
HSA |
43 |
6.0 ± 0.1 |
8.8 ± 0.2 |
2.8 ± 0.2 |
0.8 ± 0.4 |
0.7 ± 0.2 |
23 ± 2 |
39
|
| FePt |
1.6 ± 0.2 |
PMA |
apo-Tf |
RT |
5.1 ± 0.2 |
12.1 ± 0.4 |
7.0 ± 0.4 |
26 ± 6 |
1.7 ± 0.2 |
23 ± 3 |
65
|
| FePt |
1.7 ± 0.3 |
PMA |
apo-Tf |
9 |
5.1 ± 0.2 |
15.1 ± 0.8 |
10.0 ± 0.8 |
13 ± 4 |
0.6 ± 0.1 |
47 ± 7 |
39
|
| FePt |
1.7 ± 0.3 |
PMA |
apo-Tf |
22 |
5.0 ± 0.2 |
14.3 ± 0.7 |
9.3 ± 0.7 |
16 ± 6 |
0.7 ± 0.1 |
40 ± 6 |
39
|
| FePt |
1.7 ± 0.3 |
PMA |
apo-Tf |
43 |
5.3 ± 0.1 |
11.0 ± 0.4 |
5.7 ± 0.4 |
5 ± 1 |
0.7 ± 0.1 |
17 ± 2 |
39
|
| FePt |
1.6 ± 0.2 |
PMA |
apoA-I |
RT |
6.0 ± 0.1 |
10.8 ± 1.4 |
4.8 ± 1.4 |
140 ± 60 |
1.0 ± 0.3 |
52 ± 10 |
66
|
| FePt |
1.6 ± 0.2 |
PMA |
apoE4 |
RT |
6.0 ± 0.1 |
11.7 ± 0.2 |
5.7 ± 0.2 |
0.021 ± 0.003 |
1.4 ± 0.2 |
65 ± 3 |
66
|
| Au |
2.3 ± 0.6 |
P(−) |
HSA |
RT |
7.9 ± 0.2 |
10.4 ± 0.3 |
2.5 ± 0.3 |
1.5 ± 0.8 |
0.8 ± 0.3 |
32 ± 4 |
35
|
| Au |
2.3 ± 0.6 |
P(+) |
HSA |
RT |
5.1 ± 0.1 |
9.4 ± 0.4 |
4.3 ± 0.4 |
1.0 ± 0.3 |
0.8 ± 0.3 |
35 ± 3 |
35
|
| CdSe/ZnS |
6 × 12 |
PAA |
HSA |
RT |
7.9 ± 0.3 |
11.1 ± 0.4 |
3.2 ± 0.5 |
37 ± 12 |
0.8 ± 0.2 |
36 ± 8 |
54
|
Future perspectives
As discussed in this review, there is no need to reinvent the wheel in regard to characterization of the protein corona because a body of work from protein biochemistry can be adapted to this problem. Further continuing along this path will lead to more quantitative data, for example, dissociation constants, on- and off-rate coefficients, etc. Nowadays, the literature is mainly based on qualitative statements like “the protein corona is what the cell sees”.62 In the future, however, such statements need to be placed in the context of more quantitative data. While the protein corona is of high importance, it is not the only relevant feature of the bio-interface of NPs. Quantitative data will help to compare different systems and to better understand the underlying molecular mechanisms. In our view, the most relevant technical problems that need to be solved to obtain more solid, quantitative data are (i) insufficient NP quality, especially in regard to size distribution and agglomeration, (ii) lack of precise data on NP concentrations, and (iii) purification of protein–NP complexes from unbound protein, without changing the nature of the original protein corona. The last point maybe is the most important one and comprises also an experimental dilemma. As pointed out above, purification (as required for ex situ quantification) can change the equilibrium, and part of the original protein corona will dissociate. Whether this occurs or not is mainly determined by the koff rate coefficients. Inverse off-rates (i.e., how fast proteins can dissociate from the NP surface) can be on the minute time scale, and even faster, which is faster than possible purification steps.54 Thus, meaningful characterization of the protein corona would also involve determination of off-rates (which, together with the equilibrium dissociation coefficients, would also provide the corresponding on-rate coefficients, according to eqn (2)). Improvement regarding (i)–(iii) will help to extend future studies to new fields. Here we have only considered equilibrium conditions, but equilibrium may not always be reached if the kinetics are too slow. In this context, the determination of on- and off-rates will be crucial. We however want to point out that our models as presented here will not provide any details about the actual absorption mechanism, i.e. whether proteins are bound by electrostatic or hydrophobic interaction,32 or whether NPs change the conformation of adsorbed proteins,33,70etc.
So far, there are two distinct directions in which the analysis of the protein corona has progressed. On the one hand, model systems have been widely investigated in which NPs are incubated with only one protein species, whose behaviour can be analysed quantitatively. These systems are highly simplified, but allow for the quantitative determination of equilibrium and kinetic parameters.54 On the other hand, because nature is more complex, and hundreds of different types of proteins can adsorb from serum to the surface of NPs, we also require studies that more closely resemble the more realistic biological situation. Methods such as mass spectroscopy allow for a time-dependent analysis of the composition of the protein corona.37 However, the systems are too complex for allowing the extraction of quantitative parameters of individual protein species. In the future, both directions should be merged, leading to more complex model systems, in which, for example, replacement of one protein species by another one is investigated in detail, such as is in principle treated by eqn (9) and (10). Development of such models will again lead to quantitative investigations. While the literature is full of qualitative description about the protein corona formed around hundreds of different NPs, the future will lie towards a more quantitative analysis, which will lead to a better understanding of the underlying principles and comparability of different studies.
Acknowledgements
This work was funded in part by HFSP (project RGP0052/2012 to WJP). We thank the Deutsche Forschungsgemeinschaft (DFG) for financial support through the Priority Program SPP1313 (to GUN and WJP). QZ is grateful for a fellowship from the Chinese Government and BP for a fellowship from the Alexander von Humboldt Foundation.
References
- I. Freestone, N. Meeks, M. Sax and C. Higgitt, Gold Bull., 2007, 40, 270–277 CrossRef CAS.
- P. Rivera Gil, D. Jimenez de Aberasturi, V. Wulf, B. Pelaz, P. del Pino, Y. Zhao, J. de la Fuente, I. Ruiz de Larramendi, T. Rojo, X.-J. Liang and W. J. Parak, Acc. Chem. Res., 2013, 46, 743–749 CrossRef CAS PubMed.
- T. Pellegrino, S. Kudera, T. Liedl, A. M. Javier, L. Manna and W. J. Parak, Small, 2005, 1, 48–63 CrossRef CAS PubMed.
- H. Takeuchi, B. Omogo and C. D. Heyes, Nano Lett., 2013, 13(10), 4746–4752 CrossRef CAS PubMed.
- K. Boldt, O. T. Bruns, N. Gaponik and A. Eychmüller, J. Phys. Chem. B, 2006, 110, 1959–1963 CrossRef CAS PubMed.
- J. Aldana, Y. A. Wang and X. Peng, J. Am. Chem. Soc., 2001, 123, 8844–8850 CrossRef CAS PubMed.
- D. Gerion, F. Pinaud, S. C. Williams, W. J. Parak, D. Zanchet, S. Weiss and A. P. Alivisatos, J. Phys. Chem. B, 2001, 105, 8861–8871 CrossRef CAS.
- T. Pellegrino, L. Manna, S. Kudera, T. Liedl, D. Koktysh, A. L. Rogach, S. Keller, J. Rädler, G. Natile and W. J. Parak, Nano Lett., 2004, 4, 703–707 CrossRef CAS.
- F. Zhang, E. Lees, F. Amin, P. Rivera Gil, F. Yang, P. Mulvaney and W. J. Parak, Small, 2011, 7, 3113–3127 CrossRef CAS PubMed.
- K. E. Sapsford, W. R. Algar, L. Berti, K. B. Gemmill, B. J. Casey, E. Oh, M. H. Stewart and I. L. Medintz, Chem. Rev., 2013, 113, 1904–2074 CrossRef CAS PubMed.
- J. B. Delehanty, H. Mattoussi and I. L. Medintz, Anal. Bioanal. Chem., 2009, 393, 1091–1105 CrossRef CAS PubMed.
- E. E. Lees, T. L. Nguyen, A. H. Clayton and P. Mulvaney, ACS Nano, 2009, 3, 1121–1128 CrossRef CAS PubMed.
- C. Tassa, S. Y. Shaw and R. Weissleder, Acc. Chem. Res., 2011, 44(10), 842–852 CrossRef CAS PubMed.
- M. S. Nikolic, C. Olsson, A. Salcher, A. Kornowski, A. Rank, R. Schubert, A. Fromsdorf, H. Weller and S. Forster, Angew. Chem., Int. Ed., 2009, 48, 2752–2754 CrossRef CAS PubMed.
- V. V. Breus, C. D. Heyes, K. Tron and G. U. Nienhaus, ACS Nano, 2009, 3, 2573–2580 CrossRef CAS PubMed.
- J. Domke, S. Dannöhl, W. J. Parak, O. Müller, W. K. Aicher and M. Radmacher, Colloids Surf., B, 2000, 19, 367–379 CrossRef CAS.
- C. D. Heyes, A. Y. Kobitski, E. V. Amirgoulova and G. U. Nienhaus, J. Phys. Chem. B, 2004, 108, 13387–13394 CrossRef CAS.
- M. Mrksich and G. M. Whitesides, Annu. Rev. Biophys. Biomol. Struct., 1996, 25, 55–78 CrossRef CAS PubMed.
- E. Ostuni, R. G. Chapman, R. E. Holmlin, S. Takayama and G. M. Whitesides, Langmuir, 2001, 17, 5605–5620 CrossRef CAS.
- E. V. Amirgoulova, J. Groll, C. D. Heyes, T. Ameringer, C. Rocker, M. Moller and G. U. Nienhaus, ChemPhysChem, 2004, 5, 552–555 CrossRef CAS PubMed.
- S.-Y. Jung, S.-M. Lim, F. Albertorio, G. Kim, M. C. Gurau, R. D. Yang, M. A. Holden and P. S. Cremer, J. Am. Chem. Soc., 2003, 125, 12782–12786 CrossRef CAS PubMed.
- R. Gref, M. Lück, P. Quellec, M. Marchand, E. Dellacherie, S. Harnisch, T. Blunk and R. H. Müller, Colloids Surf., B, 2000, 18, 301–313 CrossRef CAS.
- V. C. F. Mosqueira, P. Legrand, A. Gulik, O. Bourdon, R. Gref, D. Labarre and G. Barratt, Biomaterials, 2001, 22, 2967–2979 CrossRef CAS.
- Y. Zhang, N. Kohler and M. Q. Zhang, Biomaterials, 2002, 23, 1553–1561 CrossRef CAS.
- S. M. Moghimi and J. Szebeni, Prog. Lipid Res., 2003, 42, 463–478 CrossRef CAS.
- M. Lundqvist, I. Sethson and B.-H. Jonsson, Langmuir, 2004, 20, 10639–10647 CrossRef CAS PubMed.
- K. Anikin, C. Rocker, A. Wittemann, J. Wiedenmann, M. Ballauff and G. U. Nienhaus, J. Phys. Chem. B, 2005, 109, 5418–5420 CrossRef CAS PubMed.
- G. B. Sukhorukov, A. L. Rogach, B. Zebli, T. Liedl, A. G. Skirtach, K. Köhler, A. A. Antipov, N. Gaponik, A. S. Susha, M. Winterhalter and W. J. Parak, Small, 2005, 1, 194–200 CrossRef CAS PubMed.
- T. Cedervall, I. Lynch, S. Lindman, T. Berggård, E. Thulin, H. Nilsson, K. A. Dawson and S. Linse, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 2050–2055 CrossRef CAS PubMed.
- M. Lundqvist, J. Stigler, G. Elia, I. Lynch, T. Cedervall and K. A. Dawson, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 14265–14270 CrossRef CAS PubMed.
- Z. J. Deng, M. Liang, M. Monteiro, I. Toth and R. F. Minchin, Nat. Nanotechnol., 2011, 6, 39–44 CrossRef CAS PubMed.
- R. Huang, R. P. Carney, F. Stellacci and B. L. T. Lau, Nanoscale, 2013, 5, 6928–6935 RSC.
- S. Goy-Lopez, J. Juarez, M. Alatorre-Meda, E. Casals, V. F. Puntes, P. Taboada and V. Mosquera, Langmuir, 2012, 28, 9113–9126 CrossRef CAS PubMed.
- N. Feliu, M. V. Walter, M. I. Montanez, A. Kunzmann, A. Hult, A. Nystrom, M. Malkoch and B. Fadeel, Biomaterials, 2012, 33, 1970–1981 CrossRef CAS PubMed.
- D. Hühn, K. Kantner, C. Geidel, S. Brandholt, I. De Cock, S. J. H. Soenen, P. Rivera Gil, J.-M. Montenegro, K. Braeckmans, K. Müllen, G. U. Nienhaus, M. Klapper and W. J. Parak, ACS Nano, 2013, 7, 3253–3263 CrossRef PubMed.
- J. S. Gebauer, M. Malissek, S. Simon, S. K. Knauer, M. Maskos, R. H. Stauber, W. Peukert and L. Treuel, Langmuir, 2012, 28, 9673–9679 CrossRef CAS PubMed.
- S. Tenzer, D. Docter, S. Rosfa, A. Wlodarski, J. Kuharev, A. Rekik, S. K. Knauer, C. Bantz, T. Nawroth, C. Bier, J. Sirirattanapan, W. Mann, L. Treuel, R. Zellner, M. Maskos, H. Schild and R. H. Stauber, ACS Nano, 2011, 5, 7155–7167 CrossRef CAS PubMed.
- A. Lesniak, A. Campbell, M. P. Monopoli, I. Lynch, A. Salvati and K. A. Dawson, Biomaterials, 2010, 31, 9511–9518 CrossRef CAS PubMed.
- M. Mahmoudi, A. M. Abdelmonem, S. Behzadi, J. H. Clement, S. Dutz, M. R. Ejtehadi, R. Hartmann, K. Kantner, U. Linne, P. Maffre, S. Metzler, M. K. Moghadam, C. Pfeiffer, M. Rezaei, P. Ruiz-Lozano, V. Serpooshan, M. A. Shokrgozar, G. U. Nienhaus and W. J. Parak, ACS Nano, 2013, 7, 6555–6562 CrossRef CAS PubMed.
- E. Casals, T. Pfaller, A. Duschl, G. J. Oostingh and V. F. Puntes, ACS Nano, 2010, 4, 3623–3632 CrossRef CAS PubMed.
- E. Casals, T. Pfaller, A. Duschl, G. J. Oostingh and V. F. Puntes, Small, 2011, 7, 3479–3486 CrossRef CAS PubMed.
- S. Tenzer, D. Docter, J. Kuharev, A. Musyanovych, V. Fetz, R. Hecht, F. Schlenk, D. Fischer, K. Kiouptsi, C. Reinhardt, K. Landfester, H. Schild, M. Maskos, S. K. Knauer and R. H. Stauber, Nat. Nanotechnol., 2013, 8, 772–781 CrossRef CAS PubMed.
- B. Fadeel, N. Feliu, C. Vogt, A. M. Abdelmonem and W. J. Parak, Wiley Interdiscip. Rev.: Nanomed. Nanobiotechnol., 2013, 5, 111–129 CrossRef CAS PubMed.
- A. V. Hill, J. Physiol., 1910, 40, i–vii Search PubMed.
- S. Goutelle, M. Maurin, F. Rougier, X. Barbaut, L. Bourguignon, M. Ducher and P. Maire, Fundam. Clin. Pharmacol., 2008, 22, 633–648 CrossRef CAS PubMed.
- P. Schwille, J. Bieschke and F. Oehlenschläger, Biophys. Chem., 1997, 66, 211–228 CrossRef CAS.
- L. Zemanova, A. Schenk, M. J. Valler, G. U. Nienhaus and R. Heilker, Drug Discovery Today, 2003, 8, 1085–1093 CrossRef CAS.
- V. Octeau, L. Cognet, L. Duchesne, D. Lasne, N. Schaeffer, D. G. Fernig and B. Lounis, ACS Nano, 2009, 3, 345–350 CrossRef CAS PubMed.
- W. W. Yu, L. Qu, W. Guo and X. Peng, Chem. Mater., 2003, 15, 2854–2860 CrossRef CAS.
- A. Striolo, J. Ward, J. M. Prausnitz, W. J. Parak, D. Zanchet, D. Gerion, D. J. Milliron and A. P. Alivisatos, J. Phys. Chem. B, 2002, 106, 5500–5505 CrossRef CAS.
- W. Haiss, N. T. K. Thanh, J. Aveyard and D. G. Fernig, Anal. Chem., 2007, 79, 4215–4221 CrossRef CAS PubMed.
- B. O. Dabbousi, J. Rodriguez-Viejo, F. V. Mikulec, J. R. Heine, H. Mattoussi, R. Ober, K. F. Jensen and M. G. Bawendi, J. Phys. Chem. B, 1997, 101, 9463–9475 CrossRef CAS.
- T. Liedl, S. Keller, F. C. Simmel, J. O. Rädler and W. J. Parak, Small, 2005, 1, 997–1003 CrossRef CAS PubMed.
- C. Röcker, M. Pötzl, F. Zhang, W. J. Parak and G. U. Nienhaus, Nat. Nanotechnol., 2009, 4, 577–580 CrossRef PubMed.
- M. Schaeffler, M. Semmler-Behnke, H. Sarioglu, S. Takenaka, A. Wenk, C. Schleh, S. M. Hauck, B. D. Johnston and W. G. Kreyling, Nanotechnology, 2013, 24, 265103 CrossRef CAS PubMed.
- A. S. Pitek, D. O'Connell, E. Mahon, M. P. Monopoli, F. B. Bombelli and K. A. Dawson, PLoS One, 2012, 7, e40685 CAS.
- S. Milani, F. B. Bombelli, A. S. Pitek, K. A. Dawson and J. Radler, ACS Nano, 2012, 6, 2532–2541 CrossRef CAS PubMed.
- A. Lesniak, F. Fenaroli, M. R. Monopoli, C. Aberg, K. A. Dawson and A. Salvati, ACS Nano, 2012, 6, 5845–5857 CrossRef CAS PubMed.
- M. P. Monopoli, D. Walczyk, A. Campbell, G. Elia, I. Lynch, F. B. Bombelli and K. A. Dawson, J. Am. Chem. Soc., 2011, 133, 2525–2534 CrossRef CAS PubMed.
- M. Lundqvist, J. Stigler, T. Cedervall, T. Berggard, M. B. Flanagan, I. Lynch, G. Elia and K. Dawson, ACS Nano, 2011, 5, 7503–7509 CrossRef CAS PubMed.
- A. Jedlovszky-Hajdu, F. B. Bombelli, M. P. Monopoli, E. Tombacz and K. A. Dawson, Langmuir, 2012, 28, 14983–14991 CrossRef CAS PubMed.
- D. Walczyk, F. B. Bombelli, M. P. Monopoli, I. Lynch and K. A. Dawson, J. Am. Chem. Soc., 2010, 132, 5761–5768 CrossRef CAS PubMed.
- E. E. Lees, M. J. Gunzburg, T.-L. Nguyen, G. J. Howlett, J. Rothacker, E. C. Nice, A. H. A. Clayton and P. Mulvaney, Nano Lett., 2008, 8, 2883–2890 CrossRef CAS PubMed.
- G. U. Nienhaus, P. Maffre and K. Nienhaus, Methods Enzymol., 2013, 519, 115–137 CAS.
- X. Jiang, S. Weise, M. Hafner, C. Röcker, F. Zhang, W. J. Parak and G. U. Nienhaus, J. R. Soc., Interface, 2010, 7, S5–S13 CrossRef CAS PubMed.
- P. Maffre, K. Nienhaus, F. Amin, W. J. Parak and G. U. Nienhaus, Beilstein J. Nanotechnol., 2011, 2, 374–383 CrossRef CAS PubMed.
- K. W. Mattison, P. L. Dubin and I. J. Brittain, J. Phys. Chem. B, 1998, 102, 3830–3836 CrossRef CAS.
- C.-A. J. Lin, R. A. Sperling, J. K. Li, T.-Y. Yang, P.-Y. Li, M. Zanella, W. H. Chang and W. J. Parak, Small, 2008, 4, 334–341 CrossRef CAS PubMed.
- A. D. Lehmann, W. J. Parak, F. Zhang, Z. Ali, C. Röcker, G. U. Nienhaus, P. Gehr and B. Rothen-Rutishauser, Small, 2010, 6, 753–762 CrossRef CAS PubMed.
- S. I. Yoo, M. Yang, J. R. Brender, V. Subramanian, K. Sun, N. E. Joo, S. H. Jeong, A. Ramamoorthy and N. A. Kotov, Angew. Chem., Int. Ed., 2011, 50, 5110–5115 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c3mh00106g |
|
| This journal is © The Royal Society of Chemistry 2014 |
Click here to see how this site uses Cookies. View our privacy policy here. 



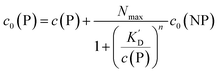
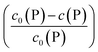 , can be calculated depending on the initial parameters c0(P), c0(NP), cf.Fig. 4. Here, c(P) needs to be derived implicitly from eqn (5). For all steps of the calculation, we refer to the ESI.† If c(P) is much greater than K′D, each NP is saturated with Nmax proteins, and the fraction becomes
, can be calculated depending on the initial parameters c0(P), c0(NP), cf.Fig. 4. Here, c(P) needs to be derived implicitly from eqn (5). For all steps of the calculation, we refer to the ESI.† If c(P) is much greater than K′D, each NP is saturated with Nmax proteins, and the fraction becomes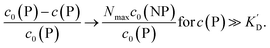

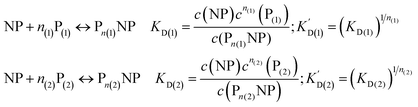
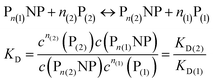


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) protein = 1
protein = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1).26 It is important to point out that in the mentioned work, the estimation of the attached protein is possible because of the working conditions (c0(P) ≈ K′D). In fact, if the experiments would have been performed at oversaturation (c0(P) ≫ K′D), these methods would not have been reliable.26 (iii) At low protein concentrations (c0(P) ≪ K′D), changes in free protein upon protein binding to NPs can be easily detected in the case of non-cooperative (n = 1) and anti-cooperative binding (n < 1) because a significant fraction of the available proteins is attached to the surface of the NPs, cf.Fig. 4. However, in the case of cooperative binding, almost all proteins are free in solution at very low protein concentrations. Due to the cooperativity of the binding process, significant binding can occur only at higher protein concentrations (c0(P) ≈ K′D), cf.Fig. 4. Thus, the predictions of Fig. 4 help in choosing the experimental conditions under which changes in protein concentration can be determined best.
1).26 It is important to point out that in the mentioned work, the estimation of the attached protein is possible because of the working conditions (c0(P) ≈ K′D). In fact, if the experiments would have been performed at oversaturation (c0(P) ≫ K′D), these methods would not have been reliable.26 (iii) At low protein concentrations (c0(P) ≪ K′D), changes in free protein upon protein binding to NPs can be easily detected in the case of non-cooperative (n = 1) and anti-cooperative binding (n < 1) because a significant fraction of the available proteins is attached to the surface of the NPs, cf.Fig. 4. However, in the case of cooperative binding, almost all proteins are free in solution at very low protein concentrations. Due to the cooperativity of the binding process, significant binding can occur only at higher protein concentrations (c0(P) ≈ K′D), cf.Fig. 4. Thus, the predictions of Fig. 4 help in choosing the experimental conditions under which changes in protein concentration can be determined best.
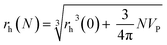


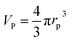 where rP = 1, 2, or 3 nm (idealized globular proteins were considered in these examples). (a) rNP = 2 nm, K′D = 100 nM, (b) rNP = 3 nm, K′D = 100 nM, (c) rNP = 2 nm, K′D = 1 mM.
where rP = 1, 2, or 3 nm (idealized globular proteins were considered in these examples). (a) rNP = 2 nm, K′D = 100 nM, (b) rNP = 3 nm, K′D = 100 nM, (c) rNP = 2 nm, K′D = 1 mM.







