DOI:
10.1039/D5SM00129C
(Paper)
Soft Matter, 2025,
21, 4533-4540
Wave front propagation in the active coagulation model
Received
5th February 2025
, Accepted 3rd May 2025
First published on 9th May 2025
Abstract
Spreading processes on top of active dynamics provide a novel theoretical framework for capturing emerging collective behavior in living systems. I consider run-and-tumble dynamics coupled with coagulation/decoagulation reactions that lead to an absorbing state phase transition. While the active dynamics does not change the location of the transition point, the relaxation toward the stationary state depends on motility parameters. Because of the competition between spreading dynamics and active motion, the system can support long-living currents whose typical time scale is a nontrivial function of motility and reaction rates. Because of this interplay between time-scales, the wave front propagation qualitatively changes from traveling to diffusive waves. Moving beyond the mean-field regime, instability at finite length scales regulates a crossover from periodic to diffusive modes. Finally, it is possible to individuate different mechanisms of pattern formation on a large time scale, ranging from the Fisher–Kolmogorov to the Kardar–Parisi–Zhang equation.
I. Introduction
In the biological world, most of the interactions do not have a strong constraint for being symmetric. Examples include social interactions,1 the synaptic dynamics in neural nets,2 and biochemical reactions.3 Breaking symmetric interaction rules is another way to fall out of equilibrium.4 Recent studies have focused on non-symmetric interactions, particularly at the mesoscopic level,5,6 in both numerical simulations and coarse-graining theory,7 as well as minimal mixed spin models with distinct interaction rules for different spin variables.8 The present work instead focuses on the simplest scenario, familiar in statistical physics: reaction rules that are inherently non-symmetrical and typically lead to absorbing states, which break detailed balance.3 A typical application of absorbing state phase transitions is the population growth of a single species, where, in the absorbing state, the population becomes extinct while, in the mixed state, the balance between birth and death processes fixes the typical population size. The birth/date processes lead to non-linear equations that, once coupled with the diffusion process, can support wave propagations. Diffusion-driven (and thus noise-driven) wave propagation plays a crucial role in many biological processes (see (ref. 9) for details). The situation is much less clear if the population rearranges itself because of active dynamics. This is a case of practical interest: for instance, when two microbial bacterial strains compete with each other, segregation patterns emerge.10 More generally, in the case of chemical waves that play an important role in developmental biology.11 This scenario naturally connects to the broader question of how spreading processes (e.g., Susceptible-Infected-Susceptible or Susceptible-Infected-Removed dynamics9), are affected by active dynamics. This is an emerging research field where the key question is what collective behavior results from the competition/cooperation of self-propelled motion and contagious dynamics.12–24
Here, I consider a minimal population growth model, the so-called coagulation model. The coagulation model describes a single species undergoing coagulation and decoagulation reactions, which change the number of particles. These reactions introduce additional time scales that compete with those of the active dynamics. Once we add self-propulsion, we can think of the model as a model of self-propelled agents that annihilate at a rate β and spontaneously duplicate at a rate μ. I will focus mostly on the mixed state, where the population size is set but the ratio μ/β. While other active matter models in which the number of particles is not a conserved quantity have been explored in connection with pattern formation,25,26 this work focuses on how the competition of time scales produces qualitative different regimes in the front wave propagation of the active particle systems. This work shows that assuming rapidly decaying currents is problematic when multiple time scales are present. This is because long-living currents arise from the density–current coupling, where the coagulation rate is the coupling constant. When this coupling is not negligible, the system requires increasingly longer times to reach a stationary state. This increased relaxation time is associated with damped traveling waves that do not always relax monotonically to the stationary state.
II. Active coagulation model
To provide a general framework for studying the impact of active motion on population dynamics, I employ the so-called coagulation model that considers just two types of reaction processes: a particle disappears with a density-dependent rate ![[small beta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10e.gif) (ρ) and appears at a constant rate μ, where ρ represents the number density of active particles. The reaction process that makes particles disappear is called coagulation, and the reason why its rate is density-dependent will be clear later. The other reaction that allows particles to appear is called decoagulation. On top of that, I consider active motion within the so-called run-and-tumble dynamics. Without loss of generality, I will focus on the one-dimensional case that is general enough to capture the salient phenomenology of active matter. In run-and-tumble dynamics, we have two species of particles: the ones moving to the right and the ones moving to the left. I will consider both species moving at constant velocity. Right-moving particles invert their direction (in one spatial dimension, there is not enough space for a rotation of a finite angle) at a rate α, usually called the tumbling rate. The same happens for the left-moving ones. Adopting the standard notation for run-and-tumble active particles in one spatial dimension, R ≡ R(x, t) and L ≡ L(x, t) indicate the fraction of right-moving and left-moving particles, respectively.27 The active motion is characterized by the self-propulsion velocity v and the tumbling rate α. In the limit v → ∞ and α → ∞ with fixed diffusion constant DA = v2/α, the random walk reduces to the standard Brownian motion. On top of the active motion, I consider a coagulation process characterized by two parameters. In the following, β indicates the reaction rate of the coagulation reaction (that is now on a density-independent rate), and with μ the rate of the offspring production (decoagulation). The microscopic picture is the following. If A indicates the presence of an active particle in some point of space at a given time, and ∅ indicates no particles, within coagulation dynamics one has to consider two elementary processes: the coagulation process that tends to annihilate particles, i.e., a particle spontaneously disappears, and the decoagulation process which introduces a new particle. After adding self-propelled motion, the set of reactions is
(ρ) and appears at a constant rate μ, where ρ represents the number density of active particles. The reaction process that makes particles disappear is called coagulation, and the reason why its rate is density-dependent will be clear later. The other reaction that allows particles to appear is called decoagulation. On top of that, I consider active motion within the so-called run-and-tumble dynamics. Without loss of generality, I will focus on the one-dimensional case that is general enough to capture the salient phenomenology of active matter. In run-and-tumble dynamics, we have two species of particles: the ones moving to the right and the ones moving to the left. I will consider both species moving at constant velocity. Right-moving particles invert their direction (in one spatial dimension, there is not enough space for a rotation of a finite angle) at a rate α, usually called the tumbling rate. The same happens for the left-moving ones. Adopting the standard notation for run-and-tumble active particles in one spatial dimension, R ≡ R(x, t) and L ≡ L(x, t) indicate the fraction of right-moving and left-moving particles, respectively.27 The active motion is characterized by the self-propulsion velocity v and the tumbling rate α. In the limit v → ∞ and α → ∞ with fixed diffusion constant DA = v2/α, the random walk reduces to the standard Brownian motion. On top of the active motion, I consider a coagulation process characterized by two parameters. In the following, β indicates the reaction rate of the coagulation reaction (that is now on a density-independent rate), and with μ the rate of the offspring production (decoagulation). The microscopic picture is the following. If A indicates the presence of an active particle in some point of space at a given time, and ∅ indicates no particles, within coagulation dynamics one has to consider two elementary processes: the coagulation process that tends to annihilate particles, i.e., a particle spontaneously disappears, and the decoagulation process which introduces a new particle. After adding self-propelled motion, the set of reactions is| |  | (1) |
The set of reactions is shown in Fig. 2, which provides a pictorial representation of a microscopic lattice–gas version of the model under consideration. However, instead of considering the lattice-based picture, I will consider a suitable coarse-grained version obtained by noticing that coagulation processes are proportional to ρ2(x, t) while decoagulation is proportional to ρ(x, t), with ρ(x, t) the density field.3 In the case of run-and-tumble dynamics, on top of that, we have other “two species” of particles: the ones moving to the right and the ones moving to the left. I will employ these three elementary processes in the following fashion| |  | (2) |
once one introduces the current J(x, t) ≡ J = v(R − L) and the probability density ρ(x, t) ≡ ρ = R + L, the equations of motion for J and ρ are| |  | (4) |
| | ![[J with combining dot above]](https://www.rsc.org/images/entities/i_char_004a_0307.gif) = −v2ρ′ − J[α + μ − βρ] = −v2ρ′ − J[α + μ − βρ] | (5) |
| |  | (6) |
The quadratic term in  generates linear interactions that tend to bring the system to extinction. Non-linear interactions with coupling constant β are therefore essential for the existence of stationary solutions with ρ ≠ 0. The nonlinearities in (4) generally render the dynamics analytically intractable. Fig. 1 depicts the typical behavior of
generates linear interactions that tend to bring the system to extinction. Non-linear interactions with coupling constant β are therefore essential for the existence of stationary solutions with ρ ≠ 0. The nonlinearities in (4) generally render the dynamics analytically intractable. Fig. 1 depicts the typical behavior of  as the mass term μ changes from negative to positive values. Since μ represents a rate, negative values are physically meaningless, however, in the spirit of critical phenomena where the mass tunes the distance from the critical point, μ should be understood in the same way as distance from the critical point where the two fixed points of the dynamics become a marginal point. In any case, from the point of view of the coarse-grained model considered here, μ can take either positive or negative values.
as the mass term μ changes from negative to positive values. Since μ represents a rate, negative values are physically meaningless, however, in the spirit of critical phenomena where the mass tunes the distance from the critical point, μ should be understood in the same way as distance from the critical point where the two fixed points of the dynamics become a marginal point. In any case, from the point of view of the coarse-grained model considered here, μ can take either positive or negative values.
 |
| | Fig. 1 Absorbing state phase transition. The function  (see (6)) develops a minimum in ρ = 0 for μ ≤ 0 that changes to ρ = μ/β ≠ 0 for μ > 0. (see (6)) develops a minimum in ρ = 0 for μ ≤ 0 that changes to ρ = μ/β ≠ 0 for μ > 0. | |
 |
| | Fig. 2 Active coagulation model. The active coagulation model involves three key processes: a run-and-tumble dynamics characterized by a tumbling rate α and self-propulsion velocity v, a coagulation process governed by the reaction rate β, and a decoagulation process controlled by the rate μ. These processes are depicted in the top row as a lattice–gas model. Moving to a coarse-grained description, active motion and decoagulation contribute terms proportional to the density field ρ(x, t), while the coagulation process introduces a nonlinear interaction term proportional to ρ2(x, t). | |
It is worth recalling the picture without coagulation dynamics, where the equations for ρ and J become
| | ![[small rho, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a6.gif) = −J′ = −J′ | (7) |
| | ![[J with combining dot above]](https://www.rsc.org/images/entities/i_char_004a_0307.gif) = −v2ρ′ − αJ. = −v2ρ′ − αJ. | (8) |
In this case, the dynamics of the system is governed by a second-order differential equation that can be obtained simply by computing
![[greek rho with two dots above]](https://www.rsc.org/images/entities/i_char_e1a8.gif)
= −
![[J with combining dot above]](https://www.rsc.org/images/entities/i_char_004a_0307.gif)
′ so that
| | ![[greek rho with two dots above]](https://www.rsc.org/images/entities/i_char_e1a8.gif) + α + α![[small rho, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a6.gif) − v2ρ′′ = 0. − v2ρ′′ = 0. | (9) |
This telegrapher equation predicts wave propagation on short-time scales that eventually diffuse.
28 One can rationalize that studying the limiting case
α → ∞ at fixed diffusive constant
DA ≡
v2/
α that reproduce the standard diffusive equation
| | ![[small rho, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a6.gif) = DAρ′′ = DAρ′′ | (10) |
while in the opposite limit
α → 0 one gets the standard wave equation
| | ![[greek rho with two dots above]](https://www.rsc.org/images/entities/i_char_e1a8.gif) = v2ρ′′, = v2ρ′′, | (11) |
so that the model interpolates between a ballistic motion on time scales
t <
α−1 and a diffusive regime for
t >
α−1. The presence of an additional dynamical process, as in the case of the coagulation dynamics considered here, introduces another time scale that enters in competition with
α−1. We also notice that, if we look at solutions of
(7) and (8) that do not depend on space,
i.e., mean-field like solutions
ρ(
x,
t) =
ρ(
t) and
J(
x,
t) =
J(
t), one has
![[small rho, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a6.gif)
= 0 and
![[J with combining dot above]](https://www.rsc.org/images/entities/i_char_004a_0307.gif)
= −
αJ,
i.e.,
ρ and
J decouple from each other, the current decays on the time scale
α−1 (
J(
t) =
J(0)e
−αt and the density is uniform
ρ(
t) =
ρ(0) = const).
Well-mixed approximation
To understand what is the effect of an additional time scale, I first study the mean-field picture that one obtains by neglecting any spatial dependency of ρ and J so that ρ′ = J′ = 0. In this limit, one can find the analytical solution of the dynamics that turns out to be different from the standard RT dynamics where ρ(t) is constant and J(t) does not depend on ρ(t) (see (7)). The equation for ρ is the well-known logistic equation| |  | (12) |
with the analytical solution (with the initial condition ρ(0) = 1)| |  | (13) |
However, in contrast with a coagulation model in the mean-field approximation, in this case, there is still the equation for the current J(t) that has to be taken into account. For the current J(t) one gets (with μ > 0)| | ![[J with combining dot above]](https://www.rsc.org/images/entities/i_char_004a_0307.gif) = −J(α + μ − βρ) = −J(α + μ − βρ) | (14) |
whose solution reads| |  | (15) |
once one plugs (13) into (15) with initial condition J(0) = 1 it follows| |  | (16) |
| | | G(t) ≡ β(1 − eμt) − μ. | (17) |
Fig. 3(a) and (b) report the typical behavior of ρ(t) and J(t). Because of the persistent motion, one obtains non-trivial dynamics of the current J that develops a peak before decaying to zero (see Fig. 3(b)). In particular, the decay rate of the current, that is α in the case of RT dynamics, increases to α + μ thanks to birth processes that produce at the same rate left-handed and right-handed particles. However, the coagulation process controlled by β tends to produce long-living currents (because of the coupling βρJ) that generate the peak shown in Fig. 3(b). One can compute the time ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) when J reaches its maximum value
when J reaches its maximum value| |  | (18) |
with ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) = 0 if β < α + μ (this condition is obtained using the fact that
= 0 if β < α + μ (this condition is obtained using the fact that ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ≥ 0 in (18)). Fig. 3(c) reports the contour plot
≥ 0 in (18)). Fig. 3(c) reports the contour plot ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) (α, β) obtained through (18) with the color indicating the magnitude of
(α, β) obtained through (18) with the color indicating the magnitude of ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) . From the equation for
. From the equation for ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) , one has
, one has  . This asymptotic limit is shown in Fig. 3(d).
. This asymptotic limit is shown in Fig. 3(d).
 |
| | Fig. 3 Mean-field approximation. (a) Time evolution of density ρ and current J for β = 0.1 (α = μ = v = 1). The dashed lines indicate the stationary values. (b) The current J develops a peak at ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) for increasing values of β (here β = 4 and α = μ = v = 1). (c) Contour plot for increasing values of β (here β = 4 and α = μ = v = 1). (c) Contour plot ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) (α, β). Below the dashed line (α, β). Below the dashed line ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) = 0. (d) = 0. (d) ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) as a function of β for α = 0.1, 1 (see legend). The dashed lines indicate the asymptotic values β → ∞. as a function of β for α = 0.1, 1 (see legend). The dashed lines indicate the asymptotic values β → ∞. | |
This happens although the stationary states are the same as the coagulation model in the well-mixed approximation:
| |  | (19) |
| |  | (20) |
as one can also check by setting
![[J with combining dot above]](https://www.rsc.org/images/entities/i_char_004a_0307.gif)
=
![[small rho, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a6.gif)
= 0 without solving the dynamics. On the other hand, while
J(
t) depends on
ρ(
t), at the mean-field level,
ρ(
t) remains independent of
J(
t). However, the mean-field computation suggests that non-trivial dynamics might be observed looking, for instance, at
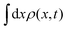
. To test the predictions of the mean-field theory,
Fig. 4(a) reports the numerical solution of the equations for
ρ and
J (here
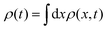
and

). The details on numerical solutions of the equations for
ρ and
J are provided in the Appendix A. As initial conditions,
ρ(
x, 0) is a Gaussian and
J(
x, 0) = 0. The numerical evolution of
ρ and
J is performed considering periodic boundary conditions. The initial Gaussian density profile evolves towards a uniform stationary state
ρ∞. The current
J, initially zero, is nonvanishing on intermediate times and eventually zero in the stationary state. The phase diagram has been obtained by varying
μ for different values of the tumbling rate
α (here
β = 1 and
v = 1). One observes apparent deviations from the mean-field prediction at small
μ as
α decreases (and thus the active motion becomes more important). Looking at the dynamics of
ρ(
t), one obtains that at small
α (panel (b) in
Fig. 4)
ρ(
t) approaches its stationary mean-field value very slowly. On the contrary, as
α increases
ρ(
t) quickly converges to
ρ∞. One can connect this behavior with the fact that there is a characteristic time
![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif)
which maximizes the current
J. In other words, long-living currents slow down the relaxation time of
ρ(
t) producing an apparent violation of the mean-field prediction.
 |
| | Fig. 4 Phase Diagram. (a) Stationary density ρ∞ as a function of μ for different values of α (increasing values from violet to yellow, see legend). The dashed red line is the mean-field prediction. (b) Time evolution of ρ(t) at α = 0.05 for different values of μ (the ones shown in (a), with μ increasing from violet to yellow). (c) ρ(t) at α = 2 for the same μ values shown in (b). Dashed red lines represent the mean-field stationary values. | |
Linear stability analysis
From the previous section, it follows that the characteristic time scale on which J decays depends on ρ because it is coupled to J through the coupling constant β. This coupling, at the mean-field level, produces excess in J that decays on a longer time scale (larger than α−1). Numerical solutions of the actual dynamics suggest that this effect impact also the dynamics of ρ (that is transparent to J in the mean-field picture). I now explore the spatiotemporal evolution of the spreading process combined with active motion in finite dimensions through the linear stability analysis of the stationary well-mixed configurations against small perturbations. As a standard procedure, one starts with| |  | (21) |
the linearized dynamics for the perturbations (δρ, δJ) reads| | δ![[small rho, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a6.gif) = −δJ′−μδρ = −δJ′−μδρ | (23) |
| | δ![[J with combining dot above]](https://www.rsc.org/images/entities/i_char_004a_0307.gif) = −v2δρ′ − δJ(α + μ). = −v2δρ′ − δJ(α + μ). | (24) |
Once one introduces  it is possible to rewrite in the compact form
it is possible to rewrite in the compact form| |  | (25) |
| |  | (26) |
Looking at damped plane wave solutions  the dispersion relation σ(k) controls the stability of the perturbation. σ(k) is the solution of the eigenvalues equation
the dispersion relation σ(k) controls the stability of the perturbation. σ(k) is the solution of the eigenvalues equation| | 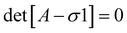 | (27) |
with eigenvalues| | 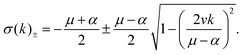 | (28) |
The stability condition requires 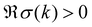 and thus, for k → 0, one obtains σ+ = −α and σ− = −μ, so that the long-wavelength perturbation is always damped ensuring that density fluctuations are diffuse. However, for finite k values, σ(k) can acquire an imaginary part so that density fluctuations are dumped oscillations that propagate as waves. This happens whenever
and thus, for k → 0, one obtains σ+ = −α and σ− = −μ, so that the long-wavelength perturbation is always damped ensuring that density fluctuations are diffuse. However, for finite k values, σ(k) can acquire an imaginary part so that density fluctuations are dumped oscillations that propagate as waves. This happens whenever| | | Δ ≡ (μ − α)2 − (2vk)2 < 0 | (29) |
and thus there is a critical wavelength kc given by| |  | (30) |
that separates purely diffusive excitations for k < kc from dumped travelling waves for k > kc. From (30) it follows that there is a limit where propagating waves dominate up to the macroscopic scale. This happen for α → μ so that kc → 0. On the other hand, in the large tumbling rate limit α → ∞ there are only diffusive excitations. The linear stability analysis produces the phase diagram shown in Fig. 5(a) that has been obtained for μ = β = v = 1. To test this prediction one can solve numerically (4) and (5) (the initial condition is a small perturbation of the uniform profile  with k0 = 2π and periodic boundary conditions), with the initial condition on the current J(x, 0) = 0 (with v = β = μ = 1, α = 0.5, 15). In the case α = 0.5, one has k0 > kc(α) so that linear stability predicts traveling waves. As one can see in Fig. 5(b), that shows δρ(x, t) ≡ ρ(x, t) − μ/β, the initial plane wave persists in the system while, in the second case α = 15 (Fig. 5(c)), k0 < kc(α), the initial wave dissipate fast into a uniform configuration without oscillations.
with k0 = 2π and periodic boundary conditions), with the initial condition on the current J(x, 0) = 0 (with v = β = μ = 1, α = 0.5, 15). In the case α = 0.5, one has k0 > kc(α) so that linear stability predicts traveling waves. As one can see in Fig. 5(b), that shows δρ(x, t) ≡ ρ(x, t) − μ/β, the initial plane wave persists in the system while, in the second case α = 15 (Fig. 5(c)), k0 < kc(α), the initial wave dissipate fast into a uniform configuration without oscillations.
 |
| | Fig. 5 Linear stability. (a) Contour plot of Δ(α,k) for β = v = μ = 1. The critical wave number kc(α) is the dashed blue line. For k > kc, before relaxing, a perturbation propagates as a wave, for k < kc relaxes diffusively to the uniform configuration. (b) Wave-like perturbation for k = 2π and α = 0.5 (see the black square in (a)). (c) Diffusive perturbation for k = 2π and α = 15 (see the red star in (a)). Different curves are taken at different times (time increases from violet to yellow). | |
Dynamics towards the stationary state
Although one cannot analytically solve the non-linear dynamics in finite dimensions, it is possible to gain some insight into limiting cases. First, I consider the large α limit. In this case, there are two possibilities: if the ratio DA = v2/α is maintained finite, i.e., the Brownian limit of the run-and-tumble walker, the model reduces to reaction–diffusion in one spatial dimension. This limiting case can be understood by setting (5) in the following form| | α−1![[J with combining dot above]](https://www.rsc.org/images/entities/i_char_004a_0307.gif) = −DAρ′ − J[1 + μ/α − βρ/α] = −DAρ′ − J[1 + μ/α − βρ/α] | (31) |
once the limit α → ∞ is performed, one arrives at the following constitutive relation for the currentonce this expression of J is inserted into the equation for ρ, one arrives at the Fisher–Kolmogorov equation (see for instance (ref. 9))| |  | (33) |
Performing the same limit but at finite velocity v, the diffusivity drops to zero, i.e., vρ′/α → 0, and thus one ends with the well-mixed case because J = 0 so that the dynamics reduces to (13). In this situation, the spreading process drives the system to uniform configurations ρ∞ = μ/β so fast that active motion is irrelevant. This is also the case of β → ∞ with v finite. There is another limit that is not trivial that I mention but I will not discuss. The case is β → ∞ and v → ∞. In this limit, one can introduce a diffusion constant of the spreading process defined as Ds ≡ v2/β. Since β−1J → 0, the constitutive relation is J[ρ] = Ds(log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ρ)′ that inserted into (6) brings to the following non-linear diffusion equation
ρ)′ that inserted into (6) brings to the following non-linear diffusion equation| |  | (34) |
In the opposite limit, one has β as a small parameter so that the dynamics of ρ and J is the same as obtained within the linear stability analysis.
The numerical integration of the equations for ρ and J is the primary tool for making progress in intermediate regimes. As suggested by linear stability analysis, one should appreciate some crossover from a situation where the stationary state is approached through dumped traveling waves to another situation where the wave front relaxes following a purely dissipative dynamics. One can move between these two situations by varying the tumbling rate α (keeping the other time scales fixed).
To test the existence of these different scenarios, eqn (4) and (5) have been solved numerically with a Gaussian profile for ρ(x, 0) as the initial condition (while J(x, 0) is set to zero). Fig. 6 reports the typical time evolution of the density field ρ(x, t) and the current field J(x, t) for two values of tumbling rate (α = 0.5, 2). The reaction parameters are set μ = 1 and β = 0.5 so that the stationary state is mixed (ρ∞ > 0). In the case α = 0.5, the initial Gaussian profile propagates ballistically with a minimal attenuation, this is also mirrored by the behavior of J(x, t) that does not decay. On the contrary, as α increases the traveling wave and currents tend to disappear rapidly. These long-living currents can be interpreted as Fisher waves preventing the system from quickly reaching a stationary uniform state.
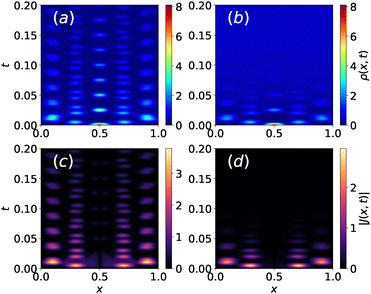 |
| | Fig. 6 Dynamics. The color map indicates the time evolution of the density field ρ(x, t) from an initial Gaussian distribution centered in L/2 (L = 1). Different panels display different values of the tumbling rate α = 0.1,2 (panels (a) and (b), respectively). Panels (c) and (d) show the intensity of the corresponding current fields |J(x, t)|. At small α value, the system clearly support traveling damped waves that become more and more damped as α increases. | |
Diffusive limit and pattern formation
In the case of time scales larger than the typical time scale of relaxation of J(x, t), one can get rid of J and write a closed equation for ρ(x, t). This is because once one imposes ![[J with combining dot above]](https://www.rsc.org/images/entities/i_char_004a_0307.gif) = 0, it returns a constitutive relation J = J[ρ]. I refer to this situation as the diffusive limit. The link between J and ρ is
= 0, it returns a constitutive relation J = J[ρ]. I refer to this situation as the diffusive limit. The link between J and ρ is| |  | (36) |
That brings us to the following diffusive equation| |  | (37) |
In this limit, there is a problem related to the behavior of D[ρ] because it becomes negative for large enough β values. It is well known that the changing of sign in the diffusion coefficient is a signal of pattern formation.9 Moreover, a negative diffusion coefficient can be regularized by inserting surface terms that are proportional to ∇4ρ (see, for instance, (ref. 17 and 25)). This is because the linear stability analysis of (37) leads to a second-order equation for the wave-length k in Fourier space that defines the dispersion relation σ(k). A change of sign of the diffusion coefficient indicates that σ(k) changes sign too, and thus an initially small perturbation undergoes an uncontrolled growth. Once we consider the ∇4ρ term, this brings a k4 contribution that in turn stabilizes the emerging patterns in the region of the phase diagram where the diffusion coefficient is negative. However, (37) has a much serious problem because D[ρ], in changing its sign, diverges at α + μ − βρ = 0 whose meaning has to be understood. We notice that this divergency happens at a critical density 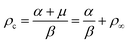 . We can get rid of the divergence in the small β regime, i.e., assuming μ and β both small so that ρ∞ is kept fixed. This limit means assuming the spreading process is so slow that variation in the local density due to birth/death processes is so rare that the change in ρ due to them causes a small fluctuation in J that quickly relaxes towards J = 0.
. We can get rid of the divergence in the small β regime, i.e., assuming μ and β both small so that ρ∞ is kept fixed. This limit means assuming the spreading process is so slow that variation in the local density due to birth/death processes is so rare that the change in ρ due to them causes a small fluctuation in J that quickly relaxes towards J = 0.
If β is small enough, the diffusive limit is well-defined and thus the diffusion constant is not diverging and remains positive with D < DA. The dynamics is governed by an effective Fisher–Kolmogorov equation whose typical time-evolution is shown in Fig. 7.
 |
| | Fig. 7 Diffusive Limit. (a) Relaxation of a Gaussian density profile towards homogeneous configurations (time increases from violet to yellow). Panel (b) reports the same profile as a color map ρ(x, t). | |
Going back to (37), in the case of a perturbation δρ around the uniform stationary state ρ∞ = μ/β (we consider μ > 0), the dynamics of δρ is controlled by
| | δ![[small rho, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a6.gif) = [Dδρ′]′ − μδρ. = [Dδρ′]′ − μδρ. | (38) |
Again, this equation does not generally make sense unless one considers a small
β regime so that
D[
ρ] remains positive and finite. In the small
β limit, at the zero order in δ
ρ,
D[δ
ρ] can be replaced by
D ≃
![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) A
A, with
![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) A
A renormalized by the spreading process,
i.e.,
![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) A
A ≡
v2/(
α +
μ), so that one ends with a diffusive equation for the perturbation
| | δ![[small rho, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a6.gif) = = ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) Aρ′′ − μδρ. Aρ′′ − μδρ. | (39) |
A more interesting situation can be obtained if one keeps the first order in δ
ρ in the expression of
D =
D[
ρ]. In particular, considering small perturbation so that |δ
ρ| < 1, upon defining
| | 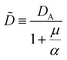 | (40) |
| |  | (41) |
for
![[small beta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10e.gif)
< 1, one has
D ≃
![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif)
[1 +
![[small beta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10e.gif)
δ
ρ] and thus
| | δ![[small rho, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a6.gif) = D[δρ]δρ′′ + = D[δρ]δρ′′ + ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) ![[small beta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10e.gif) (δρ′)2 − μδρ. (δρ′)2 − μδρ. | (42) |
Adding a noise term to this equation (representing the effect of the fast degrees of freedom), brings us to
| | δ![[small rho, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a6.gif) = D[δρ]δρ′′ + = D[δρ]δρ′′ + ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) ![[small beta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10e.gif) (δρ′)2 − μδρ + η (δρ′)2 − μδρ + η | (43) |
with
η ≡
η(
x,
t), 〈
η(
x,
t)〉 = 0, and 〈
η(
x,
t)
η(
y,
s)〉 = 2
Tδ(
x −
y)δ(
t −
s) (with
T setting the strength of the noise). Considering fluctuations due to the noise around the absorbing state critical point
μ = 0, it follows that
(43) is formally equivalent to Kardar–Parisi–Zhang equation (KPZ) model
29 (but with a non-linear diffusion coefficient). This mapping suggests that pattern formation at criticality should fall into the KPZ universality class. It is interesting to note that the strength of the KPZ term depends on the ratio
μ/
α, and thus on both autonomous motion and replication.
III. Conclusions and outlook
This work addresses a simple one-dimensional continuum model that combines two non-equilibrium phenomena: active dynamics and absorbing state phase transitions. Wave-front propagation in biological systems is a typical example of the application of the model introduced here. The continuum model consists of a gas of run-and-tumble particles that interacts via a reaction process. This process annihilates particles at a rate β and produces new particles at a rate μ. Although the presence of active motion does not change the stationary properties of the system, the dynamics towards the absorbing or mixed state qualitatively changes with α from a situation where the system fast relaxes because of diffusive modes, to another situation, for small α, where the system can support propagating waves. Consequently, the relaxation time towards the stationary state strongly depends on the interplay of active motion with the spreading process. It is possible to rationalize this interplay already at level of a men-field approximation where ρ(t) does not vary in space. In mean-field, while ρ(t) follows the standard logistic evolution, the current J(t) does not decay monotonously because of its coupling with ρ(t): interaction that is generated by the coagulation dynamics. In particular, J(t) admits a local maximum for large β. This prediction agrees with the behavior of integrated quantities such as 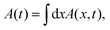 with A = ρ, J. These quantities were computed numerically beyond the mean-field regime by solving the full dynamics. Spatial heterogeneities couple currents and density, causing ρ(t) to relax very slowly to ρ∞ at small α. This dynamical slowing down is distinct from the usual critical slowing down typical of critical phenomena, having a genuinely non-equilibrium origin. The density–current coupling generates damped waves that can propagate up to macroscopic scales or rapidly diffuse, depending on the interplay between the spreading process and active motion.
with A = ρ, J. These quantities were computed numerically beyond the mean-field regime by solving the full dynamics. Spatial heterogeneities couple currents and density, causing ρ(t) to relax very slowly to ρ∞ at small α. This dynamical slowing down is distinct from the usual critical slowing down typical of critical phenomena, having a genuinely non-equilibrium origin. The density–current coupling generates damped waves that can propagate up to macroscopic scales or rapidly diffuse, depending on the interplay between the spreading process and active motion.
Considering the system's dynamics on time scales where the current is stationary (i.e., J = 0), I also demonstrated that, in general, it is not safe to consider the diffusive limit of the model due to the competition between the spreading dynamics and active motion. This is manifested by a pathological diffusive limit that leads to diverging and eventually a negative diffusion constant. On phenomenological grounds, the negative diffusion constant in the diffusive continuum model indicates pattern formation and can be cured by introducing appropriate surface tension terms. The model admits a well-defined diffusive limit in the small β limit, with fluctuation dynamics governed by a KPZ-like equation.
The independence of the stationary state from non-equilibrium active dynamics may be a model-dependent feature of the continuum description considered here. Like its equilibrium counterpart, the active coagulation model belongs to the directed percolation universality class. Future work should investigate the effects of activity near the critical point, using both lattice models and continuum descriptions, to determine whether activity alters the morphology of pattern formation.
Data availability
All the data are included as figures in the manuscript.
Conflicts of interest
There are no conflicts to declare.
Appendix
A Numerical solution of the dynamics
The equations for ρ and J given by (4) have been solved numerically using the Euler scheme for the time integration. The numerical implementation consists in mesh the space in Ngrid space interval of size Δx = 1/Ngrid (with periodic boundary conditions) and the time in Nt intervals of size Δt. The value of the fields on the lattice point i = 1, …, Ngrid at time t + δt are updated as follows| | | fiρ ≡ −∇Jti + ρit(μ − βρit) | (A2) |
| | | fiJ ≡ −v2∇ρi − Jit(α + μ − βρit) | (A4) |
where the gradients ∇gi of a generic function gi defined on the mesh have been computed using the central finite difference method| | 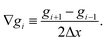 | (A5) |
The initial condition is a Gaussian profile for ρ(x, 0) with zero current J(x, 0) = 0. The time spacing is fixed by the Courant–Friedrichs–Lewy condition  with Da ≡ v2/α. In the case of (A1)
with Da ≡ v2/α. In the case of (A1) with Ngrid = 400, and Nt = 107. The dynamics in the diffusive limit (37) has been solved in the same way
with Ngrid = 400, and Nt = 107. The dynamics in the diffusive limit (37) has been solved in the same way| |  | (A7) |
| |  | (A8) |
with Ngrid = 200, Nt = 2 × 106, and  .
.
Acknowledgements
M. P. acknowledges funding from the Italian Ministero dellUniversità e della Ricerca under the programme PRIN 2022 (“re-ranking of the final lists”), number 2022KWTEB7, cup B53C24006470006.
References
- M. Fruchart, R. Hanai, P. B. Littlewood and V. Vitelli, Nature, 2021, 592, 363–369 CrossRef CAS.
- H. Sompolinsky, A. Crisanti and H. J. Sommers, Phys. Rev. Lett., 1988, 61, 259–262 CrossRef PubMed.
- H. Hinrichsen, Adv. Phys., 2000, 49, 815–958 CrossRef CAS.
- A. Crisanti, A. Puglisi and D. Villamaina, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 061127 CrossRef CAS.
- S. Saha, J. Agudo-Canalejo and R. Golestanian, Phys. Rev. X, 2020, 10, 041009 CAS.
- G. Pisegna, S. Saha and R. Golestanian, Proc. Natl. Acad. Sci. U. S. A., 2024, 121, e2407705121 CrossRef CAS.
- A. Dinelli, J. OByrne, A. Curatolo, Y. Zhao, P. Sollich and J. Tailleur, Nat. Commun., 2023, 14, 7035 CrossRef CAS PubMed.
- Y. Avni, M. Fruchart, D. Martin, D. Seara and V. Vitelli, Phys. Rev. E, 2025, 111, 034124 CrossRef CAS.
-
J. D. Murray, Mathematical biology: I. An introduction, Springer Science & Business Media, 2007, vol. 17 Search PubMed.
- O. Hallatschek, P. Hersen, S. Ramanathan and D. R. Nelson, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 19926–19930 CrossRef CAS.
- V. E. Deneke and S. Di Talia, J. Cell Biol., 2018, 217, 1193–1204 CrossRef CAS PubMed.
- F. Peruani and G. J. Sibona, Phys. Rev. Lett., 2008, 100, 168103 CrossRef PubMed.
- F. Peruani and G. J. Sibona, Soft Matter, 2019, 15, 497–503 RSC.
- H.-M. Gascuel, P. Rahmani, R. Bon and F. Peruani, Phys. Rev. Lett., 2024, 133, 058301 CrossRef CAS PubMed.
- J. P. Rodríguez, M. Paoluzzi, D. Levis and M. Starnini, Phys. Rev. Res., 2022, 4, 043160 CrossRef.
- D. Levis, A. Diaz-Guilera, I. Pagonabarraga and M. Starnini, Phys. Rev. Res., 2020, 2, 032056 CrossRef CAS.
- M. Paoluzzi, M. Leoni and M. C. Marchetti, Soft Matter, 2020, 16, 6317–6327 RSC.
- M. Paoluzzi, M. Leoni and M. C. Marchetti, Phys. Rev. E, 2018, 98, 052603 CrossRef CAS.
- B. Marcolongo, F. Peruani and G. J. Sibona, Phys. A, 2024, 648, 129916 CrossRef.
- F. Peruani and C. F. Lee, Europhys. Lett., 2013, 102, 58001 CrossRef.
- A. Norambuena, F. J. Valencia and F. Guzmán-Lastra, Sci. Rep., 2020, 10, 20845 CrossRef CAS.
- P. de Castro, F. Urbina, A. Norambuena and F. Guzmán-Lastra, Phys. Rev. E, 2023, 108, 044104 CrossRef CAS PubMed.
- A. Libál, P. Forgács, A. Néda, C. Reichhardt, N. Hengartner and C. J. O. Reichhardt, Phys. Rev. E, 2023, 107, 024604 CrossRef.
- P. Forgács, A. Libál, C. Reichhardt, N. Hengartner and C. J. Reichhardt, Commun. Phys., 2023, 6, 294 CrossRef.
- M. E. Cates, D. Marenduzzo, I. Pagonabarraga and J. Tailleur, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 11715–11720 CrossRef CAS PubMed.
- A. Curatolo, N. Zhou, Y. Zhao, C. Liu, A. Daerr, J. Tailleur and J. Huang, Nat. Phys., 2020, 16, 1152–1157 Search PubMed.
- M. J. Schnitzer, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1993, 48, 2553–2568 CrossRef CAS PubMed.
- M. Kac, Rocky Mt. J. Math., 1974, 4, 497–509 Search PubMed.
- M. Kardar, G. Parisi and Y.-C. Zhang, Phys. Rev. Lett., 1986, 56, 889–892 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2025 |
Click here to see how this site uses Cookies. View our privacy policy here. 
![[small beta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10e.gif) (ρ) and appears at a constant rate μ, where ρ represents the number density of active particles. The reaction process that makes particles disappear is called coagulation, and the reason why its rate is density-dependent will be clear later. The other reaction that allows particles to appear is called decoagulation. On top of that, I consider active motion within the so-called run-and-tumble dynamics. Without loss of generality, I will focus on the one-dimensional case that is general enough to capture the salient phenomenology of active matter. In run-and-tumble dynamics, we have two species of particles: the ones moving to the right and the ones moving to the left. I will consider both species moving at constant velocity. Right-moving particles invert their direction (in one spatial dimension, there is not enough space for a rotation of a finite angle) at a rate α, usually called the tumbling rate. The same happens for the left-moving ones. Adopting the standard notation for run-and-tumble active particles in one spatial dimension, R ≡ R(x, t) and L ≡ L(x, t) indicate the fraction of right-moving and left-moving particles, respectively.27 The active motion is characterized by the self-propulsion velocity v and the tumbling rate α. In the limit v → ∞ and α → ∞ with fixed diffusion constant DA = v2/α, the random walk reduces to the standard Brownian motion. On top of the active motion, I consider a coagulation process characterized by two parameters. In the following, β indicates the reaction rate of the coagulation reaction (that is now on a density-independent rate), and with μ the rate of the offspring production (decoagulation). The microscopic picture is the following. If A indicates the presence of an active particle in some point of space at a given time, and ∅ indicates no particles, within coagulation dynamics one has to consider two elementary processes: the coagulation process that tends to annihilate particles, i.e., a particle spontaneously disappears, and the decoagulation process which introduces a new particle. After adding self-propelled motion, the set of reactions is
(ρ) and appears at a constant rate μ, where ρ represents the number density of active particles. The reaction process that makes particles disappear is called coagulation, and the reason why its rate is density-dependent will be clear later. The other reaction that allows particles to appear is called decoagulation. On top of that, I consider active motion within the so-called run-and-tumble dynamics. Without loss of generality, I will focus on the one-dimensional case that is general enough to capture the salient phenomenology of active matter. In run-and-tumble dynamics, we have two species of particles: the ones moving to the right and the ones moving to the left. I will consider both species moving at constant velocity. Right-moving particles invert their direction (in one spatial dimension, there is not enough space for a rotation of a finite angle) at a rate α, usually called the tumbling rate. The same happens for the left-moving ones. Adopting the standard notation for run-and-tumble active particles in one spatial dimension, R ≡ R(x, t) and L ≡ L(x, t) indicate the fraction of right-moving and left-moving particles, respectively.27 The active motion is characterized by the self-propulsion velocity v and the tumbling rate α. In the limit v → ∞ and α → ∞ with fixed diffusion constant DA = v2/α, the random walk reduces to the standard Brownian motion. On top of the active motion, I consider a coagulation process characterized by two parameters. In the following, β indicates the reaction rate of the coagulation reaction (that is now on a density-independent rate), and with μ the rate of the offspring production (decoagulation). The microscopic picture is the following. If A indicates the presence of an active particle in some point of space at a given time, and ∅ indicates no particles, within coagulation dynamics one has to consider two elementary processes: the coagulation process that tends to annihilate particles, i.e., a particle spontaneously disappears, and the decoagulation process which introduces a new particle. After adding self-propelled motion, the set of reactions is


![[J with combining dot above]](https://www.rsc.org/images/entities/i_char_004a_0307.gif) = −v2ρ′ − J[α + μ − βρ]
= −v2ρ′ − J[α + μ − βρ]
 generates linear interactions that tend to bring the system to extinction. Non-linear interactions with coupling constant β are therefore essential for the existence of stationary solutions with ρ ≠ 0. The nonlinearities in (4) generally render the dynamics analytically intractable. Fig. 1 depicts the typical behavior of
generates linear interactions that tend to bring the system to extinction. Non-linear interactions with coupling constant β are therefore essential for the existence of stationary solutions with ρ ≠ 0. The nonlinearities in (4) generally render the dynamics analytically intractable. Fig. 1 depicts the typical behavior of 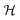 as the mass term μ changes from negative to positive values. Since μ represents a rate, negative values are physically meaningless, however, in the spirit of critical phenomena where the mass tunes the distance from the critical point, μ should be understood in the same way as distance from the critical point where the two fixed points of the dynamics become a marginal point. In any case, from the point of view of the coarse-grained model considered here, μ can take either positive or negative values.
as the mass term μ changes from negative to positive values. Since μ represents a rate, negative values are physically meaningless, however, in the spirit of critical phenomena where the mass tunes the distance from the critical point, μ should be understood in the same way as distance from the critical point where the two fixed points of the dynamics become a marginal point. In any case, from the point of view of the coarse-grained model considered here, μ can take either positive or negative values.

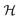 (see (6)) develops a minimum in ρ = 0 for μ ≤ 0 that changes to ρ = μ/β ≠ 0 for μ > 0.
(see (6)) develops a minimum in ρ = 0 for μ ≤ 0 that changes to ρ = μ/β ≠ 0 for μ > 0.![[small rho, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a6.gif) = −J′
= −J′![[J with combining dot above]](https://www.rsc.org/images/entities/i_char_004a_0307.gif) = −v2ρ′ − αJ.
= −v2ρ′ − αJ.![[greek rho with two dots above]](https://www.rsc.org/images/entities/i_char_e1a8.gif) = −
= −![[J with combining dot above]](https://www.rsc.org/images/entities/i_char_004a_0307.gif) ′ so that
′ so that![[greek rho with two dots above]](https://www.rsc.org/images/entities/i_char_e1a8.gif) + α
+ α![[small rho, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a6.gif) − v2ρ′′ = 0.
− v2ρ′′ = 0.![[small rho, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a6.gif) = DAρ′′
= DAρ′′![[greek rho with two dots above]](https://www.rsc.org/images/entities/i_char_e1a8.gif) = v2ρ′′,
= v2ρ′′,![[small rho, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a6.gif) = 0 and
= 0 and ![[J with combining dot above]](https://www.rsc.org/images/entities/i_char_004a_0307.gif) = −αJ, i.e., ρ and J decouple from each other, the current decays on the time scale α−1 (J(t) = J(0)e−αt and the density is uniform ρ(t) = ρ(0) = const).
= −αJ, i.e., ρ and J decouple from each other, the current decays on the time scale α−1 (J(t) = J(0)e−αt and the density is uniform ρ(t) = ρ(0) = const).


![[J with combining dot above]](https://www.rsc.org/images/entities/i_char_004a_0307.gif) = −J(α + μ − βρ)
= −J(α + μ − βρ)

![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) when J reaches its maximum value
when J reaches its maximum value
![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) = 0 if β < α + μ (this condition is obtained using the fact that
= 0 if β < α + μ (this condition is obtained using the fact that ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ≥ 0 in (18)). Fig. 3(c) reports the contour plot
≥ 0 in (18)). Fig. 3(c) reports the contour plot ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) (α, β) obtained through (18) with the color indicating the magnitude of
(α, β) obtained through (18) with the color indicating the magnitude of ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) . From the equation for
. From the equation for ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) , one has
, one has  . This asymptotic limit is shown in Fig. 3(d).
. This asymptotic limit is shown in Fig. 3(d).


![[J with combining dot above]](https://www.rsc.org/images/entities/i_char_004a_0307.gif) =
= ![[small rho, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a6.gif) = 0 without solving the dynamics. On the other hand, while J(t) depends on ρ(t), at the mean-field level, ρ(t) remains independent of J(t). However, the mean-field computation suggests that non-trivial dynamics might be observed looking, for instance, at
= 0 without solving the dynamics. On the other hand, while J(t) depends on ρ(t), at the mean-field level, ρ(t) remains independent of J(t). However, the mean-field computation suggests that non-trivial dynamics might be observed looking, for instance, at 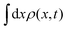 . To test the predictions of the mean-field theory, Fig. 4(a) reports the numerical solution of the equations for ρ and J (here
. To test the predictions of the mean-field theory, Fig. 4(a) reports the numerical solution of the equations for ρ and J (here 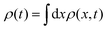 and
and  ). The details on numerical solutions of the equations for ρ and J are provided in the Appendix A. As initial conditions, ρ(x, 0) is a Gaussian and J(x, 0) = 0. The numerical evolution of ρ and J is performed considering periodic boundary conditions. The initial Gaussian density profile evolves towards a uniform stationary state ρ∞. The current J, initially zero, is nonvanishing on intermediate times and eventually zero in the stationary state. The phase diagram has been obtained by varying μ for different values of the tumbling rate α (here β = 1 and v = 1). One observes apparent deviations from the mean-field prediction at small μ as α decreases (and thus the active motion becomes more important). Looking at the dynamics of ρ(t), one obtains that at small α (panel (b) in Fig. 4) ρ(t) approaches its stationary mean-field value very slowly. On the contrary, as α increases ρ(t) quickly converges to ρ∞. One can connect this behavior with the fact that there is a characteristic time
). The details on numerical solutions of the equations for ρ and J are provided in the Appendix A. As initial conditions, ρ(x, 0) is a Gaussian and J(x, 0) = 0. The numerical evolution of ρ and J is performed considering periodic boundary conditions. The initial Gaussian density profile evolves towards a uniform stationary state ρ∞. The current J, initially zero, is nonvanishing on intermediate times and eventually zero in the stationary state. The phase diagram has been obtained by varying μ for different values of the tumbling rate α (here β = 1 and v = 1). One observes apparent deviations from the mean-field prediction at small μ as α decreases (and thus the active motion becomes more important). Looking at the dynamics of ρ(t), one obtains that at small α (panel (b) in Fig. 4) ρ(t) approaches its stationary mean-field value very slowly. On the contrary, as α increases ρ(t) quickly converges to ρ∞. One can connect this behavior with the fact that there is a characteristic time ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) which maximizes the current J. In other words, long-living currents slow down the relaxation time of ρ(t) producing an apparent violation of the mean-field prediction.
which maximizes the current J. In other words, long-living currents slow down the relaxation time of ρ(t) producing an apparent violation of the mean-field prediction.

![[small rho, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a6.gif) = −δJ′−μδρ
= −δJ′−μδρ![[J with combining dot above]](https://www.rsc.org/images/entities/i_char_004a_0307.gif) = −v2δρ′ − δJ(α + μ).
= −v2δρ′ − δJ(α + μ). it is possible to rewrite in the compact form
it is possible to rewrite in the compact form

 the dispersion relation σ(k) controls the stability of the perturbation. σ(k) is the solution of the eigenvalues equation
the dispersion relation σ(k) controls the stability of the perturbation. σ(k) is the solution of the eigenvalues equation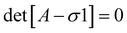
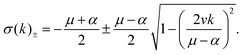
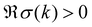 and thus, for k → 0, one obtains σ+ = −α and σ− = −μ, so that the long-wavelength perturbation is always damped ensuring that density fluctuations are diffuse. However, for finite k values, σ(k) can acquire an imaginary part so that density fluctuations are dumped oscillations that propagate as waves. This happens whenever
and thus, for k → 0, one obtains σ+ = −α and σ− = −μ, so that the long-wavelength perturbation is always damped ensuring that density fluctuations are diffuse. However, for finite k values, σ(k) can acquire an imaginary part so that density fluctuations are dumped oscillations that propagate as waves. This happens whenever
 with k0 = 2π and periodic boundary conditions), with the initial condition on the current J(x, 0) = 0 (with v = β = μ = 1, α = 0.5, 15). In the case α = 0.5, one has k0 > kc(α) so that linear stability predicts traveling waves. As one can see in Fig. 5(b), that shows δρ(x, t) ≡ ρ(x, t) − μ/β, the initial plane wave persists in the system while, in the second case α = 15 (Fig. 5(c)), k0 < kc(α), the initial wave dissipate fast into a uniform configuration without oscillations.
with k0 = 2π and periodic boundary conditions), with the initial condition on the current J(x, 0) = 0 (with v = β = μ = 1, α = 0.5, 15). In the case α = 0.5, one has k0 > kc(α) so that linear stability predicts traveling waves. As one can see in Fig. 5(b), that shows δρ(x, t) ≡ ρ(x, t) − μ/β, the initial plane wave persists in the system while, in the second case α = 15 (Fig. 5(c)), k0 < kc(α), the initial wave dissipate fast into a uniform configuration without oscillations.
![[J with combining dot above]](https://www.rsc.org/images/entities/i_char_004a_0307.gif) = −DAρ′ − J[1 + μ/α − βρ/α]
= −DAρ′ − J[1 + μ/α − βρ/α]
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ρ)′ that inserted into (6) brings to the following non-linear diffusion equation
ρ)′ that inserted into (6) brings to the following non-linear diffusion equation
![[J with combining dot above]](https://www.rsc.org/images/entities/i_char_004a_0307.gif) = 0, it returns a constitutive relation J = J[ρ]. I refer to this situation as the diffusive limit. The link between J and ρ is
= 0, it returns a constitutive relation J = J[ρ]. I refer to this situation as the diffusive limit. The link between J and ρ is

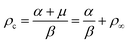 . We can get rid of the divergence in the small β regime, i.e., assuming μ and β both small so that ρ∞ is kept fixed. This limit means assuming the spreading process is so slow that variation in the local density due to birth/death processes is so rare that the change in ρ due to them causes a small fluctuation in J that quickly relaxes towards J = 0.
. We can get rid of the divergence in the small β regime, i.e., assuming μ and β both small so that ρ∞ is kept fixed. This limit means assuming the spreading process is so slow that variation in the local density due to birth/death processes is so rare that the change in ρ due to them causes a small fluctuation in J that quickly relaxes towards J = 0.
![[small rho, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a6.gif) = [Dδρ′]′ − μδρ.
= [Dδρ′]′ − μδρ.![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) A, with
A, with ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) A renormalized by the spreading process, i.e.,
A renormalized by the spreading process, i.e., ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) A ≡ v2/(α + μ), so that one ends with a diffusive equation for the perturbation
A ≡ v2/(α + μ), so that one ends with a diffusive equation for the perturbation![[small rho, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a6.gif) =
= ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) Aρ′′ − μδρ.
Aρ′′ − μδρ.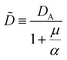

![[small beta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10e.gif) < 1, one has D ≃
< 1, one has D ≃ ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) [1 +
[1 + ![[small beta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10e.gif) δρ] and thus
δρ] and thus![[small rho, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a6.gif) = D[δρ]δρ′′ +
= D[δρ]δρ′′ + ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif)
![[small beta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10e.gif) (δρ′)2 − μδρ.
(δρ′)2 − μδρ.![[small rho, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a6.gif) = D[δρ]δρ′′ +
= D[δρ]δρ′′ + ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif)
![[small beta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10e.gif) (δρ′)2 − μδρ + η
(δρ′)2 − μδρ + η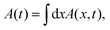 with A = ρ, J. These quantities were computed numerically beyond the mean-field regime by solving the full dynamics. Spatial heterogeneities couple currents and density, causing ρ(t) to relax very slowly to ρ∞ at small α. This dynamical slowing down is distinct from the usual critical slowing down typical of critical phenomena, having a genuinely non-equilibrium origin. The density–current coupling generates damped waves that can propagate up to macroscopic scales or rapidly diffuse, depending on the interplay between the spreading process and active motion.
with A = ρ, J. These quantities were computed numerically beyond the mean-field regime by solving the full dynamics. Spatial heterogeneities couple currents and density, causing ρ(t) to relax very slowly to ρ∞ at small α. This dynamical slowing down is distinct from the usual critical slowing down typical of critical phenomena, having a genuinely non-equilibrium origin. The density–current coupling generates damped waves that can propagate up to macroscopic scales or rapidly diffuse, depending on the interplay between the spreading process and active motion.
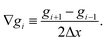
 with Da ≡ v2/α. In the case of (A1)
with Da ≡ v2/α. In the case of (A1) with Ngrid = 400, and Nt = 107. The dynamics in the diffusive limit (37) has been solved in the same way
with Ngrid = 400, and Nt = 107. The dynamics in the diffusive limit (37) has been solved in the same way

 .
.






