DOI:
10.1039/D4SM01255K
(Paper)
Soft Matter, 2025,
21, 1085-1112
Dynamic electroosmotic flow and solute dispersion through a nanochannel filled with an electrolyte surrounded by a layer of a dielectric and immiscible liquid†
Received
26th October 2024
, Accepted 19th December 2024
First published on 14th January 2025
Abstract
The present article deals with the modulation of oscillatory electroosmotic flow (EOF) and solute dispersion across a nanochannel filled with an electrolyte solution surrounded by a layer of a dielectric liquid. The dielectric permittivity of the liquid layer adjacent to supporting rigid walls is taken to be lower than that of the electrolyte solution. Besides, the aforesaid liquid layer may bear additional mobile charges, e.g., free lipid molecules, charged surfactant molecules etc., which in turn lead to a nonzero charge along the liquid–liquid interface. Such a layer of a dielectric liquid resembles the membrane of various biological cells. An AC voltage is applied to generate the fluid motion. Note that among others, the major advantage of AC voltage is that it can suppress the formation of gas bubbles that are often very detrimental in flow through microdevices. Considering the combined impact of ion partitioning and ion steric effects, we have studied the EOF modulation and its impact on the dispersion of the solute band of given width placed initially at the middle of the channel. The full scale numerical results for flow modulation induced by an AC electric field and its impact on the solute transport are presented considering a wide range of pertinent parameters. It is observed that the molar concentration of additional charge present in the dielectric liquid layer and its thickness, interfacial charge, and concentration of the bulk electrolyte, ion partitioning and ion steric effects, frequency of oscillatory electric field, channel height etc., have a substantial impact on the flow modulation, effective dispersion coefficient as well as broadening of the solute band across the channel. We have further highlighted the impact of the Péclet number on the transport and dispersion of solutes. Along with the numerical results, several benchmark analytical results under various limits are deduced for electrostatic potential, flow velocity and various quantities associated with the dispersion process.
1 Introduction
Hydrodynamic dispersion of a solute band placed inside a fluidic channel occurs due to the combined impacts of molecular diffusion and fluid convection. For such cases, an additional convective flux due to the flow velocity is added with the flux due to molecular diffusion, which further intensifies the broadening of the solute band. The dispersion of a solute in the presence of the fluid convection has either favourable or adverse effects depending on the type of the processes.1 For example, the dispersion is favourable in the mixing process, which leads to a faster and enhanced mixing of samples with the background liquid medium.2 In contrast, hydrodynamic dispersion has detrimental effects on the separation process as it reduces the resolution of the analytical separation.3 Thus, a complete knowledge on the interplay between the fluid convection and the molecular diffusion in the dispersion process is essential to achieve a precise and controlled dispersion of a solute band across fluidic devices that deal with the analytical separation or mixing processes.
Historically, solute dispersion through a circular tube under laminar pressure driven Hagen–Poiseuille flow was studied by Taylor.4 Shortly after, using the method of moments, Aris obtained the expression for the effective dispersion coefficient of passive solutes, which are generally uncharged or at their isoelectric point.5,6 Note that the Taylor–Aris dispersion coefficient is often used to determine the material properties, e.g., the molecular diffusion coefficient and the hydrodynamic radius of solutes.7 The fundamental mechanism that leads to an enhanced dispersion is the impact of a nonuniform velocity gradient on the molecular diffusion, and thus a stronger velocity gradient may lead to an enhanced dispersion. It is important to note that the Taylor–Aris dispersion coefficient depends on other associated physical parameters but not on the time. Thus, the analysis based on the Taylor–Aris model may be applied only at a long time limit.8 Such an inherent assumption of the Taylor–Aris model was further relaxed by Gill and Sankarasubramanian.9 They proposed a general dispersion model which is capable of estimating the dispersion coefficient and the area-averaged concentration of a solute for all values of time. Thereafter, a remarkable advancement in the study of solute dispersion is made by several researchers. Fife and Nicholes studied the dispersion of a solute band across a tube of arbitrary cross section under a time-dependent flow field.10 The impact of the catalytic wall reaction on the dispersion of passive contaminants through a circular tube under time dependent laminar flow is studied numerically by Mazumder and Das.11 The transport and dispersion of solutes in open channels was further studied by Ng and Yip using homogenization methods.12 Ng further studied the dispersion of chemical species through a tube under steady and oscillatory pressure driven flow considering a reversible or an irreversible wall reaction.13 The dispersion of passive solutes suspended in a liquid flowing through a parallel plate channel under time dependent Couette–Poiseuille flow was studied by Paul and Mazumder.14 Using a multi-scale perturbation method, Karmakar et al. further analysed the impact of transient Couette–Poiseuille flow on the dispersion of passive contaminants through a porous channel.15
All the studies indicated above deal with the dispersion due to nonuniform flow velocity across a channel where the characteristic length scale is exactly the same as that characterizes the cross-sectional geometry. In contrast, for the dispersion process driven by electrokinetic transport of an ionized liquid flowing through microfluidic devices, the length scale is the thickness of the electric double layer (EDL).16 Besides, it is further difficult to utilize the pressure driven flow for channels with size down to micrometer or even less. Note that an electrokinetic transport phenomenon, e.g., electroosmosis induced by the interaction of an external electric field with the excess counterions present in the EDL. The hydrodynamic dispersion through microfluidic devices due to electroosmosis does not require any movable mechanical part, and thus offers long-term stability as well as ability to achieve a precise control of fluid flow driven by externally applied voltage drop.17 Compared to the purely pressure driven flow, the electroosmotic flow (EOF) through microdevices with uniform wall charge properties leads to a weaker hydrodynamic dispersion and produces a high device resolution with the same throughput.18 Thus, the hydrodynamic dispersion due to the EOF is beneficial in designing various tools for analytical separation and detection of samples. In recent years significant attention has been paid to design various microdevices that combine the mechanical and electrical components. The readers are referred to recent articles which paid significant attention to design various electrified lab-on-disc systems, intelligent nanochannels, etc. as well as to study the electrokinetically driven flow across such tiny devices.19–24 Motivated by this trend, several researchers further studied the hydrodynamic dispersion through microdevices considering the EOF with uniform surface ζ-potential (the key parameter that indicates the electrostatic charge of the supporting walls of the conduits).25–29 Hoshyargar et al. studied the dispersion of solutes considering the EOF of viscoelastic fluids within a slit microchannel.30 Existing studies indicate that a substantial dispersion of a solute band interacting with the EOF through microdevices is further possible. The same can be done by modifying the geometry of microdevices and/or by considering spatially varying the ζ-potential of supporting walls.31–34 For such a case an additional pressure field is created, which in turn leads to an enhanced hydrodynamic dispersion that is often beneficial for the mixing process.
The works indicated above have considered the solute dispersion under a steady DC electric field. However, there are several advantages of EOF under an AC electric field. Gas bubbles are often very detrimental in microchannels, since they may block the flow passage. It is noteworthy to mention that an AC electric based EOF has one major advantage over DC EOF: under DC field gas bubbles are produced at the electrodes driving the flow, while bubble formation is suppressed under AC fields. Besides, the AC electric field based EOF requires lower voltage drop compared to the DC EOF, which reduces the chances of damage of electrodes, requires a less response time leading to a faster detection time as well as minimizes the electrode erosion, to name a few.35–37 Note that the AC electric field based EOF is further desirable for many practical applications, e.g., electrokinetic manipulation of nanoparticulates, rapid medical diagnosis, etc.38,39 There are several studies dealing with electrohydrodynamics through microdevices under an AC electric field,40–47 however little attention is paid to study the solute dispersion under AC electric field based EOF. Huang and Lai studied the impact of AC electric field based EOF on the transport and separation phenomena through a two dimensional microchannel.48 Ramon et al. studied the dispersion of solutes under an oscillatory EOF across a cylindrical tube considering the reversible mass exchange along the walls and it is observed that the separation of species can be done in a better way under an AC electric field.49 The solute dispersion through a microchannel considering the combined impact of time dependent electric field as well as wall ζ-potential was studied by Paul and Ng.50 Teodoro et al. have investigated the impact of oscillatory EOF on the solute dispersion under various periodic electric fields (e.g., sawtooth, square, and parabolic waveforms, etc.) and they observed that an enhanced mass transport can be achieved suitably regulating the field signal.51 Li and Jian studied solute dispersion under an AC electric field driven EOF and deduced the results for the dispersion coefficient and the mean concentration of the solutes across a microtube.52
The aforesaid articles deal with the solute dispersion in fluidic devices with bare walls (or rigid walls) and a single phase fluidic medium under an AC electric field driven oscillatory EOF. Kumar and De studied the hydrodynamic dispersion of solutes under an oscillatory EOF across microtubes with porous walls.53 Li and Jian studied the impact of an AC field induced EOF on the solute dispersion across a soft nanochannel.54 Reshadi and Saidi studied the solute dispersion through a soft nanochannel under steady as well as oscillatory electroosmotic-Poiseuille flow.55 Note that the soft nanochannels are conduits in which the inner side of the supporting rigid walls are coated with a soft polyelectrolyte layer. It is shown in the existing studies that the presence of polyelectrolyte layers can have a substantial impact on the dispersion process.56,57 Note that solute dispersion driven by an oscillatory electric field finds potential application in various fields, including biological or physiological transport, drug delivery systems, and chromatographic separation and mixing, to name a few.58–62
In recent years, a significant work is done on the flow modulation and transport of ionic species through various shaped engineered soft nanochannels. Karimzadeh et al. studied the impact of the shape of soft nanochannels on the overall EOF modulation and transport of ionic species.63 Dartoomi et al. have shown the importance of the shape of nanochannels on the blue energy generation.64 Such an extensive study indicates an alternate way to extract the energy. Ashrafizadeh and co-researchers studied extensively the role of nanochannel geometry and soft layers in the salinity gradient driven energy harvesting through various shaped soft nanochannels.65–67 In addition to the flow modulation through a soft nanochannel, another important electrokinetic phenomenon is ionic current rectification (ICR). Note that the ICR is a consequence of symmetry breaking either in channel geometry, charge distribution, the applied potential gradient, etc.68 For such cases, depending on the voltage bias the ion transport is preferential along a particular direction. In recent years, several researchers studied extensively the ICR phenomenon though various engineered microdevices for which there is some underlying asymmetry.69–72 It is noteworthy to mention that in the absence of any asymmetry along the lateral dimension, the no current rectification is possible.73
In addition to soft nanochannels, a huge body of literature is further available on the modulation of electrokinetic flow through microfluidic devices filled with two or more liquids. The existing studies in this direction are carried out under DC or AC electric fields and are restricted only with the study on electrohydrodynamics.74–81 In the present article, we focus on dispersion of passive solutes under an AC electric field driven EOF across a channel filled with an electrolyte solution surrounded with a layer of a membrane of various biological cells. Such a membrane layer may bear additional mobile charges (e.g., free lipid molecules, charged surfactant molecules in the form of dimer micelles or small micelles with very low aggregation numbers). The presence of free charges across the membrane layer gives rise to non zero charge density along the liquid–liquid interface.82,83 According to the fluid mosaic model of Singer and Nicolson,84 the membrane layer can be treated as a two-dimensional oriented viscous liquid with low dielectric constant. The difference in dielectric permittivity of the aqueous electrolyte solution and the membrane layer leads to the ion partitioning effect.85,86 Depending on the Born energies of both the phases with possible mismatch in dielectric permittivity, the electrolyte ions will penetrate inside the peripheral membrane layer in a discontinuous manner. It is noteworthy to mention that in a recent article we have studied the solute dispersion through a soft nanochannel under the EOF induced by the applied DC electric field.57 In contrast, the present article deals with the flow modulation and the solute dispersion under applied AC electric field. Furthermore, instead of a soft nanochannel we consider the EOF modulation and solute dispersion in a nanochannel filled with electrolyte solution surrounded by a layer of a dielectric liquid that resembles membranes of various biological cells. Note that there is no available study in this direction that deals with the flow modulation under an oscillatory electric field and the impact of modulated EOF on the dispersion of solutes across such a channel.
In order to fill the aforesaid research gap, we aim to study the flow modulation and solute dispersion across such a channel indicated above under applied AC electric field. A mathematical study is thus performed to evaluate the EOF field and its impact on solute dispersion considering the combined impact of the ion partitioning and the ion steric effects. Note that a steric effect is induced by the interaction of finite sized ions. We adopt the Carnahan and Starling model to take into account the ion steric effect,87 which is however best suited to characterize the said effect for a moderate to highly charged electrohydrodynamic systems.88,89 Considering the impact of molecular diffusion and modulated AC field based EOF, the band broadening process is analysed by the generalized dispersion model introduced by Gill and Sankarasubramanian.9 Note that the AC electric field driven EOF prevents the formation of gas bubbles within the flow passage, and thus the fluid convection is expected to have a substantial impact on the solute dispersion process.
The rest of the article is organized as follows. The problem formulation is summarized in Section 2. The mathematical model and methodology are presented in Section 3, which includes a brief description of the distribution of electrostatic EDL potential, AC electric field driven oscillatory EOF and the solute dispersion process. We developed a numerical scheme to simulate the governing equations. In addition, we obtained closed forms of analytical results that describe the EOF field as well as the dispersion process under various limiting cases. Results and discussion on the modulation of EOF and its impact on the solute dispersion process are included in Section 4 followed by a brief summary of all the results and future scope of study in Section 5.
2 Problem formulation
Fig. 1 systematically depicts a parallel plate slit nanochannel of height 2H filled with an electrolyte solution surrounded by a layer of an immiscible and dielectric liquid with thickness δ (<H). We neglect the end effects considering the width and length of the channel are much larger than its height. A Cartesian coordinate system (x, y) with the origin located at the channel center is employed to analyze the EOF field and solute dispersion under the influence of an AC electric field  where E0 indicates the magnitude of applied oscillatory electric field. Here
where E0 indicates the magnitude of applied oscillatory electric field. Here  ; ω and t indicate the angular frequency of the oscillatory electric field and time, respectively, and
; ω and t indicate the angular frequency of the oscillatory electric field and time, respectively, and  indicates the real part of a complex number
indicates the real part of a complex number  . The concentration and valence of additional mobile ions in the form of surfactant molecules present in the membrane layer are denoted as N0 (in mM) and Z, respectively. We have assumed that the concentration of such molecules with in an aqueous medium is zero.
. The concentration and valence of additional mobile ions in the form of surfactant molecules present in the membrane layer are denoted as N0 (in mM) and Z, respectively. We have assumed that the concentration of such molecules with in an aqueous medium is zero.
 |
| | Fig. 1 Schematic representation of the EOF through an infinitely long nanochannel filled with an electrolyte solution surrounded by a layer of a dielectric liquid. The dielectric permittivity, fluidic mass density and viscosity of the liquid layer and ambient electrolyte solutions are denoted as  ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) d, ηd and d, ηd and  ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) e, ηe, respectively. The uncharged solute with concentration C0 is placed initially along the middle of the channel with bandwidth 2L, which is further exposed to a back and forth fluid motion under an oscillating electric field E0 e, ηe, respectively. The uncharged solute with concentration C0 is placed initially along the middle of the channel with bandwidth 2L, which is further exposed to a back and forth fluid motion under an oscillating electric field E0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ωt). cos(ωt). | |
This is a reasonable assumption as their solubility in the aqueous phase is negligibly small.82,90 The presence of the additional mobile charges within the dielectric liquid layer induces nonzero interfacial charge σ, which further leads to the formation of two EDLs along the liquid–liquid interface. Such EDLs may form due to attraction of counterions by the charged liquid–liquid interface from the adjacent liquid medium. An EDL may form at the interface towards the side of aqueous medium with thickness κ−1, while an equivalent EDL with thickness κd−1 further forms at the liquid–liquid interface towards the dielectric liquid layer side. A detailed description of the same may be found elsewhere.82,86 We consider the background electrolyte as a binary symmetric z:z electrolyte with bulk concentration n0 (in mM). The viscosity and dielectric permittivity of the membrane layer are denoted as ηd, ηe and  respectively. The dielectric constant of the membrane layer is in general lower than that of the electrolyte medium.83,91 Thus, the penetration of electrolyte ions within the membrane layer occurs in a discontinuous manner due to the presence of the ion partitioning effect. The concentration of electrolyte ions (nj, j = 1, 2) along the liquid–liquid interface is discontinuous and satisfies the following relation92–95
respectively. The dielectric constant of the membrane layer is in general lower than that of the electrolyte medium.83,91 Thus, the penetration of electrolyte ions within the membrane layer occurs in a discontinuous manner due to the presence of the ion partitioning effect. The concentration of electrolyte ions (nj, j = 1, 2) along the liquid–liquid interface is discontinuous and satisfies the following relation92–95
| | | nj{(−H + δ)−} = fjnj{(−H + δ)+}, j = 1, 2 | (1) |
where
fj indicates the ion partitioning coefficient of the
jth (
j = 1, 2) ions and is defined as ref.
96| |  | (2) |
Here
kB,
T and
e are the Boltzmann constant, the absolute temperature and the elementary charge, respectively, and the radius of the
jth ion is denoted as
rj (
j = 1, 2). In our present study, we consider the size of the cation and anion to be the same denoted as
r, and thus
f1 =
f2 =
f. It is evident from the relation
(2) that for a two-phase fluidic system with different dielectric permittivities of liquids in the adjacent phases, an increase in the ion size increases the value of ion partitioning coefficient
f. Thus, an increase in the ion size reduces the dielectric-gradient mediated ion partitioning effect. Thus, both the ion steric and ion partitioning effects are coupled together. However, for similar dielectric permittivity of the adjacent phases, the ion partitioning effect is absent.
Using the Carnahan and Starling model,87 the spatial distribution of the concentration of mobile electrolyte ions (nj, j = 1, 2) with finite size follows the modified Boltzmann distribution, given as97
| |  | (3) |
The terms
ψ,
F and
R indicate the electrostatic potential, Faraday constant and gas constant, respectively. The above expression further involves the steric factor
P, defined as
P = 8
ϕB/(1 + 8
ϕB), where
ϕB is the volume fraction of mobile ions, defined as
ϕB = (4π
r3/3)2
NAn0. Here
NA is the Avogadro number. In addition, the spatial distribution of the concentration of additional mobile ions present in the dielectric liquid layer, considering its nonzero volume fraction
ϕd, is given as follows
83,97| |  | (4) |
where
Ω = 8
ϕd/(1 + 8
ϕd). The volume fraction
ϕd is defined as
ϕd = (4π
ad3/3)2
NAN0, where
ad indicates the size of the additional ion. The expression
(4) involves the Donnan potential
ψD which indicates the potential deep inside the dielectric liquid layer.
83–98 Explicit expression for the same is deduced later. The readers are further referred to the Section S.1 (ESI
†) for a detailed derivation of relation
(4).
The EOF field across the considered channel is in general lies in the creeping flow regime and there is no instability occurring in the present two-liquid systems. As indicated earlier the liquid in the dielectric liquid layer and the aqueous medium are immiscible in nature, so the liquid in the layer adjacent to the supporting walls and the aqueous medium cannot permeate each other. Furthermore, we assume that the uniformly charged liquid–liquid interface remains planar, which is in fact the basic state of a general stability problem. Note that for the considered parameter space, the Capillary number is far smaller than unity, and accordingly, warrants our analysis without accounting the deformation of the liquid–liquid interface. Such a consideration is rather common in transient EOF involving liquid–liquid interface.74–78,80,81 A small amount of passive solute is placed along the channel center with a given bandwidth, and it faces the back and forth EOF induced by an applied AC electric field. The flow background liquid medium is not affected by the presence of a dilute band of sufficiently small soluble solutes. The details of the mathematical model and methods to solve the set of model equations are described below.
3 Mathematical model and methodology
In this section, we present the detailed mathematical model and methodology to solve the set of governing equations. For the considered flow geometry, the EDL potential, flow field and spatial distribution of the concentration are symmetric with respect to the central line of the channel. Without loss of generality we present the governing equations pertaining to the EDL potential, EOF field as well as concentration distribution of solutes along the lower half of the channel. We first present the electrostatic EDL potential followed by the calculation of AC electric field based EOF. With the known flow field, the dispersion characteristics of the injected solute under oscillatory EOF field are further analyzed.
3.1 Electrostatic EDL potential and EOF field under AC electric field
The electrostatic EDL potential considering the combined impact of the ion steric and the ion partitioning effects is described by the modified Poisson–Boltzmann equation, given as| |  | (5a) |
| |  | (5b) |
where ρd(y) and ρe(y) represent the volumetric charges due to mobile ions inside and outside of the dielectric liquid layer, respectively, and are defined as| | | ρd(y) = F[f{zn1(y) − zn2(y)} + Znd(y)] −H < y ≤ −H + δ | (6a) |
| | | ρe(y) = F[zn1(y) − zn2(y)] −H + δ < y ≤ 0 | (6b) |
Substituting the relations (3) and (6) into the eqn (5) yields| |  | (7a) |
| |  | (7b) |
The channel walls are considered to be uncharged. We adopt the continuity of electrostatic EDL potential along the liquid–liquid interface. In the presence of interfacial charge, the displacement vector along the liquid–liquid interface is discontinuous. Along the central line, the gradient of potential vanishes due to symmetry. We use the scale ϕ0 = RT/zF to non-dimensionalize the EDL potential (ψ(y)) as well as the Donnan potential (ψD) and the space coordinate y is scaled by the half height of the channel, i.e., H. Using the above scales the governing equation and associated boundary conditions for the EDL potential in the scaled form may be deduced as follows| |  | (8a) |
| |  | (8b) |
subject to the boundary conditions| |  | (9a) |
| |  | (9b) |
| |  | (9c) |
| |  | (9d) |
Eqn (8a) involves the scaled parameter M, defined as M = ZN0/2zfn0. The quantities ![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) (ȳ),
(ȳ), ![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) D indicate the scaled EDL potential and Donnan potential, respectively. The scaled interfacial charge
D indicate the scaled EDL potential and Donnan potential, respectively. The scaled interfacial charge ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) is defined as
is defined as  and
and  indicates the liquid layer to electrolyte permittivity ratio with
indicates the liquid layer to electrolyte permittivity ratio with ![[small delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c5.gif) = δ/H being the scaled thickness of the liquid layer. The quantity κ appearing in eqn (8) indicates the inverse of the EDL thickness (which forms towards the side of the aqueous phase), defined as
= δ/H being the scaled thickness of the liquid layer. The quantity κ appearing in eqn (8) indicates the inverse of the EDL thickness (which forms towards the side of the aqueous phase), defined as  and the quantity κ1 appearing in eqn (8) is defined as
and the quantity κ1 appearing in eqn (8) is defined as  . The scaled Donnan potential can be obtained by setting the right hand side of eqn (8a) to zero, and thus we may write
. The scaled Donnan potential can be obtained by setting the right hand side of eqn (8a) to zero, and thus we may write| |  | (10) |
Solution of (10) provides the explicit expression for the scaled Donnan potential, given as| |  | (11) |
The time dependent axial flow velocity component u(y, t) is governed by the unsteady Stokes equations with the electric body force term, and is given as| |  | (12a) |
| |  | (12b) |
subject to the boundary conditions| | | u(y, t)|y=(−H+δ)− = u(y, t)|y=(−H+δ)+ | (13b) |
| |  | (13c) |
| |  | (13d) |
where the mass density of the liquid in the peripheral layer and electrolyte solution are ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) d and
d and ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) e, respectively. We consider the no-slip velocity boundary condition along the supporting rigid walls of the channel as indicated in the relation (13a). The continuity of flow velocity along the liquid–liquid interface is adopted, which is further indicated in the relation (13b). We adopt the EDL plus surface charge (SC) model to study the considered electrokinetic flow involving a two-liquid system.74 It is noteworthy to mention that such an EDL plus SC model can successfully describe the experimental observation on the electrokinetic behavior of two-phase liquid systems.99 Such a consideration may leads to the condition indicated in (13c). We further adopt symmetry condition for flow velocity along the central line of the channel, which is indicated in (13d).
e, respectively. We consider the no-slip velocity boundary condition along the supporting rigid walls of the channel as indicated in the relation (13a). The continuity of flow velocity along the liquid–liquid interface is adopted, which is further indicated in the relation (13b). We adopt the EDL plus surface charge (SC) model to study the considered electrokinetic flow involving a two-liquid system.74 It is noteworthy to mention that such an EDL plus SC model can successfully describe the experimental observation on the electrokinetic behavior of two-phase liquid systems.99 Such a consideration may leads to the condition indicated in (13c). We further adopt symmetry condition for flow velocity along the central line of the channel, which is indicated in (13d).
We consider the oscillatory EOF under AC electric field  and thus the back and forth oscillatory axial velocity may be written as
and thus the back and forth oscillatory axial velocity may be written as  where u0(y) is the complex amplitude of the velocity field. We consider the Helmoltz–Smoluchowsky reference velocity
where u0(y) is the complex amplitude of the velocity field. We consider the Helmoltz–Smoluchowsky reference velocity  as the velocity scale. Below we recast the governing equations and boundary conditions associated with the velocity field in the scaled form
as the velocity scale. Below we recast the governing equations and boundary conditions associated with the velocity field in the scaled form
| |  | (14a) |
| |  | (14b) |
subject to
| | ū0(ȳ)|ȳ=(−1+![[small delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c5.gif) )− = ū0(ȳ)|ȳ=(−1+ )− = ū0(ȳ)|ȳ=(−1+![[small delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c5.gif) )+ )+ | (15b) |
| |  | (15c) |
| |  | (15d) |
where
ū0(
ȳ) is the scaled value
u0(
y) and
ηR =
ηd/
ηe is the viscosity ratio. Solving the above
eqn (14a) and (14b) subject to the given boundary conditions
(15a)–(15d) yields the explicit form of
ū0(
ȳ), given as
| |  | (16) |
The above expression
(16) contains several constants,
e.g.,
mi (
i = 1, 2, 3) and
Ci (
i = 1, 2, 3, 4) and integrals
Ji(
ȳ) (
i = 1, 2, 3, 4), which are are provided in Appendix-A.
It is evident that one can deduce the results for the axial velocity field with the known value of the electrostatic EDL potential. In Appendix-B, we have deduced the approximate semi-analytical results for EDL potential valid for the low to higher regime of electrostatic charge. In addition, we have further deduced exact analytical results for electrostatic potential as well as velocity field within the Debye–Hückel electrostatic limit and are summarized in Appendix-C. However to consider a broad range of electrostatic charge as well as other model parameters, we have deduced numerical results for EDL potential using the finite difference based numerical scheme. The discretized equation for EDL potential based on the central difference scheme is solved iteratively using the tridiagonal matrix algorithm. The iterations are continued until the difference in two successive steps becomes smaller than the tolerance limit. A comparison of the numerical results for EDL potential with the deduced semi-analytical results are shown in Appendix-B and the exact theoretical results under the Debye–Hückel limit are shown in Appendix-C. With the known value of EDL potential and the integrals mentioned above, we have further deduced the numerical results of axial velocity using the expression (16). Note that the main complexity to deduce the axial velocity is to calculate the integrals Ji (i = 1, 2, 3, 4) and for the same we have used MATHEMATICA software. The validation of dynamic axial velocity field with the deduced analytical results is provided in Appendix-C. The results for the velocity field are further used to study the dispersion characteristics of the solute band placed inside the channel. A detailed description of the dispersion process is summarized below.
3.2 Dispersion of solutes
In this subsection we have presented the governing equation for the concentration of solutes and the relevant initial and boundary conditions to study the dispersion process. A solute with bandwidth 2L, diffusivity D0 and initial concentration C0 is placed at the channel center and is exposed under oscillatory EOF. The concentration distribution of the solutes is governed by the unsteady convective–diffusion equation, given as| |  | (17) |
where C(x, y, t) indicates the concentration of solutes. The initial distribution of the concentration of solutes is given as| |  | (18) |
Along x → ±∞, the concentration of the solute vanishes. Besides, there is no mass transfer across the supporting rigid walls. We further adopt the symmetry condition along the central line of the channel. Thus, the boundary conditions associated with the solute concentration are as follows| |  | (19b) |
The reference concentration C0 is considered as the scale for the solute concentration. The y-coordinate is scaled by the half-height of the channel, i.e., H. Besides, the x-coordinate is scaled by H2UHS/D0 and the time is scaled by H2/D0. Using these scales, we may obtain the governing equation and associated initial and boundary conditions in the nondimensional form, given as| |  | (20) |
subject to the initial conditions| |  | (21) |
and boundary conditions| | ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) (±∞, ȳ, (±∞, ȳ, ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) = 0 ) = 0 | (22a) |
| |  | (22b) |
where ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) = C/C0,
= C/C0, ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) = D0x/H2UHS,
= D0x/H2UHS, ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) = D0t/H2 and
= D0t/H2 and ![[L with combining macron]](https://www.rsc.org/images/entities/i_char_004c_0304.gif) = D0L/H2UHS. The non-dimensional parameter Pe indicates the ratio of the rate of transport caused by convection and molecular diffusion, and is defined as Pe = HUHS/D0. To analyze the dispersion of solutes we introduce a moving coordinate system, comoving with the cross-sectional mean fluid velocity
= D0L/H2UHS. The non-dimensional parameter Pe indicates the ratio of the rate of transport caused by convection and molecular diffusion, and is defined as Pe = HUHS/D0. To analyze the dispersion of solutes we introduce a moving coordinate system, comoving with the cross-sectional mean fluid velocity  . Thus, the new axial coordinate
. Thus, the new axial coordinate ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) u(
u(![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) ,
, ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) (in the scaled form) in the moving frame of reference may be defined as
) (in the scaled form) in the moving frame of reference may be defined as| |  | (23) |
Using this transformation, we may recast the unsteady convection–diffusion equation as follows| |  | (24) |
The method used by Gill and Sankarasubramanian9 is adopted to study the dispersion process. Thus, the local concentration of solutes can be written in terms of series expansion in axis gradients of cross-sectional averaged concentration ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) m, given as
m, given as| |  | (25) |
where| |  | (26) |
The terms fk(ȳ, ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) (k = 1, 2, 3, …) are the coefficients of series expansion. Substituting (26) into (25) yields
) (k = 1, 2, 3, …) are the coefficients of series expansion. Substituting (26) into (25) yields| |  | (27) |
We consider that the dispersion process is diffusive right from the time zero and thus the cross-sectional averaged concentration ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) m follows the given equation100
m follows the given equation100| |  | (28) |
where the coefficients Ki(![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) are the periodic function of time due to an oscillatory flow of the background aqueous medium. Considering k-times the partial derivative of the above eqn (28) with respect to space coordinate
) are the periodic function of time due to an oscillatory flow of the background aqueous medium. Considering k-times the partial derivative of the above eqn (28) with respect to space coordinate ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) u, we may deduce the following relation
u, we may deduce the following relation| |  | (29) |
Now substituting eqn (28) and (29) into eqn (27) and after algebraic simplification yields| |  | (30) |
From the above equation we may set the coefficients of ∂k![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) m/∂
m/∂![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) ku (k = 1, 2, 3, …) to zero, which yields the following differential equations involving fk
ku (k = 1, 2, 3, …) to zero, which yields the following differential equations involving fk| |  | (31a) |
| |  | (31b) |
| |  | (31c) |
The index k in eqn (31c) takes the values k = 1, 2, 3, …. It is worth noting that the initial and boundary conditions for ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) are also satisfied by
are also satisfied by ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) m. Thus, substituting (25) into (21) and (22) yieldsand
m. Thus, substituting (25) into (21) and (22) yieldsand| |  | (33) |
Besides, eqn (26) requires| |  | (34) |
Integrating (31a)–(31c) with respect to ȳ from −1 to 0, one can easily check that the coefficient K1(![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) vanishes and the other coefficients are derived as follows
) vanishes and the other coefficients are derived as follows| |  | (35) |
and| |  | (36) |
Note that the term K1(![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) indicates the convection coefficient due to the velocity of solutes and thus vanishes as we are in a moving frame of reference. Besides, the term K2(
) indicates the convection coefficient due to the velocity of solutes and thus vanishes as we are in a moving frame of reference. Besides, the term K2(![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) indicates the effective dispersion coefficient due to the molecular diffusion and fluid convection, which is renamed as K(
) indicates the effective dispersion coefficient due to the molecular diffusion and fluid convection, which is renamed as K(![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ). The terms Ki (i ≥ 3) are very small compared to the value of K2. So, we can neglect the contribution of all Ki when i ≥ 3.9 Thus, eqn (28) takes the simplified form as follows
). The terms Ki (i ≥ 3) are very small compared to the value of K2. So, we can neglect the contribution of all Ki when i ≥ 3.9 Thus, eqn (28) takes the simplified form as follows| |  | (37) |
The expression of K2(![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) (renamed afterwards as K(
) (renamed afterwards as K(![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) )) requires the value of f1(ȳ,
)) requires the value of f1(ȳ, ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ), which is governed by eqn (31b) subject to the conditions (32) and (33). Thus, to evaluate the cross-sectional averaged concentration of the solute, one need to calculate f1(ȳ,
), which is governed by eqn (31b) subject to the conditions (32) and (33). Thus, to evaluate the cross-sectional averaged concentration of the solute, one need to calculate f1(ȳ, ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ). It may be noted that under the AC field based EOF, we may write
). It may be noted that under the AC field based EOF, we may write  , where
, where  and
and  . With the same analogy we may further rewrite
. With the same analogy we may further rewrite  . Substituting the same into (31a), (32) and (34) we may formulate the boundary value problem involving F(ȳ), and the same is summarized below
. Substituting the same into (31a), (32) and (34) we may formulate the boundary value problem involving F(ȳ), and the same is summarized below| |  | (38) |
subject to the boundary conditions| |  | (39a) |
| | F{(−1 + ![[small delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c5.gif) )−} = F{(−1 + )−} = F{(−1 + ![[small delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c5.gif) )+} )+} | (39b) |
| |  | (39c) |
| |  | (39d) |
where  . Solving (38) subject to the boundary conditions (39a)–(39d) yields
. Solving (38) subject to the boundary conditions (39a)–(39d) yields| |  | (40) |
The above expression (40) contains the constants Di (i = 1, 2, 3, 4) and integrals Ji(ȳ) (i = 5, 6, 7, 8), which are summarized in Appendix-A.
The relation for dispersion coefficient K(![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) may be written in terms of F(ȳ) and is given below
) may be written in terms of F(ȳ) and is given below
| |  | (41) |
We further introduce a new time dependent variable
ξ(
![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif)
), defined as
| |  | (42) |
Note that

indicates the standard deviation of distribution of
![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) m
m at a given time
![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif)
. Such a quantity measures the width of the dispersed zone of the solutes. Using the above transformation
(42), we may transform
eqn (37) and the associated initial and boundary conditions as follows
| |  | (43) |
subject to
| | ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) m( m(![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) u, 0) = 2 u, 0) = 2![[L with combining macron]](https://www.rsc.org/images/entities/i_char_004c_0304.gif) δ δ![[L with combining macron]](https://www.rsc.org/images/entities/i_char_004c_0304.gif) , , ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) m(±∞, m(±∞, ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) = 0 ) = 0 | (44) |
where
| |  | (45) |
Using the Fourier transformation, we can easily transform
eqn (43) and (44) into the following equations
| | 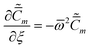 | (46) |
and,
| |  | (47) |
where

, and
![[small omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0da.gif)
represents the scaled spatial wave number, defined earlier. The solution of
eqn (46) subject to conditions indicated in
(47) is given as follows
| |  | (48) |
Using inverse Fourier transform on the function

we may deduce the time evolution of the spatially dependent area-averaged solute concentration as follows
| |  | (49) |
where erf(
χ) indicates the error function, defined as

. It is worth noting that the quantities which provide the measurement of the dispersion process are
![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) m
m(
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) u
u,
![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif)
),
K(
![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif)
) and

respectively. In addition, we have further indicated the results for time-averaged effective dispersion coefficient
Kavg over one oscillation period
τ0 = 2π/
ω, defined as
| |  | (50) |
In order to obtain the aforesaid quantities, the main input is the axial velocity profile and the method to deduce the same is already indicated. To obtain the dispersion coefficient K(![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ), we need to calculate the function F(ȳ) using the closed form relation (40), which further involves the axial velocity. Note that the main complexity to deduce F(ȳ) is to calculate the integrals Ji (i = 5, 6, 7, 8), which are calculated using MATHEMATICA software. With the known values of axial velocity and F(ȳ), the relation (41) is implemented to calculate K(
), we need to calculate the function F(ȳ) using the closed form relation (40), which further involves the axial velocity. Note that the main complexity to deduce F(ȳ) is to calculate the integrals Ji (i = 5, 6, 7, 8), which are calculated using MATHEMATICA software. With the known values of axial velocity and F(ȳ), the relation (41) is implemented to calculate K(![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ). The relations (42), (49) and (50) are further implemented to derive the results for
). The relations (42), (49) and (50) are further implemented to derive the results for 
![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) m(
m(![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) u,
u, ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) and Kavg, respectively.
) and Kavg, respectively.
It is noteworthy to mention that within the Debye–Hückel electrostatic framework and the limit of ω → 0 we have further deduced the closed form analytical results for all the quantities associated with the dispersion process, e.g., 
![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) m(
m(![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) u,
u, ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) and Kavg, respectively. The detailed description of the same is further summarized in Appendix-D. In addition, we have further performed the validation of numerical quantities associated with the dispersion process with the aforesaid analytical results. The readers are referred to Appendix-D for more details related to the same.
) and Kavg, respectively. The detailed description of the same is further summarized in Appendix-D. In addition, we have further performed the validation of numerical quantities associated with the dispersion process with the aforesaid analytical results. The readers are referred to Appendix-D for more details related to the same.
4 Results and discussion
The main objective of the present study is to provide a quantitative measurement of the modulation EOF under an AC electric field in a channel filled with an electrolyte solution surrounded by a layer of a dielectric liquid. In addition to that, we further investigate the impact of flow of the background fluidic medium on the dispersion of the solute across such a channel. The pertinent parameters that affect the fluid flow and thereby the dispersion process are dielectric permittivity, viscosity and thickness of the dielectric liquid layer, electrolyte concentration, ion size, concentration of additional mobile ions present within the liquid layer, interfacial surface charge along the liquid–liquid interface, channel height, frequency of the applied electric field, etc. For solute dispersion, another additional intrinsic parameter is mass diffusivity of the solute. As indicated earlier, the dielectric permittivity of the membrane layer is in general lower than that of the electrolyte medium. We have varied systematically the dielectric constant of the membrane layer to account for the ion partitioning effect. Besides, the ion steric effect further plays a prominent role in the flow modulation specially for the case when the electrostatic charge carried by the considered fluidic system (i.e., interfacial charge and molar concentration of additional mobile ions of the dielectric liquid layer) is moderate to high. The impact of the steric effect depends on the finite size of ions and electrolyte concentration, which we have varied systematically to produce the results for flow field and thereby the solute dispersion. For the EOF under AC electric field, the oscillating Reynolds number Rej = ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) jωH2/ηj dictates the back and forth motion of the background medium, where the subscript j = d or e is associated with the dielectric liquid layer or the electrolyte medium, respectively. We present the results for various choices of the channel height and frequency of the applied AC electric field.
jωH2/ηj dictates the back and forth motion of the background medium, where the subscript j = d or e is associated with the dielectric liquid layer or the electrolyte medium, respectively. We present the results for various choices of the channel height and frequency of the applied AC electric field.
Unless stated otherwise, the dielectric liquid which surrounds the electrolytic solution is considered as the oily organic solvent cyclohexyl bromide (CHB) for which the dielectric constant  , viscosity ηd = 2.269 mPa s and mass density
, viscosity ηd = 2.269 mPa s and mass density ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) d = 1345 kg m−3, respectively.101 For such a choice of liquid layer, the viscosity ratio ηR = 2.54, dielectric permittivity ratio
d = 1345 kg m−3, respectively.101 For such a choice of liquid layer, the viscosity ratio ηR = 2.54, dielectric permittivity ratio  and the interfacial tension is 9.2 × 10−3 N m−1, respectively. The electric strength of electric field E0 is taken as E0 = 103 V m−1. Thus, the Capillary number Ca ≪ 1. In addition to the CHB solvent, we have further presented the results changing suitably the dielectric permittivity as well as viscosity of the liquid layer adjacent to the supporting walls. For each of the cases, we found the Capillary number is far smaller than unity. A relatively broad range in frequency ω/2π is considered, e.g., 105 Hz to 108 Hz, and such choices of frequency are rather common in the AC electric field driven EOF.102,103
and the interfacial tension is 9.2 × 10−3 N m−1, respectively. The electric strength of electric field E0 is taken as E0 = 103 V m−1. Thus, the Capillary number Ca ≪ 1. In addition to the CHB solvent, we have further presented the results changing suitably the dielectric permittivity as well as viscosity of the liquid layer adjacent to the supporting walls. For each of the cases, we found the Capillary number is far smaller than unity. A relatively broad range in frequency ω/2π is considered, e.g., 105 Hz to 108 Hz, and such choices of frequency are rather common in the AC electric field driven EOF.102,103
4.1 Modulation of EOF
To illustrate the impact of pertinent parameters on the flow modulation we present the results for dimensionless velocity amplitude |ū0(ȳ)|. In Fig. 2 we have shown the results to discuss the impact of the Debye–Hückel parameter of κH with fixed ion size r = 3.3 Å (Fig. 2a) and the ion steric effect with fixed κH (Fig. 2b). The dielectric liquid which surrounds the electrolytic solution is considered as oily organic solvent cyclohexyl bromide (CHB). Choice of such a liquid in the layer adjacent to the supporting walls is reasonable as its dielectric permitivity is much lower than that of the aqueous medium and the liquid in adjacent phases in immiscible in nature. Thus, for the considered two-phase fluidic system, the ion partitioning effect arises due to a significant difference in dielectric permittivity of both the phases. Since the viscosity of the CHB solvent is high compared to that of the aqueous medium, the magnitude of |ū0(ȳ)| within the liquid layer is substantially small compared to that in the electrolyte phase. We further observed that the strength of flow field reduces with the increase in κH (Fig. 2a). The accumulation of counterions near the charged interface enhances with the increase in κH, and thus, the impact of effective interfacial charge reduces, which leads to a significant reduction in flow strength. We observed that the velocity amplitude reduces with the increase in the size of electrolyte ions (Fig. 2b). In general, the finite sized ion restricts the accumulation of arbitrary number of counterions near the charged interface as well within the dielectric liquid layer. On the other hand, the increase in the ion size reduces the impact of the dielectric-gradient mediated ion partitioning effect. Combination of these two effects reduces the net neutralization mobile charge entrapped within the dielectric liquid layer, which enhances with the increase in the ion size and leads to a reduction in net electromotive force. As a result, the velocity amplitude |ū0(ȳ)| reduces with increasing ion size.
 |
| | Fig. 2 The results for scaled velocity amplitude |ū0(ȳ)| are shown for various values of (a) κH (= 2.5, 5, 10, and 25) with fixed r = 3.3 Å and (b) r (= 3.3 Å, 4 Å, 5 Å, and 6 Å) with fixed κH = 2.5. The results are presented for fixed H = 25 nm, δ = 5 nm, N0 = 1 mM, ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) = 2 and = 2 and ![[small omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0da.gif) = 10 (i.e., ω/2π = 2.5 × 106 Hz), respectively. = 10 (i.e., ω/2π = 2.5 × 106 Hz), respectively. | |
In Fig. 3, we have shown the results for the velocity amplitude considering different values of dielectric permittivity and viscosity of the liquid in the layer adjacent to the supporting walls. We present the results for various choices of  with fixed viscosity ηR = 2.54 (Fig. 3a) and in Fig. 3b we have shown the results for various choices of ηR with fixed dielectric permittivity
with fixed viscosity ηR = 2.54 (Fig. 3a) and in Fig. 3b we have shown the results for various choices of ηR with fixed dielectric permittivity  . The results are presented for fixed values of other model parameters, which are summarized in the figure caption. As indicated earlier for CHB solvent
. The results are presented for fixed values of other model parameters, which are summarized in the figure caption. As indicated earlier for CHB solvent  and ηR = 2.54, which is taken as the base value and an increase in
and ηR = 2.54, which is taken as the base value and an increase in  and ηR indicates that the liquid in the dielectric layer is more polarizable in response to an electric field and more viscous compared to the CHB solvent, respectively. Besides, the increase in
and ηR indicates that the liquid in the dielectric layer is more polarizable in response to an electric field and more viscous compared to the CHB solvent, respectively. Besides, the increase in  with fixed dielectric constant of the aqueous medium leads to an increase in dielectric permittivity of the liquid in the layer adjacent to the channel wall. Thus, the impact of ion partitioning reduces, which in turn allows the accumulation of more counterions within the dielectric liquid layer. As a result, the neutralization of effective charge inside the liquid layer enhances and leads to a reduction in velocity amplitude |ū0(ȳ)|. As expected the velocity amplitude |ū0(ȳ)| reduces with the increase in viscosity of the liquid layer adjacent to the supporting walls. Note that the increase in velocity amplitude |ū0(ȳ)| within the liquid layer with its lower viscosity leads to an enhancement in |ū0(ȳ)| within the aqueous phase so as to satisfy the continuity in flow velocity along the liquid–liquid interface.
with fixed dielectric constant of the aqueous medium leads to an increase in dielectric permittivity of the liquid in the layer adjacent to the channel wall. Thus, the impact of ion partitioning reduces, which in turn allows the accumulation of more counterions within the dielectric liquid layer. As a result, the neutralization of effective charge inside the liquid layer enhances and leads to a reduction in velocity amplitude |ū0(ȳ)|. As expected the velocity amplitude |ū0(ȳ)| reduces with the increase in viscosity of the liquid layer adjacent to the supporting walls. Note that the increase in velocity amplitude |ū0(ȳ)| within the liquid layer with its lower viscosity leads to an enhancement in |ū0(ȳ)| within the aqueous phase so as to satisfy the continuity in flow velocity along the liquid–liquid interface.
 |
| | Fig. 3 The results for scaled velocity amplitude |ū0(ȳ)| are shown for various values of (a)  (= 0.1, 0.5, 0.75, and 0.9) with fixed ηR = 2.54 and (b) ηR (= 0.1, 0.7, 2.54, and 10) with fixed (= 0.1, 0.5, 0.75, and 0.9) with fixed ηR = 2.54 and (b) ηR (= 0.1, 0.7, 2.54, and 10) with fixed  . Other model parameters are H = 25 nm, κH = 2.5, δ = 5 nm, N0 = 1 mM, ρR = 1.35, r = 3.3 Å, . Other model parameters are H = 25 nm, κH = 2.5, δ = 5 nm, N0 = 1 mM, ρR = 1.35, r = 3.3 Å, ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) = 2, = 2, ![[small omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0da.gif) = 10. = 10. | |
In Fig. 4, we have presented the cross-sectional averaged velocity amplitude |um|/UHS (in the scaled form) as a function of Debye–Hückel parameter κH and dielectric permittivity ratio  . The results are presented here for various choices of ion size. Other model parameters for Fig. 4 are summarized in the figure caption. The impact of the ion size on overall flow modulation is prominent for lower ranges of κH and
. The results are presented here for various choices of ion size. Other model parameters for Fig. 4 are summarized in the figure caption. The impact of the ion size on overall flow modulation is prominent for lower ranges of κH and  . An increase in κH for a fixed channel height strengthens the shielding effect and thus leads to an enhanced charge neutralization. Besides, an increase in
. An increase in κH for a fixed channel height strengthens the shielding effect and thus leads to an enhanced charge neutralization. Besides, an increase in  reduces the impact of the ion partitioning effect and thus enhances the accumulation of counterions within the liquid layer as well as near the charged interface. Thus, for a smaller range of κH or
reduces the impact of the ion partitioning effect and thus enhances the accumulation of counterions within the liquid layer as well as near the charged interface. Thus, for a smaller range of κH or  where the net charge of the fluidic system is high, the impact of the ion steric effect is prominent. However, its impact gradually diminishes with the increase in κH and
where the net charge of the fluidic system is high, the impact of the ion steric effect is prominent. However, its impact gradually diminishes with the increase in κH and  . As expected the increase in the ion size reduces the net throughput due to the enhanced impact of the ion partitioning effect.
. As expected the increase in the ion size reduces the net throughput due to the enhanced impact of the ion partitioning effect.
 |
| | Fig. 4 The results for scaled cross-sectional averaged velocity amplitude |um|/UHS are shown as a function of (a) Debye–Hückel parameter κH for various values of r (= 3.3 Å, 5 Å, and 6 Å) with fixed  and (b) dielectric permittivity ratio and (b) dielectric permittivity ratio  for various values of r (= 3.3 Å, 5 Å, and 6 Å) with fixed κH = 2.5. Other model parameters are for various values of r (= 3.3 Å, 5 Å, and 6 Å) with fixed κH = 2.5. Other model parameters are ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) = 2, N0 = 1 mM, H = 25 nm, = 2, N0 = 1 mM, H = 25 nm, ![[small delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c5.gif) = 0.2, ρR = 1.35, ηR = 2.54, = 0.2, ρR = 1.35, ηR = 2.54, ![[small omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0da.gif) = 10, respectively. = 10, respectively. | |
In Fig. 5 we have shown the results for dimensionless velocity amplitude |ū0(ȳ)| for different values of interfacial charge ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) (Fig. 5a), molar concentration N0 of additional mobile ions within the membrane layer (Fig. 5b) and its thickness
(Fig. 5a), molar concentration N0 of additional mobile ions within the membrane layer (Fig. 5b) and its thickness ![[small delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c5.gif) (Fig. 5c). Rise in interfacial charge density for fixed values of N0 and
(Fig. 5c). Rise in interfacial charge density for fixed values of N0 and ![[small delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c5.gif) leads to an enhanced electrostatic potential in the membrane layer as well as in the aqueous medium and thus leads to an enhanced throughput. The impact of interfacial charge on the overall flow modulation further augments with the increase in N0 and
leads to an enhanced electrostatic potential in the membrane layer as well as in the aqueous medium and thus leads to an enhanced throughput. The impact of interfacial charge on the overall flow modulation further augments with the increase in N0 and ![[small delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c5.gif) . Note that the increase in both of these quantities enhances the net effective charge density entrapped in the membrane layer. In Appendix-E, we have further shown the results for electrostatic potential distribution as well as net charge density considering different values of concentration of mobile charges in the dielectric liquid layer. A detailed discussion on the same is made thereat. Thus, the effective electromotive force further enhances with the increase in N0 and
. Note that the increase in both of these quantities enhances the net effective charge density entrapped in the membrane layer. In Appendix-E, we have further shown the results for electrostatic potential distribution as well as net charge density considering different values of concentration of mobile charges in the dielectric liquid layer. A detailed discussion on the same is made thereat. Thus, the effective electromotive force further enhances with the increase in N0 and ![[small delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c5.gif) , which in turn leads to an enhanced velocity amplitude |ū0(ȳ)|. Unlike that increase in interfacial charge or N0, an increase in δ further leads to an enhanced motion deterring drag force due to higher viscosity of the dielectric liquid layer. Thus, it is expected that the interfacial charge and N0 have more impacts on the flow modulation compared to the thickness δ of the dielectric liquid layer.
, which in turn leads to an enhanced velocity amplitude |ū0(ȳ)|. Unlike that increase in interfacial charge or N0, an increase in δ further leads to an enhanced motion deterring drag force due to higher viscosity of the dielectric liquid layer. Thus, it is expected that the interfacial charge and N0 have more impacts on the flow modulation compared to the thickness δ of the dielectric liquid layer.
 |
| | Fig. 5 The results for scaled velocity amplitude |ū0(ȳ)| for various values of (a) ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) (= 0, 2, 5, and 10) with fixed N0 = 1 mM, δ = 5 nm; (b) N0 (= 0, 1 mM, 10 mM, and 20 mM) with fixed (= 0, 2, 5, and 10) with fixed N0 = 1 mM, δ = 5 nm; (b) N0 (= 0, 1 mM, 10 mM, and 20 mM) with fixed ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) = 2, δ = 5 nm; and (c) δ (= 2.5 nm, 5 nm, and 7.5 nm) with fixed = 2, δ = 5 nm; and (c) δ (= 2.5 nm, 5 nm, and 7.5 nm) with fixed ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) = 2, N0 = 1 mM. The results are shown here considering fixed values of other model parameters, e.g., H = 25 nm, κH = 2.5, r = 3.3 Å and = 2, N0 = 1 mM. The results are shown here considering fixed values of other model parameters, e.g., H = 25 nm, κH = 2.5, r = 3.3 Å and ![[small omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0da.gif) = 10, respectively. = 10, respectively. | |
Fig. 6 further shows the impact of the channel height and frequency of the applied oscillatory electric field on the overall flow modulation. Note that these two parameters are directly related to the oscillating Reynolds number. As expected, with the increase in the channel height with fixed value of the scaled thickness of the dielectric liquid layer and other model parameters, the net charge carried by the system enhances and leads to an enhanced velocity amplitude |ū0(ȳ)| (Fig. 6a). We have further shown the results for scaled and cross-sectional averaged velocity amplitude as a function of oscillating frequency and the results are shown for various channel heights (Fig. 6b). We observe that the impact of oscillating frequency on the flow modulation is significant when the channel height is large. The increase in oscillating frequency accelerates the back and forth motion of the fluid medium. At a smaller range in oscillating frequency, the average velocity amplitude increases with the increase in the channel height. However, the averaged velocity amplitude reduces with the increase in frequency of the applied oscillatory electric field and its impact is prominent for the channel with larger height. Note that unlike the DC-EOF, the background fluidic medium requires the transient time to respond to the AC electric field. Besides, the increase in ω enhances the oscillatory Reynolds number, which actually measures the relative importance of dynamic inertial force and viscous force. Thus, the increased impact of the inertial effect due to the increase in oscillatory frequency leads to a substantial reduction in the average velocity amplitude. The impact of the oscillatory frequency on the overall reduction in the average velocity amplitude is further augmented for channels with larger height for which the oscillatory Reynolds number is large.
 |
| | Fig. 6 (a) Scaled velocity amplitude |ū0(ȳ)| is shown for various values of H (= 25 nm, 50 nm, 100 nm, and 200 nm) with fixed ![[small omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0da.gif) = 10 (i.e., ω/2π = 2.5 × 106 Hz) and (b) scaled cross-sectional averaged velocity amplitude |um|/UHS is shown as a function of frequency ω/2π (Hz) for various values of H (= 25 nm, 50 nm, 100 nm, and 200 nm). The results are shown here considering the fixed values of other model parameters, e.g., κH = 2.5, r = 3.3 Å, N0 = 1 mM and = 10 (i.e., ω/2π = 2.5 × 106 Hz) and (b) scaled cross-sectional averaged velocity amplitude |um|/UHS is shown as a function of frequency ω/2π (Hz) for various values of H (= 25 nm, 50 nm, 100 nm, and 200 nm). The results are shown here considering the fixed values of other model parameters, e.g., κH = 2.5, r = 3.3 Å, N0 = 1 mM and ![[small delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c5.gif) = 0.2, respectively. = 0.2, respectively. | |
From the results presented in Fig. 2–6 we have observed that a significant flow enhancement is possible for the electrolyte with low concentration (e.g., a lower range of κH) and small size of electrolyte ions. Besides, the choice of liquid in the layer adjacent to the walls further plays a significant role in the maximum throughput. For example, when the dielectric permittivity of the liquid layer is small compared to the liquid layer, a significant flow modulation is possible. Furthermore the net effective charge of the liquid layer enhances the flow strength, which can be achieved by increasing thickness and the concentration of mobile charge of the said layer as well as the interfacial charge. In addition, the flow strength across the channel is high for a smaller range of frequencies of the oscillatory electric field, and a reduction in the average throughput is possible with the increase in frequency of the applied AC electric field. Next we have discussed the impact of the modulated flow field on the dispersion process considering various mass diffusivity of the solutes.
4.2 Dispersion of solutes
In this section we have illustrated the results to highlight the dispersion of the solute band placed initially along the middle of the channel with a given bandwidth 2![[L with combining macron]](https://www.rsc.org/images/entities/i_char_004c_0304.gif) = 0.2 (in the scaled form). The band of solutes was dispersed due to molecular diffusion and fluid convection was induced by an applied oscillatory electric field. Note that the mass diffusivity of the uncharged solutes in general ranges from 10−12 m2 s−1 to 10−9 m2 s−1.104 Thus, for the considered flow geometry with a given channel height, the Péclet number (Pe) associated with the dispersion process ranges from 0.05 to 50. To analyze the findings related to solute dispersion we present the results for time evolution of cross-sectional averaged solute concentration
= 0.2 (in the scaled form). The band of solutes was dispersed due to molecular diffusion and fluid convection was induced by an applied oscillatory electric field. Note that the mass diffusivity of the uncharged solutes in general ranges from 10−12 m2 s−1 to 10−9 m2 s−1.104 Thus, for the considered flow geometry with a given channel height, the Péclet number (Pe) associated with the dispersion process ranges from 0.05 to 50. To analyze the findings related to solute dispersion we present the results for time evolution of cross-sectional averaged solute concentration ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) m, effective dispersion coefficient K(
m, effective dispersion coefficient K(![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ), standard deviation
), standard deviation  of the distribution of
of the distribution of ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) m and time-averaged effective dispersion coefficient Kavg over one oscillation period τ0 = 2π/ω, respectively.
m and time-averaged effective dispersion coefficient Kavg over one oscillation period τ0 = 2π/ω, respectively.
To start with, we have first presented the results for time evolution of the cross-sectional averaged solute concentration ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) m(
m(![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) u,
u, ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ). We have shown the results for time evolution of
). We have shown the results for time evolution of ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) m(
m(![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) u,
u, ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) at a fixed value of Pe = 25 (Fig. 7a). The corresponding line plots for
) at a fixed value of Pe = 25 (Fig. 7a). The corresponding line plots for ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) m(
m(![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) u,
u, ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) for discrete values of scaled time
) for discrete values of scaled time ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) are further shown in Fig. 7b. We observed that as the time grows, the dispersion of solutes under the combined impact of molecular diffusion and oscillatory convective effect increases and leads to a significant band broadening of the solute placed inside the channel. The impact of the Péclet number on the spatial distribution of averaged concentration
are further shown in Fig. 7b. We observed that as the time grows, the dispersion of solutes under the combined impact of molecular diffusion and oscillatory convective effect increases and leads to a significant band broadening of the solute placed inside the channel. The impact of the Péclet number on the spatial distribution of averaged concentration ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) m is shown in Fig. 7c, where we have presented the results indicating the line plots for
m is shown in Fig. 7c, where we have presented the results indicating the line plots for ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) m for various choices of Péclet numbers at a given time. In addition, we have further shown the results in Fig. S.1 (ESI†) to indicate the time evolution of
m for various choices of Péclet numbers at a given time. In addition, we have further shown the results in Fig. S.1 (ESI†) to indicate the time evolution of ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) m(
m(![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) u,
u, ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) for various values of Pe, where the Péclet number is varied by suitably changing the mass diffusivity of the solutes with fixed values of other model parameters. For such cases, an increase in the Péclet number indicates a reduction in mass diffusivity of the solutes. As expected the broadening is higher at smaller values of Pe due to enhanced mass diffusivity of the solutes. For such cases the molecular diffusion dominates over the convective dispersion process. The quantitative measurement of band broadening is dictated by the time evolution of standard deviation
) for various values of Pe, where the Péclet number is varied by suitably changing the mass diffusivity of the solutes with fixed values of other model parameters. For such cases, an increase in the Péclet number indicates a reduction in mass diffusivity of the solutes. As expected the broadening is higher at smaller values of Pe due to enhanced mass diffusivity of the solutes. For such cases the molecular diffusion dominates over the convective dispersion process. The quantitative measurement of band broadening is dictated by the time evolution of standard deviation  of the distribution of
of the distribution of ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) m, as presented in Fig. 7d. Such a quantity indicates the width of the sample zone at a specified time. The oscillatory behaviour of the time evolution of
m, as presented in Fig. 7d. Such a quantity indicates the width of the sample zone at a specified time. The oscillatory behaviour of the time evolution of  is prominent for a larger range of Péclet numbers for which the oscillatory convection effect dominates over the diffusion process. However, the width of the sample zone is higher for small Péclet numbers due to a strong diffusion effect.
is prominent for a larger range of Péclet numbers for which the oscillatory convection effect dominates over the diffusion process. However, the width of the sample zone is higher for small Péclet numbers due to a strong diffusion effect.
 |
| | Fig. 7 (a) The time evolution of cross sectional averaged mean concentration distribution ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) m is shown as a function of moving co-ordinate system m is shown as a function of moving co-ordinate system ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) u and scaled time u and scaled time ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) for Pe = 25. (b) The time evolution of for Pe = 25. (b) The time evolution of ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) m for discrete values of time, i.e., m for discrete values of time, i.e., ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) (= 0.1, 0.3, 0.5, and 0.9) is further shown. (c) The results for (= 0.1, 0.3, 0.5, and 0.9) is further shown. (c) The results for ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) m for various choices of Péclet number Pe (= 5, 10, 15, and 25) at a fixed time m for various choices of Péclet number Pe (= 5, 10, 15, and 25) at a fixed time ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) = 0.5. (d) The results indicating the time evolution of = 0.5. (d) The results indicating the time evolution of  as a function of scaled time as a function of scaled time ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) for various values of Pe (= 5, 10, 15 and 25). The results are shown here considering fixed values of other model parameters, e.g., r = 3.3 Å, H = 25 nm, κH = 2.5, δ = 5 nm, N0 = 1 mM, for various values of Pe (= 5, 10, 15 and 25). The results are shown here considering fixed values of other model parameters, e.g., r = 3.3 Å, H = 25 nm, κH = 2.5, δ = 5 nm, N0 = 1 mM, ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) = 2, = 2, ![[small omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0da.gif) = 10 and = 10 and ![[L with combining macron]](https://www.rsc.org/images/entities/i_char_004c_0304.gif) = 0.1, respectively. = 0.1, respectively. | |
In Fig. 8–10 (and Fig. S.3–S.6 shown in the ESI†), we have presented the results to indicate the impact of pertinent parameters associated with the flow modulation on the dispersion coefficient K(![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) (the influence of the axial diffusion 1/Pe2 is deduced). In Fig. 8 the results for K(
) (the influence of the axial diffusion 1/Pe2 is deduced). In Fig. 8 the results for K(![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) − 1/Pe2 are presented for fixed Pe with a similar set of other model parameters as considered in Fig. 2. Impact of convective transport on the dispersion process is evident from the results presented in Fig. 8. As observed in Fig. 2, the velocity amplitude |ū0(ȳ)| increases (decreases) with the increase in the EDL thickness (ion size). As a result the amplitude of the oscillatory dispersion coefficient increases with the reduction in κH (Fig. 8a), and it reduces with the increase in the ion size (Fig. 8b). In addition, the oscillatory behavior of the dispersion coefficient enhances with the increase in the impact of fluid convection. In Fig. S.2 (ESI†) we have further shown the corresponding results for time evolution of
) − 1/Pe2 are presented for fixed Pe with a similar set of other model parameters as considered in Fig. 2. Impact of convective transport on the dispersion process is evident from the results presented in Fig. 8. As observed in Fig. 2, the velocity amplitude |ū0(ȳ)| increases (decreases) with the increase in the EDL thickness (ion size). As a result the amplitude of the oscillatory dispersion coefficient increases with the reduction in κH (Fig. 8a), and it reduces with the increase in the ion size (Fig. 8b). In addition, the oscillatory behavior of the dispersion coefficient enhances with the increase in the impact of fluid convection. In Fig. S.2 (ESI†) we have further shown the corresponding results for time evolution of  (Fig. S.2a and b, ESI†) and cross-sectional averaged
(Fig. S.2a and b, ESI†) and cross-sectional averaged ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) m at a given time
m at a given time ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) = 0.5 (Fig. S.2c and d, ESI†) for different values of κH and ion size. The model parameters in Fig. S.2 (ESI†) are the same as considered in Fig. 8. It is evident that the band broadening is higher for the cases when the impact of fluid convection is strong. The larger dispersion coefficient K(
= 0.5 (Fig. S.2c and d, ESI†) for different values of κH and ion size. The model parameters in Fig. S.2 (ESI†) are the same as considered in Fig. 8. It is evident that the band broadening is higher for the cases when the impact of fluid convection is strong. The larger dispersion coefficient K(![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) − 1/Pe2 is a direct consequence of the larger effective Péclet number based on the overall strength of the flow field with fixed molecular diffusion of solutes. Thus, the peak of mean concentration
) − 1/Pe2 is a direct consequence of the larger effective Péclet number based on the overall strength of the flow field with fixed molecular diffusion of solutes. Thus, the peak of mean concentration ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) m decreases with the reduction in κH as well as with the reduction in the ion size for which the velocity amplitude |ū0(ȳ)| is enhanced.
m decreases with the reduction in κH as well as with the reduction in the ion size for which the velocity amplitude |ū0(ȳ)| is enhanced.
 |
| | Fig. 8 Time periodic dispersion coefficients K(![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) − 1/Pe2 are shown as a function of scaled time ) − 1/Pe2 are shown as a function of scaled time ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) for various values of (a) κH (= 2.5, 5, 10, and 25) with fixed r = 3.3 Å and (b) r (= 3.3 Å, 4 Å, 5 Å, and 6 Å) with fixed κH = 2.5. The results are presented here considering the fixed values of other model parameters, e.g., H = 25 nm, δ = 5 nm, N0 = 1 mM, for various values of (a) κH (= 2.5, 5, 10, and 25) with fixed r = 3.3 Å and (b) r (= 3.3 Å, 4 Å, 5 Å, and 6 Å) with fixed κH = 2.5. The results are presented here considering the fixed values of other model parameters, e.g., H = 25 nm, δ = 5 nm, N0 = 1 mM, ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) = 2 and = 2 and ![[small omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0da.gif) = 10 and = 10 and ![[L with combining macron]](https://www.rsc.org/images/entities/i_char_004c_0304.gif) = 0.1, respectively. = 0.1, respectively. | |
 |
| | Fig. 9 Time periodic dispersion coefficients K(![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) − 1/Pe2 are shown as a function of scaled time ) − 1/Pe2 are shown as a function of scaled time ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) for various values of (a) for various values of (a)  (= 0.1, 0.5, 0.75, and 1) with fixed ηR = 2.54 and (b) ηR (= 0.1, 0.7, 2.54, and 10) with fixed (= 0.1, 0.5, 0.75, and 1) with fixed ηR = 2.54 and (b) ηR (= 0.1, 0.7, 2.54, and 10) with fixed  . The results are presented here considering fixed values of other model parameters, e.g., H = 25 nm, κH = 2.5, δ = 5 nm, N0 = 1 mM, r = 3.3 Å, . The results are presented here considering fixed values of other model parameters, e.g., H = 25 nm, κH = 2.5, δ = 5 nm, N0 = 1 mM, r = 3.3 Å, ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) = 2, = 2, ![[small omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0da.gif) = 10 and = 10 and ![[L with combining macron]](https://www.rsc.org/images/entities/i_char_004c_0304.gif) = 0.1, respectively. = 0.1, respectively. | |
 |
| | Fig. 10 Time periodic dispersion coefficients K(![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) − 1/Pe2 are shown as a function of scaled time ) − 1/Pe2 are shown as a function of scaled time ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) for various values of (a) H (= 25 nm, 50 nm, and 100 nm) for fixed for various values of (a) H (= 25 nm, 50 nm, and 100 nm) for fixed ![[small omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0da.gif) = 10 and (b) = 10 and (b) ![[small omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0da.gif) (= 10, 20, and 40) for fixed H = 25. The results are presented here considering the fixed values of other model parameters, e.g., r = 3.3 Å, N0 = 1 mM, κH = 2.5 nm, (= 10, 20, and 40) for fixed H = 25. The results are presented here considering the fixed values of other model parameters, e.g., r = 3.3 Å, N0 = 1 mM, κH = 2.5 nm, ![[small delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c5.gif) = 0.2, = 0.2, ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) = 2, = 2, ![[small omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0da.gif) = 10, and = 10, and ![[L with combining macron]](https://www.rsc.org/images/entities/i_char_004c_0304.gif) = 0.1, respectively. = 0.1, respectively. | |
In Fig. 9, we have presented the results for K(![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) − 1/Pe2 for various choices of dielectric permittivity ratios
) − 1/Pe2 for various choices of dielectric permittivity ratios  (Fig. 9a) and viscosity ratios (ηR) (Fig. 9) for fixed values of other model parameters. In addition, the time evolution of
(Fig. 9a) and viscosity ratios (ηR) (Fig. 9) for fixed values of other model parameters. In addition, the time evolution of  and
and ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) m at a given time
m at a given time ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) = 0.5 is presented in Fig. S.3 (ESI† for a similar set of pertinent parameters. As indicated earlier, the flow strength enhances with the reduction in
= 0.5 is presented in Fig. S.3 (ESI† for a similar set of pertinent parameters. As indicated earlier, the flow strength enhances with the reduction in  (stated differently, an increase in the difference between the dielectric permittivity of both the phases or in other words, an increase in the ion partitioning effect). In addition, a reduction in viscosity of the liquid layer adjacent to the supporting walls further rises the velocity amplitude. Thus, the enhanced flow strength achieved in a smaller range of
(stated differently, an increase in the difference between the dielectric permittivity of both the phases or in other words, an increase in the ion partitioning effect). In addition, a reduction in viscosity of the liquid layer adjacent to the supporting walls further rises the velocity amplitude. Thus, the enhanced flow strength achieved in a smaller range of  and ηR leads to a larger dispersion coefficient (K(
and ηR leads to a larger dispersion coefficient (K(![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) − 1/Pe2) as well as a larger band broadening, which results in a smaller peak of the mean concentration. We further observed an enhanced dispersion of the solute band for increasing values of thickness and molar concentration of additional mobile ions present in the liquid layer adjacent to the supporting walls as well as interfacial charge density. The same is graphically illustrated in Fig. S.4 and S.5 (ESI†) which can further be justified with a similar analogy.
) − 1/Pe2) as well as a larger band broadening, which results in a smaller peak of the mean concentration. We further observed an enhanced dispersion of the solute band for increasing values of thickness and molar concentration of additional mobile ions present in the liquid layer adjacent to the supporting walls as well as interfacial charge density. The same is graphically illustrated in Fig. S.4 and S.5 (ESI†) which can further be justified with a similar analogy.
The dispersion coefficients K(![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) − 1/Pe2 are further shown for various channel heights (Fig. 10a) and frequency of the oscillatory electric field (Fig. 10b). The results are presented here for the given value of other model parameters. As indicated earlier, an increase in the channel height leads to an enhanced flow rate. Thus, an enhanced dispersion coefficient and a larger dispersion occur in the wider channel as a consequence of an enhanced effective Péclet number (Fig. 10a and Fig. S.6a, ESI†). As a result the peak of the mean concentration profile reduces with the increase in the channel height (Fig. S.6c, ESI†). We observe that the increase in oscillatory frequency reduces the effective dispersion coefficient (Fig. 10b), and results in a reduced bandwidth (Fig. S.6b, ESI†) and hence the larger peak in the mean solute concentration (Fig. S.6d, ESI†). Note that for higher frequency, the diffusion time is much higher than the oscillating period of applied AC electric field. Thus, the solute band does not have enough time to diffuse in a larger area. In addition, an increase in frequency and the increased inertia effect lead to a reduction in velocity amplitude. As a result the convective dispersion process with the increase in oscillatory frequency becomes weaker.
) − 1/Pe2 are further shown for various channel heights (Fig. 10a) and frequency of the oscillatory electric field (Fig. 10b). The results are presented here for the given value of other model parameters. As indicated earlier, an increase in the channel height leads to an enhanced flow rate. Thus, an enhanced dispersion coefficient and a larger dispersion occur in the wider channel as a consequence of an enhanced effective Péclet number (Fig. 10a and Fig. S.6a, ESI†). As a result the peak of the mean concentration profile reduces with the increase in the channel height (Fig. S.6c, ESI†). We observe that the increase in oscillatory frequency reduces the effective dispersion coefficient (Fig. 10b), and results in a reduced bandwidth (Fig. S.6b, ESI†) and hence the larger peak in the mean solute concentration (Fig. S.6d, ESI†). Note that for higher frequency, the diffusion time is much higher than the oscillating period of applied AC electric field. Thus, the solute band does not have enough time to diffuse in a larger area. In addition, an increase in frequency and the increased inertia effect lead to a reduction in velocity amplitude. As a result the convective dispersion process with the increase in oscillatory frequency becomes weaker.
We have further presented the results for time-averaged effective dispersion coefficient Kavg over one oscillation period τ0 = 2π/ω. Such a quantity is an important parameter to analyze the broadening of the solute band placed in an oscillatory flow field. In Fig. 11a–c we have shown the results for Kavg as a function of frequency of the applied oscillatory electric field. We present the results for various choices of κH (Fig. 11a), ion size (Fig. 11b) and dielectric permittivity ratio  (Fig. 11c). Other model parameters are indicated in the caption of the said figure. As expected the time-averaged effective dispersion Kavg reduces with the increase in oscillatory frequency. Such a reduction is due to enhanced periodical expansion and contraction of the solute band placed under the oscillatory flow field. For a smaller range of oscillatory frequencies, due to an enhanced flow strength with reduction in κH, ion size as well as
(Fig. 11c). Other model parameters are indicated in the caption of the said figure. As expected the time-averaged effective dispersion Kavg reduces with the increase in oscillatory frequency. Such a reduction is due to enhanced periodical expansion and contraction of the solute band placed under the oscillatory flow field. For a smaller range of oscillatory frequencies, due to an enhanced flow strength with reduction in κH, ion size as well as  , the magnitude in Kavg increases. However, their impact on Kavg gradually diminishes with the increase in frequency of the oscillatory electric field. In Fig. S.7 (ESI†) we have further shown the impact of other pertinent parameters associated with flow modulation (e.g., viscosity ratio ηR, thickness
, the magnitude in Kavg increases. However, their impact on Kavg gradually diminishes with the increase in frequency of the oscillatory electric field. In Fig. S.7 (ESI†) we have further shown the impact of other pertinent parameters associated with flow modulation (e.g., viscosity ratio ηR, thickness ![[small delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c5.gif) , interfacial charge
, interfacial charge ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) and molar concentration N0). The viscosity ratio ηR has little effect on the time-averaged effective dispersion Kavg, however,
and molar concentration N0). The viscosity ratio ηR has little effect on the time-averaged effective dispersion Kavg, however, ![[small delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c5.gif) ,
, ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) and N0 have a substantial impact on Kavg, when frequency of the oscillatory electric field is small. We observed that when ω/2π is smaller than 6 × 105 Hz, the impact of oscillatory electric field on the flow modulation, dispersion coefficient as well as band broadening is prominent. However, beyond this limit of frequency, an increase in oscillatory frequency ω reduces the impact of pertinent parameters on the flow modulation and hence the dispersion characteristics.
and N0 have a substantial impact on Kavg, when frequency of the oscillatory electric field is small. We observed that when ω/2π is smaller than 6 × 105 Hz, the impact of oscillatory electric field on the flow modulation, dispersion coefficient as well as band broadening is prominent. However, beyond this limit of frequency, an increase in oscillatory frequency ω reduces the impact of pertinent parameters on the flow modulation and hence the dispersion characteristics.
 |
| | Fig. 11 Time average dispersion coefficient Kavg is shown as a function of frequency ω/2π (Hz) for various values of (a) κH (= 2.5, 5, 10, and 25) with fixed r = 3.3 Å,  ; (b) r (= 3.3 Å, 4 Å, 5 Å, and 6 Å) with fixed κH = 2.5, ; (b) r (= 3.3 Å, 4 Å, 5 Å, and 6 Å) with fixed κH = 2.5,  and (c) and (c)  (= 0.1, 0.5, 0.75, and 0.9) with fixed r = 3.3 Å, κH = 2.5. The results are presented for fixed H = 25 nm, δ = 5 nm, N0 = 1 mM, ρR = 1.35, ηR = 2.54, Pe = 25 and (= 0.1, 0.5, 0.75, and 0.9) with fixed r = 3.3 Å, κH = 2.5. The results are presented for fixed H = 25 nm, δ = 5 nm, N0 = 1 mM, ρR = 1.35, ηR = 2.54, Pe = 25 and ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) = 2, respectively. = 2, respectively. | |
In Fig. 12, we have shown the results for time-averaged dispersion coefficient Kavg over one oscillation period as a function of oscillatory frequency and the results are shown here for various choices of Péclet number. We have systematically changed the Péclet number either by varying mass diffusivity with fixed channel height (Fig. 12a), or by varying the channel height at a given mass diffusivity (Fig. 12b) and the results are presented for fixed values of the other model parameters. As expected, a larger Kavg is achieved with large (small) values of mass diffusivity (Péclet number). The magnitude of Kavg further reduces with the increase in oscillatory frequency for which the impact of effective fluid convection reduces. We further observe an enhanced Kavg for an increasing channel height. The same is however possible due to the enhanced fluid convection effect, especially for a smaller range of oscillatory frequencies. Moreover, for the considered problem dealing with solute dispersion under AC EOF, a change in sign of Kavg is observed, especially for channels with a larger size and at larger oscillatory frequency. Note that the variance of the solute dispersion is always positive, however, it does not ensure that differential variance, referred to as the effective dispersion coefficient, remains always positive. The occurrence of the negative effective dispersion coefficient for oscillatory flow field is rather common.55,105–107 As indicated earlier, the increase in the channel height results in an enhanced dispersion. The transition from the positive to negative value of Kavg is caused by a rapid change in periodical expansion and contraction of the solute band under EOF induced by an oscillatory electric field with large frequency.
 |
| | Fig. 12 The time-averaged effective dispersion coefficient Kavg over one oscillation period is shown as a function of frequency ω/2π (Hz) for various values of (a) Pe (= 5, 10, 15, and 25) with fixed channel height H = 25 nm and (b) H (= 25 nm, 50 nm, and 100 nm) with fixed mass diffusion coefficient D0 = 2.05 × 10−10 m2 s−1. The results are presented here considering the fixed values of other model parameters, e.g., r = 3.3 Å, N0 = 1 mM, κH = 2.5, ![[small delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c5.gif) = 0.2 and = 0.2 and ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) = 2, respectively. = 2, respectively. | |
5 Conclusion
The present article provides an extensive study on the modulation of EOF involving a two-phase liquid system under an oscillatory electric field and its impact on the transport and dispersion processes of the solute band placed along the middle of the channel. In the considered two-phase liquid system, the electrolyte medium is surrounded by a layer of a dielectric liquid, which resembles a membrane of biological cells containing additional mobile charges. The difference in dielectric permittivity of both the phases induces an ion partitioning effect, which plays a significant role in the flow modulation and therefore in solute dispersion. In addition, the ion steric effect comes into play, specifically when the charge carried by the system is moderate to high. We have presented the results for flow modulation under an applied AC electric field across such a channel and further studied the dispersion of the solute band. We measured the magnitude of complex amplitude of the velocity field as well as the cross-sectional averaged velocity to dictate the impact of pertinent parameters on the overall flow modulation. Besides, to provide quantitative measurement of the dispersion process, we deduce the results for the cross-sectional averaged concentration ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) m of the solute band, standard deviation of distribution of
m of the solute band, standard deviation of distribution of ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) m, and the time dependent dispersion coefficient as well as the time-averaged effective dispersion coefficient over one oscillation period. The numerical results are presented for a wide range of pertinent parameters. Besides, benchmark analytical results within the Debye–Hückel electrostatic framework for EDL potential and EOF velocity are deduced. The numerical calculations should pave the way for novel AC electric field based EOF pumping mechanisms and therefore the band broadening process. In addition, we deduced the analytical results for the said quantities associated with the dispersion process under the Debye–Hückel limit with vanishing frequency of the AC electric field. These benchmark theoretical results are however important for validation purposes of the numerical scheme adopted in this study as well as for future applications.
m, and the time dependent dispersion coefficient as well as the time-averaged effective dispersion coefficient over one oscillation period. The numerical results are presented for a wide range of pertinent parameters. Besides, benchmark analytical results within the Debye–Hückel electrostatic framework for EDL potential and EOF velocity are deduced. The numerical calculations should pave the way for novel AC electric field based EOF pumping mechanisms and therefore the band broadening process. In addition, we deduced the analytical results for the said quantities associated with the dispersion process under the Debye–Hückel limit with vanishing frequency of the AC electric field. These benchmark theoretical results are however important for validation purposes of the numerical scheme adopted in this study as well as for future applications.
We observe an enhanced flow strength and band broadening when the difference in dielectric permittivity of both the phases is high for which the impact of the ion partitioning effect is prominent. Reduction in the effect of ion partitioning reduces the flow strength, and thus molecular diffusion dominates over the convective dispersion process. The size in mobile ions is further related to the ion partitioning effect. An increase in the ion size reduces the effective electromotive force and leads to a reduction in the flow rate and dispersion coefficient. An augmented flow strength and enhanced convective dispersion process are observed with the increase in interfacial charge, thickness and additional mobile charge of the dielectric liquid layer. The impact of the ion steric effect is further augmented when the net charge within the fluidic system is high. A rise in the electrolyte concentration leads to an enhanced shielding effect and leads to a reduced strength of flow field, and thus reduces the convective effect on the dispersion process. As expected, due to the enhanced effective Péclet number, an enhanced dispersion coefficient and larger dispersion occur in the wider channel. An increase in oscillatory frequency causes a reduction in velocity amplitude due to the increased inertia effect, and thus the convective counterpart of the dispersion coefficient reduces. We further witness the negative value of the dispersion coefficient for a large channel height and a large frequency of the dispersion coefficient.
Finally, the present article provides an improved theory of modulation of oscillatory electroosmotic flow and solute dispersion considering a planar liquid–liquid interface, which indicates the basic state of a general stability problem. In our subsequent article we aim to study the instabilities associated with two-layer EOF under an oscillatory electric field and the present study will be a benchmark for such future studies. Besides, the study of ICR considering a two-phase liquid in the presence of any sort of asymmetries along the lateral dimension may be an important topic of future research.
Data availability
The authors confirm that the data supporting the findings of this study are available within the article. Additional supporting data, such as numerical data corresponding to the data presented in the figures, are available upon request to the corresponding author.
Conflicts of interest
The authors report no conflict of interest.
Appendices
Appendix-A: summary of various constants appearing in the velocity field and F(ȳ)
The expression (16) for velocity field presented in main article contains several constants, which are summarized below| |  | (A.1) |
Various constants appearing in the above relation (A.1) are summarized below| |  | (A.2) |
The function F(ȳ) appearing in eqn (40) of the main article involves the following constants| |  | (A.3) |
Several constants appearing in (A.3) are summarized below| |  | (A.4) |
Appendix-B: approximate analytical results for EDL potential
The analytical results for scaled EDL potential may be deduced as follows| |  | (B.1) |
The above expression involves the following constants| |  | (B.2) |
where ![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) (−1 +
(−1 + ![[small delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c5.gif) ) represents the scaled interfacial potential at the liquid–liquid interface ȳ = −1 +
) represents the scaled interfacial potential at the liquid–liquid interface ȳ = −1 + ![[small delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c5.gif) (i.e., at the liquid/liquid interface), and the functions h1(
(i.e., at the liquid/liquid interface), and the functions h1(![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) (−1 +
(−1 + ![[small delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c5.gif) )), h2(
)), h2(![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) (−1 +
(−1 + ![[small delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c5.gif) )) are defined by
)) are defined by| |  | (B.3) |
Note that the interfacial potential ![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) (−1 +
(−1 + ![[small delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c5.gif) ) and the Donnan potential
) and the Donnan potential ![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) D are implicitly connected to each other. The implicit relationship between both of them may be deduced as follows
D are implicitly connected to each other. The implicit relationship between both of them may be deduced as follows| |  | (B.4) |
We adopt a suitable numerical scheme to deduce the interfacial potential from the relation (B.4) with the known Donnan potential. Note that the explicit form of Donnan potential is given in the relation (11) appearing in the main manuscript (MS). With the known interfacial potential as well as Donnan potential we further obtain the spatial distribution of EDL potential using the relation (B.1). We have now presented a comparison of EDL potential obtained from the numerical scheme indicated in the main manuscript (MS) and the results obtained in this section. In Fig. 13a we have shown the spatial distribution of the EDL potential in the scaled form for various choices of κH with fixed values of other model parameters. We have further presented the results for EDL potential for increasing molar concentration of additional ions present in the dielectric liquid layer (Fig. 13b). We observe a close agreement in the numerical results with deduced analytical results for EDL potential for any choices of Debye–Hückel parameter and concentration of additional ions present in the dielectric liquid layer.
 |
| | Fig. 13 Scaled potential distributions ![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) (ȳ) are shown as a function of scaled spatial coordinate ȳ for various values of (a) κH (= 2.5, 5, 10, and 25) with fixed N0 = 1 mM and (b) N0 (= 1 mM, 5 mM, and 10 mM) with fixed κH = 25. Other model parameters are H = 25 nm, δ = 5 nm, (ȳ) are shown as a function of scaled spatial coordinate ȳ for various values of (a) κH (= 2.5, 5, 10, and 25) with fixed N0 = 1 mM and (b) N0 (= 1 mM, 5 mM, and 10 mM) with fixed κH = 25. Other model parameters are H = 25 nm, δ = 5 nm, ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) = 2, = 2,  , and r = 3.3 Å, respectively. , and r = 3.3 Å, respectively. | |
Appendix-C: closed form analytical results for EDL potential and EOF field under the Debye–Hückel limit
Under the Debye–Hückel limit (![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) (ȳ) ≪ 1), the linearized form of the EDL potential equation (in the scaled form) may be written as
(ȳ) ≪ 1), the linearized form of the EDL potential equation (in the scaled form) may be written as| |  | (C.1a) |
| |  | (C.1b) |
where| |  | (C.2) |
Solving the governing equations (C.1a) and (C.1b) subject to the boundary conditions (9a)–(9d) yields the explicit form of the EDL potential, given as| |  | (C.3) |
where the constants Q1 and Q2 appearing in (C.3) are as follows| |  | (C.4) |
Within the Debye–Hückel electrostatic framework, the oscillatory EOF velocity may be deduced as follows| |  | (C.5) |
The above expression for the velocity field involves various constants, e.g. Ci (i = 1, 2, 3, 4); mi (i = 1, 2, 3), which are summarized in relation (A.1) appearing in the main MS. In order to validate the numerical results deduced in this present study, we have further shown the comparison for the EDL potential and the axial velocity in Fig. 14.
 |
| | Fig. 14 In Fig. (a) and (b) we have shown the scaled velocity amplitude  as a function of ȳ for various values of as a function of ȳ for various values of  (= 0.1, 0.5, and 0.9) with fixed κH = 2.5; and various values of κH (= 2.5, 5, 10, and 25) with fixed (= 0.1, 0.5, and 0.9) with fixed κH = 2.5; and various values of κH (= 2.5, 5, 10, and 25) with fixed  . Other model parameters are H = 25 nm, δ = 5 nm, N0 = 1 mM, ρR = 1.35, ηR = 2.54, . Other model parameters are H = 25 nm, δ = 5 nm, N0 = 1 mM, ρR = 1.35, ηR = 2.54, ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) = 1 and = 1 and ![[small omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0da.gif) = 10, respectively. = 10, respectively. | |
In Fig. 14a and b, we have shown the scaled velocity amplitude |ū0(ȳ)| for various choices of  and κH. The model parameters are indicated in the figure caption and they are chosen in such a way that the Debye–Hückel limit for EDL potential holds good. The deduced theoretical results are shown by solid lines and numerical results are further included by dashed lines. We have detailed the methods to deduce the numerical results for velocity amplitude in the main article. We observe a close agreement in the numerical results with the analytical results deduced in this section. It is noteworthy to mention that we may have a discrepancy in the numerical results with the analytical results presented in this section. The reason is the results presented in Appendix-C is valid only for low charge limits. Thus, for the case when the system charge is moderate to high, we need to use either semi-analytical results presented in Appendix-B or the complete numerical solution for electrostatic potential and hence the velocity amplitude.
and κH. The model parameters are indicated in the figure caption and they are chosen in such a way that the Debye–Hückel limit for EDL potential holds good. The deduced theoretical results are shown by solid lines and numerical results are further included by dashed lines. We have detailed the methods to deduce the numerical results for velocity amplitude in the main article. We observe a close agreement in the numerical results with the analytical results deduced in this section. It is noteworthy to mention that we may have a discrepancy in the numerical results with the analytical results presented in this section. The reason is the results presented in Appendix-C is valid only for low charge limits. Thus, for the case when the system charge is moderate to high, we need to use either semi-analytical results presented in Appendix-B or the complete numerical solution for electrostatic potential and hence the velocity amplitude.
Appendix-D Analytical results for several quantities associated with solute dispersion deduced under the Debye–Hückel electrostatic framework with ω → 0
The electroosmotic velocity distribution under Debye–Hückel approximation and externally applied electric field with ω → 0 may be written in the scaled form as follows| |  | (D.1) |
where Q1, Q2 are defined in (C.4) and Q3 is defined as follows| |  | (D.2) |
Using the expression of ū0(ȳ), we may find the explicit analytical expression for cross-sectional mean fluid velocity ūm, given as| |  | (D.3) |
Now under the Debye–Hückel framework and externally applied electric field with ω → 0, the reduced form of the governing equation for F(ȳ) associated with dispersion process indicated earlier can be rewritten as| |  | (D.4) |
In order to solve the function F(ȳ), the required conditions are given below| |  | (D.5a) |
| |  | (D.5b) |
Note that for applied electric field with ω → 0, the dispersion coefficient is free form time. We further denote the dispersion coefficient K(![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) as Keff. Thus, for ω → 0, the dispersion coefficient Keff may be deduced from (35), as follows
) as Keff. Thus, for ω → 0, the dispersion coefficient Keff may be deduced from (35), as follows| |  | (D.6) |
Solving F(ȳ), the relation (D.6) may be rewritten as follows| |  | (D.7) |
where| |  | (D.8) |
The expression G(ȳ) involves Qi (1, 2, 3, 4). Note that Qi (i = 1, 2, 3) are defined earlier and Q4 is defined as follows| |  | (D.9) |
Substituting (D.8) into (D.7) yields the analytical expression of Keff, given as| |  | (D.10) |
where the constants involved in the above relation (D.10) are given below| |  | (D.11) |
Under the limit of ω → 0, the governing equation for the cross sectional average concentration distribution ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) m(
m(![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) u,
u, ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) may be written as
) may be written as| |  | (D.12) |
Solving eqn (D.12) subject to the initial condition (21) and boundary conditions (22a) and (22b), we may deduce the analytical expression of ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) m(
m(![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) u,
u, ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) as given below
) as given below| |  | (D.13) |
In order to validate the numerical results for the solute dispersion process, we have shown the comparison of the numerically obtained effective dispersion coefficient and the cross-sectional averaged concentration in Fig. 15 and 16, respectively. The effective dispersion coefficient is shown as a function of κH for various choices of  (Fig. 15a) and Pe (Fig. 15b). The time evolution of cross-sectional averaged solute concentration
(Fig. 15a) and Pe (Fig. 15b). The time evolution of cross-sectional averaged solute concentration ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) m is shown in Fig. 16a. We have further shown the results for
m is shown in Fig. 16a. We have further shown the results for ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) m in Fig. 16b for various choices of Pe with fixed channel height. From all the results, it is clear that the numerical results are in close agreement in with the theoretical results deduced in this section.
m in Fig. 16b for various choices of Pe with fixed channel height. From all the results, it is clear that the numerical results are in close agreement in with the theoretical results deduced in this section.
 |
| | Fig. 15 The dispersion coefficient Keff is shown as a function of κH for various values of (a)  (= 0.1, 0.5, and 0.9) with fixed Pe = 25 and (b) Pe (= 5, 15, and 25) with fixed (= 0.1, 0.5, and 0.9) with fixed Pe = 25 and (b) Pe (= 5, 15, and 25) with fixed  . Other model parameters are H = 25 nm, δ = 5 nm, N0 = 1 mM, . Other model parameters are H = 25 nm, δ = 5 nm, N0 = 1 mM,  , ηR = 2.54, , ηR = 2.54, ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) = 1 and = 1 and ![[L with combining macron]](https://www.rsc.org/images/entities/i_char_004c_0304.gif) = 0.1, respectively. = 0.1, respectively. | |
 |
| | Fig. 16 The cross-sectional averaged ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) m is shown for various values of (a) m is shown for various values of (a) ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) (= 0.1, 0.5, and 0.9) with fixed Pe = 25 and (b) Péclet numbers Pe (= 5, 15, and 25) at time (= 0.1, 0.5, and 0.9) with fixed Pe = 25 and (b) Péclet numbers Pe (= 5, 15, and 25) at time ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) = 0.5. The results are shown here considering dielectric liquid which surrounds the electrolytic solution as oily organic solvent cyclohexyl bromide (CHB) with fixed values of other model parameters, e.g., H = 25 nm, κ−1 = 10 nm, = 0.5. The results are shown here considering dielectric liquid which surrounds the electrolytic solution as oily organic solvent cyclohexyl bromide (CHB) with fixed values of other model parameters, e.g., H = 25 nm, κ−1 = 10 nm, ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) = 1 and r = 3.3 Å. = 1 and r = 3.3 Å. | |
Appendix-E: impact of the concentration of mobile ions N0 on the overall charge distribution and electrostatic potential
Here we have shown the impact of concentration N0 of additional ions within the surrounding liquid layer on the overall charge distribution (Fig. 17a and b) and electrostatic potential (Fig. 17c and d). We denote the overall charge density (in the scaled form) as ![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) c(ȳ), which indicates the scaled form of ρd(y) within the dielectric liquid layer and ρe(y) within the electrolyte medium. The results are presented for two different values of
c(ȳ), which indicates the scaled form of ρd(y) within the dielectric liquid layer and ρe(y) within the electrolyte medium. The results are presented for two different values of  (say,
(say,  and
and  ). When the permitivity ratio is far smaller than 1, say
). When the permitivity ratio is far smaller than 1, say  , the impact of the ion partitioning effect is prominent, however the ion partitioning effect is absent for
, the impact of the ion partitioning effect is prominent, however the ion partitioning effect is absent for  . Thus, for
. Thus, for  , the penetration of the counterion across the dielectric liquid layer is less and leads to a higher value of net charge density within the liquid layer. As a result the magnitude in electrostatic potential is high, which in turn leads to a large value in electric driving force that leads to fluid motion. On the other hand, for
, the penetration of the counterion across the dielectric liquid layer is less and leads to a higher value of net charge density within the liquid layer. As a result the magnitude in electrostatic potential is high, which in turn leads to a large value in electric driving force that leads to fluid motion. On the other hand, for  , the accumulation of counterions within the dielectric liquid layer is sufficiently high and leads to a significant reduction in the overall charge distribution and hence a lower magnitude in the electrostatic potential.
, the accumulation of counterions within the dielectric liquid layer is sufficiently high and leads to a significant reduction in the overall charge distribution and hence a lower magnitude in the electrostatic potential.
 |
| | Fig. 17 Charge distribution of mobile ions ![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) c(ȳ) (in the scaled form) and scaled potential distributions ( c(ȳ) (in the scaled form) and scaled potential distributions (![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) (ȳ)) are shown as a function of scaled spatial coordinate ȳ for various values of N0 (0, 1 mM, 5 mM, and 10 mM). In (a) and (c) we consider (ȳ)) are shown as a function of scaled spatial coordinate ȳ for various values of N0 (0, 1 mM, 5 mM, and 10 mM). In (a) and (c) we consider  and in (b) and (d) the value of dielectric permitivity ratio and in (b) and (d) the value of dielectric permitivity ratio  . Other model parameters are H = 25 nm, δ = 5 nm, κH = 25, . Other model parameters are H = 25 nm, δ = 5 nm, κH = 25, ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) = 2, and r = 3.3 Å, respectively. = 2, and r = 3.3 Å, respectively. | |
Acknowledgements
S. C. wishes to acknowledge National Institute of Technology Durgapur for financial support in the form of Institute funded Senior Research Fellowship.
References
- H. A. Stone, A. D. Stroock and A. Ajdari, Engineering flows in small devices: microfluidics toward a lab-on-a-chip, Annu. Rev. Fluid Mech., 2004, 36(1), 381–411 CrossRef
 .
.
- M. H. Oddy, J. G. Santiago and J. C. Mikkelsen, Electrokinetic Instability Micromixing, Anal. Chem., 2001, 73(24), 5822–5832 CrossRef CAS PubMed
 .
.
- M. T. Kreutzer, A. Günther and K. F. Jensen, Sample Dispersion for Segmented Flow in Microchannels with Rectangular Cross Section, Anal. Chem., 2008, 80(5), 1558–1567 CrossRef CAS PubMed
 .
.
- G. Taylor, Dispersion of Soluble Matter in Solvent Flowing Slowly through a Tube, Proc. R. Soc. London, Ser. A, 1953, 219(1137), 186–203 CAS
 .
.
- R. Aris, On the Dispersion of a Solute in a Fluid Flowing through a Tube, Proc. R. Soc. London, Ser. A, 1956, 235(1200), 67–77 Search PubMed
 .
.
- R. Aris, On the Dispersion of a Solute in Pulsating Flow Through a Tube, Proc. R. Soc. London, Ser. A, 1960, 259(1298), 370–376 CAS
 .
.
- S. Latunde-Dada, R. Bott, K. Hampton and O. I. Leszczyszyn, Application of the Exact Dispersion Solution to the Analysis of Solutes beyond the Limits of Taylor Dispersion, Anal. Chem., 2015, 87(15), 8021–8025 CrossRef CAS
 .
.
- V. Ananthakrishnan, W. N. Gill and A. J. Barduhn, Laminar dispersion in capillaries: Part I. Mathematical analysis, AIChE J., 1965, 11(6), 1063–1072 CrossRef CAS
 .
.
- W. N. Gill and R. Sankarasubramanian, Exact Analysis of Unsteady Convective Diffusion, Proc. R. Soc. London, Ser. A, 1970, 316(1526), 341–350 Search PubMed
 .
.
- P. C. Fife and K. R. K. Nicholes, Dispersion in Flow Through Small Tubes, Proc. R. Soc. London, Ser. A, 1975, 344(136), 131–145 Search PubMed
 .
.
- B. S. Mazumder and S. K. Das, Effect of boundary reaction on solute dispersion in pulsatile flow through a tube, J. Fluid Mech., 1992, 239(1), 523 CrossRef CAS
 .
.
- C.-O. Ng and T. L. Yip, Effects of kinetic sorptive exchange on solute transport in open-channel flow, J. Fluid Mech., 2001, 446, 321–345 CrossRef CAS
 .
.
- C.-O. Ng, Dispersion in steady and oscillatory flows through a tube with reversible and irreversible wall reactions, Proc. R. Soc. London, Ser. A, 2005, 462(2066), 481–515 Search PubMed
 .
.
- S. Paul and B. S. Mazumder, Dispersion in unsteady Couette-Poiseuille flows, Int. J. Eng. Sci., 2008, 46(12), 1203–1217 CrossRef CAS
 .
.
- T. Karmakar, S. Barik and G. P. Raja Sekhar, Multi-scale analysis of concentration distribution in unsteady Couette-Poiseuille flows through a porous channel, Proc. R. Soc. London, Ser. A, 2023, 479(2269), 20220494 Search PubMed
 .
.
-
R. F. Probstein, Physicochemical Hydrodynamics, Wiley, New York, 2nd edn, 1994, pp. 53–164 Search PubMed
 .
.
- C.-O. Ng and Q. Zhou, Dispersion due to electroosmotic flow in a circular microchannel with slowly varying wall potential and hydrodynamic slippage, Phys. Fluids, 2012, 24(11), 112002 CrossRef
 .
.
- H. Stefan and R. Zengerle, Microfluidic platforms for lab-on-a-chip applications, Lab Chip, 2007, 7(9), 1094–1110 RSC
 .
.
- V. K. Kermani, M. Madadelahi, S. N. Ashrafizadeh, L. Kulinsky, S. O. Martinez-Chapa and M. J. Madou, Electrified lab on disc systems: a comprehensive review on electrokinetic applications, Biosens. Bioelectron., 2022, 214, 114381 CrossRef
 .
.
- M. Khatibi and S. N. AshrafizadehIon, Transport in Intelligent Nanochannels: A Comparative Analysis of the Role of Electric Field, Anal. Chem., 2023, 95(49), 18188–18198 CrossRef CAS
 .
.
- V. Hoshyargar, S. N. Ashrafizadeh and A. Sadeghi, Drastic alteration of diffusioosmosis due to steric effects, Phys. Chem. Chem. Phys., 2015, 17(43), 29193–29200 RSC
 .
.
- S. N. Ashrafizadeh, M. Zare and M. Khatibi, A Comprehensive Review of Pinch Flow Fractionation in Microfluidics: From Principles to Practical Applications, Chem. Eng. Process., 2024, 110087 Search PubMed
 .
.
- A. Alinezhad, M. Khatibi and S. N. Ashrafizadeh, Impact of surface
charge density modulation on ion transport in heterogeneous nanochannels, Sci. Rep., 2024, 14, 18409 CrossRef CAS
 .
.
- M. Khatibi, A. Aminnia and S. N. Ashrafizadeh, The role of ionic concentration polarization on the behavior of nanofluidic membranes, Chem. Eng. Process., 2024, 202, 109849 CrossRef CAS
 .
.
- S. Levine, J. R. Marriott, G. Neale and N. Epstein, Theory of electrokinetic flow in fine cylindrical capillaries at high zeta-potentials, J. Colloid Interface Sci., 1975, 52(1), 136–149 CrossRef
 .
.
- M. Martin and G. Guiochon, Axial dispersion in open-tubular capillary liquid chromatography with electroosmotic flow, Anal. Chem., 1984, 56(4), 614–620 CrossRef CAS
 .
.
- S. K. Griffiths and R. H. Nilson, Hydrodynamic Dispersion of a Neutral Nonreacting Solute in Electroosmotic Flow, Anal. Chem., 1999, 71(24), 5522–5529 CrossRef CAS
 .
.
- S. K. Griffiths and R. H. Nilson, Electroosmotic Fluid Motion and Late-Time Solute Transport for Large Zeta Potentials, Anal. Chem., 2000, 72(20), 4767–4777 CrossRef CAS
 .
.
- D. Dutta, Electrokinetic Transport of Charged Samples through Rectangular Channels with Small Zeta Potentials, Anal. Chem., 2008, 80(12), 4723–4730 CrossRef CAS PubMed
 .
.
- V. Hoshyargar, M. Talebi, S. N. Ashrafizadeh and A. Sadeghi, Hydrodynamic dispersion by electroosmotic flow of viscoelastic fluids within a slit microchannel, Microfluid. Nanofluid., 2017, 22(1), 1–15 Search PubMed
 .
.
- A. E. Herr, J. I. Molho, J. G. Santiago, M. G. Mungal, T. W. Kenny and M. G. Garguilo, Electroosmotic Capillary Flow with Nonuniform Zeta Potential, Anal. Chem., 2000, 72(5), 1053–1057 CrossRef CAS PubMed
 .
.
- S. Ghosal, Band Broadening in a Microcapillary with a Stepwise Change in the ζ-potential, Anal. Chem., 2002, 74(16), 4198–4203 CrossRef CAS PubMed
 .
.
- E. K. Zholkovskij, J. H. Masliyah and A. E. Yaroshchuk, Broadening of neutral analyte band in electroosmotic flow through slit channel with different ζ-potentials of the walls, Microfluid. Nanofluidics, 2012, 15(1), 35–47 CrossRef
 .
.
- J. C. Arcos, F. Méndez, E. G. Bautista and O. Bautista, Dispersion coefficient in an electro-osmotic flow of a viscoelastic fluid through a microchannel with a slowly varying wall zeta potential, J. Fluid Mech., 2018, 839, 348–386 CrossRef CAS
 .
.
- A. Ramos, H. Morgan, N. G. Green and A. Castellanos, Ac electrokinetics: a review of forces in microelectrode structures, J. Phys. D: Appl. Phys., 1998, 31(18), 2338–2353 CrossRef CAS
 .
.
- J. Experton, X. Wu and C. Martin, From Ion Current to Electroosmotic Flow Rectification in Asymmetric Nanopore Membranes, Nanomaterials, 2017, 7(12), 445 CrossRef
 .
.
- M. R. Hossan, D. Dutta, N. Islam and P. Dutta, Review: electric field driven pumping in microfluidic device, Electrophoresis, 2018, 39, 702–731 CrossRef CAS PubMed
 .
.
- S. Talapatra and S. Chakraborty, Double layer overlap in ac electroosmosis, Eur. J. Mech. B Fluids, 2008, 27(3), 297–308 CrossRef
 .
.
- M. Selmi and H. Belmabrouk, AC Electroosmosis Effect on Microfluidic Heterogeneous Immunoassay Efficiency, Micromachines, 2020, 11(4), 342 CrossRef PubMed
 .
.
- P. Dutta and A. Beskok, Analytical Solution of Time Periodic Electroosmotic Flows: Analogies to Stokes Second Problem, Anal. Chem., 2001, 73(21), 5097–5102 CrossRef CAS
 .
.
- X. Xuan and D. Li, Electroosmotic flow in microchannels with arbitrary geometry and arbitrary distribution of wall charge, J. Colloid Interface Sci., 2005, 289(1), 291–303 CrossRef CAS
 .
.
- W.-J. Luo, Transient electroosmotic flow induced by AC electric field in micro-channel with patchwise surface heterogeneities, J. Colloid Interface Sci., 2006, 295(2), 551–561 CrossRef CAS PubMed
 .
.
- S. Chakraborty, Augmentation of peristaltic microflows through electro-osmotic mechanisms, J. Phys. D: Appl. Phys., 2006, 39(24), 5356–5363 CrossRef CAS
 .
.
- S. Bhattacharyya and A. K. Nayak, Time periodic electro-osmotic transport in a charged micro/nano-channel, Colloids Surf., A, 2008, 325(3), 152–159 CrossRef CAS
 .
.
- Q. Liu, Y. Jian and L. Yang, Time periodic electroosmotic flow of the generalized Maxwell fluids between two micro-parallel plates, J. Non-Newtonian Fluid Mech., 2011, 166(9–10), 478–486 CrossRef CAS
 .
.
- A. J. Moghadam, Thermal characteristics of time-periodic electroosmotic flow in a circular microchannel, Heat Mass Transfer, 2015, 51(10), 1461–1473 CrossRef CAS
 .
.
- A. Haque, A. K. Nayak, B. Weigand and A. Banerjee, Time dependent electroosmotic flow in micro-channels with variable wall slip zones, Ind. Eng. Chem. Res., 2019, 59(2), 942–955 CrossRef
 .
.
- H. F. Huang and C. L. Lai, Enhancement of mass transport and separation of species by oscillatory electroosmotic flows, Proc. R. Soc. London, Ser. A, 2006, 462(2071), 2017–2038 CAS
 .
.
- G. Ramon, Y. Agnon and C. Dosoretz, Solute dispersion in oscillating electro-osmotic flow with boundary mass exchange, Microfluid. Nanofluidics, 2010, 10(1), 97–106 CrossRef
 .
.
- S. Paul and C.-O. Ng, Dispersion in electroosmotic flow generated by oscillatory electric field interacting with oscillatory wall potentials, Microfluid. Nanofluidics, 2011, 12(1–4), 237–256 Search PubMed
 .
.
- C. Teodoro, O. Bautista and F. Mendez, Mass transport and separation of species in an oscillating electroosmotic flow caused by distinct periodic electric fields, Phys. Scr., 2019, 94, 115012 CrossRef CAS
 .
.
- H. Li and Y. Jian, Dispersion for periodic electro-osmotic flow of Maxwell fluid through a microtube, Int. J. Heat Mass Transfer, 2017, 115, 703–713 CrossRef CAS
 .
.
- A. Kumar and S. De, Effect of AC electric field in mass transport of a neutral solute in a microtube with porous wall, Chem. Eng. Sci., 2024, 288, 119832 CrossRef CAS
 .
.
- F. Li and Y. Jian, Solute dispersion generated by alternating current electric field through polyelectrolyte-grafted nanochannel with interfacial slip, Int. J. Heat Mass Transfer, 2019, 141, 1066–1077 CrossRef CAS
 .
.
- M. Reshadi and M. H. Saidi, Tuning the dispersion of reactive solute by steady and oscillatory electroosmotic-Poiseuille flows in polyelectrolyte-grafted micro/nanotubes, J. Fluid Mech., 2019, 880, 73–112 CrossRef CAS
 .
.
- V. Hoshyargar, A. Khorami, S. N. Ashrafizadeh and A. Sadeghi, Solute dispersion by electroosmotic flow through soft microchannels, Sens. Actuators, B, 2018, 255, 3585–3600 CrossRef CAS
 .
.
- B. Saha, S. Chowdhury, S. Sarkar and P. P. Gopmandal, Electroosmotic flow modulation and dispersion of uncharged solutes in soft nanochannel, Soft Matter, 2024, 20(32), 6458–6489 Search PubMed
 .
.
- S. Debesset, C. J. Hayden, C. Dalton, J. C. T. Eijkel and A. Manz, An AC electroosmotic micropump for circular chromatographic applications, Lab Chip, 2004, 4(4), 396 RSC
 .
.
- G. Yan, S. K. Li and W. I. Higuchi, Evaluation of constant current alternating current iontophoresis for transdermal drug delivery, J. Controlled Release, 2005, 110(1), 141–150 CrossRef CAS
 .
.
- H. Gaikwad, G. Kumar and P. Mondal, Efficient Electroosmotic Mixing in a Narrow-Fluidic Channel: The Role of a Patterned Soft Layer, Soft Matter, 2020, 27, 1–29 Search PubMed
 .
.
- J. Song, C.-O. Ng and W.-K. A. Law, Dispersion in oscillatory electro-osmotic flow through a parallel-plate channel with kinetic sorptive exchange at walls, J. Hydrodyn., Ser. B, 2014, 26(3), 363–373 CrossRef
 .
.
- I. Medina, M. Toledo, F. Méndez and O. Bautista, Pulsatile electroosmotic flow in a microchannel with asymmetric wall zeta potentials and its effect on mass transport enhancement and mixing, Chem. Eng. Sci., 2018, 184, 259–272 CrossRef CAS
 .
.
- M. Karimzadeh, Z. Seifollahi, M. Khatibi and S. N. Ashrafizadeh, Impacts of the shape of soft nanochannels on their ion selectivity and current rectification, Electrochim. Acta, 2021, 399, 139376 CrossRef CAS
 .
.
- H. Dartoomi, M. Khatibi and S. N. Ashrafizadeh, Importance of nanochannels shape on blue energy generation in soft nanochannels, Electrochim. Acta, 2022, 431, 141175 CrossRef CAS
 .
.
- H. Dartoomi, M. Khatibi and S. N. Ashrafizadeh, Nanofluidic Membranes to Address the Challenges of Salinity Gradient Energy Harvesting: Roles of Nanochannel Geometry and Bipolar Soft Layer, Langmuir, 2022, 38(33), 10313–10330 CrossRef CAS PubMed
 .
.
- M. Karimzadeh, M. Khatibi, S. N. Ashrafizadeh and P. K. Mondal, Blue energy generation by the temperaturedependent properties in funnel-shaped soft nanochannels, Softmatter, 2022, 24, 20303 CAS
 .
.
- D. Jafari, M. Khatibi and S. N. Ashrafizadeh, Blue energy conversion utilizing smart ionic nanotransistors, Electrochim. Acta, 2024, 507, 145186 CrossRef
 .
.
- N. Qiao, Z. Zhang, A. Liu, W. Lu and C. Li, Ion current rectification in asymmetric nanochannels: effects of nanochannel shape and surface charge, Int. J. Heat Mass Transfer, 2023, 208, 124038 CrossRef CAS
 .
.
- H. Dartoomi, M. Khatibi and S. N. Ashrafizadeh, Enhanced Ionic Current Rectification through Innovative Integration of Polyelectrolyte Bilayers and Charged-Wall Smart Nanochannels, Anal. Chem., 2023, 95(2), 1522–1531 CAS
 .
.
- M. Karimzadeh, M. Khatibi and S. N. Ashrafizadeh, Boost ionic selectivity by coating bullet-shaped nanochannels with dense polyelectrolyte brushes, Phys. Fluids, 2022, 34, 122008 CrossRef CAS
 .
.
- A. Alinezhad, M. Khatibi and S. N. Ashrafizadeh, Impact of asymmetry soft layers and ion partitioning on ionic current rectification in bipolar nanochannels, J. Mol. Liq., 2022, 347, 118324 CrossRef CAS
 .
.
- A. Alinezhad, M. Khatibi and S. N. Ashrafizadeh, Ionic transfer behavior of bipolar nanochannels resembling PNP nanotransistor, Electrochim. Acta, 2023, 460, 142625 CrossRef CAS
 .
.
- R. Chein and B. Chung, Numerical study of ionic current rectification through non-uniformly charged micro/nanochannel systems, J. Appl. Electrochem., 2013, 43, 1197–1206 CrossRef CAS
 .
.
- Y. Gao, T. N. Wong, C. Yang and K. T. Ooi, Transient two-liquid electroosmotic flow with electric charges at the interface, Colloids Surf., A, 2005, 266(1–3), 117–128 CrossRef CAS
 .
.
- C. Wang, Q. Gao and Y. Song, Electrokinetic Effect of a Two-Liquid Interface within a Slit Microchannel, Langmuir, 2023, 39, 17529–17537 CrossRef CAS
 .
.
- L. Haiwang, T. N. Wong and N.-T. Nguyen, Time-dependent model of mixed electroosmotic/pressure-driven three immiscible fluids in a rectangular microchannel, Int. J. Heat Mass Transfer, 2010, 53(4), 772–785 CrossRef CAS
 .
.
- J. Su, Y.-J. Jian, L. Chang and Q.-S. Li, Transient electro-osmotic and pressure driven flows of two-layer fluids through a slit microchannel, Acta Mech. Sin., 2013, 29(4), 534–542 CrossRef CAS
 .
.
- M. Mayur, S. Amiroudine, D. Lasseux and S. Chakraborty, Effect of interfacial Maxwell stress on time periodic electro-osmotic flow in a thin liquid film with a flat interface, Electrophoresis, 2013, 35(5), 670–680 CrossRef
 .
.
- S. Mandal, U. Ghosh, A. Bandopadhyay and S. Chakraborty, Electro-osmosis of superimposed fluids in the presence of modulated charged surfaces in narrow confinements, J. Fluid Mech., 2015, 776, 390–429 CrossRef
 .
.
- A. Navarkar, S. Amiroudine and E. A. Demekhin, On two-liquid AC electroosmotic system for thin films, Electrophoresis, 2016, 37(5–6), 727–735 CrossRef CAS PubMed
 .
.
- S. Deng, T. Xiao and C. Liang, Analytical study of unsteady two-layer combined electroosmotic and pressure-driven flow through a cylindrical microchannel with slip-dependent zeta potential, Chem. Eng. Sci., 2024, 283, 119327 CrossRef CAS
 .
.
- H. Ohshima, K. Nomura, H. Kamaya and I. Ueda, Liquid membrane: equilibrium potential distribution across lipid monolayer-coated oil/water interface, J. Colloid Interface Sci., 1985, 106(2), 470–478 CrossRef CAS
 .
.
- P. Mahapatra, H. Ohshima and P. P. Gopmandal, Electrophoresis of Liquid-Layer Coated Particles: Impact of Ion Partitioning and Ion Steric Effects, Langmuir, 2021, 37(38), 11316–11329 CrossRef CAS PubMed
 .
.
- S. J. Singer and G. L. Nicolson, The Fluid Mosaic Model of the Structure of Cell Membranes, Science, 1972, 175(4023), 720–731 CrossRef CAS PubMed
 .
.
- H. G. L. Coster, The Double Fixed Charge Membrane, Biophys. J., 1973, 13(2), 133–142 CrossRef CAS PubMed
 .
.
- P. Goswami, S. De and P. P. Gopmandal, Streaming Potential and Associated Electrokinetic Effects through a Channel Filled with Electrolyte Solution Surrounded by a Layer of Immiscible and Dielectric Liquid, Langmuir, 2024, 40(22), 11695–11712 Search PubMed
 .
.
- N. F. Carnahan and K. E. Starling, Equation of State for Nonattracting Rigid Spheres, J. Chem. Phys., 1969, 51(2), 635–636 CrossRef CAS
 .
.
- J. J. López-García, J. Horno and C. Grosse, Influence of steric interactions on the dielectric and electrokinetic properties in colloidal suspensions, J. Colloid Interface Sci., 2015, 458, 273–283 CrossRef
 .
.
- H. Ohshima, A simple algorithm for the calculation of an approximate electrophoretic mobility of a spherical colloidal particle based on the modified Poisson-Boltzmann equation, Colloid Polym. Sci., 2017, 295(4), 543–548 CrossRef CAS
 .
.
- P. P. Gopmandal and H. Ohshima, Modulation of electroosmotic flow through electrolyte column surrounded by a dielectric oil layer, Colloid Polym. Sci., 2017, 295(7), 1141–1151 CrossRef CAS
 .
.
- H. Jing and S. Das, Electric double layer electrostatics of lipid-bilayer-encapsulated nanoparticles: toward a better understanding of protocell electrostatics, Electrophoresis, 2018, 39(5–6), 752–759 CrossRef CAS
 .
.
- Z. Seifollahi and S. N. Ashrafizadeh, Effect of charge density distribution of polyelectrolyte layer on electroosmotic flow and ion selectivity in a conical soft nanochannel, Chem. Eng. Sci., 2022, 261, 117986 CrossRef CAS
 .
.
- A. Ganjizade, S. N. Ashrafizadeh and A. Sadeghi, Effect of ion partitioning on the electrostatics of soft particles with a volumetrically charged core, Electrochem. Commun., 2017, 84, 19–23 CrossRef CAS
 .
.
- A. Ganjizade, S. N. Ashrafizadeh and A. Sadeghi, Significant alteration in DNA electrophoretic translocation velocity through soft nanopores by ion partitioning, Anal. Chim. Acta, 2019, 1080, 66–74 CrossRef CAS
 .
.
- M. Reshadi and M. H. Saidi, The role of ion partitioning in electrohydrodynamic characteristics of soft nanofluidics: inclusion of EDL overlap and steric effects, Chem. Eng. Sci., 2018, 190, 443–458 CrossRef CAS
 .
.
-
J. N. Israelachvili, Intermolecular and surface forces, Academic Press, 3rd edn, 2011, pp. 273–277 Search PubMed
 .
.
- H. Ohshima, An approximate analytic solution to the modified Poisson–Boltzmann equation: effects of ionic size, Colloid Polym. Sci., 2016, 294(12), 2121–2125 CrossRef CAS
 .
.
- H. Ohshima, Theory of electrostatics and electrokinetics of soft particles, Sci. Technol. Adv. Mater., 2009, 10(6), 063001 CrossRef
 .
.
- J. S. H. Lee, I. Barbulovic-Nad, Z. Wu, X. Xuan and D. Li, Electrokinetic flow in a free surface-guided microchannel, J. Appl. Phys., 2006, 99(5), 054905 CrossRef
 .
.
- W. N. Gill, Analysis of axial dispersion with time variable flow, Chem. Eng. Sci., 1967, 22(7), 1013–1017 CrossRef CAS
 .
.
- M. E. Leunissen, J. Zwanikken, R. van Roij, P. M. Chaikin and A. van Blaaderen, Ion partitioning at the oil-water interface as a source of tunable electrostatic effects in emulsions with colloids, Phys. Chem. Chem. Phys., 2007, 9(48), 6405 RSC
 .
.
- A. R. Kneller, D. G. Haywood and S. C. Jacobson, AC Electroosmotic Pumping in Nanofluidic Funnels, Anal. Chem., 2016, 88(12), 6390–6394 CrossRef CAS PubMed
 .
.
- A. J. Moghadam and P. Akbarzadeh, AC two-immiscible-fluid EOF in a microcapillary, J. Braz. Soc. Mech. Sci. Eng., 2019, 41, 194 CrossRef
 .
.
- A. Sadeghi, Analytical solutions for mass transport in hydrodynamic focusing by considering different diffusivities for sample and sheath flows, J. Fluid Mech., 2019, 862, 517–551 CrossRef CAS
 .
.
- S. Vedel and H. Bruus, Transient Taylor-Aris dispersion for time-dependent flows in straight channels, J. Fluid Mech., 2011, 691, 95–122 CrossRef
 .
.
- H. Li and Y. Jian, Dispersion for periodic electro-osmotic flow of Maxwell fluid through a microtube, Int. J. Heat Mass Transfer, 2017, 115, 703–713 CrossRef CAS
 .
.
- A. Mukherjee and B. S. Mazumder, Dispersion of contaminant in oscillatory flows, Acta Mech., 1988, 74(1–4), 107–122 CrossRef
 .
.
Footnote |
| † Electronic supplementary information (ESI) available: Nomenclature, the spatial distribution of the concentration of additional mobile ions present in the dielectric liquid layer and some additional results to support the findings. See DOI: https://doi.org/10.1039/d4sm01255k |
|
| This journal is © The Royal Society of Chemistry 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  a,
Sanjib Kr
Pal
a,
Sanjib Kr
Pal
 b and
Partha P.
Gopmandal
b and
Partha P.
Gopmandal
 *a
*a
 where E0 indicates the magnitude of applied oscillatory electric field. Here
where E0 indicates the magnitude of applied oscillatory electric field. Here  ; ω and t indicate the angular frequency of the oscillatory electric field and time, respectively, and
; ω and t indicate the angular frequency of the oscillatory electric field and time, respectively, and  indicates the real part of a complex number
indicates the real part of a complex number  . The concentration and valence of additional mobile ions in the form of surfactant molecules present in the membrane layer are denoted as N0 (in mM) and Z, respectively. We have assumed that the concentration of such molecules with in an aqueous medium is zero.
. The concentration and valence of additional mobile ions in the form of surfactant molecules present in the membrane layer are denoted as N0 (in mM) and Z, respectively. We have assumed that the concentration of such molecules with in an aqueous medium is zero.
 respectively. The dielectric constant of the membrane layer is in general lower than that of the electrolyte medium.83,91 Thus, the penetration of electrolyte ions within the membrane layer occurs in a discontinuous manner due to the presence of the ion partitioning effect. The concentration of electrolyte ions (nj, j = 1, 2) along the liquid–liquid interface is discontinuous and satisfies the following relation92–95
respectively. The dielectric constant of the membrane layer is in general lower than that of the electrolyte medium.83,91 Thus, the penetration of electrolyte ions within the membrane layer occurs in a discontinuous manner due to the presence of the ion partitioning effect. The concentration of electrolyte ions (nj, j = 1, 2) along the liquid–liquid interface is discontinuous and satisfies the following relation92–95












![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) (ȳ),
(ȳ), ![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) D indicate the scaled EDL potential and Donnan potential, respectively. The scaled interfacial charge
D indicate the scaled EDL potential and Donnan potential, respectively. The scaled interfacial charge ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) is defined as
is defined as  and
and  indicates the liquid layer to electrolyte permittivity ratio with
indicates the liquid layer to electrolyte permittivity ratio with ![[small delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c5.gif) = δ/H being the scaled thickness of the liquid layer. The quantity κ appearing in eqn (8) indicates the inverse of the EDL thickness (which forms towards the side of the aqueous phase), defined as
= δ/H being the scaled thickness of the liquid layer. The quantity κ appearing in eqn (8) indicates the inverse of the EDL thickness (which forms towards the side of the aqueous phase), defined as  and the quantity κ1 appearing in eqn (8) is defined as
and the quantity κ1 appearing in eqn (8) is defined as  . The scaled Donnan potential can be obtained by setting the right hand side of eqn (8a) to zero, and thus we may write
. The scaled Donnan potential can be obtained by setting the right hand side of eqn (8a) to zero, and thus we may write





![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) d and
d and ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) e, respectively. We consider the no-slip velocity boundary condition along the supporting rigid walls of the channel as indicated in the relation (13a). The continuity of flow velocity along the liquid–liquid interface is adopted, which is further indicated in the relation (13b). We adopt the EDL plus surface charge (SC) model to study the considered electrokinetic flow involving a two-liquid system.74 It is noteworthy to mention that such an EDL plus SC model can successfully describe the experimental observation on the electrokinetic behavior of two-phase liquid systems.99 Such a consideration may leads to the condition indicated in (13c). We further adopt symmetry condition for flow velocity along the central line of the channel, which is indicated in (13d).
e, respectively. We consider the no-slip velocity boundary condition along the supporting rigid walls of the channel as indicated in the relation (13a). The continuity of flow velocity along the liquid–liquid interface is adopted, which is further indicated in the relation (13b). We adopt the EDL plus surface charge (SC) model to study the considered electrokinetic flow involving a two-liquid system.74 It is noteworthy to mention that such an EDL plus SC model can successfully describe the experimental observation on the electrokinetic behavior of two-phase liquid systems.99 Such a consideration may leads to the condition indicated in (13c). We further adopt symmetry condition for flow velocity along the central line of the channel, which is indicated in (13d).
 and thus the back and forth oscillatory axial velocity may be written as
and thus the back and forth oscillatory axial velocity may be written as  where u0(y) is the complex amplitude of the velocity field. We consider the Helmoltz–Smoluchowsky reference velocity
where u0(y) is the complex amplitude of the velocity field. We consider the Helmoltz–Smoluchowsky reference velocity  as the velocity scale. Below we recast the governing equations and boundary conditions associated with the velocity field in the scaled form
as the velocity scale. Below we recast the governing equations and boundary conditions associated with the velocity field in the scaled form

![[small delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c5.gif) )− = ū0(ȳ)|ȳ=(−1+
)− = ū0(ȳ)|ȳ=(−1+![[small delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c5.gif) )+
)+







![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) (±∞, ȳ,
(±∞, ȳ, ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) = 0
) = 0
![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) = C/C0,
= C/C0, ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) = D0x/H2UHS,
= D0x/H2UHS, ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) = D0t/H2 and
= D0t/H2 and ![[L with combining macron]](https://www.rsc.org/images/entities/i_char_004c_0304.gif) = D0L/H2UHS. The non-dimensional parameter Pe indicates the ratio of the rate of transport caused by convection and molecular diffusion, and is defined as Pe = HUHS/D0. To analyze the dispersion of solutes we introduce a moving coordinate system, comoving with the cross-sectional mean fluid velocity
= D0L/H2UHS. The non-dimensional parameter Pe indicates the ratio of the rate of transport caused by convection and molecular diffusion, and is defined as Pe = HUHS/D0. To analyze the dispersion of solutes we introduce a moving coordinate system, comoving with the cross-sectional mean fluid velocity  . Thus, the new axial coordinate
. Thus, the new axial coordinate ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) u(
u(![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) ,
, ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) (in the scaled form) in the moving frame of reference may be defined as
) (in the scaled form) in the moving frame of reference may be defined as

![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) m, given as
m, given as

![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) (k = 1, 2, 3, …) are the coefficients of series expansion. Substituting (26) into (25) yields
) (k = 1, 2, 3, …) are the coefficients of series expansion. Substituting (26) into (25) yields
![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) m follows the given equation100
m follows the given equation100
![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) are the periodic function of time due to an oscillatory flow of the background aqueous medium. Considering k-times the partial derivative of the above eqn (28) with respect to space coordinate
) are the periodic function of time due to an oscillatory flow of the background aqueous medium. Considering k-times the partial derivative of the above eqn (28) with respect to space coordinate ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) u, we may deduce the following relation
u, we may deduce the following relation

![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) m/∂
m/∂![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) ku (k = 1, 2, 3, …) to zero, which yields the following differential equations involving fk
ku (k = 1, 2, 3, …) to zero, which yields the following differential equations involving fk


![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) are also satisfied by
are also satisfied by ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) m. Thus, substituting (25) into (21) and (22) yields
m. Thus, substituting (25) into (21) and (22) yields

![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) vanishes and the other coefficients are derived as follows
) vanishes and the other coefficients are derived as follows

![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) indicates the convection coefficient due to the velocity of solutes and thus vanishes as we are in a moving frame of reference. Besides, the term K2(
) indicates the convection coefficient due to the velocity of solutes and thus vanishes as we are in a moving frame of reference. Besides, the term K2(![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) indicates the effective dispersion coefficient due to the molecular diffusion and fluid convection, which is renamed as K(
) indicates the effective dispersion coefficient due to the molecular diffusion and fluid convection, which is renamed as K(![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ). The terms Ki (i ≥ 3) are very small compared to the value of K2. So, we can neglect the contribution of all Ki when i ≥ 3.9 Thus, eqn (28) takes the simplified form as follows
). The terms Ki (i ≥ 3) are very small compared to the value of K2. So, we can neglect the contribution of all Ki when i ≥ 3.9 Thus, eqn (28) takes the simplified form as follows
![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) (renamed afterwards as K(
) (renamed afterwards as K(![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) )) requires the value of f1(ȳ,
)) requires the value of f1(ȳ, ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ), which is governed by eqn (31b) subject to the conditions (32) and (33). Thus, to evaluate the cross-sectional averaged concentration of the solute, one need to calculate f1(ȳ,
), which is governed by eqn (31b) subject to the conditions (32) and (33). Thus, to evaluate the cross-sectional averaged concentration of the solute, one need to calculate f1(ȳ, ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ). It may be noted that under the AC field based EOF, we may write
). It may be noted that under the AC field based EOF, we may write  , where
, where  and
and  . With the same analogy we may further rewrite
. With the same analogy we may further rewrite  . Substituting the same into (31a), (32) and (34) we may formulate the boundary value problem involving F(ȳ), and the same is summarized below
. Substituting the same into (31a), (32) and (34) we may formulate the boundary value problem involving F(ȳ), and the same is summarized below

![[small delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c5.gif) )−} = F{(−1 +
)−} = F{(−1 + ![[small delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c5.gif) )+}
)+}

 . Solving (38) subject to the boundary conditions (39a)–(39d) yields
. Solving (38) subject to the boundary conditions (39a)–(39d) yields
![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) may be written in terms of F(ȳ) and is given below
) may be written in terms of F(ȳ) and is given below
![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ), defined as
), defined as
 indicates the standard deviation of distribution of
indicates the standard deviation of distribution of ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) m at a given time
m at a given time ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) . Such a quantity measures the width of the dispersed zone of the solutes. Using the above transformation (42), we may transform eqn (37) and the associated initial and boundary conditions as follows
. Such a quantity measures the width of the dispersed zone of the solutes. Using the above transformation (42), we may transform eqn (37) and the associated initial and boundary conditions as follows
![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) m(
m(![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) u, 0) = 2
u, 0) = 2![[L with combining macron]](https://www.rsc.org/images/entities/i_char_004c_0304.gif) δ
δ![[L with combining macron]](https://www.rsc.org/images/entities/i_char_004c_0304.gif) ,
, ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) m(±∞,
m(±∞, ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) = 0
) = 0
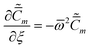

 , and
, and ![[small omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0da.gif) represents the scaled spatial wave number, defined earlier. The solution of eqn (46) subject to conditions indicated in (47) is given as follows
represents the scaled spatial wave number, defined earlier. The solution of eqn (46) subject to conditions indicated in (47) is given as follows
 we may deduce the time evolution of the spatially dependent area-averaged solute concentration as follows
we may deduce the time evolution of the spatially dependent area-averaged solute concentration as follows
 . It is worth noting that the quantities which provide the measurement of the dispersion process are
. It is worth noting that the quantities which provide the measurement of the dispersion process are ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) m(
m(![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) u,
u, ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ), K(
), K(![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) and
) and  respectively. In addition, we have further indicated the results for time-averaged effective dispersion coefficient Kavg over one oscillation period τ0 = 2π/ω, defined as
respectively. In addition, we have further indicated the results for time-averaged effective dispersion coefficient Kavg over one oscillation period τ0 = 2π/ω, defined as
![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ), we need to calculate the function F(ȳ) using the closed form relation (40), which further involves the axial velocity. Note that the main complexity to deduce F(ȳ) is to calculate the integrals Ji (i = 5, 6, 7, 8), which are calculated using MATHEMATICA software. With the known values of axial velocity and F(ȳ), the relation (41) is implemented to calculate K(
), we need to calculate the function F(ȳ) using the closed form relation (40), which further involves the axial velocity. Note that the main complexity to deduce F(ȳ) is to calculate the integrals Ji (i = 5, 6, 7, 8), which are calculated using MATHEMATICA software. With the known values of axial velocity and F(ȳ), the relation (41) is implemented to calculate K(![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ). The relations (42), (49) and (50) are further implemented to derive the results for
). The relations (42), (49) and (50) are further implemented to derive the results for 
![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) m(
m(![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) u,
u, ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) and Kavg, respectively.
) and Kavg, respectively.
![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) m(
m(![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) u,
u, ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) and Kavg, respectively. The detailed description of the same is further summarized in Appendix-D. In addition, we have further performed the validation of numerical quantities associated with the dispersion process with the aforesaid analytical results. The readers are referred to Appendix-D for more details related to the same.
) and Kavg, respectively. The detailed description of the same is further summarized in Appendix-D. In addition, we have further performed the validation of numerical quantities associated with the dispersion process with the aforesaid analytical results. The readers are referred to Appendix-D for more details related to the same.![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) jωH2/ηj dictates the back and forth motion of the background medium, where the subscript j = d or e is associated with the dielectric liquid layer or the electrolyte medium, respectively. We present the results for various choices of the channel height and frequency of the applied AC electric field.
jωH2/ηj dictates the back and forth motion of the background medium, where the subscript j = d or e is associated with the dielectric liquid layer or the electrolyte medium, respectively. We present the results for various choices of the channel height and frequency of the applied AC electric field.
 , viscosity ηd = 2.269 mPa s and mass density
, viscosity ηd = 2.269 mPa s and mass density ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) d = 1345 kg m−3, respectively.101 For such a choice of liquid layer, the viscosity ratio ηR = 2.54, dielectric permittivity ratio
d = 1345 kg m−3, respectively.101 For such a choice of liquid layer, the viscosity ratio ηR = 2.54, dielectric permittivity ratio  and the interfacial tension is 9.2 × 10−3 N m−1, respectively. The electric strength of electric field E0 is taken as E0 = 103 V m−1. Thus, the Capillary number Ca ≪ 1. In addition to the CHB solvent, we have further presented the results changing suitably the dielectric permittivity as well as viscosity of the liquid layer adjacent to the supporting walls. For each of the cases, we found the Capillary number is far smaller than unity. A relatively broad range in frequency ω/2π is considered, e.g., 105 Hz to 108 Hz, and such choices of frequency are rather common in the AC electric field driven EOF.102,103
and the interfacial tension is 9.2 × 10−3 N m−1, respectively. The electric strength of electric field E0 is taken as E0 = 103 V m−1. Thus, the Capillary number Ca ≪ 1. In addition to the CHB solvent, we have further presented the results changing suitably the dielectric permittivity as well as viscosity of the liquid layer adjacent to the supporting walls. For each of the cases, we found the Capillary number is far smaller than unity. A relatively broad range in frequency ω/2π is considered, e.g., 105 Hz to 108 Hz, and such choices of frequency are rather common in the AC electric field driven EOF.102,103 with fixed viscosity ηR = 2.54 (Fig. 3a) and in Fig. 3b we have shown the results for various choices of ηR with fixed dielectric permittivity
with fixed viscosity ηR = 2.54 (Fig. 3a) and in Fig. 3b we have shown the results for various choices of ηR with fixed dielectric permittivity  . The results are presented for fixed values of other model parameters, which are summarized in the figure caption. As indicated earlier for CHB solvent
. The results are presented for fixed values of other model parameters, which are summarized in the figure caption. As indicated earlier for CHB solvent  and ηR = 2.54, which is taken as the base value and an increase in
and ηR = 2.54, which is taken as the base value and an increase in  and ηR indicates that the liquid in the dielectric layer is more polarizable in response to an electric field and more viscous compared to the CHB solvent, respectively. Besides, the increase in
and ηR indicates that the liquid in the dielectric layer is more polarizable in response to an electric field and more viscous compared to the CHB solvent, respectively. Besides, the increase in  with fixed dielectric constant of the aqueous medium leads to an increase in dielectric permittivity of the liquid in the layer adjacent to the channel wall. Thus, the impact of ion partitioning reduces, which in turn allows the accumulation of more counterions within the dielectric liquid layer. As a result, the neutralization of effective charge inside the liquid layer enhances and leads to a reduction in velocity amplitude |ū0(ȳ)|. As expected the velocity amplitude |ū0(ȳ)| reduces with the increase in viscosity of the liquid layer adjacent to the supporting walls. Note that the increase in velocity amplitude |ū0(ȳ)| within the liquid layer with its lower viscosity leads to an enhancement in |ū0(ȳ)| within the aqueous phase so as to satisfy the continuity in flow velocity along the liquid–liquid interface.
with fixed dielectric constant of the aqueous medium leads to an increase in dielectric permittivity of the liquid in the layer adjacent to the channel wall. Thus, the impact of ion partitioning reduces, which in turn allows the accumulation of more counterions within the dielectric liquid layer. As a result, the neutralization of effective charge inside the liquid layer enhances and leads to a reduction in velocity amplitude |ū0(ȳ)|. As expected the velocity amplitude |ū0(ȳ)| reduces with the increase in viscosity of the liquid layer adjacent to the supporting walls. Note that the increase in velocity amplitude |ū0(ȳ)| within the liquid layer with its lower viscosity leads to an enhancement in |ū0(ȳ)| within the aqueous phase so as to satisfy the continuity in flow velocity along the liquid–liquid interface. . The results are presented here for various choices of ion size. Other model parameters for Fig. 4 are summarized in the figure caption. The impact of the ion size on overall flow modulation is prominent for lower ranges of κH and
. The results are presented here for various choices of ion size. Other model parameters for Fig. 4 are summarized in the figure caption. The impact of the ion size on overall flow modulation is prominent for lower ranges of κH and  . An increase in κH for a fixed channel height strengthens the shielding effect and thus leads to an enhanced charge neutralization. Besides, an increase in
. An increase in κH for a fixed channel height strengthens the shielding effect and thus leads to an enhanced charge neutralization. Besides, an increase in  reduces the impact of the ion partitioning effect and thus enhances the accumulation of counterions within the liquid layer as well as near the charged interface. Thus, for a smaller range of κH or
reduces the impact of the ion partitioning effect and thus enhances the accumulation of counterions within the liquid layer as well as near the charged interface. Thus, for a smaller range of κH or  where the net charge of the fluidic system is high, the impact of the ion steric effect is prominent. However, its impact gradually diminishes with the increase in κH and
where the net charge of the fluidic system is high, the impact of the ion steric effect is prominent. However, its impact gradually diminishes with the increase in κH and  . As expected the increase in the ion size reduces the net throughput due to the enhanced impact of the ion partitioning effect.
. As expected the increase in the ion size reduces the net throughput due to the enhanced impact of the ion partitioning effect.![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) (Fig. 5a), molar concentration N0 of additional mobile ions within the membrane layer (Fig. 5b) and its thickness
(Fig. 5a), molar concentration N0 of additional mobile ions within the membrane layer (Fig. 5b) and its thickness ![[small delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c5.gif) (Fig. 5c). Rise in interfacial charge density for fixed values of N0 and
(Fig. 5c). Rise in interfacial charge density for fixed values of N0 and ![[small delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c5.gif) leads to an enhanced electrostatic potential in the membrane layer as well as in the aqueous medium and thus leads to an enhanced throughput. The impact of interfacial charge on the overall flow modulation further augments with the increase in N0 and
leads to an enhanced electrostatic potential in the membrane layer as well as in the aqueous medium and thus leads to an enhanced throughput. The impact of interfacial charge on the overall flow modulation further augments with the increase in N0 and ![[small delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c5.gif) . Note that the increase in both of these quantities enhances the net effective charge density entrapped in the membrane layer. In Appendix-E, we have further shown the results for electrostatic potential distribution as well as net charge density considering different values of concentration of mobile charges in the dielectric liquid layer. A detailed discussion on the same is made thereat. Thus, the effective electromotive force further enhances with the increase in N0 and
. Note that the increase in both of these quantities enhances the net effective charge density entrapped in the membrane layer. In Appendix-E, we have further shown the results for electrostatic potential distribution as well as net charge density considering different values of concentration of mobile charges in the dielectric liquid layer. A detailed discussion on the same is made thereat. Thus, the effective electromotive force further enhances with the increase in N0 and ![[small delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c5.gif) , which in turn leads to an enhanced velocity amplitude |ū0(ȳ)|. Unlike that increase in interfacial charge or N0, an increase in δ further leads to an enhanced motion deterring drag force due to higher viscosity of the dielectric liquid layer. Thus, it is expected that the interfacial charge and N0 have more impacts on the flow modulation compared to the thickness δ of the dielectric liquid layer.
, which in turn leads to an enhanced velocity amplitude |ū0(ȳ)|. Unlike that increase in interfacial charge or N0, an increase in δ further leads to an enhanced motion deterring drag force due to higher viscosity of the dielectric liquid layer. Thus, it is expected that the interfacial charge and N0 have more impacts on the flow modulation compared to the thickness δ of the dielectric liquid layer.![[L with combining macron]](https://www.rsc.org/images/entities/i_char_004c_0304.gif) = 0.2 (in the scaled form). The band of solutes was dispersed due to molecular diffusion and fluid convection was induced by an applied oscillatory electric field. Note that the mass diffusivity of the uncharged solutes in general ranges from 10−12 m2 s−1 to 10−9 m2 s−1.104 Thus, for the considered flow geometry with a given channel height, the Péclet number (Pe) associated with the dispersion process ranges from 0.05 to 50. To analyze the findings related to solute dispersion we present the results for time evolution of cross-sectional averaged solute concentration
= 0.2 (in the scaled form). The band of solutes was dispersed due to molecular diffusion and fluid convection was induced by an applied oscillatory electric field. Note that the mass diffusivity of the uncharged solutes in general ranges from 10−12 m2 s−1 to 10−9 m2 s−1.104 Thus, for the considered flow geometry with a given channel height, the Péclet number (Pe) associated with the dispersion process ranges from 0.05 to 50. To analyze the findings related to solute dispersion we present the results for time evolution of cross-sectional averaged solute concentration ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) m, effective dispersion coefficient K(
m, effective dispersion coefficient K(![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ), standard deviation
), standard deviation  of the distribution of
of the distribution of ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) m and time-averaged effective dispersion coefficient Kavg over one oscillation period τ0 = 2π/ω, respectively.
m and time-averaged effective dispersion coefficient Kavg over one oscillation period τ0 = 2π/ω, respectively.
![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) m(
m(![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) u,
u, ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ). We have shown the results for time evolution of
). We have shown the results for time evolution of ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) m(
m(![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) u,
u, ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) at a fixed value of Pe = 25 (Fig. 7a). The corresponding line plots for
) at a fixed value of Pe = 25 (Fig. 7a). The corresponding line plots for ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) m(
m(![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) u,
u, ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) for discrete values of scaled time
) for discrete values of scaled time ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) are further shown in Fig. 7b. We observed that as the time grows, the dispersion of solutes under the combined impact of molecular diffusion and oscillatory convective effect increases and leads to a significant band broadening of the solute placed inside the channel. The impact of the Péclet number on the spatial distribution of averaged concentration
are further shown in Fig. 7b. We observed that as the time grows, the dispersion of solutes under the combined impact of molecular diffusion and oscillatory convective effect increases and leads to a significant band broadening of the solute placed inside the channel. The impact of the Péclet number on the spatial distribution of averaged concentration ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) m is shown in Fig. 7c, where we have presented the results indicating the line plots for
m is shown in Fig. 7c, where we have presented the results indicating the line plots for ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) m for various choices of Péclet numbers at a given time. In addition, we have further shown the results in Fig. S.1 (ESI†) to indicate the time evolution of
m for various choices of Péclet numbers at a given time. In addition, we have further shown the results in Fig. S.1 (ESI†) to indicate the time evolution of ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) m(
m(![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) u,
u, ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) for various values of Pe, where the Péclet number is varied by suitably changing the mass diffusivity of the solutes with fixed values of other model parameters. For such cases, an increase in the Péclet number indicates a reduction in mass diffusivity of the solutes. As expected the broadening is higher at smaller values of Pe due to enhanced mass diffusivity of the solutes. For such cases the molecular diffusion dominates over the convective dispersion process. The quantitative measurement of band broadening is dictated by the time evolution of standard deviation
) for various values of Pe, where the Péclet number is varied by suitably changing the mass diffusivity of the solutes with fixed values of other model parameters. For such cases, an increase in the Péclet number indicates a reduction in mass diffusivity of the solutes. As expected the broadening is higher at smaller values of Pe due to enhanced mass diffusivity of the solutes. For such cases the molecular diffusion dominates over the convective dispersion process. The quantitative measurement of band broadening is dictated by the time evolution of standard deviation  of the distribution of
of the distribution of ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) m, as presented in Fig. 7d. Such a quantity indicates the width of the sample zone at a specified time. The oscillatory behaviour of the time evolution of
m, as presented in Fig. 7d. Such a quantity indicates the width of the sample zone at a specified time. The oscillatory behaviour of the time evolution of  is prominent for a larger range of Péclet numbers for which the oscillatory convection effect dominates over the diffusion process. However, the width of the sample zone is higher for small Péclet numbers due to a strong diffusion effect.
is prominent for a larger range of Péclet numbers for which the oscillatory convection effect dominates over the diffusion process. However, the width of the sample zone is higher for small Péclet numbers due to a strong diffusion effect.![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) (the influence of the axial diffusion 1/Pe2 is deduced). In Fig. 8 the results for K(
) (the influence of the axial diffusion 1/Pe2 is deduced). In Fig. 8 the results for K(![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) − 1/Pe2 are presented for fixed Pe with a similar set of other model parameters as considered in Fig. 2. Impact of convective transport on the dispersion process is evident from the results presented in Fig. 8. As observed in Fig. 2, the velocity amplitude |ū0(ȳ)| increases (decreases) with the increase in the EDL thickness (ion size). As a result the amplitude of the oscillatory dispersion coefficient increases with the reduction in κH (Fig. 8a), and it reduces with the increase in the ion size (Fig. 8b). In addition, the oscillatory behavior of the dispersion coefficient enhances with the increase in the impact of fluid convection. In Fig. S.2 (ESI†) we have further shown the corresponding results for time evolution of
) − 1/Pe2 are presented for fixed Pe with a similar set of other model parameters as considered in Fig. 2. Impact of convective transport on the dispersion process is evident from the results presented in Fig. 8. As observed in Fig. 2, the velocity amplitude |ū0(ȳ)| increases (decreases) with the increase in the EDL thickness (ion size). As a result the amplitude of the oscillatory dispersion coefficient increases with the reduction in κH (Fig. 8a), and it reduces with the increase in the ion size (Fig. 8b). In addition, the oscillatory behavior of the dispersion coefficient enhances with the increase in the impact of fluid convection. In Fig. S.2 (ESI†) we have further shown the corresponding results for time evolution of  (Fig. S.2a and b, ESI†) and cross-sectional averaged
(Fig. S.2a and b, ESI†) and cross-sectional averaged ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) m at a given time
m at a given time ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) = 0.5 (Fig. S.2c and d, ESI†) for different values of κH and ion size. The model parameters in Fig. S.2 (ESI†) are the same as considered in Fig. 8. It is evident that the band broadening is higher for the cases when the impact of fluid convection is strong. The larger dispersion coefficient K(
= 0.5 (Fig. S.2c and d, ESI†) for different values of κH and ion size. The model parameters in Fig. S.2 (ESI†) are the same as considered in Fig. 8. It is evident that the band broadening is higher for the cases when the impact of fluid convection is strong. The larger dispersion coefficient K(![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) − 1/Pe2 is a direct consequence of the larger effective Péclet number based on the overall strength of the flow field with fixed molecular diffusion of solutes. Thus, the peak of mean concentration
) − 1/Pe2 is a direct consequence of the larger effective Péclet number based on the overall strength of the flow field with fixed molecular diffusion of solutes. Thus, the peak of mean concentration ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) m decreases with the reduction in κH as well as with the reduction in the ion size for which the velocity amplitude |ū0(ȳ)| is enhanced.
m decreases with the reduction in κH as well as with the reduction in the ion size for which the velocity amplitude |ū0(ȳ)| is enhanced.![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) − 1/Pe2 for various choices of dielectric permittivity ratios
) − 1/Pe2 for various choices of dielectric permittivity ratios  (Fig. 9a) and viscosity ratios (ηR) (Fig. 9) for fixed values of other model parameters. In addition, the time evolution of
(Fig. 9a) and viscosity ratios (ηR) (Fig. 9) for fixed values of other model parameters. In addition, the time evolution of  and
and ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) m at a given time
m at a given time ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) = 0.5 is presented in Fig. S.3 (ESI† for a similar set of pertinent parameters. As indicated earlier, the flow strength enhances with the reduction in
= 0.5 is presented in Fig. S.3 (ESI† for a similar set of pertinent parameters. As indicated earlier, the flow strength enhances with the reduction in  (stated differently, an increase in the difference between the dielectric permittivity of both the phases or in other words, an increase in the ion partitioning effect). In addition, a reduction in viscosity of the liquid layer adjacent to the supporting walls further rises the velocity amplitude. Thus, the enhanced flow strength achieved in a smaller range of
(stated differently, an increase in the difference between the dielectric permittivity of both the phases or in other words, an increase in the ion partitioning effect). In addition, a reduction in viscosity of the liquid layer adjacent to the supporting walls further rises the velocity amplitude. Thus, the enhanced flow strength achieved in a smaller range of  and ηR leads to a larger dispersion coefficient (K(
and ηR leads to a larger dispersion coefficient (K(![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) − 1/Pe2) as well as a larger band broadening, which results in a smaller peak of the mean concentration. We further observed an enhanced dispersion of the solute band for increasing values of thickness and molar concentration of additional mobile ions present in the liquid layer adjacent to the supporting walls as well as interfacial charge density. The same is graphically illustrated in Fig. S.4 and S.5 (ESI†) which can further be justified with a similar analogy.
) − 1/Pe2) as well as a larger band broadening, which results in a smaller peak of the mean concentration. We further observed an enhanced dispersion of the solute band for increasing values of thickness and molar concentration of additional mobile ions present in the liquid layer adjacent to the supporting walls as well as interfacial charge density. The same is graphically illustrated in Fig. S.4 and S.5 (ESI†) which can further be justified with a similar analogy.![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) − 1/Pe2 are further shown for various channel heights (Fig. 10a) and frequency of the oscillatory electric field (Fig. 10b). The results are presented here for the given value of other model parameters. As indicated earlier, an increase in the channel height leads to an enhanced flow rate. Thus, an enhanced dispersion coefficient and a larger dispersion occur in the wider channel as a consequence of an enhanced effective Péclet number (Fig. 10a and Fig. S.6a, ESI†). As a result the peak of the mean concentration profile reduces with the increase in the channel height (Fig. S.6c, ESI†). We observe that the increase in oscillatory frequency reduces the effective dispersion coefficient (Fig. 10b), and results in a reduced bandwidth (Fig. S.6b, ESI†) and hence the larger peak in the mean solute concentration (Fig. S.6d, ESI†). Note that for higher frequency, the diffusion time is much higher than the oscillating period of applied AC electric field. Thus, the solute band does not have enough time to diffuse in a larger area. In addition, an increase in frequency and the increased inertia effect lead to a reduction in velocity amplitude. As a result the convective dispersion process with the increase in oscillatory frequency becomes weaker.
) − 1/Pe2 are further shown for various channel heights (Fig. 10a) and frequency of the oscillatory electric field (Fig. 10b). The results are presented here for the given value of other model parameters. As indicated earlier, an increase in the channel height leads to an enhanced flow rate. Thus, an enhanced dispersion coefficient and a larger dispersion occur in the wider channel as a consequence of an enhanced effective Péclet number (Fig. 10a and Fig. S.6a, ESI†). As a result the peak of the mean concentration profile reduces with the increase in the channel height (Fig. S.6c, ESI†). We observe that the increase in oscillatory frequency reduces the effective dispersion coefficient (Fig. 10b), and results in a reduced bandwidth (Fig. S.6b, ESI†) and hence the larger peak in the mean solute concentration (Fig. S.6d, ESI†). Note that for higher frequency, the diffusion time is much higher than the oscillating period of applied AC electric field. Thus, the solute band does not have enough time to diffuse in a larger area. In addition, an increase in frequency and the increased inertia effect lead to a reduction in velocity amplitude. As a result the convective dispersion process with the increase in oscillatory frequency becomes weaker. (Fig. 11c). Other model parameters are indicated in the caption of the said figure. As expected the time-averaged effective dispersion Kavg reduces with the increase in oscillatory frequency. Such a reduction is due to enhanced periodical expansion and contraction of the solute band placed under the oscillatory flow field. For a smaller range of oscillatory frequencies, due to an enhanced flow strength with reduction in κH, ion size as well as
(Fig. 11c). Other model parameters are indicated in the caption of the said figure. As expected the time-averaged effective dispersion Kavg reduces with the increase in oscillatory frequency. Such a reduction is due to enhanced periodical expansion and contraction of the solute band placed under the oscillatory flow field. For a smaller range of oscillatory frequencies, due to an enhanced flow strength with reduction in κH, ion size as well as  , the magnitude in Kavg increases. However, their impact on Kavg gradually diminishes with the increase in frequency of the oscillatory electric field. In Fig. S.7 (ESI†) we have further shown the impact of other pertinent parameters associated with flow modulation (e.g., viscosity ratio ηR, thickness
, the magnitude in Kavg increases. However, their impact on Kavg gradually diminishes with the increase in frequency of the oscillatory electric field. In Fig. S.7 (ESI†) we have further shown the impact of other pertinent parameters associated with flow modulation (e.g., viscosity ratio ηR, thickness ![[small delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c5.gif) , interfacial charge
, interfacial charge ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) and molar concentration N0). The viscosity ratio ηR has little effect on the time-averaged effective dispersion Kavg, however,
and molar concentration N0). The viscosity ratio ηR has little effect on the time-averaged effective dispersion Kavg, however, ![[small delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c5.gif) ,
, ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) and N0 have a substantial impact on Kavg, when frequency of the oscillatory electric field is small. We observed that when ω/2π is smaller than 6 × 105 Hz, the impact of oscillatory electric field on the flow modulation, dispersion coefficient as well as band broadening is prominent. However, beyond this limit of frequency, an increase in oscillatory frequency ω reduces the impact of pertinent parameters on the flow modulation and hence the dispersion characteristics.
and N0 have a substantial impact on Kavg, when frequency of the oscillatory electric field is small. We observed that when ω/2π is smaller than 6 × 105 Hz, the impact of oscillatory electric field on the flow modulation, dispersion coefficient as well as band broadening is prominent. However, beyond this limit of frequency, an increase in oscillatory frequency ω reduces the impact of pertinent parameters on the flow modulation and hence the dispersion characteristics.![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) m of the solute band, standard deviation of distribution of
m of the solute band, standard deviation of distribution of ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) m, and the time dependent dispersion coefficient as well as the time-averaged effective dispersion coefficient over one oscillation period. The numerical results are presented for a wide range of pertinent parameters. Besides, benchmark analytical results within the Debye–Hückel electrostatic framework for EDL potential and EOF velocity are deduced. The numerical calculations should pave the way for novel AC electric field based EOF pumping mechanisms and therefore the band broadening process. In addition, we deduced the analytical results for the said quantities associated with the dispersion process under the Debye–Hückel limit with vanishing frequency of the AC electric field. These benchmark theoretical results are however important for validation purposes of the numerical scheme adopted in this study as well as for future applications.
m, and the time dependent dispersion coefficient as well as the time-averaged effective dispersion coefficient over one oscillation period. The numerical results are presented for a wide range of pertinent parameters. Besides, benchmark analytical results within the Debye–Hückel electrostatic framework for EDL potential and EOF velocity are deduced. The numerical calculations should pave the way for novel AC electric field based EOF pumping mechanisms and therefore the band broadening process. In addition, we deduced the analytical results for the said quantities associated with the dispersion process under the Debye–Hückel limit with vanishing frequency of the AC electric field. These benchmark theoretical results are however important for validation purposes of the numerical scheme adopted in this study as well as for future applications.






![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) (−1 +
(−1 + ![[small delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c5.gif) ) represents the scaled interfacial potential at the liquid–liquid interface ȳ = −1 +
) represents the scaled interfacial potential at the liquid–liquid interface ȳ = −1 + ![[small delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c5.gif) (i.e., at the liquid/liquid interface), and the functions h1(
(i.e., at the liquid/liquid interface), and the functions h1(![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) (−1 +
(−1 + ![[small delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c5.gif) )), h2(
)), h2(![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) (−1 +
(−1 + ![[small delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c5.gif) )) are defined by
)) are defined by
![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) (−1 +
(−1 + ![[small delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c5.gif) ) and the Donnan potential
) and the Donnan potential ![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) D are implicitly connected to each other. The implicit relationship between both of them may be deduced as follows
D are implicitly connected to each other. The implicit relationship between both of them may be deduced as follows
![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) (ȳ) ≪ 1), the linearized form of the EDL potential equation (in the scaled form) may be written as
(ȳ) ≪ 1), the linearized form of the EDL potential equation (in the scaled form) may be written as





 and κH. The model parameters are indicated in the figure caption and they are chosen in such a way that the Debye–Hückel limit for EDL potential holds good. The deduced theoretical results are shown by solid lines and numerical results are further included by dashed lines. We have detailed the methods to deduce the numerical results for velocity amplitude in the main article. We observe a close agreement in the numerical results with the analytical results deduced in this section. It is noteworthy to mention that we may have a discrepancy in the numerical results with the analytical results presented in this section. The reason is the results presented in Appendix-C is valid only for low charge limits. Thus, for the case when the system charge is moderate to high, we need to use either semi-analytical results presented in Appendix-B or the complete numerical solution for electrostatic potential and hence the velocity amplitude.
and κH. The model parameters are indicated in the figure caption and they are chosen in such a way that the Debye–Hückel limit for EDL potential holds good. The deduced theoretical results are shown by solid lines and numerical results are further included by dashed lines. We have detailed the methods to deduce the numerical results for velocity amplitude in the main article. We observe a close agreement in the numerical results with the analytical results deduced in this section. It is noteworthy to mention that we may have a discrepancy in the numerical results with the analytical results presented in this section. The reason is the results presented in Appendix-C is valid only for low charge limits. Thus, for the case when the system charge is moderate to high, we need to use either semi-analytical results presented in Appendix-B or the complete numerical solution for electrostatic potential and hence the velocity amplitude.





![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) as Keff. Thus, for ω → 0, the dispersion coefficient Keff may be deduced from (35), as follows
) as Keff. Thus, for ω → 0, the dispersion coefficient Keff may be deduced from (35), as follows





![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) m(
m(![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) u,
u, ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) may be written as
) may be written as
![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) m(
m(![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) u,
u, ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) as given below
) as given below
 (Fig. 15a) and Pe (Fig. 15b). The time evolution of cross-sectional averaged solute concentration
(Fig. 15a) and Pe (Fig. 15b). The time evolution of cross-sectional averaged solute concentration ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) m is shown in Fig. 16a. We have further shown the results for
m is shown in Fig. 16a. We have further shown the results for ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) m in Fig. 16b for various choices of Pe with fixed channel height. From all the results, it is clear that the numerical results are in close agreement in with the theoretical results deduced in this section.
m in Fig. 16b for various choices of Pe with fixed channel height. From all the results, it is clear that the numerical results are in close agreement in with the theoretical results deduced in this section.![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) c(ȳ), which indicates the scaled form of ρd(y) within the dielectric liquid layer and ρe(y) within the electrolyte medium. The results are presented for two different values of
c(ȳ), which indicates the scaled form of ρd(y) within the dielectric liquid layer and ρe(y) within the electrolyte medium. The results are presented for two different values of  (say,
(say,  and
and  ). When the permitivity ratio is far smaller than 1, say
). When the permitivity ratio is far smaller than 1, say  , the impact of the ion partitioning effect is prominent, however the ion partitioning effect is absent for
, the impact of the ion partitioning effect is prominent, however the ion partitioning effect is absent for  . Thus, for
. Thus, for  , the penetration of the counterion across the dielectric liquid layer is less and leads to a higher value of net charge density within the liquid layer. As a result the magnitude in electrostatic potential is high, which in turn leads to a large value in electric driving force that leads to fluid motion. On the other hand, for
, the penetration of the counterion across the dielectric liquid layer is less and leads to a higher value of net charge density within the liquid layer. As a result the magnitude in electrostatic potential is high, which in turn leads to a large value in electric driving force that leads to fluid motion. On the other hand, for  , the accumulation of counterions within the dielectric liquid layer is sufficiently high and leads to a significant reduction in the overall charge distribution and hence a lower magnitude in the electrostatic potential.
, the accumulation of counterions within the dielectric liquid layer is sufficiently high and leads to a significant reduction in the overall charge distribution and hence a lower magnitude in the electrostatic potential.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.




![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(
cos(

































