Spatiotemporal pattern formation of membranes induced by surface molecular binding/unbinding

Abstract

Nonequilibrium membrane pattern formation is studied using meshless membrane simulation. We consider that molecules bind to either surface of a bilayer membrane and move to the opposite leaflet by flip–flop. When binding does not modify the membrane properties and the transfer rates among the three states are cyclically symmetric, the membrane exhibits spiral-wave and homogeneous-cycling modes at high and low binding rates, respectively, as in an off-lattice cyclic Potts model. When binding changes the membrane spontaneous curvature, these spatiotemporal dynamics are coupled with microphase separation. When two symmetric membrane surfaces are in thermal equilibrium, the membrane domains form 4.8.8 tiling patterns in addition to stripe and spot patterns. In nonequilibrium conditions, moving biphasic domains and time-irreversible fluctuating patterns appear. The domains move ballistically or diffusively depending on the conditions.

---

1 Introduction

Various spatiotemporal patterns, such as traveling waves, have been observed in living cells.^1–6 Recent experiments have revealed that the oscillation of membrane shapes can be accompanied by wave propagation.^7,8 Membrane shape transformations are important processes in various functions, such as molecular transport, locomotion, and mitosis.^9–15 For example, spherical buds are formed by curvature-inducing proteins such as clathrin and coat protein complexes in vesicle transports.^{12,13,16–19} The cell division position during mitosis is determined by the standing wave of Min proteins.^7,15,20 The cell polarity of eukaryotic embryos is determined by a PAR protein pattern.^1,15,21 Other membrane shape transformations can also be regulated by chemical waves.

The thermal equilibrium states of lipid membranes have been extensively studied and are sufficiently understood. The morphology of liposomes and phase separation are well-understood based on the free energy, including bending energy.^22–28 Curvature-inducing proteins bend the bound membrane and sense the membrane curvature (i.e., concentrate on the membranes of their preferred curvatures).^29–32 The curvature dependencies of these proteins have been reproduced using mean-field theories.^33–35 The assembly of these proteins produces not only spherical buds and cylindrical membrane tubes^29,36–41 but also periodic patterns such as hexagonal⁴² and checkerboard⁴³ arrays of curved domains and beaded-necklace-like membrane tubes.⁴⁴ In contrast to membranes in equilibrium, membranes in nonequilibrium have been much less explored. The coupling of membrane deformation and reaction-diffusion dynamics has been simulated for traveling waves and Turing patterns.^8,45–49 On a flat surface, nucleation and growth can induce spatiotemporal patterns, such as the homogeneous-cycling (HC) and spiral-wave (SW) modes.^50–52 However, the effects of thermal fluctuations on the spatiotemporal patterns of deformable membranes have not been investigated.

This study aims to clarify the spatiotemporal patterns of membranes caused by active phase separation with nucleation and growth. We consider the binding/unbinding of molecules to/from both membrane surfaces. In our previous study,⁴³ we found stripe, checkerboard, and kagome-lattice patterns in thermal equilibrium. In this study, we examined dynamic patterns in nonequilibrium conditions. Nonequilibrium conditions can be generated by the differences in binding chemical potentials with the two surfaces and active flip or flop by proteins (flippase or floppase, respectively). We observed various patterns, such as spiral waves, moving biphasic domains, and time-irreversible fluctuations.

The simulation model and method are described in Section 2. The results are presented and discussed in Section 3. The binding/unbinding of molecules with zero and finite spontaneous curvatures are described in Sections 3.1 and 3.2, respectively. Finally, a summary is presented in Section 4.

2 Simulation model and method

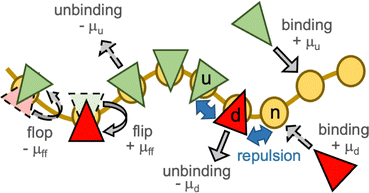
In a meshless membrane model, membrane particles self-assemble into a one-layer sheet in a fluid phase.^53–56 Proteins or surfactant molecules bind to and unbind from the membrane. Here, each membrane particle is a binding site and has three states: unbound membrane (bare, denoted by “n”), bound to the upper surface of the membrane (denoted by “u”), bound to the lower surface of the membrane (denoted by “d”), as shown in Fig. 1. We call these membrane particles unbound and bound particles, respectively. The particle diameter σ is considered to be the size of a binding site, so that it is varied from σ = 5 to 100 nm depending on binding molecules. The molecules bind to the upper and lower membrane surfaces with binding chemical potentials μ_u and μ_d, respectively. The chemical potential for the molecular flip from the upper to the lower surface is μ_ff, while that for flop from the lower to the upper surface is −μ_ff. In thermal equilibrium, μ_d = μ_u + μ_ff. The different binding chemical potentials (μ_u ≠ μ_d) can be generated by the concentration difference between the upper and the lower solutions. Flip–flop is considered to occur spontaneously or actively via an enzyme through ATP hydrolysis.

Fig. 1 Schematic of the binding and unbinding of curvature-inducing molecules (proteins or surfactants) that have a zero or finite spontaneous curvature. The brown curve and yellow circles represent membrane and membrane binding sites, respectively. The molecules (green and red triangles) bind to the membrane from the upper and lower solutions with binding chemical potentials μ_u and μ_d, respectively. The molecules also move between the upper and lower membrane surfaces with the flip–flop chemical potential μ_ff. The three states of the membrane are represented by “n” (unbound), “u” (bound to the upper surface), and “d” (bound to the lower surface). The solid and dashed gray arrows represent the dominant and secondary processes, respectively, in the nonequilibrium simulations.

The position and orientational vectors of the i-th particle are r_i and u_i, respectively. The membrane particles interact with each other via a potential U = U_rep + U_att + U_bend + U_tilt + U_pp. The potential U_rep is an excluded volume interaction with diameter σ for all pairs of particles. The solvent is implicitly accounted for by an effective attractive potential as follows:

where , ρ* is the characteristic density with ρ* = 7, ε_att = 8 and k_BT is the thermal energy, as in our previous studies.^42,43f_cut(r) is a C^∞ cutoff function⁵⁴ and r_i,j = |r_i,j|, with r_i,j = r_i − r_j:where Θ(x) is the unit step function, n = 6, b = ln(2){(r_cut/r_att)ⁿ − 1}, r_att = 1.9σ, and r_cut = 2.4σ. The bending and tilt potentials are given bywhere r̂_i,j = r_i,j/r_i,j and w_cv(r_i,j) is a weight function. The spontaneous curvature is given by C₀ = C_bd/2σ.⁵⁵

The repulsive interactions of different states (u, d, and n) are represented by

where b₀ = r_cut/(r_cut − σ).⁵⁷ At r_ij = σ, the potential height is ε_p,sisjk_BT, where s_i,s_j ∈ {u, d, n}. In our previous study,⁴³ we used this repulsive interaction only between the bound particles (u and d). In this study, we applied it for all three pairs (u–d, u–n, and d–n) to induce phase separation between all types of domain pairs.

The position r_i and orientation u_i of membrane particles are updated by underdamped Langevin equations, which are integrated by the leapfrog algorithm^58,59 with Δt = 0.002τ. The time unit is τ = σ²/D₀, where D₀ is the diffusion coefficient of the free membrane particles. Two types of states [binding/unbinding (u vs. n and d vs. n) and flip–flop (u vs. d)] are stochastically switched by a Metropolis Monte Carlo (MC) procedure with the acceptance rate p_acpt:

where the + and − signs refer to the forward and backward processes, respectively. Here, ΔH = ΔU − μ_α where ΔU is the energy difference between the two states and μ_α is the chemical potential of each process (α ∈ {u, d, ff}). Thermal equilibrium states do not depend on the frequencies of these MC processes. Conversely, in nonequilibrium, the dynamics can be varied by these frequencies. For binding/unbinding and flip–flop, Γ_bind and Γ_flip MC trials are performed, respectively, per particle at every MC step of τ_MC = 0.01τ.

A membrane consisting of 25 600 membrane particles is simulated under periodic boundary conditions. The NγT ensemble is used, where N is the total number of particles and γ is the surface tension, so that the projected area of the square membrane thermally fluctuates and can be varied by the membrane deformation.^60,61 Unless otherwise specified, we use a tension of γ = 0.5 k_BT/σ², which is sufficiently large to prevent the budding of a bound domain.^42,43 This tension corresponds to an average tension ≈0.02 mN m⁻¹, which is well below the usual lysis tension (1–25 mN m⁻¹),^62–64 (σ ≈ 10 nm and k_BT ≈ 4 × 10⁻²¹ J). For the unbound particles, C₀ = 0 and k_bend = k_tilt = 10 (corresponding bending rigidity κ_n/k_BT = 16.1 ± 1) are used. The saddle-splay modulus [small kappa, Greek, macron] is proportional to κ, as [small kappa, Greek, macron]/κ = −0.9 ± 0.1.⁶⁵ These are typical values for lipid membranes.^66–68

For the bound states, we examined two types of conditions: (1) no or slight changes of the membrane properties with a zero spontaneous curvature and (2) generation of a finite spontaneous curvature. In the first case, cyclically symmetric and quasi-symmetric conditions are considered. The bound particles have no spontaneous curvature (C₀ = 0) and identical or slightly high bending rigidities, κ_p. We use κ_p/κ_n = 1–1.6 (k_bend = k_tilt = 10–15), since the bending rigidity linearly depends on k_bend = k_tilt as κ_p/k_BT = 1.83 k_bend − 2.2.⁵⁵ The other parameters are symmetrically set as μ_u = −μ_d = μ_ff = μ and ε_p,αβ = 3 for α,β ∈ {u, d, n}, and the MC rates are Γ_bind = Γ_flip = Γ_MC. We use Γ_MC = 0.5 unless otherwise specified. This model is an off-lattice version of the three-state cyclic Potts model.^50,51 Here, the particles (flipping sites) laterally diffuse, and their heights vertically fluctuate, unlike those in the lattice Potts models. Note that this cyclic condition can be alternatively realized by the binding only on one leaflet of the bilayer and chemical reaction instead of the flip–flop.⁵⁰

In the second case, the binding of curvature-inducing molecules (proteins or surfactants) is considered. The molecule bound to the upper and lower surfaces induces positive and negative spontaneous curvatures of C₀σ = ±0.1, respectively, and their bending rigidities are high as κ_u/k_BT = κ_d/k_BT = 144 ± 7 (k_bend = k_tilt = 80). We use ε_p,ud = 3, ε_p,un = ε_p,dn = 2, Γ_bind = 1, and Γ_flip = 0.01. This parameter set is identical to that in our previous study,⁴³ except for the repulsion strength (ε_p,un = ε_p,dn = 0 in ref. 43) for bound and unbound particles. In ref. 43, we obtained only steady spatial patterns in nonequilibrium. A sufficiently large repulsion to form three types of domains is key to obtaining spatiotemporal patterns. The equilibrium membrane behaviors of membranes without molecular binding, with binding to the upper surface, and binding to both surfaces are described in ref. 42, 43 and 55, respectively.

The mean cluster sizes are calculated to characterize various phases. Two membrane particles of each state are considered to belong to the same cluster when the inter-particle distance is less than r_att. The mean size of the clusters is given by , where n_i^s,cl is the number of clusters of size i_s,cl and N_s is the total number of each state (s ∈ {u, d, n}). The mean cluster size of each state is normalized by the mean total number as χ_s = 〈N_s,cl〉/〈N_s〉. A large percolated cluster results in χ ≃ 1. The vertical span of the membrane is calculated from the membrane height variance as , where . The statistical errors are calculated from three or more independent runs.

3 Simulation results

3.1 Membrane with zero-spontaneous-curvature

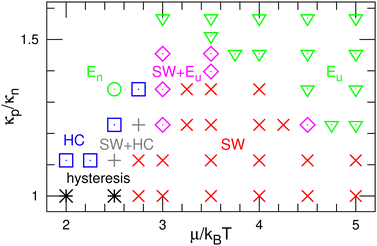
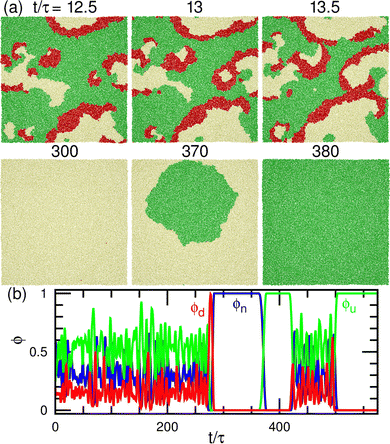
First, we describe the pattern formation of membranes with a zero spontaneous curvature. The cyclic dynamics reported in the square-lattice Potts model^50,51 are also obtained in this off-lattice model (see Fig. 2–5). Three dynamic modes (SW, HC, and steady one-phase mode (E_s)) and their temporal coexistence are obtained (see the phase diagram shown in Fig. 2). The temporal coexistence of SW and HC (SW + HC) is shown in Fig. 3, where “+” represents the temporal coexistence. In SW mode, the boundary of the u and d phases (or the d and n and the n and u phases) moves in the direction of the u phase (or d and n phases,  respectively), and the contact point of the three phases becomes the center of a spiral wave (see the upper three snapshots in Fig. 3(a) and Movie S1, ESI†). In HC mode, the membrane is dominantly occupied by one of the three phases for most of the period, and the dominant phases change cyclically as s = n → u → d → n. These phase changes are caused by nucleation and growth, as shown in the lower three snapshots in Fig. 3(a).

Fig. 2 Phase diagram of the binding molecules of zero spontaneous curvatures (C₀ = 0). The (green) down-pointing triangles and circles represent the homogeneous phases of the upper-bound (E_u) and unbound (E_n) states, respectively. The (red) crosses and (blue) squares represent the spiral-wave (SW) and homogeneous-cycling (HC) modes, respectively. The (magenta) diamonds or (gray) pluses represent the temporal coexistence of SW and E_u or HC, respectively. The (black) asterisks represent the hysteresis of SW and HC, in which either mode appears depending on the initial state.

Fig. 3 Temporal coexistence of the spiral-wave and homogeneous-cycling modes (SW + HC) for the binding molecules of zero spontaneous curvatures (C₀ = 0) at μ/k_BT = 2.75 and κ_p/κ_n = 1.23. (a) Sequential snapshots. Green (medium gray) and red (dark gray) spheres represent the upper and lower bound particles (u and d), respectively. Yellow (light gray) spheres represent unbound membrane particles (n). The upper and lower snapshots show the spiral-wave and homogeneous-cycling modes, respectively. (b) Time evolution of the densities of the three states.

Fig. 4 Temporal coexistence of spiral waves and homogeneous phases (SW + E_u) for the binding molecules of zero spontaneous curvatures (C₀ = 0) at μ/k_BT = 3.5 and κ_p/κ_n = 1.45. (a) Sequential snapshots. The first two snapshots show the spiral waves. (b) Time evolution of the densities of the three states.

Fig. 5 Dependence on μ and κ_p/κ_n for the binding molecules of zero spontaneous curvatures (C₀ = 0). (a) and (b) κ_p/κ_n = 1.23. (c) μ/k_BT = 3.5. (a) and (c) Mean densities 〈ϕ〉 of the three states. (b) Probabilities p_phase of a three-phase coexistence (ϕ_u > 0.05, ϕ_d > 0.05, and ϕ_n > 0.05) and one phase (ϕ_s > 0.95 with s ∈ {u, d, n}). The solid and dashed lines represent the data at Γ_MC = 0.5 and 0.005, respectively. The dynamic modes at Γ_MC = 0.5 are shown by the bidirectional arrows at the tops of (a) and (c).

The mean densities 〈ϕ〉 of the three states are identical (=1/3) in the symmetric condition (κ_p/κ_n = 1). At low μ, either the HC or SW mode appears depending on the initial state owing to hysteresis; the SW mode only appears at high μ (see the bottom of Fig. 2). This phenomenon corresponds to the discontinuous transition obtained in large systems (N > 37 000) of the lattice Potts model.⁵⁰ We also confirmed that this transition occurs in tensionless membranes (γ = 0).

As κ_p increases, 〈ϕ_u〉 increases. Subsequently, the u domain covers the whole membrane (E_u mode) (see Fig. 4 and 5(c), and Movie S2, ESI†). This E_s mode is similar to a homogeneous phase in thermal equilibrium. This change is caused by the mechanism reported for the lattice Potts model.⁵¹ At high κ_p, the unbinding is promoted since the unbound membrane has a larger undulation than the bound membrane (i.e, the unbinding gains an entropy). Hence, the duration of the d-dominant phase is reduced. This enhancement of the unbinding also suppresses the nucleation of d domains in the u-dominant phase, since small d domains disappear through the two-step process of d → n → u.⁵¹ Consequently, the duration of the E_u mode increases. When the MC rates of binding/unbinding/flip–flop are reduced to Γ_MC = 0.005, the effects of κ_p are weakened, since the membrane can relax to the preferred projected area for the local bending rigidity (compare the dashed and solid lines in Fig. 5(c)).

The modes are determined according to the manner used in ref. 50 and 51 as follows. When the probability of three-phase coexistence (〈ϕ_u〉 > 0.05, 〈ϕ_d〉 > 0.05, and 〈ϕ_n〉 > 0.05) is greater than 0.05, the SW mode exists (see the blue lines with circles in Fig. 5(b)). When that of the one-phase state (〈ϕ_s〉 > 0.95 with s ∈ {u, d, n}) is greater than 0.05, the HC or E_s mode exists. In the HC mode, all three states have a peak at ϕ_s ≈ 1. In the E_s mode, the s state has the highest peak at ϕ_s ≈ 1, and at least one of the other states does not have this peak. In the upper-right region of the phase diagram (Fig. 2), the E_u mode is formed. At κ_p/κ_n = 1.23, the mode changes from HC to SW and E_u with increasing μ through the coexistence of modes (SW + HC and SW + E_u), as shown in Fig. 5. Hence, the discontinuous transition between the SW and HC modes becomes continuous at κ_p/κ_n ≃ 1.2.

Here, the SW mode is obtained only at κ_p/κ_n < 1.5 while keeping the other properties. Therefore, a spiral wave spreading over a large membrane area is difficult to obtain when the binding largely modifies the membrane properties and/or strong interactions between the bound molecules. However, biphasic domains (Fig. 4(a)) can migrate under the conditions described in Section 3.2.2.

3.2 Binding/unbinding of curvature-inducing molecules

3.2.1 Equilibrium phases. Before discussing nonequilibrium dynamics, we briefly describe the phase behaviors under up–down symmetrical conditions in thermal equilibrium (μ_u = μ_d and μ_ff = 0) for curvature-inducing molecules of C₀σ = ±0.1. The molecules bind to the upper and lower surfaces with the same amount, as shown in Fig. 6(a) and (b). As the binding chemical potentials (μ_u = μ_d) increase, the densities of the molecules (ϕ_u = ϕ_d) increase, and eventually, the membrane is almost completely covered by the molecules (〈ϕ_u〉 = 〈ϕ_d〉 ≈ 0.5). Thus, the membrane forms a stripe of the u and d domains at μ_u/k_BT ≥ 8 (see the right snapshot in Fig. 6(a)), in which most bound u (d) particles belong to the largest u (d) domain, that is, χ_u = χ_d ≃ 1 (see Fig. 6(c)).

Fig. 6 Equilibrium states for the binding molecules of finite curvatures (C₀σ = ±0.1) in up–down symmetrical conditions (μ_u = μ_d and μ_ff = 0) (a) Snapshots. From left to right, an unbound membrane at μ_u/k_BT = 6, 4.8.8-tiling domains at μ_u/k_BT = 6, and stripe domains at μ_u/k_BT = 9. (b) Mean densities of bound molecules 〈ϕ_u〉 = 〈ϕ_d〉 and the unbound membrane 〈ϕ_n〉. (c) Mean cluster sizes normalized by the total number of each type of particle: for the u state, χ_u = 〈N_u,cl〉/〈N_u〉; for the n state (unbound), χ_n = 〈N_n,cl〉/〈N_n〉. (d) Membrane vertical span z_mb. The transition between the unbound and 4.8.8-tiling phases is first order, and two phases coexist as (meta-)stable states around the transition point.

At medium strengths of the binding potential (5.3 ≤ μ_u/k_BT ≤ 8), the u and d domains form a square lattice, and the vertices are stabilized by the n domains (see the middle snapshot in Fig. 6(a)). Owing to the symmetry, an even number of these bound domains surround the vertex. Since we added repulsion between the bound and unbound domains, the n domains at the vertices are larger than those in our previous study.⁴³ Thus, the bound (u and d) domains are shaped as octagons and the n domain is shaped as a square. When the bound domains form a regular octagon, this domain pattern corresponds to the semi-regular tessellation 4.8.8, which consists of regular octagons and squares; this pattern is one of eight tilings to cover a flat plane by two or more regular polygons. Hence, we call this state 4.8.8 tiling. Since the u and d domains bend in the positive and negative directions, respectively, the bound membrane exhibits a bumped stripe or spherical-cap shape (see Fig. 6(d)).

The transitions between the unbound and 4.8.8 tiling phases are discontinuous, and the metastable states exist around the transition point (see Fig. 6(b)–(d)). When the binding potential exceeds μ_u/k_BT = 8, the tiling membrane is ruptured from the boundaries of the n domains. This is due to the addition of the repulsion between the bound and unbound particles in the present study, since the discontinuous transition is obtained without rupture in the absence of this repulsion.⁴³ In asymmetric conditions (μ_u ≠ μ_d and μ_d = μ_u + μ_ff), kagome-lattice domain patterns reported in ref. 43 is also obtained in the present system.

3.2.2 Nonequilibrium patterns. Next, we consider a membrane far from equilibrium. Although this can be done in several ways, we select a high binding potential on the upper surface (μ_u/k_BT = 10), a low binding potential on the lower surface (0 ≤ μ_d/k_BT ≤ 4), and a low flip potential (0 ≤ μ_d/k_BT ≤ 2.5). Hence, the molecules bind to the upper surface but transfer to the lower surface and unbind in the lower solution (see Fig. 1). This cyclic sequence is identical to that in the flat membrane described in Section 3.1. However, they are coupled with the microphase separation described in Section 3.2.1.

The dynamic phase diagram is shown in Fig. 7. At a relatively large μ_d (i.e., a small difference between μ_d and μ_u), stable patterns are formed, similar to those reported in our previous study.⁴³ A hexagonal pattern consisting of large hexagonal d domains and the percolated hexagonal network of a u domain is formed at μ_d/k_BT ≃ 4 and μ_ff/k_BT ≃ 2, as shown in Fig. 7(c). Hence, the d domains have a large area fraction 〈ϕ_d〉 ≃ 0.8, the normalized mean cluster size of the domain is χ_u ≈ 1, and the bumped shape causes a large vertical span z_mb (see Fig. 8(a)–(c)). At a low flip potential μ_ff ≃ 0, the 4.8.8 tiling occurs. As μ_d decreases, the membrane is ruptured, leading to vesicle formation, as shown in Fig. 7(b).

Fig. 7 Nonequilibrium phases for the binding molecules of finite curvatures (C₀σ = ±0.1) at μ_u/k_BT = 10. (a)–(e) Snapshots. (a) Partial pattern at μ_d/k_BT = 1 and μ_ff/k_BT = 2. (b) Rupture at μ_d/k_BT = 3 and μ_ff = 0. (c) Stable pattern at μ_d/k_BT = 3.5 and μ_ff/k_BT = 2. (d) Fluctuating pattern at μ_d/k_BT = 1.5 and μ_ff = 0. The time interval of the sequential snapshots is 100τ. (e) Fluctuating pattern at μ_d/k_BT = 2.7 and μ_ff/k_BT = 2. The time interval is 60τ. (f) Phase diagram. The circles, triangles, squares, crosses, and diamonds represent the unbound membranes, partial patterns, fluctuating patterns, stable patterns, and ruptures, respectively. The letters (a–e) indicate the corresponding data points of the snapshots in (a–e).

Fig. 8 Dependence on the binding chemical potential μ_d for the binding molecules of finite curvatures (C₀σ = ±0.1) at μ_u/k_BT = 10 and μ_ff/k_BT = 2. (a) Mean densities of the three states. (b) Normalized mean cluster sizes χ_u, χ_d, and χ_n. (c) Membrane vertical span z_mb. (d) Flow rate q_f of the binding molecules from the upper to the lower solution. The dynamic modes are indicated by the bidirectional arrows at the top of the figure.

At a slightly lower μ_d than that in the stable-pattern region, it is found that the domain patterns exhibit time-irreversible fluctuations (called fluctuating patterns). At μ_d/k_BT = 1.5 and μ_ff = 0, the u and n domains form a hexagonal pattern, but a small d domain moves through a u domain, accompanied by a narrow n domain behind it (see Fig. 7(d) and Movie S3, ESI†). The backward process is negligible owing to the cyclic relation of the chemical potentials. This time-irreversible motion of d domains generates frequent changes in local patterns. At μ_d/k_BT ≃ 3 and μ_ff/k_BT = 2, an n domain appears inside of a d domain and spreads, but the resultant large n domain is rapidly replaced by u and d domains (see Fig. 7(e) and Movie S4, ESI†). In both cases, the domain-spreading process obtained in the flat membrane (Section 3.1) occurs only locally in the separated space owing to the microphase separation. Hence, the wave propagation is restricted to the inside of the domains but frequently modifies the local domain patterns. In the fluctuating patterns, the percolation of network domains is often broken so that the membranes have low values of χ_u (see Fig. 8(b) and 9(b)). In the pattern fluctuations, the domain size largely fluctuates (see Fig. 7(d)), and at μ_d/k_BT = 1 and μ_ff = 0 the formation of large spherical buds results in membrane rupture (the diamond at the bottom left in Fig. 7(f)).

Fig. 9 Dependence on the flip chemical potential μ_ff for the binding molecules of finite curvatures (C₀σ = ±0.1) at μ_u/k_BT = 10 and μ_d/k_BT = 2. (a) Mean densities of the three states. (b) Normalized mean cluster sizes χ_u, χ_d, and χ_n. (c) Membrane vertical span z_mb. (d) Flow rate q_f of the binding molecules from the upper to the lower solution. The dynamic modes are indicated by the bidirectional arrows at the top of the figure.

As μ_d further decreases at μ_ff/k_BT = 2, most of the membrane area is unbound, and isolated biphasic (u and d) domains appear (see Fig. 7(a) and 10(a) and Movies S5 and S6, ESI†). We distinguish whether the membrane is unbound or partially forms domains (called partial pattern) by the area fraction of the unbound state: unbound membranes at 〈ϕ_n〉 > 0.95 and partial patterns at 〈ϕ_n〉 ≤0.95 (see Fig. 8(a) and 9(a)). Biphasic domains are occasionally formed in the unbound membranes, whereas they appear most of the time in the partial patterns. The molecular transfer from the upper to the lower solution occurs more frequently in the partial and fluctuating patterns (see Fig. 8(d) and 9(d)).

Fig. 10 Motion of the biphasic domains of finite curvatures (C₀σ = ±0.1) at μ_u/k_BT = 10 and μ_ff/k_BT = 2. (a) Sequential snapshots with an interval of 20τ at μ_d/k_BT = 2.3. (b) Mean squared distance 〈r(t)²〉 of the center of domain u at μ_d/k_BT = 1, 1.5, 2, and 2.4. The two black straight lines represent exponents α = 1 and 2.

Last, we analyze the motion of the biphasic domains in the regions of the unbound membrane and partial pattern. The domain consisting of two (u and d) domains with equal size moves ballistically in the direction of the u  domain, as shown in Fig. 10(a) and Movie S5 (ESI†). Conversely, when the d domains are much smaller than the u domain, the domain moves diffusively (see Fig. 7(a) and Movie S6, ESI†). This is due to frequent changes in the positions of the d domains. These moving biphasic domains have a narrower size distribution than those in the flat membrane (see Fig. 11) and thus, have sufficiently long lifetimes for quantitative analysis.

Fig. 11 Size distribution of the u and d domains for μ_d/k_BT = 1, 2, and 2.4 at μ_u/k_BT = 10 and μ_ff/k_BT = 2 (corresponding to the data shown in Fig. 10). The d domains become larger with increasing μ_d.

Fig. 10(b) shows the mean squared displacement 〈r(t)²〉 of the domain center for a u domain of cluster size i_u,cl > 50. The displacement of each cluster is calculated every 2τ if both differences of the displacement and cluster size from those of the previous step are small (Δr² < (5σ)² and Δi_u,cl < 50) in order to exclude coalesced and divided clusters. Ballistic and diffusive motions exhibit 〈r²〉 ∝ t^α with exponents of α = 2 and 1, respectively. For μ_d/k_BT ≥ 2, α = 2 is obtained, i.e., it is ballistic. The biphasic domain has a maximum velocity when it consists of u and d domains with equal size at μ_d/k_BT = 2 (see Fig. 10(b) and 11). For μ_d/k_BT = 1.5, the exponent changes from α = 2 to 1 at t/τ ≃ 30, such that the ballistic domain motion becomes diffusive. For μ_d/k_BT = 1, α ∼ 1 even at t/τ < 30. The division and disappearance of d domains connecting the u domain change the moving direction so that the motion becomes diffusive. A low exponent α < 1 at t/τ ≃ 100 for μ_d/k_BT = 1 may suggest that fast-moving domains coalesce or divide earlier than slow-moving domains. The number of remaining domains decreases exponentially over time.

4 Summary

We have studied the spatiotemporal patterns of membranes with three states. When the three states are identical but separate from each other, the membrane exhibits spiral waves of domains of three states at the cyclic flipping condition as an off-lattice cyclic Potts model. At low flipping energies, the cycling of three homogeneous phases also occurs depending on the initial state. When the bending rigidities of the three states are different, the temporal coexistence of these two modes and the non-cyclic one-phase mode also appear, since the membrane undulation modifies the stability of the states.

Next, we considered that molecules (e.g., surfactants and proteins) with positive spontaneous curvatures bind to and unbind from two surfaces of the membranes and move between the two surfaces by flip–flop. In thermal equilibrium conditions, strip and 4.8.8 tiling patterns are formed. In nonequilibrium conditions, the hexagonal patterns exhibit time-irreversible fluctuations in which small domains move ballistically in the large domains of other states, and the domain patterns largely fluctuate. Moreover, biphasic domains move ballistically or diffusively depending on the conditions. These moving biphasic domains have a narrow size distribution and longer lifetime than those in the flat membrane.

In the present system, a nonequilibrium condition can be generated by the difference in chemical potential between the upper and lower solutions. Since the chemical potential can be varied by the concentration (Δμ = Δρk_BT in dilute solutions), it is easily set up in experiments. Experimentally, Miele and co-workers reported the shape transitions of the vesicles induced by the binding, unbinding, and flip–flop of surfactant molecules from the outer to the inner solutions.^69,70 Although the membrane is homogeneous in their experiments, phase separation can be induced by using two types of surfactants, in which the hydrophobic segments consist of alkyl or fluoroalkyl chains because these chains can exhibit phase separation.^71,72 Thus, the dynamic patterns obtained in the present study can be experimentally examined.

Data availability

Data for this article, including simulation data are available at ISSP Data Repository (ISSP-DR) at https://isspns-gitlab.issp.u-tokyo.ac.jp/hiroshi.noguchi/memb_pattern_2bind.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Jean-Baptiste Fournier for stimulating discussion. This work was supported by JSPS KAKENHI Grant Number JP24K06973.

Notes and references

1. A. Merino-Salomóna, L. Babla and P. Schwille, Curr. Opin. Cell Biol., 2021, 72, 106–115.
2. M. Wu and J. Liu, Curr. Opin. Cell Biol., 2021, 68, 45–54.
3. C. Beta, L. Edelstein-Keshet, N. Gov and A. Yochelis, eLife, 2023, 12, e87181.
4. H. Noguchi, ChemSystemsChem, 2024 DOI:10.1002/syst.202400042.
5. D. Taniguchi, S. Ishihara, T. Oonuki, M. Honda-Kitahara, K. Kaneko and S. Sawai, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 5016–5021.
6. M. L. Verge-Serandour and K. Alim, Annu. Rev. Condens. Matter Phys., 2024, 15, 263–289.
7. T. Litschel, B. Ramm, R. Maas, M. Heymann and P. Schwille, Angew. Chem., 2018, 57, 16286–16290.
8. Z. Wu, M. Su, C. Tong, M. Wu and J. Liu, Nat. Commun., 2018, 9, 136.
9. H. T. McMahon and J. L. Gallop, Nature, 2005, 438, 590–596.
10. J. Zimmerberg and M. M. Kozlov, Nat. Rev. Mol. Cell Biol., 2006, 7, 9–19.
11. S. Suetsugu, S. Kurisu and T. Takenawa, Physiol. Rev., 2014, 94, 1219–1248.
12. M. Kaksonen and A. Roux, Nat. Rev. Mol. Cell Biol., 2018, 19, 313–326.
13. J. Béthune and F. T. Wieland, Annu. Rev. Biophys., 2018, 47, 63–83.
14. T. Svitkina, Cold Spring Harbor Perspect. Biol., 2018, 10, a018267.
15. J. Lutkenhaus, Trends Microbiol., 2012, 20, 411–418.
16. L. Johannes, R. G. Parton, P. Bassereau and S. Mayor, Nat. Rev. Mol. Cell Biol., 2015, 16, 311–321.
17. F. Brandizzi and C. Barlowe, Nat. Rev. Mol. Cell Biol., 2013, 14, 382–392.
18. J. H. Hurley, E. Boura, L.-A. Carlson and B. Różycki, Cell, 2010, 143, 875–887.
19. H. T. McMahon and E. Boucrot, Nat. Rev. Mol. Cell Biol., 2011, 12, 517–533.
20. S. Takada, N. Yoshinaga, N. Doi and K. Fujiwara, Sci. Adv., 2022, 8, eabm8460.
21. C. Hoege and A. A. Hyman, Nat. Rev. Mol. Cell Biol., 2013, 14, 315–322.
22. Structure and Dynamics of Membranes, ed. R. Lipowsky and E. Sackmann, Elsevier Science, Amsterdam, 1995.
23. U. Seifert, Adv. Phys., 1997, 46, 13–137.
24. S. Svetina and B. Žekš, Adv. Colloid Interface Sci., 2014, 208, 189–196.
25. A. R. Honnerkamp-Smith, S. L. Veatch and S. L. Keller, Biochim. Biophys. Acta, Biomembr., 2009, 1788, 53–63.
26. T. Baumgart, S. T. Hess and W. W. Webb, Nature, 2003, 425, 821–824.
27. S. Veatch and S. L. Keller, Biophys. J., 2003, 85, 3074–3083.
28. M. Yanagisawa, M. Imai and T. Taniguchi, Phys. Rev. Lett., 2008, 100, 148102.
29. T. Baumgart, B. R. Capraro, C. Zhu and S. L. Das, Annu. Rev. Phys. Chem., 2011, 62, 483–506.
30. C. Has and S. L. Das, Biochim. Biophys. Acta, Gen. Subj., 2021, 1865, 129971.
31. C. Prévost, H. Zhao, J. Manzi, E. Lemichez, P. Lappalainen, A. Callan-Jones and P. Bassereau, Nat. Commun., 2015, 6, 8529.
32. F.-C. Tsai, M. Simunovic, B. Sorre, A. Bertin, J. Manzi, A. Callan-Jones and P. Bassereau, Soft Matter, 2021, 17, 4254–4265.
33. H. Noguchi, Int. J. Mod. Phys. B, 2022, 36, 2230002.
34. H. Noguchi, N. Walani and M. Arroyo, Soft Matter, 2023, 19, 5300–5310.
35. H. Noguchi, Phys. Rev. E, 2024, 109, 024403.
36. C. Mim and V. M. Unger, Trends Biochem. Sci., 2012, 37, 526–533.
37. A. Frost, R. Perera, A. Roux, K. Spasov, O. Destaing, E. H. Egelman, P. De Camilli and V. M. Unger, Cell, 2008, 132, 807–817.
38. J. Adam, N. Basnet and N. Mizuno, Sci. Rep., 2015, 5, 15452.
39. N. Ramakrishnan, R. P. Bradley, R. W. Tourdot and R. Radhakrishnan, J. Phys.: Condens. Matter, 2018, 30, 273001.
40. H. Noguchi, Sci. Rep., 2016, 6, 20935.
41. H. Noguchi, J. Chem. Phys., 2022, 157, 034901.
42. Q. Goutaland, F. van Wijland, J.-B. Fournier and H. Noguchi, Soft Matter, 2021, 17, 5560–5573.
43. H. Noguchi, Soft Matter, 2023, 19, 679–688.
44. H. Noguchi, Soft Matter, 2021, 17, 10469–10478.
45. B. Peleg, A. Disanza, G. Scita and N. Gov, PLoS One, 2011, 6, e18635.
46. N. Tamemoto and H. Noguchi, Sci. Rep., 2020, 10, 19582.
47. N. Tamemoto and H. Noguchi, Soft Matter, 2021, 17, 6589–6596.
48. N. Tamemoto and H. Noguchi, Phys. Rev. E, 2022, 106, 024403.
49. H. Noguchi, Sci. Rep., 2023, 13, 6207.
50. H. Noguchi, F. van Wijland and J.-B. Fournier, J. Chem. Phys., 2024, 161, 025101.
51. H. Noguchi and J.-B. Fournier, New J. Phys., 2024, 26, 093043.
52. H. Noguchi, Sci. Rep., 2025, 15, 674.
53. H. Noguchi, J. Phys. Soc. Jpn., 2009, 78, 041007.
54. H. Noguchi and G. Gompper, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 021903.
55. H. Shiba and H. Noguchi, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 031926.
56. H. Noguchi, Soft Matter, 2019, 15, 8741–8748.
57. H. Noguchi, Soft Matter, 2012, 8, 8926–8935.
58. M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Clarendon Press, Oxford, 1987.
59. H. Noguchi, J. Chem. Phys., 2011, 134, 055101.
60. S. E. Feller, Y. Zhang, R. W. Pastor and B. R. Brooks, J. Chem. Phys., 1995, 103, 4613–4621.
61. H. Noguchi, Soft Matter, 2012, 8, 3146–3153.
62. E. A. Evans and F. Ludwig, J. Phys.: Condens. Matter, 2000, 12, A315–A320.
63. E. A. Evans, V. Heinrich, F. Ludwig and W. Rawicz, Biophys. J., 2003, 85, 2342–2350.
64. H. V. Ly and M. L. Longo, Biophys. J., 2004, 87, 1013–1033.
65. H. Noguchi, J. Chem. Phys., 2019, 151, 094903.
66. M. A. S. Karal, M. M. Billah, M. Ahmed and M. K. Ahamed, Soft Matter, 2023, 19, 8285–8304.
67. R. Dimova, Adv. Colloid Interface Sci., 2014, 208, 225–234.
68. M. Hu, J. J. Briguglio and M. Deserno, Biophys. J., 2012, 102, 1403–1410.
69. Y. Miele, Z. Medveczky, G. Holló, B. Tegze, I. Derényi, Z. Hórvölgyi, E. Altamura, I. Lagzi and F. Rossi, Chem. Sci., 2020, 11, 3228–3235.
70. G. Holló, Y. Miele, F. Rossi and I. Lagzi, Phys. Chem. Chem. Phys., 2021, 23, 4262–4270.
71. Q. Xiao, J. D. Rubien, Z. Wang, E. H. Reed, D. A. Hammer, D. Sahoo, P. A. Heiney, S. S. Yadavalli, M. Goulian, S. E. Wilner, T. Baumgart, S. A. Vinogradov, M. L. Klein and V. Percec, J. Am. Chem. Soc., 2016, 138, 12655–12663.
72. R. Wakabayashi, R. Imatani, M. Katsuya, Y. Higuchi, H. Noguchi, N. Kamiya and M. Goto, Chem. Commun., 2022, 58, 585–588.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm01277a

---