DOI:
10.1039/D4SM00839A
(Paper)
Soft Matter, 2025,
21, 670-686
Multiscale modelling of active hydrogel elasticity driven by living polymers: softening by bacterial motor protein FtsZ†
Received
10th July 2024
, Accepted 24th December 2024
First published on 27th December 2024
Abstract
We present a neo-Hookean elasticity theory for hybrid mechano-active hydrogels, integrating motor proteins into polymer meshes to create composite materials with active softening due to modulable chain overlaps. Focusing on polyacrylamide (PA) hydrogels embedded with FtsZ, a bacterial cytokinetic protein powered by GTP, we develop a multiscale model using microscopic Flory theory of rubbery meshes through mesoscopic De Gennes’ scaling concepts for meshwork dynamics and phenomenological Landau's formalism for second-order phase transitions. Our theoretical multiscale model explains the active softening observed in hybrid FtsZ-PA hydrogels by incorporating modulable meshwork dynamics, such as overlapping functionality and reptation dynamics, into an active mean-field of unbinding interactions. The novel FtsZ-based metamaterial and companion multiscale theory offer insights for designing, predicting, and controlling complex active hydrogels, with potential applications in technology and biomedicine.
1. Introduction
Polymer hydrogels are soft, porous materials with water-filled pockets held within a crosslinked gel structure.1,2 Due to these polymer crosslinks, they maintain mechanical integrity while retaining water content. Hence, some synthetic hydrogels exhibit unusual mechanical properties akin to biological tissues.3 Indeed, swellable hydrogels hold biomedical potential for creating artificial tissues in reconstructive surgery,4–7 and in synthetic biotechnologies e.g., for controlled drug release.8 Nowadays, active gels represent a novel class of mechanically tunable polymer networks actuated by biomolecular motors.9,10 Unlike contractile filaments that constrain thermal fluctuations,11–15 living polymers with directed motion can act as extensile agents amplifying fluctuations, hence driving active swelling through matrix extensibility.16,17 Here, we propose modelling mechanically active hydrogels based on polyacrylamide (PA) with polymer-interconnected porosity that supports extensile softness (as depicted in Fig. 1).
 |
| | Fig. 1 Cellular structure of active hydrogels with living polymers embedded. On the left panel cartoon we depict the cellular microstructure of the polyacrylamide (PA) hydrogel with the aqueous shells as a reservoir for the FtsZ monomer dissolved in the physiological solvent with the essential components. On the right panel, we zoom on the shell hybrid hydrogel walls formed by chemical crosslinking and disrupted physical overlaps of the polymer PA chains under hydrolytic (GTP/GDP-driven) treadmilling motions of the living FtsZ's polymers (ZLPs). In crowded aqueous environments, such as polymer hydrogel meshes, small ZLP protofilaments (100–200 nm long) polymerize in the presence of GTP above a critical concentration (ccrit ≈ 0.1 mg mL−1). Evidence shows that monomer exchange, annealing, and depolymerization create spatiotemporally randomized activity in mechanically isotropic media.18–22 Due to their small size (L ≈ 100–200 nm), FtsZ protofilaments diffuse more quickly within solvent-filled interstices than their treadmilling motion allows for directed propulsion across the mesh. Typical FtsZ dynamic parameters: treadmilling speed (v ≈ 0.03 μm s−1);21 protofilament diffusivity (D ≈ 10−2 μm2 s−1);23 globular protein diffusivity (D0 ≈ 1 μm2 s−1);23 Peclet number Pe = vL/D ≪ 1, giving dimensionless ratio between advective and diffusive transport rates.24 | |
These active hydrogels are designed as cellular structures with solid shell walls being mechanically active as driving by living polymers (Fig. 1; left panel). They are composed of passively crosslinked PA chains with an active elasticity driven by the “Filamentous temperature-sensitive mutant Z” (FtsZ), the motor protein responsible for cytokinesis in bacteria.25 Living FtsZ polymers (ZLPs) exert out-of-equilibrium remodelling to cause processive treadmilling motion under GTP-hydrolysis.18–20 Backed on experimental evidence,18–21 treadmilling involves the continuous addition of FtsZ monomers at one end of flexible protofilaments and their simultaneous dissociation at the opposite end,22 leading to momentum fluctuations randomized in an isotropic milieu (Fig. 1; right panel). Specifically, we model active mesoporous hydrogels composed of hybrid PA–FtsZ meshes considered isotropic, combining covalent crosslinks with physical entanglements formed by ZLP actuators undergoing treadmilling in the polymer meshwork at the shell edges. More active binding overlaps in the meshwork are expected to cause greater level of active softening at the mesoscale.3 Hence, we focus on the steady-state mechanics of active PA–FtsZ gels considered structurally isotropic, where GTP-powered ZLP actuators soften deformability and enhance fluidity. Furthermore, enhanced cell connectivity and a high porosity within the PA matrix should actively participate to augment swelling and permeability.26 Likewise, active PA–FtsZ hydrogels should adapt to tuneable mechanical changes, making them ideal for technological and biomedical applications. To understand their biomechanical properties under stationary swelling-elastic forces tradeoff, we need to quantify force balances in non-equilibrium steady states and their adaptive response to stationary stimuli, leading to mechanical pseudo-equilibrium. Using a quasi-static approach, we present a constrained mixing theory,27 which balances meshwork elasticity with polymer–solvent interactions to model mechanical remodeling in active matter under stationary deformation conditions.17,24
In this work, we propose the mechanical stresses induced by treadmilling ZLP activity driving directed movements within the crosslinked PA-meshwork, whether living FtsZ protofilaments are constrainedly embedded in the flexible cellular structure swollen by solvent under osmotic equilibrium (Fig. 1; left). As more active FtsZ motors are integrated within crosslinked PA chains, we anticipate that the hybrid ZLP–PA hydrogel would soften and become more fluid under GTP consumption, resulting in structural weakening and extensibility with increased FtsZ treadmilling (Fig. 1; right). The macroscopic rheological response is expected to reflect active De Gennes’ reptation dynamics driven by the active ZLP–PA meshwork.28–30 This active rheology is fuelled by biochemical free energy (GTP), which generates mechanical softness across meso- and microscales.31–33 The observed plasticity of the overlapping polymers present at the shell edges aligns with active reptation theory.34,35 Moreover, the active softening gradually observed can be viewed as a structural weakening transition within the framework of mean-field Landau's theory of order–disorder phase transitions.36 The Landau's free energy functional is defined by an order parameter linked to the concentration of active ZLP elements, driving phase separation into two opposing states: (a) active treadmilling chains that induce mesh softening and osmotic swelling under unbinding disentanglement, and (b) passive crosslinking interactions that lead to hardening and osmotic shrinking. Our multiscale theory describes the coexistence of two metastable states in the swollen mesh: the one actively weakened by treadmilling motions, and the other strengthened by passive filaments filling the mesh with additional chain overlapping. These antagonist states dynamically exchange through mechanical balance with the active chemo-elasticity of the polymer matrix.17 A quasi-static approach to model the steady mechanical response is justified by the predominantly random treadmilling activity of FtsZ protofilaments, where random diffusivity exceeds their slow directed propulsion.21,23 Hence, the active hydrogel dynamics are modeled within a quasi-static generalized framework of constrained FtsZ-PA mixing,27 further modified by FtsZ-induced pseudo-equilibrium reptation,28,29 overly governed by nonlinearly balanced swelling-elasticity interactions.37 Therefore, we propose the weakening/strengthening changes caused by FtsZ polymerization through respective active ZLP treadmilling, or passive filament reinforcement, thus influencing the complex active rheology of the hybrid gels compared to their passive counterparts. We theorize on quasi-static chemoelasticity connections between molecular polymer conformations, mesoscopic mesh overlaps, and macroscopic mean-field interactions leading to effective elasticity. The multiscale model of active elasticity is validated with experimental rheological data from hybrid PA–ZLP hydrogels with varying FtsZ concentrations in the passive polymer matrix.
2. Results: multiscale theory of active elasticity and experimental validation
2.1. Active neo-Hookean elasticity in hybrid gels
2.1.1. Hydrogel elasticity: structural interactions between passive mesh and FtsZ living polymer.
As depicted in Fig. 2, we have devised a mesoscopic model with the structural attributes of the hybrid hydrogel. SEM imaging unveils a swollen cellular framework (Fig. 2a), featuring liquid-filled cells primarily comprising water and solid-like shell walls made up of a crosslinked PA matrix embedded with FtsZ protein (Fig. 2b). This hybrid PA–ZLP hydrogel showcases active deformability due to the treadmilling motions of FtsZ filaments within the PA meshwork in the solid-like walls (see also Fig. 1). To explain the nonlinear active softening of hybrid PA–ZLP hydrogels under oscillatory shear, we develop a mesoscopic pseudo-equilibrium model based on Flory's theory of crosslinked polymer networks,38 with superposed treadmilling activity as fluctuations in average randomized assuming effective steady-state nonequilibrium.39 These swollen hydrogels have a high-water content (the volume fractions ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) w = Vw/V ≈ 0.9, thus
w = Vw/V ≈ 0.9, thus ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) p = Vp/V ≈ 0.1), and a relatively low polymer fraction (ϕ), making them practically incompressible.40 Under the high hydrogel swelling considered (
p = Vp/V ≈ 0.1), and a relatively low polymer fraction (ϕ), making them practically incompressible.40 Under the high hydrogel swelling considered (![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) p ≈ 0.1 ≪
p ≈ 0.1 ≪ ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) w), and relatively low PA-crosslinking degree (ϕPA = 0.025), the polymer matrix provides shear rigidity through the flexible edges of the cellular structure (Fig. 2a). These solidlike elements are made up of a chemically crosslinked and physically entangled polymer network essentially characterized by the overall density of its binding junctions.3,41,42 Actively treadmilling ZLP-actuators, driven by living FtsZ polymerization under GTP hydrolysis,18–20 generate spatially randomized extensile fluctuations in the absence of directional anisotropy.21 In the hybrid PA–ZLP system, nonequilibrium steady states arise,39 where oscillatory shear maintains a stationary elasticity-swelling constrained imbalance.27 Despite being out-of-equilibrium, this mechanical tradeoff results in an effective constant rigidity considered stationary (Supplementary Note N1, ESI†).
w), and relatively low PA-crosslinking degree (ϕPA = 0.025), the polymer matrix provides shear rigidity through the flexible edges of the cellular structure (Fig. 2a). These solidlike elements are made up of a chemically crosslinked and physically entangled polymer network essentially characterized by the overall density of its binding junctions.3,41,42 Actively treadmilling ZLP-actuators, driven by living FtsZ polymerization under GTP hydrolysis,18–20 generate spatially randomized extensile fluctuations in the absence of directional anisotropy.21 In the hybrid PA–ZLP system, nonequilibrium steady states arise,39 where oscillatory shear maintains a stationary elasticity-swelling constrained imbalance.27 Despite being out-of-equilibrium, this mechanical tradeoff results in an effective constant rigidity considered stationary (Supplementary Note N1, ESI†).
 |
| | Fig. 2 Mesoscopic architecture of the hybrid PA–FtsZ hydrogel under high swelling conditions; (a) experimental ultrastructure as revealed by scanning electron microscopy (SEM). We performed ambiental SEM imaging of minimally dehydrated hydrogel samples in a low vacuum device (SEM Hitachi TM1000). We imaged the remaining swollen hydrogel structure by fixing specimens under chemical crosslinking at avoiding highly desiccating metal sputtering. The showed SEM photograph corresponds to a highly swollen hydrogel structure (90% water/10% PA), composed only by a 10% solid fraction with a relatively low degree of PA crosslinking (ϕ = 2.5%) and relatively high content of FtsZ (cFtsZ > 5 mg mL−1). On the right, we show a legend for the different chemical ingredients and crosslinking interactions involved in the hybrid hydrogel further considered for theoretical modelling. (b) Theoretical model: mesoscopic hybridization of the crosslinked PA hydrogel under ZLP activation in quasi-equilibrium moderate deformation regimes. On the left panel, we depict the schematic cartoon that initially describes the polymeric network constituted by the interaction between the FtsZ monomers acting as a filler, and the rigid crosslinks of characteristic length (ξ0), associated with the passive PA-gel (black circles). On the central panel, we represent the strengthening effect further caused by the physical crosslinks, i.e., “entanglements” of the polymerized FtsZ filaments bounded to the hybrid meshwork (red circles). The Rouse tubes for filamentous FtsZ reptation are established by their broaden chain contours as reversibly (un)bounded in the hybrid crosslinked meshwork (passive tubes in yellow). On the right panel, we depict how active structural weaking happens in a phantom network (ξ > ξ0), with disentangling interactions due to disrupted bonds under active reptation of ZLPs i.e., the FtsZ living (active) polymers (see main text for details). The Rouse tube is in this case consequently broaden as corresponding to the active reptation of ZLP chains undergoing disordering treadmilling by opening/reorganizing/reclosing motions in the interstitial spaces of the hydrogel (reddish active tubes). | |
2.1.2. Neo-Hookean model.
Hence, we described the hybrid PA–ZLP hydrogel with an active deformability based on the living treadmilling motions of the FtsZ filaments across the polymerized PA-meshwork in the solidlike walls (as also depicted in Fig. 1). The mechanical counterbalance between these deformable elements was described by the free energy functional:37,43| |  | (1) |
which combines constrained mixing elasticity,27 and phase-separation interaction theory,36 integrating polymer–solvent deformations,  while allowing each material element to evolve into an equilibrium configuration (Supplementary Note N1, ESI†).
while allowing each material element to evolve into an equilibrium configuration (Supplementary Note N1, ESI†).
Here, the nonlinear elastic component  represents the mechanical rigidness of the hydrogel as depending on the Cauchy-Green (CG) stress tensor
represents the mechanical rigidness of the hydrogel as depending on the Cauchy-Green (CG) stress tensor 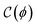 .44,45 For given deformation strain (γ), this equilibrium term is essentially determined upon structural mesh variables (ϕ), constitutionally describing matrix crosslinking degrees and compositional concentrations.41,42,46 Additionally, the strain-dependent interaction term
.44,45 For given deformation strain (γ), this equilibrium term is essentially determined upon structural mesh variables (ϕ), constitutionally describing matrix crosslinking degrees and compositional concentrations.41,42,46 Additionally, the strain-dependent interaction term  describes the nonlinear interactions between the passive hydrogel matrix and the active additive leading to non-equilibrium elasticity (either weakening or strengthening). The interaction energy depends on both passive deformations and active phase interactions, coupled through an order parameter
describes the nonlinear interactions between the passive hydrogel matrix and the active additive leading to non-equilibrium elasticity (either weakening or strengthening). The interaction energy depends on both passive deformations and active phase interactions, coupled through an order parameter  which is dependent on the additive concentration variable
which is dependent on the additive concentration variable  describing the effective driving effect from the active component. This crucial interaction parameter will be further described in Section 2.3. The neo-Hookean CG tensor includes components relevant to both compression and shear deformations, governed by effective osmotic/swelling interactions between reconfigurable binding points.29,41,45 A detailed analysis is provided as ESI† (Supplementary Note N1, ESI†). These interactions, either active or passive, are described by the effective interaction parameter
describing the effective driving effect from the active component. This crucial interaction parameter will be further described in Section 2.3. The neo-Hookean CG tensor includes components relevant to both compression and shear deformations, governed by effective osmotic/swelling interactions between reconfigurable binding points.29,41,45 A detailed analysis is provided as ESI† (Supplementary Note N1, ESI†). These interactions, either active or passive, are described by the effective interaction parameter  which depends on FtsZ concentration
which depends on FtsZ concentration  . Thus, the constitutional CG-tensor can vary with elastic changes in network interactions modulated under deformation i.e.,
. Thus, the constitutional CG-tensor can vary with elastic changes in network interactions modulated under deformation i.e.,  for a given strain (γ).37–41,45,47 Regarding macroscopic solid-like elasticity under shear, a constitutive relationship is established for the applied stress (σ), as
for a given strain (γ).37–41,45,47 Regarding macroscopic solid-like elasticity under shear, a constitutive relationship is established for the applied stress (σ), as  calculated for a given shear strain (γ).41,47 The stress–strain relationship is determined in terms of a generalized rigidity
calculated for a given shear strain (γ).41,47 The stress–strain relationship is determined in terms of a generalized rigidity  assumed to include linear and nonlinear components. Here, the strain tensor
assumed to include linear and nonlinear components. Here, the strain tensor  is considered invariant under rotation, representing the squared value of the local change in relative distances in the solid body due to shear deformation.41,47 At low strain (γ → 0), the constitutional relationship is linear, corresponding to the harmonic response of the polymer chains i.e.,
is considered invariant under rotation, representing the squared value of the local change in relative distances in the solid body due to shear deformation.41,47 At low strain (γ → 0), the constitutional relationship is linear, corresponding to the harmonic response of the polymer chains i.e.,  , where
, where  is the Hookean rigidity modulus.41 Above a yield point
is the Hookean rigidity modulus.41 Above a yield point  the stress response becomes nonlinear, entering an intermediate plastic plateau (i.e., constant
the stress response becomes nonlinear, entering an intermediate plastic plateau (i.e., constant  at γ → γY), followed by a hyper-elastic regime under large deformation (i.e.,
at γ → γY), followed by a hyper-elastic regime under large deformation (i.e.,  at γ ≫ γY). For simplicity, we consider the elastic energy as neo-Hookean strain function:45,47
at γ ≫ γY). For simplicity, we consider the elastic energy as neo-Hookean strain function:45,47
| |  | (2) |
Here,
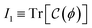
is the first invariant (trace) of the right Cauchy-Green strain tensor expressed uniquely in terms of the principal deformations.
41,45,47 For an incompressible neo-Hookean material considered internally isotropic under simple (uniaxial) shear strain, then
I1 = 3
γ2.
43,45 Under these isotropic straining conditions, the hydrogel's nonlinear elasticity is effectively described by the neo-Hookean energy density function within an effective rigidity modulus,

balancing shear rigidity (
G) and osmotic/swelling ratio (
J) (see Supplementary Note N1 for details, ESI
†). Below, we argue how mesoscopic mechanostructural factors are encapsulated in the effective rigidity.
2.1.3. Mesoscopic elasticity of polymer networks: variable binding functionality into neo-Hookean plasticity.
On the one hand, the affine model of rubber-like elasticity is often used to describe rigid networks fixed by chemical crosslinks (Fig. 2b; left panel). In an affine network, the crosslinks move proportionally to the applied strain without rearrangement, stretching or coiling the polymer chains to adapt deformation.48,49 Nonetheless, Flory argued that in dense, rubbery networks, even fixed junctions are influenced by the movements of surrounding chains.48,49 On the other hand, for swollen hydrogels containing semiflexible FtsZ filaments, we assume a superposed phantom meshwork (Fig. 2b; center panel). This reconfigurable phantom meshwork is more flexible than the rigidly affine counterpart as far as can reorganize between movable entanglements. Indeed, the phantom crosslinking is suitable for active hydrogels to work as swellable structures,49 where solvent allocation occurs from the passive matrix into more diffusible regions.50 In this active meshwork weakening setup, treadmilling ZLPs broaden the Rouse tubes, leading to local dilation and minimized mechanical stress as chains actively disentangle and slide each other (Fig. 2b; right panel). Hence, for describing harmonic deformations in the hybrid PA–ZLP meshwork, we consider both affine (rigid) and phantom (flexible) models. In the affine PA matrix, each crosslinked strand end is pinned to the deformable embedding.41 Described by the Flory theory of entropic rubber elasticity with a fixed chain binding functionality (f = 4),41,49 this rigidly affine network results in a Hookean modulus proportional to the bulk density of crosslinked strands that are tightly bounded each other i.e. K(0)aff(ϕ) ≅ ϕ(N/V)kBT (essentially determined by the passive crosslinking fraction ϕ ≅ ϕpass). In the phantom meshwork, however, binding ends can slide each other under external deformation, leading to structural liquidlike softening characterized by varying functionality (4 ≥ f ≥ 2).41,49 Hence, the effective rigidity in the phantom meshwork is disrupted by unbinding interactions, leading to an apparent decrease in functionality,41,49 which accounts for ZLP-driven activity as K(0)ph[ϕ, f(Γ)] ≈ 2K(0)aff(ϕ)[1 − 2/f(Γ)]. Here, f(Γ) refers to the crosslinking functionality dependent on the interaction parameter Γ(c), which is ultimately dependent on the concentration of living ZLP filaments.49 Hence, the effective Hookean modulus is given by active changes in crosslinking functionality due to unbinding interactions; expanding to first order, we get K(0)ph(c, ϕ) ≈ K0(ϕ)[1 + (4/f2)(df/dΓ)] (see discussion below). Nonetheless, entropic flexible forces and active disentangling interactions are limited by the constrained motion of fluctuating junctions under volume conservation.48–50
Therefore, we assume a generalized neo-Hookean plasticity model with effective rigidity determined under variable binding i.e., K[f(Γ)]. Beyond critical structural thresholds (ϕPA > ϕ* and c > ccrit), the model predicts active softening at a tipping point on the Cauchy tensor  when sufficient deformation exceeds the plasticity onset (γ > γY).41,47 Hence,
when sufficient deformation exceeds the plasticity onset (γ > γY).41,47 Hence,  for
for  resembling effective rubber-like plasticity.48,49 The nonlinear affine model accurately describes plastic deformations up to 40% beyond the yield point (γ ≤ 1.4γY) but may not predict further strengthening at larger strains limited by chain stretching.47 Although the model assumes reversible solidlike plasticity, no dissipative energy release is considered during fluidization. The extensible phantom chains may strengthen from a certain onset of stretching up to the maximum strain supported by chemical crosslinks (at γstr ≫ γY), hence resulting in an effective still reversible strengthening (i.e., Kstr ≫ K0 at γ < γstr) (see Fig. 3c). These models have been shown to capture hardening effects due to transient reconfiguration after plastic fluidization51 or bursting damage under critical hydrogel swelling.52 We will address these modelling issues when discussing the experimental data later.
resembling effective rubber-like plasticity.48,49 The nonlinear affine model accurately describes plastic deformations up to 40% beyond the yield point (γ ≤ 1.4γY) but may not predict further strengthening at larger strains limited by chain stretching.47 Although the model assumes reversible solidlike plasticity, no dissipative energy release is considered during fluidization. The extensible phantom chains may strengthen from a certain onset of stretching up to the maximum strain supported by chemical crosslinks (at γstr ≫ γY), hence resulting in an effective still reversible strengthening (i.e., Kstr ≫ K0 at γ < γstr) (see Fig. 3c). These models have been shown to capture hardening effects due to transient reconfiguration after plastic fluidization51 or bursting damage under critical hydrogel swelling.52 We will address these modelling issues when discussing the experimental data later.
 |
| | Fig. 3 (a) Mechanical mesoscopic modelling for the hybrid hydrogels as composed by passive PA-crosslinks (black dots), and disrupted bonds elicited by active ZLPs (red dots). The elastic meshwork is characterized by the correlation length (ξ), the effective entanglement length. (Upper inset) Schematics for the free-energy landscape of binding elasticity describing the polymeric network constituted by the interaction between rigid bonds associated with the PA-gel and disrupted bonds due to the reptation of the ZLPs, the living (active) FtsZ polymers (see main text for details). (b) Mass action relationships proposed at dependence of strain as a dynamic equilibrium between the passive (n bounded crosslinks), and active polymers (m unbounded crosslinks) (see eqn (3)–(5)). The hydrogel system is composed by fixed crosslinks (m), and a variable amount of ZLPs that depends on the status of strain (n(γ) see eqn (5)). Below the yield strain (at γ ≤ γY), the bound fraction is majoritarian making the solid body essentially rigid (i.e., n ≫ m thus K ≈ K0). Well above the yield strain (at γ > γY), the unbounded fraction becomes conversely majoritarian hence making the body to soften (i.e., n ≪ m thus K < K0). (c) Nonlinear stress–strain relation expected from the proposed neo-Hookean model (see eqn (1) and (2)) for different compositions of active ZLPs (m), and passive PA-polymers (n); from top to down: (green) passively rigid meshwork with a plastic plateau leading to elongational chain strengthening under hybrid filament reinforcement (m ≪ n); (red) plasticized meshwork by active ZLP unbounding (m < n); (blue) active meshwork softening and fluidization under collective activation (m ≈ n); see also main text for further theoretical details. | |
2.1.4. Passive rigid chains vs. active flexible treadmilling filaments.
The synthetic PA-gel serves as a passive elastic scaffold of flexible segments embedded by active ZLP polymers, as depicted in Fig. 3. The softening effect of the active polymer is accounted for within the neo-Hookean elastic strain energy K(ϕ, c) (as expressed in eqn (1)). The total fraction of crosslinks is given by contributing with the passive matrix response (f = 4), and n denotes the active filaments that soften the network due to ZLP treadmilling (i.e., f(c) < 4 under apparent concentration c ⇔ cFtsZ = n/V = ϕactN/V). According to Flory's theory of dilute polymer solutions,29 the effective size of an isolated chain, expressed as the hydrodynamic radius RF ≈ aNν, depends on polymer solubility and effective interactions (here, a is the monomer size, and the Flory exponent 0 < ν < 1 accounts for interactions). A real polymer chain consists of rigid segments, or strands, with an effective persistence length lp ≈ aeκ(ν)/kBT(≥a). This Kuhn length represents a competition between conformational persistence and thermal randomness leading to segmental stiffness κ(ν).53 Three configurational reference states can be considered at dependence of effective interactions: (A) rigid chains stretched in a good solvent (ν = 1, κrig → ∞); they adopt an ordered rodlike configuration compatible with strengthening (cohesive) interactions with the environment (Rstr ≈ lp ≈ lc = aN). (B) Random coils under “theta-solvent” solubility and excluded volume conditions (ν = 1/2, κflex ≪ κrig); the disordered strands adopt a quite flexible self-avoiding configuration compatible with balanced interactions (Rflex ≈ aN1/2 ≪ Rrig and lp ≈ a ≪ lc). (C) Collapsed chains in bad-solvent conditions (ν → 0, κcol → 0); completely random polymer strands do collapse in bad solvents (Rcol ≈ a and lp → 0).48 For a complex polymer mesh, we assume the Flory exponent is embedded within the interaction parameter Γ(ν), which accounts for the effective interactions among the many individual components in the meshwork. In the reference (critical) state (Γ1/2 = 0 for ν = 1/2), we represent flexible chains with no net apparent interaction. However, neatly cohesive interactions lead to chain strengthening i.e., structural hardening (Γhard > 0 for ν > 1/2), while neatly repulsive interactions lead to effective softening (Γsoft < 0 for ν < 1/2). As representing mean-field interactions, the Flory exponent  is determined by the activity concentration variable
is determined by the activity concentration variable  .
.
2.1.5. Correlation length: mean-field approach to critical meshwork overlapping.
Understanding the mechanical properties of a polymer mesh involves defining a fundamental correlation length ξ, as first described by De Gennes for overlapping chains.29,54 This characteristic length – in general denoted  represents the distance for binding correlations between polymer stands (see Fig. 3a), where
represents the distance for binding correlations between polymer stands (see Fig. 3a), where  denotes a reduced distance to a critical point for ordering.29 In the hybrid mesh considered here, this constitutional parameter should depend on compositional variables in a complex way i.e.,
denotes a reduced distance to a critical point for ordering.29 In the hybrid mesh considered here, this constitutional parameter should depend on compositional variables in a complex way i.e., 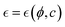 . Specifically, it depends on the fixed number of passive polymer PA-crosslinks (ϕ ≅ ϕPA), and the variable number of actively flexible ZLP-elements (c ≅ cFtsZ). Generally, the composition-dependent length
. Specifically, it depends on the fixed number of passive polymer PA-crosslinks (ϕ ≅ ϕPA), and the variable number of actively flexible ZLP-elements (c ≅ cFtsZ). Generally, the composition-dependent length  is larger at dependence of effective interactions than the persistence length lp, but smaller than the Flory radius RF.41 In chemically crosslinked polymer gels, for instance, this universal length diverges at the percolation threshold (ϕ*), but decreases essentially with the ordering degree of crosslinking as ξ(ϕ) ∼ (ϕ − ϕ*)−νd (here, ν is the Flory exponent and d represents dimensionality).29 For physically entangled gels, De Gennes stablished his famous scaling law for the characteristic entanglement length ξ(c)/lp ≈ (c*/c)δ(ν,d), defined above the critical concentration (c > c*); at the critical overlapping concentration ξ(c*) ≈ lp.28,29 In those cases, the critical amplitude is
is larger at dependence of effective interactions than the persistence length lp, but smaller than the Flory radius RF.41 In chemically crosslinked polymer gels, for instance, this universal length diverges at the percolation threshold (ϕ*), but decreases essentially with the ordering degree of crosslinking as ξ(ϕ) ∼ (ϕ − ϕ*)−νd (here, ν is the Flory exponent and d represents dimensionality).29 For physically entangled gels, De Gennes stablished his famous scaling law for the characteristic entanglement length ξ(c)/lp ≈ (c*/c)δ(ν,d), defined above the critical concentration (c > c*); at the critical overlapping concentration ξ(c*) ≈ lp.28,29 In those cases, the critical amplitude is  (with N being the calibrated chain length), and the scaling exponent δ(ν,d) = νd/(νd − 1) > νd, both modulated by interactions.41 De Gennes considered calibrated polymer overlapping (constant N), but he postulated that the same results also apply to the swelling of more complex networks.29 Specifically, the hybrid meshwork represented in Fig. 3a consists of passive (affine) crosslinks between bound strands, interspersed with active (phantom) entanglements that disrupt polymer bonds, resulting in unbound strands leading to neo-Hookean response. Despite the differences between dimensional random models describing hybrid affine and active phantom phases, a mean-field approach can recapitulate their mechanical behaviour into a simpler ordered mesoscopic model that is mechanically isotropic but compositionally heterogeneous at coexistence (see Sections 2.8–2.9).36
(with N being the calibrated chain length), and the scaling exponent δ(ν,d) = νd/(νd − 1) > νd, both modulated by interactions.41 De Gennes considered calibrated polymer overlapping (constant N), but he postulated that the same results also apply to the swelling of more complex networks.29 Specifically, the hybrid meshwork represented in Fig. 3a consists of passive (affine) crosslinks between bound strands, interspersed with active (phantom) entanglements that disrupt polymer bonds, resulting in unbound strands leading to neo-Hookean response. Despite the differences between dimensional random models describing hybrid affine and active phantom phases, a mean-field approach can recapitulate their mechanical behaviour into a simpler ordered mesoscopic model that is mechanically isotropic but compositionally heterogeneous at coexistence (see Sections 2.8–2.9).36
Henceforth, the mesoscale De Gennes’ length is averaged over internal degrees of freedom as  expanded in series from the perturbative distance
expanded in series from the perturbative distance  defined as a critical concentration for phase segregation. The scaling exponent δ(ν, d) reflects dimension (d), and effective mean-field interactions Γ(ν), as above mentioned. The unperturbed Rouse tube size ξ0 ≅ lp(κ) denotes the isotropic length determined by the intrinsic chain rigidness in the unperturbed meshwork conditions; these are Γ(νcrit) = 0, for
defined as a critical concentration for phase segregation. The scaling exponent δ(ν, d) reflects dimension (d), and effective mean-field interactions Γ(ν), as above mentioned. The unperturbed Rouse tube size ξ0 ≅ lp(κ) denotes the isotropic length determined by the intrinsic chain rigidness in the unperturbed meshwork conditions; these are Γ(νcrit) = 0, for 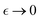 . Hence, this reference size determines the bare Hookean rigidity K0 ≅ kBT/ξd0.29 Analogous to the Landau–De Gennes’ c* – theorem,29,55,56 which states that structural deformation is constrained by local connectivity akin to short-range ordering effects in liquid crystal phases, this mesoscopic scenario allows for effective crosslink adjustments above the critical overlapping concentration (c ≥ ccrit).29 Referred to the critical interactions (at νcrit), they are either unbinding due to softening interactions i.e., ξ > ξ0 (for ν < νcrit, thus Γsoft < 0), or strengthening from hardening interactions i.e., ξ < ξ0 (for ν > νcrit, thus Γhard > 0). For a hybrid neo-Hookean meshwork approaching the critical point (
. Hence, this reference size determines the bare Hookean rigidity K0 ≅ kBT/ξd0.29 Analogous to the Landau–De Gennes’ c* – theorem,29,55,56 which states that structural deformation is constrained by local connectivity akin to short-range ordering effects in liquid crystal phases, this mesoscopic scenario allows for effective crosslink adjustments above the critical overlapping concentration (c ≥ ccrit).29 Referred to the critical interactions (at νcrit), they are either unbinding due to softening interactions i.e., ξ > ξ0 (for ν < νcrit, thus Γsoft < 0), or strengthening from hardening interactions i.e., ξ < ξ0 (for ν > νcrit, thus Γhard > 0). For a hybrid neo-Hookean meshwork approaching the critical point ( for ν = νcrit), the interaction-dependent characteristic size
for ν = νcrit), the interaction-dependent characteristic size  may accommodate both, the strengthening effect of fixed passive crosslinks in the affine network (δ > 0), and the softening effect of sliding entanglements enabled by ATP-dependent ZLP treadmilling (δ < 0). Notably, Active FtsZ-driven entanglements may further increase this correlation length
may accommodate both, the strengthening effect of fixed passive crosslinks in the affine network (δ > 0), and the softening effect of sliding entanglements enabled by ATP-dependent ZLP treadmilling (δ < 0). Notably, Active FtsZ-driven entanglements may further increase this correlation length  contingent upon a supercritical concentration c > ccrit(Γ), and the repulsive nature of the interaction Γsoft(ν) < 0. To model the mesoscopic behaviour of the hybrid PA–ZLP meshwork, we use a self-consistent mean-field theory that simplifies this high-dimensional polymer system into a one-dimensional model governed by the interaction parameter Γ(ν).56 Similarly to the Landau–Ginzburg (LG) theory of phase transitions,57 our mean-field quasi-chemical approach approximates the complex hydrogel neo-Hookean elasticity by averaging correlated interactions Γ(ν).56 With the mesoscopic overlapping length defining the apparent size of the Rouse tube
contingent upon a supercritical concentration c > ccrit(Γ), and the repulsive nature of the interaction Γsoft(ν) < 0. To model the mesoscopic behaviour of the hybrid PA–ZLP meshwork, we use a self-consistent mean-field theory that simplifies this high-dimensional polymer system into a one-dimensional model governed by the interaction parameter Γ(ν).56 Similarly to the Landau–Ginzburg (LG) theory of phase transitions,57 our mean-field quasi-chemical approach approximates the complex hydrogel neo-Hookean elasticity by averaging correlated interactions Γ(ν).56 With the mesoscopic overlapping length defining the apparent size of the Rouse tube  relative to the critical distance to the critical point
relative to the critical distance to the critical point 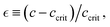 hence, we stablish the multiscale connection
hence, we stablish the multiscale connection  (see Section 2.3).
(see Section 2.3).
2.1.6. Active reptation: treadmilling leads to effective disentanglement.
For active gels containing ZLPs, we consider an effective De Gennes’ reptation dynamics perturbed by treadmilling chains that can remove binding points in the Rouse tube.29,30 The effective interaction Γ(ν) between passive PA polymers and active ZLP filaments involves reconfigurable bonds with kinetic barriers and binding energy significantly higher than thermal energy (i.e., Eξ(ξ) > Eb(ξ) ≫ 10kBT), thus leading to an activated reptation dynamics controlled by the overlapping length 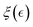 . Indeed, active reptation systems with slipping linkages behave like physically entangled gels with a variable mesh size
. Indeed, active reptation systems with slipping linkages behave like physically entangled gels with a variable mesh size  58 where sliding interactions maintain a reversible two-state equilibrium between reptation states either passive or active.59 When macroscopic shear deformation occurs slower than reptation dynamics (as in rheological experiments), softening interactions emerge leading above the onset of plasticity at
58 where sliding interactions maintain a reversible two-state equilibrium between reptation states either passive or active.59 When macroscopic shear deformation occurs slower than reptation dynamics (as in rheological experiments), softening interactions emerge leading above the onset of plasticity at  – the yield point. Hence, active elasticity can be expressed as a weakening interaction considered neo-Hookean i.e., the apparent modulus is
– the yield point. Hence, active elasticity can be expressed as a weakening interaction considered neo-Hookean i.e., the apparent modulus is 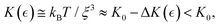 under structural rigidity K0 ≅ kBT/ξ03, considering an effective softening
under structural rigidity K0 ≅ kBT/ξ03, considering an effective softening 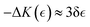 (for δ < 0). This active softening is ultimately determined by treadmilling assisted reptation, which causes effective unbinding interactions leading to an apparent reduction in the overlap functionality i.e., −ΔK ≈ K0(4/f2)(df/dΓ) (assuming df/dΓ ≤ 0). Hence, we have related the changes in overlapping functionality with the effective interactions modulated by FtsZ activity as follows
(for δ < 0). This active softening is ultimately determined by treadmilling assisted reptation, which causes effective unbinding interactions leading to an apparent reduction in the overlap functionality i.e., −ΔK ≈ K0(4/f2)(df/dΓ) (assuming df/dΓ ≤ 0). Hence, we have related the changes in overlapping functionality with the effective interactions modulated by FtsZ activity as follows  . This differential relationship establishes the multiscale connection between the microscopic interactions and the macroscopic order i.e.,
. This differential relationship establishes the multiscale connection between the microscopic interactions and the macroscopic order i.e.,  otherwise stated, the better effective polymer–solvent interaction with increasing δ(ν, d), the higher effective change of overlapping functionality under given activity
otherwise stated, the better effective polymer–solvent interaction with increasing δ(ν, d), the higher effective change of overlapping functionality under given activity  . Therefore, we can stablish the active softening governed by a mass action equilibrium between unbound (ub) and bound (b) overlapping states:60
. Therefore, we can stablish the active softening governed by a mass action equilibrium between unbound (ub) and bound (b) overlapping states:60| |  | (3) |
Here, the weakening (neo-Hookean) term ΔK is determined by the ratio of pub(n), the probability of an overlapping element being unbounded (slipping entangled or simply not linked), to pb(m), the probability of it being meshwork bound (or crosslinked) (hence pb + pub = 1). In this context, Eb is the free energy difference between these states, and wext (≥Eb) is the external work causing unbinding by overpassing the kinetic barrier needed for yielding plasticity (see Fig. 3a). The bound (elastic) state is the preferred low-energy equilibrium at zero force (i.e., pb ≫ pub when wext = 0), while the unbound (plastic) state has higher free energy under stress (i.e., pub ≫ pb when wext ≫ Eξ). The crucial point now is to explain how the applied force determines the extent of softening at dependence of interactions. Based on the statistics in eqn (3), Fig. 3b shows the actual number of passive crosslinks contributing to rigidness (m = pbmmax), and actively sliding entanglements responsible for plasticity (n = pbnmax), both relative to their maximum populations.
From the above discussion on Rouse tube broadening under FtsZ treadmilling, the active population ratio is favoured by a larger mesh size (ξ), and lower intrinsic chain rigidity (κ). Both factors contribute to effective softening by relaxation of internal stress, leading plasticity by yielding i.e.,  . Moreover, the detaching energy sets the yield strain for plasticity (γY), which depends on the remanent force i.e.,
. Moreover, the detaching energy sets the yield strain for plasticity (γY), which depends on the remanent force i.e.,  (defined for Δσ = ΔKγY). Hence, we redefine the external unbinding force as the yield stress that causes disentangling equivalent to macroscopic plastic strain, wext = Fξ ⇔ K(γ − γY) (where F(γ) is the unbinding force and
(defined for Δσ = ΔKγY). Hence, we redefine the external unbinding force as the yield stress that causes disentangling equivalent to macroscopic plastic strain, wext = Fξ ⇔ K(γ − γY) (where F(γ) is the unbinding force and  the effective entanglement size also dependent on the applied strain). Therefore, the unbinding driving force can be expressed in terms of elasticity as
the effective entanglement size also dependent on the applied strain). Therefore, the unbinding driving force can be expressed in terms of elasticity as  (where γY(ξ) is the yield strain essentially fixed by the entanglement length, and K(f, γ) is the effective strain-dependent value of shear modulus). Ultimately, the effective stress–strain relationship holds plasticity as a function of
(where γY(ξ) is the yield strain essentially fixed by the entanglement length, and K(f, γ) is the effective strain-dependent value of shear modulus). Ultimately, the effective stress–strain relationship holds plasticity as a function of  the apparent binding functionality dependent on activity; in the first order approximation, this is
the apparent binding functionality dependent on activity; in the first order approximation, this is  . Therefore, the key structural characteristics for plastic yielding leading to active-passive phase segregation are: (a) the entanglement size itself
. Therefore, the key structural characteristics for plastic yielding leading to active-passive phase segregation are: (a) the entanglement size itself  ; (b) the active decrease in entanglement functionality
; (b) the active decrease in entanglement functionality  ; both determined under effective interactions Γ(ν), in approaching the critical point
; both determined under effective interactions Γ(ν), in approaching the critical point 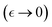 (discussed in Section 2.3). Fig. 3c shows expected nonlinear stress–strain plots dependent on the interaction-driven crosslinking activity of the meshwork.
(discussed in Section 2.3). Fig. 3c shows expected nonlinear stress–strain plots dependent on the interaction-driven crosslinking activity of the meshwork.
2.1.7. Local chain persistence: strain-dependent rigidness.
We estimate the near-equilibrium mechanical properties from a mesoscopic perspective, using the strain-dependent characteristic length  and interaction energies summarized by the order parameter Γ(ν),29,30,34,35 as depicted in Fig. 3. First, local Hookean rigidity is determined by the conformational chain persistence along the m crosslinked strands in the meshwork i.e., K0(ξ) ≈ lpkBT/ξ03 ≪ Eξ/lc2 ⇔ mκ. Second, the effective work exerted by the external force causing plastic deformation is proportional to the number n of unbounded strands i.e.,
and interaction energies summarized by the order parameter Γ(ν),29,30,34,35 as depicted in Fig. 3. First, local Hookean rigidity is determined by the conformational chain persistence along the m crosslinked strands in the meshwork i.e., K0(ξ) ≈ lpkBT/ξ03 ≪ Eξ/lc2 ⇔ mκ. Second, the effective work exerted by the external force causing plastic deformation is proportional to the number n of unbounded strands i.e.,  . Third, stable nonlinear deformation within the hardening regime must be compatible with the maximum stretching work i.e.,
. Third, stable nonlinear deformation within the hardening regime must be compatible with the maximum stretching work i.e.,  (at γY < γ ≪ γstr). Hence, these arguments support passive stiffness based on the passive overlapping length proportional to chain persistence ξ ∝ lp(≪ lc), which is compatible with apparent Hookean rigidity as K0(ξ) ≅ mlp/ξ ⇔ mκ.29 Therefore, we primarily establish rigidity governed by the balance between the binding energy of the m crosslinks and the imposed strain:
(at γY < γ ≪ γstr). Hence, these arguments support passive stiffness based on the passive overlapping length proportional to chain persistence ξ ∝ lp(≪ lc), which is compatible with apparent Hookean rigidity as K0(ξ) ≅ mlp/ξ ⇔ mκ.29 Therefore, we primarily establish rigidity governed by the balance between the binding energy of the m crosslinks and the imposed strain:| |  | (4) |
Hence, higher unbinding interactions cause more open overlaps leading to a weaker mesh i.e.,  . Otherwise stated in the context of ZLP activity, the mesh weakens due to treadmilling-assisted reptation in regimes of active softening i.e.,
. Otherwise stated in the context of ZLP activity, the mesh weakens due to treadmilling-assisted reptation in regimes of active softening i.e.,  (see Fig. 2b, right panel).
(see Fig. 2b, right panel).
2.2. Active neo-Hookean mesoscopic plasticity
2.2.1. Plastic yield under active crosslink unbinding: action mass balance.
We consider kinetic unbinding transitions to lead to plasticization when active treadmilling stresses cause the meshwork to disentangle. Based on the population statistics (see eqn (3)), Fig. 3 shows a two-state mechano-statistical model as a kinetic process, with characteristic energies mainly determined by the mesh size ξ (Fig. 3a; lower). The mass action process involves three competing energies: (i) binding energy related to static overlapping rigidity Eb(ξ; γ → 0) ≈ K0ξ3, assumed within the semiflexible persistence regime (K0 ≈ mκ); (ii) reptation-controlled kinetic barrier Eξ(ξ;γ)/Eb ≈ (m/n)lpa/ξ2, inversely proportional to the actual tube section (S ≡ ξ2); (iii) external deformation work wext = F(γ)(ξ − ξ0) ≥ Eξ ≫ Eb, under effective elastic force  (see eqn (4)). The barrier separates two (un)bounded states with differential energy Eb, constrained by shear rigidity K(γ), under strain γ (Fig. 3a; upper inset). For passive hydrogels, ξ ≈ lp ≪ lc, thus Eb(ξ) ≲ K0(ξ)lp3 ≈ mκ. In the plastic regime, if the injected work exceeds the kinetic barrier wext(γ) ≥ Eξ ≫ Eb, the mesh undergoes chain unbinding i.e., pub(γ) ≥ pb. Hence, the plastic threshold for retaining the chains bound is given by wext(γ) − Eξ ≈ Eb + (alp/lcξ)γ (at γ = γY, then wext(γY) − Eξ = 0). Therefore, the yield strain necessary to plastic unbinding can be expressed in terms of structural energies as:
(see eqn (4)). The barrier separates two (un)bounded states with differential energy Eb, constrained by shear rigidity K(γ), under strain γ (Fig. 3a; upper inset). For passive hydrogels, ξ ≈ lp ≪ lc, thus Eb(ξ) ≲ K0(ξ)lp3 ≈ mκ. In the plastic regime, if the injected work exceeds the kinetic barrier wext(γ) ≥ Eξ ≫ Eb, the mesh undergoes chain unbinding i.e., pub(γ) ≥ pb. Hence, the plastic threshold for retaining the chains bound is given by wext(γ) − Eξ ≈ Eb + (alp/lcξ)γ (at γ = γY, then wext(γY) − Eξ = 0). Therefore, the yield strain necessary to plastic unbinding can be expressed in terms of structural energies as:| | 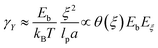 | (5) |
which is determined by the binding ratio. (see eqn (3)). For high kinetic barriers to unbinding (Eξ ≫ Eb), the yield strain is high (γY ≫ γ), representing a passive crosslinked network. Conversely, in the absence of a barrier (ξ ≫ ξ0, thus Eξ ≈ 0), the yield strain vanishes in a very active mesh (γY → 0). In practice, when wext(γ) ≫ Eξ (corresponding to pub ≫ pb, hence θ(ξ) ≈ 0), the system effectively plasticizes (at γ > γY). Generally, the strain-dependent mesh size ξ(γ) defines the onset of plasticization, set by the kinetic barrier Eξ/kBT ≈ lpa/ξ2.
For the proposed mesoscopic model of a bistable overlapping system (passive fixed crosslinks vs. active sliding entanglements; see Fig. 3a), Hookean rigidity arises from the binding energy K0(ξ) ≅ mEb/ξ3, while yielding plasticity is determined by the strain-regulated kinetic barrier ΔK(ξ)/K0(ξ) ≅ n/mEbEξ ∼ θ−1, meaning more unbound crosslinks result in lower effective rigidity. We assume the effective number of crosslinked elements in the bound state m = mmaxpb (where mmax the maximal number of passive crosslinks), hence the population of bounded crosslinks dependent on shear strain is expected as:
| |  | (6a) |
where the mesoscopic energy barrier appears fixed by the microscopic stiffness defined as
κ ≈
lpa/
ξ2 ≈
K/
K0 ≈
Eb/
kBT (see
eqn (4)), determining the sharpness of the plastic transition between the bounded and unbounded state. Because persistent (semiflexible) filaments strengthen the mesh by creating stiffer reptation chains in narrower tubes, for high chain stiffness (
lpa ≫
ξ2), we expect
m ≈
mmax (see
Fig. 3b). Conversely, actively broadened tubes contribute to plasticization.
34,35 Hence, the number of crosslinked elements that become unbound under plasticizing strain can be calculated
n(
γ) =
nmaxpub =
nmax[1 −
m(
γ)/
mmax] (for
nmax =
N −
mmax, taking
pub = 1 −
pb). By considering
eqn (6a), we get:
| |  | (6b) |
2.2.2. Intrinsic mesh plasticity: phenomenological regimes.
Three mechanical response regimes can be predicted based on the yield point (fixed at γ = γY), where unbinding and binding probabilities are equal (pub = pb = 0.5), and crosslink populations equalize (m(γY) = n(γY) = N/2), thus θY = 1 and wY = Eξ. (A) Linear regime (for γ ≪ γY); Hookean rigidity is high (κ0 ≡ lpa/ξ02 ≈ a/lp, then K0 = mκ0 ≫ 0). (B) Plastic regime (for γ ≈ γY); the system becomes effectively plasticized (κ ≪ κ0, then K ≈ 0). Essentially, the yield point is fixed by binding energies γY ≈ EbEξ/θY ≈ EbEξ. Higher binding energy makes the system more thermodynamically inaccessible, while a higher barrier makes it more kinetically limited (see Fig. 3a). (C) Stiffening regime (for γ ≫ γY); the single polymer chains become stretched (thus κ ≫ 0). Remaining binding crosslinks become stable, and transition probability is low, so the mesh behaves like a solid (K ≫ K0).59,61 Therefore, depending on the systemic parameters γY and κ, the relative populations of active and passive crosslinks can be determined (see Fig. 3b). Moreover, three constitutionally related domains of plasticity are expected in function of ZLP treadmilling activity concurrent with passive PA crosslinks (see Fig. 3c). Specifically, for low activity (n ≪ m), the elastic response resembles a passive rigid gel (K ≈ K0). For moderate activity (n ≈ m), the hybrid gel explores metastable states, leading to active plasticization (K ≪ K0). For high activity (n ≫ m), effective crosslink unbinding activity results in dominant fluidization (K → 0). To provide quantitative support for these qualitative expectations of modulated plasticity, we use phase transition arguments, specifically mean-field Landau theory applied to soft matter mechanics.62
2.2.3. Quasi-chemical approach to active plasticity: order parameter.
We explore the Landau–Ginzburg energy interactions between FtsZ living polymers (ZLP chains) and a passive PA hydrogel. Beyond the mesoscopic binding energy (Eb) and kinetic barrier (Eξ), we consider quasi-chemical order/disorder interactions coupled to deformation strain Ψint[Γ(Eb, Eξ, c), C] (see eqn (1)). This term accounts for the nonlinear interplay between active ZLPs and the passive PA matrix, characterized by an “activity concentration” c = cFtsZ ∝ θ−1, defined inversely proportional to the binding fraction θ ≡ m/n. This interaction arises from an active order parameter determined by the unbinding fraction Γ(c) ≡ Γ[θ−1(n/m)], which minimizes elastic energy leading to hydrogel weakening at a critical point (ccrit). Using a Landau–Ginzburg formalism for macroscopic phase transitions, we describe the transition from a solid-like gel to a liquid-like state. Our model leverages mean-field interactions, leading to hydrogel stiffening or softening depending on ZLP activation. This process is controlled by the concentration-dependent order parameter Γ(c, Eξ, Eb), regulated by the kinetic ratio Eξ/Eb ≈ (m/n)lpa/ξ2 (see Fig. 3a). For subcritical chemical potential (![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) <
< ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) crit), ZLP filaments do not activate enough to cause macroscopic softening. For supercritical states (
crit), ZLP filaments do not activate enough to cause macroscopic softening. For supercritical states (![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) >
> ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) crit), ZLPs activate sufficiently to enable swelling and fluidization, decreasing crosslinking and weakening the hydrogel (i.e., Γ(
crit), ZLPs activate sufficiently to enable swelling and fluidization, decreasing crosslinking and weakening the hydrogel (i.e., Γ(![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) ) < 0). When focussing on the plasticity ZLP effects under controlled PA crosslinking, we examine the critical phenomena encoded in the interaction functional by the critical distance
) < 0). When focussing on the plasticity ZLP effects under controlled PA crosslinking, we examine the critical phenomena encoded in the interaction functional by the critical distance  i.e.,
i.e.,  . Additionally, we consider constant elastic energy Ψelas(c), at least when the activity concentration approaches the critical point (c → ccrit), where the interaction parameter is small (Γ ≈ 0), as describable by Landau theory of phase transitions.36
. Additionally, we consider constant elastic energy Ψelas(c), at least when the activity concentration approaches the critical point (c → ccrit), where the interaction parameter is small (Γ ≈ 0), as describable by Landau theory of phase transitions.36
2.3. Landau model of plastic remodelling interactions
2.3.1. Effective mean-field model of active hydrogel remodelling.
The Landau theory describes the interaction energy, ψint, complementing the neo-Hookean elastic response, ψelas (see eqn (1)). This phenomenological mean-field approach captures mechanical remodeling (strengthening/softening) driven by the interaction (contractile/extensile) between the active component and the supporting matrix. We focus on the key terms in the Taylor expansion of the order parameter:36,57| |  | (7) |
where α(![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) ) and
) and  are systemic parameters controlling the structural phase transition, with Γ(c) as the activity order parameter.
are systemic parameters controlling the structural phase transition, with Γ(c) as the activity order parameter.
Here, the quadratic term α(Eξ, ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) ) ≤ 0, represents the quasi-chemical energy barrier between equilibrium phases barely determined by the chemical potential (
) ≤ 0, represents the quasi-chemical energy barrier between equilibrium phases barely determined by the chemical potential (![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) ). The critical condition, α(Eξ,
). The critical condition, α(Eξ, ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) ) = 0, occurs when
) = 0, occurs when ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) =
= ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) crit(Eb, ccrit). The quartic term β[C(γ)], depends on the concentration of actively disentangling elements and deformation status by coupling to the elastic energy through the Cauchy-Green strain tensor
crit(Eb, ccrit). The quartic term β[C(γ)], depends on the concentration of actively disentangling elements and deformation status by coupling to the elastic energy through the Cauchy-Green strain tensor  . A positive β implies stable strain-dependent strengthening (i.e., stiffening order), while a negative β suggests weakening instabilities (softening disorder like active swelling and hyperfluidity). Assuming the system is near the critical point (at α ≈ α0 → 0), this model captures the interplay between extrinsic deformation and intrinsic changes in rigidity. Because the control parameter changes sign across the critical point, it can be expanded as α(
. A positive β implies stable strain-dependent strengthening (i.e., stiffening order), while a negative β suggests weakening instabilities (softening disorder like active swelling and hyperfluidity). Assuming the system is near the critical point (at α ≈ α0 → 0), this model captures the interplay between extrinsic deformation and intrinsic changes in rigidity. Because the control parameter changes sign across the critical point, it can be expanded as α(![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) ) ≈ −Eξ(c − ccrit)/ccrit, where −Eξ reflects the kinetic dependence on the barrier height for mesh disentanglement.
) ≈ −Eξ(c − ccrit)/ccrit, where −Eξ reflects the kinetic dependence on the barrier height for mesh disentanglement.
For the Landau mean-field remodelling transition between hydrogel phases, we assume repulsive interaction for the high-activity (fluid-like) state (α < 0 at c > ccrit), and attractive interaction for the inactive (solid-like) state (α > 0 at c < ccrit). Minimizing the free energy with respect to the order parameter gives:
| |  | (8) |
which yields the binodal condition
![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) eq
eq =
![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) solid
solid =
![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) fluid
fluid, where the chemical potential is equal in both phases. Consequently, the equilibrium value of the interaction parameter is:
| |  | (9) |
Below the critical threshold (
c <
ccrit), the interaction parameter is zero (
Γ = 0). Above the critical point (
c ≥
ccrit), it scales approximately as

where

is the reduced distance to the critical point as considered in our mesoscopic depiction of effective mean-field interactions. The scaling ordering amplitude is
Γ0(
c) ≡ (
Eξ/2|
β|)
1/2, determined by the ratio of the kinetic barrier height to the nonlinear change in structural binding interaction.
From a mesoscopic perspective, the binding energy comprises neo-Hookean energy Eb(ξ, β) ≅ E0b ± ΔEbK(β)ξ3, with a barely Hookean leading component E0b(ξ0, β = 0) ≅ K0(ξ0)ξ03, perturbed under nonlinear remodelling energy ±ΔEb ≅ ΔK(β)ξ3 (here, the sign ± holds for stiffening/softening, respectively). The interaction order parameter is positive (repulsive) in disordered, fluid-like states, indicating weakening instabilities that lead to liquid-like phase fluidization (i.e., Γfluid > 0 for β < 0). However, it becomes negative (attractive) in ordered, solid-like states, indicating structural reinforcement under mechanical strengthening (i.e., Γsolid < 0 for β > 0). These states define the internal variables that encode the mechanical interplay between the passive solid-like and active fluid-like phases in equilibrium, connected by the interaction parameter  . Fig. 4 illustrates the mesoscopic hypotheses for evaluating the phase space of hybrid PA–FtsZ hydrogels and performing stress–strain response calculations that predict a neo-Hookean plasticity. Particularly, mesh hybridization affects the yield point of the hydrogel (γ0), shifting it as
. Fig. 4 illustrates the mesoscopic hypotheses for evaluating the phase space of hybrid PA–FtsZ hydrogels and performing stress–strain response calculations that predict a neo-Hookean plasticity. Particularly, mesh hybridization affects the yield point of the hydrogel (γ0), shifting it as  (Fig. 4a). These mean-field predictions are discussed individually below in the context of the mesoscopic mesh model described in previous sections.
(Fig. 4a). These mean-field predictions are discussed individually below in the context of the mesoscopic mesh model described in previous sections.
 |
| | Fig. 4 Mesoscopic scenarios for swelling phase behavior in hybrid PA–FtsZ hydrogels: softened fluid-like phase by active ZLPs contributing to fluidity (upper panels); strengthened solid-like phase by passivated semiflexible filaments of FtsZ contributing to rigidity (lower panels). (a) Population shifts causing yield perturbations (for a given mesoscopic rigidness κ). Lowering the yield strain causes an increase in the population of fluidizing ZLPs undergoing active reptation inside broadened tubes (upper panel); conversely, an increase in the yield point leads to a net decrease in active ZLPs as they convert into inactivated filaments that contribute to strengthening the mesh (lower panel). (b) Structural depictions of the mesoscopic scenarios described in (a). Mesh weakening occurs under active reptation by chain slipping (upper panel); mesh strengthening occurs under hybrid physical crosslinking by semiflexible FtsZ filaments (lower panel). (c) Phase diagram as predicted by the Landau functional to describe the effect of strengthening/fluidization in hybrid hydrogels under critical ordering/disordering interactions (eqn (5)–(7)). The equilibrium surface for phase coexistence corresponds to the Landau binodal (eqn (6)). | |
2.3.2. Active reptation dynamics: treadmilling ZLPs induce structural softening.
ZLP treadmilling weakens the ordered state in a GTP-dependent manner (for ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) >
> ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) crit at c > ccrit), leading to supercritical mesh softening through repulsive, crosslink-disruptive interactions (weakening, liquidlike Γfluid > 0; Fig. 4a; top). In passive reptation theory, the polymer chain is confined to a narrow tube formed by closely spaced sticking linkages.28–30 These constraints are represented in our case by the persistent crosslinks of the passive PA matrix (ξ0 ≈ lp). In Fig. 4b, we illustrate how active ZLP entanglements are created and destroyed during treadmilling under GTP hydrolysis (top panel). Relative to passive ones, active ZLPs fluctuate within a broader reptation tube interacting with the surrounding matrix where movable entanglement links are continuously remodelled across slipping linkages. Similar to the Rouse size of the reptation tube for a passive chain (ξ0), we assume the characteristic length between the passively crosslinked PA gel and the active ZLPs is uniformly distributed along the FtsZ filament, with spacing comparable to the passive entanglement size but smaller than the contour length (ξ0 ≤ ξ ≪ lc; Fig. 4b, top). Therefore, structural softening under active ZLP hybridization is promoted by an effective decrease of chain overlapping m(f, γ) = mmax(γ, f0) − n(γ, f) < mmax (relative to the maximal equilibrium value mmax), under effectively lower crosslinking functionality i.e.,
crit at c > ccrit), leading to supercritical mesh softening through repulsive, crosslink-disruptive interactions (weakening, liquidlike Γfluid > 0; Fig. 4a; top). In passive reptation theory, the polymer chain is confined to a narrow tube formed by closely spaced sticking linkages.28–30 These constraints are represented in our case by the persistent crosslinks of the passive PA matrix (ξ0 ≈ lp). In Fig. 4b, we illustrate how active ZLP entanglements are created and destroyed during treadmilling under GTP hydrolysis (top panel). Relative to passive ones, active ZLPs fluctuate within a broader reptation tube interacting with the surrounding matrix where movable entanglement links are continuously remodelled across slipping linkages. Similar to the Rouse size of the reptation tube for a passive chain (ξ0), we assume the characteristic length between the passively crosslinked PA gel and the active ZLPs is uniformly distributed along the FtsZ filament, with spacing comparable to the passive entanglement size but smaller than the contour length (ξ0 ≤ ξ ≪ lc; Fig. 4b, top). Therefore, structural softening under active ZLP hybridization is promoted by an effective decrease of chain overlapping m(f, γ) = mmax(γ, f0) − n(γ, f) < mmax (relative to the maximal equilibrium value mmax), under effectively lower crosslinking functionality i.e.,  (relative to mmax). The decreased yield point reduces the Hookean range of the solidlike regime through weakening interaction leading fluidization
(relative to mmax). The decreased yield point reduces the Hookean range of the solidlike regime through weakening interaction leading fluidization 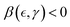 (Fig. 4c; upper regime).
(Fig. 4c; upper regime).
2.3.3. Inactive FtsZ filaments induce strengthening.
The presence of non-activated semiflexible FtsZ filaments (nonhydrolyzed GTP) enhances the stiffness of the PA matrix. Hence, the passive FtsZ filaments contribute to reinforce the mesh with additional fixed overlaps leading to hardening. In Fig. 4a, we illustrate the increased strengthening population with reference to the plastic yield point. In this case, the inactive FtsZ filaments lead to expand the Hookean regime up to higher  driven by a negative interaction parameter (hardening, solidlike, Γsolid < 0; Fig. 4b, bottom). Such effective subcritical hardening resulted from the increase in the polymer crosslink density m(c, γ) → m0(c = 0,γ)|Γ(c)|, modulated by the interaction parameter Γ(c), with respect to reference values considered at zero FtsZ concentration m0. The hardening change (Δm(c, γ) = m − m0 > 0) represents the positive order parameter that enhances rigidity upon passive FtsZ hybridization (for
driven by a negative interaction parameter (hardening, solidlike, Γsolid < 0; Fig. 4b, bottom). Such effective subcritical hardening resulted from the increase in the polymer crosslink density m(c, γ) → m0(c = 0,γ)|Γ(c)|, modulated by the interaction parameter Γ(c), with respect to reference values considered at zero FtsZ concentration m0. The hardening change (Δm(c, γ) = m − m0 > 0) represents the positive order parameter that enhances rigidity upon passive FtsZ hybridization (for ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) <
< ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) crit). From a mesoscopic perspective, this structural strengthening raises the yield point with increasing concentration of inactive FtsZ filaments; for c ≥ ccrit (i.e., if
crit). From a mesoscopic perspective, this structural strengthening raises the yield point with increasing concentration of inactive FtsZ filaments; for c ≥ ccrit (i.e., if  ), this is
), this is  (Fig. 4b; bottom). In a composite passive gel, the first term represents the characteristic yield strain for the matrix (γ0), plus a perturbation controlled by a cohesive additive interaction modulated by the chemical potential in the equilibrated system (
(Fig. 4b; bottom). In a composite passive gel, the first term represents the characteristic yield strain for the matrix (γ0), plus a perturbation controlled by a cohesive additive interaction modulated by the chemical potential in the equilibrated system (![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) <
< ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) crit). Therefore, structural hydrogel stiffening under passive FtsZ hybridization is undergone by the effective increase of crosslinking m(f, γ) = mmax(γ, f0) − n(γ, f) > mmax, under higher effective functionality i.e.,
crit). Therefore, structural hydrogel stiffening under passive FtsZ hybridization is undergone by the effective increase of crosslinking m(f, γ) = mmax(γ, f0) − n(γ, f) > mmax, under higher effective functionality i.e.,  . The reinforced yield point extends over a strengthened solidlike regime through enhanced strengthening interaction
. The reinforced yield point extends over a strengthened solidlike regime through enhanced strengthening interaction  (Fig. 4c; lower regime).
(Fig. 4c; lower regime).
2.3.4. Active ZLP plasticization: stress–strain neo-Hookean relationship.
We propose an active plasticization process based on structural weakening above a yield point (at γ ≥ γY and  ). In the active FtsZ hydrogel, the Landau model predicts a reduced density of chain overlaps due to the cooperation of treadmilling ZLPs (for
). In the active FtsZ hydrogel, the Landau model predicts a reduced density of chain overlaps due to the cooperation of treadmilling ZLPs (for  ), and decreasing interaction energy over fluidized bonds, limited by the kinetic barrier and reduced mesh chemical potential (i.e.,
), and decreasing interaction energy over fluidized bonds, limited by the kinetic barrier and reduced mesh chemical potential (i.e., 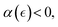 thus
thus  ). Conversely, passive stiffening occurs through strengthening interactions (for
). Conversely, passive stiffening occurs through strengthening interactions (for 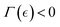 ), promoted by inactive FtsZ filaments, which reinforce crosslinking leading to higher kinetic barrier followed by increasing chemical potential (i.e.,
), promoted by inactive FtsZ filaments, which reinforce crosslinking leading to higher kinetic barrier followed by increasing chemical potential (i.e.,  and
and  ). Here, the effective crosslinking energy (Eb) has been defined by reference to the mesoscopic model as Eb ∝ κγY (where κ represents an effective mesoscopic stiffness, and γY the critical shear strain for yielding). Additionally, the kinetic barrier energy (Eξ) defines the critical amplitude in the phase-transition Landau model
). Here, the effective crosslinking energy (Eb) has been defined by reference to the mesoscopic model as Eb ∝ κγY (where κ represents an effective mesoscopic stiffness, and γY the critical shear strain for yielding). Additionally, the kinetic barrier energy (Eξ) defines the critical amplitude in the phase-transition Landau model  (see eqn (7)). A positive barrier to unbinding results in subcritical strengthening, while a negative barrier leads to supercritical fluidization. Therefore, we propose a theoretical expression for the effective nonlinear shear modulus, defining the neo-Hookean stress–strain relationship as a trade-off between passive and active element concentrations; referred to sections S ≅ ξ2 of the Rouse's tube (see Section 2); this is:
(see eqn (7)). A positive barrier to unbinding results in subcritical strengthening, while a negative barrier leads to supercritical fluidization. Therefore, we propose a theoretical expression for the effective nonlinear shear modulus, defining the neo-Hookean stress–strain relationship as a trade-off between passive and active element concentrations; referred to sections S ≅ ξ2 of the Rouse's tube (see Section 2); this is:| |  | (10a) |
where ± sign refers to either passive strengthening under additive mesh hybridization, or active ZLP softening by treadmilling. The key mesoscopic ingredients are the apparent activity fraction θ−1 ≡ n/m (with reference non-interaction value θmax−1 = nmax/mmax), and the reduced chain rigidity κ ≡ K/K0 (in the Hookean limit, κ0 = 1). They can be expanded from their equilibrium values by respective perturbations on the interaction parameter:| |  | (11) |
where the subscript “0” represents equilibrium (unperturbed) values, and  the order parameter that fixes the effective interaction
the order parameter that fixes the effective interaction 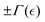 (see Fig. 4a).
(see Fig. 4a).
We investigate how perturbations affect remodelling variables such as stiffening  mechanically neutral
mechanically neutral 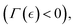 or softening
or softening  . Drawing from Landau's theory, which will be further validated, we interpret experimental findings in a weakly perturbed regime consistent with chain overlap binding energy (i.e., for
. Drawing from Landau's theory, which will be further validated, we interpret experimental findings in a weakly perturbed regime consistent with chain overlap binding energy (i.e., for  ). As a practical parametrization for the chemical potential, we consider a constant unbinding ratio determined by the maximum proportion of active ZLPs relative to chemically fixed crosslinking in the PA matrix, θmax−1 = (n/m)max ≅ cFtsZ with (δθ ≅ 0). For small deformations well below the yield point
). As a practical parametrization for the chemical potential, we consider a constant unbinding ratio determined by the maximum proportion of active ZLPs relative to chemically fixed crosslinking in the PA matrix, θmax−1 = (n/m)max ≅ cFtsZ with (δθ ≅ 0). For small deformations well below the yield point  , rigidity is nearly independent of nonlinear interaction (thus E0b ≅ K0ξ03). In the case of a reference passive meshwork
, rigidity is nearly independent of nonlinear interaction (thus E0b ≅ K0ξ03). In the case of a reference passive meshwork  assuming
assuming  we find the bare passive rigidity as
we find the bare passive rigidity as 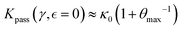 . Fully passive gels
. Fully passive gels  exhibit Hookean elasticity with K0(γ → 0) ≈ κ0. For active gels
exhibit Hookean elasticity with K0(γ → 0) ≈ κ0. For active gels  near the yield point under high plasticity (δγ ≡ γ − γY → 0), the effective modulus changes as
near the yield point under high plasticity (δγ ≡ γ − γY → 0), the effective modulus changes as  . In the fully active gel (θmax−1 → 1), corresponding to critical softening at
. In the fully active gel (θmax−1 → 1), corresponding to critical softening at 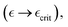 we found
we found  . Generally, above the yield point
. Generally, above the yield point  a strain-dependent shear rigidity defines the actively softened state under active plasticization; to lowest perturbative order (eqn (11)), one gets the active neo-Hookean elasticity modulus (by approximating eqn (10a) in the plastic regime):
a strain-dependent shear rigidity defines the actively softened state under active plasticization; to lowest perturbative order (eqn (11)), one gets the active neo-Hookean elasticity modulus (by approximating eqn (10a) in the plastic regime):
| |  | (10b) |
The actively softened modulus is influenced by the binding fraction (
θ =
m/
n ≥ 0), with strain-dependent effects governed by the maximum unbinding ratio
θmax−1 =
nmax/
mmax ≅
cFtsZ ≥ 0. Its apparent softening strength diminishes as fewer matrix crosslinks remain bound under strain-induced activity, expressed as

. This plastic modulus is further affected by the microscopic binding energy required to detach a fixed crosslink through active reptation, denoted as

. In the first-order approximation, the effective excess strain beyond the yield point

and the corresponding mesoscopic softness

both decrease proportionally with the chain overlap disruptive force of the softening interaction

.
2.4. Experimental results and numerical validation of the active softening model with hybrid PA hydrogels embedded with FtsZ living polymers
Rheological experiments were conducted as depicted in Fig. 5, using hybrid ZLP–PA hydrogels to study the mechanical response under GTP hydrolysis. The biocompatible PA-hydrogel was synthesized with acrylamide–bisacrylamide crosslinking under mild conditions using bio-orthogonal chemistry.63 Hydrogels with 2.5% crosslinking were prepared following standard procedures involving TEMED and APS initiation. Rheological tests were performed using an oscillatory shear rheometer in controlled strain mode (Hybrid Rheometer 2, cone-plate geometry; TA Instruments, USA) (Fig. 5a).64 We evaluated the stress–strain behavior of the hybrid ZLP–PA hydrogel at a constant PA gel concentration (2.5% crosslinks) and varied concentrations of active FtsZ filaments (cFtsZ = (0–5) × 10−3 mol L−1; see Fig. 5b), covering both, linear and nonlinear regimes within amplitude sweeps from 0.1% to 100% deformation strain. All experiments were conducted at a constant temperature of 25 °C. To ensure FtsZ bioactivity, a buffer solution containing FtsZ, KCl (100 mM), GTP (5 mM), and Tris–HCl (50 mM) in Milli-Q water was prepared. The passive hydrogel consisted of PA-gel and FtsZ monomers in Z-solution without Mg2+ (depleted with 10 mM EDTA). Activation of ZLPs was achieved by adding excess MgCl2 (10 mM) to catalyze FtsZ polymerization under GTP hydrolysis in vitro.65 Rheological measurements were performed on both passive (without catalytic Mg2+) and active ZLP–PA hydrogel samples (with MgCl2 at 10 mM and excess GTP at 10 mM). Swelling equilibration under constant osmotic pressure was achieved by immersing the sample in excess buffer within a water-saturated atmosphere. Rheological monitoring confirmed a steady oscillatory response 10 minutes after Mg2+ activation. The measured rigidity modulus remained stable for at least 2 hours after hydrogel formation.
 |
| | Fig. 5 (a) Rheometry station with the oscillatory shear rheometer used for the experimental measurements. (b) Stress strain plots obtained in rheological experiments for hybrid PA–FtsZ hydrogels at 2.5% crosslinking for variable concentrations of FtsZ in different mechanical realizations: (Reference) Pristine PA hydrogel without FtsZ (green symbols). (Strengthened) Passive PA–FtsZ hydrogel containing 2 mM FtsZ in the absence of catalytic Mg2+ (EDTA 10 mM; blue symbols in the upper reference region; undashed). These realizations exhibit a Hookean response in the whole range of shear strain (up to 100%). (Fluidized) Active PA–FtsZ hydrogels containing variable concentration of FtsZ monomers (see legend). The living polymerization is triggered out by adding excess Mg2+ (10 mM), which activates the FtsZ filaments into ZLPs. The stress–strain plots decay into the fluidized region (reddish dashed) in which active yielding is clearly observed as an increasing fluidization with increasing the ZLP-amount (curves legend: 1 mM (blue); 2 mM (red); 5 mM (yellow)). | |
2.4.1. Hookean regime and plastic yielding.
Stress–strain plots were analyzed to compare the mechanical properties of active and passive ZLP–PA gels alongside a pure PA gel. Oscillatory shear experiments were conducted on hybrid gels with FtsZ concentrations ranging from 0 to 5 mM. When hydrolyzable GTP (10 mM) was present, FtsZ filaments exhibited behavior akin to living polymers (ZLPs).66–69 In contrast, without GTP, FtsZ polymers remained semiflexible, contributing to hydrogel strengthening.65Fig. 5b presents shear rheology results plotted logarithmically, revealing distinct mechanical responses from Hookean, through plastic neo-Hookean to stretch strengthening. The linear regime, characterized by initial slope and intercept, indicates the Hookean modulus (K0). The plastic regime is marked by the yield strain point (γY), which defines the onset of neo-Hookean plasticity leading to active softening i.e., K(γ) < K0. These experimental data align with our theoretical predictions of both strengthening and weakening behaviours (see caption for details). The barely Hookean response (green) corresponds to the crosslinked PA-hydrogel without FtsZ (control), showing no yielding within the explored shear strain range. In hybrid PA–FtsZ hydrogels without GTP activation, structural stiffening was observed due to semiflexible FtsZ filaments (brown). Conversely, with GTP present, experiments demonstrated increased softening and plastic yielding with higher concentrations of polymerized FtsZ. Our findings for the active hydrogels (cFtsZ ≫ 0) indicate a decrease in the Hookean modulus and reduced yielding stress and strain, consistent with our theoretical framework.
2.4.2. Active nonlinear behaviour: plastic yield and active softening.
To validate the proposed mean-field model for active neo-Hookean elasticity, we analysed the mechanical data from the mesoscopic perspective described earlier. Fig. 6 focuses on the nonlinear regime of the stress–strain plots, providing experimental evidence of transitional behavior towards a softening regime as theorized. We observed a drop in Hookean stiffness and yielding point with increasing ZLP activity, both in empirical evidence and theoretical predictions (best fits of eqn (10) to the experimental data; see caption for details). This validates the active Landau theory as a reasonable descriptor of active mechanics in hybrid ZLP–PA hydrogels driven by living polymers of FtsZ under GTP hydrolysis. As FtsZ concentration increases, yielding stress and strain decrease, and the drop after yielding becomes sharper. Specifically, Fig. 6a shows the strain–stress plots from a predictive perspective, demonstrating that the mechanical Landau model accurately describes the experimental results as presented in eqn (10) (see caption for details). Furthermore, we obtained the best fits to the perturbative mesoscopic parameters defined in eqn (11). By considering the adjustable parameters κ0, δκ, γ0 and δγY, and fixing cFtsZ → θmax−1 = nmax/mmax (for δθ = 0, and c(max)FtsZ = 5 mM), the theoretical model is able to describe the initial neo-Hookean performance followed by a marked plastic yield regime characterized by the stress softening parameter Δσ (see theoretical fitting curves in Fig. 6a, and best fit parameters in Table 1).
 |
| | Fig. 6 Validating stress–strain nonlinearity in hybrid PA–FtsZ hydrogels with active ZLPs (under increasing concentration from top to bottom). The experimental measurements appear in the left panels (symbols): triangles: experimental measurements. Continuous line: theory (best fittings to eqn (10a)). (a) Experimental stress–strain curves showing the nonlinear elastic response at large deformations regime for different levels of concentration of FtsZ and its comparison with the theoretical prediction of the model. (b) Neo-Hookean plasticity calculated as values of shear modulus. In the right panel, we plot the associated neo-Hookean shear modulus K = dσ/dγ calculated from theoretical predictions in this work. | |
Table 1 Parametric description for stress–strain nonlinearity in hybrid PA–FtsZ hydrogels with active ZLPs. The table includes phenomenological information obtained from theoretical fittings of the Landau interaction model to experimental data
|
c
FtsZ (mM) |
w/w (%) |
K
0 (Pa) |
κ
0 (−) |
δκ (−) |
Δσ (Pa) |
γ
Y (EXP) (%) |
γ
0 (THY) (%) |
| 0.0 |
0.0 |
9.8 ± 1.5 |
1.0 |
0 |
0 |
— |
— |
| 1.0 |
0.01 |
8.6 ± 1.2 |
0.8 ± 0.2 |
0.2 ± 0.1 |
0.8 ± 0.2 |
22 |
25 ± 8 |
| 2.0 |
0.02 |
3.2 ± 0.8 |
0.3 ± 0.1 |
0.3 ± 0.2 |
1.8 ± 0.8 |
7.5 |
8.0 ± 1.5 |
| 5.0 |
0.05 |
0.4 ± 0.3 |
0.1 ± 0.1 |
0.5 ± 0.2 |
3.2 ± 1.2 |
3.5 |
3.7 ± 1.2 |
By comparing experimental descriptors with the best fitted model parameters, we achieve the following conclusions: first, the polymer chain persistence correlates well with the Hookean rigidity of the passive meshwork (i.e., κ0 ∝ K0). Second, the active decrease in chain persistence correlates with the observed stress softening (i.e., −δκ ∝ Δσ). Third, the values of the plastic yield observed in the experiments match accurately the theoretical values calculated from fittings to the stress–strain plots using eqn (10a). Finally, and most notably, all observed activity parameters, both experimental and theoretical, vary almost linearly with the FtsZ concentration as derived from eqn (10b). Our results show the softening neo-Hookean instability caused by the active reptation of ZLPs under plastic strain. The yield strain matches the experimental value (γ0 ≈ γY) and the yield perturbations are consistently positive  as expected for structurally weakening interactions i.e.,
as expected for structurally weakening interactions i.e.,  . Additionally, the softening stress correlates with the unbinding ratio (i.e., Δσ ∝ n/m → θ−1).
. Additionally, the softening stress correlates with the unbinding ratio (i.e., Δσ ∝ n/m → θ−1).
Also, we calculate the effective shear modulus as a function of strain, K(γ) = σ(γ)/γ (see Fig. 6b). The results show significant structural neo-Hookean softening in the hydrogel under ZLP activation, both experimentally and theoretically. We observe increasing plasticization under shear deformation (i.e., K(γ) < K0 for any γ). This nonlinear activity is marked by softening and fluidization above the yield point (i.e., K(γ) → 0 at γ ≥ γY). Higher ZLP concentrations shift the plastic yield to lower strains, even causing a hyperfluidity instability with an effective negative modulus (Khyp < 0). At high strain, the active hybrid gel stabilizes, behaving like a highly softened solid (i.e., K(γ) ≈ 0 at γ ≫ γY). No structural strengthening was observed in the experiments.
As a rule of thumb, model evaluation shows good agreement with the experimental data, capturing the neo-Hookean yielding transition controlled by structural parameters dependent on the ZLP-interaction energy parameter  . Fig. 7 demonstrates that the proposed phase transition model predicts a scaling relation for the interaction parameter
. Fig. 7 demonstrates that the proposed phase transition model predicts a scaling relation for the interaction parameter 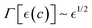 (with the order parameter
(with the order parameter  ; see eqn (7)). This relation effectively captures the softening and fluidization trends due to changes in the stiffness of the hybrid gel caused by active FtsZ filaments (see Fig. 7a). According to the active reptation model, the effective density of entanglement points θ(Γ) ≅ [m − n(Γ)]/nmax is controlled by the activity of the living polymer
; see eqn (7)). This relation effectively captures the softening and fluidization trends due to changes in the stiffness of the hybrid gel caused by active FtsZ filaments (see Fig. 7a). According to the active reptation model, the effective density of entanglement points θ(Γ) ≅ [m − n(Γ)]/nmax is controlled by the activity of the living polymer  (with
(with  ), and excess shear strain δγ = γ − γY. Then, the statistical population relationships in eqn (5a) and (5b) holds non-linearly and effectively active, resulting from a larger population of unbounded chains at larger strains (as shown in Fig. 7b, with the vertical axis in logarithmic scale to better illustrate the distinct regimes when the structure is active or inactive). As far the activation level increases, the density of entanglements decreases due to disruption by the active FtsZ gel. To summarize, the level of structural softening scales with the active interaction ratio
), and excess shear strain δγ = γ − γY. Then, the statistical population relationships in eqn (5a) and (5b) holds non-linearly and effectively active, resulting from a larger population of unbounded chains at larger strains (as shown in Fig. 7b, with the vertical axis in logarithmic scale to better illustrate the distinct regimes when the structure is active or inactive). As far the activation level increases, the density of entanglements decreases due to disruption by the active FtsZ gel. To summarize, the level of structural softening scales with the active interaction ratio  ultimately depending on the theoretically modelled Landau order parameter
ultimately depending on the theoretically modelled Landau order parameter  i.e., the observable softening
i.e., the observable softening  (see eqn (7)).
(see eqn (7)).
 |
| | Fig. 7 Landau's theory validation. (a) Functional relation for the interaction parameter Γ(c) as a function of the FtsZ concentration (cFtsZ). The different dimensionless structural parameters  follow the follow the  – scaling as predicted from the Landau's theory (see eqn (7); experimental data taken from Table 1). (b) Strain dependence of the nonlinear stiffness of the hybrid gel for different levels of shear strain (γ) and concentration of active polymer FtsZ (cFtsZ). – scaling as predicted from the Landau's theory (see eqn (7); experimental data taken from Table 1). (b) Strain dependence of the nonlinear stiffness of the hybrid gel for different levels of shear strain (γ) and concentration of active polymer FtsZ (cFtsZ). | |
3. Discussion
The bacterial cytoskeletal motor-protein FtsZ forms self-assembling filaments crucial for the cytokinetic ring in cell division.25,70–72 This Z ring serves dual roles: as a scaffold for divisome protein recruitment,66 and for generating contractile force.73–75In vitro, FtsZ assemblies exhibit diverse mechanical behaviours depending on conditions.76–82 They can orderly contract in tubular liposomes with matching bacterial geometry,83 but extend in nearly flat geometries due to disordered movements.67,68,84–86 A key feature is their “living” behaviour, dynamically reconfiguring by treadmilling under GTP/GDP turnover.68,69 These dynamic FtsZ polymers, termed ZLP chains, constantly exchange monomers and rearrange, creating longitudinal disorder while condensing laterally.66,68,69 This treadmilling allows ZLPs to elongate lengthwise and condense crosswise, enhancing elastic efficiency and reducing deformation constraints compared to passive counterparts.
In this study, we have explored novel mechanical behaviours of hybrid active gels combining a polyacrylamide (PA) matrix with FtsZ motor proteins, or ZLPs, obtained from E. coli. We find that bioactive matter interacting with a passive hydrogel PA-matrix can induce active gel fluidization through neo-Hookean meshwork dilation. This “active matter” effect has suggested new possibilities to create “smart” structures capable of induced softening by living ZLPs undergoing treadmilling under GTP hydrolysis—chains that grow continuously and depolymerize from their ends. Our multiscale model for active PA–ZLP hybrid structure features ZLP treadmilling chains in a reconfigurable entangled matrix, with companioning theory based on active disentangling reptation and mean-field softening interactions offering new insights into hybrid metamaterial functionalities. In summary, the phenomenological Landau model of phase transition has explained the remarkable mechanical response from active softening induced from lower scales, linking polymer expandability due to ZLPs with the flexible meshwork structure through FtsZ treadmilling powered by GTP hydrolysis. By linking active matrix expansibility due to ZLP reptation with reconfigurable chain overlaps, those molecular building blocks engender the multiscale structure–function connection into an active neo-Hookean response, which emerges from the microscopic layers of polymer conformations and interactions with the embedding, leading to macroscopically softened elasticity Ultimately, the Landau formalism for phase transitions connects the macroscopic elasticity with the underlying mesoscopic mesh structure and microscopic structural levels of molecular complexity.
As depicted in Fig. 8 (scaling bottom-up), we have linked conformational descriptors from microscopic polymer components (monomer size a, interaction exponent ν, related Flory radius RF, chain rigidness κ, and persistence Kuhn length lp, specified in the Flory scale), through the mesoscopic characteristics of the polymer meshwork (overlapping functionality f, and mesh size ξ in the De Gennes’ scale), up to the mean-field interactions that lead to effective neo-Hookean elasticity at the macroscale (governed by the order parameter  in the Landau's macroscopic scale). In summary, we demonstrate these multiscale characteristics and their quantitative dependence on the apparent concentration of the FtsZ additive
in the Landau's macroscopic scale). In summary, we demonstrate these multiscale characteristics and their quantitative dependence on the apparent concentration of the FtsZ additive  defined relative to a critical concentration ccrit. Furthermore, the phenomenological order parameter
defined relative to a critical concentration ccrit. Furthermore, the phenomenological order parameter  has been identified as an effective mean-field descriptor for the PA–FtsZ interaction. This order parameter differentiates two elasticity scenarios (Fig. 8; rightmost panels): (A) active softening by FtsZ treadmilling in a supercritical regime of structural weakening interactions (repulsive bi-phasic separation
has been identified as an effective mean-field descriptor for the PA–FtsZ interaction. This order parameter differentiates two elasticity scenarios (Fig. 8; rightmost panels): (A) active softening by FtsZ treadmilling in a supercritical regime of structural weakening interactions (repulsive bi-phasic separation  ; upper panel); (B) meshwork strengthening by interstitial mesh filling in a subcritical regime relative to the barely passive state (attractive monophase
; upper panel); (B) meshwork strengthening by interstitial mesh filling in a subcritical regime relative to the barely passive state (attractive monophase  ; lower panel). Such multiscale predictive modeling is crucial for bioengineering materials, allowing us to forecast mechanical properties, functional performance under strain, and diffusivity and transport in composite hydrogels with active elasticity. Future designs aim to develop cellular structures similar to thin-walled polymer capsules for biomedical applications, capable of expanding or bursting tumor cell aggregates87–90 and serving as smart drug delivery vehicles.91,92 Controlled hydrogel bursting is essential for effective delivery, balancing therapeutic benefits with potential adverse effects.93
; lower panel). Such multiscale predictive modeling is crucial for bioengineering materials, allowing us to forecast mechanical properties, functional performance under strain, and diffusivity and transport in composite hydrogels with active elasticity. Future designs aim to develop cellular structures similar to thin-walled polymer capsules for biomedical applications, capable of expanding or bursting tumor cell aggregates87–90 and serving as smart drug delivery vehicles.91,92 Controlled hydrogel bursting is essential for effective delivery, balancing therapeutic benefits with potential adverse effects.93
 |
| | Fig. 8 Multiscale model of active elasticity in a hybrid polymer meshwork crossbred with FtsZ living polymers (polyacrylamide (PA) and treadmilling FtsZ (ZLP). Microscale) Individual polymer chains at interaction with the solvent (Flory scale; here, RF ≈ aNν is the Flory radius, as fixed by the monomer size a, and the interaction exponent ν). The microscopic interactions determine the molecular conformation, specifically chain rigidness (κ), and the Kuhn's persistence length (lp), which fixes the size of the flexible strands leading to microscopic elasticity. (Mesoscale) Hybrid polymer mesh constituted by fixed chemical crosslinks (passive PA overlaps as spots in black), and reconfigurable physical entanglements driven by FtsZ treadmiller (active ZLP overlaps as spots in red). A mesoscopic density variable 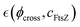 recapitulates the degree of crosslinking (ϕcross), and the concentration of FtsZ monomers (cFtsZ). The mesoscopic structure is depicted as a passive crosslinked meshwork with embedded active ZLP treadmillers able to locally reconfigure the physical entanglements (De Gennes’ scale, characterized by effective mesh length recapitulates the degree of crosslinking (ϕcross), and the concentration of FtsZ monomers (cFtsZ). The mesoscopic structure is depicted as a passive crosslinked meshwork with embedded active ZLP treadmillers able to locally reconfigure the physical entanglements (De Gennes’ scale, characterized by effective mesh length  leading to Rouse tube broadening under treadmilling activity, and effective meshwork functionality leading to Rouse tube broadening under treadmilling activity, and effective meshwork functionality  leading to effective disentanglement). (Macroscale) A two-component interacting system recapitulates both, passive elastic attractiveness among the rigid crosslinks leading to narrow reptation tubes (black particles) and active repulsiveness elicited by ZLP (dis)entanglements leading to faster reptation into broader tubes (red particles). As a multiscale connection, the macroscopic order parameter leading to effective disentanglement). (Macroscale) A two-component interacting system recapitulates both, passive elastic attractiveness among the rigid crosslinks leading to narrow reptation tubes (black particles) and active repulsiveness elicited by ZLP (dis)entanglements leading to faster reptation into broader tubes (red particles). As a multiscale connection, the macroscopic order parameter  of the nonlinear Landau's functional (eqn (7)) is equivalent to the microscopic interaction parameter Γ(ν, d) (determined by the Flory exponent ν, and dimensionality d; see Section 2.1 for details). The phenomenological Landau–Ginzburg model of phase separation predicts both macroscopic scenarios (see free-energy Landau's scale landscapes in the right panels); (a) active softening under repulsive phase segregation of disentangling living polymers into a systemic weakening state (supercritical; of the nonlinear Landau's functional (eqn (7)) is equivalent to the microscopic interaction parameter Γ(ν, d) (determined by the Flory exponent ν, and dimensionality d; see Section 2.1 for details). The phenomenological Landau–Ginzburg model of phase separation predicts both macroscopic scenarios (see free-energy Landau's scale landscapes in the right panels); (a) active softening under repulsive phase segregation of disentangling living polymers into a systemic weakening state (supercritical;  for for  ); (b) passive strengthening under attractive aggregation of the crosslinking elements (subcritical; ); (b) passive strengthening under attractive aggregation of the crosslinking elements (subcritical;  for for  ). ). | |
4. Conclusions
We developed a novel hybrid material with active elasticity based on living polymers of the bacterial motor protein FtsZ embedded in polyacrylamide (PA). The passive PA hydrogel matrix was physically interspersed with living FtsZ filaments, named ZLPs, as undergoing treadmilling motions under GTP-consumption. Using polymer physics concepts, specifically, De Gennes’ polymer reptation theory and Landau's mean-field theory of phase transitions, we have formulated a multiscale model to explain the active plasticity observed as softening in hybrid PA–ZLP hydrogels. Under material engineering guided by our physical model of active structural plasticity, the FtsZ-PA gel prototype demonstrates a transition from neo-Hookean passive behaviour to active softening facilitated by the living FtsZ polymers. Our quasi-static approach provides a useful framework for mapping active material behavior by embedding activity effects into equilibrium parameters, capturing key outcomes like active reversible plasticity and passive strengthening. However, it has two key limitations: (1) it lacks explicit incorporation of treadmilling dynamics; (2) it does not fully account for a comprehensive nonequilibrium thermodynamic formalism. While our simplified quasi-equilibrium approach appears as a crucial stepping stone that facilitates analytical tractability and provides insights into effective mechanical properties, it cannot fully explain the inherently dynamic and nonequilibrium nature of active hydrogels driven by living polymers. These weaknesses underline the need for future efforts to extend this effective model toward a more comprehensive out-of-equilibrium framework for active systems. Understanding the synthetic components, biological modules and multiscale interactions involved is crucial for interfacing materials with biological driving systems in vivo, such as cytokinetic proteins and motile cells and bacteria, ensuring effective biocompatibility and enhanced functionality. Further research integrating theoretical insights with experimental advancements on synthetic biological hybridization will identify potential design enhancements on novel active hydrogels under swellable conditions and their engineering adaptations for future applications in biomedical innovation and soft robotics.
Author contributions
HLM, CLR, MK and DHA conducted research, provided experimental data, contributed to analysing data. HLM, JAS and FM supervised research and drafted the manuscript. FM supported the search for funding, planning the research, supervised the research, contributed to analysing data, and wrote the manuscript.
Data availability
The raw data that support the findings of this study are available on reasonable request from the corresponding author.
Conflicts of interest
The authors declare no conflicts of interest.
Acknowledgements
We thank Prof. G. Rivas and Prof. M. Vicente for providing the purified FtsZ samples. This work was supported by Spanish Ministry of Science and Innovation (MICINN) – Agencia Estatal de Investigación (AEI) under grants TED2021-132296B-C52, PID2019-108391RB-I00 and FIS2015-70339-C2-1-R, and Comunidad de Madrid (CAM) under grants S2018/NMT-4389 and Y2018/BIO-5207. This study was also funded by the REACT-EU program PR38-21-28 ANTICIPA-CM, a grant by Comunidad de Madrid and European Union under FEDER program, from European Union in response to COVID-19 pandemics. The RSS of Instituto de Catálisis y Petroleoquímica (ICP)-CSIC, Spain is acknowledged for making SEM available for use.
References
- E. M. Ahmed, J. Adv. Res., 2015, 6(2), 105–121 CrossRef CAS PubMed
 .
.
- Z. Kaberova, E. Karpushkin, M. Nevoralová, M. Vetrík, M. Slouf and M. D. Smrcková, Polymers, 2020, 12(3), 578 CrossRef CAS PubMed
 .
.
- J. Zhu and R. E. Marchant, Expert Rev. Med. Devices, 2011, 8(5), 607–626 CrossRef CAS PubMed
 .
.
- I. V. Yannas, J. F. Burke, D. P. Orgill and E. M. Skrabut, Science, 1982, 215(4529), 174–176 CrossRef CAS PubMed
 .
.
- S. O. Blacklow, J. Li, B. R. Freedman, M. Zeidi, C. Chen and D. J. Mooney, Sci. Adv., 2019, 5(7), 3963 CrossRef PubMed
 .
.
- C. A. Cezar, E. T. Roche, H. H. Vandenburgh, G. N. Duda, C. J. Walsh and D. J. Mooney, Proc. Natl. Acad. Sci. U. S. A., 2016, 113(6), 1534–1539 CrossRef CAS PubMed
 .
.
- X. Liu, J. Liu, S. Lin and X. Zhao, Mater. Today, 2020, 36, 104–124 Search PubMed
 .
.
-
B. D. Ratner, A. S. Hoffman, F. J. Schoen and J. E. Lemons, Biomaterials Science An Introduction to Materials in Medicine, Elsevier, 2004 Search PubMed
 .
.
- J. Prost, F. Jülicher and J. F. Joanny, Nat. Phys., 2015, 11, 111–117 Search PubMed
 .
.
- M. H. Ayoubi-Joshaghani,
et al.
, Adv. Funct. Mater., 2020, 30(45), 2004098 CrossRef CAS
 .
.
- V. S. Deshpande, R. M. McMeeking and A. G. Evans, Proc. Natl. Acad. Sci. U. S. A., 2006, 103(38), 14015–14020 CrossRef CAS PubMed
 .
.
- D. Mizuno, C. Tardin, C. F. Schmidt and F. C. MacKintosh, Science, 2007, 315(5810), 370–373 CrossRef CAS PubMed
 .
.
- J. Alvarado, M. Sheinman, A. Sharma, F. C. MacKintosh and G. H. Koenderink, Soft Matter, 2017, 13(34), 5624–5644 RSC
 .
.
- M. Curatolo, P. Nardinocchi and L. Teresi, J. Mech. Phys. Solids, 2020, 135, 103807 CrossRef CAS
 .
.
- M. Ferraresso, A. Kong, M. Hasan, D. Agostinelli, G. J. Elfring and M. Bacca, Soft Matter, 2023, 19(29), 5430–5442 RSC
 .
.
- D. A. Gagnon, C. Dessi, J. P. Berezney, R. Boros, D. T. N. Chen, Z. Dogic and D. L. Blair, Phys. Rev. Lett., 2020, 125, 178003 CrossRef CAS PubMed
 .
.
- M. Kumar, A. Murali and A. G. Subramaniam,
et al.
, Nat. Commun., 2024, 15, 4903 CrossRef CAS PubMed
 .
.
- A. W. Bisson-Filho, Y. P. Hsu, G. R. Squyres, E. Kuru, F. Wu, C. Jukes, Y. Sun, C. Dekker, S. Holden and M. S. Van Nieuwenhze, Science, 2017, 355(6326), 739–743 CrossRef CAS PubMed
 .
.
- X. Yang, Z. Lyu, A. Miguel, R. McQuillen, K. C. Huang and J. Xiao, Science, 2017, 355(6326), 744–747 CrossRef CAS PubMed
 .
.
- J. M. Monteiro, A. R. Pereira, N. T. Reichmann, B. M. Saraiva, P. B. Fernandes, H. Veiga, A. C. Tavares, M. Santos, M. T. Ferreira and V. Macário, Nature, 2018, 554(7693), 528–532 CrossRef CAS PubMed
 .
.
- J. W. McCausland, X. Yang and G. R. Squyres,
et al.
, Nat. Commun., 2021, 12, 609 CrossRef CAS PubMed
 .
.
- P. Mateos-Gil, A. Paez, I. Hörger, G. Rivas and M. Vicente, Proc. Natl. Acad. Sci. U. S. A., 2012, 109(21), 8133–8138 CrossRef CAS PubMed
 .
.
- L. Niu and J. Yu, Biophys. J., 2008, 95(4), 2009–2016 CrossRef CAS PubMed
 .
.
- G. Gonnella, D. Marenduzzo, A. Suma and A. Tiribocchi, C. R. Phys., 2015, 16(3), 316–331 CrossRef CAS
 .
.
- E. Bi and J. Lutkenhaus, Nature, 1991, 354(6349), 161–164 CrossRef CAS PubMed
 .
.
- Y. Gombert, F. Roncoroni, A. Sánchez-Ferrer and N. D. Spencer, Soft Matter, 2020, 16(42), 9789–9798 RSC
 .
.
- J. D. Humphrey and K. R. Rajagopal, Math. Mod. Meth. Appl. Sci., 2002, 12(3), 407–430 CrossRef
 .
.
- P. G. De Gennes, Nature, 1976, 282, 367–370 CrossRef
 .
.
-
P. G. de Gennes. Scaling Concepts in Polymer Physics, Cornell University Press, 1979 Search PubMed
 .
.
-
M. Doi and S. F. Edwards, The Theory of Polymer Dynamics, Clarendon Press, 1988 Search PubMed
 .
.
- M. Curatolo, P. Nardinocchi, E. Puntel and L. Teresi, J. Appl. Phys., 2017, 122(14), 145109 CrossRef
 .
.
- M. Curatolo, P. Nardinocchi and L. Teresi, J. Mech. Phys. Solids, 2020, 135, 103807 CrossRef CAS
 .
.
- R. Brighenti and M. P. Cosma, J. Mech. Phys. Solids, 2020, 104011 CrossRef CAS
 .
.
- M. E. Cates, Macromolecules, 1987, 20(9), 2289–2296 CrossRef CAS
 .
.
- A. R. Tejedor and J. Ramirez, Macromolecules, 2019, 52(22), 8788–8792 CrossRef CAS
 .
.
-
L. D. Landau and E. M. Lifshitz, Course of Theoretical Physics, Statistical Physics, Elsevier, 2013, vol. 5 Search PubMed
 .
.
-
R. W. Ogden, Non-Linear Elastic Deformations, Courier Corp., 2013 Search PubMed
 .
.
- P. J. Flory and J. Rehner, J. Chem. Phys., 1943, 11, 512–520 CrossRef CAS
 .
.
- M. Lax, Rev. Mod. Phys., 1960, 32(1), 25–64 CrossRef CAS
 .
.
- K. D. Schulze, S. M. Hart, S. L. Marshall, C. S. O’Bryan, J. M. Urueña, A. A. Pitenis, W. G. Sawyer and T. E. Angelini, Biotribology, 2017, 11, 3–7 CrossRef
 .
.
- L. R. G. Treloar, Trans. Faraday Soc., 1943, 39, 241–246 RSC
 .
.
-
M. Rubinstein and R. H. Colby. Polymer Physics, Oxford University Press, 2003 Search PubMed
 .
.
- H. López-Menéndez, J. Mech. Behav. Biomed. Mater., 2020, 101, 103432 CrossRef PubMed
 .
.
- A. Kaye, R. F. T. Stepto, W. J. Work, J. V. Aleman and A. Y. Malkin, Pure Appl. Chem., 1998, 70(3), 701–754 CrossRef CAS
 .
.
-
G. A. Holzapfel. Nonlinear Solid Mechanics: A Continuum Approach for Engineering, Wiley, 2000 Search PubMed
 .
.
- T. J. Pence and K. Gou, Math. Mech. Solids, 2015, 20(2), 157–182 CrossRef
 .
.
-
A. N. Gent. Engineering with Rubber, Carl Hanser Verlag, 2001 Search PubMed
 .
.
- P. J. Flory, J. Chem. Phys., 1977, 66(12), 5720–5729 CrossRef CAS
 .
.
- P. J. Flory, Polym. J., 1985, 17(1), 1–12 CrossRef CAS
 .
.
- G. W. Scherer, J. Non-Cryst. Solids, 1989, 108(1), 18–27 CrossRef CAS
 ; 1989, 108(1), 28–36.
; 1989, 108(1), 28–36.
- F. Meng and E. M. Terentjev, Macromolecules, 2018, 51(12), 4660–4669 CrossRef CAS
 .
.
- V. Zamani and T. J. Pence, Int. J. Solids Struct., 2017, 125, 134–149 CrossRef
 .
.
- W. Kuhn and F. Grün, J. Polym. Sci., 1946, 1, 183 CrossRef CAS
 .
.
- P. G. De Gennes, Macromolecules, 1976, 9(4), 587 CrossRef CAS
 .
.
- P. G. De Gennes, Phys. Lett. A, 1969, 30(8), 454–455 CrossRef
 .
.
-
P. M. Chaikin and T. C. Lubensky, Principles of Condensed Matter Physics, Cambridge University Press, 2007 Search PubMed
 .
.
- L. D. Landau, Zh. Eksp. Teor. Fiz., 1937, 7, 19–32 CAS
 .
.
- J. Cheng, Z. Jia, H. Guo, Z. Nie and T. Li, J. Mech. Phys. Solids, 2019, 124, 143–158 CrossRef CAS
 .
.
- W. Hong, X. Zhao, J. Zhou and Z. Suo, J. Mech. Phys. Solids, 2008, 56(5), 1779–1793 CrossRef CAS
 .
.
- H. Lopez-Menendez and L. Gonzalez-Torres, J. Mech. Phys. Solids, 2019, 127, 208–220 CrossRef CAS
 .
.
- T. Bertrand, J. Peixinho, S. Mukhopadhyay and C. W. MacMinn, Phys. Rev. Appl., 2016, 6(6), 064010 CrossRef
 .
.
- E. Peña, J. Mech. Phys. Solids, 2011, 59(9), 1808–1822 CrossRef
 .
.
-
M. Funaki and P. A. Janmey. Technologies to Engineer Cell Substrate Mechanics in Hydrogels, Biology and Engineering of Stem Cell Niches, Academic Press, 2017, ch. 23 Search PubMed
 .
.
- M. Kharbedia, N. Caselli, H. López-Menéndez, E. Enciso, J. A. Santiago and F. Monroy, Nat. Commun., 2021, 12, 1130 CrossRef CAS PubMed
 .
.
- J. M. González, M. Jiménez, M. Vélez, J. Mingorance, J. M. Andreu, M. Vicente and G. Rivas, J. Biol. Chem., 2003, 278(39), 37664–37671 CrossRef PubMed
 .
.
- X. Ma, D. W. Ehrhardt and W. Margolin, Proc. Natl. Acad. Sci. U. S. A., 1996, 93(23), 12998–13003 CrossRef CAS PubMed
 .
.
- P. González de Prado Salas, I. Hörger, F. M. García, J. Mendieta, Á. Alonso, M. Encinar, P. G. Puertas, M. Vélez and P. Tarazona, Soft Matter, 2014, 10(12), 1977–1986 RSC
 .
.
- P. M. Gil, A. Paez, I. Hörger, G. Rivas, M. Vicente, P. Tarazona and M. Vélez, Proc. Natl. Acad. Sci. U. S. A., 2012, 109(21), 8133–8138 CrossRef PubMed
 .
.
- P. Caldas, M. L. Pelegrín, D. Pearce, N. B. Budanur, J. Brugués and M. Loose, Nat. Commun., 2019, 10(1), 1–13 CrossRef PubMed
 .
.
- N. W. Goehring and J. Beckwith, Curr. Biol., 2005, 15(13), 514–526 CrossRef PubMed
 .
.
- J. Errington, R. A. Daniel and D. J. Scheffers, Microbiol. Mol. Biol. Rev., 2003, 67(1), 52–65 CrossRef CAS PubMed
 .
.
- D. P. Haeusser and W. Margolin, Nat. Rev. Microbiol., 2016, 14(5), 305–319 CrossRef CAS PubMed
 .
.
- H. P. Erickson, Proc. Natl. Acad. Sci. U. S. A., 2009, 106(23), 9238–9243 CrossRef CAS PubMed
 .
.
- Z. Zhang, J. J. Morgan and P. A. Lindahl, J. Math. Biol., 2014, 68(4), 911–930 CrossRef PubMed
 .
.
- R. McQuillen and J. Xiao, Ann. Rev. Biophys., 2020, 49, 309–341 CrossRef CAS PubMed
 .
.
- H. P. Erickson, D. E. Anderson and M. Osawa, MMBR, 2010, 74(4), 504–528 CrossRef CAS PubMed
 .
.
- G. Lan, A. Dajkovic, D. Wirtz and S. X. Sun, Biophys. J., 2008, 95(8), 4045–4056 CrossRef CAS PubMed
 .
.
- K. H. Huang, J. Durand-Heredia and A. Janakiraman, J. Bacteriol., 2013, 195(9), 1859–1868 CrossRef CAS PubMed
 .
.
- M. Encinar, A. V. Kralicek, A. Martos, M. Krupka, S. Cid, A. Alonso, I. Rico, A. M. Jiménez and M. Vélez, Langmuir, 2013, 29(30), 9436–9446 CrossRef CAS PubMed
 .
.
- S. Huecas, E. Ramírez-Aportela, A. Vergoñós, R. Núñez-Ramírez, O. Llorca, J. Fernando Díaz, D. J. Rodríguez, M. A. Oliva, P. Castellen and J. M. Andreu, Biophys. J., 2017, 113(8), 1831–1844 CrossRef CAS PubMed
 .
.
- P. Mateos-Gil, P. Tarazona and M. Vélez, Microbiol. Rev., 2019, 43(1), 73–87 CAS
 .
.
- M. Rahman, Z. Li, T. Zhang, S. Du, X. Ma, P. Wang and Y. Chen, Sci. Rep., 2020, 10(1), 1–12 CrossRef PubMed
 .
.
- M. Osawa, D. E. Anderson and H. P. Erickson, Science, 2008, 320(5877), 792–794 CrossRef CAS PubMed
 .
.
- I. Hörger, E. Velasco, G. Rivas, M. Vélez and P. Tarazona, Biophys. J., 2008, 94(11), 81–83 CrossRef PubMed
 .
.
- I. L. Montero, P. M. Gil, M. Sferrazza, P. L. Navajas, M. Vélez and F. Monroy, Langmuir, 2012, 28(10), 4744–4753 CrossRef PubMed
 .
.
- I. L. Montero, P. L. Navajas, J. Mingorance, M. Vélez, M. Vicente and F. Monroy, Biochim. Biophys. Acta, 2013, 1828(2), 687–698 CrossRef PubMed
 .
.
- T. Lu, L. An, J. Li, C. Yuan and T. J. Wang, J. Mech. Phys. Solids, 2015, 85, 160–175 CrossRef
 .
.
- S. Mytnyk, I. Ziemecka, A. G. L. Olive, J. W. M. van der Meer, K. A. Totlani, S. Oldenhof, M. T. Kreutzer, V. van Steijn and J. H. van Esch, RSC Adv., 2017, 7(19), 11331–11337 RSC
 .
.
- W. Song, Y. C. Lu, A. S. Frankel, D. An, R. E. Schwartz and M. Ma, Sci. Rep., 2015, 5(1), 1–13 CAS
 .
.
- S. Zhao, P. Agarwal, W. Rao, H. Huang, R. Zhang, Z. Liu, J. Yu, N. Weisleder, W. Zhang and X. He, Int. Biol., 2014, 6(9), 874–884 CAS
 .
.
- D. R. Griffin, W. M. Weaver, P. O. Scumpia, D. Di Carlo and T. Segura, Nat. Mater., 2015, 14(7), 737–744 CrossRef CAS PubMed
 .
.
- Y. Wang and J. Wang, Analyst, 2014, 139(10), 2449–2458 RSC
 .
.
- R. M. Olabisi, Z. Waunyka, W. Lazard, C. L. Franco, M. A. Hall, S. K. Kwon, E. M. Sevick-Muraca, J. A. Hipp, A. R. Davis, E. A. Olmsted-Davis and J. L. West, Tissue Eng., Part A, 2010, 16(12), 3727–3736 CrossRef CAS PubMed
 .
.
|
| This journal is © The Royal Society of Chemistry 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *ab
*ab

![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) w = Vw/V ≈ 0.9, thus
w = Vw/V ≈ 0.9, thus ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) p = Vp/V ≈ 0.1), and a relatively low polymer fraction (ϕ), making them practically incompressible.40 Under the high hydrogel swelling considered (
p = Vp/V ≈ 0.1), and a relatively low polymer fraction (ϕ), making them practically incompressible.40 Under the high hydrogel swelling considered (![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) p ≈ 0.1 ≪
p ≈ 0.1 ≪ ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) w), and relatively low PA-crosslinking degree (ϕPA = 0.025), the polymer matrix provides shear rigidity through the flexible edges of the cellular structure (Fig. 2a). These solidlike elements are made up of a chemically crosslinked and physically entangled polymer network essentially characterized by the overall density of its binding junctions.3,41,42 Actively treadmilling ZLP-actuators, driven by living FtsZ polymerization under GTP hydrolysis,18–20 generate spatially randomized extensile fluctuations in the absence of directional anisotropy.21 In the hybrid PA–ZLP system, nonequilibrium steady states arise,39 where oscillatory shear maintains a stationary elasticity-swelling constrained imbalance.27 Despite being out-of-equilibrium, this mechanical tradeoff results in an effective constant rigidity considered stationary (Supplementary Note N1, ESI†).
w), and relatively low PA-crosslinking degree (ϕPA = 0.025), the polymer matrix provides shear rigidity through the flexible edges of the cellular structure (Fig. 2a). These solidlike elements are made up of a chemically crosslinked and physically entangled polymer network essentially characterized by the overall density of its binding junctions.3,41,42 Actively treadmilling ZLP-actuators, driven by living FtsZ polymerization under GTP hydrolysis,18–20 generate spatially randomized extensile fluctuations in the absence of directional anisotropy.21 In the hybrid PA–ZLP system, nonequilibrium steady states arise,39 where oscillatory shear maintains a stationary elasticity-swelling constrained imbalance.27 Despite being out-of-equilibrium, this mechanical tradeoff results in an effective constant rigidity considered stationary (Supplementary Note N1, ESI†).

 while allowing each material element to evolve into an equilibrium configuration (Supplementary Note N1, ESI†).
while allowing each material element to evolve into an equilibrium configuration (Supplementary Note N1, ESI†).
 represents the mechanical rigidness of the hydrogel as depending on the Cauchy-Green (CG) stress tensor
represents the mechanical rigidness of the hydrogel as depending on the Cauchy-Green (CG) stress tensor  .44,45 For given deformation strain (γ), this equilibrium term is essentially determined upon structural mesh variables (ϕ), constitutionally describing matrix crosslinking degrees and compositional concentrations.41,42,46 Additionally, the strain-dependent interaction term
.44,45 For given deformation strain (γ), this equilibrium term is essentially determined upon structural mesh variables (ϕ), constitutionally describing matrix crosslinking degrees and compositional concentrations.41,42,46 Additionally, the strain-dependent interaction term  describes the nonlinear interactions between the passive hydrogel matrix and the active additive leading to non-equilibrium elasticity (either weakening or strengthening). The interaction energy depends on both passive deformations and active phase interactions, coupled through an order parameter
describes the nonlinear interactions between the passive hydrogel matrix and the active additive leading to non-equilibrium elasticity (either weakening or strengthening). The interaction energy depends on both passive deformations and active phase interactions, coupled through an order parameter  which is dependent on the additive concentration variable
which is dependent on the additive concentration variable  describing the effective driving effect from the active component. This crucial interaction parameter will be further described in Section 2.3. The neo-Hookean CG tensor includes components relevant to both compression and shear deformations, governed by effective osmotic/swelling interactions between reconfigurable binding points.29,41,45 A detailed analysis is provided as ESI† (Supplementary Note N1, ESI†). These interactions, either active or passive, are described by the effective interaction parameter
describing the effective driving effect from the active component. This crucial interaction parameter will be further described in Section 2.3. The neo-Hookean CG tensor includes components relevant to both compression and shear deformations, governed by effective osmotic/swelling interactions between reconfigurable binding points.29,41,45 A detailed analysis is provided as ESI† (Supplementary Note N1, ESI†). These interactions, either active or passive, are described by the effective interaction parameter  which depends on FtsZ concentration
which depends on FtsZ concentration  . Thus, the constitutional CG-tensor can vary with elastic changes in network interactions modulated under deformation i.e.,
. Thus, the constitutional CG-tensor can vary with elastic changes in network interactions modulated under deformation i.e.,  for a given strain (γ).37–41,45,47 Regarding macroscopic solid-like elasticity under shear, a constitutive relationship is established for the applied stress (σ), as
for a given strain (γ).37–41,45,47 Regarding macroscopic solid-like elasticity under shear, a constitutive relationship is established for the applied stress (σ), as  calculated for a given shear strain (γ).41,47 The stress–strain relationship is determined in terms of a generalized rigidity
calculated for a given shear strain (γ).41,47 The stress–strain relationship is determined in terms of a generalized rigidity  assumed to include linear and nonlinear components. Here, the strain tensor
assumed to include linear and nonlinear components. Here, the strain tensor  is considered invariant under rotation, representing the squared value of the local change in relative distances in the solid body due to shear deformation.41,47 At low strain (γ → 0), the constitutional relationship is linear, corresponding to the harmonic response of the polymer chains i.e.,
is considered invariant under rotation, representing the squared value of the local change in relative distances in the solid body due to shear deformation.41,47 At low strain (γ → 0), the constitutional relationship is linear, corresponding to the harmonic response of the polymer chains i.e.,  , where
, where  is the Hookean rigidity modulus.41 Above a yield point
is the Hookean rigidity modulus.41 Above a yield point  the stress response becomes nonlinear, entering an intermediate plastic plateau (i.e., constant
the stress response becomes nonlinear, entering an intermediate plastic plateau (i.e., constant  at γ → γY), followed by a hyper-elastic regime under large deformation (i.e.,
at γ → γY), followed by a hyper-elastic regime under large deformation (i.e.,  at γ ≫ γY). For simplicity, we consider the elastic energy as neo-Hookean strain function:45,47
at γ ≫ γY). For simplicity, we consider the elastic energy as neo-Hookean strain function:45,47
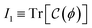 is the first invariant (trace) of the right Cauchy-Green strain tensor expressed uniquely in terms of the principal deformations.41,45,47 For an incompressible neo-Hookean material considered internally isotropic under simple (uniaxial) shear strain, then I1 = 3γ2.43,45 Under these isotropic straining conditions, the hydrogel's nonlinear elasticity is effectively described by the neo-Hookean energy density function within an effective rigidity modulus,
is the first invariant (trace) of the right Cauchy-Green strain tensor expressed uniquely in terms of the principal deformations.41,45,47 For an incompressible neo-Hookean material considered internally isotropic under simple (uniaxial) shear strain, then I1 = 3γ2.43,45 Under these isotropic straining conditions, the hydrogel's nonlinear elasticity is effectively described by the neo-Hookean energy density function within an effective rigidity modulus,  balancing shear rigidity (G) and osmotic/swelling ratio (J) (see Supplementary Note N1 for details, ESI†). Below, we argue how mesoscopic mechanostructural factors are encapsulated in the effective rigidity.
balancing shear rigidity (G) and osmotic/swelling ratio (J) (see Supplementary Note N1 for details, ESI†). Below, we argue how mesoscopic mechanostructural factors are encapsulated in the effective rigidity.
 when sufficient deformation exceeds the plasticity onset (γ > γY).41,47 Hence,
when sufficient deformation exceeds the plasticity onset (γ > γY).41,47 Hence,  for
for  resembling effective rubber-like plasticity.48,49 The nonlinear affine model accurately describes plastic deformations up to 40% beyond the yield point (γ ≤ 1.4γY) but may not predict further strengthening at larger strains limited by chain stretching.47 Although the model assumes reversible solidlike plasticity, no dissipative energy release is considered during fluidization. The extensible phantom chains may strengthen from a certain onset of stretching up to the maximum strain supported by chemical crosslinks (at γstr ≫ γY), hence resulting in an effective still reversible strengthening (i.e., Kstr ≫ K0 at γ < γstr) (see Fig. 3c). These models have been shown to capture hardening effects due to transient reconfiguration after plastic fluidization51 or bursting damage under critical hydrogel swelling.52 We will address these modelling issues when discussing the experimental data later.
resembling effective rubber-like plasticity.48,49 The nonlinear affine model accurately describes plastic deformations up to 40% beyond the yield point (γ ≤ 1.4γY) but may not predict further strengthening at larger strains limited by chain stretching.47 Although the model assumes reversible solidlike plasticity, no dissipative energy release is considered during fluidization. The extensible phantom chains may strengthen from a certain onset of stretching up to the maximum strain supported by chemical crosslinks (at γstr ≫ γY), hence resulting in an effective still reversible strengthening (i.e., Kstr ≫ K0 at γ < γstr) (see Fig. 3c). These models have been shown to capture hardening effects due to transient reconfiguration after plastic fluidization51 or bursting damage under critical hydrogel swelling.52 We will address these modelling issues when discussing the experimental data later.
 is determined by the activity concentration variable
is determined by the activity concentration variable  .
.
 represents the distance for binding correlations between polymer stands (see Fig. 3a), where
represents the distance for binding correlations between polymer stands (see Fig. 3a), where  denotes a reduced distance to a critical point for ordering.29 In the hybrid mesh considered here, this constitutional parameter should depend on compositional variables in a complex way i.e.,
denotes a reduced distance to a critical point for ordering.29 In the hybrid mesh considered here, this constitutional parameter should depend on compositional variables in a complex way i.e., 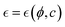 . Specifically, it depends on the fixed number of passive polymer PA-crosslinks (ϕ ≅ ϕPA), and the variable number of actively flexible ZLP-elements (c ≅ cFtsZ). Generally, the composition-dependent length
. Specifically, it depends on the fixed number of passive polymer PA-crosslinks (ϕ ≅ ϕPA), and the variable number of actively flexible ZLP-elements (c ≅ cFtsZ). Generally, the composition-dependent length  is larger at dependence of effective interactions than the persistence length lp, but smaller than the Flory radius RF.41 In chemically crosslinked polymer gels, for instance, this universal length diverges at the percolation threshold (ϕ*), but decreases essentially with the ordering degree of crosslinking as ξ(ϕ) ∼ (ϕ − ϕ*)−νd (here, ν is the Flory exponent and d represents dimensionality).29 For physically entangled gels, De Gennes stablished his famous scaling law for the characteristic entanglement length ξ(c)/lp ≈ (c*/c)δ(ν,d), defined above the critical concentration (c > c*); at the critical overlapping concentration ξ(c*) ≈ lp.28,29 In those cases, the critical amplitude is
is larger at dependence of effective interactions than the persistence length lp, but smaller than the Flory radius RF.41 In chemically crosslinked polymer gels, for instance, this universal length diverges at the percolation threshold (ϕ*), but decreases essentially with the ordering degree of crosslinking as ξ(ϕ) ∼ (ϕ − ϕ*)−νd (here, ν is the Flory exponent and d represents dimensionality).29 For physically entangled gels, De Gennes stablished his famous scaling law for the characteristic entanglement length ξ(c)/lp ≈ (c*/c)δ(ν,d), defined above the critical concentration (c > c*); at the critical overlapping concentration ξ(c*) ≈ lp.28,29 In those cases, the critical amplitude is  (with N being the calibrated chain length), and the scaling exponent δ(ν,d) = νd/(νd − 1) > νd, both modulated by interactions.41 De Gennes considered calibrated polymer overlapping (constant N), but he postulated that the same results also apply to the swelling of more complex networks.29 Specifically, the hybrid meshwork represented in Fig. 3a consists of passive (affine) crosslinks between bound strands, interspersed with active (phantom) entanglements that disrupt polymer bonds, resulting in unbound strands leading to neo-Hookean response. Despite the differences between dimensional random models describing hybrid affine and active phantom phases, a mean-field approach can recapitulate their mechanical behaviour into a simpler ordered mesoscopic model that is mechanically isotropic but compositionally heterogeneous at coexistence (see Sections 2.8–2.9).36
(with N being the calibrated chain length), and the scaling exponent δ(ν,d) = νd/(νd − 1) > νd, both modulated by interactions.41 De Gennes considered calibrated polymer overlapping (constant N), but he postulated that the same results also apply to the swelling of more complex networks.29 Specifically, the hybrid meshwork represented in Fig. 3a consists of passive (affine) crosslinks between bound strands, interspersed with active (phantom) entanglements that disrupt polymer bonds, resulting in unbound strands leading to neo-Hookean response. Despite the differences between dimensional random models describing hybrid affine and active phantom phases, a mean-field approach can recapitulate their mechanical behaviour into a simpler ordered mesoscopic model that is mechanically isotropic but compositionally heterogeneous at coexistence (see Sections 2.8–2.9).36
 expanded in series from the perturbative distance
expanded in series from the perturbative distance  defined as a critical concentration for phase segregation. The scaling exponent δ(ν, d) reflects dimension (d), and effective mean-field interactions Γ(ν), as above mentioned. The unperturbed Rouse tube size ξ0 ≅ lp(κ) denotes the isotropic length determined by the intrinsic chain rigidness in the unperturbed meshwork conditions; these are Γ(νcrit) = 0, for
defined as a critical concentration for phase segregation. The scaling exponent δ(ν, d) reflects dimension (d), and effective mean-field interactions Γ(ν), as above mentioned. The unperturbed Rouse tube size ξ0 ≅ lp(κ) denotes the isotropic length determined by the intrinsic chain rigidness in the unperturbed meshwork conditions; these are Γ(νcrit) = 0, for 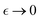 . Hence, this reference size determines the bare Hookean rigidity K0 ≅ kBT/ξd0.29 Analogous to the Landau–De Gennes’ c* – theorem,29,55,56 which states that structural deformation is constrained by local connectivity akin to short-range ordering effects in liquid crystal phases, this mesoscopic scenario allows for effective crosslink adjustments above the critical overlapping concentration (c ≥ ccrit).29 Referred to the critical interactions (at νcrit), they are either unbinding due to softening interactions i.e., ξ > ξ0 (for ν < νcrit, thus Γsoft < 0), or strengthening from hardening interactions i.e., ξ < ξ0 (for ν > νcrit, thus Γhard > 0). For a hybrid neo-Hookean meshwork approaching the critical point (
. Hence, this reference size determines the bare Hookean rigidity K0 ≅ kBT/ξd0.29 Analogous to the Landau–De Gennes’ c* – theorem,29,55,56 which states that structural deformation is constrained by local connectivity akin to short-range ordering effects in liquid crystal phases, this mesoscopic scenario allows for effective crosslink adjustments above the critical overlapping concentration (c ≥ ccrit).29 Referred to the critical interactions (at νcrit), they are either unbinding due to softening interactions i.e., ξ > ξ0 (for ν < νcrit, thus Γsoft < 0), or strengthening from hardening interactions i.e., ξ < ξ0 (for ν > νcrit, thus Γhard > 0). For a hybrid neo-Hookean meshwork approaching the critical point ( for ν = νcrit), the interaction-dependent characteristic size
for ν = νcrit), the interaction-dependent characteristic size  may accommodate both, the strengthening effect of fixed passive crosslinks in the affine network (δ > 0), and the softening effect of sliding entanglements enabled by ATP-dependent ZLP treadmilling (δ < 0). Notably, Active FtsZ-driven entanglements may further increase this correlation length
may accommodate both, the strengthening effect of fixed passive crosslinks in the affine network (δ > 0), and the softening effect of sliding entanglements enabled by ATP-dependent ZLP treadmilling (δ < 0). Notably, Active FtsZ-driven entanglements may further increase this correlation length  contingent upon a supercritical concentration c > ccrit(Γ), and the repulsive nature of the interaction Γsoft(ν) < 0. To model the mesoscopic behaviour of the hybrid PA–ZLP meshwork, we use a self-consistent mean-field theory that simplifies this high-dimensional polymer system into a one-dimensional model governed by the interaction parameter Γ(ν).56 Similarly to the Landau–Ginzburg (LG) theory of phase transitions,57 our mean-field quasi-chemical approach approximates the complex hydrogel neo-Hookean elasticity by averaging correlated interactions Γ(ν).56 With the mesoscopic overlapping length defining the apparent size of the Rouse tube
contingent upon a supercritical concentration c > ccrit(Γ), and the repulsive nature of the interaction Γsoft(ν) < 0. To model the mesoscopic behaviour of the hybrid PA–ZLP meshwork, we use a self-consistent mean-field theory that simplifies this high-dimensional polymer system into a one-dimensional model governed by the interaction parameter Γ(ν).56 Similarly to the Landau–Ginzburg (LG) theory of phase transitions,57 our mean-field quasi-chemical approach approximates the complex hydrogel neo-Hookean elasticity by averaging correlated interactions Γ(ν).56 With the mesoscopic overlapping length defining the apparent size of the Rouse tube  relative to the critical distance to the critical point
relative to the critical distance to the critical point 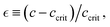 hence, we stablish the multiscale connection
hence, we stablish the multiscale connection  (see Section 2.3).
(see Section 2.3).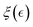 . Indeed, active reptation systems with slipping linkages behave like physically entangled gels with a variable mesh size
. Indeed, active reptation systems with slipping linkages behave like physically entangled gels with a variable mesh size  58 where sliding interactions maintain a reversible two-state equilibrium between reptation states either passive or active.59 When macroscopic shear deformation occurs slower than reptation dynamics (as in rheological experiments), softening interactions emerge leading above the onset of plasticity at
58 where sliding interactions maintain a reversible two-state equilibrium between reptation states either passive or active.59 When macroscopic shear deformation occurs slower than reptation dynamics (as in rheological experiments), softening interactions emerge leading above the onset of plasticity at  – the yield point. Hence, active elasticity can be expressed as a weakening interaction considered neo-Hookean i.e., the apparent modulus is
– the yield point. Hence, active elasticity can be expressed as a weakening interaction considered neo-Hookean i.e., the apparent modulus is 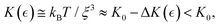 under structural rigidity K0 ≅ kBT/ξ03, considering an effective softening
under structural rigidity K0 ≅ kBT/ξ03, considering an effective softening 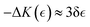 (for δ < 0). This active softening is ultimately determined by treadmilling assisted reptation, which causes effective unbinding interactions leading to an apparent reduction in the overlap functionality i.e., −ΔK ≈ K0(4/f2)(df/dΓ) (assuming df/dΓ ≤ 0). Hence, we have related the changes in overlapping functionality with the effective interactions modulated by FtsZ activity as follows
(for δ < 0). This active softening is ultimately determined by treadmilling assisted reptation, which causes effective unbinding interactions leading to an apparent reduction in the overlap functionality i.e., −ΔK ≈ K0(4/f2)(df/dΓ) (assuming df/dΓ ≤ 0). Hence, we have related the changes in overlapping functionality with the effective interactions modulated by FtsZ activity as follows  . This differential relationship establishes the multiscale connection between the microscopic interactions and the macroscopic order i.e.,
. This differential relationship establishes the multiscale connection between the microscopic interactions and the macroscopic order i.e.,  otherwise stated, the better effective polymer–solvent interaction with increasing δ(ν, d), the higher effective change of overlapping functionality under given activity
otherwise stated, the better effective polymer–solvent interaction with increasing δ(ν, d), the higher effective change of overlapping functionality under given activity  . Therefore, we can stablish the active softening governed by a mass action equilibrium between unbound (ub) and bound (b) overlapping states:60
. Therefore, we can stablish the active softening governed by a mass action equilibrium between unbound (ub) and bound (b) overlapping states:60
 . Moreover, the detaching energy sets the yield strain for plasticity (γY), which depends on the remanent force i.e.,
. Moreover, the detaching energy sets the yield strain for plasticity (γY), which depends on the remanent force i.e.,  (defined for Δσ = ΔKγY). Hence, we redefine the external unbinding force as the yield stress that causes disentangling equivalent to macroscopic plastic strain, wext = Fξ ⇔ K(γ − γY) (where F(γ) is the unbinding force and
(defined for Δσ = ΔKγY). Hence, we redefine the external unbinding force as the yield stress that causes disentangling equivalent to macroscopic plastic strain, wext = Fξ ⇔ K(γ − γY) (where F(γ) is the unbinding force and  the effective entanglement size also dependent on the applied strain). Therefore, the unbinding driving force can be expressed in terms of elasticity as
the effective entanglement size also dependent on the applied strain). Therefore, the unbinding driving force can be expressed in terms of elasticity as  (where γY(ξ) is the yield strain essentially fixed by the entanglement length, and K(f, γ) is the effective strain-dependent value of shear modulus). Ultimately, the effective stress–strain relationship holds plasticity as a function of
(where γY(ξ) is the yield strain essentially fixed by the entanglement length, and K(f, γ) is the effective strain-dependent value of shear modulus). Ultimately, the effective stress–strain relationship holds plasticity as a function of  the apparent binding functionality dependent on activity; in the first order approximation, this is
the apparent binding functionality dependent on activity; in the first order approximation, this is  . Therefore, the key structural characteristics for plastic yielding leading to active-passive phase segregation are: (a) the entanglement size itself
. Therefore, the key structural characteristics for plastic yielding leading to active-passive phase segregation are: (a) the entanglement size itself  ; (b) the active decrease in entanglement functionality
; (b) the active decrease in entanglement functionality  ; both determined under effective interactions Γ(ν), in approaching the critical point
; both determined under effective interactions Γ(ν), in approaching the critical point 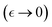 (discussed in Section 2.3). Fig. 3c shows expected nonlinear stress–strain plots dependent on the interaction-driven crosslinking activity of the meshwork.
(discussed in Section 2.3). Fig. 3c shows expected nonlinear stress–strain plots dependent on the interaction-driven crosslinking activity of the meshwork. and interaction energies summarized by the order parameter Γ(ν),29,30,34,35 as depicted in Fig. 3. First, local Hookean rigidity is determined by the conformational chain persistence along the m crosslinked strands in the meshwork i.e., K0(ξ) ≈ lpkBT/ξ03 ≪ Eξ/lc2 ⇔ mκ. Second, the effective work exerted by the external force causing plastic deformation is proportional to the number n of unbounded strands i.e.,
and interaction energies summarized by the order parameter Γ(ν),29,30,34,35 as depicted in Fig. 3. First, local Hookean rigidity is determined by the conformational chain persistence along the m crosslinked strands in the meshwork i.e., K0(ξ) ≈ lpkBT/ξ03 ≪ Eξ/lc2 ⇔ mκ. Second, the effective work exerted by the external force causing plastic deformation is proportional to the number n of unbounded strands i.e.,  . Third, stable nonlinear deformation within the hardening regime must be compatible with the maximum stretching work i.e.,
. Third, stable nonlinear deformation within the hardening regime must be compatible with the maximum stretching work i.e.,  (at γY < γ ≪ γstr). Hence, these arguments support passive stiffness based on the passive overlapping length proportional to chain persistence ξ ∝ lp(≪ lc), which is compatible with apparent Hookean rigidity as K0(ξ) ≅ mlp/ξ ⇔ mκ.29 Therefore, we primarily establish rigidity governed by the balance between the binding energy of the m crosslinks and the imposed strain:
(at γY < γ ≪ γstr). Hence, these arguments support passive stiffness based on the passive overlapping length proportional to chain persistence ξ ∝ lp(≪ lc), which is compatible with apparent Hookean rigidity as K0(ξ) ≅ mlp/ξ ⇔ mκ.29 Therefore, we primarily establish rigidity governed by the balance between the binding energy of the m crosslinks and the imposed strain:
 . Otherwise stated in the context of ZLP activity, the mesh weakens due to treadmilling-assisted reptation in regimes of active softening i.e.,
. Otherwise stated in the context of ZLP activity, the mesh weakens due to treadmilling-assisted reptation in regimes of active softening i.e.,  (see Fig. 2b, right panel).
(see Fig. 2b, right panel).
 (see eqn (4)). The barrier separates two (un)bounded states with differential energy Eb, constrained by shear rigidity K(γ), under strain γ (Fig. 3a; upper inset). For passive hydrogels, ξ ≈ lp ≪ lc, thus Eb(ξ) ≲ K0(ξ)lp3 ≈ mκ. In the plastic regime, if the injected work exceeds the kinetic barrier wext(γ) ≥ Eξ ≫ Eb, the mesh undergoes chain unbinding i.e., pub(γ) ≥ pb. Hence, the plastic threshold for retaining the chains bound is given by wext(γ) − Eξ ≈ Eb + (alp/lcξ)γ (at γ = γY, then wext(γY) − Eξ = 0). Therefore, the yield strain necessary to plastic unbinding can be expressed in terms of structural energies as:
(see eqn (4)). The barrier separates two (un)bounded states with differential energy Eb, constrained by shear rigidity K(γ), under strain γ (Fig. 3a; upper inset). For passive hydrogels, ξ ≈ lp ≪ lc, thus Eb(ξ) ≲ K0(ξ)lp3 ≈ mκ. In the plastic regime, if the injected work exceeds the kinetic barrier wext(γ) ≥ Eξ ≫ Eb, the mesh undergoes chain unbinding i.e., pub(γ) ≥ pb. Hence, the plastic threshold for retaining the chains bound is given by wext(γ) − Eξ ≈ Eb + (alp/lcξ)γ (at γ = γY, then wext(γY) − Eξ = 0). Therefore, the yield strain necessary to plastic unbinding can be expressed in terms of structural energies as: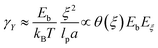


![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) <
< ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) crit), ZLP filaments do not activate enough to cause macroscopic softening. For supercritical states (
crit), ZLP filaments do not activate enough to cause macroscopic softening. For supercritical states (![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) >
> ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) crit), ZLPs activate sufficiently to enable swelling and fluidization, decreasing crosslinking and weakening the hydrogel (i.e., Γ(
crit), ZLPs activate sufficiently to enable swelling and fluidization, decreasing crosslinking and weakening the hydrogel (i.e., Γ(![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) ) < 0). When focussing on the plasticity ZLP effects under controlled PA crosslinking, we examine the critical phenomena encoded in the interaction functional by the critical distance
) < 0). When focussing on the plasticity ZLP effects under controlled PA crosslinking, we examine the critical phenomena encoded in the interaction functional by the critical distance  i.e.,
i.e.,  . Additionally, we consider constant elastic energy Ψelas(c), at least when the activity concentration approaches the critical point (c → ccrit), where the interaction parameter is small (Γ ≈ 0), as describable by Landau theory of phase transitions.36
. Additionally, we consider constant elastic energy Ψelas(c), at least when the activity concentration approaches the critical point (c → ccrit), where the interaction parameter is small (Γ ≈ 0), as describable by Landau theory of phase transitions.36

![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) ) and
) and  are systemic parameters controlling the structural phase transition, with Γ(c) as the activity order parameter.
are systemic parameters controlling the structural phase transition, with Γ(c) as the activity order parameter.
![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) ) ≤ 0, represents the quasi-chemical energy barrier between equilibrium phases barely determined by the chemical potential (
) ≤ 0, represents the quasi-chemical energy barrier between equilibrium phases barely determined by the chemical potential (![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) ). The critical condition, α(Eξ,
). The critical condition, α(Eξ, ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) ) = 0, occurs when
) = 0, occurs when ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) =
= ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) crit(Eb, ccrit). The quartic term β[C(γ)], depends on the concentration of actively disentangling elements and deformation status by coupling to the elastic energy through the Cauchy-Green strain tensor
crit(Eb, ccrit). The quartic term β[C(γ)], depends on the concentration of actively disentangling elements and deformation status by coupling to the elastic energy through the Cauchy-Green strain tensor  . A positive β implies stable strain-dependent strengthening (i.e., stiffening order), while a negative β suggests weakening instabilities (softening disorder like active swelling and hyperfluidity). Assuming the system is near the critical point (at α ≈ α0 → 0), this model captures the interplay between extrinsic deformation and intrinsic changes in rigidity. Because the control parameter changes sign across the critical point, it can be expanded as α(
. A positive β implies stable strain-dependent strengthening (i.e., stiffening order), while a negative β suggests weakening instabilities (softening disorder like active swelling and hyperfluidity). Assuming the system is near the critical point (at α ≈ α0 → 0), this model captures the interplay between extrinsic deformation and intrinsic changes in rigidity. Because the control parameter changes sign across the critical point, it can be expanded as α(![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) ) ≈ −Eξ(c − ccrit)/ccrit, where −Eξ reflects the kinetic dependence on the barrier height for mesh disentanglement.
) ≈ −Eξ(c − ccrit)/ccrit, where −Eξ reflects the kinetic dependence on the barrier height for mesh disentanglement.
![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) eq =
eq = ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) solid =
solid = ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) fluid, where the chemical potential is equal in both phases. Consequently, the equilibrium value of the interaction parameter is:
fluid, where the chemical potential is equal in both phases. Consequently, the equilibrium value of the interaction parameter is:
 where
where  is the reduced distance to the critical point as considered in our mesoscopic depiction of effective mean-field interactions. The scaling ordering amplitude is Γ0(c) ≡ (Eξ/2|β|)1/2, determined by the ratio of the kinetic barrier height to the nonlinear change in structural binding interaction.
is the reduced distance to the critical point as considered in our mesoscopic depiction of effective mean-field interactions. The scaling ordering amplitude is Γ0(c) ≡ (Eξ/2|β|)1/2, determined by the ratio of the kinetic barrier height to the nonlinear change in structural binding interaction.
 . Fig. 4 illustrates the mesoscopic hypotheses for evaluating the phase space of hybrid PA–FtsZ hydrogels and performing stress–strain response calculations that predict a neo-Hookean plasticity. Particularly, mesh hybridization affects the yield point of the hydrogel (γ0), shifting it as
. Fig. 4 illustrates the mesoscopic hypotheses for evaluating the phase space of hybrid PA–FtsZ hydrogels and performing stress–strain response calculations that predict a neo-Hookean plasticity. Particularly, mesh hybridization affects the yield point of the hydrogel (γ0), shifting it as  (Fig. 4a). These mean-field predictions are discussed individually below in the context of the mesoscopic mesh model described in previous sections.
(Fig. 4a). These mean-field predictions are discussed individually below in the context of the mesoscopic mesh model described in previous sections.
![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) >
> ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) crit at c > ccrit), leading to supercritical mesh softening through repulsive, crosslink-disruptive interactions (weakening, liquidlike Γfluid > 0; Fig. 4a; top). In passive reptation theory, the polymer chain is confined to a narrow tube formed by closely spaced sticking linkages.28–30 These constraints are represented in our case by the persistent crosslinks of the passive PA matrix (ξ0 ≈ lp). In Fig. 4b, we illustrate how active ZLP entanglements are created and destroyed during treadmilling under GTP hydrolysis (top panel). Relative to passive ones, active ZLPs fluctuate within a broader reptation tube interacting with the surrounding matrix where movable entanglement links are continuously remodelled across slipping linkages. Similar to the Rouse size of the reptation tube for a passive chain (ξ0), we assume the characteristic length between the passively crosslinked PA gel and the active ZLPs is uniformly distributed along the FtsZ filament, with spacing comparable to the passive entanglement size but smaller than the contour length (ξ0 ≤ ξ ≪ lc; Fig. 4b, top). Therefore, structural softening under active ZLP hybridization is promoted by an effective decrease of chain overlapping m(f, γ) = mmax(γ, f0) − n(γ, f) < mmax (relative to the maximal equilibrium value mmax), under effectively lower crosslinking functionality i.e.,
crit at c > ccrit), leading to supercritical mesh softening through repulsive, crosslink-disruptive interactions (weakening, liquidlike Γfluid > 0; Fig. 4a; top). In passive reptation theory, the polymer chain is confined to a narrow tube formed by closely spaced sticking linkages.28–30 These constraints are represented in our case by the persistent crosslinks of the passive PA matrix (ξ0 ≈ lp). In Fig. 4b, we illustrate how active ZLP entanglements are created and destroyed during treadmilling under GTP hydrolysis (top panel). Relative to passive ones, active ZLPs fluctuate within a broader reptation tube interacting with the surrounding matrix where movable entanglement links are continuously remodelled across slipping linkages. Similar to the Rouse size of the reptation tube for a passive chain (ξ0), we assume the characteristic length between the passively crosslinked PA gel and the active ZLPs is uniformly distributed along the FtsZ filament, with spacing comparable to the passive entanglement size but smaller than the contour length (ξ0 ≤ ξ ≪ lc; Fig. 4b, top). Therefore, structural softening under active ZLP hybridization is promoted by an effective decrease of chain overlapping m(f, γ) = mmax(γ, f0) − n(γ, f) < mmax (relative to the maximal equilibrium value mmax), under effectively lower crosslinking functionality i.e.,  (relative to mmax). The decreased yield point reduces the Hookean range of the solidlike regime through weakening interaction leading fluidization
(relative to mmax). The decreased yield point reduces the Hookean range of the solidlike regime through weakening interaction leading fluidization 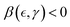 (Fig. 4c; upper regime).
(Fig. 4c; upper regime).
 driven by a negative interaction parameter (hardening, solidlike, Γsolid < 0; Fig. 4b, bottom). Such effective subcritical hardening resulted from the increase in the polymer crosslink density m(c, γ) → m0(c = 0,γ)|Γ(c)|, modulated by the interaction parameter Γ(c), with respect to reference values considered at zero FtsZ concentration m0. The hardening change (Δm(c, γ) = m − m0 > 0) represents the positive order parameter that enhances rigidity upon passive FtsZ hybridization (for
driven by a negative interaction parameter (hardening, solidlike, Γsolid < 0; Fig. 4b, bottom). Such effective subcritical hardening resulted from the increase in the polymer crosslink density m(c, γ) → m0(c = 0,γ)|Γ(c)|, modulated by the interaction parameter Γ(c), with respect to reference values considered at zero FtsZ concentration m0. The hardening change (Δm(c, γ) = m − m0 > 0) represents the positive order parameter that enhances rigidity upon passive FtsZ hybridization (for ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) <
< ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) crit). From a mesoscopic perspective, this structural strengthening raises the yield point with increasing concentration of inactive FtsZ filaments; for c ≥ ccrit (i.e., if
crit). From a mesoscopic perspective, this structural strengthening raises the yield point with increasing concentration of inactive FtsZ filaments; for c ≥ ccrit (i.e., if  ), this is
), this is  (Fig. 4b; bottom). In a composite passive gel, the first term represents the characteristic yield strain for the matrix (γ0), plus a perturbation controlled by a cohesive additive interaction modulated by the chemical potential in the equilibrated system (
(Fig. 4b; bottom). In a composite passive gel, the first term represents the characteristic yield strain for the matrix (γ0), plus a perturbation controlled by a cohesive additive interaction modulated by the chemical potential in the equilibrated system (![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) <
< ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) crit). Therefore, structural hydrogel stiffening under passive FtsZ hybridization is undergone by the effective increase of crosslinking m(f, γ) = mmax(γ, f0) − n(γ, f) > mmax, under higher effective functionality i.e.,
crit). Therefore, structural hydrogel stiffening under passive FtsZ hybridization is undergone by the effective increase of crosslinking m(f, γ) = mmax(γ, f0) − n(γ, f) > mmax, under higher effective functionality i.e.,  . The reinforced yield point extends over a strengthened solidlike regime through enhanced strengthening interaction
. The reinforced yield point extends over a strengthened solidlike regime through enhanced strengthening interaction  (Fig. 4c; lower regime).
(Fig. 4c; lower regime).
 ). In the active FtsZ hydrogel, the Landau model predicts a reduced density of chain overlaps due to the cooperation of treadmilling ZLPs (for
). In the active FtsZ hydrogel, the Landau model predicts a reduced density of chain overlaps due to the cooperation of treadmilling ZLPs (for  ), and decreasing interaction energy over fluidized bonds, limited by the kinetic barrier and reduced mesh chemical potential (i.e.,
), and decreasing interaction energy over fluidized bonds, limited by the kinetic barrier and reduced mesh chemical potential (i.e., 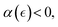 thus
thus  ). Conversely, passive stiffening occurs through strengthening interactions (for
). Conversely, passive stiffening occurs through strengthening interactions (for 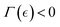 ), promoted by inactive FtsZ filaments, which reinforce crosslinking leading to higher kinetic barrier followed by increasing chemical potential (i.e.,
), promoted by inactive FtsZ filaments, which reinforce crosslinking leading to higher kinetic barrier followed by increasing chemical potential (i.e.,  and
and  ). Here, the effective crosslinking energy (Eb) has been defined by reference to the mesoscopic model as Eb ∝ κγY (where κ represents an effective mesoscopic stiffness, and γY the critical shear strain for yielding). Additionally, the kinetic barrier energy (Eξ) defines the critical amplitude in the phase-transition Landau model
). Here, the effective crosslinking energy (Eb) has been defined by reference to the mesoscopic model as Eb ∝ κγY (where κ represents an effective mesoscopic stiffness, and γY the critical shear strain for yielding). Additionally, the kinetic barrier energy (Eξ) defines the critical amplitude in the phase-transition Landau model  (see eqn (7)). A positive barrier to unbinding results in subcritical strengthening, while a negative barrier leads to supercritical fluidization. Therefore, we propose a theoretical expression for the effective nonlinear shear modulus, defining the neo-Hookean stress–strain relationship as a trade-off between passive and active element concentrations; referred to sections S ≅ ξ2 of the Rouse's tube (see Section 2); this is:
(see eqn (7)). A positive barrier to unbinding results in subcritical strengthening, while a negative barrier leads to supercritical fluidization. Therefore, we propose a theoretical expression for the effective nonlinear shear modulus, defining the neo-Hookean stress–strain relationship as a trade-off between passive and active element concentrations; referred to sections S ≅ ξ2 of the Rouse's tube (see Section 2); this is:

 the order parameter that fixes the effective interaction
the order parameter that fixes the effective interaction 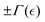 (see Fig. 4a).
(see Fig. 4a).
 mechanically neutral
mechanically neutral 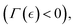 or softening
or softening  . Drawing from Landau's theory, which will be further validated, we interpret experimental findings in a weakly perturbed regime consistent with chain overlap binding energy (i.e., for
. Drawing from Landau's theory, which will be further validated, we interpret experimental findings in a weakly perturbed regime consistent with chain overlap binding energy (i.e., for  ). As a practical parametrization for the chemical potential, we consider a constant unbinding ratio determined by the maximum proportion of active ZLPs relative to chemically fixed crosslinking in the PA matrix, θmax−1 = (n/m)max ≅ cFtsZ with (δθ ≅ 0). For small deformations well below the yield point
). As a practical parametrization for the chemical potential, we consider a constant unbinding ratio determined by the maximum proportion of active ZLPs relative to chemically fixed crosslinking in the PA matrix, θmax−1 = (n/m)max ≅ cFtsZ with (δθ ≅ 0). For small deformations well below the yield point  , rigidity is nearly independent of nonlinear interaction (thus E0b ≅ K0ξ03). In the case of a reference passive meshwork
, rigidity is nearly independent of nonlinear interaction (thus E0b ≅ K0ξ03). In the case of a reference passive meshwork  assuming
assuming  we find the bare passive rigidity as
we find the bare passive rigidity as 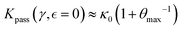 . Fully passive gels
. Fully passive gels  exhibit Hookean elasticity with K0(γ → 0) ≈ κ0. For active gels
exhibit Hookean elasticity with K0(γ → 0) ≈ κ0. For active gels  near the yield point under high plasticity (δγ ≡ γ − γY → 0), the effective modulus changes as
near the yield point under high plasticity (δγ ≡ γ − γY → 0), the effective modulus changes as  . In the fully active gel (θmax−1 → 1), corresponding to critical softening at
. In the fully active gel (θmax−1 → 1), corresponding to critical softening at  we found
we found  . Generally, above the yield point
. Generally, above the yield point  a strain-dependent shear rigidity defines the actively softened state under active plasticization; to lowest perturbative order (eqn (11)), one gets the active neo-Hookean elasticity modulus (by approximating eqn (10a) in the plastic regime):
a strain-dependent shear rigidity defines the actively softened state under active plasticization; to lowest perturbative order (eqn (11)), one gets the active neo-Hookean elasticity modulus (by approximating eqn (10a) in the plastic regime):
 . This plastic modulus is further affected by the microscopic binding energy required to detach a fixed crosslink through active reptation, denoted as
. This plastic modulus is further affected by the microscopic binding energy required to detach a fixed crosslink through active reptation, denoted as  . In the first-order approximation, the effective excess strain beyond the yield point
. In the first-order approximation, the effective excess strain beyond the yield point  and the corresponding mesoscopic softness
and the corresponding mesoscopic softness  both decrease proportionally with the chain overlap disruptive force of the softening interaction
both decrease proportionally with the chain overlap disruptive force of the softening interaction  .
.

 as expected for structurally weakening interactions i.e.,
as expected for structurally weakening interactions i.e.,  . Additionally, the softening stress correlates with the unbinding ratio (i.e., Δσ ∝ n/m → θ−1).
. Additionally, the softening stress correlates with the unbinding ratio (i.e., Δσ ∝ n/m → θ−1). . Fig. 7 demonstrates that the proposed phase transition model predicts a scaling relation for the interaction parameter
. Fig. 7 demonstrates that the proposed phase transition model predicts a scaling relation for the interaction parameter 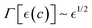 (with the order parameter
(with the order parameter  ; see eqn (7)). This relation effectively captures the softening and fluidization trends due to changes in the stiffness of the hybrid gel caused by active FtsZ filaments (see Fig. 7a). According to the active reptation model, the effective density of entanglement points θ(Γ) ≅ [m − n(Γ)]/nmax is controlled by the activity of the living polymer
; see eqn (7)). This relation effectively captures the softening and fluidization trends due to changes in the stiffness of the hybrid gel caused by active FtsZ filaments (see Fig. 7a). According to the active reptation model, the effective density of entanglement points θ(Γ) ≅ [m − n(Γ)]/nmax is controlled by the activity of the living polymer  (with
(with  ), and excess shear strain δγ = γ − γY. Then, the statistical population relationships in eqn (5a) and (5b) holds non-linearly and effectively active, resulting from a larger population of unbounded chains at larger strains (as shown in Fig. 7b, with the vertical axis in logarithmic scale to better illustrate the distinct regimes when the structure is active or inactive). As far the activation level increases, the density of entanglements decreases due to disruption by the active FtsZ gel. To summarize, the level of structural softening scales with the active interaction ratio
), and excess shear strain δγ = γ − γY. Then, the statistical population relationships in eqn (5a) and (5b) holds non-linearly and effectively active, resulting from a larger population of unbounded chains at larger strains (as shown in Fig. 7b, with the vertical axis in logarithmic scale to better illustrate the distinct regimes when the structure is active or inactive). As far the activation level increases, the density of entanglements decreases due to disruption by the active FtsZ gel. To summarize, the level of structural softening scales with the active interaction ratio  ultimately depending on the theoretically modelled Landau order parameter
ultimately depending on the theoretically modelled Landau order parameter  i.e., the observable softening
i.e., the observable softening  (see eqn (7)).
(see eqn (7)).
 follow the
follow the  – scaling as predicted from the Landau's theory (see eqn (7); experimental data taken from Table 1). (b) Strain dependence of the nonlinear stiffness of the hybrid gel for different levels of shear strain (γ) and concentration of active polymer FtsZ (cFtsZ).
– scaling as predicted from the Landau's theory (see eqn (7); experimental data taken from Table 1). (b) Strain dependence of the nonlinear stiffness of the hybrid gel for different levels of shear strain (γ) and concentration of active polymer FtsZ (cFtsZ). in the Landau's macroscopic scale). In summary, we demonstrate these multiscale characteristics and their quantitative dependence on the apparent concentration of the FtsZ additive
in the Landau's macroscopic scale). In summary, we demonstrate these multiscale characteristics and their quantitative dependence on the apparent concentration of the FtsZ additive  defined relative to a critical concentration ccrit. Furthermore, the phenomenological order parameter
defined relative to a critical concentration ccrit. Furthermore, the phenomenological order parameter  has been identified as an effective mean-field descriptor for the PA–FtsZ interaction. This order parameter differentiates two elasticity scenarios (Fig. 8; rightmost panels): (A) active softening by FtsZ treadmilling in a supercritical regime of structural weakening interactions (repulsive bi-phasic separation
has been identified as an effective mean-field descriptor for the PA–FtsZ interaction. This order parameter differentiates two elasticity scenarios (Fig. 8; rightmost panels): (A) active softening by FtsZ treadmilling in a supercritical regime of structural weakening interactions (repulsive bi-phasic separation  ; upper panel); (B) meshwork strengthening by interstitial mesh filling in a subcritical regime relative to the barely passive state (attractive monophase
; upper panel); (B) meshwork strengthening by interstitial mesh filling in a subcritical regime relative to the barely passive state (attractive monophase  ; lower panel). Such multiscale predictive modeling is crucial for bioengineering materials, allowing us to forecast mechanical properties, functional performance under strain, and diffusivity and transport in composite hydrogels with active elasticity. Future designs aim to develop cellular structures similar to thin-walled polymer capsules for biomedical applications, capable of expanding or bursting tumor cell aggregates87–90 and serving as smart drug delivery vehicles.91,92 Controlled hydrogel bursting is essential for effective delivery, balancing therapeutic benefits with potential adverse effects.93
; lower panel). Such multiscale predictive modeling is crucial for bioengineering materials, allowing us to forecast mechanical properties, functional performance under strain, and diffusivity and transport in composite hydrogels with active elasticity. Future designs aim to develop cellular structures similar to thin-walled polymer capsules for biomedical applications, capable of expanding or bursting tumor cell aggregates87–90 and serving as smart drug delivery vehicles.91,92 Controlled hydrogel bursting is essential for effective delivery, balancing therapeutic benefits with potential adverse effects.93
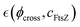 recapitulates the degree of crosslinking (ϕcross), and the concentration of FtsZ monomers (cFtsZ). The mesoscopic structure is depicted as a passive crosslinked meshwork with embedded active ZLP treadmillers able to locally reconfigure the physical entanglements (De Gennes’ scale, characterized by effective mesh length
recapitulates the degree of crosslinking (ϕcross), and the concentration of FtsZ monomers (cFtsZ). The mesoscopic structure is depicted as a passive crosslinked meshwork with embedded active ZLP treadmillers able to locally reconfigure the physical entanglements (De Gennes’ scale, characterized by effective mesh length  leading to Rouse tube broadening under treadmilling activity, and effective meshwork functionality
leading to Rouse tube broadening under treadmilling activity, and effective meshwork functionality  leading to effective disentanglement). (Macroscale) A two-component interacting system recapitulates both, passive elastic attractiveness among the rigid crosslinks leading to narrow reptation tubes (black particles) and active repulsiveness elicited by ZLP (dis)entanglements leading to faster reptation into broader tubes (red particles). As a multiscale connection, the macroscopic order parameter
leading to effective disentanglement). (Macroscale) A two-component interacting system recapitulates both, passive elastic attractiveness among the rigid crosslinks leading to narrow reptation tubes (black particles) and active repulsiveness elicited by ZLP (dis)entanglements leading to faster reptation into broader tubes (red particles). As a multiscale connection, the macroscopic order parameter  of the nonlinear Landau's functional (eqn (7)) is equivalent to the microscopic interaction parameter Γ(ν, d) (determined by the Flory exponent ν, and dimensionality d; see Section 2.1 for details). The phenomenological Landau–Ginzburg model of phase separation predicts both macroscopic scenarios (see free-energy Landau's scale landscapes in the right panels); (a) active softening under repulsive phase segregation of disentangling living polymers into a systemic weakening state (supercritical;
of the nonlinear Landau's functional (eqn (7)) is equivalent to the microscopic interaction parameter Γ(ν, d) (determined by the Flory exponent ν, and dimensionality d; see Section 2.1 for details). The phenomenological Landau–Ginzburg model of phase separation predicts both macroscopic scenarios (see free-energy Landau's scale landscapes in the right panels); (a) active softening under repulsive phase segregation of disentangling living polymers into a systemic weakening state (supercritical;  for
for  ); (b) passive strengthening under attractive aggregation of the crosslinking elements (subcritical;
); (b) passive strengthening under attractive aggregation of the crosslinking elements (subcritical;  for
for  ).
)..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
; 1989, 108(1), 28–36.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.


