Thermogelation of nanoemulsions stabilized by a commercial pea protein isolate: high-pressure homogenization defines gel strength

Abstract

The impact of animal-based food production on climate change drives the development of plant-based alternatives. We demonstrate the use of colloidal thermogelation on a real nanoemulsion system to create structured gels that could be of interest for thermo-mechanical processing of next-generation plant-based food applications. We use a commercial pea protein isolate (PPI) without further purification to stabilize a 20 vol% peanut oil-in-water nanoemulsion at pH = 7 by high-pressure homogenization (HPH) and demonstrate the temperature induced gelation behavior of the nanoemulsion as a function of the HPH processing parameters. Bright-field and laser scanning confocal fluorescence microscopy reveals a diverse microstructure of the aqueous PPI dispersions, with a large amount of insoluble protein particles, cell-wall debris particles, and lipid inclusions. Sedimentation of particulates is prevented by HPH treatment and leads to a loss of the dispersion's thermogelation properties. The non-gelling PPI dispersion stabilizes nanoemulsions and the insoluble components of the PPI dispersions persist throughout the HPH processing. We perform a systematic rheological investigation of the effect of HPH processing on thermogelation and demonstrate that the number of HPH passes n and HPH pressure P control the average nanoemulsion droplet size measured by DLS at a 90° scattering angle. We show that the droplet size defines the final gel strength with a strong inverse dependence of the elastic modulus on droplet size. Furthermore, processing can lead to heterogeneously structured gels that yield over a large strain amplitude range.

---

1 Introduction

Advancements in modern agriculture increased the supply of secure, affordable, and appetizing foods, and helped to reduce world hunger throughout the last century. However, the growing world population requires an increased food production to meet the United Nation's Sustainable Development Goal 2 to strengthen food security by 2030.¹ Furthermore, current food production practices contribute considerably to climate change because rearing livestock is very resource intensive in water and land use, and contributes to greenhouse gas emissions and pollution, and loss of biodiversity compared to growing plants for direct consumption.² Therefore, plant-based foods are a promising approach for a much more sustainable alternative.³

A major challenge for plant-based proteins to find their application as analogues in next-generation plant-based foods is to generate a structured morphology from their predominantly globular protein conformation that can imitate animal-based products such as meat, fish, or seafood. Some protocols are reported for fibril formation of pea protein,⁴ thermo-mechanical processing,⁵ and thermal templating by the application of a well-defined thermal history to a combined pea protein–curdlan gum system⁶ and emulsion systems.⁷ Furthermore, a plant-based diet is not necessarily better than an omnivore diet with respect to nutritional value and can lead to chronic diseases and deficiencies of essential nutrients.⁸ This outlines the necessity for next-generation plant-based foods to take an integral approach and focus not only on sustainability, but also take nutrition, taste, availability, and affordability into consideration.⁹ Furthermore, next-generation plant-based foods should not solely include meat analogues, but also be applied to all animal-based foods, such as dairy products, fish and seafood, and egg analogues.¹⁰

Oil-in-water nanoemulsions can be used to encapsulate hydrophobic nutrients in the dispersed oil droplets, which is called fortification of a food product.¹¹ Nanoemulsions contain droplets with diameters below 1 μm and are kinetically stabilized by an interfacial tension reducing agent in contrast to microemulsions, which are thermodynamically equilibrated systems and therefore react sensitively to environmental changes, or macro-emulsions, which tend to undergo phase separation.^12,13 The small droplet size results in a very large interfacial area and hence a large bioavailability of the encapsulated nutrients is achieved. Furthermore, similar concepts are applied, where nanoemulsions are loaded with hydrophobic pharmaceutically active ingredients and engineered for controlled drug release.¹⁴

The temperature induced gelation – or thermogelation – of nanoemulsions has been studied with various model systems. Polymers with associative end-groups whose partition coefficient to the dispersed phase increases with temperature can be used to induce bridging of nanoemulsion droplets at a well-defined temperature.¹⁵ The transition from a viscous liquid to an elastic solid is reversible, and the final gel structure can be tuned from homogeneous percolation to arrested phase separation by tuning parameters such as the volume fraction of the dispersed oil phase ϕ or heating range.^16–18 The mechanical properties and microstructure of these model materials can be tuned precisely by the processing parameters of said nanoemulsions where the gel strength is defined by an inverted power-law of nanoemulsion droplet size. The gelation is not a result of jamming as a consequence of a large volume fraction ϕ of the dispersed phase, as observed for colloidal hard spheres at the glass transition¹⁹ or repulsive emulsions at high volume fractions,²⁰ but due to an increase in attractive interactions between the droplets, where the interaction strength ε (units of k_BT) is given by the partitioning of the polymer end-groups into the droplets, and the interaction range λ given by the linking polymer radius of gyration R_g.^21–23 Similar systems use a thermally triggered surfactant displacement to tune repulsive interactions of emulsion droplets,²⁴ and telechelic triblock copolymers have been used as linkers to study the bridging mechanism between emulsion droplets²⁵ elucidating the chemical properties of the linker protein on their rheological properties in shear flows.²⁶

Proteins of yellow peas (Pisum sativum L.) are attractive candidates for formulation of plant-based foods because of their high nutritional value and low allergenic potential.^27,28 The commercial pea protein isolate (PPI) used in this study consists of a collection of storage proteins with diverse primary structures.^29,30 These are mostly legumin, vicilin, and convicilin with few albumins, and are present as heteromers with hydrophobically linked subunits, as shown for a similar PPI.³¹ Furthermore, the PPI can contain a large amount of other particles such as cell-wall debris or lipid phases. The different fractions of a PPI differ in functional properties.³² Furthermore, the functional properties between different pea protein isolates usually differ strongly, and variations even between seeds of the same variety can be substantial.³³ A stronger protein purification can lead to the loss of protein nativity and therefore limits their functional properties such as surface activity, emulsification, and gelation.^34–39

Only a small amount of the proteins in PPI are soluble in water, and the majority forms insoluble particles on the order of 50 μm and sediments quickly.⁴⁰ The soluble fraction contains a higher concentration of proteins with charged amino acids and is surface active and hence stabilizes oil droplets or air bubbles in water. The insoluble particles are stabilized by hydrogen bonds, hydrophobic interactions, and disulphide bonds and are suitable to increase water holding.⁴¹ High-pressure homogenization (HPH) of the combined PPI increases the protein solubility drastically by reducing the size of the insoluble particles where Brownian dynamics prevents sedimentation.^31,42 Furthermore, the insoluble protein particles can be functionalized by HPH treatment and properties such as solubility, surface activity, and gel properties can be boosted through HPH treatment.^42–47 However, the large mechanical impact during HPH processing can lead to partial protein denaturation, hence reducing other functional properties.

The temperature induced gelation of PPI solutions or dispersions has been studied extensively.^37,48 The mechanism is based on denaturation of the proteins at their denaturation temperatures. The unfolding exposes the hydrophobic groups of the proteins, hence increasing the hydrophobic interaction between proteins, leading to a percolating network. The properties of the heat-set PPI gels can be manipulated by pH and salt concentration. Setting the pH close to the isoelectric point reduces the electrostatic repulsion between proteins and hence they typically aggregate and sediment, while an increased ionic strength can stabilize the proteins from unfolding.^49,50 Bivalent ions can also be used to control the properties of the protein gel.⁵¹ Furthermore, HPH treatment can functionalize the insoluble pea protein fraction for synergistic contributions to gelation,⁵² but there is limited systematic investigation of HPH processing parameters on the rheology of heat induced gelation of PPI emulsions.

Only a few examples can be found in the literature where the application of emulsion systems is not just limited to fortification, but also serve as a structural component to the plant-based food.^7,53 In this paper, we demonstrate the temperature induced gelation of nanoemulsions stabilized by a commercial plant-based protein isolate and the effect of processing parameters on the final gel structure. We use high-pressure homogenization to both process the PPI and synthesize nanoemulsions stabilized by PPI. We perform a systematic rheological investigation of the effect of processing on the gel properties. The results are interesting for applications in thermo-mechanical processing of next-generation plant-based food products.

2 Materials and methods

2.1 Chemicals

Pea protein isolate (PPI) S85XF was kindly provided by Roquette (France). Peanut oil and Nile blue A were purchased from Thermo Scientific Chemicals. Sodium chloride (ACS reagent, ≥99.0%), sodium phosphate monobasic dihydrate (BioUltra, ≥99.0%), mineral oil (light), Nile red (for microscopy), and Calcofluor white stain (for microscopy) were purchased from Sigma-Aldrich. Sodium phosphate dibasic anhydrous (ACS, ≥99.0%) and 2-propanol (ACS, ≥99.5%) were purchased from VWR Chemicals. Ethanol absolute (KOPTEC, USP 200 Proof) was purchased from Decon Labs (USA). Deionized water was used for buffer preparation and cleaning.

2.2 Differential scanning calorimetry

7.4 mg PPI powder was sealed in a Tzero aluminium hermetic pan and loaded together with an empty pan as a reference in a DSC 2500 (TA instruments). Heating rates of +2 °C min⁻¹ and −5 °C min⁻¹ were applied in the temperature range from 20 °C to 120 °C. The endothermic peak was analysed using DSC software (Trios v5.6.0.87).

2.3 High-pressure homogenization

A high-pressure homogenizer (Emulsiflex-C3, Avestin) was first cleaned by feeding successively 2-propanol, ethanol, and water at pressures ranging from 0 kpsi to 30 kpsi through the homogenizer. The sample was loaded by rinsing the homogenizer with a 20 mL sample to displace the water from the cleaning step. The first four and two pump strokes were discarded for HPH passes n ≤ 4 and n > 4, respectively. The heat exchanger at the outlet of the homogenizer was set to 4 °C and the sample was allowed to cool in an ice bath and equilibrated for 10 min after each HPH pass.

2.4 PPI dispersion sample preparation

A 10 mmol L⁻¹ phosphate buffer with pH = 7 (Orion Star A125 pH/conductivity meter, Thermo Fisher Scientific) and 0.1 mol L⁻¹ NaCl were prepared and stored in a fridge. A 10 wt% PPI dispersion was prepared by slowly adding the PPI powder to the buffer while gently stirring. 0.1 wt% Nile blue, 0.02 wt% Nile red and 1% v/w Calcofluor-white with respect to PPI powder mass were added for staining. The dispersion was stirred overnight at 4 °C to ensure full hydration. The dispersion was then homogenized for up to n = 6 consecutive passes at P = 10 kpsi and stored at 4 °C.

2.5 PPI nanoemulsion sample preparation

A 10 wt% PPI dispersion passed for n = 4 times at P = 10 kpsi was used as a precursor and mixed with peanut oil containing 0.01 wt% Nile red for staining to reach an oil volume fraction of ϕ = 0.2 while stirring. A pre-emulsion was formed by ultrasonication at 20 kHz for 10 min sonication time with a tip probe (Cole-Palmer Ultrasonic Processor CPX750; 30 s cycles with 10 s on, 20 s off, and amplitude 30%) while the emulsion was stirred in an ice bath to keep the temperature below 4 °C. The pre-emulsion was then homogenized up to n = 20 consecutive passes at various P. Samples were collected from the emulsion after every four passes and analyzed immediately while transported at 4 °C.

2.6 Dynamic light scattering

A Brookhaven NanoBrook 90Plus PALS with a wavelength of 640 nm at a fixed scattering angle of 90° was used (a comparison of scattering angles is shown in Fig. S1, ESI†). PPI dispersions and PPI emulsions were diluted by a factor of 1 × 10³ and 2 × 10⁴ in filtered (20 nm, Whatman Anotop 25 syringe filters) buffer, respectively, to avoid multiple scattering during the DLS experiment. After equilibration for 2 min at 25 °C, nine measurements were performed for each sample. The acquisition time was 1 s and data were averaged over 2 min for each measurement. Average diameter (D_eff) and polydispersity were calculated by the standard second-order cumulant analysis using the instrument software. A refractive index of 1.45 for the insoluble PPI particles³¹ and 1.46 for the peanut oil droplets⁵⁴ were used for the dispersed phase of the PPI dispersion and nanoemulsion samples, respectively, and the refractive index of water was used for the continuous phase.

2.7 Rheology

Rheological oscillatory shear tests were conducted with a Discovery Hybrid Rheometer 3 (DHR3, TA Instruments) and concentric cylinder geometry with Peltier temperature control. The geometry was successively cleaned with 2-propanol, ethanol, and water. Instrument calibration including the measurement of the instrument and geometry inertia, geometry friction, and a rotational mapping (three iterations in precision mode) was performed. The sample was stored at 4 °C and loaded in the equilibrated geometry at 20 °C without creating air bubbles. After lowering the rotating bob to the measuring position, the exposed sample surface was covered with mineral oil to avoid evaporation. The sample was pre-sheared at a shear rate of [small gamma, Greek, dot above] = 290 s⁻¹ for 60 s before performing rheological tests. The sample was conditioned for one period, and data were acquired for three periods in strain-controlled mode while motor mode was set to 'auto'. Rheological tests were performed with frequency f = 1 Hz, shear strain amplitude γ = 1%, and a heating rate of 2 °C min⁻¹ if not specified differently. A minimum torque value of 5 × 10⁻⁹ was used as the lower measurement limit.⁵⁵

2.8 Optical microscopy

A laser scanning confocal microscope (Zeiss LSM 980 with Airyscan 2) was used in oil-immersion mode with a 63× objective (numerical aperture = 1.4, Plan Apochromat). Three imaging channels were defined with excitation wavelengths [emission windows] of 405 nm [429 nm to 509 nm], 514 nm [535 nm to 579 nm], and 639 nm [667 nm to 693 nm], corresponding to the Calcofluor-white, Nile red, and Nile blue fluorescent dyes. The same setup was equipped with a bright-field transmission imaging camera (Axiocam 305 mono). Samples were prepared by placing a 25 μL sample between two cover slides separated by a frame-seal from Bio-Rad Laboratories (USA). All measurements were conducted at room temperature. Images were analysed with a 5D contrast optimizer of the BioVoxxel Figure Tools⁵⁶ in Fiji. Pixel saturation was set to 0.00% and 0.01% for the PPI dispersions and PPI nanoemulsions, respectively.

3 Results and discussion

An overview of the sample processing parameters is sketched in Fig. 1. Pea protein isolate (PPI) dispersions and nanoemulsions (PPI–NE) were prepared following Methods A and B, respectively, and are presented in separate subsections. The processing parameters for high-pressure homogenization (HPH) are detailed in Fig. 1 as the number of passes n and pressure P. We focus on a nanoemulsion composition of 10 wt% PPI and 20 vol% oil. This provides a sufficiently high surfactant-to-oil ratio for the stabilization of the oil droplets, and an adequate gel strength based on preliminary data presented in Fig. S2 (ESI†).

Fig. 1 Visualization of the sample processing methods. (Method A) Preparation of a 10 wt% pea protein isolate (PPI) dispersion with n number of high-pressure homogenization (HPH) passes at P = 10 kpsi. (Method B) Preparation of a 10 wt% PPI + 20 vol% oil nanoemulsion (PPI–NE) with n number of HPH passes at pressure P.

3.1 PPI dispersion (Method A)

First, the morphology of the pristine PPI dispersion is discussed in terms of bright-field and fluorescence microscopy, followed by the effect of HPH passes n at P = 10 kpsi on the microscopic morphology. The discussion is complimented by dynamic light scattering (DLS) measurements at a 90° scattering angle to relate the average effective PPI particle diameter as a function of n. The section is concluded by the effect of the number of HPH passes n at P = 10 kpsi on the rheological behavior of the PPI dispersions while increasing the temperature from 20 °C to 80 °C.

3.1.1 PPI dispersions have a diverse morphology – fluorescence confocal microscopy. A representative bright-field and fluorescence microscopy image of an unprocessed PPI10 dispersion is shown in the first column of Fig. 2. The bright-field image (Fig. 2A) of the pristine sample reveals the presence of large particles on the order of 50 μm. These large particles are insoluble PPI particles and sediment within seconds if stirring of the sample ceases. Individual components of the PPI10 dispersions are highlighted by the channels isolating different fluorescent dyes within the sample.

Fig. 2 (A) Bright-field and fluorescence confocal images with channels (B) Nile blue (protein), (C) Calcofluor-white (cell-wall debris), (D) Nile red (lipid phases) with arrows highlighting the presence of small lipid phases, and (E) the composite of (B)–(D) of a 10 wt% PPI dispersion after n = 0 (pristine), 1, 2, and 5 passes at P = 10 kpsi. Images were recorded at room temperature and the scale bar represents 20 μm.

Nile blue binds to proteins and appears as yellow color in Fig. 2B. This channel not only confirms that the large particles in the bright-field image are insoluble PPI particles, but also reveals the presence of smaller insoluble PPI particles, and hence their particle size is highly polydisperse. The irregular shape of the insoluble PPI particles suggests that they broke off, and some neighboring particles are actually connected in the z-direction and just cracked open. Video S1 (ESI†) provides a z-scan of the pristine sample in Fig. 2 and highlights a high polydispersity in insoluble PPI particle size, particles connected through the z-direction, and the presence of hollow particles.

Some areas are not stained by Nile blue, but are visible in the Calcofluor-white channel in Fig. 2C. This dye binds to polysaccharides of chitin and cellulose that are present in cell walls and hence this channel is highlighting cell-wall debris particles. The presence of cell-wall debris particles in a similar PPI has been quantified as 2.6 ± 0.4 g per 100 g dry mass.³¹ Furthermore, Nile red is only fluorescent in lipid solvents, and the Nile red channel (Fig. 2D) shows the presence of small bright spots. Some lipid phases are highlighted with arrows. This confirms the presence of lipid phases in PPI, which is in agreement with composition analysis reported for similar commercial PPI powders and can be as high as 10 wt%.^31,41 The three fluorescence channels are combined in the composite image in Fig. 2E. Cell-wall debris can be present as particles of their own but are more often embedded as thin sheets within the large PPI particles. The lipid phases are present as inclusions within the large protein particles, as highlighted by arrows. All of these features can be seen in the z-scan provided in Video S1 (ESI†).

A selection of representative bright-field and fluorescence microscopy images of the processed PPI10 dispersions after n = 1, 2, and 5 HPH passes are assembled in the remaining columns of Fig. 2. The bright-field images and Nile-blue channel confirm that passing the sample through the high-pressure homogenizer at 10 kpsi decreases the protein particle size with each consecutive pass. The large insoluble protein particles are broken down to diameters on the order of 10 μm. The difference in insoluble protein particle size is strongest between the pristine and first HPH pass and the particle size after more than two passes appears qualitatively identical (images for all HPH passes shown in Fig. S3, ESI†). The cell-wall debris shown in the Calcofluor-white channel persists throughout all HPH passes and the particles do not seem to significantly reduce in size. However, they appear more freely and are less frequently attached to the green protein particles, as shown in the composite image. The apparent increase in number is most likely a consequence of this detachment, which allows for independent sedimentation of the cell-wall debris particles from the insoluble protein particles. Interestingly, the embedded lipid phases, which are visible in the Nile red channel (highlighted by arrows), become also more evenly distributed throughout the sample and appear not only within the large protein particles anymore.

The fluorescence microscopy reveals that the dispersions remain heterogeneous even after 6 HPH passes at P = 10 kpsi, but the insoluble protein particle size is strongly reduced and the cell-wall debris and some of the lipid inclusions are freed from the insoluble protein particles. The size of the cell-wall debris particles appears to be least affected by the processing parameters. The dark areas in the bright-field images are not stained by any of the three fluorescent dyes and are most likely ashes, as quantified by the supplier for a similar PPI to approximately 5 wt%, and also reported in the literature for comparable PPI powders.^31,41

3.1.2 Average effective particle size – dynamic light scattering. The estimation of particle size distributions from fluorescence microscopy is difficult because of the large polydispersity and difference in sedimentation of the dissimilar particles. Therefore, the average particle sizes of the PPI10 dispersions are measured by DLS at a 90° scattering angle, which measures ensemble averages of all particles in the sample that contribute to the scattered light signal at this scattering angle. As discussed previously, the pristine dispersions with no HPH processing contain large particles (see the first column in Fig. 2A). They are non-Brownian and sediment immediately. After one HPH pass at 10 kpsi, the particle size is reduced such that the particles become Brownian and sedimentation is not observed on the time scale of an experiment. Therefore, DLS measurements are not performed on pristine samples.

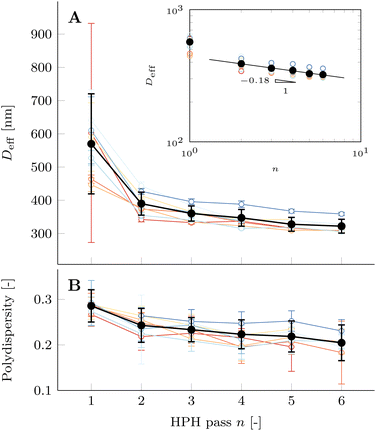
The average effective diameter D_eff of PPI10 dispersions decreases with each subsequent HPH pass n, as shown in Fig. 3A, and the strong decrease of D_eff weakens after two homogenization passes. This is in agreement with the confocal microscopy study presented in Fig. 2. The decrease in particle size for a larger number of HPH passes can be quantified by DLS and the inset in Fig. 3A confirms a power-law dependence of D_eff on n for more than one HPH pass. Measurements of individual samples are shown by colored open symbols. Their standard deviations are large at n = 1 pass but decrease with increasing passes where the variability between individual samples becomes dominant to the total average. The confocal images show larger insoluble particles, which is a consequence of capturing the images at the bottom of the imaging cell where large particles sediment, while smaller particles have a different sedimentation profile and are located at higher z-values. On the contrary, DLS averages all the particles in the sample, therefore measuring a smaller average effective diameter D_eff. Another contributing factor for the cutoff of particles of larger size in the DLS data is due to measurements at a scattering angle of 90°.

Fig. 3 DLS data of 10 wt% PPI dispersions after n ∈ [1,6] consecutive HPH passes at P = 10 kpsi. (A) Mean effective diameter D_eff and (B) polydispersity. The colored open symbols are averages of individual samples with at least eight repetitions, while the black data are the average of all samples. Error bars correspond to standard deviations and measurements were performed at 25 °C and a scattering angle of 90°. The inset shows the data of (A) in log–log scale with a power-law fit (R² = 0.99), error bars not shown.

The polydispersity in Fig. 3B is large for all individual samples. The average polydispersity decreases with each subsequent HPH pass. This is reflected by the microscopy images in Fig. 2 where the large particles are strongly reduced in size with each consecutive HPH pass.

3.1.3 Effect of HPH on thermogelation. The rheological behavior of PPI10 dispersions during a temperature increase from 20 °C to 80 °C is presented in Fig. 4. A time sweep at 20 °C for equilibration preceding the temperature increase is shown in the gray shaded area. The pristine PPI10 dispersion behaves like a viscous liquid with constant loss modulus G′′ and storage modulus G′ below the minimum torque limit of the rheometer and hence the phase angle δ is close to 90°. The initial decrease in G′′ upon increasing the temperature represents the dependence of the dispersion's viscosity on temperature. Further heating of the pristine PPI10 dispersion leads to gelation at a gel point of 77 °C where G′ crosses G′′ in Fig. 4A. Another representation of the gelation behavior is the decrease of the phase angle δ to values smaller than 45° in Fig. 4B. We posit that the dissolved proteins denature upon heating and lose their secondary structure. The unfolding exposes hydrophobic groups to the aqueous phase and hydrophobic interactions between different proteins are formed, which result in a sample spanning network at the gel point. The increasing G′ in the subsequent time sweep at 80 °C (see the subsequent orange shaded area in Fig. 4) indicates a slow gelation process that is still ongoing once 80 °C has been reached, but the final G′ at the end of the time sweep remains small with less than 1 Pa. Furthermore, the gelation occurs at higher temperatures compared to the endothermic peak temperature (66 °C) of the PPI powder measured by differential scanning calorimetry (see Fig. S4, ESI†). The low peak temperature compared to reported denaturation temperatures of pea globulins suggests that the detected endothermic peak represents complete unfolding of the already partially denatured pea proteins. The extraction process in commercial PPI is known to reduce protein nativity. This is supported by the relatively small enthalpy measured with DSC and small final G′, and the dissolved PPI appears already partially denatured. However, the absence of peaks in the cooling and second heating cycles in the DSC data is typical for the irreversible mechanism of protein unfolding and does not comply with phase transitions of a lipid phase. Therefore, the measured endothermic peak might not correspond with the actual denaturation temperature of the purely native pea proteins, but represents the final unfolding of an already partially denatured pea protein isolate.

Fig. 4 Rheological temperature sweeps of a 10 wt% PPI dispersion homogenized at 10 kpsi from n = 0 (pristine) to 5 HPH passes labeled by the legend. (A) Full and empty symbols are the storage modulus G′ and loss modulus G′′, respectively. A low torque limit is indicated by the solid horizontal line. (B) Phase angle δ. δ = 45° is indicated by the solid line. Equilibration time sweeps at 20 °C and 80 °C are shown in the preceding gray and subsequent orange shaded areas, respectively. Data were measured at f = 1 Hz, γ = 1%, and a heating rate of 2 °C min⁻¹. Every tenth point is shown for clarity.

Homogenizing the PPI10 dispersion at 10 kpsi leads to an increase in the viscous modulus at 20 °C. The measuring position of the concentric cylinder geometry leaves a gap of 5.9 mm between the bottom of the rotating bob and the cup, and the lower end of the rotating bob has a conical shape with a relatively large angle. This geometry results in a large volume at the bottom of the measuring cup that is not sheared during the rheological measurement. It can be expected that the short time scale of sedimentation observed in the pristine sample results in a significant fraction of the large insoluble PPI particles to sediment into this gap volume. Therefore, they do not contribute to the rheological signal. As discussed earlier, one HPH pass reduces the insoluble PPI particle size to prevent visual sedimentation on time scales of the experiment. The increase in G′′ is in agreement with a higher volume fraction of dispersed solid particles. The application of more than one HPH pass further reduces the particle size and their anisotropy, but does not change the volume fraction of insoluble PPI particles within the sheared section of the sample. Therefore, a viscosity reduction with each subsequent HPH pass is expected and has been reported for similar systems.⁴⁵

An even more striking difference between the homogenized and pristine PPI10 dispersions is the absence of a gel point of the processed samples and G′′ is larger than G′ across the entire temperature range. This difference is also present in Fig. 4B where the phase angle δ remains well above 45° for the homogenized dispersions. The higher volume fraction of the insoluble particles as well as the higher amount of free cell-wall debris particles and lipid phases (cf.Fig. 2) prevents the formation of a sample spanning network. The thermogelation experiments of pristine samples show poor repeatability, as shown in Fig. S5 and S6 (ESI†). The rheological properties seem to be highly sensitive to sedimentation of the insoluble PPI particles.

Changes in the rheological properties for more than n = 3 HPH passes at 10 kpsi are below the sensitivity limit of the rheometer. We apply n = 4 HPH passes for all further use of PPI10 dispersions in the emulsion synthesis. The small inconsistencies in G′ when switching from a time sweep to temperature ramp or vice versa are a result of G′ values close to the low torque limit and the feedback loop for the strain-controlled mode of the rheometer.

3.2 PPI nanoemulsions (Method B)

As outlined in the previous section, the rheological and morphological properties are qualitatively similar for HPH passes n ≥ 4. Therefore, 10 wt% PPI dispersions homogenized with n = 4 passes at P = 10 kpsi are used as a precursor for all nanoemulsion samples (Method B in Fig. 1), where the HPH parameters of the homogenization step are varied.

We first discuss the morphology of PPI–NE nanoemulsions with fluorescence confocal microscopy images followed by the effect of high-pressure homogenization (HPH) during the emulsification process on the said morphology. This is supported by dynamic light scattering (DLS) measurements at a 90° scattering angle of the average effective droplet diameter size as a function of the number of HPH passes. The thermogelation behavior of the nanoemulsions depending on the number of HPH passes n and pressure P is discussed, resulting in a strong inverse dependence of the storage modulus after gelation as a function of average effective droplet size. The section is concluded by a detailed focus on frequency and amplitude sweeps after gelation to investigate the structure of the gel.

3.2.1 Microstructure – fluorescence confocal images. The morphology of a PPI10–Oil20 nanoemulsion homogenized for n = 20 passes at 10 kpsi is shown by the fluorescence confocal microscopy images assembled in Fig. 5. The composite image in Fig. 5A reveals a diverse microstructure that is composed of differently sized and shaped particles, which are detected in different fluorescence channels (B–D).

Fig. 5 Fluorescence confocal microscopy images of a 10 wt% PPI + 20 vol% oil nanoemulsion after n = 20 HPH passes at P = 10 kpsi. (A) Composite of the channels separately shown in channels (B) Nile red (oil), (C) Nile blue (protein), and (D) Calcofluor-white (cell-wall debris). The images (E)–(G) are magnifications of the areas indicated by the white frame in the large images (B)–(D). The scale bar for (A)–(D) is 20 μm and for images (E)–(G) is 1 μm. Images were recorded at room temperature.

The Nile red channel in Fig. 5B labels lipid phases in the emulsion and highlights the oil droplets. Large droplets with diameters on the order of a few μm are clearly visible. However, the magnified image in Fig. 5E reveals a significant population of droplets with diameters smaller than 1 μm. Evidently, the droplet size distribution of this emulsion is very broad after n = 20 HPH passes. The signal of the added oil dominates the signal of the lipid phases already present in the PPI (see Fig. 2).

The Nile blue fluorescence dye stains proteins and its channel is shown in Fig. 5C. It confirms the presence of insoluble PPI particles in the emulsion. The high number of HPH passes reduces the insoluble PPI particle drastically and they appear less frequent compared to the PPI10 dispersions after n = 5 HPH passes (Fig. 2) but are still anisotropic. Furthermore, a decreased intensity of the Nile blue signal can be seen in locations where large oil droplets or other particles are located. The magnified image in Fig. 5F does not suggest that the presence of insoluble PPI particles leads to Pickering emulsions but rather hints at solubilized proteins stabilizing the oil droplets. However, the optical resolution could be too small to identify the smallest insoluble PPI particles to give a definitive conclusion.

The Calcofluor-white dye binds to cellulose which is common in plant cell walls and highlights cell-wall debris. Large particles are visible in Fig. 5D similar in size but less frequent compared to the PPI10 dispersions discussed earlier (see Fig. 2). These particles seem to exhibit a different sedimentation profile since they are typically found at higher z-values within the imaging sample cell. The presence of the nanoemulsion droplets could lead to a small yield-stress, which traps the large particles and ultimately prevents them from sedimentation. Furthermore, the cell-wall debris particles are the last to break down by the homogenization processing. They even persist the n = 20 passes at the highest homogenization pressure of 30 kpsi (see Fig. S7, ESI†).

Fig. 5 confirms that the PPI10(4) precursor is able to stabilize a peanut oil-in-water nanoemulsion despite the presence of insoluble protein and cell-wall debris particles, and results in a very broad droplet size distribution. A confocal z-scan of the sample is presented in Video S2 (ESI†) to show the heterogeneity of the sample.

3.2.2 HPH effect on oil droplet morphology. This section focuses on the Nile red channel of fluorescence confocal microscopy images since this dye highlights the oil droplets within the sample. A representative microscopy image selection of differently processed PPI10–Oil20 nanoemulsion samples recorded at room temperature is assembled in Fig. 6.

Fig. 6 Fluorescence confocal microscopy images of 10 wt% PPI + 20 vol% oil nanoemulsions. The rows and columns correspond to HPH pressure P and the number of passes n, respectively. Shown are the stained oil droplets in the Nile red channel. The scale bar is 1 μm. Images were recorded at room temperature.

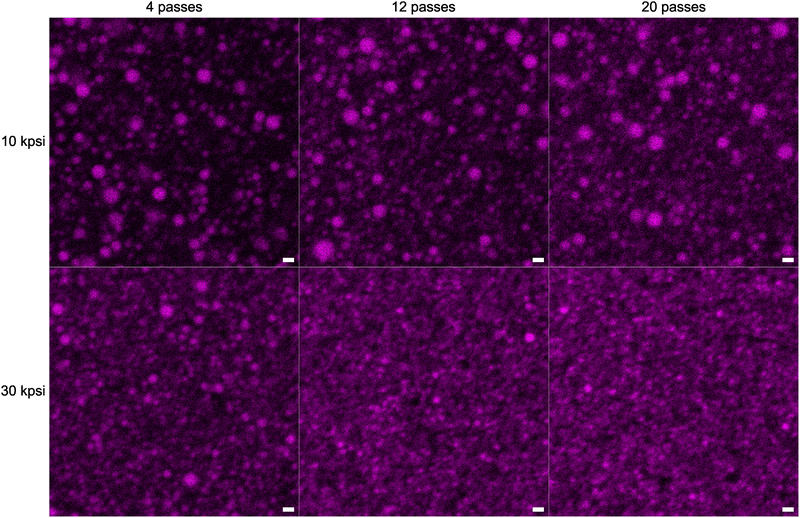
The microscopy image for n = 4 and P = 10 kpsi shows predominantly droplets with diameters on the order of a few μm. However, careful inspection reveals the presence of a significant population of droplets with diameters below 1 μm, and therefore confirms the presence of a broad droplet size distribution. Increasing the number of HPH passes at P = 10 kpsi to n = 12 increases the fraction of the small droplet population compared to the large droplets. The same trend can be observed for n = 20 where the background appears more densely populated with droplets, of which some are below the optical resolution limit, but large droplets persist throughout the 20 passes.

An increase of HPH pressure to P = 30 kpsi qualitatively increases the population of small particles at n = 4 passes compared to the same n at lower pressure. However, a significant number of larger droplets are still present. Similar to the case at P = 10 kpsi, the population of droplets with a radius below 1 μm is increased with increasing the number of passes to n = 12 at P = 30 kpsi but becomes dominant compared to the lower P at the same n. There are no large droplets in the presented field-of-view and hence the polydispersity is significantly decreased with increasing P. An increase to n = 20 passes at P = 30 kpsi suggests an increase in the number of droplets with diameters below the optical detection limit, but qualitative differences to n = 12 passes are less obvious.

3.2.3 Average effective droplet size – dynamic light scattering. As mentioned in the previous section, the individual droplet size can be close to the diffraction limit, especially for a large number of HPH passes n at P = 30 kpsi. Hence, it is difficult to measure the droplet size distribution of these emulsions quantitatively with optical microscopy methods. We use DLS at a 90° scattering angle to measure an average effective droplet diameter, which represents an ensemble average of all droplet populations that are present in the nanoemulsion sample. In contrast, the confocal microscopy images serve to qualitatively investigate the nanoemulsion droplet morphology.

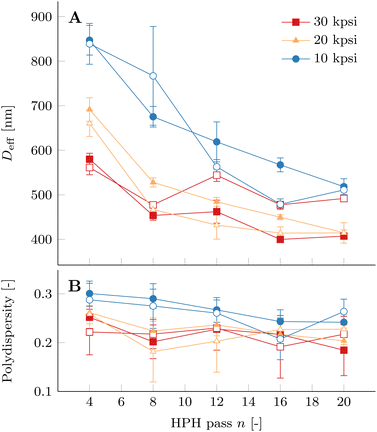
We did not observe a change in droplet size over the time of at least 10 consecutive DLS experiments, i.e. 20 min. This confirms that PPI is able to stabilize a nanoemulsion prepared with the presented processing parameters. The average effective droplet diameter D_eff of PPI10–Oil20 nanoemulsions decreases as a function of HPH passes n for each HPH pressure P, as shown in Fig. 7A. However, the relatively large minimum D_eff compared to droplet sizes of model-nanoemulsions is probably caused by the increased viscosity of the peanut oil (η_d = 81 mPa s at T = 20 °C).⁵⁷

Fig. 7 DLS data of 10 wt% PPI + 20 vol% oil nanoemulsions after n = 4 to 20 consecutive HPH passes at different pressures P as labeled in the legend: (A) effective diameter and (B) polydispersity. Open and closed symbols are repetitions of individually prepared nanoemulsions at the same P. Error bars correspond to standard deviations of at least 9 measurements. Measurements were performed at 25 °C and a scattering angle of 90°.

Homogenizing with larger pressures P results in smaller average droplet size. However, this is strictly true only for n ≤ 4. The variability of D_eff between different samples prepared at the same P becomes comparable to the difference in D_eff as a function of P with increasing n. Not all samples homogenized at 30 kpsi have smaller droplet size averages than the ones processed at 20 kpsi. This variability is likely to be a consequence of the heterogeneous nature and presence of insoluble PPI particles and cell-wall debris particles of the PPI dispersions used as a precursor to stabilize the oil droplets. Furthermore, repetitions of DLS experiments with fresh dilutions from the same nanoemulsion show an increase of D_eff and polydispersity. This indicates aggregation of the droplets even when the nanoemulsions are stored at 4 °C (see Fig. S8, ESI†). As a consequence, the measurements of the nanoemulsion samples appear to be very time sensitive and the time delay between processing and sample analysis is kept as small as possible for the presented data in Fig. 7.

The D_eff of nanoemulsion samples homogenized at 10 kpsi plotted with empty circles and 30 kpsi plotted with empty squares are comparable for n = 12, 16, and 20 passes. Fluorescence microscopy images corresponding to these two samples are shown in Fig. 6 and show strong differences in their morphology, as discussed previously. On the one hand, this is a consequence of the ensemble averaging of the DLS technique and due to measuring at a constant scattering angle of 90°. Furthermore, the scattering cross section is larger for larger droplets and hence D_eff is biased towards large droplets and the presence of a population of smaller droplets can remain hidden even if it is higher in number. On the other hand, optical microscopy captures the morphology of a very localized volume in the nanoemulsion sample. The absence of droplets with diameters larger than 1 μm in the nanoemulsion homogenized for n = 20 times at 30 kpsi is not likely to be representative of the entire sample. This emphasizes the importance of using both techniques complementary to each other to understand the morphological features of the processed nanoemulsions.

The polydispersity in Fig. 3B decreases with increasing HPH pass number n for each HPH pressure. The effect of HPH pressure can be seen in a consistently reduced polydispersity between the 10 kpsi and 30 kpsi processed samples. The intermediate pressure of 20 kpsi is not always located within the other samples, which is caused by the same reason that leads to the variability between individual samples processed at the same P. We present our data analysed using the CONTIN method, which takes a wide size distribution into account, in Fig. S9 (ESI†) to demonstrate that our results are only marginally affected by the analysis method.

3.2.4 Thermogelation of a PPI nanoemulsion. A PPI10–Oil20(20) nanoemulsion homogenized at 30 kpsi following Method B in Fig. 1 undergoes a temperature induced gelation as shown by its rheological properties in Fig. 8. The nanoemulsion behaves predominantly like a viscous liquid at 20 °C. Upon increasing the temperature, a gel point at 53 °C is clearly defined by the crossover of G′ and G′′. The gel point is close to the measured unfolding temperature of the PPI powder by differential scanning calorimetry (see Fig. S4, ESI†). G′ is increasing two orders of magnitude during the gelation process and the gelled nanoemulsion is stable during the time sweep at 80 °C where a weak strengthening (aging) of G′ can be observed. Furthermore, the gelation of the nanoemulsion is not reversible. G′ increases with decreasing temperature after the time sweep at 80 °C. This is different compared to thermogelling nanoemulsion model systems which use polymers with associative end groups as linkers¹⁵ or reversible hydrophobic^14,58 and surfactant displacement²⁴ interactions and exhibit strong reversibility of thermogelation. The measured behavior for PPI–NE proposes the gelation mechanism to be based on protein unfolding or denaturation. The unfolding of the pea proteins exposes hydrophobic groups to the aqueous phase. Newly exposed hydrophobic groups between different proteins can interact and form a network. The proteins remain unfolded when the temperature is reduced and these newly formed network connections persist. Interactions between other constituents of the PPI such as the formation of disulphide bonds have been found to play a minor role in gel formation and could contribute to the aging during the equilibration at 80 °C.^48,50

Fig. 8 Rheological temperature sweeps of a 10 wt% PPI dispersion after n = 4 HPH passes at P = 10 kpsi (PPI, blue squares) and a 10 wt% PPI + 20 vol% oil nanoemulsion after n = 20 HPH passes at P = 30 kpsi (NE, red circles). The rheology of a pure oil sample is shown by the data without symbols. An equilibration time sweep at 80 °C between the heating and cooling steps is shown in the shaded area. Full and empty symbols are the storage modulus G′ and loss modulus G′′, respectively. The maximal storage modulus after gelation at 80 °C is indicated as . Data were measured at f = 1 Hz, γ = 1%, and a heating rate of 2 °C min⁻¹. Every tenth point is shown for clarity.

The rheological properties of a PPI10(4) dispersion, which is prepared following Method A in Fig. 1, are plotted for comparison in Fig. 8. In contrast to the nanoemulsion, the PPI dispersion does not gel in the temperature sweep or the equilibration step at 80 °C. During the cooling step, G′ does increase slightly more strongly than G′′, but the phase angle δ is 46° at T = 20 °C, and hence G′′ is still weakly dominant and the dispersion is not gelled at the end of the cooling temperature ramp. Furthermore, we show that the thermogelation properties of a PPI dispersion after n = 4 HPH passes at P = 10 kpsi are not affected by sonication (Fig. S10, ESI†).

The maximal storage modulus after gelation for the nanoemulsion is indicated as in Fig. 8 at 80 °C in the heating temperature sweep. The stark difference of between the PPI10–Oil20(20) nanoemulsion and PPI10(4) dispersion is a result of the assembly of the PPI at the water–oil interfaces of the oil droplets within the nanoemulsion. The comparison of the PPI dispersion to the PPI nanoemulsion leads to the conclusion that the gelation mechanism is based on the attractive droplet–droplet interactions (increase in ε) which emerge with an increase of temperature. The PPI dispersion itself does not gel, and therefore droplet–droplet interactions are dominant and lead to a colloidal arrest even at a volume fraction of ϕ = 0.2, which is much smaller compared to the packing fraction usually observed for the glass transition in colloidal systems (ϕ = 0.58).⁵⁹

The loss modulus of a pure peanut oil sample is plotted in Fig. 8 to demonstrate that the oil can only explain the elevated G′′ of the nanoemulsion prior to the temperature increase from 20 °C, but the oil is not responsible for the thermogelation behavior of the nanoemulsion. The oil behaves as a Newtonian viscous liquid with a phase angle close to 90° (G′ → 0 Pa and outside of the plotted axis limits) and viscosity at T = 20 °C.

3.2.5 Effect of HPH passes n on thermogelation of a PPI nanoemulsion. The rheological properties of a PPI10–Oil20 nanoemulsion homogenized for up to n = 20 consecutive passes at P = 10 kpsi are shown in Fig. 9. All samples are predominantly viscous during the equilibration time sweep at 20 °C prior to the temperature increase. A difference to the PPI dispersions discussed earlier is the steady increase of G′ with time despite the constant temperature. An increase in G′ is associated with the generation of a structure that has elastic properties and is an indication of nanoemulsion droplet aggregation, which is in agreement with earlier observations with DLS (see Fig. S8, ESI†). This instability underlines the importance of measuring the rheological properties and droplet size with as little time delay after processing as possible and keeping the sample at low temperature at all times.

Fig. 9 Thermogelation of a 10 wt% PPI + 20 vol% oil nanoemulsion homogenized during the emulsification process at P = 10 kpsi for up to n = 20 consecutive passes labeled by the legend. (A) Full and empty symbols are the storage modulus G′ and loss modulus G′′, respectively. (B) Phase angle δ. δ = 45° is indicated by the solid line. Equilibration time sweeps at 20 °C and 80 °C are shown in the gray and orange shaded areas, respectively. Data were measured at f = 1 Hz, γ = 1%, and a heating rate of 2 °C min⁻¹. Every tenth point is shown for clarity.

All of the nanoemulsion samples in Fig. 9 undergo thermogelation with a resulting dominant G′ at 80 °C. The sample with n = 4 HPH passes (circles) shows a gel point at a temperature of 64 °C, which is 10 °C larger compared to the samples with a larger n. Furthermore, the relaxation (or rejuvenation) of G′ during the time sweep at 80 °C is distinct and almost leads to the loss of the dominant elastic modulus, as well shown by the rebounce of δ towards 45°. This sample contains droplets on the order of a few μm, which could not be stabilized by thermal fluctuations. However, no macroscopic creaming or phase separation on the time scale of the measurement is observed.

The final gel strength after gelation is increasing with increasing number of HPH passes n and plateaus for the shown sample at n = 16. The correlation of decreasing oil droplet size with the HPH pass number (see DLS data in Fig. 7) suggests that smaller emulsion droplets (D_eff) lead to stronger gels (). Furthermore, the gels are stable at 80 °C for n > 4.

3.2.6 Effect of HPH pressure P on thermogelation of PPI nanoemulsions. Three samples of PPI10–Oil20(20) nanoemulsions homogenized at different pressures P for the same amount of passes n = 20 are shown in Fig. 10. A higher homogenization pressure leads to less stable gels in the time sweep at 20 °C prior to increasing the temperature. The phase angle δ of the 30 kpsi sample in Fig. 10B decreases to values very close to 45° towards the end of the time sweep. This trend suggests that the large mechanical impact during the processing at 30 kpsi leads to partial denaturation of the proteins. Furthermore, the mechanical impact at this P leads to a significant increase of temperature during the homogenization process. Temperatures measured at the outer side of the outlet pipe in between the piston and the heat exchanger can reach up to 28.7 °C for 10 kpsi, 38.8 °C for 20 kpsi, and 55.1 °C for 30 kpsi. Because the PPI consists of a collection of proteins rather than an isolated molecule, the denaturation temperature of the PPI powder is spread out over a temperature region and unfolding onset is measured by DSC as low as 52 °C while the denaturation peak is at 66 °C (see Fig. S4, ESI†). The temperature during HPH processing at P = 30 kpsi is larger than the onset of the unfolding temperature of the PPI powder. As a consequence, it is likely that the pea protein is already partially denatured despite keeping the sample at 4 °C in between passes. Therefore, the high mechanical impact and temperature increase during HPH processing can induce partial unfolding and breakup of protein heteromers and aggregates. This changes the strength ε and range λ of the interaction potential between droplets in addition to the droplet size change. Furthermore, the increase in temperature during the HPH processing depends on sample volume because small volumes need less pump strokes and hence the sample can already complete the HPH pass before reaching the equilibrium temperature during processing. The data in Fig. 8 represent a temperature sweep of an independent nanoemulsion sample prepared in a batch with a smaller volume. The smaller value of G′ at 20 °C prior to the temperature increase for the smaller badge supports this hypothesis.

Fig. 10 Thermogelation of 10 wt% PPI + 20 vol% oil nanoemulsions homogenized during the emulsification process for n = 20 consecutive passes at the pressure P indicated by the legend. (A) Full and empty symbols are the storage modulus G′ and loss modulus G′′, respectively. (B) Phase angle δ. δ = 45° is indicated by the solid line. Equilibration time sweeps at 20 °C and 80 °C are shown in the gray and orange shaded areas, respectively. Data were measured at f = 1 Hz, γ = 1%, and a heating rate of 2 °C min⁻¹. Every tenth point is shown for clarity.

The samples in Fig. 10 correspond to the filled symbols in Fig. 7. Higher HPH pressure leads generally to stronger gels (larger 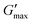). This supports the hypothesis that smaller droplets lead to stronger gels. The thermogelling nanoemulsion is a complex mixture of particles with polydisperse size (cf. DLS data in Fig. 7) and of different nature (oil droplets, cell-wall debris, and insoluble protein particles; see the microscopy images in Fig. 5). As a consequence, it is likely that the evolution of G′ and G′′ deviates from a gelation process with a single underlying mechanism as seen for model nanoemulsions.¹⁵ Nevertheless, the increased thermogelation with HPH pressure is reproducible (see Fig. S11, ESI†).

An interesting behavior is the unsteady relaxation of the nanoemulsion processed at 30 kpsi at 80 °C in Fig. 10. Repetition of a fresh nanoemulsion sample with the same processing parameters does not show the said instability (see Fig. 8). The applied shear strain of 1% was chosen carefully to probe the sample within the linear viscoelastic regime. Nevertheless, there could be an influence of the applied shear strain on certain components of the gel, e.g. rearrangements of droplets within the gel. However, the relaxation of G′′ prior to G′ in the time sweep is not typical for a weakening of the gel due to a large strain amplitude. The subtle increase in G′ at the end of the temperature sweep and before the time sweep at 80 °C indicates that the material is not in equilibrium.

3.2.7 Nanoemulsion droplet size controls final gel strength. The results presented so far indicate that the material properties of the gelled nanoemulsion can be manipulated by the number of high-pressure homogenization passes n and pressure P. Since the nanoemulsion droplets are detrimental for the colloidal gelation and serve as building blocks for the final gel structure, we propose to use the measured average effective droplet size D_eff to compare the final gel strength at 80 °C, , as indicated in Fig. 8, of differently processed nanoemulsions. The data of the three HPH pressures P align on the graph in Fig. 11. Since DLS measurements are conducted at a fixed scattering angle of 90°, the observed trends should be analysed with caution to avoid over-interpretation. Nevertheless, it is worthwhile to compare the dependence of on D_eff qualitatively with reported scalings in the literature. Furthermore, the strong inverse dependence of 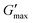with D_eff suggests that the large droplets visible in the microscopy images actually make a negligible contribution to the gel elasticity.

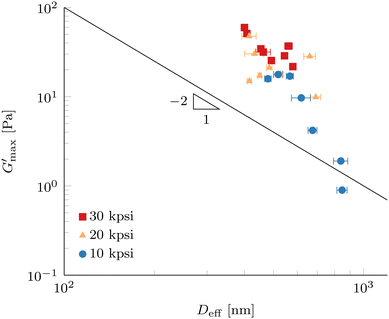Fig. 11 Maximum gel strength after gelation (G′ at 80 °C) as a function of effective droplet size D_eff of 10 wt% PPI + 20 vol% oil nanoemulsions processed according to Method B in Fig. 1. Error bars represent standard deviations of 9 DLS measurements at a scattering angle of 90°. The solid line shows a power-law with exponent −2 as a guide to the eye.

The elasticity for emulsions with repulsive interactions at high volume fraction originates by the resistance against droplet deformation described by the Laplace pressure, which scales as σ/D, where σ is the interfacial tension and D is the droplet radius.^20,60 Scaling of the plateau modulus for emulsions with attractive depletion interactions has shown to scale in the same way as repulsive interactions,⁶¹ but other dependencies have been reported.⁶² For attractive interactions originating by associating linker proteins, a scaling of plateau modulus as a function of D_eff with a power-law exponent of −1.7 has been reported,¹⁵ which could be described by cluster mode coupling theory.²³ Exponents between −2 and −3 were reported for attractive colloidal systems.⁶³

Since the measured dependence shown in Fig. 11 is stronger than a power-law scaling with exponent −2, we expect that not only the amount of interface present in our attractive nanoemulsion system is dictating the elasticity, but the load bearing gel structure is changed by the processing as well. We note that our data do not span a full decade for D_eff and so comparisons to power-law scalings are tentative. As discussed in the previous section, the increase in G′ at 20 °C prior to temperature increase in Fig. 10 suggests an increase in the well depth ε and changes in the range λ of the interaction potential between the droplets. A change in the interaction potential results in a different path in the colloidal phase diagram during gelation, hence leading to different load bearing structures. A larger ε usually results in a smaller percolation threshold leading to earlier onset of a percolating network or increases the quenching depth which gives rise to different non-ergodic states, e.g., homogeneous percolation or arrested phase separation.^21,64–66 The coupled effects of processing on droplet diameter and interaction potential (both ε and λ) render predictions of a percolation threshold non-trivial but could explain a stronger dependence compared to a power-law exponent of −2. Furthermore, the diverse nature of our system with multiple proteins and insoluble particles is contributing to the complexity and multiple effects can be present under the same conditions, such as partial unfolding of the protein molecules and also increased depletion interactions by polymers or small particles in solution.

The dispersion of the data in Fig. 11 can be a consequence of the use of a commercial protein isolate powder, which contains not only one well-defined protein, but a collection of extractable proteins with a range of sizes, solubilities, and denaturation temperatures, where a large portion of the protein remains in insoluble particles. Furthermore, the presence of lipid phases and large resilient cell-wall debris particles is confirmed by fluorescence microscopy (Fig. 2 and 5) as well by other authors.³¹ Even after forming the nanoemulsions, a significant number of insoluble pea protein particles withstand the processing parameters and the cell-wall debris particles are only marginally reduced in size. This complex mixture inevitably leads to a higher polydispersity of the homogenized nanoemulsions compared to a model system. Furthermore, most theories assume a monodisperse colloidal system in contrast to our polydisperse nanoemulsions. The results in Fig. 11 are only marginally affected by analysing the DLS data with the CONTIN method (see Fig. S9, ESI†). Furthermore, the measurement of such a system with a fixed scattering angle requires a careful analysis to prevent over-interpretation.

Nevertheless, is significantly different for D_eff below and above 500 nm, which are fabricated with low and high HPH pressures, respectively. This result reveals the droplet size D_eff to be a very strong handle to control the elasticity of nanoemulsion gels formed with a commercial pea protein isolate. Exploration of a smaller droplet limit will be interesting to generate stronger nanoemulsion gels and ultimately increase the range of applications in the plant-based food space.

3.2.8 Rheological investigation of the gel structure. To investigate the gel structure of the thermally gelled PPI10–Oil20 nanoemulsions, frequency and strain amplitude sweeps are performed after the time sweep at 80 °C (i.e. after aging). A representative selection is shown in Fig. 12. Data show the processing parameters have a strong influence on the viscoelastic properties.

Fig. 12 (A) and (B) Frequency sweep, (C) and (D) applied strain amplitude sweep, and (E) and (F) the resulting stress amplitude sweep of 10 wt% PPI + 20 vol% oil nanoemulsions at 80 °C and processed as labeled by the legend. (A)–(C) Full and empty symbols are the storage modulus G′ and loss modulus G′′, respectively. (D)–(F) Phase angle δ. δ = 45° is indicated by the solid line. The solid line in (A) indicates the contribution of instrument inertia. Data were measured at a frequency of 1 Hz and a shear strain amplitude of 1%, if not stated otherwise.

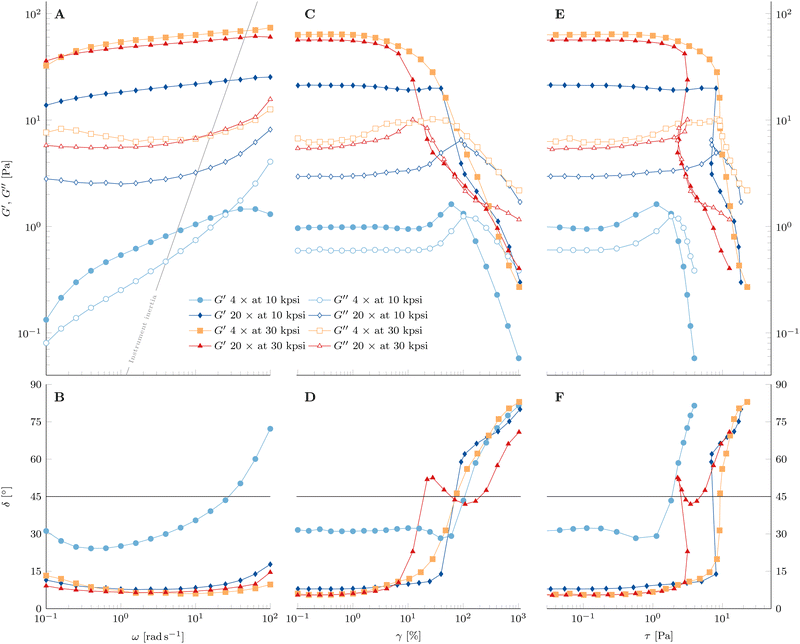
3.2.8.1 Frequency sweep. The nanoemulsion homogenized with n = 4 passes at 10 kpsi shows a positive slope of G′ with frequency ω in Fig. 12A. Furthermore, no plateau of G′ is visible in the entire measured frequency range. The crossover of the two moduli at large ω is due to instrument inertial effects, which become dominant at frequencies indicated by the solid line⁶⁷ and do not represent the material property. The rheometer software corrects for inertia to allow accurate measurement beyond the solid line to some extent, but this only applies to uncorrected raw phase signals smaller than 175° (raw phase shown in Fig. S12–S14, ESI†).

In contrast, there seems to be a crossover of the viscoelastic moduli close to the lower limit of the measured frequency range. This indicates the presence of a terminal region at low frequencies. Hence, the material behaves rather like a viscoelastic liquid with a long relaxation time than an elastic solid. Another representation of this behavior can be seen in the phase angle in Fig. 12B. The value of δ = 31° at the smallest frequency and its negative slope indicate a crossover of δ = 45° not far below the lower limit of applied frequencies. As stated above, instrument inertial effects are responsible for the increase of δ at large ω.

Increasing the number of HPH passes at 10 kpsi to n = 20 changes the rheological properties of the gel drastically. Besides the strong increase in both viscoelastic moduli, G′ is larger than G′′ in the entire accessible frequency range of Fig. 12A. Furthermore, there is a definite minimum in G′′, which defines a plateau modulus of that represents the overall elasticity of the gel. Hence, this nanoemulsion behaves like a viscoelastic solid. The phase angle δ in Fig. 12B is smaller and less dependent on frequency compared to the PPI10–Oil20(4) gelled nanoemulsion. The slight increase at large frequencies is again a result of instrument inertial effects. Increasing the homogenizing pressure P from 10 kpsi to 30 kpsi does not change the qualitative behavior of the gel, but generally leads to a larger plateau modulus ( for n = 20). A low number of passes at high HPH pressures leads to a more pronounced minimum in G′′ as well as a stronger decrease in G′ with decreasing frequency.

3.2.8.2 Strain amplitude sweep. After completing the frequency sweeps, the strain amplitude sweeps in Fig. 12C and D are performed and give insights into the material's behavior with increasing strain amplitudes at f = 1 Hz.

The PPI10–Oil20(4) at 10 kpsi has a linear viscoelastic regime up to strain amplitudes of 10%. The increase of G′ towards a maximum with increasing strain amplitude before the strong decrease is not common in strain amplitude sweeps and is known as large strain overshoot.⁶⁸ However, this behavior has been observed for associative polymers such as hydrophobically modified alkali-swellable emulsion (HASE) polymers, which interact through hydrophobic groups along their backbone^69,70 or polyelectrolytes with electrostatic interactions,⁷¹ and in some fractal colloidal gels.⁷² The proposed mechanism is the increased rate of association compared to the rate of dissociation because of the applied strain combined with straightening of stress bearing gel components in the flow direction or stretching of said gel backbone components (molecules in the case of the reported polymer system) beyond their linear Hookean limit. The occurrence of the rejuvenation during the time sweep at 80 °C (see Fig. 9) suggests that some bonds dissociate from the gel network, which leads to an increased number of free interaction sites and results in a less dense gel. Additionally, the interaction range between droplets λ is given by the radius of gyration R_g of the adsorbed pea protein (9.47 nm reported from small-angle X-ray scattering measurements⁷³), which is not expected to be a well-defined length scale because of the diverse composition of pea proteins. The application of shear strain compresses the gel with increasing strain amplitude, reducing the interdroplet distance, hence leading to the association of the free interaction sites and aligning the stress bearing gel backbone. This requires a large enough bond strength to withstand the increased strain amplitude. The behavior is reproducible and seen for all PPI10–Oil20 gels undergoing rejuvenation during the time sweep at 80 °C. Further increase in strain amplitude eventually overcomes the bond strength in the gel and the dissociation rate becomes larger than the association rate and hence G′ decreases and the network disintegrates. The small decrease of G′ at around γ = 10% prior to the increase has been observed and characterized in polyvinyl alcohol–borate hydrogels and is a consequence of an intermediate number of free reaction sites, where the association rate increase is delayed slightly with respect to the strain induced dissociation rate.⁷⁴

The loss modulus G′′ shows a maximum which is typical for many soft materials (weak stress overshoot) and is related to the network breakup and increased energy dissipation during plastic deformations of the droplet network.^59,75 We define the yield point where G′ crosses G′′. The phase angle δ in Fig. 12D displays a minimum where the maximum in G′ is located and a steady increase after the yielding occurs. Therefore, the yielding behavior of the gelled PPI10–Oil20 nanoemulsion sample processed for n = 4 passes at 10 kpsi shows a simple yielding of the strengthened gel. The corresponding representation of the same data as a function of resulting stress amplitude in Fig. 12E shows a very strong decrease of the viscoelastic moduli after the yield point.

Increasing the number of passes to n = 20 at 10 kpsi results in not only a strong increase of the viscoelastic moduli and a decrease of the phase angle, but also a drastic change of the yielding process. There is a slight increase in G′′ at γ = 3%, accompanied by a decrease of G′. However, G′′ plateaus after this first increase before exhibiting the characteristic maximum as a function of strain amplitude. Furthermore, the decrease in the storage modulus is stopped and G′ remains constant. The yielding is delayed after the first increase of G′′ for more than an order of magnitude in strain amplitude where it occurs instantaneously at around γ = 75%, similar to a brittle fracture. The sudden yielding and strong change of G′ lead to a recoil when the data are plotted against the resulting stress amplitude τ in Fig. 12E. This is a consequence of using the hybrid rheometer, which is in fact a stress controlled rheometer and uses a feedback loop to constantly adjust the applied torque for reaching the desired strain amplitudes in the strain-controlled mode. This can be seen by the larger applied strain amplitude for the first data point after yielding compared to the expected logarithmic distributed value (see Fig. S15, ESI†). The abrupt yielding highlights the presence of a population of strong bonds that break at a well-defined critical stress. The presence of a local maximum in G′′ has been connected to the breaking of weak links in the gel structure in attractive emulsion systems before the shear induced configurational rearrangements of the droplets where G′′ displays the maximum at larger strain amplitudes.^61,76 This two-step yielding has also been observed in attractive colloidal systems.⁷⁷ Furthermore, these “weak bonds” are dissociated with increasing strain amplitude and contribute to free network sites available for the strain induced network formation, resulting in a constant G′ before the abrupt yielding. After the instantaneous yielding, the phase angle in Fig. 12F shows a shallower slope compared to the nanoemulsion passed 4 times at 10 kpsi. These observations indicate a more complex yielding process, where not all components of the gel structure disintegrate at the same critical strain amplitude but are spread out in a wider strain regime.

Nanoemulsions prepared with n = 4 passes at an increased homogenization pressure of P = 30 kpsi exhibit again not only an increase of viscoelastic moduli, but also a change in the yielding behavior. The local maximum and broad plateau of G′′ are much more pronounced in Fig. 12C compared to the sample prepared with n = 20 passes at P = 10 kpsi. A decrease of G′ is accompanied by the first increase of G′′ and G′ shows a constant non-zero slope during the plateau of G′′. Once the gel yields, the slope of G′ decreases further. This behavior is also visible in the phase angle in Fig. 12D. Plotted as a function of the resulting stress amplitude in Fig. 12E, the decrease is sudden with a steep decay of both moduli at the end of the G′′ plateau, similar to the nanoemulsion homogenized for n = 4 passes at 10 kpsi. However, the slopes seem to level off towards very large stress amplitudes. The larger HPH pressure leads to stronger interactions between the droplets on average and hence the availability of free network sites is not sufficient for the gel to undergo the large strain overshoot.

Increasing the number of passes to n = 20 at P = 30 kpsi shows similarities to increasing the number of passes at 10 kpsi. The maximum in G′′ is more distinct, and there is a recoil in the resulting stress amplitude. A big difference is the more gradual occurrence of the yielding and the constant non-zero slope in G′ is absent. A stark contrast to the other samples is the recoil of the phase angle towards 45° over a broad strain (and resulting stress) amplitude range before eventually increasing towards 90° (see Fig. 12D). The wide range of δ close to 45° indicates the presence of a heterogeneously structured gel whose structural components yield over a broad range of strain/stress amplitudes. The recoil of the moduli as a function of stress amplitude is again the result of a very abrupt yielding (see Fig. 12E).

In conclusion, the HPH processing parameters n and P control the rheological properties of the gelled nanoemulsions and a higher degree of processing leads to more heterogeneously structured gels.

4 Conclusions

Bright-field and fluorescence confocal microscopy show that the aqueous redispersed commercial PPI consists of a considerable amount of insoluble protein particles, cell-wall debris particles, and lipid inclusions. These large insoluble particles sediment quickly and the temperature induced gelation of the PPI dispersion is very sensitive to sample loading and hence repeatability of the thermogelation is low. Sedimentation can be prevented by just one high-pressure homogenization pass due to insoluble particle size reduction. As a consequence, the PPI dispersion loses its gelling ability and stays viscous for the entire temperature range with good repeatability.

The non-gelling PPI dispersion is able to stabilize a nanoemulsion with ϕ = 0.2 oil volume fraction and exhibits a complex microscopic morphology, which is composed of not only emulsion oil droplets, but insoluble protein particles, and cell-wall debris particles persist to varying degrees throughout all processing steps. The emulsion droplet size and polydispersity can be modified by varying the number of HPH passes n and pressure P and both fluorescence microscopy and dynamic light scattering show the presence of sub-micron sized droplets. Furthermore, the nanoemulsions stabilized by the non-gelling PPI dispersion show strong thermogelation upon heating to 80 °C, which is associated to an increase in attractive interaction between droplets as a result of the denaturation and unfolding of the adsorbed protein molecules. Hence, the pea protein isolate acts not only as a nanoemulsion stabilizer, but also as a linker for thermogelation. We show that the average droplet size measured by DLS at a 90° scattering angle is a strong handle to control nanoemulsion gel stiffness after gelation at 80 °C despite the underlying complexity in composition and morphology of the commercial pea protein isolate. Furthermore, the rheological properties of the formed nanoemulsion gel can be manipulated by the parameters n and P, ranging from a strong stress overshoot and almost brittle fraction to multi-step yielding over a broad strain range, which indicates the presence of free network sites, a homogeneous, and a heterogeneously structured gel that yields over a range of critical strain amplitudes, respectively.

In conclusion, we demonstrate the use of nanoemulsion droplets stabilized by a commercial pea protein isolate as building blocks to control the mechanical properties of thermogelled nanoemulsions with droplet size and processing parameters as controlling parameters. This study serves as a first step of structure formation by colloidal thermogelation in a real system with a commercial pea protein isolate. Extending the lower droplet size limit to smaller values will be interesting to fabricate stronger gels. The investigation of sedimenting large particles with z-dependent turbidity scan measurements prior to gelation will be helpful to identify the nature of these particles. They can then be removed for future formulation to avoid perturbation of the gelation process. Furthermore, interfacial rheology will be interesting to gain more detailed insights into the adsorption kinetics of the proteins depending on the pre-processed PPI and the interfacial shear modulus will reveal structural changes of these adsorbed proteins as a function of temperature. This will be useful for optimizing the thermogelation process, e.g., selecting a specific protein fraction with beneficial interfacial properties. Detailed knowledge of the interfacial behavior of a specific protein fraction as a function of HPH processing will help to deconvolute the effect of HPH processing on droplet diameter and interaction potential (ε and λ) between the droplets. Using hydrophobic colloidal particles instead of oil droplets in combination with adsorbing PPI dispersions could potentially further decouple these effects and lead to mechanistic insights of the colloidal physics and potentially allow for predictions of the percolation threshold. Additionally, tuning the oil volume fraction ϕ could potentially lead to different gel structures as has been shown for model nanoemulsions.¹⁶ However, it is crucial to keep the surfactant-to-oil ratio constant to avoid droplet size change which drastically affects the gel elasticity. Furthermore, an extensive rheological investigation with the underlying constant shear strain rate paired with parallel and orthogonal superposition oscillatory shear measurements can give a more profound insight into the formed heterogeneous structure, which will be interesting for application as a precursor in thermo-mechanical processing for next-generation plant-based foods.

Author contributions

Damian Renggli: conceptualization, formal analysis, funding acquisition, investigation, visualization, and writing – original draft. Patrick S. Doyle: conceptualization, supervision, funding acquisition, resources, and writing – review & editing.

Data availability

All data of the results presented in the manuscript titled “Thermogelation of Nanoemulsions Stabilized by a Commercial Pea Protein Isolate: High-Pressure Homogenization Defines Gel Strength” are presented in the manuscript and the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

DR is supported by the Swiss National Science Foundation (Grant No. P500PN_210761) and partially through the Robert T. Haslam (1911) chair to PSD. Roquette is acknowledged for providing the pea protein isolate powder. The use of the DSC was made available by the Institute for Soldier Nanotechnologies, a university-affiliated research center at MIT. The confocal microscopy was made available by the Whitehead Institute for Biomedical Research at MIT.

Notes and references

1. D. K. Ray, L. L. Sloat, A. S. Garcia, K. F. Davis, T. Ali and W. Xie, Nat. Food, 2022, 3, 367–374.
2. J. Poore and T. Nemecek, Science, 2018, 360, 987–992.
3. W. Willett, J. Rockström, B. Loken, M. Springmann, T. Lang, S. Vermeulen, T. Garnett, D. Tilman, F. DeClerck, A. Wood, M. Jonell, M. Clark, L. J. Gordon, J. Fanzo, C. Hawkes, R. Zurayk, J. A. Rivera, W. De Vries, L. Majele Sibanda, A. Afshin, A. Chaudhary, M. Herrero, R. Agustina, F. Branca, A. Lartey, S. Fan, B. Crona, E. Fox, V. Bignet, M. Troell, T. Lindahl, S. Singh, S. E. Cornell, K. Srinath Reddy, S. Narain, S. Nishtar and C. J. L. Murray, Lancet, 2019, 393, 447–492.
4. C. D. Munialo, A. H. Martin, E. van der Linden and H. H. J. de Jongh, J. Agric. Food Chem., 2014, 62, 2418–2427.
5. K. J. Grabowska, S. Tekidou, R. M. Boom and A.-J. van der Goot, Food Res. Int., 2014, 64, 743–751.
6. Y. Wang, W. Kim, R. R. Naik, P. T. Spicer and C. Selomulya, Food Hydrocolloids, 2023, 140, 108611.
7. K. Kobata, Z. Zhang and D. J. McClements, Colloids Interfaces, 2023, 7, 65.
8. E. C. Hemler and F. B. Hu, Curr. Atheroscler. Rep., 2019, 21, 18.
9. D. J. McClements and L. Grossmann, npj Sci. Food, 2021, 5, 17.
10. D. J. McClements and L. Grossmann, Compr. Rev. Food Sci. Food Saf., 2021, 20, 4049–4100.
11. C. Tan and D. J. McClements, Foods, 2021, 10, 812.
12. A. Gupta, H. B. Eral, T. A. Hatton and P. S. Doyle, Soft Matter, 2016, 12, 2826–2841.
13. M. N. Yukuyama, D. D. M. Ghisleni, T. J. A. Pinto and N. A. Bou-Chacra, Int. J. Cosmet. Sci., 2015, 38, 13–24.
14. L. Chen and P. S. Doyle, Adv. Mater., 2021, 33, 2008618.
15. M. E. Helgeson, S. E. Moran, H. Z. An and P. S. Doyle, Nat. Mater., 2012, 11, 344–352.
16. M. E. Helgeson, Y. Gao, S. E. Moran, J. Lee, M. Godfrin, A. Tripathi, A. Bose and P. S. Doyle, Soft Matter, 2014, 10, 3122.
17. L. C. Hsiao and P. S. Doyle, Soft Matter, 2015, 11, 8426–8431.
18. L.-C. Cheng, P. D. Godfrin, J. W. Swan and P. S. Doyle, Soft Matter, 2018, 14, 5604–5614.
19. T. G. Mason and D. A. Weitz, Phys. Rev. Lett., 1995, 75, 2770–2773.
20. T. G. Mason, J. Bibette and D. A. Weitz, Phys. Rev. Lett., 1995, 75, 2051–2054.
21. M. E. Cates, M. Fuchs, K. Kroy, W. C. K. Poon and A. M. Puertas, J. Phys.: Condens. Matter, 2004, 16, S4861–S4875.
22. Y.-L. Chen and K. S. Schweizer, J. Chem. Phys., 2004, 120, 7212–7222.
23. K. Kroy, M. E. Cates and W. C. K. Poon, Phys. Rev. Lett., 2004, 92, 148302.
24. L.-C. Cheng, Z. M. Sherman, J. W. Swan and P. S. Doyle, Langmuir, 2019, 35, 9464–9473.
25. D. P. Keane, M. D. Mellor and R. Poling-Skutvik, ACS Appl. Nano Mater., 2022, 5, 5934–5943.
26. D. P. Keane, C. J. Constantine, M. D. Mellor and R. Poling-Skutvik, Langmuir, 2023, 39, 7852–7862.
27. A. Gharsallaoui, R. Saurel, O. Chambin and A. Voilley, Food Bioprocess Technol., 2011, 5, 2211–2221.
28. F. Roy, J. Boye and B. Simpson, Food Res. Int., 2010, 43, 432–442.
29. P. R. Shewry, J. A. Napier and A. S. Tatham, Plant Cell, 1995, 7, 945.
30. B. G. Swanson, J. Am. Oil Chem. Soc., 1990, 67, 276–280.
31. E. Keuleyan, P. Gélébart, V. Beaumal, A. Kermarrec, L. Ribourg-Birault, S. Le Gall, A. Meynier, A. Riaublanc and C. Berton-Carabin, Food Hydrocolloids, 2023, 141, 108671.
32. A. P. Adebiyi and R. E. Aluko, Food Chem., 2011, 128, 902–908.
33. M. Taghvaei, R. Sadeghi and B. Smith, PLoS One, 2022, 17, e0271887.
34. M. E. Geerts, C. V. Nikiforidis, A. J. van der Goot and A. van der Padt, Food Struct., 2017, 14, 104–111.
35. S. Sridharan, M. B. Meinders, J. H. Bitter and C. V. Nikiforidis, Food Hydrocolloids, 2020, 101, 105533.
36. X. D. Sun and S. D. Arntfield, Food Res. Int., 2010, 43, 509–515.
37. Y. Rodriguez and M. Beyrer, Food Struct., 2023, 37, 100340.
38. E. B. A. Hinderink, C. C. Berton-Carabin, K. Schroën, A. Riaublanc, B. Houinsou-Houssou, A. Boire and C. Genot, J. Agric. Food Chem., 2021, 69, 6601–6612.
39. A. K. Stone, A. Karalash, R. T. Tyler, T. D. Warkentin and M. T. Nickerson, Food Res. Int., 2015, 76, 31–38.
40. J.-L. Mession, M. L. Chihi, N. Sok and R. Saurel, Food Hydrocolloids, 2015, 46, 233–243.
41. P. Moll, H. Salminen, O. Seitz, C. Schmitt and J. Weiss, J. Dispersion Sci. Technol., 2022, 44, 2417–2428.
42. P. Moll, H. Salminen, C. Schmitt and J. Weiss, Eur. Food Res. Technol., 2021, 247, 545–554.
43. Z.-L. Kang, R. Bai, F. Lu, T. Zhang, Z.-S. Gao, S.-M. Zhao, M.-M. Zhu and H.-J. Ma, Food Hydrocolloids, 2022, 124, 107261.
44. S. Melchior, M. Moretton, S. Calligaris, L. Manzocco and M. C. Nicoli, Food Bioprod. Process., 2022, 131, 77–85.
45. P. Moll, H. Salminen, E. Griesshaber, C. Schmitt and J. Weiss, J. Food Sci., 2022, 87, 4622–4635.
46. S. Zhao, Y. Huang, D. J. McClements, X. Liu, P. Wang and F. Liu, Food Hydrocolloids, 2022, 126, 107441.
47. G. DAlessio, F. Flamminii, M. Faieta, R. Prete, A. Di Michele, P. Pittia and C. D. Di Mattia, Curr. Res. Food Sci., 2023, 6, 100499.
48. X. D. Sun and S. D. Arntfield, Food Hydrocolloids, 2012, 28, 325–332.
49. X. D. Sun and S. D. Arntfield, J. Food Eng., 2011, 105, 577–582.
50. C. Tanger, M. Müller, D. Andlinger and U. Kulozik, Food Hydrocolloids, 2022, 123, 106903.
51. W. Ren, W. Xia, D. Z. Gunes and L. Ahrné, Food Hydrocolloids, 2024, 147, 109417.
52. S. W. Janssen, L. Pouvreau and R. J. de Vries, Food Hydrocolloids, 2024, 154, 110049.
53. D. J. McClements, Prog. Lipid Res., 2021, 81, 101081.
54. S. Xu and X. Li, J. Innovative Opt. Health Sci., 2021, 14, 2140010.
55. D. Renggli, A. Alicke, R. H. Ewoldt and J. Vermant, J. Rheol., 2020, 64, 141–160.
56. J. Brocher, biovoxxel/BioVoxxel-Figure-Tools: BioVoxxel Figure Tools – v2.3.0, 2024.
57. A. Gupta, H. B. Eral, T. A. Hatton and P. S. Doyle, Soft Matter, 2016, 12, 1452–1458.
58. P. Nasatto, F. Pignon, J. Silveira, M. Duarte, M. Noseda and M. Rinaudo, Polymers, 2015, 7, 777–803.
59. Y. M. Joshi, Annu. Rev. Chem. Biomol. Eng., 2014, 5, 181–202.
60. H. Princen and A. Kiss, J. Colloid Interface Sci., 1986, 112, 427–437.
61. S. S. Datta, D. D. Gerrard, T. S. Rhodes, T. G. Mason and D. A. Weitz, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 041404.
62. V. V. Erramreddy and S. Ghosh, Colloids Surf., A, 2015, 484, 144–152.
63. R. Buscall, P. D. A. Mills, J. W. Goodwin and D. W. Lawson, J. Chem. Soc., Faraday Trans. 1, 1988, 84, 4249.
64. S. A. Safran, I. Webman and G. S. Grest, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 32, 506–511.
65. E. Zaccarelli, J. Phys.: Condens. Matter, 2007, 19, 323101.
66. A. Zaccone, J. J. Crassous and M. Ballauff, J. Chem. Phys., 2013, 138, 104908.
67. R. H. Ewoldt, M. T. Johnston and L. M. Caretta, Experimental Challenges of Shear Rheology: How to Avoid Bad Data, Springer, New York, 2014, pp. 207–241.
68. K. Hyun, S. H. Kim, K. H. Ahn and S. J. Lee, J. Non-Newtonian Fluid Mech., 2002, 107, 51–65.
69. V. Tirtaatmadja, K. C. Tam and R. D. Jenkins, Macromolecules, 1997, 30, 3271–3282.
70. J. Mewis, B. Kaffashi, J. Vermant and R. J. Butera, Macromolecules, 2001, 34, 1376–1383.
71. F. Bossard, V. Sfika and C. Tsitsilianis, Macromolecules, 2004, 37, 3899–3904.
72. T. Gisler, R. C. Ball and D. A. Weitz, Phys. Rev. Lett., 1999, 82, 1064–1067.
73. E. Adal, A. Sadeghpour, S. Connell, M. Rappolt, E. Ibanoglu and A. Sarkar, Biomacromolecules, 2017, 18, 625–635.
74. G. Huang, H. Zhang, Y. Liu, H. Chang, H. Zhang, H. Song, D. Xu and T. Shi, Macromolecules, 2017, 50, 2124–2135.
75. G. J. Donley, P. K. Singh, A. Shetty and S. A. Rogers, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 21945–21952.
76. P. L. Fuhrmann, S. Breunig, G. Sala, L. Sagis, M. Stieger and E. Scholten, J. Colloid Interface Sci., 2022, 607, 389–400.
77. N. Koumakis and G. Petekidis, Soft Matter, 2011, 7, 2456.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm00687a

---