Theoretical studies on the spectroscopic properties of porphyrin derivatives for dye-sensitized solar cell application†
Miao Xie,
Jian Wang,
Hong-Qiang Xia,
Fu-Quan Bai*,
Ran Jia,
Jin-Gun Rim and
Hong-Xing Zhang*
State Key Laboratory of Theoretical and Computational Chemistry, Institute of Theoretical Chemistry, Jilin University, 130023 Changchun, China. E-mail: baifq@jlu.edu.cn; zhanghx@mail.jlu.edu.cn; Tel: +86 431 88498966
First published on 30th March 2015
Abstract
Dye sensitizers play an important role in dye-sensitized solar cells (DSSCs). Owing to the synthetic challenge and cost of precious metal-complex dyes, increasing research has been focused on organic molecule dyes, porphyrin and light metal porphyrin dyes. In this paper, three natural porphyrin derivatives as dyes with the TiO2 nanoparticulate model are studied theoretically using density functional theory (DFT) approaches to explore their spectroscopic properties and application future in DSSCs. The detailed orbital components and absorption transitions of these porphyrin derivatives are analyzed from the calculated results. Key parameters of the short-circuit current density (Jsc) including light harvesting efficiency (LHE), electron injection driving force (ΔGinject) and nonlinear optical properties (NLO) were discussed. In addition, the calculated values of open circuit photovoltage (Voc) for these dyes were also presented. The tetrapyrrole macrocycle of porphyrin with central metals Mg or Zn can enrich the absorption strength greatly. Our research reveals that the Zn–porphyrin sensitizer can be used as a potential sensitizer for DSSCs due to its good electronic and optical properties and good photovoltaic parameters. This study is expected to understand natural dye sensitizers and assist the molecular design of new dyes for further DSSC improvement.
1. Introduction
Due to the issue of anthropogenic global warming and widespread environmental pollution damage since the end of 20th century, more and more scientists are devoted to developing renewable energy. Dye-sensitized solar cells (DSSCs) have attracted considerable attention since the pioneering work by Grätzel and O'Regan in 1991.1 DSSCs have been regarded as an economical energy conversion device because of their low cost and high efficiency.1–5 A typical DSSC is constructed with four major parts: metal oxide semiconductor electrode, dye sensitizers, liquid redox electrolyte and platinum-coated counter electrode. Among these aspects, the dye sensitizer plays an important role in photovoltaic conversion. An ideal dye should have the following characteristics: anchoring to the surface of metal oxide semiconductor electrode stably, absorb as much visible light as possible and having redox potentials to match the electron injection, as well as regeneration of semiconductor and electrolyte.5To increase the DSSC's efficiency, many researchers are trying to find a promising sensitizer from large numbers of synthesized complexes.6–18 The dye sensitizers in early design scheme involved transition metal compounds for their strong visible light absorption, long-lived excited state and high thermal stability.19–22 Due to the synthetic challenge and precious metals needed for multipyridine ruthenium complex dyes, the cheaper, safer and cleaner alternatives are desirable. Nature pigments, such as chlorophyll, carotene and cyanin, are the most abundant available in plant leaves, flowers and fruits. Experimentally, natural dye sensitized solar cells with high stability have reached an efficiency of 7.1%.23 Recently, the cobalt redox-based DSSCs allow the record conversion efficiency to exceed 12% (12.3% with YD2-o-C8 dye and 13% with SM315 dye),24,25 stimulating the further development of the photovoltaic devices.
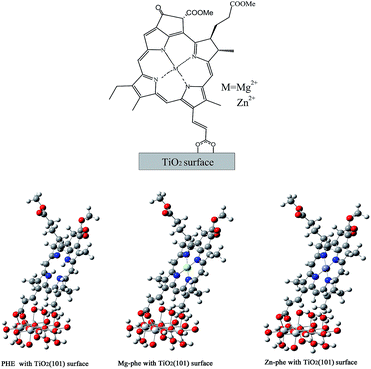
The photosynthesis has been adopted to be an opportunity to build a new type of dye-sensitizers based on nature dyes. Chlorophyll-a (Chl) is a natural photosynthetic pigment playing important roles in the electron-transferring reaction in the midst of light-harvesting pigment–protein complexes. Thus, in this study, the chlorophyll-a is taken as a parent model, and theoretical calculations are performed on regulating of the tetrapyrrole macrocycle with different central metals in order to enhance the absorption of the dye.26–28 Fig. 1 shows the chemical structures of the three sensitizers investigated in this work. The new dye Mg–PHE (PHE = pheophorbide) and Zn–PHE compared to the organic dye PHE were designed on account of two factors: (1) the dye Mg–porphyrin is the main structure of natural chlorophyll-a. It is the most abundant pigments contained in the plant. Moreover, we think that chlorophyll-a have evolved long time, and it can provide hints regarding some possible material for improving the performance of DSSCs. (2) The efficiency of the Zn–porphyrin is relatively high in all kinds of dye sensitizers.24,25 Many Zn–porphyrin derivatives have been used as organic sensitizers for DSSCs.29,30 Actually, porphyrins are molecules containing a heterocyclic macrocycle with a π-aromatic core, and showing an intense Soret band at 400–450 nm and weak Q bands at 500–650 nm. The Soret and Q absorption bands are generated based on electric charge conversion between four molecular orbitals, HOMO−1, HOMO, LUMO and LUMO+1.31,32 The Q band is constitutive of degenerate pairs of states called Qx and Qy, respectively.31 The position of Chl derivative with a carboxyl group located at the Qy axis might be more efficient in electron injection to TiO2 semiconductor electrode.33 Thus, these Chl derivatives with a carboxy group located at the Qy axis were considered in this work. Moreover, the structures of three Chl derivatives were optimized and then simplified by removing some factors unrelated to absorption spectra.
Another important part of DSSC, the titanium dioxide in nanoparticulate form has been also attracted much attention in photovoltaic solar cells application.34–36 TiO2 is used as a semiconductor in dye-sensitized solar cells. Though TiO2 absorbs light in the ultraviolet spectrum, the TiO2 surface covered with dye-sensitizer molecules can absorb light in the visible region in DSSCs. The light-induced excited dye-sensitizer molecule subsequently injects electrons into the TiO2 conduction band. The sensitized mechanism and electronic coupling between the TiO2 surface and the dye molecule, especially the natural one, has rare been involved. Therefore, we aimed to further study of the photophysical properties of three porphyrin analogues on TiO2 surface, and research the structure–performance relationships and the efficiency dyes for DSSCs.
2. Theoretical background
As well known, the overall efficiency (η) of the DSSCs is defined as the ratio of the maximum output electrical power of the DSSC to the energy of incident sunlight (Pin) and, therefore, η is determined by the short-circuit current density (Jsc), the open-circuit photovoltage (Voc), the fill factor (ff) and Pin (generally AM 1.5, 100 mW cm−2). It can be expressed by the following equation:37
 | (1) |
2.1 Short-circuit current density Jsc
Correspondingly, the Jsc value is the photocurrent per unit area (mA cm−2) when a DSSC under irradiation is short-circuited. It is related to the interaction between TiO2 and dye as well as the absorption coefficient of the dye. The Jsc in DSSCs can be expressed as:38
 | (2) |
| LHEλ = 1 − 10−A = 1 − 10−f | (3) |
| Φinject ∝ f(−ΔGinject) | (4) |
| ΔGinject = Edye* − ECB = Edye − E0–0 − ECB | (5) |
2.2 Open circuit photovoltage Voc
Voc is defined as the voltage difference between the electrolyte redox potential (Eredox/q) and the quasi-Fermi potential of electrons (EF,n/q) in the TiO2 semiconductor. As for Voc in DSSCs, it could be described by:44
 | (6) |
 | (7) |
2.3 The nonlinear optical properties (NLO)
Additionally, the good nonlinear optical properties (NLO) which include polarizability and hyperpolarizability could influence the short-circuit current density. Namely, the larger value of the nonlinear optical properties, the better photoelectric conversion property will be. The mean molecular isotropic polarizability, a, is defined as the mean value of three diagonal elements of the polarizability tensor and the anisotropy of polarizability is expressed by following:
 | (8) |
The tensor of the static first-order hyperpolarizability is a result of the third derivative of the energy with respect to the electric field components. The total first-order hyperpolarizability, βtotal, is calculated as
| βtot = [(βxxx + βxyy + βzxx)2 + (βyyy + βyzz + βyxx)2 + (βzzz + βzxx + βzyy)2]1/2 | (9) |
The chemical hardness (η) is the resistance of the species to liberate or accept electrons. It can be calculated in terms of the vertical ionization potential (IP) and vertical electron affinity (EA) values as follows:
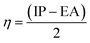 | (10) |
The IP and EA can be calculated from
| IP = E0+ − E0 and EA = E0 − E0− | (11) |
3. Computational details
Dye molecules were fully optimized using DFT with the B3LYP functional (Becke's three parameter functional and the Lee–Yang–Parr functional) after the functional comparative trial.45 On the basis of such calculations, spectroscopic absorption of dyes lined to TiO2 films was obtained by time-dependent density functional theory (TD-DFT) method.46–48 The polarizable continuum model (PCM)49–52 was employed to simulate the solvent effects of ethanol solvent molecules.In the calculations, quasi-relativistic pseudopotential of Ti atom was carried out by CEP-31G basis set and other atoms are described by a split valence basis set 6-31G(d). Therefore, the optimized ground state geometry and UV/Vis spectra were obtained by the use of DFT and TD-DFT method with B3LYP functional and 6-31G(d) basis set (CEP-31G for Ti atom). All UV/Vis spectra of the current system were reflected with Gaussian curves under full-width at half-maximum (FWHM) of 0.10 eV.
Oxidation potentials were determined from vertical ΔSCF energy calculated by a single-point energy calculation from ground-state geometries of the neutral and oxidized species in ethanol. In addition, the nonlinear optical (NLO) properties were calculated in gas phase using the finite field approach from ground-state geometries with the strength of electric field set at 0.001 au. All calculations have been performed with the Gaussian09 program package53 (Revision D.01) with a tight self-consistent filed convergence threshold.
4. Results and discussion
4.1 Molecular structure and absorption spectra
The molecular structure of the dye PHE, Mg–PHE and Zn–PHE was fully optimized. The tetrapyrrole macrocycle holds one β-substituent acted as an anchoring group for adsorption. This substituent is a conjugated double bond with a carboxylic group that is help to bond tightly to the TiO2 surface. Meanwhile, compared with dye PHE, Mg–PHE and Zn–PHE are modified by metal ions (Mg2+ and Zn2+, respectively) in the center of tetrapyrrole macrocycle. The central metal ions of Mg–PHE and Zn–PHE lie in the plane formed by the four central N atoms of the tetrapyrrole macrocycle. The average metal ions–N bond lengths of Mg–PHE and Zn–PHE are 2.068 and 2.053 Å, respectively. It should be noted that the bond length of Zn–N is shorter than that Mg–N by 0.015 Å, which can probably be interpreted as the difference of the atomic radius of between Zn and Mg. In conclusion, the results of calculated geometrical parameters for PHE, Mg–PHE and Zn–PHE are similar.It will be useful to examine the frontier molecular orbitals (FMOs) of three complexes to provide a detailed framework of the electronic structure. To show the effect of central metals, the energy and compositions of the selected FMOs are given in Fig. 2. Furthermore, the frontier molecular orbital energies and compositions of three complexes in ethanol are collected in Table 1. We display the electron density diagrams of the important frontier molecular orbitals for complex PHE, Mg–PHE and Zn–PHE in ethanol in Fig. 3.
 | ||
| Fig. 2 Plot of the frontier MOs relevant to the absorptions for dye PHE, Mg–PHE and Zn–PHE in ethanol solution. | ||
| Analogues | Molecular orbital | Energy (eV) | Main component (%) | Assignment | |||
|---|---|---|---|---|---|---|---|
| MC | TM | π-bridge | COOH | ||||
| PHE | LUMO+3 | −1.157 | 79 | 11 | 10 | π*(TM) | |
| LUMO+2 | −1.579 | 68 | 19 | 13 | π*(TM) + π*(π-bridge) | ||
| LUMO+1 | −2.247 | 85 | 9 | 6 | π*(TM) | ||
| LUMO | −2.996 | 88 | 8 | 4 | π*(TM) | ||
| ΔE(HOMO − LUMO) = 2.305 | |||||||
| HOMO | −5.301 | 98 | 1 | 1 | π(TM) | ||
| HOMO−1 | −5.488 | 98 | 2 | π(TM) | |||
| HOMO−2 | −6.201 | 100 | π(TM) | ||||
| HOMO−3 | −6.682 | 62 | 31 | 7 | π(TM) + π(π-bridge) | ||
| Mg–PHE | LUMO+3 | −1.037 | 85 | 8 | 7 | π*(TM) | |
| LUMO+2 | −1.394 | 65 | 20 | 15 | π*(TM) + π*(π-bridge) | ||
| LUMO+1 | −2.087 | 82 | 11 | 17 | π*(TM) + p(COOH) | ||
| LUMO | −2.887 | 89 | 7 | 4 | π*(TM) | ||
| ΔE(HOMO − LUMO) = 2.219 | |||||||
| HOMO | −5.106 | 98 | 2 | π(TM) | |||
| HOMO−1 | −5.387 | 2 | 97 | π(TM) | |||
| HOMO−2 | −6.234 | 89 | 8 | 2 | π(TM) | ||
| HOMO−3 | −6.337 | 1 | 78 | 16 | 4 | π(TM) + π(π-bridge) | |
| HOMO−4 | −6.804 | 1 | 94 | 1 | 4 | π(TM) | |
| Zn–PHE | LUMO+2 | −1.412 | 64 | 20 | 15 | π*(TM) + π*(π-bridge) | |
| LUMO+1 | −2.094 | 82 | 11 | 7 | π*(TM) | ||
| LUMO | −2.874 | 89 | 7 | 4 | π*(TM) | ||
| ΔE(HOMO − LUMO) = 2.255 | |||||||
| HOMO | −5.129 | 98 | 1 | π(TM) | |||
| HOMO−1 | −5.460 | 2 | 96 | π(TM) | |||
| HOMO−2 | −6.262 | 93 | 6 | 1 | π(TM) | ||
| HOMO−3 | −6.376 | 2 | 76 | 18 | 4 | π(TM) + π*(π-bridge) | |
| HOMO−4 | −6.474 | 18 | 82 | π(TM) | |||
| HOMO−5 | −6.853 | 2 | 96 | 2 | π(TM) | ||
For all of the researched complexes, the patterns of the occupied MOs and unoccupied MOs are qualitatively analogous. The unoccupied MOs orbitals and occupied MOs can be classified as similar character, which are labeled as contribution coming from the π or π* orbital of tetrapyrrole macrocycle. When the tetrapyrrole macrocycle connect with different central metals, the HOMO and LUMO energy levels changed, while the band gap changes with the order of Mg–PHE < Zn–PHE < PHE. All the highest occupied molecular orbitals (HOMOs) of the three complexes are mainly composed by the tetrapyrrole macrocycle. It can be noted, the HOMOs of PHE, Mg–PHE and Zn–PHE are similar not only in composition but also in energy level. And all the lowest unoccupied molecular orbitals (LUMOs) of the three complexes are qualitatively similar. They are mainly composed by the tetrapyrrole macrocycle and carboxyl group, as illustrated in Fig. 3.
From the above analysis, the frontier molecular orbital energies are influenced by the central metals. This is an important feature for the complex to act as the sensitizer in DSSC. Since the complex can interact with the semiconductor via the carboxyl group, the transferred electron can reach the conduction band of the semiconductor via the virtual orbitals attached by carboxyl group. With the decrease of HOMO–LUMO energy gap, the dyes would absorb more photons in the longer-wavelength range and excite more electrons transited into the unoccupied orbitals, leading to the results that the short circuit current density increases and the conversion efficiency of the dye-sensitized solar cell further enhances. Moreover, according to the analysis of the electron density diagram of four orbitals in Fig. 3, it could be concluded that the four orbitals of each dye are similar and the effect has nothing to do with the center of the metal. However, it has been shown with porphyrins that the main effect of a metal in the system is conjugation of its pπ orbital with the π electrons of the tetrapyrrole macrocycle. Because of the nodal properties of the HOMOs, the centred metal orbital can only interact with the HOMO−1 type orbital (such as the HOMO−4 of the Zn–PHE system in Fig. S1†). Thus, these predicted effects can be seen in the electronic structures, and the red-shift of the absorption bands.
The electronic transition between 350 and 800 nm for PHE, Mg–PHE and Zn–PHE in ethanol calculated by TD-B3LYP method are listed in Table 2. For each complex only the dominant excitations in the absorption process are summarized. The fitted Gaussian-type absorption curves which are based on the calculated absorption data of PHE, Mg–PHE and Zn–PHE are shown in Fig. 4.
| Analogues | Excitation (CI coeff) | ΔEcal (eV) | λcal (nm) | f | Character |
|---|---|---|---|---|---|
| PHE | HOMO → LUMO (0.65) | 2.00 | 621 | 0.3325 | π(TM) → π*(TM) |
| HOMO−1 → LUMO (0.63) | 2.20 | 564 | 0.1040 | π(TM) → π*(TM) | |
| HOMO → LUMO+1 (0.53) | 2.89 | 428 | 0.6224 | π(TM) → π*(TM) | |
| HOMO−1 → LUMO+1 (0.55) | 2.92 | 425 | 0.4428 | π(TM) → π*(TM) | |
| HOMO−3 → LUMO (0.65) | 3.23 | 384 | 0.1250 | π(TM) + π(π-bridge) → π*(TM) | |
| HOMO−2 → LUMO+1 (0.61) | 3.29 | 376 | 0.1104 | π(TM) → π*(TM) | |
| HOMO → LUMO+2 (0.60) | 3.37 | 367 | 0.4470 | π(TM) → π*(TM) + π*(π-bridge) | |
| HOMO−1 → LUMO+2 (0.48) | 3.50 | 354 | 0.3721 | π(TM) → π*(TM) + π*(π-bridge) | |
| HOMO → LUMO+2 (0.36) | π(TM) → π*(TM) + π*(π-bridge) | ||||
| Mg–PHE | HOMO → LUMO (0.67) | 1.96 | 631 | 0.4359 | π(TM) → π*(TM) |
| HOMO → LUMO+1 (0.62) | 2.82 | 438 | 0.3510 | π(TM) → π*(TM) + p(COOH) | |
| HOMO−1 → LUMO+1 (0.55) | 2.95 | 419 | 0.4405 | π(TM) → π*(TM) + p(COOH) | |
| HOMO → LUMO+2 (0.51) | 3.34 | 371 | 0.1310 | π(TM) → π*(TM) + π*(π-bridge) | |
| HOMO−4 → LUMO (0.55) | 3.41 | 363 | 0.3132 | π(TM) → π*(TM) | |
| HOMO−2 → LUMO+1 (0.42) | 3.48 | 356 | 0.1378 | π(TM) → π*(TM) + p(COOH) | |
| HOMO−1 → LUMO+2 (0.41) | π(TM) → π*(TM) + π*(π-bridge) | ||||
| HOMO−2 → LUMO+1 (0.44) | 3.53 | 350 | 0.1530 | π(TM) → π*(TM) + p(COOH) | |
| HOMO → LUMO+3 (0.40) | |||||
| Zn–PHE | HOMO → LUMO (0.68) | 1.99 | 621 | 0.4328 | π(TM) → π*(TM) |
| HOMO → LUMO+1 (0.60) | 2.84 | 436 | 0.3603 | π(TM) → π*(TM) | |
| HOMO−3 → LUMO (0.56) | 3.01 | 412 | 0.2920 | π(TM) + π*(π-bridge) → π*(TM) | |
| HOMO−1 → LUMO+1 (0.52) | 3.02 | 410 | 0.2531 | π(TM) → π*(TM) | |
| HOMO → LUMO+2 (0.58) | 3.37 | 368 | 0.2433 | π(TM) → π*(TM) + π*(π-bridge) | |
| HOMO−5 → LUMO (0.63) | 3.45 | 359 | 0.2021 | π(TM) → π*(TM) |
In generally, the UV-Vis absorption spectrums of three complexes are characterized by a weak Q band and a Soret band at a higher energy region. The studied dye shows the Q broad band in the region between 550 and 650 nm, and the Soret band at around 400 nm. The excitation energies are in very good agreement with the experimental data reported in ref. 27.
Take dye PHE as an example, three strong absorption bands were obtained peaking at 367, 428, and 621 nm, respectively. The absorption at 367 nm is contributed by excitation HOMO → LUMO+2. As can be seen from Fig. 3, the HOMO is localized on tetrapyrrole macrocycle and virtual LUMO+2 is localized on tetrapyrrole macrocycle and carboxyl group. At 428 and 621 nm, the excitations responsible for them originated from four molecular orbitals (HOMO−1, HOMO, LUMO and LUMO+1). At 428 nm, the excitation is contributed by HOMO−1 → LUMO+1. On the other hand, the excitation of HOMO → LUMO leads to the absorption band at 621 nm. According to the analysis about the frontier molecular orbital (see Fig. 3), these excitation can be ascribed to the Gouterman four molecular orbitals transition and the COOH groups involved in the transition process.
The simulated absorption spectra of Mg–PHE and Zn–PHE are similar to that of PHE but with some difference in the oscillator strength. The calculated absorptions at λ > 550 nm of both Mg–PHE and Zn–PHE have a higher oscillator strength than PHE. The PHE, Mg–PHE and Zn–PHE have the identical HOMO → LUMO transition character. But the HOMO–LUMO energy gaps of Mg–PHE and Zn–PHE are smaller than PHE (see Fig. 2), namely the light harvesting capability of the complex can be improved. This improvement is helpful to enhance the incident photon to current efficiency (IPCE) of the dye.
In order to demonstrate the effect of charge transfer states from ligand to metal, we further studied the partial molecular orbital compositions. As shown in Tables 1 and S1,† the metal center is not directly involved in the charge transfer transition. The change of MO energy levels of the dye Mg–PHE and Zn–PHE is obvious. Compared to the results of dye PHE, the metal center can evidently improve the orbital symmetry, thereby enhance the intensity of the absorptions.
4.2 The dye with TiO2 (101) surface
Besides, the electronic structure of the TiO2 model was analyzed. The density of states (DOS) is presented in Fig. S2.† Moreover, to illustrate the electronic structure, the frontier molecular orbital compositions are listed in following Table S2.† These characters are in accord with that of the understanding in TiO2 semiconductor material. Compared with the conduction band edge position of −4.3 eV for anatase, the LUMO energy level of single-crystal anatase (TiO2)5 model (location at −4.281 eV) has provided the more approximate and corresponding result. Lastly, the electronic structure and related results of the single-crystal anatase (TiO2)5 model is reasonable and accurate for describing the conduction band properties of semiconductor.
Finally, anatase (101) surface carved from crystal structures was adopted as the surface of TiO2 film. Ti5O20H22 (101) model from crystal structures was adopted as surface of TiO2 film in current work.56 In this model, H atoms were used to saturate the covalent bond of O atoms, and this method not only maintains bond-orientation in crystal, but also avoids the chaos of charge and multiplicity in the whole system. All the coordinates of the atoms in the TiO2 surface were kept frozen during the calculation. According to the scale of our model, a single carboxyl–titanium dioxide connection was selected to simulate the charge-transfer on the anatase (101) surface.
The type of anchoring functionality and linker between the dye-sensitizer and nanocrystal semiconductor surface can enhance electronic coupling and/or alter the surface state energetics so that electron injection is faster and more efficient. There are various connection types between dye molecules and TiO2 film, including the physical adsorption by electrostatic attraction/hydrogen chemical bond formation of chelating, ester-type linkage and bidentate bridging linkage.57,58 Generally, the monodentate ester-type is the most basic connection model. But in the PHE system, the number of carboxylic group for connection is only one. It is not reasonable about one steady single-bond connections in our systems, moreover, the characteristic of one monodentate ester-type is whirling, and the steady configuration is not exclusive. At last, bidentate bridging type is appropriate in this work. The bidentate bridging type is firm, which is the most important connection type in our systems for the strength and absorption efficiency. The calculated bond lengths between two carboxylate oxygens and connected titanium atoms on the TiO2 film of the PHE, Mg–PHE and Zn–PHE system are: 2.148/2.236 Å, 2.144/2.230 Å and 2.144/2.231 Å, respectively. Compared with the bond length data of TiO2 film (1.930 and 1.973 Å) and calculated data, the latter has provided the more proximate result. In this contribution, the bidentate bridging type is considered throughout for reasonable connection mode and suitable distance within binding structures (see Fig. 5).
| Analogues | Molecular orbital | Main component (%) | Energy (eV) | ||
|---|---|---|---|---|---|
| Tetrapyrrole macrocycle | COO– | TiO2 | |||
| PHE | LUMO+7 | 54 | 18 | 28 | −2.251 |
| LUMO+3 | 12 | 3 | 85 | −2.743 | |
| LUMO+1 | 58 | 22 | 19 | −3.100 | |
| LUMO | 3 | 3 | 94 | −3.213 | |
| HOMO | 98 | 2 | 0 | −5.248 | |
| HOMO−1 | 98 | 2 | 0 | −5.415 | |
| HOMO−6 | 49 | 35 | 15 | −6.634 | |
| Mg–PHE | LUMO+7 | 55 | 24 | 21 | −2.063 |
| LUMO+2 | 28 | 8 | 63 | −2.871 | |
| LUMO+1 | 21 | 11 | 68 | −2.938 | |
| LUMO | 0 | 1 | 99 | −3.237 | |
| HOMO | 98 | 2 | 0 | −5.012 | |
| HOMO−1 | 99 | 1 | 0 | −5.243 | |
| Zn–PHE | LUMO+9 | 0 | 0 | 99 | −1.843 |
| LUMO+7 | 55 | 24 | 21 | −2.067 | |
| LUMO+6 | 13 | 3 | 84 | −2.516 | |
| LUMO+3 | 23 | 4 | 73 | −2.747 | |
| LUMO+2 | 28 | 10 | 62 | −2.871 | |
| LUMO | 0 | 1 | 99 | −3.244 | |
| HOMO | 98 | 2 | 0 | −5.030 | |
| HOMO−1 | 99 | 1 | 0 | −5.320 | |
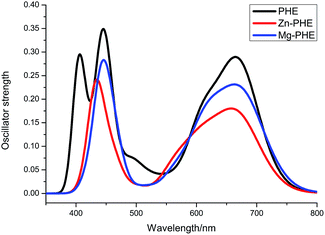 | ||
| Fig. 7 Simulated absorption spectra of dye PHE, Mg–PHE and Zn–PHE connected to TiO2 (101) surface in ethanol solution. | ||
The frontier molecular orbitals which responsible for absorption wavelength (λ) longer than 350 nm (see Fig. 8), are plotted according to their energies. For all of the complexes studied, the patterns of the occupied MOs and unoccupied MOs are qualitatively different. As depicted in Fig. 6, all the occupied MOs orbitals can be classified into one type, which are labeled as contribution coming from the π to π* orbit of tetrapyrrole macrocycle. Dye molecules connect to TiO2 film in (101) surface, and mainly alters the distribution of the unoccupied MOs orbitals can be classified as three types, which are labeled as a, b, and c, respectively. Type a is the contribution from the π to π*orbit of tetrapyrrole macrocycle and carboxyl group, type b is mainly localized on the d orbitals of the Ti atoms, and type c is mixed contribution from both a and b type.
 | ||
| Fig. 8 Electron density diagrams of the frontier molecular orbitals relevant to the absorptions of dye PHE connected to TiO2 (101) surface in ethanol solution. | ||
When the dye molecules with different central metals connect to TiO2 film in (101) surface, the LUMO energy levels of three complexes change slightly. However, the HOMOs energy levels would change notably, the HOMO energy levels of three complexes changes in the order of Mg–PHE > Zn–PHE > PHE. Thus the gap energy between HOMO and LUMO changes with the reverse sequence.
From the above analysis, it could be concluded that the frontier molecular orbitals of PHE–TiO2 derivatives are also influenced by the central metals, which is particularly reflected in the change of the energy of the unoccupied orbitals and the gap energy decrease between HOMO and LUMO. These are important features for the dyes to act in DSSC, which is conducive to the abundant absorption in long-wavelength region.
The main absorption peaks between 350 and 800 nm for three systems in ethanol solution are listed in Table 4. For each complex only the dominant excitations in the absorption process are summarized. The fitted Gaussian-type absorption curves based on the calculated absorption data are shown in Fig. 7.
| Analogues | Excitation (CI coeff) | ΔEcal (eV) | λcal | f |
|---|---|---|---|---|
| PHE | HOMO → LUMO (0.70) | 1.73 | 715 | 0.0161 |
| HOMO → LUMO+1 (0.68) | 1.85 | 671 | 0.3129 | |
| HOMO−1 → LUMO+1 (0.66) | 2.02 | 614 | 0.1801 | |
| HOMO−1 → LUMO+3 (0.60) | 2.36 | 525 | 0.0220 | |
| HOMO → LUMO+7 (0.61) | 2.72 | 455 | 0.1073 | |
| HOMO−1 → LUMO+7 (0.57) | 2.79 | 443 | 0.2927 | |
| HOMO−6 → LUMO+1 (0.51) | 3.05 | 406 | 0.2466 | |
| Mg–PHE | HOMO → LUMO+2 (0.68) | 1.85 | 671 | 0.2299 |
| HOMO−1 → LUMO+1 (0.64) | 2.00 | 621 | 0.0930 | |
| HOMO → LUMO+7 (0.63) | 2.66 | 466 | 0.1047 | |
| HOMO−1 → LUMO+7 (0.58) | 2.80 | 443 | 0.2786 | |
| Zn–PHE | HOMO → LUMO+2 (0.68) | 1.87 | 665 | 0.2211 |
| HOMO → LUMO+3 (0.69) | 2.00 | 621 | 0.1349 | |
| HOMO → LUMO+6 (0.67) | 2.20 | 565 | 0.0680 | |
| HOMO → LUMO+7 (0.62) | 2.68 | 463 | 0.1057 | |
| HOMO−1 → LUMO+7 (0.44) | 2.86 | 432 | 0.1796 | |
| HOMO → LUMO+9 (0.33) |
Compared with the experimental spectrum of dye PHE deposited on TiO2 film,27 the simulated spectra not only has a similar profile but also possesses the same absorption range. Hence, the calculated absorption spectra of dye connected to TiO2 surface model are reasonable and creditable.
For dye PHE system, the electron density diagrams of the frontier molecular orbitals in ethanol media are given in Fig. 8. Three strong absorption peaks were simulated with the absorption peaking at 406, 443, and 671 nm (Fig. 7 and Table 4), respectively. The strongest absorption at 443 nm is contributed by excitation HOMO−1 → LUMO+7. As shown in Fig. 8 and Table 3, the HOMO−1 is consisted of tetrapyrrole macrocycle and the virtual orbital LUMO+7 is consisted of π* orbitals of tetrapyrrole macrocycle (54%) and d orbitals of Ti atoms (28%), therefore this excitation can be partly assigned as dye sensitizer to TiO2 film charge transfer. For the other two strong absorption at 406 and 671 nm, the excitations mostly originate from the different occupied orbital but terminate in the same virtual orbital LUMO+1, and is consisted of both π* orbitals of dye sensitizer and d orbitals of Ti atoms. The excitation of HOMO−6 → LUMO+1 is in charge of absorption at 406 nm and can be assigned as charge transfer transition from dye sensitizer to TiO2 film, in which the COOH group has some contributions. In addition, the excitation of HOMO → LUMO+1 leads to the absorption at 671 nm, which can also be assigned as dye sensitizer to TiO2 film charge transfer. In the λ > 650 nm range, the contribution of long-wavelength absorption is more related to the d orbitals of Ti atoms (19%). Thus, the long-wavelength absorption conduces to ultrafast, excited electron injection in PHE to TiO2.
Moreover, there is a weak peak located at about 500 nm in absorption spectra for PHE system. It is contributed by excitation HOMO−1 → LUMO+3 that lead to the quite weak oscillator strength among the calculated absorptions. The calculated lowest energy absorption at 715 nm is contributed by HOMO–LUMO excitation. This excitation transition process is also from dye sensitizer to TiO2 film charge transfer.
The simulated absorption spectra of Mg–PHE and Zn–PHE system are similar with each other, but different from that of PHE system. The calculated absorptions (λ < 500 nm) in both Mg–PHE and Zn–PHE system show the strongest absorption band at 443 nm and 432 nm, respectively. The strongest absorption of Mg–PHE system is contributed by excitation HOMO−1 → LUMO+7. While the strongest absorption band of the Zn–PHE system at 432 nm is contributed by excitation HOMO−1 → LUMO+7 and HOMO → LUMO+9. These excitation transition processes are charge transfer from dye sensitizer to TiO2 film and the COOH groups are involved in the transition process. The simulated absorption spectra of Mg–PHE and Zn–PHE system (λ > 500 nm) are similar to that of PHE system but with oscillator strength weakened a little bit. The absorption of Mg–PHE system at 671 nm is contributed by excitation HOMO → LUMO+2. Meanwhile, for Zn–PHE system, the absorption at 665 nm is also contributed by excitation HOMO → LUMO+2. These excitation transition processes are different from PHE system. The excitation transition processes are all from dye sensitizer to TiO2 film charge transfer transitions.
Finally, similar to the isolated dyes, the simulated electronic absorption spectra of these systems can also be divided into two regions and the bands also red shift and become broader. It could be seen that a small modulation such as different central metals would influence the integral efficiency of DSSCs to a certain extent.
4.3 Nonlinear optical properties
Nonlinear optical properties (NLO, such as polarizability and hyperpolarizability) were determined by the intra-molecular charge delocalization in π-electron-conjugated molecules. Thus, the NLO properties could be used as a tool to describe the efficiency of electron charge transfer of the sensitizer, which could also influence the short-circuit current density and the solar cell efficiency. It has been reported that the porphyrin analogues59,60 and other organic dye sensitizer systems,61 which have good NLO property. And so usually it possesses good photoelectric conversion property. The calculated mean isotropic polarizabilities (a), polarizability anisotropies (Δa), and first-order hyperpolarizability (βtot), together with chemical hardness (η) values are listed in Table 5. As observed in Table 5, the Mg–PHE and Zn–PHE have similar NLO properties as compared with the dye PHE due to the analogues structure. In general, the chemical hardness values of metalloporphyrins are less than that of PHE. The dye Mg–PHE has the lowest η, suggesting that its electron density was more readily influenced and that Mg–PHE would be the most reactive among the analogues.| Analogues | a (au) | Δa (au) | βtot (au) | η (eV) |
|---|---|---|---|---|
| PHE | 614 | 579 | 6965 | 2.30 |
| Mg–PHE | 620 | 578 | 6659 | 2.26 |
| Zn–PHE | 617 | 571 | 6588 | 2.28 |
Since the mean isotropic polarizabilities (a) and polarizability anisotropies (Δa) are a measure of the response of electrons against electric field, the large a means that the electrons are easier to move from the donor to the acceptor group. The polarizability anisotropies (Δa) of the PHE, Mg–PHE and Zn–PHE are 579, 578 and 571 (in au), respectively, and the values are almost the same. The calculated isotropic polarizability of dye PHE is slightly less than that of the Mg–PHE and Zn–PHE. This may be resulted from that the tetrapyrrole macrocycle of PHE is stronger than the tetrapyrrole macrocycle with central metal in the Mg–PHE and Zn–PHE. And then the electronic structure of tetrapyrrole macrocycle is more stable than that of tetrapyrrole macrocycle with central metal, thus the response of external field for PHE is weaker than that for Mg–PHE and Zn–PHE.
The computed βtot values in Table 5 are consistent with the donor and acceptor strengths of the analogues. And PHE gave the highest βtot compared with the Mg–PHE and Zn–PHE because of the planar configuration and π-conjugation of the PHE. Although regulating the tetrapyrrole macrocycle with central metal has brought an effective electronic π-coupling between the porphyrin macrocycle and the central metal, it also resulted in βtot values slightly less than the PHE without central metal. It demonstrates that βtot was greatly influenced by the character of the donor and acceptor groups.
4.4 Photovoltaic properties
The high photo-electricity conversion efficiency of DSSCs requires rapid and efficient electron injection from the excited state of the dyes into the CB of TiO2. To fully understand the influence of the tetrapyrrole macrocycle with central metal in DSSCs, we must take the quality of electron injection into consideration. Herein, one method was adopted to assess the electron injection of all systems; it is calculations of the ΔGinject of the PHE, Mg–PHE and Zn–PHE systems. The electronic injection free enthalpy ΔGinject, ground (Edye) and excited state (Edye*) oxidation potentials computed for the PHE, Mg–PHE and Zn–PHE systems are summarized in Table 6.| Analogues | Edye | E0–0 | Edye* | ΔGinject |
|---|---|---|---|---|
| PHE | 4.93 | 2.00 | 2.93 | −1.07 |
| Mg–PHE | 4.78 | 1.96 | 2.82 | −1.18 |
| Zn–PHE | 4.79 | 1.99 | 2.80 | −1.20 |
The ground state oxidation potential (GSOP) is related to the total electron attachment energy in solution. The rigorous way to obtain the GSOP (ΔGox) is to compute free energy different between the neutral and the oxidized ground-state species, (G0 − G+)GS.62 The Gibbs free energy in solution of a species i (Gisolv) is defined as
| Gisolv = Givac + ΔGisolv | (12) |
All the ΔGinject is in negative value for all porphyrin analogues, thus the excited state energy level of dye lies above the ECB of TiO2 and the electron injection from the dye to TiO2 is spontaneous. As shown in Table 6, the calculated ΔGinject are increasing in the order: Zn–PHE < Mg–PHE < PHE. Therefore, the driving force of systems are in the opposite order Zn–PHE > Mg–PHE > PHE. This result vindicates that the dye Zn–PHE and Mg–PHE have the relatively higher electron injection efficiency than that of PHE.
Another factor related to efficiency of DSSC is the performance of the dyes in responsibility to the incident light. Based on the LHE of the dyes, the performance value has to be as high as possible to maximize the photocurrent response. In this work, we use peak area (A) calculation method which is more precise and accurate than the maximum absorption method as it covers all excited state transitions, even low intensity transitions, and now quantitative study would be possible. Moreover, this method was used in previous work.63 The peak area for all porphyrin analogues has been calculation and listed in Table 7. For all porphyrin analogues, the peak area is calculated through following equation:
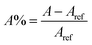 | (13) |
| Analogues | A | ΔA | A% | µx-bare (Debye) | µx-ads (Debye) |
|---|---|---|---|---|---|
| PHE | 49.43 | — | — | 0.9004 | 15.09 |
| Mg–PHE | 63.20 | 13.77 | 27.86 | 1.0682 | 17.09 |
| Zn–PHE | 67.19 | 17.67 | 35.93 | 0.9334 | 17.30 |
In this equation, the peak area for the PHE in ethanol solution is selected to serve as an A-reference (Aref) for the Mg–PHE and Zn–PHE. As the data from Table 7, the peak area is increased in metalloporphyrin, which is a result of peak broadening and red-shifted. Take into account of peak area, it is indicated that the Mg–PHE and Zn–PHE have an efficient LHE as compared to the PHE. Thus, we can conclude that metalloporphyrin (the Mg–PHE and Zn–PHE) can lead to higher photon to current response than the PHE.
As discussed above, besides the short-circuit current density Jsc, the overall power conversion efficiency also could be influenced by the open-circuit voltage (Voc). The shift in the conduction band of the semiconductor could lead to an increasing Voc. This shift can be assessed based on the increase in the dipole moment µnormal of the adsorbed molecules pointing outward from the semiconductor surface. In this work, the adsorbed system dipole moment µx-ads symbol was used to instead of µnormal and bare dyes dipole moment of (µx-bare). As shown in Table 7, the variation trends of the µx-bare and the µx-ads are the consistent. Namely, the PHE has lower dipole moment values compare to the Mg–PHE and Zn–PHE. And the metalloporphyrin (the Mg–PHE and Zn–PHE) increases the µx-ads values more than 13%. The Mg–PHE and Zn–PHE would shift the CB of the semiconductor toward the vacuum energy level than the PHE, thus, produce qualitatively higher Voc values.
As a consequence, we could draw a conclusion that dyes with the large LHE, ΔGinject and Voc have higher IPCE efficiency. Thus, the performance of DSSCs sensitized by dyes Mg–PHE and Zn–PHE might superior than PHE, due to their favourable performances of the above factors based on our computed results.
4.5 The mechanism of photo-induced electron transfer
Towards an understanding of the processes involved in the photo-induced electron transfer from the dye to the semiconductor are very important for DSSCs. Generally, for n-type semiconductor (such as TiO2 and ZnO64), they are further classified into type-I and type-II:65,66 (1) the type-I is the excited electron moves from the LUMO of the dye to the CB of the semiconductor. (2) The type-II is a direct charge-transfer excitation of electron from the HOMO of the dye to the CB of the semiconductor. In order to gain insight of the mechanism of photo-induced electron transfer, the relative energies for all systems are reported in Table 8. Furthermore, Fig. 9 shows schematically the proposed mechanism of type-I and type-II electron transfer between the dye and semiconductor (pathway A and pathway B).| System | HOMO (eV) | Edye (eV) | LUMO (eV) | Edye* (eV) | E0–0 (eV) | ε1 (eV) | ε2 (eV) | ε3 (eV) |
|---|---|---|---|---|---|---|---|---|
| TiO2 | −6.520 | −4.281 | ||||||
| PHE | −5.301 | 4.93 | −2.996 | 2.93 | 2.00 | |||
| PHE–TiO2 | −5.248 | −3.213 | ||||||
| Energy difference | 1.004 | 0.217 | 0.787 | |||||
| Mg–PHE | −5.106 | 4.78 | −2.887 | 2.82 | 1.96 | |||
| Mg–PHE–TiO2 | −5.012 | −3.237 | ||||||
| Energy difference | 1.113 | 0.350 | 0.763 | |||||
| Zn–PHE | −5.129 | 4.79 | −2.874 | 2.80 | 1.99 | |||
| Zn–PHE–TiO2 | −5.030 | −3.244 | ||||||
| Energy difference | 1.126 | 0.370 | 0.756 |
 | ||
| Fig. 9 The mechanism of type-I (pathway A) and type-II (pathway B) electron transfer between the dye and semiconductor. | ||
Essentially, as shown in Fig. 9, the type-I (pathway A) electron transfer mechanism must be operative through the photo-excited electron hops from the LUMO of the dye sensitizer to the LUMO of the dye–TiO2 complex, and finally gets transferred to the CB of the semiconductor. Hence, it is not only the LUMO level of the dye needs to be above the ECB of the semiconductor, but also the energy difference between the LUMO level of the dye sensitizer and the LUMO level of the dye–TiO2 system and the energy difference between the LUMO level of the dye–TiO2 system and ECB of the semiconductor need to be individually positive. In other words, the positive energies of ε1, ε2 and ε3 are expectant. Moreover, the type-II (pathway B) electron transfer mechanism is electron transitions directly from the dye to the semiconductor. For effective charge injection from dye to semiconductor, it is seen from Table 8 that the energy difference between the LUMO level of the dye–TiO2 system and ECB of the semiconductor is still larger. The positive values for ε1, ε2 and ε3 of all the systems make efficient for light harvesting. And, the LUMO level of the dye sensitizer should be at least ∼0.5 eV higher than the ECB has recommended by Grätzel for efficient solar energy-to-current conversion.67 For PHE–TiO2, Mg–PHE–TiO2 and Zn–PHE–TiO2 system, the energies of ε3 are more than 0.5 eV, thus making them appealing prospective candidates for DSSCs.
From above discussion, it is demonstrated that the type-I processes is dominated when TiO2 surface was adsorbed.
5. Conclusion
Electronic structures and spectroscopic properties of several typical dye molecules of porphyrin and metal porphyrin derivatives absorbed to TiO2 film was investigated theoretically. Based upon the calculated results, the role of different center metals in the tetrapyrrole macrocycle was analyzed, and the following conclusions can be drawn.For isolated dye molecule, the absorption spectra, photovoltaic properties as well as nonlinear optical properties have been calculated. It is indicate that the PHE with efficient electronic injection free enthalpy ΔGinject was made for electron injection, as well as a long range of absorption spectra and high nonlinear optical response. Moreover, the calculated results indicate that different central metals employed to adjust porphyrin macrocycle is a crucial factor to affect the gap energy between HOMO and LUMO of porphyrin, electron transition, and the electron transfer activity in DSSC. When the tetrapyrrole macrocycle was inserted with different central metals, the dyes can produce higher nonlinear optical response and electronic injection free enthalpy ΔGinject as well as enrich the absorptions greatly, especially at the Q-bonds. This improvement is helpful to obtain a higher Jsc compared with the PHE, and benefit to enhance the power conversion efficiency (η).
In addition, the analysis of the absorption spectra for dye PHE connecting to TiO2 in (101) surface shows the orbital-coupling between dye PHE and TiO2 film is satisfactory. However, for Mg–PHE and Zn–PHE systems, the central metal effect leads to a sizable difference in the electronic structures. In the case of absorption, the charge transfer transition processes of Mg–PHE and Zn–PHE system have significant differences with PHE system, and more energy is needed. Although the HOMO–LUMO energy gaps of Mg–PHE–TiO2 and Zn–PHE–TiO2 systems are smaller than that PHE–TiO2 system, the weaker orbital-coupling effects of Mg–PHE–TiO2 and Zn–PHE–TiO2 system are harmful to LHE, because the energy mismatching renders electron transition to TiO2 difficulty. But on the other hand, the Mg–PHE and Zn–PHE system can produce higher dipole moment, thus producing qualitatively higher Voc values. Thus, the performance of DSSCs sensitized by dyes Mg–PHE and Zn–PHE might superior than PHE. Lastly, the mechanism of photo-induced electron transfer for the entire system has been discussed. Our calculations show that the type-I processes is dominated when TiO2 surface was adsorbed. Overall, it has been shown that tetrapyrrole macrocycle with different central metals has an important effect on the energy levels and absorptions, which would help to improve the efficiency of DSSCs. These results should be helpful to design new sensitizers in DSSC. We hope that our calculations could facilitate future experimental.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant no. 21173096 and 21203071) and the State Key Development Program for Basic Research of China (Grant no. 2013CB834801) and the Jilin Provincial Natural Science Foundation (Grant no. 201215031) and the Graduate Innovation Fund of Jilin University (Grant no. 2014005).Notes and references
- B. O'Regan and M. Grätzel, Nature, 1991, 353, 737–740 CrossRef.
- K. Kalyanasundaram and M. Grätzel, Coord. Chem. Rev., 1998, 177, 347–414 CrossRef CAS.
- A. I. Philippopoulos, A. Terzis, C. P. Raptopoulou, V. J. Catalano and P. Falaras, Eur. J. Inorg. Chem., 2007, 2007, 5633–5644 CrossRef PubMed.
- M. Green, Appl. Phys. A: Mater. Sci. Process., 2009, 96, 153–159 CrossRef CAS.
- M. Grätzel, Nature, 2001, 414, 338–610 CrossRef PubMed.
- K. Hara, T. Sato, R. Katoh, A. Furube, Y. Ohga, A. Shinpo, S. Suga, K. Sayama, H. Sugihara and H. Arakawa, J. Phys. Chem. B, 2002, 107, 597–606 CrossRef.
- T. Horiuchi, H. Miura, K. Sumioka and S. Uchida, J. Am. Chem. Soc., 2004, 126, 12218–12219 CrossRef CAS PubMed.
- E. A. Gibson, A. L. Smeigh, L. Le Pleux, J. Fortage, G. Boschloo, E. Blart, Y. Pellegrin, F. Odobel, A. Hagfeldt and L. Hammarström, Angew. Chem., 2009, 121, 4466–4469 CrossRef PubMed.
- S. Ito, S. M. Zakeeruddin, R. Humphry-Baker, P. Liska, R. Charvet, P. Comte, M. K. Nazeeruddin, P. Péchy, M. Takata, H. Miura, S. Uchida and M. Grätzel, Adv. Mater., 2006, 18, 1202–1205 CrossRef CAS PubMed.
- D. Kuciauskas, M. S. Freund, H. B. Gray, J. R. Winkler and N. S. Lewis, J. Phys. Chem. B, 2000, 105, 392–403 CrossRef.
- A. Islam, H. Sugihara, K. Hara, L. P. Singh, R. Katoh, M. Yanagida, Y. Takahashi, S. Murata, H. Arakawa and G. Fujihashi, Inorg. Chem., 2001, 40, 5371–5380 CrossRef CAS PubMed.
- Q. Wang, W. M. Campbell, E. E. Bonfantani, K. W. Jolley, D. L. Officer, P. J. Walsh, K. Gordon, R. Humphry-Baker, M. K. Nazeeruddin and M. Grätzel, J. Phys. Chem. B, 2005, 109, 15397–15409 CrossRef CAS PubMed.
- M. Grätzel, Inorg. Chem., 2005, 44, 6841–6851 CrossRef PubMed.
- N. Robertson, Angew. Chem., 2006, 118, 2398–2405 CrossRef PubMed.
- F. O. Lenzmann and J. M. Kroon, Adv. OptoElectron., 2007, 2007 Search PubMed.
- F.-T. Kong, S.-Y. Dai and K.-J. Wang, Adv. OptoElectron., 2007, 2007 Search PubMed.
- A. S. Shalabi, A. M. El Mahdy, M. M. Assem, H. O. Taha and W. S. Abdel Halim, Mol. Phys., 2013, 112, 22–34 CrossRef.
- C. I. Oprea, P. Panait, B. F. Minaev, H. Ågren, F. Cimpoesu, M. Ferbinteanu and M. A. Gîrţu, Mol. Phys., 2013, 111, 1526–1538 CrossRef CAS.
- M. K. Nazeeruddin, A. Kay, I. Rodicio, R. Humphry-Baker, E. Mueller, P. Liska, N. Vlachopoulos and M. Graetzel, J. Am. Chem. Soc., 1993, 115, 6382–6390 CrossRef CAS.
- M. K. Nazeeruddin, S. M. Zakeeruddin, R. Humphry-Baker, M. Jirousek, P. Liska, N. Vlachopoulos, V. Shklover, C.-H. Fischer and M. Grätzel, Inorg. Chem., 1999, 38, 6298–6305 CrossRef CAS PubMed.
- P. Péchy, T. Renouard, S. M. Zakeeruddin, R. Humphry-Baker, P. Comte, P. Liska, L. Cevey, E. Costa, V. Shklover, L. Spiccia, G. B. Deacon, C. A. Bignozzi and M. Grätzel, J. Am. Chem. Soc., 2001, 123, 1613–1624 CrossRef PubMed.
- N. Onozawa-Komatsuzaki, M. Yanagida, T. Funaki, K. Kasuga, K. Sayama and H. Sugihara, Sol. Energy Mater. Sol. Cells, 2011, 95, 310–314 CrossRef CAS PubMed.
- W. M. Campbell, K. W. Jolley, P. Wagner, K. Wagner, P. J. Walsh, K. C. Gordon, L. Schmidt-Mende, M. K. Nazeeruddin, Q. Wang, M. Grätzel and D. L. Officer, J. Phys. Chem. C, 2007, 111, 11760–11762 CAS.
- A. Yella, H.-W. Lee, H. N. Tsao, C. Yi, A. K. Chandiran, M. K. Nazeeruddin, E. W.-G. Diau, C.-Y. Yeh, S. M. Zakeeruddin and M. Grätzel, Science, 2011, 334, 629–634 CrossRef CAS PubMed.
- S. Mathew, A. Yella, P. Gao, R. Humphry-Baker, B. F. Curchod, N. Ashari-Astani, I. Tavernelli, U. Rothlisberger, M. K. Nazeeruddin and M. Grätzel, Nat. Chem., 2014, 6, 242–247 CrossRef CAS PubMed.
- X.-F. Wang, H. Tamiaki, L. Wang, N. Tamai, O. Kitao, H. Zhou and S.-I. Sasaki, Langmuir, 2010, 26, 6320–6327 CrossRef CAS PubMed.
- X.-F. Wang, O. Kitao, H. Zhou, H. Tamiaki and S.-I. Sasaki, Chem. Commun., 2009, 1523–1525, 10.1039/b820540j.
- S.-I. Sasaki, M. Yoshizato, M. Kunieda and H. Tamiaki, Eur. J. Org. Chem., 2010, 2010, 5287–5291 CrossRef PubMed.
- M. S. Kang, S. H. Kang, S. G. Kim, I. T. Choi, J. H. Ryu, M. J. Ju, D. Cho, J. Y. Lee and H. K. Kim, Chem. Commun., 2012, 48, 9349–9351 RSC.
- S. H. Kang, I. T. Choi, M. S. Kang, Y. K. Eom, M. J. Ju, J. Y. Hong, H. S. Kang and H. K. Kim, J. Mater. Chem. A, 2013, 1, 3977–3982 CAS.
- M. Gouterman, J. Chem. Phys., 1959, 30, 1139–1161 CrossRef CAS PubMed.
- M. Gouterman, J. Mol. Spectrosc., 1961, 6, 138–163 CrossRef CAS.
- X.-F. Wang, O. Kitao, H. Zhou, H. Tamiaki and S.-I. Sasaki, J. Phys. Chem. C, 2009, 113, 7954–7961 CAS.
- W.-J. Chen, P.-J. Tsai and Y.-C. Chen, Small, 2008, 4, 485–491 CrossRef CAS PubMed.
- Z.-Y. Chen, Y. Hu, T.-C. Liu, C.-L. Huang and T.-S. Jeng, Thin Solid Films, 2009, 517, 4998–5000 CrossRef CAS PubMed.
- P. Tengvall and I. Lundström, Clin. Mater., 1992, 9, 115–134 CrossRef CAS.
- M. R. Narayan, Renewable Sustainable Energy Rev., 2012, 16, 208–215 CAS.
- J. Zhang, H.-B. Li, S.-L. Sun, Y. Geng, Y. Wu and Z.-M. Su, J. Mater. Chem., 2012, 22, 568–576 RSC.
- W. Sang-aroon, S. Saekow and V. Amornkitbamrung, J. Photochem. Photobiol., A, 2012, 236, 35–40 CrossRef CAS PubMed.
- R. Katoh, A. Furube, T. Yoshihara, K. Hara, G. Fujihashi, S. Takano, S. Murata, H. Arakawa and M. Tachiya, J. Phys. Chem. B, 2004, 108, 4818–4822 CrossRef CAS.
- Z. Ning, Y. Fu and H. Tian, Energy Environ. Sci., 2010, 3, 1170–1181 CAS.
- W.-L. Ding, D.-M. Wang, Z.-Y. Geng, X.-L. Zhao and W.-B. Xu, Dyes Pigm., 2013, 98, 125–135 CrossRef CAS PubMed.
- J. Wang, H. Li, N.-N. Ma, L.-K. Yan and Z.-M. Su, Dyes Pigm., 2013, 99, 440–446 CrossRef CAS PubMed.
- J. Feng, Y. Jiao, W. Ma, M. K. Nazeeruddin, M. Grätzel and S. Meng, J. Phys. Chem. C, 2013, 117, 3772–3778 CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS PubMed.
- M. E. Casida, C. Jamorski, K. C. Casida and D. R. Salahub, J. Chem. Phys., 1998, 108, 4439–4449 CrossRef CAS PubMed.
- R. E. Stratmann, G. E. Scuseria and M. J. Frisch, J. Chem. Phys., 1998, 109, 8218–8224 CrossRef CAS PubMed.
- N. N. Matsuzawa, A. Ishitani, D. A. Dixon and T. Uda, J. Phys. Chem. A, 2001, 105, 4953–4962 CrossRef CAS.
- M. Cossi, G. Scalmani, N. Rega and V. Barone, J. Chem. Phys., 2002, 117, 43–54 CrossRef CAS PubMed.
- V. Barone, M. Cossi and J. Tomasi, J. Chem. Phys., 1997, 107, 3210–3221 CrossRef CAS PubMed.
- B. Mennucci and J. Tomasi, J. Chem. Phys., 1997, 106, 5151–5158 CrossRef CAS PubMed.
- M. Cossi and V. Barone, J. Chem. Phys., 2001, 115, 4708–4717 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. E. Gomperts, O. Stratmann, A. J. Yazyev, R. Austin, C. Cammi, J. W. Pomelli, R. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01., Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- U. Diebold, N. Ruzycki, G. S. Herman and A. Selloni, Catal. Today, 2003, 85, 93–100 CrossRef CAS.
- M. Lazzeri, A. Vittadini and A. Selloni, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 155409 CrossRef.
- K. Syres, A. Thomas, F. Bondino, M. Malvestuto and M. Grätzel, Langmuir, 2010, 26, 14548–14555 CrossRef CAS PubMed.
- P. Falaras, Sol. Energy Mater. Sol. Cells, 1998, 53, 163–175 CrossRef CAS.
- Y.-X. Weng, L. Li, Y. Liu, L. Wang and G.-Z. Yang, J. Phys. Chem. B, 2003, 107, 4356–4363 CrossRef CAS.
- M. P. Balanay and D. H. Kim, Curr. Appl. Phys., 2011, 11, 109–116 CrossRef PubMed.
- M.-J. Lee, M. Balanay and D. Kim, Theor. Chem. Acc., 2012, 131, 1–12 CAS.
- C.-R. Zhang, Z.-J. Liu, Y.-H. Chen, H.-S. Chen, Y.-Z. Wu, W. Feng and D.-B. Wang, Curr. Appl. Phys., 2010, 10, 77–83 CrossRef PubMed.
- M. Pastore, S. Fantacci and F. De Angelis, J. Phys. Chem. C, 2010, 114, 22742–22750 CAS.
- O. M. Sarhangi, S. M. Hashemianzadeh, M. M. Waskasi and A. P. Harzandi, J. Photochem. Photobiol., A, 2011, 225, 95–105 CrossRef CAS PubMed.
- Q. Zhang, C. S. Dandeneau, X. Zhou and G. Cao, Adv. Mater., 2009, 21, 4087–4108 CrossRef CAS PubMed.
- E. L. Tae, S. H. Lee, J. K. Lee, S. S. Yoo, E. J. Kang and K. B. Yoon, J. Phys. Chem. B, 2005, 109, 22513–22522 CrossRef CAS PubMed.
- S. M. Pratik and A. Datta, Phys. Chem. Chem. Phys., 2013, 15, 18471–18481 RSC.
- M. Grätzel, Acc. Chem. Res., 2009, 42, 1788–1798 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4ra17080f |
| This journal is © The Royal Society of Chemistry 2015 |