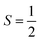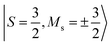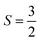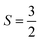Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Accurate and interpretable representation of correlated electronic structure via Tensor Product Selected CI†
Nicole M.
Braunscheidel
,
Arnab
Bachhar
and
Nicholas J.
Mayhall
 *
*
Department of Chemistry, Virginia Tech, Blacksburg, VA 24060, USA. E-mail: nmayhall@vt.edu
First published on 28th March 2024
Abstract
The task of computing wavefunctions that are accurate, yet simple enough mathematical objects to use for reasoning, has long been a challenge in quantum chemistry. The difficulty in drawing physical conclusions from a wavefunction is often related to the generally large number of configurations with similar weights. In Tensor Product Selected Configuration Interaction (TPSCI), we use a locally correlated tensor product state basis, which has the effect of concentrating the weight of a state onto a smaller number of physically interpretable degrees of freedom. In this paper, we apply TPSCI to a series of three molecular systems ranging in separability, one of which is the first application of TPSCI to an open-shell bimetallic system. For each of these systems, we obtain accurate solutions to large active spaces, and analyze the resulting wavefunctions through a series of different approaches including (i) direct inspection of the TPS basis coefficients, (ii) construction of Bloch effective Hamiltonians, and (iii) computation of cluster correlation functions.
1. Introduction
Computational electronic structure theory has developed into an indisputably powerful tool for understanding the quantum mechanical origins of molecular structure and chemical transformations. Progress over the past several decades (in both hardware and algorithmic improvements) has advanced quantum chemistry to the point where the accuracy can often rival that of experiments, particularly for low-energy molecules near equilibrium. However, as the accuracy of a computation increases, so to does the numerical complexity of the solution, making interpretation more challenging.The need for achieving both quantitative accuracy and qualitative richness was recognized early on, as computers were first becoming increasingly powerful.1–3 Gaining access to the underlying driving forces of reactions or structure has proven to be one of the most valuable aspects of quantum chemistry. As such, the ability to extract qualitative insight is perhaps more important than simply arriving at a quantitatively accurate result.
Many approaches to extracting conceptual insight from ab initio calculations involves some sort of “localization”. This is because much of our chemical vocabulary is inherently local (oxidation states, bond order, partial charges, hybridization, etc.). The abundance of local chemical constructs is not an accident; molecular structure is generally highly local. For example, the alcohol group in 1-hexanol behaves very similarly to that in 1-heptanol. As such, understanding the local structure of a functional group in one system extends significant reasoning power to other systems. Consequently, much of the effort spent toward extracting qualitative insight involves the localization of orbitals, such as with natural bond orbital methods (NBOs),4–7 atomic localized molecular orbital methods (ALMOs),8–10 localization of the density as in atoms in molecules (AIM),11 or even many-electron states12–19 (though this list is necessarily far from comprehensive). Localization has also been leveraged extensively for reducing computational complexity. Underlying many of these developments is the fact that the density matrix asymptotically approaches linearly scaling for gapped systems in a localized basis.20
All (most) of the methods discussed above ultimately leverage the fact that a Slater determinant wavefunction (or MP2 or CCSD) is invariant with respect to orbital rotations within the occupied or virtual spaces. Orbitals can be mixed to maximize some localizing objective function, and the resulting wavefunctions can then be analyzed in terms of local or non-local contributions.
In contrast, a tensor product space permits a much more explicit notion of locality, one that naturally exposes the ability to factorize into local quantities (entanglement) and allows clear labeling of the entire Hilbert space in terms of unambiguously local quantities. Recently, we have explored the ability to leverage features of tensor product spaces to decrease the computational cost of large active-space calculations.21–25 In ref. 23 and 24, we introduced a method called Tensor Product Selected Configuration Interaction (TPSCI), which uses a selected CI algorithm to assemble a basis of tensor products of locally correlated wavefunctions, which can provide accurate approximations to full configuration interaction (FCI). In this paper, we demonstrate the ability of these (still expansive) TPSCI wavefunctions to be meaningfully analyzed and interpreted across a rather wide range of physical systems, including non-bonded chromophores, dichromium spin coupling, and the fully delocalized π system of a graphene nano-flake.
2. Theory
We will start by expressing the electronic Hamiltonian in a basis of active orbitals (p, q, r, s),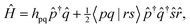 | (1) |
2.1 Orbital clustering
To make progress toward a compact and interpretable representation, we will assume that the active orbitals can be partitioned into disjoint clusters, or groups of orbitals. We will generally use capital letters, I, to index clusters. This orbital partitioning (or “clustering”) is chosen to maximize the interactions within a cluster while minimizing the interactions between clusters. For example, if one had a bimetallic compound (as we consider later in the paper) then one might define each cluster to include all the orbitals centered on a given metal, such that all local dynamical correlation is included as intra-cluster correlation, and weak spin-coupling is considered as an inter-cluster correlation.Physically, we will assume that the interactions within a cluster are stronger than the interactions between clusters. This is not a formal requirement, but rather one that affects the convergence of the calculations. Each cluster is effectively a new smaller active space, and thus we can construct correlated many-body wavefunctions, |αI〉, that are completely localized to each local active space (cluster), I. We will refer to these locally correlated states as cluster states, using them to form an orthonormal basis for the full Fock space on each cluster. Likewise, the list of all tensor products of cluster states forms an orthonormal basis for the global Fock space on the full orbital active space. This allows us to represent an arbitrary wavefunction with s states as a linear combination of cluster-state tensor products:
 | (2) |
However, interesting molecular systems generally have non-trivial interactions between clusters, and so this becomes a rather poor approximation in practice. Fortunately, one can easily obtain a much-improved ground-state estimate by including a mean-field description of the inter-cluster interactions when defining the local cluster Hamiltonian, instead of simply projecting out the inter-cluster terms. An approach, called Cluster Mean-Field (cMF) theory, was introduced by Scuseria and coworkers,30–33 and used by Gagliardi and coworkers under the name variational localized active-space self-consistent field (vLASSCF).34 In this work, we construct correlated cluster states by diagonalizing the local cMF effective Hamiltonian, ĤcMFI, for each cluster:
 | (3) |
![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) †ŝ|0J〉. The cMF Hamiltonian for cluster I depends on the one-particle reduced density matrix (1RDM) of all the other clusters, requiring the cMF solution to be obtained self-consistently.
†ŝ|0J〉. The cMF Hamiltonian for cluster I depends on the one-particle reduced density matrix (1RDM) of all the other clusters, requiring the cMF solution to be obtained self-consistently.
Bearing a strong resemblance to traditional Hartree–Fock (HF) theory, the self-consistent solution corresponds to the variational minimization of an unentangled (product state) wavefunction ansatz,
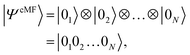 | (4) |
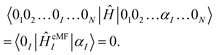 | (5) |
2.2 Tensor product selected CI (TPSCI)
While cMF provides a qualitatively attractive approximation for the ground state of a clustered molecular system, quantitative accuracy is clearly missing due to the neglect of all inter-cluster entanglement. Analogous to the common approach of using substituted Slater determinants for a basis, we will use substituted tensor product states as a basis for the full Hilbert space, where each TPS is typically taken to be an eigenstate of a cluster's cMF Hamiltonian. This is similar to a CI analogue of the Block-Correlated Coupled Cluster (BCCC) approach of Li.35The Hartree–Fock-based Slater determinant basis and the TPS basis are equivalent, in that both span the full space. However, as soon as truncations are made, the two bases span different spaces. One benefit of working in a TPS basis where the local Hamiltonians are diagonal is that, due to the fact that local correlation is folded into the basis states themselves, the low-energy solutions become more heavily concentrated on a smaller number of basis states. Consequently, computational methods that exploit sparsity (e.g., selected CI) might be expected to be more performant in the correlated TPS basis than in a Slater determinant basis. In ref. 23 and 24 we demonstrated that this is often true, and can sometimes be leveraged for computational benefit.
In the Tensor Product Selected CI (TPSCI) method,23 we use the general CIPSI36 algorithm to discover and exploit, in a bottom-up fashion, the sparsity of the exact wavefunction in a TPS basis. This uses perturbation theory to iteratively discover the non-negligible TPSs that are needed to accurately approximate the exact solution. This is done via the following steps:
(1) Diagonalize Ĥ in the current variational space (this being a list of TPS basis states that are expected to have large amplitude in the exact solution).
(2) Apply the Ĥ to the current variational space eigenvector. This couples the variational space to the external space.
(3) Compute the first-order wavefunction in the external space.
(4) Move the external configurations with large first-order coefficients from the external space to the variational space.
(5) If the variational dimension increases, go back to step 1. If not, exit.
This overall iterative loop is shown in Fig. 1. In principle, all local FCI cluster states would be computed and used to form the basis for state space. While this is tractable for small clusters, for larger clusters, this becomes computationally prohibitive, and high-energy states are generally discarded prior to running TPSCI. We generally use M to refer to the maximum number of cluster states kept in a particular Fock sector of a cluster. For each particle number subspace included, the corresponding lowest M eigenstates are computed. Then the Ŝ+ and Ŝ− operators are applied to those cluster states to generate the basis for the higher Ms sectors. More details can be found in ref. 24.
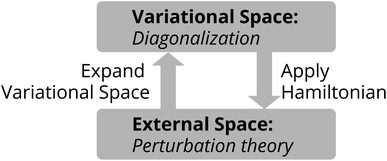 | ||
| Fig. 1 Schematic illustration of the selected CI algorithm used in TPSCI to build a basis of tensor product states. This is iterated until the dimension of the variational space stops growing. | ||
The computational limitations of conventional (determinant basis) CIPSI are generally determined by the size of the dimension of the variational space. Because TPSCI uses correlated TPS basis vectors, more correlation energy is typically recovered with smaller variational spaces, addressing the most significant bottleneck. This comes at a cost, however, during the matrix-element evaluation. Whereas evaluating matrix elements in the Slater determinant basis is extremely efficient, matrix elements in the TPS basis are significantly more expensive. For a 3-cluster example, consider the following Hamiltonian contribution that contains three operators (![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) †
†![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) †r) on cluster 1, and one operator (s) on cluster 2:
†r) on cluster 1, and one operator (s) on cluster 2:
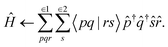 | (6) |
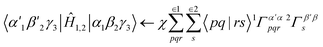 | (7) |
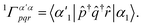 | (8) |
We start by defining a “model space”, {|ϕi〉}, which is taken to be the set of physically meaningful TPSs that qualitatively define the structure or process. To ensure that the model space is actually relevant to the physics computed, the exact low-energy states of the system, |Ψs〉, should have relatively large projections onto the model space, i.e.,
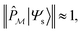 | (9) |
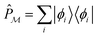 . Next, we seek a Hermitian effective Hamiltonian which exists only in the model space, but that yields the exact energy spectrum. While this is often done in a bottom-up fashion through approaches like quasi-degenerate perturbation theories or Schrieffer–Wolff transformations, if one already has access to the exact target eigenstates, an effective Hamiltonian (specifically, a Bloch effective Hamiltonian) can be obtained simply in a top-down fashion by direct projection,
. Next, we seek a Hermitian effective Hamiltonian which exists only in the model space, but that yields the exact energy spectrum. While this is often done in a bottom-up fashion through approaches like quasi-degenerate perturbation theories or Schrieffer–Wolff transformations, if one already has access to the exact target eigenstates, an effective Hamiltonian (specifically, a Bloch effective Hamiltonian) can be obtained simply in a top-down fashion by direct projection,ĤBloch = |![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) s〉Es〈 s〉Es〈![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) s| s| | (10) |
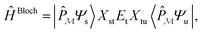 | (11) |
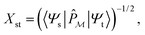 | (12) |
Following the recent work of Luzanov, Krylov, and Casanova,48,49 the local TPS representation makes it simple to compute cluster correlation functions of various local cluster operators to characterize states in terms of observables. A two-cluster correlation function for operator Ô is given as the covariance between the operator localized onto each individual cluster:
| cov(ÔI,ÔJ) = 〈Ψs|ÔIÔJ|Ψs〉 − 〈Ψs|ÔI|Ψs〉〈Ψs|ÔJ|Ψs〉 | (13) |
![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) I, local spin projection, ŜzI, local spin Ŝ2I, and local excitation,
I, local spin projection, ŜzI, local spin Ŝ2I, and local excitation, ![[Q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0051_0302.gif) I =
I = ![[1 with combining circumflex]](https://www.rsc.org/images/entities/char_0031_0302.gif) − |0I〉〈0I|, which indicates that cluster I is excited out of its cMF ground cluster state.
− |0I〉〈0I|, which indicates that cluster I is excited out of its cMF ground cluster state.
3. Results
In the following sections, we explore the ability to simultaneously obtain quantitative yet interpretable approximations to large active spaces. Because our representation is ideal for separable clusters, to obtain insight into the transferability of the formalism, we explore systems that span a broad spectrum in terms of clusterability, going from a non-bonded tetracene tetramer (Sec. 3 3.1), to an anti-ferromagnetically coupled dichromium complex (Sec. 3 3.2), to a completely delocalized graphene-flake model, hexabenzocoronene (Sec. 3 3.3).We use PySCF software for performing any necessary geometry optimizations, Hartree–Fock calculations, and integral generation.50 All TPSCI calculations are performed using our open-source FermiCG software.51
3.1 Singlet-fission: tetracene tetramer
Singlet fission is the photophysical process by which a bright singly excited state, |S1〉, is converted into two lower-energy triplet states, |T1〉 + |T1〉, by way of a multiexcitonic intermediate state, |1TT〉.52 Because this process converts a single photon into two excitons (each of which can split into charge carriers), materials that exhibit singlet fission have promising applications in solar cells due to the possibility of overcoming the Shockley–Queisser limit for efficiency.53A dimer model description of the singlet-fission process requires a total of 8 states: the ground state, |S0S0〉, two local bright states, |S1S0〉 and |S0S1〉, two local triplet states, |S0T1〉 and |T1S0〉, and the three biexcitonic states arising from the product of two triplet states, |T1T1〉. The biexcitonic state is characterized as an entangled pair of local triplets, which can be spin-coupled into either a singlet |1TT〉, triplet |3TT〉, or quintet |5TT〉, represented in the diabatic basis via their Clebsch–Gordan coefficients,
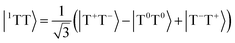 | (14) |
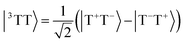 | (15) |
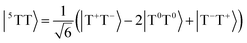 | (16) |
While a dimer model captures the key intermediates, it is too small to describe additional physical effects that occur in bulk systems. For example, the initial bright state is generally understood to delocalize over several monomers, increasing the number of localized biexcitons to which it can couple. Further, it has been seen that singlet fission rates are increased by the involvement of a non-nearest-neighbor biexciton |1T⋯T〉, which is absent from the dimer model by construction.55,56 Recent work has further demonstrated the importance of beyond-dimer effects.57,58
Because methods that rely on single or even double excitations struggle to accurately describe two-electron excitations, multireference methods, such as CASPT2, are often required to capture the wide range of electronic character. While this is suitable for a couple chromophores, active-space methods typically grow exponentially with the number of chromophores, making it difficult to extend to larger systems.
TPSCI (similar to ASD, which preceded it27–29) is well-suited for treating collections of chromophores because the physical system efficiently maps onto the tensor product basis. In a recent paper,24 we demonstrated that TPSCI was able to provide accurate approximations to complete active space configuration interaction (CASCI) for a large (40e, 40o) active space, which incorporated 10 active orbitals for each of the four tetracene chromophores. In this paper, we explore this further, using the TPS structure to facilitate further analysis and characterization of the resulting wavefunctions.
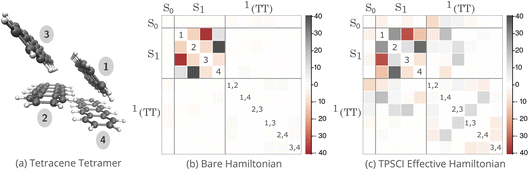
In this subsection, we use TPSCI to go beyond the minimal dimer example for singlet fission and explore dressed Hamiltonains and local cluster operator correlations for a tetracene tetramer (shown in Fig. 2(a)) using a large (40e, 40o) active space.
In Fig. 2(b) and (c), we plot the bare Hamiltonian and effective Hamiltonian in the model space as described above, with the columns arranged to correspond with the cluster labels in Fig. 2(a). The diagonal energies are subtracted to better reveal the off-diagonal activity in meV. In both plots, the Hamiltonian is blocked by state type: the ground state, four singlet excited states, and six singlet biexcitons, where the non-singlet states have been omitted for clarity. As expected, the singlet excitons couple very strongly to each other, both in the bare and effective Hamiltonians, which ultimately gives rise to bright-state delocalization. There is only negligible coupling between the S1 and biexcitons in the bare plot, but after including external space correlations, we see a significant growth in the strength of the effective coupling. These are listed explicitly in Table 1. Whereas the |1TT〉 states on the 3 herringbone dimers develop significant S1 coupling after the inclusion of the external space, the planar dimers remain uncoupled from the bright spectrum. In addition to strengthening the coupling between the bright states and the biexcitonic states, the inclusion of higher-energy states also induces couplings between the biexcitons themselves.
| Ĥ eff | |1TT〉 | ||||||
|---|---|---|---|---|---|---|---|
| 1,2 | 1,4 | 2,3 | 1,3 | 2,4 | 3,4 | ||
| 〈S1| | 1 | −6.43 | 19.46 | 0.33 | 0.80 | 1.31 | 0.01 |
| 2 | 3.66 | 2.47 | 10.16 | 1.04 | 0.50 | 0.00 | |
| 3 | 0.37 | −0.82 | 14.36 | −0.64 | −0.08 | −0.07 | |
| 4 | −0.23 | −6.62 | 0.42 | 0.10 | 0.37 | 0.08 | |
![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) I), cluster spin projections (ŜzI), and cluster excitations (
I), cluster spin projections (ŜzI), and cluster excitations (![[Q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0051_0302.gif) I) for each of the six singlet biexcitons 1(TT) and four bright states.
I) for each of the six singlet biexcitons 1(TT) and four bright states.
![[Q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0051_0302.gif) I =
I = ![[1 with combining circumflex]](https://www.rsc.org/images/entities/char_0031_0302.gif) − |0I〉〈0I|. A value of 0 indicates that the cluster is in its local ground state. A value of 1 indicates that the cluster is always in a local excited state. All the local excitation ranks of the states are summed
− |0I〉〈0I|. A value of 0 indicates that the cluster is in its local ground state. A value of 1 indicates that the cluster is always in a local excited state. All the local excitation ranks of the states are summed
| State | 〈![[Q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0051_0302.gif) 1〉 1〉 |
〈![[Q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0051_0302.gif) 2〉 2〉 |
〈![[Q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0051_0302.gif) 3〉 3〉 |
〈![[Q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0051_0302.gif) 4〉 4〉 |
Excitation rank |
|---|---|---|---|---|---|
| 6 | 0.90 | 0.89 | 0.20 | 0.04 | 2.01 |
| 7 | 0.63 | 0.54 | 0.81 | 0.03 | 2.02 |
| 10 | 0.95 | 0.10 | 0.01 | 0.95 | 2.01 |
| 12 | 0.45 | 0.54 | 1.00 | 0.02 | 2.01 |
| 19 | 0.05 | 0.11 | 0.91 | 0.95 | 2.02 |
| 21 | 0.05 | 0.86 | 0.11 | 0.99 | 2.01 |
| 24 | 0.63 | 0.27 | 0.13 | 0.11 | 1.14 |
| 25 | 0.24 | 0.57 | 0.08 | 0.16 | 1.05 |
| 28 | 0.18 | 0.08 | 0.81 | 0.02 | 1.09 |
| 31 | 0.06 | 0.20 | 0.01 | 0.80 | 1.07 |
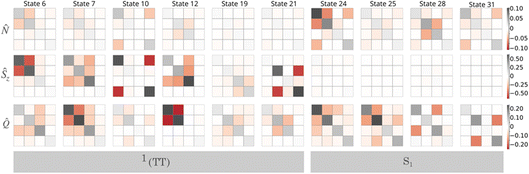 | ||
Fig. 3 Tetracene tetramer correlation functions. (top row) Particle number, ![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) I. (middle row) Spin projection, ŜzI. (bottom row) Cluster excitation, I. (middle row) Spin projection, ŜzI. (bottom row) Cluster excitation, ![[Q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0051_0302.gif) I. The first 6 plots from the left are for the |1TT〉 states. The last 4 plots from the left are for the |S1〉 states. Each matrix column/row corresponds to cluster 1 to 4, as labeled in Fig. 2. The color scale for each correlation function is shown on the far right. I. The first 6 plots from the left are for the |1TT〉 states. The last 4 plots from the left are for the |S1〉 states. Each matrix column/row corresponds to cluster 1 to 4, as labeled in Fig. 2. The color scale for each correlation function is shown on the far right. | ||
Looking first at the particle number correlations, ![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) I, we see that overall, the “dark” |TT〉 states are relatively quiet compared to the charge correlations present in the bright states. This is entirely expected based on the physical characteristics of the bright vs. dark states. Bright states have relatively large amounts of charge-transfer character mixed in. The presence of charge transfer makes the local particle number less well defined, which increases a cluster's charge variance, and similarly increases the anti-correlation between two clusters' charge states (when the donor is cationic, the acceptor has a high probability of being anionic). Although weaker than the lowest S1 state, we see clear signatures of charge correlation present in a couple of the biexcitons (state 6 and 10). This is consistent with an analysis of the wavefunction itself. If we compute the amount of charge transfer present in each state, we find that out of all of the biexcitons, states 6 and 10 have the highest percentage of CT character, 4.6% and 4.5%, respectively (see the ESI† for all state CT compositions). Charge correlations between clusters entangled into a biexciton also indicate significant superexchange, which stabilizes the low-spin biexciton.62,63
I, we see that overall, the “dark” |TT〉 states are relatively quiet compared to the charge correlations present in the bright states. This is entirely expected based on the physical characteristics of the bright vs. dark states. Bright states have relatively large amounts of charge-transfer character mixed in. The presence of charge transfer makes the local particle number less well defined, which increases a cluster's charge variance, and similarly increases the anti-correlation between two clusters' charge states (when the donor is cationic, the acceptor has a high probability of being anionic). Although weaker than the lowest S1 state, we see clear signatures of charge correlation present in a couple of the biexcitons (state 6 and 10). This is consistent with an analysis of the wavefunction itself. If we compute the amount of charge transfer present in each state, we find that out of all of the biexcitons, states 6 and 10 have the highest percentage of CT character, 4.6% and 4.5%, respectively (see the ESI† for all state CT compositions). Charge correlations between clusters entangled into a biexciton also indicate significant superexchange, which stabilizes the low-spin biexciton.62,63
Considering next the ŜzI correlations, we see the opposite trend, where the biexciton states have significantly more pronounced correlations, and the bright states are featureless (as would be expected from the lack of local triplet character). This is also consistent with the nature of the different sets of states. A |1TT〉 biexciton is characterized as two entangled triplet states coupled into a singlet state. Because the total Ms is zero, when the first monomer is in the Ms = 1 microstate, the entangled partner is very likely to be found in the Ms = −1 microstate. This entanglement leads to a very strong ŜzI covariance.
Using the spin correlation as a way to label the biexcitons,48 we can identify that state 6 is a (1,2) biexciton (meaning that it primarily exists on chromophores 1 and 2), states 7 and 12 are superpositions of (1,3) and (2,3) biexcitons, and state 21 is a (2,4) biexciton. Looking at state 19, we see what resembles a (3,4) biexciton, although the overall magnitude is much smaller. In order to understand this, we can look at the Ŝ2 expectation value of the state (shown in the ESI†). We find that in this case, the (what we labeled to be) |1TT〉 state has significant spin contamination of about 1.1. This is a consequence of the fact that the |1TT〉 and |3TT〉 states are approximately degenerate, meaning that any arbitrary mixing of the two states is also an eigenstate. This mixing of the two spin states essentially creates a “broken-symmetry” state, where one chromophore is Ms = 1 and the other is Ms = −1. By locking the local spin vectors, the local ŜzI fluctuations are diminished, and hence the ability to have significant covariance with any other cluster. This could be corrected by tightening our TPSCI convergence, or by rediagonalizing Ŝ2 in nearly-degenerate subspaces.
Looking more closely at state 12, we see that clusters 1, 2, and 3 all have significant ŜzI fluctuations, but only the 1,3 and 2,3 pairs are spin correlated. Considering the cluster excitation ![[Q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0051_0302.gif) I covariance plot, we see that while cluster three has zero fluctuations (it is consistently excited), clusters 1 and 2 are strongly correlated. This means that cluster 3 is always excited, but when cluster 1 is excited, cluster 2 is most likely in the ground state, and vice versa. This suggests a situation where a triplet state on cluster 3 forms a biexciton with a triplet delocalized between clusters 1 and 2. This is consistent with an analysis of the individual TPS state coefficients, were we find that 98% of the wavefunction is characterized as a superposition of the 1,3 and 2,3 biexcitons, ψ12 ≈ 0.671(T1S0T1S0) + 0.73t1(S0T1T1S0).
I covariance plot, we see that while cluster three has zero fluctuations (it is consistently excited), clusters 1 and 2 are strongly correlated. This means that cluster 3 is always excited, but when cluster 1 is excited, cluster 2 is most likely in the ground state, and vice versa. This suggests a situation where a triplet state on cluster 3 forms a biexciton with a triplet delocalized between clusters 1 and 2. This is consistent with an analysis of the individual TPS state coefficients, were we find that 98% of the wavefunction is characterized as a superposition of the 1,3 and 2,3 biexcitons, ψ12 ≈ 0.671(T1S0T1S0) + 0.73t1(S0T1T1S0).
3.2 Cr2-complex effective Hamiltonian
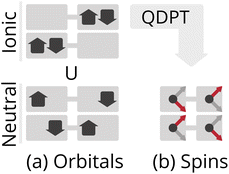
Multi-center organometallic complexes often exhibit interesting physics, such as single-molecule magnetism,64,65 or valuable catalytic capabilities, such as water oxidation,66 or nitrogen fixation.67 While having a computational method that could efficiently compute the low-energy structure of organometallic compounds would be highly valuable, several physical features of these systems make this challenging. When multiple weakly interacting metal centers possess unpaired electrons, the resulting low-energy states are highly multiconfigurational, making conventional approaches like perturbation theory or coupled cluster theory inappropriate, as they require a qualitatively correct single determinant wavefunction as a reference.Because the product of multiple high-spin centers leads to a large number of spin states, it is not always possible to predict, a priori, the spin multiplicity of a multi-center organometallic complex. Consider a simple biradical Hubbard model, represented in a local minimal orbital basis, as shown in Fig. 4(a). Here, the low-energy configurations are both open-shell broken-symmetry states, and proper eigenstates must be superpositions of these two configurations, one being a singlet, and the other the Ms = 0 component of the triplet. Because the ionic (or charge transfer) configurations are both singlets, they can only mix with the singlet combination of neutral configurations, which is ultimately the origin of the antiferromagnetic coupling in biradicals.
This picture can often be simplified significantly. For systems where the electron repulsion is sufficiently large, such that hopping of an electron from one center to another incurs a high energy barrier (i.e., U ≫ t), the influence of charge fluctuations can be approximately downfolded using quasi-degenerate perturbation theory into an effective spin Hamiltonian, called the Heisenberg–Dirac–van Vleck Hamiltonian:68
| ĤHDvV = −2JŜ1Ŝ2, | (17) |
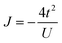 . For this model, the low-energy spectrum is completely determined by the value of J.
. For this model, the low-energy spectrum is completely determined by the value of J.
Starting from the ab initio Hamiltonian instead of the Hubbard model, one finds that the zeroth-order term also contains the non-local direct exchange integral. Since bare exchange stabilizes the high-spin states, and the second-order super-exchange term stabilizes the low-spin states, even getting the sign correct for the exchange coupling constant can be difficult, as the value of J is determined by the subtle interactions coupling the metals with each other and with the ligands. However, once known, the relative ordering of the spin states can be directly written down in terms of J. While this is indeed an approximate description of the low-energy electronic structure, it is profoundly useful, as the prediction of J is also often what connects experiment to theory, where J is commonly fitted to experimental magnetic susceptibility measurements.
The most common approach to computing J from ab initio quantum chemistry is to use DFT, where one of the degenerate broken-symmetry configurations is optimized, followed by a spin projection formula, originally proposed by Noodleman,69 and then improved by Yamaguchi.70,71 While this approach has been widely used due to its conceptual simplicity and computational efficiency, there are downsides. First, the formalism doesn't actually ever compute the proper low-spin wavefunction, and so only the energy is generally able to be extracted. Second, the results become highly functional-dependent. While all systems demonstrate some density-functional dependence, spin-coupled complexes are intrinsically more sensitive because the percentage of exact exchange directly affects the relative energies of the high-spin and broken-symmetry states.72,73 Finally, DFT doesn't offer a path toward systematic improvements, making it difficult to compare results.
Because of these reasons, multireference methods like CASSCF and CASPT2 are often used to model exchange-coupled systems. However, the associated computational cost limits the active-space size, making it difficult to converge results to the point where quantitative comparison to experiment is possible. Often one finds that dynamical correlation (involving interactions with non-magnetic orbitals) has a significant impact on the value of J, generally strengthening the antiferromagnetic interactions. As such, density matrix renormalization group algorithm (DMRG) has emerged as the standard benchmark method for computing exchange coupling constants in organometallic compounds,74–83 although if only the value of J is needed, efficient approaches that combine spin-flip methods have also been useful.44,45,47,84
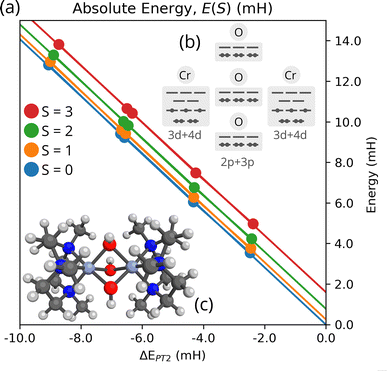
In this subsection, we present the first application of TPSCI to a transition-metal compound, a tris-hydroxy-bridged Cr(III) dimer, [L2Cr(III)2(μ-OH)3]+3 (L = N,N′,N′′-trimethyl-1,4,7-triazacyclononane (Fig. 5(c)), which has a J value that was experimentally fitted to a value of −66 cm−1.85 Recently, Pantazis studied this system using DMRG to solve the low-energy states in a large orbital active space of up to (30e, 22o),74 calculating an exchange coupling constant of −23.9 cm−1.
As is commonly done with selected CI approaches, significantly improved approximations to the energy can obtained by performing a series of selected CI calculations with varying thresholds and extrapolating to the zero-error limit, which is taken as an approximation to full CI. While more sophisticated extrapolation schemes have been proposed,87 we use the common approach of assuming a linear relationship between the variational energies and the PT2 correction.88 In Fig. 5(a), we plot the variational TPSCI energy of the 4 lowest eigenstates as a function of the PT2 correction to each state. By extrapolating this linear relationship to zero PT2 correction, we can obtain an estimate of the exact eigenvalues of the Hilbert space defined by M. In Fig. 5(a), we show the extrapolation for the M = 100 calculations.
In order to compute J, we can use the Landé interval rule derived from the energy spectrum of a two-site Heisenberg model, J = (E(S − 1) − E(S))/2S. After computing the lowest energy S = 0, 1, 2, and 3 spin states, we could use any of the gaps to compute J. If the ab initio system was to be perfectly described by the Heisenberg model, then the computed J value would be independent of the particular energy gaps we were to choose. However, the Heisenberg model is rarely exact, and so we can partially quantify how approximate the model is by comparing J values computed with different energy gaps. We list the various J values in Table 3, using either the best variational TPSCI energies, the TPSCI + PT2 corrected energies, or the extrapolated energies. Results for both M = 100 and M = 200 are included.89
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 357 for M = 100 and 127
357 for M = 100 and 127![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 493 for M = 200
493 for M = 200
| J (S0,S1) | J (S1,S2) | J (S2,S3) | |
|---|---|---|---|
| TPSCI | |||
| M = 100 | −25.4 | −25.7 | −26.6 |
| M = 200 | −26.6 | −27.0 | −27.7 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| TPSCI + PT2 | |||
| M = 100 | −26.7 | −27.3 | −28.3 |
| M = 200 | −28.3 | −28.9 | −29.9 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Extrapolated | |||
| M = 100 | −28.0 | −28.7 | −30.0 |
| M = 200 | −29.3 | −30.3 | −31.3 |
Inspecting first the effect of energy extrapolation, we find that the extrapolated J values are larger than the TPSCI + PT2 values by only around 1 cm−1, and that doubling the size of M from 100 to 200 only increases the J value by another 1 cm−1, despite the fact that this also increases the dimension of the total accessible Hilbert space significantly from 2.7 × 1014 to 6.1 × 1015. Compared to the recent (30e, 22o) DMRG-SCF calculations, which yielded a J value of −23.9 cm−1,74 our computed values are slightly larger, in good agreement with the reported CASSCF(6e,10o)-NEVPT2 value of −31.8 cm−1.74
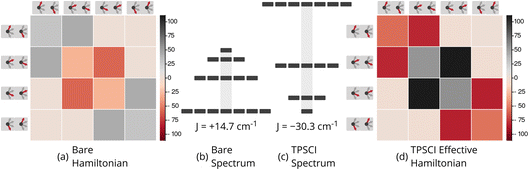
 . As such, the low-energy spectrum is expected to be dominated by the 16 spin configurations that form a basis for the S = 3, 2, 1, and 0 states, providing a clear definition for our model space. However, because the Hamiltonian preserves spin, we can restrict our focus to only the global Ms = 0 subspace, and take our model space to be the corresponding 4-dimensional subspace. In Fig. 6, we plot both the bare Hamiltonian (Fig. 6(a)) and the Bloch-effective Hamiltonian (Fig. 6(d)) in the model space. The corresponding low-energy spectra are provided in Fig. 6(b) and (c), respectively.
. As such, the low-energy spectrum is expected to be dominated by the 16 spin configurations that form a basis for the S = 3, 2, 1, and 0 states, providing a clear definition for our model space. However, because the Hamiltonian preserves spin, we can restrict our focus to only the global Ms = 0 subspace, and take our model space to be the corresponding 4-dimensional subspace. In Fig. 6, we plot both the bare Hamiltonian (Fig. 6(a)) and the Bloch-effective Hamiltonian (Fig. 6(d)) in the model space. The corresponding low-energy spectra are provided in Fig. 6(b) and (c), respectively.
There are two main features of the effective Hamiltonian that emerge from the implicit inclusion of the external space correlation: the spin-coupling interactions have their signs flipped, and their magnitudes are increased. The result of this is that the system changes from ferromagnetic to antiferromagnetic coupling and the gaps between the spin states are approximately doubled.
This qualitative result is consistent with a recent study (ref. 90) where J values for a similar dichromium(III) complex were computed using the vLASSCF-SI method. Because the vLASSCF method works in a similar TPS basis, they were able to evaluate the impact of explicitly including some charge-transfer configurations. They, too, found that this effected a qualitative change in the sign of J, switching from ferromagnetic to anti-ferromagnetic.
In order to further analyze this Cr2(III) system, we can compute cumulants of local observables, as mentioned above.48,49 In Table 4, we list the expectation values, the variances, and the covariances of a few operators local to the Cr2(III) centers, including the local particle number, ŜzCr, and Ŝ2Cr. We also include the global Ŝ2 because our basis is not spin-adapted, so there is potential for spin-contamination, although our calculations are converged tightly enough to reduce spin-contamination to the 4th decimal place.
| Root | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 〈Ŝ2〉 | 0.000 | 2.000 | 6.000 | 12.000 |
〈![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) Cr〉 Cr〉 |
7.010 | 7.010 | 7.010 | 7.010 |
var(![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) Cr) Cr) |
0.019 | 0.018 | 0.016 | 0.014 |
cov(![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) Cr, Cr,![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) Cr) Cr) |
−0.004 | −0.004 | −0.002 | 0.000 |
| 〈ŜzCr〉 | 0.019 | 0.013 | 0.003 | 0.003 |
| var(ŜzCr) | 1.248 | 2.042 | 1.246 | 0.453 |
| cov(ŜzCr,ŜzCr) | −1.245 | −2.039 | −1.242 | −0.449 |
| 〈Ŝ2Cr〉 | 3.741 | 3.742 | 3.745 | 3.750 |
| var(Ŝ2Cr) | 0.064 | 0.061 | 0.056 | 0.047 |
| cov(Ŝ2Cr,Ŝ2Cr) | 0.017 | 0.014 | 0.008 | −0.001 |
Considering first the local particle number values, we find that the average number of electrons is quite consistent across the different spin states, staying just barely above 7 electrons (which corresponds to a Cr(III) oxidation state, with 2 doubly occupied ligand orbitals). However, the fluctuations in the oxidation state noticeably depend on the spin state, increasing as the global spin is decreased. This is easily understood as a consequence of the super-exchange mechanism, whereby coupling to electron-transfer states stabilizes the low-spin states relative to the high-spin states. Again, this is consistent with what is seen in ref. 90, and the more general treatment of formal magnetic interactions from Malrieu and coworkers.43 For the global singlet state, the statistical correlation between the oxidation-state fluctuations on the two Cr centers is only 21.1%, indicating that the majority of the oxidation-state fluctuations are due to electron exchanges with the bridging ligands.
Because both Cr centers are re-coupled into global eigenvectors of Ŝ2, the local ŜzCr is no longer a good quantum number, and becomes maximally uncertain. In fact, we can further test how closely the system follows Heisenberg–Dirac–von Vleck physics by comparing the analytic values of the local SzCr variance using the Clebsch–Gordon coefficients for a product of two  spins. For the singlet, triplet, quintet, and heptet states, the analytic var(ŜzCr) values are −1.25, −2.05, −1.25, and −0.45, respectively. Our computed correlations are only slightly different from these analytical values: −1.245, − 2.039, − 1.242, and − 0.449, further indicating good consistency with the Heisenberg model.
spins. For the singlet, triplet, quintet, and heptet states, the analytic var(ŜzCr) values are −1.25, −2.05, −1.25, and −0.45, respectively. Our computed correlations are only slightly different from these analytical values: −1.245, − 2.039, − 1.242, and − 0.449, further indicating good consistency with the Heisenberg model.
Inspecting the local Ŝ2Cr values, we see a complementary picture to that provided by the particle-number fluctuations. As the global spin is decreased, the local S2 values also tend to decrease, while the variance increases. This is consistent with the superexchange mechanism stabilizing global low-spin states by coupling to charge-transfer states. When an electron transfers from one Cr to the another, the number of unpaired electrons decreases. As a result, the local S2Cr values decrease, and develop a positive covariance between the centers.
3.3 Conjugation in 2D
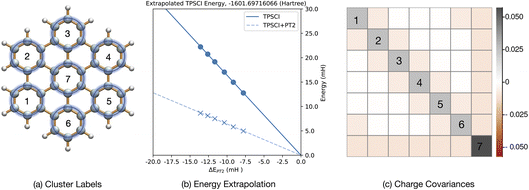
In the earlier sections, the tetracene tetramer (Sec. 3 3.1) served as an example of a completely non-bonded system, which is clearly quite easily clusterable. In Sec. 3 3.2, we demonstrated that the concepts of oxidation state and local spin allowed us to treat the Cr2(III) complex in a clustered representation. In contrast, conjugated π-systems are characterized primarily by the highly delocalized nature of their electronic structure. In this section, we investigate the ability to compute and analyze the full π active space for a large delocalized π system.Hexabenzocoronene (C42H18) is a polycyclic aromatic hydrocarbon (shown in Fig. 7(a)) where an additional benzene ring is fused to the outside of a central coronene ring. The π electrons are delocalized across the entire molecule, which contributes to its unique electronic properties. As we have seen previously,23 the delocalized hexabenzocoronene system serves as a nice edge case for evaluating the ability of TPSCI to provide both accurate and insightful results for systems that are not obviously clusterable.
We note that the performance of TPSCI on such delocalized π systems depends significantly on the topology of the molecule. For the complex considered here, there is a well defined Clar's structure that suggests a unique clustering. We expect this to be key to achieving accurate solutions. In contrast, our recent work23 revealed that π systems without a well-defined clustering into a Clar's structure (such as coronene) are significantly slower to converge. We plan to explore this topic in the future for a more extensive set of polyaromatic hydrocarbons.
![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) I is the number operator for cluster I. ŜzI is the spin magnetization operator for cluster I.
I is the number operator for cluster I. ŜzI is the spin magnetization operator for cluster I. ![[Q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0051_0302.gif) I is the projector onto the orthogonal complement of the cMF ground state for cluster I. Cluster pair indices correspond to the labeling in Fig. 7(a) with the description of the interaction type in parenthesises
I is the projector onto the orthogonal complement of the cMF ground state for cluster I. Cluster pair indices correspond to the labeling in Fig. 7(a) with the description of the interaction type in parenthesises
| Cluster pair | cov(![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) i, i,![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) j) j) |
cov(Ŝzi,Ŝzj) | cov(![[Q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0051_0302.gif) i, i,![[Q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0051_0302.gif) j) j) |
|---|---|---|---|
| 1,1 (outer) | 0.02551 | 0.00925 | 0.03307 |
| 7,7 (inner) | 0.05729 | 0.02103 | 0.06867 |
| 1,2 (nearest neighbor) | −0.00759 | −0.00276 | 0.01079 |
| 1,3 (meta) | −0.00018 | −0.00005 | −0.00010 |
| 1,4 (para) | −0.00040 | −0.000134 | −0.00006 |
| 1,7 (outer-inner) | −0.00956 | −0.00350 | 0.01342 |
By considering the wavefunction directly, we notice that about 89.6% of the wavefunction is attributable to TPSs that have 6α and 6β in each cluster, whereas 9.1% is due to charge-transfer configurations, and 1.3% is due to local spin-flip configurations.
We also note that in Table 5, we see stronger particle number and spin correlations between benzenes connected in the para position than between those with meta connections, despite being further in distance, indicating a slight directing effect of the central benzene. However, the opposite is seen with the cluster excitation, ![[Q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0051_0302.gif) I, correlations.
I, correlations.
Although the particle number covariance between each pair of neighboring clusters is negative (indicating charge transfer), the Ŝ2I correlations are positive between neighboring clusters. This is consistent with the description of charge correlation. When an electron from a cluster hops into another cluster, then a doublet state will be formed in both of the clusters. One cluster will be one electron deficient, giving rise to a cationic doublet state, and the extra electron forms an anionic doublet state in the neighboring cluster. Consequently, when one cluster is in a doublet state, its neighbors have a higher probability of also being found in a doublet state, making the correlation positive. The entanglement between clusters leads each to acquire a non-zero average Ŝ2I value. The outer clusters have total spin of 0.034 ± 0.55, whereas the central cluster as a local S2I value of 0.078 ± 0.84, where uncertainty is given as 3σ.
4. Conclusions
In this paper, we have explored the ability of TPSCI to provide accurate yet interpretable approximations to FCI on relatively large orbital active spaces. Because TPSCI works in a basis consisting of products of local FCI states, the more separable a system is, the easier it should be to simulate. As such, in this paper, we consider three example systems, which range in the degree of separability: (i) a completely non-bonded tetramer of tetracene molecules, (ii) a more strongly interacting dichromium organometallic complex that, while bonded, is still characterized with local quantities like oxidation state, and (iii) a completely delocalized π system of hexabenzocoronene.For the dichromium example, this was the first TPSCI calculation applied to open-shell biradical systems. We found that TPSCI was able to compute exchange coupling constants that are larger in magnitude (presumably more accurate) than recent DMRG calculations.
For each of these systems, we characterized the resulting wavefunctions using quantities that are easily accessible from the TPS basis. By leveraging the natural diabatic character of the TPS basis, we are able to easily construct Bloch effective Hamiltonians, which provide quantitative relationships between physically relevant degrees of freedom. This provided access to quantities such as the effective coupling between the bright states and the multiexcitonic states, 〈S1|Ĥeff|1TT〉, which implicitly includes the downfolded effects from charge-transfer couplings, which are substantially enhanced compared to the direct coupling.
We additionally used correlation functions of quantities like particle number, spin, and cluster excitation to provide a more detailed analysis of the various variational TPSCI eigenstates, and ultimately compare the results to inspection of the wavefunction itself, which is particularly interpretable due to the diabatic nature of the basis. This work helps lay out approaches for extracting more insight from TPSCI wavefunctions (and other TPS-based wavefunctions) in the future.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Science Foundation (Award No. 1752612). NMB also acknowledges the support provided by the Graduate School Doctoral Assistantship from the Department of Chemistry at Virginia Tech.References
- K. Ruedenberg, M. W. Schmidt, M. M. Gilbert and S. T. Elbert, Are atoms intrinsic to molecular electronic wavefunctions? I. The FORS model, Chem. Phys., 1982, 71, 41–49 CrossRef CAS.
- K. Ruedenberg, M. W. Schmidt, M. M. Gilbert and S. T. Elbert, Are atoms intrinsic to molecular electronic wavefunctions? III. Analysis of FORS configurations, Chem. Phys., 1982, 71, 65–78 CrossRef CAS.
- K. Ruedenberg, M. W. Schmidt and M. M. Gilbert, Are atoms sic to molecular electronic wavefunctions? II. Analysis of fors orbitals, Chem. Phys., 1982, 71, 51–64 CrossRef CAS.
- J. P. Foster and F. Weinhold, Natural hybrid orbitals, J. Am. Chem. Soc., 1980, 102, 7211–7218 CrossRef CAS.
- E. D. Glendening, C. R. Landis and F. Weinhold, Natural bond orbital methods, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2012, 2, 1–42 CrossRef CAS.
- E. D. Glendening and A. Streitwieser, Natural energy decomposition analysis: An energy partitioning procedure for molecular interactions with application to weak hydrogen bonding, strong ionic, and moderate donor–acceptor interactions, J. Chem. Phys., 1994, 100, 2900–2909 CrossRef CAS.
- A. E. Reed, R. B. Weinstock and F. Weinhold, Natural population analysis, J. Chem. Phys., 1985, 83, 735–746 CrossRef CAS.
- R. Z. Khaliullin, M. Head-Gordon and A. T. Bell, An efficient self-consistent field method for large systems of weakly interacting components, J. Chem. Phys., 2006, 124, 204105 CrossRef PubMed.
- R. Z. Khaliullin, E. A. Cobar, R. C. Lochan, A. T. Bell and M. Head-Gordon, Unravelling the Origin of Intermolecular Interactions Using Absolutely Localized Molecular Orbitals, J. Phys. Chem. A, 2007, 111, 8753–8765 CrossRef CAS PubMed.
- Y. Mao, M. Loipersberger, P. R. Horn, A. Das, O. Demerdash, D. S. Levine, S. Prasad Veccham, T. Head-Gordon and M. Head-Gordon, From Intermolecular Interaction Energies and Observable Shifts to Component Contributions and Back Again: A Tale of Variational Energy Decomposition Analysis, Annu. Rev. Phys. Chem., 2021, 72, 641–666, DOI:10.1146/annurev-physchem-090419-115149.
- R. F. W. Bader, A quantum theory of molecular structure and its applications, Chem. Rev., 1991, 91, 893–928 CrossRef CAS.
- R. J. Cave and M. D. Newton, Calculation of electronic coupling matrix elements for ground and excited state electron transfer reactions: Comparison of the generalized Mulliken–Hush and block diagonalization methods, J. Chem. Phys., 1997, 106, 9213–9226 CrossRef CAS.
- R. J. Cave and M. D. Newton, Generalization of the Mulliken-Hush treatment for the calculation of electron transfer matrix elements, Chem. Phys. Lett., 1996, 249, 15–19 CrossRef CAS.
- H.-C. Chen, Z.-Q. You and C.-P. Hsu, The mediated excitation energy transfer: Effects of bridge polarizability, J. Chem. Phys., 2008, 129, 084708 CrossRef PubMed.
- S. Fatehi, E. Alguire and J. E. Subotnik, Derivative couplings and analytic gradients for diabatic states, with an implementation for Boys-localized configuration-interaction singles, J. Chem. Phys., 2013, 139, 124112 CrossRef PubMed.
- C.-P. Hsu, Z.-Q. You and H.-C. Chen, Characterization of the Short-Range Couplings in Excitation Energy Transfer, J. Phys. Chem. C, 2008, 112, 1204–1212 CrossRef CAS.
- K. Ruedenberg and G. J. Atchity, A quantum chemical determination of diabatic states, J. Chem. Phys., 1993, 99, 3799–3803 CrossRef CAS.
- J. E. Subotnik, S. Yeganeh, R. J. Cave and M. A. Ratner, Constructing diabatic states from adiabatic states: Extending generalized Mulliken–Hush to multiple charge centers with Boys localization, J. Chem. Phys., 2008, 129, 244101 CrossRef PubMed.
- J. Zheng, Y. K. Kang, M. J. Therien and D. N. Beratan, Generalized Mulliken-Hush analysis of electronic coupling interactions in compressed pi-stacked porphyrin-bridge-quinone systems, J. Am. Chem. Soc., 2005, 127, 11303–11310 CrossRef CAS PubMed.
- R. Baer and M. Head-Gordon, Sparsity of the Density Matrix in Kohn-Sham Density Functional Theory and an Assessment of Linear System-Size Scaling Methods, Phys. Rev. Lett., 1997, 79, 3962–3965 CrossRef CAS.
- V. Abraham and N. J. Mayhall, Cluster many-body expansion: A many-body expansion of the electron correlation energy about a cluster mean field reference, J. Chem. Phys., 2021, 155, 054101 CrossRef CAS PubMed.
- V. Abraham and N. J. Mayhall, Coupled Electron Pair-Type Approximations for Tensor Product State Wave Functions, J. Chem. Theory Comput., 2022, 18, 4856–4864 CrossRef CAS PubMed.
- V. Abraham and N. J. Mayhall, Selected Configuration Interaction in a Basis of Cluster State Tensor Products, J. Chem. Theory Comput., 2020, 16, 6098–6113 CrossRef CAS PubMed.
- N. M. Braunscheidel, V. Abraham and N. J. Mayhall, Generalization of the Tensor Product Selected CI Method for Molecular Excited States, J. Phys. Chem. A, 2023, 127, 8179–8193 CrossRef CAS PubMed.
- N. J. Mayhall, Using Higher-Order Singular Value Decomposition To Define Weakly Coupled and Strongly Correlated Clusters: The n -Body Tucker Approximation, J. Chem. Theory Comput., 2017, 13, 4818–4828 CrossRef CAS PubMed.
- N. P. Bauman, E. J. Bylaska, S. Krishnamoorthy, G. H. Low, N. Wiebe, C. E. Granade, M. Roetteler, M. Troyer and K. Kowalski, Downfolding of many-body Hamiltonians using active-space models: Extension of the sub-system embedding sub-algebras approach to unitary coupled cluster formalisms, J. Chem. Phys., 2019, 151, 014107 CrossRef PubMed.
- S. M. Parker, T. Seideman, M. A. Ratner and T. Shiozaki, Communication: Active-space decomposition for molecular dimers, J. Chem. Phys., 2013, 139, 021108 CrossRef PubMed.
- S. M. Parker and T. Shiozaki, Quasi-diabatic States from Active Space Decomposition, J. Chem. Theory Comput., 2014, 10, 3738–3744 CrossRef CAS PubMed.
- S. M. Parker, T. Seideman, M. A. Ratner and T. Shiozaki, Model Hamiltonian Analysis of Singlet Fission from First Principles, J. Phys. Chem. C, 2014, 118, 12700–12705 CrossRef CAS.
- C. A. Jiménez-Hoyos and G. E. Scuseria, Cluster-based mean-field and perturbative description of strongly correlated fermion systems: Application to the one- and two-dimensional Hubbard model, Phys. Rev. B, 2015, 92, 085101 CrossRef.
- A. Papastathopoulos-Katsaros, C. A. Jiménez-Hoyos, T. M. Henderson and G. E. Scuseria, Coupled Cluster and Perturbation Theories Based on a Cluster Mean-Field Reference Applied to Strongly Correlated Spin Systems, J. Chem. Theory Comput., 2022, 18, 4293–4303 CrossRef CAS PubMed.
- A. Papastathopoulos-Katsaros, T. M. Henderson and G. E. Scuseria, Linear combinations of cluster mean-field states applied to spin systems, arXiv, 2024, arXiv:2402.06760 [cond-mat, physics:physics] version: 1 DOI:10.48550/arXiv.2402.06760.
- A. Papastathopoulos-Katsaros, T. M. Henderson and G. E. Scuseria, Symmetry-projected cluster mean-field theory applied to spin systems, J. Chem. Phys., 2023, 159, 084107 CrossRef CAS PubMed.
- M. R. Hermes and L. Gagliardi, The Variational Localized Active Space Self-Consistent Field Method, arXiv, 2020, arXiv:2003.02995 [physics] DOI:10.48550/arXiv.2003.02995.
- S. Li, Block-correlated coupled cluster theory: The general formulation and its application to the antiferromagnetic Heisenberg model, J. Chem. Phys., 2004, 120, 5017 CrossRef CAS PubMed.
- B. Huron, J. P. Malrieu and P. Rancurel, Iterative perturbation calculations of ground and excited state energies from multiconfigurational zeroth-order wavefunctions, J. Chem. Phys., 1973, 58, 5745 CrossRef CAS.
- A. A. Holmes, N. M. Tubman and C. J. Umrigar, Heat-Bath Configuration Interaction: An Efficient Selected Configuration Interaction Algorithm Inspired by Heat-Bath Sampling, J. Chem. Theory Comput., 2016, 12, 3674–3680 CrossRef CAS PubMed.
- C. Bloch, Sur la théorie des perturbations des états liés, Nucl. Phys., 1958, 6, 329–347 CrossRef CAS.
- J. des Cloizeaux and J. J. Pearson, Spin-Wave Spectrum of the Antiferromagnetic Linear Chain, Phys. Rev., 1962, 128, 2131–2135 CrossRef.
- C. J. Calzado, J. Cabrero, J. P. Malrieu and R. Caballol, Analysis of the magnetic coupling in binuclear complexes. II. Derivation of valence effective Hamiltonians from ab initio CI and DFT calculations, J. Chem. Phys., 2002, 116, 3985–4000 CrossRef CAS.
- R. Maurice, R. Bastardis, C. d. Graaf, N. Suaud, T. Mallah and N. Guihéry, Universal Theoretical Approach to Extract Anisotropic Spin Hamiltonians, J. Chem. Theory Comput., 2009, 5, 2977–2984 CrossRef CAS PubMed.
- A. Monari, D. Maynau and J.-P. Malrieu, Determination of spin Hamiltonians from projected single reference configuration interaction calculations. I. Spin 1/2 systems, J. Chem. Phys., 2010, 133, 044106 CrossRef CAS PubMed.
- J. P. Malrieu, R. Caballol, C. J. Calzado, C. de Graaf and N. Guihéry, Magnetic Interactions in Molecules and Highly Correlated Materials: Physical Content, Analytical Derivation, and Rigorous Extraction of Magnetic Hamiltonians, Chem. Rev., 2014, 114, 429–492 CrossRef CAS PubMed.
- N. J. Mayhall, P. R. Horn, E. J. Sundstrom and M. Head-Gordon, Spin-flip non-orthogonal configuration interaction: a variational and almost black-box method for describing strongly correlated molecules, Phys. Chem. Chem. Phys., 2014, 16, 22694–22705 RSC.
- N. J. Mayhall and M. Head-Gordon, Computational Quantum Chemistry for Multiple-Site Heisenberg Spin Couplings Made Simple: Still Only One Spin–Flip Required, J. Phys. Chem. Lett., 2015, 6, 1982–1988 CrossRef CAS PubMed.
- N. J. Mayhall, From Model Hamiltonians to ab Initio Hamiltonians and Back Again: Using Single Excitation Quantum Chemistry Methods To Find Multiexciton States in Singlet Fission Materials, J. Chem. Theory Comput., 2016, 12, 4263–4273 CrossRef CAS PubMed.
- P. Pokhilko and A. I. Krylov, Effective Hamiltonians derived from equation-of-motion coupled-cluster wave functions: Theory and application to the Hubbard and Heisenberg Hamiltonians, J. Chem. Phys., 2020, 152, 094108 CrossRef CAS PubMed.
- D. Casanova and A. I. Krylov, Quantifying local exciton, charge resonance, and multiexciton character in correlated wave functions of multichromophoric systems, J. Chem. Phys., 2016, 144, 014102 CrossRef PubMed.
- A. V. Luzanov, D. Casanova, X. Feng and A. I. Krylov, Quantifying charge resonance and multiexciton character in coupled chromophores by charge and spin cumulant analysis, J. Chem. Phys., 2015, 142, 224104 CrossRef PubMed.
- Q. Sun, et al., Recent developments in the PySCF program package, J. Chem. Phys., 2020, 153, 024109 CrossRef CAS PubMed.
- N. J. Mayhall, V. Abraham, N. M. Braunscheidel and A. Bachhar, FermiCG, 2024, https://github.com/mayhallgroup/FermiCG, accessed 03-03-2024.
- M. B. Smith and J. Michl, Recent Advances in Singlet Fission, Annu. Rev. Phys. Chem., 2013, 64, 361–386 CrossRef CAS PubMed.
- M. C. Hanna and A. J. Nozik, Solar conversion efficiency of photovoltaic and photoelectrolysis cells with carrier multiplication absorbers, J. Appl. Phys., 2006, 100, 074510 CrossRef.
- J. C. Johnson, Open questions on the photophysics of ultrafast singlet fission, Commun. Chem., 2021, 4, 1–3 CrossRef PubMed.
- R. D. Pensack, A. J. Tilley, S. R. Parkin, T. S. Lee, M. M. Payne, D. Gao, A. A. Jahnke, D. G. Oblinsky, P.-F. Li, J. E. Anthony, D. S. Seferos and G. D. Scholes, Exciton delocalization drives rapid singlet fission in nanoparticles of acene derivatives, J. Am. Chem. Soc., 2015, 137, 6790–6803 CrossRef CAS PubMed.
- G. D. Scholes, Correlated Pair States Formed by Singlet Fission and Exciton-Exciton Annihilation, J. Phys. Chem. A, 2015, 119, 12699–12705 CrossRef CAS PubMed.
- T. C. Berkelbach, M. S. Hybertsen and D. R. Reichman, Microscopic theory of singlet exciton fission. III. Crystalline pentacene, J. Chem. Phys., 2014, 141, 074705 CrossRef PubMed.
- T. C. Berkelbach, in Advances in Chemical Physics, Vol 162, ed. S. A., Rice, A. R., Dinner, 2017, vol. 162, pp. 1–38 Search PubMed.
- Y. Shu, E. G. Hohenstein and B. G. Levine, Configuration interaction singles natural orbitals: an orbital basis for an efficient and size intensive multireference description of electronic excited states, J. Chem. Phys., 2015, 142, 024102 CrossRef PubMed.
- R. Ditchfield, W. J. Hehre and J. A. Pople, Self-Consistent Molecular-Orbital Methods. IX. An Extended Gaussian-Type Basis for Molecular-Orbital Studies of Organic Molecules, J. Chem. Phys., 1971, 54, 724–728 CrossRef CAS.
- S. Lehtola and H. Jónsson, Pipek–Mezey Orbital Localization Using Various Partial Charge Estimates, J. Chem. Theory Comput., 2014, 10, 642–649 CrossRef CAS PubMed.
- T. C. Berkelbach, M. S. Hybertsen and D. R. Reichman, Microscopic theory of singlet exciton fission. II. Application to pentacene dimers and the role of superexchange, J. Chem. Phys., 2013, 138, 114103 CrossRef PubMed.
- V. Abraham and N. J. Mayhall, Simple Rule To Predict Boundedness of Multiexciton States in Covalently Linked Singlet-Fission Dimers, J. Phys. Chem. Lett., 2017, 8, 5472–5478 CrossRef CAS PubMed.
- A. Caneschi, D. Gatteschi, R. Sessoli, A. L. Barra, L. C. Brunel and M. Guillot, Alternating current susceptibility, high field magnetization, and millimeter band EPR evidence for a ground S = 10 state in [Mn12O12(Ch3COO)16(H2O)4].2CH3COOH.4H2O, J. Am. Chem. Soc., 1991, 113, 5873–5874 CrossRef CAS.
- S. Demir, M. I. Gonzalez, L. E. Darago, W. J. Evans and J. R. Long, Giant coercivity and high magnetic blocking temperatures for N2 3- radical-bridged dilanthanide complexes upon ligand dissociation, Nat. Commun., 2017, 8, 2144 CrossRef PubMed.
- M. Gil-Sepulcre and A. Llobet, Molecular water oxidation catalysts based on first-row transition metal complexes, Nat. Catal., 2022, 5, 79–82 CrossRef CAS.
- Y. Tanabe and Y. Nishibayashi, Recent advances in catalytic nitrogen fixation using transition metal–dinitrogen complexes under mild reaction conditions, Coord. Chem. Rev., 2022, 472, 214783 CrossRef CAS.
- This is true for the Hubbard model at half-filling. Situations with away-from half-filling can be mapped onto different Hamiltonians, such as the tJ model.
- L. Noodleman, Valence bond description of antiferromagnetic coupling in transition metal dimers, J. Chem. Phys., 1981, 74, 5737–5743 CrossRef CAS.
- K. Yamaguchi, F. Jensen, A. Dorigo and K. N. Houk, A spin correction procedure for unrestricted Hartree–Fock and Møller-Plesset wavefunctions for singlet diradicals and polyradicals, Chem. Phys. Lett., 1988, 149, 537–542 CrossRef CAS.
- S. Yamanaka, T. Kawakami, H. Nagao and K. Yamaguchi, Effective exchange integrals for open-shell species by density functional methods, Chem. Phys. Lett., 1994, 231, 25–33 CrossRef CAS.
- M. Reiher, O. Salomon and B. Artur Hess, Reparameterization of hybrid functionals based on energy differences of states of different multiplicity, Theor. Chem. Acc., 2001, 107, 48–55 Search PubMed.
- M. Reiher, Theoretical Study of the Fe(phen)2(NCS)2 Spin-Crossover Complex with Reparametrized Density Functionals, Inorg. Chem., 2002, 41, 6928–6935 CrossRef CAS PubMed.
- D. A. Pantazis, Meeting the Challenge of Magnetic Coupling in a Triply-Bridged Chromium Dimer: Complementary Broken-Symmetry Density Functional Theory and Multireference Density Matrix Renormalization Group Perspectives, J. Chem. Theory Comput., 2019, 15, 938–948 CrossRef CAS PubMed.
- S. Szalay, M. Pfeffer, V. Murg, G. Barcza, F. Verstraete, R. Schneider and r. Legeza, Tensor product methods and entanglement optimization for ab initio quantum chemistry, Int. J. Quantum Chem., 2015, 115, 1342–1391 CrossRef CAS.
- A. Baiardi and M. Reiher, The density matrix renormalization group in chemistry and molecular physics: Recent developments and new challenges, J. Chem. Phys., 2020, 152, 040903 CrossRef CAS PubMed.
- U. Schollwöck, The density-matrix renormalization group in the age of matrix product states, Ann. Phys., 2011, 326, 96–192 Search PubMed.
- S. Wouters and D. Van Neck, The density matrix renormalization group for ab initio quantum chemistry, Eur. Phys. J. D, 2014, 68, 272 CrossRef.
- J. J. Eriksen, et al., The Ground State Electronic Energy of Benzene, J. Phys. Chem. Lett., 2020, 11, 8922–8929 CrossRef CAS PubMed.
- R. Olivares-Amaya, W. Hu, N. Nakatani, S. Sharma, J. Yang and G. K.-L. Chan, The ab-initio density matrix renormalization group in practice, J. Chem. Phys., 2015, 142, 034102 CrossRef PubMed.
- S. Sharma, K. Sivalingam, F. Neese and G. K.-L. Chan, Low-energy spectrum of iron-sulfur clusters directly from many-particle quantum mechanics, Nat. Chem., 2014, 6, 927–933 CrossRef CAS PubMed.
- S. Sharma, G. Jeanmairet and A. Alavi, Quasi-degenerate perturbation theory using matrix product states, J. Chem. Phys., 2016, 144, 034103 CrossRef PubMed.
- T. V. Harris, Y. Kurashige, T. Yanai and K. Morokuma, Ab initio density matrix renormalization group study of magnetic coupling in dinuclear iron and chromium complexes, J. Chem. Phys., 2014, 140, 054303 CrossRef PubMed.
- N. J. Mayhall and M. Head-Gordon, Computational quantum chemistry for single Heisenberg spin couplings made simple: Just one spin flip required, J. Chem. Phys., 2014, 141, 134111 CrossRef PubMed.
- A. Niemann, U. Bossek, K. Wieghardt, C. Butzlaff, A. X. Trautwein and B. Nuber, A New Structure–Magnetism Relationship for Face-Sharing Transition-Metal Complexes with d3–d3 Electronic Configuration, Angew. Chem., Int. Ed. Engl., 1992, 31, 311–313 CrossRef.
- For each active space, we solve for the lowest M states in the lowest Ms-subspace, and then generate the higher Ms vectors by directly applying Ŝ±. This is done to, not only reduce the cost, but also to ensure that every TPS in our basis can be properly spin-adapted to form proper eigenstates of Ŝ2, as first noted in ref. 24.
- H. G. A. Burton and P.-F. Loos, Rationale for the Extrapolation Procedure in Selected Configuration Interaction, arXiv, 2024, arXiv:2312.12530 [cond-mat, physics:nucl-th, physics:physics] DOI:10.48550/arXiv.2312.12530.
- A. A. Holmes, C. J. Umrigar and S. Sharma, Excited states using semistochastic heat-bath configuration interaction, J. Chem. Phys., 2017, 147, 164111 CrossRef PubMed.
- We have also explored directly extrapolating the J values themselves, and found the results to be essentially the same.
- R. Pandharkar, M. R. Hermes, C. J. Cramer and L. Gagliardi, Localized Active Space-State Interaction: a Multireference Method for Chemical Insight, J. Chem. Theory Comput., 2022, 18, 6557–6566 CrossRef CAS PubMed.
- T. H. Dunning, Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- N. J. Mayhall, V. Abraham, N. M. Braunscheidel and A. Bachhar, ClusterMeanField.jl, 2023, https://github.com/nmayhall-vt/ClusterMeanField.jl, accessed 11-24-2023.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4fd00049h |
| This journal is © The Royal Society of Chemistry 2024 |