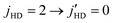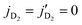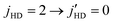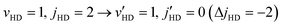Open Access Article
Open Access ArticleStereodynamical control of cold HD + D2 collisions†
Bikramaditya
Mandal
 a,
James F. E.
Croft
a,
James F. E.
Croft
 b,
Pablo G.
Jambrina
b,
Pablo G.
Jambrina
 c,
Hua
Guo
c,
Hua
Guo
 d,
F. Javier
Aoiz
d,
F. Javier
Aoiz
 e and
Naduvalath
Balakrishnan
e and
Naduvalath
Balakrishnan
 *a
*a
aDepartment of Chemistry and Biochemistry, University of Nevada, Las Vegas, Nevada 89154, USA. E-mail: naduvala@unlv.nevada.edu
bDepartment of Chemistry, Durham University, South Road, Durham, DH1 3LE, UK
cDepartamento de Química Física, University of Salamanca, Salamanca 37008, Spain
dDepartment of Chemistry and Chemical Biology, University of New Mexico, Albuquerque, New Mexico 87131, USA
eDepartamento de Química Física, Universidad Complutense, Madrid 28040, Spain
First published on 24th June 2024
Abstract
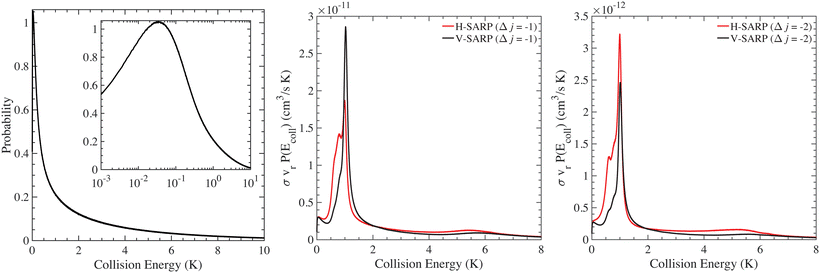
We report full-dimensional quantum calculations of stereodynamic control of HD(v = 1, j = 2) + D2 collisions that has been probed experimentally by Perreault et al. using the Stark-induced adiabatic Raman passage (SARP) technique. Computations were performed on two highly accurate full-dimensional H4 potential energy surfaces. It is found that for both potential surfaces, rotational quenching of HD from 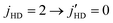 with concurrent rotational excitation of D2 from
with concurrent rotational excitation of D2 from 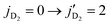 is the dominant transition with cross sections four times larger than that of elastically scattered D2
is the dominant transition with cross sections four times larger than that of elastically scattered D2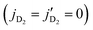 for the same quenching transition in HD. This process was not considered in the original analysis of the SARP experiments that probed ΔjHD = −2 transitions in HD(vHD = 1, jHD = 2) + D2 collisions. Cross sections are characterized by an l = 3 resonance for ortho-D2(jD2 = 0) collisions, while both l = 1 and l = 3 resonances are observed for the para-D2(jD2 = 1) partner. While our results are in excellent agreement with prior measurements of elastic and inelastic differential cross sections, the agreement is less satisfactory with the SARP experiments, in particular for the
for the same quenching transition in HD. This process was not considered in the original analysis of the SARP experiments that probed ΔjHD = −2 transitions in HD(vHD = 1, jHD = 2) + D2 collisions. Cross sections are characterized by an l = 3 resonance for ortho-D2(jD2 = 0) collisions, while both l = 1 and l = 3 resonances are observed for the para-D2(jD2 = 1) partner. While our results are in excellent agreement with prior measurements of elastic and inelastic differential cross sections, the agreement is less satisfactory with the SARP experiments, in particular for the 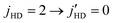 transition for which the theoretical calculations indicate that D2 rotational excitation channel is the dominant inelastic process.
transition for which the theoretical calculations indicate that D2 rotational excitation channel is the dominant inelastic process.
1 Introduction
Inelastic and reactive collisions of small molecules have received much interest due to their importance in the chemistry of the early universe,1–7 Earth's atmosphere, interstellar media (ISM),4,8,9 and star formation regions.10–12 Being the most abundant molecule in astrophysical environments, H2 and its isotopic counterparts HD and D2, were a major focus of experimental and theoretical studies.1,13 Unlike H2 which lacks a permanent dipole moment, which makes its detection more challenging, the isotopologue HD possesses a non-zero dipole moment.4,13 The signatures of j = 1 → j′ = 0 rotational transition in HD were observed by the Herschel space observatory14,15 and by the long wavelength spectrometer at the Infrared space observatory (ISO).16,17 The prospects of detecting the j = 4 → j′ = 3 transition in HD by the Atacama large millimeter array (ALMA),18 as well as other transitions by the Spitzer space telescope16,19 have led to much interest in collisions of rotationally excited HD. Due to its small dipole moment the HD molecule is also thought to play an important role in the cooling of the primordial gas despite its relatively small abundance compared to H2.1,4,13,20,21 Major advancements in ab initio electronic structure calculations in the last decade, coupled with high-performance computing and machine-learning algorithms have led to the availability of high quality potential energy surfaces (PESs) for the interaction between two H2 molecules.22–24 These surfaces have formed the basis of a number of full-dimensional quantum calculations of H2–H2 and H2–HD collisions of interest in astrophysics.4,5,13,25 Very recently, a full-dimensional PES for the H4 system that accounts for four-center exchange reactions and collision-induced dissociation channels in H2 + H2 collisions have also been reported.26Recent advances in molecular cooling and trapping technologies have also led to renewed interest in inelastic and reactive collisions of atom–molecule and molecule–molecule systems. Indeed, collisions of cold and ultracold diatomic molecules are an active area of experimental and theoretical research due to their applications to quantum sensing, ultracold chemistry, quantum computing, and quantum information processing.27–43 Molecular collisions in this regime are characterized by large de Broglie wavelengths and are strongly influenced by long-range intermolecular forces. Although, diatomic species such as CaF, SrF, RbCs, KRb, NaK, etc. are preferred molecules for such applications,44–48 their small rotational constants lead to high densities of states making rigorous quantum calculations of diatom–diatom collisions involving these molecules computationally intractable.43,49,50 Therefore, lighter diatomic molecules, such as H2 and its isotopologues, are generally preferred to benchmark theoretical studies against experiments. These systems are characterized by large rotational constants and low densities of states, thus requiring only a small number of orbital angular momentum partial waves to yield converged cross sections in the 1 kelvin range of collision energies.43
Zare and coworkers have recently developed a coherent optical technique, called Stark-induced adiabatic Raman passage (SARP), to study quantum controlled cold collisions of light molecular systems, such as H2, HD and D2.51–63 The SARP technique allows preparation of a phase-coherent superposition of degenerate alligned states (mj) within a single ro-vibrational state.64 Additionally, the colliding partners are adiabatically expanded and co-propagated in the same molecular beam, yielding relative collision energies in the 1 kelvin regime for collisions involving H2 and its isotopologues. This provides a powerful approach to probe stereodynamics in collision of quantum state-prepared and aligned molecules.65 The SARP technique has recently been extended to chemical reactions of state-prepared HD with H atoms leading to the D + H2 product using a crossed molecular beam technique but at thermal and superthermal collision energies or collision energies above 0.5 eV.66
Zare, Mukherjee and collaborators have published a series of papers applying the SARP technique to rotational quenching of HD and D2 by collisions with H2, D2, and He.51–63 These systems are amenable to full-dimensional quantum calculations and allow direct comparisons between theory and experiment. Their first experiment involved rotational quenching of aligned HD prepared in the v = 1, j = 2 initial state colliding with unpolarized D2.53,63 Subsequent studies involved colliding partners of H2,53 D2,63 and He,58,60 all of which were unprepared (unpolarized). They also applied the SARP technique to D2 + He55,57 and D2 + Ne collisions.56 In their most recent work rotational quenching in collisions of two aligned D2 molecules prepared in the v = 2, j = 2 initial state61 was reported.
The SARP experiments stimulated a series of theoretical studies aimed at gaining more insight into the quantum dynamics and relevant partial waves that control the collision outcome.23,31,43,67–73 Quantum dynamical studies of stereodynamic control of reactive collisions of F + HD74 and H + D2/D + HD75 systems have also been reported recently. While analysis of the experimental data and the experimental relative velocity distribution can discern the relevant partial waves involved in the collision dynamics, theoretical studies are needed to identify specific partial-wave resonances that control the collision outcome. Theory is particularly useful as the experimental measurements were not done with energy resolution, and averaging over the relative collision energy is needed.
Theoretical investigations of HD + H2,68,73 HD + He,69,70 D2 + D2,43,71 and D2 + He72 yielded results in reasonable agreement with experiments for the angular distribution though assignments of specific resonances that contribute to signatures of the measured angular distribution differed between theory and experiment. This is due in part to the lack of energy resolution in the experiment. Though the HD + D2 system was the topic of the first SARP experiment by Perreault et al.,53 no theoretical studies have been reported so far. For this system experimental data was reported for both ΔjHD = −1 and −2 transitions with HD prepared initially in the vHD = 1, jHD = 2 state, while the D2 molecule is unprepared.53,54 The measured angular distributions of the HD molecule for the 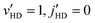 and
and 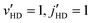 final states involve a convolution of relative collision energies in the 1 mK–10 K range with the peak of the energy distribution centered around 1 K. Here, we report the first theoretical study of this process using full-dimensional quantum scattering calculations on two highly accurate interaction potentials for the H2–H2 system.22,23 Besides its importance in astrophysics, this system also serves as a benchmark for inelastic diatom–diatom collisions.
final states involve a convolution of relative collision energies in the 1 mK–10 K range with the peak of the energy distribution centered around 1 K. Here, we report the first theoretical study of this process using full-dimensional quantum scattering calculations on two highly accurate interaction potentials for the H2–H2 system.22,23 Besides its importance in astrophysics, this system also serves as a benchmark for inelastic diatom–diatom collisions.
The article is organized as follows: Section II provides a brief description of the two potential energy surfaces, quantum scattering methods, and the SARP preparation. A detailed discussion of our findings, state-to-state cross sections, partial wave analysis, and comparisons between theory and experiments are provided in Section III. Finally, in Section IV, we summarize the key findings.
2 Methods
2.1 Potential energy surface
The H4 system is the simplest neutral four atom system; so high quality full-dimensional PESs are available for this molecular system.22–24 In this study, we adopt the PESs by Zuo, Croft, Yao, Balakrishnan, and Guo (ZCYBG)23 and by Hinde22 (hereafter referred to as the ZCYBG PES and Hinde PES, respectively). A detailed comparison between the two surfaces was reported in previous studies and is not our focus here.23,43 The interaction potential is represented in Jacobi coordinates (R, r1, r2, θ1, θ2, ϕ12) where R is the center-of-mass (COM) separation between the two molecules, r1 and r2 are the two diatomic vibrational coordinates, θ1 and θ2 are the two Jacobi angles of![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) with
with ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 1 and
1 and ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 2, and ϕ12 is the dihedral angle. The current system of interest, HD–D2, has the same interaction potential as the H2–H2 system within the Born–Oppenheimer approximation, except that the COM of the HD molecule is shifted compared to the H2 COM. Thus, the interaction potential for HD + D2 is expressed in this coordinate system as described in our prior studies of HD + H2 collisions.4,5
2, and ϕ12 is the dihedral angle. The current system of interest, HD–D2, has the same interaction potential as the H2–H2 system within the Born–Oppenheimer approximation, except that the COM of the HD molecule is shifted compared to the H2 COM. Thus, the interaction potential for HD + D2 is expressed in this coordinate system as described in our prior studies of HD + H2 collisions.4,5
The angular dependence of the PESs was parameterized by the following spherical harmonic expansion as described in detail elsewhere:23,43
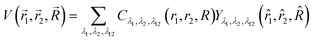 | (1) |
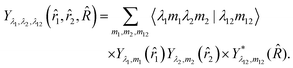 | (2) |
First, we present a brief comparison between the two PESs. Fig. 1 displays the five leading terms in the angular dependence of the interaction potential obtained from the ZCYBG PES (solid lines) and the Hinde PES (dashed lines) with the HD and D2 bond lengths fixed at their equilibrium value of re = 1.401 a0. The isotropic term derived from the ZCYBG and Hinde PESs is found to be about 993 cm−1 and 1032 cm−1 deep, respectively, at a HD–D2 COM separation of R = 6.55 a0 (∼3.47 Å). We also compare the five leading expansion terms (Cλ1,λ2,λ12) with a previous study available in the literature from 1980s by Buck et al.76,77 In their joint theory-experiments, Buck et al. adopted an ab initio PES, named M80, to derive the expansion coefficients using an expression similar to eqn (1). The comparison is provided in Fig. 2 in the same energy units reported by Buck et al.76,77 As Fig. 2 illustrates, the expansion terms are in excellent agreement with both PESs used in this work. The potential minimum for the isotropic terms for all three potentials occurs at an intermolecular separation of R ∼ 3.5 Å. The well-depth of the isotropic term differs by about 0.46% and 3.46% compared to the ZCYBG PES and Hinde PES, respectively. The isotropic, leading anisotropic, and other terms show maximum deviation in the highly repulsive region, not sampled at low and moderate collision energies.
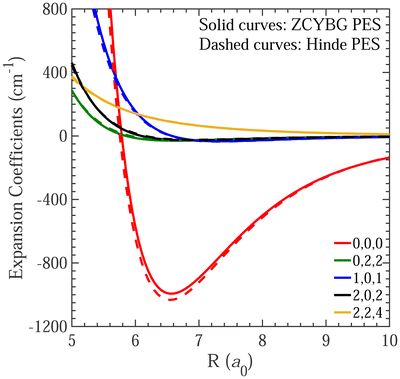 | ||
| Fig. 1 The dominant expansion terms in the angular dependence of the HD–D2 PESs as a function of the intermolecular separation. The solid curves represent the results from the ZCYBG PES,23 while dashed curves are obtained using the Hinde PES.22 The numbers in the legends correspond to λ1, λ2, and λ12, respectively. | ||
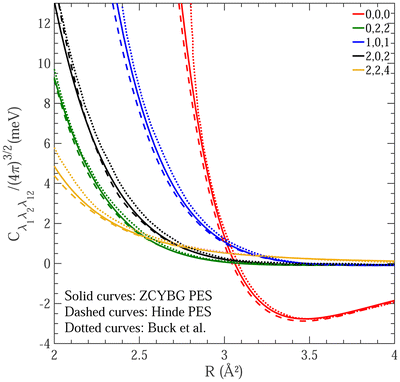 | ||
| Fig. 2 Same as Fig. 1. In addition to the solid curves obtained from the ZCYBG PES23 and dashed curves from the Hinde PES,22 the dotted curves show available results using the M80 PES reported by Buck et al.76 Note the different units for the energy and R compared to Fig. 1. | ||
For the scattering calculations of HD + D2, it was found that λ1 ≤ 2 and λ2 ≤ 6 for HD and D2, respectively, were sufficient to yield converged results for both the ZCYBG and Hinde PESs.
2.2 Scattering calculations
Full-dimensional quantum scattering calculations were carried out using a modified version of the TwoBC code.78 The methodology for rovibrational scattering of two 1Σ diatomic molecules is well established, and several benchmark calculations of the H2–H2 system and its isotopic variants have been reported in the literature.5,79–82 Here we provide a brief outline to introduce the necessary quantum numbers and parameters involved in the calculations. A time-independent quantum approach within the close-coupling method is used for the scattering calculations.82 This yields the scattering matrix, S, from which observable quantities are calculated. To label the initial and final states, we introduce the combined molecular state (CMS), n ≡ v1j1v2j2 where v1 and j1 are the initial vibrational and rotational quantum numbers of asymptotic channels for the HD molecule while v2 and j2 denote the same for D2. Similarly, we define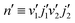 for the final channels of HD and D2. The state-to-state integral cross section (ICS) for ro-vibrationally inelastic scattering at a collision energy Ec is given by
for the final channels of HD and D2. The state-to-state integral cross section (ICS) for ro-vibrationally inelastic scattering at a collision energy Ec is given by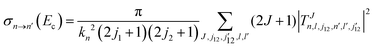 | (3) |
The differential cross section (DCS) is given in terms of the scattering amplitude q as a function of the scattering angle, θ and the azimuthal angle ϕ. The θ dependence of the scattering amplitude is evaluated within the helicity representation, as given by Schaefer and Meyer:83
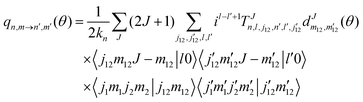 | (4) |
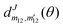 is an element of the Wigner reduced rotation matrix,
is an element of the Wigner reduced rotation matrix, 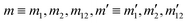 , and the quantities in angular brackets 〈….|‥〉 are Clebsch–Gordan coefficients. For isotropic collisions, the differential rovibrational state resolved cross sections are obtained by summing over all final m′-states and averaging over initial m-states as given below:
, and the quantities in angular brackets 〈….|‥〉 are Clebsch–Gordan coefficients. For isotropic collisions, the differential rovibrational state resolved cross sections are obtained by summing over all final m′-states and averaging over initial m-states as given below: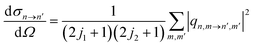 | (5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θdθdϕ is the solid angle.
θdθdϕ is the solid angle.
The expressions given above for integral and differential cross sections assume that the colliding entities are unpolarized. In the SARP experiments of Perreault et al., rotational quenching of HD by D2 was explored by controlling the alignment of HD relative to the SARP laser polarization.53,54 This is achieved by selecting appropriate mj components of the rotational state j of the HD molecule relative to the polarization of the SARP laser.84,85 A rotational state of the HD molecule |j,![[m with combining tilde]](https://www.rsc.org/images/entities/i_char_006d_0303.gif) 〉 prepared by the SARP method can be expressed as
〉 prepared by the SARP method can be expressed as
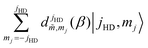 | (6) |
![[m with combining tilde]](https://www.rsc.org/images/entities/i_char_006d_0303.gif) = 0 preparation is considered. An angle β = 0° corresponds to a horizontal alignment of the molecular bond axis with respect to the initial velocity vector. This is referred to as the H-SARP preparation, and for the HD molecule in the j = 2 rotational state, it corresponds to |j = 2, mj = 0〉 initial state. For the same j = 2 rotational state of the HD molecule, a vertical alignment of the HD bond axis corresponding to
= 0 preparation is considered. An angle β = 0° corresponds to a horizontal alignment of the molecular bond axis with respect to the initial velocity vector. This is referred to as the H-SARP preparation, and for the HD molecule in the j = 2 rotational state, it corresponds to |j = 2, mj = 0〉 initial state. For the same j = 2 rotational state of the HD molecule, a vertical alignment of the HD bond axis corresponding to 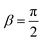 , known as V-SARP, includes a superposition of mj states given by
, known as V-SARP, includes a superposition of mj states given by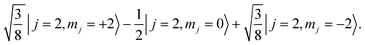 | (7) |
In the HD + D2 experiments of Perreault et al.,53,54 both H-SARP and V-SARP preparations of the HD molecule were realized for the initial rovibrational state of vHD = 1, jHD = 2. The corresponding DCSs for the SARP preparations are given by
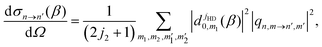 | (8) |
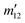 are omitted in the summation. Note that the experimental results correspond to an integration over the azimuthal angle which washes out any interference between different m1 states in the initial preparation.67,71 Thus, the overall effect of the initial alignment is captured by the weight factor
are omitted in the summation. Note that the experimental results correspond to an integration over the azimuthal angle which washes out any interference between different m1 states in the initial preparation.67,71 Thus, the overall effect of the initial alignment is captured by the weight factor 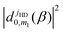 attached to each |q|2 term for a given m1.
attached to each |q|2 term for a given m1.
In the computations, a basis set including three vibrational levels v = 0–2 was considered for both molecules. For the HD molecule, within each vibrational level six rotational states j = 0–6 were included while for the D2 molecule three rotational states, j = 0, 2, and 4 were considered, which led to nearly 200 CMSs. Calculations were done for total angular momentum quantum numbers J = 0–8. The coupled-channel equations resulting from the time-independent Schrödinger equation were integrated from R = 3 to R = 103 a0 with a step size of ΔR = 0.05 a0. This choice of parameters yield results converged to within 1% in the collision energy regime of 1 mK to 10 K reported here. Additional calculations were carried out at higher collision energies to compare against the experimental and theoretical results of Buck et al.76,77 as discussed in the next section. These calculations adopted the same rotational basis sets for both molecules but limited to the v = 0 vibrational level.
3 Results
3.1 Comparisons with prior theory and experimental results
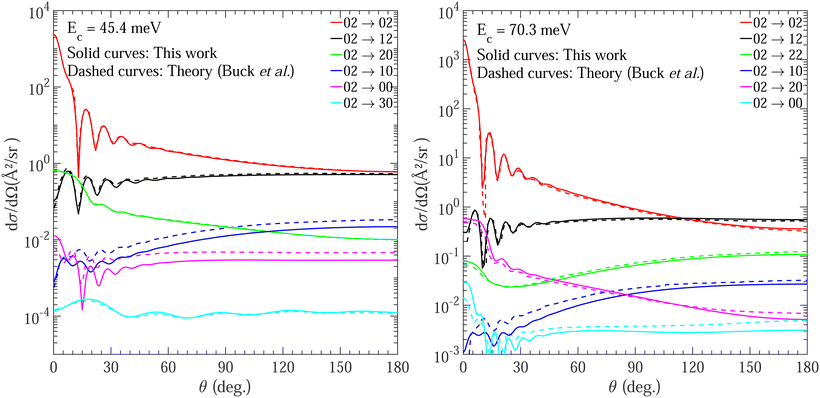
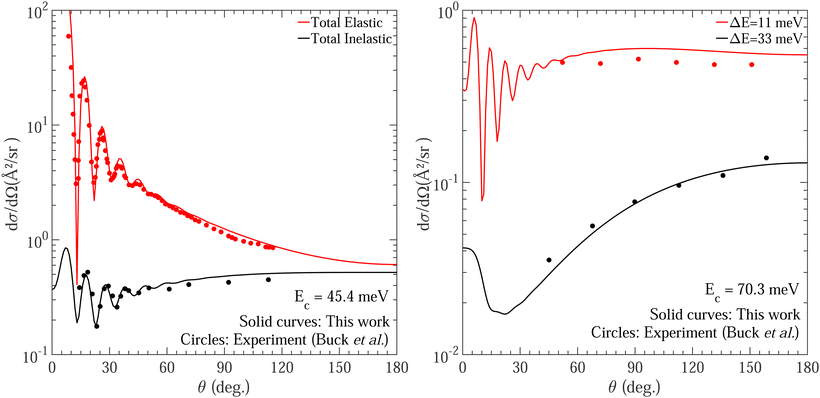
First, we benchmark our results against available experimental and theoretical results. Unfortunately, very limited data exist for this system and the available experimental and theoretical results correspond to the work of Buck et al.76,77 four decades ago. The measurements were reported at collision energies of 45.4 meV (∼527 K) and 70.3 meV (∼816 K)76,77 and the corresponding theoretical calculations adopted a rigid rotor formalism for both molecules. Because the previous calculations and measurements correspond to fairly high collision energies we include total angular momentum quantum number J up to 80 to achieve a convergence within 1% with respect to summation over J. Fig. 3 shows a comparison of DCS from our calculation for both elastic and inelastic collisions on the ZCYBG PES with the theoretical results of Buck et al. at collision energies of 45.4 and 70.3 meV. Our results correspond to both molecules in the ground vibrational state. Similar comparisons using the Hinde PES are provided in the ESI.† The agreement between the two results is excellent for both collision energies for the entire range of scattering angle despite the large variation in the magnitude of the DCS for the different transitions. It is remarkable to see the oscillatory behavior of the DCS arising from interference between different partial wave contributions quantitatively reproduced by the two calculations. The DCSs for the elastic transition, 02→02 and the dominant inelastic transition, namely 02→12 (where the numbers denote jHDjD2 before and after collision; see figure caption for the notation), are almost identical from the two calculations for both collision energies. Slight differences seen for the weaker 02→10 and 02→00 transitions can be attributed to differences in the potential expansion term λ2,0,2 as illustrated in Fig. 2. However, even for these weaker transitions with 2–3 orders of magnitude smaller DCSs than the elastic and leading inelastic transitions, the oscillatory behavior as a function of the scattering angle is nearly identical in both calculations.In Fig. 4 we compare our DCS results on the ZCYBG PES with the experimental results of Buck et al.76 for the two collision energies of 45.4 and 70.3 meV. A similar comparison for the Hinde PES is provided in the ESI.† To compare with the experimental results, we used the same procedure as in Buck et al.77 where we summed over contributions from different thermally populated rotational levels of the D2 collision partner. The total elastic cross sections in the left panel at a collision energy of 45.4 meV were obtained by taking a weighted sum of transitions 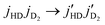 for 00→00, 01→01, 02→02 with weights 0.27, 0.33 and 0.40 for D2 rotational states j = 0, 1, and 2, respectively. Similarly, the total inelastic cross sections were obtained by a weighted sum of the transitions 00→10, 01→11, 02→12, and 02→20. For details, see Buck et al.76,77 In the right panel of Fig. 4, the filled circles represent the experimental data, while the solid curves show our results. Here, ΔE refers to the energy difference between the combined molecular states of HD + D2. Specifically, ΔE = 11 meV includes transitions 02→20, 00→10, 01→11, and 02→12 while ΔE = 33 meV includes 00→20, 01→21, 02→22, and 00→12. The total cross sections corresponding to the energy gaps are then obtained by taking a weighted sum of D2 rotational states j = 0, 1 and 2 with weights of 0.62, 0.33, and 0.05, respectively. The agreement is excellent, for both elastic and inelastic collisions, including scattering angles where the DCS shows strong oscillatory pattern. The excellent agreement between our results and the theoretical and experimental results of Buck et al. at the level of differential cross sections validates the accuracy of the results presented here and the quality of the PESs adopted for the scattering calculations.
for 00→00, 01→01, 02→02 with weights 0.27, 0.33 and 0.40 for D2 rotational states j = 0, 1, and 2, respectively. Similarly, the total inelastic cross sections were obtained by a weighted sum of the transitions 00→10, 01→11, 02→12, and 02→20. For details, see Buck et al.76,77 In the right panel of Fig. 4, the filled circles represent the experimental data, while the solid curves show our results. Here, ΔE refers to the energy difference between the combined molecular states of HD + D2. Specifically, ΔE = 11 meV includes transitions 02→20, 00→10, 01→11, and 02→12 while ΔE = 33 meV includes 00→20, 01→21, 02→22, and 00→12. The total cross sections corresponding to the energy gaps are then obtained by taking a weighted sum of D2 rotational states j = 0, 1 and 2 with weights of 0.62, 0.33, and 0.05, respectively. The agreement is excellent, for both elastic and inelastic collisions, including scattering angles where the DCS shows strong oscillatory pattern. The excellent agreement between our results and the theoretical and experimental results of Buck et al. at the level of differential cross sections validates the accuracy of the results presented here and the quality of the PESs adopted for the scattering calculations.
3.2 Sensitivity of low-energy collisions to potential energy surfaces
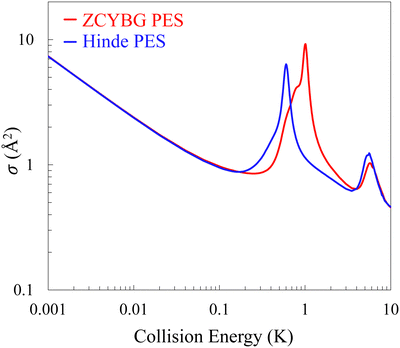
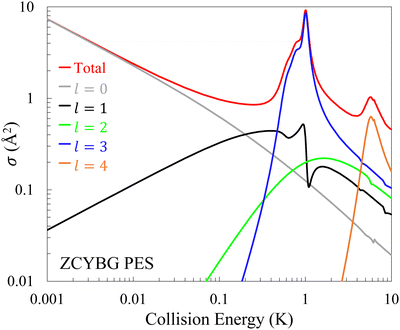
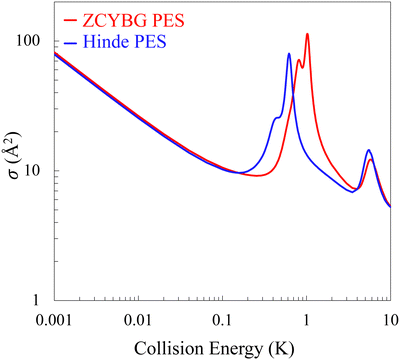
The experimental data by Perreault et al.53,54 corresponds to pure rotational quenching of the HD molecule from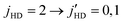 within the vHD = 1 vibrational level in collisions with n-D2(vD2 = 0) but with a thermal population of rotational levels. Since the D2 molecules were used without state preparation D2 is considered as an isotropic collision partner. The experiment involves a broad distribution of collision energies centered around ∼1 K with the higher energy tail extending to about ∼8 K. To what extent energies below 1 K contribute to the measured angular distribution is not clear but we first explore sensitivity of rotationally inelastic cross sections to the interaction potential at collision energies relevant to the experiment. Fig. 5 shows the integral cross-section as a function of the collision energy for the
within the vHD = 1 vibrational level in collisions with n-D2(vD2 = 0) but with a thermal population of rotational levels. Since the D2 molecules were used without state preparation D2 is considered as an isotropic collision partner. The experiment involves a broad distribution of collision energies centered around ∼1 K with the higher energy tail extending to about ∼8 K. To what extent energies below 1 K contribute to the measured angular distribution is not clear but we first explore sensitivity of rotationally inelastic cross sections to the interaction potential at collision energies relevant to the experiment. Fig. 5 shows the integral cross-section as a function of the collision energy for the 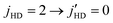 transition for
transition for 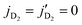 . Results are presented for both the Hinde and ZCYBG PESs. As shown in the figure the newer ZCYBG PES predicts slightly higher values of cross sections, ∼9 Å2 near the peak of the primary resonance at about ∼1 K compared to ∼6 Å2 on the Hinde PES. Also, the resonance occurs at about 1.01 K for the ZCYBG PES compared to 0.62 K for the Hinde PES, which is also narrower. In contrast, the Hinde PES yields slightly higher values (less than 0.2 Å2) of the cross section for the secondary resonance at 5.6 K even though the resonance energy differs by only ∼0.1 K for the two PESs. Apart from these differences in the resonance region, it is striking to note that the background cross section, including the ultracold s-wave limit, is nearly identical for both PESs. We note that below ∼10 mK, the cross sections exhibit the well-known Wigner threshold behavior where they vary inversely as the velocity or
. Results are presented for both the Hinde and ZCYBG PESs. As shown in the figure the newer ZCYBG PES predicts slightly higher values of cross sections, ∼9 Å2 near the peak of the primary resonance at about ∼1 K compared to ∼6 Å2 on the Hinde PES. Also, the resonance occurs at about 1.01 K for the ZCYBG PES compared to 0.62 K for the Hinde PES, which is also narrower. In contrast, the Hinde PES yields slightly higher values (less than 0.2 Å2) of the cross section for the secondary resonance at 5.6 K even though the resonance energy differs by only ∼0.1 K for the two PESs. Apart from these differences in the resonance region, it is striking to note that the background cross section, including the ultracold s-wave limit, is nearly identical for both PESs. We note that below ∼10 mK, the cross sections exhibit the well-known Wigner threshold behavior where they vary inversely as the velocity or 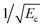 .86,87 Such resonance features supported by the entrance channel van der Waals potentials have been reported for many atom–diatom and diatom–diatom systems, including the benchmark F + H2 and F + HD chemical reactions.88,89 The properties of these resonances are generally very sensitive to the choice of the interaction potential, in particular, if they occur close to the entrance channel threshold.72,88,89
.86,87 Such resonance features supported by the entrance channel van der Waals potentials have been reported for many atom–diatom and diatom–diatom systems, including the benchmark F + H2 and F + HD chemical reactions.88,89 The properties of these resonances are generally very sensitive to the choice of the interaction potential, in particular, if they occur close to the entrance channel threshold.72,88,89
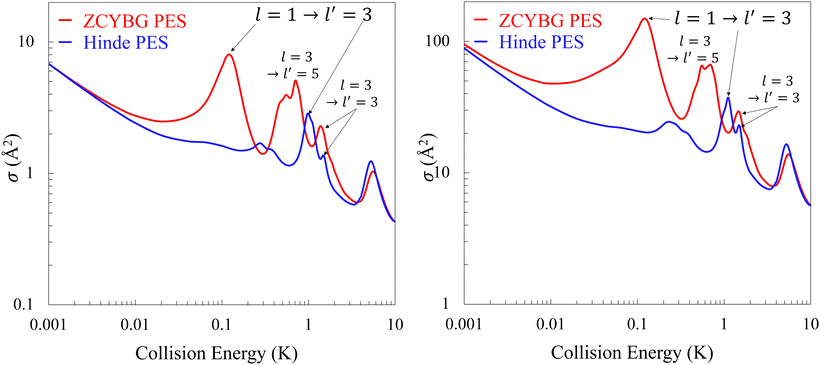
A partial wave analysis of the cross sections for the 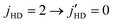 transition shows that the primary peak corresponds to an l = 3 shape resonance originating from total angular momentum quantum number J = 3. The partial wave resolved cross sections on the ZCYBG PES is shown in Fig. 6. The shoulder feature seen on the left side of the primary resonance peak also arises from l = 3 but from J = 5. A similar analysis on the Hinde PES is shown in the ESI† that also features an l = 3 resonance for the primary peak. The secondary resonance corresponds to l = 4 arising from J = 2, 4, and 6 coinciding with the same collision energy on both the PESs.
transition shows that the primary peak corresponds to an l = 3 shape resonance originating from total angular momentum quantum number J = 3. The partial wave resolved cross sections on the ZCYBG PES is shown in Fig. 6. The shoulder feature seen on the left side of the primary resonance peak also arises from l = 3 but from J = 5. A similar analysis on the Hinde PES is shown in the ESI† that also features an l = 3 resonance for the primary peak. The secondary resonance corresponds to l = 4 arising from J = 2, 4, and 6 coinciding with the same collision energy on both the PESs.
Fig. 7 shows integral cross sections for the ΔjHD = −1 transition in HD for the same initial state on the two PESs. Results correspond to elastically scattered D2, i.e., 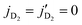 . For this case, the quenching cross section is an order of magnitude larger than the ΔjHD = −2 transition, as it is driven by the leading anisotropic term of the interaction potential depicted in Fig. 1. Similar to the ΔjHD = −2 transition, the primary resonance peak is observed at 1.02 and 0.62 K, respectively, on the ZCYBG and Hinde PESs. A partial wave analysis reveals that the same partial waves are responsible for the resonances in both ΔjHD = −1 and ΔjHD = −2 transitions. For ΔjHD = −1, the l = 3 resonance originates from J = 2, 5 (shoulder region) and J = 3, 4 (main peak). The secondary resonance peak is also observed at the same energy as the
. For this case, the quenching cross section is an order of magnitude larger than the ΔjHD = −2 transition, as it is driven by the leading anisotropic term of the interaction potential depicted in Fig. 1. Similar to the ΔjHD = −2 transition, the primary resonance peak is observed at 1.02 and 0.62 K, respectively, on the ZCYBG and Hinde PESs. A partial wave analysis reveals that the same partial waves are responsible for the resonances in both ΔjHD = −1 and ΔjHD = −2 transitions. For ΔjHD = −1, the l = 3 resonance originates from J = 2, 5 (shoulder region) and J = 3, 4 (main peak). The secondary resonance peak is also observed at the same energy as the 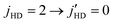 transition, and the Hinde PES predicts slightly larger cross sections compared to the ZCYBG PES (less than 2 Å2).
transition, and the Hinde PES predicts slightly larger cross sections compared to the ZCYBG PES (less than 2 Å2).
3.3 Effect of ortho and para-D2 colliders
The experiments of Perreault et al.53,54 employed n-D2 collision partner with populations of 59% in j = 0, 33% in j = 1 and 8% in j = 2, all in the v = 0 vibrational level. Results presented in Fig. 5–7 correspond to D2(jD2 = 0). Cross sections for D2(jD2 = 1) collisions are shown in Fig. 8 for both Hinde and ZCYBG PESs. The dominant peaks on both PESs arise from l = 1 and l′ = 3 partial waves while the secondary peaks correspond to l = 3, l′ = 3, 5 though the l′ = 5 feature is absent for the Hinde PES. The resonance positions predicted by the two potentials are somewhat different for the two low-energy resonances illustrating the sensitivity of the resonance features to the attractive part of the two PESs. However, both potentials predict the same position and similar magnitudes for the resonance near 6 K. The primary peak in the cross section is an l = 1 → l′ = 3 resonance, which is more prominent on the ZCYBG PES, occurring at about 0.15 K compared to about 1 K for the Hinde PES. This could be attributed to the small differences in the well-depth of the isotropic potential as shown in Fig. 1. This applies to both ΔjHD = −2 and ΔjHD = −1 transitions shown in Fig. 8. Compared to ortho-D2(jD2 = 0) collider, for which the dominant resonance was found for l = 3, for para-D2(jD2 = 1) both l = 1 and l = 3 contribute to the resonance features.In the low-energy limit, both ortho and para-D2 are dominated by s-wave scattering, and the cross sections are nearly identical for the ZCYBG and Hinde PESs. While low-energy scattering is generally very sensitive to the fine details of the interaction potential, the fact that the cross sections are identical on the two PESs, implies that the long-range part of the two PESs is accurately described. We also note that in the scattering calculations, we use the same diatomic potential energy function for HD and D2 molecules, the H2 potential of Schwenke.90
3.4 Energy transfer from HD to D2
In their analysis of the experiments, Perreault et al.53,54 treated the D2 collision partner as a spectator, i.e., its rotational level is considered to be unchanged during the collision. Because the rotational constant of D2 (∼43 K for v = 0) is significantly smaller than that of HD (∼64 K for v = 0 and ∼61 K for v = 1) this assumption may not be valid as a ΔjHD = −2 transition in HD can accompany a ΔjD2 = +2 transition in D2. Indeed, the energy difference of j = 0 and j = 2 state of the HD molecule in v = 1 is about ∼367 K, while the same for D2(v = 0) is about ∼258 K. Therefore, the energy released from quenching of HD in a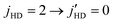 transition is sufficient to excite ortho-D2 molecule from
transition is sufficient to excite ortho-D2 molecule from 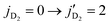 . This energy transfer is only possible for the ortho-D2 collision partner in jD2 = 0 because the released energy from the quenching of HD is not sufficient to excite para-D2 molecule from
. This energy transfer is only possible for the ortho-D2 collision partner in jD2 = 0 because the released energy from the quenching of HD is not sufficient to excite para-D2 molecule from 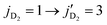 state. Also, the energy released from HD quenching from
state. Also, the energy released from HD quenching from 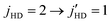 transition in v = 1 is about ∼245 K, and thus, not sufficient to excite the ortho-D2 molecule from
transition in v = 1 is about ∼245 K, and thus, not sufficient to excite the ortho-D2 molecule from 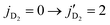 . Therefore, an accurate characterization of the experimental results of Perreault et al.53 must include concurrent excitation of D2 from
. Therefore, an accurate characterization of the experimental results of Perreault et al.53 must include concurrent excitation of D2 from 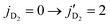 in the quenching of HD from
in the quenching of HD from 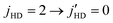 .
.
We investigated this process of energy exchange between HD and D2, and the resulting cross section is shown in Fig. 9 as a function of the collision energy. The results show that this process has a cross section that is a factor of 4 greater than pure rotational quenching of HD from 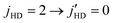 without D2 rotational excitation. Except for the resonance peaks both PESs predict similar results. A partial wave analysis reveals that the resonance peaks arise from the same partial waves as in elastically scattered D2 (ΔjD2 = 0).
without D2 rotational excitation. Except for the resonance peaks both PESs predict similar results. A partial wave analysis reveals that the resonance peaks arise from the same partial waves as in elastically scattered D2 (ΔjD2 = 0).
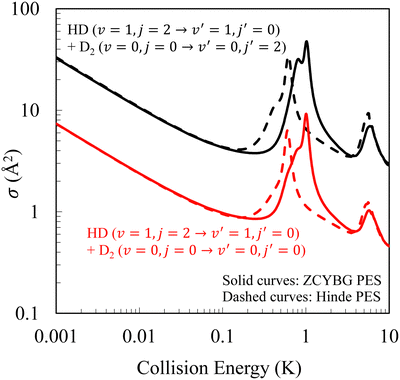 | ||
Fig. 9 Integral cross sections as function of the collision energy for rotational quenching of HD from from 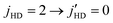 with and without rotational excitation of the D2 molecule from jD2 = 0 to with and without rotational excitation of the D2 molecule from jD2 = 0 to 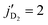 . The red curves represent the elastic transition in D2 (ΔjD2 = 0) (cross sections depicted in Fig. 5) while the black curves denote the D2 rotational excitation channel. The solid and dashed curves show results computed on the ZCYBG and Hinde PES, respectively. . The red curves represent the elastic transition in D2 (ΔjD2 = 0) (cross sections depicted in Fig. 5) while the black curves denote the D2 rotational excitation channel. The solid and dashed curves show results computed on the ZCYBG and Hinde PES, respectively. | ||
Results in Fig. 9 illustrate that the energy exchange process between HD and D2 cannot be ignored in the 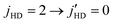 rotational quenching of the HD molecule in HD(vHD = 1, jHD = 2) + D2(jD2 = 0) collisions. As such, this transition is more important, and should be considered together with other transitions in characterizing the experimental data. However, this process was not included in the original analysis of the experimental data,54 presumably due to lack of information on the cross section for this process. Instead, the experimental studies explained their results using a partner reorientation theory that accounts for m′ changing collisions of the para-D2(jD2 = 1) partner. While such collisions may indeed occur in the scattering experiment, and the experimental data may well be reproduced by a model including this effect, a correct description should also account for rotational excitation of D2 in jD2 = 0 collisions. As mentioned above the cross sections for
rotational quenching of the HD molecule in HD(vHD = 1, jHD = 2) + D2(jD2 = 0) collisions. As such, this transition is more important, and should be considered together with other transitions in characterizing the experimental data. However, this process was not included in the original analysis of the experimental data,54 presumably due to lack of information on the cross section for this process. Instead, the experimental studies explained their results using a partner reorientation theory that accounts for m′ changing collisions of the para-D2(jD2 = 1) partner. While such collisions may indeed occur in the scattering experiment, and the experimental data may well be reproduced by a model including this effect, a correct description should also account for rotational excitation of D2 in jD2 = 0 collisions. As mentioned above the cross sections for 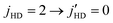 transitions in HD(vHD = 1) by para and ortho-D2 have similar magnitude for elastically scattered D2, but the energy exchange process between HD and D2 yields cross sections that are four times larger, making it an important mechanism in interpreting the experimental data. This is further supported by the comparisons with the results of Buck et al. shown in Fig. 3. Among the various transitions reported in Fig. 3, we would like to draw attention to the 02 → 20 transition. This is the reverse process in which HD is excited from
transitions in HD(vHD = 1) by para and ortho-D2 have similar magnitude for elastically scattered D2, but the energy exchange process between HD and D2 yields cross sections that are four times larger, making it an important mechanism in interpreting the experimental data. This is further supported by the comparisons with the results of Buck et al. shown in Fig. 3. Among the various transitions reported in Fig. 3, we would like to draw attention to the 02 → 20 transition. This is the reverse process in which HD is excited from 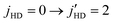 while D2 relaxes from
while D2 relaxes from 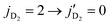 . The agreement between the two calculations is excellent over the entire range of the scattering angle for both collision energies reported in Fig. 3. This further validates the importance of the D2 rotational excitation process in the ΔjHD = −2 quenching of the HD molecule. We note that the cross sections for HD(v = 1, j = 2 → v′ = 1, j′ = 0) + D2(v = 0, j = 0 → v′ = 0, j′ = 2) and its reverse process are connected by the principle of microscopic reversibility.
. The agreement between the two calculations is excellent over the entire range of the scattering angle for both collision energies reported in Fig. 3. This further validates the importance of the D2 rotational excitation process in the ΔjHD = −2 quenching of the HD molecule. We note that the cross sections for HD(v = 1, j = 2 → v′ = 1, j′ = 0) + D2(v = 0, j = 0 → v′ = 0, j′ = 2) and its reverse process are connected by the principle of microscopic reversibility.
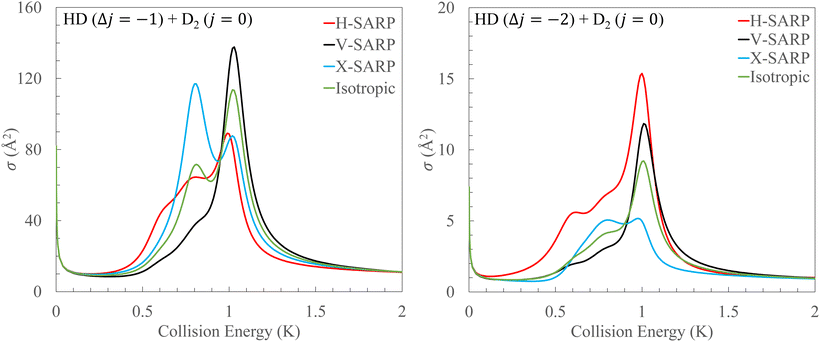
The ICSs for the different processes discussed thus far correspond to isotropic preparations of the collision partners. The various SARP prepared ICSs are compared against their isotropic counterpart in Fig. 10 for ΔjHD = −1 (left panel) and ΔjHD = −2 (right panel) in HD(vHD = 1, jHD = 2) + D2(jD2 = 0) collisions. It is seen that the cross sections are strongly sensitive to the SARP preparation, in particular, in the vicinity of the resonance. The X-SARP preparation corresponds to β = ±45° and refers to a bi-axial state that involves linear combinations of mjHD = ±1 states.64 For the ΔjHD = −1 transition the V-SARP preparation maximizes the cross section at the resonance peak near 1 K while for the ΔjHD = −2 transition it is the H-SARP preparation that maximizes the cross section. For ΔjHD = −2, the X-SARP preparation leads to the smallest ICS. However, for the ΔjHD = −1 transition, the less prominent shoulder peak on the left of the main peak near 1 K becomes even more prominent for the X-SARP preparation and becomes comparable in magnitude to the main peak of the isotropic case. Thus, strong stereodynamic effect is seen in the resonance region that allows considerable control of the ICS through alignment of the HD rotational angular momentum.
3.5 Comparisons with SARP experiments
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ, where χ is the crossing angle between the two beams of HD and D2. A beam divergence of 12 mrad in the transverse direction has been reported by Perreault et al.54 In the analysis of the experimental data by Perreault et al.53,54 a simpler 1-dimensional (1D) relative velocity distribution corresponding to χ = 0 is used. A 3D relative velocity distribution obtained from a Monte-Carlo sampling of χ consistent with the reported beam divergence is used in our analysis. However, we have verified that a 1D velocity distribution yields nearly identical results.
χ, where χ is the crossing angle between the two beams of HD and D2. A beam divergence of 12 mrad in the transverse direction has been reported by Perreault et al.54 In the analysis of the experimental data by Perreault et al.53,54 a simpler 1-dimensional (1D) relative velocity distribution corresponding to χ = 0 is used. A 3D relative velocity distribution obtained from a Monte-Carlo sampling of χ consistent with the reported beam divergence is used in our analysis. However, we have verified that a 1D velocity distribution yields nearly identical results.
In constructing the velocity averaged differential rate, the ortho and para-D2 contributions are weighted by their populations of 59% and 33%, respectively for j = 0 and 1. There is a minor 8% contribution from j = 2 but it is neglected in our calculations. While we have computed the DCS on both PESs, we present the results from the ZCYBG PES in the main text, and provide that of the Hinde PES in the ESI.†
The collision energy distribution evaluated from the 3D relative velocity distribution is shown in the left panel of Fig. 11. In the middle and the right panel of Fig. 11, we show ICS for H-SARP and V-SARP preparations multiplied by the relative velocity and the corresponding energy distribution as a function of the collision energy in Kelvin for ΔjHD = −1 and −2, respectively. For both cases, the collision partner is D2(j = 0) and the ΔjHD = −2 process does not include contributions from rotational excitation of the D2 molecule. As can be seen, for both H-SARP and V-SARP preparations, the energy dependent rate coefficients convoluted with the energy distribution peak near 1 K, and are dominated by contributions from the l = 3 partial wave resonance. We note that the analysis of the experimental data is limited to l = 0 and l = 1 and that the experimental results are not energy resolved.53,54 Thus, the energy dependent rate coefficient weighted with the collision energy distribution presented here can provide key insights into specific partial wave resonances that contribute to the measured angular distribution.
Fig. 12 shows a comparison of the experimental angular distribution of Perreault et al.53 and our theoretical results for the 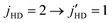 transition in HD(vHD = 1, ΔjHD = −1). The left panel shows the results for the H-SARP preparation while the right panel shows that for the V-SARP case. We note that the experimental data are reported in arbitrary units and they do not correspond to absolute cross sections (rates). Thus, to enable comparison with experiments, the experimental results are scaled appropriately. The comparison is overall good for both H-SARP and V-SARP preparations. However, the peaks in the experimental and theory results are largely out-of-phase except for the forward scattering peak in the H-SARP result.
transition in HD(vHD = 1, ΔjHD = −1). The left panel shows the results for the H-SARP preparation while the right panel shows that for the V-SARP case. We note that the experimental data are reported in arbitrary units and they do not correspond to absolute cross sections (rates). Thus, to enable comparison with experiments, the experimental results are scaled appropriately. The comparison is overall good for both H-SARP and V-SARP preparations. However, the peaks in the experimental and theory results are largely out-of-phase except for the forward scattering peak in the H-SARP result.
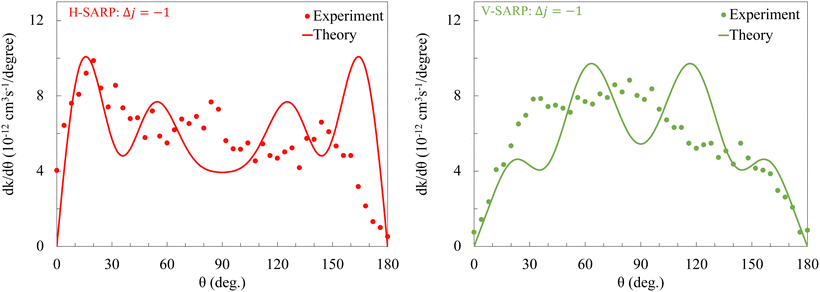 | ||
Fig. 12 A comparison between experiment and theory of the differential rate coefficients averaged over the relative energy distribution for rotational quenching of HD for 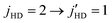 transition. The left and right panels correspond to H-SARP and V-SARP preparations, respectively. The experimental data by Perreault et al.53 are shown by filled circles while the theoretical results are shown by solid and dashed curves. transition. The left and right panels correspond to H-SARP and V-SARP preparations, respectively. The experimental data by Perreault et al.53 are shown by filled circles while the theoretical results are shown by solid and dashed curves. | ||
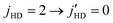 rotational transition in HD(vHD = 1).54Fig. 13 provides a comparison between experiment and theory with filled circles representing the experimental results and solid curves denoting theoretical results. For this case, Perreault et al.54 have proposed a partner re-orientation theory that involves mj changing collisions of the D2(j = 1) partner to account for the experimental findings (strictly speaking, we believe “partner re-orientation” is a misleading terminology because the D2 molecule is un-prepared initially and its angular momentum is not polarized. We believe, “collision-induced alignment” is a more appropriate terminology and we adopt in our discussions here). Specifically, the H-SARP angular distribution could not be reproduced by their non-linear fitting scheme when mj changing collisions of D2(j = 1) are not considered.54 Thus, three different scenarios have been examined from a theoretical standpoint: (i) mj changing collisions of D2(j = 1) is not invoked (shown by the green curve); (ii) mj changing collisions of D2(j = 1) are considered with the corresponding results shown by the black curve. In both these cases, we have omitted contributions from the rotational excitation channel in D2(j = 0) collisions, i.e., only direct relaxation of HD is considered. Both yield comparable results and display strong deviation from the experiment for H-SARP and V-SARP preparations. Lastly, (iii) we include the D2 rotational excitation channel in D2(j = 0) collisions as well as collision-induced alignment of the D2(j = 1) partner. Note that the D2 rotational excitation channel has the largest cross section as shown in Fig. 9. Despite including all possible processes the agreement between theory and experiment is not significantly improved, although the V-SARP results depict a broad central peak consistent with sideways scattering. The experimental data display very similar features for both H-SARP and V-SARP preparations, which is very different from the
rotational transition in HD(vHD = 1).54Fig. 13 provides a comparison between experiment and theory with filled circles representing the experimental results and solid curves denoting theoretical results. For this case, Perreault et al.54 have proposed a partner re-orientation theory that involves mj changing collisions of the D2(j = 1) partner to account for the experimental findings (strictly speaking, we believe “partner re-orientation” is a misleading terminology because the D2 molecule is un-prepared initially and its angular momentum is not polarized. We believe, “collision-induced alignment” is a more appropriate terminology and we adopt in our discussions here). Specifically, the H-SARP angular distribution could not be reproduced by their non-linear fitting scheme when mj changing collisions of D2(j = 1) are not considered.54 Thus, three different scenarios have been examined from a theoretical standpoint: (i) mj changing collisions of D2(j = 1) is not invoked (shown by the green curve); (ii) mj changing collisions of D2(j = 1) are considered with the corresponding results shown by the black curve. In both these cases, we have omitted contributions from the rotational excitation channel in D2(j = 0) collisions, i.e., only direct relaxation of HD is considered. Both yield comparable results and display strong deviation from the experiment for H-SARP and V-SARP preparations. Lastly, (iii) we include the D2 rotational excitation channel in D2(j = 0) collisions as well as collision-induced alignment of the D2(j = 1) partner. Note that the D2 rotational excitation channel has the largest cross section as shown in Fig. 9. Despite including all possible processes the agreement between theory and experiment is not significantly improved, although the V-SARP results depict a broad central peak consistent with sideways scattering. The experimental data display very similar features for both H-SARP and V-SARP preparations, which is very different from the 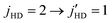 transition. In general, for H-SARP collisions, two dominant peaks are observed at forward and backward scattering angles with a less prominent peak at 90 degrees. This appears to be the case for all of the atom–molecule and molecule–molecule collisions for which SARP experiments have been reported so far.55–58,60–62 A strong central peak is typical for the V-SARP case. Such features are also implied by the values of the reduced rotation matrix elements that characterize these preparations (e.g., see Fig. 2 of ref. 67). It is unlikely that the lack of agreement with experiment for this case is due to the PES employed as corresponding results on the Hinde PES presented in the ESI† also depict similar comparisons. At this point we can only speculate on the source of the discrepancy but energy-resolved measurements may yield more insight.
transition. In general, for H-SARP collisions, two dominant peaks are observed at forward and backward scattering angles with a less prominent peak at 90 degrees. This appears to be the case for all of the atom–molecule and molecule–molecule collisions for which SARP experiments have been reported so far.55–58,60–62 A strong central peak is typical for the V-SARP case. Such features are also implied by the values of the reduced rotation matrix elements that characterize these preparations (e.g., see Fig. 2 of ref. 67). It is unlikely that the lack of agreement with experiment for this case is due to the PES employed as corresponding results on the Hinde PES presented in the ESI† also depict similar comparisons. At this point we can only speculate on the source of the discrepancy but energy-resolved measurements may yield more insight.
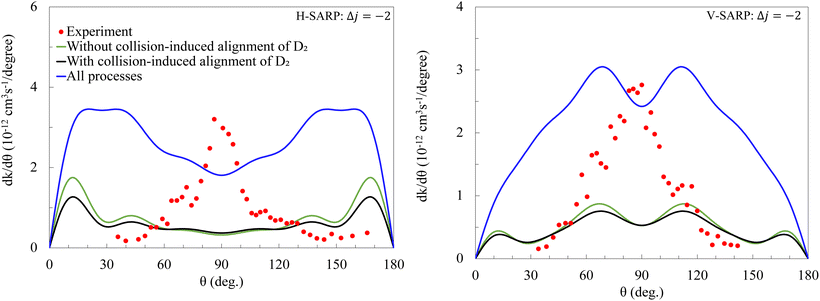 | ||
Fig. 13 Differential rates in H-SARP and V-SARP for  rotational transition in HD induced by collisions with D2. H-SARP (left panel) and V-SARP (right panel) results from Perreault et al.54 (red dots) are compared against theoretical results (solid curves) from this work using the ZCYBG PES. Black and green curves represent, respectively, results with and without considering collision-induced alignment of D2 in D2(j = 1) collisions, while blue curve includes this process and the D2 excitation from j = 0 → j′ = 2. rotational transition in HD induced by collisions with D2. H-SARP (left panel) and V-SARP (right panel) results from Perreault et al.54 (red dots) are compared against theoretical results (solid curves) from this work using the ZCYBG PES. Black and green curves represent, respectively, results with and without considering collision-induced alignment of D2 in D2(j = 1) collisions, while blue curve includes this process and the D2 excitation from j = 0 → j′ = 2. | ||
Perreault et al.54 have discussed the possibility of including the D2 rotational excitation channel in their analysis of the experimental data. However, they excluded this process in favor of mj changing collisions of D2(j = 1) as the measured time-of-flight spectrum of the scattered HD molecules appeared to be consistent with this mechanism. The D2 rotational excitation channel would require lower HD speeds based on energy conservation but this seems to be not supported by the time-of-flight data. Beam-divergence is not considered in the experiments and it is not clear whether this would have an impact on the measured time-of-flight spectrum. We would like to point out that angular momentum conservation effects would produce similar outgoing partial waves regardless of whether the D2 rotational excitation process or mj changing collisions of the D2(j = 1) partner is invoked in fitting the experimental data. In our prior simulations of HD(v = 1, j = 2) + H2 collisions where  collisions were probed by the SARP techniques54 excellent agreement with experiment is observed without invoking mj changing collisions of the H2(j = 1) partner.68 In this case, rotational excitation of H2(j = 0) is not energetically possible at the collision energies involved in the experiment. Similarly, we have obtained excellent agreement with the SARP experiments for aligned collisions of two D2(v = 2, j = 2) molecules using the ZCYBG PES adopted in this study.43,71 Indeed, in this case it was important to include the effect of four-vector correlations in the theoretical formalism as well as collisions involving aligned D2(v = 2, j = 2) and unpolarized D2(v = 0, j = 1, 2) molecules present in the beam in reproducing key features of the measured H-SARP angular distribution. Thus, all relevant processes should be taken into account in the analysis of the experimental data as done in this work for HD + D2.
collisions were probed by the SARP techniques54 excellent agreement with experiment is observed without invoking mj changing collisions of the H2(j = 1) partner.68 In this case, rotational excitation of H2(j = 0) is not energetically possible at the collision energies involved in the experiment. Similarly, we have obtained excellent agreement with the SARP experiments for aligned collisions of two D2(v = 2, j = 2) molecules using the ZCYBG PES adopted in this study.43,71 Indeed, in this case it was important to include the effect of four-vector correlations in the theoretical formalism as well as collisions involving aligned D2(v = 2, j = 2) and unpolarized D2(v = 0, j = 1, 2) molecules present in the beam in reproducing key features of the measured H-SARP angular distribution. Thus, all relevant processes should be taken into account in the analysis of the experimental data as done in this work for HD + D2.
4 Conclusions
In this paper, we report theoretical studies of the stereodynamics and quantum-controlled scattering of HD and D2 for the first time. It is found that the dominant inelastic channel in the rotational quenching of HD from involves an energy transfer to D2 leading to
involves an energy transfer to D2 leading to 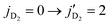 rotational excitation of the D2 molecule. This transition conserves the total molecular rotational angular momentum and has a cross section that is 4 times larger than that of direct relaxation of HD without D2 rotational excitation. A partial wave analysis shows a dominant l = 3 resonance for both ΔjHD = −2 and ΔjHD = −1 transition in HD for ortho-D2(j = 0), while both l = 1 and l = 3 resonances contribute to para-D2(j = 1) collisions. These results are found to be largely insensitive to the choice of the potential energy surfaces for the H2–H2 system adopted in the scattering calculations. Our computed results are in excellent agreement with prior calculations and measurements of differential cross sections for elastic and rotationally inelastic collisions of HD and D2 at higher collision energies. However, the agreement is less satisfactory with recent SARP experiments that report stereodynamic control of rotational quenching in HD(vHD = 1, jHD = 2) + D2 collisions. While our results generally agree with experiments for the
rotational excitation of the D2 molecule. This transition conserves the total molecular rotational angular momentum and has a cross section that is 4 times larger than that of direct relaxation of HD without D2 rotational excitation. A partial wave analysis shows a dominant l = 3 resonance for both ΔjHD = −2 and ΔjHD = −1 transition in HD for ortho-D2(j = 0), while both l = 1 and l = 3 resonances contribute to para-D2(j = 1) collisions. These results are found to be largely insensitive to the choice of the potential energy surfaces for the H2–H2 system adopted in the scattering calculations. Our computed results are in excellent agreement with prior calculations and measurements of differential cross sections for elastic and rotationally inelastic collisions of HD and D2 at higher collision energies. However, the agreement is less satisfactory with recent SARP experiments that report stereodynamic control of rotational quenching in HD(vHD = 1, jHD = 2) + D2 collisions. While our results generally agree with experiments for the 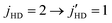 transition, a significant discrepancy is observed for the
transition, a significant discrepancy is observed for the 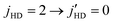 transition in HD. The discrepancy persists regardless of whether D2 rotational excitation channel is considered in the theoretical simulations. We believe, a re-analysis of the experimental data including the D2 rotational excitation channel in D2(j = 0) collisions or measurements of energy resolved cross sections may help resolve the discrepancy.
transition in HD. The discrepancy persists regardless of whether D2 rotational excitation channel is considered in the theoretical simulations. We believe, a re-analysis of the experimental data including the D2 rotational excitation channel in D2(j = 0) collisions or measurements of energy resolved cross sections may help resolve the discrepancy.
Author contributions
Quantum scattering calculations were primarily carried out by B. M. with assistance from N. B. and J. F. E. C. All authors contributed to data analysis, manuscript preparation, and editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Dick Zare, Nandini Mukherjee, William Perreault, and Haowen Zhou for many stimulating discussions and sharing their experimental data. This work is supported in part by NSF grant No. PHY-2110227 (N. B.) and by a DoD MURI grant from Army Research Office (Grant No. W911NF-19-1-0283 to H. G. and N. B.). F. J. A. acknowledges funding by the Spanish Ministry of Science and Innovation (grant PID2021-122839NB-I00). P. G. J. acknowledges Grant No. PID2020-113147GA-I00 funded by MCIN/AEI/10.13039/501100011033 (Spanish Ministry of Science and Innovation). J. F. E. C. acknowledges support from the U.K. Engineering and Physical Sciences Research Council (EPSRC) Grant No. EP/W00299X/1.Notes and references
- P. C. Stancil, S. Lepp and A. Dalgarno, Astrophys. J., 1998, 509, 1 CrossRef CAS.
- S. C. O. Glover and T. Abel, Mon. Not. R. Astron. Soc., 2008, 388, 1627–1651 CrossRef CAS.
- D. Galli and F. Palla, Astron. Astrophys., 1998, 335, 403 CAS.
- Y. Wan, N. Balakrishnan, B. H. Yang, R. C. Forrey and P. C. Stancil, Mon. Not. R. Astron. Soc., 2019, 488, 381 CrossRef CAS.
- N. Balakrishnan, J. F. E. Croft, B. H. Yang, R. C. Forrey and P. C. Stancil, Astrophys. J., 2018, 866, 95 CrossRef.
- D. Puy, G. Alecian, J. L. Bourlot, J. Leorat and G. D. Forets, Astron. Astrophys., 1993, 267, 337 CAS.
- D. Galli and F. Palla, Planet. Space Sci., 2002, 50, 1197 CrossRef CAS.
- S. Lacour, M. K. André, P. Sonnentrucker, F. L. Petit, D. E. Welty, J. M. Desert, R. Ferlet, E. Roueff and D. G. York, Astron. Astrophys., 2005, 430, 967 CrossRef CAS.
- H. S. Liszt, Astrophys. J., 2015, 799, 66 CrossRef.
- I. D. McGreer and G. L. Bryan, Astrophys. J., 2008, 685, 8 CrossRef CAS.
- S. Hirano, T. Hosokawa, N. Yoshida, K. Omukai and H. W. Yorke, Mon. Not. R. Astron. Soc., 2015, 448, 568 CrossRef CAS.
- E. Ripamonti, Mon. Not. R. Astron. Soc., 2007, 376, 709 CrossRef CAS.
- Y. Wan, B. H. Yang, P. C. Stancil, N. Balakrishnan, N. J. Parekh and R. C. Forrey, Astrophys. J., 2018, 862, 132 CrossRef.
- C. Joblin, E. Bron, C. Pinto, P. Pilleri, F. L. Petit, M. Gerin, J. L. Bourlot, A. Fuente, O. Berne and J. R. Goicoechea, et al. , Astron. Astrophys., 2018, 615, A129 CrossRef PubMed.
- E. A. Bergin, L. I. Cleeves, U. Gorti, K. Zhang, G. A. Blake, J. D. Green, S. M. Andrews, N. J. Evans II, T. Henning and K. Öberg, et al. , Nature, 2013, 493, 644 CrossRef CAS PubMed.
- C. M. Wright, E. F. V. Dishoeck, P. Cox, S. D. Sidher and M. F. Kessler, Astrophys. J., 1999, 515, L29 CrossRef CAS.
- E. T. Polehampton, J. P. Baluteau, C. Ceccarelli, B. M. Swinyard and E. Caux, Astron. Astrophys., 2002, 388, L44 CrossRef CAS.
- H. Kamaya and J. Silk, Mon. Not. R. Astron. Soc., 2003, 339, 1256 CrossRef CAS.
- D. A. Neufeld, J. D. Green, D. J. Hollenbach, P. Sonnentrucker, G. J. Melnick, E. A. Bergin, R. L. Snell, W. J. Forrest, D. M. Watson and M. J. Kaufman, Astrophys. J., 2006, 647, L33 CrossRef CAS.
- D. Flower, Molecular collisions in the interstellar medium, Cambridge University Press, 2007, vol. 42 Search PubMed.
- D. R. Flower, Mon. Not. R. Astron. Soc., 2000, 318, 875 CrossRef CAS.
- R. J. Hinde, J. Chem. Phys., 2008, 128, 154308 CrossRef PubMed.
- J. Zuo, J. F. E. Croft, Q. Yao, N. Balakrishnan and H. Guo, J. Chem. Theory Comput., 2021, 17, 6747 CrossRef CAS PubMed.
- G. Garberoglio, P. Jankowski, K. Szalewicz and A. H. Harvey, J. Chem. Phys., 2012, 137, 154308 CrossRef PubMed.
- S. F. dos Santos, N. Balakrishnan, S. Lepp, G. Quéméner, R. C. Forrey, R. J. Hinde and P. C. Stancil, J. Chem. Phys., 2011, 134, 214303 CrossRef PubMed.
- Y. Liu, P. G. Jambrina, J. F. E. Croft, N. Balakrishnan, F. J. Aoiz and H. Guo, J. Chem. Theory Comput., 2024, 1829 CrossRef CAS PubMed.
- J. L. Bohn, A. M. Rey and J. Ye, Science, 2017, 357, 1002 CrossRef CAS PubMed.
- V. V. Albert, J. P. Covey and J. Preskill, Phys. Rev. X, 2020, 10, 31050 CAS.
- J. Toscano, H. J. Lewandowski and B. R. Heazlewood, Phys. Chem. Chem. Phys., 2020, 22, 9180 RSC.
- M. G. Hu, Y. Liu, M. A. Nichols, L. Zhu, G. Quéméner, O. Dulieu and K. K. Ni, Nat. Chem., 2021, 13, 435 CrossRef CAS PubMed.
- P. G. Jambrina, J. F. E. Croft, N. Balakrishnan and F. J. Aoiz, Phys. Chem. Chem. Phys., 2021, 23, 19364 RSC.
- B. K. Kendrick, H. Li, M. Li, S. Kotochigova, J. F. E. Croft and N. Balakrishnan, Phys. Chem. Chem. Phys., 2021, 23, 5096 RSC.
- Y. Segev, M. Pitzer, M. Karpov, N. Akerman, J. Narevicius and E. Narevicius, Nature, 2019, 572, 189 CrossRef CAS PubMed.
- H. Son, J. J. Park, W. Ketterle and A. O. Jamison, Nature, 2020, 580, 197 CrossRef CAS PubMed.
- L. Anderegg, L. W. Cheuk, Y. Bao, S. Burchesky, W. Ketterle, K. K. Ni and J. M. Doyle, Science, 2019, 365, 1156 CrossRef CAS PubMed.
- Y. Liu and K. K. Ni, Annu. Rev. Phys. Chem., 2022, 73, 73 CrossRef CAS PubMed.
- R. V. Krems, Phys. Chem. Chem. Phys., 2008, 10, 4079 RSC.
- L. D. Carr, D. DeMille, R. V. Krems and J. Ye, New J. Phys., 2009, 11, 55049 CrossRef.
- B. K. Stuhl, M. T. Hummon and J. Ye, Annu. Rev. Phys. Chem., 2014, 65, 501 CrossRef CAS PubMed.
- Y. Liu, M. G. Hu, M. A. Nichols, D. Yang, D. Xie, H. Guo and K. K. Ni, Nature, 2021, 593, 379 CrossRef CAS PubMed.
- N. Balakrishnan, J. Chem. Phys., 2016, 145, 150901 CrossRef CAS PubMed.
- B. R. Heazlewood and T. P. Softley, Nat. Rev. Chem., 2021, 5, 125 CrossRef CAS PubMed.
- J. F. E. Croft, P. G. Jambrina, F. J. Aoiz, H. Guo and N. Balakrishnan, J. Phys. Chem. A, 2023, 127, 1619 CrossRef CAS PubMed.
- J. A. Blackmore, L. Caldwell, P. D. Gregory, E. M. Bridge, R. Sawant, J. Aldegunde, J. M. Petit, D. Jaksch, J. M. Hutson and B. E. Sauer, et al. , Quantum Sci. Technol., 2018, 4, 14010 CrossRef.
- L. W. Cheuk, L. Anderegg, Y. Bao, S. Burchesky, S. Y. Scarlett, W. Ketterle, K. K. Ni and J. M. Doyle, Phys. Rev. Lett., 2020, 125, 43401 CrossRef CAS PubMed.
- P. Aggarwal, Y. Yin, K. Esajas, H. L. Bethlem, A. Boeschoten, A. Borschevsky, S. Hoekstra, K. Jungmann, V. R. Marshall and T. B. Meijknecht, et al. , Phys. Rev. Lett., 2021, 127, 173201 CrossRef CAS PubMed.
- S. Jurgilas, A. Chakraborty, C. J. H. Rich, L. Caldwell, H. J. Williams, N. J. Fitch, B. E. Sauer, M. D. Frye, J. M. Hutson and M. R. Tarbutt, Phys. Rev. Lett., 2021, 126, 153401 CrossRef CAS PubMed.
- L. Anderegg, B. L. Augenbraun, Y. Bao, S. Burchesky, L. W. Cheuk, W. Ketterle and J. M. Doyle, Nat. Phys., 2018, 14, 890 Search PubMed.
- J. F. E. Croft, J. L. Bohn and G. Quéméner, Phys. Rev. A, 2020, 102, 33306 CrossRef CAS.
- D. Yang, J. Huang, X. Hu, D. Xie and H. Guo, J. Chem. Phys., 2020, 152, 241103 CrossRef CAS PubMed.
- N. Mukherjee and R. N. Zare, J. Chem. Phys., 2011, 135, 024201 CrossRef PubMed.
- N. Mukherjee, W. E. Perreault and R. N. Zare, J. Phys. B: At., Mol. Opt. Phys., 2017, 50, 144005 CrossRef.
- W. E. Perreault, N. Mukherjee and R. N. Zare, Science, 2017, 358, 356 CrossRef CAS PubMed.
- W. E. Perreault, N. Mukherjee and R. N. Zare, Nat. Chem., 2018, 10, 561 CrossRef CAS PubMed.
- H. Zhou, W. E. Perreault, N. Mukherjee and R. N. Zare, J. Chem. Phys., 2021, 154, 104309 CrossRef CAS PubMed.
- W. E. Perreault, H. Zhou, N. Mukherjee and R. N. Zare, J. Chem. Phys., 2022, 157, 144301 CrossRef CAS PubMed.
- H. Zhou, W. E. Perreault, N. Mukherjee and R. N. Zare, Science, 2021, 374, 960 CrossRef CAS PubMed.
- W. E. Perreault, H. Zhou, N. Mukherjee and R. N. Zare, J. Phys. Chem. Lett., 2022, 13, 10912 CrossRef CAS PubMed.
- W. E. Perreault, N. Mukherjee and R. N. Zare, J. Chem. Phys., 2016, 145, 154203 CrossRef PubMed.
- W. E. Perreault, N. Mukherjee and R. N. Zare, J. Chem. Phys., 2019, 150, 174301 CrossRef PubMed.
- H. Zhou, W. E. Perreault, N. Mukherjee and R. N. Zare, Nat. Chem., 2022, 14, 658 CrossRef CAS PubMed.
- W. E. Perreault, H. Zhou, N. Mukherjee and R. N. Zare, Phys. Rev. Lett., 2020, 124, 163202 CrossRef CAS PubMed.
- W. E. Perreault, N. Mukherjee and R. N. Zare, Chem. Phys., 2018, 514, 150 CrossRef CAS.
- N. Mukherjee, J. Phys. Chem. A, 2023, 127, 418 CrossRef CAS PubMed.
- N. Balakrishnan, P. G. Jambrina, J. F. E. Croft, H. Guo and F. J. Aoiz, Chem. Commun., 2024, 60, 1239 RSC.
- Y. Wang, J. Huang, W. Wang, T. Du, Y. Xie, Y. Ma, C. Xiao, Z. Zhang, D. H. Zhang and X. Yang, Science, 2023, 379, 191 CrossRef CAS PubMed.
- J. F. E. Croft and N. Balakrishnan, J. Chem. Phys., 2019, 150, 164302 CrossRef CAS PubMed.
- J. F. E. Croft, N. Balakrishnan, M. Huang and H. Guo, Phys. Rev. Lett., 2018, 121, 113401 CrossRef CAS PubMed.
- M. Morita and N. Balakrishnan, J. Chem. Phys., 2020, 153, 184307 CrossRef CAS PubMed.
- M. Morita and N. Balakrishnan, J. Chem. Phys., 2020, 153, 091101 CrossRef CAS PubMed.
- P. G. Jambrina, J. F. E. Croft, J. Zuo, H. Guo, N. Balakrishnan and F. J. Aoiz, Phys. Rev. Lett., 2023, 130, 33002 CrossRef CAS PubMed.
- P. G. Jambrina, M. Morita, J. F. E. Croft, F. J. Aoiz and N. Balakrishnan, J. Phys. Chem. Lett., 2022, 13, 4064 CrossRef CAS PubMed.
- P. G. Jambrina, J. F. E. Croft, H. Guo, M. Brouard, N. Balakrishnan and F. J. Aoiz, Phys. Rev. Lett., 2019, 123, 43401 CrossRef CAS PubMed.
- V. Sáez-Rábanos, J. E. Verdasco, F. J. Aoiz and V. J. Herrero, Phys. Chem. Chem. Phys., 2021, 23, 8002 RSC.
- H. da Silva, B. K. Kendrick and N. Balakrishnan, J. Chem. Phys., 2022, 156, 044305 CrossRef CAS PubMed.
- U. Buck, F. Huisken, G. Maneke and J. Schaefer, J. Chem. Phys., 1983, 78, 4430 CrossRef CAS.
- U. Buck, F. Huisken, J. Schleusener and J. Schaefer, J. Chem. Phys., 1981, 74, 535 CrossRef CAS.
- R. V. Krems, TwoBC – quantum scattering program, University of British Columbia, Vancouver, Canada, 2006 Search PubMed.
- G. Quéméner, N. Balakrishnan and R. V. Krems, Phys. Rev. A: At., Mol., Opt. Phys., 2008, 77, 30704 CrossRef.
- G. Quéméner and N. Balakrishnan, J. Chem. Phys., 2009, 130, 114303 CrossRef PubMed.
- J. P. Ríos, M. Bartolomei, J. C. Martínez, M. I. Hernández and R. H. Lamoneda, J. Phys. Chem. A, 2009, 113, 14952 CrossRef PubMed.
- A. M. Arthurs and A. Dalgarno, Proc. R. Soc. London, Ser. A, 1960, 256, 540 Search PubMed.
- J. Schaefer and W. Meyer, J. Chem. Phys., 1979, 70, 344 CrossRef CAS.
- R. N. Zare, Ber. Bunsenges. Phys. Chem., 1982, 86, 422 CrossRef CAS.
- N. Mukherjee, W. E. Perreault and R. N. Zare, Stark-induced adiabatic passage processes to selectively prepare vibrationally excited single and superposition of quantum states, Elsevier, 2018, p. 1 Search PubMed.
- N. Balakrishnan, R. C. Forrey and A. Dalgarno, Chem. Phys. Lett., 1997, 280, 1 CrossRef CAS.
- E. P. Wigner, Phys. Rev., 1948, 73, 1002 CrossRef CAS.
- D. D. Fazio, V. Aquilanti and S. Cavalli, J. Phys. Chem. A, 2020, 124, 12 CrossRef PubMed.
- D. D. Fazio, V. Aquilanti and S. Cavalli, Front. Chem., 2019, 7, 328 CrossRef PubMed.
- D. W. Schwenke, J. Chem. Phys., 1988, 89, 2076 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Stereodynamical control of cold HD + D2 collisions. It includes similar results as those presented in the main text but obtained using the full-dimensional H4 PES by Hinde. Also, contour plots of differential cross sections for the H-SARP and V-SARP preparations as a function of the collision energy and scattering angle are included. See DOI: https://doi.org/10.1039/d4cp01737d |
| This journal is © the Owner Societies 2024 |