 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Mass and mole fractions in calibration-free LIBS
Tobias
Völker
 * and
Igor B.
Gornushkin
* and
Igor B.
Gornushkin

Bundesanstalt für Materialforschung und –prüfung (BAM), Richard-Willstätter-Straße 11, 12489, Berlin, Germany. E-mail: tobias.voelker@bam.de
First published on 27th February 2024
Abstract
This technical note highlights the fact that CF-LIBS algorithms work in mole fractions, while results of spectrochemical analysis are usually reported in mass fractions or mass percent. Ignoring this difference and not converting mole fractions to mass fractions can lead to errors in reported concentrations determined by the CF-LIBS method and inadequate comparison of these concentrations with certified concentrations. Here, the key points of the CF-LIBS algorithm are reproduced and the formulae for converting a mole fraction to a mass fraction and vice versa are given. Several numerical examples are also given, which show that the greater the difference between the molar mass of an individual element in a sample and the average molar mass, the greater the discrepancy between the mole and mass fractions.
1 Introduction
Calibration-free LIBS (CF-LIBS) has received considerable attention as an alternative approach to analysis using reference samples because it does not require a laborious calibration procedure. The element concentrations are found directly from the measured spectrum using a simplified laser-induced plasma model. This approach was first proposed by Ciucci et al.1 using the assumptions of stoichiometric ablation and homogeneous optically thin plasma in local thermodynamic equilibrium (LTE). Special efforts have been made to investigate the accuracy of the method by analyzing errors associated with plasma inhomogeneity, line overlap, noise, spectral resolution, self-absorption, or inaccurate path length.2,3 It was shown that the CF-LIBS method is not error-free even for synthetic spectra that fully correspond to the mathematical model.3The purpose of this technical note is to eliminate another potential error in the presentation of CF-LIBS results that can occur if the fact that CF-LIBS algorithms work with mole fractions rather than mass fractions is neglected. Since mass percentages (mass fractions) are more commonly used when reporting spectrochemical analysis data, CF-LIBS results assume conversion of mole fractions to mass fractions. The importance of such a conversion was emphasized in ref. 4, however, most publications on CF-LIBS avoid mentioning it, leaving the impression that work with mass percent is taken for granted. Meanwhile, the lack of conversion of mole fraction to mass fractions can lead to overestimations or underestimations of concentrations. Here we discuss this issue by highlighting the difference between the mole and mass fractions and estimating errors due to misassignment of concentrations.
2 Relative concentrations in the Boltzmann plot method
The most used expression for the Boltzmann plot in the CF-LIBS application is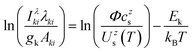 | (1) |
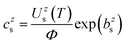 | (2) |
The unknown factor Φ is found from the requirement that all mole fractions add up to one, Σs,zczs = 1.
It should be emphasized again that the above equations work with number densities, so that relative concentrations of elements are expressed in mole fractions. Since the concentrations in standard reference samples are usually given in mass fractions, the results of the CF-LIBS analysis cannot be directly compared with these reference values. For a correct comparison, either the CF-LIBS results should be converted from mole fractions cs to mass fractions wsvia
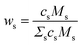 | (3) |
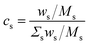 | (4) |
3 Mass fraction versus mole fraction examples
Table 1 shows the relative concentrations of elements in Portland cement, stainless steel, alnico, and soda-lime glass. The mass percentage are sourced from the literature,6–9 and the mole percentage are calculated according to eqn (4). For Portland cement, the relative error (RE = |c − w|/w·100%) between the mass fractions and the mole fractions falls in the range of about 3–57%, with an average relative error about 35%. The largest error is observed for iron and titanium due to the largest deviations of their molar masses (respectively 56 and 48 g mol−1) from the average molar mass![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) = (Σiwi/Mi)−1 ≈ 25 g mol−1. In contrast, sodium, magnesium, and aluminum with molar masses close to the average molar mass (respectively 23, 24, and 27 g mol−1) show the smallest error. For the Alnico sample, which is composed of aluminum, cobalt, copper, iron, nickel and titanium, the latter five have close molar masses, while aluminum has a molar mass of almost less than half that. Therefore, the relative error of aluminum is the highest, about 83%, and the relative errors of the remaining elements are within 3–22%. A similar analysis can be carried out for the other two samples shown in Table 1: stainless steel and soda-lime glass. Wherever the molar mass of an element differs significantly from the average molar mass, a deviation between mole and mass concentration becomes apparent. This is also illustrated in Fig. 1.
= (Σiwi/Mi)−1 ≈ 25 g mol−1. In contrast, sodium, magnesium, and aluminum with molar masses close to the average molar mass (respectively 23, 24, and 27 g mol−1) show the smallest error. For the Alnico sample, which is composed of aluminum, cobalt, copper, iron, nickel and titanium, the latter five have close molar masses, while aluminum has a molar mass of almost less than half that. Therefore, the relative error of aluminum is the highest, about 83%, and the relative errors of the remaining elements are within 3–22%. A similar analysis can be carried out for the other two samples shown in Table 1: stainless steel and soda-lime glass. Wherever the molar mass of an element differs significantly from the average molar mass, a deviation between mole and mass concentration becomes apparent. This is also illustrated in Fig. 1.
| Element | M g mol−1 | w wt% | c mol% | RE % |
|---|---|---|---|---|
Portland cement (![[M with combining macron]](https://www.rsc.org/images/entities/b_i_char_004d_0304.gif) = 25 g mol−1) = 25 g mol−1) |
||||
| Al | 26.98 | 2.51 | 2.34 | 7 |
| Ca | 40.08 | 47.37 | 29.72 | 37 |
| Fe | 55.84 | 1.77 | 0.80 | 55 |
| K | 39.10 | 0.74 | 0.47 | 36 |
| Mg | 24.31 | 1.38 | 1.43 | 3 |
| Na | 22.99 | 0.15 | 0.17 | 9 |
| O | 16.00 | 35.46 | 55.72 | 57 |
| S | 32.06 | 1.07 | 0.84 | 22 |
| Si | 28.09 | 9.45 | 8.46 | 10 |
| Ti | 47.87 | 0.11 | 0.06 | 47 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
Alnico (![[M with combining macron]](https://www.rsc.org/images/entities/b_i_char_004d_0304.gif) = 52 g mol−1) = 52 g mol−1) |
||||
| Al | 26.98 | 13.96 | 25.49 | 83 |
| Co | 58.93 | 36.09 | 30.17 | 16 |
| Cu | 63.55 | 2.50 | 1.94 | 22 |
| Fe | 55.84 | 28.50 | 25.14 | 12 |
| Ni | 58.69 | 11.75 | 9.86 | 16 |
| Ti | 47.87 | 7.20 | 7.41 | 3 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
Stainless steel (![[M with combining macron]](https://www.rsc.org/images/entities/b_i_char_004d_0304.gif) = 54 g mol−1) = 54 g mol−1) |
||||
| C | 12.01 | 0.20 | 0.90 | 353 |
| Cr | 52.00 | 13.00 | 13.59 | 5 |
| Fe | 55.84 | 84.25 | 81.99 | 3 |
| Mn | 54.94 | 1.50 | 1.48 | 1 |
| P | 30.97 | 0.04 | 0.07 | 75 |
| S | 32.06 | 0.01 | 0.03 | 70 |
| Si | 28.09 | 1.00 | 1.94 | 94 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
Soda-lime glass (![[M with combining macron]](https://www.rsc.org/images/entities/b_i_char_004d_0304.gif) = 21 g mol−1) = 21 g mol−1) |
||||
| Al | 26.98 | 0.74 | 0.57 | 24 |
| Ca | 40.08 | 5.62 | 2.89 | 49 |
| Fe | 55.84 | 0.04 | 0.02 | 63 |
| K | 39.10 | 0.12 | 0.06 | 47 |
| Mg | 24.31 | 1.44 | 1.22 | 15 |
| Na | 22.99 | 11.77 | 10.56 | 10 |
| O | 16.00 | 46.48 | 59.89 | 29 |
| Si | 28.09 | 33.79 | 24.80 | 27 |
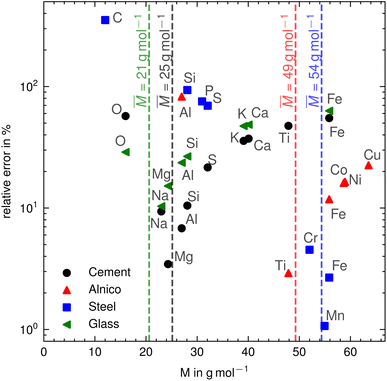 | ||
| Fig. 1 Comparison between molar mass and relative error of mass and mole fraction for different materials. | ||
4 Conclusion
An important feature of the CF-LIBS algorithms is that element concentrations are expressed in mole fractions rather than mass fractions, as opposed to the typical representation of concentrations in mass percentages or mass fractions. For an adequate presentation of CF analysis results, the conversion of mole fractions to mass fractions should not be overlooked, otherwise errors in reported concentrations and incorrect comparisons with certified concentrations will occur. If elements with close molar masses are analyzed, such as transition metals in steel, the difference between mole fraction and mass fraction is small. However, it becomes larger the greater the difference between the molar masses of the individual elements in the sample.Author contributions
Tobias Völker: conceptualization, methodology, formal analysis, visualization, writing – original draft, writing – review & editing, Igor B. Gornushkin: validation, writing – review & editing.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Acknowledgements
The authors are grateful to Dr E. Niederleithinger and Dr J. Riedel (BAM) for their continued support of this collaboration. All authors have read and agreed to the published version of the manuscript. The authors would like to thank the unknown reviewers for taking the time and effort to review the manuscript and provide valuable comments and suggestions.References
- A. Ciucci, M. Corsi, V. Palleschi, S. Rastelli, A. Salvetti and E. Tognoni, New Procedure for Quantitative Elemental Analysis by Laser-Induced Plasma Spectroscopy, Appl. Spectrosc., 1999, 53(8), 960–964, DOI:10.1366/0003702991947612.
- E. Tognoni, G. Cristoforetti, S. Legnaioli, V. Palleschi, A. Salvetti, M. Mueller, U. Panne and I. Gornushkin, A numerical study of expected accuracy and precision in calibration-free laser-induced breakdown spectroscopy in the assumption of ideal analytical plasma, Spectrochim. Acta, Part B, 2007, 62(12), 1287–1302, DOI:10.1016/j.sab.2007.10.005.
- I. B. Gornushkin, T. Völker and A. Y. Kazakov, Extension and investigation by numerical simulations of algorithm for calibration-free laser induced breakdown spectroscopy, Spectrochim. Acta, Part B, 2018, 147, 149–163, DOI:10.1016/j.sab.2018.06.011.
- E. Tognoni, G. Cristoforetti, S. Legnaioli and V. Palleschi, Calibration-free laser-induced breakdown spectroscopy: State of the art, Spectrochim. Acta, Part B, 2010, 65(1), 1–14, DOI:10.1016/j.sab.2009.11.006.
- T. Völker and I. B. Gornushkin, Importance of physical units in the Boltzmann plot method, J. Anal. At. Spectrom., 2022, 37(10), 1972–1974, 10.1039/d2ja00241h.
- T. Völker, S. Millar, C. Strangfeld and G. Wilsch, Identification of type of cement through laser-induced breakdown spectroscopy, Constr. Build. Mater., 2020, 258, 120345, DOI:10.1016/j.conbuildmat.2020.120345.
- E. White, E. Rinko, T. Prost, T. Horn, C. Ledford, C. Rock and I. Anderson, Processing of alnico magnets by additive manufacturing, Appl. Sci., 2019, 9(22), 4843, DOI:10.3390/app9224843.
- DIN EN 10088-1, Stainless Steels – Part 1: List of Stainless Steels, 2014, DOI:10.31030/2102106.
- W. Lanford, K. Davis, P. Lamarche, T. Laursen, R. Groleau and R. Doremus, Hydration of soda-lime glass, J. Non-Cryst. Solids, 1979, 33(2), 249–266, DOI:10.1016/0022-3093(79)90053-x.
| This journal is © The Royal Society of Chemistry 2024 |
