DOI:
10.1039/C9NA00372J
(Paper)
Nanoscale Adv., 2020,
2, 1214-1227
Nanodiamonds as a state-of-the-art material for enhancing the gamma radiation resistance properties of polymeric membranes†
Received
13th June 2019
, Accepted 29th January 2020
First published on 31st January 2020
Abstract
We report, for the first time, the development of gamma radiation resistant polysulfone (Psf)–nanodiamond (ND) composite membranes with varying concentrations of NDs, ranging up to 2 wt% of Psf. Radiation stability of the synthesized membranes was tested up to a dose of 1000 kGy. To understand the structure–property correlationship of these membranes, multiple characterization techniques were used, including field-emission scanning electron microscopy, atomic force microscopy, drop shape analysis, Fourier-transform infrared spectroscopy, X-ray photoelectron spectroscopy, gel permeation chromatography, positron annihilation spectroscopy, and small angle X-ray scattering. All the composite membranes exhibited enhanced radiation resistance properties, with 0.5% loading of NDs as the optimum. Compared to the radiation stability of Psf membranes up to a dose of 100 kGy, the optimum composite membranes are found to be stable up to a radiation dose of 500 kGy, owing to the unique surface chemistry of NDs and interfacial chemistry of Psf–ND composites. Experimental findings along with the Monte Carlo simulation studies confirmed a five times enhanced life-span of the composite membranes in an environment of the intermediate level radioactive waste, compared to the control Psf membrane.
1 Introduction
A broad spectrum of radioactive wastes (low, intermediate, and high level) is generated at various stages of nuclear fuel processing (uranium ore mining and milling, fuel fabrication, reactor operation, and spent fuel reprocessing).1 Hence, safe and effective management of radioactive wastes is of utmost importance.2,3 Various methods have been established to treat and manage radioactive wastes. These processes typically include chemical treatment,4 adsorption,5 filtration,6 evaporation, ion exchange,7 extraction8etc. However, these processes have limitations in terms of the efficiency of eliminating all the contaminants, high operating cost and/or production of secondary solid wastes.9
Membrane technology has been demonstrated to be successful in removal of radioactive substances with significant advantages over the above-mentioned conventional processes.10 For a unit operation, membranes can be used independently, or in combination with conventional technologies, for treatment of complex waste streams.11 These hybrid technologies provide excellent capability for treating radioactive wastes by improving the efficiency and effectiveness of conventional processes. Inorganic (ceramic) membranes have been found to have excellent stability against the radioactive environment,12 but their application is limited owing to the difficulty in their fabrication, inherent brittleness, and more importantly, the limitation in fine-tuning the pore sizes.
Polymeric membranes have gained attention due to their higher flexibility, processability, simple pore formation mechanism, tailorable properties, and low cost as well as negligible secondary waste generation.13 Also, the properties of polymeric membranes can be altered for specific application by functionalization and/or modification of their internal structure (pores/porosity, internal network etc.), with enhanced thermal, chemical, and mechanical stability.14 However, the application of polymeric membranes is limited in the radioactive domain, owing to their low radiation stability.15
Though polysulfone (Psf) is regarded as a heat-resistant, high performance engineering thermoplastic, it has gamma radiation stability up to 1000 kGy.16 It is important to note that polysulfone-based membranes still have reduced radiation stability up to 25 kGy.17 When exposed to radiation, free radicals induced by gamma-ray irradiation lead to chain scission and/or cross-linking, and change the crosslink density of the polymer matrix.18 This causes degradation in the performance of the polymeric membranes. Hence, there is extensive interest in establishing new membrane materials that are resistant to gamma radiation.
Since nanomaterials have unique properties such as a high surface area, tunability, low density, high porosity etc.,19 they offer unprecedented opportunities to tailor make membranes with desirable attributes taking into account the targeted applications.20 In polymer-nano composites, a larger surface-to-volume ratio of nanofillers results in a significant increase in the volume of interphase between nanomaterials and polymers, which makes the properties of the polymer-nano composites different from those of bulk polymers.21 Among different nanofillers, carbonaceous nanoparticles such as 2D graphene, 1D carbon nanotubes, and 0D nanodiamonds (NDs) are very promising due to their unique combination of properties, such as mechanical strength, chemical stability, electrical conductivity, aspect ratio etc.22 NDs have exceptional mechanical (superior hardness, fracture strength and Young's modulus), chemical (resistance to harsh environments), thermal (high thermal conductivity), electronic (electrical resistivity) and optical properties.23 Additionally, they are non-toxic (biocompatible), have excellent structural properties (high surface area and tunable surface structures),24 and high radiation resistance.25 Furthermore, their properties can be modified through surface doping,26 interior doping,27 introduction of functional groups28etc. In line with this, several nanoparticles with surface modification were utilized as additives in the polymer matrix to enhance the properties of membranes, like performance,29 mechanical properties,30 thermal properties,31 anti(bio)fouling properties,32 antibacterial properties33etc.
The confined size of NDs (in all dimensions; zero-dimensional) is favorable in terms of larger loading of particles in the polymeric host matrix relative to the other materials (which have at least one larger dimension; one-dimensional or two-dimensional). Hence, they provide a greater interface volume in the polymer–nanomaterial composite matrix. Furthermore, due to their spherical shape, ND particles do not stack together and do not create bundles (theoretically).34 NDs provide better dispersion as compared to one-dimensional or two-dimensional nanomaterials.35 NDs are promising materials, owing to their prosperous surface chemistry and sp3 hybridization, and show diverse viable chemistries and allow introduction of a variety of surface functional groups on them, and hence they are pronounced as potential nano-filler materials.36 Several research studies confirm the thermodynamic compatibility of NDs with different polymers37 and Psf,38 in terms of strong mixed-matrix interaction through homogeneous dispersion.
In studies, various polymers were embedded with NDs to observe their effect on mechanical, thermal, tribiological, optical and rheological properties, as well as biocompatibility of polymers. These effects on the properties were identified by their influence on morphology, polymer/ND interface, functionality, and processing conditions. Ayatollahi et al. investigated the mechanical and tribological properties of an epoxy/ND composite.39 Rheological characteristics of PDMS influenced by NDs were reported by Gavrilov and Voznyakovskii.40 Effects of NDs on the thermal properties of crosslinked high density polyethylene were established by Roumeli et al.41 The wear performance of PTFE films was enhanced by incorporation of NDs.42 High refractive index materials were attained by incorporating NDs into polymer matrices.43 Biocompatibility of PLLA/ND-ODA composites was observed by Zhang et al.44 However, radiation resistant properties of a polymer/ND composite have not been explored in the literature.
Radiolysis of water results in the production of highly reactive species, e.g. eaq−, HO˙, H˙, 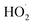 , H2O2, H3O+, OH−, and H2.45 These can react with Psf chains and create defects in the Psf matrix. Carboxyl and hydroxyl groups present on the surface of NDs could interact with these free radicals and protect the Psf matrix from radiation-induced damage caused by the radiolysed products of water. The possible mechanism of interaction of free radicals with carboxyl and hydroxyl groups is given in eqn (1)–(4).
, H2O2, H3O+, OH−, and H2.45 These can react with Psf chains and create defects in the Psf matrix. Carboxyl and hydroxyl groups present on the surface of NDs could interact with these free radicals and protect the Psf matrix from radiation-induced damage caused by the radiolysed products of water. The possible mechanism of interaction of free radicals with carboxyl and hydroxyl groups is given in eqn (1)–(4).
| | 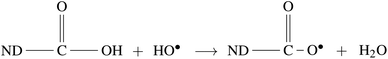 | (1) |
| | | ND–OH + HO˙ → ND–O˙ + H2O | (2) |
| | 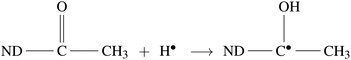 | (3) |
| | | ND−OH + H˙ → ND˙ + H2O | (4) |
In the present work, the unique radiation-resistant properties of NDs have been exploited to develop Psf–ND composite membranes with improved gamma radiation resistant behavior, which can have potential applications in radioactive effluent treatment. To the best of our knowledge, this is the first time such a study on enhancing the radiation stability of a polymeric membrane through composite fabrication is being reported. The findings clearly confirmed that Psf–ND composite membranes with 0.5% ND loading can be operated in a radiation environment up to 500 kGy of gamma dose, compared to Psf membranes that have stability up to 100 kGy.
2 Materials and methods
2.1 Materials
Polysulfone (Psf) was procured from Solvay Specialties India Pvt. Ltd, India. N-methyl-2-pyrrolidone (NMP, ≥99.5% purity) and polyvinyl pyrrolidone (PVP, K-30; molecular weight: 40 kDa) of AR grade were obtained from SRL Pvt. Ltd, India. The nanodiamond powder (ND, particle size <10 nm, assay ≥97%, MW: 12.01 g mol−1, density: 3.5 g mL−1) and polyethylene oxide (PEO, molecular weight: 100 kDa) were purchased from Sigma-Aldrich.
2.2 Fabrication of membranes
Psf–ND composite membranes were fabricated by a phase inversion technique as shown in Fig. 1. To prepare the dope solution, different weight fractions of NDs (0.1-ND, 0.5-ND, 1-ND, and 2-ND wt% of Psf) were taken as filler materials and dispersed separately in 100 mL NMP by sonication in a sonication bath for 30 minutes. Each of these solutions was then mixed with base polymer Psf (25 g) and additive PVP (7.5 g). The mixed dope solutions were stirred continuously for up to 24 h until a homogeneous casting solution was obtained. Psf–ND composite membranes with a thickness of 200 μm were prepared using an automatic flat-sheet table top casting machine at ambient temperature and gelled in de-mineralized water. The control Psf membrane was prepared without addition of NDs.
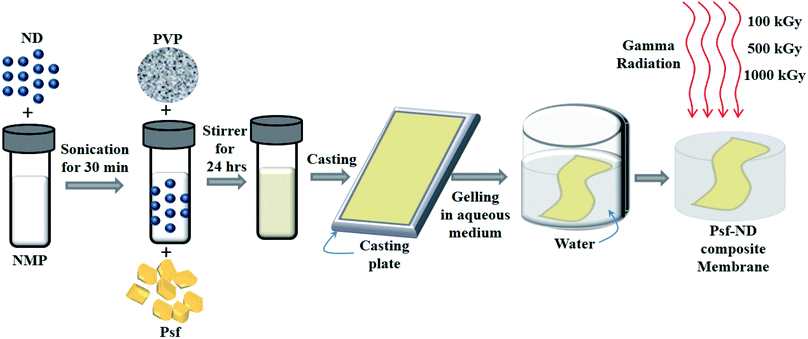 |
| | Fig. 1 Schematic representation of the fabrication of Psf–ND composite membranes by a phase inversion technique. | |
2.3 Irradiation of membranes
Fabricated Psf and Psf–ND composite membranes were exposed to 100 (Psf-100, 0.1-ND-100, 0.5-ND-100, 1-ND-100, and 2-ND-100), 500 (Psf-500, 0.1-ND-500, 0.5-ND-500, 1-ND-500, and 2-ND-500), and 1000 kGy (Psf-1000, 0.1-ND-1000, 0.5-ND-1000, 1-ND-1000, and 2-ND-1000) of radiation using a 60Co source Gamma Chamber GC-5000 (Board of Radiation & Isotope Technology, BRIT, India) with a dose rate of about 1.5 kGy per h (Fricke dosimetry). The individual membranes immersed in de-mineralized water were sealed in the zip-lock polyethylene bags for irradiation.
2.4 Morphological characterization by field emission scanning electron microscopy (FESEM)
The surface and cross-sectional morphology of membranes were observed using a FESEM (AURIGA 4553) at 20 and 5 kV operating voltages, respectively. For this purpose, membranes were made electrically conducting using a sputter coater with a gold–palladium alloy target at a current of 15 mA for 100 seconds.
2.5 Topography analysis by atomic force microscopy (AFM)
The topography of the membrane surface was analyzed using an atomic force microscope (AFM, Model: SOLVER next, NT-MDT, Russia). A small (1 cm2) dry membrane piece was taken for the AFM analysis and pasted onto the metal substrate. The AFM images were acquired in tapping mode with the aid of a silicon cantilever NSG 10 (NT-MDT, Russia) with a spring constant of 11.8 N m−1 and a resonating frequency of 240 kHz. The imaging was carried out at room temperature and ambient pressure, and the surface roughness of these membranes was obtained using NOVA-P9 software. The effect of ND loading and irradiation dose on the surface roughness of the membrane was examined within a scan range 3 μm × 3 μm.
2.6 Water contact angle measurements using a drop shape analyzer
The water contact angle at the membrane surface was measured through a KRUSS Advance drop shape analyzer (DSA100, Germany) under ambient conditions. In order to measure the contact angle, a small membrane piece was placed on the glass slide and water was dropped onto the surface of the membrane. The drop was illuminated from one side and a camera at the opposite side records an image of the drop. The drop image was analyzed using KRUSS Advance software. Contact angles in three different regions for each sample were measured and averaged.
2.7 Functional group characterization by attenuated total reflectance Fourier-transform infrared spectroscopy (ATR-FTIR)
Vibrational spectra of the membranes were observed through an attenuated total reflectance Fourier-transform infrared spectrometer (ATR-FTIR; IR Affinity-1 spectrometer, Shimadzu, Japan) in single reflectance ATR mode. The results were evaluated and substantiated by taking 50 scans with a 4 cm−1 spectral resolution. The surface of the membranes was in contact with the ATR crystal element and a slight pressure was applied using a high pressure clamp (MIRacle) with torque-limited press. The infrared spectrum was recorded in absorbance mode in the range from 400 to 4000 cm−1 at room temperature with a radiation penetration depth of 2 mm.
2.8 Elemental composition determination by X-ray photoelectron spectroscopy (XPS)
X-ray photoelectron spectroscopy (XPS) measurements of the air dried membranes were accomplished using a Mg Kα (1253.6 eV) source and a DESA-150 electron analyzer (Staib Instruments, Germany). The binding-energy scale was calibrated using the Au-4f7/2 line of 84.0 eV. The analyzer was operated at 40 eV pass energy. Pressure in the chamber during analysis was ∼7 × 10−9 Torr. The surface composition (Ci) and the percentage of C, S, and O were calculated by the binding energy value obtained from the XPS spectrum, using eqn (5).46,47| | 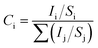 | (5) |
where, i and j are the elements C, S and O. Here Ii is the intensity of the C-1s, S-2p and O-1s peaks determined by the total area under the core level peak (by least-squares fitting of the Gaussian curve). Si represents the atomic sensitivity factor with values 0.296, 0.666 and 0.711 for C-1s, S-2p and O-1s peaks, respectively.
2.9 Average molecular weight determination by gel permeation chromatography (GPC)
The average molecular weight of the membrane samples was determined using a GPC system (Malvern 270 dual detector, UK) equipped with a refractive index detector and a light scattering detector (λ = 670 nm, consisting of two scattering angles: 7° and 90°) along with T6000M, a general mixed organic column (300 × 8 mm) (Viscotek, Malvern, UK). The detector and column were kept at a temperature of 22 °C. The mobile phase consisted of tetrahydrofuran (SD Fine Chemicals Ltd., India) at a flow rate of 0.5 mL min−1. The samples were filtered through a PTFE syringe filter with a 0.22 μm pore size and a 25 mm diameter (Axiva Sichem Biotech, India). The sample volume injected was 100 μL. Both detectors were calibrated with polystyrene standards having a narrow molecular-weight distribution. Data were analyzed using Viscotek OmniSEC 5.12 software.
2.10 Free volume estimation by positron annihilation lifetime spectroscopy (PALS)
Positron annihilation lifetime (PAL) of membranes was determined at room temperature using two scintillation detectors (BaF2) connected to a fast–fast coincidence system. 22Na (∼10 μCi) wrapped in thin Kapton foil (∼8 μm thick) was used as the positron source which was sandwiched between stacks of polymer films. The source-sample assembly was kept between two BaF2 detectors. The time resolution of the spectrometer measured with a 60Co prompt gamma source in 22Na window setting was 250 ps. The time calibration was fixed at 25 ps per channel. The spectrum with approximately 5 × 106 counts was acquired for each measurement. The positron lifetime histogram is a multi-exponential decay curve as shown in eqn (6).| | 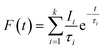 | (6) |
Here, F(t) is the number of counts at time t, k represents the number of exponential decays, τi and Ii are the corresponding lifetime and intensity of the ith component, respectively. The lifetime spectra were fitted to four discrete components with minimum χ2 using the PALSfit analysis program.48
The third lifetime component within the range of 1.8–1.9 ns corresponds to spin-triplet ortho-positronium (o-Ps) pick-off annihilation with an electron from the inner surface of the free volume. The fourth component with lifetime in the range of 10–30 ns corresponds to o-Ps annihilation in the intergranular region. The intensity of the third lifetime component is within the range of 14–17%, whereas the intensity of the fourth component is very small (<0.6%). So we will not consider this fourth component for further discussion. The third lifetime component was converted into the average radius (R) of the spherical free volume using the following empirical relation from the well-known Tao-Eldrup model (eqn (7)).49,50
| | 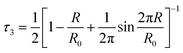 | (7) |
Here,
τ3 is the third lifetime component and
R0 = R + 0.166 nm. The relative fractional free volume (
f) was calculated by
eqn (8).
| | 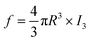 | (8) |
Here,
τ3 is the relative intensity (in %) of the third lifetime component (
τ3).
2.11 Membrane molecular structure interpretation by small angle X-ray scattering (SAXS)
SAXS experiments were performed using a laboratory-based SAXS instrument with Cu Kα (λ = 1.54 Å) as probing radiation. Radial averaged scattering intensity (I(q)) was obtained within a wave vector transfer (q = 4π![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(θ)/λ, where λ is the wavelength and 2θ is the scattering angle) range from ∼0.1 to 2.5 nm−1. The sample to detector distance was nearly 1 m. It was found that three cumulative power law scattering contributions could explain fairly well the scattering profile of the Psf membrane. Thus, for the Psf membrane, the model of eqn (9) was used.
sin(θ)/λ, where λ is the wavelength and 2θ is the scattering angle) range from ∼0.1 to 2.5 nm−1. The sample to detector distance was nearly 1 m. It was found that three cumulative power law scattering contributions could explain fairly well the scattering profile of the Psf membrane. Thus, for the Psf membrane, the model of eqn (9) was used.| | | IPsf(q) = C1q−k + C2q−m + C3q−n + C4 | (9) |
Here C1, C2, C3, and C4 are q independent constant parameters, and were estimated by fitting this model to the scattering data using a non-linear least squares method. The scattering data from the ND impregnated membranes were analyzed by adding an extra scattering term as shown in eqn (10) and (11).| | | Itotal(q) = IPsf(q) + IND(q) | (10) |
| | 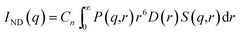 | (11) |
Here, P(q,r) represents the form factor of a spherical particle of radius r. D(r) is the particle size distribution and S(q,r) represents the structural factor of the particles. A fractal like structural factor51 was considered for the present data. D(r) was estimated from the scattering profile of the ND powder. Cn is a q-independent constant and is proportional to the product of the number density of the particle and the respective scattering contrast. The particle size distribution of the NDs was calculated from the virgin ND powder (Fig. S-VI†), and the same size distribution was used during the fitting of the SAXS curve for Psf–ND composite membranes.
2.12 Evaluation of the mechanical properties using a universal testing machine (UTM)
A universal testing machine (UTM, Hemetek Techno Instrument, model LRX Plus, India) was used to measure the mechanical properties of the membranes at room temperature and 40–50% relative humidity. Dumbbell shaped specimens of the membranes each of 5 cm length and 0.6 cm width were prepared for analysis. During the analysis, a constant deformation rate of 100 mm min−1 was applied. The NEXYGEN plus software was used to calculate tensile strength (TS) and percent elongation at maximum force for the membrane.
2.13 Permeability measurement of the membranes
The pure water permeability measurements of the membranes were carried out in an ultrafiltration test skid (cross-sectional area A = 14.5 cm2) at room temperature and 1 bar trans-membrane pressure. Steady state pure water permeability (PWP) was determined by the measurement of permeate flow in terms of liters per square meter per hour (LMH). The PWP (LMH) through the membrane area A (m2) was measured by the volume V (L) collected during a time period T (h) and illustrated using eqn (12).| | 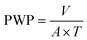 | (12) |
To achieve stabilized performance, membranes were initially placed for compaction for 1 hour in water under standard ultrafiltration test conditions.
2.14 Solute rejection study of the membranes
The membrane samples were placed in an ultrafiltration test skid for cross-flow permeation measurement, with an effective membrane area of 14.5 cm2. Polyethylene oxide (PEO, molecular weight: 100 kDa) was used as a solute for the measurement. The PEO solution (200 ppm) was prepared in distilled water by dissolving pre-weighed amounts of PEO. Solute rejection studies were carried out at room temperature and 1 bar transmembrane pressure. The concentration of PEO was determined by measuring the total organic carbon (TOC) content of the samples (in both feed and product) using a TOC analyzer (ANATOC, SGE Analytical Science, Australia). The rejection of PEO (R) was calculated using eqn (13).| | 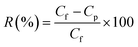 | (13) |
Here, Cf is the concentration in the feed and Cp is the concentration in the permeate side.
2.15 Monte Carlo simulation studies for life-cycle assessment of membranes
The dose absorbed by the membranes in the intermediate level radioactive waste environment was calculated using Monte Carlo simulations. The Monte Carlo method involves actual mathematical simulations of transport of particles through the medium using random sampling techniques with the help of high speed computers. This method is considered to be the most accurate method of solving radiation transport problems, which takes care of the complicated and heterogeneous geometries and source emission. The various information such as the energy imparted, fluence, and energy distribution of the radiation can be scored during the transport. A validated Fluka (FLUKA2011.2x-3)52,53 code was used for this purpose. The FLUKA code can simulate the propagation and interaction of photons of energies from 1 keV to thousands of TeV in very complex geometries, modeled using the Combinatorial Geometry (CG) package.
A Psf membrane of a cross sectional area of 1 m2 with a thickness of 150 μm and a density of 1.02 g cm−3 was dipped in a radioactive effluent cylindrical column. The modeled geometry is shown in Fig. 2. As a close approximation to the reality, it is assumed that the radioactive effluent contains 50% of Cs-137 and Sr/Y-90 radionuclides each. The emission particulars of these radionuclides are shown in Table 1. The length of the effluent column used for simulations is 100 cm and 2 cm for gamma and beta radiation, respectively. The beta spectrum used for calculations is taken from the RAdiation Dose Assessment Resource (RADAR). The energy absorbed by the membrane was scored when the radiation was emitted uniformly from the cylindrical volume of effluent isotropically. The dose absorbed by the membrane enclosed by the liquid radioactive effluent is obtained using USRBIN region based scoring.
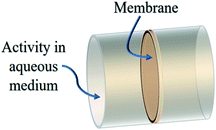 |
| | Fig. 2 Monte Carlo simulated geometry for membrane performance in the liquid radioactive waste environment. | |
Table 1 The energy emission from radionuclides
| Radionuclide |
Emission |
Energy (MeV) |
Yield% |
| Cs-137 |
Gamma |
0.662 |
85.1 |
| Sr/Y-90 |
Beta |
0.546 (max) |
100 |
|
|
Beta |
2.284 (max) |
100 |
3 Results and discussion
3.1 Membrane surface morphology and topography studies
Surface and cross-sectional morphology of the membranes, as observed using a FESEM, is shown in Fig. 3 and 4, respectively, for different ND concentrations and irradiation doses. The top surface morphology of the control Psf and the Psf–ND composite membranes is indistinguishable, except for the presence of NDs on the composite systems, as shown in Fig. 3. The ND particles are homogeneously distributed on the composite membrane surface. However, with increased loading of NDs, the proportion of ND particles has increased on the top surface of the membrane, leading to agglomeration at 1% ND loading (Fig. 3(c), (f) and (i)). The fingering has been observed in all the membranes, as clearly seen in Fig. 4, which is a characteristic of membranes synthesized by a nonsolvent-induced phase inversion technique.54 The cross-sectional images of the composite membranes show the presence of NDs in the bulk of the membrane matrix, offering mechanical strength to the membrane,55 as discussed later in Section 3.4 of the mechanical properties of the membranes. The FESEM images (insets of Fig. 4(a)–(c)) reveal that an increase in ND loading results in a decrease in pore density and an increase in the pore size. This can be explained by the delay in exchange between the solvent and water during phase inversion due to the increased viscosity of dope solution by added ND nanoparticles.56 With radiation exposure, different phenomena like pore closure, pore merger and pore splitting57 are observed because of cross linking and chain scissioning,58 as shown in Fig. 4. With an increase in the radiation dose, the Psf membranes showed significant pore closure, leading to a reduction in pore density, as shown in Fig. 4(a), (d) and (g). However, on exposure to radiation, for the composite membranes, 0.5-ND and 1-ND, pore splitting and pore merger phenomena occur statistically, but simultaneously, leading to an overall reduction in pore density of membranes, as shown in Fig. 4(e), (f) and (i). A similar finding has been observed in SAXS studies as shown in Fig. 11. The reduced pore density of composite membranes resulted in reduced permeability, as discussed later (Fig. 13). Interestingly, membrane 0.5-ND shows comparatively less changes with radiation in porosity. The SEM studies clearly indicate that the presence of NDs has got a profound positive implication on the structure and morphology of the composite membranes, and the effects are more pronounced in the presence of gamma radiation.
 |
| | Fig. 3 SEM images of the top surface of the membranes with and without NDs: (a–c) unirradiated (UR) membranes, (a) Psf, (b) 0.5-ND, and (c) 1-ND; (d–f) exposure to a 500 kGy radiation dose, (d) Psf-500, (e) 0.5-ND-500, and (f) 1-ND-500; (g–i) exposure to a 1000 kGy radiation dose, (g) Psf-1000, (h) 0.5-ND-1000, and (i) 1-ND-1000. | |
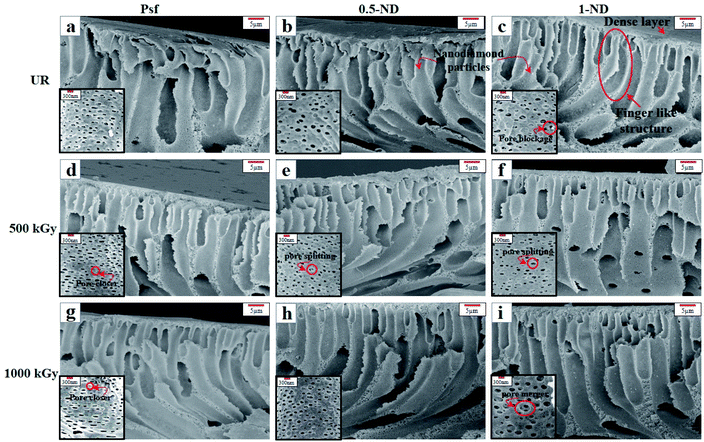 |
| | Fig. 4 SEM images of the cross-section of the membrane with and without NDs: (a–c) unirradiated (UR) membranes, (a) Psf, (b) 0.5-ND, and (c) 1-ND; (d–f) exposure to a 500 kGy radiation dose, (d) Psf-500, (e) 0.5-ND-500, and (f) 1-ND-500; (g–i) exposure to a 1000 kGy radiation dose, (g) Psf-1000, (h) 0.5-ND, and (i) 1-ND-1000. Inset in the images shows the pores in the respective membranes. | |
The root mean square (RMS) roughness of the membranes, obtained from AFM studies, is shown in Fig. 5. The RMS roughness of the control Psf membrane was found to be 2.02 nm. The surface roughness increases with the ND loading and a RMS roughness value of 3.20 nm was obtained for 2% loading. This is due to interfacial defects created between the NDs and the Psf matrix (as observed by PALS analysis shown in Fig. 10). The surface roughness of membranes increases with radiation dose due to deterioration of the membrane structure, which results in a rough topography. Psf membranes undergo chain scissioning and crosslinking phenomena, which increase the surface roughness even at a 100 kGy radiation dose. For Psf–ND composite membranes, the change in roughness is not significant up to a radiation dose of 100 kGy, while an appreciable change was observed for radiation doses of 500 and 1000 kGy, which leads to an increase in surface roughness up to 4.6 nm (2-ND-500) and 5.2 nm (2-ND-1000). Up to a radiation dose of 100 kGy, the presence of NDs prevents the Psf membrane matrix from the effect of gamma-radiation. On the other hand, beyond a 500 kGy radiation dose the chain scissioning and crosslinking phenomena deteriorate the Psf membrane matrix, as evident from the surface roughness values (maximum of 76.2% increase for 0.5-ND-1000). These findings indicate that least deterioration of the membrane structure has occurred at 2% loading, with 60.3% increase in the roughness value (2-ND-1000). The chain scissioning and cross-linking phenomena of the polymer (polysulfone) chains lead to the creation of defects (which is statistical in nature) in the host membrane matrix, which is related to the decomposition of the Psf backbone. With an increase in the radiation dose, the extent of decomposition of the polymer backbone, and in turn the defects in the membrane matrix, increases, which is reflected in the increase in surface roughness values of the membrane surface. The AFM results demonstrate that the control Psf membrane surface starts deteriorating even at a 100 kGy radiation dose, while Psf–ND composite membranes showed significant changes in surface roughness only after a 500 kGy radiation dose.
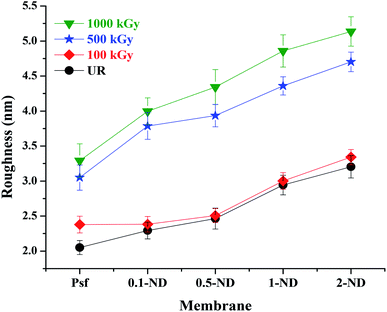 |
| | Fig. 5 Variations of RMS roughness of membranes at different loadings of NDs and radiation dose. | |
3.2 Physico-chemical properties of the membranes
The water contact angle studies were carried out to determine the hydrophilicity/hydrophobicity of membranes, as shown in Fig. 6. The water contact angle of the control Psf membrane was found to be 80°, which decreases with loadings of NDs (74.2° for 0.1-ND and 70.2° for 0.5-ND) because of the enhanced surface hydrophilicity due to the presence of hydrophilic (hydroxyl and carboxyl) groups of NDs (observed in the FTIR spectra shown in Fig. 7).59 However, beyond 0.5% loading, the contact angle increases (75.4° for 1-ND and 76.1° for 2-ND), which could be the result of less physical interaction of NDs with the Psf matrix due to aggregation. The contact angle values of the membranes irradiated up to 1000 kGy remained almost similar, and in line with the trend observed for the unirradiated (UR) membranes, with the 2% loaded one being the exception. At a 100 kGy radiation dose, a significant change of the contact angle has been observed only in the case of the control Psf membrane due to enhancement of hydrophilicity because of the increase in surface roughness (as reflected in the surface roughness values, Fig. 5). At a 500 kGy radiation dose the contact angle decreases, which is due to pore splitting, increasing the pore density and thus the hydrophilicity. Almost similar values of contact angles, 72°, 71.2°, and 76.2°, in the cases of 0.1-ND-1000, 0.5-ND-1000, and 1-ND-1000 membranes, respectively, with their unirradiated counterparts (70.2° and 75.4°), is one important observation to be made here. However, the dip in the contact angle values of the irradiated membranes at 2% ND loading is due to the agglomeration of NDs at a high concentration. The less interaction between NDs and the polymer at 2% loading could be responsible for having a similar trend in the contact angle values of 2-ND membranes to that of the control Psf membrane.
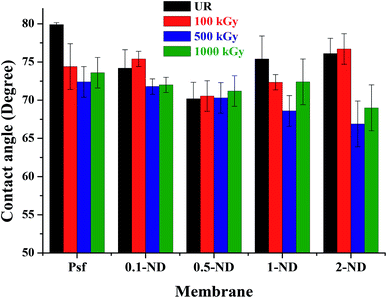 |
| | Fig. 6 Variation of the water contact angle at the membrane surface with the loading of NDs in the membrane matrix, before and after irradiation. | |
 |
| | Fig. 7 ATR-FTIR spectrum of the unirradiated control Psf and Psf–ND composite membranes. | |
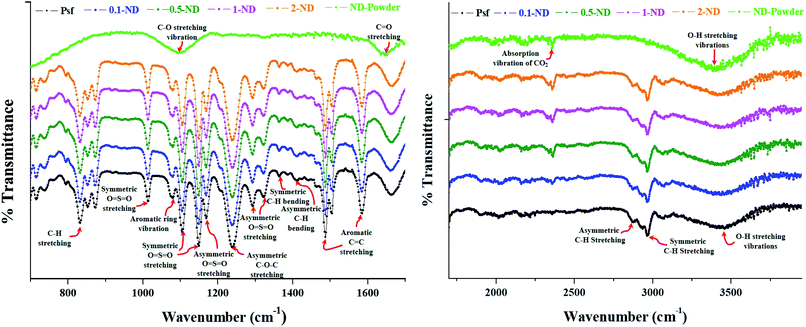
The ATR-FTIR spectra, as shown in Fig. 7, exhibit a significant absorption band around 834 cm−1 (C–H stretching of the aromatic ring of Psf), 1014 cm−1 (symmetric O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S
S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching of the sulfone group), 1080 and 1105 cm−1 (aromatic ring vibrations), 1149 cm−1 (symmetric O
O stretching of the sulfone group), 1080 and 1105 cm−1 (aromatic ring vibrations), 1149 cm−1 (symmetric O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S
S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching of the sulfone group), 1168 cm−1 (asymmetric O
O stretching of the sulfone group), 1168 cm−1 (asymmetric O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S
S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching of the sulfone group), 1238 cm−1 (asymmetric C–O–C stretching of the aryl ether group), 1293 and 1322 cm−1 (asymmetric O
O stretching of the sulfone group), 1238 cm−1 (asymmetric C–O–C stretching of the aryl ether group), 1293 and 1322 cm−1 (asymmetric O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S
S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching of the sulfone group), 1364 cm−1 (symmetric C–H bending deformation of the methyl group), 1411 cm−1 (asymmetric C–H bending deformation of the methyl group), 1487 and 1586 cm−1 (aromatic C
O stretching of the sulfone group), 1364 cm−1 (symmetric C–H bending deformation of the methyl group), 1411 cm−1 (asymmetric C–H bending deformation of the methyl group), 1487 and 1586 cm−1 (aromatic C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching), 2873 and 2968 cm−1 (asymmetric and symmetric C–H stretching vibrations include the complete methyl group), and 3440 cm−1 (O–H stretching vibrations). The FTIR spectra of the pure ND powder show major absorption bands around 3410 cm−1 (O–H stretching vibrations), 2359 cm−1 (absorption vibrations of CO2), 1647 cm−1 (C
C stretching), 2873 and 2968 cm−1 (asymmetric and symmetric C–H stretching vibrations include the complete methyl group), and 3440 cm−1 (O–H stretching vibrations). The FTIR spectra of the pure ND powder show major absorption bands around 3410 cm−1 (O–H stretching vibrations), 2359 cm−1 (absorption vibrations of CO2), 1647 cm−1 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching of the carboxyl groups), and 1100 cm−1 (C–O stretching vibrations of the –COOH groups). This validates the presence of carboxyl and hydroxyl functional groups on the surface of NDs. The hydroxyl and carboxyl groups present over NDs are responsible for scavenging the secondary free radicals generated during radiolysis of water, which in turn protects the composite membranes leading to an enhanced life-span in a radioactive environment. This finding has also been corroborated with our in-house data for radiation stability of composite membranes with carboxyl-functionalised NDs (being considered for publication elsewhere). No shift in the characteristic absorption bands of Psf–ND composite membranes indicates the fact that impregnation of NDs in the control Psf matrix does not affect the internal molecular structure of membranes. The characteristic band of NDs at 2359 cm−1 shows the physical presence of NDs, whose intensity increases with loading of NDs, as seen in Fig. 7.
O stretching of the carboxyl groups), and 1100 cm−1 (C–O stretching vibrations of the –COOH groups). This validates the presence of carboxyl and hydroxyl functional groups on the surface of NDs. The hydroxyl and carboxyl groups present over NDs are responsible for scavenging the secondary free radicals generated during radiolysis of water, which in turn protects the composite membranes leading to an enhanced life-span in a radioactive environment. This finding has also been corroborated with our in-house data for radiation stability of composite membranes with carboxyl-functionalised NDs (being considered for publication elsewhere). No shift in the characteristic absorption bands of Psf–ND composite membranes indicates the fact that impregnation of NDs in the control Psf matrix does not affect the internal molecular structure of membranes. The characteristic band of NDs at 2359 cm−1 shows the physical presence of NDs, whose intensity increases with loading of NDs, as seen in Fig. 7.
The XPS spectra of the C-1s peak of the membranes, as shown in Fig. 8, exhibit a binding energy peak for the C–C bond around 284.9 eV, for the C–OH bond around 286.3 eV, and for the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond around 287.5 eV. The XPS spectra of S-2p and O-1s peaks of the membranes are shown in Fig. S-II and S-III,† respectively. No shift in the XPS peaks of the bonds confirms that there is no chemical interaction between the NDs and Psf, even at an increased loading of NDs, indicating only physical entrapment of nanomaterials in the membrane matrix. The absence of additional peaks in the membrane samples exposed to gamma irradiation confirms no adduct formation with irradiation (Fig. S-IV†).
O bond around 287.5 eV. The XPS spectra of S-2p and O-1s peaks of the membranes are shown in Fig. S-II and S-III,† respectively. No shift in the XPS peaks of the bonds confirms that there is no chemical interaction between the NDs and Psf, even at an increased loading of NDs, indicating only physical entrapment of nanomaterials in the membrane matrix. The absence of additional peaks in the membrane samples exposed to gamma irradiation confirms no adduct formation with irradiation (Fig. S-IV†).
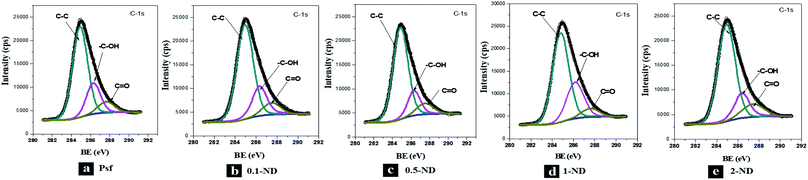 |
| | Fig. 8 XPS spectra of the unirradiated membranes: (a) Psf, (b) 0.1-ND, (c) 0.5-ND, (d) 1-ND, and (e) 2-ND. | |
As seen in Table 2, the atom ratio of carbon to sulfur (C/S) was found to be increasing with the loading of NDs, owing to the increase in the concentration of carbon resulting from ND addition. Also, the ratio of C/S was found to be increasing with radiation dose for both the control Psf and the composite membranes, which is mainly attributable to the elimination of the sulfone group with irradiation due to chain scissioning.18,54 It is interesting to see that the increase in the C/S ratio from 20.9 for 0.5-ND to 26.5 for 0.5-ND-1000 was minimal in the case of a membrane with 0.5% loading of NDs, indicating this membrane to be the most radiation resistant amongst all the composites. The results indicate that a better interaction of the polymeric chain with the NDs exists at an optimum loading of NDs, which is 0.5%. At loadings lower than 0.5, the concentration of NDs in the polymeric host matrix is not reasonable enough to bring about the significant interfacial interactions, whereas, at loadings beyond 0.5% (that is for 1-ND & 2-ND membranes), the agglomeration of NDs and interfacial defects lead to a reduced interaction between the inter- and intra-polymeric chains.
Table 2 The carbon to sulfur atom ratio (C/S) obtained from XPS: for different concentrations of NDs in the membrane at different doses of gamma radiation
| C/S |
| Radiation dose |
Psf |
0.1-ND |
0.5-ND |
1-ND |
2-ND |
| UR |
20.6 |
20.7 |
20.9 |
22.7 |
25.3 |
| 100 kGy |
21.1 |
21.4 |
21.2 |
28.7 |
30.9 |
| 500 kGy |
29.1 |
23.4 |
21.4 |
35.5 |
43.2 |
| 1000 kGy |
38.8 |
47.6 |
26.5 |
42.1 |
53.4 |
The weighted average molecular weight (Mw) values of the un(irradiated) Psf and composite membranes are shown in Fig. 9. At a gamma radiation dose of 100 kGy, there is no significant change observed in terms of Mw, as compared to their unirradiated counterparts. At a 500 kGy irradiation dose, Mw decreased by 25.6, 2.6 and 16.7% for Psf-500, 0.1-ND-500 and 2-ND-500 membranes, respectively, compared to their unirradiated counterparts. This is because the chain-scission of the Psf chain dominates, which leads to a reduction in the molecular weight.17,60 The 0.5-ND-500 and 1-ND-500 membranes show a negligible increase (i.e., 1.4 and 8.1%, respectively) compared to their unirradiated counterparts, might be due to the dominant crosslinking of Psf chains. The extent of change in Mw of 0.1-ND, 0.5-ND, and 1-ND membranes is much less up to a 500 kGy radiation dose, compared to their unirradiated counterparts. This reveals the least effect of chain scissioning in the case of 0.5-ND and 1-ND membranes. It is important to note that the polydispersity index (PI is the ratio of the weighted average to the number average molecular weight of a polymer) of the unirradiated membranes (control Psf and composite membranes) is found in the range of 2 to 2.5. After a 1000 kGy of radiation dose, the PI for Psf membranes reached ∼3.8, while it varied in the range of 2.3 to 3.1 for the Psf–ND composite membranes, with an optimum value of ∼2.3 for the 0.5-ND membrane. Higher PI values for the Psf membrane indicate the pronounced effect of chain scissioning in the control matrix at a 1000 kGy of radiation dose, while the stability of the Psf–ND composite membranes is restored in the radiation environment.
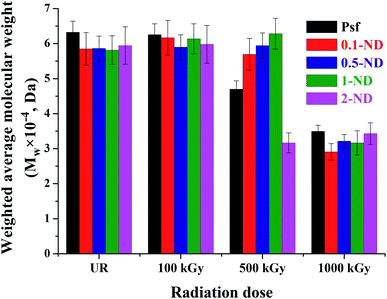 |
| | Fig. 9 Weighted average molecular weight obtained from gel permeation chromatography of the membranes: with the variation of ND loading and radiation dose. | |
3.3 Internal structure of the membrane matrix
The free volume in the membrane matrix was investigated with the help of positron annihilation lifetime spectroscopy (PALS)61 and the results are shown in Fig. 10. There is an increase from 960 (Psf) to 1270 (0.1-ND) in the relative fractional free volume after impregnation of NDs in the membrane matrix. This is due to the formation of an interfacial free volume at the interface on nanodiamond particles and the polymer matrix in the composite membranes.62 The interfacial free volume initially increases with the ND loading (up to 1373 for the 0.5-ND membrane), due to an increase in the number density of particles. However, a further increase in the ND loading (beyond 0.5%) leads to agglomeration of the ND particles resulting in the reduction of the overall interfacial free volume, and hence a reduction in the relative fractional free volume (1254 and 1158 for 1-ND and 2-ND membranes, respectively). On exposure to radiation up to 1000 kGy, there is an increase in the relative fractional free volume by 35.2, 8, 8.9, 8.2, and 9.3% for Psf-1000, 0.1-ND-1000, 0.5-ND-1000, 1-ND-1000, and 2-ND-1000 membranes, respectively, due to the defects created in the membrane matrix as a result of structural rearrangement of polymer chains. The extent of change in the relative fractional free volume is less in the case of ND impregnated membranes as compared to that of Psf membranes. Hence, Psf–ND composite membranes are structurally more radiation resistant at all reported loadings.
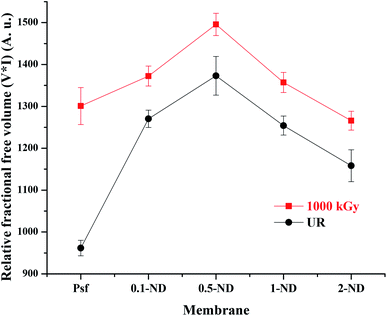 |
| | Fig. 10 Variation of the relative fractional free volume with loading of NDs in the membrane matrix and radiation dose obtained from PALS. | |
Structural evolution as probed by small angle X-ray scattering (SAXS) analysis is shown in Fig. 11. The increased relative number density with an increase in the ND loading confirms an even distribution of the NDs in the membrane matrix. On the other hand, the relative scattering contrast is found to be decreasing with the radiation dose, which is due to the reduction in pore density. This is because of the pore-closure and pore merger phenomenon, as observed in SEM images (inset of Fig. 4). The value of relative “number density × contrast” has been calculated by taking Psf membranes as a reference. After irradiation, the variation in relative contrast increases with increasing ND loading with respect to Psf membranes. This indicates that after irradiation the reduction in pore density is more pronounced at higher loadings of NDs.
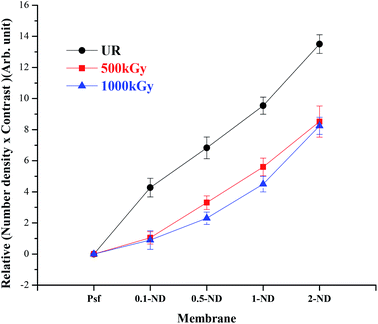 |
| | Fig. 11 Variation of relative “number density × contrast” of the membrane matrix obtained from SAXS with the loading of NDs at different radiation doses. | |
3.4 Mechanical properties of the membrane
The UTM analysis (Fig. 12(a)) shows that the tensile strength of the Psf membrane is 3.07 MPa, which remained almost the same (3.11 MPa) after impregnating 0.1% ND (0.1-ND). A further increase in ND loading up to 0.5% reduced the tensile strength to 2.88 MPa, as the hard ND is expected to introduce rigidity between the polymer chains. A further increase in the concentration of NDs in the composite membrane enhances its tensile strength to 3.25 and 3.36 MPa for 1-ND and 2-ND membranes, respectively, which may be due to the reduced physical interaction between the NDs and polymeric chains at higher loadings, owing to the agglomeration.63 The percentage elongation at maximum force of the unirradiated membranes decreases from 14.2 (for Psf membranes) to 13, 9.1, and 12.7% for 0.1-ND, 0.5-ND, and 1-ND membranes, respectively (Fig. 12(b)), owing to the impregnation of nanomaterials onto the porous polymeric host matrix, which in turn reduces the ductility of the membranes. The lowest percentage elongation for the 0.5-ND membrane is due to the rigidity introduced by the NDs in remaining homogeneously distributed in the membrane matrix up to a loading of 0.5%. However, with further loading beyond 0.5%, the agglomeration of ND particles essentially nullifies the effect of ND impregnation on the Psf host matrix, leading to an increase in the percentage elongation. These findings are well in agreement with the distribution of ND particles in the polymer host matrix, as observed in SAXS studies (Fig. 10). No significant changes were observed in tensile strength and percentage elongation upto a 100 kGy radiation dose.
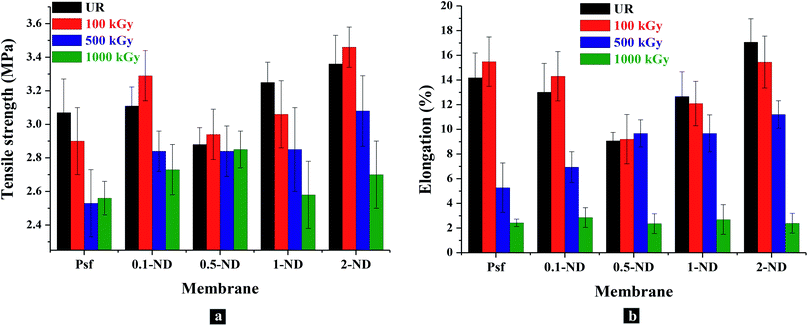 |
| | Fig. 12 Mechanical properties of membranes with the loading of NDs in the membrane matrix and gamma radiation dose: (a) variations in the tensile strength with loading of NDs into the membrane matrix and radiation dose; (b) changes in the percentage elongation at break of the membranes at maximum force with the loading of NDs and the radiation dose. | |
Further irradiation of the membranes leads to the degradation in terms of chain scissioning of polymer chains and hence a reduction in the tensile strength. At 500 kGy irradiation, membranes show 17.5, 9, 1.4, 12.6, and 6.7% reduction in tensile strength for Psf-500, 0.1-ND-500, 0.5-ND-500, 1-ND-500, & 2-ND-500 ND loaded membranes, compared to their unirradiated counterparts. Interestingly, a negligible change in tensile strength (1.4%) confirms the stability of the 0.5-ND membrane up to 500 kGy of radiation dose, which indicates that a 0.5% loading of NDs is capable of protecting the Psf host matrix from extensive chain scissioning, while being responsible for scavenging of the radiolysed products (free radicals) of water. This is also corroborated in GPC studies (Fig. 9). Furthermore, at 1000 kGy irradiation, the Psf membrane (Psf-1000) shows 16.6% reduction in tensile strength as compared to the unirradiated membrane (Psf). The membranes impregnated with NDs show 12.2, 0.7%, 20.9%, and 18.2% reduction in tensile strength at 1000 kGy for 0.1-ND-1000, 0.5-ND-1000, 1-ND-1000 and 2-ND-1000 membranes, respectively, compared to their unirradiated counterparts. This shows that the membrane with 0.5% loading of NDs restores its mechanical properties even after exposed to 1000 kGy radiation.
The percentage elongation at maximum force decreases with a higher radiation dose,64 as the chain scissioning of polymer reduces the ductility of the membranes. At 500 kGy irradiation, a reduction in percentage elongation by 62.8, 46.7, 23.6, and 34.3% was observed for Psf-500, 0.1-ND-500, 1-ND-500 and 2-ND-500 membranes, respectively, compared to their unirradiated counterparts. However, the membrane with 0.5% loading has not shown any significant change. This confirms that the Psf–ND composite membranes are stable up to 500 kGy of radiation dose, compared to Psf membranes, with the 0.5-ND membrane being the most stable composite membrane (a similar trend has been observed for tensile strength). Further irradiation up to 1000 kGy shows a significant reduction in the percentage elongation by 83%, 78%, 74%, 78.8%, and 86% for Psf-1000, 0.1-ND-1000, 0.5-ND-1000, 1-ND-1000 and 2-ND-1000 membranes, respectively, compared to their unirradiated counterparts. Thus, ductility of the membranes is lost and they become brittle at an irradiation dose of 1000 kGy, making the membranes unusable.
3.5 Performance study of the membranes
The permeability offered by the composite membranes shows around 32, 38.5, 44.9 and 61.5% enhancement with the 0.1, 0.5, 1, and 2% impregnation of NDs, respectively, in the Psf matrix, compared to the control Psf membrane, as shown in Fig. 13(a). The increase in permeability is attributed to the increase in surface hydrophilicity due to the presence of hydroxyl functional groups of NDs (as verified by water contact angle Fig. 6). As membranes were exposed to gamma radiation, simultaneous chain scissioning and cross linking events take place in the polymer chains. As a result, the internal structure of the membrane gets altered leading to pore closure, pore merger, pore splitting, creation of defects, etc. When membranes were exposed to 100 kGy of gamma radiation, Psf–ND composite membranes did not show any observable changes in permeability, while a slight reduction (9%) in permeability has been observed for the control Psf membrane. This is attributed to the reduction of free volume (pore closure, reduction in pore density) within the polymer matrix. At 500 kGy of radiation dose, a further reduction in pore density and porosity decreases the permeabilty, as a result of radiation dose (as verified by the SAXS results in Fig. 11). The reduction in permeability of membranes exposed to up to a 1000 kGy radiation dose is due to excessive pore closure, as evident in the FESEM images (Fig. 4) and SAXS analysis (Fig. 11). Permeability of the control Psf membrane reduces by 23% on exposure to 1000 kGy of radiation dose (Psf-1000). At 1000 kGy, the changes in permeability of Psf–ND composite membranes are 41.7, 31.4, 41.6, and 42.8% for 0.1-ND-1000, 0.5-ND-1000, 1-ND-1000 and 2-ND-1000 membranes, respectively, compared to their unirradiated counterparts. The trend of permeability with radiation dose indicates that the 0.5-ND membrane is the most stable one in terms of restoration of performance subsequent to radiation exposure.
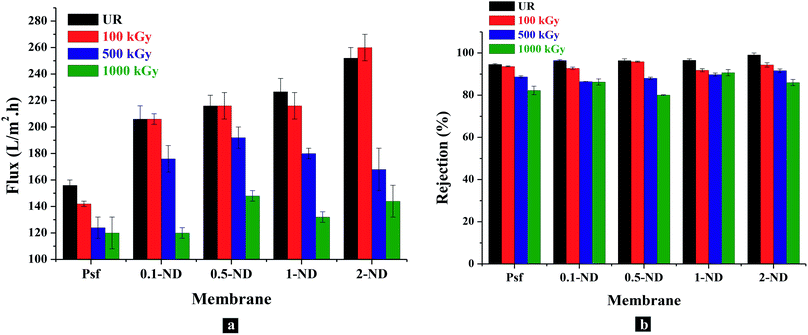 |
| | Fig. 13 Performance of the control Psf and Psf–ND composite membranes with loading of NDs and radiation dose: (a) permeability of membranes in terms of the flux of water through membranes (LMH), (b) rejection of polyethylene oxide (PEO, molecular weight 100 KDa) by the membranes. | |
The solute rejection attributes of the Psf–ND composite membranes remain unaffected with ND loading, with PEO (Mw = 100 kDa) rejection in the range of 94.63% (for Psf membranes) to 99.11% (for 2% ND loaded membranes), as shown in Fig. 13(b). This indicates the absence of defects in the composite membranes because of ND impregnation. The rejection rate increases from 94.63 to 96.5% with increasing loading of NDs (from 0.1 to 1%). Further higher loading of NDs (2-ND membrane) contributes to a higher rejection of up to 99.11%, which is due to blockage of the pores. Membranes exposed to 100 kGy of radiation do not show much variation in terms of the rejection rate which varies from 92–94%. For membranes irradiated up to 1000 kGy, the solute rejection was found to be 82, 86.2, 80, 90.7 and 80% for Psf-1000, 0.1-ND-1000, 0.5-ND-1000, 1-ND-1000 and 2-ND-1000 membranes, respectively. Considering the permeability and solute rejection capability, the 0.5–1% ND impregnated membranes were found to be promising.
3.6 Life-span analysis of membranes using Monte Carlo simulation studies
An intermediate level liquid radioactive waste (ILLRW) stream has a maximum activity of 1 Ci L−1.65 The radiation dose rate offered by this stream, as determined by Monte Carlo simulation, was found to be 115.4 Gy per h. From our studies, the Psf membranes were found to be stable up to 100 kGy. Whereas, all the Psf–ND composite membranes were established to be stable up to 500 kGy, with the 0.5-ND membrane being the most stable one. The dose rate obtained from Monte Carlo simulation studies was used to calculate the life span of the membranes in an actual ILLRW environment. It was found that, to absorb a radiation dose of 500 kGy, a Psf–ND composite membrane would take 3 years and 8 months. Thus, the 0.5-ND membrane can be operated for about 3 years and 8 months. On the other hand, a Psf membrane, which is claimed to be stable up to 100 kGy, shall deteriorate in about 9 months. Thus, the Psf–ND composite membrane with an optimum loading of 0.5% ND is a radiation resistant membrane material, which can extend the application of polymeric membranes in the radioactive domain.
4 Conclusions
Gamma radiation resistant Psf–ND composite membranes were developed, with 0.5% loading of NDs as optimum. These membranes were found to be stable up to a radiation dose of 500 kGy, without compromise in the performance and in the mechanical and structural properties of the membranes. The radiation resistance properties of the composite membranes were attributed to the unique surface chemistry of NDs, having hydroxyl and carboxyl groups over them, which are responsible for ensuring homogeneous and enhanced interaction of the nanomaterials with the Psf host matrix. Interestingly, these groups play a pivotal role in protecting the polymer backbone from disintegration by scavenging the secondary free radicals generated in situ in gamma-induced radiolysis, as confirmed in the pulse radiolysis studies (ESI Section S4†). This is in addition to the most important feature of the NDs, that is the hardness, which brings in further stability to the composite in acting as a potential barrier to the gamma radiation. The Monte Carlo simulation studies coupled with the experimental findings confirm that these composite membranes with optimum loading of NDs will have a 5 times enhanced life span in an intermediate liquid radioactive effluent, compared to the control Psf membranes. Thus, it is exciting to claim, for the first time, that these Psf–ND composite membranes can have the potential applications in the nuclear fuel cycle, circumventing the practical limitations encountered in the deployment of polymeric membranes in this domain.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
The authors would like to acknowledge Dr Nilanjal Misra and Dr N. K. Goel, RTDD (BARC) for FTIR and contact angle analysis; Mr P. P. Surve and Mr R. B. Bramhane of Membrane Development Section (BARC) for assisting in the fabrication of membranes using a table top membrane casting machine.
Notes and references
-
The nuclear fuel cycle from ore to wastes, ed. P. D. Wilson, Oxford University Press, United Kingdom, 1996 Search PubMed.
- L. E. Roberts, Annu. Rev. Nucl. Part. Sci., 1990, 40, 79–112 CrossRef CAS.
-
R. E. Berlin and C. C. Stanton, Radioactive waste management, John Wiley and Sons Inc, United States, 1988 Search PubMed.
- J. Lento and R. Harjula, Solvent Extr. Ion Exch., 1987, 5, 343–352 CrossRef.
- S. A. Khan and M. A. Khan,
et al.
, Waste Manag., 1995, 15, 271–282 CrossRef CAS.
- K. Raj, K. Prasad and N. Bansal, Nucl. Eng. Des., 2006, 236, 914–930 CrossRef CAS.
- E. P. Horwitz, M. L. Dietz, R. Chiarizia, H. Diamond, S. L. Maxwell III and M. R. Nelson, Anal. Chim. Acta, 1995, 310, 63–78 CrossRef CAS.
- X. Sun, H. Luo and S. Dai, Chem. Rev., 2011, 112, 2100–2128 CrossRef PubMed.
-
M. I. Ojovan and W. E. Lee, An introduction to nuclear waste immobilisation, Newnes, 2013 Search PubMed.
-
C. Hill, J.-F. Dozol, V. Lamare, H. Rouquette, S. Eymard, B. Tournois, J. Vicens, Z. Asfari, C. Bressot and R. Ungaro, et al., Calixarenes 50th Anniversary: Commemorative Issue, Springer, 1994, pp. 399–408 Search PubMed.
-
International Atomic Energy Agency, Application of Membrane Technologies for Liquid Radioactive Waste Processing, International Atomic Energy Agency, Vienna, 2004 Search PubMed.
- Y. Lu, T. Chen, X. Chen, M. Qiu and Y. Fan, J. Membr. Sci., 2016, 514, 476–486 CrossRef CAS.
- W. Koros, G. Fleming, S. Jordan, T. Kim and H. Hoehn, Prog. Polym. Sci., 1988, 13, 339–401 CrossRef CAS.
- S. A. Piletsky, H. Matuschewski, U. Schedler, A. Wilpert, E. V. Piletska, T. A. Thiele and M. Ulbricht, Macromolecules, 2000, 33, 3092–3098 CrossRef CAS.
- N. Combernoux, L. Schrive, V. Labed, Y. Wyart, E. Carretier, A. Benony-Rhodier and P. Moulin, J. Membr. Sci., 2015, 480, 64–73 CrossRef CAS.
- J. Brown and J. O'Donnell, J. Appl. Polym. Sci., 1979, 23, 2763–2775 CrossRef CAS.
- N. N. Rupiasih and P. Vidyasagar, Polym. Degrad. Stab., 2008, 93, 1300–1307 CrossRef CAS.
- K. Murakami and H. Kudo, Nucl. Instrum. Methods Phys. Res., Sect. B, 2007, 265, 125–129 CrossRef CAS.
-
A. S. Edelstein and R. Cammaratra, Nanomaterials: synthesis, properties and applications, CRC press, 1998 Search PubMed.
- R. A. Damodar, S.-J. You and H.-H. Chou, J. Hazard. Mater., 2009, 172, 1321–1328 CrossRef CAS PubMed.
- D. Ciprari, K. Jacob and R. Tannenbaum, Macromolecules, 2006, 39, 6565–6573 CrossRef CAS.
- E. Kablov, S. Kondrashov and G. Y. Yurkov, Nanotechnol. Russ., 2013, 8, 163–185 CrossRef.
- J.-Y. Raty and G. Galli, J. Electroanal. Chem., 2005, 584, 9–12 CrossRef CAS.
- R. Mishra, A. Chhalodia and S. Tiwari, Recent progress in nanodiamonds: Synthesis, properties and their potential applications, Veruscript Functional Nanomaterials, 2018, 2, 8W2EG0 CrossRef.
- R. J. Trew, J.-B. Yan and P. M. Mock, Proc. IEEE, 1991, 79, 598–620 CrossRef CAS.
- T. Petit, J.-C. Arnault, H. A. Girard, M. Sennour, T.-Y. Kang, C.-L. Cheng and P. Bergonzo, Nanoscale, 2012, 4, 6792–6799 RSC.
- Y. Liu, S. Chen, X. Quan and H. Yu, J. Am. Chem. Soc., 2015, 137, 11631–11636 CrossRef CAS PubMed.
- A. Krueger and D. Lang, Adv. Funct. Mater., 2012, 22, 890–906 CrossRef CAS.
- P. Kanagaraj, S. Neelakandan, A. Nagendran, D. Rana, T. Matsuura and A. Muthumeenal, RSC Adv., 2015, 5, 27594–27602 RSC.
- U. Maitra, K. E. Prasad, U. Ramamurty and C. Rao, Solid State Commun., 2009, 149, 1693–1697 CrossRef CAS.
- Y.-C. Wang, S.-C. Fan, K.-R. Lee, C.-L. Li, S.-H. Huang, H.-A. Tsai and J.-Y. Lai, J. Membr. Sci., 2004, 239, 219–226 CrossRef CAS.
- Y. Kim, D. Rana, T. Matsuura and W.-J. Chung, Chem. Commun., 2012, 48, 693–695 RSC.
- S. R. Lakhotia, M. Mukhopadhyay and P. Kumari, Sci. Rep., 2018, 8, 4976 CrossRef PubMed.
- V. N. Mochalin and Y. Gogotsi, Diamond Relat. Mater., 2015, 58, 161–171 CrossRef CAS.
- E. Alishahi, S. Shadlou, S. Doagou-R and M. R. Ayatollahi, Macromol. Mater. Eng., 2013, 298, 670–678 CrossRef CAS.
- P. Karami, S. S. Khasraghi, M. Hashemi, S. Rabiei and A. Shojaei, Adv. Colloid Interface Sci., 2019, 269, 122–151 CrossRef CAS PubMed.
- S. Kumar, M. Nehra, D. Kedia, N. Dilbaghi, K. Tankeshwar and K.-H. Kim, Carbon, 2019, 143, 678–699 CrossRef CAS.
- A. Tizchang, Y. Jafarzadeh, R. Yegani and E. Shokri, J. Water Environ. Nanotechnol., 2019, 4, 213–226 Search PubMed.
- M. Ayatollahi, E. Alishahi, S. Doagou-R and S. Shadlou, Composites, Part B, 2012, 43, 3425–3430 CrossRef CAS.
- A. Gavrilov and A. Voznyakovskii, Russ. J. Appl. Chem., 2009, 82, 1041–1045 CrossRef CAS.
- E. Roumeli, E. Pavlidou, A. Avgeropoulos, G. Vourlias, D. N. Bikiaris and K. Chrissafis, J. Phys. Chem. B, 2014, 118, 11341–11352 CrossRef CAS PubMed.
- J.-Y. Lee and D.-S. Lim, Surf. Coat. Technol., 2004, 188, 534–538 CrossRef.
- L. L. Beecroft and C. K. Ober, Chem. Mater., 1997, 9, 1302–1317 CrossRef CAS.
- Q. Zhang, V. N. Mochalin, I. Neitzel, I. Y. Knoke, J. Han, C. A. Klug, J. G. Zhou, P. I. Lelkes and Y. Gogotsi, Biomaterials, 2011, 32, 87–94 CrossRef CAS.
- S. Le Caër, Water, 2011, 3, 235–253 CrossRef.
- J. Castle, Surf. Interface Anal., 1984, 6, 302 CrossRef.
-
J. F. Moulder, Physical electronics, 1995, pp. 230–232 Search PubMed.
-
P. Kirkegaard, J. V. Olsen, M. M. Eldrup and N. J. Pedersen, PALSfit: A computer program for analysing positron lifetime spectra, Risø National Laboratory for Sustainable Energy, Technical University of Denmark, Roskilde, Denmark, 2009 Search PubMed.
- S. Tao, J. Chem.
Phys., 1972, 56, 5499–5510 CrossRef CAS.
- M. Eldrup, D. Lightbody and J. N. Sherwood, Chem. Phys., 1981, 63, 51–58 CrossRef CAS.
- T. Freltoft, J. Kjems and S. Sinha, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 269 CrossRef CAS PubMed.
-
A. Ferrari, P. R. Sala, A. Fasso and J. Ranft, FLUKA: A multi-particle transport code (Program version 2005), 2005 Search PubMed.
- T. Böhlen, F. Cerutti, M. Chin, A. Fassò, A. Ferrari, P. Ortega, A. Mairani, P. R. Sala, G. Smirnov and V. Vlachoudis, Nucl. Data Sheets, 2014, 120, 211–214 CrossRef.
- C. Barth, M. Goncalves, A. Pires, J. Roeder and B. Wolf, J. Membr. Sci., 2000, 169, 287–299 CrossRef CAS.
- J. Yin and B. Deng, J. Membr. Sci., 2015, 479, 256–275 CrossRef CAS.
- H. Zhao, L. Wu, Z. Zhou, L. Zhang and H. Chen, Phys. Chem. Chem. Phys., 2013, 15, 9084–9092 RSC.
- L. Varshney, Nucl. Instrum. Methods Phys. Res., Sect. B, 2007, 255, 343–349 CrossRef CAS.
- D. R. Sekulić, B. M. Babić, L. M. Kljajević, J. M. Stašić and B. V. Kaluđerović, J. Serb. Chem. Soc., 2009, 74, 1125–1132 CrossRef.
- Y. Li, S. Huang, S. Zhou, A. G. Fane, Y. Zhang and S. Zhao, J. Membr. Sci., 2018, 556, 154–163 CrossRef CAS.
- A. Zegaoui, A.-r. Wang, A. Q. Dayo, B. Tian, W.-b. Liu, J. Wang and Y.-g. Liu, Radiat. Phys. Chem., 2017, 141, 110–117 CrossRef CAS.
- G. Choudalakis and A. Gotsis, Curr. Opin. Colloid Interface Sci., 2012, 17, 132–140 CrossRef CAS.
-
P. Tewari, Nanocomposite Membrane Technology: Fundamentals and Applications, CRC Press, 2015 Search PubMed.
- Y. Zhang, K. Y. Rhee, D. Hui and S.-J. Park, Composites, Part B, 2018, 143, 19–27 CrossRef CAS.
- H. Shintani, Trends in Biomaterials & Artificial Organs, 2004, 18, 36–40 Search PubMed.
- M. Carter, H. Li, Y. Zhang, E. Vance and D. Mitchell, J. Nucl. Mater., 2009, 384, 322–326 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9na00372j |
|
| This journal is © The Royal Society of Chemistry 2020 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article ab,
Nitesh
Goswami
b,
Amit K.
Singha
b,
Virendra
Kumar
c,
Anil K.
Debnath
d,
Debasis
Sen
ab,
Nitesh
Goswami
b,
Amit K.
Singha
b,
Virendra
Kumar
c,
Anil K.
Debnath
d,
Debasis
Sen
 ae,
Vinod K.
Aswal
ae,
Sanjay
Kumar
f,
Dhanadeep
Dutta
g,
Biju
Keshavkumar
h,
Sharwari
Ghodke
i,
Ratnesh
Jain
i,
Beena G.
Singh
aj,
Pradeep K.
Tewari
a,
Ramesh C.
Bindal
ab and
Soumitra
Kar
ae,
Vinod K.
Aswal
ae,
Sanjay
Kumar
f,
Dhanadeep
Dutta
g,
Biju
Keshavkumar
h,
Sharwari
Ghodke
i,
Ratnesh
Jain
i,
Beena G.
Singh
aj,
Pradeep K.
Tewari
a,
Ramesh C.
Bindal
ab and
Soumitra
Kar
 *ab
*ab
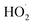 , H2O2, H3O+, OH−, and H2.45 These can react with Psf chains and create defects in the Psf matrix. Carboxyl and hydroxyl groups present on the surface of NDs could interact with these free radicals and protect the Psf matrix from radiation-induced damage caused by the radiolysed products of water. The possible mechanism of interaction of free radicals with carboxyl and hydroxyl groups is given in eqn (1)–(4).
, H2O2, H3O+, OH−, and H2.45 These can react with Psf chains and create defects in the Psf matrix. Carboxyl and hydroxyl groups present on the surface of NDs could interact with these free radicals and protect the Psf matrix from radiation-induced damage caused by the radiolysed products of water. The possible mechanism of interaction of free radicals with carboxyl and hydroxyl groups is given in eqn (1)–(4).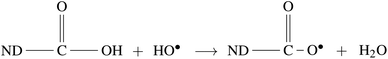
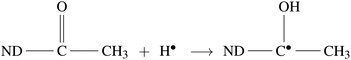

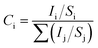
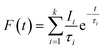
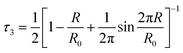
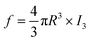
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(θ)/λ, where λ is the wavelength and 2θ is the scattering angle) range from ∼0.1 to 2.5 nm−1. The sample to detector distance was nearly 1 m. It was found that three cumulative power law scattering contributions could explain fairly well the scattering profile of the Psf membrane. Thus, for the Psf membrane, the model of eqn (9) was used.
sin(θ)/λ, where λ is the wavelength and 2θ is the scattering angle) range from ∼0.1 to 2.5 nm−1. The sample to detector distance was nearly 1 m. It was found that three cumulative power law scattering contributions could explain fairly well the scattering profile of the Psf membrane. Thus, for the Psf membrane, the model of eqn (9) was used.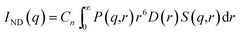
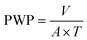
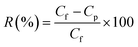


![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S
S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching of the sulfone group), 1080 and 1105 cm−1 (aromatic ring vibrations), 1149 cm−1 (symmetric O
O stretching of the sulfone group), 1080 and 1105 cm−1 (aromatic ring vibrations), 1149 cm−1 (symmetric O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S
S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching of the sulfone group), 1168 cm−1 (asymmetric O
O stretching of the sulfone group), 1168 cm−1 (asymmetric O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S
S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching of the sulfone group), 1238 cm−1 (asymmetric C–O–C stretching of the aryl ether group), 1293 and 1322 cm−1 (asymmetric O
O stretching of the sulfone group), 1238 cm−1 (asymmetric C–O–C stretching of the aryl ether group), 1293 and 1322 cm−1 (asymmetric O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S
S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching of the sulfone group), 1364 cm−1 (symmetric C–H bending deformation of the methyl group), 1411 cm−1 (asymmetric C–H bending deformation of the methyl group), 1487 and 1586 cm−1 (aromatic C
O stretching of the sulfone group), 1364 cm−1 (symmetric C–H bending deformation of the methyl group), 1411 cm−1 (asymmetric C–H bending deformation of the methyl group), 1487 and 1586 cm−1 (aromatic C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching), 2873 and 2968 cm−1 (asymmetric and symmetric C–H stretching vibrations include the complete methyl group), and 3440 cm−1 (O–H stretching vibrations). The FTIR spectra of the pure ND powder show major absorption bands around 3410 cm−1 (O–H stretching vibrations), 2359 cm−1 (absorption vibrations of CO2), 1647 cm−1 (C
C stretching), 2873 and 2968 cm−1 (asymmetric and symmetric C–H stretching vibrations include the complete methyl group), and 3440 cm−1 (O–H stretching vibrations). The FTIR spectra of the pure ND powder show major absorption bands around 3410 cm−1 (O–H stretching vibrations), 2359 cm−1 (absorption vibrations of CO2), 1647 cm−1 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching of the carboxyl groups), and 1100 cm−1 (C–O stretching vibrations of the –COOH groups). This validates the presence of carboxyl and hydroxyl functional groups on the surface of NDs. The hydroxyl and carboxyl groups present over NDs are responsible for scavenging the secondary free radicals generated during radiolysis of water, which in turn protects the composite membranes leading to an enhanced life-span in a radioactive environment. This finding has also been corroborated with our in-house data for radiation stability of composite membranes with carboxyl-functionalised NDs (being considered for publication elsewhere). No shift in the characteristic absorption bands of Psf–ND composite membranes indicates the fact that impregnation of NDs in the control Psf matrix does not affect the internal molecular structure of membranes. The characteristic band of NDs at 2359 cm−1 shows the physical presence of NDs, whose intensity increases with loading of NDs, as seen in Fig. 7.
O stretching of the carboxyl groups), and 1100 cm−1 (C–O stretching vibrations of the –COOH groups). This validates the presence of carboxyl and hydroxyl functional groups on the surface of NDs. The hydroxyl and carboxyl groups present over NDs are responsible for scavenging the secondary free radicals generated during radiolysis of water, which in turn protects the composite membranes leading to an enhanced life-span in a radioactive environment. This finding has also been corroborated with our in-house data for radiation stability of composite membranes with carboxyl-functionalised NDs (being considered for publication elsewhere). No shift in the characteristic absorption bands of Psf–ND composite membranes indicates the fact that impregnation of NDs in the control Psf matrix does not affect the internal molecular structure of membranes. The characteristic band of NDs at 2359 cm−1 shows the physical presence of NDs, whose intensity increases with loading of NDs, as seen in Fig. 7.![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond around 287.5 eV. The XPS spectra of S-2p and O-1s peaks of the membranes are shown in Fig. S-II and S-III,† respectively. No shift in the XPS peaks of the bonds confirms that there is no chemical interaction between the NDs and Psf, even at an increased loading of NDs, indicating only physical entrapment of nanomaterials in the membrane matrix. The absence of additional peaks in the membrane samples exposed to gamma irradiation confirms no adduct formation with irradiation (Fig. S-IV†).
O bond around 287.5 eV. The XPS spectra of S-2p and O-1s peaks of the membranes are shown in Fig. S-II and S-III,† respectively. No shift in the XPS peaks of the bonds confirms that there is no chemical interaction between the NDs and Psf, even at an increased loading of NDs, indicating only physical entrapment of nanomaterials in the membrane matrix. The absence of additional peaks in the membrane samples exposed to gamma irradiation confirms no adduct formation with irradiation (Fig. S-IV†).









