Open Access Article
Open Access ArticleVibrational dynamics in lead halide hybrid perovskites investigated by Raman spectroscopy†
Josefa
Ibaceta-Jaña
 a,
Ruslan
Muydinov
*a,
Pamela
Rosado
b,
Hossein
Mirhosseini
a,
Ruslan
Muydinov
*a,
Pamela
Rosado
b,
Hossein
Mirhosseini
 c,
Manjusha
Chugh
c,
Olga
Nazarenko
de,
Dmitry N.
Dirin
c,
Manjusha
Chugh
c,
Olga
Nazarenko
de,
Dmitry N.
Dirin
 de,
Dirk
Heinrich
b,
Markus R.
Wagner
de,
Dirk
Heinrich
b,
Markus R.
Wagner
 b,
Thomas D.
Kühne
c,
Bernd
Szyszka
b,
Thomas D.
Kühne
c,
Bernd
Szyszka
 a,
Maksym V.
Kovalenko
a,
Maksym V.
Kovalenko
 de and
Axel
Hoffmann
b
de and
Axel
Hoffmann
b
aTechnology for Thin-Film Devices, Technische Universitat Berlin, Einsteinufer 25, 10587 Berlin, Germany. E-mail: ruslan.muydinov@tu-berlin.de
bInstitute of Solid State Physics, Technische Universitat Berlin, Hardenbergstr. 36, 10623 Berlin, Germany
cDynamics of Condensed Matter and Center for Sustainable Systems Design, Department of Chemistry, University of Paderborn, Warburger Str. 100, D-33098 Paderborn, Germany
dInstitute of Inorganic Chemistry, Department of Chemistry and Applied Biosciences, ETH Zürich, Vladimir-Prelog-Weg 1-5/10, 8093 Zürich, Switzerland
eLaboratory for Thin Films and Photovoltaics, Empa-Swiss Federal Laboratories for Materials Science and Technology, Überlandstrasse 129, CH-8600 Dübendorf, Switzerland
First published on 26th February 2020
Abstract
Lead halide perovskite semiconductors providing record efficiencies of solar cells have usually mixed compositions doped in A- and X-sites to enhance the phase stability. The cubic form of formamidinium (FA) lead iodide reveals excellent opto-electronic properties but transforms at room temperature (RT) into a hexagonal structure which does not effectively absorb visible light. This metastable form and the mechanism of its stabilization by Cs+ and Br− incorporation are poorly characterized and insufficiently understood. We report here the vibrational properties of cubic FAPbI3 investigated by DFT calculations on phonon frequencies and intensities, and micro-Raman spectroscopy. The effects of Cs+ and Br− partial substitution are discussed. We support our results with the study of FAPbBr3 which expands the identification of vibrational modes to the previously unpublished low frequency region (<500 cm−1). Our results show that the incorporation of Cs+ and Br− leads to the coupling of the displacement of the A-site components and weakens the bonds between FA+ and the PbX6 octahedra. We suggest that the enhancement of α-FAPbI3 stability can be a product of the release of tensile stresses in the Pb–X bond, which is reflected in a red-shift of the low frequency region of the Raman spectrum (<200 cm−1).
Introduction
Lead halide perovskites (LHPs = A[Pb]X3) have attracted the curiosity of researchers owing to their outstanding optoelectronic properties such as a sharp absorption edge, high absorption coefficients, the large diffusion length of free charge carriers, and low recombination rates.1,2 Furthermore, the band gap tunability,3–7 the small difference between the band gap size and the open circuit voltage,8 easy processing, and the high defect tolerance9,10 of LHPs make these compounds suitable for a variety of applications including light emitting devices,11 solar cells,3,12,13 photo-transistors,14,15 lasers,16,17 and detectors.18–21 Among various LHPs, formamidinium (CH(NH2)2+ = FA+) lead iodide (FAPbI3) is of particular interest for solar cell applications due to its narrow band gap of around 1.55 eV, its improved thermal stability compared to that of methylammonium (CH3NH3+ = MA+) lead iodide (MAPbI3) and the easier solution processability compared to CsPbI3.22–25 The main challenge for this material is the structural instability: at room temperature (RT) it transforms into the non-photoactive yellow δ-phase in 1 to 10 days depending on the environment.25,26 A common way to circumvent this is to combine different cations on the A-site or halides on the X-site featuring quinary CsxFA1−xPb(I1−yBry)3 composition with x and y about 10% each. This strategy has been shown to improve the phase stability in bulk, microcrystalline and nanocrystalline forms. In solar cells, this is translated into improved photo and moisture stability under environmental conditions and reduction of trap density, which consequently increases the efficiency by more than 1%.3,12,20,27–29Even though impressive progress in synthesis and device engineering has been made, some fundamental properties of LHPs remain poorly investigated. Particularly, the understanding of the lattice dynamics of LHPs is crucial for the further optimization of their performance due to the unusually high softness of LHPs compared to conventional semiconductors30–32 and the additional dynamic effects caused by the non-spherical geometry of organic A-cations. Their dipole moments in combination with the X-ion migration33 and the reorientation of A-cations within the BX6-octahedral frame34 result in a structural phase transition.35
Raman spectroscopy has already disclosed the lattice dynamics for some LHPs. The experimental Raman spectra of LHPs have been supported with Density Functional Theory (DFT) calculations only for MAPbX3 (X = I and Br). The interesting range of the vibrational spectrum of these materials is 10–3100 cm−1 where the most pronounced peaks are correlated with the motion of the PbX6 octahedra and the reorientation of the MA+ cation. These peaks appear in the spectra below and above 200 cm−1, respectively.36–39 Dynamic disorder of MA+ causes splittings of independent harmonic modes, resulting in a larger number of Raman peaks at high frequencies.37 The variation of halogens in MAPbX3 shifts the Raman peaks in accordance to the Pb–X bond strength.38,39 There are experimentally measured Raman spectra of FAPbBr3 and CsPbBr3 up to 3500 cm−1 and 320 cm−1, respectively, but the specific modes have not been ascribed for the whole spectrum.36,40–42 For FAPbBr3, the attribution is well-made for molecular modes (>500 cm−1), associating them with the Raman modes of the isolated FA+ molecular ion.43 For CsPbBr3, a general description of modes was done on the basis of atomic trajectories, which reveals that Cs+ atoms perform a head-to-head motion, which is the displacement of two neighboring Cs+ atoms towards the same face, along the 〈100〉 directions. Comparative studies of MAPbX3 and CsPbX3 demonstrated a number of correlating Raman peaks representing the analogous motions for both compounds.36,42 Despite the existence of molecular dynamics simulations performed for FAPbI3,44,45 its vibrational behavior and internal dynamics have not been correlated with experimental data so far. Only one Raman peak at 110 cm−1 has been experimentally determined.25 There are also no experimental data for the mixed FA-based compounds at all. Therefore, the effect of Cs+ and Br− doping in the lattice dynamics also remains poorly understood.
In this work we investigate FAPbI3 and FAPbBr3 by means of Raman spectroscopy and identify the origin of the different vibrational modes with the support of DFT calculations.46 The measurements were conducted on single crystal perovskites which exhibit less defects compared to their polycrystalline counterparts. Solution based growth provides an even distribution of components and a good level of the process control. We intend to understand the impact of Cs+ and Br− incorporation into FAPbI3 through the quantification of Raman modes and Raman shifts. A compositional cross-check is performed: single crystalline FAPbI3 and FAPbBr3 are compared to identify the sublattice PbX6 modes and FA+ movements. Comparing FAPbBr3 with CsPbBr3 enables the identification of Br− related vibrational modes and to differentiate between FA+ and Cs+ cations. A complex effect of the partial cation and anion substitutions is observed in relatively stable Cs0.1FA0.9PbI3 and Cs0.1FA0.9PbI2.6Br0.4 compositions. By analyzing the cooperative effects of the noticed substitutions we propose an explanation for the observed stabilization of the cubic structure at RT.
Methods
Sample preparation
Single crystalline samples of the compositions presented in Fig. 1 were prepared using the modified inverse temperature crystallization (ITC) method reported elsewhere.20,25,26,47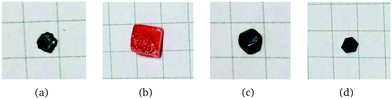 | ||
| Fig. 1 Photographs of single crystals: (a) FAPbI3, (b) FAPbBr3, (c) Cs0.1FA0.9PbI3 and (d) Cs0.1FA0.9PbI2.6Br0.4. | ||
The γ-butyrolactone (GBL) based-solutions were prepared in ambient air (RT = 17 °C) and next filtered through a 0.2 μm polytetrafluoroethylene syringe filter. The filtered precursor solution of 3 ml volume was poured into a 20 ml vial, closed with a cap, and placed into a preheated (90 °C) glycerol bath. The temperature was elevated in 5 °C h−1 steps up to 130 °C maximum and kept for 3 h. The crystals formed were wiped with a filter paper and dried under ambient conditions. To grow large enough crystals of the Cs0.1FA0.9PbI3 and FAPbI3 compositions, a previously obtained seed was introduced at 95 °C into the solution. Seeds were obtained using the method of Han et al.25 by keeping a not-filtered 1 M precursor solution at 70 °C for 6 hours followed by their growth in a freshly prepared and filtered solution at 115 °C for 3 h.
Analytical methods
Powder X-ray diffraction (XRD) patterns were collected in transmission (Debye–Scherrer-geometry) with a STADI P diffractometer (STOE & Cie GmbH), equipped with a silicon strip MYTHEN 1K Detector (DECTRIS) with a curved Ge(111)-Monochromator. For the measurement, single crystals were ground and placed between adhesive tapes.Raman spectroscopy was performed on a high-resolution LabRAM HR800 spectrometer from Horiba. It included an ultra-low frequency (ULF) unit capable of measuring Raman spectra from 10 cm−1 at an excitation wavelength of 633 nm. Spectra were recorded with gratings of 600 and 1800 lines per millimeter at RT in an ambient environment. The laser beam was focused using a 50×/NA = 0.75 microscope objective, with a spot diameter of 1.03 μm and a power intensity in the range from 6 μW to 280 μW. This results in a power density in the range from 0.8 kW cm−2 to 35.6 kW cm−2.
We notice here that the acquisition and interpretation of Raman spectra are challenging in the case of the LHPs, due to the combination of two counteracting effects: (i) the low relative intensity of Raman scattering compared to the primary excitation power and (ii) the high rate of degradation of LHPs under laser induced heating.48 For a laser wavelength λ = 532 nm, the LHPs are degraded at a beam power higher than >10 μW. We detected degradation of FA-based LHPs at >1 mW at an excitation wavelength λ = 633 nm. Consequently, the excitation power and integration times were optimized for each LHP to ensure good signal to noise ratios while avoiding laser induced material degradation during the measurements. To avoid parasitic light signals, the measurements were performed in the dark. Due to the onset of strong luminescence in FAPbI3 (PL signal around λ = 827 nm), the Raman spectrum of this compound is only shown up to 200 cm−1. The same limitation applies for mixed compounds at frequencies above 1200 cm−1. For CsPbBr3, the spectra were found to be informative up to 400 cm−1. Despite the limitation in the measured range, the source at λ = 633 nm gives the sharpest peaks and lowest noise. A less energetic excitation source (λ = 830 nm) also excites FAPbI3, emitting photoluminescence that reduces the possibility of identifiable peaks.
Expecting exclusively molecular (FA+) modes in Zone III, we considered the FAPbBr3 compound as a reference. Besides, among FA-based LHPs, only this compound is experimentally characterized by Raman spectroscopy in the literature.40
Computational details
DFT based total energy and force calculations were performed using the Vienna Ab initio Simulation Package (VASP) code.49 The projector augmented (PAW) potentials50,51 that describe electron–ion interactions were constructed such that the 5d electrons of Pb, 4s and 4p electrons of Br, and 5s and 5p electrons of I are treated as valence electrons. The plane-wave cutoff energy was set to 700 eV. A force convergence criterion of 1 meV Å−1 and an energy convergence of 10−6 eV were used for all geometry optimizations. A Gamma-centered Monkhorst–Pack set of k-points of 6 × 6 × 6 was used for Brillouin zone integration. To take the weak van der Waals interactions into account, the optB88-vdW functional52 with default setting of the VASP was used. Cubic phases of FAPbI3 and FAPbBr3 perovskite compounds with experimentally measured lattice parameters (6.36 and 5.99 AA, respectively) were considered. Spin-polarized calculations for the primitive cells and 2 × 2 × 2 cells showed no change in the atomic configuration, therefore, the rest of the calculations were performed on primitive cells. First-principles lattice dynamics (phonon spectrum) calculations were performed for the cubic phases of FAPbI3 and FAPbBr3 by diagonalizing the Hessian matrix within the Harmonic approximation.53 We used the finite difference method to calculate the force constants. The eigenvectors of the Hessian matrix give the normal modes of the vibrations of the atoms, whereas the eigenvalues represent their frequencies. After obtaining the normal modes, Raman intensities (activities) of these modes were obtained by calculating the change in polarizability (macroscopic dielectric tensor) of each normal mode. Diagonalization of the Hessian matrix gives imaginary frequencies if the structure is not well optimized. Hence, we first optimized the atomic structures with a rather tight convergence criterion as mentioned above.Results and discussion
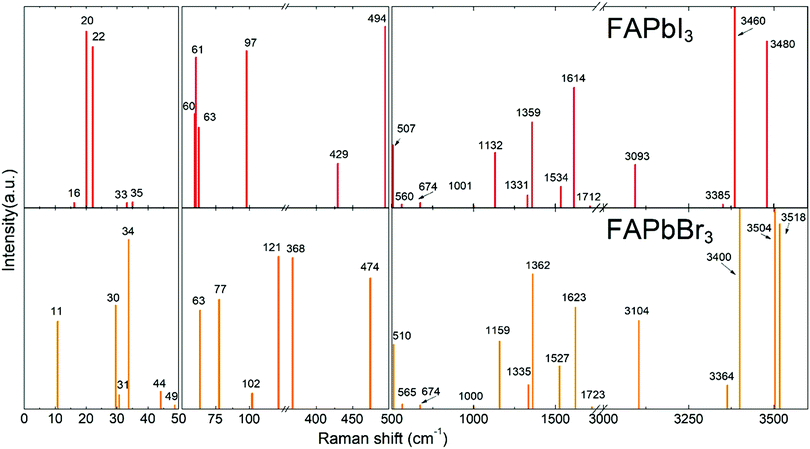
Theoretical Raman spectra of FAPbBr3 and FAPbI3
DFT calculations were performed to attribute the modes in the case of poorly investigated FAPbBr3 and FAPbI3. To validate our model, we performed DFT calculations for MAPbI3 (see Fig. S1, ESI†) and our results were found to be in good agreement with the data published previously.37 The calculated Raman spectra of FAPbX3 are shown in Fig. 2. The modes of the high frequency range (500–3500 cm−1) for some FA-based compounds were also explored experimentally40,43 and our DFT data agree well with the experimental data for FAPbBr3.40Raman spectra of hybrid perovskites are usually analyzed in three spectral ranges which correspond to different sources of vibrations.37 The low-energy range from 10 to 50 cm−1 (Zone I) contains PbX6 sublattice modes. Zone II, from 50 to 500 cm−1, corresponds to the coupled modes, which appear exclusively in LHPs. They present the FAPbX3 molecular reorientation of FA+ influenced by the PbX6 octahedral framework. Zone III, the high-energy zone from 500 to 3500 cm−1, includes individual molecular modes. It is worth noticing that all modes are affected by the coupling, however, this coupling is the source of the vibration only in Zone II. The modes of Zones I and III are present in isolated octahedra and isolated molecules, respectively.
The following results are structured in accordance with these three zones. We explain the modes of Zones I and III by comparison with theoretical modes from the literature.37,43 The modes of Zone II are extensively explained due to the absence of references in the literature.
In Zone I, our calculations show peaks related to the octahedral modes, which are twist and distortion vibrations characteristic for the Oh symmetry (see Fig. S2, ESI†). For FAPbI3, the twist mode is present at 16, 20 and 22 cm−1 and the distortion mode is present at 33 and 35 cm−1. For FAPbBr3, these modes are present at 30 and 31 cm−1 and at 34, 44 and 63 cm−1, respectively.
A comparison between our calculated modes of Zone I with experimental Raman modes cannot be made due to the lack of Raman data of FAPbX3 compositions in the literature. We can directly compare FAPbX3 with other hybrid LPHs, such as MAPbI3, considering that the molecular response does not affect the frequencies of the octahedral modes significantly. This is a consequence of the lower mass of the molecules compared to the inorganic frame (FA+ = 46 u. compared to PbX6 = 1000 u.). The modes of MAPbI3 were thoroughly ascribed on the basis of DFT calculations37 and corroborated by experiments.37,38 According to these data the peak associated with the octahedral twist in iodide appears at energies below 30 cm−1, whereas the octahedral distortion peak appears between 30 and 50 cm−1. In bromide, these modes shift about 15 cm−1 to higher frequencies. This happens due to the higher strength of the Pb–Br bond (0.66 in the Pauling scale) compared to Pb–I (0.33 in the Pauling scale) as well as due to the smaller atomic mass of Br (79.9 u.) compared to I (126.9 u.). The latter impacts peak positions as 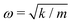 , according to the harmonic oscillator model.54 This model is the solution of the Schrödinger equation that describes the atomic vibrations in a system. For a simple scheme, in a diatomic molecule the frequency of the vibration “ω” depends directly on “m”, that represents the reduced mass, and “k”, that represents the spring constant, which is related to the strength of the chemical bond between the involved atoms.
, according to the harmonic oscillator model.54 This model is the solution of the Schrödinger equation that describes the atomic vibrations in a system. For a simple scheme, in a diatomic molecule the frequency of the vibration “ω” depends directly on “m”, that represents the reduced mass, and “k”, that represents the spring constant, which is related to the strength of the chemical bond between the involved atoms.
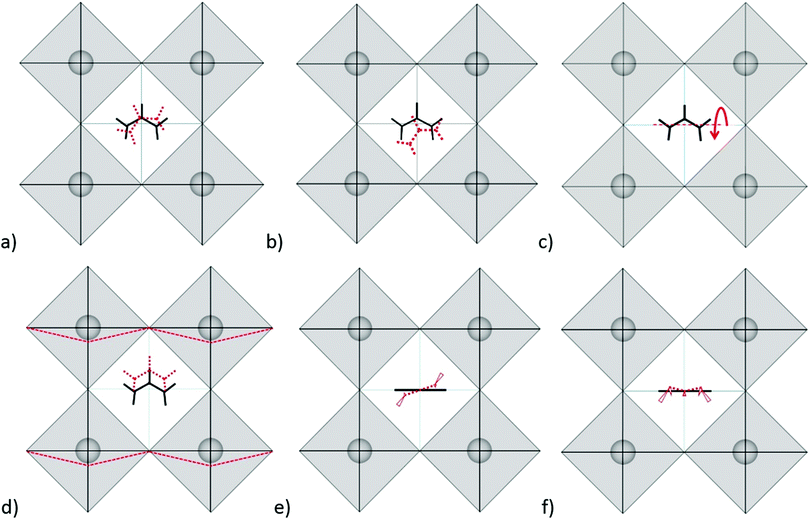
Modes in Zone II for FAPbX3 have not been described in the literature so far. For this zone, our calculations showed mainly six modes which are (a) in-plane rotation around the center of mass, (b) in-plane rotation around corner hydrogen, (c) out-of-plane rotation around the N–N axis, (d) molecular translation, and (e) asymmetric and (f) symmetric out-of-plane bending of H2N–C–NH2 (see Fig. 3). The 2D representation of the HP modes shown in the figure is a schematization of the 3D models of the vibrations given by DFT calculations, in which the displacements are represented by arrows. FAPbI3 reveals these modes at 60, 61, 63, 97, 429, and 494 cm−1, whereas FAPbBr3 peaks (excluding mode b) appear at 11, 77, 102/121, 368 and 474 cm−1, respectively.
As we can observe, the substitution of the halide is not reflected in a unidirectional shift of the modes. Thus, the large shift of mode (a) in FAPbI3 at 60 cm−1 as compared to 11 cm−1 in FAPbBr3 may be related to the following fact: the plane in which the rotation takes place is parallel to the crystallographic plane in FAPbBr3 but slightly tilted in the case of FAPbI3 due to the larger free space of the last one. The absence of mode (b) in FAPbBr3 may be explained by the smaller size of the unit cell that makes unfavorable such a notable shift of FA+. Modes (c) and (d) shift from the iodide to bromide in accordance to the halide mass difference, however modes (e) and (f) do not follow this rule. Mode (e) is governed by displacements of hydrogen atoms at the corners of the FAPbI3 unit cell (see Fig. 3e), whereas, in FAPbBr3, these hydrogen atoms remain almost static while Br− ions displace (figure is not presented in this work). We suggest that the magnitude of the displacement of the hydrogen atoms is a consequence of the interaction H<–>X, which is lower for X = I− than X = Br−. Therefore, it stipulates a higher frequency of mode (e) for FAPbI3 than for FAPbBr3, whose Raman peaks are present at 429 cm−1 and 368 cm−1, respectively. The higher energy of mode (f) in FAPbI3 is expected to originate from the larger free space provided by the PbI6 octahedra that allow the FA+ molecules to vibrate without valuable interactions with the surrounding halides as compared to FAPbBr3.
For Zone III, we compare our calculations of the Raman modes with the specific modes of the isolated FA+ ions, disclosed in the theoretical work of Kucharska et al.43 In this work, they present 18 internal modes according to the C2v symmetry of the FA+ molecule, distributed as Γ = 7A1+ 2A2 + B1+ 3B2. Our calculations are slightly red-shifted with respect to the isolated cation. This phenomenon is already known for MAPbX3, in which the molecular modes are shifted around 200 cm−1 for MAPbI3 and 350 cm−1 for MAPbBr3. The dependency of the shift magnitude with the halide is due to the formation of hydrogen bonds or other non-covalent interactions, resulting from the difference in elecronegativity.55 Our predicted Raman modes for FAPbI3 and FAPbBr3 differ on average ca. 50 cm−1 from the isolated cation. According to Kucharska et al., FA+ molecular modes should appear above 521 cm−1.43 Our DFT calculations predict modes already at 507 and 510 cm−1 for FAPbI3 and FAPbBr3, respectively.
Experimental Raman spectra of the FA-based compounds
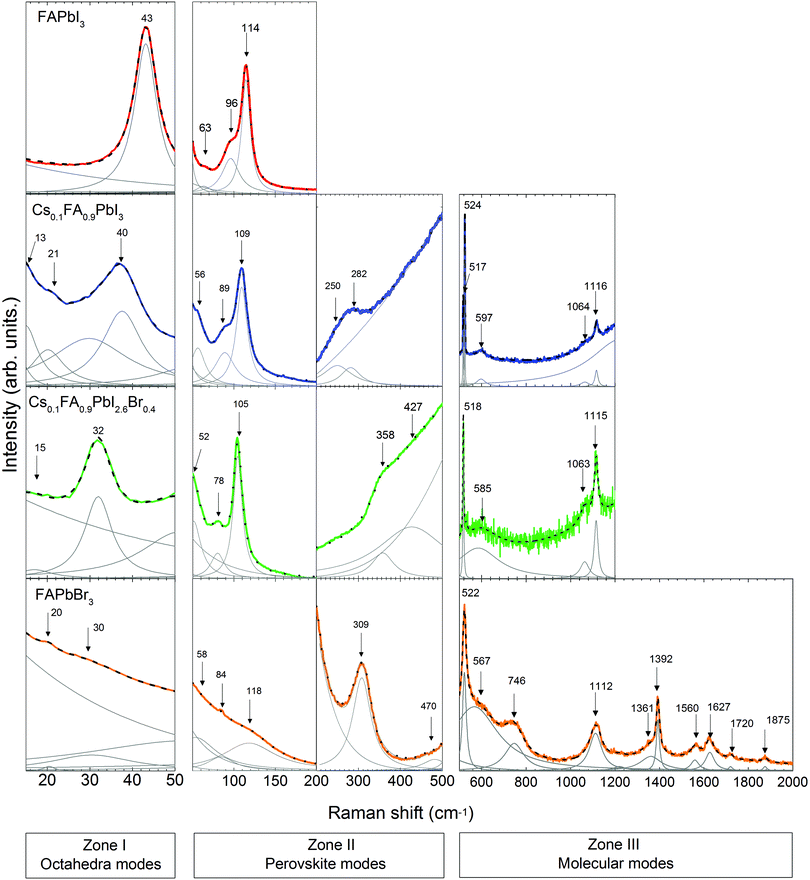
Following the discussion of DFT calculations, we focus next on the experimental Raman modes of FAPbI3 and FAPbBr3. In accordance with the previously established order, we discuss the experimental phonon modes in spectral ranges. The Raman spectra of the LHPs containing FA+ are shown in Fig. 4. Supporting experimental data for MAPbI3 and CsPbBr3 compounds are provided in the ESI† (Fig. S3).In Zone I of the experimental spectrum, FAPbI3 and FAPbBr3 present the twist and distortion modes represented by a single peak. The absence of splitting peaks indicated a cubic structure for both of them.
Compared to the other LHPs, FAPbBr3 shows broad modes that basically reflect low octahedral activity. This is likely due to the stronger Pb–Br bonds than the Pb–I bonds and the closer-to-unity Goldschmidt Tolerance Factor (GTF) ensuring better fit of FA+ to the octahedral cage and therefore a less flexible lattice.
Zone II is analyzed in two sub-zones: a high-coupling range (50–200 cm−1) and a low-coupling one (200–500 cm−1). The spectrum of FAPbI3 in the high-coupling range shows a sharp peak at 114 cm−1 and two broad peaks at 63 cm−1 and 96 cm−1. The spectrum of FAPbBr3 presents broad peaks in this range. In the low-coupling range, the spectrum of FAPbBr3 shows a sharp peak at 308 cm−1 and a broad peak at 470 cm−1.
Assigning the modes of this zone is especially challenging. The experimentally visible modes of FAPbX3 are more frequent than those theoretically predicted in the first sub-zone. Such a difference may be caused by a non-uniform disposition of FA+ cations resulting from the head-to-tail ordering and the neglect of spin–orbit-coupling interactions.1,56,57 The head-to-tail ordering was proposed for FAPbI3 as a low energetic arrangement of the molecules in which the N–N axis of one FA+ is perpendicular to the same axis of the adjacent molecules.
To validate the attribution of the experimental modes of FAPbX3 to the mode description given by the DFT calculations, we compare the coupled modes for FAPbI3 and MAPbI3. It is worth remarking significant differences between MA+ and FA+ for further discussion (Fig. S4, ESI†). In the FA+ ion, the positive charge is delocalized between two nitrogen atoms, whereas in MA+ it remains only on the –NH3+ group. The N–C–N chain becomes more rigid and deflects with an interatomic angle of 125° due to proton embedding.58 According to theoretical calculations, FA+ possesses a much lower dipole moment (0.21 D) than MA+ (2.29 D).59 The experimentally determined value for MA+ is quite low –0.854 D60 resulting in an expected dipole moment of the FA+ cation close to zero. Finally, FA+ adopts a planar symmetrical structure.61 Such 2D disposition and weaker polarization enables FA+ to vibrate out-of-plane without significant interactions with the surrounding sublattice PbX6. Therefore, the associated Raman modes may present higher frequencies compared to analogous modes of MAPbX3.
Taking into account these differences we can now compare the corresponding coupled modes. In the case of MAPbI3 (see Fig. S2a, ESI†) these modes derive from the active reorientation of MA+, which mainly rotates in a cone around N (58, 66 cm−1) with a period of 0.3 ps.34 Other coupled modes represent rotation in a cone around C and N (117, 133 cm−1), molecular translations (69, 75, 81 and 92 cm−1), rotation around C–N (128 cm−1) and C–N torsion (315 cm−1).37 The molecular reorientation of FA+ is distinctly slower and therefore the corresponding modes shift to lower frequencies. In contrast to that, a dominating movement of the molecules in FAPbI3 is a single roll-over with a time constant of 2 ps. The C–H bonds remain parallel to the {100} planes.34,62 Analogous modes of rotation around C or N and C–N torsion are not expected in FAPbI3 due to the rigid N–C–N frame. Translation modes in MAPbI3 are expected at lower frequencies as compared to FAPbI3. The main reason is the stronger ionic bonding between MA+ and X− because MA+ has a larger dipole moment and a smaller size than FA+. The large size, rigidity and twist of a dipole moment stipulate slower rotation of FA+ around the N–N axis in contrast to more frequent MA+ rotations around the C–N axis. In this way, we attributed the experimental modes of FAPbI3 at Zone II and correlated them with the DFT calculated data (see Table 1). Analogously, we attribute the Raman modes for FAPbBr3. As discussed before, the exception is the “in-plane rotation” mode, which is restricted due to the more compact lattice structure.
| Literature | Description | DFT-FAPbI3 | FAPbI3 | Cs0.1FA0.9PbI3 | Cs0.1FA0.9PbI2.6Br0.4 | FAPbBr3 | DFT-FAPbBr3 |
|---|---|---|---|---|---|---|---|
| 19,2937 | Octahedral twist | 16, 20, 22 | 13#,21# | 15 | 20# | 30, 31 | |
| 3537 | Octahedral distortion | 33, 35 | 43 | 40 | 32 | 58# | 34, 44, 63 |
| In-plane rotation around a corner H | 61 | 63# | 52# | 50# | |||
| 12537 | Out-of-plane rotation around N–N axis | 63 | 96# | 89# | 78# | 84# | 77 |
| 105*40 | FA+ Translation | 97 | 114 | 109 | 105 | 118# | 102, 121 |
| 64,75,81,9237 | |||||||
| 310*,4031537 | Out-of-plane sym. + bending HN–C–NH | 429 | 250 | 358 | 309 | 368 | |
| 485*40 | Out-of-plane asym. + bending H2N–C–NH2 | 494 | 282# | 427# | 470# | 474 | |
| 521*,4052143 | H2N–C–NH2 bending | 507 | 517, 524 | 518 | 522 | 510 | |
| 587*,4058743 | NH2 wagging | 560 | 597 | 585 | 567 | 565 | |
| 71843 | NH2torsion + C–H | 674 | 746 | 672 | |||
| out-of-plane bending | |||||||
| 104743 | NH2 rocking | 1001 | 1064# | 1063# | 1000 | ||
| 1120*,40113043 | C–N sym. stretching | 1132 | 1116 | 1115 | 1112 | 1159 | |
| 138843 | C–H in-plane bending + | 1359 | 1351#, 1393 | 1362 | |||
| C–N asym. stretching | |||||||
| 1500*,40141943 | C–H in-plane bending | 1534 | 1560 | 1527 | |||
| 1620*,40164543 | NH2 scissoring | 1614 | 1623, 1627# | 1623 | |||
| 1720*,40174143 | NH2 scissoring | 1712 | 1720 | 1723 | |||
| 178943 | NH2,C–H scissoring + | 1875 | |||||
| C–N asym. Stretching |
For the Raman modes of FAPbBr3 at Zone III, we found close agreement between the experimental data and the results from DFT calculations (see Table 1). It is worth noticing that the frequencies of those modes are only slightly shifted with respect to the phonon modes of the isolated FA+, which indicates a weak interaction between the molecules and the PbBr6 octahedra.
To summarize, we have identified the vibrational modes existing in FAPbI3 above 200 cm−1 using DFT calculations. Additionally, we have correlated the DFT results with experimental data obtained for FAPbBr3 single crystals. Table 1 summarizes all modes discussed above and lists their attribution based on the experimental spectra shown in Fig. 2 and 4.
Effect of the partial Cs+ and Br− substitutions
Following the previous discussion, we focus on the effect of partial substitution of FA+ by Cs+ and I− by Br− on the vibrational behaviour of LHPs and the stabilization of the cubic form. We refer here to XRD and PL measurements (Fig. S5 and S6, ESI†) of the chosen mixed compounds to support the comparison of the Raman spectra (Fig. 5).In analogy to the Raman spectra, we compare the XRD patterns of FAPbI3 and the mixed compounds (Fig. S5, ESI†). Due to the similarity of the patterns, we fit them to the phase structure of FAPbI3 presented in the literature, a cubic Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m symmetry.62 The (100) diffraction maximum shifts only when Cs+ and Br− are incorporated. The corresponding lattice constants were found to be 6.357 Å for FAPbI3 and Cs0.1FA0.9PbI3, and 6.293 Å for Cs0.1FA0.9PbI2.6Br0.4. The comparison of the reported lattice constants of the pure compounds FAPbI3 (6.3620 Å62) and CsPbI3 (6.242 Å63) in cubic form suggests a continuity of the phase-structure of FAPbI3 with the incorporation of Cs+. The substitution of I− by Br− results in the expected decrease of the lattice constant due to the smaller size and more electronegative character of the incorporated halide.
m symmetry.62 The (100) diffraction maximum shifts only when Cs+ and Br− are incorporated. The corresponding lattice constants were found to be 6.357 Å for FAPbI3 and Cs0.1FA0.9PbI3, and 6.293 Å for Cs0.1FA0.9PbI2.6Br0.4. The comparison of the reported lattice constants of the pure compounds FAPbI3 (6.3620 Å62) and CsPbI3 (6.242 Å63) in cubic form suggests a continuity of the phase-structure of FAPbI3 with the incorporation of Cs+. The substitution of I− by Br− results in the expected decrease of the lattice constant due to the smaller size and more electronegative character of the incorporated halide.
For further consideration we assume a homogeneous distribution of Cs+ and Br− in the mixed compositions, which is indirectly proven by the PL measurements (Fig. S6, ESI†) due to the absence of a secondary peak related to separated cesium-rich or bromide-rich zones. We also expect no symmetry change with respect to the cubic FAPbI3.
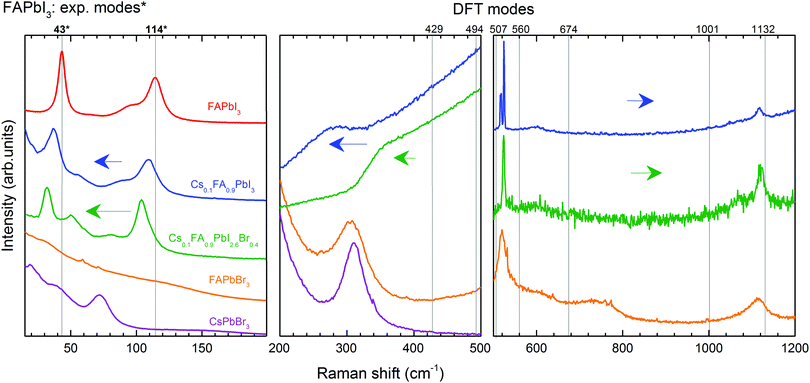
We discuss first the Raman spectrum of Cs0.1FA0.9PbI3. Within the range between 15 and 200 cm−1, it demonstrates a slight red-shift with respect to the spectrum of FAPbI3: the modes observed at 40 and 109 cm−1 of the mixed compound appear at 43 and 114 cm−1 in FAPbI3, respectively (see Fig. 5). The observed shift of phonon modes to lower frequencies correlates with the previously suggested release of stresses in the FAPbI3 single crystals upon Cs+ substitution. The magnitude of this reduction is probably not valuable enough to represent the prolonged stabilization of the cubic structure, which is observed in the degradation of this compound after a few weeks.
In Zone I, the appearance of the twist modes at 13 and 21 cm−1 implies some local distortion due to the incorporation of the Cs+ cation. Indeed, it can be expected that the heavier and more electronically spherical Cs+ atoms should have notably stronger ionic interaction with the PbX6 framework than the FA+ molecules.
The influence of the incorporation of the Cs+ atoms and the effect on the modes of Zone II are analyzed according to the Cs+ atoms displacement from the A-position, considering that they are contained in a FAPbI3 matrix. For this, we compared the mixed compound Cs0.1FA0.9PbI3 with CsPbBr3 in which the atomic trajectories of Cs+ are known.42 In CsPbBr3, the Cs+ cations have 0.85 Å displacement in a head-to-head motion which is stabilized by a cooperative motion of Br− ions. This means that the octahedral sub-cages that are approached by Cs+ ions expand due to Pauli repulsion forces. Therefore, the translation of Cs+ in the mixed compound is likely coordinated with the surrounding FA+ molecules to reduce the energy of the system during the distortion of the octahedral cages, which results in a shift of the corresponding translation mode from 114 cm−1 in FAPbI3 to 109 cm−1.
In the range from 200 to 500 cm−1, we observe two modes at 250 cm−1 and 282 cm−1. Compared to the DFT calculations of FAPbI3, they may be related to the out-of-plane FA+ bending modes which are predicted at 429 and 494 cm−1, respectively (see Table 1). The higher energies of these modes of FAPbI3 basically mean an overestimation of the FA+–I− interaction in our theoretical model. This may originate from deviations from the assumed Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group and/or considerable contributions of Cs+ to this interaction. CsPbBr3 reveals a second-order-phonon mode at 312 cm−1 related to Cs+ translations, which may influence the FA+-bending via variations of the internal electric field. The same modes appear in FAPbBr3 at 309 and 470 cm−1 respectively.
m space group and/or considerable contributions of Cs+ to this interaction. CsPbBr3 reveals a second-order-phonon mode at 312 cm−1 related to Cs+ translations, which may influence the FA+-bending via variations of the internal electric field. The same modes appear in FAPbBr3 at 309 and 470 cm−1 respectively.
The Raman spectrum of Cs0.1FA0.9PbI3 in Zone III presents peaks at frequencies in good agreement with the predicted ones by the DFT calculations of the molecular modes of FAPbI3. One noticeable difference between them is the splitting of the mode around 520 cm−1 present only for the former case. This may be related to the previously discussed lowering of symmetry. In this case, the frequency of the mode “molecular bending” depends on the position of the molecule inside the cage. This distortion in the structure was previously discussed from the presence of an additional peak for the “octahedral twist” mode.
To summarize, the effect of Cs+ substitution in the Raman spectrum of FAPbI3 can be appreciated in a red-shift of the medium-frequency spectrum (<500 cm−1) due to the release of stresses of the Pb–I bonds and the coordination of the translations of Cs+ and FA+.
The Raman spectrum of Cs0.1FA0.9PbI2.6Br0.4 shows a red shift compared to the spectrum of Cs0.1FA0.9PbI3 for low frequencies (<200 cm−1). The octahedral distortion peak shifts from 40 to 32 cm−1 and the translation one from 109 to 105 cm−1. This is counterintuitive as the lighter Br ions are expected to cause a shift to higher phonon frequencies. We observe a similar unexplained red shift effect in CsPbBr3 as compared to CsPbI3. For these materials, the most prominent peaks that we can ascribe to the Raman modes “distortion of the octahedra” and “translation of Cs+” are present at 55 and 108 cm−1 in CsPbI364 and at 40 and 73 cm−1 in CsPbBr3 (see Fig. S3, ESI†), respectively. The structure of CsPbBr3 is more compact compared to CsPbI3, as suggested by a GTF closer to 1 (0.974 vs. 0.836, respectively). Therefore, we suggest an effect of the strength release of the Pb–X bonds as in both cases a red shift is accompanied by an increase of the GTF (see Table S2, ESI†).
In Zone I, the disappearance of the second peak of the “octahedral twist” mode at 21 cm−1 of Cs0.1FA0.9PbI3 suggests that the emergence of additional stresses in the PbX6 structure caused by the incorporation of Cs+ somehow counteracts the distortion introduced by Br−1.
The peaks of the high-coupling range of Zone II (50–200 cm−1) are red-shifted as previously discussed. In the low-coupling range (200–500 cm−1), the modes at 250 and 282 cm−1 expectedly shift to higher energies: 358 and 427 cm−1 respectively. Similar Raman mode frequencies of 429 and 494 cm−1 are found for pure FAPbI3. This can be understood considering that the modes in this frequency range are influenced by the internal electric field which determines the strength of the coupling. A combination of the less frequent translation of Cs+ atoms with the stronger PbX6 octahedral bonds results in the weakening of the interaction between FA+ molecules and the PbX6 octahedra.
The Raman modes of Zone III of Cs0.1FA0.9PbI2.6Br0.4 have quite similar frequencies to the modes of Cs0.1FA0.9PbI3. The splitting of the mode around 520 cm−1 is absent in the former case, which supports the lowering of the distortion created by the incorporation of Cs+. Compared to FAPbBr3, the mixed compounds do not present a peak at 740 cm−1, related to the combined vibration of NH2 torsion and C–H out plane bending and predicted for FAPbI3 at 674 cm−1. Instead, they present a broad peak around 1064 cm−1 assigned to NH2 rocking. The activation of different modes is likely a consequence of the lattice size.
In conclusion, the incorporation of Br− affects the dynamics of Cs+, hindering the frequency of the atomic displacement due to enhanced lattice compactness. This is expressed in the red-shift of the low-frequency range (<200 cm−1). A blue shift of the low-coupled modes (from 200 to 500 cm−1) of Cs0.1FA0.9PbI2.6Br0.4 towards the frequencies of the Raman modes of FAPbI3 indicates softening in the interaction of the FA+ molecules and the octahedra. Therefore, the structure is stabilized in a cubic form due to the reduction of the stresses in the Pb–X bonds, resulting in a more compact crystalline lattice. In this case, the frequency of cooperative translation in the A-site is hindered by the surrounding Br− atoms.
Conclusions
We have reported the vibrational properties of formamidinium (FA)-based LHPs investigated by micro-Raman spectroscopy. The experimental spectra were presented for the first time for the cubic forms of FAPbI3, Cs0.1FA0.9PbI3 and Cs0.1FA0.9PbI2.6Br0.4 hybrid perovskites. Theoretical Raman spectra were obtained for FAPbBr3 and FAPbI3 using DFT calculations to support the identification of the experimental Raman modes.Low frequency Raman modes of LHPs (<50 cm−1 for I-based and <65 cm−1 for Br-based) can be assigned to the vibrational modes of the Oh symmetry, twist and distortion of the octahedra. Medium frequency Raman modes (from 50 to 500 cm−1) of FA-containing LHPs are derived for molecular reorganization and the consequent octahedral response, which are in-plane and out-of-plane rotations, and symmetric and asymmetric out-of-plane bending. The closeness of energies of FA+ modes above 500 cm−1 for FAPbBr3 and the isolated FA+ ions denotes a low interaction between the molecules and the PbBr6 octahedra. This is presumed to result from the neglectable dipole moment of the FA+ ions.
The improved stability of FAPbI3 due to the incorporation of Cs+ and Br− is the result of the combined effect of both components. It is explained by the release of stresses of the Pb–X bonds, which is a consequence of a more compact lattice and a less frequent displacement of the FA+ ions resulting from the coupling with the Cs+ atoms. This is expressed in the Raman spectrum as a red-shift of the octahedra related modes (<500 cm−1).
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge the financial support provided by the Scholarship Becas Chile-DAAD 2017/91645541 and the German Research Foundation within the Collaborative Research Center 787 (SFB 787), and the Paderborn Center for Parallel Computing (PC2) for computing time on OCuLUS and FPGA-based supercomputer NOCTUA. This work was also supported by the German Federal Ministry for Economic Affairs and Energy (BMWi) under contract number 0324095H (speedCIGS).References
- C. C. Stoumpos, C. D. Malliakas and M. G. Kanatzidis, Inorg. Chem., 2013, 52, 9019–9038 CrossRef CAS PubMed.
- J. Chen, S. Zhou, S. Jin, H. Li and T. Zhai, J. Mater. Chem. C, 2016, 4, 11–27 RSC.
- D. P. McMeekin, G. Sadoughi, W. Rehman, G. E. Eperon, M. Saliba, M. T. Hoerantner, A. Haghighirad, N. Sakai, L. Korte and B. Rech, et al. , Science, 2016, 351, 151–155 CrossRef CAS PubMed.
- J. H. Noh, S. H. Im, J. H. Heo, T. N. Mandal and S. I. Seok, Nano Lett., 2013, 13, 1764–1769 CrossRef CAS PubMed.
- Z. Yang, C.-C. Chueh, P.-W. Liang, M. Crump, F. Lin, Z. Zhu and A. K.-Y. Jen, Nano Energy, 2016, 22, 328–337 CrossRef CAS.
- G. E. Eperon, S. D. Stranks, C. Menelaou, M. B. Johnston, L. M. Herz and H. J. Snaith, Energy Environ. Sci., 2014, 7, 982–988 RSC.
- C. M. Sutter-Fella, Y. Li, M. Amani, J. W. Ager III, F. M. Toma, E. Yablonovitch, I. D. Sharp and A. Javey, Nano Lett., 2015, 16, 800–806 CrossRef PubMed.
- H. J. Snaith, J. Phys. Chem. Lett., 2013, 4, 3623–3630 CrossRef CAS.
- X.-Y. Zhu and V. Podzorov, Charge carriers in hybrid organic–inorganic lead halide perovskites might be protected as large polarons, 2015.
- K. Miyata, D. Meggiolaro, M. T. Trinh, P. P. Joshi, E. Mosconi, S. C. Jones, F. De Angelis and X.-Y. Zhu, Sci. Adv., 2017, 3, e1701217 CrossRef PubMed.
- X. Zhao, J. D. A. Ng, R. H. Friend and Z.-K. Tan, ACS Photonics, 2018, 5, 3866–3875 CrossRef CAS.
- C. Yi, J. Luo, S. Meloni, A. Boziki, N. Ashari-Astani, C. Graetzel, S. M. Zakeeruddin, U. Röthlisberger and M. Graetzel, Energy Environ. Sci., 2016, 9, 656–662 RSC.
- A. Kojima, K. Teshima, Y. Shirai and T. Miyasaka, J. Am. Chem. Soc., 2009, 131, 6050–6051 CrossRef CAS PubMed.
- Y. Wang, Y. Zhang, Y. Lu, W. Xu, H. Mu, C. Chen, H. Qiao, J. Song, S. Li and B. Sun, et al. , Adv. Opt. Mater., 2015, 3, 1389–1396 CrossRef CAS.
- F. Li, C. Ma, H. Wang, W. Hu, W. Yu, A. D. Sheikh and T. Wu, Nat. Commun., 2015, 6, 8238 CrossRef PubMed.
- X. Wang, H. Zhou, S. Yuan, W. Zheng, Y. Jiang, X. Zhuang, H. Liu, Q. Zhang, X. Zhu and X. Wang, et al. , Nano Res., 2017, 10, 3385–3395 CrossRef CAS.
- H. Zhu, Y. Fu, F. Meng, X. Wu, Z. Gong, Q. Ding, M. V. Gustafsson, M. T. Trinh, S. Jin and X. Zhu, Nat. Mater., 2015, 14, 636 CrossRef CAS PubMed.
- Q. Dong, Y. Fang, Y. Shao, P. Mulligan, J. Qiu, L. Cao and J. Huang, Science, 2015, 347, 967–970 CrossRef CAS PubMed.
- S. Yakunin, D. N. Dirin, Y. Shynkarenko, V. Morad, I. Cherniukh, O. Nazarenko, D. Kreil, T. Nauser and M. V. Kovalenko, Nat. Photonics, 2016, 10, 585 CrossRef CAS.
- O. Nazarenko, S. Yakunin, V. Morad, I. Cherniukh and M. V. Kovalenko, NPG Asia Mater., 2017, 9, e373 CrossRef CAS.
- H. Wei, Y. Fang, P. Mulligan, W. Chuirazzi, H.-H. Fang, C. Wang, B. R. Ecker, Y. Gao, M. A. Loi and L. Cao, et al. , Nat. Photonics, 2016, 10, 333 CrossRef CAS.
- Y. Zhao, H. Tan, H. Yuan, Z. Yang, J. Z. Fan, J. Kim, O. Voznyy, X. Gong, L. N. Quan and C. S. Tan, et al. , Nat. Commun., 2018, 9, 1607 CrossRef PubMed.
- S. Pang, H. Hu, J. Zhang, S. Lv, Y. Yu, F. Wei, T. Qin, H. Xu, Z. Liu and G. Cui, Chem. Mater., 2014, 26, 1485–1491 CrossRef CAS.
- N. Pellet, P. Gao, G. Gregori, T.-Y. Yang, M. K. Nazeeruddin, J. Maier and M. Graetzel, Angew. Chem., 2014, 126, 3215–3221 CrossRef.
- Q. Han, S.-H. Bae, P. Sun, Y.-T. Hsieh, Y. Yang, Y. S. Rim, H. Zhao, Q. Chen, W. Shi and G. Li, et al. , Adv. Mater., 2016, 28, 2253–2258 CrossRef CAS PubMed.
- M. I. Saidaminov, A. L. Abdelhady, G. Maculan and O. M. Bakr, Chem. Commun., 2015, 51, 17658–17661 RSC.
- Z. Li, M. Yang, J.-S. Park, S.-H. Wei, J. J. Berry and K. Zhu, Chem. Mater., 2015, 28, 284–292 CrossRef.
- D. Forgács, D. Pérez-del Rey, J. Ávila, C. Momblona, L. Gil-Escrig, B. Daenekamp, M. Sessolo and H. J. Bolink, J. Mater. Chem. A, 2017, 5, 3203–3207 RSC.
- I. Lignos, V. Morad, Y. Shynkarenko, C. Bernasconi, R. M. Maceiczyk, L. Protesescu, F. Bertolotti, S. Kumar, S. T. Ochsenbein and N. Masciocchi, et al. , ACS Nano, 2018, 12, 5504–5517 CrossRef CAS.
- M. A. Becker, R. Vaxenburg, G. Nedelcu, P. C. Sercel, A. Shabaev, M. J. Mehl, J. G. Michopoulos, S. G. Lambrakos, N. Bernstein and J. L. Lyons, et al. , Nature, 2018, 553, 189 CrossRef CAS.
- V. V. Belykh, D. R. Yakovlev, M. M. Glazov, P. S. Grigoryev, M. Hussain, J. Rautert, D. N. Dirin, M. V. Kovalenko and M. Bayer, Nat. Commun., 2019, 10, 673 CrossRef.
- M. Puppin, S. Polishchuk, N. Colonna, A. Crepaldi, D. Dirin, O. Nazarenko, R. De Gennaro, G. Gatti, S. Roth and T. Barillot, et al., 2019, arXiv preprint arXiv:1909.00248.
- E. T. Hoke, D. J. Slotcavage, E. R. Dohner, A. R. Bowring, H. I. Karunadasa and M. D. McGehee, Chem. Sci., 2015, 6, 613–617 RSC.
- A. A. Bakulin, O. Selig, H. J. Bakker, Y. L. Rezus, C. Mueller, T. Glaser, R. Lovrincic, Z. Sun, Z. Chen and A. Walsh, et al. , J. Phys. Chem. Lett., 2015, 6, 3663–3669 CrossRef CAS.
- S. Brittman, G. W. P. Adhyaksa and E. C. Garnett, MRS Commun., 2015, 5, 7–26 CrossRef CAS.
- Y. Guo, O. Yaffe, D. W. Paley, A. N. Beecher, T. D. Hull, G. Szpak, J. S. Owen, L. E. Brus and M. A. Pimenta, Phys. Rev. Mater., 2017, 1, 042401 CrossRef.
- A. M. Leguy, A. R. Goñi, J. M. Frost, J. Skelton, F. Brivio, X. Rodrguez-Martnez, O. J. Weber, A. Pallipurath, M. I. Alonso and M. Campoy-Quiles, et al. , Phys. Chem. Chem. Phys., 2016, 18, 27051–27066 RSC.
- R. G. Niemann, A. G. Kontos, D. Palles, E. I. Kamitsos, A. Kaltzoglou, F. Brivio, P. Falaras and P. J. Cameron, J. Phys. Chem. C, 2016, 120, 2509–2519 CrossRef CAS.
- A. Y. Lee, D. Y. Park and M. S. Jeong, J. Alloys Compd., 2018, 738, 239–245 CrossRef CAS.
- L. Wang, K. Wang and B. Zou, J. Phys. Chem. Lett., 2016, 7, 2556–2562 CrossRef CAS PubMed.
- J.-H. Cha, J. H. Han, W. Yin, C. Park, Y. Park, T. K. Ahn, J. H. Cho and D.-Y. Jung, J. Phys. Chem. Lett., 2017, 8, 565–570 CrossRef CAS PubMed.
- O. Yaffe, Y. Guo, L. Z. Tan, D. A. Egger, T. Hull, C. C. Stoumpos, F. Zheng, T. F. Heinz, L. Kronik and M. G. Kanatzidis, et al. , Phys. Rev. Lett., 2017, 118, 136001 CrossRef PubMed.
- E. Kucharska, J. Hanuza, A. Ciupa, M. Maczka and L. Macalik, Vib. Spectrosc., 2014, 75, 45–50 CrossRef CAS.
- M. Carignano, Y. Saeed, S. A. Aravindh, I. S. Roqan, J. Even and C. Katan, Phys. Chem. Chem. Phys., 2016, 18, 27109–27118 RSC.
- M. A. Carignano, S. A. Aravindh, I. S. Roqan, J. Even and C. Katan, J. Phys. Chem. C, 2017, 121, 20729–20738 CrossRef CAS.
- R. O. Jones, Rev. Mod. Phys., 2015, 87, 897–923 CrossRef.
- D. N. Dirin, I. Cherniukh, S. Yakunin, Y. Shynkarenko and M. V. Kovalenko, Chem. Mater., 2016, 28, 8470–8474 CrossRef CAS PubMed.
- M. Ledinsky, P. Loeper, B. Niesen, J. Holovsky, S.-J. Moon, J.-H. Yum, S. De Wolf, A. Fejfar and C. Ballif, J. Phys. Chem. Lett., 2015, 6, 401–406 CrossRef CAS PubMed.
- P. E. Bloechl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef CAS PubMed.
- G. Kresse and J. Furthmueller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmueller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- J. Klimeš, D. R. Bowler and A. Michaelides, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 195131 CrossRef.
- A. Fonari and S. Stauffer, VASP Raman, 2013, https://github.com/raman-sc/VASP/.
- J. Weidlein, U. Mueller and K. Dehnicke, Schwingungsspektroskopie: eine Einfuehrung, Thieme, 1982 Search PubMed.
- T. Glaser, C. Mueller, M. Sendner, C. Krekeler, O. E. Semonin, T. D. Hull, O. Yaffe, J. S. Owen, W. Kowalsky and A. Pucci, et al. , J. Phys. Chem. Lett., 2015, 6, 2913–2918 CrossRef CAS.
- A. Amat, E. Mosconi, E. Ronca, C. Quarti, P. Umari, M. K. Nazeeruddin, M. Graetzel and F. De Angelis, Nano Lett., 2014, 14, 3608–3616 CrossRef CAS PubMed.
- C. Quarti, G. Grancini, E. Mosconi, P. Bruno, J. M. Ball, M. M. Lee, H. J. Snaith, A. Petrozza and F. De Angelis, J. Phys. Chem. Lett., 2013, 5, 279–284 CrossRef PubMed.
- J. Oszczapowicz, C. U. Regelmann and G. Haefelinger, J. Chem. Soc., Perkin Trans. 2, 1990, 1551–1557 RSC.
- J. M. Frost, K. T. Butler, F. Brivio, C. H. Hendon, M. Van Schilfgaarde and A. Walsh, Nano Lett., 2014, 14, 2584–2590 CrossRef CAS PubMed.
- A. Poglitsch and D. Weber, J. Chem. Phys., 1987, 87, 6373–6378 CrossRef CAS.
- A. A. Petrov, E. A. Goodilin, A. B. Tarasov, V. A. Lazarenko, P. V. Dorovatovskii and V. N. Khrustalev, Acta Crystallogr., Sect. E: Crystallogr. Commun., 2017, 73, 569–572 CrossRef CAS PubMed.
- M. T. Weller, O. J. Weber, J. M. Frost and A. Walsh, J. Phys. Chem. Lett., 2015, 6, 3209–3212 CrossRef CAS.
- M. Ahmad, G. Rehman, L. Ali, M. Shafiq, R. Iqbal, R. Ahmad, T. Khan, S. Jalali-Asadabadi, M. Maqbool and I. Ahmad, J. Alloys Compd., 2017, 705, 828–839 CrossRef CAS.
- G. Yuan, S. Qin, X. Wu, H. Ding and A. Lu, Phase Transitions, 2018, 91, 38–47 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp06568g |
| This journal is © the Owner Societies 2020 |