Open Access Article
Open Access ArticleWhy ammonium detection is particularly challenging but insightful with ionophore-based potentiometric sensors – an overview of the progress in the last 20 years
María
Cuartero
 *,
Noemi
Colozza
,
Bibiana M.
Fernández-Pérez
*,
Noemi
Colozza
,
Bibiana M.
Fernández-Pérez
 and
Gastón A.
Crespo
and
Gastón A.
Crespo
 *
*
Department of Chemistry, School of Engineering Sciences in Chemistry, Biotechnology and Health, KTH Royal Institute of Technology, 10044 Stockholm, Sweden. E-mail: mariacb@kth.se; gacp@kth.se
First published on 12th March 2020
Abstract
The monitoring of ammonium ion concentration has gained the attention of researchers from multiple fields since it is a crucial parameter with respect to environmental and biomedical applications. For example, ammonium is considered to be a quality indicator of natural waters as well as a potential biomarker of an enzymatic byproduct in key physiological reactions. Among the classical analytical methods used for the detection of ammonium ions, potentiometric ion-selective electrodes (ISEs) have attracted special attention in the scientific community because of their advantages such as cost-effectiveness, user-friendly features, and miniaturization ability, which facilitate easy portable measurements. Regarding the analytical performance, the key component of ISEs is the selective receptor, labelled as an ionophore in ISE jargon. Indeed, the preference of an ionophore for ammonium amongst other ions (i.e., selectivity) is a factor that primarily dictates the limit of detection of the electrode when performing measurements in real samples. A careful assessment of the literature for the last 20 years reveals that nonactin is by far the most employed ammonium ionophore to date. Despite the remarkable cross-interference of potassium over the ammonium response of nonactin-based ISEs, analytical applications comprising water quality assessment, clinical tests in biological fluids, and sweat monitoring during sports practice have been successfully researched. Nevertheless, there is evident difficulty in the determination of close-to-micromolar levels of ammonium in real samples with a significant potassium background level (i.e., millimolar concentration). This fact has fostered the search for a large variety of ammonium ionophores over the years, which are critically inspected herein. Overall, we provide an easily readable state of the art accompanied by a comprehensive description of other types of ammonium electrodes, including commercially available units. We conclude that newer breakthroughs are still required in the field to reach the desired analytical applications.
1. Introduction
In the last few decades, potentiometric ion-selective electrodes (ISEs) have been proposed as effective analytical tools in multifaceted applications where ion detection is essential. Indeed, the utilization of ISEs is currently preferred over other analytical techniques because of their cost-effectiveness, user-friendly features, and miniaturization capability. Moreover, ISEs are some of the few analytical techniques that provide in situ real-time measurements of the target concentration with total reliability.1–5 Major examples that evidence the success of ISEs are the membrane-based design of a sensor and have been applied for ion determination mainly in water quality assessment,1,6,7 clinical analyses,8–11 and monitoring of sport practices.2,12–14Looking back at the development history of ISEs, the integration of ion-selective membranes (ISMs) as the sensing element has undoubtedly been a disruptive event in this field.15 Today, the technology involving ISM fabrication is well entrenched and the criteria for selecting components/materials as well as the necessary features have been known for decades.15 One remarkable aspect is the tuning of membrane selectivity towards the target ions by the incorporation of a specific receptor (labelled as ionophore in ISE terminology) in the ISM. Traditionally, ionophores are embedded into a plasticized polymeric matrix with intrinsic ion-exchange properties, which is provided by a mixture of a polymer, plasticizer, and ion exchanger.16,17 The selectivity pattern of the ionophore is the primary factor that dictates the limit of detection (LOD) of ISE measurements for any sample.
Essentially, the role of the ionophore is to promote a drastic change in the response pattern found in ionophore-free membranes exclusively containing the polymer, plasticizer, and ion exchanger.16,17 Therefore, the ion-exchange process at the sample–membrane interphase relies on the extraction of the target ion from the solution (i.e., solvated state of the ion in the aqueous phase) to the ISM (i.e., formation of the ion–ionophore complex at the organic phase). If the formation of the ion–ionophore complex is sufficiently accessible thermodynamically, the hydration energy of ions in the aqueous phase can be overcome and ion exchange becomes an assisted process.16 As a result, the order for ion preference to be exchanged at the sample–membrane interphase is not based anymore on regular lipophilicity distribution (i.e., following the Hofmeister series) as that occurring in ionophore-free membranes or even with ionophores that are not sufficiently selective for a single ion.17–19
Ideally, to ensure the reliable analytical detection of an individual ion (i.e., no interference) using the corresponding ISE, the ionophore should uniquely bind with that ion. Unfortunately, this is beyond reality and every ISM—comprising a distinct ionophore—presents a response (or selectivity) pattern toward the ion analyte together with a number of interferences. Notably, it is typically more challenging to develop effective ISEs for highly hydrophilic small ions (for example, fluorides and sulfates with high hydration energies).20 These species have to overcome the enthalpically unfavorable phase transfer from an aqueous solution into the membrane owing to the presence of the ionophore. However, it is challenging to access receptors (particularly for anions) that fulfill such a requirement. Consequently, as a general trend, the literature comprises several studies regarding cation ionophores, whereas there is a lack of studies on effective anion ionophores.18,21–23
Among the cation ionophores, the case of the ammonium ion (NH4+) is particularly interesting. Even though research on the provision of NH4+-selective electrodes has been really active over the past few decades, the very first ionophore investigated for this purpose is indeed the most widely used until now. Nonactin is one of the earliest tested antibiotics for cation-selective electrodes. Indeed, the first studies on the suitability of nonactin and its homologous materials as ionophores in ISMs were carried out with potassium (K+) as the target cation, but its selectivity in favor of NH4+ was soon evident.24,25 This preference could be attributed to the ad hoc properties of nonactin when binding with NH4+.26–29 Nevertheless, both ionic size and monovalent charge of K+ are competitively suitable with the receptor site features of nonactin.26 Consequently, the presence of K+ in the matrix in which NH4+ needs to be measured represents an interference that sometimes—depending on the nature of the sample—impedes the reliable detection of NH4+ using ISEs based on nonactin.
The accurate detection of NH4+ is needed in samples comprising many different compositions and from totally different fields, ranging from agricultural water to tissues and cell media.30,31 In all these samples, the molar ratio of NH4+/K+ (and probably other side-interfering ions) dictates the suitability of nonactin-based NH4+-selective electrodes for the consequent analysis. Hence, in this review, we firstly investigate the performances of nonactin implemented as NH4+ ionophore in ISMs with different architectures. A comprehensive evaluation of collected papers reported in the last 20 years can shed light on certain samples that are still inaccessible due to the intrinsic selectivity limitations of nonactin. On the other hand, other receptors and strategies have been explored, as evident in the literature, in an attempt to provide alternatives to the use of nonactin as an ionophore. Herein, we report the entire scenario created for NH4+ sensing using potentiometric electrodes designed over the last 20 years, mainly focusing on the use of ionophores, but also discussing certain other highlighted contributions and commercially available devices. Beyond providing an updated collection of published papers on NH4+ potentiometric detection until now, this review critically analyzes the advantages and drawbacks of the selected papers in order to provide guidance toward the definitive solution for NH4+ detection in the presence of primary interferences.
It should be noted that we do not intend to deviate from our discussions any of the manuscripts related to NH4+ electrodes over the selected period; if this has inadvertently been the case, the aim was not to undervalue any of the related publications. Overall, we consider that the selected papers offer a true vision of the field. In addition, all the analytical parameters discussed throughout this review were obtained from the original sources (published papers), and the main aim when analyzing them was not to criticize the manner in which these values were calculated. However, selectivity coefficients require special attention; accordingly, the reader should carefully consider our discussions. It is rather common in the literature to find biased calculations if the experiments were not meticulously performed and the equations were not used appropriately (e.g., the necessity of considering any deviation from the Nernstian slope of the interfering ion response). Indeed, while a majority of the inspected papers use the well-known “separate solution method” for the calculation of selectivity coefficients, we could not find the description of the corresponding calculations/methods in other works. A very useful guide to avoid systematic errors was reported by Bakker and co-workers in 1997, which has been revised over the years.32–34
2. Ammonium-selective electrodes based on nonactin as the ionophore
Inspired by the behavior of ions in physiological membranes in the presence of macrotetrolide-like antibiotics,35 Simon and co-workers pioneered the use of nonactin as the ionophore in liquid membranes in the 70s.24,36,37 The authors evaluated the selectivity pattern of the membrane and calculated the potentiometric selectivity coefficients for NH4+ against alkaline cations and calcium ions. Remarkable interference from K+ was already evident in the results of that study, affording a logarithmic potentiometric selectivity coefficient of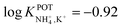 .25 This value revealed that only when the K+ concentration is within 1 and 2 orders of magnitude higher than the NH4+ concentration in the sample, nonnegligible interference can be obtained. Beyond that, NH4+ detection in the sample becomes difficult.
.25 This value revealed that only when the K+ concentration is within 1 and 2 orders of magnitude higher than the NH4+ concentration in the sample, nonnegligible interference can be obtained. Beyond that, NH4+ detection in the sample becomes difficult.
The first implementation of nonactin in polymeric membranes was reported by Meyerhoff and co-workers,38,39 who developed a potentiometric sensor for detecting ammonia gas in blood samples based on the use of a buffer solution phase placed between NH4+–ISM and a gas-permeable membrane in order to convert ammonia into NH4+. This work paved the way for a large number of studies regarding nonactin-based NH4+-selective electrodes (NH4–ISEs) until now. Here, it is anticipated that the optimization of the membrane components may provide a marginal improvement in the analytical performances of nonactin-based NH4–ISEs. However, overall, K+ interference is always evident to a rather similar extent that can be expressed by the comparable binding affinity of nonactin toward either NH4+ and K+, because both these ions have very similar ionic radii (1.38 and 1.43 Å, respectively).26
Nonactin (Fig. 1a) is a spherical compound characterized by a well-defined spatial cavity that can accommodate cations, such as the ones from alkaline metal groups.28,29 In addition, nonactin presents the possibility for hydrogen binding when the cation is present in an organic solvent. In particular, in the case of NH4+, four H-bonds are formed between the cation and four ether oxygens of nonactin (Fig. 1b), as demonstrated by 13C NMR, IR, and crystallography studies.28,29 This is the primary difference between NH4+ and K+ binding with nonactin, thereby yielding a slightly higher preference toward NH4+ as compared to that toward K+, regardless of the plausibility of the described H-bonds in the complex medium/environment.26
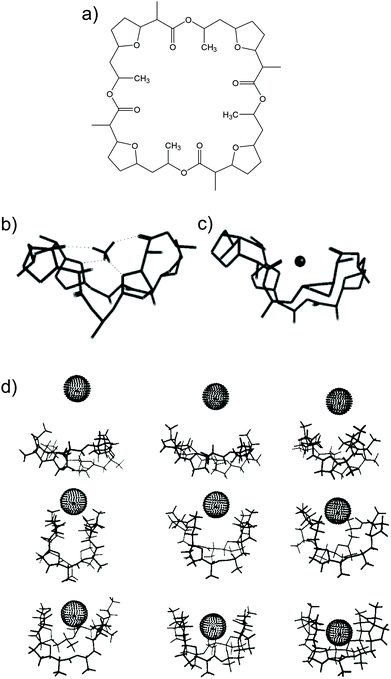 | ||
| Fig. 1 (a) Nonactin. (b) Minimized structure of nonactin-complexed NH4+. Reprinted from ref. 26 with permission from the American Chemical Society, Copyright 2019. (c) Representative structures of nonactin-complexed K+ upon approximation: 9, 8, 7, 6, 5, 4, 3, 2, and 1 Å from the top to the bottom/left to the right. Minimized structure of nonactin-complexed NH4+. Reprinted from ref. 113 with permission from the American Chemical Society, Copyright 2019. | ||
Table 1 lists a summary of nonactin-based NH4–ISEs reported over the last few years, mainly focusing on the last two decades (1998–2019), but also summarizes earlier papers that we considered to be important in this case. In the review by Bühlmann et al., all NH4–ISEs published until 1998 were evaluated; therefore, the present review complements that manuscript.18 The authors already discussed the possibility of incorporating nonactin as an NH4+ ionophore in plasticized polyvinyl chloride (PVC) membranes (mainly with nitrophenyl octyl ether (NPOE)), silicone rubber polyurethane, and cellulose acetate membranes; however, all these electrodes reported similar K+ interference levels.27,40–44 For overcoming this issue, the chemometric correction of K+ interference using an array of inner-filling solution-type ISEs for NH4+, K+, Na+, and Ca2+ in flow injection analysis (FIA) has been proposed by Diamond and co-workers in 1994.45 Indeed, this approach was later used by the group of Del Valle with all-solid-state electrodes.46,47 Importantly, this array of ISEs was demonstrated to be suitable for the detection of NH4+ at the millimolar level; at the same time, the array was used to estimate the content of K+ (∼1 mM) in river water and wastewater.
| Type of electrode | Membrane composition (wt%) | Calibration parameters | NH4+/K+ selectivity | Application | Ref. |
|---|---|---|---|---|---|
| a Calculated from the creatinine response considering stoichiometric enzymatic conversion to NH4+. b The electrode developed by Ding et al. was based on a GCE modified with POT with a nonactin membrane on top. Subsequently, a PVA hydrogel film (pH 7.0) and a gas-permeable Ag/AgCl electrode were implemented. c These electrodes are based on photocurable compounds. d The value of this slope was calculated from one figure provided in the ESI of the corresponding ref. 49. ISE: ion-selective electrode. LOD: limit of detection. LRR: linear range. FIA: flow injection analysis. GCE: glassy carbon electrode. PPy: polypyrrole. ISFET: ion-selective field-effect transistor. PVC: polyvinyl chloride. PVC-COOH: carboxylated PVC. MMA-DMA: methyl methacrylate decyl methacrylate. o-NPOE: o-nitrophenyl octyl ether. DOS: bis(2-ethylhexyl) sebacate. DBP: dibutyl phthalate. BBPA: bis(1-butylpentyl) adipate. TDACl: tetradodecylammonium chloride. NaTFPB: sodium tetrakis[3,5-bis-(trifluoromethyl)-phenyl]borate. KTpClPB: potassium tetrakis(4-chlorophenyl) borate. IL: ionic liquid. POT: poly(3-octylthiophene). CRE: creatinine. tPB: tetraphenylborate. | |||||
| Inner-filling solution | 30.7% PVC | LRR = 10−4–10−2 M | −0.6 | Sensor array in FIA | 45 |
| 72% DOS | |||||
| 1.9% nonactin | |||||
| 0.5% KTpClPB | |||||
| Solid-state (graphite-epoxy composite) | 33% PVC | LOD in the millimolar level | – | Electronic tongue. | 46 |
| 66% BBPA | Synthetic water samples | ||||
| 1% nonactin | |||||
| No cation-exchanger | |||||
| Solid-state (graphite-epoxy composite) | 33% PVC | LOD in the millimolar level | – | Electronic tongue. | 47 |
| 66% BBPA | River water and wastewater | ||||
| 1% nonactin | |||||
| No cation-exchanger | |||||
| Inner-filling solution (multisensor module) | 28.6% PVC | Slope = 56 mV dec−1 | – | Application promised in ground water (not shown) | 48 |
| 64.3% DBP | LOD = 8 × 10−6 M | ||||
| 7% nonactin | LRR = 10−5–10−1 M | ||||
| No cation-exchanger | |||||
| Inner-filling solution (flow cell in an automated platform) | 30% PVC | Slope = ca. 55d mV dec−1 | – | Profiling of NH4+ concentration in a lake | 49 |
| 68% o-NPOE | LOD = 10−5 M | ||||
| 3 mmol kg−1 nonactin | LRR = 10−4–10−2 M | ||||
| No cation-exchanger | |||||
| Inner-filling solution (CRE deiminase immobilized in the membrane) | 32% PVC-COOH | LOD = 0.015 mMa | Strong K+ interference | Indirect detection of CRE in urine and serum (after K+, Na+ and NH4+ removal with Dowex resin) | 50 |
| 65% DOS | LRR = 0.02–20.0 mMa | ||||
| 3% nonactin | |||||
| No cation-exchanger | |||||
| EC-NH4-03 (likely inner-filling solution and urease immobilized in the membrane) | No information available | Slope = 55.07 ± 3.80 mV dec−1 | – | Urea detection in milk samples | 62 |
| LRR = 0.55 × 10−6–0.55 × 10−11 M | |||||
| Solid-state (silver substrate) | 32.2% PVC | Slope = 54.4 mV dec−1 | −0.8 | – | 64 |
| 66.8% DOS | LOD = 5 × 10−6 M | ||||
| 1.0% nonactin | LRR = 3.2 × 10−6 M | ||||
| No cation-exchanger | |||||
| Solid-state (screen-printed electrode and membrane) | 21.5% DOS | Slope = 53 mV dec−1 | −1.4 | – | 65 |
| 1.0% nonactin | LOD = 5 × 10−6 M | ||||
| 0.50% KTpClPB | LRR = 5 × 10−5–10−2 M | ||||
| Solid-state (screen-printed electrode, CRE iminohydrolize immobilized in the membrane) | 66% PVC-COOH | Slope = 51.01 ± 1.55 mV dec−1 | −1.2 | Indirect detection of CRE in synthetic samples | 52 |
| 33% DOS | LOD = 10−5 M | ||||
| 1% nonactin | LRR = 10−4–1 M | ||||
| No cation-exchanger | |||||
| Solid-state (temporary tattoo) | 30.8% PVC | Slope = 59.2 ± 0.3 mV dec−1 | −1.8 | On-body sweat analysis | 53 |
| 69.0% o-NPOE | LOD = 1.2 × 10−5 M | ||||
| 0.2% nonactin | LRR = 10−4–10−1 M | ||||
| No cation-exchanger | |||||
| Solid-state (screen-printed electrode) | 92.4% o-NPOE | Slope = 59.3 ± 11.2 mV dec−1 | – | On-body sweat analysis | 54 |
| 6.9% nonactin | LRR = 10−5–10−1 M | ||||
| 0.7% KTpClPB | |||||
| Solid-state (GCE) | 32.8% DMA-MMA | Slope = 59.2 ± 0.3 mV dec−1 | −0.8 | In situ depth profiling in a lake | 5 and 55 |
| 65.9% o-NPOE | LOD = 1.2 × 10−5 M | ||||
| 15 mmol kg−1 nonactin | LRR = 10−4–10−1 M | ||||
| 5 mmol kg−1 NaTFPB | |||||
| Solid-state (GCE) | 32.8%PVC | Slope = 59.5 ± 2.9 mV dec−1 | −0.90 | TAN in seawater | 56 |
| 65.9% o-NPOE | LOD = 3.2 × 10−7 M | ||||
| 1% nonactin | LRR = 10−6–10−3 M | ||||
| 0.3% NaTFPBb | |||||
| Solid-state (GCE + PPy) | 30% PVC | Slope = 56.3 mV dec−1 | −1.0 | Natural water (high content of inorganic and organic substrates) | 68 |
| 67% BBPA | LRR = 10−5–10−1 M | ||||
| 1% KTFPB | |||||
| 3% nonactin/monactin | |||||
| Solid-state (pencil-draw graphite electrode) | 33% DMA-MMA | Slope = 52.96 ± 0.5 mV dec−1 | −0.65 | Water sample and soil | 57 |
| 10 mmol kg−1 nonactin | LOD = 4 × 10−6 M | ||||
| 5 mmol kg−1 NaTFPB | LRR = 10−4–10−2 M | ||||
| Solid-state (graphite paste) | 32.2% PVC | Slope ≈ 52 mV dec−1 | −0.85 | Tap and well water | 69 |
| 68.8% BBPA | LOD < 10−6 M | ||||
| 1% nonactin | LRR = 10−6–10−1 M | ||||
| No cation-exchanger | |||||
| Solid-state (gold electrode) | 33% PVC-COOH | Slope = 55 ± 0.7 mV dec−1 | – | Tap water and sewage water | 58 |
| 66% DOS | LOD = (4 ± 0.81) 10−5 M | ||||
| 2% nonactin | LRR = 10−4–4 × 10−2 M | ||||
| No cation-exchanger | |||||
| Solid-state (ISFETs with SiO2/Ta2O5 gate insulators)c | 34.5% DOS | Slope = 55–59 mV dec−1 | −1.2 | – | 75 |
| 63% Ebecryl | LRR = 10−5–10−1 M | ||||
| 1.9% nonactin | |||||
| 0.6% KTpClPB | |||||
| Inner-filling solutionc | 34.5% DOS | Slope = 55.5 mV dec−1 | −1.2 | – | 51 |
| 63% Ebecryl | LOD = 10−5 M | ||||
| 2% nonactin | LRR = 10−5–10−1 M | ||||
| 0.5% KTpClPB | |||||
| Solid-state (silver)c | 23.5% o-NPOE | Slope = 49.2 ± 1.0 mV dec−1 | −1.7 | Hydroponic solution and wastewater | 59 |
| 34.4% Ebecryl | LOD = 10−7 M | ||||
| 34.4% HDDA | LRR = 10−5–10−2 M | ||||
| 5.3% nonactin | |||||
| 1.6% KTpClPB | |||||
| Solid-state (Ag/AgCl electrode)c | 1.9% nonactin | Slope = 58.5 ± 0.1 mV dec−1 | −1.4 | Sewage water | 60 |
| 43 mol% relative to Ionophore of KTpClPB | LOD = 1.3 × 10−6 M | ||||
| LRR = 10−5–10−1 M | |||||
| Solid-state (carbon tape) | 66.8% DOS | Slope = 57.01 ± 0.02 mV dec−1 | −0.8 | Human urine | 76 |
| 32.2% PU | LOD = 10−7 M | ||||
| 0.44% NaTFPB | LRR = 10−6–10−1 M | ||||
| 1% nonactin | |||||
| Inner-filling microelectrode | 89% NPOE | Slope = 50–55 mV dec−1 | −0.42 | Synthetic and real freshwater soils (depth of 15 mm) | 78 and 79 |
| 1% tPB | LRR = 10−5–10−1 M | ||||
10% nonactin/monactin (75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25) 25) |
|||||
Aligned with the development of ISE technology from the inner-filling solution type to the all-solid-state concept, all NH4–ISEs that initially appeared in the literature were based on the inner-filling solution-type design (Table 1).45,48–51 Subsequently, coinciding with the boom in the introduction of solid ion-to-electron transducers in the late 90s, investigations regarding all-solid-state NH4+–ISEs were started, fostering a number of analytical applications.45–50,52–60 Nevertheless, the use of NH4+–ISEs is more evident in two types of samples (as observed in Table 1): environmental water and biological fluids analyses.
Initially, we inspected the inner-filling solution-type NH4–ISEs: three corresponding contributions are highlighted here (see Table 1). Schwarz et al. embedded a NH4–ISE together with a nitrate–ISE into a multisensor module for the analysis of natural groundwater.48 Although this multisensor appeared to have suitable resistance for in situ applications of water quality monitoring, no discussions about the NH4+/K+ selectivity and natural consequence affecting the reliability of the outcomes were offered.
Pankratova et al. developed an automated monitoring platform based on an ISE array for multi-ion monitoring in a lake.49 With the aim to monitor ions involved in the nitrogen/carbon cycle, namely, hydrogen, carbonate, calcium, nitrate, and ammonium ions, the authors proved the suitability of different ISEs for the continuous evaluation of the ecological status of a natural water environment. The potentiometric platform was conceived to be able to perform automated sampling at different depths in an aquatic resource (e.g., lake) by means of an external pump. Then, the collected water directly passed through a flow cell containing the ISEs. In particular, the response of the NH4–ISE was corrected by applying the Nikolsky equation for K+ interference (based on the selectivity coefficient). Interestingly, the developed platform was applied to water monitoring (concentrations versus depth) in a natural lake over a period of 4 days. However, the NH4+ content was found to be lower than the LOD of ISE, which was about 10 μM for a K+ background of 100 μM; therefore, no clear trends whatsoever could be reported for this ion.
With regard to biomedical applications, Radomska et al.50 developed a biosensor for creatinine analysis in biological samples using FIA based on NH4+ detection. The authors immobilized creatinine deiminase on the nonactin-based ISM to indirectly measure creatinine by NH4+ monitoring, since this is a product of an enzymatic reaction. In order to overcome the interference from the rich contents of K+ and Na+ in biological samples (i.e., dialysate solutions, human serum, and human urine), as well as from endogenous NH4+, a resin (4 cm-long exchanger column based on Dowex 50WX8) was used to remove the interfering cations. Importantly, creatinine was not retained in the column because it is present in the zwitterionic form at physiological pH (pH 8). The biosensor was found to be suitable for creatinine detection in clinical samples, covering a range of 0.02–20 mM with a LOD of 0.015 mM; therefore, it was applicable for serum (0.05–0.11 mM) and post-dialysate (0.06–0.35 mM) samples, as well as detecting pathological levels (>0.14 mM). Indeed, acceptable correlation with the classical colorimetric Jaffe method61 used as the standard technique was found for all the analyzed samples. Interestingly, the biosensor was found to be more reliable than the reference method in the case of non-deproteinized serum samples, probably because of the nonspecificity of the reference method for higher content of proteins in the samples. Moreover, the biosensor showed remarkable operational and storage stability, i.e., maintaining over 70% of the initial sensitivity after 72 days of operation and without deteriorating the sensitivity over half a year of storage at 4 °C.
Along the same direction, the indirect detection of urea by means of NH4–ISEs was also reported.62 The sensor was based on the immobilization of urease enzyme, which was present in a microbial culture isolated from different soil sources, in the membrane of a commercial NH4+ electrode (EC-NH4-03: we could not find any indication of the type of this electrode as inner-filling solution or solid state; however, from some descriptions in the paper, one may intuitively understand that it is of the inner-filling solution type). The reported linear range of response (LRR; NH4+ concentration ranging from 0.55 × 10−6 to 0.55 × 10−11 M) for the electrode is surprisingly much lower than those reported for NH4+ detection in the literature while exhibiting a Nernstian response (55.07 ± 3.80 mV dec−1). Interestingly, the authors demonstrated urea detection in different milk samples at the millimolar level, which was indeed fairly different from the reported (and unusual) LRR values. This approach was discussed in the review by de Marco et al. together with other nonactin-based electrodes that have been applied to detect NH4+ essentially in contaminated natural waters.7 Furthermore, Lei et al. provided a comprehensive review on microbial biosensors, particularly describing the coupling with pH, NH4+, and Cl− ISEs by immobilizing them in the membrane of the corresponding enzyme.63
To the best of our knowledge, the very first all-solid-state potentiometric NH4+–ISE based on nonactin was reported by Knoll and co-workers.64 This electrode comprised a silver wire modified with a plasticized polymeric membrane that displayed analytical performances that were fairly similar to those of the analogous inner-filling solution-type electrode. Later on, Koncki et al. used nonactin-based membranes in the fabrication of screen-printed electrodes.65 The strategy was based on the ad hoc integration of the membrane components (i.e., plasticizer, cation exchanger, and nonactin) into the insulating ink (made of graphite), which was screen-printed onto a conductive carbon-based electrode substrate; however, there were no improvements in the analytical features.
In another approach, Chou et al.52 used a carbon-based screen-printed electrode coated with a thin SnO2 film as the support for nonactin-based ISMs. Then, a creatinine imino-hydrolyzed enzyme was immobilized on the membrane. In addition, the SnO2-coated electrode was used to prepare a pH sensor. Then, both NH4+ and pH levels were monitored for the indirect detection of creatinine in the synthesized samples. Such samples were prepared using 20 mM Tris-HCl buffer and 5 mM phosphate buffer (both at pH 7.5) for NH4+ and pH measurements, respectively. Unfortunately, the authors did not prove the suitability of the sensor in real samples, but they reported an interesting selectivity study. Therefore, they investigated the ISE performances at different concentrations of Na+, K+, Mg2+, and Ca2+ in buffer solutions. As expected, the highest interference was caused by K+, displaying similar selectivity coefficient as those in earlier papers (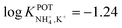 ).
).
The three all-solid-state NH4–ISEs discussed up to now exhibit very similar analytical performances and NH4+/K+ selectivities (i.e., 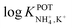 ranging from −0.8 to −1.4). Notably, none of these electrodes presented an analytical application (see Table 1). While these works shed light on the preparation of all-solid-state NH4+–ISEs, the demonstration of electrode suitability in real samples is lacking, likely due to NH4+/K+ selectivity. Indeed, the first application in real samples of an all-solid-state NH4+–ISE was reported by Guinovart et al.53 in 2013. This electrode was integrated in a temporary tattoo by the screen-printing technique and was used for the on-body detection of NH4+ in sweat in an accumulative manner while practicing sports. Along the same direction, Struck and co-workers developed a three-electrode screen-printed sensor conceived to be embedded in a wearable device for the noninvasive monitoring of NH4+ in sweat during sports activity.54
ranging from −0.8 to −1.4). Notably, none of these electrodes presented an analytical application (see Table 1). While these works shed light on the preparation of all-solid-state NH4+–ISEs, the demonstration of electrode suitability in real samples is lacking, likely due to NH4+/K+ selectivity. Indeed, the first application in real samples of an all-solid-state NH4+–ISE was reported by Guinovart et al.53 in 2013. This electrode was integrated in a temporary tattoo by the screen-printing technique and was used for the on-body detection of NH4+ in sweat in an accumulative manner while practicing sports. Along the same direction, Struck and co-workers developed a three-electrode screen-printed sensor conceived to be embedded in a wearable device for the noninvasive monitoring of NH4+ in sweat during sports activity.54
However, the K+ interference expected in sweat is a critical issue that requires special efforts in developing NH4–ISEs for on-body wearable applications. The temporary tattoo sensor developed by Guinovart et al.53 showed a linear range from 10–4 to 10–1 M and a NH4+/K+ selectivity of 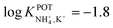 , which was demonstrated to be suitable for NH4+ detection in sweat considering the expected amount of endogenous NH4+ and K+ (0.1–1 and 0.2–6 mM, respectively).66,67 On the other hand, Struck and co-workers54 did not evaluate the NH4+/K+ selectivity related to the corresponding NH4+–ISE. Overall, it is possible to estimate the NH4+/K+ selectivity coefficient that is needed for reliable measurements in any biological fluid by considering the expected levels of these two ions. For example, average values of NH4+ and K+ in serum equal to 4 mM and lower than 0.05 mM, respectively, were recently reported in an experimental survey.9 Considering these values and those reported for sweat (see above), a selectivity coefficient of
, which was demonstrated to be suitable for NH4+ detection in sweat considering the expected amount of endogenous NH4+ and K+ (0.1–1 and 0.2–6 mM, respectively).66,67 On the other hand, Struck and co-workers54 did not evaluate the NH4+/K+ selectivity related to the corresponding NH4+–ISE. Overall, it is possible to estimate the NH4+/K+ selectivity coefficient that is needed for reliable measurements in any biological fluid by considering the expected levels of these two ions. For example, average values of NH4+ and K+ in serum equal to 4 mM and lower than 0.05 mM, respectively, were recently reported in an experimental survey.9 Considering these values and those reported for sweat (see above), a selectivity coefficient of 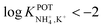 is necessary for the reliable detection of NH4+ in either serum or sweat. This value is closer to that reported by Guinovart et al.;53 with this exception, the required selectivity is fairly different from all the values reported in the literature for NH4+–ISEs (
is necessary for the reliable detection of NH4+ in either serum or sweat. This value is closer to that reported by Guinovart et al.;53 with this exception, the required selectivity is fairly different from all the values reported in the literature for NH4+–ISEs (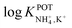 from −0.65 to −1.4; see Table 1). It would be very useful to further explore the reasons for which the electrode reported by Guinovart et al. yielded such a negative (and very close to the required value of −2) value for the logarithmic selectivity coefficient in order to formulate processes for the reliable on-body detection of NH4+ using wearable sensors. However, we could not find any information in the related paper.53
from −0.65 to −1.4; see Table 1). It would be very useful to further explore the reasons for which the electrode reported by Guinovart et al. yielded such a negative (and very close to the required value of −2) value for the logarithmic selectivity coefficient in order to formulate processes for the reliable on-body detection of NH4+ using wearable sensors. However, we could not find any information in the related paper.53
With regard to urine samples, NH4+ concentration is expected to be in the order of 10 mM, but K+ concentration can be significantly higher.9 Moreover, the relative concentrations of NH4+ and K+ can undergo important variations in the case of kidney or renal diseases. These evidences clearly indicate the need of improving NH4+/K+ selectivity in order to undertake NH4+ detection in biological fluids different than sweat.
All-solid-state NH4–ISEs containing nonactin have also been applied for the analysis of different types of natural waters (see Table 1). Crespo and co-workers were the first (and only ones, as far as we know) to demonstrate in situ and real-time NH4+ detection by integrating all-solid-state NH4–ISEs in a submersible probe (called a profiling ion analyzer (PIA)), which was employed for the dynamic monitoring of a lake.55 The authors explored the in situ performances of the electrodes based on different ion-to-electron transducers (mainly poly(3-octylthiophene), POT, and carbon nanotubes, CNTs), as well as membranes based on different polymeric matrices (PVC and the acrylic copolymer methyl methacrylate decyl methacrylate (MMA-DMA)) with handmade glassy carbon electrode (GCE) as the substrate. The best analytical performances, also considering electrode durability and light influence, were provided by the electrode based on CNTs and MMA-DMA. In an attempt to deal with K+ interference, the authors implemented an algorithm to correct the measured electrode potential according to the in situ calibration of ISE, primary interferences, and drift correction.55 Accordingly, the in situ calibration curve (plot of EMF values at respective depth points against the logarithm of NH4+ concentration obtained from spectrophotometric analysis) was plotted by high-resolution sampling during profile recording using syringe samples and therefore excluding spatiotemporal misalignment between the measurements. The additional analysis of the other ions in these samples permitted the determination of the concentrations of interfering ions and subsequently the potential measured by the NH4–ISE was corrected using the selectivity coefficients that were calculated earlier. Drift correction considers in situ changes in the standard potential of the electrode together with parallel drifts by minimizing the least-squares difference, leading to a single drift value. This algorithm is indeed applicable to any kind of ISE.
With regard to the profiling of NH4+ at different depths in a water column, at depths <5 m, the NH4+ concentration was <5 μM, which is outside the LOD of the ISE; further, higher K+ interference was detected in this case because of its higher content. As a result, the NH4+ concentration until this depth could not be accurately calculated, despite the formulated algorithm. In the underlying 5–10 m of the water column, slight oscillations in the NH4+ concentration were observed, while profiling beyond 11 m revealed a disturbance in the potentiometric response during the in situ measurements, which also yielded unreliable results. Overall, while this approach was promising toward in situ depth-dependent measurements, more efforts are needed in the direction of providing more reliable measurements within the expected NH4+ concentration levels.
Later on, Ding et al. reported the application of all-solid-state NH4–ISEs for the detection of total ammonia nitrogen (TAN) in seawater.56 The electrode consisted of a GCE modified with POT as an ion-to-electron transducer with a nonactin-based membrane on top. Subsequently, a polyvinyl alcohol (PVA) hydrogel film (pH 7.0) and a gas-permeable Ag/AgCl electrode were placed on the top of the membrane. The entire amount of NH3 gas dissolved in the seawater sample passed through the gas-permeable layer and then converted into NH4+ at the local pH of 7.0. The generated NH4+ was finally detected by the nonactin-based membrane. Advantageously, the initial gas-permeable film avoided the interference of any cation in the potentiometric response of the electrode and consequently the response toward NH4+ could be uniquely ascribed to the NH3 present in the seawater sample. This contribution is an elegant approach that utilizes an all-solid-state NH4+–ISE based on nonactin as the ionophore for indirect NH3 detection without any cationic interference.
Another ion-to-electron transducer explored in solid-contact NH4–ISEs was polypyrrole (PPy). One example is the work by Quan et al. based on electrodes fabricated with electropolymerized PPy and a membrane containing a nonactin/monactin mixture as the ionophore;68 however, there were no significant improvements in the analytical performances. The electrode was applied for NH4+ analysis in natural water with higher contents of inorganic and organic substrates, i.e., with higher NH4+ concentrations (order of millimoles).
Choosang et al. explored the suitability of phosphonium-based ionic liquids (ILs) as plasticizers in PVC and MMA-DMA membranes containing nonactin as the NH4+ ionophore.57 The associated investigations aimed at developing ISEs that were suitable for the monitoring of both NH4+ and NO3− in the agriculture field. The authors examined the role of two ILs (trihexyl(tetradecyl) phosphoniumbis(trifluoromethanesulfonyl) [P6,6,6,14][TFMS] and trihexyl(tetradecyl) phosphoniumdicyanamide[P6,6,6,14][DCA]), conceived as membrane plasticizers for realizing both a nonactin-based ISE and an ionophore-free nitrate-selective ISE. The electrodes were prepared by drop-casting ISMs comprising several compositions (to test different combinations of ILs and/or dioctyl sebacate (DOS)) on pencil-drawn graphite electrodes. Although the use of both ILs resulted in Nernstian responses in the case of nitrate electrodes, the responses for nonactin-based ISEs were not Nernstian. The authors hypothesized that the higher lipophilicity of the cationic part of the IL with respect to the anionic counterion resulted in the preferential extraction of NO3− instead of NH4+. Hence, ILs can be used as plasticizers for PVC-based ISMs, but the intrinsic ion-exchange properties have to be essentially considered if the selective detection of one target ion is desired. In particular, in the case of NH4+, the best analytical performances could be achieved with a MMA-DMA membrane without ILs, resulting in the regularly found NH4+/K+ selectivity coefficient (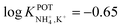 ). Notably, MMA-DMA ISEs could be applied to real environmental samples, including water and soils; the results were compared with those obtained from the traditional colorimetric assay when used as the reference method, and the results were in good agreement with each other.
). Notably, MMA-DMA ISEs could be applied to real environmental samples, including water and soils; the results were compared with those obtained from the traditional colorimetric assay when used as the reference method, and the results were in good agreement with each other.
With regard to all-solid-state NH4–ISEs, Schwarz et al.69 applied them for the analysis of tap and well water and Gallardo-Gonzalez et al.58 applied them for the analysis of sewage water. Both of them used a similar approach based on electropolymerized PPy as the ion-to-electron transducer in nonactin-based ISEs. Graphite-based sensors were first used as the basis of NH4–ISEs (also nitrate–ISEs) that displayed worthwhile analytical performances and NH4+/K+ selectivity in the range of 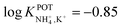 .69 Similarly, gold microelectrodes doped with cesium cosine in the substrate were also investigated.58 Interestingly, these electrodes were implemented into a lab-on-a-chip concept for the in situ and real-time potentiometric monitoring of NH4+ in tap and sewage water, where the obtained NH4+/K+ selectivity seemingly provided trustworthy results even in the absence of earlier studies on selectivity.
.69 Similarly, gold microelectrodes doped with cesium cosine in the substrate were also investigated.58 Interestingly, these electrodes were implemented into a lab-on-a-chip concept for the in situ and real-time potentiometric monitoring of NH4+ in tap and sewage water, where the obtained NH4+/K+ selectivity seemingly provided trustworthy results even in the absence of earlier studies on selectivity.
In general, the membrane compositions of all the described NH4–ISEs were based on different polymers and plasticizers in a weight ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, similar to that in a traditional ISM format. Apparently, the uses of PVC as a polymer and sebacate-based compound (e.g., DOS) as a plasticizer are preferred, but we could not find strong foundations for this trend in the analyzed papers. It is indeed surprising that a common polymer such as polyurethane has not yet been incorporated in nonactin-based ISMs, particularly in electrodes applied for biological fluids. Another surprising tendency is the indistinct use of the cation exchanger in the membrane (i.e., with and without its presence). While it is well known that ISMs based on neutral receptors for cations exhibit a potentiometric response in the absence of any cation exchanger owing to the impurities present in the membrane (arising from the plasticizer, polymer, and/or the appropriate ionophore),70 it was additionally demonstrated that the incorporation of a cation exchanger is convenient for better electrode reproducibility and therefore superior reliability.17,23 Unfortunately, in the case of nonactin-based membranes, we could not find the origin of the preferred absence of the cation exchanger in the membrane composition, which indeed contradicts the tendencies found in other ionophore-based membranes. In our opinion, this strategy may arise from the idea of providing a membrane that is initially free of any cation (to avoid K+ interference).
2, similar to that in a traditional ISM format. Apparently, the uses of PVC as a polymer and sebacate-based compound (e.g., DOS) as a plasticizer are preferred, but we could not find strong foundations for this trend in the analyzed papers. It is indeed surprising that a common polymer such as polyurethane has not yet been incorporated in nonactin-based ISMs, particularly in electrodes applied for biological fluids. Another surprising tendency is the indistinct use of the cation exchanger in the membrane (i.e., with and without its presence). While it is well known that ISMs based on neutral receptors for cations exhibit a potentiometric response in the absence of any cation exchanger owing to the impurities present in the membrane (arising from the plasticizer, polymer, and/or the appropriate ionophore),70 it was additionally demonstrated that the incorporation of a cation exchanger is convenient for better electrode reproducibility and therefore superior reliability.17,23 Unfortunately, in the case of nonactin-based membranes, we could not find the origin of the preferred absence of the cation exchanger in the membrane composition, which indeed contradicts the tendencies found in other ionophore-based membranes. In our opinion, this strategy may arise from the idea of providing a membrane that is initially free of any cation (to avoid K+ interference).
Another strategy that has been used with nonactin-based ISMs is the substitution of PVC by polymers with crosslink properties upon exposure to UV light. This type of polymer allows a reduction in the plasticizer content in the membrane, which may consequently improve three aspects: adhesion of the ISM to the electrode substrate, biocompatibility, and reduction in excessive leaching.51,71,72 The reduction in excessive leaching is indeed important in the case of nonactin because of its low lipophilicity and therefore its lowered tendency to remain in the membrane (i.e., remarkable leaching from the ISM). Notably, ionophore lipophilicity is usually expressed by the partition coefficient between octanol and water, i.e., log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Poctanol/water, measured by means of thin-layer chromatography. For ionophores with log
Poctanol/water, measured by means of thin-layer chromatography. For ionophores with log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Poctanol/water < 6, leaching is generally expected after 2–3 days from the prepared membrane under common storage conditions (e.g., millimolar concentrations of the primary ion).73 In the case of nonactin, log
Poctanol/water < 6, leaching is generally expected after 2–3 days from the prepared membrane under common storage conditions (e.g., millimolar concentrations of the primary ion).73 In the case of nonactin, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Poctanol/water = 5.8,74 thereby representing a limitation on the lifetime of nonactin-based ISEs.
Poctanol/water = 5.8,74 thereby representing a limitation on the lifetime of nonactin-based ISEs.
Bratov et al. proposed the fabrication of photocurable membranes primarily comprising aliphatic urethane diacrylate, i.e., Ebecryl 270, and hexanediol diacrylate in both inner-filling solution- and all-solid-state-type electrode formats.51,75 In the first work of its kind, a photocurable membrane (63% Ebecryl and 34.5% DOS) was deposited on an ion-sensitive field-effect transistor (ISFET).75 Overall, performances comparable with those of conventional PVC-based ISMs can be obtained with a reduced amount of plasticizer. Subsequently, the same approach was applied to fabricate an inner-filling solution-type electrode and the authors further optimized the membrane composition according to improvement in the analytical features.51 Therefore, several membrane compositions were examined that employed different plasticizers, revealing that the best option was DOS. The authors also investigated the effect of PVC addition (7%) in the photocurable membrane, observing a marginal enhancement in the sensitivity as well as lower LOD values, but without any remarkable improvement in NH4+/K+ selectivity.51
Alexander et al.59 employed a photocurable NH4+ membrane based on an aromatic epoxy diacrylate polymer (Ebecryl 600) crosslinked to an acrylate ester (1,6-hexanedioldiacrylate). This polymer was demonstrated to act as an inner plasticizer, further decreasing the required amount of external plasticizer: o-NPOE was decreased down to 23.5 wt% from the traditionally required 66 wt%. Photocured NH4–ISE showed remarkable NH4+/K+ selectivity (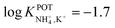 ), allowing NH4+ determination in hydroponic nutrient solutions and wastewater samples in the FIA. The validation of the analytical application was carried out with a commercially available NH4+ test based on spectrophotometric measurements (in compliance with EPA 350.1, APHA 4500-NH3 F, ISO 7150-1, and DIN 38406-5).
), allowing NH4+ determination in hydroponic nutrient solutions and wastewater samples in the FIA. The validation of the analytical application was carried out with a commercially available NH4+ test based on spectrophotometric measurements (in compliance with EPA 350.1, APHA 4500-NH3 F, ISO 7150-1, and DIN 38406-5).
A self-plasticized nonactin-based ISM (i.e., with no plasticizer in the membrane) was reported by Heng et al. using photocurable poly(n-butyl acrylate).60 The analytical performances displayed by this electrode were consistent with the photocurable ISEs described earlier. In addition, this NH4–ISE was applied for the analysis of sewage samples, demonstrating good agreement with the results obtained from the Nessler method used as the reference. Advantageously, the photocurable membranes may be additionally patterned by using conventional photolithography, instead of the manual deposition (drop-casting) of the cocktail. This approach would be very convenient for improving the between-electrode reproducibility in a further manufacturing process. Moreover, the photocured membranes seem to exhibit better adherence to the surface of solid-state electrodes with respect to the common PVC-based membranes (water-layer tests).
To the best of our knowledge, the most recent paper on NH4+ detection based on nonactin as the ionophore was published by our research group.76 It is based on using thin-layer potentiometry for the indirect detection of creatinine in urine after its reaction with the enzyme creatinine deiminase, stoichiometrically producing NH4+. We have presented a new microfluidic chip that separates two thin-layer reservoirs: one for the urine sample and the other for the enzyme and embedding the electrodes. The separation of the reservoirs is accomplished by using an anion–exchange membrane. The membrane allows the transport of neutral molecules (i.e., creatinine) and anions from the urine to the reservoir containing the enzyme and the electrodes, while significantly repelling cations. Then, creatinine is quantitively converted into NH4+ by the enzyme, where NH4+ formation is monitored by the nonactin-based electrodes. The incorporation of the anion–exchange membrane as a barrier to interfering ions (cations) in response to nonactin-based electrodes might be an elegant way to suppress K+ influence on NH4+ sensing.76
After inspecting all these papers, it seems clear that the main field of application of nonactin-based ISEs is the detection of NH4+ in water. Indeed, this fact has been extensively reviewed over the years, e.g., de Marco,7 Winkler,77 Crespo,3 and Cuartero.1,6 In this context, it is noteworthy to mention the work by de Beer and co-workers that included measuring NH4+ profiles in freshwater sediments,78,79 even if those papers were published prior to the established screening time in the present review. In the first paper of its kind, the development and characterization of nonactin-based inner-filling solution-type microelectrodes (diameter: 1 μM) were reported, showing analytical performance that was rather close to any nonactin-based ISE.79 The authors highlighted that the microelectrode was suitable for the detection of NH4+ concentration when it is at least equal to 0.1 times the Na+ concentration and 10 times the K+ concentration in the sample; this was as per the calculated selectivity coefficients. Macrokinetic data about the products’ gradients (i.e., NH4+) in gel beads containing crosslinked urease were demonstrated. After this success, the electrode was directly applied in freshwater soils, showing depth profiles of NH4+ concentrations along 15 mm.78
3. Ammonium-selective electrodes based on ionophores different than nonactin
The development of tailor-made synthetic receptors to be used as NH4+ ionophores in ISMs has its root in the NH4+–nonactin complexing efficiency, which is a well-tuned compromise between the affinity and reversibility of binding. Therefore, in these receptors, the binding site for NH4+ has to be designed considering both structural requirements and thermodynamic constants that govern the binding process. The general criteria for designing a receptor suitable to act as an NH4+ ionophore are based on the possibility to provide a tetrahedral binding site capable of coordinating NH4+ by H-bonds, ion–π, and/or ion–dipole interactions. In particular, designing the tetrahedral symmetry of the binding site, with a coordination number of four, may play a key role in facilitating the binding of NH4+ with respect to K+: indeed, K+ is characterized by spherical symmetry and the preference for ionic bonds with coordination number of six or more.26,27,80One example of the described strategy was presented in the study by Graf et al.81 performed back in the 80s. They discussed spherical macrotricyclic cryptands designed with tetrahedral geometry to provide four H-bond acceptors for the coordination of NH4+. Moreover, 5–6 oxygen atoms were present at the binding site to stabilize the NH4+–receptor complex with electrostatic interactions. X-ray analysis revealed that NH4+ was effectively placed at the center of a tetrahedron formed by the four nitrogen atoms of the receptor. The NH4+/K+ selectivity was 250-fold higher than that of the nonactin–NH4+ complex, but the dissociation constant turned to be considerably smaller, leading to poor reversibility of binding and hence being unsuitable for the development of an ISE. However, this study demonstrated the primary importance of both H-bond configuration and symmetry of the binding site in the design of effective NH4+ receptors.
Until now, considerable attention has been paid to macrocyclic compounds as NH4+ receptors that are capable of mimicking the binding features of nonactin. However, a majority of the reported studies have focused on the synthesis and/or physicochemical characterization of the structure of the binding site, giving poor or no information about its applicability as an ionophore for use in ISEs.81 Truly, these studies have been crucial toward the understanding of the host–guest chemistry that is the most suitable for NH4+ binding; however, the present review focuses on the receptors applied to NH4+–ISEs; their structures are shown in Fig. 2–10. Table 2 summarizes the electrode type, membrane composition, certain analytical features, and applications of these electrodes. In addition, because some of these ISEs reported on 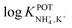 using nonactin-based ISEs as control experiments, these values are included in the table for comparison purposes. Notably, for Table 2, potentiometry is the primary readout technique used for the ISEs: the use of any other technique is particularly indicated.
using nonactin-based ISEs as control experiments, these values are included in the table for comparison purposes. Notably, for Table 2, potentiometry is the primary readout technique used for the ISEs: the use of any other technique is particularly indicated.
 | ||
| Fig. 2 Dibenzyl ether derivates, reported by Siswanta et al., as NH4+ ionophores.44 | ||
 | ||
| Fig. 3 Aza-crown ether derivates, reported by Moriuchi-Kawakami et al., as NH4+ ionophores.82 | ||
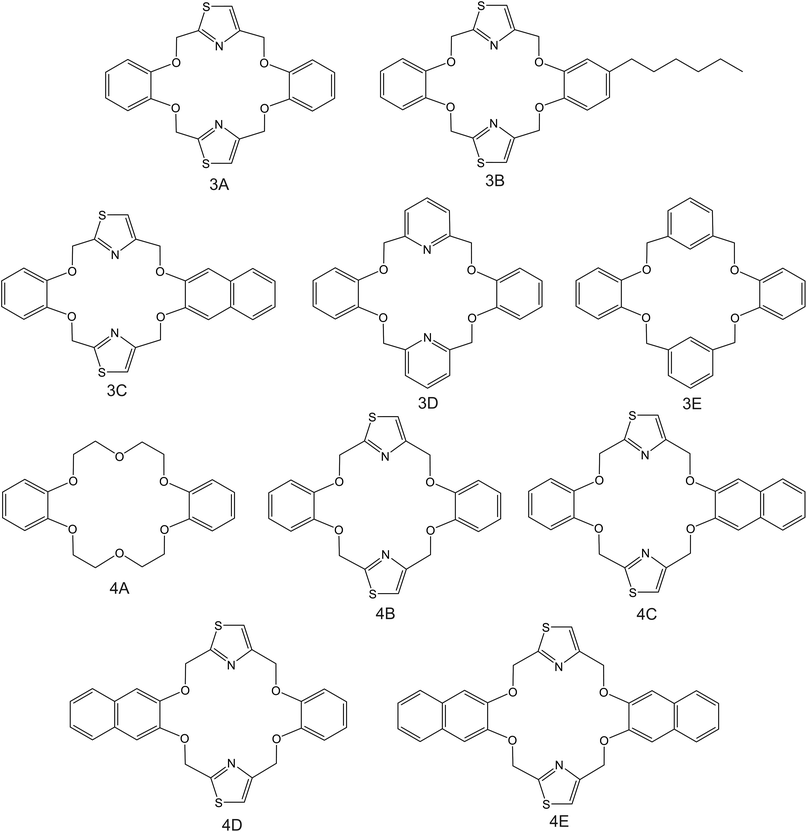 | ||
| Fig. 4 DB18C6 derivates, reported in the works by Kim et al. (3A–3E;83 4A–4E85), as NH4+ ionophores. | ||
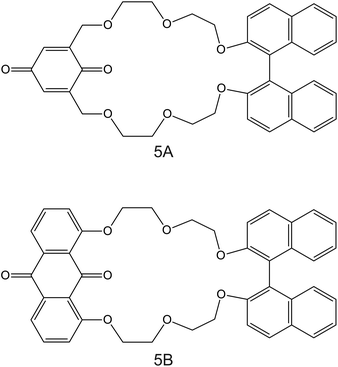 | ||
| Fig. 5 Structures of (1,1′-bi-2-naphthyl)-23-crown-6 ether derivates modified with 1,4-benzoquinone (5A) and 9,10-anthraquinone (5B), reported in the work of Rahman et al., as NH4+ ionophores.86 | ||
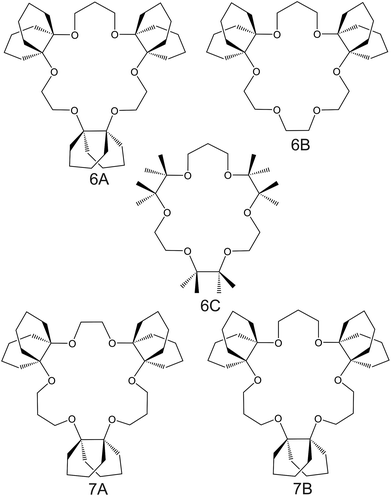 | ||
| Fig. 6 Crown ether derivates substituted with decalino subunits and methyl groups, reported in the works of Suzuki et al.74 (6A–6C) and Sasaki et al.89 (7A and 7B), as NH4+ ionophores. | ||
 | ||
| Fig. 7 6-Fold substituted benzene tripodal derivates, reported in the work of Sasaki et al.,89 as NH4+ ionophores. | ||
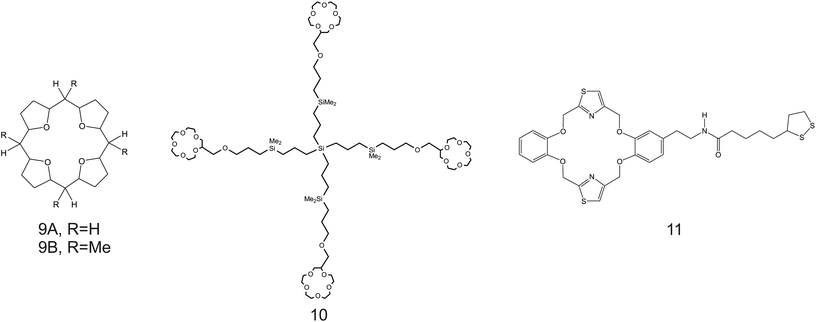 | ||
| Fig. 8 THF-containing 16-crown-4 derivative (9A and 9B), 15-crown-5 substituted carbosilane dendrimer (10), and DB18C6 (11) reported in the works of Jin et al.,90 Chandra et al.,91 and Jin et al.,92 respectively, as NH4+ ionophores. | ||
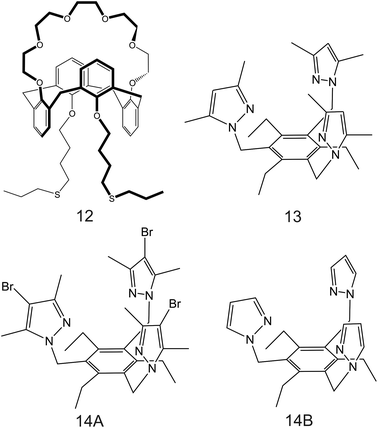 | ||
| Fig. 9 Calix[4]arene-crown-6 (12) functionalized with alkyl sulfide units reported in the work of Saiapina and co-workers.93 The 6-fold substituted benzene tripodal derivates, reported in the works of Chin et al. (13;80 14A and 14B95), as NH4+ ionophores. | ||
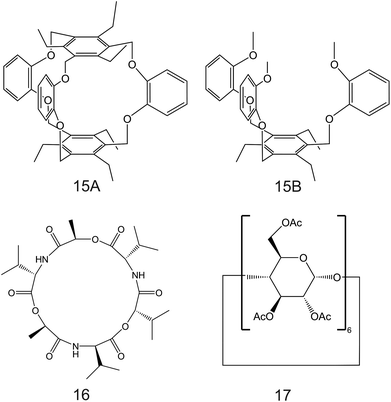 | ||
| Fig. 10 6-Fold substituted benzene tripodal derivates (15A and 15B), cyclic depsipeptide (16), and α-cyclodextrin derivate (17), reported in the works of Jon et al.,96 Benco et al.,26 and Ribeiro et al.,98 respectively, as NH4+ ionophores. | ||
| NH4+ Ionophore | Type of electrode | Membrane (wt%) | Analytical Parameters | NH4+/K+ selectivity | Application | Ref. |
|---|---|---|---|---|---|---|
| ISE: ion-selective electrode. LOD: limit of detection. LRR: linear range. o-NPOE: o-nitrophenyl octyl ether. BBPA: bis(1-butylpentyl) adipate. DBE: dibenzyl ether. TEHP: bis(2-ethylhexyl) phthalate. DEHA: bis(2-ethylhexyl) adipate. DOA: dioctyl adipate. TDACl: tetradodecylammonium chloride. NaTFPB: sodium tetrakis[3,5-bis-(trifluoromethyl)-phenyl]borate. KTpClPB: potassium tetrakis(4-chlorophenyl) borate. | ||||||
| 1E | Inner-filling solution | 30% PVC | – | −1.7 | 44 | |
| 69% DBE and derivates | Nonactin: −1.0 | |||||
| No cation-exchanger | ||||||
| 2A | Solid state ISE kit (DKK Co. Ltd Tokyo) | 27.6% PVC | Slope = 58.7 mV dec−1 | −1.2 | – | 82 |
| 69% DBE | LRR = 5 × 10−5–10−1 M | |||||
| 2.8% ionophore | ||||||
| 0.5% NaTFPB | ||||||
| 3A | Inner filling solution | PVC/o-NPOE 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 w/w 2 w/w |
Slope = 59.4 mV dec−1 | −1.1 | – | 83 |
| 1.9 mmol kg−1 KTpClPB | LOD = 3 × 10−6 M | Nonactin: −1.0 | ||||
| LRR = 10−5–10−1 M | ||||||
| 4D | Inner filling solution | 33% PVC | Slope = 57.6 mV dec−1 | −1.3 | – | 85 |
| 66% o-NPOE | LOD = 5 × 10−6 M | |||||
| 1% ionophore | LRR = 10−5–10−1 M | |||||
| No cation-exchanger | ||||||
| 5A and 5B | Solid state ISE (glassy carbon electrode) (amperometric readout) | 10 mM Ionophore | Slope = 59.4 mV dec−1 | – | – | 86 |
| 1.0% Nafion coating | LOD = 5 × 10−6 M | |||||
| LRR = 10−5–10−1 M | ||||||
| 6A | Inner filling solution | 30% PVC | Slope = 58.1 mV dec−1 | −1.0 | – | 74 |
| 67% BBPA | LRR = 5 × 10−6–10−1 M | |||||
| 3% ionophore | ||||||
| 10 mol% KTpClPB | ||||||
| 7B | Inner filling solution | 30% PVC | Slope = 59.3 mV dec−1 | −1.6 | – | 89 |
| 67% BBPA | LOD < 10−5 M | |||||
| 3% ionophore | LRR = 10−5–10−1 M | |||||
| 10 mol% KTpClPB | ||||||
| 8A | Inner filling solution | 30% PVC | LOD = 10−3 M | −2.1 | – | 89 |
| 67% BBPA | ||||||
| 3% ionophore | ||||||
| 10 mol% KTpClPB | ||||||
| 9A | Inner filling solution | 32.8% PVC | Slope = 53.9 mV dec−1 | −1.8 | – | 90 |
| 65.4% TEHP | LOD = 10−5 M | |||||
| 1.39% ionophore | LRR = 5 × 10−6–10−1 M | |||||
| 32.4% KTpClPB | ||||||
| 10 | Inner filling solution | 42.4% PVC | Slope = 53.3 mV dec−1 | −1.8 | – | 91 |
| 53% DBP | LOD = 3.9 × 10−6 M | |||||
| 3.5% ionophore | LRR = 7.6 × 10−6–10−1 M | |||||
| 1% NaTFPB | ||||||
| 11 | Inner-filling solution | 32.9% PVC | LRR = 10−4–10−1 M | – | – | 92 |
| 65.9% o-NPOE | ||||||
| 1% ionophore | ||||||
| 0.2% KTpClPB | ||||||
| 11 | Solid state ISE (gold electrode) (voltammetric readout) | The ionophore was immobilized in a self-assembled monolayer | LRR = 10−4–10−1 M | −1.1 | – | 92 |
| Nonactin: −0.9 | ||||||
| 12 | Solid state ISE (gold electrode) (conductimetric readout) | The ionophore was immobilized in a self-assembled monolayer | LOD = 10−6 M | −1.1 | Environmental samples (river waters) | 93 |
| LRR = 10−5–1.5 × 10−3 M | ||||||
| 13 | Inner filling solution | 33% PVC | LRR = 10−3–10−1 M | −2.6 | – | 80 |
| 66% DEHA | Nonactin: −1.0 | |||||
| 1% ionophore | ||||||
| No cation-exchanger | ||||||
| 14A | Inner filling solution | 33% PVC | LOD = 2.5 × 10−5 M | −2.3 | – | 95 |
| 66% DOA | LRR = 10−4–10−1 M | |||||
| 1% ionophore | Nonactin; −1.3 | |||||
| No cation-exchanger | ||||||
| 15A | Inner filling solution | Not indicated | LOD = 3.2 × 10−6 M | −0.97 | – | 96 |
| Nonactin: −0.88 | ||||||
| LRR = 10−5–10−1 M | ||||||
| 16 | Solid state planar electrode | 30% PVC | Slope = 55.8 mV dec−1 | −1.0 | – | 26 |
| 69% o-NPOE | LRR = 10−4–10−1 M | |||||
| 1% ionophore | ||||||
| 50 mol% KTpClPB | ||||||
| 17 | Solid state micro-hole array (voltammetric/amperometric readout) | 32.2% PVC | Slope = 53.3 mV dec−1 | k amp = 2.9 × 10−4 | – | 98 |
| 68.8% BBPA | LOD = 1.2 × 10−7 M | |||||
| 1% ionophore | LRR = (4.2–66)x10−6 M | |||||
| No cation exchanger | ||||||
In the early 90s, Siswanta et al. observed that a membrane based on dibenzyl ether (DBE) exhibited improved NH4+/K+ selectivity, which was ascribed to the preference of DBE in forming tetracoordinate complexes. Therefore, the authors explored the use of certain DBE derivates (Fig. 2, 1A–1E) for the development of ISMs for NH4+ detection.44 It should be noted that these compounds were used in a large amount in the membrane composition (i.e., 69% w/w) in order to act as both plasticizer and ionophore. A comparison of all the different ISMs showed that NH4+/K+ selectivity was slightly improved when using a DBE derivate containing a butylene glycol unit disubstituted with dimethyl groups (1E,  ) with respect to the selectivity afforded by unsubstituted DBE (1A,
) with respect to the selectivity afforded by unsubstituted DBE (1A, 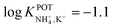 ); the values obtained from the latter were closer to the average values afforded by nonactin-based membranes (see Table 1). Despite the fact that the selectivity coefficient was sufficient for certain analytical applications, the sensors were never tested in real samples.44
); the values obtained from the latter were closer to the average values afforded by nonactin-based membranes (see Table 1). Despite the fact that the selectivity coefficient was sufficient for certain analytical applications, the sensors were never tested in real samples.44
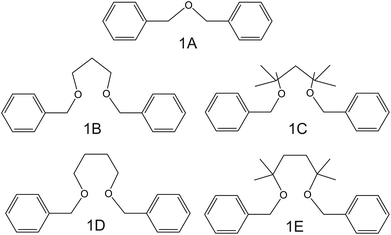
Importantly, after nonactin, the family of aza-crown ethers has been widely tested as NH4+ ionophores for use in ISEs. Among the first authors that reported on these ionophores, Moriuchi-Kawakami et al.82 introduced carbonyl groups and pyrazole rings into an aza-crown backbone. The authors fabricated 12 different compounds (Fig. 3, 2A–2L) with distinct macrocyclic sizes and substituents on the sp3-hybridized nitrogen of the pyrazole ring. They found that the selectivity changed depending on the macrocyclic size as well as on the substituents. Importantly, all the ionophores showed selectivity favorable for NH4+ with respect to other cations in regular experiments based on organic solvents as well as in ISM. The best NH4+/K+ selectivity was observed for 18-membered crown ethers with carbonyl groups (Fig. 3, 2A–2D). Among them, the selectivity was seemingly dependent on the steric hindrance of the substituents on the sp3-hybridized pyrazolic nitrogens, i.e., it decreased according to the substituents’ bulkiness (selectivity order: H < Me < Bn < Oct). Conversely, the 18-membered crown ethers without the carbonyl groups (Fig. 3, 2E and 2F) were revealed to be poorly selective to NH4+ with respect to K+, thereby highlighting the importance of carbonyl contribution in the selective binding of NH4+. Overall, the best NH4+/K+ selectivity was given by the 18-membered crown ether with unsubstituted pyrazoles and carbonyl groups (Fig. 3, 2A) using DBE as a plasticizer and NaTFPB as the ion exchanger. Importantly, it was also observed that other plasticizers (i.e., DOS or o-NPOE) and the absence of NaTFPB negatively influenced the NH4+/K+ selectivity.
Kim et al.83 were inspired by the structure of dibenzo-18-crown-6 ether (DB18C6), which was previously found to present remarkable affinity to NH4+;84 they synthesized a number of thiazole derivates (Fig. 4, 3A–3C). ISMs based on these ionophores showed NH4+/K+ selectivity similar to those of nonactin-based ISEs (from −1.1 to −1). Notably, unsubstituted thiazole-containing DB18C6 (Fig. 4, 3A) was found to form both 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexes with NH4+. In contrast to earlier examples examined herein, the use of DBE plasticizer resulted in worse NH4+/K+ selectivity. Analogous DB18C6-type macrocycles having pyridine or benzene groups instead of thiazole (Fig. 4, 3D and 3E, respectively) exhibited poor or no preference toward NH4+ with respect to K+. Hence, the proper ability of DB18C6 in binding NH4+ was attributed to the presence of thiazole units.
2 complexes with NH4+. In contrast to earlier examples examined herein, the use of DBE plasticizer resulted in worse NH4+/K+ selectivity. Analogous DB18C6-type macrocycles having pyridine or benzene groups instead of thiazole (Fig. 4, 3D and 3E, respectively) exhibited poor or no preference toward NH4+ with respect to K+. Hence, the proper ability of DB18C6 in binding NH4+ was attributed to the presence of thiazole units.
Subsequently, the same research group investigated the binding properties of thiazole-based receptors comprising naphto-crown ether derivates (Fig. 4, 4B–4E) and compared their observations with DB18C6 (Fig. 4, 4A).85 In principle, the authors expected a preference for 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex with NH4+, favoring its access to the binding site with the incorporation of naphthalene groups. In particular, molecular modeling for NH4+ complexation by ionophores 4C and 4D displayed very similar results based on H-bonds between NH4+ and the nitrogens of the thiazole rings, which were oriented in facial alignment. Overall, these receptors were arranged in a saddle-like structure by establishing both electrostatic interactions and H-bonds. Extraction studies in water/1,2-dichloroethane showed a significant preference of ionophores 4B, 4C, and 4D for NH4+ with respect to K+, following the trend 4C ≈ 4D > 4B. Because of its poor solubility in 1,2-dichloroethane, 4E was not included in the subsequent study. However, 4A was included for comparison purposes. The ratio between the percentage extractability of NH4+versus K+ was equal to 1.2 for 4A, suggesting that the absence of thiazole units in the naphto-crown ether structure drastically decreased the selectivity properties toward NH4+. When these compounds were incorporated into the polymeric membranes, all of them presented similar K+ interference:
1 complex with NH4+, favoring its access to the binding site with the incorporation of naphthalene groups. In particular, molecular modeling for NH4+ complexation by ionophores 4C and 4D displayed very similar results based on H-bonds between NH4+ and the nitrogens of the thiazole rings, which were oriented in facial alignment. Overall, these receptors were arranged in a saddle-like structure by establishing both electrostatic interactions and H-bonds. Extraction studies in water/1,2-dichloroethane showed a significant preference of ionophores 4B, 4C, and 4D for NH4+ with respect to K+, following the trend 4C ≈ 4D > 4B. Because of its poor solubility in 1,2-dichloroethane, 4E was not included in the subsequent study. However, 4A was included for comparison purposes. The ratio between the percentage extractability of NH4+versus K+ was equal to 1.2 for 4A, suggesting that the absence of thiazole units in the naphto-crown ether structure drastically decreased the selectivity properties toward NH4+. When these compounds were incorporated into the polymeric membranes, all of them presented similar K+ interference: 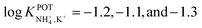 for 4B, 4C, and 4D, respectively. No special improvements with respect to the presence of nonactin were reported, despite the fact that traditional extraction experiments revealed remarkable selectivity for NH4+ against K+.
for 4B, 4C, and 4D, respectively. No special improvements with respect to the presence of nonactin were reported, despite the fact that traditional extraction experiments revealed remarkable selectivity for NH4+ against K+.
The electrodes developed by Rahmen et al. are particularly interesting. The authors implemented a redox active group comprising 9,10-anthraquinone (BNBQ) and 1,4-benzoquinone (BNAQ) in the backbone of (1,1′-bi-2-naphthyl)-23-crown-6 ethers (Fig. 5, 5A and 5B, respectively).86 These compounds were then immobilized on a GCE; finally, a layer of Nafion was added. When the electrode was investigated using cyclic voltammetry (CV), the quinone redox peak was found to decrease with the NH4+ concentration in the sample solution, thereby indicating that NH4+ was complexed by the compound and its redox properties could not be revealed. Importantly, a negligible effect was observed on the redox peak of quinone with increasing K+ concentrations. Indeed, the CV data were used to calculate the binding constants of 5A and 5B with NH4+ and K+, yielding values of two orders of magnitude greater for NH4+ than those for K+: 4000 ± 77 M−1 for 5A–NH4+, 4300 ± 120 M−1 for 5B–NH4+, 18.0 ± 0.8 M−1 for 5A–NH4+, and 19.0 ± 0.5 M−1 for 5B–K+. Additional NMR studies revealed that NH4+ is complexed in a tetrahedral conformation through H-bonds with three ether oxygen atoms and one quinone oxygen atom in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry. Advantageously, the electrode based on 5B was further explored in the amperometric mode (applied potential of −680 mV, coinciding with the quinone voltammetric peak), showing LRR from 10–6 to 10–3 M and LOD at the micrometer levels. Nevertheless, the analytical applicability of the electrode was not demonstrated, despite its proven potential. Although this electrode is not based on a potentiometric readout, it represents a clear example on how electrodes based on ISMs (in this case, NH4+ ionophore in a Nafion-based environment) can be investigated under a dynamic electrochemical protocol and therefore can yield a different selectivity dimension.87,88 In the inspected paper, it would be worthwhile to compare the reported results with those observed with regular potentiometric ISEs based on the same ionophore.
1 stoichiometry. Advantageously, the electrode based on 5B was further explored in the amperometric mode (applied potential of −680 mV, coinciding with the quinone voltammetric peak), showing LRR from 10–6 to 10–3 M and LOD at the micrometer levels. Nevertheless, the analytical applicability of the electrode was not demonstrated, despite its proven potential. Although this electrode is not based on a potentiometric readout, it represents a clear example on how electrodes based on ISMs (in this case, NH4+ ionophore in a Nafion-based environment) can be investigated under a dynamic electrochemical protocol and therefore can yield a different selectivity dimension.87,88 In the inspected paper, it would be worthwhile to compare the reported results with those observed with regular potentiometric ISEs based on the same ionophore.
Suzuki and collaborators reported 19–21-membered crown ethers having decalino subunits in the macrocyclic system.74 In particular, 19-membered crowns were first functionalized with 2 or 3 decalino or dimethyl units (Fig. 6, 6A–6C). The higher rigidity of such kinds of macrocyclic compounds was supposed to allow for improving the NH4+ selectivity versus other alkaline cations. Therefore, bulky subunits were expected to play a dual role: to hinder the formation of sandwich-type complexes with larger cations due to a “block-wall effect” and to deter the formation of wrapping-type complexes with smaller cations owing to the low flexibility of the macrocycles. Indeed, X-ray analysis revealed that the cavity size of the most rigid ionophore included in this group (6B) was proven to perfectly fit in the tetrahedral coordination of NH4+, while other alkaline cations were rather small to be retained or rather large to get access to the binding site. In detail, the authors highlighted that only three hydrogens of NH4+ were involved in the complex via H-bonds, leaving one hydrogen oriented out of the ring plan to be coordinated by the counterion. Regarding NH4+/K+ selectivity, a lower K+ influence was presented for 6A (with two decalino units) in comparison with 6B and 6C (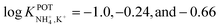 , respectively). One advantage of this compound as compared to nonactin (while presenting similar NH4+/K+ selectivity) is the higher lipophilicity (log
, respectively). One advantage of this compound as compared to nonactin (while presenting similar NH4+/K+ selectivity) is the higher lipophilicity (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Poctanol/water = 13.5 ± 0.7) compatible with the use of bis(1-butylpentyl) adipate (BBPA) in the membrane, even though the plasticizers exhibit a low dielectric constant.
Poctanol/water = 13.5 ± 0.7) compatible with the use of bis(1-butylpentyl) adipate (BBPA) in the membrane, even though the plasticizers exhibit a low dielectric constant.
Subsequently, the authors investigated two crown ethers presenting three decalino units to enlarge the macrocycles to 20- and 21-membered crowns (Fig. 6, 7A and 7B).89 In the same paper, the authors additionally evaluated another type of receptor consisting of noncyclic 6-fold substituted benzene tripodal compounds (Fig. 7, 8A–8E), aiming to promote the formation of a tetrahedral binding site instead of the spherical arrangement to favor NH4+ selectivity versus K+. In particular, the use of 1,3,5-tributylbenzene as the backbone for the further introduction of three substituents (i.e., pyrazole rings, phenolic ethers, and amide carbonyl groups) confer a preorganized structure to these receptors, where the three butyl units were placed on the same side of the benzene ring by the steric hindrance of the substituents. Once incorporated into the membrane matrix, the 20- and 21-membered tridecalino-crown ethers (Fig. 6, 7A and 7B) exhibited NH4+/K+ selectivity (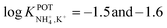 , respectively) better than that of the 19-membered compound previously reported (6B,
, respectively) better than that of the 19-membered compound previously reported (6B, 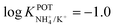 ) and really close to the best values reported for nonactin (−1.7 and −1.8).53,58 This may be attributed to the fact that the larger cavities in 7A and 7B are disadvantageous for K+ complexing. Furthermore, the lipophilicity values calculated for these two compounds were greater than that for nonactin (log
) and really close to the best values reported for nonactin (−1.7 and −1.8).53,58 This may be attributed to the fact that the larger cavities in 7A and 7B are disadvantageous for K+ complexing. Furthermore, the lipophilicity values calculated for these two compounds were greater than that for nonactin (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Poctanol/water = 14.6 and 15.2 for 7A and 7B, respectively, against log
Poctanol/water = 14.6 and 15.2 for 7A and 7B, respectively, against log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Poctanol/water = 5.8 for nonactin), implying that plasticized polymeric membranes based on either 7A or 7B may exhibit reduced leaching, resulting in longer lifetimes. In the case of tripodal ionophores (Fig. 7), only the pyrazole-containing compound (Fig. 7, 8A) showed significant NH4+/K+ selectivity (i.e.,
Poctanol/water = 5.8 for nonactin), implying that plasticized polymeric membranes based on either 7A or 7B may exhibit reduced leaching, resulting in longer lifetimes. In the case of tripodal ionophores (Fig. 7), only the pyrazole-containing compound (Fig. 7, 8A) showed significant NH4+/K+ selectivity (i.e.,  ), but with a LOD at the millimolar level. As a result, none of these compounds were further used in analytical applications.
), but with a LOD at the millimolar level. As a result, none of these compounds were further used in analytical applications.
Despite the considerations reported so far highlighting the necessity of increasing the cavity size of the crown ether compounds to promote NH4+ binding against K+, unexpectedly, the use of smaller ones was reported along the same directions. For example, Jin et al.90 examined 16-crown-4 derivatives based on 4 units of tetrahydrofuran (THF), namely, 1,4,6,9,11,14,16,19-tetraoxocycloeicosane (Fig. 8, 9A) and its tetramethyl derivate (5,10,15,20-tetramethyl-1,4,6,9,11,14,16,19-tetraoxocycloeicosane, 9B) as NH4+ ionophores. The presence of methyl groups in the meso positions of the compound was found to negatively affect NH4+-selective binding; 9A presented a higher capability to selectively bind NH4+. The authors additionally ascribed the different behaviors by the two compounds to changes in the electronegativity of the ether oxygen atoms in the crown backbone when the four methyl substituents were present (9B). Advantageously, the NH4+/K+ selectivity of 9A was found to be better than the average value for nonactin (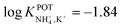 versus −1.0) when dioctyl phenylphosphonate (DOPP) was used as the plasticizer. However, the selectivity values with respect to other cations belonging to the alkaline and earth alkaline groups were rather worse as compared to that when using nonactin.
versus −1.0) when dioctyl phenylphosphonate (DOPP) was used as the plasticizer. However, the selectivity values with respect to other cations belonging to the alkaline and earth alkaline groups were rather worse as compared to that when using nonactin.
The use of even smaller crown ethers was explored by Chandra et al. by placing units of 15-crown-5 ethers as the branches of a dendrimer (Fig. 8, 10).91 Interestingly, the authors accomplished a comparison of the use of different plasticizers, namely, dibutyl phthalate (DBP), diphenyl ether (DPE), dioctyl phthalate (DOP), and dibutyl amine (DBA) in the membrane composition. Wider linear range and lower LOD could be obtained when using DBP and NaTFPB as the ion exchangers, with remarkable selectivity toward NH4+ over K+ (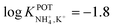 ). Moreover, the lifetimes of these electrodes were found to be at least 45 days after ISM preparation.
). Moreover, the lifetimes of these electrodes were found to be at least 45 days after ISM preparation.
More recently, Jin et al.92 employed a thiazole-derivate benzo-crown ether functionalized with ethylamine-thioctic acid (TBCEAT; Fig. 8, 11) to form ionophore-based self-assembled monolayers on a gold disk electrode via a thiol linker. In addition, the behavior of this ionophore was investigated using a regular membrane incorporated in inner-filling solution-type ISEs (see Table 2). Regarding the self-assembled monolayer, its redox peak in Ru(NH3)6Cl3 solution was found to decrease with increasing NH4+ concentrations as a result of the binding of the cation with the ionophore, thereby blocking the monolayer from any redox conversion. However, in none of the explored electrodes (neither voltammetry nor potentiometry), the ionophore exhibited better performances than those obtained from nonactin-based electrodes (see Table 2).
Along the same direction, Saiapina et al.93 explored a self-assembled monolayer on gold electrodes based on calixarene-type ionophores as the selective element of a differential conductometric transducer. In particular, 25,27-di-(5-thio-octyloxy)calix[4]arene-crown-6 (Fig. 9, 12) was used. This is a cryptand-like ionophore that was expected to provide dual coordination sites: via ether oxygens of the crown unit and via cation–π interactions. However, the NH4+/K+ selectivity coefficient calculated with the Cammann method,94 which is similar to the fix interference method applied in potentiometry, was very similar to the nonactin one (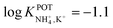 ). Thereafter, the analytical performance of the sensor revealed a linear range of 10–5–1.5 × 10–3 M as well as higher operational stability. The conductimetric ISE was applied for NH4+ detection in river water samples, which were filtered and spiked with a known amount of NH4+, yielding recoveries between 93% and 106%. Nevertheless, the authors did not report the spiked NH4+ concentrations in the samples: without this information, it is not possible to further evaluate the potential of this electrode to detect NH4+ in real samples at the expected levels.
). Thereafter, the analytical performance of the sensor revealed a linear range of 10–5–1.5 × 10–3 M as well as higher operational stability. The conductimetric ISE was applied for NH4+ detection in river water samples, which were filtered and spiked with a known amount of NH4+, yielding recoveries between 93% and 106%. Nevertheless, the authors did not report the spiked NH4+ concentrations in the samples: without this information, it is not possible to further evaluate the potential of this electrode to detect NH4+ in real samples at the expected levels.
The use of tripodal nonmacrocyclic receptors based on a 6-fold substituted benzene ring as NH4+ ionophores was also reported. One of the first studies by Chin et al.80 investigated the compound 1,3,5-tri(3,5-dimethylpyrazol-1-ylmethyl)-2,4,6-triethylbenzene receptor (Fig. 9, 13) with a worthwhile design to improve NH4+ selectivity. The key feature of the tripodal compound reported by them was its tendency toward forming tetracoordinated complexes instead of spherical ones. Therefore, the 6-fold substituted benzene ring was predicted to assume a preorganized structure, driven by the steric repulsions among the ethyl and dimethylpyrazole substituents (Fig. 9, 13). Indeed, the molecular computation showed that the three dimethylpyrazole groups were not placed on the same side of the benzene ring in the crystal structure, but they were found to converge toward the internal region of the receptor in the presence of NH4+. In this configuration, NH4+ was captured by three H-bonds established with the sp2-hybridized nitrogen atoms of the pyrazole groups and stabilized by cation–π interactions with the benzene ring. Furthermore, the size and symmetry of the designed receptor cavity was proven to effectively fit with the tetrahedral conformation of NH4+, while being disadvantageous for spherical symmetry coordination as well as being largely wider for smaller cations. These structural findings were supported by remarkable NH4+/K+ selectivity when the receptor was incorporated into a plasticized polymeric membrane as a part of an inner-filling solution-type ISE (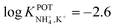 ). Importantly, this represents the best NH4+/K+ selectivity reported in the literature so far. However, the sensitivity of 13 was rather poor to allow for its effective application in the analysis of real samples (i.e., LRR ≈ 10–3–10–1 M). A subsequent study was carried out,95 aiming to improve the sensitivity of 13 by designing new tripodal derivates. The authors synthesized two analogous tripodal compounds by introducing bromide atoms in the fourth position of the pyrazole units in one case (Fig. 9, 14A) and removing the dimethyl substituents from the pyrazole units in the other case (Fig. 9, 14B) in order to deepen both steric and electronic effects on the binding properties.
). Importantly, this represents the best NH4+/K+ selectivity reported in the literature so far. However, the sensitivity of 13 was rather poor to allow for its effective application in the analysis of real samples (i.e., LRR ≈ 10–3–10–1 M). A subsequent study was carried out,95 aiming to improve the sensitivity of 13 by designing new tripodal derivates. The authors synthesized two analogous tripodal compounds by introducing bromide atoms in the fourth position of the pyrazole units in one case (Fig. 9, 14A) and removing the dimethyl substituents from the pyrazole units in the other case (Fig. 9, 14B) in order to deepen both steric and electronic effects on the binding properties.
The presence of electronegative bromide atoms in 14A allowed an improvement in the LOD (2.5 × 10–5 M against 1.0 × 10–4 M, as reported for 13), but also resulting in slightly lower NH4+/K+ selectivity (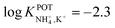 ). This decrease could be attributed to the electronegativity in the ion complexation provided by bromide atoms, thereby decreasing the preference toward tetrahedral configuration over the spherical one demonstrated in 13. In addition, the authors observed that the sensitivity of 14A improved when the pH was increased from neutral (7) to 9, which could be attributed to the ability of the protonated receptor to coordinate with water molecules and therefore interfering with NH4+ acquisition, as demonstrated by the X-ray experiments. As a result, the sensitivity of the pyrazole-containing receptor could be correlated with the basicity of the pyrazole units; therefore, competitive NH4+/H2O could be modulated. However, this need for pH adjustment to obtain the best sensitivity is not convenient for the analysis of real samples. Subsequently, with regard to NH4+/K+ selectivity in 14B, the analysis of the crystal structures suggested that the methyl groups at the third positions of the pyrazole units provided a shielding effect, deterring the formation of a 2
). This decrease could be attributed to the electronegativity in the ion complexation provided by bromide atoms, thereby decreasing the preference toward tetrahedral configuration over the spherical one demonstrated in 13. In addition, the authors observed that the sensitivity of 14A improved when the pH was increased from neutral (7) to 9, which could be attributed to the ability of the protonated receptor to coordinate with water molecules and therefore interfering with NH4+ acquisition, as demonstrated by the X-ray experiments. As a result, the sensitivity of the pyrazole-containing receptor could be correlated with the basicity of the pyrazole units; therefore, competitive NH4+/H2O could be modulated. However, this need for pH adjustment to obtain the best sensitivity is not convenient for the analysis of real samples. Subsequently, with regard to NH4+/K+ selectivity in 14B, the analysis of the crystal structures suggested that the methyl groups at the third positions of the pyrazole units provided a shielding effect, deterring the formation of a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex that was found to be more favorable for K+ binding as compared to 13 and 14A, thereby explaining the reported selectivity order for 13, 14A, and 14B:
1 complex that was found to be more favorable for K+ binding as compared to 13 and 14A, thereby explaining the reported selectivity order for 13, 14A, and 14B: 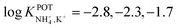 , respectively.
, respectively.
In a further study by the same research group,96 a cage-type tripodal derivate with three dialkoxybenzene units coupled to two benzene rings was reported (Fig. 10, 15A). Obviously, the receptor was designed on the basis of a rigid framework, providing a cavity with a tailor-made size for binding NH4+; this was recognized not only by H-bonds, but also by double-sided cation–π interactions. The suitability of phenolic oxygen atoms as H-bond acceptors instead of pyrazolic nitrogen atoms was tested, thereby decreasing the pH dependence owing to the lower basicity of the former. Indeed, X-ray analyses demonstrated that the distance between the two benzene rings is larger when NH4+ is bound, being placed in the middle of the cavity and stabilized by H-bonds. This receptor showed comparable analytical performances to those observed for nonactin, both in terms of sensitivity and selectivity. In addition, a derivate with an open structure was also synthesized without one of the two benzene rings (Fig. 10, 15B). By calculating the association constants of 15A and 15B (i.e., 3.3 × 107 and 1.9 × 106, respectively) and the corresponding binding energies (i.e., 62.3 and 58.2 kcal mol−1, respectively), the authors confirmed that the cage-type structure could enhance the binding efficiency toward NH4+; unfortunately, they could never overcome the performances of nonactin-based compounds.
Benco et al.26 reported a cyclic depsipeptide (Fig. 10, 16) that possessed alternating amide and ester groups in order to achieve a valinomycin-inspired structure. Molecular modeling suggested that this valinomycin-like receptor could provide more favorable coordination for NH4+ than that for K+, owing to five H-bond acceptors (i.e., carbonyl groups) available for the tetrahedral binding of NH4+. Furthermore, the rather high rigidity of this ionophore with respect to nonactin was responsible in deterring the binding of K+, which prefers spherical symmetry coordination. All these aspects were evidenced in an organic solution. In addition, ionophore 16 was incorporated in a planar ISE with a polymeric solid contact material. The membrane composition was examined using DOP or o-NPOE as the plasticizer and the presence or absence of potassium tetrakis (4-chlorophenyl) borate (KtpClPB) as the ion exchanger. The potentiometric responses obtained with o-NPOE resulted in close-to-Nernstian slopes, while DOP-based membranes yielded lower values. The authors ascribed this behavior to the different dielectric constants of the plasticizers, favoring the formation of H-bonding.97 Although the closest slope to the Nernstian behavior was obtained without the ion exchanger (60.1 mV dec−1), the best NH4+/K+ selectivity was observed with the KtpClPB-based membrane (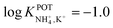 ) with a slightly lower slope (55.8 mV dec−1). Overall, the analytical performances were comparable with the traditional nonactin-based ISEs without improvements, despite the fact that the selectivity in organic solutions was promising.
) with a slightly lower slope (55.8 mV dec−1). Overall, the analytical performances were comparable with the traditional nonactin-based ISEs without improvements, despite the fact that the selectivity in organic solutions was promising.
Ribeiro et al.98 investigated the facilitated transport of NH4+ at aqueous/organic interfaces driven by an electrochemical potential variation (i.e., the study of a polarized interface between two immiscible electrolyte solutions, known as ITIES). For this purpose, synthetic hexakis(2,3,6-tri-O-acetyl)-α-cyclodextrin (Fig. 10, 17) was used as the ionophore that could promote the transfer of NH4+via the water/1,6-dichlorohexane interface. Essentially, it was observed that compound 17 formed stable complexes with NH4+, with a relatively high association constant (logβ of 7.9). In particular, NH4+ transfer was investigated using CV, differential pulse voltammetry, and squarewave voltammetry, where the final option was the optimal readout mechanism for the calibration graph. Therefore, the squarewave voltammetric peak increases with the extraction of NH4+ in the organic phase within a linear range from 4 to 66 μM. Although the authors proposed the concept as the basis of an amperometric sensor for NH4+ detection, this application was not reported until now. In addition, when interferences were evaluated, K+ as well as Na+ had a fair influence on the analytical response. Accordingly, the authors suggested the need for combining an ion chromatography system with the detector in the subsequent development of this system.
After inspecting the selected papers, the overview for NH4+ sensing using ionophore-based sensors is fairly clear. As far as we know, none of the ionophores reported in the literature over the last 20 years provide analytical features that can overcome the performance of nonactin-based electrodes. The confirmation of this statement relies on the higher number of applications reported for nonactin-based electrodes when compared with other ionophores (see Tables 1 and 2). However, the use of nonactin-based electrodes for NH4+ sensing in real samples is significantly restricted by K+ interference. As a result, NH4+ is detectable using ISEs only in certain specific samples where its concentration is typically higher than the micromolar level; in addition, the K+ concentration is higher than the NH4+ concentration by no more than 1.5 orders of magnitude (e.g., well water, hydroponic solution, wastewater, sewage, and some natural waters).5,48,49,55,57–60,69 Importantly, this seems to also be the situation for NH4+ detection in sweat.53,54 Although NH4+ detection in sweat using wearables has been reported in the literature, K+ interference is on the borderline; further, an exhaustive analysis of the associated error is mandatory to establish the accuracy of on-body analysis. On the other hand, NH4+ electrodes based on nonactin can be used as a part of a sensor array (together with statistical treatments)45–47 along with any other technique to detect K+ concentrations in the sample and subsequently correcting the electrode response according to the NH4+/K+ selectivity coefficient (by using specific algorithms)55 after a separation column50 or the indirect detection of creatinine in urine (also using anion–exchange membranes to avoid K+ interference).76 From this assessment, it is evident that NH4+ detection cannot be currently resolved by ISEs. However, in the subsequent section, we inspect the electrodes fabricated without any kind of ionophores as well as commercial devices to confirm this absence.
4. Other ammonium electrodes without ionophores
Kan et al. reported a potentiometric sensor fabricated on the basis of an Ag/AgCl wire modified first with a film of PANI as an ion-to-electron transducer and then with poly(o-phenylenediamine) (POPD) as the sensing membrane.99 POPD has an affinity toward NH4+via hydrogen binding and acts as a membrane when electropolymerized at the PANI surface. Overall, it can be assumed that POPD plays the role of an ionophore, but this was not really investigated by the authors. Despite the fact that the calibration parameters in potentiometry were within the expected values, the selectivity toward K+ and Na+ did not overcome the performances reported for ionophore-based electrodes (close to −0.9 in both the cases, see Table 3). The authors demonstrated the application of the electrode in tap water containing really high concentrations of NH4+ without being specific about these unusual levels.| Type of electrode | Readout | Analytical parameters | NH4+/K+ selectivity | Application | Ref. |
|---|---|---|---|---|---|
| POPD: poly(o-phenylenediamine). ZTP: zirconium–titanium phosphate. LOD: limit of detection. LRR: linear range of response. | |||||
| Ag/AgCl wire + PANI (transducer) + POPD (sensing element) | Potentiometry | LOD = 1.2 × 10−5 M | −0.9 | Tap water with 0.1, 1.4 × 10−3 and 4 × 10−4 M NH4+ concentration | 99 |
| Slope = 54.99–55.70 mV dec−1 | |||||
| LRR = 2 × 10−5–0.1 M | |||||
| GC + SiO2/ZrO2/phosphate–NH4+ composite | Potentiometry | Slope = sub-Nernstian | −1.2 | Natural waters in the range from 1 to 14 mM | 100 |
| LOD = 1.6 × 10−7 M | |||||
| LRR = 7.7 × 10−7–4.0 × 10−2 M | |||||
| ZTP ion-exchanger | Potentiometry | Slope = 38–48 mV dec−1 | – | – | 101 |
| LRR = 1 × 10−5–1.0 M | |||||
| Natural zeolite clinoptilolite | Conductometric | LOD = 1 × 10−8 M | 0 | – | 102 |
| LLR = 0–8 mM | |||||
Coutinho and co-workers published the analytical performances and applications of a GCE modified with SiO2/ZrO2/phosphate–NH4+ composite.100 This composite presented reproducible exchange properties toward NH4+ in the pH range from 6 to 7.5, which may be an inconvenience for certain applications. In addition, again, the selectivity coefficient for K+ did not improve the values as compared to those reported for electrodes analyzed in the earlier sections (see Table 3). As a result, the authors demonstrated NH4+ detection in natural waters at fairly high concentrations (1–14 mM). Most probably, the developed electrode has its roots in earlier investigations reported by the group of Hassan about a zirconium–titanium phosphate ion exchanger capable of measuring NH4+ concentrations between 1 × 10−5 and 1.0 M in the pH range of 4.0–7.5.101 While the electrode was implemented in a FIA system, no analytical applications could be unfortunately reported.
The natural zeolite, clinoptilolite, was also explored as a sensing element for NH4+-conductometric electrodes.102 A specific ion-exchange process occurred between NH4+ from the aqueous solution and Na+ from the sensitive zeolitic membrane, resulting in a change in the interfacial resistance. This paper interestingly revised the data from certain electrodes reported till the date of publication, highlighting the primary existence of potentiometric electrodes prepared on the basis of ionophore-based polymeric membranes. Although a zeolite-based electrode yielded promising LOD (NH4+ concentration in the order of 10−8 M) along with the intrinsic characteristics of conductimetric sensors versus potentiometric ones (essentially simplicity and lifetime), the selectivity is rather poor and the electrode response is similar to all the cations tested (particularly K+ and Na+). In our opinion, and in view of the impressive LOD of this sensor, it would be interesting to investigate modified zeolites in the direction of providing more selective sensors for NH4+.
5. Commercially available ammonium electrodes
In this last section, we offer an overview of commercially available NH4+ electrodes: a summary of its main features are listed in Table 4. In general, a vast majority of the brands do not provide a detailed description of the sensor in terms of membrane composition. Essentially, the operation principle always follows two different alternatives: (i) gas membrane for NH3 detection (consequently, NH4+ has to be converted into NH3 to be detected in the sample) or (ii) NH4+-selective membranes. Regarding the formulation of the latter, some brands indicate that this is a PVC-based membrane,103–108 but the presence of an ionophore is uncertain. However, we may anticipate that all these electrodes are based on nonactin after inspecting the analytical performances reported on the corresponding webpages (i.e., LRR from 5 × 10–6 to 1 M and K+ interference, see Table 4).| Brand | Detected specie (s) | Sensing principle | Electrode design | pH range for operation | T range for operation | Analytical parameters | Interferences | Applications |
|---|---|---|---|---|---|---|---|---|
| ISE: ion-selective electrode. LRR: linear range. PVC: polyvinyl chloride. POM: polyoxometalate. | ||||||||
| Bante instruments109 | NH4+ | Direct NH4+ detection in aqueous solutions | Not described | 4–10 | 0–50 °C | LRR = 5 × 10−6–1 M | Cs+, K+, Tl+, H+, Ag+, tris+, Li+, Na+ | Laboratory measurements |
| Metrohm110 | NH3/NH4+ | Direct NH3 detection in aqueous solutions and NH4+ after conversion to NH3 | Gas membrane | 0–14 | 0–50 °C | LRR = 5 × 10−6–10−2 M | Water vapor | Contaminated water |
| Metrohm110 | NH3/NH4+ | Direct NH3 detection in aqueous solutions and NH4+ after conversion to NH3 | Gas membrane | 0–14 | 0–50 °C | LRR = 10−4–1 M | Water vapor | Contaminated water |
| Nico 2000103 | NH4+ | Direct NH4+ detection in aqueous solutions | Solid-state PVC membrane | 0–8.5 | 0–50 °C | LRR = 2 × 10−6–0.1 M | Na+, K+, Li+, Ca2+, Mg2+ | Laboratory measurements |
| HORIBA Advanced Techno105 | NH4+ | Direct NH4+ detection in aqueous solutions | pH glass ISE membrane | >12 | 0–50 °C | LRR = 5 × 10−7–1 M | Gas into the internal solution | Laboratory measurements |
| Cole-Parmer111 | NH3/NH4+ | Direct NH3 detection in aqueous solutions and NH4+ after conversion to NH3 | Gas sensing electrode | >11 | 0–50 °C | LRR = 5 × 10−7–1 M | Not found | Laboratory measurements |
| Hanna Instruments104 | NH4+ | Direct NH4+ detection in aqueous solutions | PVC membrane | >11 | 0–40 °C | LRR = 0.02–200 ppm | Not found | Fresh water |
| Hanna Instruments104 | NH3/NH4+ | Direct NH4+ detection in aqueous solutions | Gas membrane | >11 | 0–40 °C | LRR = 10−6–1 M | Not found | Natural water, wine, beer, ground water |
| YSI a Xylen Brand108 | NH3/NH4+ | Direct NH3 detection in aqueous solutions | Gas sensing electrode | ISA buffers to >11 | 0–50 °C | LRR = 0.02–17000 ppm | Volatile amines | Laboratory measurements |
| YSI a Xylen Brand108 | NH4+ | Direct NH4+ detection in aqueous solutions | PVC membrane | 4–10 | −5–100 °C | LRR = 0.02–1800 ppm | Na+, K+ | Laboratory measurements |
| Thermo Fisher112 | NH3/NH4+ | Direct NH3 detection in aqueous solutions and NH4+ after conversion to NH3 | Gas sensing electrode | 11 | 0–50 °C | LRR = 5 × 10−7–1 M | Water vapor | Laboratory measurements |
| Vernier107 | NH4+ | Direct NH4+ detection in aqueous solutions | PVC membrane | 4–7.5 | 0–40 °C | LRR = 1–18000 ppm | K+ | Laboratory measurements |
| NT Sensors106 | NH4+ | Direct NH4+ detection in aqueous solutions | POM/PVC | 2–9 | 0–50 °C | LRR = 10−5–1 M | Not found | Laboratory measurements |
| NT Sensors106 | NH3/NH4+ | Direct NH3 detection in aqueous solutions | Gas sensing electrode | Not described | 0–50 °C | LRR = 0.02–17000 ppm | Hydrazine | Laboratory measurements |
With regard to selectivity, it is normally mentioned (prospect and webpages) that cations or other compounds may influence the electrode signal. However, no quantification of this influence is provided, which somehow complicates the advance determination of whether the electrode suits any desired application. Only Nico2000 lists the potentiometric selectivity coefficients for K+ (0.1), Na+ (0.002), Mg2+ (0.0002), Ca2+ (0.00006), and Li+ (0.00003), which are in good agreement with the values reported for nonactin-based polymeric membranes (see Table 1). On the other hand, regardless of the principle of operation used for sensor fabrication, a wide range of operating temperatures are generally described (between 0 and 50 °C as a trend), while no trend is found for an appropriate pH range.
In general, a more comprehensive inspection of commercial NH4+ electrodes can confirm that there is no clear solution that is currently available, whereas these electrodes can be used for academic purposes and some specific applications comprising water samples with a relatively high concentration of NH4+ (see Table 4).
6. Conclusions
An overview of ammonium-selective electrodes reported over the last 20 years is presented in this paper, considering electrodes based on nonactin or other ionophores, electrodes without any ionophore, and commercially available devices. After a comprehensive analysis, it is evident that none of the ionophore-based electrodes can overcome the analytical features demonstrated by nonactin-based electrodes; further, there is clear evidence of a higher number of analytical applications reported for nonactin-based electrodes as compared to the other electrodes. However, these analytical applications are limited by K+ interference present in the electrode response. Therefore, seemingly, the detection of ammonium ions is primarily possible in some kinds of (contaminated) water samples as well as sweat. Moreover, the indirect detection of creatinine and urea is also achievable by nonactin-based electrodes by monitoring the formed ammonium during the respective enzymatic reactions based on hydrolases enzymes. Unfortunately, despite the fact that the authors in the field working along the direction of providing new alternatives for use as ionophores, there is no tangible solution available. In general, the incorporation of newer receptors to be explored as ammonium ionophores is based on preliminary considerations involving NMR and extractability data, which indicate the preference of the receptor for ammonium over potassium. Nevertheless, these investigations do not correlate with the results observed in the membrane phase and therefore the associated analytical features do not improve. On the other hand, when analyzing ammonium-selective electrodes that are commercially available, the same conclusion can be obtained. Nevertheless, we have identified two potential paths to follow toward a suitable ammonium detection system using ISEs. One is the use of zeolite-based sensors, on the basis of the publication by Saiapina et al.,102 and the other is the integration of ionophore-based membranes by dynamic electrochemical protocols, analogous to the paper by Rahmen and co-workers,86 thereby yielding newer selectivity dimensions. In our opinion, this is the time to question why ammonium detection is not entirely possible using ISEs, and researchers in the field have to act accordingly by searching for newer strategies as well as readout mechanisms.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This project has received funding from the European Union's Horizon 2020 research and innovation programme under Marie Skłodowska-Curie grant agreement No. 792824. M. C. acknowledges the support from the ÅForsk Foundation (Grant Agreement 19-464) and the Swedish Research Council (VR-2019-04142). N. C. thanks the scholarship program from The Foundation Blanceflor. B. F. acknowledges the Wenner-Gren Foundation (Scholarship UPD2019-0038). G. C. gratefully thanks KTH Royal Institute of Technology (K-2017-0371) and the Swedish Research Council (Project Grant VR-2017–4887).References
- M. Cuartero and G. A. Crespo, Curr. Opin. Electrochem., 2018, 10, 98–106 CrossRef.
- M. Parrilla, R. Canovas, I. Jeerapan, F. J. Andrade and J. Wang, Adv. Healthcare Mater., 2016, 5, 996–1001 CrossRef PubMed.
- G. A. Crespo, Electrochim. Acta, 2017, 245, 1023–1034 CrossRef.
- A. J. Bandodkar and J. Wang, Trends Biotechnol., 2014, 32, 363–371 CrossRef PubMed.
- R. Athavale, C. Dinkel, B. Wehrli, E. Bakker, G. A. Crespo and A. Brand, Environ. Sci. Technol. Lett., 2017, 4, 286–291 CrossRef.
- M. Cuartero and E. Bakker, Curr. Opin. Electrochem., 2017, 3, 97–105 CrossRef.
- R. De Marco, G. Clarke and B. Pejcic, Electroanalysis, 2007, 19, 1987–2001 CrossRef.
- M. C. Frost and M. E. Meyerhoff, Annu. Rev. Anal. Chem., 2015, 8, 171–192 CrossRef PubMed.
- R. Koncki, Anal. Chim. Acta, 2007, 599, 7–15 CrossRef PubMed.
- M. Gutierrez, S. Alegret and M. del Valle, Biosens. Bioelectron., 2007, 22, 2171–2178 CrossRef PubMed.
- R. G. Yan, S. Qiu, L. Tong and Y. Qian, Chem. Speciation Bioavailability, 2016, 28, 1–1 CrossRef.
- M. Parrilla, M. Cuartero and G. A. Crespo, TrAC, Trends Anal. Chem., 2019, 110, 303–320 CrossRef.
- M. Parrilla, I. Ortiz-Gomez, R. Canovas, A. Salinas-Castillo, M. Cuartero and G. A. Crespo, Anal. Chem., 2019, 91, 8644–8651 CrossRef PubMed.
- J. R. Sempionatto, A. Martin, L. Garcia-Carmona, A. Barfidokht, J. F. Kurniawan, J. R. Moreto, G. D. Tang, A. Shin, X. F. Liu, A. Escarpa and J. Wang, Electroanalysis, 2019, 31, 239–245 CrossRef.
- E. Bakker and E. Pretsch, Angew. Chem., Int. Ed., 2007, 46, 5660–5668 CrossRef.
- P. Buhlmann and L. D. Chen, in Supramolecular Chemistry: From Molecules to Nanomaterials, Wiley&Sons, 2012 Search PubMed.
- E. Bakker, P. Buhlmann and E. Pretsch, Chem. Rev., 1997, 97, 3083–3132 CrossRef.
- P. Bühlmann, E. Pretsch and E. Bakker, Chem. Rev., 1998, 98, 1593–1688 CrossRef PubMed.
- E. Bakker, in Encyclopedia of Analytical Science, 2019 Search PubMed.
- M. Mas-Montoya, M. Cuartero, D. Curiel, J. A. Ortuno, M. S. Garcia and A. Tarraga, Analyst, 2015, 140, 287–294 RSC.
- E. Bakker and E. Pretsch, Anal. Chem., 2002, 74, 420a–426a CrossRef.
- A. Bratov, N. Abramova and A. Ipatov, Anal. Chim. Acta, 2010, 678, 149–159 CrossRef.
- E. Bakker and K. Chumbimuni-Torres, J. Braz. Chem. Soc., 2008, 19, 621–629 CrossRef.
- L. A. Pioda, H. Wachter, R. Dohner and W. Simon, Helv. Chim. Acta, 1967, 50, 1373–1376 CrossRef.
- W. Simon, Pure Appl. Chem., 1971, 25, 811–824 Search PubMed.
- J. S. Benco, H. A. Nienaber and W. G. McGimpsey, Anal. Chem., 2003, 75, 152–156 CrossRef.
- J. Schindler, R. Schindler and O. Aziz, Clin. Chem. Lab. Med., 1978, 16, 441–446 Search PubMed.
- K. Neupert-Laves and M. Dobler, Helv. Chim. Acta, 1976, 59, 614–623 CrossRef.
- M. Dobler and R. P. Phizackerley, Helv. Chim. Acta, 1974, 57, 664–674 CrossRef.
- E. Boyle, Science, 2017, 356, 700–701 CrossRef.
- E. Stokstad, Science, 2014, 343, 238–238 CrossRef.
- E. Bakker, Anal. Chem., 1997, 69, 1061–1069 CrossRef.
- E. Bakker, E. Pretsch and P. Buhlmann, Anal. Chem., 2000, 72, 1127–1133 CrossRef.
- M. Rich, L. Mendecki, S. T. Mensah, E. Blanco-Martinez, S. Armas, P. Calvo-Marzal, A. Radu and K. Y. Chumbimuni-Torres, Anal. Chem., 2016, 88, 8404–8408 CrossRef.
- A. Birch and J. Robinson, in Genetics and Biochemistry of Antibiotic Production, Elsevier, 1995, pp. 443–476 Search PubMed.
- Z. Stefanac and W. Simon, Chimica, 1966, 20, 436–440 Search PubMed.
- Z. Štefanac and W. Simon, Microchem. J., 1967, 12, 125–132 CrossRef.
- M. Meyerhoff and R. Robins, Anal. Chem., 1980, 52, 2383–2387 CrossRef.
- M. E. Meyerhoff, Anal. Chem., 1980, 52, 1532–1534 CrossRef.
- G. S. Cha and M. E. Meyerhoff, Talanta, 1989, 36, 271–278 CrossRef.
- M. Ghauri and J. Thomas, Analyst, 1994, 119, 2323–2326 RSC.
- D. Liu, M. E. Meyerhoff, H. D. Goldberg and R. B. Brown, Anal. Chim. Acta, 1993, 274, 37–46 CrossRef.
- I. Mostert, P. Anker, H.-B. Jenny, U. Oesch, W. Morf, D. Ammann and W. Simon, Microchim. Acta, 1985, 85, 33–38 CrossRef.
- D. Siswanta, H. Hisamoto, H. Tohma, N. Yamamoto and K. Suzuki, Chem. Lett., 1994, 23, 945–948 CrossRef.
- F. S. de Viteri and D. Diamond, Electroanalysis, 1994, 6, 9–16 CrossRef.
- J. Gallardo, S. Alegret, M. A. de Roman, R. Munoz, P. R. Hernandez, L. Leija and M. del Valle, Anal. Lett., 2003, 36, 2893–2908 CrossRef.
- J. Gallardo, S. Alegret, R. Munoz, M. De-Roman, L. Leija, P. R. Hernandez and M. del Valle, Anal. Bioanal. Chem., 2003, 377, 248–256 CrossRef CAS.
- J. Schwarz, H. Kaden and G. Pausch, Fresenius’ J. Anal. Chem., 2000, 367, 396–398 CrossRef CAS.
- N. Pankratova, G. A. Crespo, M. G. Afshar, M. C. Crespi, S. Jeanneret, T. Cherubini, M. L. Tercier-Waeber, F. Pomati and E. Bakker, Environ. Sci.: Processes Impacts, 2015, 17, 906–914 RSC.
- A. Radomska, E. Bodenszac, S. Glab and R. Koncki, Talanta, 2004, 64, 603–608 CrossRef CAS.
- A. Bratov, N. Abramova, J. Muñoz, C. Domínguez, S. Alegret and J. Batrolí, J. Electrochem. Soc., 1997, 144, 617–621 CrossRef CAS.
- N. H. Chou, J. C. Chou, T. P. Sun and S. K. Hsiung, IEEE Sens. J., 2009, 9, 665–672 CAS.
- T. Guinovart, A. J. Bandodkar, J. R. Windmiller, F. J. Andrade and J. Wang, Analyst, 2013, 138, 7031–7038 RSC.
- S. Oertel, M. P. Jank, L. Frey, C. Hofmann, N. Lang and M. Struck, Conference in Biodevices, 2016 Search PubMed.
- R. Athavale, I. Kokorite, C. Dinkel, E. Bakker, B. Wehrli, G. A. Crespo and A. Brand, Anal. Chem., 2015, 87, 11990–11997 CrossRef CAS.
- L. Ding, J. W. Ding, B. J. Ding and W. Qin, Int. J. Electrochem. Sci., 2017, 12, 3296–3308 CrossRef CAS.
- J. Choosang, A. Numnuam, P. Thavarungkul, P. Kanatharana, T. Radu, S. Ullah and A. Radu, Sensors, 2018, 18, 3555 CrossRef.
- J. Gallardo-Gonzalez, A. Baraket, S. Boudjaoui, T. Metzner, F. Hauser, T. Rossler, S. Krause, N. Zine, A. Streklas, A. Alcacer, J. Bausells and A. Errachid, Sci. Total Environ., 2019, 653, 1223–1230 CrossRef CAS PubMed.
- P. W. Alexander, T. Dimitrakopoulos and D. B. Hibbert, Electroanalysis, 1997, 9, 1331–1336 CrossRef CAS.
- L. Y. Heng, S. Alva and M. Ahmad, Sens. Actuators, B, 2004, 98, 160–165 CrossRef CAS.
- R. Canovas, M. Cuartero and G. A. Crespo, Biosens. Bioelectron., 2019, 130, 110–124 CrossRef CAS.
- N. Verma and M. Singh, Biosens. Bioelectron., 2003, 18, 1219–1224 CrossRef CAS.
- Y. Lei, W. Chen and A. Mulchandani, Anal. Chim. Acta, 2006, 568, 200–210 CrossRef CAS PubMed.
- C. Dumschat, M. Borchardt, C. Diekmann, J. Hepke, K. Cammann and M. Knoll, Fresenius’ J. Anal. Chem., 1994, 348, 553–555 CrossRef CAS.
- R. Koncki, S. Głąb, J. Dziwulska, I. Palchetti and M. Mascini, Anal. Chim. Acta, 1999, 385, 451–459 CrossRef CAS.
- M. Bariya, H. Y. Y. Nyein and A. Javey, Nat. Electron., 2018, 1, 160–171 CrossRef.
- D. Czarnowski, J. Gorski, J. Jóźwiuk and A. Boroń-Kaczmarska, Eur. J. Appl. Physiol. Occup. Physiol., 1992, 65, 135–137 CrossRef CAS PubMed.
- D. P. Quan, C. X. Quang, L. T. Duan and P. H. Viet, Environ. Monit. Assess., 2001, 70, 153–165 CrossRef CAS.
- J. Schwarz, K. Trommer and M. Mertig, Am. J. Anal. Chem., 2018, 9, 591–601 CrossRef CAS.
- A. Van den Berg, P. D. Van der Wal, M. Skowronska-Ptasinska, E. J. Sudholter, D. N. Reinhoudt and P. Bergveld, Anal. Chem., 1987, 59, 2827–2829 CrossRef CAS.
- S. S. Levichev, A. V. Bratov and Y. G. Vlasov, Sens. Actuators, B, 1994, 19, 625–628 CrossRef CAS.
- A. Bratov, N. Abramova, J. Munoz, C. Dominguez, S. Alegret and J. Bartroli, Anal. Chem., 1995, 67, 3589–3595 CrossRef CAS.
- R. Canovas, S. P. Sanchez, M. Parrilla, M. Cuartero and G. A. Crespo, ACS Sens., 2019, 4, 2524–2535 CrossRef CAS.
- K. Suzuki, D. Siswanta, T. Otsuka, T. Amano, T. Ikeda, H. Hisamoto, R. Yoshihara and S. Ohba, Anal. Chem., 2000, 72, 2200–2205 CrossRef CAS PubMed.
- A. Bratov, N. Abramova, J. Muñoz, C. Domínguez, S. Alegret and J. Bartrolí, J. Electrochem. Soc., 1994, 141, L111–L112 CrossRef CAS.
- Y. Liu, R. Canovas, G. A. Crespo and M. Cuartero, Anal. Chem., 2020, 92, 3315–3323 CrossRef CAS PubMed.
- S. Winkler, L. Rieger, E. Saracevic, A. Pressl and G. Gruber, Water Sci. Technol., 2004, 50, 105–114 CrossRef CAS.
- D. de Beer, J.-P. R. A. Sweerts and J. C. van den Heuvel, FEMS Microbiol. Ecol., 1991, 86, 1–6 CrossRef CAS.
- D. Debeer and J. C. Vandenheuvel, Talanta, 1988, 35, 728–730 CrossRef CAS.
- J. Chin, C. Walsdorff, B. Stranix, J. Oh, H. J. Chung, S. M. Park and K. Kim, Angew. Chem., Int. Ed., 1999, 38, 2756–2759 CrossRef CAS.
- E. Graf, J. P. Kintzinger, J. M. Lehn and J. LeMoigne, J. Am. Chem. Soc., 1982, 104, 1672–1678 CrossRef CAS.
- T. Moriuchi-Kawakami, S. Nakazawa, M. Ota, M. Nishihira, H. Hayashi, Y. Shibutani and T. Shono, Anal. Sci., 1998, 14, 1065–1068 CrossRef CAS.
- H. S. Kim, H. J. Park, H. J. Oh, Y. K. Koh, J. H. Choi, D. H. Lee, G. S. Cha and H. Nam, Anal. Chem., 2000, 72, 4683–4688 CrossRef CAS.
- U. S. Hong, H. K. Kwon, G. S. Cha, H. Nam, S. H. Chang and K. B. Chung, J. Korean Chem. Soc., 1995, 39, 698–704 CAS.
- H.-S. Kim, K. S. Do, K. S. Kim, J. H. Shim, G. S. Cha and H. Nam, Bull. Korean Chem. Soc., 2004, 25, 1465–1470 CrossRef CAS.
- M. A. Rahmen, N.-H. Kwon, M.-S. Won, M.-H. Hyun and Y.-B. Shim, Anal. Chem., 2004, 76, 3660–3665 CrossRef PubMed.
- K. Q. Xu, M. Cuartero and G. A. Crespo, Sens. Actuators, B, 2019, 297, 126781 CrossRef CAS.
- G. A. Crespo and E. Bakker, RSC Adv., 2013, 3, 25461–25474 RSC.
- S.-I. Sasaki, T. Amano, G. Monma, T. Otsuka, N. Iwasawa, D. Citterio, H. Hisamoto and K. Suzuki, Anal. Chem., 2002, 74, 4845–4848 CrossRef CAS.
- H.-Y. Jin, T.-H. Kim, J.-E. Kim, S.-S. Lee and J.-S. Kim, Bull. Korean Chem. Soc., 2004, 25, 59–62 CrossRef CAS.
- S. Chandra, R. Buschbeck and H. Lang, Talanta, 2006, 70, 1087–1093 CrossRef CAS PubMed.
- S. Jin, J. S. Lee, Y. Kang, M. Heo, J. H. Shin, G. S. Cha, H. Nam, J. Y. Lee, A. Helal and H.-S. Kim, Sens. Actuators, B, 2015, 207, 1026–1034 CrossRef CAS.
- O. Saiapina, S. Kharchenko, S. Vishnevskii, V. Pyeshkova, V. Kalchenko and S. Dzyadevych, NRL, 2016, 11, 105 CAS.
- K. Cammann, Working with ion-selective electrodes: chemical laboratory practice, Springer Science & Business Media, 2012 Search PubMed.
- J. Chin, J. Oh, S. Y. Jon, S. H. Park, C. Walsdorff, B. Stranix, A. Ghoussoub, S. J. Lee, H. J. Chung and S.-M. Park, J. Am. Chem. Soc., 2002, 124, 5374–5379 CrossRef CAS PubMed.
- S. Y. Jon, J. Kim, M. Kim, S. H. Park, W. S. Jeon, J. Heo and K. Kim, Angew. Chem., Int. Ed., 2001, 40, 2116–2119 CrossRef CAS.
- M. Cuartero, J. A. Ortuno, M. S. Garcia, G. Sanchez, M. Mas-Montoya and D. Curiel, Talanta, 2011, 85, 1876–1881 CrossRef CAS.
- J. A. Ribeiro, F. Silva and C. M. Pereira, Talanta, 2012, 88, 54–60 CrossRef CAS.
- Y. T. Kan, C. H. Han, Y. Ye, X. Zhang, Y. F. Huang, L. Xing, Y. F. Zhou and H. W. Qin, Int. J. Electrochem. Sci., 2016, 11, 9928–9940 CrossRef CAS.
- C. Coutinho, A. Muxel, C. Rocha, D. de Jesus, R. Alfaya, F. Almeida, Y. Gushikemb and A. Alfaya, J. Braz. Chem. Soc., 2007, 18, 189–194 CrossRef CAS.
- S. Hassan, S. Marei, I. Badr and H. Arida, Anal. Chim. Acta, 2001, 427, 21–28 CrossRef CAS.
- O. Y. Saiapina, S. V. Dzyadevych, A. Walcarius and N. Jaffrezic-Renault, Anal. Lett., 2012, 45, 1467–1484 CrossRef CAS.
- http://www.nico2000.net/analytical/ammonium.htm .
- https://www.hannainst.es/parametros/4292-electrodo-ise-de-amonio-para-multiparam-hi9829.html .
- https://www.horiba.com/sg/application/material-property-characterization/water-analysis/water-quality-electrochemistry-instrumentation/electrodes-accessories/ion-selective-electrodes/details/ammonia-electrode-combination-5002s-10c-32811/ .
- https://www.ntsensors.com/parameters/ammonium/ .
- https://www.vernier.com/products/sensors/ion-selective-electrodes/labquest-ise/nh4-bta/ .
- https://www.ysi.com/Product/id-400371/TruLine-Ammonium-Electrode-Kit .
- http://www.bante-china.com/enproductsview/764.html .
- https://www.metrohm.com/en/applications/AB-133 .
- https://www.coleparmer.com/i/thermo-scientific-9512bnwp-ise-ammonia-ammonium-electrode-with-bnc-connector/0572216 .
- https://www.thermofisher.com/order/catalog/product/9512HPBNWP .
- T. J. Marrone and K. M. Merz, J. Am. Chem. Soc., 1992, 114, 7542–7549 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2020 |