Open Access Article
Open Access ArticleAmmonia decomposition catalysis using non-stoichiometric lithium imide†
Joshua W.
Makepeace
ab,
Thomas J.
Wood
a,
Hazel M. A.
Hunter
a,
Martin O.
Jones
a and
William I. F.
David
*ab
aISIS Facility, Rutherford Appleton Laboratory, Harwell Oxford, Didcot, OX11 0QX, UK. E-mail: bill.david@stfc.ac.uk
bInorganic Chemistry Laboratory, University of Oxford, Oxford, OX1 3QR, UK
First published on 7th May 2015
Abstract
We demonstrate that non-stoichiometric lithium imide is a highly active catalyst for the production of high-purity hydrogen from ammonia, with superior ammonia decomposition activity to a number of other catalyst materials. Neutron powder diffraction measurements reveal that the catalyst deviates from pure imide stoichiometry under ammonia flow, with active catalytic behaviour observed across a range of stoichiometry values near the imide. These measurements also show that hydrogen from the ammonia is exchanged with, and incorporated into, the bulk catalyst material, in a significant departure from existing ammonia decomposition catalysts. The efficacy of the lithium imide–amide system not only represents a more promising catalyst system, but also broadens the range of candidates for amide-based ammonia decomposition to include those that form imides.
Introduction
Among hydrogen storage candidates, ammonia has one of the highest volumetric (121 kg H2 m−3 at 10 bar) and gravimetric (17.8 wt%) hydrogen densities. At room temperature, it can be stored as a liquid under moderate pressures (∼10 bar), which allows for conformable, cheap and lightweight plastic tanks and a distribution network similar to that of liquefied petroleum gas (LPG). These characteristics make it an attractive alternative fuel and energy buffer.1–3 However, it has been overlooked as a viable hydrogen storage system because of real and perceived safety issues associated with its use, and the unavailability of an effective and inexpensive method of cracking ammonia at moderate temperatures to release its stored hydrogen (eqn (1)):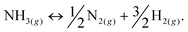 | (1) |
A 2006 U.S. Department of Energy report4 concluded that the current ammonia cracking technology was too large and expensive to be viable for mobile applications. It was also noted that a high temperature of operation is required to drive the ammonia decomposition reaction to completion and thus produce hydrogen of very high purity. This purity is required because proton exchange membrane (PEM) fuel cells are irreparably degraded by low part-per-million concentrations of ammonia. While some energy must be expended to release the stored hydrogen from ammonia (the thermodynamic minimum energy to completely crack ammonia is 12.7% of the energy release from the subsequent oxidation reaction), the requirement of excessively high temperatures for the cracking reaction reduces the effective volumetric energy density of the system, which is particularly detrimental for mobile applications.‡
Three possible solutions could be employed to mitigate these issues. Firstly, significant progress has been made in the development of ammonia-capture materials (metal halide ammines) on porous supports for the purpose of removing small amounts of ammonia from hydrogen gas streams,5 which could assist in lowering the operating temperature required of the ammonia decomposition catalyst. These materials have been shown to be capable of delivering <0.1 ppm ammonia down from an inlet concentration in excess of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ppm. Secondly, an alternative fuel cell technology such as alkaline fuel cells, which have been shown to be unaffected by quite high levels (up to 9%) of ammonia in the hydrogen stream,6 could be used. Although these fuel cells have not been developed as intensively as PEM fuel cells over the last few decades, the technology is known to be effective.7 Thirdly, the ammonia may be combusted instead of used in a fuel cell; ammonia alone is difficult to ignite, but mixtures of ammonia containing as little as 10 vol% hydrogen gas have been shown to combust well.8
000 ppm. Secondly, an alternative fuel cell technology such as alkaline fuel cells, which have been shown to be unaffected by quite high levels (up to 9%) of ammonia in the hydrogen stream,6 could be used. Although these fuel cells have not been developed as intensively as PEM fuel cells over the last few decades, the technology is known to be effective.7 Thirdly, the ammonia may be combusted instead of used in a fuel cell; ammonia alone is difficult to ignite, but mixtures of ammonia containing as little as 10 vol% hydrogen gas have been shown to combust well.8
Regardless of which of these technological solutions is employed, the need to optimise the efficiency of the ammonia cracking reaction will drive the search for more active catalysts for the decomposition reaction, forming a central hurdle to the development of ammonia as an alternative to fossil fuels.4 The state-of-the-art ammonia cracking technology for the production of high purity hydrogen streams at high flow rates is based on ruthenium, often with complex support architecture and promoter species.9,10 Ruthenium is a rare and expensive metal, and so the search for replacement catalysts is an important part of the effort to make ammonia cracking feasible for transport and stationary applications.
We have recently reported a method for the decomposition of ammonia, showing similar performance to a ruthenium-based system,11 that is effected by the concurrent formation and decomposition of sodium amide. The generalised mechanism drawn from the sodium-based system facilitates the decomposition of ammonia through the decomposition and formation of the metal amide (MNH2) from the metal (M),
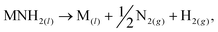 | (2) |
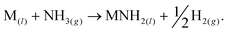 | (3) |
Other metal amides known to thermally decompose via this route (such as potassium and rubidium amides12) should display ammonia decomposition activity through a similar mechanism. Conversely, amides which form the corresponding imide upon heating are not expected to follow the stoichiometric ammonia decomposition indicated in eqn (2). In this paper, we test the ammonia decomposition activity of lithium amide, an imide-forming metal amide.
Lithium amide (LiNH2), a compound widely investigated for its hydrogen storage potential,13–15 shows reversible, ammonia-mediated thermal decomposition to form lithium imide (Li2NH),
| 2LiNH2(s) ↔ Li2NH(s) + NH3(g). | (4) |
Accordingly, lithium amide is not expected to show appreciable ammonia decomposition efficiency by the mechanism outlined in eqn (2) and (3). However, testing and understanding ammonia decomposition activity across the metal amides is an important step in assessing the potential of this new class of ammonia decomposition catalyst, and in developing an understanding of the relevant reaction mechanisms.
Experimental section
Ammonia decomposition
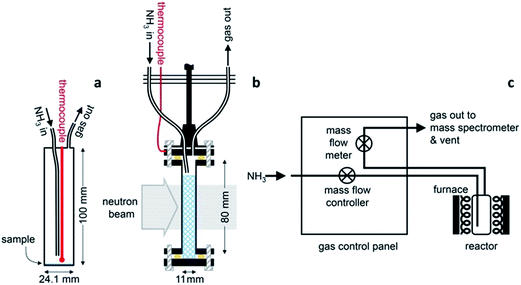
The ammonia decomposition activity measurements in this study were determined in an identical manner to that described for the sodium system.11 Ammonia decomposition reactions using various catalyst materials were performed in one of two cylindrical, 316 stainless steel reactors with internal volumes of 46.9 cm3 and 21.3 cm3. The reactors were fitted with an inlet gas pipe running from the reactor lid to approximately 10 mm from the base of the reactor, an outlet gas pipe from the lid, and a thermocouple monitoring the internal temperature (Fig. 1a). Gas was flowed through the reactor via a custom-designed gas control panel (Fig. 1c) with the inlet gas flow controlled using a mass flow controller (HFC-302, Teledyne Hastings Instruments) and the outlet gas flow measured using a mass flow meter (HFM-300, Teledyne Hastings Instruments). The gas species exiting the reactor were characterised by Quantitative Gas Analysis (QGA) using a Hiden Analytical HPR-20 QIC R&D mass spectrometer system. The mass-to-charge (m/z) values routinely monitored in these experiments were 2 (H2), 17 (NH3), 28 (N2), 32 (O2) and 40 (Ar). The gas flow rates in to and out of the reactor, the reactor temperature and system pressure were also recorded.Variable temperature ammonia decomposition experiments were performed by loading 0.5 g of the catalyst powder into the reactor in an argon-filled glove box. Sodium amide (95%, Sigma Aldrich) and lithium amide (hydrogen storage grade, Sigma Aldrich) were used as received. Samples of silica/alumina-supported nickel (66 ± 5% nickel, Alfa Aesar) or alumina-supported ruthenium (5% ruthenium, Alfa Aesar) were lightly ground to remove any agglomeration and were reduced under flowing ammonia for 5 hours at 680 °C prior to the decomposition experiment. Once loaded with the sample, the reactor was sealed, transferred to a vertical tube furnace (Severn Thermal Solutions) and connected to the gas control panel. The panel was first flushed with argon and then evacuated up to the reactor, before flushing the panel and reactor with ammonia prior to heating.
The ammonia conversion efficiency of each catalyst (along with that of the empty reactor as a baseline) was measured under an ammonia flow of 60 standard cubic centimetres per minute (sccm) in the temperature range of 250–650 °C. Conversion efficiencies were calculated using a customised computer program, which removes background signals and accounts for the signal discontinuities which occur when the detector range switches (see ESI†). Following these corrections, the ammonia conversion efficiency was calculated by determining the ammonia signal as a percentage of the total signal. The conversion values reported are based on average conversion values from a 2–3 h dwell at each temperature.
Gravimetric analysis
The decomposition of lithium amide under ammonia was monitored using the Intelligent Gravimetric Analysis for Neutrons apparatus (IGAn, Hiden Isochema) at the ISIS Neutron and Muon Facility, UK. A sample of lithium amide (390 mg) was loaded into a stainless steel bucket and attached to the IGAn balance in an argon-filled glove box. The apparatus was sealed and evacuated, then refilled with 1100 mbar of ammonia. The sample was then heated to 450 °C at 1 °C min−1, with the mass and temperature of the sample recorded simultaneously.Neutron powder diffraction
Time-of-flight neutron powder diffraction measurements were collected on the POLARIS diffractometer16 at the ISIS Neutron and Muon Facility, UK. A deuterated sample of lithium imide was prepared for these experiments to optimise the coherent neutron scattering from the sample. Deuterated lithium amide (LiND2) was prepared by the reaction of deuterated ammonia (ND3) with lithium nitride (Li3N),| Li3N(s) + 2ND3(g) ↔ 3LiND2(s), | (5) |
| Li3N(s) + LiND2(s) ↔ 2Li2ND(s), | (6) |
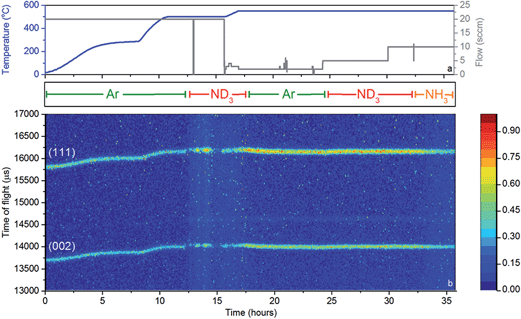
A 11 mm i.d., 0.35 mm wall thickness cylindrical stainless steel flow-through cell (Fig. 1b) was chosen in order to maximise exposure of the ammonia gas to the powder sample. The gas flowed into the sample cell via a pipe which extended 14.5 mm down from the top of the cell into the cell volume, and out through a hole in the top of the cell. This minimised the potential for a blockage of the cell, and permitted the collection of data under flowing ammonia. The cell was filled with approximately 2.7 g of deuterated lithium imide in an argon-filled glove box and assembled into the rest of the POLARIS in situ stick in an argon-filled glove bag. Once sealed, the cell was encased in a boron-nitride collimation shell, with extra gadolinium shielding, to remove the diffraction signal of the stainless steel sample cell from the collected diffraction data.
Once loaded, the sample cell was attached to the same gas delivery panel used in the laboratory ammonia decomposition experiments (Fig. 1c), equipped with argon, ammonia and deuterated ammonia. The sample was then placed within a furnace held in the diffractometer, and an initial 75 minutes diffraction dataset was collected at room temperature under flowing argon (20 sccm). The sample was then heated under flowing argon, first to 300 °C (2 °C min−1) and then to 500 °C (5 °C min−1). After stabilising at that temperature for approximately 30 minutes, the flow was then switched to deuterated ammonia at various flow rates and two temperatures (500 and 550 °C). Finally the sample was exposed to ammonia at 550 °C to perform an H–D isotope exchange reaction experiment. Diffraction data were collected every three minutes throughout the experiment, and the gas flow from the sample cell was monitored by mass spectrometry using the QGA, as described for the ammonia decomposition experiments. The following m/z values were monitored: 2 (H2), 3 (HD), 4 (D2), 17 (NH3), 18 (NH2D), 19 (NHD2), 20 (ND3), 28 (N2), 32 (O2) and 40 (Ar).
The experimental conditions were additionally replicated with an empty sample cell, without the simultaneous collection of diffraction data, in order to assess the background ammonia decomposition levels as measured by the QGA.
Crystallographic analysis
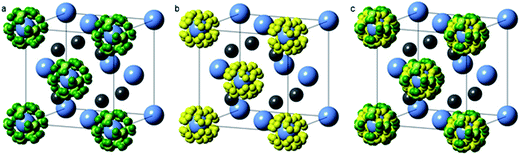
Neutron powder diffraction data were analysed using the TOPAS Academic software package.18 The LiNH2–Li2NH system is known to form a continuum of non-stoichiometric intermediates (Li1+xNH2−x, 0 ≤ x ≤ 1) which adopt the same average cubic structure as Li2NH, with an increasing lattice parameter as the stoichiometry approaches LiNH2.19,20 In contrast to previous X-ray scattering investigations,20 where the scattering of the hydrogen atoms could essentially be ignored, the deuterium atoms contribute a significant proportion of the scattering in the neutron powder diffraction experiment.21 This affords the opportunity to determine the stoichiometry of the sample through Rietveld analysis, but also requires a more carefully constructed structural model to account for the presence of the deuterium atoms in a non-stoichiometric continuum between lithium amide and lithium imide.The a × a × 2a tetragonal lithium amide structure was reduced into a cubic anti-fluorite Li2ND cell (see ESI† for details of the reduction), resulting in a unit cell with half-occupied lithium sites and deuterium atoms on two disordered sites around the nitrogen atoms. This disordered lithium amide structure is shown in Fig. 2a.
For the lithium imide stoichiometry, the tetrahedral lithium site is fully occupied while the deuterium atoms occupy a single disordered site similar to one of the amide positions, Fig. 2b.
With these models representing disordered structures of the end-member stoichiometries, lithium amide and lithium imide, only a single parameter, p, is required to determine the average imide–amide stoichiometry, by varying the occupancy of these sites between fully-occupied amide deuterium sites and a fully-occupied imide deuterium site (0 ≤ p ≤ 1; 0 = Li2ND, 1 = LiND2). This p value also determines the lithium occupancy in the structure, ranging from full occupancy (p = 0) to half occupancy (p = 1). The value of p thus determines the average stoichiometry of the sample with a structural model shown in Fig. 2c. The crystallographic positions and site occupancies for the end members and non-stoichiometric phases described above are summarised in Table 1.
| Atom | x | y | z | Li2ND, p = 0 | LiND2, p = 1 | Li2−pND1+p, 0 < p < 1 |
|---|---|---|---|---|---|---|
| Occupancy | Occupancy | Occupancy | ||||
| Li | 1/4 | 1/4 | 1/4 | 1 | 0.5 | 1 − p/2 |
| N | 0 | 0 | 0 | 1 | 1 | 1 |
| D1 | 0.163 | 0.106 | 0.058 | 1/48 | — | (1 − p)/48 |
| D2 | 0 | −0.081 | 0.186 | — | 1/24 | p/24 |
| D3 | 0.165 | 0.118 | 0 | — | 1/24 | p/24 |
Results and discussion
Ammonia decomposition activity
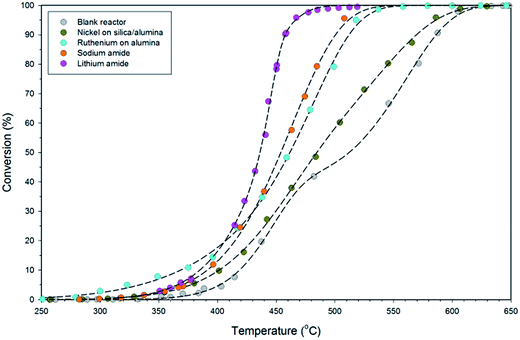
The variable-temperature ammonia decomposition efficiency of 0.5 g lithium amide is shown in Fig. 3 and is compared with equivalent masses of sodium amide, silica/alumina-supported nickel and alumina-supported ruthenium catalysts, and the empty (blank) reactor. The ammonia flow rate was constant at 60 sccm for all of the experiments.LiNH2 reaches high conversion at moderate temperatures, attaining 90.7% conversion at 458 °C, compared with 54.9% for sodium amide, 53.7% for alumina-supported ruthenium, 34.0% for silica/alumina-supported nickel and 32.0% for the blank reactor. Although the ruthenium catalyst has superior performance at lower temperatures, LiNH2 displays a steeper rise than the other systems in Fig. 3, which explains its superior high-conversion performance. The steepness of the sigmoidal function is indicative of higher activation energy for the ammonia decomposition reaction for LiNH2. While a large value for the activation energy might be thought of as a detrimental characteristic, this example shows the importance of considering both the activation energy and the pre-exponential factor within the empirical Arrhenius relationship as the determinants of reaction kinetics. LiNH2 has a larger pre-exponential factor which compensates for its high activation energy.
A range of metrics of catalyst performance are offered in existing literature concerned with catalytic decomposition of ammonia. A number of these metrics for the data presented in Fig. 3 are given in Table 2. The turnover frequency (TOF) indicates the number of catalytic cycles performed by each active site of the catalyst per hour. In the transition metal catalysts, the active site is taken to be the metal itself, with the support excluded. In sodium amide and lithium amide, it is reasonable to assert that the metal ions are the active sites, as it is they that form the strong bond with ammonia on formation of the amide. No account for particle size is made in the TOF calculation; the high TOF for the ruthenium catalyst demonstrates the value of generating dispersed nanoparticles. Given the low cost of alkali metals relative to noble metals, a lower TOF can be tolerated, with the mass-based reaction rate being the most relevant comparator for catalytic performance.
| Catalyst | NH3 conversion (%) | Reaction rate (kgNH3 kgcat−1 h−1) | TOFa (h−1) |
|---|---|---|---|
| a The TOF was calculated as the ratio of the number of moles of ammonia decomposed by the catalyst (molar flow rate × fractioned conversion) per hour and the number of moles of the active metal. | |||
| Ni–SiO2/Al2O3 | 34.0 | 1.78 | 9.31 |
| Ru–Al2O3 | 53.7 | 2.81 | 334 |
| NaNH2 | 54.9 | 2.88 | 6.59 |
| LiNH2 | 90.7 | 4.75 | 6.42 |
Thermogravimetric analysis
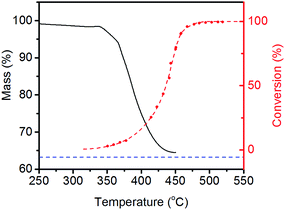
It is clear from Fig. 3 that LiNH2 shows superior ammonia decomposition activity to all of the other materials at temperatures above 420 °C per unit mass of catalyst. The decomposition of LiNH2 has received only limited attention to date; its examination has largely been confined to its role in the production of hydrogen in the lithium amide–lithium hydride hydrogen storage system.22–26 These studies generally consider the decomposition of LiNH2 under an inert atmosphere, where it melts and then decomposes to Li2NH above 360 °C. Examination of LiNH2 under an ammonia atmosphere is limited to a single study of the thermodynamic parameters of eqn (4) through the measurement of pressure-composition isotherms.27In order to probe the decomposition of LiNH2 under relevant conditions for ammonia decomposition, a thermogravimetric analysis (TGA) experiment was performed under a 1 bar ammonia atmosphere. The variation in the mass of the sample under these conditions between 50–450 °C is shown in Fig. 4, and compared against the ammonia decomposition efficiency data from Fig. 3 over the same temperature range.
The percentage mass loss in the TGA experiment indicates that the same Li2NH product is obtained as under inert atmospheres. Importantly, the onset of significant levels of ammonia decomposition appears to be correlated with the onset of decomposition of the amide, indicating that it is reasonable to suggest that LiNH2 will have partially or completely decomposed in the temperature region where it is active in the decomposition of ammonia.
This could be an important factor in the practicability of the use of alkali metal amides for ammonia decomposition. LiNH2 melts at 360 °C, which, although significantly higher than the melting point of sodium amide (210 °C), still means that difficulties are encountered with the effective containment of the catalyst. However, Li2NH is solid until its decomposition at around 600 °C.25,28 Thus, operating at a temperature at which only the imide is stable would allow for the catalyst to be kept solid during the ammonia decomposition reaction.
From the perspective of practicality, the ability to maintain the amide catalyst as a solid at high temperatures has important implications, potentially giving a lithium-based catalyst an additional advantage over the sodium system, aside from its higher catalytic activity. Working with a solid catalyst allows for traditional catalysis routes to higher turnover frequency to be explored, such as the use of support structures. The task of containing the catalyst within the reactor is also significantly simpler. A typical experimental run with the sodium amide catalyst (99.75% conversion, 600 °C, 100 sccm NH3, 3 hours) results in material recoveries from the reactor of between 5–20%, as the sodium amide, while still contained within the reactor, coats the reactor and outlet tubing with a fine powder. In contrast, lithium imide, heated to 500 °C under argon before switching to ammonia in order to avoid amide formation and consequent melting, shows material recoveries from the base of the reactor in excess of 80% after similar reaction conditions (99.85% conversion, 590 °C, 100 sccm NH3, 3 hours).
Neutron powder diffraction
While these results give a reasonable indication that the catalyst has, at least to some extent, decomposed to lithium imide during ammonia decomposition, an in situ probe is the most reliable means for determining the active form of the catalyst. Neutron powder diffraction (NPD) measurements were performed using a stainless steel flow cell (Fig. 1b). Although this setup differs from that used to obtain the results presented in Fig. 3, the flow-through setup ensures that the bulk of the sample is exposed to ammonia and thus the data collected reflect the sample in its active form.Fig. 5 shows a section of the NPD data which includes the (111) and (002) reflections of Li2ND, along with the temperature, gas flow, and input gas species. The sample was heated to 500 °C under argon, and remained crystalline throughout this heating process.
First inspection of the diffraction data shows that lithium imide is present throughout the reaction. Some diffraction peaks are observed from the boron nitride collimation around the reaction cell, and a small amount of lithium oxide is formed during the reaction (see ESI†). Recent reports have shown that the formation of mixed lithium-transition metal nitrides results in high ammonia decomposition activity.29,30 However, lithium imide is the only active species observed in this experiment.
Upon the introduction of ND3 at approximately 12 hours, the intensities of the Li2ND Bragg peaks change dramatically. Firstly the sample appears to melt, which is indicative of the formation of a LiND2-like species, which would be molten at 500 °C. The flow-through cell suffered a significant blockage at this point. Thus, in the absence of further ND3 flow, the sample forms solid Li2ND again, and the Bragg peak intensities return. This cycle of blocking and unblocking repeated a number of times before it was decided to elevate the temperature of the sample under an argon atmosphere in an effort to reform crystalline Li2ND and thus unblock the cell. Heating of the sample to 550 °C did achieve this goal, and the subsequent reintroduction of ND3 at 23 hours did not result in the loss of Bragg peak intensity, nor the blocking of the sample cell. The ammonia decomposition efficiency at 500 °C was approximately 50%, increasing to 74% at 550 °C, compared with 23% and 39% using the same reaction conditions with the blank sample cell (see ESI†). Clearly the sample was involved in the enhanced decomposition of the ammonia in this experiment. Interestingly, the efficiencies for both the blank cell and the catalyst are lower than those presented in Fig. 3. This is a consequence both of the different geometry of the reaction zone in the in situ cell, and the use of deuterated ammonia.
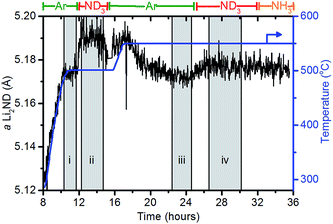
When under isothermal conditions, the a lattice parameter is a good guide to the changes in stoichiometry of the sample. The variation of the a lattice parameter of Li2ND extracted via a Pawley refinement of the diffraction data and the temperature for a portion of the experiment are shown in Fig. 6. The datasets in the shaded areas (i)–(iv) were summed and analysed by the Rietveld method to determine more accurately the lattice parameter and stoichiometry of the sample. The outputs of these refinements are shown in Table 3.
| Segment | Temp. (°C) | Gas | a Li2ND (Å) | p value/average stoichiometry |
|---|---|---|---|---|
| i | 500 | Ar | 5.174(3) | 0.002(33)/Li1.998ND1.002 |
| ii | 500 | ND3 | 5.190(5) | 0.37(3)/Li1.63ND1.37 |
| iii | 550 | Ar | 5.172(2) | 0.19(2)/Li1.81ND1.19 |
| iv | 550 | ND3 | 5.177(3) | 0.24(2)/Li1.76ND1.24 |
The behaviour of the lattice parameter shows that the addition of ND3, both at 500 °C and 550 °C, results in an increase in the lattice parameter of Li2ND. Furthermore, when the sample is exposed to argon from 17–24 hours, the lattice parameter decreases. This anticipated change is consistent with a change in stoichiometry as outlined above.
The crystallographic reduction of the LiND2 structure into the cubic form allowed for the continuum of stoichiometry between Li2ND and LiND2 to be modelled as a single phase in the Rietveld refinement, as described in the Experimental section and ESI.† The stoichiometry determined using this model is presented in Table 3. The initial stoichiometry was close to pure lithium imide, as expected for the as-synthesised sample. On exposure to ND3, the stoichiometry shifts to an intermediate stoichiometry between lithium amide and lithium imide. This value represents the average stoichiometry of the crystalline species. The switch back to argon caused the stoichiometry to return to a value close to lithium imide. The second addition of ND3 again caused a shift towards amide stoichiometry, though to a lesser extent due to the higher temperature.
As a check of the stoichiometry value obtained from the Rietveld refinement, the change in the lattice parameter can be compared with the change observed in the previous in situ XRD study on the decomposition of the Li–N–H hydrogen store.20 In this study, the increase in the lattice parameter from Li2NH to LiNH2 is approximately 1.5% at ∼290 °C. Assuming a linear variation in the lattice parameter with stoichiometry change, the stoichiometry predicted from the magnitude of the changes in the a lattice constant mirror those obtained from the Rietveld refinement fairly well, predicting a stoichiometry of Li1.79(2)ND1.21(2) for segment (ii)—a 0.31% increase in a from segment (i)—and Li1.76(2)ND1.24(2) for segment (iv)—a 0.097% increase in a from segment (iii). The most significant discrepancy between these two approaches of determining the stoichiometry is in the comparison of the lattice parameters in segments (i) and (iii). The lattice parameter in segment (iii) is smaller than that in segment (i) despite being at a higher temperature and a more amide-like stoichiometry. One hypothesis for the origin of this observation is that the sample underwent a melting process between 12 and 15 hours, which may have introduced internal strains that caused the change in the lattice parameter. There is some evidence supporting this assertion as the intensity of the Bragg peaks shown in Fig. 5 is higher after 15 hours than for the initial sample.
These stoichiometry values are indicative of the equilibrium position of eqn (4) under the mixed ammonia–hydrogen–nitrogen atmosphere. These values also provide insight into the mechanism by which the LiNH2–Li2NH system decomposes ammonia. As stated earlier, comparison of the TGA and ammonia decomposition data indicates that the decomposition of NH3 becomes favourable once LiNH2 is no longer stable. This assertion is corroborated by the in situ NPD data, which shows that the active form of the catalyst is a non-stoichiometric lithium imide.
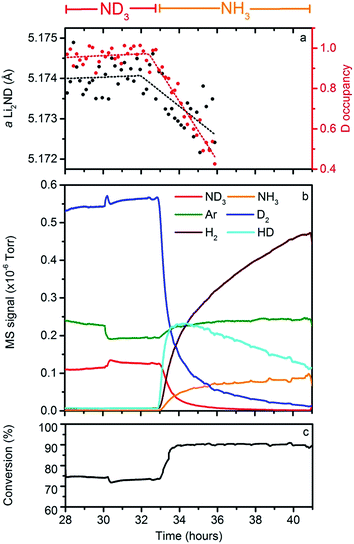
Hydrogen–deuterium exchange experiment
In order to provide experimental data to assess the validity of these hypotheses, an isotope exchange experiment was conducted between 28–36 hours of the data collection, where the flow through the Li2ND sample was switched from ND3 to NH3 at 32.5 hours. The collection of mass spectrometry data was continued for a further five hours after the neutron diffraction experiment finished. These data are presented in Fig. 7.It can be seen in Fig. 5 that the peak-to-background ratio of the neutron diffraction data decreases steadily after the switch to NH3; this is attributable to incoherent neutron scattering arising from the replacement of deuterium by hydrogen in the Li2ND structure.21 It is possible to quantify the extent of this isotope exchange through Rietveld analysis. To do this, the stoichiometry of the sample was fixed in the refinement model, and a set of hydrogen positions were added to the structural model outlined previously. These hydrogen atoms have identical locations and thermal parameters to the deuterium atoms. A single parameter was then introduced to vary the fractional occupancy of the hydrogen and deuterium positions, summing to the fixed overall stoichiometry. Fig. 7a shows the refined value of the deuterium occupancy obtained from this analysis, along with the lattice parameter of the sample. These data show that the deuterium occupancy remains close to 1.0 until the NH3 is introduced, and then decreases for the remainder of the experiment; the lattice parameter mirrors this behaviour. At the point at which the NPD experiment was terminated, Rietveld analysis of the diffraction data suggests that 58(4)% of the deuterium in the structure was replaced by hydrogen.
Fig. 7b shows the mass spectrometry data collected during the isotope exchange reaction, with the ND3/NH3 conversion percentage indicated in Fig. 7c. As can be seen, the isotope exchange reaction continued after the collection of NPD data finished. The most striking feature of the QGA data is that HD is produced as the supply of ND3 into the reactor is replaced with NH3. There are three potential sources of gaseous HD:
(i) the decomposition of NH3 over the surface of Li2ND resulting in the formation of Li2NH and the evolution of N2, HD and H2.
(ii) scrambling from the interaction of NH3 with residual ND3 still within the reactor or the Li2ND catalyst to form a NDxH3−x species, which subsequently decomposes.
(iii) scrambling of H2 with residual D2.
Our laboratory tests indicate that the scrambling effects detailed in (i) and (ii) can occur under the reaction conditions used, making detailed analysis of the QGA data from this experiment difficult. However, the persistence of a strong HD signal in the QGA and the exchange observed in the NPD data, both after the ND3 and D2 signals have diminished significantly indicates that large components of those observed effects relate to the active participation of the bulk catalyst material with the ammonia decomposition reaction.
The absence of sample-related line broadening in the diffraction data indicates that the particle size of the lithium imide in this experiment was greater than 1 μm. High decomposition activity despite this large particle size provides corroborative evidence for the bulk reaction mechanism.
Based on the early observation of HD together with the substitution of deuterium with hydrogen in the catalyst structure it is possible to write an overall equation for this reaction as follows:
| 2Li2ND + 2NH3 ↔ 2Li2NH + 2HD + H2 + N2. | (7) |
This reaction is consistent with the high initial rate of HD formation compared with that of H2. This reaction is also consistent with a calculation from the gas flow and ammonia conversion which suggests that, on average, 0.93(4) hydrogens were exchanged per NH3 molecule decomposed by the catalyst.§ However, it is highly unlikely that this reaction is stoichiometric. Although the change in the deuterium occupancy in Fig. 7a is fitted to a linear function, this may be a consequence of the low precision of the refined data.
In the early stages of the reaction, it is likely that the rate of isotope exchange is even higher than that suggested by eqn (7). Indeed, simple exponential fits to the HD and H2 traces (see ESI†) suggest that the rate of HD production is initially three times that of H2, although some of this increase may be due to the contribution of scrambling effects. As the reaction proceeds, an increasing amount of Li2NH is produced, making further exchange less likely, and thus an increasing contribution to the outgas will be from the following reaction:
| 2Li2NH + 2NH3 ↔ 2Li2NH + N2 + 3H2 | (8) |
This is reflected in the QGA data, where the HD signal plateaus and then decreases, and the H2 signal continues to rise over the course of the experiment.
The decomposition of ammonia on traditional metal catalysts is rationalised in terms of sequential breaking of N–H bonds in ammonia and then recombination of pairs of nitrogen atoms and hydrogen atoms to form molecular nitrogen and hydrogen, respectively. Similar reactions most likely also occur here, with the proviso that the bulk of the catalyst is more actively involved in the decomposition reaction than in surface catalysis.
Given that the stoichiometry of the sample is observed to deviate from Li2ND in the presence of ammonia, it is evident that when the Li2ND is exposed to NH3, there will be some amide formation, as described in eqn (9). This process provides a route for the incorporation of hydrogen into the Li2ND structure and, since it involves the breaking of N–H bonds, could be reasonably considered to be part of the ammonia decomposition reaction at a lithium imide–amide surface. Density functional theory studies on lithium imide and amide suggest that the energy barrier for the migration of protons between imide and amide groups is low,31,32 so once the amide unit forms, the hydrogen atom can diffuse into the structure, presumably by the Frenkel defect mechanism discussed for the Li–N–H hydrogen store. The extent of the H–D exchange observed here suggests that the rate of diffusion of hydrogen into the imide structure according to eqn (10) is more rapid than the recombinative desorption of hydrogen from the surface.
| Li2ND + NH3 ↔ LiNDH + LiNH2 | (9) |
| NDH− + ND2− ↔ ND2− + NDH− | (10) |
Although this mechanism seems most likely given these experimental observations, the absence of direct evidence means that alternative or additional mechanisms cannot be excluded from consideration. The decomposition may involve intermediate formation of lithium metal, and subsequent reformation of the imide by interaction of the metal with ammonia. However, more detailed experimental work would be required to unambiguously determine the reaction mechanism.
The temperature and flow conditions were kept constant under both ND3 and NH3 for the exchange experiment. Examination of the mass spectrometry data shows that the conversion for the ND3 was ∼73%, while under NH3, the conversion was ∼91%. This difference in the conversion efficiency may reflect a kinetic isotope effect, indicating that the deuterium/hydrogen atoms are involved in the rate determining step of the ammonia decomposition reaction. This effect could result from the breaking of N–H/D bonds, H/D diffusion or H2/D2 formation/desorption.
In each of the substantive density functional theory studies on the decomposition of LiNH2, hydrogen is involved in the rate-determining step.31–34 Miceli et al. found that the cleavage of the N–H bond to form an interstitial proton had the equal-highest activation energy together with that of the formation of the lithium ion Frenkel defect pair, while Wang et al. and Hazrati et al. determined it to have significantly higher activation energy than the lithium pair. Hoang et al. proposed two different mechanisms: for large particles, the cleavage of the N–H bond was again the rate-determining step, and for small particles, diffusion of H+ to the surface of the particle had the highest activation energy. All of these mechanisms would be expected to show a kinetic isotope effect. Our observation of such an effect in the ammonia decomposition reaction for lithium imide is consistent with these analyses, indicating that the elementary steps used to explain the reaction mechanism of hydrogen storage and release in the Li–N–H system may go some way to explaining the mechanism of ammonia decomposition using lithium imide–amide.
Aside from the observed kinetic isotope effect, the ammonia conversion levels were stable across the 15 hours of continuous operation, indicating good catalyst stability over this time period. In a practical setting, the sensitivity of light metal amides to water, reacting to form the hydroxide, may also represent a concern for the longevity of their catalytic activity. In order to probe these effects, long-duration experiments on the performance of lithium imide were conducted. After 250 hours of exposure to refrigerant grade ammonia (99.98% purity), the performance of a 0.5 g sample of lithium imide at 550 °C and 60 sccm of ammonia flow changed from a peak conversion of 99.3% to 97.5% (see ESI†). These results are encouraging, though more detailed experiments studying the stability of the catalyst over even longer timescales will be necessary. In particular, investigations of the relative contributions of (i) reaction of the catalyst with water in the ammonia stream and (ii) the loss of active material from the reactor to any observed reduction in catalytic performance would be instructive.
Conclusions
The lithium imide–amide system shows superior ammonia decomposition activity to both sodium amide and ruthenium- or nickel-based catalysts. A combination of gravimetric and diffraction data identified that the activity of the catalyst is related to an intermediate stoichiometry that is closer to lithium imide than lithium amide. This stoichiometry is temperature-dependent under ammonia flow.By demonstrating that imide-forming amides can be active ammonia decomposition catalysts, in addition to metal-forming amides, the lithium imide–amide system suggests a significantly broader range of metal amide-based materials might be expected to show appreciable ammonia decomposition activity. It indicates that a range of reaction mechanisms may operate in this catalyst family.
The observation of hydrogen–deuterium exchange in this system indicates that the bulk of the material is active in the decomposition reaction. Further experimental and computational studies are required to unravel the precise mechanism of action of this and other metal imides/amides on ammonia.
The catalytic activity of lithium imide, which has been shown to remain solid under particular operating conditions, makes a number of strategies for improving the turnover frequency, such as the development of appropriate support architecture, more accessible than for sodium amide. This enhanced practicality may indicate that an imide or amide material could be developed into an ammonia decomposition catalyst of sufficiently high activity for the production of high purity hydrogen for transport applications.
Funding sources
This work was financially supported by an STFC Innovations Proof of Concept Award (Phase 3 POCF1213-14).Conflict of interest
The authors declare no competing financial interest.Acknowledgements
The authors acknowledge the technical assistance of Mark Kibble, Richard Haynes and Chris Goodway in the setup of the POLARIS experiment, James Taylor for laboratory management, and Kate Ronayne, Beth Evans, Steven Wakefield, Tim Bestwick and Andrew Taylor for project management and useful guidance. The authors would also like to thank STFC for the provision of experimental time on the POLARIS diffractometer at the ISIS Facility, and to Ronald Smith for his extensive assistance running the diffractometer. J.W.M. thanks the Rhodes Trust for additional funding.References
- L. Green Jr, An ammonia energy vector for the hydrogen economy, Int. J. Hydrogen Energy, 1982, 7, 355–359 CrossRef
.
- W. H. Avery, A role for ammonia in the hydrogen economy, Int. J. Hydrogen Energy, 1988, 13, 761–773 CrossRef CAS
.
- R. Lan, J. T. S. Irvine and S. Tao, Ammonia and related chemicals as potential indirect hydrogen storage materials, Int. J. Hydrogen Energy, 2012, 37, 1482–1494 CrossRef CAS PubMed
.
-
G. Thomas and G. Parks, Potential Roles of Ammonia in a Hydrogen Economy, U.S. Department of Energy, 2006 Search PubMed
.
- B. A. van Hassel, J. R. Karra, J. Santana, S. Saita, A. Murray, D. Goberman, R. Chahine and D. Cossement, Ammonia sorbent development for on-board H2 purification, Sep. Purif. Technol., 2015, 142, 215–226 CrossRef CAS PubMed
.
- T. Hejze, J. O. Besenhard, K. Kordesch, M. Cifrain and R. R. Aronsson, Current status of combined systems using alkaline fuel cells and ammonia as a hydrogen carrier, J. Power Sources, 2008, 176, 490–493 CrossRef CAS PubMed
.
-
K. Kordesch and M. Cifrain, Comparison between the alkaline fuel cell (AFC) and the polymer electrolyte membrane (PEM) fuel cell, in Handbook of Fuel Cells—Fundamentals, Technology and Applications, ed. W. Vielstich, A. Lamm and H. A. Gasteiger, John Wiley & Sons, 2003, vol. 4, pp. 789–793 Search PubMed
.
- C. S. Mørch, A. Bjerre, M. P. Gøttrup, S. C. Sorenson and J. Schramm, Ammonia/hydrogen mixtures in an SI-engine: Engine performance and analysis of a proposed fuel system, Fuel, 2011, 90, 854–864 CrossRef PubMed
.
- S. F. Yin, B. Q. Xu, S. J. Wang, C. F. Ng and C. T. Au, Magnesia-carbon nanotubes (MgO-CNTs) nanocomposite: novel support of Ru catalyst for the generation of COx-free hydrogen from ammonia, Catal. Lett., 2004, 96, 113–116 CrossRef CAS
.
- S. F. Yin, B. Q. Xu, X. P. Zhou and C. T. Au, A mini-review on ammonia decomposition catalysts for on-site generation of hydrogen for fuel cell applications, Appl. Catal., A, 2004, 277, 1–9 CrossRef CAS PubMed
.
- W. I. F. David, J. W. Makepeace, S. K. Callear, H. M. A. Hunter, J. D. Taylor, T. J. Wood and M. O. Jones, Hydrogen Production from Ammonia Using Sodium Amide, J. Am. Chem. Soc., 2014, 136, 13082–13085 CrossRef CAS PubMed
.
- R. Juza, Amides of the Alkali and the Alkaline Earth Metals, Angew. Chem., Int. Ed., 1964, 3, 471–481 CrossRef PubMed
.
- D. H. Gregory, Lithium nitrides, imides and amides as lightweight, reversible hydrogen stores, J. Mater. Chem., 2008, 18, 2321–2330 RSC
.
- P. Chen, Z. Xiong, G. Wu, Y. Liu, J. Hu and W. Luo, Metal–N–H systems for the hydrogen storage, Scr. Mater., 2007, 56, 817–822 CrossRef CAS PubMed
.
- P. Chen, Z. Xiong, J. Luo, J. Lin and K. L. Tan, Interaction of hydrogen with metal nitrides and imides, Nature, 2002, 420, 302–304 CrossRef CAS PubMed
.
- S. Hull, R. I. Smith, W. I. F. David, A. C. Hannon, J. Mayers and R. Cywinski, The Polaris powder diffractometer at ISIS, Phys. B, 1992, 180-181, 1000–1002 CrossRef
.
- Y. H. Hu and E. Ruckenstein, Ultrafast Reaction between Li3N and LiNH2 To Prepare the Effective Hydrogen Storage Material Li2NH., Ind. Eng. Chem. Res., 2006, 45, 4993–4998 CrossRef CAS
.
-
A. Coelho, TOPAS Academic, version 5 Search PubMed
.
- W. I. F. David, M. O. Jones, D. H. Gregory, C. M. Jewell, S. R. Johnson, A. Walton and P. P. Edwards, A Mechanism for Non-stoichiometry in the Lithium-Amide Lithium Imide Hydrogen Storage Reaction, J. Am. Chem. Soc., 2007, 129, 1594–1601 CrossRef CAS PubMed
.
- J. W. Makepeace, M. O. Jones, S. K. Callear, P. P. Edwards and W. I. F. David,
In situ X-ray powder diffraction studies of hydrogen storage and release in the Li-N-H system, Phys. Chem. Chem. Phys., 2014, 16, 4061–4070 RSC
.
- National Institute of Standards and Technology, Neutron scattering lengths and cross sections, http://www.ncnr.nist.gov/resources/n-lengths, accessed December 1, 2014.
- T. Ichikawa, N. Hanada, S. Isobe, H. Leng and H. Fujii, Mechanism of Novel Reaction from LiNH2 and LiH to Li2NH and H2 as a Promising Hydrogen Storage System, J. Phys. Chem. B, 2004, 108, 7887–7892 CrossRef CAS
.
- O. Palumbo, A. Paolone, P. Rispoli, A. D'Orazio, R. Cantelli and D. Chandra, The decomposition reaction of lithium amide studied by anelastic spectroscopy and thermogravimetry, Int. J. Mater. Res., 2008, 99, 487–490 CrossRef CAS
.
- Y. H. Hu and E. Ruckenstein, Ultrafast Reaction between LiH and NH3 during H2 Storage in Li3N, J. Phys. Chem. A, 2003, 107, 9737–9739 CrossRef CAS
.
- J. Zhang and Y. H. Hu, Decomposition of Lithium Amide and Lithium Imide with and without Anion Promoter, Ind. Eng. Chem. Res., 2011, 50, 8058–8064 CrossRef CAS
.
- T. Markmaitree, R. Ren and L. L. Shaw, Enhancement of Lithium Amide to Lithium Imide transition via Mechanical Activation, J. Phys. Chem. B, 2006, 110, 20710–20718 CrossRef CAS PubMed
.
- S. Hino, T. Ichikawa and Y. Kojima, Thermodynamic properties of metal amides determined by ammonia pressure-composition isotherms, J. Chem. Thermodyn., 2010, 42, 140–143 CrossRef CAS PubMed
.
- J. Zhang and Y. H. Hu, Intermediate species and kinetics of lithium imide decomposition, Int. J. Hydrogen Energy, 2012, 37, 10467–10472 CrossRef CAS PubMed
.
- J. Guo, P. Wang, G. Wu, A. Wu, D. Hu, Z. Xiong, J. Wang, P. Yu, F. Chang, Z. Chen and P. Chen, Lithium imide synergy with 3d Transition-Metal Nitrides leading to Unprecedented Catalytic Activities for Ammonia Decomposition, Angew. Chem., Int. Ed., 2015, 54, 2950–2954 CrossRef CAS PubMed
.
- J. Guo, F. Chang, P. Wang, D. Hu, P. Yu, G. Wu, Z. Xiong and P. Chen, Highly Active MnN-Li2NH Composite Catalyst for Producing COx-Free Hydrogen, ACS Catal., 2015, 5, 2708–2713 CrossRef CAS
.
- G. Miceli, C. S. Cucinotta, M. Bernasconi and M. Parrinello, First Principles Study of the LiNH2/Li2NH Transformation, J. Phys. Chem. C, 2010, 114, 15174–15183 CAS
.
- E. Hazrati, G. Brocks, B. Buurman, R. A. de Groot and G. A. de Wijs, Intrinsic defects and dopants in LiNH2: a first-principles study, Phys. Chem. Chem. Phys., 2011, 13, 6043–6052 RSC
.
- K. Hoang, A. Janotti and C. G. Van de Walle, Mechanisms for the decomposition and dehydrogenation of Li amide/imide, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 064115 CrossRef
.
- J. Wang, Y. Du, H. Xu, C. Jiang, Y. Kong, L. Sun and Z.-K. Liu, Native defects in LiNH2: A first-principles study, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 024107 CrossRef
.
Footnotes |
| † Electronic supplementary information (ESI) available: Data analysis procedures, data fitting procedures, X-ray diffraction pattern of Li2ND, details of reduction of LiND2 unit cell, POLARIS blank cell results, NPD patterns, exponential fits to QGA data and long-duration reaction data. See DOI: 10.1039/c5sc00205b |
| ‡ It is worth noting here the comparative advantage in system efficiency expected using ammonia as a source of hydrogen, where only the gas being used at the time must be heated. For a solid state hydrogen store, in contrast, the whole store, or successive portions of it, must be kept heated in order to deliver hydrogen to the fuel cell. |
| § The average NH3 flow is 5.70 sccm for the 210 minutes of the exchange reaction, giving a total volume of approximately 1200 cm3. The conversion of NH3 in that period is around 90%, giving a volume of reacted NH3 of 1080 cm3. Given the density of ammonia gas at STP is 0.771 g L−1, the mass of reacted NH3 is 0.832 g, corresponding to 0.0489 moles; the mass of Li2ND is 2.70 g, which equates to 0.0905 moles. The H–D conversion obtained from the Rietveld analysis was determined to be 58(4)% and this equates to (0.0489/0.0905)/0.58 = 0.93(4) hydrogens exchanged per ammonia molecule. |
| This journal is © The Royal Society of Chemistry 2015 |