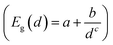Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Germanium nanoparticles with non-diamond core structures for solar energy conversion
Márton
Vörös
ab,
Stefan
Wippermann
c,
Bálint
Somogyi
b,
Adam
Gali
bd,
Dario
Rocca
ef,
Giulia
Galli
ag and
Gergely T.
Zimanyi
*a
aPhysics Department, University of California, Davis, California 95616, USA. E-mail: zimanyi@physics.ucdavis.edu
bDepartment of Atomic Physics, Budapest University of Technology and Economics, Budafoki út 8., H-1111, Budapest, Hungary
cInterface Chemistry and Surface Engineering Department, Max-Planck-Institute for Iron Research GmbH, Max-Planck-Str. 1, 40237 Düsseldorf, Germany
dInstitute for Solid State Physics and Optics, Wigner Research Center for Physics, Hungarian Academy of Sciences, P.O. Box 49, H-1525, Budapest, Hungary
eUniversité de Lorraine, CRM2, UMR 7036, Institut Jean Barriol, 54506 Vandoeuvre-lès-Nancy, France
fCNRS, CRM2, UMR 7036, 54506 Vandoeuvre-lès-Nancy, France
gInstitute for Molecular Engineering, University of Chicago, 5801 South Ellis Avenue, Chicago, Illinois 60637, USA
First published on 1st May 2014
Abstract
Multiple Exciton Generation (MEG) in nanoparticle-based solar cells promises to increase the cell-efficiency above the Shockley–Queisser limit. However, utilizing MEG is hampered by the Quantum Confinement Dilemma (QCD): quantum confinement advantageously increases the effective Coulomb interaction, but at the same time disadvantageously increases the electronic gap. Using ab initio calculations we showed that germanium nanoparticles with core structures of high pressure phases of bulk Ge can transcend the QCD, by simultaneously lowering gaps and increasing the MEG rates above those of NPs with a cubic diamond core. Synthesis routes to obtain Ge colloidal ST12 core structures are available and hence we propose that exploring ST12 Ge NPs for MEG solar cells is a promising research effort.
1 Introduction
Efficient conversion of solar energy is one of the greatest challenges of our times. Single junction solar cells are limited by the theoretical bound of about 33%, which was outlined in the seminal work by Shockley and Queisser (SQ).1 In the SQ analysis all photons with energies higher than the band gap generate an electron–hole pair. However, as these pairs relax to the band edges via phonon emission, part of the energy of the incoming photons is lost as heat.Several ideas were put forward to overcome the SQ limit by retaining a higher fraction of the absorbed solar energy in the electronic sector.2 One exciting proposal is the Multiple Exciton Generation (MEG) paradigm: electrons that absorb an energy exceeding twice the bandgap 2Eg relax by exciting additional electron–hole pairs, e.g. by impact ionization, instead of emitting phonons. The excess electrons enhance the photo-current and increase the quantum efficiency.
Interestingly, MEG was reported long ago in bulk semiconductors, such as silicon3 and germanium,3,4 where this effect was referred to as (band-to-band) impact ionization. However, the efficiency of MEG was disappointingly low in these bulk systems, because the phonon-assisted decay was much faster than MEG in almost the entire energy range of interest for solar applications.
Nozik proposed to enhance the efficiency of MEG via enhancement of the effective Coulomb interaction by quantum confining the electrons to nanoparticles (NPs).5,6 This proposal generated a wealth of papers investigating the exciton dynamics of quantum confined systems, e.g. in colloidal nanoparticles. Encouragingly, early papers reported a strongly enhanced MEG in lead salts,7–9 and other group III–V semiconductor NPs such as InP10 and InAs.11,12 After a detailed analysis of experimental circumstances, a consensus emerged about the enhancement of MEG in nanoparticles, compared to bulk semiconductors, on relative energy scales, in units of the gap Eg.13–16
However the use of MEG in NPs, faces the Quantum Confinement Dilemma (QCD): quantum confinement enhances the efficiency of MEG but it also leads to the increase of the nanoparticle gap, and thus on absolute scales the onset of MEG is pushed to higher energies, undermining their utility for solar energy conversion. In addition, several experiments15,16 reported that even on relative energy scales the onset of MEG is around 2.5–2.7Eg. This is substantially higher than 2Eg, the minimum energy required by energy conservation.
To date, nearly all experiments investigating MEG projects were carried out on colloidal NPs, with no demonstration of charge extraction. However recently it was demonstrated that the MEG-generated charge carriers can be extracted in a PbSe NP solar cell:17 a quantum efficiency in excess of 120% was reported in a certain energy range. A parallel work on PbSxSe1−x NP solar cells also reported quantum efficiencies above 100%.18
Although interesting, lead based materials raise toxicity concerns; the only Earth abundant and non toxic material for which MEG was explored is Si, with experiments reported for both colloidal19 and embedded20–22 nanoparticles. The results for embedded Si nanoparticles were analyzed in the framework of energy transfer between nanoparticles, driven by the Coulomb interaction, a process also known as “quantum cutting”.20 According to a recent study, the onset of MEG in silicon nanoparticles may be essentially at the energy conservation threshold of 2Eg.23
The theoretical description of MEG requires complex models and elaborate calculations. Some of the early works used empirical pseudopotential methods,24,25 or tight-binding models,26,27 yet others focused on the coherent nature of the process28 or by introducing virtual states to explain MEG.29 More recently, Rabani30 and Velizhanin31 introduced model Hamiltonians and Green's function techniques that take into account several possible relaxation mechanisms and incorporate band structure effects empirically. Importantly, according to Velizhanin,32,33 impact ionization may be the most relevant channel of MEG, at least in the case of PbSe. Other papers, e.g.ref. 34, focused on ab initio models to study the effects of non-adiabatic electron–phonon coupling on MEG processes. Our own recent work concentrated on introducing an ab initio framework that uses density functional perturbation theory techniques. This framework was first applied to Si nanoparticles.35 In a parallel effort, impact ionization processes in nanostructured Si were also investigated in ref. 36. Other recent applications to group IV nanoparticles came from Delerue's group37 that considered Sn, which is a metal in the bulk and exhibits a small gap in nanoparticles.
In this paper, we address the Quantum Confinement Dilemma by utilizing Ge nanoparticles for MEG-based solar cells. We focus on Ge because (1) it is environmentally friendly, (2) Earth-abundant, (3) the MEG was shown to be more efficient in bulk Ge than in Si, and (4) Ge has a lower bulk gap of 0.66 eV at room temperature (RT) than bulk Si (1.11 eV at RT). For reason (4), the onset of MEG on absolute energy scales is lower in Ge than in Si: this is a crucial advantage for solar energy conversion. Lower gaps are especially relevant for concentrating solar cells, where the optimum electronic gap has been shown to be as low as a few tenth of an eV.38 In spite of all of these advantages, to the best of our knowledge, no experimental study of MEG in Ge nanoparticles has yet been reported.
In our previous work on Si,39 we determined that hydrogen terminated nanoparticles with a BC8/Si-III core-structure exhibited a gap lower than that of the Si NPs with a cubic-diamond core by 20–40%. This gap reduction has the potential to greatly enhance the utility of MEG for solar applications.
Inspired by the promise of the Si study, we explored Ge nanoparticles with core structures derived from those of high pressure phases of the bulk. The stable form of crystalline Ge at ambient conditions is the cubic diamond (CD) structure (Ge I phase). Upon applying pressure, at about 10 GPa, the structure transforms to the metallic β-tin phase (Ge II). The release of pressure leads to the formation of a variety of metastable phases at ambient conditions depending on the kinetics of the release. Slow decompression leads preferentially to the formation of the ST12 phase (Ge III),40 while faster decompression to that of the BC8 phase (Ge IV).41 However the Ge BC8 phase is only observed for a few hours upon release of pressure to ambient values, before a transition to hexagonal diamond occurs.42 Hence BC8 is most likely metastable. Recent reports confirmed the existence of additional phases in germanium,43–45 such as the R8 phase,44 and the hexagonal diamond phase (Ge V),45 but these were not yet fully characterized.
The ST12 phase of Ge behaves as a semiconductor according to early experiments,40,46 but the size of its electronic gap is still unknown. Empirical pseudopotential calculations suggest that it has an electronic gap larger than that of CD (≈1.4 eV),47 possibly due to the presence of odd-fold rings.47Ab initio calculations suggested that in ST12 the states around the valence band edge have a flat dispersion, yielding an enhancement of the density of states (DOS) compared to the CD diamond phase.48 While the increased gap may be detrimental for MEG, the enhanced DOS would be advantageous.39
The BC8 phase of Ge is likely to be metallic,47,48 in contrast to the ST12 phase, and thus one may expect that NPs with a BC8 core may have a small gap, which would be useful for solar applications.
Theoretical calculations suggested that ST12 nanoparticles are less stable than diamond ones when formed under equilibrium conditions. However, kinetic trapping may stabilize the ST12 structure at the nanoscale, e.g. by crystallizing under pressure an initially amorphous NP.49 Similar kinetic trapping may have occurred in the recent study of Kim et al., where colloidal Ge NPs were successfully synthesized in the ST12 structure.50 Cluster-beam evaporated Ge NPs also showed signatures of ST12 core structures.51 More recently, ST12 Ge NPs were reported to form during lithiation processes in lithium ion batteries with Ge being the active anode material.52,53
We carried out density functional theory (DFT) calculations of MEG in germanium nanoparticles with high pressure core structures. We found that, in an experimentally attainable size-range, these NPs may provide an improvement for both aspects of the Quantum Confinement Dilemma: they have (1) lower gaps, and (2) higher absorption, and correspondingly higher impact ionization rates, than the CD Ge NPs. In particular we found that ST12 and BC8 nanoparticles are the most advantageous for solar applications, with BC8 superior to ST12, given their lower gaps.
The rest of the paper is organized as follows: in Section 2 we describe our theoretical and computational approach to calculate the optical and impact ionization properties of nanoparticles; in Section 3 we report our results on germanium nanoparticles with high pressure core structures. This is followed by our conclusions in Section 4.
2 Methods
We built structural models of germanium nanoparticles with cubic diamond, BC8 and ST12 structures from the corresponding bulk structures so as to have at most two dangling bonds per surface atom. The diameters, defined as the largest distance between two Ge atoms, ranged from ≈1.0 nm to ≈2.6 nm. Remaining dangling bonds were passivated by hydrogen atoms. The formulas of the nanoparticles considered here are the following; cubic diamond NPs: Ge35H36, Ge66H64, Ge87H76, Ge123H100, Ge172H120, Ge281H172, Ge452H232; BC8 NPs: Ge34H38, Ge64H60, Ge76H72, Ge102H80, Ge144H114, Ge302H180; ST12 NPs: Ge46H52, Ge60H60, Ge124H100, Ge206H140, Ge317H188. Some selected NPs are shown in Fig. 1. All structures were locally optimized using density functional theory, and the PBE approximation,54 as implemented in the Quantum-ESPRESSO code,55 allowing for at least 10 Å NP–NP separation between periodic replica.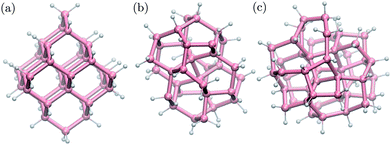 | ||
| Fig. 1 Ball-and-stick geometries of selected nanoparticles with 1 nm diameter: (a) cubic diamond, (b) BC8 (d) ST12 core structures. Pink (white) spheres represent germanium (hydrogen) atoms. | ||
Single particle wave functions were expanded in a plane wave basis and the interaction between valence electrons and ionic cores was described by norm-conserving pseudopotentials. The 3d electrons of Ge were included in the valence partition and hence a high plane wave cutoff, 150 Ry, was used. For the largest nanoparticles we used projector augmented wave (PAW) pseudopotentials56,57 for computational convenience.
The inclusion of the 3d electrons in the valence is necessary for an accurate determination of the atomic structure. However we found that the electronic structure of the NP computed with and without the 3d electrons in the valence partition is similar, provided the same geometry – determined with 3d electrons in the valence – was used. Single particle eigenvalues differed by about 50 meV and the energy gaps by about 30 meV. Freezing the 3d electrons into the core allowed us to reduce the kinetic energy cutoff to 35 Ry.
In order to estimate the effect of spin–orbit coupling (SOC) on the computed eigenvalues, we calculated the electronic structure of the Ge10H16 diamond-like nanoparticle using the self-consistent two-component relativistic PAW formalism,58 and we found that the HOMO level splitted by 0.07 eV. Moreover, recent calculations59 showed that in the case of a larger CD NP, Ge41H60, explicit inclusion of SOC resulted in a splitting of the first peak in the optical absorption spectrum by about 0.2 eV, probably driven by the SOC splitting of the highest occupied molecular orbital (HOMO). In the bulk, the split off valence band is downshifted by about 0.3 eV, according to the experiments.60 Based on these representative examples, we decided to omit SOC from our calculations. We estimate that doing so restricts the accuracy of our results to 0.1–0.2 eV.
The absorption spectra in a wide energy range were calculated using time-dependent density functional perturbation theory (TDDFPT) within the adiabatic approximation, as implemented in QUANTUM-ESPRESSO,61,62 where explicit summations over unoccupied single particle states are avoided. The absorption intensity A(ω) was calculated by averaging the dipole polarizability χ over spatial directions: 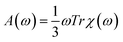 . We also determined the low-energy part of the TDDFT spectrum of selected nanoparticles using the TURBOMOLE cluster code63 with Gaussian basis sets. We used a double-ζ polarized basis set and effective core potentials, and we calculated the excitation energies within the Casida formalism at fixed nanoparticle geometries.64 The use of the TURBOMOLE code allowed us to compute the eigenvectors of the initial and final states of low-lying transitions. We checked that single particle energy levels calculated by the TURBOMOLE code agreed with those obtained by QUANTUM-ESPRESSO within 0.1 eV for all tested nanoparticles.
. We also determined the low-energy part of the TDDFT spectrum of selected nanoparticles using the TURBOMOLE cluster code63 with Gaussian basis sets. We used a double-ζ polarized basis set and effective core potentials, and we calculated the excitation energies within the Casida formalism at fixed nanoparticle geometries.64 The use of the TURBOMOLE code allowed us to compute the eigenvectors of the initial and final states of low-lying transitions. We checked that single particle energy levels calculated by the TURBOMOLE code agreed with those obtained by QUANTUM-ESPRESSO within 0.1 eV for all tested nanoparticles.
Finally, we calculated the multiple exciton generation rates assuming impact ionization is the major contributing process. We used the Fermi's golden rule to evaluate the decay rate ΓII of excitons to bi-excitons:
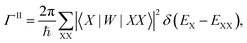 | (1) |
The MEG transition proceeds through separate electron (a) and hole (j) relaxation channels. The overall MEG rate is a sum of these two contributions (ΓIIja = ΓII+j + ΓII−a):
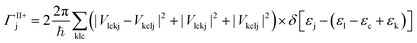 | (2a) |
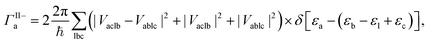 | (2b) |
Here Vrsut is a six-dimensional integral of the screened Coulomb interaction. We averaged over all excitons having the same energy to obtain an averaged impact ionization rate:
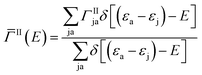 | (3) |
The energy levels in eqn (2) and (3) were broadened with a width Δ to ensure energy conservation. The independence of our results from Δ was extensively verified in the energy range of interest. The energy summations were properly normalized by the corresponding number of excitons.
The inverse dielectric matrix entering the calculation of the matrix elements of W was obtained using the spectral decomposition technique proposed in ref. 65–67: 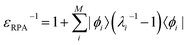 , where ϕi is the ith eigenpotential of the static dielectric function with eigenvalue λi. We used M = 600 for the largest system (690 electrons) considered here.
, where ϕi is the ith eigenpotential of the static dielectric function with eigenvalue λi. We used M = 600 for the largest system (690 electrons) considered here.
3 Results and discussion
In this section first we present our calculation of the electronic states and the spectrum of Ge NPs. We then characterize their absorption properties and we analyze the MEG process based on the electronic states and absorption characteristics.1 Electronic structure
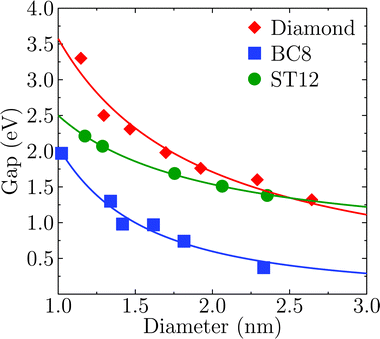
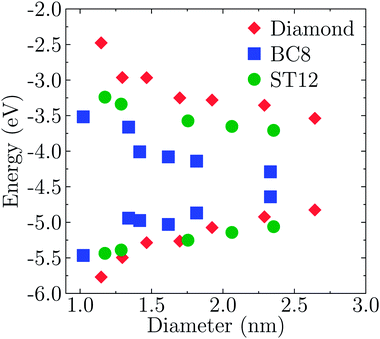
Fig. 2 shows the effect of quantum confinement on the Kohn–Sham gap of the nanoparticles as a function of size, where the gap was defined as the energy difference between the highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO). As a guide to the eye, the calculated gaps were fitted with a power law: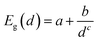 , where a was the known bulk theoretical limit: 0 eV for diamond and BC8, and 0.6 eV for ST12. The latter values were obtained by calculations using 8 × 8 × 8 Monkhorst–Pack k-point grids at relaxed geometries (cell and atomic positions).
, where a was the known bulk theoretical limit: 0 eV for diamond and BC8, and 0.6 eV for ST12. The latter values were obtained by calculations using 8 × 8 × 8 Monkhorst–Pack k-point grids at relaxed geometries (cell and atomic positions).
Fig. 2 shows that BC8 nanoparticles had by far the smallest gaps in the entire diameter range. In addition, the energy gap of the ST12 particles is smaller than that of CD ones, for diameters below 2.5 nm. The reduction of the gap of ST12 and BC8 nanoparticles relative to that of the diamond structures is our first major result regarding the QCD, as it shows that considering high pressure structures may bring gaps to values interesting for solar applications, in spite of quantum confinement effects.
Fig. 3 shows the energy of HOMO and LUMO levels of the NPS as a function of size, which provide relevant information, e.g. if one is interested in band offsets of the NP with embedding matrices or electrodes. A common zero of energy of the eigenvalues of the various structures was determined by using the average electrostatic potential at the edge of the supercells and the monopole Makov–Payne correction.68 We verified that the Martyna–Tuckerman correction approach69 yielded numerically identical results for the largest simulation volumes. Further tests on the smallest nanoparticles with very large simulation volumes of about 110 Bohr of vacuum showed that absolute energies were converged within 0.02 eV.
 | ||
| Fig. 3 Size dependence of the HOMO and LUMO levels of Ge NPs with different core structures. The diameter was defined as the largest distance between any of two Ge atoms. | ||
The effects of quantum confinement are clearly visible for both the HOMO and LUMO levels in all considered structures: the energy of the LUMO level increases and that of the HOMO decreases, as the size of the NP decreases. The dependence on size is weaker in the case of ST12 and BC8 than for CD. Although the absolute values of the energies shown in Fig. 3 are not quantitative estimates of ionization potentials and electron affinities, the trends as a function of size revealed by density functional calculations are expected to be correct.70,71
We now turn to the analysis of the two-step MEG process. In the first step, the NP absorbs a single high energy photon with an energy at least twice the gap Eg, and a valence electron is excited into the conduction band |0〉 → |X〉. In a subsequent step, the high energy exciton formed in the first step relaxes into a low energy exciton by creating an additional low energy exciton |X〉 → |XX〉. The former process is characterized by the absorption rate, while the latter by the multiple exciton generation rate. In what follows, we compute and analyze both of these rates to characterize the entire MEG process.
2 Absorption spectrum
Fig. 4 shows the absorption spectra A(E) for the CD, BC8 and ST12 core structures obtained by using TDDFT and the PBE functional. Our results for cubic diamond NPs are in agreement with those of previous calculations.72,73 In the case of BC8, the presence of low gaps is accompanied by a higher absorption intensity at low energies. ST12 nanoparticles, however, did not appear to absorb more efficiently than CD NPs.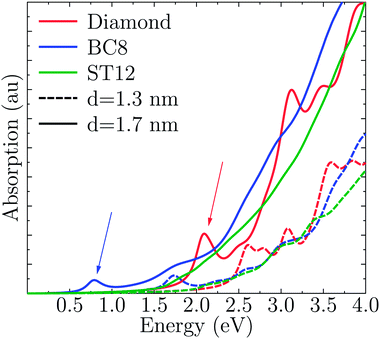 | ||
| Fig. 4 Computed optical absorption spectra of Ge NPs, as a function of NP size and for different core structures. | ||
Interestingly, while the spectra of BC8 and cubic diamond NPs had clearly identifiable peaks in the low energy regime (denoted by arrows in Fig. 4), the spectra for ST12 NPs was featureless. We used the cluster code Turbomole to analyze the low energy features of the spectra of diamond and BC8 NPs. For NPs with cubic diamond cores, we found that the first peaks corresponded to band edge excitations of the type HOMO → LUMO. This was not the case for NPs with BC8 core structures, where HOMO → LUMO transitions turned out to be forbidden by symmetry, as the near spherical shape resulted in a S6 NP point group symmetry. The first visible peak was dominated by the HOMO−2 → LUMO transition in the case of the d = 1.1 nm NP, and by the HOMO → LUMO+1 transition in the case of the d = 1.3 nm NP. The corresponding wave functions of these transitions are shown in Fig. 5.
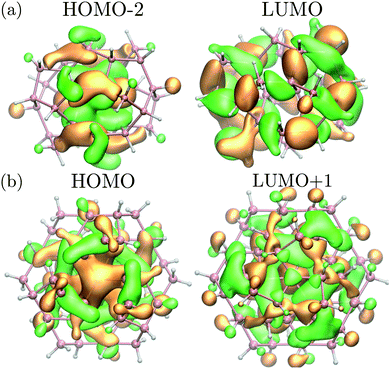 | ||
| Fig. 5 (a) Square moduli of the (HOMO−2) and LUMO wave functions of the BC8 NP with d = 1.1 nm multiplied by their sign. (b) Square moduli of the HOMO and (LUMO+1) wave functions of the BC8 NP with d = 1.3 nm multiplied by their sign. These states are the initial and final states of the optical transition responsible for the first absorption peak (see Fig. 4 for the absorption of d = 1.3 nm NP). Orange (green) isosurfaces represent the positive (negative) part of the isosurfaces of the corresponding wavefunction. Pink (white) spheres represent germanium (hydrogen) atoms. | ||
3 MEG transition rates
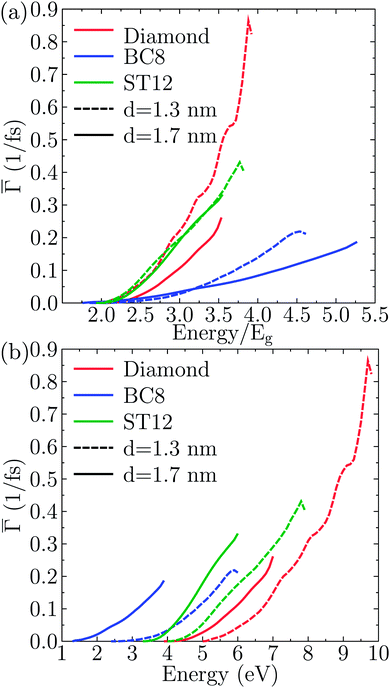
These rates were approximated by the probability per unit time of the impact ionization process Γ(E), as described by eqn (1).To identify the effect of the NP core structure on the strength of the effective Coulomb interactions, in Fig. 6(a) we plotted the single-particle-averaged impact ionization rates Γ(E) as a function of the energy E/Eg of the initial exciton in units of the gap. Remarkably, the ST12 core NP has a higher Γ(E) than the cubic diamond one for the largest diameter. Since the ST12 NPs also had a gap lower than that of the CD NPs for diameters below 2.5 nm, we conclude that ST12 NPs are more advantageous than CD ones for both their lower gap and an enhanced effective Coulomb interaction.
In Fig. 6(b) we plotted the single-particle-averaged impact ionization rates Γ(E) as a function of the absolute energy E of the initial exciton, with two major findings:
(i) For the ST12 phase the reduced gap and the enhanced effective Coulomb interaction combined into a robust enhancement of the MEG rate, demonstrating that ST12 core NPs offers marked improvement for both competing factors of the QCD.
(ii) While the BC8 core NPs did not offer an improvement for both QCD factors, the large gap reduction alone was capable of making the BC8 core NPs the overall winners, with the highest MEG rate on absolute energy scales.
4 Summary and conclusions
In conclusion, we performed ab initio calculations of the electronic, absorption and MEG rates of germanium nanoparticles with cubic diamond and high pressure core structures. We found that ST12 core nanoparticles had lower electronic gaps than diamond NPs for diameters less than 2.5 nm. The gaps of BC8 core NPs were smaller than those of CD NPs for all diameters. The lower gaps translated into higher absorption rates only in the case of BC8 nanoparticles.Investigation of the MEG rates on relative energy scales revealed that in ST12 core NPs the gap reduction was not accompanied by a reduced effective Coulomb interaction. In fact, the effective Coulomb interactions in ST12 core NPs exceeded that of the CD core NPs. The BC8 core NPs behaved differently: the effective Coulomb interaction was reduced relative to CD NPs.
Shifting to absolute energy scales to evaluate the combined effect of the competing factors of the Quantum Confinement Dilemma, we found that:
(i) For the ST12 core NPs the reduced gap and the enhanced effective Coulomb interaction combined into a robust enhancement of the MEG rate, demonstrating that ST12 core NPs indeed transcended the QCD by improving both of its competing factors.
(ii) While the BC8 core NPs did not offer an improvement for both QCD factors, the large gap reduction made the BC8 core NPs the overall winners with the highest MEG rate on absolute energy scales.
In summary, our work has established that some high-pressure core Ge nanoparticles are capable of transcending the Quantum Confinement Dilemma over the regular diamond core Ge nanoparticles. For this reason, we propose that exploring high-pressure core Ge NPs for multiple exciton generation solar cells may be worth the effort. The first steps seem to have already been taken by the fabrication of colloidal ST12 Ge NPs.50
Acknowledgements
We thank François Gygi for useful discussions. The authors acknowledge support from NSF Solar Collaborative DMR-1035468. Work was also supported by DOE DE-FG02-06ER46262, Grant NSF CHE-0802907, Deutsche Forschungsgemeinschaft (grant no. WI3879/1). SW acknowledges BMBF grant no. 13N12972 and AG acknowledges the support from “MTA Lendület” program (Hungarian Academy of Sciences). Supercomputer access at the NIIF centre in Debrecen is gratefully acknowledged. This research used computational resources of the National Energy Research Scientific Computing Center (NERSC) grant NISE-35687. NERSC is supported by the Office of Science of the U.S. Department of Energy under Contract no. DE-AC02-05CH11231.References
- W. Shockley and H. J. Queisser, J. Appl. Phys., 1961, 32, 510–519 CrossRef CAS PubMed.
- M. Green, Third generation photovoltaics: advanced solar energy conversion, Springer, 2006 Search PubMed.
- M. Wolf, R. Brendel, J. H. Werner and H. J. Queisser, J. Appl. Phys., 1998, 83, 4213–4221 CrossRef CAS PubMed.
- S. Koc, Cechoslovackij fiziceskij zurnal, 1957, 7, 91–95 CAS.
- A. J. Nozik, Annu. Rev. Phys. Chem., 2001, 52, 193 CrossRef CAS PubMed.
- A. J. Nozik, Phys. E, 2002, 14, 115–120 CrossRef CAS.
- R. D. Schaller and V. I. Klimov, Phys. Rev. Lett., 2004, 92, 186601 CrossRef CAS.
- R. J. Ellingson, M. C. Beard, J. C. Johnson, P. Yu, O. I. Micic, A. J. Nozik, A. Shabaev and A. L. Efros, Nano Lett., 2005, 5, 865–871 CrossRef CAS PubMed.
- S. J. Kim, W. J. Kim, Y. Sahoo, A. N. Cartwright and P. N. Prasad, Appl. Phys. Lett., 2008, 92, 031107 CrossRef PubMed.
- S. K. Stubbs, S. J. O. Hardman, D. M. Graham, B. F. Spencer, W. R. Flavell, P. Glarvey, O. Masala, N. L. Pickett and D. J. Binks, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 081303 CrossRef.
- J. J. H. Pijpers, E. Hendry, M. T. W. Milder, R. Fanciulli, J. Savolainen, J. L. Herek, D. Vanmaekelbergh, S. Ruhman, D. Mocatta, D. Oron, A. Aharoni, U. Banin and M. Bonn, J. Phys. Chem. C, 2007, 111, 4146–4152 CAS.
- R. D. Schaller, J. M. Pietryga and V. I. Klimov, Nano Lett., 2007, 7, 3469–3476 CrossRef CAS PubMed.
- A. Shabaev, C. S. Hellberg and A. L. Efros, Acc. Chem. Res., 2013, 46, 1242–1251 CrossRef CAS PubMed.
- L. A. Padilha, J. T. Stewart, R. L. Sandberg, W. K. Bae, W.-K. Koh, J. M. Pietryga and V. I. Klimov, Acc. Chem. Res., 2013, 46, 1261–1269 CrossRef CAS PubMed.
- M. C. Beard, J. M. Luther, O. E. Semonin and A. J. Nozik, Acc. Chem. Res., 2013, 46, 1252–1260 CrossRef CAS PubMed.
- G. Nair, L.-Y. Chang, S. M. Geyer and M. G. Bawendi, Nano Lett., 2011, 11, 2145–2151 CrossRef CAS PubMed.
- O. E. Semonin, J. M. Luther, S. Choi, H.-Y. Chen, J. Gao, A. J. Nozik and M. C. Beard, Science, 2011, 334, 1530–1533 CrossRef CAS PubMed.
- G. Zhai, C. P. Church, A. J. Breeze, D. Zhang, G. B. Alers and S. A. Carter, Nanotechnology, 2012, 23, 405401 CrossRef PubMed.
- M. C. Beard, K. P. Knutsen, P. Yu, J. M. Luther, Q. Song, W. K. Metzger, R. J. Ellingson and A. J. Nozik, Nano Lett., 2007, 7, 2506–2512 CrossRef CAS PubMed.
- D. Timmerman, I. Izeddin, P. Stallinga, I. N. Yassievich and T. Gregorkiewicz, Nat. Photonics, 2008, 2, 105 CrossRef CAS.
- D. Timmerman, J. Valenta, K. Dohnalova, W. D. A. M. de Boer and T. Gregorkiewicz, Nat. Nanotechnol., 2011, 6, 710–713 CrossRef CAS PubMed.
- M. T. Trinh, R. Limpens, W. D. A. M. de Boer, J. M. Schins, L. D. A. Siebbeles and T. Gregorkiewicz, Nat. Photonics, 2012, 6, 316 CrossRef CAS.
- M. Sagar Dodderi, J. Yang, U. Kortshagen, E. Whitney, O. Semonin, A. Nozik and M. C. Beard, APS Meeting Abstracts, 2013, p. 38015 Search PubMed.
- A. Franceschetti, J. M. An and A. Zunger, Nano Lett., 2006, 6, 2191–2195 CrossRef CAS PubMed.
- C. Sevik and C. Bulutay, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 125414 CrossRef.
- G. Allan and C. Delerue, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 205423 CrossRef.
- J. Pijpers, R. Ulbricht, K. Tielrooij, A. Osherov, Y. Golan, C. Delerue, G. Allan and M. Bonn, Nat. Phys., 2009, 5, 811–814 CrossRef CAS.
- A. Shabaev, A. L. Efros and A. J. Nozik, Nano Lett., 2006, 6, 2856–2863 CrossRef CAS PubMed.
- R. D. Schaller, V. M. Agranovich and V. I. Klimov, Nat. Phys., 2005, 1, 189–194 CrossRef CAS.
- E. Rabani and R. Baer, Chem. Phys. Lett., 2010, 496, 227–235 CrossRef CAS PubMed.
- A. Piryatinski and K. A. Velizhanin, J. Chem. Phys., 2010, 133, 084508 CrossRef PubMed.
- K. A. Velizhanin and A. Piryatinski, Phys. Rev. Lett., 2011, 106, 207401 CrossRef.
- K. A. Velizhanin and A. Piryatinski, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 165319 CrossRef.
- H. M. Jaeger, K. Hyeon-Deuk and O. V. Prezhdo, Acc. Chem. Res., 2013, 46, 1280–1289 CrossRef CAS PubMed.
- M. Vörös, D. Rocca, G. Galli, G. T. Zimanyi and A. Gali, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 155402 CrossRef.
- M. Govoni, I. Marri and S. Ossicini, Nat. Photonics, 2012, 6, 672–679 CrossRef CAS.
- G. Allan and C. Delerue, ACS Nano, 2011, 5, 7318–7323 CrossRef CAS PubMed.
- M. C. Hanna, M. C. Beard and A. J. Nozik, J. Phys. Chem. Lett., 2012, 3, 2857–2862 CrossRef CAS.
- S. Wippermann, M. Vörös, D. Rocca, A. Gali, G. Zimanyi and G. Galli, Phys. Rev. Lett., 2013, 110, 046804 CrossRef.
- F. P. Bundy and J. S. Kasper, Science, 1963, 139, 340–341 CAS.
- C. H. Bates, F. Dachille and R. Roy, Science, 1965, 147, 860–862 CAS.
- R. J. Nelmes, M. I. McMahon, N. G. Wright, D. R. Allan and J. S. Loveday, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 9883–9886 CrossRef CAS.
- D. Selli, I. A. Baburin, R. Martoňák and S. Leoni, Sci. Rep., 2013, 3, 1466 Search PubMed.
- B. C. Johnson, B. Haberl, S. Deshmukh, B. D. Malone, M. L. Cohen, J. C. McCallum, J. S. Williams and J. E. Bradby, Phys. Rev. Lett., 2013, 110, 085502 CrossRef.
- J. S. Williams, B. Haber, S. Deshmukh, B. C. Johnson, B. D. Malone, M. L. Cohen and J. E. Bradby, Phys. Status Solidi RRL, 2013, 7, 355–359 CrossRef CAS.
- F. P. Bundy, J. Chem. Phys., 1964, 41, 3809–3814 CrossRef CAS PubMed.
- J. D. Joannopoulos and M. L. Cohen, Phys. Rev. B: Solid State, 1973, 7, 2644–2657 CrossRef CAS.
- B. D. Malone and M. L. Cohen, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 054101 CrossRef.
- L. Pizzagalli, G. Galli, J. E. Klepeis and F. Gygi, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 165324 CrossRef.
- S. J. Kim, O. K. Quy, L.-S. Chang, E. A. Stach, C. A. Handwerker and A. Wei, J. Mater. Chem., 2010, 20, 331–337 RSC.
- S. Sato, S. Nozaki and H. Morisaki, Appl. Phys. Lett., 1998, 72, 2460–2462 CrossRef CAS PubMed.
- Y. J. Cho, H. S. Im, Y. Myung, C. H. Kim, H. S. Kim, S. H. Back, Y. R. Lim, C. S. Jung, D. M. Jang, J. Park, E. H. Cha, S. H. Choo, M. S. Song and W. I. Cho, Chem. Commun., 2013, 49, 4661–4663 RSC.
- Y. J. Cho, H. S. Im, H. S. Kim, Y. Myung, S. H. Back, Y. R. Lim, C. S. Jung, D. M. Jang, J. Park, E. H. Cha, W. I. Cho, F. Shojaei and H. S. Kang, ACS Nano, 2013, 7, 9075–9084 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. D. Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- A. Dal Corso, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 085135 CrossRef.
- H.-C. Weissker, N. Ning, F. Bechstedt and H. Vach, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 125413 CrossRef.
- C. Kittel, Introduction to Solid State Physics, Wiley, 2004 Search PubMed.
- D. Rocca, R. Gebauer, Y. Saad and S. Baroni, J. Chem. Phys., 2008, 128, 154105 CrossRef PubMed.
- O. B. Malcıoğlu, R. Gebauer, D. Rocca and S. Baroni, Comput. Phys. Commun., 2011, 182, 1744–1754 CrossRef PubMed.
- R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169 CrossRef CAS.
- R. Bauernschmitt and R. Ahlrichs, Chem. Phys. Lett., 1996, 256, 454–464 CrossRef CAS.
- H. F. Wilson, F. Gygi and G. Galli, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 113303 CrossRef.
- H. F. Wilson, D. Lu, F. Gygi and G. Galli, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 245106 CrossRef.
- H.-V. Nguyen and S. de Gironcoli, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 205114 CrossRef.
- G. Makov and M. C. Payne, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 4014–4022 CrossRef CAS.
- G. J. Martyna and M. E. Tuckerman, J. Chem. Phys., 1999, 110, 2810–2821 CrossRef CAS PubMed.
- D. V. Melnikov and J. R. Chelikowsky, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 113305 CrossRef.
- M. Marsili, S. Botti, M. Palummo, E. Degoli, O. Pulci, H.-C. Weissker, M. A. L. Marques, S. Ossicini and R. Del Sole, J. Phys. Chem. C, 2013, 117, 14229–14234 CAS.
- A. Tsolakidis and R. M. Martin, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 125319 CrossRef.
- G. Nesher, L. Kronik and J. R. Chelikowsky, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 035344 CrossRef.
| This journal is © The Royal Society of Chemistry 2014 |