SANS and rheology of elongated SDS–DDAO mixed micelles near the phase boundary

Abstract

We examine the micellar phase of sodium dodecyl sulphate (SDS) and N,N-dimethyldodecylamine N-oxide (DDAO) in water, a synergistic anionic/amphoteric mixed surfactant system, in the vicinity of the phase boundary, employing small angle neutron scattering (SANS) and rheology. Specifically, we investigate the role of the SDS : DDAO mixing ratio at a fixed concentration at room temperature. While neat SDS and DDAO form near-spherical micelles with radius ≈20 Å, these elongate into prolates with ≈90 Å polar axis, at intermediate 60–70% mol DDAO ratios. Micellar charge remains largely invariant with a surfactant ratio up to ≤80% DDAO, decreasing thereafter towards uncharged, neat DDAO, except for a large increase in charge, and up to 4 orders of magnitude in solution viscosity (from ≈1 to in excess of 10⁴ mPa s), accompanied by scattering anisotropy, at those intermediate ratios and in 500 mM solutions. A strong correlation is found between solution viscosity and micellar dimensions (and structure factor peak) in the vicinity of the phase boundary.

---

1 Introduction

Surfactant mixtures are ubiquitous in everyday liquid formulations across a range of applications.¹ A vast literature has examined the relationship between the solution structure and rheological properties in mixed-surfactant systems.^2–14 In ionic–nonionic and cationic–anionic surfactant pairs, viscosity generally increases with mixing due to micelle elongation.^8,9,15,16 Upon increasing surfactant concentration, such systems can transition from spheres, to rods, and wormlike micelle networks with mixing, due to an increase in the aggregation number, associated with the electrostatic screening of charged headgroups, effectively decreasing the effective headgroup area. At even higher concentrations, solution viscosity generally drops due to the prevalent formation of 3-way junctions, over end-caps, in the wormlike micelle network.^3,4,10

The effect of additives and environmental conditions on solution viscosity is also well documented: for instance, an increase in temperature leading to an increase in viscosity due to the formation of wormlike micelles;¹⁷ the addition of inorganic salts that screen electrostatic interactions (yielding so-called ‘salt curves’^4,14,18–20), yielding a rise and drop in viscosity accompanying the formation of wormlike micelle networks and solution de-mixing respectively; or changing solution pH, thus modulating the fraction of charged surfactant headgroups available for hydrogen bonding and electrostatic interactions, generally leading to an increase in viscosity due to micelle elongation and wormlike micelle formation.²¹

1.1 Synergy in the SDS–DDAO mixed surfactant system

Sodium dodecylsulfate (SDS) and N,N-dimethyl dodecylanime N-oxide (DDAO) form a model anionic-amphoteric surfactant pair, due to a rich synergy,^15,22–24 manifested in a range of physical–chemical properties. Aqueous mixtures of SDS–DDAO exhibit a pronounced decrease in critical micelle concentration (cmc) and surface tension,^22,25 shifting phase boundaries (including precipitation and Krafft point) upon mixing,^15,26–29 increasing solution pH,^22,30,31 induced transitions from spherical to rod-like micelles in the micellar phase (L₁), and increase in micellar charge and aggregation number.^24,32–34 The SDS:DDAO stoichiometry corresponding to maximum synergy was recently reported to be concentration dependent, ranging from a 1 : 4 to 1 : 1 molar ratio, between 5–80 mM (≈0.1–2% w/w).²⁴ This synergistic behaviour has been rationalised in terms of their strong electrostatic interactions between the sulfate and amine oxide headgroups,^15,22,24 favourable at all ratios, forming mixed monolayers and micelles,^22,24 with negative, parabolic interaction parameters β_ij,^22,35 and interactions well described by regular solution theory.^24,36 Furthermore, the ionisation of the SDS headgroup favours the protonation of the DDAO headgroup (whose amine oxide permanent dipole has a low pK_a ≃ 5),³⁷ which in turn contributes to screening of the sulfate headgroup repulsions, and leads to further dissociation of Na⁺ ions, generating a feedback mechanism.²⁴ The strong headgroup interactions of SDS and DDAO, and the similarity of their hydrocarbon tails, is reminiscent of twin-tail or gemini molecular surfactant architectures.

The effect of SDS–DDAO synergy on solution viscosity has also been reported. Safonova et al.¹⁶ carried out dynamic light scattering (DLS) and rheology measurements finding a pronounced viscosity increase with maxima around 1 : 4 to 1 : 1 molar ratios of SDS : DDAO (within 1–15 wt%, ≈50–500 mM in water), and reporting multimodal decays in DLS (up to 3 at the highest concentrations), interpreted in terms of populations of aggregates with various hydrodynamic radii. Weers et al.¹⁵ studied a very similar system of SDS and N,N-dimethyl tetradecylamine N-oxide (TDAO) by Fourier transform infrared (FTIR) spectroscopy and rheology, to higher concentrations (to ≈30% w/w, ≈1 M, total surfactant concentration) including the hexagonal liquid-crystalline phase (H₁). The authors examined changes in the wavenumber of the CH₂ symmetric stretch (of the surfactant tails) with mixing, inferring that a sphere-to-rod transition in micelle shape accompanied the viscosity increase in the L₁ phase.

1.2 SANS and rheology study of SDS–DDAO solutions

Building upon the early works of Weers et al.¹⁵ and Safonova et al.¹⁶ employing FTIR and DLS (with well known limitations^38,39 for charged, non-spherical and concentrated systems) for solution characterisation, we employ small angle neutron scattering (SANS), accompanied by rheology experiments of mixed SDS–DDAO systems in the micellar phase (L₁), in the vicinity of the phase boundary. We focus on the impact of SDS : DDAO ratio at constant total surfactant concentrations, with no added salt as illustrated in Fig. 1a. We selected the concentration range, 300–500 mM, bound by the previously investigated 1–100 mM range,^24,32,40 where no appreciable increase in solution viscosity was observed with surfactant ratio, and the L₁ + H₁ phase boundary (estimated at 550–575 mM at 70% mol DDAO), as shown in Fig. 1a.

Fig. 1 (a) Ternary composition diagram of SDS:DDAO:H₂ O showing the compositions (∘) of mixed micellar surfactant solutions investigated at fixed overall concentration (300, 400, and 500 mM respectively in blue, purple, and red) and varying SDS : DDAO ratio. Black dashed lines indicate the approximate phase boundaries estimated by polarised optical microscopy (ESI,† Fig. S1). (b) Schematic of SANS experiment and analysis in terms of a core–shell ellipsoidal micelle form factor P(q) and Hayter–MSA and hard sphere (for pure DDAO) structure factors, S(q); the 2D pattern and 1D profiles correspond to composition “A”.

2 Experimental

2.1 Materials

Sodium dodecyl sulfate (SDS, BioReagent ≥98.5%, Sigma-Aldrich 151213), and N,N-dimethyl dodecylamine N-oxide (DDAO, BioXtra, ≥99.0%, Sigma-Aldrich 1643205) were used as received. For SANS experiments, stock solutions of pure SDS and DDAO samples (at 300, 400, and 500 mM) were prepared volumetrically by the addition of heavy water (D₂O, filtered, 99.8% atom, Sigma-Aldrich 7789200) to the SDS and DDAO solids as received, and were homogenised using a roller mixer for 24 h. At each fixed concentration, the pure aqueous samples were mixed at appropriate ratios to make all samples illustrated in Fig. 1a, e.g. for the 10 mol% DDAO samples, 90% by volume of the pure SDS and 10% by volume of the pure DDAO samples were separately prepared and then mixed. All solutions were then homogenised for 24 h prior to measurements (greatly exceeding timescales of monomer exchange kinetics in micelles⁴¹). Selected viscous samples were heated in an oven at 50 °C for 30 min intervals to aid mixing. For rheology measurements, solutions were instead prepared in ultra-pure water (Milli-Q 18.2 kΩ cm) and using aqueous DDAO solutions (30 wt% in H₂O, Sigma-Aldrich 1643205).

2.2 Rheology

The steady state shear viscosity of micellar solutions shown in Fig. 1 was measured using an Anton Paar MCR 302 rheometer in a concentric cylinder geometry (with 20 mL sample volume) operated with RheoCompass (v.1.24) software. Measurements were carried out at 25 °C over a shear rate range of 0.1–1000 s⁻¹ (narrower for less viscous samples), and all data acquired once ‘steady state’ had been reached (to ±0.2% variation tolerance). Shear rate curves showing shear-thinning behaviour were fitted to the Carreau model,⁴²where η([small gamma, Greek, dot above]) is the dynamic viscosity at shear rate [small gamma, Greek, dot above], η₀ is the zero-shear viscosity, τ the relaxation time corresponding to the inverse of the shear rate at which shear thinning commences, and p characterises the power law in the shear thinning regime. Flow curves exhibiting shear-independent viscosities (Newtonian behaviour) were fitted to a straight line.

2.3 Small angle neutron scattering

SANS measurements were carried out at the ISIS pulsed neutron and muon source (Oxfordshire, UK) on the time-of-flight SANS2D diffractometer, equipped with two detectors (at 2.4 and 4 m sample-to-detector distances), and incident neutron wavelengths λ ≈ 1.75–16.5 Å, yielding an elastic wavenumber q = (4π/λ)sin(θ/2), where θ is the scattering angle, of 0.005 ⪅ q ⪅ 1 Å⁻¹.

Surfactant solutions of selected compositions (Fig. 1a) were loaded into 1 mm pathlength quartz glass banjo cells (Hellma 120-QS) and mounted onto a temperature-controlled sample changer set to at 25 °C. The most viscous samples were pre-heated to 50 °C before loading into Hellma cells, and allowed to rest for >1 h. Simultaneous scattering and transmission measurements were then acquired using a 12 mm diameter circular aperture.

MANTID software (v.6.8.0)⁴³ was used to bin, merge data from both detectors, reduce and subtract the empty cell, and calibrate the data to absolute units (cm⁻¹) using an isotropic polystyrene blend of known radius of gyration.⁴⁴ The 2D spectra were then radially averaged to obtain 1D profiles, illustrated in Fig. 1b. Selected 2D spectra were azimuthally averaged in SASView (v5.0.6),⁴⁵ within a defined q-window.

The 1D scattering profiles for the micellar solutions were analysed in terms of their form, P(q), and structure, S(q), factors,⁴⁶

I(q) = kP(q)S(q) + B, (2)

where pre-factor k = (N/V)V_p²Δρ², with (N/V) being the number density of micelles, V_p their volume, Δρ the scattering length density (SLD) difference between micelles and solution, and B is a scattering background, mostly comprising incoherent scattering from hydrogen. The data are analysed in SASView employing a micellar core–shell ellipsoid form factor,^47,48 and a Hayter–Penfold mean spherical approximation (Hayter–MSA)^49,50 structure factor, with the exception of pure DDAO solutions (with charge ∼0) for which a hard-sphere structure factor^47,51 was used instead. Alternative fitting approaches, explicitly accounting for non-sphericity of the structure factor,⁴⁷ and distinct form factors were explored and compared (in terms of fitting quality across the q-range and overall χ²) as detailed in the ESI† (Fig. S2–S6 and Table S1). The scattering profiles were fitted assuming a single population of mixed SDS–DDAO micelles, in agreement with infrared spectroscopy studies^22–24 on this system, which provide evidence of a single micellar population (instead of, for instance, a bimodal distribution) based on wavenumber shifts of surfactant C–H and S–O bonds upon mixing. The approach from the micellar phase towards the hexagonal phase could be expected to result in a large increase in solution viscosity, and increased positional correlation between surfactant aggregates, leading eventually to anisotropic scattering (or local order albeit exhibiting isotropic scattering in spatial, or ‘powder’ average). For the composition space explored, SANS data were we generally isotropic and could be well described by a relatively simple ellipsoid model and Hayter–MSA structure factor (further discussed below and in the ESI†).

3 Results & discussion

3.1 Solution rheology

Fig. 2a shows the rheology data obtained from a shear sweep of solutions at a constant surfactant concentration of 500 mM and varying SDS : DDAO ratio (corresponding to the red isopleth in Fig. 1a with two additional compositions (65% and 75% mol DDAO) to better resolve the maximum in η₀; data for 300 mM and 400 mM solutions are provided in Fig. S7 of the ESI.† Fitting data to the descriptive Carreau model (eqn (1)), we obtain the zero shear rate viscosities shown in Fig. 2b, the relaxation times τ in the inset of Fig. 2a, and p is given in the legend. A range of stoichiometries (0–50% and 90–100% mol DDAO at 400 and 500 mM, and 0–70% and 90–100% mol DDAO at 300 mM) are effectively Newtonian within this shear rate range, and viscosity data were fitted to a constant value; the corresponding τ values are shown as <10⁻³ s, the inverse of the maximum shear rate measured.

Fig. 2 (a) Dynamic viscosity dependence on shear rate for the 500 mM surfactant solutions at varying mol% DDAO. Lines are linear fits, and fits to the Carreau model for 60–80% data. The inset shows the relaxation times obtained from the Carreau fit with other compositions set to <10⁻³ s, and the dashed line showing a guide to the eye. (b) Zero shear viscosities (η₀) for 300 mM (blue), 400 mM (purple), and 500 mM (red) solutions of varying SDS : DDAO ratios, obtained from linear extrapolations of data in (a) and fitting of the Carreau model. Dashed lines are guides to the eye.

Increasing DDAO ratio at constant 500 mM concentration leads to an increase in solution viscosity up to 70% mol, spanning ∼4 orders of magnitude, decreasing thereafter towards pure DDAO; approximately ∼3 orders of magnitude increase is measured for the 400 mM solutions up to a peak at 75% mol DDAO, and a more modest increase (of ∼2 orders of magnitude) is observed for 300 mM, progressively away from the phase boundaries and continuing the shift towards pure DDAO, with a maximum at 80% DDAO. Shear thinning behaviour is observed for 60–80% mol DDAO solutions, with most other ratios having viscosities in the range of 1–10 mPa s.

These data are reminiscent of so-called ‘salt curves’ (characterising the change in zero-shear viscosity with concentration of added salt), where the viscosity increase is associated with micelle elongation, the formation of wormlike micelle networks, and the eventual viscosity decrease with the formation of 3-way junctions over end-caps, and finally phase separation (‘salting out’).^4,14,19,20 In contrast, here we examine the effect of the SDS–DDAO ratio at a constant surfactant concentration. In mixed systems, in the absence of salt, or at fixed salt content, changes in solution viscosity with mixing have been rationalised in terms of micelle elongation (sphere-to-rod transition^2,14–16) or the formation of entangled wormlike micelle networks.^3–5

For this SDS–DDAO system, maximum synergy (deviation from neat solution properties due to favourable interactions of headgroups^15,22,24) away from the equimolar ratio has been observed for the similar system of SDS and TDAO by Weers et al.¹⁵ where maximum zero-shear viscosity was observed in the range ∼70–80% mol DDAO. Furthermore, the higher viscosities observed (up to 10 kPa s) were attributed to the formation of rod-like micelles, inferred from changes in the S=O absorption band in Fourier transform infrared (FTIR) spectroscopy in the study and in previous studies.^22,24 Furthermore, correlations between viscosities¹⁶ and multimodal DLS decays, interpreted as surfactant aggregate populations, have been proposed.^16,24 To elucidate the molecular origin of such large viscosity increases and evaluate their dependence on the aspect ratio of micelles, we have carried out a series of SANS measurements near the phase boundaries, complementing our previous work on the characterisation of this system at lower (0.1–100 mM) concentrations.²⁴ Albeit within a narrow range investigated, the solution viscosity at fixed SDS–DDAO stoichiometry and varying concentration can be reasonably well described by a power law with exponents ranging from ∼1.4 to 14 (with stoichiometry), as detailed in Fig. S8 of the ESI.†

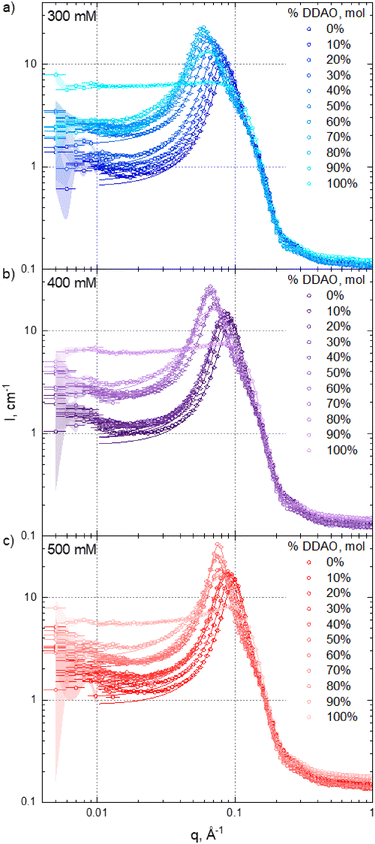
3.2 Micellar structure and interactions

Fig. 3 shows SANS intensity profiles (circles) and model fits (solid lines) for (a) 300 mM, (b) 400 mM, and (c) 500 mM total surfactant concentrations of varying SDS : DDAO ratios. Data fits were carried out between 0.01 ≤ q ≤ 1 Å, as scattering data at lower q exhibit higher uncertainty and may contain contributions from larger clusters.⁴⁰ Porod representations of selected datasets and fits are provided in the ESI,† Fig. S6 to illustrate the model agreement across the q-range investigated. As expected, neat DDAO solutions (100%) do not show appreciable structure factor contribution, as this amphoteric surfactant (pK_a ≈ 5) forms approximately uncharged micelles at neutral pH ≈ 7 (detailed in Fig. 3 of Soontravanich et al.³⁷). By contrast, the remaining SDS–DDAO mixtures and neat SDS solutions exhibit a pronounced structural peak.

Fig. 3 Radially-averaged (1D) SANS scattering profiles for (a) 300 mM, (b) 400 mM, and (c) 500 mM isopleths, of fixed overall surfactant concentration, with varying SDS : DDAO ratio. Open circles (∘) show data points and the solid lines are model fits using a core–shell form factor, P(q), and Hayter–MSA structure factor, S(q) (except for 100% DDAO, for which a hard sphere structure factor was used).

Fig. 4 summarises the estimated micelle dimensions, strength of inter-micellar interactions by the model's ‘charge’ parameter, and aggregation numbers N_agg. All fitting parameters are provided in the ESI† (core and shell SLDs used and the background in Fig. S2 (ESI†) with all other fitting parameters and χ² in Table S1, ESI†). The scattering background B shows little variation with SDS:DDAO stoichiometry, which is expected well above cmc.

Fig. 4 Micelle characteristics estimated by SANS for the 300 mM (blue), 400 mM (purple), and 500 mM (red) constant concentration isopleths. (a) The total (core + shell) equatorial (Δ) and polar (∘) micelle radii. (b) Interactions estimated by the micelle charge by the Hayter–MSA model, and set to zero for pure DDAO by use of the hard sphere model. (c) Aggregation numbers of micelles based on the micelle core volume and the Tanford equation.⁵⁴ Dashed lines are guides to the eye across all concentrations.

The micelle radii plotted in Fig. 4a correspond to the sum of the core radii and shell thickness (provided in Fig. S9 in the ESI†). The equatorial micellar radius remained approximately constant across all concentrations and ratios investigated (exhibiting a gentle maximum at ≈70% mol DDAO, shown in the inset) such that the aspect ratio, AR, is approximately proportional to the polar radius. Neat DDAO and SDS micelles are approximately spherical with radius ≈2 nm and their mixing results in a significant increase of polar radius, thus forming prolate ellipsoidal micelles, with the longest radii found at 60–70% mol DDAO, for all concentrations investigated. This behaviour is consistent with previous observations at lower surfactant concentrations, viz. 5–50 mM²⁴ and 80 mM.³² However, the overall trend is non-monotonic, increasing modestly between 0–40% DDAO, and varying abruptly between 40–100% DDAO. Refitting the data with alternative model assumptions and parameters to impose a smoother behaviour, appreciably degraded the quality of the fits as measured by χ².

Close inspection of the polar radii suggests a comparatively ‘smoother’ elongation for 300 mM concentration series, around the 30–50% DDAO ratios, with respect to that at 400–500 mM. The latter approach a plateau (and slight decrease), followed by a doubling of the polar radius between a narrow stoichiometric range of 40–50% DDAO. We are unsure of the physical origin of this non-monotonic trend, and speculate it could be associated with an evolution of the average partitioning of the mixed surfactant monomers in micelles: below 50% DDAO, micelles will have on average a greater proportion of SDS monomers and thus an average SDS : DDAO ratio below the stoichiometry of most favourable interactions between headgroups, this ‘most favourable ratio’ defined as giving rise to previously measured e.g. lowest surface tension (at 1 : 1 ratio),²² and greatest micellar aggregation numbers and charge (maximal in the range of 1 : 1 to 1 : 4 depending on concentration).²⁴ The amphoteric nature of DDAO (neutral or cationic depending on pH)^23,37 and the favourable electrostatic interaction between the cationic DDAO headgroup and anionic sulphate on SDS^15,22–24 appears to relieve packing frustration of anionic SDS headgroups above 40% ratios, leading to a rapid increase in prolate dimensions. For the lower 0–40% DDAO ratios, we speculate that the inability of micelles to adopt SDS–DDAO monomer ratios close to the ‘favourable’ stoichiometry, and therefore the non-optimal alleviation of SDS packing frustration gives rise to the more modest increase in polar radius. We cannot rule out more complex interpretations based on various micellar populations of different average composition, and fast exchange kinetics, but we do not have experimental evidence for those from FTIR spectroscopy or SANS. Albeit challenging due to low scattering intensity, precise contrast-matching^52,53 of the aqueous medium D₂O/H₂O to the expected averaged SLD of the mixed core–shell micelles (possibly augmented by molecular dynamic simulations) could provide further physical insight.

Fig. 4b shows the strength of interactions between micelles (interpreted as the micellar charge in the Hayter–MSA structure factor model, and set to zero for pure DDAO where a hardsphere model was used for all solutions). For both 300 mM and 400 mM solutions, the data suggest that the addition of DDAO does not modify the micelle interactions significantly up to ∼90% mol DDAO where the charge drops. By contrast, for the 500 mM solution we observe a steep increase in charge for the 60% and 70% mol DDAO solutions. The equivalent charge per monomer and surface charge density have also been calculated and are provided in Fig. S10 in the ESI.† This behaviour of constant charge with DDAO addition shown in the 300–400 mM solutions extends the previous observations of Kakitani et al.³² at 80 mM, those of Torquato et al.²⁴ at 50 mM, and in the work of Khodaparast et al.³³ at ∼700 mM SDS doped with ≤5% w/w DDAO. This has been rationalised in terms of the equilibrium between the dissociation of Na⁺ cations from SDS, the resulting increased counterion concentration near the surface of micelles, the subsequent increased protonation of DDAO, and therefore greater dissociation of Na⁺ cations.^15,22,24,30 The increase in interactions strength for the 500 mM solutions at 60–70% mol DDAO thus appears to correspond to the samples in proximity to the hexagonal phase boundary, and coinciding with micelle elongation at this higher concentration and thus volume fraction relative to the 300 mM and 400 mM solutions. A modest alignment of micelles is observed from a small (⪅5% variation in intensity with azimuthal angle) anisotropy in the 2D scattering profiles (ESI,† Fig. S11) likely related to interactions with sample holder walls, as observed in some polyelectrolyte solutions.⁵⁵ We verified that the bulk of the surfactant solution had relaxed by obsessing the decay of flow-induced birefringence shown in the ESI,† Fig. S12, well described by a double exponential fit with a 1 s decay constant, commensurate with the relaxation time from the Carreau fitting of the respective flow curve, and a much longer time constant.

Finally, Fig. 4c shows the aggregation numbers for all solutions studied. These were calculated by dividing the micelle core volume by the volume of a liquid dodecane molecule, V_Tail = 347.5³, calculated using the Tanford equation, V_Tail = 24.7 + 26.9n_c,⁵⁴ with n_c = 12, the number of carbons. As expected, the trends here mirror that of the micellar radii with maxima at ∼60–70% mol DDAO.

The viscosity of colloidal suspensions is generally described in terms of the concentration, or volume fraction, of the colloids in solution (e.g., ref. 56–58). In our experiments, however, the large variations in viscosity take place at a largely constant overall surfactant concentration and volume fraction (as shown in Fig. S2 in the ESI†); specifically, our constant volume fractions from SANS fitting suggest that the increase in volume fraction from the growth of micelles must be offset by the number of micelles decreasing. The viscosity and packing of ellipsoids is also well-known to depend on their shape and size (e.g., ref. 59 and 60) and thus we next focus on extracting correlations with the SDS : DDAO ratio and the structure factor related to the solution structure due to micelle interactions.

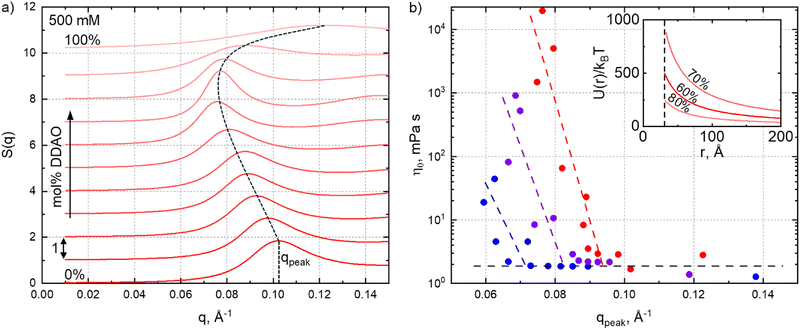
Fig. 5a shows the structure factors S(q) estimated from the scattering data (using SASView ‘integrated theory mode’) for the 500 mM series (offset +1 for clarity). Structure factors for the for 300 mM and 400 mM data are provided in the ESI,† Fig. S13. The dashed line indicates the location of the peak upon varying SDS : DDAO ratio, decreasing for mixed micelles as their interactions and dimensions increase. We find an interesting correlation between peak position, q_peak, roughly correlated to the average inter-micellar distance, and solution viscosity, shown in Fig. 5b.

Fig. 5 (a) Structure factors, S(q), estimated from fitting SANS data for the 500 mM surfactant solutions of increasing mol% DDAO in steps of 10% from bottom to top. Curves are shifted vertically by +1 increments for clarity, and the dashed line shows the position of the maximum (first peak) in S(q), and the corresponding q_peak value. (b) Zero shear viscosity dependence on q_peak for the 300 mM (blue), 400 mM (purple), and 500 mM (red) concentration series, with dashed lines showing the plateau and pronounced increasing regions of the data. The inset illustrates the repulsive electric double-layer potential, U(r), compared to the thermal energy, k_BT, as a function of distance, r, computed from the SANS parameters, showing a greater range of the most viscous, 70% mol DDAO, ratio. The vertical dashed line indicates the hard-wall limit of the Hayter–MSA model, below which U(r) = ∞.

For very low viscosities (≃2 mPa s), the viscosity appears largely independent of q_peak. By contrast, below a certain value q*, solution viscosity increases (approximately exponentially) with decreasing q_peak, associated with longer-range interactions. These are illustrated through the repulsive interaction potential, calculated from SANS parameters and assuming an electric double-layer interaction,⁴⁹ shown in the inset. The 70% mol DDAO solution (of highest viscosity in the series), exhibits a longer range repulsive potential (U(r)/k_BT is greater at all distances, r) compared to the 60% and 80% DDAO solutions, for which the viscosity decreases. We define q* as the intercept of the two regions shown in Fig. 5b, where q* ≃ 0.07, 0.08, or 0.09 Å⁻¹, respectively, for the 300 mM, 400 mM or 500 mM series, corresponding to an effective lengthscale of r* ≡ 2π/q* in the range of 90 Å, 80 Å and 70 Å.

Comparing these critical dimensions to the micelle size, specifically the polar radius (shown in Fig. 4a), we find that if the diameter of the micelle along the polar axis 2R_Polar < r*, the q_peak appears to be independent of viscosity, while for 2R_Polar > r*, a decrease in q_peak leads to a large viscosity increase. The latter condition corresponds to solutions where the average inter-micellar distance is smaller than the diameter of the polar axis and we therefore qualitatively interpret r* as a crossover interaction lengthscale (or corresponding q*), above which if the micelle dimensions become commensurate, further elongation leads to a large increase in viscosity. This correlation is reminiscent to the characteristic crossovers (such as the overlap concentration c*) in polymer solutions, or network percolation, and associated structural and rheological regimes.⁶¹ In our data, an analogous crossover is found in terms of SDS–DDAO stoichiometry and manifested in an onset q* below which the viscosity rises rapidly.

Previous literature has suggested correlations between micellar shape and viscosity; Weers et al.¹⁵ attributed the viscosity increase in SDS and TDAO to a sphere-to-rod transition in the micelle shape inferred by FTIR (CH₂ symmetric stretch); Safonova et al.¹⁶ correlated the viscosity of SDS–DDAO solutions to large aggregates (>100 nm) inferred by DLS. Our work explicitly measures the shape, size and interactions of micelles via SANS, and their impact on viscosity.

3.3 Micellar geometry scaling with solution viscosity

Fig. 6 summarises correlations between fitting parameters from the core–shell form factor and Hayter–MSA structure factor models to the viscosity of the systems. For the 500 mM series, we find that an exponential relationship of the form η₀ = 0.042e^0.144R_Polar with an R² = 0.833, satisfactorily describes the correlation between micelle elongation (in terms of the polar radius) and viscosity, whereby the viscosity of near-spherical micelles increases slowly with R_Polar, while the same increase in R_Polar results in a large viscosity change for elongated micelles. This exponential relationship is of interest as the nearly doubling in the polar radius (25–41 Å) between 0–30% mol DDAO is accompanied by a near proportionate increase in viscosity (2.8–3.5 mPa s). By contrast, doubling the radius between 30% and 70% mol DDAO (41–85 Å) leads to a nearly 10⁴ increase in solution viscosity (3.5–21 000 mPa s), while the volume fraction remains relatively constant, as here the increase in viscosity is due to the changing of mixed surfactant ratio at constant total concentration.

Fig. 6 (a) Zero shear viscosities, η₀, for 300 mM (blue), 400 mM (purple), and 500 mM (red) samples plotted against parameters interpreted through the SANS fitting, namely the polar radius, R_Polar, volume fraction, V_Frac, and micelle charge, Q_Micelle. The red dashed line represents the general trend in R_Polar with η₀ for 500 mM data, and the vertical blue, purple, and red bars show the spread in 300 mM, 400 mM, and 500 mM volume fractions respectively. (b) The relation between the viscosity and micelle volume, V_Micelle = (4/3)πR_Equatorial²R_Polar. The dashed line highlights the exponential increase in η₀ with increasing V_Micelle approximately ∝ R_Polar. (c) Schematic of 500 mM 0%, 40%, 70%, 100% mol DDAO micelles (R_Polar : R_Equatorial to scale).

Further away from the phase boundaries, for the 300 mM and 400 mM series, we do not observe such simple correlations between R_Polar and viscosity (as opposed to the correlation with S(q) above), or with other parameters such as micellar volume fraction or charge (Fig. 6a). This is surprising, as variations in zero-shear viscosity in mixed micelles are often associated to a sphere-to-rod (and reverse) transition.^2,5,7,14,15 Furthermore, we observe an offset between the DDAO ratio of maximum polar radius and that of maximum viscosity; the maximum R_Polar occurs at 60% mol DDAO for both 300 mM and 400 mM solutions, while the viscosity is maximum at 80% and 75% mol DDAO respectively. The correlation between micelle elongation and viscosity thus seems to apply solely at the higher concentration, in proximity of the phase boundary. Modest changes in viscosity have been reported to correlate well with micellar dimensions; for example, in the work of Christov et al.² an increase in viscosity of only ≈8 mPa s in changing the surfactant ratio for an SDS-cocoamidopropyl betaine (CAPB) system, shows good correlation to the R_H of micelles measured by DLS. More complex nano-structural correlations likely influence the solution viscosity across the concentration-composition space.

Since the equatorial radius of SDS–DDAO micelles remains largely constant for the concentrations series investigated, we expect a favourable relationship between micellar volume and viscosity, and calculate V_Micelle = (4/3)πR_Equatorial²R_Polar taking into account the slight variation in the equatorial radius (ΔR_Equatorial ≈ 1.5 Å). This correlation is shown in Fig. 6b, with the dashed line now representing an exponential fit of the form, η₀ = 0.089e^{8.6×10−5R_Polar} with an improved R² = 0.910. Fig. 6c illustrates our conclusion, that in the proximity of the H₁ phase boundary, the SDS:DDAO surfactant ratio has a pronounced effect on the micelle elongation (with other geometric considerations discussed in Fig. S14 of the ESI†) which closely follows the increase in solution viscosity.

4 Conclusions

SDS–DDAO synergy is observed in both micelle structure and interactions through a sphere to prolate elongation along the polar radius (up to 5×) at intermediate 60–70% DDAO surfactant ratios, in the proximity of the phase boundary. By contrast, the equatorial radius exhibits a modest variation (<10%) with stoichiometry, and the micellar charge remains all but constant, except in the proximity of uncharged neat DDAO, and nearest to the phase boundary. The solution rheology is also found to exhibit a pronounced variation with SDS:DDAO stoichiometry, at constant overall concentration (and thus micellar volume fraction), with the zero shear-rate viscosity increasing by up to 4 orders of magnitude at these intermediate ratios. This viscosity increase is also most pronounced for the concentration isopleth nearest to the phase boundary. We find a strong correlation between solution rheology and micelle geometry, namely that the viscosity increases near exponentially with micellar volume (or equivalently with polar radius, since the equatorial dimensions remain effectively unchanged) but only for our highest concentration series (500 mM), near the phase boundaries.

These findings should be relevant to formulation science and engineering, seeking to manipulate macroscopic properties by solution design. It would be of great interest to expand this study to other classes of mixed surfactant systems, beyond anionic-amphoteric SDS–DDAO, and examine the generality of our findings and possible quantitative correlations to surfactant thermodynamics and proximity to the phase boundaries.

Data availability

All SANS and rheology data supporting this article are available on Zenodo (https://doi.org/10.5281/zenodo.14765827).

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank EPSRC and Procter & Gamble for funding an iCASE PhD studentship for LMGT and the ANTENNA prosperity partnership (EP/V056891/1). JTC thanks the Royal Academy of Engineering (RCSRF1920/10/60) for funding a Research chair and the Royal Society (IES/R2/222241) for an international exchange grant. We acknowledge the Science and Technology Facilities Council (STFC) for access to neutron beamtime at ISIS (DOI: 10.5286/ISIS.E.RB2310627). This work benefited from the use of the SasView application, originally developed under NSF award DMR-0520547. SasView contains code developed with funding from the European Union's Horizon 2020 research and innovation programme under the SINE2020 project, grant agreement No. 654000. We thank Stephen King (ISIS) for discussions on non-spherical corrections of the structure factors and William Sharratt (Liverpool) for discussions on data fitting.

Notes and references

1. T. F. Tadros, Applied surfactants: principles and applications, John Wiley & Sons, 2006.
2. N. C. Christov, N. D. Denkov, P. A. Kralchevsky, K. P. Ananthapadmanabhan and A. Lips, Langmuir, 2004, 20, 565–571.
3. D. P. Acharya and H. Kunieda, Adv. Colloid Interface Sci., 2006, 123–126, 401–413.
4. B. A. Schubert, E. W. Kaler and N. J. Wagner, Langmuir, 2003, 19, 4079–4089.
5. R. A. Abdel-Rahem, R. Martin, H. Matthias and H. Hoffmann, J. Dispersion Sci. Technol., 2014, 35, 64–75.
6. R. D. Koehler, S. R. Raghavan and E. W. Kaler, J. Phys. Chem. B, 2000, 104, 11035–11044.
7. J. Bhattacharjee, G. Verma, V. K. Aswal, A. A. Date, M. S. Nagarsenker and P. A. Hassan, J. Phys. Chem. B, 2010, 114, 16414–16421.
8. S. Kumar, V. K. Aswal, H. N. Singh and P. S. Goyal, Langmuir, 1994, 10, 4069–4072.
9. D. Varade, K. Ushiyama, L. K. Shrestha and K. Aramaki, J. Colloid Interface Sci., 2007, 312, 489–497.
10. V. Croce, T. Cosgrove, C. A. Dreiss, G. Maitland, T. Hughes and G. Karlsson, Langmuir, 2004, 20, 7984–7990.
11. A. Shiloach and D. Blankschtein, Langmuir, 1998, 14, 7166–7182.
12. T. Joshi, J. Mata and P. Bahadur, Colloids Surf., A, 2005, 260, 209–215.
13. T. Iwasaki, M. Ogawa, K. Esumi and K. Meguro, Langmuir, 1991, 7, 30–35.
14. V. I. Yavrukova, G. M. Radulova, K. D. Danov, P. A. Kralchevsky, H. Xu, Y. W. Ung and J. T. Petkov, Adv. Colloid Interface Sci., 2020, 275, 102062.
15. J. Weers, J. Rathman and D. Scheuing, Colloid Polym. Sci., 1990, 268, 832–846.
16. E. Safonova, M. Alekseeva, S. Filippov, T. Durrschmidt, L. Mokrushina, H. Hoffmann and N. Smirnova, Russ. J. Phys. Chem., 2006, 80, 915–921.
17. G. C. Kalur, B. D. Frounfelker, B. H. Cipriano, A. I. Norman and S. R. Raghavan, Langmuir, 2005, 21, 10998–11004.
18. T. Vu, P. Koenig, M. Weaver, H. D. Hutton and G. B. Kasting, Colloids Surf., A, 2021, 626, 127040.
19. W. Zhang, J. Mao, X. Yang, H. Zhang, J. Zhao, J. Tian, C. Lin and J. Mao, Chem. Eng. Sci., 2019, 207, 688–701.
20. A. Parker and W. Fieber, Soft Matter, 2013, 9, 1203–1213.
21. J. Yang, S. Chen and Y. Fang, Carbohydr. Polym., 2009, 75, 333–337.
22. G. Tyagi, D. Seddon, S. Khodaparast, W. N. Sharratt, E. S. Robles and J. T. Cabral, Colloids Surf., A, 2021, 618, 126414.
23. G. Tyagi, W. N. Sharratt, S. Erikson, D. Seddon, E. S. Robles and J. T. Cabral, Langmuir, 2022, 38, 7198–7207.
24. L. M. Torquato, G. Tyagi, W. N. Sharratt, Z. Ahmad, N. Mahmoudi, J. Gummel, E. S. Robles and J. T. Cabral, Langmuir, 2024, 40, 7433–7443.
25. M. Rosen and X. Hua, J. Am. Oil Chem. Soc., 1982, 59, 582–585.
26. K. Tsujii, K. Okahashi and T. Takeuchi, J. Phys. Chem., 1982, 86, 1437–1441.
27. K. L. Stellner, J. C. Amante, J. F. Scamehorn and J. H. Harwell, J. Colloid Interface Sci., 1988, 123, 186–200.
28. N. Smirnova, B. Murch, I. Pukinsky, T. Churjusova, M. Alexeeva, A. Y. Vlasov and L. Mokrushina, Langmuir, 2002, 18, 3446–3453.
29. H. Hoffmann, S. Hofmann and J. Illner, Trends in Colloid and Interface Science VIII, 1994, pp. 103–109.
30. M. Abe, K. Kato and K. Ogino, J. Colloid Interface Sci., 1989, 127, 328–335.
31. T. Imae and M. Kakitani, Colloid Polym. Sci., 1996, 274, 1170–1175.
32. M. Kakitani, T. Imae and M. Furusaka, J. Phys. Chem., 1995, 99, 16018–16023.
33. S. Khodaparast, W. N. Sharratt, G. Tyagi, R. M. Dalgliesh, E. S. Robles and J. T. Cabral, J. Colloid Interface Sci., 2021, 582, 1116–1127.
34. H. Pilsl, H. Hoffmann, S. Hofmann, J. Kalus, A. Kencono, P. Lindner and W. Ulbricht, J. Phys. Chem., 1993, 97, 2745–2754.
35. R. De Lisi, A. Inglese, S. Milioto and A. Pellerito, Fluid Phase Equilib., 1996, 126, 273–287.
36. M. Bakshi, R. Crisantino, R. De Lisi and S. Milioto, J. Phys. Chem., 1993, 97, 6914–6919.
37. S. Soontravanich, J. A. Munoz, J. F. Scamehorn, J. H. Harwell and D. A. Sabatini, J. Surfactants Deterg., 2008, 11, 251–261.
38. D. N. Petsev, N. D. Denkov and P. A. Kralchevsky, J. Dispersion Sci. Technol., 1997, 18, 647–659.
39. M. Corti and V. Degiorgio, J. Phys. Chem., 1981, 85, 711–717.
40. B. Hammouda, J. Res. Natl. Inst. Stand. Technol., 2013, 118, 151.
41. T. Shoaib, J.-M. Ha, Y. Han, W.-R. Chen and C. Do, Phys. Chem. Chem. Phys., 2022, 24, 16988–16996.
42. J. M. Dealy and K. F. Wissbrun, Melt Rheology and Its Role in Plastics Processing: Theory and Applications, Springer Science & Business Media, 2012.
43. O. Arnold, J.-C. Bilheux, J. Borreguero, A. Buts, S. I. Campbell, L. Chapon, M. Doucet, N. Draper, R. F. Leal and M. Gigg, et al., Nucl. Instrum. Methods Phys. Res., Sect. A, 2014, 764, 156–166.
44. G. T. Wignall and F. Bates, J. Appl. Crystallogr., 1987, 20, 28–40.
45. SASView, https://www.sasview.org/, (accessed: 31.10.2023).
46. B. Hammouda, Probing nanoscale structures – the SANS toolbox, https://www.nist.gov/system/files/documents/2023/04/14/the_sans_toolbox.pdf.
47. M. Kotlarchyk and S.-H. Chen, J. Chem. Phys., 1983, 79, 2461–2469.
48. S. Berr, J. Phys. Chem., 1987, 91, 4760–4765.
49. J. B. Hayter and J. Penfold, Mol. Phys., 1981, 42, 109–118.
50. J.-P. Hansen and J. B. Hayter, Mol. Phys., 1982, 46, 651–656.
51. J. K. Percus and G. J. Yevick, Phys. Rev., 1958, 110, 1.
52. M. Adamo, A. S. Poulos, R. M. Miller, C. G. Lopez, A. Martel, L. Porcar and J. T. Cabral, Lab Chip, 2017, 17, 1559–1569.
53. M. Adamo, A. S. Poulos, C. G. Lopez, A. Martel, L. Porcar and J. T. Cabral, Soft Matter, 2018, 14, 1759–1770.
54. C. Tanford, J. Phys. Chem., 1972, 76, 3020–3024.
55. R. Wang, V. V. Ginzburg, J. Jiang and Z.-G. Wang, Macromolecules, 2023, 56, 7653–7662.
56. R. Roscoe, British J. Appl. Phys., 1952, 3, 267.
57. I. M. Krieger and T. J. Dougherty, Trans. Soc. Rheol., 1959, 3, 137–152.
58. G. K. Batchelor, J. Fluid Mech., 1977, 83, 97–117.
59. A. Donev, I. Cisse, D. Sachs, E. A. Variano, F. H. Stillinger, R. Connelly, S. Torquato and P. M. Chaikin, Science, 2004, 303, 990–993.
60. A. Donev, F. H. Stillinger, P. Chaikin and S. Torquato, Phys. Rev. Lett., 2004, 92, 255506.
61. M. Rubinstein and R. H. Colby, Polymer physics, Oxford University Press, 2003.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5sm00437c

---