Open Access Article
Open Access ArticlePredefined attention-focused mechanism using center-environment features: a machine learning study of alloying effects on the stability of Nb5Si3 alloys†
Yuchao
Tang
ab,
Bin
Xiao
a,
Shuizhou
Chen
c,
Quan
Qian
c and
Yi
Liu
 *a
*a
aMaterials Genome Institute, Shanghai Engineering Research Center for Integrated Circuits and Advanced Display Materials, Shanghai University, Shanghai 200444, China. E-mail: yiliu@shu.edu.cn
bState Key Laboratory of Functional Materials for Informatics, Shanghai Institute of Micro-system and Information Technology, Chinese Academy of Sciences, Shanghai 200050, China
cSchool of Computer Engineering & Science, Shanghai University, Shanghai, 200444, China
First published on 14th June 2025
Abstract
Digital encoding of material structures using graph-based features combined with deep neural networks often lacks local specificity. Additionally, incorporating a self-attention mechanism increases architectural complexity and demands extensive data. To overcome these challenges, we developed a Center-Environment (CE) feature representation—a less data-intensive, physics-informed predefined attention mechanism. The pre-attention mechanism underlying the CE model shifts attention from complex black-box machine learning (ML) algorithms to explicit feature models with physical meaning, reducing data requirements while enhancing the transparency and interpretability of ML models. This CE-based ML approach was employed to investigate the alloying effects on the structural stability of Nb5Si3, guiding data-driven compositional design for ultra-high-temperature NbSi superalloys. The CE features leveraged the Atomic Environment Type (AET) method to characterize the local low-symmetry physical environments of atoms. The optimized CEAET models reasonably predicted double-site substitution energies in α-Nb5Si3, achieving a mean absolute error (MAE) of 329.43 meV per cell. The robust transferability of the CEAET models was demonstrated by their successful prediction of untrained β-Nb5Si3 structures. Site occupancy preferences were identified for B, Si, and Al at Si sites and for Ti, Hf, and Zr at Nb sites within β-Nb5Si3. This CE-based ML approach represents a broadly applicable and intelligent computational design method capable of handling complex crystal structures with strong transferability, even when working with small datasets.
1 Introduction
Nb–Si-based superalloys with high melting points and low density are expected to overcome the working temperature barrier of Ni-based superalloys and have been extensively studied as a new generation of high-temperature structural materials.1 It contains a large number of high-temperature intermetallic compounds, such as Nb5Si3, which have a high melting point (2520 °C), moderate density (7.16 g cm−3), high-temperature strength, and good creep resistance.2,3 However, single Nb5Si3 is brittle at room temperature, which seriously hinders its practical application.3,4 Nb5Si3 has both metal and ceramic properties, and its alloying elements can improve its intrinsic brittleness at room temperature. Numerous experimental works have shown that adding alloying elements is an effective way to improve the comprehensive performance of Nb–Si alloys.5–10 The alloying elements that have been reported to be incorporated in NbSi-based alloys encompass a range of metals such as Ti,11 Cr,12 Al,13 Hf,14 Sn, Mo, W,15 V, Ta, Fe, Zr, Ho,16 Sr,17 B.18 It is time-consuming and labor-intensive, requiring trial-and-error experiments. Simultaneously, the calculation method based on first principles can effectively predict the types of alloying elements and guide alloy composition design.Chen et al.19 studied the atomic occupation positions of transition group metals in different sublattices of Nb5Si3. Their findings indicate that atoms with larger radii than Nb tend to occupy NbII sites, whereas atoms with smaller radii than Nb tend to occupy NbI sites in α-Nb5Si3. Xu et al.20 studied the effects of vacancy concentration and Al substitution on the structural, electronic, and elastic properties of Nb5Si3 by first-principles calculation. Guo et al.21 systematically studied the effect of Ag addition on the structure, mechanical, and thermodynamic properties of α-Nb5Si3. Tsakiropoulos et al.22 investigated the stability and physical properties of Ti-doped α-Nb5Si3, β-Nb5Si3, and γ-Nb5Si3 alloys at different temperatures and concentrations. Xu et al.23 determined the temperature-dependent structural properties and anisotropic thermal expansion coefficients of α-/β-Nb5Si3 phases by minimizing the nonequilibrium Gibbs free energy as a function of crystal deformation. Shi et al.24 focused on the effect of alloying elements on the mechanical properties and electronic structure of α-Nb5Si3. Kang et al.25 investigated the energy, lattice parameters, electronic structure, and elastic constants of Ti-, Cr-, Al-, and Hf-doped in β-Nb5Si3. Until now, the first-principles calculations focus on only a few elements and single-site substitution of NbSi-alloys limited by cost. It is still far from adequate for screening alloying elements, considering the complex phase structure and wide range of alloying elements in multi-component NbSi-based superalloys.
Machine learning as an emerging data-driven research paradigm in materials science has proven to be effective and efficient in characterizing the complex structure–property relationships of materials.26–30 It is well known that both the chemical composition and structure of a material determine its properties. Thus, ML features should comprehensively characterize both rather than focusing only on the composition itself. To this end, Liu's group31–36 develops a Center-Environment (CE) feature model that integrates both compositional and structural information into machine learning (ML) features by mapping basic physicochemical properties onto a “core–shell” structural framework. The CE feature model considers the properties of the surrounding ambient atoms and quantifies the effect of the environment on the central atom. The CE feature models have been successfully applied to predict a variety of physicochemical properties of spinel oxides,31,36 perovskite oxides,32,35 metals,33 and surface structures,34 including formation energies, lattice parameters, band gaps, surface adsorption energies, and overpotentials for surface oxygen reactions.
In this study, the Nb5Si3 crystal structure exhibits low symmetry, possessing four non-equivalent sites and a slightly distorted local environment. The traditional method of defining nearest neighbor (NN) environment atoms encounters difficulties for local, low-symmetry, distorted configurations, as these environment atoms are not easily predetermined under different truncation conditions. Simply increasing the number of NN environment atoms does not necessarily improve the accuracy of the prediction; instead, it may introduce redundant information with adverse effects. This is because CE is essentially a localized feature representation, and an extensive truncation range may interfere with the accuracy of other localized CE atom sets. Therefore, a proper general definition of the environment atoms becomes particularly important when constructing CE features, especially for complex crystal structures. This is the primary driver of the methodological development in this work. The broader impact of this work is that it provides an alternative to current graph-based neural network methods, which have been limited in their application in materials science due to their complex architecture and the need for large amounts of training data.37–40
The conventional attention mechanism refers to the different weight parameters in the deep neural networks of large language models. The optimization of weights requires a large amount of data during the pre-trained stage that is usually not feasibly available in materials science. The CE feature model utilizes a novel pre-attention mechanism that defines attention through explicit feature models with physical meaning, rather than relying on the optimization of weights in complex black-box machine learning algorithms. This strategy can decrease data requirements and increase the transparent interpretability of ML models.
Aiming to accelerate the extended studies of new alloying elements and structures, the ML methods were developed in this work based on the previous first-principles computational data41 to investigate the structural stability properties of the alloyed α-Nb5Si3 phases. First, we developed an improved CE feature model, adapted specifically for low-symmetry crystals, by examining the different definitions of environment atoms and weights in the compound feature construction. Then, different ML algorithms were examined to obtain the optimal models of α-Nb5Si3 phases. The optimized ML models of α-Nb5Si3 were then used without modification to predict the substitution energies in new structures of the high-temperature phase β-Nb5Si3, which were not included in the original training dataset, and first-principles calculations partially confirmed this prediction.
2 Models and methods
2.1 Training dataset
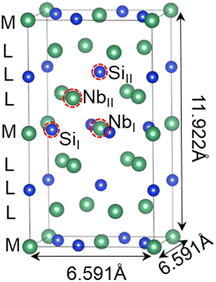
The training dataset is built based on first-principles calculations on the alloyed α-Nb5Si3.41Fig. 1 depicts the experimental structures of α-Nb5Si3 (body-centered tetragonal, BCT) crystals with the lattice parameters taken from the Materials Platform for Data Science (MPDS).42 The conventional cell of α-Nb5Si3 has two inequivalent Nb sites (dubbed NbI and NbII) and two inequivalent Si sites (dubbed SiI and SiII) for substitutions with alloying elements. In total, the 32-atom conventional cell consists of 20 Nb atoms and 12 Si atoms with four NbI, 16 NbII, 4 SiI, and 8 SiII atoms, respectively.Considering the double-site substitutions at the non-equivalent site pairs with 14 alloying elements, we collected 3528 double-site substitution energies (EDS) data in the α-Nb5Si3 phase from the literature.41 We also calculated the incremental single-site substitution energy (ESS) in the cases of double-site substitution and the local bond length change 〈Δd〉 as defined in Text S1 of ESI.† The term “substitution energy” denotes the energy change associated with the replacement of alloying constituents. It is characterized by an incremental formation energy, which measures the stabilities of the site and phase occupancy of alloying elements. The configurations of the studied substitution pair sites were depicted in Fig. S1† for α-Nb5Si3. The statistics of the numbers of corresponding substitution systems are listed in Table S1.† Fig. S2(a–c)† shows the statistical distributions of the target property data in α-Nb5Si3 that all satisfy the Gaussian distributions. Fig. S3† indicates the 14 substitution alloying elements in the periodic table.
2.2 Center-environment feature model
The CE features, which encode local structural and compositional information, have been proven effective in the study of alloys, oxides, and surface catalysis reactions.31–34 Considering the complex substitutional structure and lower symmetry of Nb5Si3 alloys, this study employs a CE feature model based on composition-structure characteristics. The CE feature model can be described as an (n + 1)-dimensional composite feature vector, as follows:| D = [D1, …, Di, …, Dn, f], (e.g., n = 20 in this work) | (1) |
| Di = [dC,i, dE,i], i = 1, 2,…, n | (2) |
| dC,i = pC, i | (3) |
 | (4) |
 | (5) |
It is well known that feature engineering determines the accuracy of ML modeling.31,43–46 The CE features were compound features consisting of an assembly of elementary property features encoded with local structural information specified by the center and environment atoms: (1) elementary property features are various elementary physicochemical properties readily available from the fundamental database,47e.g., atomic mass, radius, electronegativity, and the number of valence electrons of elements as well as density, melting temperature, and bulk modulus of pure substance among others. In total, 40 elementary properties were adopted in the feature construction, as listed in Table S2.† (2) Compound property features are constructed by a linear combination of the elementary properties of the center atom or the environment atoms with weights inversely proportional to the distance between the center atom and the environment atom (rjm, m = −1, −1⁄2). The exponent m in the decay function measures how quickly environmental effects diminish with distance. In this way, CE features can encode the elementary properties with local composition and structure information, providing a general digital representation of the material structure.
The design concepts of the CE model include the following:
(1) Localized focus: CE features explicitly define the interaction weights between the central atom and its neighboring environment through the Atomic Environment Type (AET) method. The predefined attention, achieved through a “core–shell” configuration, enables accurate local representation without requiring a large amount of data for global representation.
(2) Distance-weighted interactions: by employing decay functions based on interatomic distances, the CE method predefines the weight allocation process reflecting center-environment interactions. The reciprocal distance-dependent decay function can be attributed to the electrostatic interaction of Coulomb's law.
In contrast to the CE feature models, the Chemical Composition (CC) feature models focus solely on chemical composition without considering structural information. The construction of the CC feature is similar to that of CE except that the weight rjm(m = 0) is independent of distance (see more details in Text S2†).
2.3 Machine learning algorithms and evaluation
For this study, machine learning uses the Support Vector Regression (SVR) algorithm with an isotropic Radial Basis Function (RBF)48 kernel and the Random Forest algorithm (RF),49 both efficiently implemented via Python's Scikit-learn library. To enhance model performance, we meticulously fine-tuned the hyperparameters of both SVR and RF using a grid search approach. The optimized hyperparameters are listed in Table S3,† with corresponding discussions and analyses elaborated in Text S3.†First, we executed a randomized split of the entire original dataset into a training set and a test set with an 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ratio. The training set then underwent 20 iterations of 5-fold cross-validation, with each fold adhering to the 8
2 ratio. The training set then underwent 20 iterations of 5-fold cross-validation, with each fold adhering to the 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 partition ratio. The test set, comprising 20% of the original data, was independently retained to evaluate the performance of the trained ML models, ensuring it was not utilized during the training stage. To evaluate the performance of the regression models, the statistical metrics used were the correlation coefficient (R2), mean absolute error (MAE), and root mean square error (RMSE). These evaluation metrics are defined below:
2 partition ratio. The test set, comprising 20% of the original data, was independently retained to evaluate the performance of the trained ML models, ensuring it was not utilized during the training stage. To evaluate the performance of the regression models, the statistical metrics used were the correlation coefficient (R2), mean absolute error (MAE), and root mean square error (RMSE). These evaluation metrics are defined below:
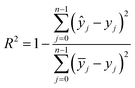 | (6) |
 | (7) |
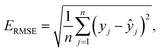 | (8) |
3 Results and discussion
3.1 Machine learning models
(I) Nearest neighbor (dubbed CENN) feature model. For crystalline materials with high symmetry, such as FCC or BCC structures, the selection of environment atoms based on the distances from the center atom to its surroundings is inherently straightforward. In this model, environmental atoms are defined as the nth-nearest neighbors to the central atom. The environmental atoms in the alloyed α-Nb5Si3 systems were identified up to the fifth nearest neighbors, with a distinction at the NbII center atom of α-Nb5Si3, where the inclusion extended to the 10th nearest neighbors.
(II) Atomic Environment Type (dubbed CEAET) feature model. For crystal structures with low symmetry, e.g., α-Nb5Si3, the distance-based cutoff definition is no longer appropriate to describe the environment. Therefore, this work employs a physics-based definition of the atomic environment to construct the CE features, utilizing the concept of AET proposed by Villars50 for the classification of inorganic compounds. The AET represents a completely enclosed physical shell surrounding the central atom based on the geometric topology rather than just distance cutoffs. To qualify as AET environmental atoms, two rules must be satisfied: the maximum distance gap (MDG) and the convex volume (CV). The MDG rule requires that AET atoms have the maximum gap in the nearest-neighbor histogram (NNH), which is a plot of the number (n) of certain interatomic distances (d) as a function of the normalized distances(d/dmin) between the central atom and surrounding atoms. The second CV rule mandates that AET atoms must enclose a convex polyhedral shape. Fig. 2 depicts the AET cluster models and their NNHs with the centers of non-equivalent sites in α-Nb5Si3. Fig. 2 shows the AET cluster models around the four non-equivalent sites of α-Nb5Si3: NbI (CN = 14, code:80.360.4), NbII (CN = 16, code: 125.046.0), SiI (CN = 9, code: 34.065.0), and SiII (CN = 10, code: 85.024.0) where CN represents coordination number. The AET code encodes the structure's topology by listing the counts of polygons (triangles, squares, pentagons, hexagons) at each vertex. For example, in Fig. 2(a), a CN of 14 is the sum of 8 and 6, indicating 8 vertices connected to 3 squares and 6 to 4 squares, with no triangles. This scheme effectively quantifies local polygonal arrangements and coordination environments, offering a detailed topological characterization. The local atomic structures of α-Nb5Si3 exhibit low symmetry, as indicated by the distorted polyhedron. For example, the AET cluster around the NbII site has up to the 9th nearest neighbor atoms with a maximum distance gap from the 10th nearest neighbor atoms by counting the distributions in the nearest-neighbor histogram (NNH) in Fig. 2(b). The number of AET atoms varies depending on the local symmetry, so it is hard to predefine the nth nearest neighbors without a careful check in advance. The inappropriate choice of the nth nearest neighbors as the environment atoms will lead to incomplete or redundant shell atoms and physically less meaningful features in the CE feature construction. The performance of ML models using CENN and CEAET features will be evaluated and compared later.
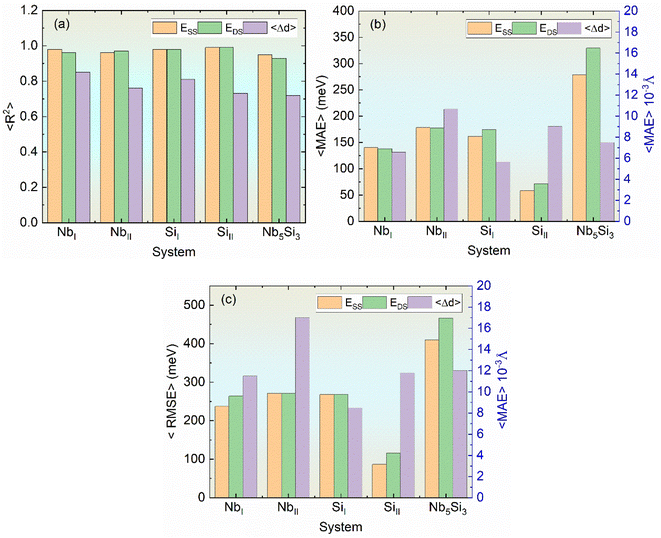
The SVR algorithm (Fig. 3) generally exhibited more accurate predictions by ∼100–200 meV per cell than the RF algorithm, using all studied features; therefore, the SVR results were primarily used for discussion. The CE feature models (Tables S4 and S5†) performed much better than the composition CC models (Table S6†), indicating that the inclusion of structural information into the feature construction via CE framework is critical to describing the complex crystal structures by ML methods. Furthermore, the CEAET models using the AET environment atoms had better prediction accuracy than the CENN models using the nearest-neighbor atoms, even though more atoms may be included in the latter cases (Fig. 3). This suggests that the physically closed shell is more appropriate to define ML features than the distance-based cutoff selection possibly with either insufficient or redundant environment atoms. Comparison among the CEAET feature models, the weight r−1j performs mostly better than r−1/2j (Fig. 3), indicating that the linear combination of elementary property features with the weight of reciprocal distance is a reasonable choice probably due to the scaling law of long-range electrostatic interactions in Coulomb's law. Based on the comparisons above, the CEAET-SVR models with weight wj = 1/r were mainly used to predict the target properties (ESS, EDS, and 〈Δd〉) of new datasets in α-Nb5Si3 hereafter. Although other algorithms, such as GBR, LGBM, and XGB, achieve high accuracy with limited samples (Table S11†), their predictions are still less precise than those of SVR. In cross-validation, SVR exhibits better generalization, likely due to the suitability of its kernel function for high-dimensional datasets with small sizes.
 | ||
| Fig. 3 MAE of prediction of α-Nb5Si3 by the (a) SVR and (b) RF methods using CENN and CEAET feature models with different weights rjm(m = −1, −1/2). | ||
Table 1 shows the prediction results of different ML models for the substitution energies at the four non-equivalent sites (NbI, NbII, SiI, and SiII) of α-Nb5Si3 in the independent test datasets. Comparing the ML results of four non-equivalent site substitutions, it is found that the graph-based deep learning model, 3D-ELAN, and the non-deep learning model, CEAET-SVR, achieved 〈R2〉 values both higher than 0.9. Specifically, the 〈MAE〉 values predicted by the 3D-ELAN model for the substitution energies of the four non-equivalent sites of α-Nb5Si3 are 248.80 meV, 307.60 meV, 419.20 meV, and 301.20 meV per supercell, respectively. The prediction had substantial errors using the other popular graph-based feature models, including GCN, GAT, and ALIGNN. In contrast, the optimal non-deep machine learning model, CEAET-SVR, has the best performance with 〈MAE〉 values of 137.95, 177.35, 174.86, and 71.39 meV per cell for the same substitution energies.
| Models | Performance metric | Non-equivalent sites | All sites | |||
|---|---|---|---|---|---|---|
| NbI | NbII | SiI | SiII | |||
| GCN32 | 〈R2〉 | 0.64 | 0.49 | 0.67 | 0.52 | — |
| 〈RMSE〉 (meV) | 943.60 | 999.01 | 956.80 | 973.30 | — | |
| 〈MAE〉 (meV) | 644.80 | 513.00 | 625.10 | 681.00 | — | |
| GAT33 | 〈R2〉 | 0.27 | 0.45 | 0.04 | 0.04 | — |
| 〈RMSE〉 (meV) | 1321.40 | 1031.70 | 1620.20 | 1377.20 | — | |
| 〈MAE〉 (meV) | 1059.70 | 727.01 | 1330.31 | 1108.82 | — | |
| ALIGNN34 | 〈R2〉 | −0.03 | 0.10 | 0.12 | 0.11 | — |
| 〈RMSE〉 (meV) | 1573.30 | 1317.90 | 1553.01 | 1334.10 | — | |
| 〈MAE〉 (meV) | 1275.50 | 1075.60 | 1264.32 | 1040.50 | — | |
| 3D-ELAN | 〈R2〉 | 0.96 | 0.93 | 0.94 | 0.90 | — |
| 〈RMSE〉 (meV) | 336.50 | 394.70 | 584.10 | 428.30 | — | |
| 〈MAE〉 (meV) | 248.80 | 307.60 | 419.20 | 301.20 | — | |
| CEAET-RF | 〈R2〉 | 0.85 | 0.82 | 0.95 | 0.92 | 0.81 |
| 〈RMSE〉 (meV) | 591.56 | 574.10 | 449.18 | 459.25 | 780.35 | |
| 〈MAE〉 (meV) | 391.11 | 454.11 | 347.70 | 359.95 | 578.16 | |
| CEAET-SVR | 〈R2〉 | 0.96 | 0.97 | 0.98 | 0.99 | 0.93 |
| 〈RMSE〉 (meV) | 263.89 | 271.01 | 268.80 | 115.34 | 465.83 | |
| 〈MAE〉 (meV) | 137.95 | 177.35 | 174.86 | 71.39 | 329.43 | |
Based on the prediction of the four non-equivalent sites, we further modeled and predicted the substitution energies for all sites in α-Nb5Si3. The results indicated that the non-deep machine learning model CEAET-SVR outperformed CEAET-RF, with predicted 〈MAE〉 values of 329.43 and 578.16 meV per cell, respectively. Notably, the errors for the four inequivalent sites are larger than any single substitution site because of the different center-environment configurations. The hundreds of meV of MAE are larger than conventional formation energies of bulk crystals because the prediction of diverse local substitutions in this work is much more challenging than traditional studies of global substitution in bulk crystals.
3.2 Construction of machine learning models for α-Nb5Si3
In the crystal structure of α-Nb5Si3, the four non-equivalent sites, NbI, NbII, SiI, and SiII, have different AET environment atoms, so we constructed the machine learning models for the substitution systems at the four non-equivalent sites, respectively.Fig. 4 shows the ESS, EDS, and 〈Δd〉 of the α-Nb5Si3 substitution systems at the four non-equivalent sites NbI, NbII, SiI, SiII, and all sites predicted by the optimal CEAET-SVR models compared with the DFT results.
The predictive performance across different sites in α-Nb5Si3 shows high accuracy, with R2 values generally above 0.9 and low 〈MAE〉 and 〈RMSE〉, indicating reliable energy predictions (Fig. 5). The models trained on a standard feature set, incorporating different AET environments, demonstrate the broad applicability of the CE approach. However, accuracy diminishes with increased system complexity. Overall, the substitution elements have minimal impact on local bond distances, with 〈Δd〉 remaining below 10−2 Å, suggesting that local structural variations are subtle across different substitution scenarios.
To understand the site dependence of substitution energies, we plot the heat maps of the double-site substitution energy EDS projection on the substitution pair sites. The distribution patterns of substitution energy predicted by the ML are very similar to those of DFT, confirming the reliability of the ML predictions. Such site-energy heat maps help identify stabilized element pairs quickly and efficiently. Fig. S8–S11† show the heat maps of the EDS projection on different site pairs containing the non-equivalent sites NbI, NbII, SiI, and SiII in α-Nb5Si3, respectively. The ML-predicted distribution patterns are consistent with those obtained from DFT. The B, Al, and Si elements preferred to occupy the Si sites, while Ti, Nb, Hf, and Zr tend to occupy Nb sites in α-Nb5Si3. Overall, the machine learning method was validated against DFT and can be used to identify new, favorable, and stabilized alloying elements in NbSi-based superalloys.
To enhance the interpretability and physical significance of the machine learning (ML) model, we employed SHAP (SHapley Additive exPlanations) methodology to analyze the contribution levels and influence trends of critical features in the optimal ML model predicting dual-site substitution energy (EDS) for Nb5Si3 superalloys. Fig. S12† presents the SHAP analysis of EDS in α-Nb5Si3. The feature importance ranking by SHAP values [Fig. S12(a)†] reveals the top five most influential features: PN_C, BM_C, TN_C, EC_E, and DV_E. As detailed in Table S2,† these features correspond to cohesive energy (EC), bulk modulus (BM), period number (PN), distance-valence moment (DV), and thermal neutron capture cross-section (TN), demonstrating their critical roles in the α-Nb5Si3 model. Notably, all significant features originate from the contributions of both central and environmental atoms. For fundamental properties of the same type, environmental atomic features depend simultaneously on elemental identity and spatial distance.
In contrast, central atomic features in the CE framework solely depend on the element type. This highlights the necessity of differentiating central and environmental atomic characteristics in feature construction for complex crystal structures. Furthermore, the α-Nb5Si3 system requires structure-dependent environmental atomic features beyond elemental chemical composition.
The SHAP value distributions [Fig. S12(b)†] qualitatively illustrate the qualitative trends of feature impacts on substitution energy. In the α-Nb5Si3 model, PN_C, BM_C, and TN_C exhibit positive correlations with substitution energy, whereas EC_E and DV_E show negative correlations. The inverse relationship between cohesive energy (EC) and substitution energy implies that higher cohesive energies correspond to more negative substitution energies. This correlation aligns with fundamental thermodynamic principles, as both increased cohesive energy and negative substitution energy values indicate enhanced system stability. The SHAP analysis in Fig. S12† reveals that the primary features influencing the substitution energy of α-Nb5Si3 with dual-site substitution (e.g., PN_C, BM_C) originate from the synergistic contributions of the central and surrounding atoms. Notably, environmental atom features depend on both element type and spatial distance, whereas central atom features are exclusively determined by element type. These findings underscore the critical importance of differentiating atomic roles when constructing features for complex crystal structures.
3.3 Applications of machine learning models
After the construction, comparison, and validation of the ML models discussed above, the optimal CEAET-SVR models with wj = 1/r were selected to study unknown systems, including new alloying elements and matrix alloys not included in the training datasets. The ML applicability would significantly extend the prediction capability and efficiency beyond expensive first-principles computations.Fig. S13† shows the performance metrics of EDS in the α-Nb5Si3 phase predicted by the CEAET-SVR models. The 〈R2〉 of Al, Co, Fe, Mo, Nb, Ti, V, and Y reached 0.86, 0.90, 0.92, 0.87, 0.91, 0.93, 0.86, and 0.86, respectively. The corresponding 〈MAE〉 were 555.94, 351.43, 301.23, 483.88, 460.88, 425.88, 518.86, and 648.72 meV per cell, respectively. The other elements had larger 〈MAE〉 with 〈R2〉 less than 0.85.
Fig. 6 summarizes the 〈MAE〉 of the substitution energies of α-Nb5Si3 in the Leave-p-out prediction of each of the 14 alloying elements using CEAET-SVR models. In the case of α-Nb5Si3 phase, the 〈MAE〉 of Fe elements were less than 300 meV per cell, and the 〈MAE〉 most elements were in 300∼600 meV per cell, e.g., Y, Ti, Zr, V, Nb, Mo, Al, and Co. While the 〈MAE〉 of B, Si, Hf, Cr, and Ni elements were greater than 600 meV per cell. It is crucial to consider the prediction errors associated with new elements when applying ML models. Specifically, larger prediction errors primarily involve the leading group of non-metals (B, Si) and elements with larger metallic radii, such as Hf, highlighting their distinct characteristics compared to transition metals. The magnitude of the 〈MAE〉 inversely correlates with the compatibility between substitution elements and host sites—smaller MAE values indicate reduced discrepancies in physicochemical properties between substituents and their host lattice positions. The divisions of three error bands are used to cover the entire range, which can serve as a quantitative metric of similarities among the various alloying effects.
The Nb–Si binary phase diagram shows that α-Nb5Si3 is the stable phase at ambient conditions while β-Nb5Si3 is more stable at the high-temperature.51 Prompting α-β phase transition at high-temperature operating conditions may improve the mechanical properties of Nb–Si alloys. Therefore, it is also interesting to find the alloying elements that can stabilize the β-Nb5Si3 phase. The conventional cell of β-Nb5Si3 crystal structure has the lattice constants of a = b= 10.06 Å, c = 5.07 Å (Fig. S14†). The β-Nb5Si3 exhibits the body-centered tetragonal structure with four non-equivalent sites: NbI (CN = 14, code: 125.026.0), NbII (CN = 15, code: 125.036.0), SiI (CN = 10, code: 24.085.0), and SiII (CN = 10, code: 34.065.016.0). Fig. 7 shows the NNH and AET cluster models of β-Nb5Si3 around the four non-equivalent sites. The local structures of β-Nb5Si3 are also complex, e.g., up to the 9th nearest-neighbor atoms are necessary to enclose the first physical shell around the NbII site. The AET type definition of the environment atoms is generally applicable to both α-Nb5Si3 and β-Nb5Si3 even though their crystal structures are different.
The optimal CEAET-SVR models were trained using all EDS of α-Nb5Si3 substituted with the 14 alloying elements: B, Al, Si, Ti, V, Cr, Fe, Co, Ni, Y, Zr, Nb, Mo, and Hf. Then, we applied these ML models directly to predict the EDS of 784 double-site substitution systems of β-Nb5Si3 doped with the same set of alloying elements. Fig. 8 shows the heat map of EDS projection on the four non-equivalent site pairs of β-Nb5Si3: XNbIYNbII, XNbIYSiI, XNbIIYSiI, and XNbIIYSiII where X, Y![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) B, Ni, Co, Fe, Si, V, Mo, Al, Ti, Nb, Hf, Zr and Y, sorted in the increasing order of metal radii.
B, Ni, Co, Fe, Si, V, Mo, Al, Ti, Nb, Hf, Zr and Y, sorted in the increasing order of metal radii.
The EDS of the XNbIYNbII@β-Nb5Si3 systems were all positive [Fig. 8(a)], indicating that the substitutions at the NbINbII site of β-Nb5Si3 were energetically not favorable. The relative preference of occupation in β-Nb5Si3 was similar to those of α-Nb5Si3: Ti, Hf, and Zr were more readily to occupy NbINbII sites than B, Si, Al, and Y. The alloying elements exhibit similar occupancy tendencies at the other three substitution sites of β-Nb5Si3, including all Nb–Si pairs: XNbIYSiII, XNbIIYSiI, and XNbIIYSiII [Fig. 8(b)–(d)]. Specifically, B, Si, and Al prefer to occupy SiI or SiII sites, while Ti, Hf, and Zr tend to occupy NbI or NbII sites. The occupancy tendency at the NbSi sites of β-Nb5Si3 is consistent with that of α-Nb5Si3. The substitution pairs that stabilized β-Nb5Si3 with negative substitution energies were HfNbIBSiII (−0.61 eV), TiNbIBSiII (−0.34 eV), and ZrNbIBSiII (−1.09 eV) at XNbIYSiII sites; ZrNbIIBSiI (−0.05 eV) and HfNbIIBSiI (−0.17 eV) at XNbIIYSiI sites; HfNbIIBSiII (−0.72 eV), HfNbIISiSiII (−0.67 eV), TiNbIIBSiII (−0.95 eV), TiNbIISiSiII (−0.78 eV), and ZrNbIIBSiII (−0.28 eV) at XNbIIYSiII sites. These results suggest that Ti, Zr, and Hf are stabilizing elements at the Nb sites of β-Nb5Si3 and may be better co-doped with B at the Si sites.
To validate the EDS of β-Nb5Si3 predicted by the ML models that were initially trained for α-Nb5Si3, we performed DFT calculations on the stabilized β-Nb5Si3 systems suggested by the ML models. The EDS of β-Nb5Si3 calculated by DFT were HfNbIBSiII (−0.19 eV), TiNbIBSiII (−0.49 eV), and ZrNbIBSiII (−0.55 eV) at XNbIYSiII sites; ZrNbIIBSiI (−0.03 eV) and HfNbIIBSiI (−0.09 eV) at XNbIIYSiI sites; TiNbIIBSiII (−0.44 eV), TiNbIISiSiII (−0.31 eV), HfNbIIBSiII (−0.28 eV), and HfNbIISiSiII (−0.48 eV), and ZrNbIIBSiII (−0.27 eV) at XNbIIYSiII sites. Fig. 9 shows the EDS of stable XNbYSi@β-Nb5Si3 predicted by DFT and ML. The comparison shows that the trends predicted by the ML models were qualitatively consistent with those of DFT. The MAE and RMSE of EDS of β-Nb5Si3 are 283.03 meV and 347.58 meV, respectively, comparable with those of α-Nb5Si3. Notably, the prediction results for the HfNbIBSiII, TiNbIIBSiII, TiNbIIBSiII, and ZrNbIBSiII systems exhibit significant discrepancies. The larger atomic radii of Hf and Zr atoms tend to favor occupying the NbII sites, whereas the smaller atomic radius of Ti favors occupancy of the NbI sites. Additionally, the smaller B atoms tend to occupy the densely packed SiI sites. These atomic site preferences in the Nb5Si3 phases are consistent with the reported first-principles calculations.41 The reliability of prediction is acceptable given that the trained ML models were directly applied across the different crystal structures without any modification of parameters.
4 Conclusions
To develop a general feature model for complex crystal structures in machine learning studies, we introduced a Center-Environment feature model with Atomic Environment Type (CEAET) to define the environment of atoms. The ML-CEAET models proved to be effective, efficient, and transferable in predicting the alloying effects on the structural stability of α/β-Nb5Si3 in NbSi-based superalloys. Comparisons between various CE construction methods revealed that: (1) the AET definition of environment atoms (CEAET) outperforms the nearest neighbor-based approach (CENN). (2) The reciprocal distance weighting function improved the performance of linear combinations of elementary features. (3) The SVR algorithm slightly outperformed RF in predicting substitution energies.The optimized CEAET-SVR models predicted the EDS of α-Nb5Si3 with an MAE of 329 meV. Direct predictions on untrained β-Nb5Si3 indicated that Ti, Zr, and Hf prefer to occupy Nb sites, while B and Al tend to occupy Si sites. These machine-learning predictions were further validated by first-principles calculations, demonstrating the reliable transferability of ML predictions using CE feature models.
This study demonstrated that non-deep machine learning models using CE feature representations based on a small computational dataset possess predictive capability for studying complex crystal structures with low symmetry and exhibit good transferability to new elements and structures. The achievement of CE feature models can be attributed to the predefined attention mechanism in feature engineering, leading to improved accuracy with reduced data requirements. Unlike traditional feature engineering, the CE feature employs a form of attention-driven information filtering through physical structure constraints rather than simple empirical feature concatenation. Compared with deep learning attention, in scenarios with limited data, physical priors serve as substitutes for data-driven weight learning, enhancing model reliability and interpretability. This CE-based ML approach provides an efficient computational tool for the compositional design of multi-component engineering alloys.
Data availability
Data for this paper are available at https://doi.org/10.1007/s11661-022-06868-y. The processing scripts are available at GitHub (https://github.com/Don-sugar/ML_script/tree/main).Author contributions
Yuchao Tang: methodology, software, investigation, data curation, visualization, writing – original draft; Bin Xiao: methodology, software; Shuizhou Chen: software, validation; Quan Qian: supervision, validation; Yi Liu: conceptualization, methodology, funding, resource, supervision, writing – review & editing.Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
This work was financially supported by the National Natural Science Foundation of China (No. 52373227, 52201016, and 91641128) and the National Key R&D Program of China (No. 2017YFB0701502, 2017YFB0702901, and 2023YFB4606200). This work was also supported by the Shanghai Technical Service Center for Advanced Ceramics Structure Design and Precision Manufacturing (No. 20DZ2294000), Key Program of Science and Technology of Yunnan Province (No. 202302AB080020), and Shanghai Technical Service Center of Science and Engineering Computing, Shanghai University. The authors acknowledge the Beijing Super Cloud Computing Center, the Hefei Advanced Computing Center, and Shanghai University for providing high-performance computing (HPC) resources.References
- J. H. Perepezko, The hotter the engine, the better, Science, 2009, 326(5956), 1068–1069, DOI:10.1126/science.1179327.
- T. M. Pollock, Alloy design for aircraft engines, Nat. Mater., 2016, 15(8), 809–815, DOI:10.1038/nmat4709.
- W. Liu, S. Huang and C. Ye, et al., Progress in Nb-Si ultra-high temperature structural materials: a review, J. Mater Sci. Technol., 2023, 149, 127–153, DOI:10.1016/j.jmst.2022.11.022.
- C. T. Sims, Niobium in superalloys: a perspective, High Temp. Technol., 1984, 2(4), 185–201, DOI:10.1080/02619180.1984.11753263.
- B. P. Bewlay, M. R. Jackson, J. C. Zhao, P. R. Subramanian, M. G. Mendiratta and J. J. Lewandowski, Ultrahigh-temperature Nb-Silicide-based composites, MRS Bull., 2003, 28(9), 646–653, DOI:10.1557/mrs2003.192.
- N. Vellios and P. Tsakiropoulos, The role of Fe and Ti additions in the microstructure of Nb–18Si–5Sn silicide-based alloys, Intermetallics, 2007, 15(12), 1529–1537, DOI:10.1016/j.intermet.2007.06.001.
- S. Zhang, X. Shi and J. Sha, Microstructural evolution and mechanical properties of as-cast and directionally-solidified Nb–15Si–22Ti–2Al–2Hf–2V–(2, 14) Cr alloys at room and high temperatures, Intermetallics, 2015, 56, 15–23, DOI:10.1016/j.intermet.2014.07.012.
- Y. Qiao, X. Guo and Y. Zeng, Study of the effects of Zr addition on the microstructure and properties of Nb–Ti–Si based ultrahigh temperature alloys, Intermetallics, 2017, 88, 19–27, DOI:10.1016/j.intermet.2017.04.008.
- S. Zhang and X. Guo, Alloying effects on the microstructure and properties of Nb–Si based ultrahigh temperature alloys, Intermetallics, 2016, 70, 33–44, DOI:10.1016/j.intermet.2015.12.002.
- J. Shu, Z. Dong and C. Zheng, et al., High-throughput experiment-assisted study of the alloying effects on oxidation of Nb-based alloys, Corros. Sci., 2022, 204, 110383, DOI:10.1016/j.corsci.2022.110383.
- T. Geng, C. Li, J. Bao, X. Zhao, Z. Du and C. Guo, Thermodynamic assessment of the Nb–Si–Ti system, Intermetallics, 2009, 17(5), 343–357, DOI:10.1016/j.intermet.2008.11.011.
- J. C. Zhao, M. R. Jackson and L. A. Peluso, Determination of the Nb–Cr–Si phase diagram using diffusion multiples, Acta Mater., 2003, 51(20), 6395–6405, DOI:10.1016/j.actamat.2003.08.007.
- G. Shao, Thermodynamic assessment of the Nb–Si–Al system, Intermetallics, 2004, 12(6), 655–664, DOI:10.1016/j.intermet.2004.03.011.
- Y. Yang, Y. A. Chang, J. C. Zhao and B. P. Bewlay, Thermodynamic modeling of the Nb–Hf–Si ternary system, Intermetallics, 2003, 11(5), 407–415, DOI:10.1016/S0966-9795(03)00021-9.
- Y. Li, C. Li, Z. Du and C. Guo, Thermodynamic optimization of the Nb–Si–W ternary system, Calphad, 2013, 43, 112–123, DOI:10.1016/j.calphad.2013.04.004.
- W. Wei, Q. Wang, R. R. Chen, C. W. Zheng and Y. Q. Su, Enhancement of comprehensive properties of Nb–Si based in-situ composites by Ho rare earth doping, Rare Met., 2024, 43(9), 4508–4520, DOI:10.1007/s12598-024-02765-y.
- Y. L. Huang, L. N. Jia, B. Kong, Y. L. Guo and N. Wang, Microstructure and room temperature fracture toughness of Nb–Si-based alloys with Sr addition, Rare Met., 2024, 43(8), 3904–3912, DOI:10.1007/s12598-018-1141-8.
- H. Guo and X. Guo, Microstructure evolution and room temperature fracture toughness of an integrally directionally solidified Nb–Ti–Si based ultrahigh temperature alloy, Scr. Mater., 2011, 64(7), 637–640, DOI:10.1016/j.scriptamat.2010.12.008.
- Y. Chen, J. X. Shang and Y. Zhang, Bonding characteristics and site occupancies of alloying elements in different Nb5Si3 phases from first principles, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76(18), 184204, DOI:10.1103/PhysRevB.76.184204.
- X. Xu, W. Zeng and S. H. Zhu, et al., Influences of vacancy concentration and Al substitution on structural, electronic, and elastic properties of Nb5Si3 from first-principles calculations, Phys. Status Solidi B, 2021, 258(5), 2000591, DOI:10.1002/pssb.202000591.
- B. Guo, J. Xu, X. L. Lu, S. Jiang, P. Munroe and Z. H. Xie, Electronic structure, mechanical and physical properties of Ag alloyed α-Nb5Si3: First-principles calculations, Phys. B, 2019, 564, 80–90, DOI:10.1016/j.physb.2019.04.013.
- I. Papadimitriou, C. Utton and P. Tsakiropoulos, The impact of Ti and temperature on the stability of Nb5Si3 phases: a first-principles study, Sci. Technol. Adv. Mater., 2017, 18(1), 467–479, DOI:10.1080/14686996.2017.1341802.
- W. Xu, J. Han and C. Wang, et al., Temperature-dependent mechanical properties of alpha-/beta-Nb5Si3 phases from first-principles calculations, Intermetallics, 2014, 46, 72–79, DOI:10.1016/j.intermet.2013.10.027.
- S. Shi, L. Zhu, L. Jia, H. Zhang and Z. Sun, Ab-initio study of alloying effects on structure stability and mechanical properties of α-Nb5Si3, Comput. Mater. Sci., 2015, 108, 121–127, DOI:10.1016/j.commatsci.2015.06.019.
- Y. Kang, Y. Han, S. Qu and J. Song, Effects of alloying elements Ti, Cr, Al, and Hf on β-Nb5Si3 from first-principles calculations, Chin. J. Aeronaut., 2009, 22(2), 206–210, DOI:10.1016/S1000-9361(08)60088-6.
- G. L. W. Hart, T. Mueller, C. Toher and S. Curtarolo, Machine learning for alloys, Nat. Rev. Mater., 2021, 6(8), 730–755, DOI:10.1038/s41578-021-00340-w.
- Y. Liu, J. Wang, B. Xiao and J. tao Shu, Accelerated development of hard high-entropy alloys with data-driven high-throughput experiments, J. Mater. Inform., 2022, 2, 3, DOI:10.20517/jmi.2022.03.
- G. Liu, L. Jia, B. Kong, K. Guan and H. Zhang, Artificial neural network application to study quantitative relationship between silicide and fracture toughness of Nb-Si alloys, Mater. Des., 2017, 129, 210–218, DOI:10.1016/j.matdes.2017.05.027.
- S. kun Xi, Yu J. xin and B. L. ke, et al., Machine learning-accelerated first-principles predictions of the stability and mechanical properties of L12-strengthened cobalt-based superalloys, J. Mater. Inform., 2022, 2(3), 15 CrossRef CAS.
- M. D. Witman and P. Schindler, MatFold: systematic insights into materials discovery models' performance through standardized cross-validation protocols, Digit Discovery, 2025 10.1039/D4DD00250D.
- Y. Li, B. Xiao and Y. Tang, et al., Center-environment feature model for machine learning study of spinel oxides based on first-principles computations, J. Phys. Chem. C, 2020, 124(52), 28458–28468, DOI:10.1021/acs.jpcc.0c06958.
- X. Wang, B. Xiao, Y. Li, Y. Tang and Y. Liu, First-principles based machine learning study of oxygen evolution reactions of perovskite oxides using a surface center-environment feature model, Appl. Surf. Sci., 2020, 531, 147323, DOI:10.1016/j.apsusc.2020.147323.
- J. Guo, B. Xiao and Y. Li, et al., Machine learning aided first-principles studies of structure stability of Co3(Al, X) doped with transition metal elements, Comput. Mater. Sci., 2021, 200, 110787, DOI:10.1016/j.commatsci.2021.110787.
- R. Chen, F. Liu and Y. Tang, et al., Combined first-principles and machine learning study of the initial growth of carbon nanomaterials on metal surfaces, Appl. Surf. Sci., 2022, 586, 152762, DOI:10.1016/j.apsusc.2022.152762.
- Y. Li, R. Zhu, Y. Wang, L. Feng and Y. Liu, Center-environment deep transfer machine learning across crystal structures: from spinel oxides to perovskite oxides, npj Comput. Mater., 2023, 9(1), 109, DOI:10.1038/s41524-023-01068-7.
- Y. Li, X. Zhang, T. Li, Y. Chen, Y. Liu and L. Feng, Accelerating materials discovery for electrocatalytic water oxidation via center-environment deep learning in spinel oxides, J. Mater. Chem. A, 2024, 12(30), 19362–19377, 10.1039/D4TA02771J.
- S. Y. Louis, Y. Zhao and A. Nasiri, et al., Graph convolutional neural networks with global attention for improved materials property prediction, Phys. Chem. Chem. Phys., 2020, 22(32), 18141–18148, 10.1039/D0CP01474E.
- J. Schmidt, L. Pettersson, C. Verdozzi, S. Botti and M. A. L. Marques, Crystal graph attention networks for the prediction of stable materials, Sci. Adv., 2021, 7(49), 7948, DOI:10.1126/sciadv.abi7948.
- K. Choudhary and B. DeCost, Atomistic Line Graph Neural Network for improved materials property predictions, npj Comput. Mater., 2021, 7(1), 185, DOI:10.1038/s41524-021-00650-1.
- A. Vasylenko, D. Antypov and S. Schewe, et al., Digital features of chemical elements extracted from local geometries in crystal structures, Digital Discovery, 2025, 4(2), 477–485, 10.1039/D4DD00346B.
- Y. Tang, B. Xiao and J. Chen, et al., Multi-component alloying effects on the stability and mechanical properties of Nb and Nb–Si alloys: a first-principles study, Metall. Mater. Trans. A, 2023, 54(2), 450–472, DOI:10.1007/s11661-022-06868-y.
- P. Villars, K. Cenzual, R. Gladyshevskii and S. Iwata, Pauling File: Toward a Holistic View, Mater. Inf., 2019, 11, 55–106, DOI:10.1002/9783527802265.ch3.
- K. T. Schütt, H. Glawe, F. Brockherde, A. Sanna, K. R. Müller and E. K. U. Gross, How to represent crystal structures for machine learning: Towards fast prediction of electronic properties, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89(20), 205118, DOI:10.1103/PhysRevB.89.205118.
- L. Ward, R. Liu and A. Krishna, et al., Including crystal structure attributes in machine learning models of formation energies via Voronoi tessellations, Phys. Rev. B: Condens. Matter Mater. Phys., 2017, 96(2), 024104, DOI:10.1103/PhysRevB.96.024104.
- R. Ouyang, S. Curtarolo, E. Ahmetcik, M. Scheffler and L. M. Ghiringhelli, SISSO: a compressed-sensing method for identifying the best low-dimensional descriptor in an immensity of offered candidates, Phys. Rev. Mater., 2018, 2(8), 083802, DOI:10.1103/PhysRevMaterials.2.083802.
- B. Shi, Y. Zhou and D. Fang, et al., Estimating the performance of a material in its service space via Bayesian active learning: a case study of the damping capacity of Mg alloys, J. Mater. Inform., 2022, 2(2), 8, DOI:10.20517/jmi.2022.06.
- S. Andrew, Database on properties of chemical elements, 2021, http://phases.imet-db.ru/elements/mendel.aspx?main=1 Search PubMed.
- H. Ducker, C. Burges, L. Kaufman, A. Smola and V. Vapnik, Support vector regression machines, Adv. Neural Inf. Process., 1997, 28(7), 779–784 Search PubMed.
- B. Leo, Random forests, Mach. Learn., 2001, 45(1), 5–32, DOI:10.1023/A:1010933404324.
- J. Daams, J. Vanvucht and P. Villars, Atomic-environment classification of the cubic “Intermetallic” structure types, J. Alloys Compd., 1992, 182(1), 1–33, DOI:10.1016/0925-8388(92)90570-Y.
- in β-Nb5Si3 Crystal Structure: Datasheet from “PAULING FILE Multinaries Edition”, ed. Villars P. and Cenzual K.Springer Materials. Springer-Verlag Berlin Heidelberg & Material Phases Data System (MPDS), Switzerland & National Institute for Materials Science (NIMS), Japan, 2012, https://materials.springer.com/isp/crystallographic/docs/sd_0533318 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5dd00079c |
| This journal is © The Royal Society of Chemistry 2025 |