Heterogeneous microstructures and dynamics of the Li-ion electrolyte with a fluorinated additive solvent from molecular dynamics simulations†
Received
21st December 2024
, Accepted 13th June 2025
First published on 26th June 2025
Abstract
Electrolytes diluted with fluorinated solvents exhibit potential qualities for improved Li-ion battery performance. Tuning the characteristics and creating novel electrolytes for rechargeable batteries requires investigating the structure and Li-ion transport. In this study, we investigated the detailed structure and dynamics of an electrolyte containing lithium hexafluorophosphate (LiPF6) in nonaqueous 3,3,3-trifluoropropylene carbonate (TFPC) in a wide range of temperatures (283.15–333.15 K) using classical molecular dynamics simulations. The analyzed results provide insights into the different microstructures, such as contact and solvent-separated ion pairs, and the effect of temperature on their existence in the electrolyte. The potential of mean force calculation shows the relative stability of microstructures consisting of ions and solvents. The diffusivity and conductivity were calculated to assess the ionic transport. The electrolyte's temperature-dependent transport properties and ion-cage dynamics have significance in understanding the atomistic details of a lithium-ion battery electrolyte. Overall, the dynamics of the electrolytes are facilitated by the balanced ion–ion and ion–solvent correlations with a vital contribution from electrostatic interactions. Our results indicate that the formation of microstructures in the fluorinated carbonate-based electrolyte shows appropriate dynamics to achieve the suitable diffusivity of the Li-ion battery electrolyte.
1. Introduction
High energy density and power-based lithium-ion batteries (LIBs) are critical given the rising need for various battery-operated devices.1–5 By raising the working voltage of LIBs, the energy density of those devices can be improved. Although high operational voltage anode and cathode materials have been available for a while, it is still challenging to discover an electrolyte that can operate at high voltages.6–9 Commercially available carbonate-based electrolytes are widely used in nonaqueous lithium-ion batteries.10–14 The high affinity of solvents with Li-ions and the flammability of carbonate electrolytes limit the operational ranges of temperature and voltage.15 Moreover, traditional carbonate-based electrolytes fail beyond 4.4 V due to parasitic reactions occurring at high voltages and oxidative decomposition of the cathode surface.16 Hence, developing a stable electrolyte with an appropriate ionic conductivity and stability at high voltage is in great demand.
The additive solvents should have a very high dielectric constant to dissociate the lithium ions from their respective anions to achieve a higher ionic conductance. However, these requirements lead to many detrimental physical and chemical characteristics, which significantly restrict the performance of batteries.17,18 Firstly, a higher dielectric constant means a stronger affinity of the solvent molecules with the Li-ions. Hence, suppressing the desolvation process on the electrode's surface limits the kinetics of lithium-ion intercalation. Secondly, the stronger binding of the lithium ions with the solvent decreases the transference. Thirdly, the higher dielectric constant enhances dipole–dipole interaction, increasing the solvent's freezing point temperature and reducing the electrolyte's low-temperature functioning. These features of the non-aqueous electrolytes create long-term challenges. Thus, this limits the voltage and temperature window as well as safety.
Fluorinated and nonflammable electrolytes have relatively higher ionic conductance, and the electrochemical stability window is wide.15,19–22 However, because of the increased interactions of the lithium ions with the fluorinated solvents, these fluorinated electrolytes fail to work below −30 °C temperature.15 To achieve a wider operating temperature range, they reduce the interactions between the lithium ions and the solvents by dissolving the fluorinated electrolyte into the highly nonpolar fluorinated solvent, forming a super electrolyte. As the affinity of the nonpolar solvents with the lithium ions was much weaker than the fluorinated carbonates with the lithium ions, the fluorinated electrolyte solvation structure was maintained in the electrolyte.15 Hence, the fluorinated electrolyte enhances its physical properties by keeping the electrochemical features. All fluorinated solvents have a higher chemical and electrochemical stability, improving the electrochemical potential window and safety.15 The change in the solvation structure of the super electrolyte is also expected to enhance the electrochemical process, charge, and mass transfer. The temperature has dramatic effects on the ionic transport properties of battery electrolytes. The electrolytes should show appropriate conductance at low temperatures to achieve the acceptable performance of a battery. The affinity between the solvent and the Li-ions was tuned by dissolving the fluorinated electrolyte into a highly fluorinated nonpolar solvent.15 Also, adding to the nonflammability characteristic, their electrolyte enabled higher electrochemical stability in the range of 0.0–5.6 V and a higher ionic conductivity in the temperature range of −125 to +70 °C.
The fluorinated electrolyte dramatically improves the safety of the battery due to its non-flammable nature.15 This design, therefore, represents a promising path for developing safe lithium batteries with a broad functional temperature range. Molecular engineering of the structure of electrolytes has successfully led to the application of 3,3,3-trifluoropropylene carbonate (TFPC), a fluorinated derivative of a traditionally used electrolyte, i.e., propylene carbonate (PC), in the next generation high-energy high-voltage lithium-ion battery.16 The Li+ solvated species intercalates in the graphene layer in propylene carbonate electrolytes, exfoliating the graphitic anode. In contrast, a TFPC-based electrolyte at lower potentials is highly compatible with the graphitic anode.16 Also, it shows excellent oxidation stability on the surface of the charged cathode electrode due to the –CF3 group present in the TFPC solvent-based electrolyte. Our work uncovers the various dynamics present in the electrolyte, which may help reach and discover a modern electrolyte required for modern energy storage devices. The electrolyte, lithium hexafluorophosphate electrolyte in TFPC (LiPF6/TFPC), was studied using molecular dynamics simulations at different temperatures. The temperatures were directly taken from the experiment for better comparison.16 Our main objective is to provide insight into the microstructures present in bulk electrolytes. We understand the dynamics of electrolytes by calculating the MSD, diffusivity, self-part of the van Hove function, non-Gaussian parameter, ionic conductivity, and ion-cage lifetime.
2. Computational method
The classical molecular dynamics simulations were performed using GROMACS 5.0.4.23,24 All-atom optimized potential for liquid simulation (OPLS-AA) force field25 parameters were used to define the bonded and nonbonded parameters. Eqn (1)–(7) depict the bonded and non-bonded interactions of the ions and molecules. The total energy of the system is the sum of bonded and non-bonded energy. The bonded energies are the sum of individual bond stretch, angle bend and torsion. In eqn (4) and (5), Kr and Kθ are force constants of bond and angle, respectively. V and fi in eqn (6) represent the Fourier coefficient and phase angle, respectively. The 1,4 non-bonded interactions are presented in eqn (7). ε and σ are the well depth and Lennard–Jones radii, respectively.| | |
Etotal = Ebonded + Enonbonded
| (1) |
| | |
Ebonded = Ebond + Eangles + Etorsion
| (2) |
| | |
Enonbonded = ECoulomb + ELJ
| (3) |
| |
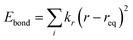 | (4) |
| |
 | (5) |
| |
 | (6) |
| |
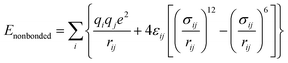 | (7) |
Individual ions were optimized in Gaussian 0926 software using the B3LYP27,28 functional with a 6-311+G(2d,p) basis set. The atomic charges were assigned to atoms of individual ions/molecules using the Antechamber package.29 Previous studies have mentioned that using a charge scaling factor could improve the system's dynamics.30–35 Therefore, we have used 0.8 e charge scaling for this work. The partial charges of Li+ and PF6− were scaled to 0.8 e to approximate the influence of charge transfer and polarizability in the bulk phase. Two hundred ion pairs of cation (Li+), and anion (PF6−) with nineteen hundred ninety-one TFPC molecules were packed in a cubic box using Packmol software.36 The chemical entities used in this study are presented in Fig. 1. The ESI† Tables S1–S3 present the non-bonded parameters used in this study. Firstly, energy minimization was done using the steepest-descent37 method. Furthermore, a 10 ns simulation within an NVT ensemble was performed to mix the solvent and ions at a 200 K higher temperature than the six targeted temperatures. After that, annealing was performed to cool down the system stepwise. The temperature was decreased by 20 K in each step, and cooling was done in 10 steps. The annealing rate is 20 K ns−1. All six systems were equilibrated to 283.15, 293.15, 303.15, 313.15, 323.15, and 333.15 K. Then, the simulations within the NPT ensemble were performed for 40 ns to equilibrate the volume of the simulation box. The leapfrog algorithm was used to integrate Newton's equation of motion with a time step of 2 fs. The electrostatic interactions were dealt with using the particle–mesh Ewald (PME)38 method. We used a short-range cut-off of 1.3 nm for all the simulations. The pressure and temperature were controlled during simulation using a Berendsen barostat39 and a V-rescale thermostat,40 respectively. The equilibrated average volume of 40 ns was used to calculate the density, and the corresponding box length was used for subsequent simulations. Furthermore, the system was equilibrated for 50 ns within the NVT ensemble. Finally, 200 ns NVE simulations were performed to calculate various properties related to the structure and dynamics of the electrolytes.
 |
| | Fig. 1 Chemical entities, (a) lithium cation, (b) hexafluorophosphate anion, and (c) 3,3,3-trifluoropropylene carbonate (TFPC), used for molecular dynamics simulations. | |
For the calculation of potential mean force (PMF) between the center of mass of the cation and anion, we performed constrained molecular dynamics simulations for three temperatures: 283.15, 303.15, and 323.15 K. We simulated a reduced system of 30 ion pairs and 299 TFPC and randomly chose two pull groups (one cation and one anion) and varied the interionic distance between them from 0.2 to 1.5 nm. A harmonic force constant of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 kJ mol−1 nm−2 was used. Multiple windows were used to separate the pull groups by 0.025 nm. Each window was energy minimized and equilibrated for 50 ns each within the NVT and NPT ensembles. The weighted histogram analysis method (WHAM), which uses the bootstrap technique for statistical error estimation, was used to calculate PMF from the constrained MD simulations.41 For the calculation of ionic conductivity, small trajectories of 1 ns were generated for each temperature by integrating equations of motion at 1 fs and saving the trajectory at every step.
000 kJ mol−1 nm−2 was used. Multiple windows were used to separate the pull groups by 0.025 nm. Each window was energy minimized and equilibrated for 50 ns each within the NVT and NPT ensembles. The weighted histogram analysis method (WHAM), which uses the bootstrap technique for statistical error estimation, was used to calculate PMF from the constrained MD simulations.41 For the calculation of ionic conductivity, small trajectories of 1 ns were generated for each temperature by integrating equations of motion at 1 fs and saving the trajectory at every step.
3. Results and discussion
3.1. Force field validation and structural analysis
Initially, we performed NPT simulations for 40 ns to obtain the density from the equilibrated volume. We calculated the density of the LiPF6/TFPC electrolyte at six different temperatures and the density of pure TFPC solvent at 298.15 K to validate the force field parameters. Densities decrease with an increase in simulation temperature. The decrease in density is due to the inefficient packing with increasing temperature. The densities of the electrolyte at different temperatures are presented in Table 1. The calculated density of TFPC solvent is 1484.94 ± 0.17 kg m−3, which is in good agreement with the experimental density of 1554 kg m−3 with 4.45% deviation.42
Table 1 The calculated simulation box length, corresponding density and concentration of the electrolyte, LiPF6 in TFPC, at different temperatures
| Temperature [K] |
Box length [nm] |
Calc. density [kg m−3] |
Calc. concentration [M] |
| 283.15 |
7.12 |
1570 |
0.922 |
| 293.15 |
7.14 |
1560 |
0.912 |
| 303.15 |
7.16 |
1540 |
0.904 |
| 313.15 |
7.19 |
1530 |
0.893 |
| 323.15 |
7.21 |
1510 |
0.886 |
| 333.15 |
7.23 |
1500 |
0.878 |
The structural properties were analyzed by studying the radial distribution function (RDF) and spatial distribution function (SDF) using the NVE simulation trajectory. The electrolyte structure was investigated by calculating the center of the mass (COM) RDF and coordination number, which are shown in Fig. 2 and 3. Eqn (8) represents the RDF, where r is the distance from the reference particle. (r) and bulk are the local density and bulk density of the observed particle, respectively. Integrating the COM RDF, we obtained the coordination number (eqn (9)).
| |
 | (8) |
| |
 | (9) |
 |
| | Fig. 2 The centre of mass radial distribution functions of (a) Li+–PF6−, (b) Li+–TFPC, and (c) PF6−–TFPC pairs, and the dashed line shows the number integrals of the same at six different temperatures. | |
 |
| | Fig. 3 Co-ordination number of (a) Li+–COM(PF6−) and (b) Li+–COM(TFPC). | |
The COM RDF of the Li+–PF6−, Li+–TFPC, and PF6−–TFPC pairs shows the first minima at 0.47, 0.8, and 0.75 nm, respectively (Fig. 2). A sharp and intense peak was observed for Li+–TFPC at 0.51 nm, indicating their utmost interactions. With the increase in temperature, the peak height of the Li+–TFPC COM RDF decreases (Fig. S1(b), ESI†), showing the change in the solvation structure of Li+–TFPC at higher temperatures. The first peak positions of Li+–PF6− and Li+–TFPC are different. The Li+–PF6−‘s first peak is observed at 0.36 nm, while Li+–TFPC's first peak is observed at 0.51 nm, indicating that PF6− ions appear closer to Li+ than TFPC's. The first peak height of Li+–PF6− RDF increases with an increase in temperature; however, the 2nd peak height decreases – this indicates that anions in the second solvation shell come into the first solvation shell with an increase in temperature. At higher temperatures (303–333 K), a peak between 0.2–0.4 nm is observed for Li+–PF6− as more anions stay in the first solvation shell. To understand the anion solvent interaction, we are looking into the PF6−–TFPC RDF (Fig. 2(c)). Sharp peaks were observed for PF6−–TFPC for different temperatures; however, the peak heights are less compared to Li+–TFPC, indicating less PF6−–TFPC interaction than Li+–TFPC.
In the case of the Li+–PF6− RDF, the first peak (g(r) > 1) is observed at 0.36 nm at higher temperatures. The g(r) being less than one at a lower temperature indicates the very low probability of finding PF6− at 0.36 nm. The first peak at 0.36 nm is due to the formation of a contact ion pair (CIP).43,44 Another peak is observed at 0.95 nm for all the temperatures, indicating the formation of solvent-separated ion pairs (SSIPs).45,46 The ion cluster analysis section presents the details of SSIP formation and other configurations.
Furthermore, to support the outcomes of RDF analysis, we calculated the coordination number (CN) of the anion and solvent around the cation in its 1st solvation shell. The cutoff for solvation was taken from the 1st minimum of RDF. Eqn (9) represents the CN. Fig. 3 shows the CN of the anion and solvent around the cation at different temperatures.
With the increase in temperature, the anion coordination number increases. But, the opposite was observed in the case of Li+–TFPC. TFPC CN decreases with temperature. As the temperature increases, the Li+–TFPC solvation environment is disturbed, and anions come closer to the cation solvation environment. Anion CN is less compared to TFPC CN with a cation. Higher coordination is due to higher interaction between the electron-rich oxygen atom of the TFPC solvent and the electron-deficient Li-ion. The coordination number of Li+–PF6− is much less (<1) at all temperatures. The previous studies showed the lower CN (<1) for Li+–PF6− in the propylene carbonate (PC)-based electrolytes at 1 M concentration.47–50 The TFPC solvates the cation, and the TFPC–Li+ interaction hinders the Li+–PF6− interaction.
To analyze the correlation in three dimensions, the spatial distribution functions (SDFs) of Li+ around TFPC were calculated and are shown in Fig. 4. The distribution of Li+ is mainly present around the oxygen atoms, as the oxygen atom tends to attract the positively charged ion. Also, the distribution became less dense as particles gain energy with increasing temperature.
 |
| | Fig. 4 A particular configuration of Li-ion interactions with TFPC is shown in the upper panel. The spatial distribution functions of Li+ around TFPC at various temperatures are shown in the lower panel. The isosurface density value is 1.5 pm−3. | |
3.2. Ion cluster analysis
Apart from the Li+–TFPC interaction, the Li+–PF6− RDF has two peaks, the first at <0.47 nm and a second peak between 0.47–1.17 nm. The first peak is due to the direct contact of PF6− with Li+, which is also known as contact ion pair (CIP) formation. The second peak is due to the interaction of PF6− with the solvated Li+ (SOLI). The interaction of solvated Li+ with PF6− forms a solvent-separated ion pair (SSIP). The cation will form CIP if the anion is within 0.47 nm of the cation. For SSIP formation, the anion will be separated from Li+ by solvent and stays between 0.8 and 1.5 nm from the cation. When the cation is only in contact with solvents within 0.8 nm, SOLI will be formed. The examples of CIP, SOLI, and SSIP extracted from the trajectory are presented in Fig. 5. Furthermore, we have calculated the percentage of Li+ forming different configurations in the electrolyte, as presented in Fig. 5(a). At 283.15 K, 6.59% of Li+ is part of CIP, and 93.17% of Li+ forms SSIP. With the increase in temperature, the percentage of Li+ forming of CIP increases to 14.36%, and SSIP decreases to 85.35% at 333.15 K. The rise in CIP percentage at higher temperatures indicates that anions are coming closer to the cation by disturbing the solvation environment of the cation at higher temperatures. Apart from SSIP and CIP, solvated Li+ (SOLI) is also present, less than 0.3% at all temperatures.
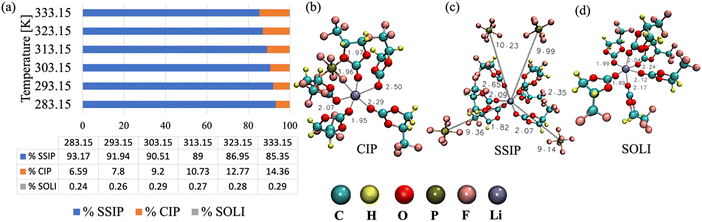 |
| | Fig. 5 (a) Percentage of Li+ forming different microstructures present in the bulk electrolyte at various temperatures, (b) example of contact ion pair (CIP), (c) solvent separated ion pair (SSIP), and (d) example of solvated Li+ (SOLI). | |
3.3. Thermodynamics of the microstructures
The ion dynamics in electrolytes depend on the formation and the thermodynamic stability of microstructures such as CIP and SSIP. The thermodynamic stability can be accessed through PMF (W(r)), as shown in eqn (10), which is calculated by integrating the mean force between the pull groups.| |
 | (10) |
| |
 | (11) |
| | |
ΔH(r) = W(r,t) + TΔS(r)
| (12) |
Here, ΔF is the mean force between the cation and anion pairs, 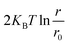 is added to consider the rotational motion of solute particles. ΔS(r), and ΔH(r) are the entropic and enthalpic contributions to the PMF. W(r,T ± ΔT) is the PMF at ± 20 K from the reference temperature of 303.15 K. The histogram shows the optimum overlap of adjacent windows, as presented in Fig. S1 of the ESI.† Fig. 6(a) shows the PMF between Li+–PF6− at three temperatures. The first minimum is observed at 0.36 nm due to CIP formation. The first minimum is followed by a transition state, and the second minimum is formed at 0.95 nm, which is due to the formation of SSIP. The energy levels of the second minimum are lower compared to the first minimum, which implies that the SSIP is more stable than the CIP. At higher temperatures, CIP shows lower energy, but a reverse scenario is observed at SSIP. To understand the thermodynamic contribution to the formation of CIP and SSIP, we calculated the ΔH(r), −TΔS(r) for each interionic distance. The finite temperature difference method was used to calculate the entropy contribution at the interionic distance presented in eqn (11),51–53 where ΔS(r) is the entropy contribution at interionic distance, W(r,t) is the PMF at temperature T, and ΔT is the temperature difference. Furthermore, eqn (12) was used to calculate the enthalpy contribution (ΔH(r)). Fig. 6(b) shows the thermodynamics of the association and solvation of the Li+–PF6− ion pair. At CIP (0.36 nm), it is stabilized by the enthalpy and destabilized by entropy. However, SSIP (0.95 nm) is stabilized by entropy.
is added to consider the rotational motion of solute particles. ΔS(r), and ΔH(r) are the entropic and enthalpic contributions to the PMF. W(r,T ± ΔT) is the PMF at ± 20 K from the reference temperature of 303.15 K. The histogram shows the optimum overlap of adjacent windows, as presented in Fig. S1 of the ESI.† Fig. 6(a) shows the PMF between Li+–PF6− at three temperatures. The first minimum is observed at 0.36 nm due to CIP formation. The first minimum is followed by a transition state, and the second minimum is formed at 0.95 nm, which is due to the formation of SSIP. The energy levels of the second minimum are lower compared to the first minimum, which implies that the SSIP is more stable than the CIP. At higher temperatures, CIP shows lower energy, but a reverse scenario is observed at SSIP. To understand the thermodynamic contribution to the formation of CIP and SSIP, we calculated the ΔH(r), −TΔS(r) for each interionic distance. The finite temperature difference method was used to calculate the entropy contribution at the interionic distance presented in eqn (11),51–53 where ΔS(r) is the entropy contribution at interionic distance, W(r,t) is the PMF at temperature T, and ΔT is the temperature difference. Furthermore, eqn (12) was used to calculate the enthalpy contribution (ΔH(r)). Fig. 6(b) shows the thermodynamics of the association and solvation of the Li+–PF6− ion pair. At CIP (0.36 nm), it is stabilized by the enthalpy and destabilized by entropy. However, SSIP (0.95 nm) is stabilized by entropy.
 |
| | Fig. 6 (a) PMF (W(r)) at three different temperatures; (b) the thermodynamic contribution as a function of distance at 303.15 K. | |
3.4. Transport properties
Transport properties like diffusion coefficient and ionic conductivities were calculated using the NVE simulation trajectory. The movement of particles leads us to different aspects of dynamics in the system that contribute to the transport properties. Ionic diffusion refers to the electrostatic interaction due to the diffusion of charged particles. Mean square displacement (MSD) was used to calculate the ionic diffusion of the particles present in the system using eqn (13). Here, ri(t) and, ri(0) are the positions of the ith particle at time t and zero, respectively. N is the number of ion pairs.| |
 | (13) |
The semilog plots of MSD of Li+, PF6−, and TFPC are shown in Fig. 7. The MSD plot of Li+ differs from PF6− and TFPC solvent; PF6− and TFPC solvent show similar diffusion and are higher than that of the cation, i.e., Li+. The lower diffusion of Li+ compared to PF6− and TFPC solvent can be attributed to the strongly correlated motion of Li+ with the PF6− ion and TFPC solvent. The oxygen and fluorine atoms in the TFPC molecule interact electrostatically with the Li+-ion, disrupting its free motion and decreasing its MSD. Also, with an increase in temperature, diffusion increases due to a gain in kinetic energy, thus starting to move faster, thereby increasing their transport properties. On the other hand, the MSD of the PF6− anion is higher than that of Li+. Therefore, the Li-ion interacts electrostatically with both the anion and the solvent very strongly, but PF6− interacts statistically only with Li+; hence, its connected interaction is relatively suppressed, increasing its diffusion property. The diffusion coefficients were obtained from appropriately selected diffusive regions from the entire simulation trajectory for each temperature. For capturing diffusive regions, the β value from MSD was calculated, as shown in eqn (14).
| |
 | (14) |
When
β is close to one, particles reach the diffusive regime. The
β plot is represented in the lower panels of
Fig. 7, and shaded parts represent the region where
β is close to one (45–135 ns). We calculated the diffusion coefficient of Li
+, PF
6−, and TFPC in the diffusive regions (45–135 ns). The diffusion coefficient of TFPC is the highest, followed by PF
6− and Li
+-ions. The diffusion coefficient was calculated from MSD by fitting the diffusive region using the following
eqn (15).
| |
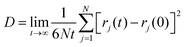 | (15) |
 |
| | Fig. 7 Semi-log plot of MSDs (a)–(c) and corresponding values of β (d)–(f). The unshaded parts, the diffusive regions of the trajectories, were used to calculate the transport properties of the electrolytes. | |
The diffusion coefficients of the ions and solvent are given in Table 2. The self-diffusion coefficient follows the same trend as the MSD. The cation diffusion is the lowest, and it increases with increasing temperature. TFPC diffuses faster than Li+ and PF6−, and its diffusivity increases with increasing temperature.
Table 2 Diffusion coefficients [×10−11 m2 s−1] of entities
| Temperature [K] |
283.15 |
293.15 |
303.15 |
313.15 |
323.15 |
333.15 |
| Li-ion |
0.65 |
1.04 |
1.65 |
3.42 |
4.85 |
6.08 |
| PF6 anion |
1.2 |
2.02 |
2.77 |
5.82 |
8.55 |
11.52 |
| TFPC |
1.34 |
2.27 |
3.12 |
6.29 |
9.12 |
12.53 |
3.5. Microheterogeneity in dynamics
To understand the distribution of displacements of entities, we calculated the self-part of the van Hove function54 (eqn (16)) of the cation and anion for three different temperatures and six different time intervals, presented in Fig. 8.| |
 | (16) |
where, GS(r,t) indicates the probability of an ion that has moved a certain distance r within the time t. The self part of the van Hove function is the spatial Fourier transform of experimentally accessible incoherent intermediate scattering function, FS(q,t). For the homogeneous dynamics, GS(r,t) follows the Gaussian approximation55,56 in eqn (17), where r(t) is the displacement of the ion.| |
 | (17) |
The deviation from the Gaussian approximation shows heterogeneous dynamics, which can be quantified by calculating the non-Gaussian parameter57,58 (α(t)), as shown in eqn (18), where r(t) is the displacement of the ion.| |
 | (18) |
Panels (a)–(c) in Fig. 8 show the van Hove function of Li+ at 283.15, 303.15, and 333.15 K, respectively. Sharp peaks are observed at shorter time intervals, and at longer time intervals, the peak shifts towards the right and becomes broader. No humps after the first peak shows the absence of an ion-hopping mechanism. So, the ions follow a diffusive mechanism. For PF6−, the shorter time interval showed humps after the first peak at 283.15 and 303.15 K, indicating the hopping mechanism. However, at a longer time, PF6− also followed a diffusive mechanism.
 |
| | Fig. 8 Panels (a), (b) and (c) show the van Hove function of Li+ at 283.15, 303.15, and 323.15 K, respectively; (d), (e) and (f) show the van Hove function of PF6− at 283.15, 303.15 and 323.15 K, respectively, for six different time intervals. | |
Fig. 9 shows the non-Gaussian parameter for cations and anions at six different temperatures to understand the heterogeneous behavior in their dynamics. The values of α(t) for the cation are higher than those of the anion at any given temperature, indicating higher dynamics in heterogeneity. At higher temperatures, cations attain a zero value of α(t) at around 30 ns, marking the start of a diffusive region. For lower temperatures, the α(t) does not attain zero at infinite time, showing that the ions are still in their sub-diffusive region.
 |
| | Fig. 9 Non-Gaussian parameter α(t) of (a) Li+ and (b) PF6− at six different temperatures. | |
3.7. Ionic conductivities
A fundamental study of ionic motion is needed to investigate the correlated and uncorrelated motions of ions and solvents in electrolytes. Uncorrelated ionic conductivity assumes that particles’ diffusion is independent of the surroundings, whereas correlated ionic conductivity considers correlations of neighboring ions. The correlated motion of cations and anions significantly decreases the ionic conductivity. Experimentally, uncorrelated ionic conductivity is calculated by the pulse–field gradient spin–echo NMR technique33 and correlated ionic conductivity can be calculated by a conductivity meter. The current–current autocorrelation function (CACF) was used to calculate the correlated ionic conductivity and proved to provide the ionic conductivity with reasonable accuracy.59–61 This method is based on the Green–Kubo62,63 relation, with J as the electrical current vector:| |
 | (19) |
J is, in turn, obtained as the product of ionic charge (q) and velocity (v) over all N species, KB is Boltzmann constant, T is temperature and V is volume.| |
 | (20) |
Appropriate ionic conductivity values can be obtained by integrating the current–current autocorrelation function. The CACFs for all the temperatures are shown in Fig. 10.
 |
| | Fig. 10 CACFs at various temperatures. | |
The values of ionic conductivities calculated from CACF are in good agreement with experimental values at lower temperatures, but deviated at higher temperatures.16 The cutoff used for the integration of CACF is 1 ps. The comparison of the experimental and correlated conductivities at six different temperatures is shown in the top panel of Fig. 11(a).16 Furthermore, to understand the temperature dependency on the ionic conductivity, we applied the Arrhenius formulation.64
| |
 | (21) |
eqn (21) can also be written as
eqn (22).
| |
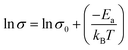 | (22) |
Eqn (22) resembles the equation of a straight line with a slope of (−
Ea/
KB).
σ0 is the pre-exponential factor. The activation energy of ionic conductivity can be derived from the slope. We have plotted the graph between ln
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σ vs.
σ vs. (
1/
T) presented in the inset of
Fig. 11(a). The linear regression fitting to the plot produces the parameters of a straight line (ln
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σ
σ = 9.55 − (2483.04/
T)). From the slope, the calculated activation energy of ionic transport is 20.64 kJ mol
−1.
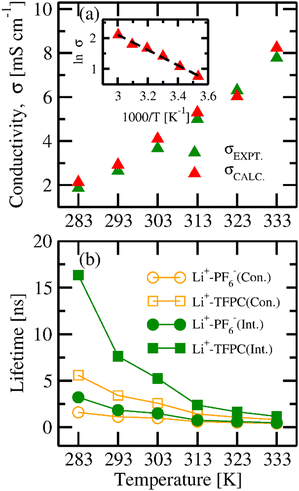 |
| | Fig. 11 (a) Conductivity and (b) lifetimes and relaxation times of the ion-cage with the variation of temperature. | |
3.8. Ion-cage dynamics and correlation with conductivity
The calculation of ion-cage dynamics65,66 was performed with the help of dimer autocorrelation functions, which are similar to the previous studies reported by Mallik and Chandra67,68 for hydrogen-bond dynamics. Ion-cage dynamics are identical to H-bond dynamics, which are the interactions of different moieties within a certain cutoff distance. These cutoff distances are taken from the 1st minimum of the COM RDF. We defined the population variable as βij, which is 1 for the moieties (ions and solvent) to be continuously in closest contact with one another; otherwise, it is zero. Eqn (23) describes the dimer autocorrelation function (DACF).| |
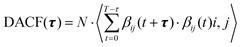 | (23) |
N represents the number of possible ion pairs within a given distance, T is the time, t is the initial time and τ is the increase in time. The term inside the parentheses represents the overall cation–anion and cation–solvent pairs. In this work, we have calculated both the continuous and intermittent autocorrelation functions for anion and solvent moieties with cations to study their existence as ion-cages. Continuous and intermittent autocorrelation functions are presented as SIC(t) and CIC(t), respectively. The continuous autocorrelation function (SIC(t)) indicates the existence of two moieties as closest neighbors until time t. We calculated the average ion-cage lifetime by stretched exponential fitting of the autocorrelation function. Eqn (24) shows the stretched exponential fitting and τa represents the ion-cage lifetime, and β is the stretching exponent.
| |
 | (24) |
On the other hand, the intermittent autocorrelation function (CIC(t)) doesn’t depend on the continuous presence of the nearest neighbor; it is unrestrained by the possible cleavage of the ion cage. The ion-cage relaxation time was calculated by the stretched exponential fitting of the intermittent autocorrelation function. The autocorrelation functions for Li+–PF6− and Li+–TFPC are shown in Fig. 12. The ion-cage lifetime and relaxation time are presented in Fig. 11(b). We observe that all the ion-cage lifetimes are smaller than the ion-cage relaxation time because the continuous correlation function depends on the first breaking of the ion-cage, but intermittent allows for the breaking and reforming of the ion-cage. The lifetimes of ion-cage formation for cation–solvent are more than that of cation–anion; this signifies that Li-ion coordinates to the solvent rather than the counter anion in the electrolyte system. As temperature increases, the mobility of ions gets faster, so there is less chance of ion-cage formation, which can be concluded from the ion-cage lifetime data.
 |
| | Fig. 12 Continuous ion-cage auto correlation functions of (a) Li+–COM(PF6−) and (b) Li+–COM(TFPC); intermittent ion-cage autocorrelation functions (c) Li+–COM(PF6−) and (d) Li+–COM(TFPC) at six different temperatures. The solid lines show the fitting data. | |
Furthermore, to understand the correlation between ion transport properties and ion-cage lifetime,69 we have plotted the graph between ionic conductivity and intermittent ion-cage lifetime as presented in Fig. 13. With the increase in ionic conductivity, the lifetime of the Li+–PF6− and Li+–TFPC pair decreases; however, the dependency is not linear. So, we have fitted the relation between ionic conductivity and lifetime with a polynomial equation fit (y = A0 + A1 × x + A2 × x2). We obtained the correlation coefficients of 0.9863 and 0.9859 for Li+–PF6− and Li+–TFPC, respectively. To achieve higher conductivity, ions must cleave the formed ion-cages in the electrolyte due to various interactions. A decrease in lifetime indicates less interaction between ion–ion and ion–solvent species, which results in higher ionic conductivity.
 |
| | Fig. 13 The correlation of conductivity vs. ion-cage lifetime of Li+–COM(PF6−) and Li+–COM(TFPC). | |
4. Conclusions
The performance and safety of a battery mainly depend on the type of electrolytes and their solvation structure. In this piece of work, we thoroughly investigated the temperature-dependent solvation structure and dynamics properties. Structural and transport properties were explored using molecular dynamics simulations at six different temperatures. The electrolyte structure was investigated by calculating the center of mass radial distribution function and coordination number. Due to electrostatic interactions, a good correlation exists between Li+–TFPC and Li+–PF6−. The Li+–PF6− CN is much lower compared to Li+–TFPC due to the formation of SSIP; anions do not stay in the first solvation shell of the cations. Three types of association are observed for the cation present in the electrolyte: CIP, SSIP, and SOLI. The ion cluster analysis shows that the percentage of Li+ forming CIP is lower and SSIP is higher at all the temperatures. With the increase in temperature, CIP formation increases; on the other hand, SSIP formation decreases. The spatial distribution of Li is mainly present around the oxygen atom, which tends to attract the positively charged Li atom. The PMF calculation shows the stability of CIP and SSIP. For CIP, the enthalpy contribution stabilizes, and entropy destabilizes, but for SSIP, entropy stabilizes.
PF6− and TFPC show similar diffusion, but higher than the cation. The lower diffusion of Li+ compared to PF6− and TFPC solvent is attributed to the strongly correlated motion of Li+ with the PF6− ion and TFPC solvent. The self part of van Hove's function calculation indicates the diffusive mechanism of ion transport for both the cation and anion. The calculation of non-Gaussian parameters shows the heterogeneous dynamics for both the cation and anion. The ionic conductivities calculated from CACF are in agreement with the experiments. The lifetime of ion-cage formation is longer for cation–TFPC compared to that of cation–PF6− and the relationship between the ion-cage lifetime and conductivity is established; moreover, the value of lifetime decreases with increased conductivity. We conducted a comprehensive set of analyses to gain deeper insights into the structural and dynamic properties of the electrolyte. These investigations include evaluations of ion coordination, solvation structure, ion-pairing behaviour, diffusivity and other key microscopic features that govern electrolyte performance. The results presented in this study provide a valuable atomistic-level understanding that can aid in developing electrolytes. Ultimately, these insights can contribute to the design of advanced electrolyte systems for improved battery performance.
Conflicts of interest
There are no conflicts to declare.
Data availability
Data for this article will be available from the authors upon reasonable request.
Acknowledgements
Ritesh Goutam Nayak would like to thank the Ministry of Education, India, for his fellowship. The authors acknowledge the financial support (CRG/2022/002187) from the Science and Engineering Research Board, Department of Science and Technology, Government of India. Part of the simulations was carried out using the Param Seva facility under the National Supercomputing Mission of India at Indian Institute of Technology Hyderabad.
References
- Y. Lu and J. Chen, Prospects of organic electrode materials for practical lithium batteries, Nat. Rev. Chem., 2020, 4, 127–142, DOI:10.1038/s41570-020-0160-9.
- H. Zhang, H. Zhao, M. A. Khan, W. Zou, J. Xu, L. Zhang and J. Zhang, Recent progress in advanced electrode materials, separators and electrolytes for lithium batteries, J. Mater. Chem. A, 2018, 6, 20564–20620, 10.1039/C8TA05336G.
- A. M. Haregewoin, A. S. Wotango and B.-J. Hwang, Electrolyte additives for lithium ion battery electrodes: progress and perspectives, Energy Environ. Sci., 2016, 9, 1955–1988, 10.1039/C6EE00123H.
- M. S. Whittingham, Electrical Energy Storage and Intercalation Chemistry, Science, 1976, 192, 1126–1127, DOI:10.1126/science.192.4244.1126.
- D. Aurbach, Y. Talyosef, B. Markovsky, E. Markevich, E. Zinigrad, L. Asraf, J. S. Gnanaraj and H.-J. Kim, Design of electrolyte solutions for Li and Li-ion batteries: a review, Electrochim. Acta, 2004, 50, 247–254, DOI:10.1016/j.electacta.2004.01.090.
- X.-G. Sun and C. A. Angell, New sulfone electrolytes for rechargeable lithium batteries.: Part I. Oligoether-containing sulfones, Electrochem. Commun., 2005, 7, 261–266, DOI:10.1016/j.elecom.2005.01.010.
- H. Cheng, Z. Ma, P. Kumar, H. Liang, Z. Cao, H. Xie, L. Cavallo, Q. Li and J. Ming, Non-Flammable Electrolyte Mediated by Solvation Chemistry toward High-Voltage Lithium-Ion Batteries, ACS Energy Lett., 2024, 9, 1604–1616, DOI:10.1021/acsenergylett.3c02789.
- S. Duan, S. Zhang, Y. Li, R. Guo, L. Lv, R. Li, Z. Wu, M. Li, S. Xiao, L. Chen, Y. Shi, T. Deng and X. Fan, H-Transfer Mediated Self-Enhanced Interphase for High-Voltage Lithium-Ion Batteries, ACS Energy Lett., 2024, 3578–3586, DOI:10.1021/acsenergylett.4c00917.
- G. Kang, G. Zhong, K. Cai, J. Ma, J. Biao, Y. Cao, S. Lu, K. Yu, F. Kang and Y. Cao, Dimethyl Sulfide Electrolyte Additive Enabled High-Voltage Lithium-Ion Battery, ACS Energy Lett., 2024, 9, 2572–2581, DOI:10.1021/acsenergylett.4c00519.
- Q. Li, J. Chen, L. Fan, X. Kong and Y. Lu, Progress in electrolytes for rechargeable Li-based batteries and beyond, Green Energy Environ., 2016, 1, 18–42, DOI:10.1016/j.gee.2016.04.006.
- J. Mu, X. Li, R. He, L. Sun, X. Bai, L. Zhang, P. Liu, Z. Liu, J. Gao and A. Wei, Effect of lithium-containing inorganic phosphate additives in stabilization of carbonate-based electrolyte for 5 V LiNi0.5Mn1.5O4-based lithium-ion batteries, J. Energy Storage, 2024, 96, 112538, DOI:10.1016/j.est.2024.112538.
- X. Zhang, P. Xu, J. Duan, X. Lin, J. Sun, W. Shi, H. Xu, W. Dou, Q. Zheng, R. Yuan, J. Wang, Y. Zhang, S. Yu, Z. Chen, M. Zheng, J.-F. Gohy, Q. Dong and A. Vlad, A dicarbonate solvent electrolyte for high performance 5 V-Class Lithium-based batteries, Nat. Commun., 2024, 15, 536, DOI:10.1038/s41467-024-44858-3.
- S. Mohapatra, H. Teherpuria, S. S. P. Chowdhury, S. J. Ansari, P. K. Jaiswal, R. R. Netz and S. Mogurampelly, Ion transport mechanisms in pectin-containing EC–LiTFSI electrolytes, Nanoscale, 2024, 16, 3144–3159, 10.1039/D3NR04029A.
- H. Teherpuria, H. Yadav, S. Mohapatra and S. Mogurampelly, Pectin alignment induced changes in ion solvation structure in ethylene carbonate-based liquid electrolytes, Int. J. Biol. Macromol., 2024, 282, 137395, DOI:10.1016/j.ijbiomac.2024.137395.
- X. Fan, X. Ji, L. Chen, J. Chen, T. Deng, F. Han, J. Yue, N. Piao, R. Wang, X. Zhou, X. Xiao, L. Chen and C. Wang, All-temperature batteries enabled by fluorinated electrolytes with non-polar solvents, Nat. Energy, 2019, 4, 882–890, DOI:10.1038/s41560-019-0474-3.
- J. Yang, Q. Liu, K. Z. Pupek, T. L. Dzwiniel, N. L. Dietz Rago, J. Cao, N. Dandu, L. Curtiss, K. Liu, C. Liao and Z. Zhang, Molecular Engineering to Enable High-Voltage Lithium-Ion Battery: From Propylene Carbonate to Trifluoropropylene Carbonate, ACS Energy Lett., 2021, 6, 371–378, DOI:10.1021/acsenergylett.0c02400.
- K. Xu, Nonaqueous Liquid Electrolytes for Lithium-Based Rechargeable Batteries, Chem. Rev., 2004, 104, 4303–4418, DOI:10.1021/cr030203g.
- X. Dong, Z. Guo, Z. Guo, Y. Wang and Y. Xia, Organic Batteries Operated at −70 °C, Joule, 2018, 2, 902–913, DOI:10.1016/j.joule.2018.01.017.
- X. Fan, L. Chen, O. Borodin, X. Ji, J. Chen, S. Hou, T. Deng, J. Zheng, C. Yang, S.-C. Liou, K. Amine, K. Xu and C. Wang, Non-flammable electrolyte enables Li-metal batteries with aggressive cathode chemistries, Nat. Nanotechnol., 2018, 13, 715–722, DOI:10.1038/s41565-018-0183-2.
- L. Dong, D. Luo, B. Zhang, Y. Li, T. Yang, Z. Lei, X. Zhang, Y. Liu, C. Yang and Z. Chen, All-Fluorinated Electrolyte Engineering Enables Practical Wide-Temperature-Range Lithium Metal Batteries, ACS Nano, 2024, 18(18), 18729–18742, DOI:10.1021/acsnano.4c06231.
- Y. Wang, Z. Wu, F. M. Azad, Y. Zhu, L. Wang, C. J. Hawker, A. K. Whittaker, M. Forsyth and C. Zhang, Fluorination in advanced battery design, Nat. Rev. Mater., 2024, 9, 119–133, DOI:10.1038/s41578-023-00623-4.
- L. Deng, L. Dong, Z. Wang, Y. Liu, J. Zhan, S. Wang, K.-P. Song, D. Qi, Y. Sang, H. Liu and H. Chen, Asymmetrically-Fluorinated Electrolyte Molecule Design for Simultaneous Achieving Good Solvation and High Inertness to Enable Stable Lithium Metal Batteries, Adv. Energy Mater., 2024, 14, 2303652, DOI:10.1002/aenm.202303652.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers, SoftwareX, 2015, 1–2, 19–25, DOI:10.1016/j.softx.2015.06.001.
- D. Van Der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. C. Berendsen, GROMACS: Fast, flexible, and free, J. Comput. Chem., 2005, 26, 1701–1718, DOI:10.1002/jcc.20291.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, Development and Testing of the OPLS All-Atom Force Field on Conformational Energetics and Properties of Organic Liquids, J. Am. Chem. Soc., 1996, 118, 11225–11236, DOI:10.1021/ja9621760.
- M. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci and G. A. Petersson, et al., Gaussian 09, Gaussian, Inc., Wallingford, CT, 2009. https://scholar.google.com/scholar?cluster=7585652766738493128&hl=en&oi=scholarr (accessed May 23, 2016) Search PubMed.
- A. D. Becke, Density-functional exchange-energy approximation with correct asymptotic behavior, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100, DOI:10.1103/PhysRevA.38.3098.
- C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789, DOI:10.1103/PhysRevB.37.785.
- J. Wang, W. Wang, P. A. Kollman and D. A. Case, Automatic atom type and bond type perception in molecular mechanical calculations, J. Mol. Graphics Modell., 2006, 25, 247–260, DOI:10.1016/j.jmgm.2005.12.005.
- T. G. A. Youngs and C. Hardacre, Application of Static Charge Transfer within an Ionic-Liquid Force Field and Its Effect on Structure and Dynamics, Chem. Phys. Chem., 2008, 9, 1548–1558, DOI:10.1002/cphc.200800200.
- N. Sieffert and G. Wipff, The [BMI][Tf2N] Ionic Liquid/Water Binary System:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A Molecular Dynamics Study of Phase Separation and of the Liquid−Liquid Interface, J. Phys. Chem. B, 2006, 110, 13076–13085, DOI:10.1021/jp061849q.
A Molecular Dynamics Study of Phase Separation and of the Liquid−Liquid Interface, J. Phys. Chem. B, 2006, 110, 13076–13085, DOI:10.1021/jp061849q. - J. Tong, X. Xiao, X. Liang, N. von Solms, F. Huo, H. He and S. Zhang, Insights into the solvation and dynamic behaviors of a lithium salt in organic- and ionic liquid-based electrolytes, Phys. Chem. Chem. Phys., 2019, 21, 19216–19225, 10.1039/C9CP01848D.
- Th. D. N. Reddy and B. S. Mallik, Solvent-Assisted Li-Ion Transport and Structural Heterogeneity in Fluorinated Battery Electrolytes, J. Phys. Chem. B, 2021, 125, 10551–10561, DOI:10.1021/acs.jpcb.1c05537.
- Dhananjay and B. S. Mallik, Cage Dynamics-Mediated High Ionic Transport in Li-O2 Batteries with a Hybrid Aprotic Electrolyte: LiTFSI, Sulfolane, and N,N-Dimethylacetamide, J. Phys. Chem. B, 2023, 127(13), 2991–3000, DOI:10.1021/acs.jpcb.2c07829.
- Y. Zhang and E. J. Maginn, A Simple AIMD Approach to Derive Atomic Charges for Condensed Phase Simulation of Ionic Liquids, J. Phys. Chem. B, 2012, 116, 10036–10048, DOI:10.1021/jp3037999.
- L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, PACKMOL: A package for building initial configurations for molecular dynamics simulations, J. Comput. Chem., 2009, 30, 2157–2164, DOI:10.1002/jcc.21224.
- M. C. Payne, M. P. Teter, D. C. Allan, T. A. Arias and J. D. Joannopoulos, Iterative minimization techniques for ab initio total-energy calculations: molecular dynamics and conjugate gradients, Rev. Mod. Phys., 1992, 64, 1045–1097, DOI:10.1103/RevModPhys.64.1045.
- T. Darden, D. York and L. Pedersen, Particle mesh Ewald: An N·log(N) method for Ewald sums in large systems, J. Chem. Phys., 1993, 98, 10089–10092, DOI:10.1063/1.464397.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, Molecular dynamics with coupling to an external bath, J. Chem. Phys., 1984, 81, 3684–3690, DOI:10.1063/1.448118.
- G. Bussi, D. Donadio and M. Parrinello, Canonical sampling through velocity rescaling, J. Chem. Phys., 2007, 126, 014101, DOI:10.1063/1.2408420.
- J. S. Hub, B. L. de Groot and D. van der Spoel, g_wham—A Free Weighted Histogram Analysis Implementation Including Robust Error and Autocorrelation Estimates, J. Chem. Theory Comput., 2010, 6, 3713–3720, DOI:10.1021/ct100494z.
- X. J. Wang, H. S. Lee, H. Li, X. Q. Yang and X. J. Huang, The effects of substituting groups in cyclic carbonates for stable SEI formation on graphite anode of lithium batteries, Electrochem. Commun., 2010, 12, 386–389, DOI:10.1016/j.elecom.2009.12.041.
- V. Ponnuchamy, S. Mossa and I. Skarmoutsos, Solvent and Salt Effect on Lithium Ion Solvation and Contact Ion Pair Formation
in Organic Carbonates: A Quantum Chemical Perspective, J. Phys. Chem. C, 2018, 122, 25930–25939, DOI:10.1021/acs.jpcc.8b09892.
- M. Takeuchi, N. Matubayasi, Y. Kameda, B. Minofar, S. Ishiguro and Y. Umebayashi, Free-Energy and Structural Analysis of Ion Solvation and Contact Ion-Pair Formation of Li+ with BF4– and PF6– in Water and Carbonate Solvents, J. Phys. Chem. B, 2012, 116, 6476–6487, DOI:10.1021/jp3011487.
- D. M. Seo, S. Reininger, M. Kutcher, K. Redmond, W. B. Euler and B. L. Lucht, Role of Mixed Solvation and Ion Pairing in the Solution Structure of Lithium Ion Battery Electrolytes, J. Phys. Chem. C, 2015, 119, 14038–14046, DOI:10.1021/acs.jpcc.5b03694.
- X. Chen, Z. Li, H. Zhao, J. Li, W. Li, C. Han, Y. Zhang, L. Lu, J. Li and X. Qiu, Dominant Solvent-Separated Ion Pairs in Electrolytes Enable Superhigh Conductivity for Fast-Charging and Low-Temperature Lithium Ion Batteries, ACS Nano, 2024, 18, 8350–8359, DOI:10.1021/acsnano.3c12877.
- A. V. Karatrantos, T. Ohba and Q. Cai, Diffusion of ions and solvent in propylene carbonate solutions for lithium-ion battery applications, J. Mol. Liq., 2020, 320, 114351, DOI:10.1016/j.molliq.2020.114351.
- M. Takeuchi, Y. Kameda, Y. Umebayashi, S. Ogawa, T. Sonoda, S. Ishiguro, M. Fujita and M. Sano, Ion–ion interactions of LiPF6 and LiBF4 in propylene carbonate solutions, J. Mol. Liq., 2009, 148, 99–108, DOI:10.1016/j.molliq.2009.07.003.
- Z. Luo, S. A. Burrows, S. K. Smoukov, X. Fan and E. S. Boek, Extension of the TraPPE Force Field for Battery Electrolyte Solvents, J. Phys. Chem. B, 2023, 127, 2224–2236, DOI:10.1021/acs.jpcb.2c06993.
- M. Mynam, B. Ravikumar and B. Rai, Molecular dynamics study of propylene carbonate based concentrated electrolyte solutions for lithium ion batteries, J. Mol. Liq., 2019, 278, 97–104, DOI:10.1016/j.molliq.2018.12.153.
- B. M. Pettitt and P. J. Rossky, Alkali halides in water: Ion–solvent correlations and ion–ion potentials of mean force at infinite dilution, J. Chem. Phys., 1986, 84, 5836–5844, DOI:10.1063/1.449894.
- N. Islam, M. Flint and S. W. Rick, Water hydrogen degrees of freedom and the hydrophobic effect, J. Chem. Phys., 2019, 150, 014502, DOI:10.1063/1.5053239.
- C. Peter, C. Oostenbrink, A. van Dorp and W. F. van Gunsteren, Estimating entropies from molecular dynamics simulations, J. Chem. Phys., 2004, 120, 2652–2661, DOI:10.1063/1.1636153.
- L. Van Hove, Correlations in Space and Time and Born Approximation Scattering in Systems of Interacting Particles, Phys. Rev., 1954, 95, 249–262, DOI:10.1103/PhysRev.95.249.
- M. G. Del Pópolo and G. A. Voth, On the Structure and Dynamics of Ionic Liquids, J. Phys. Chem. B, 2004, 108, 1744–1752, DOI:10.1021/jp0364699.
- W. Jiang, T. Yan, Y. Wang and G. A. Voth, Molecular Dynamics Simulation of the Energetic Room-Temperature Ionic Liquid, 1-Hydroxyethyl-4-amino-1,2,4-triazolium Nitrate (HEATN), J. Phys. Chem. B, 2008, 112, 3121–3131, DOI:10.1021/jp710653g.
- A. Rahman, Correlations in the Motion of Atoms in Liquid Argon, Phys. Rev., 1964, 136, A405–A411, DOI:10.1103/PhysRev.136.A405.
- Th. D. N. Reddy and B. S. Mallik, Solvent-Assisted Li-Ion Transport and Structural Heterogeneity in Fluorinated Battery Electrolytes, J. Phys. Chem. B, 2021, 125, 10551–10561, DOI:10.1021/acs.jpcb.1c05537.
- M. H. Kowsari, S. Alavi, M. Ashrafizaadeh and B. Najafi, Molecular dynamics simulation of imidazolium-based ionic liquids. II. Transport coefficients, J. Chem. Phys., 2009, 130, 014703, DOI:10.1063/1.3042279.
- M. H. Kowsari, S. Alavi, B. Najafi, K. Gholizadeh, E. Dehghanpisheh and F. Ranjbar, Molecular dynamics simulations of the structure and transport properties of tetra-butylphosphonium amino acid ionic liquids, Phys. Chem. Chem. Phys., 2011, 13, 8826–8837, 10.1039/C0CP02581J.
- A. Mondal and S. Balasubramanian, A Molecular Dynamics Study of Collective Transport Properties of Imidazolium-Based Room-Temperature Ionic Liquids, J. Chem. Eng. Data, 2014, 59, 3061–3068, DOI:10.1021/je500132u.
- C. Rey-Castro and L. F. Vega, Transport Properties of the Ionic Liquid 1-Ethyl-3-Methylimidazolium Chloride from Equilibrium Molecular Dynamics Simulation. The Effect of Temperature, J. Phys. Chem. B, 2006, 110, 14426–14435, DOI:10.1021/jp062885s.
- J. Fiates, Y. Zhang, L. F. M. Franco, E. J. Maginn and G. Doubek, Impact of anion shape on Li+ solvation and on transport properties for lithium–air batteries: a molecular dynamics study, Phys. Chem. Chem. Phys., 2020, 22, 15842–15852, 10.1039/D0CP00853B.
- A. M. Fleshman, M. Petrowsky, J. D. Jernigen, R. S. P. Bokalawela, M. B. Johnson and R. Frech, Extending the compensated Arrhenius formalism to concentrated alcohol electrolytes: Arrhenius vs. non-Arrhenius behavior, Electrochim. Acta, 2011, 57, 147–152, DOI:10.1016/j.electacta.2011.08.044.
- S. Gehrke, M. von Domaros, R. Clark, O. Hollóczki, M. Brehm, T. Welton, A. Luzar and B. Kirchner, Structure and lifetimes in ionic liquids and their mixtures, Faraday Discuss., 2017, 206, 219–245, 10.1039/C7FD00166E.
- M. Brehm and B. Kirchner, TRAVIS - A Free Analyzer and Visualizer for Monte Carlo and Molecular Dynamics Trajectories, J. Chem. Inf. Model., 2011, 51, 2007–2023, DOI:10.1021/ci200217w.
- A. Luzar and D. Chandler, Hydrogen-bond kinetics in liquid water, Nature, 1996, 379, 55–57, DOI:10.1038/379055a0.
- B. S. Mallik and A. Chandra, Hydrogen bond and residence dynamics of ion–water and water–water pairs in supercritical aqueous ionic solutions: Dependence on ion size and density, J. Chem. Phys., 2006, 125, 234502, DOI:10.1063/1.2403867.
- Y. Zhang and E. J. Maginn, Direct Correlation between Ionic Liquid Transport Properties and Ion Pair Lifetimes: A Molecular Dynamics Study, J. Phys. Chem. Lett., 2015, 6, 700–705, DOI:10.1021/acs.jpclett.5b00003.
|
| This journal is © the Owner Societies 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  *
*
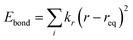


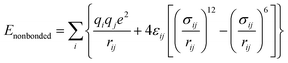

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 kJ mol−1 nm−2 was used. Multiple windows were used to separate the pull groups by 0.025 nm. Each window was energy minimized and equilibrated for 50 ns each within the NVT and NPT ensembles. The weighted histogram analysis method (WHAM), which uses the bootstrap technique for statistical error estimation, was used to calculate PMF from the constrained MD simulations.41 For the calculation of ionic conductivity, small trajectories of 1 ns were generated for each temperature by integrating equations of motion at 1 fs and saving the trajectory at every step.
000 kJ mol−1 nm−2 was used. Multiple windows were used to separate the pull groups by 0.025 nm. Each window was energy minimized and equilibrated for 50 ns each within the NVT and NPT ensembles. The weighted histogram analysis method (WHAM), which uses the bootstrap technique for statistical error estimation, was used to calculate PMF from the constrained MD simulations.41 For the calculation of ionic conductivity, small trajectories of 1 ns were generated for each temperature by integrating equations of motion at 1 fs and saving the trajectory at every step.



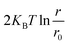 is added to consider the rotational motion of solute particles. ΔS(r), and ΔH(r) are the entropic and enthalpic contributions to the PMF. W(r,T ± ΔT) is the PMF at ± 20 K from the reference temperature of 303.15 K. The histogram shows the optimum overlap of adjacent windows, as presented in Fig. S1 of the ESI.† Fig. 6(a) shows the PMF between Li+–PF6− at three temperatures. The first minimum is observed at 0.36 nm due to CIP formation. The first minimum is followed by a transition state, and the second minimum is formed at 0.95 nm, which is due to the formation of SSIP. The energy levels of the second minimum are lower compared to the first minimum, which implies that the SSIP is more stable than the CIP. At higher temperatures, CIP shows lower energy, but a reverse scenario is observed at SSIP. To understand the thermodynamic contribution to the formation of CIP and SSIP, we calculated the ΔH(r), −TΔS(r) for each interionic distance. The finite temperature difference method was used to calculate the entropy contribution at the interionic distance presented in eqn (11),51–53 where ΔS(r) is the entropy contribution at interionic distance, W(r,t) is the PMF at temperature T, and ΔT is the temperature difference. Furthermore, eqn (12) was used to calculate the enthalpy contribution (ΔH(r)). Fig. 6(b) shows the thermodynamics of the association and solvation of the Li+–PF6− ion pair. At CIP (0.36 nm), it is stabilized by the enthalpy and destabilized by entropy. However, SSIP (0.95 nm) is stabilized by entropy.
is added to consider the rotational motion of solute particles. ΔS(r), and ΔH(r) are the entropic and enthalpic contributions to the PMF. W(r,T ± ΔT) is the PMF at ± 20 K from the reference temperature of 303.15 K. The histogram shows the optimum overlap of adjacent windows, as presented in Fig. S1 of the ESI.† Fig. 6(a) shows the PMF between Li+–PF6− at three temperatures. The first minimum is observed at 0.36 nm due to CIP formation. The first minimum is followed by a transition state, and the second minimum is formed at 0.95 nm, which is due to the formation of SSIP. The energy levels of the second minimum are lower compared to the first minimum, which implies that the SSIP is more stable than the CIP. At higher temperatures, CIP shows lower energy, but a reverse scenario is observed at SSIP. To understand the thermodynamic contribution to the formation of CIP and SSIP, we calculated the ΔH(r), −TΔS(r) for each interionic distance. The finite temperature difference method was used to calculate the entropy contribution at the interionic distance presented in eqn (11),51–53 where ΔS(r) is the entropy contribution at interionic distance, W(r,t) is the PMF at temperature T, and ΔT is the temperature difference. Furthermore, eqn (12) was used to calculate the enthalpy contribution (ΔH(r)). Fig. 6(b) shows the thermodynamics of the association and solvation of the Li+–PF6− ion pair. At CIP (0.36 nm), it is stabilized by the enthalpy and destabilized by entropy. However, SSIP (0.95 nm) is stabilized by entropy.



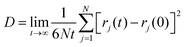






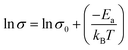
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σ vs. (1/T) presented in the inset of Fig. 11(a). The linear regression fitting to the plot produces the parameters of a straight line (ln
σ vs. (1/T) presented in the inset of Fig. 11(a). The linear regression fitting to the plot produces the parameters of a straight line (ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σ = 9.55 − (2483.04/T)). From the slope, the calculated activation energy of ionic transport is 20.64 kJ mol−1.
σ = 9.55 − (2483.04/T)). From the slope, the calculated activation energy of ionic transport is 20.64 kJ mol−1.

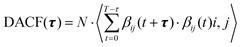

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A Molecular Dynamics Study of Phase Separation and of the Liquid−Liquid Interface, J. Phys. Chem. B, 2006, 110, 13076–13085, DOI:10.1021/jp061849q.
A Molecular Dynamics Study of Phase Separation and of the Liquid−Liquid Interface, J. Phys. Chem. B, 2006, 110, 13076–13085, DOI:10.1021/jp061849q.









