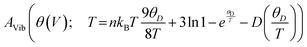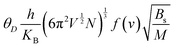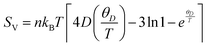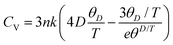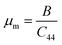Open Access Article
Open Access ArticleControl of spin on ferromagnetism and thermoelectric properties of K2GeMnX6 (X = Cl, Br, I) halide perovskites: emerging candidates for semiconductor spintronics and thermoelectric applications
Mudasir Younis
Sofi
,
Mohd Shahid
Khan
and
M. Ajmal
Khan
*
Department of Physics, Jamia Millia Islamia, New Delhi-110025, India. E-mail: majkhan@jmi.ac.in
First published on 8th May 2024
Abstract
In this systematic report, ab initio simulations based on density functional theory (DFT) have been performed to examine the structural and elastic stability, electronic profile, and transport properties of K2GeMnX6 (X = Cl, Br, I) double halide perovskites. The structural optimization, evaluation of mechanical stability criteria, and assessment of the tolerance factor collectively confirm the stability of the halide perovskites in a cubic structure with Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m symmetry. The stability of the primary magnetic phase is established through minimization of total crystal energy at the behest of Birch–Murnaghan's equation across diverse magnetic phases. The ferromagnetic state is identified as the fundamental ground state, supported by positive Curie–Weiss constant values of 101 K for K2GeMnCl6, 100 K for K2GeMnBr6 and 90 K for K2GeMnI6. Additionally, the dynamic stability has been assessed through the calculation of phonon band structures utilising density functional perturbation theory (DFPT). The electronic band structures and density of states, obtained from both the generalized gradient approximation (GGA) and the TB-mBJ potential, designate a semiconducting ferromagnetic behavior characterized by a substantial spin-splitting gap, indicating their promising potential for semiconductor spintronics. The investigation into magnetism reveals values of 5μB for each compound, primarily originating from the transition metal atom (Mn+2). Also, the Curie temperature for each compound has been determined, with values reaching 710 K for K2GeMnCl6, 650 K for K2GeMnBr6, and 570 K for K2GeMnI6, ensuring exceptional stability of the ferromagnetic phase well beyond typical ambient conditions. The analysis of the transport properties of K2GeMnX6 (X = Cl, Br, I) double perovskites involved examining both the temperature and chemical potential dependencies of thermoelectric coefficients, specifically focusing on the Seebeck coefficient, electrical conductivity, and figure of merit. The significantly low thermal conductivity values of 2.2 K W mK−1 for K2GeMnCl6, 2 K W mK−1 for K2GeMnBr6, and 1.95 K W mK−1 for K2GeMnI6 highlight their potential for efficient waste heat recovery. Furthermore, with figure of merit (zT) values of 1.01, 1.00, and 0.99 at room temperature for K2GeMnCl6, K2GeMnBr6, and K2GeMnI6 double halide perovskites respectively, these materials exhibit promising potential for both thermoelectric and renewable energy applications. The study also investigates the optical and dielectric properties, unveiling substantial absorption and photoconductivity in the visible and UV regions, thereby endorsing their potential as promising lead-free candidates for optoelectronics and solar cell applications. The comprehensive investigation overall lends support to the potential use of these materials in semiconductor spintronics, thermoelectric technology, optoelectronics, and other emerging technological domains.
m symmetry. The stability of the primary magnetic phase is established through minimization of total crystal energy at the behest of Birch–Murnaghan's equation across diverse magnetic phases. The ferromagnetic state is identified as the fundamental ground state, supported by positive Curie–Weiss constant values of 101 K for K2GeMnCl6, 100 K for K2GeMnBr6 and 90 K for K2GeMnI6. Additionally, the dynamic stability has been assessed through the calculation of phonon band structures utilising density functional perturbation theory (DFPT). The electronic band structures and density of states, obtained from both the generalized gradient approximation (GGA) and the TB-mBJ potential, designate a semiconducting ferromagnetic behavior characterized by a substantial spin-splitting gap, indicating their promising potential for semiconductor spintronics. The investigation into magnetism reveals values of 5μB for each compound, primarily originating from the transition metal atom (Mn+2). Also, the Curie temperature for each compound has been determined, with values reaching 710 K for K2GeMnCl6, 650 K for K2GeMnBr6, and 570 K for K2GeMnI6, ensuring exceptional stability of the ferromagnetic phase well beyond typical ambient conditions. The analysis of the transport properties of K2GeMnX6 (X = Cl, Br, I) double perovskites involved examining both the temperature and chemical potential dependencies of thermoelectric coefficients, specifically focusing on the Seebeck coefficient, electrical conductivity, and figure of merit. The significantly low thermal conductivity values of 2.2 K W mK−1 for K2GeMnCl6, 2 K W mK−1 for K2GeMnBr6, and 1.95 K W mK−1 for K2GeMnI6 highlight their potential for efficient waste heat recovery. Furthermore, with figure of merit (zT) values of 1.01, 1.00, and 0.99 at room temperature for K2GeMnCl6, K2GeMnBr6, and K2GeMnI6 double halide perovskites respectively, these materials exhibit promising potential for both thermoelectric and renewable energy applications. The study also investigates the optical and dielectric properties, unveiling substantial absorption and photoconductivity in the visible and UV regions, thereby endorsing their potential as promising lead-free candidates for optoelectronics and solar cell applications. The comprehensive investigation overall lends support to the potential use of these materials in semiconductor spintronics, thermoelectric technology, optoelectronics, and other emerging technological domains.
1. Introduction
The advancements in spintronics and quantum computing technology have greatly increased the speed of memory storage, endowing it with versatile capabilities. This evolving field aims to minimize the size of magnetic chips and enhance memory speed by utilizing both electron spin and charge.1,2 Advanced spintronic technology has achieved notable milestones, particularly in non-volatile magnetic random-access memory.3,4 The versatility of these advancements extends to electronic devices, offering benefits such as cost-effectiveness, faster data speed, and reduced power consumption.5,6 Additionally, contemporary quantum technology exploits electronic spin states in digital displays, departing from conventional charge-centric electronic operations. The landmark discovery of giant magnetic resistance (GMR) in 1998 played a pivotal role in advancing this technology.7 By harnessing electron spin, GMR induces a notable disparity in the resistance of different magnetic layers when subjected to external magnetic fields. Consequently, the interplay between electronic charge and spin facilitates the creation of low-powered, high-speed, non-volatile, and nano-sized memory solutions.8,9 The current scientific achievements in spintronics technology have led to improvements in magneto-resistive random-access memory (MRAM), magnetic sensors, magnetic valves, read heads for magnetic hard drives, and the giant magneto-resistive effect (GMR). Materials characterized by high spin polarization (SP) have emerged as suitable candidates for application in spintronics technology. Despite significant efforts in exploring spintronic materials, achieving 100% spin-polarized carriers at room temperature (RT) remains a major challenge. So far, numerous spintronic materials have been investigated, including spinels (NiFe2O4),10 europium chalcogenides (EuO, EuS),11,12 double perovskite oxides (Bi2FeCrO6, Sr2CrWO6),13,14 and Heusler compounds (CoVTiAl, CoVZrAl).15 However, the limited quantity of spin-polarized carriers and low Curie temperature present critical obstacles for realizing their RT spintronics.16 Prerequisites for realizing 100% spin-polarized carriers at RT involve nondegenerate electronic band structures with substantial spin splitting and a Curie temperature (TC) surpassing RT.16 While pristine halide perovskites exhibit excellent optoelectronic properties, they generally lack magnetism. Náfrádi et al.17 have documented the observation of weak magnetism in Mn-doped CH3NH3PbI3, indicating a potential avenue for halide perovskite based spintronics. However, the limited spin splitting of less than 0.2 eV and the low Curie temperature of less than 15 K in their devices must be significantly enhanced before achieving room temperature operation in spintronics. In contrast, the pursuit of intrinsic ferromagnetic semiconductors, unaided by any doping strategy, holds considerable potential for application in spintronics. Double perovskite oxides have garnered extensive attention in spintronic calculations, attributed to their straightforward crystal structures, facile modelling, a diverse array of elemental constituents, and the capacity for tuning electronic and magnetic properties. Despite these advancements, the magnetism of double perovskite halides (DPHs) remains largely unexplored to date. Recently Cai et al.18 investigated a novel class of double halide perovskites, exploring their essential characteristics in terms of stability, electronic profiles, and Curie temperature. The findings indicated that these materials exhibit both structural and dynamic stability, while displaying ferromagnetic semiconductor behavior with substantial spin splitting and significant Curie temperatures. Consequently, these materials were identified as compelling materials for semiconductor spintronics applications. Beyond their relevance in semiconductor spintronics, these halide double perovskites (DPHs) display an exceptional feature of ultra-low thermal conductivity.19 This distinctive property arises from the placement of heavier elements within the structural framework, serving as substantial rattlers and introducing lattice anharmonicity. As a result, these materials are anticipated to demonstrate a favourable thermoelectric response. In our recent study, we documented notable thermoelectric figure of merit (zT) values of 1.00 and 0.99 for K2GeNiBr6 and K2GeNiI6 halide double perovskites, respectively.20Motivated by these intriguing characteristics, we designed a novel class of double halide perovskites, systematically exploring their structural, magneto-electronic, Curie temperature, and thermoelectric properties in detail. The outcomes of our calculations on spin-polarized band structures and density of states distinctly indicate the manifestation of ferromagnetic semiconductor behaviour in K2GeMnX6 (X = Cl, Br, I) compounds, coupled with a notably high Curie temperature. Consequently, these materials exhibit promising attributes as emerging candidates for semiconductor spintronics applications. Furthermore, we conducted computations encompassing both temperature variations and chemical potential dependency to assess transport parameters such as the Seebeck coefficient, electrical conductivity, and the figure of merit (zT). The elevated room temperature zT values, stemming from the exceptionally low thermal conductivity and higher Seebeck coefficient values, endorse the suitability of these materials for application in thermoelectric technology. To forecast the comprehensive physical (structural, electronic, mechanical, phonon, thermodynamic, optical) and thermoelectric properties, the paper is structured as follows.
2. Theoretical models
The computations have been exclusively conducted utilizing the Wein2k simulation code and integrated packages associated with it.21 The iterative solution of the Kohn–Sham equation is facilitated by the generalized gradient approximation (GGA).22 Acknowledging GGA's limitations in accurately representing electronic structures of highly correlated d/f electron systems, the mBJ potential has been introduced to enhance the scrutiny of electronic structures, leading to the utilization of GGA+mBJ.23 In the FP-LAPW approach, the unit cell volume undergoes subdivision into muffin tin spheres, strategically centered at Wyckoff positions (4a, 4b, 8c, and 24e) corresponding to occupied atoms and interstitial spaces. Muffin tin radii (RMT) are carefully chosen to address charge leakage considerations while optimizing computational efficiency. A linearized augmented plane wave basis set is employed, ensuring atomic like character within MT spheres and a Bloch wave nature in interstitial spaces. The atomic wave functions within spheres extend to lmax = 10, while the plane wave cutoff condition is defined by RMTKmax = 7. Self-consistent calculations are deemed complete when the integrated charge difference between successive cycles is less than 0.0001e and the corresponding energy difference is less than or on the order of 0.0001 Ry. The Brillouin zone is discretized into 1000 k-points for the determination of magneto-electronic structures and elastic constants. To evaluate the mechanical stability, the Thomas Charpin cubic elastic package has been employed within the framework of the GGA-PBE approach.24 Thermodynamic properties were acquired through the Gibbs2 package,25 seamlessly integrated with the Wien2k code. The thermoelectric coefficients have been deduced using Boltzmann transport theory in conjunction with the rigid-band model and the constant-scattering time approximation (CSTA).26 To enhance computational accuracy, the determination of transport coefficients has been executed using a denser mesh comprising 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 k-points.
000 k-points.
3. Results and discussion
The employment of density functional theory calculations, utilizing two approximation schemes, namely PBE-GGA and TB-mBJ, has been discussed for the predictive analysis of diverse physical properties concerning the novel halide perovskites K2GeMnX6 (X = Cl, Br, I).3.1. Crystallographic structures and magnetic ground states
Crystal structures are characterized by internal structural parameters, which can be determined using experimental methods or computational approaches. Experimentalists rely on techniques such as X-ray diffraction (XRD) and Fourier-transform infrared spectroscopy (FTIR) approaches to elucidate and determine the crystal structure. In a computational context, one can predict the stability and ground state structure of a material by minimizing the crystal energy with respect to its volume. The determination of phase stability of K2GeMnX6 (X = Cl, Br, I) materials involves a computational approach, wherein the total energy is computed as a function of varying volume using distinct magnetic configurations. The optimization plots, illustrated in Fig. 1, affirm the stability of K2GeMnX6 in the cubic Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group. The energy–volume plot for the ferromagnetic phase reveals a minimum energy corresponding to the optimum volume. At this volume, the lattice constants are determined to be 10.35 Å for K2GeMnCl6, 10.61 Å for K2GeMnBr6 and 11.75 Å for K2GeMnI6 compounds. The lattice constant increases as the halide ion X (ranging from Cl to I) progresses, which can be attributed to variances in atomic sizes and interatomic interactions within the crystal lattice. Given the larger atomic radius of iodine (I) compared to bromine (Br) and chlorine (Cl), the lattice parameter of K2GeMnI6 is inherently larger, reflecting the influence of atomic dimensions on the lattice structure. The obtained values for the lattice constant are consistent with other published findings.18,20 The other equilibrium parameters defining the ground state, as determined through the minimization of total energy, are outlined in Table 1. It is worth noting that the generalized gradient approximation (GGA-PBE) yields a lattice parameter value that exhibits the closest agreement with experimental findings.
m space group. The energy–volume plot for the ferromagnetic phase reveals a minimum energy corresponding to the optimum volume. At this volume, the lattice constants are determined to be 10.35 Å for K2GeMnCl6, 10.61 Å for K2GeMnBr6 and 11.75 Å for K2GeMnI6 compounds. The lattice constant increases as the halide ion X (ranging from Cl to I) progresses, which can be attributed to variances in atomic sizes and interatomic interactions within the crystal lattice. Given the larger atomic radius of iodine (I) compared to bromine (Br) and chlorine (Cl), the lattice parameter of K2GeMnI6 is inherently larger, reflecting the influence of atomic dimensions on the lattice structure. The obtained values for the lattice constant are consistent with other published findings.18,20 The other equilibrium parameters defining the ground state, as determined through the minimization of total energy, are outlined in Table 1. It is worth noting that the generalized gradient approximation (GGA-PBE) yields a lattice parameter value that exhibits the closest agreement with experimental findings.
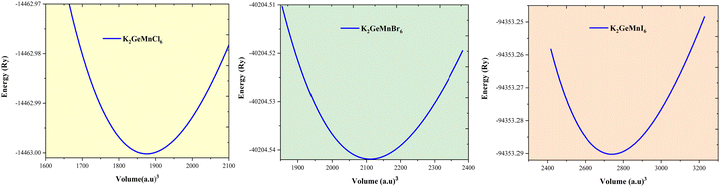 | ||
| Fig. 1 Variation in total energy against unit cell volume for K2GeMnX6 (X = Cl, Br, I) determined via the GGA-PBE functional scheme. | ||
The stability of the cubic phase is further substantiated by the computation of the tolerance factor. The tolerance factor can be derived from either ionic radii,18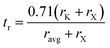 , or bond lengths,
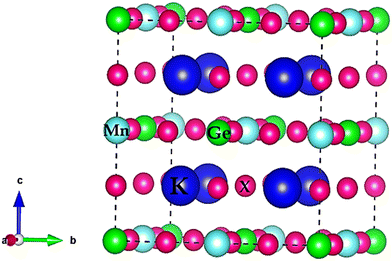
, or bond lengths, 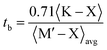 . Here rK and rX are the ionic radii of K and Cl/Br/I atoms, while ravg is the average ionic radii of Ge and Mn atoms, respectively. Besides, 〈K–X〉 signifies the interatomic distance between potassium (K) and bromine (Br)/iodine (I) atoms, whereas 〈M′–X〉avg indicates the average of germanium (Ge)–X and manganese (Mn)–X bond distances. The acquired values, as presented in Table 1, lie within the range of 0.81 < t < 1.11 for the specified materials, affirming their stability in the cubic structure. Within the unit cell, K is surrounded by a cage of twelve Cl/Br/I atoms, as depicted in Fig. 2. Meanwhile, Ge and Mn exhibit a coordination number of six with Cl/Br/I atoms, placing them in an octahedral environment of Cl/Br/I anions. The bond lengths and tolerance factor collectively contribute to determining the stable phase of these double halide perovskites.
. Here rK and rX are the ionic radii of K and Cl/Br/I atoms, while ravg is the average ionic radii of Ge and Mn atoms, respectively. Besides, 〈K–X〉 signifies the interatomic distance between potassium (K) and bromine (Br)/iodine (I) atoms, whereas 〈M′–X〉avg indicates the average of germanium (Ge)–X and manganese (Mn)–X bond distances. The acquired values, as presented in Table 1, lie within the range of 0.81 < t < 1.11 for the specified materials, affirming their stability in the cubic structure. Within the unit cell, K is surrounded by a cage of twelve Cl/Br/I atoms, as depicted in Fig. 2. Meanwhile, Ge and Mn exhibit a coordination number of six with Cl/Br/I atoms, placing them in an octahedral environment of Cl/Br/I anions. The bond lengths and tolerance factor collectively contribute to determining the stable phase of these double halide perovskites.
In the pursuit of theoretically evaluating the potential for experimental synthesis and determining the resistance of these compounds to spontaneous decomposition into other binary or elemental phases, we computed the enthalpy of formation energy, denoted as27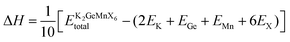 , where
, where 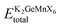 represents the equilibrium energy of the unit cell and EK, EGe, EMn, and EX illustrate the calculated DFT energies of potassium (K), germanium (Ge), manganese (Mn), and chlorine/bromine/iodine (Cl/Br/I) atoms in their stable elemental crystal structures. The negative values of ΔH obtained, as depicted in Table 1, signify the practical feasibility of experimental synthesis and production of these materials.
represents the equilibrium energy of the unit cell and EK, EGe, EMn, and EX illustrate the calculated DFT energies of potassium (K), germanium (Ge), manganese (Mn), and chlorine/bromine/iodine (Cl/Br/I) atoms in their stable elemental crystal structures. The negative values of ΔH obtained, as depicted in Table 1, signify the practical feasibility of experimental synthesis and production of these materials.
Also, we computed the cohesive energy of the materials using the formula27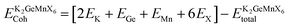 , where
, where 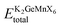 is the equilibrium energy of the unit cell and EK, EGe, EMn, and EX are the energies of the isolated atoms K, Ge, Mn, and X (Cl, Br, and I), respectively. The positive cohesive energy values, detailed in Table 1, further validate the interatomic stability of these materials.
is the equilibrium energy of the unit cell and EK, EGe, EMn, and EX are the energies of the isolated atoms K, Ge, Mn, and X (Cl, Br, and I), respectively. The positive cohesive energy values, detailed in Table 1, further validate the interatomic stability of these materials.
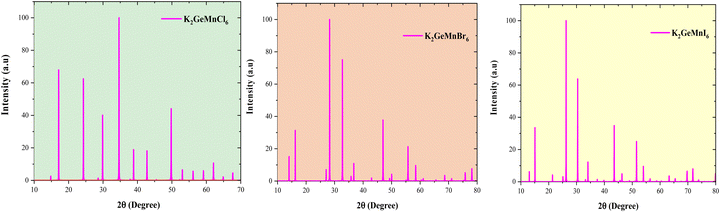
Additionally, as per the OQMD database, the energy above hull (EHull) for K2GeMnCl6 and K2GeMnBr6 is reported as 0.03 and 0.036 per atom, respectively, thus reaffirming their potential feasibility for experimental synthesis.28 Furthermore, we utilized density functional theory (DFT) simulations to generate X-ray diffraction (XRD) patterns for these compounds in the cubic configuration (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m), as illustrated in Fig. 3. These simulated patterns offer valuable guidance for potential experimental investigations into the structural properties of these materials.
m), as illustrated in Fig. 3. These simulated patterns offer valuable guidance for potential experimental investigations into the structural properties of these materials.
3.2. Phonon band structure
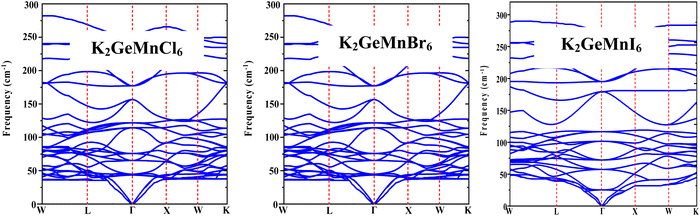
To comprehend the dynamic stability and vibrational Raman spectroscopy of crystalline solids, it is essential to explore the concept of phonon frequency dispersion. The application of density functional perturbation theory (DFPT) within the Quantum Espresso pseudopotential framework has been utilized to evaluate the dynamical stability of the specified materials at operational temperatures.29 In the realm of dynamic stability, a system is deemed stable when its phonon frequencies are real and positive; conversely, negative or imaginary frequencies indicate instability. The phonon dispersion bands depicted in Fig. 4 demonstrate the absence of negative phonon frequencies, thus confirming the dynamic stability of the materials. The phonon bands display three acoustical modes and twenty-seven optical modes, in line with the presence of ten atoms in the primitive unit cell of these materials. At the reciprocal space Γ-point (k = 0), three acoustic branches with zero frequency converge, identified as longitudinal acoustic (LA) and transverse acoustic (TA) modes. Additionally, the 27 optical modes with non-zero frequencies include Raman, infrared, and silent modes, categorized according to factor theory. The group velocity of a phonon, expressed by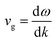 , reflects the slope of associated branches. Optical branches exhibit a flat curvature, signifying low group velocity, while longitudinal acoustical branches, characterized by linear variation, demonstrate substantial group velocity. Hence, these acoustical modes significantly contribute to thermal conduction due to their high group velocity, impacting the lattice thermal conductivity of a material.
, reflects the slope of associated branches. Optical branches exhibit a flat curvature, signifying low group velocity, while longitudinal acoustical branches, characterized by linear variation, demonstrate substantial group velocity. Hence, these acoustical modes significantly contribute to thermal conduction due to their high group velocity, impacting the lattice thermal conductivity of a material.
3.3. Thermodynamic vibrational properties
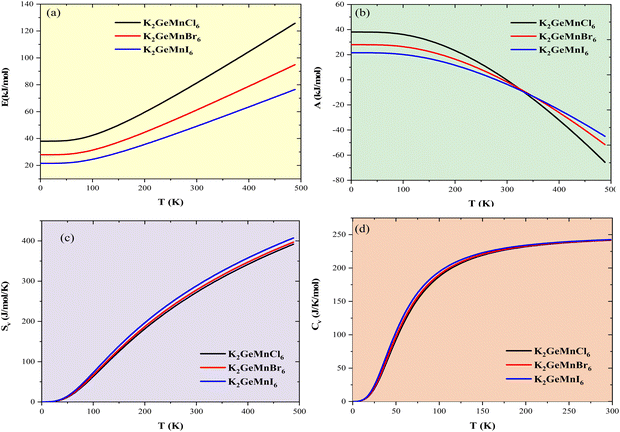
The investigation into thermodynamic vibrational functions, which encompass vibrational contributions, is aimed at comprehending phenomena such as variations in vibrational internal energy (E), vibrational Helmholtz free energy (A), vibrational entropy (SV), and specific heat at constant volume (Cv) relative to temperature (T). The quasi-harmonic Debye model is frequently employed for predicting these thermodynamic properties.30,31 As per this model, the equations for vibrational Helmholtz free energy (A), Debye temperature (θD), vibrational entropy (SV), and specific heat at constant volume (Cv) are provided as follows:Here, n symbolizes the count of atoms per formula unit, kB denotes the Boltzmann constant, Bs represents the adiabatic bulk modulus, M signifies the molecular mass per unit cell, and D stands for the Debye integral. Herein, we have investigated the fluctuations in vibrational thermodynamic functions concerning temperature, specifically focusing on variations in internal energy, Helmholtz free energy, vibrational entropy, and specific heat at constant volume.
We commence by examining vibrational internal energy (E), admitting the well-known phenomenon that sustained heat influx leads to an escalation in the kinetic energy of constituent atoms, thereby increasing atomic vibrations and consequently elevating vibrational internal energy. The variation in vibrational internal energy (E) with temperature (T), as depicted in Fig. 5(a), reveals a linear increase of E relative to T, indicating a corresponding rise in the system's enthalpy. The observed trend in vibrational Helmholtz free energy (A), illustrated in Fig. 5(b), exhibits a decrease in A with increasing T, progressing from Cl to I. This trend confirms that the thermal energy available for performing useful work reaches its maximum for K2GeMnCl6 and diminishes as X descends down the group. The level of intrinsic disorder within the system, quantified as entropy (SV), demonstrates an increase as we progress down the periodic table group from Cl to I. This trend is attributed to the expanding atomic size, facilitating greater potential orientation for subatomic particles. The calculated SV, as depicted in Fig. 5(c), emphasizes that the thermodynamic potential or thermal energy unavailable for performing useful work follows the order (X = I > Br > Cl) for K2GeMnX6 compounds. Moreover, SV increases with temperature (T), indicating an augmentation in thermally accessible vibrational states.
In the domain of thermodynamics and statistical analyses,32–34 heat capacity (CV) assumes critical importance in understanding lattice vibrational characteristics. The behavior of the CV plot delineates into two distinct regimes, as elucidated in Fig. 5(d). Initially, when temperature (T) significantly undershoots the Debye temperature (θD), it conforms to a specific relationship 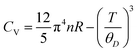 . Conversely, at high temperatures (T ≫ θD) the curve approximates the expression CV ≅ 3nR, aligning with Dulong–Petit's limit[35]. Here, n denotes the number of atoms per formula unit, R represents the universal gas constant (approximately 8.314 J K−1 mol−1), and θD stands for the Debye temperature at 0 K. The determined values for the Debye temperature (θD), the zero-point energy (E0) expressed in kilojoules per mole, and the Gruneisen parameter γ (dimensionless) are tabulated in Table 2.
. Conversely, at high temperatures (T ≫ θD) the curve approximates the expression CV ≅ 3nR, aligning with Dulong–Petit's limit[35]. Here, n denotes the number of atoms per formula unit, R represents the universal gas constant (approximately 8.314 J K−1 mol−1), and θD stands for the Debye temperature at 0 K. The determined values for the Debye temperature (θD), the zero-point energy (E0) expressed in kilojoules per mole, and the Gruneisen parameter γ (dimensionless) are tabulated in Table 2.
| Parameter | θ D | E 0 | γ |
|---|---|---|---|
| K2GeMnCl6 | 406 | 39 | 2.01 |
| K2GeMnBr6 | 300 | 28 | 2.07 |
| K2GeMnI6 | 230 | 21 | 2.10 |
The analysis of the specific heat (CV) plot portrayed in Fig. 5(d) elucidates the adherence of K2GeMnX6 (Cl, Br, I) compounds to the aforementioned principles. Remarkably, at temperatures (T) notably below the Debye temperature (θD), the observed rise in CV correlates directly with T3, confirming compliance with Debye's low-temperature specific heat law, commonly known as Debye's T3 law. Conversely, at temperatures significantly surpassing θD, CV remains nearly constant across all considered systems, approaching the Dulong–Petit limit, thereby indicating that our computational outcomes at elevated temperatures align with the classical thermodynamics embodied by the Dulong–Petit law.35 The tabulated values of θD provided in Table 2 unveil a distinct descending trend following the sequence K2GeMnCl6>K2GeMnBr6>K2GeMnI6. This trend is attributed to compounds with heavier atoms displaying a reduced average velocity of sound (Vav), stemming from an increase in density. Furthermore, the dimensionless Gruneisen parameter (γ), computed as 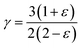 , serves as an insightful metric for predicting the anharmonic properties of the solid material. Remarkably, this parameter exhibits noteworthy consistency across all examined compounds, suggesting a uniform trend in thermodynamic properties for the scrutinized perovskites (K2GeMnX6). This consistency implies that these compounds are expected to demonstrate coherent thermodynamic behavior.
, serves as an insightful metric for predicting the anharmonic properties of the solid material. Remarkably, this parameter exhibits noteworthy consistency across all examined compounds, suggesting a uniform trend in thermodynamic properties for the scrutinized perovskites (K2GeMnX6). This consistency implies that these compounds are expected to demonstrate coherent thermodynamic behavior.
3.4. Mechanical stability
The comprehensive examination of structural properties provides additional insights into the mechanical characteristics of the materials. Furthermore, the arrangement of atoms within the structure holds significant importance in determining the material's resistance to external forces, thereby defining its mechanical stability. The assessment of mechanical stability serves as a crucial roadmap for industrial and technological applications. For the given perovskites, we ascertained elastic constants using the volume and energy approach, while maintaining tetrahedral and rhombohedral distortions within the cubic elastic package.24 The eigenvalues of the elastic constant matrix for K2GeMnX6 (X = Cl, Br, I) halide perovskites, detailed in Table 3, exhibit positivity and adhere to the Born stability conditions36 (C11 > 0, C12 > 0, C44 > 0, C11 + 2C12 > 0). This affirmation emphasizes the stability of double perovskites in the symmetric cubic phase (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m). The calculated elastic constants not only provide insights into the mechanical stability but also facilitate the analysis of various elastic parameters. Parameters like elastic moduli (bulk, shear, and Young)37–39 are derived from elastic constants through mathematical relations reported elsewhere,40 with the outcomes detailed in Table 3. The Young's modulus (Y), reflecting the stiffness of the alloy, is complemented by the bulk modulus (B), which inversely determines the resistance to volumetric deformation. The fracture strength, directly influenced by the bulk modulus, correlates with the material's resistance to volumetric changes. Shear modulus (G), indicating the resistance to plastic deformation, implies that lower G-values facilitate easier modulation of the alloy. The elastic moduli for these double perovskites follow the order of Y > B > G, suggesting that these materials exhibit easier shape deformation than volumetric deformation and possess a high-stiffness characteristic. Additionally, we computed the Kleinman coefficient (ζ) to assess the given materials' resistance to bond bending and bond angle distortions, using equations specified elsewhere.40 The Kleinman parameter (ζ), in the specified range of 0 ≤ ζ < 1, is used to evaluate the contribution of both stretching and bending of the bonds within the material. For the titled materials, a smaller Kleinman parameter (ζ) indicates more resistance to bond bending and bond angle distortions.
m). The calculated elastic constants not only provide insights into the mechanical stability but also facilitate the analysis of various elastic parameters. Parameters like elastic moduli (bulk, shear, and Young)37–39 are derived from elastic constants through mathematical relations reported elsewhere,40 with the outcomes detailed in Table 3. The Young's modulus (Y), reflecting the stiffness of the alloy, is complemented by the bulk modulus (B), which inversely determines the resistance to volumetric deformation. The fracture strength, directly influenced by the bulk modulus, correlates with the material's resistance to volumetric changes. Shear modulus (G), indicating the resistance to plastic deformation, implies that lower G-values facilitate easier modulation of the alloy. The elastic moduli for these double perovskites follow the order of Y > B > G, suggesting that these materials exhibit easier shape deformation than volumetric deformation and possess a high-stiffness characteristic. Additionally, we computed the Kleinman coefficient (ζ) to assess the given materials' resistance to bond bending and bond angle distortions, using equations specified elsewhere.40 The Kleinman parameter (ζ), in the specified range of 0 ≤ ζ < 1, is used to evaluate the contribution of both stretching and bending of the bonds within the material. For the titled materials, a smaller Kleinman parameter (ζ) indicates more resistance to bond bending and bond angle distortions.
| Parameter | C 11 | C 12 | C 44 | B | G | Y | v | B/G | C 12–C44 | ξ | A z | A U |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| K2GeMnCl6 | 57.01 | 16.08 | 9.83 | 29.72 | 16.46 | 47.03 | 0.27 | 1.80 | 6.25 | 0.43 | 0.48 | 0.30 |
| K2GeMnBr6 | 45.89 | 14.34 | 6.13 | 24.85 | 9.04 | 24.18 | 0.33 | 2.74 | 8.21 | 0.45 | 0.37 | 0.25 |
| K2GeMnI6 | 30.05 | 13.94 | 6.01 | 19.31 | 6.75 | 18.73 | 0.33 | 2.86 | 7.93 | 0.59 | 0.74 | 0.32 |
To explore the fragility aspect of the given materials, parameters such as Cauchy's pressure, Pugh's ratio, and Poisson's ratio40–42 have been computed and presented in Table 3. Cauchy's pressure, represented by the difference (C12–C44), functions as an indicator reflecting the ductile or malleable nature of a material. A positive sign denotes ductile character, while a negative sign signifies malleability. Pugh's ratio (B/G), with a critical threshold of 1.75, classifies materials as either ductile (above the threshold) or malleable (below the threshold). Poisson's ratio serves (v) as an indicator of a material's brittleness or ductility. When Poisson's ratio exceeds 0.26, the material is considered ductile, whereas a ratio below 0.26 signifies malleability. The computed values of these parameters, as outlined in Table 3, collectively indicate the ductile characteristics of the provided materials.
In the field of crystallophysics, the importance of anisotropy metrics such as Zener anisotropic metric (AZ) and universal anisotropic factor (AU) is widely recognized. Hence, we computed these parameters to assess the anisotropy within our systems, utilizing the equations43,44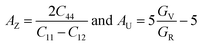 . The computed results, presented in Table 3, unequivocally indicate that the investigated compounds exhibit significant anisotropy in their nature, as both AZ and AU deviate from unity (where AZ and AU = 1 signifies isotropic materials).
. The computed results, presented in Table 3, unequivocally indicate that the investigated compounds exhibit significant anisotropy in their nature, as both AZ and AU deviate from unity (where AZ and AU = 1 signifies isotropic materials).
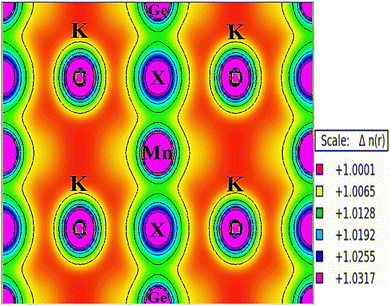
A key objective in performing mechanical constant computations is to glean insights into the average sound velocity (Vav), estimated through transverse and longitudinal velocities (Vt and Vl). These velocities are calculated using equations40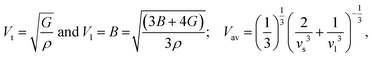 where ρ represents the density. The observed decline in Vav from Cl to I, as evident in Table 4, could be associated with the increasing density of these compounds (I > Br > Cl). Furthermore, various critical characteristics essential for real-world applications in thermoelectric materials, such as Vickers hardness (HV), machinability factor (μm), Frantsevich's ratio (G/B), and melting temperature (Tm), are also computed using the following equations:40,45–47
where ρ represents the density. The observed decline in Vav from Cl to I, as evident in Table 4, could be associated with the increasing density of these compounds (I > Br > Cl). Furthermore, various critical characteristics essential for real-world applications in thermoelectric materials, such as Vickers hardness (HV), machinability factor (μm), Frantsevich's ratio (G/B), and melting temperature (Tm), are also computed using the following equations:40,45–47
(HV)Teter = 0.151 G, (HV)Tian = 0.92(G/B)1.137![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) G0.708 G0.708 |
| Tm (K) = [553 (K) + (5.911)C11]GPa ± 300 |
| Parameter | V t | V l | V av | G/B | μ m | (HV)Teter | (HV)Tian | T m ± 300 |
|---|---|---|---|---|---|---|---|---|
| K2GeMnCl6 | 2565 | 4545 | 2978 | 0.55 | 3.02 | 2.48 | 4.53 | 890 |
| K2GeMnBr6 | 1609 | 3255 | 2395 | 0.36 | 4.04 | 1.36 | 3.67 | 824 |
| K2GeMnI6 | 1305 | 2672 | 2043 | 0.34 | 3.21 | 1.02 | 0.86 | 730 |
All these parameters are compiled in Table 4. The computed Vickers hardness (HV) values, obtained from two distinct estimations proposed by Teter et al.45 and Tian et al.,46 consistently yield positive values across all examined materials in both methods, indicating the high hardness of the given materials. The machinability factor (μm) underscores the suitable machinability level of the studied perovskites, characterized by reduced feed forces and mild lubricating properties. Furthermore, the estimated elevated melting temperature (Tm) coupled with a small G/B ratio suggests that these compounds hold promise as potential candidates for future thermoelectric materials, particularly for high-temperature applications.
3.5. Energy bands
The electronic structure of a material, elucidating the intricate arrangement and behaviour of electrons within its atomic or molecular framework, is pivotal for understanding its physical, chemical, and electronic properties. The electronic profile of the studied materials has been analyzed through spin-polarized band structure (BS) and density of states (DOS) evaluations. Utilizing both GGA and GGA+mBJ approximations, the band structures have been delineated, as depicted in Fig. 6(a–c). In the illustration, the band structure derived from GGA calculations indicates an unoccupied Fermi level in both spin directions for K2GeMnX6 (X = Cl, Br, I) halide perovskites. In the up-spin direction of all three materials, the Fermi level tangentially touches the valence band maximum, while in the spin-down direction, the Fermi level remains unoccupied. Nevertheless, a band gap exists in both spin channels, confirming the ferromagnetic semiconducting behavior of these materials. The band gap, defined as the energy separation between the top of the valence band and the minimum of the conduction band (CB), is crucial in elucidating electron behavior within the system. The computed values of the band gap obtained via GGA and GGA+mBJ potential are provided in Table 5. Considering the potential underestimation of the band gap value by the GGA approximation due to correlated d-electrons of transition atoms, the integration of the mBJ potential with GGA provides consistent electronic profiles for K2GeMnX6 (X = Cl, Br, I) perovskites, accompanied by modified band gap values, as presented in Table 5. The computed band gap values exhibit favourable agreement with analogous findings reported in the existing literature.18,20 A more in-depth examination of the energy bands indicates increased dispersion in electronic states for spin-up channels in both the valence and conduction bands, leading to a reduction in the effective mass of charge carriers. Conversely, spin-down states exhibit less dispersive electronic states, leading to relatively high effective mass. This variation in effective mass suggests promising prospects for these materials in transport dynamics. Additionally, we calculated the spin-splitting gap, which represents the energy difference between the valence band maximum (VBM) or the conduction band minimum (CBM) and the Fermi level for spin-up and spin-down channels. The computed values of the spin splitting gap, as presented in Table 5, exhibit favorable agreement with results published for analogous materials.18 These findings emphasize notable spin splitting, indicating a promising route for these materials towards advancements in semiconductor spintronics.| Parameter | Band gap | Spin-splitting gap | ||||||
|---|---|---|---|---|---|---|---|---|
| Approximation | GGA | GGA+mBJ | GGA | GGA+mBJ | ||||
| Spin channel | Up | down | Up | down | ΔECBM | ΔEVBM | ΔECBM | ΔEVBM |
| K2GeMnCl6 | 1.62 | 2.63 | 2.75 | 3.46 | 0.27 | 1.28 | 0.29 | 1.02 |
| K2GeMnBr6 | 1.09 | 2.41 | 2.01 | 3.00 | −0.08 | 1.24 | −0.04 | 0.78 |
| K2GeMnI6 | 0.61 | 1.71 | 1.21 | 2.45 | −0.34 | 0.78 | −0.32 | 0.98 |
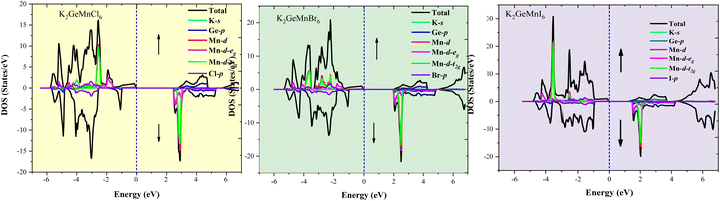 | ||
| Fig. 7 Graphical representation of total density of states (TDOS) and projected density of states (PDOS) for K2GeMnX6 (X = Cl, Br, I) double perovskites determined via the GGA+mBJ approach. | ||
The elucidation of atomic contributions to band formation and peaks in the density of states (DOS) plot is achieved through the presentation of the atomic DOS plot, as depicted in Fig. 7. In the context of these double perovskites, the halogen atom predominantly contributes to the upper valence band, whereas the Mn-d states dominate the conduction band. Notably, the d-t2g/d-eg states, positioned in the vicinity of the Fermi level, play a pivotal role in shaping the overall electronic properties of the present systems. To further elucidate the origin of semiconducting behaviour within these materials, the crystal field splitting of degenerate states of transition element Mn+2 needs to be calibrated. In the structural arrangement of K2GeMnX6 (X = Cl, Br, I), the central Mn atom is enclosed by six neighbouring Cl/Br/I atoms, acting as ligands that approach the central metal atom. To simplify, we treat these ligands as symmetrically positioned along the Cartesian coordinate system's axis, creating a spherical field with the metal ion at the center. In a spherical field, all d-orbitals are energetically elevated compared to the free ion due to negative charge repulsions. However, not all d-orbitals are affected to the same extent. Orbitals lying under the axis (dx2–y2 and dz2) experience stronger repulsion than those with lobes directed between the axes (dxy, dyz, dzx). Consequently, the d-orbitals split into two sets: d-t2g (doubly degenerate) and d-eg (triply degenerate). The extent of separation between d-t2g and d-eg states in an octahedral complex is denoted by Δ, where Δ signifies the octahedral splitting. The electronic occupation within these orbital sets involves six electrons (3↑, 3↓) for d-t2g and 4 electrons (2↑, 2↓) for d-eg, adhering to the maximum capacity of 10 electrons in d-orbitals. The electron filling, determining whether a high spin or low spin state is formed, depends on crystal field splitting and the interaction of weak or strong ligands with the central metal atom. Given the weak field ligand Cl/Br/I surrounding the central metal, the splitting is small, and electron filling aligns with Hund's rule. For Mn+2 in the Mn-d orbital, the electron filling occurs as 3t2g(↑), 2eg(↑), 0t2g(↓), and 0eg(↓). The Mn-d-t2g and Mn-d-eg orbitals each have one electron for the spin-up state, and for the opposite spin-down state, these orbitals remain empty. Consequently, the energy levels of Mn-d-t2g and Mn-d-eg manifest their presence in the valence band, forming the valence band maximum (VBM), while the unoccupied states in the spin-down channel reside in the conduction band, forming the conduction band minimum (CBM). Additionally, the p-states of Cl/Br/I, which accept electrons from cations, are situated in the valence band. The collective portrayal of these energy states thus illustrates the semiconducting electronic structure of these alloys. This semiconducting ferromagnetic behaviour certifies their potential applications in optical devices such as light-emitting diodes (LEDs) and semiconductor lasers.
| Material | Method | K (μB) | Ge (μB) | Mn (μB) | Cl/Br/I (μB) | Interstitial (μB) | Total (μB) |
|---|---|---|---|---|---|---|---|
| K2GeMnCl6 | GGA+U | 0.00 | 0.04 | 4.64 | 0.020 | 0.14 | 5.00 |
| GGA+mBJ | 0.00 | 0.03 | 4.63 | 0.026 | 0.15 | 5.00 | |
| K2GeMnBr6 | GGA+U | 0.00 | 0.06 | 4.61 | 0.022 | 0.17 | 5.00 |
| GGA+mBJ | 0.00 | 0.05 | 4.59 | 0.024 | 0.19 | 5.00 | |
| K2GeMnI6 | GGA+U | 0.00 | 0.07 | 4.52 | 0.019 | 0.23 | 5.00 |
| GGA+mBJ | 0.00 | 0.05 | 4.50 | 0.022 | 0.22 | 5.00 |
Furthermore, we determined the Curie temperature (TC), which indicates the temperature at which a ferromagnetic or ferrimagnetic substance loses its permanent magnetization. Herein, we theoretically estimated the Curie temperature using the mean-field approximation (MFT) based on the Heisenberg model. In this approach, the Curie temperature for magnetic systems is calculated as18,40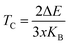 , where ΔE is a fundamental parameter in the Heisenberg model of the mean-field approximation and kB is the Boltzmann constant. The projected Curie temperatures for the compounds K2GeMnCl6, K2GeMnBr6, and K2GeMnI6 are estimated to be 710 K, 650 K, and 570 K, respectively. Notably, these values significantly surpass those typically observed in double perovskite oxides. To elucidate the exceptionally high Curie temperatures manifested by the halide double perovskites in comparison to their oxide counterparts, a comparative analysis is conducted between the present halide perovskite K2GeMnCl6 and the double perovskite Bi2CrOsO6. This comparative exploration aims to uncover the underlying factors contributing to the elevated Curie temperature (TC) in these halide perovskite systems. Exchange parameters are determined by their coupling styles. Given that the distance between two adjacent transition metal ions exceeds 7.0 Å, any direct coupling between them is expected to be negligible. Instead, the primary contributor to the ultrahigh TC is identified as the indirect exchange coupling facilitated through GeX6 groups situated between the two transition metal ions. In Fig. 7, a pronounced coupling between Mn 3d and Cl/Br/I 3p/4p/5p orbitals is evident. Consequently, the indirect coupling is elucidated as a 90° quasi-super exchange model between Mn 3d and GeBr6σs–p* orbitals. In contrast, the coupling model for double perovskite oxides (DPOs) involves an 180° super exchange mechanism, characterized by Cr(d)–O(p)–Os(d) interactions. Notably, the application of a 90° super exchange interaction is deemed more suitable for ferromagnetic interactions compared to the 180° super exchange model, aligning with Pauli's exclusion principle.
, where ΔE is a fundamental parameter in the Heisenberg model of the mean-field approximation and kB is the Boltzmann constant. The projected Curie temperatures for the compounds K2GeMnCl6, K2GeMnBr6, and K2GeMnI6 are estimated to be 710 K, 650 K, and 570 K, respectively. Notably, these values significantly surpass those typically observed in double perovskite oxides. To elucidate the exceptionally high Curie temperatures manifested by the halide double perovskites in comparison to their oxide counterparts, a comparative analysis is conducted between the present halide perovskite K2GeMnCl6 and the double perovskite Bi2CrOsO6. This comparative exploration aims to uncover the underlying factors contributing to the elevated Curie temperature (TC) in these halide perovskite systems. Exchange parameters are determined by their coupling styles. Given that the distance between two adjacent transition metal ions exceeds 7.0 Å, any direct coupling between them is expected to be negligible. Instead, the primary contributor to the ultrahigh TC is identified as the indirect exchange coupling facilitated through GeX6 groups situated between the two transition metal ions. In Fig. 7, a pronounced coupling between Mn 3d and Cl/Br/I 3p/4p/5p orbitals is evident. Consequently, the indirect coupling is elucidated as a 90° quasi-super exchange model between Mn 3d and GeBr6σs–p* orbitals. In contrast, the coupling model for double perovskite oxides (DPOs) involves an 180° super exchange mechanism, characterized by Cr(d)–O(p)–Os(d) interactions. Notably, the application of a 90° super exchange interaction is deemed more suitable for ferromagnetic interactions compared to the 180° super exchange model, aligning with Pauli's exclusion principle.
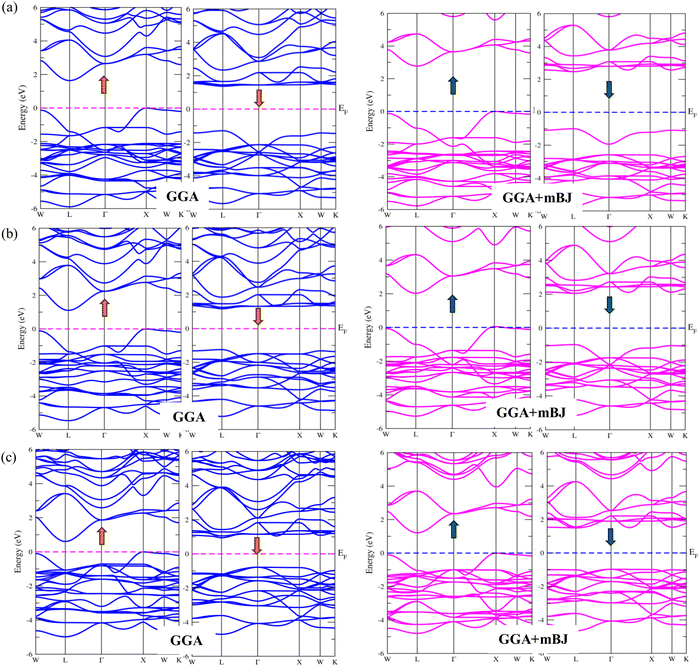
For a compound exhibiting ferromagnetic interaction, the Curie–Weiss law predicts a positive value for the Curie–Weiss constant, denoted as Tθ. Conversely, a negative Tθ value suggests the prevalence of antiferromagnetic interactions among transition metals. The calculation of magnetic susceptibility is employed to identify the magnetic ground state. The magnetic susceptibility curves in Fig. 8 distinctly reveal that the reciprocal of the susceptibility curve yields positive values for the Curie–Weiss constant (Tθ) at approximately 101 K, 100 K and 90 K for K2GeMnCl6, K2GeMnBr6 and K2GeMnI6, respectively. For Tθ > 0, signifying the presence of ferromagnetic interactions, the explanation provided by the Curie–Weiss law40 holds true. Consequently, the stable ground state for K2GeMnX6 (X = Cl, Br, I) compounds is identified as the ferromagnetic phase.
3.6. Electron charge density distribution
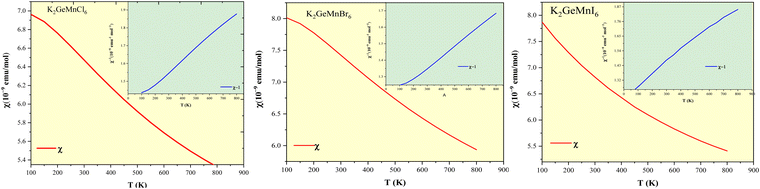
The analysis of electronic charge density provides a unique perspective for understanding the chemical stability of K2GeMnX6 (X = Cl, Br, I) perovskites. In this context, we present the spin-polarized charge densities along the (111) plane, as depicted in Fig. 9. Notably, maximum electron cloud density is observed at the atomic positions. Our investigation aims to estimate and elucidate the bonding characteristics among distinct atoms interacting within their lattice structures. In accordance with Pauling's theory, a chemical bond is deemed to exist between two atoms when the bonding force is exceptionally strong. Furthermore, electronegative atoms are those that accept electrons, while electropositive atoms are characterized by electron donation. This characterization is applicable to all the systems under consideration. The analysis discerns the presence of ionic bonding between K and X(Cl/Br/I) atoms, where the electron cloud surrounding K and X(Cl/Br/I) atoms is notably spherical. On the contrary, the bonding between Ge/Mn and X (Cl/Br/I) atoms demonstrates a purely covalent nature. This is evidenced by the presence of dumbbell-shaped electron clouds along Ge/Mn-X(Cl/Br/I) bonds, indicating the sharing of charge between Ge/Mn and X(Cl/Br/I) atoms. The overlapping charge contours signify orbital hybridization between Ge/Mn and Cl/Br/I, also confirmed by the partial density of states (PDOS) distribution, revealing Mn-3d-X-p hybridization. The overall depiction reveals the presence of polar covalent bonding, a combination of covalent and ionic bonding intrinsic to these compounds.3.7. Optical and dielectric properties
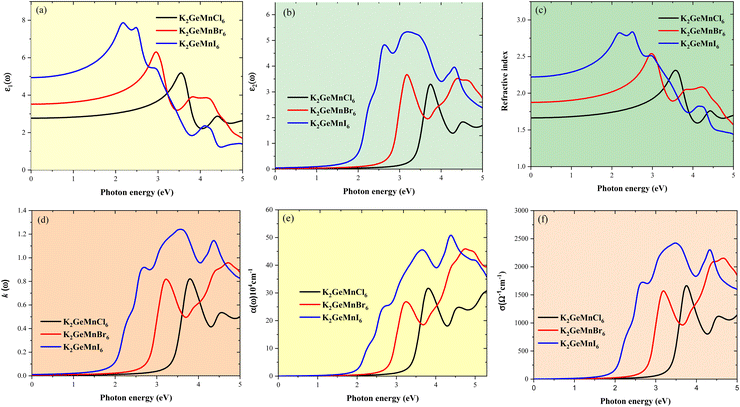
The assessment of a semiconductor's optical properties often entails the determination of band gaps and the complex dielectric function, denoted as ε(ω). This function comprises of two components, ε(ω) = ε1(ω) + iε2(ω), where ε1(ω) describes the scattering behavior of the material. Conversely, the imaginary part ε2(ω) exhibits a direct correlation with the material's band structure, reflecting its absorptive behavior and offering valuable insights into material selection for solar cell technology applications. The interplay between the dielectric constant components adheres to the principles outlined by the Kramers–Kronig relationships.34 Given the ferromagnetic semiconducting behavior observed in both spin channels of the materials under investigation, we assessed their optical properties by merging contributions from both spin channels to present a comprehensive optical response. Herein, we computed essential optical parameters for K2GeMnX6 halides as functions of photon energy, encompassing the dielectric function, refractive index, extinction coefficient, absorption coefficient, and optical conductivity, as illustrated in Fig. 10(a–f). This investigation aims to understand their capability to absorb visible light and their interaction with externally applied electromagnetic fields.We begin by examining the graphical variations in the real component of the dielectric function (ε1(ω) concerning photon energy, as depicted in Fig. 10(a). It is observed that the dielectric constant exhibits a systematic increase with changing halide ions, progressing from Cl to I. Notably, K2GeMnI6 exhibits higher static dielectric constants due to its smaller band gap, enabling reduced energy barriers for charge carrier movement. This facilitates carrier screening from charged defects within the crystal lattice, resulting in elevated dielectric constants. A high static dielectric constant facilitates the screening of carriers from charged defects within a crystal, thereby reducing carrier trapping and scattering. This reduction in scattering can result in semiconductors achieving longer carrier diffusion lengths and improved mobility lifetime outcomes. As photon energy increases, the spectra of all compounds show an upward trend. In the visible spectrum, K2GeMnI6 manifests a peak dielectric constant of about 8.0 at approximately 2.2 eV, whereas K2GeMnCl6 and K2GeMnBr6 attain maximal values of 5.1 and 6.2, respectively, at around 3.5 eV and 3 eV. Subsequently, multiple peaks are observed at different photon energies. Furthermore, Fig. 10(a) illustrates that transitioning the halide from Cl to I in K2GeMnX6 shifts the curves towards the visible energy range with increased amplitude. Consequently, there is an augmentation in the ε1 spectra, accompanied by a shift of peaks towards lower energies. The imaginary part of the dielectric function signifies the absorption or dissipation of light as it traverses through a material. In Fig. 10(b), the calculated imaginary dielectric spectra (ε2(ω) of K2GeMnX6 are presented. These spectra exhibit various peaks with varying amplitudes, resulting from potential electronic transitions from the valence band to the conduction band. Within the visible light range, the first peak in the ε2(ω) curve corresponds to optical transitions between the highest valence bands of X (Cl-3p, Br-4p, or I-5p) and the lowest conduction bands of Mn-3d states. Additionally, a second significant peak in the energy range of 3.8 to 5.7 eV arises from optical transitions between the highest valence bands of Cl-3p, Br-4p, or I-5p orbitals and the conduction bands of Ge-p orbitals, situated far from the Fermi level. For K2GeMnCl6, K2GeMnBr6, and K2GeMnI6, their respective maximum values of 3.4, 3.6, and 5.4 occur at approximately 3.8 eV, 3.3 eV, and 3.3 eV. Notably, K2GeMnI6 exhibits a significant initial peak (4.9) at 2.6 eV, indicating its robust response to visible light. The inclusive analysis highlights the potential of inorganic K2GeMnX6 perovskites as promising alternatives to organolead halide perovskites.
Next, we examine the graphical fluctuations of the refractive index, n(ω), and the extinction coefficient, k(ω), with respect to photon energy, as illustrated in Fig. 10(c) and (d) respectively. The refractive index quantifies the speed of light propagation through a material, while the extinction coefficient describes the attenuation of light as it traverses the medium due to absorption and scattering per unit distance. The static refractive index values, n(0), are determined to be 1.6, 1.8, and 2.2 for K2GeMnCl6, K2GeMnBr6, and K2GeMnI6, respectively. Beyond the zero-frequency limit, the refractive index reaches its maximum value of 2.3 at approximately 3.5 eV for K2GeMnCl6, 2.55 at 3.0 eV for K2GeMnBr6 and 2.8 at 2.2 eV for K2GeMnI6, followed by a consistent decrease with increasing photon energy. This decline in the refractive index is likely attributed to the optical dispersion behavior of these materials. Conversely, the extinction coefficient, k(ω), exhibits a profile resembling the imaginary part of the dielectric constant. Notably, significant absorption is observed in k(ω), featuring peaks situated around 2.5 eV and 3.5 eV for K2GeMnI6, and approximately 3.7 eV and 3.2 eV for K2GeMnCl6 and K2GeMnBr6.
The absorption coefficient (α(ω)) serves as a crucial parameter for characterizing the photovoltaic properties of semiconductors, governing the extent to which light penetrates a medium and indicating the semiconductor's capability to capture light effectively. Fig. 10(e) illustrates the computed absorption spectra of K2GeMnX6 compounds against photon energy, showcasing prominent peaks spanning both the visible and ultraviolet spectral regions. It is evident that the absorption coefficients surpass 104 cm−1 for all compounds, with K2GeMnBr6 and K2GeMnI6 demonstrating optimal light absorption characteristics in the visible light range, while K2GeMnCl6 exhibits optimum absorption properties in the ultraviolet region. Specifically, in the energy range of 0–5.5 eV, K2GeMnI6 and K2GeMnBr6 demonstrate maximum light absorption of 50 × 104 cm−1 and 45 × 104 cm−1 at a photon energy of 4.5 eV and 4.8 eV, whereas K2GeMnCl6 exhibits an optimal absorption value of 33 × 104 cm−1 at approximately 5.3 eV. Peaks observed away from zero energy indicate the absence of energy states at the Fermi level, confirming the semiconducting nature of these materials. The significant absorption coefficients in the visible and ultraviolet spectrum primarily stem from the abundant and localized density of states near the Fermi level, coupled with the materials’ low band gap. Moreover, as halogen anions increase in size, the absorption spectrum shifts towards the redshift direction, consistent with the band gap trend discussed above. A solar absorber characterized by a high absorption coefficient is highly advantageous for optimizing cell performance due to the minimized travel distance required for photogenerated carriers prior to recombination. This effectively diminishes non-radiative recombination processes, consequently leading to a significant enhancement in the open circuit voltage of photovoltaic cells. The utilization of thin absorber layers, facilitated by the high absorption coefficients, contributes to a reduction in the fabrication costs associated with solar cells. The optical conductivity (σ) of these halide perovskites exhibits a similar variation as the optical absorption, as depicted in Fig. 10(f). This correlation arises from the fact that absorbed photons generate conduction carriers, thereby increasing conductivity. From Fig. 10(f), it can be inferred that these perovskites display high optical conductivity in the low-energy region. Specifically, K2GeMnI6 exhibits the highest magnitude of conductivity spectra, while the remaining compounds show slightly lower values, suggesting superior optical conductivity for K2GeMnI6 compared to the others. The elevated optical conductivity values further underscore the potential of these materials for photovoltaic applications. To conclude, Ge-based halide perovskites demonstrate enhanced optical characteristics when compared to their Pb and Sn counterparts, indicating encouraging directions for further experimental exploration.
3.8. Thermoelectric coefficients
The thermoelectric effect refers to the phenomenon where a temperature gradient applied across a material results in the generation of an electric voltage or current. This effect is utilized in thermoelectric devices for various applications, including power generation and temperature regulation. The key focus in this process is the figure of merit (zT), which quantifies the efficiency of the material in terms of interdependent thermoelectric parameters. Specifically, zT is determined from the association between the Seebeck coefficient (S), electrical conductivity (σ), thermal conductivity (κ), and temperature (T) according to the equation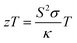 . This relationship highlights the importance of minimizing thermal conductivity (κ) while maximizing the square of the Seebeck coefficient (S) and electrical conductivity (σ) to achieve high output from a thermoelectric device. All these parameters have been determined using the Boltzmann transport theory within the rigid band approximation and constant relaxation time (τ) approximation, implemented through the BoltzTraP code.26 The electron relaxation time (τ), a crucial parameter in evaluating thermoelectric properties, represents the average duration between successive electron scattering events. The approximation assumes limited energy dependence of thermoelectric parameters at the scale of thermal agitation (kBT).48 As long as the scattering time changes gradually with energy, thermoelectric coefficients like electronic thermal conductivity (κe/τ), electrical conductivity (σ/τ), and figure of merit
. This relationship highlights the importance of minimizing thermal conductivity (κ) while maximizing the square of the Seebeck coefficient (S) and electrical conductivity (σ) to achieve high output from a thermoelectric device. All these parameters have been determined using the Boltzmann transport theory within the rigid band approximation and constant relaxation time (τ) approximation, implemented through the BoltzTraP code.26 The electron relaxation time (τ), a crucial parameter in evaluating thermoelectric properties, represents the average duration between successive electron scattering events. The approximation assumes limited energy dependence of thermoelectric parameters at the scale of thermal agitation (kBT).48 As long as the scattering time changes gradually with energy, thermoelectric coefficients like electronic thermal conductivity (κe/τ), electrical conductivity (σ/τ), and figure of merit 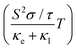 can be conveniently expressed in terms of τ.
can be conveniently expressed in terms of τ.
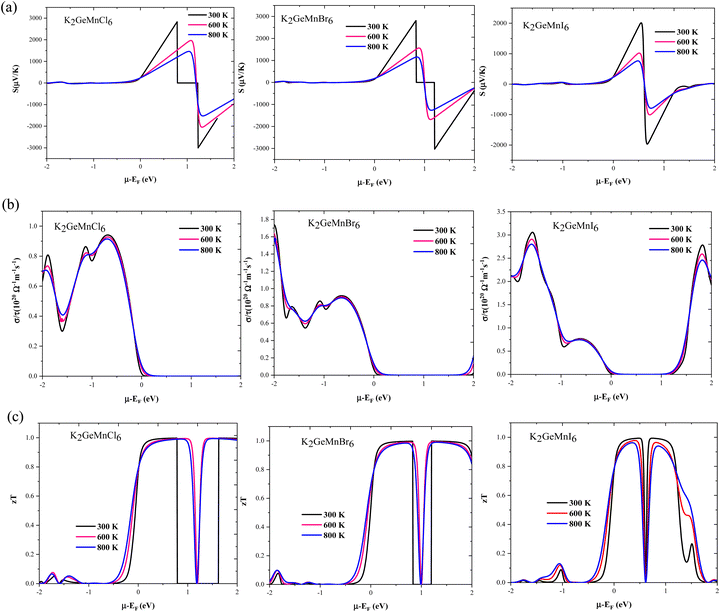
In the course of this investigation, we thoroughly examined the impact of thermoelectric coefficients on both temperature variations and chemical potential dependency, as illustrated in Fig. 11(a–e) and 12 (a–c) The anticipated ferromagnetic behavior of the investigated compounds prompts an exploration into the influence of magnetism on thermoelectric parameters. To discern this effect, we employed the two-current model,40 a theoretical framework tailored for analysing the interplay between magnetism and thermoelectric properties, particularly prevalent in ferromagnetic materials. In this model, the electronic transport is delineated separately for spin-up (↑) and spin-down (↓) electrons, acknowledging their distinct contributions owing to magnetization. Within ferromagnetic materials, magnetization induces spin-dependent electronic transport phenomena, where spin-up and spin-down electrons encounter disparate scattering mechanisms and mobility due to interactions with local magnetic moments. Consequently, quantities such as electrical conductivity (σ), electronic thermal conductivity (κe), and Seebeck coefficient (S) become spin-dependent variables, denoted as σ(↑), σ(↓), κe(↑), κe(↓), S(↑), and S(↓) respectively. Through the application of the two-current model, we computed the total electrical conductivity (σ = σ(↑) + σ(↓)), total electronic thermal conductivity (κe = κe(↑) + κe(↓)), and total Seebeck coefficient 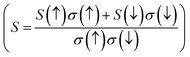 . Here, S(↑), S(↓), σ(↑), and σ(↓) represent the Seebeck coefficient and electrical conductivity for spin-up and spin-down directions, respectively.
. Here, S(↑), S(↓), σ(↑), and σ(↓) represent the Seebeck coefficient and electrical conductivity for spin-up and spin-down directions, respectively.
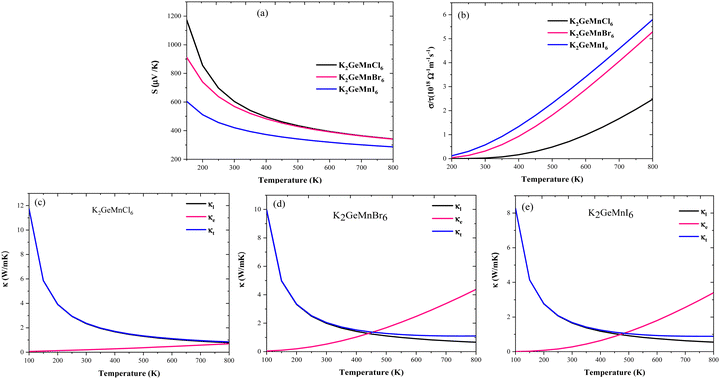 | ||
| Fig. 11 Temperature variations for (a) Seebeck coefficient, (b) electrical conductivity, and (c)–(e) lattice, electronic and total thermal conductivity of K2GeMnX6 halide perovskites. | ||
The subsequent detailed analysis of thermoelectric coefficients against temperature variations (200–800 K) and chemical potential dependency (−2 to 2 eV) is discussed below.
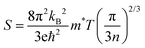 . Semiconductors behave as insulators at absolute zero (T = 0 K) due to the absence of current carriers, resulting in the expectation of an infinitely large S at absolute zero temperature. However, as the temperature rises, electrons acquire sufficient thermal energy to transition from the valence band to the conduction band, generating electron–hole pairs and consequently diminishing the magnitude of the Seebeck coefficient, as evident in Fig. 11(a).
. Semiconductors behave as insulators at absolute zero (T = 0 K) due to the absence of current carriers, resulting in the expectation of an infinitely large S at absolute zero temperature. However, as the temperature rises, electrons acquire sufficient thermal energy to transition from the valence band to the conduction band, generating electron–hole pairs and consequently diminishing the magnitude of the Seebeck coefficient, as evident in Fig. 11(a).
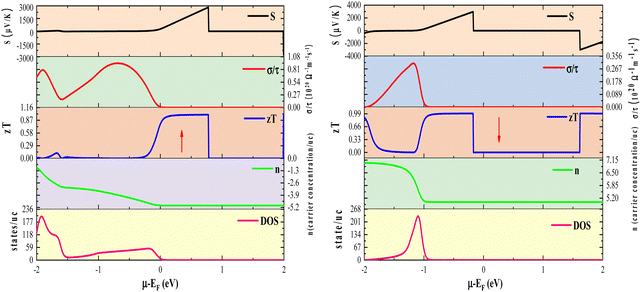
In addition to temperature, we also scrutinized the impact of chemical potential (−2 ≤ μ ≥ 2) on the total Seebeck coefficient at different temperatures (300 K, 600 K, 800 K), as illustrated in Fig. 12(a). The polarity of the Seebeck coefficient serves as an indicator of the type of charge carriers, with a positive sign denoting p-type carriers and a negative sign indicating n-type charge carriers. The magnitude of the Seebeck coefficient is intricately linked to the behaviour of energy levels in proximity to the Fermi level. Across the entire range of chemical potential (−2 to 2) eV, the Seebeck coefficient exhibits distinct peaks and valleys on either side of the Fermi level (set at zero). Particularly, prominent peaks manifest in the energy range of 0.5–2 eV for all three materials, where electronic states are either negligible or very limited, resulting in lower carrier concentration and pronounced peaks in this region. Preceding and succeeding this range, the presence of electronic states is evident, which subsequently diminishes the peaks almost to zero. At room temperature, the maximum Seebeck coefficients are ±2900 μV K−1 for K2GeMnCl6, ±2600 μV K−1 for K2GeMnBr6, and ±2000 μV K−1 for K2GeNiI6. These values are notably high, with K2GeMnCl6 exhibiting a relatively high Seebeck coefficient, attributed to its larger band gap. The elevated Seebeck coefficient values in these materials can be ascribed to their semiconducting behavior observed in both spin channels. To further elucidate the mechanism behind the high Seebeck coefficient of these compounds, we plotted the Seebeck coefficient alongside the volumetric density of states (DOS) and carrier concentration for K2GeMnCl6 in both spin channels, as depicted in Fig. 13. While a similar behavior is observed in other compounds, their data are omitted here for brevity. The Seebeck coefficient displays peaks in the energy range of 0–1 eV in the spin-up channel and −1 to 0 eV in the spin-down channel, coinciding with regions where the volumetric DOS is either low or negligible. This leads to low carrier concentration predominantly of p-type, facilitating a higher Seebeck coefficient by promoting increased carrier mobility, optimizing energy levels, and minimizing carrier scattering and Auger recombination. Furthermore, in semiconductors, the Seebeck coefficient is intricately linked to the electronic band structure near the Fermi level. At reduced carrier concentrations, the Fermi level tends to approach the band edges, leading to a pronounced gradient in the density of states. This phenomenon augments the Seebeck coefficient by enlarging the reservoir of available states accessible to charge carriers, thereby intensifying the thermoelectric response.
From Fig. 12(a), it is evident that at 800 K, the peak Seebeck coefficients experience a decrease to approximately ±1500 μV K−1 for K2GeMnCl6, ±1000 μV K−1 for K2GeMnBr6, and ±700 μV K−1 for K2GeMnI6. These results align precisely with the Mott relation, a fundamental expression capturing the dependence of the Seebeck coefficient on chemical potential and temperature, given as50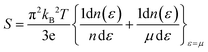 . This equation elucidates that as both chemical potential (μ) and temperature (T) increase, the Seebeck coefficient experiences a decline. This behaviour can be attributed to the stimulation of both types of carriers, resulting in a bipolar effect. Nevertheless, the given compounds effectively avoid the bipolar effect as their band gaps exceed the critical threshold of 0.64 eV, below which the bipolar effect is typically observed. Therefore, the presence of a non-zero Seebeck coefficient (S) even at elevated temperatures suggests promising potential for these materials in various applications such as thermoelectric generators, thermoelectric coolers, thermocouples, and temperature sensors.
. This equation elucidates that as both chemical potential (μ) and temperature (T) increase, the Seebeck coefficient experiences a decline. This behaviour can be attributed to the stimulation of both types of carriers, resulting in a bipolar effect. Nevertheless, the given compounds effectively avoid the bipolar effect as their band gaps exceed the critical threshold of 0.64 eV, below which the bipolar effect is typically observed. Therefore, the presence of a non-zero Seebeck coefficient (S) even at elevated temperatures suggests promising potential for these materials in various applications such as thermoelectric generators, thermoelectric coolers, thermocouples, and temperature sensors.
In the context of the chemical potential dependency of total electronic conductivity, we have graphically represented the total electrical conductivity at different temperatures (300, 600, and 800), as illustrated in Fig. 12(b). The most prominent peaks occur around −2 to 0 eV for all the three materials. Notably, K2GeMnCl6 exhibits higher band gap values in both spin channels compared to K2GeMnB6 and K2GeMnI6, leading to conductivity peaks slightly offset from the Fermi level. However, the presence of energy states at the Fermi level in one spin state contributes to the overall conductivity peaks at the Fermi value, specifically originating from spin-up electrons. Nevertheless, peaks on both sides of zero chemical potential arise from contributions by both types of spin electrons. Upon comparison of Fig. 12(a) with Fig. 12(b), it becomes evident that the Seebeck coefficient manifests peaks coinciding with conductivity minima, while conductivity exhibits peaks where the Seebeck coefficient is low or negligible. This association arises from the direct dependence of conductivity on carrier concentration (‘n’), while the Seebeck coefficient varies inversely with ‘n’.40 In order to deepen our comprehension of the relationship between electrical conductivity and chemical potential, we have constructed plots illustrating the total electrical conductivity (σ/τ), carrier concentration (n), and volumetric density of states (DOS) as functions of chemical potential at a temperature of 300 K. These plots specifically pertain to the compound K2GeMnCl6, as depicted in Fig. 13 (others are not shown for brevity). Corresponding to the pseudo gap in the band structure, carrier concentration sharply decreases, leading to peaks in the Seebeck coefficient. On the other side, conductivity demonstrates peaks at chemical potentials corresponding to densely populated bands.
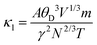 ; here, each symbol carries its usual significance. The Slack model elucidates that lattice thermal conductivity is influenced by multiple factors, including the Debye temperature (θD), Gruneisen parameter (γ), temperature (T), volume (V), average molar mass per atom (m), and the number of atoms per unit cell (N). The parameter A is determined as51A
; here, each symbol carries its usual significance. The Slack model elucidates that lattice thermal conductivity is influenced by multiple factors, including the Debye temperature (θD), Gruneisen parameter (γ), temperature (T), volume (V), average molar mass per atom (m), and the number of atoms per unit cell (N). The parameter A is determined as51A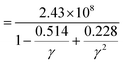 . Lattice thermal conductivity (κl), inversely proportional to temperature, diminishes as temperature rises for all three materials, as depicted in Fig. 11(c, d and e). The thermodynamic parameters required to compute lattice thermal conductivity in Slack's equation exhibit modest temperature variations, with the magnitude primarily dependent on the number of atoms per unit cell. Notably, the presence of 10 atoms per unit cell, combined with intricate cage structures housing small atoms, results in a remarkably low lattice thermal conductivity at room temperature. This phenomenon can be attributed to heightened anharmonic phonon scattering due to the clustering of heavier elements, commonly referred to as the 'phonon rattling effect'.52 Conversely, electronic thermal conductivity displays an upward trajectory with rising temperature. Higher temperatures amplify the thermal energy of carriers, consequently enhancing electronic thermal conductivity. At temperatures below 300 K, the lattice component of thermal conductivity prevails over the electronic contribution. However, with increasing temperature up to approximately 900 K, the lattice thermal conductivity of all the given materials exhibits a consistent decrease. Specifically, at 300 K, the computed lattice thermal conductivity values are 2.2 W mK−1, 2.0 W mK−1, and 1.7 W mK−1 for K2GeMnCl6, K2GeMnBr6, and K2GeMnI6, respectively. These modest κl values observed in these materials hint at a promising potential for enhanced thermoelectric performance. Notably, at higher temperatures, the total thermal conductivity is predominantly influenced by the electronic component due to the reduced contribution from the lattice. This overall low heat-carrying capacity positions these double perovskites as promising candidates for efficient waste heat harvesting applications.
. Lattice thermal conductivity (κl), inversely proportional to temperature, diminishes as temperature rises for all three materials, as depicted in Fig. 11(c, d and e). The thermodynamic parameters required to compute lattice thermal conductivity in Slack's equation exhibit modest temperature variations, with the magnitude primarily dependent on the number of atoms per unit cell. Notably, the presence of 10 atoms per unit cell, combined with intricate cage structures housing small atoms, results in a remarkably low lattice thermal conductivity at room temperature. This phenomenon can be attributed to heightened anharmonic phonon scattering due to the clustering of heavier elements, commonly referred to as the 'phonon rattling effect'.52 Conversely, electronic thermal conductivity displays an upward trajectory with rising temperature. Higher temperatures amplify the thermal energy of carriers, consequently enhancing electronic thermal conductivity. At temperatures below 300 K, the lattice component of thermal conductivity prevails over the electronic contribution. However, with increasing temperature up to approximately 900 K, the lattice thermal conductivity of all the given materials exhibits a consistent decrease. Specifically, at 300 K, the computed lattice thermal conductivity values are 2.2 W mK−1, 2.0 W mK−1, and 1.7 W mK−1 for K2GeMnCl6, K2GeMnBr6, and K2GeMnI6, respectively. These modest κl values observed in these materials hint at a promising potential for enhanced thermoelectric performance. Notably, at higher temperatures, the total thermal conductivity is predominantly influenced by the electronic component due to the reduced contribution from the lattice. This overall low heat-carrying capacity positions these double perovskites as promising candidates for efficient waste heat harvesting applications.
To elucidate the high thermoelectric figure of merit of these materials and explore avenues for further enhancing the achieved zT values, we conducted a comparative analysis of the graphical variations in density of states (DOS), carrier concentration (n), and figure of merit (zT) at 300 K for K2GeMnCl6 in both spin-up and spin-down channels, as shown in Fig. 13. Given the consistent behavior observed across all three materials, our examination focuses exclusively on the K2GeMnCl6 halide perovskite. Peaks in zT, as depicted in Fig. 13, are notably prominent within the energy range of −1 to 1 eV in both spin channels, attributable to diminishing electronic states in the DOS, resulting in a low carrier concentration, primarily of p-type, within this energy range. The reduction in the concentration of p-type carriers results in an increase in the Seebeck coefficient (S), as elucidated in the preceding discussion on the Seebeck coefficient. As a consequence, the heightened Seebeck coefficient enhances the thermoelectric voltage, thereby amplifying the zT value. However, it is pertinent to note that the attained zT values can be further enhanced through the application of strain effects or optimization of hole doping strategies, as demonstrated in previous studies.53
Conclusion
In summary, we have undertaken a comprehensive investigation into the structural, magneto-electronic, optical and transport properties of K2GeMnX6 (X = Cl, Br, I). The optimization of the structures ensures stability in the ferromagnetic phase, corroborated by positive Curie–Weiss constant values. Mechanical stability tests, tolerance factor evaluations, and negative enthalpy of formation further confirm the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m cubic stability of these materials. Through the study of phonon dispersions, we have gained insights into the dynamic characteristics of these perovskites. The electronic properties, as delineated by the TB-mBJ functional scheme, affirm the ferromagnetic semiconducting nature of all three materials, characterized by a significant spin-splitting gap (0.28–1.02 eV), indicating their promising prospects for semiconductor spintronics. The magnetic character of K2GeMnX6 (X = Cl, Br, I) perovskites has been determined to exhibit an integer value of 5μB each, validating their suitability for magneto-electronic device applications. Furthermore, the determined Curie temperatures, surpassing typical room temperature values, underscore their high-temperature phase stability. Analysis of electronic charge density plots suggests a polar covalent nature, indicating a mix of covalent and ionic bonding. Exploration of thermodynamic vibrational properties, including vibrational internal energy, vibrational Helmholtz free energy, vibrational entropy, and vibrational specific heat, indicates stability across varying temperature regimes. Moreover, the computed optical coefficients, including the dielectric constant, refractive index, and absorption coefficient, exhibit peak values within the visible spectrum. Notably, significant absorption coefficient values of 33 × 104 cm−1 for K2GeMnCl6, 45 × 104 cm−1 for K2GeMnBr6 and 50 × 104 cm−1 for K2GeMnI6 are observed across the visible and ultraviolet spectra, highlighting their promising potential for application in optoelectronic and solar cell technologies. Finally, the thermoelectric coefficients demonstrate a significant Seebeck coefficient coupled with reduced thermal conductivity, yielding high thermoelectric figure of merit (zT) values of 1.01, 1.00, and 0.99 for K2GeMnCl6, K2GeMnBr6 and K2GeMnI6, respectively. These findings highlight the potential applications of these perovskites in renewable energy technologies. The comprehensive analysis suggests that these materials hold promise for deployment in solid-state devices, green energy technologies, and various other technological domains. Despite the insightful findings, challenges persist in experimental observation. These encompass achieving uniformity in synthesis, accurately probing nanoscale structures, interpreting dynamic properties, precisely controlling doping levels, and ensuring reliable measurements of thermal and thermoelectric properties. Challenges specific to magnetism involve understanding magnetic interactions and achieving uniform magnetization, while optimizing the figure of merit (zT) requires balancing multiple thermoelectric parameters. Moreover, tackling experimental hurdles associated with comprehending and regulating optical properties, including the precise determination of dielectric constants and absorption coefficients, is paramount. Addressing these challenges is essential for unlocking the full potential of K2GeMnX6 perovskites in applications pertaining to spintronics, optoelectronics and thermoelectric devices.
m cubic stability of these materials. Through the study of phonon dispersions, we have gained insights into the dynamic characteristics of these perovskites. The electronic properties, as delineated by the TB-mBJ functional scheme, affirm the ferromagnetic semiconducting nature of all three materials, characterized by a significant spin-splitting gap (0.28–1.02 eV), indicating their promising prospects for semiconductor spintronics. The magnetic character of K2GeMnX6 (X = Cl, Br, I) perovskites has been determined to exhibit an integer value of 5μB each, validating their suitability for magneto-electronic device applications. Furthermore, the determined Curie temperatures, surpassing typical room temperature values, underscore their high-temperature phase stability. Analysis of electronic charge density plots suggests a polar covalent nature, indicating a mix of covalent and ionic bonding. Exploration of thermodynamic vibrational properties, including vibrational internal energy, vibrational Helmholtz free energy, vibrational entropy, and vibrational specific heat, indicates stability across varying temperature regimes. Moreover, the computed optical coefficients, including the dielectric constant, refractive index, and absorption coefficient, exhibit peak values within the visible spectrum. Notably, significant absorption coefficient values of 33 × 104 cm−1 for K2GeMnCl6, 45 × 104 cm−1 for K2GeMnBr6 and 50 × 104 cm−1 for K2GeMnI6 are observed across the visible and ultraviolet spectra, highlighting their promising potential for application in optoelectronic and solar cell technologies. Finally, the thermoelectric coefficients demonstrate a significant Seebeck coefficient coupled with reduced thermal conductivity, yielding high thermoelectric figure of merit (zT) values of 1.01, 1.00, and 0.99 for K2GeMnCl6, K2GeMnBr6 and K2GeMnI6, respectively. These findings highlight the potential applications of these perovskites in renewable energy technologies. The comprehensive analysis suggests that these materials hold promise for deployment in solid-state devices, green energy technologies, and various other technological domains. Despite the insightful findings, challenges persist in experimental observation. These encompass achieving uniformity in synthesis, accurately probing nanoscale structures, interpreting dynamic properties, precisely controlling doping levels, and ensuring reliable measurements of thermal and thermoelectric properties. Challenges specific to magnetism involve understanding magnetic interactions and achieving uniform magnetization, while optimizing the figure of merit (zT) requires balancing multiple thermoelectric parameters. Moreover, tackling experimental hurdles associated with comprehending and regulating optical properties, including the precise determination of dielectric constants and absorption coefficients, is paramount. Addressing these challenges is essential for unlocking the full potential of K2GeMnX6 perovskites in applications pertaining to spintronics, optoelectronics and thermoelectric devices.
Data availability
The data sets generated and thereafter analysed would be available from the corresponding author upon reasonable request.Conflicts of interest
The authors declare no competing interest.Acknowledgements
Mudasir Younis Sofi, a recipient of the Prime Minister Research Fellowship (PMRF) award (Letter No. 3302522), wishes to express sincere gratitude to the PMRF agency (Ministry of Education (MoE), Govt. of India) for the financial support.References
- T. Dietl, H. Ohno, F. Matsukura, J. Cibert and E. D. Ferrand, Zener model description of ferromagnetism in zinc blende magnetic semiconductors, Science, 2000, 287, 1019 CrossRef CAS PubMed.
- Y. Huai, F. Albert, P. Nguyen, M. Pakala and T. Valet, Observation of spin-transfer switching in deep submicron-sized and low-resistance magnetic tunnel junctions, Appl. Phys. Lett., 2004, 84, 3118 CrossRef CAS.
- C. Chappert, A. Fert, F. Nguyen and V. Dau, The emergence of spin electronics in data storage, Nat. Mater., 2007, 6, 813 CrossRef CAS PubMed.
- M. C. Prestgard, G. P. Siegel and A. Tiwari, Oxides for Spintronics: A Review of Engineered Materials for Spin Injection, Adv. Mater. Lett., 2014, 5, 242 CrossRef.
- X. Li and J. Yang, First-principles design of spintronics materials, Natl. Sci. Rev., 2016, 3, 365 CrossRef CAS.
- K. L. Wang, J. G. Alzate and P. K. Amiri, Low-power non-volatile spintronic memory: STT-RAM and beyond, J. Phys. D: Appl. Phys., 2013, 46, 074003 CrossRef CAS.
- M. N. Baibich, J. M. Broto, A. Fert, F. N. van Dau, F. Petro, P. Eitenne, G. Creuzet, A. Friederich and J. Chazelas, Giant magnetoresistance of (001) Fe/(001)Cr magnetic superlattices, Phys. Rev. Lett., 1988, 61, 2472 CrossRef CAS PubMed.
- S. A. Wolf, D. D. Awschalom, R. A. Buhrman, J. M. Daughton, S. V. Molnár, M. L. Roukes, A. Y. Chtchelkanova and D. M. Treger, Spintronics: a spin-based electronics vision for the future, Science, 2001, 294, 1488 CrossRef CAS PubMed.
- J. Puebla, J. Kim, K. Kondou and Y. Otani, Spintronic devices for energy-efficient data storage and energy harvesting, Commun. Mater., 2020, 1, 24 CrossRef.
- U. Lüders, A. Barthélémy, M. Bibes, K. Bouzehouane, S. Fusil, E. Jacquet, J. P. Contour, J. F. Bobo, J. Fontcuberta and A. Fert, NiFe2O4: A Versatile Spinel Material Brings New Opportunities for Spintronics, Adv. Mater., 2006, 18, 1733–1736 CrossRef.
- T. S. Santos and J. S. Moodera, Observation of spin filtering with a ferromagnetic EuO tunnel barrier, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 241203 CrossRef.
- J. Moodera, X. Hao, G. Gibson and R. Meservey, Electron -spin polarization in tunnel junctions in zero applied field with ferromagnetic EuS barriers, Phys. Rev. Lett., 1988, 61, 637 CrossRef CAS PubMed.
- S. Zhe-Wen and L. Bang-Gui, Electronic structure and magnetic and optical properties of double perovskite Bi2FeCrO6 from first-principles investigation, Chin. Phys. B, 2013, 22, 047506 CrossRef.
- J. Wang, J. Meng and Z. Wu, Theoretical insights on the electron doping and Curie temperature in La-doped Sr2CrWO6, J. Comput. Chem., 2011, 32, 3313–3318 CrossRef CAS PubMed.
- E. Şaşıoğlu, L. Sandratskii, P. Bruno and I. Galanakis, Exchange interactions and temperature dependence of magnetization in half-metallic Heusler alloys, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 184415 CrossRef.
- X. Li and J. Yang, First-principles design of spintronics materials, Natl. Sci. Rev., 2016, 3, 365–381 CrossRef CAS.
- B. Náfrádi, P. Szirmai, M. Spina, H. Lee, O. Yazyev, A. Arakcheeva, D. Chernyshov, M. Gibert, L. Forró and E. Horváth, Optically switched magnetism in photovoltaic perovskite CH3NH3(Mn: Pb) I3, Nat. Commun., 2016, 7, 13406 CrossRef PubMed.
- B. Cai, X. Chen, M. Xie, S. Zhang, X. Liu, J. Yang, W. Zhou, S. Guo and H. Zeng, A class of Pb-free double perovskite halide semiconductors with intrinsic ferromagnetism, large spin splitting and high Curie temperature, Mater. Horiz., 2018, 5, 961 RSC.
- E. Haque and M. A. Hossain, Origin of ultra-low lattice thermal conductivity in Cs2BiAgX6 (X= Cl, Br) and its impact on thermoelectric performance, J. Alloys Compd., 2018, 748, 63 CrossRef CAS.
- M. Younis Sofi, M. Shahid Khan, J. Ali and M. Ajmal Khan, Unlocking the role of 3d electrons on ferromagnetism and spin-dependent transport properties in K2GeNiX6 (X = Br, I) for spintronics and thermoelectric applications, J. Phys. Chem. Solids, 2024, 112022, DOI:10.1016/j.jpcs.2024.112022.
- P. Blaha, K. Schwarz, G. K. H. Madsen, D. Kvasnicka, J. Luitz, R. Laskowsk, F. Tran, L. Marks and L. Marks, WIEN2k: An Augmented Plane Wave Plus Local Orbitals Program for Calculating Crystal Properties, Techn. Universitat, Vienna, Austria, 2019, p. 287 Search PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77(18), 3865 CrossRef CAS PubMed.
- D. Koller, F. Tran and P. Blaha, Improving the modified Becke–Johnson exchange potential, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85(15), 155109 CrossRef.
- T. Charpin: A Package for Calculating Elastic Tensors of Cubic Phases Using WIEN: Laboratory of Geometrix F-75252 (Paris, France) ( 2001).
- A. tero-de-la-Roza, D. Abbasi-Pérez and V. Luaña, Gibbs2: A new version of the quasi-harmonic model code. II. Models for solid state thermodynamics, features and implementation, Comput. Phys. Commun., 2011, 182(10), 2232–2248 CrossRef.
- G. K. Madsen and D. J. Singh, BoltzTraP. A code for calculating band-structure dependent quantities, Comput. Phys. Commun., 2006, 175(1), 67–71 CrossRef CAS.
- M. Houari, B. Bouadjemi and A. Abbad, et al., Lead-Free Semiconductors with High Absorption: Insight into the Optical Properties of K2GeSnBr6 and K2GeSnI6 Halide Double Perovskites, JETP Lett., 2020, 112, 364–369 CrossRef CAS.
- J. E. Saal, S. Kirklin, M. Aykol, B. Meredig and C. Wolverton, Materials Design and Discovery with High-Throughput Density Functional Theory: The Open Quantum Materials Database (OQMD), JOM, 2013, 65, 1501–1509, DOI:10.1007/s11837-013-0755-4.
- P. Giannozzi, et al., QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- M. Blanco, E. Francisco and V. Luaña, GIBBS: isothermal-isobaric thermodynamics of solids from energy curves using a quasi-harmonic Debye model, Comput. Phys. Commun., 2004, 158, 57–72 CrossRef CAS.
- Q. Chen and B. Sundman, Calculation of Debye temperature for crystalline structures case study on Ti, Zr, and Hf, Acta Mater., 2001, 49, 947–961 CrossRef CAS.
- D. V. Schroeder and J. K. Pribram, An Introduction to Thermal Physics, Am. J. Phys., 1999, 67, 1284–1285 CrossRef.
- P. Debye, Zur Theorie der spezifischen Warmen., Ann. Phys., 1912, 344, 789–839 CrossRef.
- M. Y. Sofi, M. S. Khan and J. Ali,
et al., Exploring the lead-free halide Cs2MGaBr6 (M
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
= ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Li, Na) double perovskites for sustainable energy applications, Sci. Rep., 2024, 14, 5520 CrossRef CAS PubMed.
Li, Na) double perovskites for sustainable energy applications, Sci. Rep., 2024, 14, 5520 CrossRef CAS PubMed. - A. T. Petit and P. L. Dulong, Study on the measurement of specific heat of solids, Ann. Chim. Phys., 1819, 10, 395 Search PubMed.
- M. Born, On the stability of crystal lattices, Math. Proc. Cambridge Philos. Soc., 1940, 36, 160 CrossRef CAS.
- W. Voigt, in Textbook of Crystal Physics, ed. G. B. Teubner, 1928 Search PubMed.
- A. Reuss, Berechnung Der Fließgrenze von Mischkristallen Auf Grund Der Plastizitätsbedingung Für Einkristalle, Z. Angew. Math. Mech., 1929, 9, 49–58 CrossRef CAS.
- R. Hill, Te elastic behaviour of a crystalline aggregate, Proc. Phys. Soc., London, Sect. A, 1952, 65, 349 CrossRef.
- M. Y. Sofi and D. C. Gupta, Scrutinized the inherent spin half-metallicity and thermoelectric response of f-electron-based RbMO3 (M
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
= ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Np, Pu) perovskites: a computational assessment, Sci. Rep., 2022, 12, 19476 CrossRef CAS PubMed.
Np, Pu) perovskites: a computational assessment, Sci. Rep., 2022, 12, 19476 CrossRef CAS PubMed. - S. F. Pugh, XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals, Philos. Mag., 1954, 45, 823–843 CAS.
- I. N. Frantsevich; F. F. Voronov and S. A. Bakuta, Elastic Constants and Moduli of Elasticity of Metals and Nonmetals, Naukova Dumka: Kiev, 1982.
- W. Hume-rothery, Elasticity and anelasticity of metals, Nature, 1949, 164(4159), 84–85 CrossRef.
- S. I. Ranganathan and M. Ostoja-Starzewski, Universal elastic anisotropy index, Phys. Rev. Lett., 2008, 101(5), 055504 CrossRef PubMed.
- D. M. Teter, Computational alchemy: The search for new superhard materials, MRS Bull., 1998, 23(1), 22–27 CrossRef CAS.
- Y. Tian, B. Xu and Z. Zhao, Microscopic theory of hardness and design of novel superhard crystals, Int. J. Refract. Met. Hard Mater., 2012, 33, 93–106 CrossRef CAS.
- E. Fine, L. D. Brown and H. L. Marcus, Elastic constants versus melting temperature in metals, Scr. Metall., 1984, 18, 951–956 CrossRef.
- H. Yilin, W. Yang, L. Tingzhou, Y. Tie and W. Xiaotian, Electronic, magnetic, half-metallic, and mechanical properties of a new equiatomic quaternary Heusler compound YRhTiGe: a first-principles study, Materials, 2018, 11, 797 CrossRef PubMed.
- M. Y. Sofi, M. S. Khan, J. Ali and M. Ajmal Khan, in Novel Thermoelectric Material Ba2AlNbO6 for Energy Harvesting Applications, ed. Khan, Z. H., Jackson, M., Salah, N. A., Recent Advances in Nanotechnology, ICNOC 2022, Springer Proceedings in Materials, Springer, 2023, vol 28, Singapore, pp. 85–91 Search PubMed.
- M. Jonson and G. D. Mahan, Mott's formula for the thermopower and the Wiedemann-Franz law, Phys. Rev. B: Condens. Matter Mater. Phys., 1980, 21, 4223–4229 CrossRef CAS.
- P. Nath, et al., High throughput combinatorial method for fast and robust prediction of lattice thermal conductivity, Scr. Mater., 2017, 129, 88–93 CrossRef CAS.
- Y. Ouyang, Z. Zhang, D. Li, J. Chen and G. Zhang, Emerging theory, materials, and screening methods: New opportunities for promoting thermoelectric performance, Ann. Phys., 2019, 531, 1800437 CrossRef CAS.
- C. W. Wu, X. Ren, G. Xie, W. X. Zhou, G. Zhang and K. Q. Chen, Enhanced High-Temperature Thermoelectric Performance by Strain Engineering in BiOCl, Phys. Rev. Appl., 2022, 18(1), 014053 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2024 |