Establishing synthesis–composition–property relationships for enhanced and reproducible thermoelectric properties of MgAgSb

Abstract

α-MgAgSb is a promising p-type thermoelectric (TE) with excellent performance from room temperature up to 300 °C with a figure of merit of zT_max = 1.3. This makes MgAgSb a potential Te-free bismuth telluride (Bi₂Te₃) substitute for cooling and waste heat conversion applications. However, the material is also known for its sensitivity on synthesis conditions as indicated by various reports on the same nominal composition which show greatly differing TE properties and performance. This indicates a fundamental lack of synthesis control and synthesis–composition–property relationship knowledge. In this work, we establish a modified synthesis route with improved control over the effective sample stoichiometry which allows for reproducible high-performance properties (zT_max = 1.34 ± 0.19 at 561 K) and for systematically targeting different thermodynamic states of MgAgSb. This phase boundary mapping reveals that the homogeneity range for MgAgSb is very small (<0.1 at%) and that the TE properties are not governed by different thermodynamic states. Instead, we rationalize that the TE performance of MgAgSb is mainly controlled by the amount and type of secondary phases, mainly affecting the carrier mobility. We conclude that Sb-excess related secondary phases are the least detrimental, leading the way to upscaled synthesis of high-performance material.

---

Introduction

The development of clean and durable energy technologies is a crucial necessity following from an ever increasing energy demand and the environmental impact of fossil fuel consumption.^1,2 Solar energy from photovoltaics is an interesting alternative to current energy suppliers but cannot be used everywhere and in all conditions.³ Hence, thermoelectric generators (TEG) converting thermal energy into electricity could be used as energy harvesting devices. TEGs are becoming a promising solution for waste heat recovery to address the energy crisis, making them a possible eco-friendly solution.^4,5 Radioisotope thermoelectric generators (RTG) used for power supply in space applications such as Voyager 1 and 2 or the mars rovers Curiosity and Perseverance demonstrate the usefulness and reliability of TEG for specific applications.^6,7

The conversion efficiency of thermoelectric devices is largely governed by the thermoelectric figure of merit 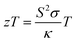, where S is the Seebeck coefficient, σ the electrical conductivity, T the absolute temperature and κ the thermal conductivity.⁸ For devices working across a temperature range from cold to hot temperature, respectively T_c to T_h, the temperature-averaged figure of merit is usually a good indicator for performance, even though it is physically not a strictly correct measure for maximum efficiency and other parameters have been introduced.^9–13 Recent works with encouraging results have shown TEGs reaching high energy conversion efficiency of around 8.5% with new types of non-toxic materials: Mg-based materials (MgAgSb and Mg₃Sb₂).¹⁴

The α-phase of MgAgSb has been identified by Kirkham et al.¹⁵ as a promising p-type thermoelectric material, and optimized by Liu et al.¹⁶ with a peak zT ∼ 1.3 at around 300 °C, which fills the performance gap between low- and high-temperature thermoelectric materials.¹⁷ Unlike Bi₂Te₃ the only state-of-the-art thermoelectric material for near room temperature applications, α-MgAgSb does not contain tellurium that is very rare (∼0.001 ppm in the Earth crust¹⁸), environmentally harmful and toxic. Furthermore, this material has many advantages such as good mechanical properties and a relatively high abundance of its constituents (Ag, Mg, Sb).^18,19

An effective synthesis route has been found by Zhao et al.²⁰ which consists of a two-step ball-milling synthesis. Liu et al. fine-tuned the nominal stoichiometry to achieve a maximal value of zT_max with the composition of MgAg_0.97Sb_0.995 which resulted in an average zT of 1.1 between room temperature and 300 °C.¹⁶ Further steps towards the technological implementation of MgAgSb-based devices have been demonstrated by Kraemer et al., continued by P. Ying et al. and numerically designed by band engineering by Tan et al.^21–23 The latter report the first performance values of thermoelectric modules assembled from Bi₂Te₃-substitute compounds, employing MgAgSb as p-type and Mg₃(Sb,Bi)₂ as n-type. Here, for a temperature difference of ∼250 K, a module using segmented n-type legs displayed a record efficiency of ∼7%, which is superior to most Bi₂Te₃-based thermoelectric modules.²² Furthermore, Liu et al. recently demonstrated an efficiency of 7.3% in a Mg₃Sb₂/MgAgSb module with a hot side temperature of 320 °C.²⁴

However, even though a synthesis route has been established²⁰ and repeatedly employed, the experimental results show that the thermoelectric properties are not easily reproducible. Indeed, several recent works on MgAgSb based devices report lower TE properties, zT_avg = 0.9,²²zT_avg = 0.9,²⁵zT_avg = 0.77,²⁶ compared to the original publication of Liu et al. reporting zT_avg = 1.1 (ref. 16) even though all followed the same synthesis route. An in-depth analysis from I. Rodriguez-Barber et al.²⁶ revealed that part of the explanation could be a variation in the formation of MgAg in the first ball milling step. He showed that the addition of a sintering step of MgAg before the addition of Sb into the mixture facilitates MgAg formation and hence improves the TE properties; this example shows how sensitive the material performance may react on synthesis details.

The TE properties of any material are a result of the properties of the main phase and the secondary phases as well as the interplay between both. It has been (re-) emphasized recently that the main phase properties of many TE materials are governed by intrinsic defects and that the TE properties of many materials can be tuned by targeting different thermodynamic states of “the same” nominal composition.^27–31 This was found to be particularly true for Mg-based materials like Mg₂(Si,Sn) and Mg₃(Sb,Bi)₂, where Mg-related intrinsic defects govern the carrier mobility and charge carrier concentration to an extent that this can be used to select the majority carrier type.^32–35 For MgAgSb, the main phase properties are likewise governed by intrinsic defects, e.g. Ag vacancies, Ag antisite defects on Mg sites, Sb vacancies^36–38 whose concentrations are linked to minimal changes in the composition. With respect to secondary phases the particular challenge for MgAgSb is first that several of the commonly found secondary phases (such as Ag₃Sb, Sb or Mg₃Sb₂) possess a high thermal stability and second that during the processing high temperature steps (>360 °C) are to be avoided as these would lead to the formation of the metallic γ-MgAgSb which shows high thermal stability below 300 °C.³⁹ While the detrimental effect of various secondary phases has been highlighted repeatedly, neither how they can be avoided nor how they impact the TE performance of MgAgSb has been addressed satisfyingly.

Therefore, a synthesis route that first allows for the reproducible fabrication of high performance MgAgSb and second for a quantitative assessment of the impact of secondary phases is needed. We achieve this by employing the following three steps: (i) fine tune the synthesis route for better reproducibility, (ii) analyze the impact of the processing changes on the resulting phases and TE properties, (iii) map the TE properties as a function of the effective composition. This allows us to identify a compositional range that leads to good TE properties and to unravel the different effects of interplay between MgAgSb matrix and different secondary phases, showing that some secondary phases are more detrimental than others regarding the TE properties. The analysis also indicates that the MgAgSb single phase region is compositionally narrow and the carrier concentration can be adjusted by the variation of intrinsic defects in a small window only, in contrast to other Mg-based TE materials. In this way, a comprehensive synthesis-composition–property relationship for MgAgSb was established.

Materials and methods

The two-step ball milling process developed by Zhao and al.²⁰ and later adapted by Liu and al.¹⁶ was used to synthesize α-MgAgSb samples. The stoichiometric amount of Mg (turnings, Merck KGaA, >99%), Ag (powder, <45 μm, Sigma Aldrich, >99.99%) was weighted according to the composition Mg_xAg_y (x = 1.02, 1.01, 1, 0.99, 0.98, 0.97, 0.94; y = 1, 0.97) and loaded in a stainless-steel jar (65 ml) with two stainless steel balls (12.7 mm diameter) under argon atmosphere. After a high-energy ball milling step for 8 hours (SPEX SamplePrep 8000D Mixer/Mill), the ball milling jar was cleaned while the Mg_xAg_y powder was hot pressed for 8 minutes at 673 K under 85 MPa using graphite foils on top and bottom in a 12.7 mm diameter graphite dies (Dr Fritsch DSP510) as introduced by Rodriguez-Baber et al.²⁶ The obtained Mg_xAg_y pellet was then crushed in the high-energy ball mill for 18 minutes, followed by the addition of Sb (granules, 3–15 mm, Sindlhauser Materials GmbH, 99.999%) according to the stoichiometry Mg_xAg_ySb_z (z = 1, 0.995). The mixture was then milled for 5 more hours under argon atmosphere and finally hot pressed for n minutes (n = 8–20–30–60 minutes) at 573 K under 85 MPa using the same graphite dies as before.

The electrical conductivity σ and the Seebeck coefficient S were measured with an in-house developed device.⁴⁰ The thermal diffusivity α was measured using an LFA 427 or an XFA 467 HTHyperflash (NETZSCH), and from this, the thermal conductivity κ was calculated as κ = αc_pρ, where c_p is the specific heat at constant pressure and ρ is the sample density. Constant c_p values can be assumed for this system and temperature range (obtained using Dulong–Petit's law)⁸ and ρ was calculated using the Archimedes method. The lattice thermal conductivity κ_lat is approximated by κ − κ_e, where κ_e is the electronic contribution to the thermal conductivity (κ_e = LσT, where L is the Lorenz number obtained from the Seebeck coefficient). The measurement uncertainties for the Seebeck coefficient, the electrical conductivity and the thermal conductivity are ±5%, ±5% and ±8%, respectively. X-ray diffraction (XRD) patterns were obtained using a Bruker D8 with a secondary monochromator, Cu-K_α radiation (1.5406 Å) and Co-K_α radiation (1.78897 Å), step size 0.01° in the 2θ range 20–80°. Microstructure characterization was performed using Secondary Electron Microscope (SEM) images and Energy Dispersive X-ray (EDX) spectroscopy using Zeiss Ultra 55 SEM device.

The carrier concentration is estimated using the measured room-temperature Seebeck coefficient and the Pisarenko plot,²⁶ calculated using a single parabolic band (SPB) model with an effective mass () estimated by Liu and et al. for MgAg_0.97Sb_0.995.¹⁶ The obtained room-temperature value of the carrier concentration n is then used to calculate the room-temperature charge carrier (drift) mobility μ following the relation .

SEM-EDX measurement procedure

Secondary Electron Microscope (SEM) images and Energy Dispersive X-ray (EDX) spectroscopy are performed using a Hitachi High Tech's SU3900 SEM device mainly to determine the average composition of the samples. The SEM-EDX measurements were performed as follows: numerous large areas (∼1 mm) are scanned on each sample and the atomic compositions are averaged to get a representative value for the whole sample. This is justified by the mesoscopic homogeneity of the samples, as can be seen from Fig. S4† in the ESI. SEM-EDX of each sample was always performed together, on the same sample holder, with the same MgAgSb sample taken as internal reference. The facility has many sample positions (it can go from 2 to 6 samples in our case). First, the composition of the reference is measured and then the composition of the different samples, one by one. For each sample, two different areas were scanned. This reference sample was the sample with the highest α-MgAgSb content (>99%) and fewest impurities (Sb, <1%) (determined by Rietveld refinement, Table S1 and Fig. S1†). It can be seen from Table 1 that the measured composition on the reference sample has a reproducibility of ∼0.2 at% but is substantially off from the nominal composition MgAg_0.97Sb_0.995 which corresponds to 33.7 at% Mg, 32.7 at% Ag and 33.6 at% Sb.

Table 1 Averaged composition of the reference sample from SEM-EDX measurements. Error bar for each element is ± 0.2

	Average composition of the reference (at%)
	Measurement date	Mg	Ag	Sb
Reference sample	Session 1: 02/12/21	31.5	34.7	33.8
	Session 2: 02/12/21	31.7	34.6	33.7
	Session 3: 03/12/21	31.5	34.7	33.8
	Session 4: 07/12/21	31.5	34.8	33.7
	Session 5: 16/12/21	31.3	34.8	33.9
	Session 6: 19/01/22	31.7	34.5	33.7

---

The same tendency of higher Ag content, lower Mg content than expected from the respective nominal stoichiometry, is observed for all other samples, and, most important, the secondary phases observed by SEM and XRD systematically do not match with the phase fields expected from the phase diagram and the average gross composition, see supplementary Fig. S2.† This indicates a shift in the SEM-EDX measurement values (lying within the certified measurement accuracy of 5 to 10 relative percent, according to the device's manual), which can be addressed with a calibration procedure. We have therefore assumed that the atomic composition of the reference sample corresponds to MgAg_0.97Sb_0.995 and then corrected the measurement results of all samples by the difference between this nominal and the composition of the respective measurement of the reference sample, as detailed in Table S2† from the ESI.

Phase diagram calculations

The phase diagram for the Mg–Ag–Sb system was calculated using a thermodynamic description for the Gibbs energies based on the work of Frost and Raynor.⁴¹ The thermodynamic database was build following the Calphad method⁴² and the Thermo-Calc software⁴³ was used as a Gibbs energy minimizer to calculate the isothermal sections. The temperature of 300 °C is of particular interest in this work as it is the samples sintering temperature. Further down to room temperature no phase transformations are expected, only slight changes on the phase boundaries.

Results

Synthesis process optimization: reproducible results

Table 2 summarizes synthesis parameters and secondary phases observed by SEM-EDX and XRD of the samples synthesized for this study. We have employed EDX spot analysis and XRD pattern matching for phase identification.

Table 2 Nominal sample compositions, sintering time t_sinter and secondary phases observed by XRD and SEM. All samples have been sintered at the same pressure (85 MPa) and temperature (300 °C). “nc” corresponds to a synthesis without jar cleaning before the MgAg + Sb ball milling step, while “c” to syntheses with the cleaning step. The first number stands for the sintering time, the last number indicates the batch number (from 1 to 14) or the Mg concentration (when <1). The fourth column is indicating visually if the sample had the Additional Cleaning Step (ACS) or not. Secondary phases identified by SEM/EDX are first recognized by microstructural analysis and then investigated with an EDX point analysis. The secondary phases are coded with the following numbers: (1) Ag_1−xSb_x (0.08 < x < 0.18) = Allargentum (2) Mg₃Sb₂ (3) MgAg (4) Ag₃Sb (5) MgAg₃ (6) Sb (7) Ag-rich solution

Sample name	Nominal composition	t sinter (min)	ACS	Secondary phases
				XRD	SEM/EDX
nc-60-1	MgAg0.97Sb0.995	60	✗	1 2 3	2 7
nc-8-2	MgAg0.97Sb0.995	8	✗	1 2 3	2 7
nc-60-2	MgAg0.97Sb0.995	60	✗	1 2 3	2 7
nc-20-2	MgAg0.97Sb0.995	20	✗	1 2 3	2 7
nc-30-3	MgAg0.97Sb0.995	30	✗	1 2	2 7
nc-8-3	MgAg0.97Sb0.995	8	✗	1 2	2 7
nc-60-3	MgAg0.97Sb0.995	60	✗	1 2 3	2 7
nc-8-4	MgAg0.97Sb0.995	8	✗	1 4 5	2 5
nc-30-4	MgAg0.97Sb0.995	30	✗	1 4 5	2 4 5
nc-60-4	MgAg0.97Sb0.995	60	✗	1 4 5	2 5
nc-8-5	MgAg0.97Sb0.995	8	✗	1 2 3	2 5
nc-8-6	MgAg0.97Sb0.995	8	✗	1 2 3	2 5
c-8-7	MgAg0.97Sb0.995	8	✓	3 6	2 6
c-8-8	MgAg0.97Sb0.995	8	✓	3 6	2 6
c-8-9	MgAg0.97Sb0.995	8	✓	3 6	2 6
c-8-10	MgAg0.97Sb0.995	8	✓	3 6	2 6
c-8-11	MgAg0.97Sb0.995	8	✓	3	6
c-20-12	MgAg0.97Sb0.995	20	✓	3	4 6
c-20-13	MgAg0.97Sb0.995	20	✓	3	4 6
nc-20-1.01	Mg1.01Ag0.97Sb0.995	20	✗	1 2 3	2 7
nc-20-1.02	Mg1.02Ag0.97Sb0.995	20	✗	1 2 3	2 7
nc-30-0.98	Mg0.98Ag0.97Sb0.995	30	✗	1 2 3	7 2 5
nc-30-0.99	Mg0.99Ag0.97Sb0.995	30	✗	1 2 3	2 7
nc-30-0.97	Mg0.97Ag0.97Sb0.995	30	✗	4 5 6	7 4
c-8-0.94	Mg0.94AgSb	8	✓	4 6	4 6
c-8-14	MgAg0.94Sb1.3	8	✓	2 3 6	2 6

---

Usually, when allargentum (Ag_1−xSb_x, 0.08 < x < 0.18) is detected with XRD, some Ag-rich solution will be identified with SEM. Also, in all cases where MgAg was detected by XRD, no separate phase domains or inclusions of MgAg could be observed in the EDX analysis. Furthermore, if there is peak overlapping between the XRD pattern of one or several secondary phases with the main phase α-MgAgSb, phase quantification by Rietveld refinement is unreliable for the available data. Precise quantification of small amounts of secondary phases as observed for our sample is generally challenging and therefore the above described EDX area scan method was chosen in preference over Rietveld refinement for the effective composition measurement, while XRD is primarily used for the secondary phases' identification.

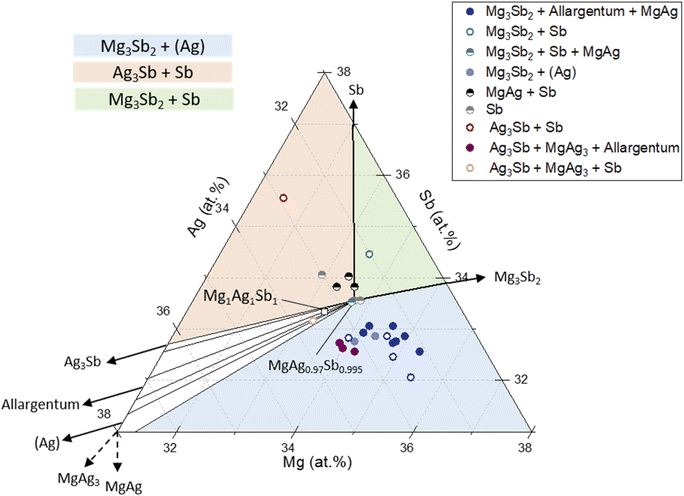
The measured effective compositions by EDX including the reference-based correction of the samples are plotted on the calculated ternary phase diagram at 300 °C in Fig. 1. The results of the calculated isothermal section at 300 °C are used in this work to compare the different phase fields with the samples composition. With our thermodynamic description the phase diagram results reproduce the experimental determinations of Frost and Raynor⁴¹ at 450 °C and allows the calculation of isothermal sections at lower/higher temperatures. At 300 °C, all two and three-phase fields as expected from higher temperatures are present. In Fig. 1, a zoom-in of the composition region near the MgAgSb ternary phase is presented with the following two-phase equilibrium regions visible: MgAgSb + Ag₃Sb, MgAgSb + Allargentum, MgAgSb + (Ag), MgAgSb + Mg₃Sb₂ and MgAgSb + Sb. The indicated three-phase equilibria with widest composition range are MgAgSb + (Ag) + Mg₃Sb₂ (light blue), MgAgSb + Sb + Mg₃Sb₂ (light green) and MgAgSb + Sb + Ag₃Sb (light orange), while two very narrow three-phase fields are also visible (white) MgAgSb + Ag₃Sb + Allargentum and MgAgSb + (Ag) + Allargentum. These phase diagram results were used along the rest of the manuscript for comparing phase fields with measured compositions and determined thermoelectric properties.

Fig. 1 Mg–Ag–Sb phase diagram at 300 °C with the sample positions according to their measured effective compositions. Full markers represent samples with the nominal stoichiometry Mg₁Ag_0.97Sb_0.995, synthesized without cleaning step while samples with cleaning step and Mg₁Ag_0.97Sb_0.995 stoichiometry are represented with a half-filled circle marker. Empty markers correspond to samples with a different nominal stoichiometry. The empty black square visualizes the Mg₁Ag₁Sb₁ position. Full arrows indicate the secondary phase present in the specific zone in the phase diagram. Further secondary phases that are observed in the full MgAgSb phase diagram but not in the shown section are indicated by dashed arrows at the margin of the diagram pointing towards their respective composition.

Employing the calibration procedure outlined in the Methods section, we find a satisfactory agreement between the secondary phases identified using XRD and the expected ones according to the location of the effective sample composition in the phase diagram. In Fig. 1 we have assumed MgAg_0.97Sb_0.995 as the single-phase stoichiometry with unresolved homogeneity region. This is based on experimental results which seem to indicate that the single-phase region for MgAgSb would rather be slightly off-centered towards the Mg-rich and Sb-rich area,^38,44,45 showing a lower impurity content compared to Mg₁Ag₁Sb₁. The exact phase boundaries of the single-phase region are unknown and its determination is beyond the present study. Samples with the same composition MgAg_0.97Sb_0.995 are used to study reproducibility and investigate the effect of modifications of the synthesis process. These are labeled by full and half-filled circle markers in Fig. 1. Empty markers representing samples synthesized with variation of Mg, Ag or Sb content will be additionally considered in the discussion part together with the other samples to better illustrate the complex relation between TE properties and average composition. Fig. S3† from the ESI section allows the identification of each sample from the study in the phase diagram.

Exemplary results of the figure of merit of the samples without cleaning step are shown in Fig. 2a, the full TE properties are presented in Fig. S6.† It can clearly be discerned that the TE properties are, firstly varying significantly and are, secondly, inferior to those of the best sample with the same composition reported by Liu et al.¹⁶

Fig. 2 Figure of merit of samples made (a) without the additional cleaning step, (b) with the additional cleaning step. “Lit” refers to MgAg_0.97Sb_0.995 from Liu et al.¹⁶

During the synthesis process, we observed that after the 8 hours of high-energy ball milling of Mg and Ag to Mg_xAg_y not all material could be removed from the jar walls. As the amount of Sb in the second ball milling step is based on the target stoichiometry and the weight of the Mg_xAg_y pellet after sintering, the residues from the first ball milling step might lead to some varying shift of the overall stoichiometry towards Mg and Ag. To increase the reproducibility of the synthesis and improve the thermoelectric properties we introduced an additional cleaning step of the jar after the 8 hours of high energy ball milling of Mg and Ag. Fig. 2b shows the figure of merit of several samples synthesized with the routine containing the additional cleaning step. It can be seen that the figure of merit is now much more reproducible (Fig. 2a, standard deviation <18% at 560 K compared to 8% at 560 K for Fig. 2b) and its value is significantly improved, matching the so far best result from Liu et al.¹⁶

The observed differences in TE properties and the impact of the adjusted synthesis procedure can be correlated with the observed secondary phases of the samples. For the sample nc-8-2, SEM images indicate the formation of Mg₃Sb₂ and Ag-rich solution (Ag) as secondary phases (Fig. S4(a) and (c)†). We also identify MgAg precursor in addition to Mg₃Sb₂ and (Ag) from the XRD pattern shown in Fig. 3. The noticed discrepancy would come from the sensitivity of XRD as well as from the SEM detector (probably due to low contrast of the phases identifying MgAg against the MgAgSb matrix in SEM). Correlating this with the phase diagram in Fig. 1, it implies that the overall stoichiometry of sample nc-8-2 is antimony deficient with MgAg being some precursor leftovers from the first HEBM step. No antimony impurity was detected, which means that for these samples all the Sb reacted with MgAg. On the other hand, sample c-8-9 is composed of MgAgSb + Mg₃Sb₂ + Sb (SEM images (b) and (d) from Fig. S4†) while the XRD pattern reveals the presence of Mg₃Sb₂, Sb and MgAg, indicating the unfinished reaction between MgAg and Sb throughout the second HEBM step. Hence, c-8-9 composition points toward an excess of antimony. Note that square root intensities are plotted for better visualization of the secondary phases, which are not discernible on the often-employed linear plots.^8,16,26 If one compares the XRD scans of nc-8-2 and c-8-9, it is likely that c-8-9 contains less Mg₃Sb₂ than nc-8-2 (lower intensity of the Mg₃Sb₂ peaks of 25.5° or 34.5° in Fig. 3). The additional cleaning step is expected to reduce the amount of Mg_xAg_y powder reacting with antimony in the second ball mill step. This should lead to an overall Sb-richer effective stoichiometry of the targeted composition, in line with the observed secondary phases that are expected at the Sb rich side of the phase diagram.

Fig. 3 XRD patterns of nc-8-2 (without additional cleaning step) and c-8-9 (with additional cleaning step).

This is confirmed by Fig. 1 which shows the average composition of the samples obtained from calibrated EDX mappings, with the color coding according to the secondary phases observed in the samples by XRD. The samples synthesized including the cleaning step (half-filled markers) have relatively similar average compositions, while the samples without cleaning step (full markers) show more scattering. It can also be seen that the first group of samples are richer in Sb, in agreement with the XRD results, confirming the hypothesized impact of the cleaning step. The composition thus changed from Sb-poor to Sb-rich. Furthermore, Fig. S7† indicates that we now have similar TE properties batch-to-batch (nearly superimposed) with the added cleaning step in the synthesis route. Besides the improvement of the reproducibility of the TE properties for c-8-7/8/9/10, their figure of merits has been systematically improved with a zT_max = 1.34 at 550 K for c-8-9 (Fig. 2b), being in the same range as the best literature reference.¹⁶ Thus, both TE property reproducibility as well as performance have been improved by addition of the cleaning step between first and second ball mill steps.

Discussion: analysis of effective composition vs. TE properties

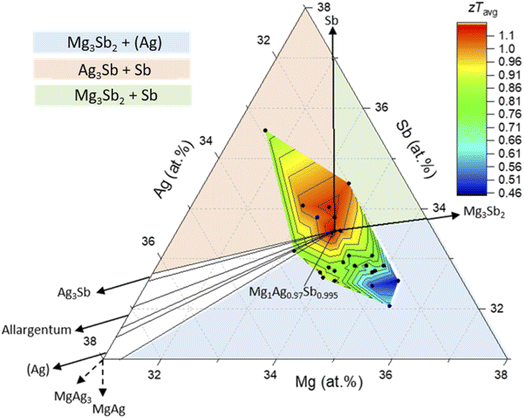
Comparing Fig. 1 and 2 reveals a strong but complex relation between TE properties and the average composition, suggesting a strong impact of secondary phases and/or matrix composition on the TE material performance. This is in line with earlier results and speculations.^16,25,26 The effective composition was determined for each sample in order to observe its influence on the thermoelectric properties.

The average zT is represented with respect to the effective composition in Fig. 4, where a hotspot can be observed for compositions around MgAg_0.97Sb_0.995 (corresponding to 33.7 at% of Mg, 32.7 at% of Ag and 33.6 at% of Sb) and those slightly richer in Sb (≤0.5 at%). Samples with other effective compositions show a clearly inferior figure of merit with zT decreasing systematically when going away from the “ideal” composition. Together with Fig. 1 it also links good samples (zT_avg > 1) with Mg₃Sb₂, Sb and MgAg as secondary phases. MgAg precursor and MgAg₃ are thermodynamically unstable secondary phases, as it can be seen in the phase diagram (Fig. 1) where they do not appear in the center region. When comparing the TE properties of samples with and without MgAg, no systematic differences are observable. We therefore conclude that its effect on the TE properties is weak. Its impact will therefore not be discussed in more details in this paper.

Fig. 4 The average figure of merit versus the effective composition determined by EDX. Averaged figure of merit is more relevant to get a device efficiency. Hence, the average figure of merit was preferred to zT_max to get an idea on how good the samples are.

Taking a closer look at the data in Fig. 4, we find that, for a given deviation from the ideal stoichiometry, samples with a Sb-rich stoichiometry have a higher zT_avg than Sb-poor ones. We observe that a deviation between 1 and 2 at% in Mg and in Sb from the Mg₁Ag_0.97Sb_0.995 stoichiometry corresponds to a reduction in zT_avg by 50% when going in Mg-rich–Sb-poor direction, but only 20% in the Mg-poor–Sb-rich direction, respectively. This is illustrated by comparing the sample pictured by the empty blue marker as shown in Fig. 1, close to the 35 at% Mg line (nominal composition Mg_1.02Ag_0.97Sb_0.995) with an Mg deficient sample represented by the empty red marker (nominally Mg_0.94Ag_0.97Sb_0.995). Even though the shift in composition compared to MgAg_0.97Sb_0.995 is larger for Mg_0.94Ag_0.97Sb_0.995 sample, the reduction in zT_avg is much less (−18% compared to −50% for the 2 at% excess of Mg).

With the average zT being a combined quantity, it is necessary to analyze the individual thermoelectric properties to better understand the behavior of the figure of merit. As seen in Fig. 5a, the Seebeck coefficient at room temperature differs significantly between the samples. Samples with the highest Seebeck are abundant the MgAgSb + Mg₃Sb₂ + (Ag) region. One can observe an almost monotonous decrease of Seebeck with an increase in Sb content when starting from the defined single-phase position. Conversely, when the Mg content increases, the Seebeck coefficient tends to increase (loss of the charge carrier concentration), followed by a decrease beyond approximately 35 at% of magnesium.

Fig. 5 (a) Seebeck coefficient (b) electrical conductivity (c) charge carrier concentration (d) charge carrier mobility versus the effective composition determined by EDX at room temperature. The charge carrier concentration and mobility are calculated using a single parabolic band model.

The electrical conductivity shows a different behavior versus the effective composition than the Seebeck coefficient (Fig. 5b). The hotspot identified for the zT_avg is also identifiable for the electrical conductivity. For the sample with the highest Sb content the highest electrical conductivity value is obtained, in line with this sample being the one with the lowest Seebeck coefficient, reflecting the usual interplay between S and σ. This compensates in zT and explains why the sample is not remarkable in Fig. 4. When moving towards Mg-rich regions, the electrical conductivity is drastically decreasing.

The Seebeck coefficient as well as the electrical conductivity are both influenced by the charge carrier concentration. In this study, the obtained values range from 3.5 × 10¹⁹ cm⁻³ to 8.4 × 10¹⁹ cm⁻³ with the highest values in Mg-poor and Sb-rich region, where the sample with the highest electrical conductivity is localized, as shown in Fig. 5c. When comparing our calculated data from an SPB model to measured Hall data from literature (from 3 × 10¹⁹ cm⁻³ up to 7.3 × 10¹⁹ cm⁻³), our values cover a similar range.^8,16,44,46 Note that carrier concentration (and hence also mobility) are obtained using a single parabolic band model, which is in principle valid for single phase materials, not composites. However, it has been argued that the impact of secondary phases on a Hall measurement is small for comparable cases⁴⁷ and the amount of secondary phases in our samples is small and not forming connected networks. We therefore understand them as effective properties, where in particular the carrier concentration is governed by the MgAgSb matrix properties.

As no external dopant was used to adjust the carrier concentration, observed changes of the matrix properties must be related to the intrinsic point defects. If, for simplicity, one assumes that all changes in charge carrier concentration are related to a change in Ag and Sb content (p of MgAgsb is mostly affected by point defects being Ag vacancy (V_Ag), Ag on Mg site (Ag_Mg) in the case of Mg-poor stoichiometry and Sb vacancy (V_Sb) for MgAgSb^36–38), then one can translate changes in p into changes in the Ag and Sb content and obtain a lower estimate of the size of the single-phase region. Here, a simplified defect chemistry model is used considering only V_Sb (produces one electron), V_Ag and Ag_Mg (each of both produces one hole). Indeed, excess of Mg is contributing to the formation of vacancies V_Ag.^36,38 For one formula unit of MgAg_1−xSb_1−y, the number of electrons is then given by y and the number of holes by x. α-MgAgSb has a tetragonal crystal structure (a = b ≠ c) with 48 atoms in the lattice, such as Mg₁₆Ag_(4a,4b,8e)Sb₁₆ which means that there are 16 formula units per unit cell.³⁹ We measure the charge carrier concentration as the hole density minus electron density (in a p-type material) which can be rearranged to , normalized by the unit cell volume. With this it is possible to calculate the expected p for a given x and y. If one furthermore assumes that all changes in p are due to changes in Ag content x, (Sb content y remaining constant) one obtains . Hence, for an observed maximum variation of 5 × 10¹⁹ cm⁻³ between the samples one obtains Δx = 0.003 atom of Ag per formula unit i.e. a width of the homogeneity range of ∼0.1 at% for Ag. We note that this is an upper limit and a rough estimate for the homogeneity range as we have used the carrier concentration data of all samples, which might be affected to a small extent by the observed secondary phases.

Even though no precise extension of the MgAgSb single-phase region can be given, it is clear that it is much smaller than the region spanned by the samples of this report. According to the defect model estimation, the size of the single-phase region (δ_Ag = 0.1 at%) is much smaller than what can be resolved by EDX analysis. The effective bulk properties of a composite will be affected by the properties of the matrix phase, the properties of the secondary phases, the properties of interfaces and the possible interactions between them. If we disregard the latter in the case of p, one might therefore expect sharp changes within the single-phase region (due to a change in defect densities in the matrix phase) and, following the effective medium theory,^48,49 slowly changing values outside the single-phase region due to the increasing fraction of secondary phases. The effect of the secondary phases depends obviously on their properties (more precise on the difference of these to the matrix properties) and can be modelled using effective medium theories. Moderate and continuous changes for the charge carrier concentration are indeed observed in Fig. 5c, in particular towards Mg-rich compositions, where a plateau can be observed. Comparing nc-8-4 with nc-8-3 which have a very similar composition, might also show an effect of the secondary phases on the carrier concentration. nc-8-4- has a higher p and Ag₃Sb, Allargentum, MgAg₃ as secondary phases while nc-8-3 has a lower p and Mg₃Sb₂ and (Ag). This gives evidence on a substantial effect of at least one among the side phases. Beyond this plateau an increase of the charge carrier concentration can be noticed, possibly related to the properties of the secondary phases themselves: (Ag) is metallic and Mg₃Sb₂ a semiconductor.⁵⁰ What we do not observe is a clear change around the single-phase region, as e.g. observed for Mg₃Sb₂ and Mg₂Si systems, where going from Mg-rich to Mg-poor can change the carrier concentration by ∼10²⁰ cm⁻³ and even switch polarity.^{33,35,51–54} This indicates that (at least with the employed synthesis approach) the carrier concentration range of single phase MgAg_0.97Sb_0.995 is relatively narrow and the phase width is hence small or the compensation between different defect types is strong.

Knowing the defect concentration, it should be possible to determine if this narrow single-phase is in line with DFT calculations and if the expected compensation by coexistence of donor and acceptor state is small or not. To do so, we can use the defect density equation: ⁵⁵ where E_f(D^q) is the charged defect formation energy of the defect D, q is the charge state, n_lat is the available sites in the material, k_B is the Boltzmann constant and T_S is the sintering temperature. The defect formation energy of the defects considered (V_Ag, Ag_Mg and V_Sb) where determined by DFT calculation.^36,37 Since our samples are p-type and undoped we compare the defect formation energies at the Fermi level E_F = 0 eV and k_BT = 0.049 eV with T = 573 K. At this low Fermi level, the difference in defect formation energy for each of both defects V_Ag and Ag_Mg doesn't change between Ag-rich and Ag-poor stoichiometry, hence not affecting the charge carrier concentration.³⁶ This happens to be in line with what we observe in Fig. 5c. When going from Ag-rich to Ag-poor, there is basically no change in our samples, indicating that the phase width of MgAgSb even smaller than obtained from the simple defect chemistry model above. It also makes it plausible that the secondary phases have a minor effect on the carrier concentration, in addition to variations in intrinsic defect concentrations. In this sense the obtained TE properties are effective ones and the precise determination of the matrix properties would require usage of a composite material model. However, the obtained conclusions on impact of effective composition remain valid. We furthermore note that the finding of a narrow homogeneity range is in apparent contradiction to the assumed composition of MgAg_0.97Sb_0.995, which would correspond to a high carrier concentration according to the employed, possibly oversimplifying defect chemistry model. However, while we and others have targeted this composition, the true composition and hence the true defect concentrations remain unknown.

The (effective) charge carrier mobility is higher in the central zone (near MgAg_0.97Sb_0.995), where the secondary phase content is the lowest (from SEM images and XRD). As shown in Fig. 5d, the mobility is decreasing when moving away from it, but it does not decrease at the same rate in every direction. Samples in the MgAgSb + Mg₃Sb₂ + (Ag) region have the lowest charge carrier mobilities indicating that these phase impurities have a stronger impact than other combinations of secondary phases on the charge carrier mobility. Even though Sb secondary phases are smaller than (Ag) impurities, and more finely dispersed (Fig. S4†), Sb seems to matter less than (Ag). Indeed, Sb is a semimetal not far from a semiconducting state, with lower carrier concentration and higher mobility rather than Ag, a typical metal with much larger carrier concentration.

Mg-poor samples are the ones with the highest electrical conductivity and the lowest Seebeck coefficient. This could be explained by the fact that samples are composed of the matrix, metallic (Ag) rich solution, and Mg₃Sb₂, which is a semiconductor (n- or p-type depending on its magnesium content³⁵), and which is therefore affecting the thermoelectric properties in different ways. In this region of the phase diagram, Mg₃Sb₂ is Mg-rich so it should be n-type. It is plausible that n-type impurities in a p-type matrix lead to local charge depletion which might affect the mobility and thus the electrical conductivity which decreases. On the other hand, Mg₃Sb₂ + Sb secondary phases are less degrading for MgAgSb thermoelectric properties. Indeed, Mg-poor Mg₃Sb₂ contains free holes and is a p-type semiconductor.⁵⁶ It can therefore be concluded that the combination of n-type Mg₃Sb₂ and (Ag) impurities is worse for our p-type TE material than with p-type impurity combination, seeming to decrease drastically the charge carrier mobility, thus the electrical conductivity and the figure of merit. Going towards Mg one can see a continuous decrease in mobility. Besides the direct effect of the secondary phases it is also possible that the type and amount of secondary phase influences the grain size which could via grain boundary scattering also influence electrical (and thermal) transport.^57,58

One can suppose that part of the improvement of the thermoelectric properties of MgAgSb giving rise to the best zT is reached close to the homogeneity region in the ternary phase diagram mainly because of a higher mobility (due to lowest phase impurity content). Interestingly, the charge carrier concentration does not vary a lot between the samples around the supposed single-phase region. This indicates first that this region is small and second that the TE properties can only marginally be controlled by intrinsic defect variation due to variation of nominal stoichiometry (Fig. 5c).

Our results indicate that carrier mobility and with it zT are governed by secondary phase content and type, with the secondary phases in the Mg-rich section of the phase diagram being much more detrimental.

Conclusion

We developed a modified route for the synthesis of MgAgSb which consists of adding a cleaning step of the milling jar after the MgAg precursor synthesis by HEBM right before the 2^nd HEBM step with the added antimony powder. This modification improved the reproducibility of the TE properties between several batches in addition to enhancing the achieved figure of merit (zT_max = 1.34 ± 0.19 at 561 K). The addition of this cleaning step also had an influence on the resulting secondary phases observed in the samples. The cleaning step proved to be effective in reducing the amount of (Ag) phase, showing higher amount of Sb secondary phases. Furthermore, a study on the effective composition and the effect of secondary phases on the TE properties was conducted. It appears that (Ag) + Mg₃Sb₂ (n-type) is degrading the overall figure of merit while Sb + Mg₃Sb₂ (p-type) are least relevant in affecting zT. Finally, the single-phase compositional range was studied by correlating charge carrier concentration and point defect calculations. Our results show a compositional width <0.1 at% of Ag, clarifying why a 100% purity is difficult to reach. Thus, one can conclude that α-MgAgSb is a sensitive material yet thermoelectric properties can be obtained reproducibly high with good synthesis control.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

The author would like to acknowledge the endorsement from the DLR Executive Board Member for Space Research and Technology and the financial support from the Young Research Group Leader Program. Financial support was also provided by the European Astronaut Centre of the European Space Agency, making this study possible thanks to the Spaceship EAC Initiative. The authors thank P. Blaschkewitz (DLR) for his support with the thermoelectric measurements and Gustavo Castillo Hernandez for the XRD measurements.

References

1. D. Gielen, F. Boshell and D. Saygin, Climate and energy challenges for materials science, Nat. Mater., 2016, 15(2), 117–120.
2. S. Chu and A. Majumdar, Opportunities and challenges for a sustainable energy future, Nat. Mater., 2012, 488, 294–303.
3. N. Kannan and D. Vakeesan, Solar energy for future world: - A review, Renewable Sustainable Energy Rev., 2016, 62, 1092–1105.
4. H. J. Goldsmid, Introduction to Thermoelectricity, ed. R. Hull and et al., Springer Series in Material Science 2010.
5. M. Zebarjadi, et al., Perspectives on thermoelectrics: from fundamentals to device applications, Energy Environ. Sci., 2012, 5(1), 5147–5162.
6. R. C. O'Brien, et al., Safe radioisotope thermoelectric generators and heat sources for space applications, J. Nucl. Mater., 2008, 377(3), 506–521.
7. L. Yang, et al., High Performance Thermoelectric Materials: Progress and Their Applications, Adv. Energy Mater., 2017, 8(6), 1701797.
8. P.-J. Ying, High performance alpha_mgagsb thermoelectric material for low temperature power generation, Chem. Mater., 2015, 27, 909–913.
9. H. Armstrong, et al., Estimating Energy Conversion Efficiency of Thermoelectric Materials: Constant Property Versus Average Property Models, J. Electron. Mater., 2016, 46(1), 6–13.
10. P. Ponnusamy, J. de Boor and E. Müller, Using the constant properties model for accurate performance estimation of thermoelectric generator elements, Appl. Energy, 2020, 262, 114587.
11. P. Ponnusamy, et al., Efficiency as a performance metric for material optimization in thermoelectric generators, J. Phys.: Energy, 2021, 3(4), 044006.
12. H. S. Kim, et al., Relationship between thermoelectric figure of merit and energy conversion efficiency, Proc. Natl. Acad. Sci. U. S. A., 2015, 112(27), 8205–8210.
13. G. J. Snyder and T. S. Ursell, Thermoelectric efficiency and compatibility, Phys. Rev. Lett., 2003, 91(14), 148301.
14. P. Ying, et al., A robust thermoelectric module based on MgAgSb/Mg3(Sb,Bi)2 with a conversion efficiency of 8.5% and a maximum cooling of 72 K, Energy Environ. Sci., 2022, 15(6), 2557–2566.
15. M. J. Kirkham, et al., Abinitio determination of crystal structures of the thermoelectric material MgAgSb, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85(14), 144120.
16. Z. Liu, et al., Effects of antimony content in MgAg0.97Sbx on output power and energy conversion efficiency, Acta Mater., 2016, 102, 17–23.
17. T. Zhu, et al., Compromise and Synergy in High-Efficiency Thermoelectric Materials, Adv. Mater., 2017, 29(14), 1605884.
18. R. Amatya and R. J. Ram, Trend for Thermoelectric Materials and Their Earth Abundance, J. Electron. Mater., 2011, 41(6), 1011–1019.
19. G. Li, et al., Intrinsic mechanical behavior of MgAgSb thermoelectric material: An ab initio study, J. Materiomics, 2020, 6(1), 24–32.
20. H. Zhao, et al., High thermoelectric performance of MgAgSb-based materials, Nano Energy, 2014, 7, 97–103.
21. D. Kraemer, et al., High thermoelectric conversion efficiency of MgAgSb-based material with hot-pressed contacts, Energy Environ. Sci., 2015, 8(4), 1299–1308.
22. P. Ying, et al., Towards tellurium-free thermoelectric modules for power generation from low-grade heat, Nat. Commun., 2021, 12(1), 1121.
23. X. Tan, et al., Improving Thermoelectric Performance of α-MgAgSb by Theoretical Band Engineering Design, Adv. Energy Mater., 2017, 7(18), 1700076.
24. Z. Liu, et al., Demonstration of ultrahigh thermoelectric efficiency of ∼7.3% in Mg3Sb2/MgAgSb module for low-temperature energy harvesting, Joule, 2021, 5(5), 1196–1208.
25. J. Camut, et al., Insight on the Interplay between Synthesis Conditions and Thermoelectric Properties of alpha-MgAgSb, Materials, 2019, 12(11), 1857.
26. I. Rodriguez-Barber, et al., On the influence of AgMg precursor formation on MgAgSb microstructure and thermoelectric properties, J. Alloys Compd., 2021, 860, 158384.
27. Y. Tang, et al., Impact of Ni content on the thermoelectric properties of half-Heusler TiNiSn, Energy Environ. Sci., 2018, 11(2), 311–320.
28. Y. Tang, et al., Phase diagram of In–Co–Sb system and thermoelectric properties of In-containing skutterudites, Energy Environ. Sci., 2014, 7(2), 812–819.
29. X. Li, et al., Phase Boundary Mapping in ZrNiSn Half-Heusler for Enhanced Thermoelectric Performance, Research, 2020, 2020, 4630948.
30. E. Visnow, et al., On the True Indium Content of In-Filled Skutterudites, Inorg. Chem., 2015, 54(16), 7818–7827.
31. F. Han, N. Andrejevic and M. Li, A Hidden Dimension to Explore New Thermoelectrics, Joule, 2018, 2(1), 16–18.
32. M. Wood, et al., Improvement of Low-Temperature zT in a Mg3 Sb2 -Mg3 Bi2 Solid Solution via Mg-Vapor Annealing, Adv. Mater., 2019, 31(35), e1902337.
33. D. Kato, et al., Significant effect of Mg-pressure-controlled annealing: non-stoichiometry and thermoelectric properties of Mg2-deltaSi1-xSbx, Phys. Chem. Chem. Phys., 2018, 20(40), 25939–25950.
34. A. Sankhla, et al., On the role of Mg content in Mg2(Si,Sn): Assessing its impact on electronic transport and estimating the phase width by in situ characterization and modelling, Mater. Today Phys., 2021, 21, 100471.
35. S. Ohno, et al., Phase Boundary Mapping to Obtain n-type Mg3Sb2-Based Thermoelectrics, Joule, 2018, 2(1), 141–154.
36. Z. Feng, et al., Ag-Mg antisite defect induced high thermoelectric performance of alpha-MgAgSb, Sci. Rep., 2017, 7(1), 2572.
37. D. Li, et al., Atomic Disorders Induced by Silver and Magnesium Ion Migrations Favor High Thermoelectric Performance in α-MgAgSb-Based Materials, Adv. Funct. Mater., 2015, 25(41), 6478–6488.
38. Z. Liu, et al., Understanding and manipulating the intrinsic point defect in α-MgAgSb for higher thermoelectric performance, J. Mater. Chem. A, 2016, 4(43), 16834–16840.
39. J.-L. Mi, et al., Elaborating the Crystal Structures of MgAgSb Thermoelectric Compound: Polymorphs and Atomic Disorders, Chem. Mater., 2017, 29(15), 6378–6388.
40. J. de Boor, et al., High-Temperature Measurement of Seebeck Coefficient and Electrical Conductivity, J. Electron. Mater., 2013, 42(7), 1711–1718.
41. F. a. Raynor, The system silver-magnesium-antimony, with reference to the theory of alloy formation, Proc. R. Soc. London, Ser. A, 1950, 203(1072), 132–147.
42. H. Lukas, S. G. Fries and B. Sundman, Computational Thermodynamics: the Calphad Method, Cambridge University Press, 2007.
43. J.-O. Andersson, et al., THERMO-CALC & DICTRA, Computational Tools For MAterials Science, Calphad, 2002, 26, 273–312.
44. Y. Liu, et al., Unusual consequences of donor and acceptor doping on the thermoelectric properties of the MgAg0.97Sb0.99 alloy, J. Mater. Chem. A, 2018, 6(6), 2600–2611.
45. Z. Liu, et al., High thermoelectric performance of α-MgAgSb for power generation, Energy Environ. Sci., 2018, 11(1), 23–44.
46. T. Zhang, B. Dong and X. Wang, Optimization of the thermoelectric performance of α-MgAgSb-based materials by Zn-doping, J. Mater. Sci., 2021, 56(24), 13715–13722.
47. Y. Lin, et al., Expression of interfacial Seebeck coefficient through grain boundary engineering with multi-layer graphene nanoplatelets, Energy Environ. Sci., 2020, 13(11), 4114–4121.
48. J. B. Vaney, et al., Effective medium theory based modeling of the thermoelectric properties of composites: comparison between predictions and experiments in the glass–crystal composite system Si10As15Te75–Bi0.4Sb1.6Te3, J. Mater. Chem. C, 2015, 3(42), 11090–11098.
49. D. J. Bergman and O. Levy, Thermoelectric properties of a composite medium, J. Appl. Phys., 1991, 70(11), 6821–6833.
50. A. Li, et al., High-Performance Mg3Sb2-xBix Thermoelectrics: Progress and Perspective, Research, 2020, 2020, 1934848.
51. A. Sankhla, et al., Analyzing thermoelectric transport in n-type Mg2Si0.4Sn0.6 and correlation with microstructural effects: An insight on the role of Mg, Acta Mater., 2020, 199, 85–95.
52. D. Kato and K. Iwasaki, Mg-pressure-controlled annealing for tuning Mg content and thermoelectric properties of Mg2–(Si0.5Sn0.5)1–Sb, J. Alloys Compd., 2021, 856, 157351.
53. D. Kato, et al., Control of Mg content and carrier concentration via post annealing under different Mg partial pressures for Sb-doped Mg2Si thermoelectric material, J. Solid State Chem., 2018, 258, 93–98.
54. A. Sankhla, et al., On the role of Mg content in Mg2(Si,Sn): Assessing its impact on electronic transport and estimating the phase width by in situ characterization and modelling, Mater. Today Phys., 2021, 21, 100471.
55. S. Ayachi, et al., On the relevance of point defects for the selection of contacting electrodes: Ag as an example for Mg2(Si,Sn)-based thermoelectric generators, Mater. Today Phys., 2021, 16, 100309.
56. Y. Wang, et al., Optimizing the thermoelectric performance of p-type Mg3Sb2 by Sn doping, Vacuum, 2020, 177, 109388.
57. J. J. Kuo, et al., Grain boundary dominated charge transport in Mg3Sb2-based compounds, Energy Environ. Sci., 2018, 11(2), 429–434.
58. J. de Boor, et al., Microstructural effects on thermoelectric efficiency: A case study on magnesium silicide, Acta Mater., 2014, 77, 68–75.

---

Footnote

† Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2ta05936c

---