DOI:
10.1039/C5RA08476H
(Paper)
RSC Adv., 2015,
5, 53497-53503
Exploration of stable stoichiometries, physical properties and hardness in the Rh–Si system: a first-principles study†
Received
7th May 2015
, Accepted 11th June 2015
First published on 11th June 2015
Abstract
To understand the structural stability, physical properties, and hardness of the Rh–Si system, we have performed systematic first-principles crystal structure searches for various stoichiometries of rhodium silicides, utilizing the particle swarm optimization method. A new stable stoichiometry, Rh4Si5 with space group P21/m, has been found at atmospheric pressure, complementing the three well-known rhodium silicides of Rh2Si (Pnma), Rh5Si3 (Pbam), and RhSi (Pnma). Our calculations of the structural and mechanical properties of the known phases are in excellent agreement with the available experimental data and similar theoretical calculations. The elastic, electronic, and hardness properties of the Rh–Si stoichiometries are discussed. Our results suggest that the new rhodium silicide Rh4Si5 (P21/m) is a potentially hard material with the hardness of 20.1 GPa.
I. Introduction
Binary intermetallic compounds of transition metals and silicon constitute an important and diverse family of inorganic solids. They have been extensively investigated both experimentally and theoretically in recent years, due to their hardness, resistance to oxidation, useful electronic properties, and compatibility with silicon-based microelectronics. They find application in many fields, which include the use as high temperature structural materials for rocket- and jet-engine parts, for furnace construction, i.e. Super Kanthal, as temperature sensors in turbine engines, in manufacturing of ceramic materials and in the production of high-temperature coatings.1–6 Rhodium is a hard and chemically inert 4d transition metal. In line with its position in the periodic table of elements and its electronic structure, it is found to be a fast diffusing impurity in Si. In these contexts, the exploration of stable stoichiometries of rhodium silicides is of interest both to confirm the role of transition metal Rh in Si, and to understand the basic physical behaviors of transition metal silicides.
Many studies have explored the crystal structures and physical properties of rhodium silicides and a broad range of stoichiometries, including Rh2Si, Rh5Si3 and RhSi, have been synthesized and characterized by various experimental methods.6–8 Great efforts have been made and opened up an interdisciplinary research field. Engström carried out a detailed X-ray powder and single crystal diffraction (XRD) analysis of metal-rich phases in Rh–Si system and reported the crystal structure refinements of Rh2Si and Rh5Si3.7 Finnie and Searcy presented XRD measurements on the high-temperature CsCl structure of RhSi, and described its preparation by heating rhodium and an excess of silicon (atomic ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3), in finely divided form, for one hour at 1200 °C and then for one-half hour at 1550 °C.8 To investigate the influence of silicon on the chemical composition and the crystallinity of these crystals, Marot et al. conducted comparative measurements on rhodium/silicon films of Rh2Si, Rh5Si3, RhSi and Rh3Si4 at room temperature using X-ray and ultraviolet photoelectron spectroscopy (XPS), ultraviolet photoemission spectroscopy (UPS), scanning electron microscope (SEM) and XRD techniques. The formation of Rh2Si at 300 °C, Rh5Si3 at 500 °C and 600 °C, RhSi as well as Rh5Si3 at 800 °C and 900 °C was reported.6 In order to gain a deeper insight into the Rh–Si system, Niranjan performed calculations on the structural, electronic and elastic properties of RhSi both in the cubic and orthorhombic phase, and found that relatively strong three centre (Rh–Si–Rh) directional bonds are formed in both phases due to the hybridization between Rh-4d orbitals and Si-3p orbitals.9 However, there have been several open questions for rhodium silicides: (i) do other stable or metastable stoichiometries in the Rh–Si system exist, besides the already known stoichiometries? (ii) What are their structural and mechanical properties? (iii) Are these metallic phases or, unusually, insulators?
3), in finely divided form, for one hour at 1200 °C and then for one-half hour at 1550 °C.8 To investigate the influence of silicon on the chemical composition and the crystallinity of these crystals, Marot et al. conducted comparative measurements on rhodium/silicon films of Rh2Si, Rh5Si3, RhSi and Rh3Si4 at room temperature using X-ray and ultraviolet photoelectron spectroscopy (XPS), ultraviolet photoemission spectroscopy (UPS), scanning electron microscope (SEM) and XRD techniques. The formation of Rh2Si at 300 °C, Rh5Si3 at 500 °C and 600 °C, RhSi as well as Rh5Si3 at 800 °C and 900 °C was reported.6 In order to gain a deeper insight into the Rh–Si system, Niranjan performed calculations on the structural, electronic and elastic properties of RhSi both in the cubic and orthorhombic phase, and found that relatively strong three centre (Rh–Si–Rh) directional bonds are formed in both phases due to the hybridization between Rh-4d orbitals and Si-3p orbitals.9 However, there have been several open questions for rhodium silicides: (i) do other stable or metastable stoichiometries in the Rh–Si system exist, besides the already known stoichiometries? (ii) What are their structural and mechanical properties? (iii) Are these metallic phases or, unusually, insulators?
To address these issues, we present here a comprehensive theoretical study on binary rhodium silicide with various stoichiometries, based on the recently developed particle swarm optimization (PSO) technique as implemented in the CALYPSO (crystal structure analysis by particle swarm optimization) code. We study the Rh–Si system by a systematic combination of first-principles calculations. In a first step, the stable structures for a range of chemical compositions are identified by global crystal structure prediction. Subsequently, relevant candidate phases are re-optimized and their properties studied in more detail. These calculations are performed using density functional theory within generalized gradient approximation of the exchange-correlation energy functional. In a final step, we combine the ground state enthalpies of formation and dynamic stabilities to confirm the possible stoichiometries that can be synthetized.
II. Computational details
The search for stable structures of the Rh–Si system was based on global minimization of free energy surfaces using ab initio total energy calculations and the particle-swarm-optimization scheme as implemented in the CALYPSO (Crystal structure AnaLYsis by Particle Swarm Optimization) code.10–12 It has been successful in correctly predicting structures for various systems including elements, binary and ternary compounds.13–15 The structure searches were performed at ambient pressure, with a simulation cell consisting of one to four formula units. Each generation contains 30 structures, 60% of which are generated from previous low-energy structures following the particle swarm method, while 40% will be generated randomly. We optimized 50 generations to achieve a thorough sampling of the crystal configuration space. The stoichiometries that were considered are listed in Table S1 (in the ESI†). The total energy calculations and structural relaxations were carried out with the Cambridge Serial Total Energy Package (CASTEP) plane-wave code, ultrasoft pseudopotentials and the Perdew–Burke–Ernzerhof (PBE) generalized gradient approximation functional.16–18 The crystal structure parameters, formation enthalpy, and electronic properties are also checked by the LDA+U (local density approximation) method.19,20 The ultrasoft pseudopotentials include 4d85s1 and 3s23p2 as the valence space for the Rh and Si atoms, respectively. A cutoff energy of 500 eV for the expansion of the wave function into plane waves and sufficiently fine Monkhorst-Pack k-point sampling meshes21 were chosen to ensure that all the enthalpy calculations are converged to better than 1 meV per atom. Phonon frequencies were calculated by the finite displacement method.22
III. Results and discussion
In order to explore potential binary structures of the RhxSiy rhodium silicides, we first focused on structure searches of Rh2Si, Rh5Si3 and RhSi, using only the respective chemical compositions as input information. The crystal structure searches readily reproduced the experimental structures of Rh2Si (Pnma), Rh5Si3 (Pbam) and RhSi (P21/c, Pnma, P213 and Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) as the lowest ground state energy phases.7,8,22 This gives us confidence in the applicability of our method to this and other transition metal silicides. The crystal structure information of the lowest energy structures for each stoichiometry considered at GGA level is presented in Table 1, along with the theoretical values and available experimental data of the rhodium silicides Rh2Si (Pnma), Rh5Si3 (Pbam) and RhSi (Pnma).7,23,24 Complete crystal structure information for the considered phases of RhxSiy are listed in Tables S1 and S2 (in the ESI†). The energetic stability of RhxSiy stoichiometries can be quantified by constructing the ground state convex hull, which is constructed from the formation enthalpy per atom of the most stable structures at each stoichiometry: ΔH = {E (RhxSiy) − x*E (Rh) − y*E (Si)}/(x + y). Here ΔH is the relative ground state enthalpy of formation per atom and E is the calculated enthalpy per formula unit for each stoichiometry. Any structure with an enthalpy on the convex hull is energetically stable towards decomposition into other unary or binary phases, and thus experimentally accessible.25 The convex hull of Rh–Si phases at ambient pressure, with the optimized lowest energy structures of RhxSiy is presented in Fig. 1. From Fig. 1, it is clearly seen that the convex hull is composed of four stable phases denoted as Rh2Si (Pnma), Rh5Si3 (Pbam), RhSi (Pnma) and Rh4Si5 (P21/m); their structures are shown in Fig. 2 and 3. Under well-controlled experimental conditions (e.g. regarding relative stoichiometries), these could be synthesized and confirmed by experiments. In order to check the reliability of our calculations, we recalculate the crystal structure parameters and formation enthalpies of Rh–Si system using LDA+U method (see Fig. S1 in the ESI†). The calculated crystal structure parameters and formation enthalpies of the four stable stoichiometries are listed in Table S3 (in the ESI†). We clearly note that the LDA+U calculated results are in good agreement with the GGA–PBE calculations, providing important support for the reliability of present GGA–PBE calculations. Interestingly, several new metastable structures of rhodium silicides with various silicon concentrations have also been found (see Fig. S2 in the ESI†).
m) as the lowest ground state energy phases.7,8,22 This gives us confidence in the applicability of our method to this and other transition metal silicides. The crystal structure information of the lowest energy structures for each stoichiometry considered at GGA level is presented in Table 1, along with the theoretical values and available experimental data of the rhodium silicides Rh2Si (Pnma), Rh5Si3 (Pbam) and RhSi (Pnma).7,23,24 Complete crystal structure information for the considered phases of RhxSiy are listed in Tables S1 and S2 (in the ESI†). The energetic stability of RhxSiy stoichiometries can be quantified by constructing the ground state convex hull, which is constructed from the formation enthalpy per atom of the most stable structures at each stoichiometry: ΔH = {E (RhxSiy) − x*E (Rh) − y*E (Si)}/(x + y). Here ΔH is the relative ground state enthalpy of formation per atom and E is the calculated enthalpy per formula unit for each stoichiometry. Any structure with an enthalpy on the convex hull is energetically stable towards decomposition into other unary or binary phases, and thus experimentally accessible.25 The convex hull of Rh–Si phases at ambient pressure, with the optimized lowest energy structures of RhxSiy is presented in Fig. 1. From Fig. 1, it is clearly seen that the convex hull is composed of four stable phases denoted as Rh2Si (Pnma), Rh5Si3 (Pbam), RhSi (Pnma) and Rh4Si5 (P21/m); their structures are shown in Fig. 2 and 3. Under well-controlled experimental conditions (e.g. regarding relative stoichiometries), these could be synthesized and confirmed by experiments. In order to check the reliability of our calculations, we recalculate the crystal structure parameters and formation enthalpies of Rh–Si system using LDA+U method (see Fig. S1 in the ESI†). The calculated crystal structure parameters and formation enthalpies of the four stable stoichiometries are listed in Table S3 (in the ESI†). We clearly note that the LDA+U calculated results are in good agreement with the GGA–PBE calculations, providing important support for the reliability of present GGA–PBE calculations. Interestingly, several new metastable structures of rhodium silicides with various silicon concentrations have also been found (see Fig. S2 in the ESI†).
Table 1 Calculated relative enthalpy of formation ΔH per atom; lattice parameters, a, b, and c; volume per atom; and mass density for various rhodium silicides, compared with experimental and other theoretical data
| Phase |
Space group |
ΔH (eV) |
a (Å) |
b (Å) |
c (Å) |
V (Å3) |
ρ (g cm−3) |
| |
Expt. |
Theor. |
|
Expt. |
Theor. |
|
Expt. |
Theor. |
| Ref. 7. Ref. 21. Ref. 22. |
| Rh3Si |
Pnma |
−0.56 |
5.36 |
|
|
7.99 |
|
|
5.27 |
|
|
14.12 |
9.90 |
| Rh5Si2 |
P41212 |
−0.51 |
9.53 |
|
|
9.53 |
|
|
8.80 |
|
|
14.25 |
9.50 |
| Rh2Si |
Pnma |
−0.82 |
5.58 |
5.41a |
|
3.99 |
3.93a |
|
7.40 |
7.38a |
|
13.72 |
9.44 |
| Rh5Si3 |
Pbam |
−0.86 |
5.45 |
5.32a |
|
10.32 |
10.13a |
|
3.90 |
3.90a |
|
13.72 |
9.06 |
| Rh3Si2 |
Cmc21 |
−0.68 |
13.29 |
|
|
11.43 |
|
|
7.50 |
|
|
14.25 |
8.50 |
| RhSi |
Pnma |
−0.91 |
5.60 |
5.56b |
5.60c |
3.11 |
3.70b |
3.11c |
6.45 |
6.38b |
6.45c |
14.05 |
7.74 |
| Rh4Si5 |
P21/m |
−0.82 |
12.47 |
|
|
3.55 |
|
|
6.01 |
|
|
14.53 |
7.01 |
| Rh3Si4 |
Pnma |
−0.56 |
20.57 |
|
|
4.45 |
|
|
4.50 |
|
|
14.71 |
6.79 |
| Rh2Si3 |
P63/mmc |
−0.62 |
3.76 |
|
|
3.76 |
|
|
12.52 |
|
|
15.36 |
6.27 |
| Rh3Si5 |
P21/c |
−0.65 |
6.48 |
|
|
14.24 |
|
|
11.64 |
|
|
14.99 |
6.22 |
| RhSi2 |
Cmce |
−0.55 |
6.98 |
|
|
6.98 |
|
|
8.09 |
|
|
15.46 |
5.70 |
| RhSi3 |
P63mc |
−0.03 |
4.81 |
|
|
4.81 |
|
|
6.36 |
|
|
15.95 |
4.87 |
 |
| | Fig. 1 Relative enthalpies of formation for rhodium silicides at GGA level. The solid line denotes the ground state convex hull. | |
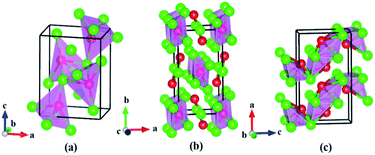 |
| | Fig. 2 Experimental observed structures of rhodium silicides at 1 atm: (a) Rh2Si (Pnma), (b) Rh5Si3 (Pbam), and (c) RhSi (Pnma). The green and red spheres represent rhodium and silicon atoms, respectively. | |
 |
| | Fig. 3 Predicted crystal structure and electron localization function (ELF) of Rh4Si5 (P21/m). The green and red spheres represent rhodium and silicon atoms, respectively. The ELF isosurfaces value is 0.8. | |
In fact, three phases have already been synthesized, while our structure searches uncovered a new stable Rh4Si5 phase, of monoclinic P21/m symmetry, with two Rh4Si5 formula units per unit cell (a = 12.47 Å, b = 3.55 Å, c = 6.01 Å, and beta = 100.1 deg). This new phase is stable by 10.3 meV per atom with respect towards decomposition into RhSi and pure Si. The structure contains four Rh atoms on the 2e Wyckoff sites (0.0499, 1/4, 0.2091), (0.2731, 1/4, 0.1070), (0.5001, 1/4, 0.2994) and (0.7308, 1/4, 0.2866), and five Si atoms also 2e at (0.6350, 1/4, 0.6385), (0.4221, 1/4, 0.8933), (0.2237, 1/4, 0.4649), (0.9229, 1/4, 0.4876) and (0.1395, 3/4, 0.97903). Each Si atom in the Rh4Si5 (P21/m) structure is surrounded by 4 or 6 Rh atoms, which is similar to the Pnma structure of RhSi. Intriguingly, Rh atoms in the P21/m structure of Rh4Si5 exhibit mixed six and seven-fold coordination to Si atoms (see Fig. 3), with Rh–Si separations in the range of 2.324 to 2.687 Å. These are significantly longer than the bond length in gas-phase RhSi (2.12 Å).26 Rhodium polyhedra in rhodium silicides, such as Rh octahedra in RhSi and Rh5Si3 type structures, are known. However, to the best of our knowledge, Rh atoms with a seven-fold coordination to Si atoms, have not been seen in rhodium silicides. Remarkably, upon comparing the coordination environments of Rh atoms in the new Rh4Si5 (P21/m) compound with those of the most stable known Rh2Si (Pnma), Rh5Si3 (Pbam) and RhSi (Pnma) rhodium silicides, it can be clearly observed that the coordination of Rh atoms with Si atoms change from four-fold coordinated (Rh2Si) to six-fold coordinated (Rh5Si3 and RhSi) and further, mixed six- and seven-fold coordinated (Rh4Si5) with the increased Si content.
To compare the structural parameters of the calculated rhodium silicides with those seen experimentally, we calculated the powder X-ray diffraction (XRD) patterns of the different structures. Schematic X-ray stick spectra, together with the available experimental data, are shown in Fig. 4. The overall agreement between simulated and measured spectra by Engström et al.7,23 is very satisfactory, demonstrating the validity of the structure search approach. We also show the simulated XRD patterns of the Rh4Si5 (P21/m) structure in Fig. 4. While no experimental spectra on this phase have been reported, the XRD pattern is sufficiently distinct from those of the hitherto known phases, that it should be easily identifiable in a successful synthesis experiment; further experimental studies are necessary. To study the dynamical stability of the RhxSiy phases, the phonon dispersion curves of the new phase Rh4Si5 (P21/m) as well as of the known crystalline structures Rh2Si (Pnma), Rh5Si3 (Pbam) and RhSi (Pnma) were calculated and shown in Fig. 5, respectively. The new phase Rh4Si5 (P21/m) is dynamically stable, as there are no imaginary phonon frequencies detected in the whole Brillouin zone. The previously proposed phases, Rh2Si (Pnma), Rh5Si3 (Pnam) and RhSi (Pnma), are also found to be dynamically stable in the calculations.
 |
| | Fig. 4 Simulated X-ray diffraction pattern of (a) Rh2Si (Pnma), (c) Rh5Si3 (Pbam), (e) RhSi (Pnma), and (g) Rh4Si5 (P21/m), while (b), (d), (f) show the experimental data for Rh2Si (Pnma), Rh5Si3 (Pbam), and RhSi (Pnma), respectively. | |
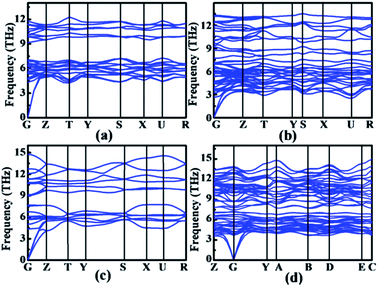 |
| | Fig. 5 Calculated phonon spectra of (a) Rh2Si (Pnma), (b) Rh5Si3 (Pbam), (c) RhSi (Pnma), and (d) Rh4Si5 (P21/m). | |
In order to further establish the mechanical stability of the various Rh–Si phases, we have calculated the elastic constants by a direct method, i.e. ab initio stress–strain relations.27 There, stress is calculated as a function of strain, with the internal coordinates optimized under each strain application, and the elastic constants are found as derivates of the stress with respect to the strain.28 The calculation of the elastic constants is straightforward and the calculated results together with the experimental values and similar theoretical calculations are summarized in Table 2. The key criteria for mechanical stability of a crystal are that the strain energy must be positive. For orthorhombic lattices, the elastic constants should satisfy the following inequalities:29
| | |
C11 > 0, C22 > 0, C33 > 0, C44 > 0, C55 > 0, C66 > 0, [C11 + C22 + C33 + 2(C12 + C13 + C23)] > 0, (C11 + C22 − 2C12) > 0, (C11 + C33 − 2C13) > 0, (C22 + C33 − 2C23) > 0.
| (1) |
Table 2 Calculated elastic constants (GPa) of various rhodium silicides
| |
Rh2Si (Pnma) |
Rh5Si3 (Pbam) |
RhSi (Pnma) |
Rh4Si5 (P21/m) |
| Ref. 22. Ref. 9. |
| C11 |
246.4 |
268.8 |
416.2 |
416.5a |
417.3b |
351.3 |
| C22 |
331.4 |
256.7 |
228.7 |
227.6a |
230.1b |
256.5 |
| C33 |
332.5 |
357.9 |
358.0 |
315.5a |
359.9b |
285.0 |
| C44 |
86.1 |
102.4 |
110.2 |
100.7a |
116.2b |
104.5 |
| C55 |
73.6 |
124.0 |
112.8 |
114.0a |
114.8b |
106.4 |
| C66 |
123.0 |
91.9 |
87.7 |
86.4a |
95.4b |
88.9 |
| C12 |
173.6 |
164.8 |
113.8 |
110.7a |
130.9b |
115.7 |
| C13 |
216.6 |
185.8 |
142.2 |
139.3a |
145.9b |
112.3 |
| C23 |
194.1 |
184.1 |
161.6 |
162.1a |
165.1b |
148.6 |
| C15 |
— |
— |
— |
|
|
−1.4 |
| C25 |
— |
— |
— |
|
|
4.4 |
| C35 |
— |
— |
— |
|
|
−5.8 |
| C46 |
— |
— |
— |
|
|
4.1 |
For the monoclinic crystals, the corresponding mechanical stability criterion is more complex:27
| | |
C11 > 0, C22 > 0, C33 > 0, C44 > 0, C55 > 0, C66 > 0, (C22 + C33 − 2C23) > 0, (C33C55 − C352) > 0, (C44C66 − C462) > 0, [C11 + C22 + C33 + 2(C12 + C13 + C23)] > 0, [C22(C33C55 − C352) + 2C23C25C35 − C232C55 − C252C33] > 0, 2[C15C25(C33C12 − C13C23) + C15C35(C22C13 − C12C23) + C25C35(C11C23 − C12C13)] − [C152(C22C33 − C232) + C252(C11C33 − C132) + C352(C11C22 − C122)] + gC55 > 0, g = C11C22C33 − C232C11 − C132C22 − C122C33 + 2C12C13C23.
| (2) |
The P21/m structure of Rh4Si5 satisfies all twelve criteria in eqn (2) and it follows, in conjunction with the phonon calculations presented above, that Rh4Si5 rhodium silicide in the P21/m structure is mechanically stable.
The bulk modulus (B) and shear modulus (G) are directly derived from the calculated elastic constants by using the Voigt–Reuss–Hill method,30 and the results are tabulated in Table 3. The Young's modulus (E) and the Poisson's ratio (ν) can also be calculated from B and G using the following formulae:29
| |
 | (3) |
Table 3 Calculated bulk modulus B (GPa), shear modulus G (GPa), Young's modulus E (GPa), Poisson's ratio ν, and Debye temperature ΘD (K) of various rhodium silicides
| |
Rh2Si (Pnma) |
Rh5Si3 (Pbam) |
RhSi (Pnma) |
Rh4Si5 (P21/m) |
| Ref. 22. Ref. 9. |
| BV |
231.0 |
217.0 |
204.2 |
202.2a |
210.1b |
182.9 |
| BR |
222.0 |
209.5 |
190.2 |
188.6a |
196.4b |
182.0 |
| GV |
78.3 |
86.9 |
101.2 |
99.1a |
102.9b |
94.4 |
| GR |
65.4 |
77.4 |
93.2 |
90.9a |
94.3b |
89.5 |
| B |
226.5 |
213.2 |
197.2 |
195.4a |
203.3b |
182.5 |
| G |
71.8 |
82.2 |
97.2 |
95.0a |
98.6b |
91.9 |
| B/G |
3.15 |
2.60 |
2.03 |
|
|
1.98 |
| E |
194.9 |
218.4 |
250.4 |
254.3a |
254.7b |
236.2 |
| ν |
0.36 |
0.33 |
0.29 |
|
|
0.28 |
| νt |
2.76 |
3.01 |
3.54 |
|
|
4.72 |
| νl |
5.84 |
5.97 |
6.50 |
|
|
8.60 |
| νm |
3.11 |
3.38 |
3.95 |
|
|
5.26 |
| ΘD |
409.3 |
439.0 |
487.6 |
482.3a |
490.5b |
526.4 |
| Hν |
11.9 |
12.0 |
14.7 |
14.8a |
|
20.1 |
In general, the bulk modulus B characterizes a material's resistance against volume change, while the shear modulus G estimates a material's ability to resist shear strain, and Young's modulus E denotes the resistance against longitudinal tensions.31 It is worth noting that, among the four phases, Rh4Si5 (P21/m) has the lowest value of bulk modulus and the second largest shear modulus, revealing that it is the most compressible while being able to withstand shear strain to a large extent. In order to evaluate the ductility of the material, the B/G values are calculated and summarized in Table 3. The critical value of B/G, which separates ductile and brittle materials, is about 1.75.32 The B/G ratio of all Rh–Si phases are all larger than 1.75, reflecting their ductile nature, with the new found Rh4Si5 phase being the most brittle. Poisson's ratio is an important parameter to describe the degree of directionality of the covalent bonding.31 The smallest Poisson's ratio of 0.28 for Rh4Si5 (P21/m) suggests its strong degree of covalent bonding. It is also worth noting that the large shear modulus and Young's modulus E, together with the smallest value of the B/G ratio and Poisson's ratio ν for Rh4Si5 (P21/m), entails the potential of high hardness.
One of the standard methods for calculating the Debye temperature ΘD, is from elastic constants, since in Debye's approximation the vibrations of the solid are considered as elastic waves. The Debye temperature can be estimated from the average sound velocity νm, by using the following expressions:28
| |
 | (4) |
where
| |
 | (5) |
and
h is Planck's constant,
kB is Boltzmann's constant,
NA is Avogadro's number. Using the Voigt–Reuss–Hill method, the calculated
ΘD, together with
νm,
νt and
νl for the considered structures of rhodium silicides are listed in
Table 3. In general, a higher Debye temperature indicates a larger thermal conductivity and microhardness. Thus, Rh
4Si
5 (
P2
1/
m), owing the highest
ΘD (526.4 K), promises to show the largest thermal conductivity and microhardness amongst the rhodium silicides.
We now turn to the rhodium silicides' electronic structures. Total and partial densities of states (DOS) were calculated and shown in Fig. 6. As seen there, all phases are found to be metallic, with a finite electronic DOS at the Fermi level. This is corroborated by the electronic band structures, shown in Fig. 7. The projected density of states reveals that the states just below the Fermi energy are mainly Rh 4d, whereas the states just above the Fermi energy consists of more Si 3p orbitals. It is worth mentioning that, for all the phases, the Rh 4d orbital hybridizes significantly with the Si 3p orbital, indicating a strong Rh–Si covalent bonding nature. The strong covalent bonding between Rh and neighboring Si atoms can also be seen from the electron localized function (ELF), as illustrated for the Rh4Si5 phase in Fig. 3 and S5 (in the ESI†). Although the localization of the electrons is not very strong in those metallic phases, it still indicates significant covalent bonding between neighboring Rh and Si atoms.
 |
| | Fig. 6 Calculated total and partial DOSs of (a) Rh2Si (Pnma), (b) Rh5Si3 (Pbam), (c) RhSi (Pnma), and (d) Rh4Si5 (P21/m) at GGA level. The Fermi level is at 0 eV. | |
 |
| | Fig. 7 Calculated band structures of (a) Rh2Si (Pnma), (b) Rh5Si3 (Pbam), (c) RhSi (Pnma), and (d) Rh4Si5 (P21/m). The Fermi level is at 0 eV. | |
From the discussion above, regarding the large shear modulus G and Young's modulus E, and the small values for the B/G ratio and Poisson's ratio ν, together with the strong covalent bonding of Rh4Si5 (P21/m), a potential of high hardness is recognizable. Thus, we estimated the theoretical hardness of rhodium silicides using the semiempirical method by Dai et al.33 The expression of the hardness for a multi-component compound can be written as34,35
| |
 | (6) |
where
| |
 | (7) |
| |
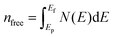 | (8) |
| |
 | (9) |
and
Pμ is the Mulliken overlap population,
V is the volume,
nμ is the number of chemical bonds of type
μ,
dμ the respective bond length, and
Nbν the number of bonds of type
μ per unit volume.
P′ is the metallic population,
nfree is the number of free electrons per unit cell,
V is the volume of the cell, and
EF is the Fermi energy. The calculated hardness values for all phases are listed in
Table 3, and the detailed bond parameters of hardness calculations can be found in Table S4 (in the ESI
†). As shown in
Table 3, the values of the hardness for the considered structures increase with increasing Si contents, in the order Rh
2Si (
Pnma) < Rh
5Si
3 (
Pbam) < RhSi (
Pnma) < Rh
4Si
5 (
P2
1/
m). It also reveals that the predicted hardness of the Rh
4Si
5 (
P2
1/
m) phase is approximately 20.1 GPa, which is obviously larger than the hardness of the pure Si in
Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m
m phase (11.1 GPa), implying it is a potential hard material at ambient conditions (see Table S3 in the ESI
†).
IV. Conclusions
In summary, the structural, dynamical, and electronic properties as well as the hardness of various stoichiometric rhodium silicides have been studied from unbiased CALYPSO structure searches in conjunction with first-principles calculations. Our calculations find an unusual monoclinic rhodium silicide, Rh4Si5 with the space group P21/m, to be stable at 1 atm. Our results on the known Rh–Si binary phases are consistent with available experimental data and previous calculations, and fall in line with the trends expected in the transition metal silicides. Based on a detailed analysis of the chemical bonds and by employing a semi-empirical model, the Vickers hardness of all stable rhodium silicides is estimated. Amongst those, the newly proposed stable compound, the P21/m structure Rh4Si5, is the hardest material, with a hardness of about 20.1 GPa. Experimental synthesis and characterization efforts would greatly complement the theoretical considerations presented in this paper, and allow for a more complete picture of the binary Rh–Si phase diagram.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (nos. 11274235 and 11304167), Postdoctoral Science Foundation of China (nos. 20110491317 and 2014T70280), Program for Science & Technology Innovation Talents in Universities of Henan Province (no. 15HASTIT020), Open Project of State Key Laboratory of Superhard Materials (no. 201405), and Young Core Instructor Foundation of Henan Province (no. 2012GGJS-152). The results presented here were computed by using supercomputers at RIKEN.
References
- X. Chen, J. Guan, G. Sha, Z. Gao, C. T. Williams and C. Liang, RSC Adv., 2014, 4, 653–659 RSC.
- R. Hao, X. Y. Zhang, J. Q. Qin, S. H. Zhang, J. L. Ning, N. Sun, M. Z. Ma and R. P. Liu, RSC Adv., 2015, 5, 36779–36786 RSC.
- P. K. Dutta, S. Panda, D. Chaudhuri and S. S. Zade, RSC Adv., 2014, 4, 33955–33957 RSC.
- C. M. Fang, R. S. Koster, W. F. Li and M. A. van Huis, RSC Adv., 2014, 4, 7885–7899 RSC.
- Y. K. Shi, X. J. Hu, B. L. Zhu, S. R. Wang, S. M. Zhang and W. P. Huang, RSC Adv., 2014, 4, 62215–62222 RSC.
- L. Marot, R. Schoch, R. Steiner, V. Thommen, D. Mathys and E. Meyer, Nanotechnology, 2010, 21, 365707 CrossRef CAS PubMed.
- I. Engström, Acta Chem. Scand., 1963, 17, 775–784 CrossRef PubMed.
- L. N. Finnie and A. W. Searcy, Acta Cryst., 1959, 12, 260 CrossRef CAS.
- M. K. Niranjan, Intermetallics, 2012, 26, 150–156 CrossRef CAS PubMed.
- J. Lv, Y. C. Wang, L. Zhu and Y. M. Ma, J. Chem. Phys., 2012, 137, 084104 CrossRef PubMed.
- Y. C. Wang, J. Lv, L. Zhu and Y. M. Ma, Comput. Phys. Commun., 2012, 183, 2063–2070 CrossRef CAS PubMed.
- Y. C. Wang, J. Lv, L. Zhu and Y. M. Ma, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 094116 CrossRef.
- Y. C. Wang, M. S. Miao, J. Lv, L. Zhu, K. T. Yin, H. Y. Liu and Y. M. Ma, J. Chem. Phys., 2012, 137, 224108 CrossRef PubMed.
- L. Zhu, H. Y. Liu, C. J. Pickard, G. T. Zou and Y. M. Ma, Nat. Chem., 2014, 6, 644–648 CAS.
- S. H. Lu, Y. C. Wang, H. Y. Liu, M. S. Miao and Y. M. Ma, Nat. Commun., 2014, 5, 3666 CAS.
- M. D. Segall, P. J. D. Lindan, M. J. Probert, C. J. Pickard, P. J. Hasnip, S. J. Clark and M. C. Payne, J. Phys.: Condens. Matter, 2002, 14, 2717–2744 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892–7895 CrossRef.
- V. I. Anisimovy, F. Aryasetiawanz and A. I. Lichtenstein, J. Phys.: Condens. Matter, 1997, 9, 767–808 CrossRef.
- P. Guss, M. E. Foster, B. M. Wong, F. P. Doty, K. Shah, M. R. Squillante, U. Shirwadkar, R. Hawrami, J. Tower and D. Yuan, J. Appl. Phys., 2014, 115, 034908 CrossRef PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192 CrossRef.
- M. T. Yin and M. L. Cohen, Phys. Rev. B: Condens. Matter Mater. Phys., 1982, 26, 3259–3272 CrossRef CAS.
- K. Göransson, I. Engström and B. Nölang, J. Alloys Compd., 1995, 219, 107–110 CrossRef.
- J. J. Wang, X. Y. Kuang, Y. Y. Jin, C. Lu and X. F. Huang, J. Alloys Compd., 2014, 592, 42–47 CrossRef CAS PubMed.
- G. Ghosh, A. van de Walle and M. Asta, Acta Mater., 2008, 56, 3202–3221 CrossRef CAS PubMed.
- Z. Y. Ren, R. Hou, P. Guo, J. K. Gao, G. H. Du and Z. Y. Wen, Chin. Phys. B, 2008, 17, 2116–2123 CrossRef CAS.
- J. P. Poirier, Introduction to the Physics of the Earth’s Interior, Cambridge University Press, Cambridge, 2000 Search PubMed.
- C. Lu, X. Y. Kuang, S. J. Wang, Y. R. Zhao and X. M. Tan, Europhys. Lett., 2010, 91, 16002 CrossRef.
- Z. J. Wu, E. J. Zhao, H. P. Xiang, X. F. Hao, X. J. Liu and J. Meng, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 054115 CrossRef.
- J. H. Dai, Y. Song, W. Li, R. Yang and L. Vitos, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 014103 CrossRef.
- C. Z. Fan, J. Li and L. M. Wang, Sci. Rep., 2014, 4, 6786 CrossRef CAS PubMed.
- M. M. Zhong, X. Y. Kuang, Z. H. Wang, P. Shao, L. P. Ding and X. F. Huang, J. Phys. Chem. C, 2013, 117, 10643–10652 CAS.
- C. Z. Fan, Y. Jin, J. Li and X. Dong, Sci. Rep., 2014, 4, 6993 CrossRef CAS PubMed.
- F. M. Gao, J. L. He, E. D. Wu, S. M. Liu, D. L. Yu, D. C. Li, S. Y. Zhang and Y. J. Tian, Phys. Rev. Lett., 2003, 91, 015502 CrossRef.
- F. M. Gao, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 132104 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Crystal structure and hardness of RhxSiy. See DOI: 10.1039/c5ra08476h |
|
| This journal is © The Royal Society of Chemistry 2015 |
Click here to see how this site uses Cookies. View our privacy policy here. ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3), in finely divided form, for one hour at 1200 °C and then for one-half hour at 1550 °C.8 To investigate the influence of silicon on the chemical composition and the crystallinity of these crystals, Marot et al. conducted comparative measurements on rhodium/silicon films of Rh2Si, Rh5Si3, RhSi and Rh3Si4 at room temperature using X-ray and ultraviolet photoelectron spectroscopy (XPS), ultraviolet photoemission spectroscopy (UPS), scanning electron microscope (SEM) and XRD techniques. The formation of Rh2Si at 300 °C, Rh5Si3 at 500 °C and 600 °C, RhSi as well as Rh5Si3 at 800 °C and 900 °C was reported.6 In order to gain a deeper insight into the Rh–Si system, Niranjan performed calculations on the structural, electronic and elastic properties of RhSi both in the cubic and orthorhombic phase, and found that relatively strong three centre (Rh–Si–Rh) directional bonds are formed in both phases due to the hybridization between Rh-4d orbitals and Si-3p orbitals.9 However, there have been several open questions for rhodium silicides: (i) do other stable or metastable stoichiometries in the Rh–Si system exist, besides the already known stoichiometries? (ii) What are their structural and mechanical properties? (iii) Are these metallic phases or, unusually, insulators?
3), in finely divided form, for one hour at 1200 °C and then for one-half hour at 1550 °C.8 To investigate the influence of silicon on the chemical composition and the crystallinity of these crystals, Marot et al. conducted comparative measurements on rhodium/silicon films of Rh2Si, Rh5Si3, RhSi and Rh3Si4 at room temperature using X-ray and ultraviolet photoelectron spectroscopy (XPS), ultraviolet photoemission spectroscopy (UPS), scanning electron microscope (SEM) and XRD techniques. The formation of Rh2Si at 300 °C, Rh5Si3 at 500 °C and 600 °C, RhSi as well as Rh5Si3 at 800 °C and 900 °C was reported.6 In order to gain a deeper insight into the Rh–Si system, Niranjan performed calculations on the structural, electronic and elastic properties of RhSi both in the cubic and orthorhombic phase, and found that relatively strong three centre (Rh–Si–Rh) directional bonds are formed in both phases due to the hybridization between Rh-4d orbitals and Si-3p orbitals.9 However, there have been several open questions for rhodium silicides: (i) do other stable or metastable stoichiometries in the Rh–Si system exist, besides the already known stoichiometries? (ii) What are their structural and mechanical properties? (iii) Are these metallic phases or, unusually, insulators?![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) as the lowest ground state energy phases.7,8,22 This gives us confidence in the applicability of our method to this and other transition metal silicides. The crystal structure information of the lowest energy structures for each stoichiometry considered at GGA level is presented in Table 1, along with the theoretical values and available experimental data of the rhodium silicides Rh2Si (Pnma), Rh5Si3 (Pbam) and RhSi (Pnma).7,23,24 Complete crystal structure information for the considered phases of RhxSiy are listed in Tables S1 and S2 (in the ESI†). The energetic stability of RhxSiy stoichiometries can be quantified by constructing the ground state convex hull, which is constructed from the formation enthalpy per atom of the most stable structures at each stoichiometry: ΔH = {E (RhxSiy) − x*E (Rh) − y*E (Si)}/(x + y). Here ΔH is the relative ground state enthalpy of formation per atom and E is the calculated enthalpy per formula unit for each stoichiometry. Any structure with an enthalpy on the convex hull is energetically stable towards decomposition into other unary or binary phases, and thus experimentally accessible.25 The convex hull of Rh–Si phases at ambient pressure, with the optimized lowest energy structures of RhxSiy is presented in Fig. 1. From Fig. 1, it is clearly seen that the convex hull is composed of four stable phases denoted as Rh2Si (Pnma), Rh5Si3 (Pbam), RhSi (Pnma) and Rh4Si5 (P21/m); their structures are shown in Fig. 2 and 3. Under well-controlled experimental conditions (e.g. regarding relative stoichiometries), these could be synthesized and confirmed by experiments. In order to check the reliability of our calculations, we recalculate the crystal structure parameters and formation enthalpies of Rh–Si system using LDA+U method (see Fig. S1 in the ESI†). The calculated crystal structure parameters and formation enthalpies of the four stable stoichiometries are listed in Table S3 (in the ESI†). We clearly note that the LDA+U calculated results are in good agreement with the GGA–PBE calculations, providing important support for the reliability of present GGA–PBE calculations. Interestingly, several new metastable structures of rhodium silicides with various silicon concentrations have also been found (see Fig. S2 in the ESI†).
m) as the lowest ground state energy phases.7,8,22 This gives us confidence in the applicability of our method to this and other transition metal silicides. The crystal structure information of the lowest energy structures for each stoichiometry considered at GGA level is presented in Table 1, along with the theoretical values and available experimental data of the rhodium silicides Rh2Si (Pnma), Rh5Si3 (Pbam) and RhSi (Pnma).7,23,24 Complete crystal structure information for the considered phases of RhxSiy are listed in Tables S1 and S2 (in the ESI†). The energetic stability of RhxSiy stoichiometries can be quantified by constructing the ground state convex hull, which is constructed from the formation enthalpy per atom of the most stable structures at each stoichiometry: ΔH = {E (RhxSiy) − x*E (Rh) − y*E (Si)}/(x + y). Here ΔH is the relative ground state enthalpy of formation per atom and E is the calculated enthalpy per formula unit for each stoichiometry. Any structure with an enthalpy on the convex hull is energetically stable towards decomposition into other unary or binary phases, and thus experimentally accessible.25 The convex hull of Rh–Si phases at ambient pressure, with the optimized lowest energy structures of RhxSiy is presented in Fig. 1. From Fig. 1, it is clearly seen that the convex hull is composed of four stable phases denoted as Rh2Si (Pnma), Rh5Si3 (Pbam), RhSi (Pnma) and Rh4Si5 (P21/m); their structures are shown in Fig. 2 and 3. Under well-controlled experimental conditions (e.g. regarding relative stoichiometries), these could be synthesized and confirmed by experiments. In order to check the reliability of our calculations, we recalculate the crystal structure parameters and formation enthalpies of Rh–Si system using LDA+U method (see Fig. S1 in the ESI†). The calculated crystal structure parameters and formation enthalpies of the four stable stoichiometries are listed in Table S3 (in the ESI†). We clearly note that the LDA+U calculated results are in good agreement with the GGA–PBE calculations, providing important support for the reliability of present GGA–PBE calculations. Interestingly, several new metastable structures of rhodium silicides with various silicon concentrations have also been found (see Fig. S2 in the ESI†).









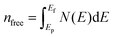

![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase (11.1 GPa), implying it is a potential hard material at ambient conditions (see Table S3 in the ESI†).
m phase (11.1 GPa), implying it is a potential hard material at ambient conditions (see Table S3 in the ESI†).



