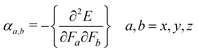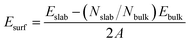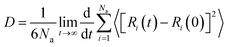DOI:
10.1039/C4RA04931D
(Paper)
RSC Adv., 2014,
4, 41956-41967
Theoretical challenges in understanding the inhibition mechanism of copper corrosion in acid media in the presence of three triazole derivatives†
Received
25th May 2014
, Accepted 26th August 2014
First published on 29th August 2014
Abstract
Using quantum chemical and molecular dynamics approaches, we investigated the corrosion inhibition mechanism of the Cu/HNO3 system in the presence of three triazole derivatives. The interactions between inhibitors and copper substrates were described by the periodic slab model using density functional theory calculations. Dispersion forces are taken into account in the OBS (Ortmann, Bechstedt, and Schmidt) framework correcting both energies and gradients. It was found that the perpendicular configuration is energetically more stable than the parallel configuration for all three inhibitors. A diffusion model was also employed to compare the protective effect of the inhibitor membranes. A good correlation was observed between the related parameters and inhibition efficiency data reported in the literature.
1. Introduction
Copper metal is widely used in microelectronic packaging. The advantages of copper over aluminium are lower resistance and higher reliability. But copper is an active metal, which readily undergoes corrosion in acid medium. Corrosion is a destructive phenomenon by which the metallic structures are destroyed gradually through chemical or electrochemical reactions. Therefore, various attempts must be employed to prevent or retard these undesired reactions. The application of inhibitors, viz. specific organic compounds containing heteroatoms, aromatic rings or π electrons, is one of the most practical methods to combat corrosion.1–3
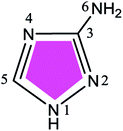
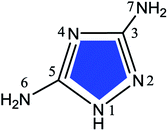
Nowadays, N- and S-containing triazole derivatives have attracted more attention for their excellent corrosion inhibition performance.4–7 Zarrouk et al.8–10 have recently reported considerable inhibition efficiencies of such three compounds, that is, 3-amino-1,2,4-triazole (ATA), 3,5-diamino-1,2,4-triazole (DAT), and 4-amino-3-hydrazino-5-mercapto-1,2,4-triazole (AHMT) (see Table 1), for copper corrosion in 2 M HNO3 medium. The results of their electrochemical and weight loss measurements showed that all three compounds reduce the corrosion rate of copper substantially in HNO3 medium. At any given inhibitor concentration, the corrosion rate follows the order: ν(AHMT) < ν(DAT) < ν(ATA), which indicates that AHMT exhibits the best inhibitive performance among these additives. A recondite explanation was suggested that the inhibitor molecules hinder the dissolution of copper by forming a protective hydrophobic film on the surface.
Table 1 Percent inhibition efficiency, IE (%), of three triazole derivatives as corrosion inhibitors of copper in nitric acid solution (0.01 M, 303 K)a
| Taken from ref. 8–10, obtained through weight loss experiments. |
 |
 |
 |
| 3-Amino-1,2,4-triazole |
3,5-Diamino-1,2,4-triazole |
4-Amino-3-hydrazino-5-mercapto-1,2,4-triazole |
| ATA |
DAT |
AHMT |
| 82.2 |
86.5 |
91.7 |
Although their experimental work has shown that the inhibitor molecules act by adsorption at the metal interface, the protection mechanism of organic corrosion inhibitors has not been clearly understood. Actually, little attention has been paid to how these organic surface modifiers bind to metal surfaces, and why seemingly minor modifications in the structures of organic active compounds can have a profound effect on their efficacy. The advancements in computer simulation techniques hold promise that questions regarding the inhibitive properties of such compounds can be addressed at the atomic level. Therefore, there is a wealth of theoretical studies concerning the associations between molecular mechanism and inhibition effect.11–15
In this work, prompted by the successful application of theoretical calculations in corrosion inhibitor research, an attempt is devoted to elucidate the inhibition mechanism of ATA, DAT and AHMT compounds and to give a suitable explanation to the experimental results by using quantum mechanics and molecular dynamics methods, which have proven to be very suitable methods for gaining new physical insight into the actual inhibition mechanism.
2. Methods and definitions
2.1. Computational details
The geometry pre-optimizations of the molecules studied have been carried out by applying the molecular-mechanics method. Thereafter, the optimized equilibrium structures of molecules have been calculated by DFT methods, B3LYP and PW91 functionals, using 6-311++G** basis set, which are embodied in Gaussian 03 program package.16 Frequency calculation was executed simultaneously, and no imaginary frequency was found, confirming the minimum-energy structures. The global and local indexes of reactivity were calculated with Koopmans approximation.17
A prediction of copper crystal morphology was necessary before the simulation process. Three representative algorithms, i.e., the Bravais–Friedel–Donnay–Harker (BFDH) method, the surface free-energy (SFE) model, and the attachment energy (AE) method, were utilized to predict crystal structures. More detailed descriptions about these models can be found in ref. 18 and the references therein.
The interactions between interested inhibitors and the Cu(111) surface was carried out in a simulation box with periodic boundary conditions using the DMol3 program.19 The Cu(111) surface was modelled with a four-layer slab model. In this model, there were 25 copper atoms in each layer representing a (5 × 5) unit cell, and a 20 Å vacuum region between two adjacent layers to ensure the repeated slabs decoupled. The generalized gradient approximation (GGA) functional developed by Perdew and Wang (PW91)20,21 has been employed in conjunction with a double numeric quality basis set with polarization functions (DNP), where the reliability of this level of theory in studying the metal surface has been confirmed.22–24 The electron–ion interaction was described by density functional semi-core pseudopotentials for metals, which are intended for use with density functional local orbital methods. A Monkhorst–Pack grid of 6 × 6 × 1 was used to simple the Brillouin zone. The tolerances of energy, gradient, and displacement convergence were 1 × 10−5 Ha, 2 × 10−3 Ha Å−1, and 5 × 10−3 Å, respectively. A Fermi smearing of 0.001 Ha and a real space cutoff of 4.4 Å were used to improve computational performance. To explore the influence of van der Waals (vdW) forces on the adsorption geometry, the calculations were also performed by the PW91-D scheme, which includes a semiempirical dispersion correction of OBS25 (Ortmann, Bechstedt, and Schmidt) that consists of employing a damped C6·R−6 energy term applied on top of the PW91 functional. We used a damping constant (λ = 3.0 × 10−5), in order to confirm the universality and transferability of this parameter, some solids and molecular systems (including Fe, Ar2, benzene dimer, etc.) were studied (see Table S in the ESI†). For the PW91-D set of calculations, the Cu bulk lattice parameter has been recalculated with the PW91-D functional, which gives a slightly smaller value of 3.645 Å compared to the PW91 value of 3.650 Å.
After above calculations, the possible bonding modes between Cu atoms and the inhibitors were straightforward. Thus, all the most probable Cu–inhibitor (using a single Cu atom for simplicity) geometries have been fully optimized at the B3LYP/6-311++G** level using Gaussian 03. To better clarify the nature of the intermolecular contact, the QTAIM (quantum theory of atoms in molecules)26 analysis was performed with the help of Multiwfn software27 on the basis of the optimized structures.
Finally, diffusion model was selected to compare the protective effect of the inhibitor membranes. As shown in Fig. 1, the model consists of three regions, the substrate, middle layer and top layer. The substrate is Cu(111) surface. It contains five layers of copper atoms consisted of 405 frozen copper atoms. The middle layer contains an amorphous system of inhibitor membranes (composed of 50 inhibitors) and three H3O+ corrosive particles. The top layer is a 30 Å vacuum slab. To obtain the equilibrium density of inhibitor membrane, molecular dynamics (MD) simulations were carried out under NPT ensemble. The pressure was 1 × 10−4 GPa controlled by means of Berendsen Barostat method.28 The temperature and simulation time are set to 303 K and 300 ps, respectively. Then, the middle layer was rebuilt with the calculated density by the Amorphous Cell module. After a molecular mechanics optimization, three diffusion models were submitted to a 1 ns MD run under the NVT ensemble. All the MD simulations were performed under COMPASS29 force field, which was parameterized to predict various properties (molecular structures, vibrational frequencies, conformation energies, etc.) for molecules in isolation and in condensed phases (equations of state, cohesive energy density, etc.).
 |
| | Fig. 1 Schematic of interface supercell (the design in the vacuum region is just for aesthetics). | |
In all our simulations, we have neglected charge and solvent effects and performed the calculations at the neutral forms of the molecules. Although this is clearly an oversimplification of the factual situation, it is adequate to qualitatively illustrate the differences in the adsorption behaviour of three molecules and provide sufficient insight to rationalize previous experimental findings.
2.2. Definitions of global reactivity descriptors
Within the conceptual framework of DFT, the chemical potential σ, which measures the escape tendency of an electron from equilibrium, is defined as:where σ is the first derivative of the total energy E relative to the electron number N, ν is the external potential exerted by the nucleus and χ is the electronegativity.
The global hardness η can be seen as the resistance to charge transfer and is defined as:
Using a finite difference approximation and Koopmans's theorem, the above expressions can be written as:
| | |
σ ≈ (I + A)/2 ≈ (EHOMO + ELUMO)/2 = −χ
| (3) |
| | |
η ≈ (I − A)/2 = (ELUMO − EHOMO)/2
| (4) |
where
EHOMO and
ELUMO represent the energies of the highest occupied and the lowest unoccupied molecular orbitals (HOMO and LUMO), respectively,
I is the ionization potential and
A is the electron affinity. When two systems, Cu and inhibitor, are brought together, electrons will flow from (to) inhibitor to (from) Cu, until the chemical potentials become equal. As a first approximation, the fraction of transferred electrons (Δ
N) was calculated according to Pearson theory
30 as follows:
| |
 | (5) |
where work function (
Φ) is uesd for the electronegativity of metal surface, and the global hardness is neglected by assuming that for a metallic bulk
I =
A because they are softer than the neutral metallic atoms.
31
3. Results and discussion
3.1. Molecular reactivity
Quantum chemical calculations were performed to investigate the inhibition efficiencies of mentioned inhibitors. Table 2 shows the calculated theoretical parameters such as total energy, EHOMO, ELUMO, and ΔE, which provide information about the reactive behavior. In some ways, though, different calculation methods produced some changes in the electronic structure of the inhibitor molecules, but they follow the same trend for the presented properties of three molecules. However, the hybrid B3LYP functional is the most popular and reasonably accurate functional for the description of organic molecules. Thus, in subsection 3.1, unless explicitly attributed to PW91, the results refer to B3LYP/6-311++G** approach.
Table 2 Calculated quantum chemical properties for triazole derivatives ATA, BAT and AHMT
| Molecule |
|
EHOMO (eV) |
ELUMO (eV) |
ΔE (eV) |
μ (Debye) |
〈α〉 (Å3) |
χ |
η |
ΔN |
| ATA |
B3LYP |
−6.26 |
−0.38 |
5.88 |
2.06 |
7.63 |
3.32 |
2.94 |
0.24 |
| PW91 |
−5.33 |
−0.98 |
4.34 |
1.95 |
8.02 |
3.15 |
2.17 |
0.37 |
| DAT |
B3LYP |
−5.81 |
−0.65 |
5.16 |
2.60 |
9.15 |
3.23 |
2.58 |
0.29 |
| PW91 |
−4.86 |
−1.11 |
3.75 |
2.51 |
9.66 |
2.98 |
1.87 |
0.47 |
| AHMT |
B3LYP |
−6.42 |
−1.06 |
5.37 |
4.99 |
13.62 |
3.74 |
2.68 |
0.19 |
| PW91 |
−5.53 |
−1.66 |
3.87 |
4.93 |
14.41 |
3.59 |
1.93 |
0.30 |
The electric dipole polarizability is a measure of the linear response of the electron density in the presence of an infinitesimal electric field, F, and represents a second-order variation in the energy, viz.:32
| |
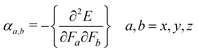 | (6) |
The mean polarizability 〈α〉 is a property observed when a molecule presents all orientations to the applied field and is evaluated by 〈α〉 = (αxx + αyy + αzz)/3. As seen in Table 2, the polarizability values of ATA, DAT, and AHMT calculated with B3LYP are 7.63, 9.15, and 13.62 Å3, respectively. It means that the higher values of α facilitate the strong adsorption process, resulting in an increase in the inhibition efficiency.
The interaction between the inhibitor and the metal can be understood in the light of the frontier molecular orbital theory. In general, high lying HOMO favors the donation of molecular charge to metal, whereas low lying LUMO induces a back-donation of charge from metal to the molecule.33,34 Both effects contribute to the enhanced molecule–metal interaction. It is understandable that the less negative HOMO and the smaller energy gap reflects a stronger chemisorbed bond and greater inhibitor efficiency. We regrettably find out that there is no direct correlation between EHOMO, ΔE and inhibition efficiency determined experimentally. Consequently, this make the related descriptors (including χ, η and ΔN) invalid. Similar cases have been reported elsewhere.35,36 It demonstrates that some molecular electronic properties cannot be used in a blind fashion to judge the inhibition effectiveness.
Actually, the chemisorption through the nitrogen lone-pair electrons is very common for nitrogen-containing aromatic rings; Moreover, in the previous DFT study it has been shown that several high-lying orbitals mix with metal states, yet the interaction is mainly due to σ-type molecular orbitals.37,38 The high-lying molecular orbitals (including HOMO-n and LUMO) are plotted in Fig. 2 for three azole derivatives. For all the molecules, the HOMO is a π-type orbital and is spread throughout the whole molecular skeleton. On the other hand, if the energy of the σ orbital was decisive for the inhibitor properties, the ranking of the compounds should be: EHOMO-1 (AHMT) > EHOMO-2 (DAT) > EHOMO-1 (ATA). This agrees well with the experimental observations.
 |
| | Fig. 2 Isosurface plots of HOMO-n (n = 0, 1, and 2) and LUMO molecular orbitals for the molecules studied. The number below each molecular orbital plot is the energy (in eV) of the orbital. | |
Dipole moment (μ) is another often used parameter in the corrosion inhibition studies.39 There is no consensus on the influence of the dipole moment on corrosion inhibition. Some authors think that an increase of the dipole moment leads to decrease of inhibition, suggesting that a lower value of dipole moment will favour accumulation of the inhibitor in the surface layer.40,41 Others argue that the increase of the dipole moment can lead to increase of inhibition, which could be related to the dipole–dipole interaction of molecules and metal surface.42,43 Kokalj does not see this as a conflict and he demonstrates that the role of the molecular dipole depends on its orientation.35 The dipole is almost parallel to the molecular plain for DAT (see Fig. 3a), whereas for ATA/AHMT the dipole points outward slightly. The higher value of μ obtained for AHMT is coherent with the second explanation indicating stronger dipole–dipole interactions of AHMT molecules and metallic surface in comparison to that of ATA/DAT.
 |
| | Fig. 3 (a) Molecular dipoles shown as the arrows pointing from the barycenter of the molecules. (b and c) Contour and isosurface representation of electrostatic potential, respectively. Negative (positive) regions are colored blue (red). | |
The local reactivity has been analyzed by means of Fukui function, which are an indication of the reactive centers within the molecules. In the finite difference approximation, the condensed Fukui functions at the atom k can be calculated unambiguously for two situations:44
| | |
f+ = q(N) − q(N + 1) (for nucleophilic attack)
| (7) |
| | |
f− = q(N − 1) − q(N) (for electrophilic attack)
| (8) |
herein,
q(
N + 1),
q(
N) and
q(
N − 1) are the charges at atom
k of the anionic, neutral and cationic species, respectively. The definition of the dual descriptor Δ
f has close relationship with Fukui function:
45
Unlike Fukui function, via Δf both types of reactive sites can be revealed simultaneously. If Δf > 0, then the site is favorable for a nucleophilic attack, whereas if Δf < 0, then the site is favorable for an electrophilic attack.
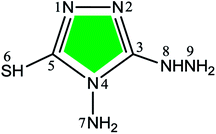
Table 3 shows the atomic charges and condensed Fukui functions for the three inhibitors, which were easily evaluated from the Hirshfeld population analysis.46 By examination of the f+ values, it is evident that the preferred sites for nucleophilic attack in ATA, DAT and AHMT are near C5, N6 and S6 atoms, respectively. As for f−, the N atoms of amino group are substantially charged, but they are passivated with H atom. So we thought that their reaction activities were reduced to some extent in neutral/vacuum condition. Moreover, the f− values for N2 atoms were relatively larger for all three molecules, which implied that these atoms preferred to provide electrons to form coordinate bonds with the metal atoms, so they were the electrophilic reactive sites during absorption. These results are basically consistent with previous HOMO/LUMO analysis. Besides, the adsorption geometries of the inhibitors can be anticipated from the electrostatic potential plots presented in Fig. 3b and c. These negative regions would be preferred sites for adsorption to metal surfaces. On this basis, it can be anticipated that ATA/DAT would adsorb through either N2 or N4 atoms, whereas AHMT would adsorb via N1 and N2 atoms.
Table 3 Calculated Hirshfeld atomic charges and condensed Fukui functions for ATA, BAT and AHMT (numbers of atoms were shown in Table 1)
| ATA |
DAT |
AHMT |
| # |
q |
f+ |
f− |
Δf |
q |
f+ |
f− |
Δf |
# |
q |
f+ |
f− |
Δf |
| N1 |
−0.01 |
0.02 |
0.10 |
−0.07 |
−0.04 |
0.02 |
0.09 |
−0.07 |
N1 |
−0.16 |
0.03 |
0.10 |
−0.06 |
| N2 |
−0.20 |
0.03 |
0.16 |
−0.14 |
−0.22 |
0.03 |
0.19 |
−0.16 |
N2 |
−0.20 |
0.03 |
0.13 |
−0.10 |
| C3 |
0.10 |
0.03 |
0.08 |
−0.06 |
0.10 |
0.02 |
0.08 |
−0.06 |
C3 |
0.11 |
0.02 |
0.06 |
−0.04 |
| N4 |
−0.23 |
0.03 |
0.08 |
−0.05 |
−0.25 |
0.02 |
0.06 |
−0.04 |
N4 |
0.01 |
0.00 |
0.02 |
−0.02 |
| C5 |
0.05 |
0.06 |
0.10 |
−0.05 |
0.12 |
0.02 |
0.07 |
−0.04 |
C5 |
0.03 |
0.01 |
0.09 |
−0.07 |
| N6 |
−0.17 |
0.03 |
0.21 |
−0.18 |
−0.16 |
0.04 |
0.10 |
−0.06 |
S6 |
−0.02 |
0.16 |
0.13 |
0.02 |
| N7 |
|
|
|
|
−0.17 |
0.02 |
0.15 |
−0.13 |
N7 |
−0.12 |
0.04 |
0.02 |
0.02 |
| |
|
|
|
|
|
|
|
|
N8 |
−0.08 |
0.01 |
0.14 |
−0.13 |
| |
|
|
|
|
|
|
|
|
N9 |
−0.16 |
0.02 |
0.07 |
−0.05 |
3.2. Copper surfaces survey
We calculated the surface energy (Esurf) in a slab model as47| |
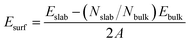 | (10) |
where Eslab and Ebulk are the total energies of the surface slab and the bulk unit cell, respectively. Nslab and Nbulk are the number of atoms contained in the slab and the bulk unit cells, respectively, and ‘A’ is the area of the surface unit cell. For each slab model, the work function (Φ) is obtained as follows:48where Evac is the vacuum local potential energy and EF is the Fermi level.
The calculated surface energies, work functions, as well as the morphology results for copper crystal are listed in Table 4. Our results are in reasonable agreement with the available literature data.49–51 After careful analysis of the simulated crystal morphology for copper, one will notice that the (111) face accounts for at least 42.0% of the crystal surface, and the most 77.6% in the BFDH model. The calculated surface energies decrease in the following sequence: (110) > (100) > (111). Additionally, a more intuitive micromorphology comparison diagram is produced, as shown in Fig. 4. Based on Fig. 4d, the regular (110), (100), and (111) surfaces have one type of surface atom with coordination numbers 7, 8, and 9, respectively. The calculated surface work functions were found to be strongly dependent on the surface atom coordination number, and follow the expected trend (111) > (100) > (110), which means that the lower the coordination number of the surface atom the lower the work function value.52 Consequently, the densely packed Cu(111) surface model was chosen as representative to address the inhibitor adsorption-study because it is the most stable low Miller index copper surface and then the most abundant. In addition, the Cu(111) surface symmetry provides an advantage to systematically explore the potential energy surface of the adsorption system.
Table 4 Surface atom coordination number (N, #), surface energy, work function and morphology results for the clean copper surfaces studied here
| hkl |
Multiplicitya |
% Total facet area |
Surface energy (J m−2) |
Work function (eV) |
N |
| BFDH |
SFE |
AE |
BFDH |
SFE |
AE |
This work |
Calc.49,50 |
This work |
Calc.50 |
Expt.51 |
| Symmetry multiplicity of the growth form. |
| (110) |
12 |
12 |
12 |
– |
26.5 |
– |
1.60 |
1.47 |
4.23 |
4.39 |
4.48 |
7 |
| (100) |
6 |
6 |
6 |
22.4 |
31.5 |
28.5 |
1.45 |
1.44 |
4.42 |
4.60 |
4.59 |
8 |
| (111) |
8 |
8 |
8 |
77.6 |
42.0 |
71.5 |
1.37 |
1.30 |
4.76 |
4.83 |
4.94 |
9 |
 |
| | Fig. 4 (a–c) The crystal habits of copper simulated by BFDH, SFE, and AE algorithms, respectively. (d) Upper views of the Cu (3 × 3) surface models. | |
3.3. Adsorption at Cu(111) surface
3.3.1. Adsorption geometries and energies. Following a strategy similar to that used in previous works,53,54 both parallel and perpendicular adsorption orientations of the inhibitor on to Cu(111) surface have been considered. The geometries of inhibitor molecules adsorbed on the Cu(111) surface with a perpendicular (parallel) initial adsorption configuration were investigated and the most stable optimized structures are displayed in the upper (lower) panels of Fig. 5. To quantitatively appraise the interaction between each molecule and the copper surface, the adsorption energy (Eads) was calculated using following formula| | |
Eads = Emol/surf − (Esurf + Emol)
| (12) |
where Emol, Esurf, and Emol/surf are the total energies of isolated adsorbate, Cu(111) slab, and mol/Cu(111) system, respectively. Based on this definition, a negative value of Eads corresponds to a stable adsorption structure. Calculated adsorption energies and structure parameters of inhibitor molecules adsorbed on the Cu(111) surface are summarized in Table 5.
 |
| | Fig. 5 Geometry optimized structures of ATA, DAT, and AHMT adsorbed on Cu(111). Only parts of the atoms of the slab model are shown for clarity. | |
Table 5 Structural parameters and adsorption energies of inhibitor molecules adsorbed on Cu(111) as obtained with the PW91 and PW91-D functionalsa
| Molecule@Cu(111) |
Perpendicular |
Initially parallel |
| Bond lengths (Å) |
ΔhCub (Å) |
Eads (eV) |
Eads (eV) |
θc (deg) |
| Values in parentheses are those from PW91-D functional. ΔhCu denotes the distance that the copper has moved up. The angle θ is defined by the two planes of molecular cyclic skeleton and the horizontal substrate. |
| ATA |
R[N2–Cu] |
2.06 (2.05) |
0.25 (0.21) |
−0.67 (−0.84) |
−0.26 (−0.76) |
3.8 (59.9) |
| DAT |
R[N4–Cu] |
2.11 (2.10) |
0.22 (0.21) |
−0.76 (−0.99) |
−0.61 (−0.94) |
69.9 (27.2) |
| R[N7–Cu] |
2.22 (2.21) |
0.12 (0.08) |
| AHMT |
R[N1–Cu] |
2.01 (2.02) |
0.06 (0.06) |
−1.12 (−1.29) |
−0.86 (−1.26) |
64.2 (58.3) |
| R[N2–Cu] |
2.11 (2.09) |
0.12 (0.10) |
For perpendicular adsorption modes, the PW91 and PW91-D functionals give almost identical structures (just give the structures of the former for simplicity), but discrepancies appear for initially parallel modes. These discrepancies can be seen in the lower panels of Fig. 5, where the PW91-D gives a more tilted adsorption configuration. Similar results were obtained by Kokalj et al.53 in their study of the adsorption of dehydrogenated benzotriazole on perfect copper surfaces. ATA is a very special case since PW91 shows nearly parallel structure, and the molecule surface height of 3.0 Å (substantially equal to the sum of the van der Waals radii rNvdw+ rCuvdw = 1.55 + 1.40 = 2.95 Å)55 indicates a physisorption nature. As for the adsorption energies, it can be seen that the perpendicular configuration is energetically more stable than the initially parallel configuration for all the three inhibitors. This confirms that azoles bond perpendicularly with σ-orbitals to transition metals with fully occupied d-band (such as copper).56 The non-perpendicular state appears to be either unstable or metastable, it is either a very shallow minimum or a flat plateau, and the molecules are steered directly into perpendicular (chemisorbed) state.
Analysis of the frozen perpendicular configurations reveals that inhibitors actually bond directly with Cu through nitrogen atoms. Concrete speaking, ATA molecule is adsorbed on top of a Cu atom with a single N2 atom; DAT molecule mainly adsorbs via N4 atom, as well as a relatively weak interaction via N7 atom; whereas AHMT is boned through the bridge-N1, N2 atoms. These results indeed confirm above active site analysis. As evident from Table 5, the N–Cu bond lengths are in the range between 2.0–2.2 Å thus being comparable to the sum of N and Cu covalent radii (rNcov + rCucov = 0.71 + 1.32 = 2.03 Å), which be categorized as chemisorption. The three molecules interact strongly with the surface and the strength of the chemisorption increases in the order ATA < DAT < AHMT with the adsorption energies of −0.67, −0.76, and −1.12 eV, respectively. Due to the strong interaction, the adsorption induced corrugation, as measured by ΔhCu (defined in Table 5), is about 0.06–0.25 Å. The PW91-D gives more exothermic adsorption energies than the PW91, although it may more appropriately capture the relative stability of different adsorption modes, we hold that under current circumstance the PW91 results should be more appropriate than the PW91-D results, because it is known that PW91 functional often overestimates the chemisorption energies.57,58 The absolute value of adsorption energy for ATA (i.e., 0.67 eV) is slightly higher than the earlier reported PBE result (0.6 eV),33,55 this can be considered acceptable, since PW91 gives slightly higher adsorption energy than PBE for molecule—metal (hkl) system (as reviewed by Hammer and Norskov).59
3.3.2. Projected density of states. Insights into the interaction between inhibitor molecule and Cu(111) surface can be obtained from the projected density of states (PDOS), as shown in Fig. 6 (PW91 results). A Gaussian broadening width of 0.04 eV has been applied. The Fermi level is set to zero, as shown by the vertical line.
 |
| | Fig. 6 Superimposed density of states for ATA, DAT, and AHMT projected to the molecule (blue) and to the Cu atoms that bond with the molecule (red) (upper panels: inhibitor above Cu(111); lower panels: perpendicular adsorption configurations in Fig. 5). | |
Fig. 6 shows the PDOS of the inhibitor/Cu(111) system before and after molecule–surface interaction: the upper panels presents the PDOS for the molecule located 7 Å above the Cu(111) surface, while the lower panels shows the PDOS for the molecule with the perpendicular adsorption mode. The upper panels can be used to highlight the high-lying molecular valence states before the interaction occurs.33,60,61 It is obvious that several molecular states lie at the position of the copper d-band, which can be considered to describe the molecule–surface bonding upon adsorption. When the inhibitor molecule adsorbs on the copper surface (shown in the lower panels), the molecular peaks broadened slightly due to the hybridization between molecular and metal states. As a consequence, the distributions of density of states for both Cu and adsorbates are skewed toward the lower energy values. In the energy range from −4.5 to −1.5 eV, the molecular PDOS of AHMT is considerably less spiky compared to that of ATA/DAT, suggesting the stronger molecule–surface bond.
3.3.3. Charge density difference. The corresponding rearrangement of electronic charge upon the adsorbed inhibitor molecules can be obtained by subtracting the charge densities of the non-interacting systems (isolated copper surface ρsurf, and isolated of inhibitor molecule ρmol, both frozen at their final equilibrium configuration upon adsorption) from those where the inhibitors interact with the Cu(111) surface ρmol/surf:| | |
Δρ = ρmol/surf − (ρmol + ρsurf)
| (13) |
The charge density difference of the most stable adsorption configuration for all three corrosion inhibitor molecules is shown in Fig. 7, this distinctly demonstrates the complex interplay between the different orbitals of metal and inhibitor molecule. The formation of direct N–Cu bonds can be seen by the charge redistribution between the corresponding N and Cu atoms, i.e., the charge flows from these atoms toward the center of N–Cu bonds. This covalent interaction is not very strong, because the Cu has the d-band completely below the Fermi energy. There is persuasive evidence that for these neutral azole/metal adsorption systems, the contribution of dipole interactions to the molecule–surface bonding is significant.50,62 Besides, there is an accumulation of charge (red regions) located in between bottommost hydrogen atoms and the copper surface, suggesting the existence of the weak X–H⋯Cu hydrogen bond (X = N or S atom).63 The adsorption between inhibitor molecules and copper surface can be strengthened through this type of bond.
 |
| | Fig. 7 Charge density difference of ATA, DAT, and AHMT molecules chemisorbed on Cu(111) surface with the perpendicular adsorption configurations (PW91 results). (The value of the mapped field is drawn in linear scale from −0.06 to +0.06 e Å−3, blue and red refer to an decrease and increase of the electronic density, respectively). | |
3.3.4. QTAIM analyses. In the QTAIM analyses, the existence of the interatomic interaction is indicated by the presence of a so-called bond critical point (BCP). The properties at the BCPs are analysed in terms of the following parameters: the electron density (ρbcp), its Laplacian (Lbcp), the electron energy density (Hbcp) and absolute ratio of kinetic and potential energies densities (−Gbcp/Vbcp). In their review Macchi and Sironi have summarized that the covalent bonds involving transition metals are characterized by: (i) the small values of ρbcp and Lbcp; (ii) negative total energy density Hbcp < 0 (that is, in covalent bonds the potential energy is dominated over kinetic energy).64 Espinosa et al. proposed use of the −Gbcp/Vbcp ratio classify different types of interactions: if −Gbcp/Vbcp > 1 the interaction is non-covalent in nature; if 0.5 < −Gbcp/Vbcp < 1, the interaction is partly covalent.65As shown in Fig. 8, the interactions between Cu and the active sites of three inhibitors can be confirmed by the existence of the BCP of the Cu⋯N contact. The corresponding topological parameters at the BCPs have been listed in Table 6. The electron density ρbcp can be used to characterize the relative strength of the Cu⋯N contact. As seen in Table 6, Cu⋯N7 exhibits weaker interactions compared with the other bonds, accompanied with a longer bond length. If considering multiple active adsorption sites, the relative order of the ρbcp for the three Cu–inhibitor complexes is: Cu–AHMT > Cu–DAT > Cu–ATA, which is consistent with the relative order of the inhibition efficiency. The positive values of Lbcp, −Gbcp/Vbcp < 1 and the nearly zero values of Hbcp suggest that the interactions between Cu and N atom of the inhibitors are predominated by the electrostatic interactions as well as partial covalent characters in nature.
 |
| | Fig. 8 The molecular graphs of the formed Cu–inhibitor complexes, where the BCPs are denoted as small red dots. | |
Table 6 Calculated topological parameters at the BCPs of the Cu⋯N contacts
| Complexes |
BCP |
ρbcp |
Lbcp |
Hbcp |
−Gbcp/Vbcp |
RCu⋯Xa |
| RCu⋯X: acceptor–donor distance in Å. |
| Cu–ATA |
Cu⋯N2 |
0.0732 |
0.3315 |
−0.0121 |
0.8870 |
2.056 |
| Cu–DAT |
Cu⋯N4 |
0.0748 |
0.3288 |
−0.0129 |
0.8798 |
2.052 |
| Cu⋯N7 |
0.0551 |
0.1999 |
−0.0107 |
0.8501 |
2.206 |
| Cu–AHMT |
Cu⋯N1 |
0.0740 |
0.3371 |
−0.0123 |
0.8871 |
2.054 |
| Cu⋯N2 |
0.0745 |
0.3372 |
−0.0125 |
0.8856 |
2.052 |
3.4. Diffusion of corrosive particle in the inhibitor membrane
The calculated densities of the inhibitor membranes are shown in Fig. 9. It is clear from Fig. 9 that three inhibitor membranes ATA, DAT, and AHMT reach equilibrium after 80 ps MD simulation. In order to obtain the accurate average density, the values from 80 ps to 300 ps are adopted. The calculated densities of three inhibitors ATA, DAT, and AHMT are 1.31, 1.49, and 1.54 g cm−3, respectively. Self-diffusion coefficient (D) of the molecule is the best measurement of the diffusion behavior. It can be used to describe the migration rate of a corrosive species in inhibitor membranes. Normally, D is calculated from the mean square displacement (MSD) by the Einstein diffusion equation:66| | |
MSD = 〈[Ri(t) − Ri(0)]2〉
| (14) |
| |
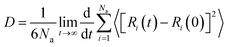 | (15) |
where Na is the number of diffusive atoms; Ri(t) and Ri(0) are positions of corrosive species at time t and 0, respectively. The limiting slope of MSD as a function of time can be used to evaluate the diffusion coefficient of a molecule undergoing random Brownian motion in the three dimensions. Fig. 10 depicts the MSD diagrams of H3O+ in the inhibitor membranes. As illustrated in Fig. 10, the MSD diagram showed a smooth increase during the initial simulation process; the anomalous diffusion67 took place between 650 ps and 1000 ps. Then the effective diffusion coefficients of H3O+ calculated from the MSD slopes over 300–650 ps by means of eqn (15) are listed in Table 7. As previously reported by Zhang and co-workers,68 the diffusion coefficient of H3O+ in water without any inhibitors is 0.831 × 10−5 cm2 s−1. The diffusion coefficients of H3O+ in the inhibitor membranes sharply decrease comparing with those in water. This indicates that these inhibitor membranes could efficiently restrain the migration of corrosive particle.
 |
| | Fig. 9 Calculated densities of inhibitor membranes ATA, DAT and AHMT. | |
 |
| | Fig. 10 MSD plot of H3O+ in the inhibitor membranes at 303 K during 1 ns MD simulation. | |
Table 7 Calculated diffusion coefficients (D) and fractional free volume (ζ) values
| Membrane |
D (×10−7 cm2 s−1) |
ζ |
| ATA |
2.154 |
0.21 |
| DAT |
1.456 |
0.14 |
| AHMT |
1.275 |
0.069 |
Furthermore, to evaluate free volume inside each inhibitor membrane, fractional free volume (ζ) is defined as follow:
| |
 | (16) |
where
Vf is the free volume, and
V0 is the volume occupied by the corrosion inhibitors in the membrane. H
3O
+ was selected as probe particle (connolly radius = 1.35 Å) in the system. It is generally recognized that a large
ζ means there are abundant cavities among the inhibition membrane, and the migration probability of corrosive particle is high, which induces to large diffusion coefficient and low inhibition efficiency.
69 On the one hand, a small
ζ infers to small diffusion coefficient and high inhibition efficiency. In this work, the last frame was extracted after 300 ps MD simulation and the fractional free volume analysis was performed. The free volume distributions of three inhibitor membranes are shown in
Fig. 11. The present
ζ values (see
Table 7) in three inhibitor membranes are in the order
ζ(AHMT) <
ζ(DAT) <
ζ(ATA). This indicates that the size of cavity which is accessible for the corrosive particle decreases in the order ATA > DAT > AHMT. It agreed well with the result of the calculated diffusion coefficient. The diffusion model results showed that it is reasonable and practical to evaluate the inhibition performance, at least qualitatively.
 |
| | Fig. 11 Free volume distributions of three inhibitor membranes probed by H3O+. | |
3.5 Mechanism of adsorption and inhibition
Now, after discussing the inhibition mechanism at molecular/atomic level, clarifying the actual reaction process is necessary. According to the potential–pH diagram shown in Fig. S in the ESI,† the protective Cu2O and CuO oxide films can be easily dissolved at low pH values. As shown in Fig. 12, the dissolution of copper in HNO3 proceeded according to the following steps:| | |
Cu − e− → Cu(I)ads (fast)
| (17) |
| | |
Cu(I)ads − e− → Cu(II) (slow)
| (18) |
where Cu(I)ads is an adsorbed species at the copper surface and does not diffuse into the bulk solution. The cathode reduction of oxygen can be expressed as follow:| | |
O2 + 4H+ + 4e− → 2H2O
| (19) |
 |
| | Fig. 12 Proposed scheme for the adsorption of inhibitors on the copper surface in acid medium. | |
Besides, the nitrate ions are readily reduced:
| | |
NO−3 + 3H+ + 2e− → HNO2 + H2O
| (20) |
| | |
NO−3 + 4H+ + 3e− → NO + 2H2O
| (21) |
According to the literatures,70,71 two mechanisms have been proposed to explain the high inhibiting efficiency recorded for the inhibitors of interest, designated as INH. One mechanism attributes the phenomenon to the formation of an adsorbed layer of INH, i.e.,
| | |
Cu(s) + INH → Cu:INH(ads)
| (22) |
where Cu:INH
(ads) refers to INH adsorbed on the copper surface. The other mechanism postulates a protective Cu(
I)IN film on the surface, which inhibits the anodic dissolution reaction,
i.e.,
| | |
Cu+(aq.) + INH(aq.) → Cu(I)IN(s) + H+(aq.)
| (23) |
The Cu(I)IN complex is favored at more anodic potentials in less acidic media; however, the adsorbed species is formed in more acidic media under cathodic potentials.
4. Conclusions
In the present study, the interactions between three triazole derivatives and copper has been systematically investigated by density functional theory in combination with the QTAIM theory and molecular dynamics. The main conclusions are summarized as follows:
(i) Quantum chemical calculation results reveal that the inhibitor molecules have strong adsorption sites by which they can directly adsorb onto copper surface via sharing of electrons with copper atoms.
(ii) The energies of the σ-molecular orbitals were decisive for the adsorption performance.
(iii) The inhibitors can chemisorb onto Cu(111) with the molecular plane being nearly perpendicular to the surface.
(iv) The agreement of the diffusion model results with the trend of inhibition efficiency (IE) indicates that the pertinent effect (the restrainment of migration of corrosive species through the inhibitor membrane) is a factor that contributes to IE of inhibitors.
Acknowledgements
This research was sponsored by the National Natural Science Foundation of China (21376282). The authors would like to thank Dong Yang for his valuable discussions. We also thank the anonymous referees for valuable criticisms and useful suggestions that helped us to improve the quality of our present and future work.
References
- B. V. Appa Rao, M. Y. Iqbal and B. Sreedhar, Electrochim. Acta, 2010, 55, 620–631 CrossRef CAS PubMed.
- S. John and A. Joseph, RSC Adv., 2012, 2, 9944–9951 RSC.
- S. Banerjee, A. Mishra, M. M. Singh, B. Maiti, B. Ray and P. Maiti, RSC Adv., 2011, 1, 199–210 RSC.
- M. L. Zheludkevich, K. A. Yasakau, S. K. Poznyak and M. G. S. Ferreira, Corros. Sci., 2005, 47, 3368–3383 CrossRef CAS PubMed.
- M. K. Awad, M. R. Mustafa and M. M. A. Elnga, J. Mol. Struct.: THEOCHEM, 2010, 959, 66–74 CrossRef CAS PubMed.
- A. Kosari, M. H. Moayed, A. Davoodi, R. Parvizi, M. Momeni, H. Eshghi and H. Moradi, Corros. Sci., 2014, 78, 138–150 CrossRef CAS PubMed.
- P. Roy, A. Pal and D. Sukul, RSC Adv., 2014, 4, 10607–10613 RSC.
- A. Zarrouk, B. Hammouti, H. Zarrok, M. Bouachrine, K. F. Khaled and S. S. Al-Deyab, Int. J. Electrochem. Sci., 2012, 7, 89–105 Search PubMed.
- A. Zarrouk, B. Hammouti, S. S. Al-Deyab, R. Salghi, H. Zarrok, C. Jama and F. Bentiss, Int. J. Electrochem. Sci., 2012, 7, 5997–6011 CAS.
- A. Zarrouk, B. Hammouti, A. Dafali and F. Bentiss, Ind. Eng. Chem. Res., 2013, 52, 2560–2568 CrossRef CAS.
- J. Zhang, W. Yu, L. Yu, Y. Yan, G. Qiao, S. Hu and Y. Ti, Corros. Sci., 2011, 53, 1331–1336 CrossRef CAS PubMed.
- J. Radilla, G. E. Negrón-Silva, M. Palomar-Pardavé, M. Romero-Romo and M. Galván, Electrochim. Acta, 2013, 112, 577–586 CrossRef CAS PubMed.
- S. Q. Hu, A. L. Guo, Y. F. Geng, X. L. Jia, S. Q. Sun and J. Zhang, Mater. Chem. Phys., 2012, 134, 54–60 CrossRef CAS PubMed.
- V. Jaiswal, R. B. Rastogi, J. L. Maurya, P. Singh and A. K. Tewari, RSC Adv., 2014, 4, 13438–13445 RSC.
- A. Kokalj, Acta Chim. Slov., 2014, 61, 340–349 CAS.
- P. C. Harihara and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213–222 CrossRef.
- G. Klopman, J. Am. Chem. Soc., 1968, 90, 223–234 CrossRef CAS.
- L. Yang and Y. Dong, Carbohydr. Res., 2011, 346, 2457–2462 CrossRef CAS PubMed.
- B. Delley, J. Chem. Phys., 2000, 113, 7756–7764 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- J. P. Perdew, K. Burke and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 16533–16539 CrossRef CAS.
- W. Wang, Z. Li, Q. Sun, A. Du, Y. Li, J. Wang, S. Bi and P. Li, Corros. Sci., 2012, 61, 101–110 CrossRef CAS PubMed.
- E. E. Oguzie, Y. Li, S. G. Wang and F. Wang, RSC Adv., 2011, 1, 866–873 RSC.
- S. H. Chen, S. Q. Sun, B. J. Lian, Y. F. Ma, Y. G. Yan and S. Q. Hu, Surf. Sci., 2014, 620, 51–58 CrossRef CAS PubMed.
- F. Ortmann, F. Bechstedt and W. Schmidt, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 205101 CrossRef.
- R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, New York, 1994 Search PubMed.
- T. Lu and F. W. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- H. J. C. Berendsen, J. P. M. Postma, W. F. Vangunsteren, A. Dinola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS PubMed.
- H. Sun, J. Phys. Chem. B, 1998, 102, 7338–7364 CrossRef CAS.
- R. G. Pearson, Inorg. Chem., 1988, 27, 734–740 CrossRef CAS.
- V. S. Sastri and J. R. Perumareddi, Corrosion, 1997, 53, 617–622 CrossRef CAS.
- R. Parthasarathi, J. Padmanabhan, V. Subramanian, B. Maiti and P. K. Chattaraj, J. Phys. Chem. A, 2003, 107, 10346–10352 CrossRef CAS.
- A. Kokalj and S. Peljhan, Langmuir, 2010, 26, 14582–14593 CrossRef CAS PubMed.
- N. Kovačević and A. Kokalj, Corros. Sci., 2011, 53, 909–921 CrossRef PubMed.
- A. Kokalj, Electrochim. Acta, 2010, 56, 745–755 CrossRef CAS PubMed.
- Y. Yan, W. H. Li, L. K. Cai and B. R. Hou, Electrochim. Acta, 2008, 53, 5953–5960 CrossRef CAS PubMed.
- Y. Jiang and J. B. Adams, Surf. Sci., 2003, 529, 428–442 CrossRef CAS.
- Y. G. Avdeev and Y. I. Kuznetsov, Russ. Chem. Rev., 2012, 81, 1133–1145 CrossRef PubMed.
- G. Gece, Corros. Sci., 2008, 50, 2981–2992 CrossRef CAS PubMed.
- N. Khalil, Electrochim. Acta, 2003, 48, 2635–2640 CrossRef CAS.
- M. Lebrini, F. Bentiss, H. Vezin and M. Lagrenee, Appl. Surf. Sci., 2005, 252, 950–958 CrossRef CAS PubMed.
- S. G. Zhang, W. Lei, M. Z. Xia and F. Y. Wang, J. Mol. Struct.: THEOCHEM, 2005, 732, 173–182 CrossRef CAS PubMed.
- H. M. Abd El-Lateef, V. M. Abbasov, L. I. Aliyeva, E. E. Qasimov and I. T. Ismayilov, Mater. Chem. Phys., 2013, 142, 502–512 CrossRef CAS PubMed.
- R. R. Contreras, P. Fuentealba, M. Galvan and P. Perez, Chem. Phys. Lett., 1999, 304, 405–413 CrossRef CAS.
- C. Morell, A. Grand and A. Toro-Labbe, J. Phys. Chem. A, 2005, 109, 205–212 CrossRef CAS PubMed.
- F. L. Hirshfeld, Theor. Chim. Acta, 1977, 44, 129–138 CrossRef CAS.
- A. Arya and E. A. Carter, Surf. Sci., 2004, 560, 103–120 CrossRef CAS PubMed.
- N. Lang and W. Kohn, Phys. Rev. B: Solid State, 1971, 3, 1215–1223 CrossRef.
- M. P. J. Punkkinen, Q. M. Hu, S. K. Kwon, B. Johansson, J. Kollar and L. Vitos, Philos. Mag., 2011, 91, 3627–3640 CrossRef CAS.
- S. Peljhan and A. Kokalj, Phys. Chem. Chem. Phys., 2011, 13, 20408–20417 RSC.
- H. L. Skriver and N. M. Rosengaard, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 7157–7168 CrossRef CAS.
- J. Radilla, M. Boronat, A. Corma and F. Illas, Phys. Chem. Chem. Phys., 2010, 12, 6492–6498 RSC.
- S. Peljhan, J. Koller and A. Kokalj, J. Phys. Chem. C, 2014, 118, 933–943 CAS.
- N. Kovacevic and A. Kokalj, Corros. Sci., 2013, 73, 7–17 CrossRef CAS PubMed.
- A. Kokalj, S. Peljhan, M. Finsgar and I. Milosev, J. Am. Chem. Soc., 2010, 132, 16657–16668 CrossRef CAS PubMed.
- N. Kovacevic and A. Kokalj, Mater. Chem. Phys., 2012, 137, 331–339 CrossRef CAS PubMed.
- S. J. Jenkins, Surf. Sci., 2006, 600, 1431–1438 CrossRef CAS PubMed.
- V. V. Mihaleva, R. A. van Santen and A. P. J. Jansen, J. Phys. Chem. B, 2001, 105, 6874–6879 CrossRef CAS.
- B. Hammer and J. K. Norskov, Adv. Catal., 2000, 45, 71–129 CAS.
- S. Sun, Y. Geng, L. Tian, S. Chen, Y. Yan and S. Hu, Corros. Sci., 2012, 63, 140–147 CrossRef CAS PubMed.
- M. Finsgar, A. Lesar, A. Kokalj and I. Milosev, Electrochim. Acta, 2008, 53, 8287–8297 CrossRef CAS PubMed.
- A. Kokalj, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 045418 CrossRef.
- R. H. Crabtree, O. Eisenstein, G. Sini and E. Peris, J. Organomet. Chem., 1998, 567, 7–11 CrossRef CAS.
- P. Macchi and A. Sironi, Coord. Chem. Rev., 2003, 238, 383–412 CrossRef.
- E. Espinosa, I. Alkorta, J. Elguero and E. Molins, J. Chem. Phys., 2002, 117, 5529–5542 CrossRef CAS PubMed.
- X. Michalet, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 059904 CrossRef.
- F. Mullerplathe, S. C. Rogers and W. F. Vangunsteren, Chem. Phys. Lett., 1992, 199, 237–243 CrossRef.
- L. F. Liu, J. X. Liu, J. Zhang, L. You, L. J. Yu and G. M. Qiao, Chem. J. Chin. Univ., 2010, 31, 537–541 CAS.
- A. L. Guo, G. C. Duan, K. He, B. Sun, C. C. Fan and S. Q. Hu, Comput. Theor. Chem., 2013, 1015, 21–26 CrossRef CAS PubMed.
- M. M. Antonijevic and M. B. Petrovic, Int. J. Electrochem. Sci., 2008, 3, 1–28 CAS.
- K. F. Khaled and M. A. Amin, Corros. Sci., 2009, 51, 2098–2106 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4ra04931d |
|
| This journal is © The Royal Society of Chemistry 2014 |
Click here to see how this site uses Cookies. View our privacy policy here.