Computational exploration of M-sites with chemical order and disorder in M′₂M′′B₂ and M′₄M′′B₃ compounds

Abstract

Boron-based materials are highly desirable for their promising mechanical properties, rendering them ideal for various industrial applications. In this study, we take advantage of the two unique metal Wyckoff sites in the prototype structures V₃B₂ (4h and 2a) and Cr₅B₃ (16h and 4c). These two sites were populated by two different metals, M′ and M′′, forming novel B-based ternary M′₂M′′B₂ and M′₄M′′B₃ compounds. A high-throughput phase stability search encompassing a total of 2738 compositions with M′ and M′′ being occupied systematically with Al, Si, Sc, Ti, V, Cr, Mn, Fe, Co, Ni, Cu, Zn, Ga, Ge, Y, Zr, Nb, Mo, Tc, Ru, Rh, Pd, Ag, Cd, In, Sn, Hf, Ta, W, Re, Os, Ir, Pt, Au, Hf, Tl, and Pb was performed. The thermodynamic phase stability of the simulated materials was assessed by evaluating the formation enthalpy, ΔH_cp for all compostions with chemical order and disorder for selective compositions. In total, 56 ternary phases were identified as stable when considering a configurational entropy contribution at 2000 K. Out of the 56 predicted stable phases, 32 displayed a preference for chemical order whereas 24 favored disorder of M′ and M′′. Initial attempts at synthesis of the predicted stable Ta₂MoB₂ compound were made, showing indications for the presence of ordered Ta₂MoB₂ or disordered (Ta_0.667Mo_0.333)₃B₂.

---

Introduction

High-throughput (HT) computational searches of materials are centered around the concepts of constructing extensive databases of materials with calculated electronic properties and then extrapolating the results based on certain criteria, i.e., predicted synthesizability,¹ or the hardness of the materials.^2,3 Notable examples of publicly accessible databases of materials, such as the Materials Project,⁴ OQMD,^5,6 and AFLOWLIB,⁷ all encompass a diverse range of both thermodynamic and electronic properties.^8,9 In practice, the construction of a materials database typically follows one of two distinct approaches. The database is formed either by focusing on a single materials system, through methodologies such as crystal structure prediction frameworks,^10–13 or by screening already known low-energy structures with the hope of discovering additional novel compounds of similar structure.^14–17

We herein consider the latter approach by focusing on two identified boron-based binary structures with two unique metal Wyckoff sites, namely V₃B₂ (P4/mbm),¹⁸ originating from U₃Si₂ discovered by Zachariasen in 1949,¹⁹ and Cr₅B₃ (I4/mcm).²⁰ The V₃B₂ and Cr₅B₃ structures were selected because of the experimentally demonstrated order of Cr and W in W₂CrB₂ (V₃B₂) and W₄CrB₃ (Cr₅B₃),²¹ and serves as the foundation for discovering additional ternary boron-based materials in this work. In addition, a multitude of materials with similar structures have previously been studied in which discussions regarding ordered and disordered lattice configurations vary.^22–28

Both V₃B₂ and Cr₅B₃ prototype structures consist of two Wyckoff sites occupied by transition metals, herein denoted as M, with a 2 : 1 and 4 : 1 ratio, respectively. The remaining sites are occupied by boron, denoted as B. To distinguish between the metal sites, we use the M′₂M′′B₂ and M′₄M′′B₃ notation to describe their compositions and the M′ : M′′ ratio. The implicated metal order in M′₂M′′B₂ and M′₄M′′B₃ herein serve as potential alloying structures in the quest for novel synthesizable boron-based materials. Multi-component boron-based materials have recently gained an extensive amount of interest due to the possibility of tuning the materials’ properties by combining atomic species of desired nature to achieve materials with exotic properties suitable for industrial applications.^29–32 The increased number of components does, however, increase the complexity of the material, which often leads to more challenging synthesis procedures. This is where theoretical studies may be used to pave the way toward the identification of stable and synthesizable materials to guide experimental procedures.

The HT phase stability screening consisted of evaluating the formation enthalpy, ΔH_cp, for 2664 ternary and 74 binary phases for the two prototype structures, M′₂M′′B₂ and M′₄M′′B₃, by systematically alloying the M′ and M′′ sites with Al, Si, Sc, Ti, V, Cr, Mn, Fe, Co, Ni, Cu, Zn, Ga, Ge, Y, Zr, Nb, Mo, Tc, Ru, Rh, Pd, Ag, Cd, In, Sn, Hf, Ta, W, Re, Os, Ir, Pt, Au, Hf, Tl and Pb. The screening considered both ordered and disordered arrangement of M′ and M′′ in which simulated solid solutions were modeled on the M-sites when ΔH_cp was in a region chosen to represent a metastable compound based on the configurational entropic contribution.

Out of 41 M′₂M′′B₂ compositions predicted to be stable, 23 favored a chemically ordered arrangement on the M-sites and 18 a disordered counterpart. The M′₄M′′B₃ compounds, with an extra MB layer, yielded 9 stable materials favoring ordered M-sites and 6 with a disordered distribution of M′ and M′′ on the M-sites. For one of the predicted stable materials, Ta₂MoB₂, initial synthesis attempts were made. Analysis of the XRD diffractogram indicated synthesis of Ta₂MoB₂. These results are further corroborated by a bonding analysis.

Theoretical and experimental methods

Density functional theory

The structural optimization procedure was performed using the density functional theory (DFT) framework. The Vienna Ab Initio Simulation Package (VASP), version 5.4.1,^33–35 was used where the exchange–correlation was modeled using the generalized gradient approximation (GGA)³⁶ with the all-electron projector augmented wave (PAW)^37,38 method. The cutoff energy was set to 520 eV, a Γ-centered 2π × 0.027 Å⁻¹k-point density was used, and with an energy and force convergence criteria of 10⁻⁷ eV and −10⁻² eV Å⁻², respectively. These settings to ensure compatability with the Materials Project database.⁴ Additional competing phases considered from ref. 14 and 39 were all reoptimized using the above VASP settings. A ferromagnetic spin configuration was considered for every material where the initial magnetic moment was set to 3 for materials with M sites populated by Cr, Mn, Fe, Co, or Ni while remaining materials had an initial spin of 0.5.

Phonon dispersion spectra were calculated for M′₂M′′B₂ and M′₄M′′B₃ through 2 × 2 × 3 (120 atoms) and 2 × 2 × 2 (128 atoms) supercells, respectively, by using the finite displacement method as implemented in Phonopy.⁴⁰ Furthermore, the LOBSTER code was used to retrieve the density of states (DOS) and crystal orbital Hamiltonian population (COHP) where the calculated band-structure energy is reconstructed into orbital interactions.^41–44 Positive COHP values indicate antibonding interactions while negative COHP values indicate bonding interactions. All crystal structures illustrated herein were generated using VESTA.⁴⁵

Phase stability predictions

The phase stability predictions was evaluated using the formation enthalpy, which compares the energy of an arbitrary M′-M′′-B phase, denoted M′_xM′′_yB_z, with all possible linear combinations of competing phases within the M′-M′′-B material system. The set of most competing phases is retrieved by solvingwhere b^M′, b^M′′, and b^B represent the compositional constraints of the competing elements M′_x, M′′_y and B_z, respectively. The terms x_i and E_i are the scaling factor and energy of phase i constituting the set of most competing phases. The formation enthalpy is further obtained by comparing the energy of an arbitrary phase with the set of most competing phases:

ΔH_cp(M′_xM′′_yB_z) = E(M′_xM′′_yB_z) − min E_cp(b^M′, b^M′′, b^B) (2)

A phase is considered stable if ΔH_cp < 0, indicating a phase being energetically favored as compared to decomposing into competing phases. ΔH_cp > 0 indicates that decomposing into identified competing phases is more energetically favorable. The complete set of competing phases considered herein is composed of data from the Materials Project database⁴ and ternary MAB phases reported in ref. 39. In addition, the considered M′₂M′′B₂ phases are included within the set of competing phases when evaluating M′₄M′′B₃ and M′₄M′′B₃ when evaluating the stability for M′₂M′′B₂. Tables of all competing phases considered in this work, with corresponding total energy values, can be found in the ESI.†

Furthermore, to model configurational disorder where M′ and M′′ are randomly mixed on the two M-sites, we use the special quasi-random structures (SQS) method.⁴⁶ The integer notations in M′₂M′′B₂ and M′₄M′′B₃ are herein used to represent chemical order of M′ and M′′ sites whereas parenthesis representation, (M′_0.67M′′_0.33)₃B₂ and (M′_0.8M′′_0.2)₅B₃, correspond to chemical disorder mixture on both M′ and M′′ sites. The corresponding mixing free energy for structures with disordered M′ and M′′ is approximated as:

ΔG^dis_cp [T] = ΔH^dis_cp − TΔS, (3)

where T is the temperature and ΔS is the entropic contribution. No mixing is assumed to take place at 0 K and thus we assumed ΔG_cp [0] = ΔH_cp. The configurational entropy of an ideal solution on the metal sublattices is given by:

ΔS = −k_B[n ln(n) + (1 − n) ln (1 − n)], (4)

in which k_B is the Boltzmann constant (units eV K⁻¹) and n is the mixing concentration of the metal sites, i.e., n = 0.333 for (M′_0.667M′′_0.333)₃B₂ and n = 0.2 for (M′_0.8M′′_0.2)₅B₃. All sublattices are assumed to be fully occupied. A size convergence of the generated SQS of supercells is found in Fig. S1.† Both SQS structures were observed to converge in terms of energy and correlation functions with respect to the cell size when occupied by 90 and 80 atoms for (M′_0.667M′′_0.333)₃B₂ and (M′_0.8M′′_0.2)₅B₃, respectively.

Synthesis of Ta₂MoB₂

The boride powder was synthesized by mixing TaB₂ (99.5%, Sigma Aldrich) and MoB (99.5%, <325 mesh, Aldrich) with elemental powders of Ta (99.97%, <325 mesh, Alfa Aesar), Mo (99.5%, APS 3–7 μm, Thermo Scientific) and amorphous B (95%, Aldrich) in molar ratios 0.66 TaB₂ + 0.66 MoB + 1.33 Ta + 0.33 Mo. The powders were mixed in an agate mortar and cold-pressed using a load corresponding to a stress of 50 MPa. The discs were placed in an alumina crucible and kept at 1600 °C for 20 h under 5 sccm of argon flow (heating and cooling rates of 5 °C min⁻¹). After cooling down to room temperature, the sintered disc was crushed and sieved through a 36 μm sieve.

Characterization methods

Structural analysis and phase identification were performed through X-ray diffraction (XRD), using a PANalytical diffractometer, with a Cu K_α radiation source and 1/2° and 5 mm divergence and receiving slits. The diffraction pattern was recorded using a step size and time per step of 0.0084° and 15.24 s, respectively. Scanning electron microscopy (SEM), using a LEO 1550 instrument, combined with an energy dispersive X-ray spectrometer (EDX), from Oxford Instruments, was used for the analysis of morphology and chemical composition, primarily the metal content. A minimum of 10 individual particles were examined.

Results & discussion

Binary boron-based precursors

Materials like V₃B₂, Cr₅B₃, and Mo₅SiB₂ all exhibit tetragonal crystal structures with two M-sites. V₃B₂ features V at Wyckoff sites 4h and 2a,¹⁸ Cr₅B₃ with Cr at Wyckoff sites 16h and 4c,²⁰ and Mo₅SiB₂ with Mo at Wyckoff sites 16h and 4c.⁴⁷ Having two different M-sites can allow for site-specific population of two carefully chosen metals that lead to formation of chemical order. Examples of such materials are W₂CrB₂ (prototype V₃B₂ with M sites 4h and 2a), W₄CrB₃ (prototype Cr₅B₃ with M sites 16h and 4c),²¹ and for Ti₄MoSiB₂ and Ta₄VSiB₂ (prototype Mo₅SiB₂ with M sites 16h and 4c).^47,48

In this work, we focus on two prototype binary structures V₃B₂ (P4/mbm) and Cr₅B₃ (I4/mcm) and take advantage of the two independent M sublattices. To distinguish the two different metal sites, we use the notation M′ and M′′, which yields the general compositions M′₂M′′B₂ and M′₄M′′B₃, respectively.

The V₃B₂ prototype structure has been identified in a total of 10 material systems forming the P4/mbm symmetry.^{18,23–27,49} However, structural information regarding the ordered or disordered arrangement on the M-sublattice is typically scarce or neglected, except in ref. 23 and 24. These two references suggest an ordered arrangement of Mo and Fe in Mo₂FeB₂ in addition to W and Cr in W₂CrB₂. This is in contrast to the Cr₅B₃ prototype structure, which has been reported in binary Cr₅B₃,²⁰ ternary W₄CrB₃,^21,50 and quaternary M′₄M′′SiB₂ systems.^47,48,51,52 However, the two identified prototype structures display a strong similarity to each other, with the Cr₅B₃ structure closely resembling the V₃B₂ structure, albeit with an additional metal and boron layer. A schematic illustration comparing the two ternary structures is shown in Fig. 1 in which the additional metal boron layer may be observed when viewed along the [100] zone axis.

Fig. 1 Schematic illustration of (a) M′₂M′′B₂ (P4/mbm) and (b) M′₄M′′B₃ (I4/mcm) along the [001] and [100] zone axes, with atoms of the two metal sites represented by blue and red while boron atoms are in green.

The M′₂M′′B₂ structure (space group P4/mbm and prototype V₃B₂) is displayed in Fig. 1a and is composed of Wyckoff sites 4h (M′), 2a (M′′), and 4g (B). A layered stacking composed of alternating layers of M′′-B and M′ is apparent along the [100] zone axis. The structure viewed from the [001] zone axis illustrates the B-layer to be composed of alternating B-pairs rotated 90 degrees around the [001] axis.

The structure of M′₄M′′B₃ (space group I4/mcm and prototype Cr₅B₃) is illustrated in Fig. 1b. This structure has additional layers of M′ and B, as compared to M′₂M′′B₂, which is apparent when viewed along the [100] zone axis. The additional B-layer contributes to a more complicated structure, where the alternating B-pairs have an additional B-layer located within the neighboring layer but rotated 90 degrees around the [001] zone axis. This structure is composed of four different sites, M′ at 16h, M′′ at 4c, and B at 8h and 4a, respectively. Note that the M′₄M′′B₃ structure bears a close resemblance to the T2 phase, in which the 4a site is occupied by Si instead of B, resulting in M′₄M′′SiB₂. The latter formula, with a different combination of M′ and M′′, has previously been predicted to include at least 11 thermodynamically stable phases energetically favoring ordered M′ and M′′ on the M sites and 40 with a disordered distribution of M′ and M′′.⁴⁷ Note that several M′₄M′′SiB₂, with ordered M′ and M′′, have been subsequently synthesized.^47,48,51,52 The close resemblance of the selected prototype structures with respect to the T2 phase, which resulted in 51 predicted stable and several synthesized materials, further strengthens the motivation for finding novel ternary compounds with chemical order of M′ and M′′.

Thermodynamical phase stability predictions

The high-throughput stability screening was performed by considering the two selected crystal structures (V₃B₂ and Cr₅B₃ prototypes) where the two M-sites were selectively populated by Al, Si, Sc, Ti, V, Cr, Mn, Fe, Co, Ni, Cu, Zn, Ga, Ge, Y, Zr, Nb, Mo, Tc, Ru, Rh, Pd, Ag, Cd, In, Sn, Hf, Ta, W, Re, Os, Ir, Pt, Au, Hf, Tl and Pb. Note the use of M′ and M′′ as general notations for elements where M′ ≠ M′′ represents ternary phases and M′ = M′′ represents binary phases. Solid solution structures (SQS) were modeled on the M′ and M′′ sites for ordered ternary phases identified as stable (ΔH_cp < 0 meV per atom) or close to stable (0 ≤ ΔH_cp < 70 meV per atom). The chosen close-to-stable energy limit of 70 meV per atom was motivated by the configurational entropy term, TΔS, which in eqn (3) for an arbitrary M′₂M′′B₂ phase and M′₄M′′B₃ phase is equal to −70 and −54 meV per atom, respectively, at 2000 K. The reason for choosing 2000 K is motivated by the typical temperature used for powder synthesis of similar boron-based materials. Since both ordered and disordered distributions of M′ and M′′ are considered herein, we choose to account for the contribution from configurational entropy to the Gibbs free energy for structures modeled with a disordered distribution of M′ and M′′ (SQS) at a temperature expected to be used for synthesis attempts. This is an approach used to identify whether an ordered or disordered distribution of M′ and M′′ are to be expected upon synthesis and has previously been demonstrated to confirm experimental observations of boron-based materials^14,47,53 and for other related layered materials.^54,55

Phase stability predictions for M′₂M′′B₂ phases

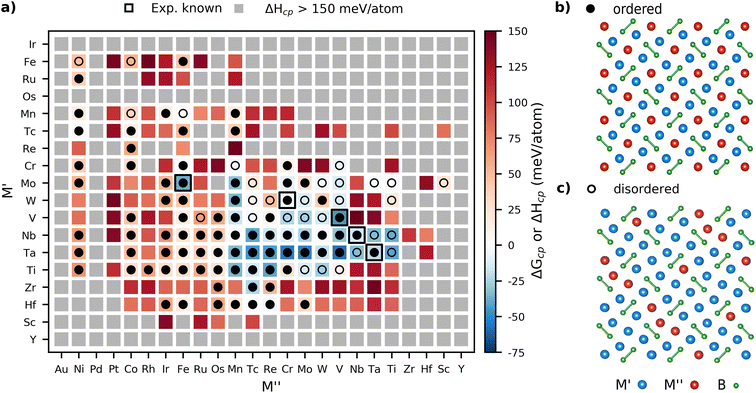
The phase stability predictions for the M′₂M′′B₂ phases are displayed in Fig. 2a for both binary (M′ = M′′) and ternary (M′ ≠ M′′) phases arranged by the group number of the considered elements, ranging from high to low. Note that a limited region of the considered M′ and M′′ combinations are shown as most of the phases located outside this region did not fulfill ΔH_cp < 150 meV per atom. The complete heatmap is displayed in Fig. S2.† Disordered phases were modeled as a solid solution of M′ and M′′ for ordered phases evaluated with ΔH_cp < 70 meV per atom. Hence, disordered configurations were evaluated as ΔG_cp according to eqn (3) in contrast to structures with ordered M sites, which were evaluated using ΔH_cp in eqn (2). The background color represents the calculated thermodynamic stability for the chemical order/disorder of lowest energy with stable phases (ΔH_cp < 0 or ΔG_cp < 0 meV per atom) in blue, and not stable or at best metastable (ΔH_cp > 0 or ΔG_cp > 0 meV per atom) phases in red. Grey represents M′₂M′′B₂ phases predicted far from stable (ΔH_cp > 150 meV per atom). The symbols used in Fig. 2a represent the M site configuration of the lowest energy evaluated at 2000 K, with filled circles illustrating ordered M′₂M′′B₂ phases and open circles disordered (M′_0.667M′′_0.333)₃B₂ phases. Experimentally known phases in which ordered and disordered configurations have been verified are marked by black squares.

Fig. 2 (a) Calculated formation enthalpy ΔH_cp (chemical order) or Gibbs free energy of formation ΔG_cp (solid solution) at 2000 K for M′₂M′′B₂ where the stability is represented by the color in blue (stable) and red (not stable). Phases with ΔH_cp > 150 meV per atom are colored grey and classified far from stable. Symbols represent the chemical order/disorder of lowest energy for a given combination of M′ and M′′ with filled circles for ordered M′₂M′′B₂ and open circles for solid solution (M′_0.667M′′_0.333)₃B₂. Black squares represent synthesized compounds. Schematic illustrations of (b) ordered and (c) disordered arrangements of M′ and M′′ when viewed along the [001] zone axis, with M′, M′′, and B in blue, red, and green, respectively.

Fig. 2a shows 44 phases predicted to be stable at 2000 K, including 3 binary and 41 ternary phases. Among the ternaries, 23 phases were predicted to energetically favor chemical order of M′ and M′′ whereas 18 were found with a disordered arrangement of M′ and M′′. The experimentally known phases, marked with black squares, display formation enthalpy values that correlate well with values found in the Materials Project database. This includes Mo₃B₂, which has been experimentally reported but is predicted to be unstable with +29 meV per atom. The majority of materials denoted as experimentally known were discovered during the mid-20^th century with, in some cases, limited information regarding the chemical composition, structural information, and arrangement of their atomic species.^{18,23–27,49} The systems modelled herein therefore represent the ideal compositions and structures, while defects and potential divergence from the ideal stoichiometry have not been considered. A complete list of predicted stable phases along with their sets of most competing phases and preferred M-arrangement at 2000 K is found in Table S1.† In addition, the phonon dispersion spectrum has been calculated for all stable M′₂M′′B₂ with order of M′ and M′′, i.e., ΔH_cp < 0. Note that Tc-based phases have not been considered due to the unstabale and radioactive Tc. These are shown in Fig. S3 to S27.† The absence of imaginary frequencies indicates that 24 out of 25 M′₂M′′B₂ are dynamically stable. The only dynamically unstable phase is Ta₂MnB₂ as indicated by the presence of imaginary frequencies.

Hu et al., previously predicted the degree of the chemical configuration of forming ordered or disordered M sites within M′₂M′′B₂ and M′₄M′′B₃ compounds to correlate with the atomic number of the alloying M′ and M′′ elements. According to Hu et al., compounds with M′ of a greater atomic number than M′′ typically displayed an ordered arrangement when considering the elements Ni, Co, Cr, W, and Mo.²¹ We herein constructed a stability heatmap with the elements arranged by their atomic number, as illustrated in Fig. S2,† to investigate this hypothesis. The results illustrate that groups of both stable and metastable phases are formed when M′ is occupied by transition metals of Period 4 (Ti, V, Cr, Mn, Fe), 5 (Zr, Nb, Mo, Tc), and Period 6 (Hf, Ta, W), whereas M′′ is occupied by elements of Period 3 (Al, Si), Period 4 (Sc, Ti, C, Cr, Mn, Fe, Co, Nu Cu), Period 5 (Nb, Mo, Tc, Ru, Rh) and Period 6 (Ta, W, Re, Os, Ir Pt). Every formed group of predicted stable compounds includes phases with both chemically ordered and disordered arrangements on the M-sites, thus illustrating no distinct connection between the M-site arrangement and the atomic number of M. This is exemplified by Ti₂ReB₂, predicted stable with ΔH_cp = −41 meV per atom, which is chemically ordered even though the atomic number of Re (Z = 75), occupying the 2a sites, is larger than Ti (Z = 22), occupying the 4h site. Furthermore, the neighboring phase (Ti_0.667W_0.333)₃B₂ is also predicted stable, with ΔG_cp = −26 meV per atom, but with a disordered distribution of M-elements when occupied by Ti and W (Z = 74).

Phase stability predictions for M′₄M′′B₃ phases

We continue the HT phase stability screening by considering the M′₄M′′B₃ structure. Fig. 3 illustrates stability for a limited elemental space whereas a complete heatmap may be found in Fig. S28.† The background color represents the calculated thermodynamic stability for the chemical order/disorder of lowest energy with blue regions representing stable phases (ΔH_cp < 0 or ΔG_cp < 0 meV per atom). The symbols, again, represent the metal arrangement of lowest energy evaluated at 2000 K with filled circles illustrating ordered M′₄M′′B₃ phases and open circles disordered (M′_0.8M′′_0.2)₅B₃ phases. Again, experimentally known phases with verified ordered or disordered configurations are marked by a black edge.

Fig. 3 (a) Calculated formation enthalpy ΔH_cp (chemical order) or Gibbs free energy of formation ΔG_cp (solid solution) at 2000 K for M′₄M′′B₃ where the stability is represented by the color ranging from blue (stable) to red (not stable). Phases with ΔH_cp > 150 meV per atom are colored grey and classified far from stable. Symbols represent the chemical order of the lowest energy for a given combination of M′ and M′′ with filled circles for ordered M′₄M′′B₂ and open circles for solid solution (M′_0.8M′′_0.2)₅B₃. Black squares mark synthesized compounds. Schematic illustrations of (b) ordered and (c) disordered arrangements of M′ and M′′ when viewed along the [001] zone axis, with M′, M′′, and B in blue, red, and green, respectively.

A total of 15 ternary phases within Fig. 3a were predicted stable out of which nine favor an ordered M-site arrangement of M′ and M′′ whereas six prefer the M-sites to be disorderly arranged at 2000 K. The only experimentally verified M′₄M′′B₃ phase, W₄CrB₃, was predicted stable with ΔH_cp = −31 meV per atom, further corroborating the formation enthalpy approach for phase stability predictions. A complete list of predicted stable phases along with their set of most competing phases and the preferred M-arrangement at 2000 K is found in Table S2.† In addition, the phonon dispersion spectrum has been calculated for all stable M′₄M′′B₃ structures with order of M′ and M′′, i.e., ΔH_cp < 0. These are shown in Fig. S29–S35.† Out of seven M′₄M′′B₃ phases, three are found to be dynamically stable, specifically Mo₄VB₃, Mo₄FeB₃, and W₄VB₃. Note that all phases identified as dynamically unstable contain magnetic elements such as Cr, Mn, or Fe. Since only non-magnetic and ferromagnetic spin configurations have been considered, a more in-depth analysis with phonon dispersion spectra calculated for various anti-ferromagnetic spin configurations may lead to dynamically stable structures.

The complete stability heatmap for the M′₄M′′B₃ compounds is shown in Fig. S28,† with metals arranged based on their atomic number, which illustrates a strikingly similar appearance to that for the M′₂M′′B₂ compounds shown in Fig. S2.† Once again, groups of stable compositions are formed when M′ is occupied by metals from Period 4 (Ti, V, Cr, Mn, Fe), Period 5 (Nb, Mo, Tc, Ru), and Period 6 (Hf, Ta, W, Re) whereas M′′ is occupied by elements from Period 3 (Al, Si), Period 4 (Ti, C, Cr, Mn, Fe, Co, Nu Cu, Zn), Period 5 (Nb, Mo, Tc, Ru, Rh, Pd) and Period 6 (Ta, W, Re, Os, Ir Pt). Similarly to the M′₂M′′B₂ composition, the complete heatmap illustrates no distinct correlation between the atomic numbers of the metal and the arrangement of the M-sites. This may, however, be traced to the few numbers of predicted disordered phases with the M′₄M′′B₃ composition. Further correlations may have been observed if chemical disorder on the M-sites was considered for the complete chemical phase space for both prototype structures, which is herein left for future studies.

Experimental realization

An attempt to verify the predicted stable compounds shown in Fig. 2 was made by selecting Ta₂MoB₂ for synthesis, with a predicted formation enthalpy ΔH_cp = −53 meV per atom with a chemically ordered M-element configuration of Ta and Mo. The selection of Ta₂MoB₂, in contrast to Ta₂VB₂ and Ta₂CrB₂, which displayed similar ΔH_cp values, is motivated by Ta and Mo being of different group numbers in addition to avoiding magnetic elements, such as Cr. The XRD pattern shown by the blue line in Fig. 4 is obtained from a sample with initial elemental powder ratios corresponding to stoichiometric Ta₂MoB₂. The data reveal the presence of TaB and Ta₂MoB₂ (peaks consistent with either chemical order or disorder on the M-sites) with a few peaks that could not be assigned to a specific compound. A comparison of the measured XRD pattern with simulated patterns of Ta₂MoB₂, (Ta_0.667Mo_0.333)₃B₂, and TaB is shown in Fig. S37.† It is worth noting that simulated XRD peaks, the positions of which are indicated by vertical bars at the bottom of Fig. 4 or in full in Fig. S37,† are slightly shifted towards lower angles, indicating larger calculated lattice parameters, which can be attributed to the underestimation of lattice parameters by GGA functionals. EDX measurements on individual particles revealed a distribution of metal concentrations, ranging from 0.8 to 2.9 in terms of Ta/Mo ratios. Importantly, certain particles were identified with Ta/Mo ratios that aligned with the correct stoichiometry, i.e., Ta/Mo = 2. To assess whether Ta₂MoB₂ is chemically ordered, we attempted to compare the theoretical XRD pattern of both chemically ordered (Ta₂MoB₂) and disordered ((Ta_0.667Mo_0.333)₃B₂) structures. However, both of these structures display very similar characteristics and could therefore not be distinguished. Thus, further insights concerning chemical order or not may be based on the performed phase stability predictions, which showed a lower formation enthalpy for the ordered Ta₂MoB₂ compared to the disordered (Ta_0.667Mo_0.333)₃B₂. Representative SEM images and the measured chemical concentrations are shown in Fig. S38 and Table S3.†

Fig. 4 XRD pattern of the sample from the attempted synthesis of Ta₂MoB₂ with assigned peaks for Ta₂MoB₂, (Ta_0.667Mo_0.333)₃B₂, and TaB, given by green, red, and yellow vertical bars respectively.

Bonding analysis

In addition, the bonding properties of the chemically ordered symmetries for both Ta₂MoB₂ and Mo₂TaB₂ were studied through the LOBSTER code, to identify possible preference for either of the metals to occupy one of the metal sites from an interaction perspective. These two phases were selected as the former compound was predicted stable (ΔH_cp = −53 meV per atom) and the latter not (ΔH_cp = +95 meV per atom). Fig. 5 displays the DOS and COHP plots for Ta₂MoB₂ and Mo₂TaB₂, respectively. The bonding characteristics for Ta₂MoB₂, shown in Fig. 5a, indicate the presence of minor to negligible bonding/antibonding states at or below the Fermi level, E_f. Notably, the total DOS exhibits a local minimum at the Fermi energy E_f that further emphasizes the preference for bonding within Ta₂MoB₂. This is in contrast to Mo₂TaB₂, in Fig. 5b, where the Fermi level is shifted away from the local minima in the total DOS, due to the presence of additional valence electrons. An examination of the DOS and COHP curves reveals a modest increase in non-bonding states for Mo₂TaB₂ compared to Ta₂MoB₂, albeit small in contrast to the difference in DOS at E_f. These observations indicate that Ta has a slight preference for occupying the majority of the 4h Wykoff sites compared to Mo. This, in combination with the XRD data and the phase stability predictions, suggests that the M-site configuration for Ta₂MoB₂ may be chemically ordered.

Fig. 5 DOS and COHP plots for (a) Ta₂MoB₂ and (b) Mo₂TaB₂, respectively, with the Fermi energy E_f denoted by a vertical dashed line.

Furthermore, a comparative analysis of bond strength for selected M′ and M′′ has been carried out for M′₂M′′B₂ in terms of the integrated projected crystal orbital Hamiltonian population (IpCOHP). A more negative value of IpCOHP indicates stronger bonding. This is shown in Fig. 6 for different interactions in M′₂M′′B₂. We find that the B–B interactions are the strongest, indicating that B plays a crucial role in stabilizing the bonding structure. B–B is also the shortest bond, around 1.7 to 1.9 Å depending on M′ and M′′. The weakest interactions are found for M′–M′ and M′′–M′′, consistent with their longer bond distance (∼<3 Å). M′–B and M′′–B, and M′–M′′ bonds are found in-between, where metals from Period 5 (Mo) or Period 6 (Hf, Ta, W) generally form stronger bonds with B than metals from Period 4 (Ti, V, Cr). Metals from Group 6 (Cr, Mo, W) show stronger bonding with B compared to metals from Groups 4 and 5. The latter (V, Ta) form moderately strong bonds with B, with Ta being stronger than V. Increased valence for M′′ generally leads to stronger M′–B and M′′–B bonds but weaker M′′–M′′ and B–B bonds. This indicates that finding the optimal bonding in M′₂M′′B₂ is challenging.

Fig. 6 Bond strengths in terms of integrated partial COHP (IpCOHP) for six different interactions in M′₂M′′B₂ where M′ = Ti, Ta, Mo and M′′ = Ti, V, Cr, Hf, Ta, Mo.

Conclusions

We have performed a high-throughput search to identify theoretically stable ternary boron-based materials that are feasible for synthesis. The thermodynamical phase stability was evaluated for a total of 2378 phases, where M′ and M′′ were systematically occupied by elements ranging from Period 3 to Period 6 and by taking advantage of the two different M sublattices in M₃B₂ (prototype V₃B₂) and M₅B₃ (prototype Cr₅B₃) structures. We identified 56 ternary materials to be stable at 2000 K, out of which 41 belong to the M′₂M′′B₂ composition and 15 to the M′₄M′′B₃ composition. Initial attempts at synthesizing the predicted stable Ta₂MoB₂ were made through powder synthesis, with XRD indicating the presence of ordered Ta₂MoB₂ or disordered (Ta_0.667Mo_0.333)₃B₂. However, distinguishing ordered (Ta₂MoB₂) from disordered ((Ta_0.66Mo_0.33)₃B₂) requires in-depth TEM analysis. The bonding characteristics of Ta₂MoB₂ and Mo₂TaB₂ were further analyzed by designing COHP and DOS plots. Ta₂MoB₂ illustrated better characteristics thus suggesting Ta occupies the 4h Wyckoff site of the ordered symmetries.

Author contributions

M.D and J.R. supervised the project, which was conducted by A.C, R.R., and M.D. The data analysis, computations, and writing of the main parts of the manuscript drafts were conducted by A.C. whereas R.R. governed the experimental procedures. All authors reviewed and edited the manuscript.

Data availability

The data supporting the results presented herein are available upon reasonable request from the corresponding author.

Conflicts of interest

The authors declare no competing interests.

Acknowledgements

M. D. and J. R. acknowledge support from the Swedish Research Council through projects 2019-05047 and 2022-06099. J. R. also acknowledges funding from the Knut and Alice Wallenberg (KAW) Foundation for a Fellowship/Scholar Grant and Project funding (KAW 2020.0033). The calculations were conducted using supercomputer resources provided by the National Academic Infrastructure for Supercomputing in Sweden (NAISS) and the Swedish National Infrastructure for Computing (SNIC) at the National Supercomputer Centre (NSC) and the High-Performance Computing Center North (HPC2N), partially funded by the Swedish Research Council through grant agreements no. 2022-06725 and no. 2018-05973.

References

1. C. J. Bartel, A. Trewartha, Q. Wang, A. Dunn, A. Jain and G. Ceder, npj Comput. Mater., 2020, 6, 97.
2. A. Mansouri Tehrani, A. O. Oliynyk, M. Parry, Z. Rizvi, S. Couper, F. Lin, L. Miyagi, T. D. Sparks and J. Brgoch, J. Am. Chem. Soc., 2018, 140, 9844–9853.
3. C. Nyshadham, C. Oses, J. E. Hansen, I. Takeuchi, S. Curtarolo and G. L. W. Hart, Acta Mater., 2017, 122, 438–447.
4. A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002.
5. J. E. Saal, S. Kirklin, M. Aykol, B. Meredig and C. Wolverton, JOM, 2013, 65, 1501–1509.
6. S. Kirklin, J. E. Saal, B. Meredig, A. Thompson, J. W. Doak, M. Aykol, S. Rühl and C. Wolverton, npj Comput. Mater., 2015, 1, 15010.
7. S. Curtarolo, W. Setyawan, S. Wang, J. Xue, K. Yang, R. H. Taylor, L. J. Nelson, G. L. W. Hart, S. Sanvito, M. Buongiorno-Nardelli, N. Mingo and O. Levy, Comput. Mater. Sci., 2012, 58, 227–235.
8. S. Curtarolo, G. L. W. Hart, M. B. Nardelli, N. Mingo, S. Sanvito and O. Levy, Nat. Mater., 2013, 12, 191–201.
9. C. J. Bartel, J. Mater. Sci., 2022, 57, 10475–10498.
10. C. W. Glass, A. R. Oganov and N. Hansen, Comput. Phys. Commun., 2006, 175, 713–720.
11. A. O. Lyakhov, A. R. Oganov, H. T. Stokes and Q. Zhu, Comput. Phys. Commun., 2013, 184, 1172–1182.
12. D. C. Lonie and E. Zurek, Comput. Phys. Commun., 2011, 182, 372–387.
13. S. Hajinazar, A. Thorn, E. D. Sandoval, S. Kharabadze and A. N. Kolmogorov, Comput. Phys. Commun., 2021, 259, 107679.
14. M. Dahlqvist, Q. Tao, J. Zhou, J. Palisaitis, P.OÅ. Persson and J. Rosen, J. Am. Chem. Soc., 2020, 142, 18583–18591.
15. V. I. Hegde, M. Aykol, S. Kirklin and C. Wolverton, Sci. Adv., 2020, 6, eaay5606.
16. G. H. Jóhannesson, T. Bligaard, A. V. Ruban, H. L. Skriver, K. W. Jacobsen and J. K. Nørskov, Phys. Rev. Lett., 2002, 88, 255506.
17. A. G. Van Der Geest and A. N. Kolmogorov, Calphad, 2014, 46, 184–204.
18. H. Nowotny and A. Wittmann, Monatsh Chem., 1958, 89, 220–224.
19. W. H. Zachariasen, Acta Cryst., 1949, 2, 94–99.
20. C. N. Guy and A. A. Uraz, J. Less-Common Met., 1976, 48, 199–203.
21. X. B. Hu, H. Y. Niu, X. L. Ma, A. R. Oganov, C. A. J. Fisher, N. C. Sheng, J. D. Liu, T. Jin, X. F. Sun, J. F. Liu and Y. Ikuhara, Acta Mater., 2018, 149, 274–284.
22. A. M. Filippi, J. Less-Common Met., 1973, 30, 153–158.
23. E. I. Gladyshevskii, T. F. Fedorov, Y. B. Kuz'ma and R. V. Skolozdra, Sov. Powder Metall. Met. Ceram., 1966, 5, 305–309.
24. V. S. Telegus and Y. B. Kuz'ma, Sov. Powder Metall. Met. Ceram., 1968, 7, 133–138.
25. A. S. Sobolev, Y. B. Kuz'ma, T. E. Soboleva and T. F. Fedorov, Sov. Powder Metall. Met. Ceram., 1968, 7, 48–51.
26. V. S. Telegus and Y. B. Kuz'ma, Sov. Powder Metall. Met. Ceram., 1971, 10, 52–56.
27. Y. B. Kuz'ma, Sov. Powder Metall. Met. Ceram., 1971, 10, 298–300.
28. Y. B. Kuz'ma, T. I. Ts'olkovskii and O. P. Baburova, Neorg. Mater., 1968, 4, 1081–1085.
29. V. Moraes, H. Riedl, C. Fuger, P. Polcik, H. Bolvardi, D. Holec and P. H. Mayrhofer, Sci. Rep., 2018, 8, 9288.
30. H. Wu, H. Fan and Y. Hu, Phys. Rev. B, 2021, 103, L041203.
31. B. D. Sahoo and K. D. Joshi, J. Appl. Phys., 2023, 134.
32. M. A. Ali, M. M. Hossain, A. K. M. A. Islam and S. H. Naqib, J. Alloys Compd., 2021, 857, 158264.
33. G. Kresse and J. Hafner, Phys. Rev. B:Condens. Matter Mater. Phys., 1993, 47, 558–561.
34. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
35. G. Kresse and J. Furthmüller, Phys. Rev. B:Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
36. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
37. P. E. Blöchl, Phys. Rev. B:Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
38. G. Kresse and D. Joubert, Phys. Rev. B:Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
39. A. Carlsson, J. Rosen and M. Dahlqvist, Phys. Chem. Chem. Phys., 2022, 24, 11249–11258.
40. A. Togo, F. Oba and I. Tanaka, Phys. Rev. B:Condens. Matter Mater. Phys., 2008, 78, 134106.
41. R. Dronskowski and P. E. Bloechl, J. Phys. Chem., 1993, 97, 8617–8624.
42. V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Phys. Chem. A, 2011, 115, 5461–5466.
43. S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Comput. Chem., 2016, 37, 1030–1035.
44. R. Nelson, C. Ertural, J. George, V. L. Deringer, G. Hautier and R. Dronskowski, J. Comput. Chem., 2020, 41, 1931–1940.
45. K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276.
46. A. Zunger, S. H. Wei, L. G. Ferreira and J. E. Bernard, Phys. Rev. Lett., 1990, 65, 353–356.
47. M. Dahlqvist, J. Zhou, I. Persson, B. Ahmed, J. Lu, J. Halim, Q. Tao, J. Palisaitis, J. Thörnberg, P. Helmer, L. Hultman, P.OÅ. Persson and J. Rosen, Adv. Mater., 2021, 33, 2008361.
48. A. S. Etman, J. Halim, H. Lind, M. Dorri, J. Palisaitis, J. Lu, L. Hultman, P.OÅ. Persson and J. Rosen, Cryst. Growth Des., 2023, 23, 4442–4447.
49. A. Wittmann, H. Nowotny and H. Boller, Monatsh Chem., 1960, 91, 608–615.
50. X. B. Hu, Y. L. Zhu, N. C. Sheng and X. L. Ma, Sci. Rep., 2014, 4, 7367.
51. J. Halim, P. Helmer, J. Palisaitis, M. Dahlqvist, J. Thörnberg, P.OÅ. Persson and J. Rosen, Inorg. Chem., 2023, 62, 5341–5347.
52. Q. Tao, J. Halim, J. Palisaitis, A. Carlsson, M. Dahlqvist, U. Wiedwald, M. Farle, P. Persson and J. Rosen, Cryst. Growth Des., 2023, 23, 3258–3263.
53. M. Dahlqvist and J. Rosen, Nanoscale, 2021, 13, 18311.
54. M. Dahlqvist and J. Rosen, Nanoscale, 2020, 12, 785–794.
55. M. Dahlqvist and J. Rosen, Nanoscale, 2022, 14, 10958–10971.

---

Footnote

† Electronic supplementary information (ESI) available: The SQS convergence, and complete heatmaps of the studied materials systems arranged based on the atomic number and tabulated formation enthalpy values, structural configuration, set of most competing phases, and phonon dispersion spectrum can be found in the attached supplementary material. See DOI: https://doi.org/10.1039/d4nr02948h

---