 Open Access Article
Open Access ArticleDensimeter-on-chip (DoC): measuring a single-cell mass density by sedimentation in microchannel flows†
David
Dannhauser‡
 *a,
Maria Isabella
Maremonti‡
*a,
Maria Isabella
Maremonti‡
 a,
Paolo Antonio
Netti
ab and
Filippo
Causa
a,
Paolo Antonio
Netti
ab and
Filippo
Causa
 a
a
aInterdisciplinary Research Centre on Biomaterials (CRIB) and, Dipartimento di Ingegneria Chimica, dei Materiali e della Produzione Industriale, University of Naples “Federico II”, 80125 Naples, Italy. E-mail: david.dannhauser@unina.it
bCenter for Advanced Biomaterials for Healthcare@CRIB, Istituto Italiano di Tecnologia, 80125 Naples, Italy
First published on 21st January 2025
Abstract
Intrinsic biophysical and morphological features are essential for the label-free identification of different cell types. Indeed, apart from object size, density could represent a key parameter for single-cell analysis. However, the measurement of such a parameter is challenging. Therefore, we present a straightforward and versatile microfluidic chip. The densimeter-on-chip (DoC) measures single-cell mass densities thanks to a hydrodynamically induced sedimentation process inside the microchannel. In detail, in-flow buoyant components become more relevant than viscoelastic alignment forces, leading to precise in-flow sedimentation. DoC is based on precise three-dimensional cell alignment, followed by an abrupt change in cross-section to induce calibrated sedimentation. Based on the balance of acting forces and tracking the in-flow cell trajectory, we have developed a self-written mathematical model to precisely measure the single-cell densities of multiple cell types of any shape. Both cell velocity and fall length define the resulting cell density. The working range of object diameters for which density can be estimated is 0.75–22.5 μm. As result, the minimum measured density is 998 kg m−3 and a sensitivity of 0.001 can be obtained. Great agreement between the computational and the literature findings about red blood cells (∼1159 ± 29.5 kg m−3), lymphocytes (∼1073 ± 49 kg m−3) and neutrophils (∼1093 ± 27 kg m−3) is obtained without chip modification. Indeed, the computational error between the mean density values is ∼1%. Thereby, DoC as an easy-to-use and reproducible solution for label-free single-cell density measurement, provides a universal approach for characterizing a wide range of cell types, independently of their size and shape.
Introduction
Cell density, regarded as the mass-to-volume ratio, is tightly regulated and varies little within a given cell type. Changes in cell density are determined by the sum of biosynthesis and degradation processes, revealing the status of a cell.1 Indeed, cells regulate their density during the cell cycle, metabolism, apoptosis, differentiation, chronic diseases or cancer progression, and in response to drugs.1,2 In fact, in the case of isolation of circulating tumour cells, tracking the physical characteristics of a cell, such as density, cell size, and electrical properties, is necessary to distinguish between healthy and unhealthy cells.3 Moreover, the way in which cell volumes change after external stimuli, as in the case of induced immune or drug responses, is strictly related to how cell size, structure and density could be rearranged.4–8 For example, changes in cellular density also occur in lymphocytes during inflammatory responses, when depletion of cytokines inactivates cells and differentiates them into memory cells.1 Therefore, detailing possible changes in cell density is relevant for both diagnostic and therapeutic applications.Typically, single-cell density values, comprising nucleus, inner fluids and organelles, range between 1060 and 1120 kg m−3.9,10 Of particular interest are changes in cytoplasm density related to alterations in protein concentration that in turn also affect the assembly of protein complexes and cell mechanics.
However, as cells consist of a unique set of morphological and biophysical features, precise characterization of this heterogeneity is still challenging.11–22 Indeed, density values show very little variation in a given cell type, with a variability 100 times smaller than the variation in cell mass among cells, since there is tight regulation of their density for maintenance of their state.23 Therefore, having a technique capable of determining, among the same type of cell, single-cell densities at high precision and specificity is crucial.
The most widely used method for cell density characterization is density gradient centrifugation, which allows one to obtain a convenient estimation of the average density of cell populations.24 However, such a technique considers a fixed density threshold (1077 kg m−3) mainly to separate lymphoblasts and monocytes from the remaining myeloblasts and red blood cells (RBCs). Moreover, this approach does not provide single-cell results for an inherent cell heterogeneity distinction and there is no correlation between size, density and shape of cells. Therefore, during the last few years, several methods, both biochemical and microfluidic/physical based, have been proposed as valid alternatives to measure the physical properties of cells.2 Typical examples are fluorescence immunoassays and bio-chemiluminescence techniques or single-cell mass cytometry,25 magnetic levitational image cytometry, suspended microchannel resonators, phase-shifting interferometry and opto-electrokinetic devices.26–29 In detail, they can be classified as active or passive methods. Magnetic and electric-based techniques are active methods, which impose external forces to displace cells for separation and characterization.16,30–32 In contrast, passive applications include hydrophoretic and hydrodynamic filtration and gravitational sedimentation.33–36 Some of them are microfluidic designs, where channels are disposed at different heights, inducing gravity-based cell sedimentation; in others, purely inertia-driven fluid flow conditions allow in-flow cell separation based on pinched flow fractionation to profile cells with different sizes and densities.37,38 As an example of these approaches, a microfluidic device where a combined effect of hydraulic jump and sedimentation for size-selective microparticle or cell separation has been proposed. Even if the resulting sorting enrichment based on size was high, the device potential was limited since a complex design and tight control over the fluid-dynamics are required to obtain the desired sorting.39
Nevertheless, other important drawbacks of both active and passive techniques need to be considered. For example, biochemical methods often have problems in achieving non-invasive, high-content and cell-specific measurement. Indeed, label-based analyses could lead to undesired cell reactions due to special preparation procedures. In contrast, physical-based techniques can measure multiple physical properties simultaneously at the single-cell level. However, the necessity to find a balance between applied flow rates, high throughput, measurement precision and multiparameter measurement, leads to unsatisfactory performance. Moreover, none of the presented techniques allow variable density levels to be recognized and measured among different cell types in the same sample.
Here, we present a densimeter-on-chip (DoC) as a new possibility to in-flow-measure single-cell density with a gravity-based approach. By first inducing a perfect viscoelastic alignment of cells, and then presenting an abrupt change in the channel geometry, in-flow cell sedimentation—where gravity (FG) and buoyancy (FB) forces matter—is promoted, since viscoelastic fluid forces dramatically reduce its lift effect. From the known laws regulating the balance of forces for viscoelastic alignment—viscoelastic (FE) and drag (FD) balance—we provide an analytical set of relations to practically estimate the density, depending on the fall length (L) of cells along the observation channel (Fig. 1).40 In particular, alignment can be achieved thanks to tight control over the imposed hydrodynamic forces ordering particles/cells on different equilibrium positions and trajectories, depending on the channel geometry, the fluid properties and the dimensions and shape of the object.41–44 Indeed, the interplay of size and shape plays a fundamental role in the definition of cell motion for alignment, separation and density measurement purposes.
We achieved precise single-cell analysis from homogenous cell types, by mapping cell diameter versus density outcomes, which comprehensively describes the biophysical characteristics of a cell population.
On the other hand, thanks to implementation of the mathematical model, the approach offers the possibility of easily and precisely in-flow-separating differently sized and weighted objects, if diameters and densities are known. With the choice of the best applied pressure conditions, we can predict the length of sedimentation of the object before starting the experiment, therefore allowing sedimentation-induced separation.
In detail, the device consists of one inlet and two outlet capillaries, which are inserted in a sandwich of engraved polymethylmethacrylate (PMMA) slides that contain the observation channel as well as the vertical fluid exit (Fig. 1 and S1†). The gravity-based sedimentation can be finely tuned with the fluid flow parameters—such as fluid viscosity and applied pressure in a working range of ∼250–2500 mbar—to ensure a precise fall length for different object types. As proof-of-concept, we decided to test both particles and peripheral blood cell sedimentation to predict the fall length and measure the density, respectively. The minimum density that can be measured is 998 kg m−3. Thanks to the in-flow observation and the relative computation, we demonstrate the possibility of profiling single-cell densities with great agreement with literature findings. Therefore, DoC is proposed as a valid, highly reproducible and easy-to-use approach to characterize and separate cells, depending on their morpho-physical properties, of prominent interest for diagnostic purposes.
Materials and methods
Densimeter-on-chip (DoC) concept
The working principle of DoC is based on two different fluid conditions, which are consecutively applied to cells of unknown density. First, cells are perfectly aligned to the centre line of a round-shaped capillary, before an abrupt change in cross-section accompanied by a subsequent change in fluid forces results in a triggered dis-alignment in-flow, mainly caused by the mass density signature of a cell. In fact, by measuring the fall length of a cell of known cell size and geometrical and fluid properties, we can calculate the density of the investigated cell.Besides the characterization, we introduced a vertical channel exit in the chip design, which can be used to collect cells of interest, while the remaining sample content can be collected in another exit at the end of the observation channel. The possibility of fine tuning the fall length by changing the flow rate and, as a consequence, the fall velocity allows precise single-cell characterization.
Microfluidic chip
The chip for density investigation in-flow consists of a cover and a base part made of PMMA, which are milled to obtain the observation channel for the density measurement (cover) and to hold in place the inlet (cover) and the outlet (cover and base) capillaries. The geometrical parameters of the observation channel are height 500 μm, width 1000 μm and length 8.5 cm (see Fig. S1†). The capillaries have a diameter of 75 μm for ‘INLET’ and ‘EXIT 2’, while 40 μm was chosen for lateral ‘EXIT 1’ (see Fig. S1 and S2†). The capillary lengths were optimized for cell alignment in the inlet as well as cell collection at the outlets, resulting in 34 cm for the inlet and 10 cm for both outlet capillaries. Due to the low-cost approach for the device, manufacturing a mismatch of ∼200 μm between the capillary centre line and the channel bottom had to be solved in designing the device. We decided to introduce into the channel design 5 steps (50 μm in depth) 9 mm before the lateral exit, which successively lowered the channel bottom in the central section of the channel to escort cells or particles of interest into the lateral exit of the device (see Fig. 1 and S2†). Furthermore, the lateral capillary enters the observation channel for ∼50 μm for smoother extraction of objects.Rheological fluid properties and fluid-flow losses
The viscoelastic measurement fluid consists of 0.3, 0.4 and 0.5 wt% of polyethylene oxide (PEO, 4 MDa, Sigma Aldrich) in phosphate-buffered saline. We investigated the fluids with a stress-controlled rheometer to obtain their rheological properties (see Fig. S4b†). The zero-shear viscosity (η0) was measured with 0.00683, 0.01002, 0.01998 Pa s for PEO 03, 04 and 05, respectively. The reported flow curves (ESI,† Fig. S4b) show that there is well-defined Newtonian behaviour up to a shear rate γ of ∼500 s−1 for PEO 04, the one we chose for the experiments. In our device, even inside the capillary, the highest estimated γ is ∼200 s−1. Therefore, non-Newtonian effects on viscosity are absent.45,46 The constant viscosity was helpful to ensure that the influence of temperature was also negligible. Indeed, there is a critical concentration (∼1.6 wt%) above which both characteristic non-Newtonian behaviour and the direct influence of temperature on viscosity values are observed.45,46Next, we investigated the hydraulic resistance of the microfluidic system, where R1 and R2 (inlet capillary and channel before EXIT 1) as well as R4 and R5 (channels after EXIT1 and EXIT 2 capillaries) are considered in series, while R3 (capillary of EXIT 1) and R4–5 (all resistance after EXIT 1) are calculated in parallel (see Fig. S3†). Note that R3 shows a ∼12-fold increase in hydraulic resistance compared to R5 when considering PEO 04 fluid. The interplay of hydraulic resistance is scaled according to the chosen PEO dilution. We optimized the capillary geometries according to the length and diameter of human bloodstream cells.
Calibration beads
Polystyrene latex beads (PSL) of different sizes (4.16 ± 0.062 μm, 6.08 ± 0.082 μm and 8.13 ± 0.09 μm from FLUKA, as well as 10.70 ± 0.25 μm and 15.66 ± 1.43 μm from PolyScience) were used for calibration of the microfluidic device (Fig. 2b). Note that PSL are known for their perfectly spherical shape and monodispersed size distribution. Beads below 10 μm have a density of 1050 kg m−3, while bigger beads were provided with a density of 1055 kg m−3.Cell sample preparation
Cells were recovered from a healthy donor after obtaining informed consent in accordance with relevant guidelines and regulations. At the time of blood donation, the donor signed an informed consent (model no. 5526 of Azienda Ospedaliera Universitaria “FEDERICO II”, Naples, Italy), which specifies that waste parts of the blood, not useful for the medical-therapeutic purposes, can be used for scientific research purposes. All experiments were performed and analysed anonymously. The collection was performed to divide peripheral blood mononuclear cells and red blood cells (RBCs) from the whole sample. To do this, we diluted the blood with phosphate-buffered saline (PBS, SIAL Srl) in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 proportion. To this solution, we added a Ficoll-Paque (Fisher Scientific) with ρ = 1077 kg m−3, still in a 1
1 proportion. To this solution, we added a Ficoll-Paque (Fisher Scientific) with ρ = 1077 kg m−3, still in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 proportion. Thanks to a density gradient, Ficoll remains on the bottom of the blood–PBS solution. Then, we centrifuged the sample at 200
1 proportion. Thanks to a density gradient, Ficoll remains on the bottom of the blood–PBS solution. Then, we centrifuged the sample at 200![[g with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0067_20d1.gif) for 30 minutes, in no-brake mode. After centrifugation, we removed the plasma and platelets, which are useless for our experimental purposes. The peripheral blood mononuclear cell (PBMC) ring was picked up and placed inside another tube rinsed with Roswell Park Memorial Institute (RPMI) 1640 medium (SIAL Srl). Note that ∼15% of the collected cells are monocytes, and although most of them adhere during the measurement procedure to the surface of the sample container, we will consider only the lymphocytes (LYM) for the microfluidic experiments. For the neutrophil (NEU) class, cells separated below the gradient medium were collected and washed with RBC lysis solution three times for 5 minutes. We centrifuged the sample three times at 200
for 30 minutes, in no-brake mode. After centrifugation, we removed the plasma and platelets, which are useless for our experimental purposes. The peripheral blood mononuclear cell (PBMC) ring was picked up and placed inside another tube rinsed with Roswell Park Memorial Institute (RPMI) 1640 medium (SIAL Srl). Note that ∼15% of the collected cells are monocytes, and although most of them adhere during the measurement procedure to the surface of the sample container, we will consider only the lymphocytes (LYM) for the microfluidic experiments. For the neutrophil (NEU) class, cells separated below the gradient medium were collected and washed with RBC lysis solution three times for 5 minutes. We centrifuged the sample three times at 200![[g with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0067_20d1.gif) for 10 minutes, then removed the supernatants and rinsed the sample with pure RPMI. Such cell populations will also contain basophils and eosinophils, although they represent only ∼3% of the collected population. In fact, we consider only NEU for our experiments. For the RBCs, a remaining part of fresh blood was used. We centrifuged it at 200
for 10 minutes, then removed the supernatants and rinsed the sample with pure RPMI. Such cell populations will also contain basophils and eosinophils, although they represent only ∼3% of the collected population. In fact, we consider only NEU for our experiments. For the RBCs, a remaining part of fresh blood was used. We centrifuged it at 200![[g with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0067_20d1.gif) for 10 minutes, in no-brake mode. Again, removing plasma and platelet parts, we collected only RBCs. In-flow measurements were performed with cell concentrations of ∼106 cells per mL to avoid cell interaction or aggregation.
for 10 minutes, in no-brake mode. Again, removing plasma and platelet parts, we collected only RBCs. In-flow measurements were performed with cell concentrations of ∼106 cells per mL to avoid cell interaction or aggregation.
Object tracking in-flow
We recorded objects in the XY-plane with an inverted bright-field microscope (IX81, Olympus) using 10× magnification and a CMOS camera (ORCA flash 4.0, Hamamatsu Photonics K.K.) with 6.5 μm pixel size. Next, we tracked cells or particles with a self-written MATLAB R2023a (MathWorks Corp.) routine, which first filtered the input frames with a set of Gaussian filters. Afterwards, we applied a threshold-based bandpass filter to obtain the object centroids for each recorded frame. Subsequently, the routine combines the tracked coordinates into single tracking information. In the case of missing centroid data in one or a maximum of 3 consecutive frames, the routine can reconstruct the missing information to guarantee the best tracking performance. However, such a tracking approach will work only in a certain range of Z-positions (∼100 μm), which is limited by the diffraction-limited focus in the recorded bright-field images. In other words, we changed the focal plane for each observed video, limiting the observation to a maximum range of ∼50 μm above and ∼50 μm below the optimal object focus. Note that the object diffraction is size dependent. Finally, the object velocity was calculated for trajectories above a minimum threshold of 5 μm s−1, which was considered to be a quiescent flow condition.Velocity field computation
Since we are interested in reconstructing the in-flow motion of particles and cells inside the microchannel, we wrote the Poiseuille velocity profile (according to the hypothesis of the Oldroyd-B fluid model, ESI†). For rectangular cross-sections with respect to a fixed Cartesian system (see Fig. 1), the profile is:47 | (1) |
| n = 2 if AR ≥ 3 |
| m = 1.7 + 0.5(AR−1)−1.4 |
 | (2) |
Results and discussion
Governing forces for DoC
Before performing the density-based cell characterization, the capability of the DoC was investigated with calibration beads. We used density standard beads (PSL) similar in size and density to peripheral blood cells. Therefore, a viscoelastic pressure-driven flow with an applied inlet pressure (ΔP) is reported by modelling the fluid according to Oldroyd-B (ESI†). In such fluid-flow conditions, suspended particles/cells experience a force FE that emerges from an imbalance of the positive N1 (ESI†), which moves them toward their equilibrium position at the channel centre line. In our case, the alignment condition has already been reached and kept stable inside the inlet capillary (Fig. 1 and 2d). When particles move from the capillary inside the bigger rectangular cross-section, a decrease in FE contribution occurs, which triggers an in-flow sedimentation effect.In detail, we describe such phenomena by defining different sedimentation falling lengths (L) for different-sized microparticles. Assuming the height (H, Fig. 1) of the rectangle is smaller than the width, we can neglect the influence of side walls and focus on forces applied along the vertical direction (z-axis). At the beginning of the observation channel (the centre line of the rectangular section), the balance of forces can be defined as follows:
| FEz + Fg − Fb − FDz = 0 | (3) |
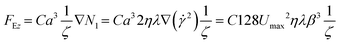 | (4) |
Therefore, we want to compute the limit velocity of the process to estimate the horizontal length at which particles reach the channel bottom (L). To do this, the following assumptions need to be made: the settling is not affected by the presence of other particles in the fluid; the fluid can be considered a continuous medium. There is no slip interaction between the particles and the fluid molecules. The settling velocity becomes greater as both particle size and density are increased; the walls of the containing duct do not exert an appreciable retarding effect: this means that the drag coefficient is not enhanced.49
When the Reynolds number (Re, ESI†) is much less than 1, such a coefficient can be expressed as:
 | (5) |
Due to sedimentation, particles assume a velocity different from that of the fluid, and the drag force can be determined from such a velocity difference. By solving the drag force expression (ESI†) as a function of the Re number, we get:
 | (6) |
and the time tL required to move along the x-direction:
From H/2 to the bottom, tz = tL and:
 | (7) |
DoC calibration
Thanks to the presented computation, we calculate first the L of PSL 6 and 10 beads for changing viscoelastic fluids as well as applied ΔP (see Fig. 2a). As expected, PSL 6 show a significantly longer L, which scales with applied η0. In addition, η0 influences the scaling of L with applied ΔP. Note that we limited our investigations to fluid conditions, which prevent fluid turbulence during the alignment section as well as the transection phase from the inlet in the observation channel. For the present microfluidic design, fluid viscosity is significant for the alignment capability in the inlet capillary, while L remains less affected (see Fig. S5†). Next, we investigated PSL 10 and 6 shortly after the channel entrance (X1 position, see Fig. 2d) for 400 and 700 mbar of applied ΔP.As shown in Fig. 2b, good agreement between calculated and measured particle velocities was observed. Note that particles are perfectly aligned at the channel centre line (YX1), where the fluid velocity is the maximum of the parabolic profile. The accord between analytical and experimental results for UX1y indicates that the change in cross-section between the capillary and observation section does not affect the alignment conditions. A knowledge of the starting position as well as the velocity is needed for a precise mass density signature calculation of single cells.
To better characterize the sedimentation process, we investigated PSL 10 beads for different values of ΔP at consecutive distances from the channel inlet (see Fig. 2c). To follow the particle trajectory, the focus was altered by manually changing the distance between the microscope objective and the channel.
In this way, we were able to compare the settling dynamics modelled by the equations with the experimental observations. We defined the settling z-displacement of the beads as a ‘reversed-migration’ of the object, since the alignment is lost as the viscoelastic lifting force capability. Such a z-position depends on the channel dimension and on the difference between the local velocity of the object compared to that of the fluid.51,52 Tracking different x locations, we estimated the variation in the object position along the channel height, since it moves at a velocity different from that of the fluid. It will migrate in reverse towards the wall, where it reaches zero-velocity and complete sedimentation. Such a dis-alignment will be faster or not, depending on the applied pressure (Fig. 2c). Higher pressure means a more sustained alignment of beads (4 cm is the length of sedimentation for the application of 700 mbar; Fig. 2c).
Therefore, from eqn (1) and the experimental bead velocity, we defined the z-coordinate at each x-position as follows:
 | (8) |
Good agreement between the computed and the experimental value of z is shown in Fig. 2c. However, as the presence of the change in cross-section (EXIT 1) becomes relevant, the difference between measurement and computation is greater far away from the inlet, since analysis of the particle motion is more challenging. Indeed, there is a match between simulated and observed particle positions up to 1.5 cm from the channel inlet.
Moreover, for higher concentrations of viscoelastic medium, we observed lower sedimentation particle velocities (see Fig. S5 and S6†). From the z-position and L computation, we show for the first time the possibility of measuring the unknown density of objects of different shapes, from their in-flow motion. To the best of our knowledge, both drag and density of objects have been studied only for streaming flows over spheres, freely falling into the fluid along a vertical direction.55 Here, we propose the possibility of computing the density of moving objects inside Poiseuille fluid-flow conditions.
In detail, according to the hypothesis of an absence of viscoelastic contribution (eqn (3) and (4)) to the fluid flow, we determined the density (ρ) of spherical objects from the expression of velocity migration due to sedimentation. As input parameters for the measure, we used the z obtained from eqn (8) compared to the initial position (H/2) of the objects at X1, Uavg of the fluid (eqn (1)) and the experimental UX3y as an estimate of the lag-motion of the particle at position X3, immediately before EXIT 1. Then, ρ was computed as:
 | (9) |
To further establish the precision of the measurement, we defined the sensitivity of the system, which is related to any possible variation in the output density result due to a change into the object velocity. In detail, sensitivity can be estimated as the ratio between the variation in the output signal (density) and the change in the input velocity, which is the experimental parameter most involved in density measurement.56 The sensitivity is found to be equal to ∼0.001. The lower the sensitivity, the better is the performance of the approach. Moreover, we found that, regardless of the imposed fluid-dynamic conditions, the limit of measurement of the density is dictated by the density of the fluid used, due to the desired buoyant effect. In our case, the limit is 998 kg m−3. Conversely, an upper limit to the measurement is essentially related to the maximum object diameter that we can align with a viscoelastic contribution. This means that the upper limit is related to the range of blockage ratios (see ESI†) useful for alignment purposes, in the range 0.01 < β < 0.3, equivalent to a diameter of 0.75–22.5 μm.57
Cell sample characterization
Mass density signatures of human cells at single-cell level are difficult to obtain. Gao et al. recently demonstrated the first method based on magnetic levitation. Nevertheless, a more precise measurement approach is needed, which is also capable of separating cells of interest. Therefore, we investigated different peripheral blood stream cells (Fig. 3: LYM, RBC and NEU) and observed their fall length and velocity in the DoC microchannel. From particle observations, we concluded that different concentrations of viscoelastic medium would result in different z-positions and consequently also different cell velocities at fixed channel positions (X-position) but would not significantly change the cell-specific fall length. Therefore, we used a viscoelastic medium concentration (PEO 04), which ensured perfect cell alignment for the whole size range of peripheral blood cells. Moreover, we applied a ΔP of 700 mbar, as the best compromise between cell alignment and measurement time.To obtain unknown cell density values, a previous knowledge of the investigated cell size is needed. Therefore, we investigated the major axis of different cell classes by bright-field observation (see Fig. S4a†). Major cell diameters of 8.70 μm (LYM), 10.98 μm (NEU) and 8.23 μm (RBC) were calculated via ImageJ observations.58 We first investigated single-cell velocities (UXy) in different observation channel positions while applying a constant pressure of 700 mbar (see Fig. 3). Directly after the inlet capillary, all cell types show similar cell velocities, in good agreement with particle investigations (see Fig. 2b). From X1 to X2, all 3 cell types significantly reduce their velocity. From measurement positions X2 to X6, RBC shows a reduction in cell velocity of ∼10 μm s−1, which indicates a long fall length, in good agreement with our simulated length. The observed cell velocity for LYM reduces significantly until the lateral exit position (X3). Some of the cells arrived at position X5, but no cells were observed in X6. Due to sample heterogeneity in the investigated lymphocyte class (T-LYM, B-LYM, natural killer cells and small fractions of monocytes) as well as the intercell type heterogeneity, no precise fall length could be established. In fact, by reducing the applied ΔP, we can tune DoC to separate all cells from the LYM class or only a part (see Fig. 5b). In the case of the NEU cell class, the major cell fraction (4.4-fold) exits laterally for an applied ΔP of 700 mbar.
Besides the cell velocity, we were also interested in the change in the Y-position of cells, which is a good indicator of whether a cell will exit laterally or not. We plotted cells for each measurement position in X in one single scatter plot (see Fig. 4) per cell class. A clear transition in cell velocity reduction to higher Y-position values was observed, which clearly shows the movement of cells in the direction of EXIT 1. Such phenomena were not observed for cell velocities greater 40 μm s−1. In fact, a cell velocity of less than 40 μm s−1 at X3 will guarantee a higher possibility of lateral collection of cells. LYM measured at YX3 below 500 μm are likely to be RBCs, showing significantly higher cell velocities compared to previous X-positions. Note that cell types were not separated with a cell-specific selection approach. A certain percentage of different cell types could be present in the measurement sample. Moreover, the self-written MATLAB routine considered all passing objects, without using any object exclusion related to the observed object size or shape. This guarantees a clear sight of possible outliers, which is fundamental for a proof-of-concept study. However, cells which reduced their velocity below 15 μm s−1 are considered as having fallen (touching the bottom of the observation channel). Note that cells tend to roll on the bottom of the microfluidic channel, so a minimum cell velocity is always present.
We investigated the cell dynamics at EXIT 1 for 400 as well as 700 mbar of ΔP (see Fig. 5a). Interestingly, LYM accelerate in the last part of journey before exiting the observation channel (see Fig. S8†). This phenomenon of lateral capillary aspiration must be considered for velocity-based cell trajectory analysis. In general, we can confirm that for higher YX3 values, a lower UX3y can be observed. In the case of NEU a ΔP of 400 mbar is insufficient to reach the lateral exit position (computed L = 3 cm), while tuning of the applied ΔP can be used to find the optimal cell class separation. For instance, in the case of LYM cells, 550 mbar showed the threshold value for EXIT 1 separation of ∼40% of cells (see Fig. S9†). Lower ΔP (e.g. 400 mbar) results in perfect separation efficiency. In the case of NEU, a value of 630 mbar was experimentally investigated, while for RBCs a significant reduction in the applied ΔP was needed (see Fig. S11†). The balance between applied ΔP and effective cell velocity during their journey in the observation channel is limited by a minimum ΔP of circa 250 mbar for the PEO 04 case (see Fig. S10†). To reduce the applied ΔP, the fluid viscosity can be reduced, which in the case of PEO 03 resulted in an applied ΔP of 150 mbar (data not shown).
We also analyzed the fractions of separated and not separated cells under two different ΔP conditions (400 and 700 mbar). NEU show a separation of 90% for 700 mbar, while LYM show their highest separation efficiency for 400 mbar, at 100% (see Fig. 5b). RBCs were found never to exit from EXIT 1. Note that cell tracking information was not filtered according to different cell classes during the measurement process. A more precise cell class selection could improve the fractioning of cells at EXIT 1. Interestingly, cells which pass EXIT 1, but significantly reduce their velocity are also likely to increase their YX3 position. An investigation of the final YX3 coordinate versus resulting UXy cell velocity could be used as an additional density-based indication (see Fig. S11†).
Therefore, from the combination of the applied fluid-flow conditions and the relative motion of cells, a single-cell characterization with diameter and density measurements was performed.
First, to predict where cells sediment, we computed the relative L for the different cell types, using density values obtained from the literature. In more detail, we used density values of 1.072 kg m−3 (LYM), 1.086 kg m−3 (NEU) and 1.099 kg m−3 (RBC), which resulted in fall lengths (see Fig. S12†) of 7.2 (LYM), 4.8 (NEU), and 9.5 cm (RBC). To guarantee the highest possible exit of cells at EXIT1 and/or at EXIT2, we used ΔP of 400 mbar, 550 mbar and 700 mbar for RBC, LYM and NEU, respectively. Secondly, we compared the obtained results with the real fall lengths measured at the same pressures used for computation. With e% < 20%, good agreement between the experimental and estimated results was found (see Fig. S13†). Then, we decided to perform single-cell measurement of cell densities, starting from an evaluation of cell diameters and velocities. The fall length used is the one measured for an entire cell population.
We found good agreement with literature values for both D and ρ (from eqn (9); see also Tables S2 and S3†). A mean value of 1093 kg m−3 for NEU was found. In the case of LYM (the most heterogenic cell class), a density between 1.005 and 1.145 kg m−3 with a mean value of 1063 kg m−3 was calculated (Fig. 6).
Despite the higher density, RBCs fall at a longer distance (EXIT 2) than other cells. This is due to the cell-specific shape being oblate. In detail, these cells have a third axis smaller than the other two axes that are equal to each other (Fig. 1). In the case of an oblate shape, the drag force is less than would be exerted on a sphere equal to the equatorial radius of the spheroid.55,59 Therefore, a scaling factor affecting the way in which drag effect changes on an oblate shape was necessary to compute ρ for RBCs. Happel and Brenner presented the correction factor in a hypothesis for a flow streaming past an oblate spheroid. The expression is:55
 , for which D and b are the diameter and the third semi-axis of the RBC, respectively. Then, a scaling of the drag coefficient (eqn (5)) as CDCorr = KCD can be written. The final expression of ρ for an oblate can be reported as:
, for which D and b are the diameter and the third semi-axis of the RBC, respectively. Then, a scaling of the drag coefficient (eqn (5)) as CDCorr = KCD can be written. The final expression of ρ for an oblate can be reported as: | (10) |
A scaling of ρ-values with respect to D and UX4,5y is presented. As expected, from the oblate shape, despite the higher density, RBCs do not fall and reach the end of the microfluidic device. Moreover, even if RBCs are similar in size range to LYM, eqn (10) well demonstrates that sedimentation behavior is influenced not only by the size but also by the shape of the object. Indeed, UX4,5y is also the highest for the RBC class (Fig. 6). NEU and LYM have lower densities than RBCs and their falling motion is dictated only by a difference in size and intrinsic ρ, which are higher for NEU than for LYM.
Conclusions
The presented densimeter-on-chip (DoC) is a label-free and easy-to-use tool for single-cell mass density measurement. During the last few years, knowledge of cell density (lower cell-to-cell variation among the same types compared to other biophysical features) has been regarded as a key factor for single-cell classification, due to the great relevance of density in cell state control and regulation. However, having an approach capable of recognizing and analysing different density levels of cells belonging to the same cell type is still challenging.Here, thanks to a triggered imbalance of hydrodynamic components—as viscoelastic, buoyant and drag forces—DoC proposes to map both single-cell diameters and densities, thanks to a non-invasive, label-free in-flow sedimentation process.
In detail, we induced the traceable gravity-based sedimentation of cells into different device exits. Additionally, the chip is designed to be versatile, with the possibility of choosing the fluid flow characteristics, such as viscosity, relaxation time and applied in-flow velocity, to achieve precise control over the sedimentation process. Moreover, since the chip is conceived to be a passive type of technique, no other operational parameters, such as external magnetic, electric or acoustic field intensities, need to be controlled. Depending on dimension and shape, the approach allows us to measure and distinguish different density levels for multiple cell types. The working range of the device is related to the applied inlet pressure and object diameters. The former varies from ∼250 mbar up to ∼2500 mbar, with the lowest detectable value of 5.134 μm s−1. The latter has a wide range of possible dimensions, from 0.75 to 22.5 μm, according to the needs of the microchannel blockage ratio. Instead, the value of 998 kg m−3 is the lowest value of measurable density. In detail, multiple types of object, such as PSL microspheres or peripheral blood stream cells—namely RBCs, LYM and NEU—are forced to pass through an inlet round capillary, where the alignment along the centre line is guaranteed by the action of a lifting viscoelastic fluid force—greater than the buoyant components—counterbalanced by the drag force. Next, cells pass from the capillary to a larger rectangular cross-section, which triggers a dramatic reduction in viscoelastic forces, which on the other hand leads to an enhancement in gravity-driven motion for a fall of cells along the vertical direction of the channel. According to the hypothesis of spherical shape, cells sediment according to their size and density. On the other hand, despite their intrinsically higher density, RBCs stably follow the centre line of the channel, thanks to a spheroidal oblate shape for which the viscoelastic force still applies a lifting effect, which results in an extended fall length. Thanks to a new formulation of governing forces, we implemented a set of equations that describe fluid flow conditions and the imbalance in forces, by setting only cell dimension and shape. In such a way, we were able to extrapolate the single-cell mass density of PSL, RBCs, LYM and NEU with a great agreement with the data in the literature. Moreover, the results from the approach are highly precise and reproducible with an intrinsically low sensitivity in density measurement of 0.001. However, in a future perspective, we would further enhance the precision and reproducibility of the system by improving the hardware for complete motion reconstruction with object acquisition in both Y and Z directions to allow an accurate reconstruction of both velocity and sedimentation profiles.
Moreover, the creation of a platform where both density and deformability measurements can be performed would allow a comprehensive characterization of cell properties, providing a complete phenotyping.
Indeed, with the capability of efficient and simple operating conditions, we believe that the proposed DoC approach provides a valid alternative for next-generation microfluidic density based single-cell characterization and manipulation platforms.
Data availability
The data supporting this article have been included as part of the ESI.† For any additional requests or queries regarding the data, please contact David Dannhauser at E-mail: david.dannhauser@unina.it.Author contributions
D. D.: conceptualization, methodology, validation, writing original draft, formal analysis. M. I. M.: conceptualization, mathematical model, validation, writing original draft, formal analysis. P. A. N.: supervision. F. C.: conceptualization, writing-review, & editing, supervision.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thanks Claudia DeClemente for valuable discussion.References
- G. E. Neurohr and A. Amon, Relevance and Regulation of Cell Density, Trends Cell Biol., 2020, 30, 213–225 CrossRef CAS PubMed.
- Y. Zhao, L. Gu, H. Sun, X. Sha and W. J. Li, Physical Cytometry: Detecting Mass-Related Properties of Single Cells, ACS Sens., 2022, 7, 21–36 CrossRef CAS PubMed.
- J. M. Park, J. Y. Lee, J. G. Lee, H. Jeong, J. M. Oh, Y. J. Kim, D. Park, M. S. Kim, H. J. Lee, J. H. Oh, S. S. Lee, W. Y. Lee and N. Huh, Highly Efficient Assay of Circulating Tumor Cells by Selective Sedimentation with a Density Gradient Medium and Microfiltration from Whole Blood, Anal. Chem., 2012, 84, 7400–7407 CrossRef CAS PubMed.
- E. M. Darling and D. Di Carlo, High-Throughput Assessment of Cellular Mechanical Properties, Annu. Rev. Biomed. Eng., 2015, 17, 35–62 CrossRef CAS PubMed.
- M. C. W. Lee, F. J. Lopez-Diaz, S. Y. Khan, M. A. Tariq, Y. Dayn, C. J. Vaske, A. J. Radenbaugh, H. J. Kim, B. M. Emerson and N. Pourmand, Single-cell analyses of transcriptional heterogeneity during drug tolerance transition in cancer cells by RNA sequencing, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, E4726–E4735 CAS.
- R. Satija and A. K. Shalek, Heterogeneity in immune responses: from populations to single cells, Trends Immunol., 2014, 35, 219–229 CrossRef CAS PubMed.
- C. Roffay, G. Molinard, M. Urbanska, V. Andrade, V. Barbarasa, P. Nowak, V. Mercier, J. Garcia-Calvo, S. Matile, R. Loewith, A. Echard, J. Guck, M. Lenz and A. Roux, Passive coupling of membrane tension and cell volume during active response of cells to osmosis, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2103228118 CrossRef CAS PubMed.
- T. Vicar, M. Raudenska, J. Gumulec and J. Balvan, The Quantitative-Phase Dynamics of Apoptosis and Lytic Cell Death, Sci. Rep., 2020, 10, 1566 CrossRef CAS PubMed.
- D. E. Goll, R. B. Young and M. H. Stromer, Separation of subcellular organelles by differential and density gradient centrifugation, Proceedings 27th Annual Reciprocal Meat Conference, National Livestock and Meat Board, Chicago, 1974 Search PubMed.
- E. Stephanova and T. Topouzova, Isolation and Purification of Cellular Organelles, National Bank For Industrial Microorganisms and Cell Cultures, 2001 Search PubMed.
- K. G. Phillips, S. L. Jacques and O. J. T. McCarty, Measurement of Single Cell Refractive Index, Dry Mass, Volume, and Density Using a Transillumination Microscope, Phys. Rev. Lett., 2012, 109, 118105 CrossRef PubMed.
- A. E. Cetin, S. N. Topkaya, O. Yalcin-Ozuysal and A. Khademhosseini, Refractive Index Sensing for Measuring Single Cell Growth, ACS Nano, 2021, 15, 10710–10721 CrossRef CAS PubMed.
- C. Honrado, P. Bisegna, N. S. Swami and F. Caselli, Single-cell microfluidic impedance cytometry: from raw signals to cell phenotypes using data analytics, Lab Chip, 2021, 21, 22–54 RSC.
- L. Huang, F. Liang, Y. Feng, P. Zhao and W. Wang, On-chip integrated optical stretching and electrorotation enabling single-cell biophysical analysis, Microsyst. Nanoeng., 2020, 6, 57 CrossRef CAS PubMed.
- P. Augustsson, J. T. Karlsen, H. W. Su, H. Bruus and J. Voldman, Iso-acoustic focusing of cells for size-insensitive acousto-mechanical phenotyping, Nat. Commun., 2016, 7, 11556 CrossRef CAS PubMed.
- Q. H. Gao, B. Wen, Y. Kang and W. M. Zhang, Pump-free microfluidic magnetic levitation approach for density-based cell characterization, Biosens. Bioelectron., 2022, 204, 114052 CrossRef CAS PubMed.
- C. Bakal, J. Aach, G. Church and N. Perrimon, Quantitative Morphological Signatures Define Local Signaling Networks Regulating Cell Morphology, Science, 2007, 316, 1753–1756 CrossRef CAS PubMed.
- W. P. J. Smith, Y. Davit, J. M. Osborne, W. Kim, K. R. Foster and J. M. Pitt-Francis, Cell morphology drives spatial patterning in microbial communities, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E280–E286 CrossRef CAS PubMed.
- A. K. Bryan, A. Goranov, A. Amon and S. R. Manalis, Measurement of mass, density, and volume during the cell cycle of yeast, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 999–1004 CrossRef CAS PubMed.
- N. Cermak, S. Olcum, F. F. Delgado, S. C. Wasserman, K. R. Payer, M. A. Murakami, S. M. Knudsen, R. J. Kimmerling, M. M. Stevens, Y. Kikuchi, A. Sandikci, M. Ogawa, V. Agache, F. Baleras, D. M. Weinstock and S. R. Manalis, High-throughput measurement of single-cell growth rates using serial microfluidic mass sensor arrays, Nat. Biotechnol., 2016, 34, 1052–1059 CrossRef CAS PubMed.
- T. A. Zangle and M. A. Teitell, Live-cell mass profiling: an emerging approach in quantitative biophysics, Nat. Methods, 2014, 11, 1221–1228 CrossRef CAS PubMed.
- Z. Zhang, T. Zheng and R. Zhu, Characterization of single-cell biophysical properties and cell type classification using dielectrophoresis model reduction method, Sens. Actuators, B, 2020, 304, 127326 CrossRef CAS.
- W. H. Grover, A. K. Bryan, M. Diez-Silva, S. Suresh, J. M. Higgins and S. R. Manalis, Measuring single-cell density, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 10992–10996 CrossRef CAS PubMed.
- A. A. Kumar, M. R. Patton, J. W. Hennek, S. Y. R. Lee, G. D'Alesio-Spina, X. Yang, J. Kanter, S. S. Shevkopyas, C. Brugnara and G. M. Whitesides, Density-based separation in multiphase systems provides a simple method to identify sickle cell disease, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 14864–14869 CrossRef CAS PubMed.
- Z. B. Bjornson, G. P. Nolan and W. J. Fantl, Single-cell mass cytometry for analysis of immune system functional states, Curr. Opin. Immunol., 2013, 25, 484–494 CrossRef CAS PubMed.
- S. Tasoglu, J. A. Khoory, H. C. Tekin, C. Thomas, A. E. Karnoub, I. C. Ghiran and U. Demirci, Levitational Image Cytometry with Temporal Resolution, Adv. Mater., 2015, 27, 3901–3908 CrossRef CAS PubMed.
- A. K. Bryan, V. C. Hecht, W. Shen, K. Payer, W. H. Grover and S. R. Manalis, Measuring single cell mass, volume, and density with dual suspended microchannel resonators, Lab Chip, 2014, 14, 569–576 RSC.
- Q. Zhang, L. Zhong, P. Tang, Y. Yuan, S. Liu, J. Tian and X. Lu, Quantitative refractive index distribution of single cell by combining phase-shifting interferometry and AFM imaging, Sci. Rep., 2017, 7, 2532 CrossRef PubMed.
- Y. Zhao, H. S. S. Lai, G. Zhang, G. B. Lee and W. J. Li, Rapid determination of cell mass and density using digitally controlled electric field in a microfluidic chip, Lab Chip, 2014, 14, 4426–4434 RSC.
- J. Y. Hwang, S. Youn and I. H. Yang, Gravitational field flow fractionation: Enhancing the resolution power by using an acoustic force field, Anal. Chim. Acta, 2019, 1047, 238–247 CrossRef CAS PubMed.
- R. J. Townsend, M. Hill, N. R. Harris and N. M. White, Modelling of particle paths passing through an ultrasonic standing wave, Ultrasonics, 2004, 42, 319–324 CrossRef CAS PubMed.
- T. Luo, Y. Zeng, S. Chen, Q. Tan, R. H. W. Lam and D. Sun, A simplified sheathless cell separation approach using combined gravitational-sedimentation-based prefocusing and dielectrophoretic separation, Lab Chip, 2018, 18, 1521–1532 RSC.
- M. A. Benincasa, L. R. Moore, P. S. Williams, E. Poptic, F. Carpino and M. Zborowski, Cell Sorting by One Gravity SPLITT Fractionation, Anal. Chem., 2005, 77, 5294–5301 CrossRef CAS PubMed.
- D. Huh, J. H. Bahng, Y. Ling, H. H. Wei, O. D. Kripfgans, J. B. Fowlkes, J. B. Grotberg and S. Takayama, Gravity-Driven Microfluidic Particle Sorting Device with Hydrodynamic Separation Amplification, Anal. Chem., 2007, 79, 1369–1376 CrossRef CAS PubMed.
- B. Roda, P. Reschiglian, A. Zattoni, P. L. Tazzari, M. Buzzi, F. Ricci and A. Bontadini, Human lymphocyte sorting by gravitational field-flow fractionation, Anal. Bioanal. Chem., 2008, 392, 137–145 CrossRef CAS PubMed.
- G. C. E. Porter, S. N. F. Sikora, J. Shim, B. J. Murray and M. D. Tarn, On-chip density-based sorting of supercooled droplets and frozen droplets in continuous flow, Lab Chip, 2020, 20, 3876–3887 RSC.
- D. Sugiyama, Y. Teshima, K. Yamanaka, M. P. Briones-Nagata, M. Maeki and K. Yamashita, Simple density-based particle separation in a microfluidic chip, Anal. Methods, 2014, 6, 308–311 RSC.
- T. Morijiri, S. Sunahiro, M. Senaha, M. Yamada and M. Seki, Sedimentation pinched-flow fractionation for size- and density-based particle sorting in microchannels, Microfluid. Nanofluid., 2011, 11, 105–110 CrossRef.
- H. Shirinkami, G. Wang, J. Park, J. Ahn, Y. Choi and H. Chun, Red blood cell and white blood cell separation using a lateral-dimension scalable microchip based on hydraulic jump and sedimentation, Sens. Actuators, B, 2020, 307, 127412 CrossRef.
- G. Romeo, G. D'Avino, F. Greco, P. A. Netti and P. L. Maffettone, Viscoelastic flow-focusing in microchannels: scaling properties of the particle radial distributions, Lab Chip, 2013, 13, 2802 RSC.
- M. I. Maremonti, D. Dannhauser, P. A. Netti and F. Causa, Circulating tumour cells deformability measurement in microfluidics, in Convegno Nazionale di Bioingegneria, Patron Editore S.r.l., 2023 Search PubMed.
- D. Dannhauser, M. I. Maremonti, P. A. Netti and F. Causa, Microfluidic platform for cell classification from optical signatures via machine learning, in Convegno Nazionale di Bioingegneria, Patron Editore S.r.l., 2023 Search PubMed.
- M. I. Maremonti, D. Dannhauser, V. Panzetta, P. A. Netti and F. Causa, Cell deformability heterogeneity recognition by unsupervised machine learning from in-flow motion parameters, Lab Chip, 2022, 22, 4871–4881 RSC.
- D. Dannhauser, D. Rossi, P. Memmolo, A. Finizio, P. Ferraro, P. A. Netti and F. Causa, Biophysical investigation of living monocytes in flow by collaborative coherent imaging techniques, Biomed. Opt. Express, 2018, 9, 5194 CrossRef PubMed.
- B. Briscoe, P. Luckham and S. Zhu, Rheological properties of poly(ethylene oxide) aqueous solutions, J. Appl. Polym. Sci., 1998, 70, 419–429 CrossRef CAS.
- M. I. Bahlouli, K. Bekkour, A. Benchabane, Y. Hemar and A. Nemdili, The effect of temperature on the rheological behavior of polyethylene oxide (PEO) solutions, Appl. Rheol., 2013, 23, 13435 Search PubMed.
- R. K. Shah and A. L. London, Laminar Flow Forced Convection in Ducts, 1978 Search PubMed.
- D. Dannhauser, M. I. Maremonti, V. Panzetta, D. Rossi, P. A. Netti and F. Causa, Mechanical phenotyping of breast cell lines by in-flow deformation-dependent dynamics under tuneable compressive forces, Lab Chip, 2020, 20, 4611–4622 RSC.
- J. F. Richardson, J. H. Harker and J. R. Backhurst, Chemical Engineering, 2002 Search PubMed.
- W. L. Murch and E. S. G. Shaqfeh, Collective effects in the sedimentation of particles in a viscoelastic fluid, Phys. Rev. Fluids, 2020, 5, 073301 CrossRef.
- A. A. Yazdi and G. D'Avino, Sedimentation and migration dynamics of a spherical particle in an elastoviscoplastic fluid near a wall, J. Non-Newtonian Fluid Mech., 2023, 314, 105004 CrossRef CAS.
- M. M. A. Spanjaards, N. O. Jaensson, M. A. Hulsen and P. D. Anderson, A Numerical Study of Particle Migration and Sedimentation in Viscoelastic Couette Flow, Fluids, 2019, 9, 25 CrossRef.
- M. Khatibi, R. W. Time and H. A. Rabenjafimanantsoa, Particles falling through viscoelastic non-Newtonian flows in a horizontal rectangular channel analyzed with PIV and PTV techniques, J. Non-Newtonian Fluid Mech., 2016, 235, 143–153 CrossRef CAS.
- B. A. Finlayson, Process fluid mechanics, by M. M. Denn. Prentice-Hall, 1980, 383 pages, $27.95, AIChE J., 1983, 29, 875 CrossRef.
- J. Happel and H. Brenner, Low Reynolds Number Hydrodynamics, Springer, 1983, vol. 1 Search PubMed.
- B. A. Prabowo, P. D. Cabral, P. Freitas and E. Fernandes, The Challenges of Developing Biosensors for Clinical Assessment: A Review, Chemosensors, 2021, 9, 299 CrossRef CAS.
- G. D'Avino, G. Romeo, M. M. Villonw, F. Greco, P. A. Netti and P. L. Maffetone, Single line particle focusing induced by viscoelasticity of the suspending liquid: theory, experiments and simulations to design a micropipe flow-focuser, Lab Chip, 2012, 12, 1638 RSC.
- C. A. Schneider, W. S. Rasband and K. W. Eliceiri, NIH Image to ImageJ: 25 years of image analysis, Nat. Methods, 2012, 9, 671–675 CrossRef CAS PubMed.
- G. D'Avino, Numerical simulations on the settling dynamics of an ellipsoidal particle in a viscoelastic fluid, J. Non-Newtonian Fluid Mech., 2022, 310, 104947 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4lc00916a |
| ‡ The authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2025 |












